Abstract
We present a first in vivo application of phase Dual-Slopes (DSϕ), measured with Frequency-Domain Near-InfraRed Spectroscopy (FD NIRS) on four healthy human subjects, to demonstrate their enhanced sensitivity to cerebral hemodynamics. During Arterial Blood Pressure (ABP) oscillations elicited at a frequency of 0.1 Hz, we compare three different ways to analyze either Intensity (I) or phase (ϕ) data collected on the subject’s forehead at multiple source-detector distances: Single-Distance (SD), Single-Slope (SS), Dual-Slope (DS). Theoretical calculations based on diffusion theory show that the method with the deepest maximal sensitivity (at about 11 mm) is DSϕ. The in vivo results indicate a qualitative difference of phase data (especially DSϕ) and intensity data (especially SDI), which we assign to stronger contributions from scalp hemodynamics to SDI and from cortical hemodynamics to DSϕ. Our findings suggest that scalp hemodynamic oscillations may be dominated by Blood Volume (BV) dynamics, whereas cortical hemodynamics may be dominated by Blood Flow velocity (BFv) dynamics.
Keywords: coherent hemodynamics, diffuse optics, functional brain imaging, near-infrared spectroscopy, photon-density waves
1. INTRODUCTION
Near-InfraRed Spectroscopy (NIRS) is a noninvasive optical method for monitoring the hemodynamics and oxygenation of target tissues. Most of the commercially available NIRS instruments are based on Continuous Wave (CW) light emission and optical detection [1]. However, richer information is provided by time-resolved methods in the Frequency-Domain (FD) and Time-Domain (TD), where the light sources are intensity modulated (at a frequency of ~100 MHz) or pulsed (with a pulse width of the order of ps), respectively. During in vivo measurements, a common problem for all these methods is the strong sensitivity to hemodynamic changes occurring in superficial tissue close to the source and detector. For example, in a typical brain experiment, the light intensity collected on the scalp, a few centimeters away from the emitting light source (usually 20-40 mm), will contain the footprint of hemodynamic changes occurring both in the scalp and skull, as well as in the brain [2]. Numerous methods have been proposed in CW to decouple superficial or systemic hemodynamic changes (occurring in scalp and skull) from those specific to the brain [3-7]. A typical approach is to collect data at short and long source-detector separations in conjunction with data processing methods such as Independent Component Analysis (ICA) [3], adaptive filtering [4], regression procedures [5], or a least-square algorithm [6]. Alternatively, physiological modeling of hemodynamic and metabolic processes in the scalp and the brain, treated as separate tissue compartments, has been proposed [7]. The vast majority of the methods for superficial hemodynamic decontamination have been introduced for functional brain studies, where one may think that the activated cortical area responds in a unique way, and independent of systemic changes occurring in both extracerebral and cerebral tissues. However, in recent years, more studies have been focusing on induced or spontaneous systemic changes in blood pressure for studying microcirculation integrity and cerebral autoregulation, for example with Coherent Hemodynamics Spectroscopy (CHS) [8-12], paced breathing [13], and spontaneous low frequency oscillations [14-16]. Further methods to induce cerebral perfusion changes include modulating the Fraction of inspired Carbon Dioxide (FiCO2) [17]. The level of success in decoupling the cerebral and scalp hemodynamics contributions to optical signals has been variable, and this remains a critical issue in the field on non-invasive NIRS. For non-invasive NIRS measurements of the brain, it would be preferable to develop methods that are intrinsically more sensitive to brain tissue by reducing contributions from the scalp and skull, thus avoiding more complicated signal processing techniques. Of course, this result would also be relevant to non-invasive measurements of other tissues (skeletal muscle, breast tissue, etc.) that are located below superficial layers (skin, adipose tissue, etc.).
Time-resolved methods have shown a higher sensitivity to deeper changes in tissues compared to CW methods, either in TD through mean time-of-flight, higher moments (like the variance), or late time gates of the photon time-of-flight distribution [8, 18-20], or in FD through phase (ϕ) measurement [21]. Moreover, slope methods based on multi-distance measurements of the first and second moments in TD [20] or ϕ in FD [22-25] have shown to feature a reduced sensitivity to superficial changes in the tissue than single-distance methods.
From a practical viewpoint, a robust method of data collection should not only use data types that are more sensitive to deeper changes in tissue, but it should also be insensitive to instrumental drifts (e.g. fluctuations in light source emission properties, detector sensitivity, or coupling between optical fibers and tissue). We recently proposed a Dual-Slope (DS) method, where we have combined the benefits of a source-detector arrangement typical of the self-calibrating approach to absolute optical properties measurements [26], which is largely insensitive to instrumental drifts and optical coupling effects, with the sole use of either Intensity (I) or, better, ϕ data in the FD [27]. Prior work inspired by the self-calibrating approach has used CW I data to measure changes in absorption or oxygen saturation of the brain (both of which require assumptions about scattering) [28,29], but to the best of our knowledge, there has been no systematic study of the associated spatial region of sensitivity.
In a theoretical work, we described how the DS with ϕ data features a region of sensitivity that does not have the typical banana shape between source and detector but it is more spatially confined in a deeper, central region between them, reaching a maximum sensitivity at a depth of ~11-13 mm (as opposed to ~5-6 mm of DS with I) for typical values of the optical properties of tissue and source-detector separations [27]. We have also shown that a DS method largely compensates for the main drawback of Single-Slope (SS) methods (i.e. slope measurements based on either a single source or a single detector), namely the presence of regions of negative sensitivity to localized absorption changes. In other words, a local increase in the absorption coefficient in tissue can result in an apparent decrease in the effective absorption coefficient recovered from SS data.
In previous work, we have reported the hemodynamics measured at a range of source-detector distances (11-40 mm) using Single-Distance (SD) intensity [9,10], and SS intensity [10]. In this article, we report human brain measurements conducted with FD NIRS during a typical CHS protocol, in which we compare six methods of data analysis. Specifically, the six methods considered are: SD, SS, and (for the first time) DS for I and ϕ, denoted as SDI, SDϕ, SSI, SSϕ, DSI, and DSϕ.
2. METHODS
2.1. Definition of Sensitivity to Local Absorption Perturbations
Below we discuss the methods relevant to Section 3.1, where we present regions of sensitivity, recovered hemodynamic phasors, and Signal-to-Noise Ratio (SNR) for the three-analysis methods SD, SS, and DS, and for the two datatypes I and ϕ. The datatype I indicates the FD Intensity (I), which represents the amplitude of the modulated I at angular frequency ω, reducing to the standard CW I at ω = 0. A general theoretical development of these methods is described in [27], but here we present all aspects of their specific implementation for this study.
2.1.1. Region of Sensitivity
Sensitivity is defined for each tissue voxel as follows:
| (1) |
where is the apparent change in absorption coefficient measured by any specific method (SDI, SDϕ, etc.) in the presence of a localized absorption perturbation centered at . The sensitivities (S) for SDY, SSY, and DSY (were Y indicates either I or ϕ) are:
| (2) |
| (3) |
| (4) |
where is the partial optical pathlength through a localized absorption perturbation centered at , and ⟨LY⟩ is the total optical pathlength, with both ⟨lY⟩ and ⟨LY⟩ depending on the position vectors of source and detector ( and , respectively) (in Equation (2) we do not explicitly list the dependence on source and detector locations to simplify notation). For the SS expression based on one source and n detectors (Equation (3)), detector positions are labeled with i = 1, … , n, so that the source-detector distances are for each detector i, and the mean source-detector distance is . Equation (4) shows that the sensitivity for DS is the average sensitivity of two paired SSs.
The complex total optical pathlength () and the partial optical pathlength () can be introduced in terms of the real optical pathlengths associated with I and ϕ as follows:
| (5) |
| (6) |
where is the imaginary unit.
The above expressions for sensitivity were implemented in MATLAB (MATrix LABoratory, MathWorks, Natick MA, USA). Expressions for the complex optical pathlength in the case of a semi-infinite geometry with extrapolated boundary condition can be found in [27] and Appendix I. If the volume of an absorption perturbation was larger than the voxel size, an array of ones of the size of the perturbation volume was convolved with the sensitivity for each voxel.
2.1.2. Modeling Absorption Oscillations and Associated Recovered Phasors
Using the sensitivity functions in Equations (2)-(4), we can calculate the recovered hemodynamic phasors of Oxyhemoglobin (O) and Deoxyhemoglobin (D) concentrations associated with any assumed and at each voxel in a semi-infinite medium (bold face notation represents phasors, which describe oscillations at a given frequency). For each voxel, was found at two wavelengths using the assumed hemodynamic phasors and the known extinction coefficients of hemoglobin [30]. Then, for each voxel and wavelength, the true absorption phasor is multiplied by the sensitivity discussed in Section 2.1.1 to yield . The recovered absorption phasors associated with absorption oscillations at each voxel are then summed over all (i.e. over the entire medium) to yield the recovered absorption phasor (μa,Recovered (λ)) the presence of absorption oscillations throughout the whole medium at each wavelength. From these recovered absorption phasors and the same hemoglobin extinction coefficients used above, ORecovered and DRecovered are calculated. Note that the above method is only valid if the perturbation volumes do not overlap and the sum of the sensitivities over all is one.
2.1.3. Noise Equivalent Absorption Change and Signal-to-Noise Ratio (SNR)
Using the sensitivity to each perturbation volume, we can calculate a SNR associated with each volume. To this aim, we define the noise equivalent absorption change as the change in absorption that results from a change in the signal at the level of the noise in that signal. We start by writing the noise equivalent absorption change (σμa) for the three methods (SD, SS DS) and data type Y (either I, ϕ):
| (7) |
| (8) |
| (9) |
the SNR for each volume at position is then given by:
| (10) |
note that this SNR is dependent not only on the analysis method, data type (with associated noise), and probe geometry, but also on the assumed true absorption perturbation and its size. In all equations, Y represents the datatype, either I or ϕ, and can be replaced by either depending on which datatype is being considered.
2.2. Experimental Setup and Measurement Protocol
FD NIRS data were collected during baseline at rest, and during induced systemic blood pressure oscillations on four healthy subjects, three females and one male aged 22-26 years old. The protocol was approved by the Tufts University Institutional Review Board (IRB) and all subjects provided a written informed consent before participating in this study. FD NIRS measurements were collected at a modulation frequency of 140.625 MHz, with wavelengths of 690 and 830 nm, and at a sampling rate of approximately 9.9 Hz (ISS Imagent, Champaign, IL, USA) (FIGURE 1(a)). A custom in-house developed probe was placed on the right side of the subject’s forehead. The probe consisted of a linear array of two 600 μm source optical fiber pairs (each pair delivered light at two wavelengths) and two 3 mm detector fiber bundles (FIGURE 1(b)). The two sources were 60 mm apart and the two detectors were 10 mm apart and located symmetrically about the midpoint between the two sources. This arrangement allowed for two SD measurements at 35 mm, two SS measurements with distances of 25 mm and 35 mm, and one DS measurement using two 25 mm and two 35 mm distances.
FIGURE 1.
(a) Diagram of experimental setup showing seated subject with Frequency Domain Near InfraRed Spectroscopy (FD NIRS, Red) probe, finger plethysmography probe measuring Arterial Blood Pressure (ABP, Green), and pneumatic thigh CUFF (CUFF, Blue) inflation system. (b) Schematic of probe geometry. Two optical sources shown as circles (1 and 2) and two optical detectors shown as squares (A and B). Source detector distance is either 25 mm or 35 mm (Gray) depending on the choice of source detector pair. Probe can make two Single-Distance (SD, Blue) measurements at 35 mm, two Single-Slope (SS, Orange) measurements with 25 mm and 35 mm distances, and one Dual-Slope (DS, Mustard) measurement with 25 mm ×2 and 35 mm ×2 distances.
The noise of the FD NIRS instrument has been measured (with the same instrumental settings as in vivo measurements) to be about 0.4% for I and 0.06° for ϕ during phantom measurements (μa = 0.016 mm−1 and 0.014 mm−1, mm−1 and 0.42 mm−1 for 690 nm and 830 nm, respectively) at a single source-detector pair. The instrument used time multiplexing to collect data from all source-detector pairs. Because of this, the two SSs used for a DS were not obtained at precisely the same time point, breaking the assumptions required for the random noise process from the instrument and setup to cancel from the self-calibrating approach. Despite this fact, the noise found from SS and DS measurements were consistent with the error propagation reported in Section 2.1.3. Thus, the noise values measured from phantoms about were used for SNR simulations and discussions according to Section 2.1.3.
The subject’s Arterial Blood Pressure (ABP) was measured continuously using a finger plethysmograph (CNSystems CNAP Monitor 500, Graz, Austria) (FIGURE 1(a)). ABP oscillations were induced by the cyclic inflation and deflation of two pneumatic thigh cuffs wrapped around both of the subject’s thighs (Hokanson CC17, Bellevue, WA, USA). The cuff’s gauge pressure was regulated between 0 mmHg and 200 mmHg (Hokanson E20, Bellevue, WA, USA) and measured using a pressure transmitter (Dwyer 626 Series, Michigan City, IN, USA). Time dynamics of the cuff’s inflation and deflation were controlled using a custom MATLAB script.
The experimental protocol consisted of 2 min of baseline when the cuffs were kept deflated. Then 3 min of oscillations when the cuffs were cyclically inflated to a pressure of 200 mmHg and deflated to 0 mmHg at a frequency of 0.1 Hz. Finally, there was 1 min of recovery when the cuffs were kept deflated. The entire protocol lasted 6 min (see FIGURE 2(a)). The frequency of 0.1 Hz was chosen because it is within the frequency range of effective cerebral autoregulation, and it is not too low, considering that measurements at lower frequencies may feature potential confounding contributions from physiological sources beside arterial blood pressure [13], or from instrumental drifts of various nature. However, the 0.1 Hz choice is not critical. In fact, CHS has been performed within the frequency range 0.04-0.20 Hz.
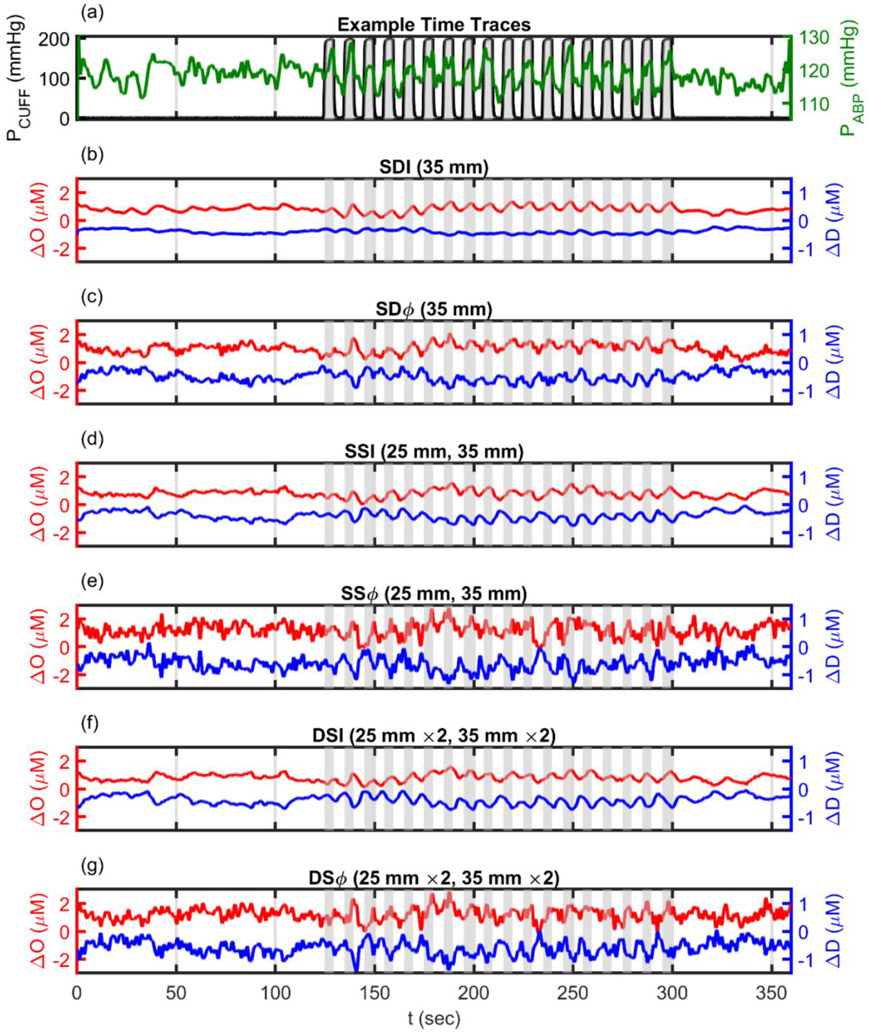
FIGURE 2.
Example time traces (Subject 4) for experimental protocol and resulting Oxyhemoglobin (O) and Deoxyhemoglobin (D) from six different data analysis methods. (a) Pneumatic thigh CUFF pressure (PCUFF, Black and Gray) and Arterial Blood Pressure (ABP, Green). (b) O (Red, mean at 0.8 μM) and D (Blue, mean at −0.4 μM) resulting from Single-Distance Intensity (SDI) analysis. (c) O (Red, mean at 1 μM) and D (Blue, mean at −0.5 μM) resulting from Single-Distance phase (SDϕ) analysis. (d) O (Red, mean at 0.8 μM) and D (Blue, mean at −0.4 μM) resulting from Single-Slope Intensity (SSI) analysis. (e) O (Red, mean at 1.2 μM) and D (Blue, mean at −0.6 μM) resulting from Single-Slope phase (SSϕ) analysis. (f) O (Red, mean at 0.8 μM) and D (Blue, mean at −0.4 μM) resulting from Dual-Slope Intensity (DSI) analysis. (g) O (Red, mean at 1.2 μM) and D (Blue, mean at −0.6 μM) resulting from Dual-Slope phase (DSϕ) analysis. Note: All signals lowpass filtered to 0.2 Hz, linearly detrended, and shifted by an arbitrary offset for visualization.
2.3. Measurements of Baseline Absolute optical Properties with Self-Calibrating Frequency-Domain (FD) Near-InfraRed Spectroscopy (NIRS)
The self-calibrating FD method [26] was used to find absolute optical properties for each of the four subjects and two wavelengths. This method involves taking the DS for both I (which here represents the amplitude of the modulated intensity at a non-zero frequency) and ϕ. This has the effect of canceling coupling and instrumental factors, thus removing the need for calibration. The absolute absorption coefficient (μa) and reduced scattering coefficient averaged over the baseline period () are given by:
| (11) |
| (12) |
where ω is the angular modulation frequency (ω = 2π × 140.625 × 106 rad/sec), n is the index of refaction of the medium (taken to be n = 1.4), and c is the speed of light in vacuum (c = 2.998 × 1011 mm/sec) [22]. These absolute values were used in the calculation of the Differential Pathlength Factor (DPF) and Differential Slope Factor (DSF) that are defined in Section 2.4. Note that the slope of I is meant to indicate the slope of ln(ρ2I(ρ)), which to a first approximation is a linear function of ρ.
2.4. Measurement of Relative Changes in Absorption with Different Methods and Datatypes
Here we describe six different methods for measuring absorption changes with the data collected with our FD NIRS probe: SDI, SDϕ, SSI, SSϕ, DSI, and DSϕ. Each of these methods yields a time trace of effective changes in the absorption coefficient at each wavelength, which were then converted into time traces of ΔO and ΔD using known extinction coefficients of hemoglobin [30]. Representative time traces are in FIGURE 2(b)(c)(d)(e)(f)(g) (showing data from Subject 4). To aid visualization, we added an arbitrary offset to the time traces of ΔO and ΔD so that they do not overlap (making their mean a non-zero value that is specified in the caption of FIGURE 2); since we are examining changes in concentration, the means of the traces are arbitrary, while the only things that matter are the timing and amplitude of fluctuations.
To simplify the notation in the following sections, we define the following quantities:
| (13a) |
| (13b) |
| (13c) |
for the CW case where ω = 0, γ = 1, , V− = 0.
We now proceed under the conditions of a homogeneous semi-infinite medium and zero-boundary conditions. However, we also performed calculations using non-zero extrapolated boundary condition. Values for DPF and DSF obtained for both zero and non-zero boundary conditions and further explanations of their calculations can be found in Appendices I and II.
2.4.1. Absorption Changes Measured with Single-Distance Intensity or Phase (SDI or SDϕ)
Intensity (I) changes measured with SD can be converted to changes in absorption using the modified Beer Lambert Law (mBLL) and the DPF [31] (denoted here with DPFI to highlight its use in conjunction with intensity measurements). One may introduce a similar, generalized DPF concept for SDϕ (denoted as DPFϕ). The time-dependent expressions for DPFI and DPFϕ can be obtained from the relationships between changes in effective (homogeneous) absorption changes, and the corresponding SDI and SDϕ:
| (14) |
| (15) |
| (16a) |
| (16b) |
| (17) |
We observe that Equations (16a), (16b), and (17) are obtained for a semi-infinite geometry under zero boundary conditions (i.e. zb = 0, with zb defined in Appendix I), at source-detector distances much greater than the depth of the effective source (ρ ≫ z1, with z1 defined in Appendix I), and for a highly scattering regime (). Representative ΔO and ΔD traces obtained from SDI and SDϕ can be seen in FIGURE 2(b)(c). The I and ϕ DPF used for each subject depended on the measured absolute optical properties at baseline; the average values of DPFI and DPFϕ were 6.3±0.2 and 0.89±0.04, respectively (see Appendix II). Note: errors in above text are Standard Errors of the Mean (SEM), and DPFs were calculated with extrapolated boundary conditions (Appendix I) from the data collected in vivo.
We opted to only analyze the SD data collected at the longest distance (35 mm) because the purpose of this work is to compare SD, SS, and DS as they would be used in non-invasive optical studies of the brain. Therefore, we considered the SD data with the deepest sensitivity (i.e., the longest source-detector distance).
2.4.2. Absorption Changes Measured with Intensity or Phase Slopes (SSI, SSϕ, DSI, or DSϕ)
Like changes in SD measurements can be converted into changes in absorption, changes in slopes (SS or DS) can also be converted into absorption changes. In the case of I, the slope refers to the linear dependence of ln(ρ2I) on ρ. The conversion of relative slope changes into apparent (homogeneous) absorption changes is:
| (18) |
| (19) |
where we introduce the intensity and phase differential slope factors (DSFs) that can be explicitly expressed as follows:
| (20) |
| (21) |
representative ΔO and ΔD traces obtained with SSI and SSϕ can be found in FIGURE 2(d)(e).
DS is an average of two SS measurements and can use the same DSF as in Equations (20) and (21). The calculation of absorption changes with DS data are as follows:
| (22) |
| (23) |
Representative ΔO and ΔD temporal traces obtained with DSI and DSϕ can be found in FIGURE 2(f)(g). Like DPF, the DSF value used for each subject depended on the measured absolute optical properties at baseline; the average DSFI and DSFϕ values were 6.9±0.2 and 1.08±0.05, respectively (see Appendix II). Note: errors in above text are SEM and DPFs were calculated with the extrapolated boundary conditions (Appendix I) from data collected in vivo.
In Section 2.3, we have reported the combined use of DSI and DSϕ to find absolute optical properties with the self-calibrating method [26]. Our novel DS method separates the use of DSI and DSϕ for measurement of absorption changes (rather than absolute values) with the explicit goal to achieve a more localized and deeper sensitivity within the investigated tissue [27]. Our DS method has the same advantages of the self-calibrating method (insensitivity to probe-tissue optical coupling, insensitivity to instrumental drifts, no need for calibration) but aims at achieving an optimal region of sensitivity for more effective spectroscopy and imaging applications. Since the primary goal of non-invasive optical studies of the brain is to maximize the sensitivity to deeper vs more superficial tissues, we focus here on DSϕ, which we showed to achieve a deeper sensitivity than DSI [27].
2.5. Signal Analysis
The coherence and signal analysis used here is the same as described in [9,10] and is only summarized here. We note that the traces in FIGURE 2 are meant only for illustration of the protocol and not for analysis of their phase and amplitude. The data analysis described here is used to determine the phase and amplitude of the coherent oscillations examined by CHS.
2.5.1. Determination of Coherence
We identify times and frequencies of significant coherence between two signals in a wavelet scalogram by comparing the measured coherence to a threshold generated with random surrogate data [32,33]. This significant coherence threshold is determined for three signal pairs: ΔT and ABP, ΔO and ABP, and ΔD and ABP (where ΔT = ΔO + ΔD are changes in Total hemoglobin concentration). Only times and frequencies that show significant coherence for ΔT and ABP are used for analysis of the phasor ratio T/ABP. Similarly, for analysis of D/O we only consider the intersection of the regions in the time-frequency space where ΔO and ABP, as well as ΔD and ABP feature a significant coherence.
2.5.2. Calculation of Phase and Amplitude
To find the phase and amplitude of T/ABP and D/O, the transfer function scalogram for each pair was found using the Continuous Wavelet Transform (CWT). For these scalograms, we averaged the transfer function during the time when the thigh cuff oscillations were applied, and we considered a frequency band centered at 0.1 Hz (with a bandwidth determined by a test sinusoidal signal’s half power point). Only pixels in the time-frequency space that featured significant coherence between the two phasors in the considered pair are used in the average. The modulus of this average represents the amplitude ratio of the two phasors, whereas the argument represents their phase difference.
3. RESULTS
3.1. Simulations of Regions of Sensitivity, Recovered Phasors, and Signal-to-Noise Ratio (SNR)
FIGURE 3(b)(c)(e)(f)(h)(i) shows the sensitivity regions of SDI, SDϕ, SSI, SSϕ, DSI, and DSϕ. Notice that SDI shows the typical photon banana with maximal sensitivity at the surface close to the source and detector, while SDϕ shows a somewhat deeper banana region that features a more uniform sensitivity along its length. Additionally, SDϕ shows a secondary negative banana near the surface. SSI and SSϕ show asymmetric bananas with slightly different sensitivities compared to their SD counterparts. However, the SS methods show a strong negative banana close to the surface. Finally, looking at DS we see that most of the SS superficial sensitivity is canceled, leaving a localized region of deeper sensitivity underneath the center of the probe. The DS region of sensitivity is nut shaped, with shapes resembling different kinds of nuts depending on the source-detector arrangement, the data type, and after considering the 3-dimentional shape of the region of sensitivity. Notably and most importantly, DSϕ has the deepest maximal sensitivity and the least superficial sensitivity.
FIGURE 3.
Example simulated phase and amplitude relationship between the Deoxyhemoglobin phasor (D) and the Oxyhemoglobin phasor (O) that would be measured from a volume with five regions containing five different true phasors. (a) Schematic of regions within the volume and true phasors. Two optical detectors (Squares) and optical sources shown. True D (Blue) and O (Red) phasors are shown in their regions Top 1 (T1, Blue), Top 2 (T2, Orange), Top 3 (T3, Mustard), Top 4 (T4, Purple), and Bottom (B, Green). [(b), (c), (e), (f), (h), and (i)] Sensitivity maps to a localized absorption perturbation for: (b) Single-Distance Intensity (SDI), (c) Single-Distance phase (SDϕ), (e) Single-Slope Intensity (SSI), (f) Single-Slope phase (SSϕ), (h) Dual-Slope Intensity (DSI), and (i) Dual-Slope phase (DSϕ) measurements. [(d), (g), and (j)] Comparison of true D and O phasor ratios (D/O) for each of the five regions to the D/O that would be measured using Intensity (I, Cyan) or phase (ϕ, Maroon) data with the: (d) Single-Distance (SD), (g) Single-Slope (SS), or (j) Dual-Slope (DS) method. Note: Extents of the five regions, their true phasor values, and other parameters can be found in Table A4 (Appendix III).
Using the sensitivity maps, we simulated five regions of hemodynamic oscillations (OTrue and DTrue), and we computed what would be measured by each method (ORecovered and DRecovered). The goal of these simulations is to provide a visual representation of the region of sensitivity in the SD, SS, and DS cases in relation to a medium geometry and optical properties that mimic the human head. FIGURE 3(a) shows the regions featuring hemodynamic oscillations, with four superficial regions and one deep region. This configuration models a heterogenous superficial layer (scalp), an intermediate non-oscillating layer, and a homogenous bottom layer (brain). FIGURE 3(d)(g)(j) shows the recovered phasor ratios and the true phasor ratios. We considered a heterogeneous superficial layer because of the possibility of heterogeneous hemodynamics in the scalp, as previously reported [5], and as would be expected in the case of a non-homogenous pressure exerted by the optical probe on the scalp. Note that all superficial regions have the same phasor ratio (despite having different absolute phasors). In general, SDI dose not accurately recover the oscillations in the deep region, while all ϕ measurements are relatively successful in doing that. All intensity measurements underestimate the amplitude of the phasor ratio. SS measurements are affected by the superficial heterogeneity and do not reconstruct the phase of the phasor ratio well. Overall, DSϕ is the most successful, closely reconstructing the amplitude and phase of the phasor ratio in the deeper region.
FIGURE 4 shows the SNR of the two DS methods. Most of the superficial sensitivity for DSϕ is below the noise level (mainly because of a low sensitivity) while DSI still has some superficial sensitivity above noise. Again, the sensitivity for DSϕ is overall deeper than that for DSI. However, overall DSϕ has lower SNR due the higher noise for ϕ.
FIGURE 4.
Signal-to-Noise Ratio (SNR) maps for Dual-Slope Intensity (DSI, (a)) and Dual-Slope phase (DSϕ, (b)). Note: Parameters can be found in TABLE A5 (Appendix III).
Input parameters to the sensitivity maps, simulated oscillations, and SNR can be found in Appendix III.
3.2. Phase and Amplitude Relationships of Total Hemoglobin (T) and Arterial Blood Pressure (ABP) during Systemic ABP Oscillations for Different Measurement Methods
FIGURE 5 shows the phase and amplitude of the phasor ratio T/ABP at 0.1 Hz during the cyclic inflation and deflation of the thigh cuffs for all four subjects and all measurement methods. Notice that SDI has a consistent T/ABP relationship across all four subjects with a mean phase difference of −40°±4° and mean amplitude ratio of 0.037±0.002 μM/mmHg (5% error). This is within the range of values for T/ABP at 0.1 Hz reported recently by our group [34]. However, the other analysis methods (SDϕ, SS, and DS) do not show this consistent relationship and feature a large variance in some cases. For example, DSϕ shows a mean phase difference and amplitude ratio of −10°±10° and 0.018±0.005 μM/mmHg (28% SEM), respectively. Generally, most other analysis methods’ vectors are in quadrant IV (same as SDI), but SDI is the only method that shows such a consistent relationship for T/ABP. Note: errors stated in above text are SEM.
FIGURE 5.
Vectors showing the phase and amplitude relationship between the Total hemoglobin phasor (T) and the Arterial Blood Pressure phasor (ABP) at 0.1 Hz. Shown for three analysis methods Single-Distance (SD, Blue), Single-Slope (SS, Orange), and Dual-Slope (DS, Mustard); two data types Intensity (I, (a) to (d)) and phase (ϕ, (e) to (h)); and four subjects Subject 1 ((a) and (e)), Subject 2 ((b) and (f)), Subject 3 ((c) and (g)), and Subject 4 ((d) and (h)).
3.3. Phase and Amplitude Relationships of Deoxyhemoglobin (D) and Oxyhemoglobin (O) during Systemic ABP Oscillations for Different Measurement Methods
FIGURE 6 shows the phase and amplitude of the phasor ratio D/O at 0.1 Hz during the cuff oscillation period for all four subjects and all measurement methods. Notice that the amplitude of D/O for SDI is smaller than for all other methods in all subjects, and that it shows no consistent value across subjects (ranging from 0.6 in Subject 1 to 0.07 in Subject 2). Similarly, the phase of D/O for SDI also does not show a consistent value (ranging from −187° in Subject 3 to −268° in Subject 2). In some cases (Subject 2) the SS measurements show different relative phase values than DS, while DS, particularly, DSϕ shows a consistent phase and amplitude of D/O across all subjects with a mean phase of −196°±2° and a mean amplitude of 0.75±0.08 (11% SEM). This compared to SDI’s inconsistent phase difference and amplitude ratio with means of −220°±10° and 0.20±0.06 (30% SEM), respectively. Note: errors stated in above text are SEM.
FIGURE 6.
Vectors showing the phase and amplitude relationship between the Deoxyhemoglobin phasor (D) and the Oxyhemoglobin phasor (O) at 0.1 Hz. Shown for three analysis methods Single-Distance (SD, Blue), Single-Slope (SS, Orange), and Dual-Slope (DS, Mustard); two data types Intensity (I, (a) to (d)) and phase (ϕ, (e) to (h)); and four subjects Subject 1 ((a) and (e)), Subject 2 ((b) and (f)), Subject 3 ((c) and (g)), and Subject 4 ((d) and (h)).
4. DISCUSSION
4.1. Phase (ϕ) is Sensitive to Deeper Absorption Perturbations Compared to Intensity (I)
Simulation results presented in Section 3.1 show a deeper sensitivity for ϕ over I regardless of the method (SD, SS, DS). Similar simulation results of a deeper ϕ sensitivity compared to I have been reported [25,27]. Experimental results also back up this conclusion. In TD NIRS, higher moments of the time-of-flight distribution (mean time-of-flight or 1st moment, ⟨t⟩, and variance or 2nd moment) show deeper sensitivity and less sensitivity to superficial layers compared to the 0th moment (i.e. the average intensity) [8,20]. Furthermore, in functional studies, the mean time-of-flight has been shown to have better correlation with functional Magnetic Resonance Imaging (fMRI) activation signals [19]. In FD NIRS, ϕ has been used to measure functional brain activation at shorter source-detector distance and to show less sensitivity to superficial hemodynamics [21]. We observe that at the frequencies typically used in FD NIRS (100-150 MHz) ϕ is proportional to the 1st moment of the photon time-of-flight distribution (ϕ ≅ ω⟨t⟩).
Compared to the results obtain with intensity, the results for D and O measured with ϕ (Section 3.3) show a closer opposition of phase (i.e. a phase closer to 180°) and a higher amplitude ratio (i.e. a ratio closer to 1) for D/O suggesting a stronger contribution from Blood Flow velocity (BFv) oscillations in the brain than in the scalp. This result is also consistent with previous studies which examined data collected at multiple source-detector distances in the range 11-40 mm [9,10], and also pointed to the deeper sensitivity of ϕ compared to I.
4.2. Advantages of the Dual-Slope (DS) over Single-Distance (SD) and Single-Slope (SS)
The simulation results in Section 3.1 show that DS has less superficial sensitivity than SD and SS. This is consistent with the development of the theory of DS [27]. Compared to SD data, slope methods in general have been shown to be less sensitive to homogeneous superficial layers using the mean time of light and variance in TD NIRS [20] and using the phase in FD NIRS [22-25]. Despite SS data having deeper sensitivity compared to SD data, SS data can be affected by heterogeneity in the superficial layer. This is supported by simulations in FIGURE 3(g), by our experimental results for Subject 2 in FIGURE 6(b), and by other work showing the possibility of heterogenous scalp hemodynamics [5]. An additional advantage of DS, inherited from the self-calibrating method [26], is the insensitivity to instrumental drifts and optical coupling with tissue. This latter feature results from the cancellation of any intensity multiplicative factors or phase additive terms associated with source emission, detector sensitivity, or other instrumental factors when the average of the paired slopes is taken [26,27]. Overall, DS has the advantage of being less sensitive to the surface, less susceptible to artifacts from superficial heterogeneities, and less sensitivity to drifts over SD and SS.
Examining our experimental results for D/O (Section 3.3), we observe robust and consistent findings from DS data across subjects. This suggests that DS is the most robust measurement method, among those presented here, for non-invasive sensing of the human brain. This is likely due to the minimal sensitivity to the superficial layer and insensitivity to drifts afforded by the DC method. Therefore, we conclude that DS coupled with ϕ (DSϕ) features the deepest maximal sensitivity, combined with the least superficial sensitivity, and is the most robust method among those considered here.
4.3. A Greater Amplitude Ratio of Deoxyhemoglobin versus Oxyhemoglobin (∣D/O∣) in the Brain Suggests a Smaller Blood Volume Change (BV)
Our experimental results for D/O (Section 3.3) show a BFv-dominated oscillation in deeper layers when examined with the eyes of CHS [11]. The closer the phase difference of D/O gets to −180° and its amplitude ratio to 1, the smaller the T oscillation amplitude. T is considered a surrogate for Blood Volume (BV). Thus, our results suggest less of a BV oscillation in the brain compared to the superficial layer, and more of a BFv oscillation in the brain. The effect of this is seen in our T/ABP results in Section 3.2, where the most superficial methods (SDI) shows the most consistent relationship for T/ABP. Recently, our group presented a model based on these consistent T/ABP results measured with SDI [34]. However, the results presented here do not show the same consistent T/ABP vector for deeper tissue, suggesting that the previous data and model may have been mostly representative of scalp hemodynamics.
It might be noted that the amplitude of T/ABP presented here is greater for all methods other than SDI. This result may be impacted by the coherence analysis (Section 2.5.1), which preferentially selects higher amplitude T oscillation periods (due to their higher coherence). However, when we examine the relationship of D/O coupled with the less consistent results for T/ABP, we can conclude that, in our results, the analysis methods sensitive to deeper tissue show either a smaller or less consistent BV oscillation.
This premise that the brain shows a small BV oscillation has been discussed in other works. Despite fMRI having consistently measured BV changes [35,36], the models involved require complicating fitting procedures and are not a direct measure of BV [36]. This, combined with the fact that the skull contains an incompressible fluid, has led to the suggestion that BV changes are in fact a redistribution of water from tissue to the vascular space [37]. NIRS methods, unlike fMRI, measure the Total concentration of hemoglobin (T). If there were a redistribution of water (leaving the amount of T the same) within the sensitivity volume of NIRS, little or no BV change would be measured with NIRS. Furthermore, work with fMRI has observed that changes resulting from brain activation are primarily caused by BFv changes rather than by BV changes [38], in agreement with the results reported here.
There has been evidence, from methods that preferentially measure the brain, in support of relatively small changes in T. Functional NIRS studies have shown this result when analyzing the optical signals with ICA [3] or a linear model [6], using a normalized time gating technique [18] or mean time-of-flight [19] in TD. Additionally, the normalized time gating technique also showed little change in T during a systemic change [18].
Our results of a BFv-dominated hemodynamic oscillation in the brain may point to a smaller BV oscillation in the brain versus the scalp, a possibility that has been discussed and presented previously (primarily concerning the incompressibility of fluid and rigidity of the skull). These results are also supported by previous work that reported hemodynamics measured at different source detector distances, in the range 11-40 mm, for SDI [9,10] and SSI [10].
4.4. Considerations on the Noise of the Two Data Types, Intensity (I) and Phase (ϕ)
The main disadvantage of ϕ measurements is their higher noise compared to I measurements. This can be seen in the SNR presented in Section 3.1. Previous works have presented ϕ [24] or mean time-of-flight and variance [8,19,20] measurements with a relative large noise. This is also seen in our representative time traces (FIGURE 2), particularly in SS that suffers from greater noise with respect to SD and DS (Section 2.1.3). However, there is room for improvement, for example by identifying optimal frequencies. In fact, a previous TD study looked at the SNR of ϕ as a function of modulation frequency [39] and showed that higher modulation frequencies (higher than the 140.625 MHz used here) may offer a better SNR for ϕ.
Furthermore, there are possible noise improvements that can be pursued in our FD NIRS instrument. First, the acquisition time or the duty cycle in a time-multiplexed scheme may be increased. Second, due to the time multiplexing of our instrument, data from different sources are not acquired simultaneously. Therefore, the ideal cancelation of noise is not achieved as described in the self-calibrating approach. Addressing these issues by using a different multiplexing scheme or frequency encoding would be a first step to improving the SNR for ϕ measurements.
4.5. Possible Enhancements of the Dual Slope (DS) Method
A number of aspects of the DS method presented here may be optimized or further developed to enhance performance in terms of SNR and depth sensitivity, and to develop imaging capabilities. For example, as mentioned above, one may identify an optimal modulation frequency to achieve a best compromise between SNR and depth of maximal sensitivity. One may also consider potential advantages of using multiple modulation frequencies. Furthermore, we have shown that multiple (more than two) source-detector distances may be used in each SS measurement [27] and this may be advantageous in some applications. Finally, the DS method may be a basis for imaging applications, for example by employing an array of sources and detectors that features a number of partially overlapping DS regions of sensitivity.
5. CONCLUSION
We have presented a first experimental demonstration of a phase Dual-Slope (DSϕ) method in healthy human subjects. We have compared this method with five other methods based on Single-Distance (SD), Single-Slope (SS) or DS Intensity (I) and phase (ϕ) data measured with Frequency-Domain Near-InfraRed Spectroscopy (FD NIRS). Theoretical predictions based on diffusion theory showed a deeper maximal sensitivity and less superficial sensitivity for the DSϕ method versus the other methods, with DSϕ also featuring the advantage of an insensitivity to instrumental drifts and to optical coupling with tissue. Our experimental results in vivo are consistent with the theoretical predictions, and indicate a stronger relative contribution of Blood Flow velocity (BFv) versus Blood Volume (BV) in brain tissue compared to scalp tissue. The DSϕ data realize the most consistent and robust measurements of D/O that we have presented, and this may have significant implications for quantitative cerebral hemodynamics measurements, especially in cases where such cerebral hemodynamics are of both systemic and local origin.
Supplementary Material
6. ACKNOWLEDGEMENTS
This work was funded by the National Institutes of Health (NIH) grant R01 NS095334.
Abbreviations:
- NIRS
Near InfraRed Spectroscopy
- CW
Continuous Wave
- FD
Frequency-Domain
- TD
Time-Domain
- I
Intensity
- ϕ
phase
- DS
Dual-Slope
- SS
Single-Slope
- SD
Single-Distance
- DPF
Differential Pathlength Factor
- DSF
Differential Slope Factor
- mBLL
modified Beer Lambert Law
- O
Oxyhemoglobin concentration
- D
Deoxyhemoglobin concentration
- T
Total hemoglobin concentration
- ABP
Arterial Blood Pressure
- CHS
Coherent Hemodynamics Spectroscopy
- BFv
Blood Flow velocity
- BV
Blood Volume
- SNR
Signal-to-Noise Ratio
- CWT
Continuous Wavelet Transform
- MATLAB
MATrix LABoratory
- ICA
Independent Component Analysis
- fMRI
functional Magnetic Resonance Imaging
- IRB
Institutional Review Board
- FiCO2
Fraction of inspired Carbon Dioxide
- SEM
Standard Error of the Mean
Footnotes
CONFLICT OF INTEREST
The authors declare no financial or commercial conflict of interest.
8 REFERENCES
- 1.Scholkmann F; Kleiser S; Metz AJ; Zimmermann R; Mata Pavia J; Wolf U; Wolf M A review on continuous wave functional near-infrared spectroscopy and imaging instrumentation and methodology. Neuroimage 2014, 85, 6–27. [DOI] [PubMed] [Google Scholar]
- 2.Tachtsidis I; Scholkmann F False positives and false negatives in functional near-infrared spectroscopy: issues, challenges, and the way forward. Neurophotonics 2016, 3, 031405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Funane T; Atsumori H; Katura T; Obata AN; Sato H; Tanikawa Y; Okada E; Kiguchi M Quantitative evaluation of deep and shallow tissue layers’ contribution to fNIRS signal using multi-distance optodes and independent component analysis. Neuroimage 2014, 85, 150–165. [DOI] [PubMed] [Google Scholar]
- 4.Zhang Q; Brown EN; Strangman GE Adaptive filtering for global interference cancellation and real-time recovery of evoked brain activity: a Monte Carlo simulation study. J. Biomed. Opt 2007, 12, 044014. [DOI] [PubMed] [Google Scholar]
- 5.Gagnon L; Yücel MA; Boas DA; Cooper RJ Further improvement in reducing superficial contamination in NIRS using double short separation measurements. Neuroimage 2014, 85, 127–135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Saager R; Berger A Measurement of layer-like hemodynamic trends in scalp and cortex: implications for physiological baseline suppression in functional near-infrared spectroscopy. J. Biomed. Opt 2008, 13, 034017. [DOI] [PubMed] [Google Scholar]
- 7.Caldwell M; Scholkmann F; Wolf U; Wolf M; Elwell C; Tachtsidis I Modelling confounding effects from extracerebral contamination and systemic factors on functional near-infrared spectroscopy. Neuroimage 2016, 143, 91–105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Kacprzak M; Sawosz P; Weigl W; Milej D; Gerega A; Liebert A Frequency analysis of oscillations in cerebral hemodynamics measured by time domain near infrared spectroscopy. Biomed. Opt. Express 2019, 10, 761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Khaksari K; Blaney G; Sassaroli A; Krishnamurthy N; Pham T; Fantini S Depth dependence of coherent hemodynamics in the human head. J. Biomed. Opt 2018, 23, 1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Blaney; Sassaroli; Pham; Krishnamurthy; Fantini Multi-Distance Frequency-Domain Optical Measurements of Coherent Cerebral Hemodynamics. Photonics 2019, 6, 83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Fantini S Dynamic model for the tissue concentration and oxygen saturation of hemoglobin in relation to blood volume, flow velocity, and oxygen consumption: Implications for functional neuroimaging and coherent hemodynamics spectroscopy (CHS). Neuroimage 2014, 85, 202–221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Kainerstorfer JM; Sassaroli A; Hallacoglu B; Pierro ML; Fantini S Practical Steps for Applying a New Dynamic Model to Near-Infrared Spectroscopy Measurements of Hemodynamic Oscillations and Transient Changes. Acad. Radiol 2014, 21, 185–196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Reinhard M; Wehrle-Wieland E; Grabiak D; Roth M; Guschlbauer B; Timmer J; Weiller C; Hetzel A Oscillatory cerebral hemodynamics—the macro- vs. microvascular level. J. Neurol. Sci 2006, 250, 103–109. [DOI] [PubMed] [Google Scholar]
- 14.Cheng R; Shang Y; Hayes D; Saha SP; Yu G Noninvasive optical evaluation of spontaneous low frequency oscillations in cerebral hemodynamics. Neuroimage 2012, 62, 1445–1454. [DOI] [PubMed] [Google Scholar]
- 15.Chernomordik V; Amyot F; Kenney K; Wassermann E; Diaz-Arrastia R; Gandjbakhche A Abnormality of low frequency cerebral hemodynamics oscillations in TBI population. Brain Res. 2016, 1639, 194–199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Peng T; Ainslie PN; Cotter JD; Murrell C; Thomas K; Williams MJA; George K; Shave R; Rowley AB; Payne SJ The effects of age on the spontaneous low-frequency oscillations in cerebral and systemic cardiovascular dynamics. Physiol. Meas 2008, 29, 1055–1069. [DOI] [PubMed] [Google Scholar]
- 17.Scholkmann F; Gerber U; Wolf M; Wolf U End-tidal CO2: An important parameter for a correct interpretation in functional brain studies using speech tasks. Neuroimage 2013, 66, 71–79. [DOI] [PubMed] [Google Scholar]
- 18.Contini D; Spinelli L; Torricelli A; Pifferi A; Cubeddu R Novel method for depth-resolved brain functional imaging by time-domain NIRS. Diffus. Opt. Imaging Tissue 2007, 6629, 662908. [Google Scholar]
- 19.Abdalmalak A; Milej D; Diop M; Shokouhi M; Naci L; Owen AM; St. Lawrence K Can time-resolved NIRS provide the sensitivity to detect brain activity during motor imagery consistently? Biomed. Opt. Express 2017, 8, 2162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Milej D; Abdalmalak A; McLachlan P; Diop M; Liebert A; St. Lawrence K Subtraction-based approach for enhancing the depth sensitivity of time-resolved NIRS. Biomed. Opt. Express 2016, 7, 4514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Doulgerakis-Kontoudis M; Eggebrecht AT; Dehghani H Information rich phase content of frequency domain functional Near Infrared Spectroscopy. In Proceedings of the Neural Imaging and Sensing 2019; Luo Q, Ding J, Fu L, Eds.; SPIE, 2019; p. 13. [Google Scholar]
- 22.Fantini S; Hueber D; Franceschini MA; Gratton E; Rosenfeld W; Stubblefield PG; Maulik D; Stankovic MR Non-invasive optical monitoring of the newborn piglet brain using continuous-wave and frequency-domain spectroscopy. Phys. Med. Biol 1999, 44, 1543–1563. [DOI] [PubMed] [Google Scholar]
- 23.Franceschini MA; Fantini S; Paunescu LA; Maier JS; Gratton E Influence of a superficial layer in the quantitative spectroscopic study of strongly scattering media. Appl. Opt 1998, 37, 7447. [DOI] [PubMed] [Google Scholar]
- 24.Toronov V; Webb A; Choi JH; Wolf M; Safonova L; Wolf U; Gratton E Study of local cerebral hemodynamics by frequency-domain near-infrared spectroscopy and correlation with simultaneously acquired functional magnetic resonance imaging. Opt. Express 2001, 9, 417. [DOI] [PubMed] [Google Scholar]
- 25.Gratton E; Toronov V; Wolf U; Wolf M; Webb A Measurement of brain activity by near-infrared light. J. Biomed. Opt 2005, 10, 011008. [DOI] [PubMed] [Google Scholar]
- 26.Hueber DM; Fantini S; Cerussi AE; Barbieri B New Optical Probe Designs for Absolute (Self-calibrating) NIR Tissue Hemoglobin Measurements. Proc. SPIE 1999, 3597, 618–631. [Google Scholar]
- 27.Sassaroli A; Blaney G; Fantini S Dual-slope method for enhanced depth sensitivity in diffuse optical spectroscopy. J. Opt. Soc. Am. A 2019, Submitted. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Scholkmann F; Metz AJ; Wolf M Measuring tissue hemodynamics and oxygenation by continuous-wave functional near-infrared spectroscopy—how robust are the different calculation methods against movement artifacts? Physiol. Meas 2014, 35, 717–734. [DOI] [PubMed] [Google Scholar]
- 29.Jenny C; Biallas M; Trajkovic I; Fauchère J-C; Bucher HU; Wolf M Reproducibility of cerebral tissue oxygen saturation measurements by near-infrared spectroscopy in newborn infants. J. Biomed. Opt 2011, 16, 097004. [DOI] [PubMed] [Google Scholar]
- 30.Bigio IJ; Fantini S Quantitative Biomedical Optics; Cambridge University Press: Cambridge, UK, 2016; ISBN 978-0-521-87656-8. [Google Scholar]
- 31.Sassaroli A; Fantini S Comment on the modified Beer–Lambert law for scattering media. Phys. Med. Biol 2004, 49, N255–N257. [DOI] [PubMed] [Google Scholar]
- 32.Sassaroli A; Tgavalekos K; Fantini S The meaning of “coherent” and its quantification in coherent hemodynamics spectroscopy. J. Innov. Opt. Health Sci 2018, 11, 1850036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Blaney G; Sassaroli A; Fantini S Algorithm for Determination of Thresholds of Significant Coherence in Time-Frequency Analysis. Biomed. Signal Process. Control 2019, Submitted. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Tgavalekos K; Pham T; Krishnamurthy N; Sassaroli A; Fantini S Frequency-resolved analysis of coherent oscillations of local cerebral blood volume, measured with near-infrared spectroscopy, and systemic arterial pressure in healthy human subjects. PLoS One 2019, 14, e0211710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Hua J; Liu P; Kim T; Donahue M; Rane S; Chen JJ; Qin Q; Kim S-G MRI techniques to measure arterial and venous cerebral blood volume. Neuroimage 2019, 187, 17–31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Gu H; Lu H; Ye FQ; Stein EA; Yang Y Noninvasive quantification of cerebral blood volume in humans during functional activation. Neuroimage 2006, 30, 377–387. [DOI] [PubMed] [Google Scholar]
- 37.Krieger SN; Streicher MN; Trampel R; Turner R Cerebral Blood Volume Changes during Brain Activation. J. Cereb. Blood Flow Metab 2012, 32, 1618–1631. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Toronov V; Walker S; Gupta R; Choi JH; Gratton E; Hueber D; Webb A The roles of changes in deoxyhemoglobin concentration and regional cerebral blood volume in the fMRI BOLD signal. Neuroimage 2003, 19, 1521–1531. [DOI] [PubMed] [Google Scholar]
- 39.Toronov V; D’Amico E; Hueber D; Gratton E; Barbieri B; Webb A Optimization of the signal-to-noise ratio of frequency-domain instrumentation for near-infrared spectro-imaging of the human brain. Opt. Express 2003, 11, 2717. [DOI] [PubMed] [Google Scholar]
- 40.Martelli F; Contini D; Taddeucci A; Zaccanti G Photon migration through a turbid slab described by a model based on diffusion approximation II Comparison with Monte Carlo results. Appl. Opt 1997, 36, 4600. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.