Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2022 Jun 8;7(24):21183–21191. doi: 10.1021/acsomega.2c01987

Optical Anisotropy and Momentum-Dependent Excitons in Dibenzopentacene Single Crystals

Lukas Graf †,*, Fupin Liu †, Marco Naumann †, Friedrich Roth ‡,§, Bipasha Debnath †, Bernd Büchner †, Yulia Krupskaya †, Alexey A Popov †, Martin Knupfer †
PMCID: PMC9219101  PMID: 35755348

Abstract

graphic file with name ao2c01987_0008.jpg

High-quality single crystals of the organic semiconductor (1,2;8,9)-dibenzopentacene were grown via physical vapor transport. The crystal structure—unknown before—was determined by single-crystal X-ray diffraction; polarization-dependent optical absorption measurements display a large anisotropy in the ac plane of the crystals. The overall Davydov splitting is ∼110 meV, which is slightly lower than that in the close relative pentacene (120 meV). Momentum-dependent electron energy-loss spectroscopy measurements show a clear exciton dispersion of the Davydov components. An analysis of the dispersion using a simple 1D model indicates smaller electron- and hole-transfer integrals in dibenzopentacene as compared to pentacene. The spectral weight distribution of the excitation spectra is strongly momentum-dependent and demonstrates a strong momentum-dependent admixture of Frenkel excitons, charge-transfer excitons, and vibrational modes.

1. Introduction

The family of Oligoacenes includes many promising organic semiconductors, such as anthracene, tetracene, and pentacene. All show relatively high charge-carrier mobilities1−4 and are already used for applications such as organic light-emitting diodes, organic field-effect transistors, and organic solar cells.5−8 Moreover, they represent model compounds for the whole class of organic semiconductors, and their investigation led to important insights into the physics of these materials.9−18

The optoelectronic properties of organic semiconductors are mostly driven by excitons, bound electron–hole pairs, lowered in energy by the Coulomb attraction and sitting on one single molecule (Frenkel exciton) or on two adjacent molecules (charge-transfer (CT) exciton). Exciton dynamics is a subject of high interest, and it has been shown in recent works that in oligoacenes neither the exciton dispersion nor the Davydov splitting (DS), an energy level splitting due to symmetrically inequivalent molecules in the unit cell,19 can be explained by the molecular Frenkel exciton picture only17,20−36 but instead are explained with an intermixing of Frenkel, CT excitations, and vibrational modes. The latest theoretical descriptions on pentacene and tetracene by the group of Spano and co-workers17,34−36 implemented this idea of an intermixing successfully into a model that describes the experimental data on tetracene and pentacene very well. On the basis of a detailed understanding of the exciton behavior in single crystals, it is also possible to predict exciton migration as it must occur, e.g., in organic solar cells for a high performance.

Starting from the well-known pentacene system, we choose 1,2;8,9-dibenzopentacene, a pentacene derivate with 2 more benzene rings, placed on the diagonal ends on the long axis of the pentacene molecule. It has strong similarities in the electron π-system with pentacene.37−39 Not as present as other Oligoacenes in research, dibenzopentacene (DBP) only received some attention as a potential superconductor40−42 in the past. On the other hand, dibenzopentacene offers the possibility to investigate the anisotropic exciton dispersion in a molecular crystal made out of molecules with a lower symmetry than that of pentacene.

To the best of our knowledge, the growth and characterization of 1,2;8,9-dibenzopentacene single crystals were not reported yet. Polarized optical absorption measurements show a strong anisotropy, and momentum-dependent electron energy-loss spectroscopy (EELS) measurements reveal the exciton dispersion in two lattice directions. Our results demonstrate that the exciton physics in dibenzopentacene is determined by a strong coupling of Frenkel and CT excitons.

2. Crystal Growth and Experimental Details

Dibenzopentacene single crystals were grown using physical vapor transport (PVT) in a furnace surrounded by a resistive heater to set up a temperature gradient at atmospheric pressure.43 Pure argon gas, 15 sccm, was used as the purging gas. Dibenzopentacene molecules (purchased from TCI Germany) were heated in the hot zone at 303 °C for 2–7 days, depending on the desired size and thickness of the crystal. Single crystals then could be collected in the crystallization zone of the furnace and processed further for measurements. The crystals showed very homogeneous shape/color, so polymorphism could be excluded.

X-ray diffraction data collection was carried out at the BESSY II storage ring (BL14.2, Berlin-Adlershof, Germany).44 XDSAPP2.0 suite was employed for data processing.45,46 The structure was solved by direct methods and refined by SHELXL-2018.47 Hydrogen atoms were added geometrically and refined with a riding model.

For optical absorption measurements, we transferred the crystals onto a glass substrate and measured the absorption spectra using a Bruker vertex spectrometer in the UV–vis and IR range at 77 K. Electron diffraction and EELS were performed with a custom-made electron energy-loss spectrometer, which could detect electronic excitations as a function of momentum transfer.48,49 The primary electron energy was 172 keV. To keep organic single crystals undamaged as long as possible, the sample temperature was always kept at 20 K, which also minimized thermal broadening in the spectra. Every sample was checked regularly for sample degradation to avoid distorted data. Electron diffraction was applied in situ prior to every measurement to ensure the quality of the sample and conformance with the measured crystal structure (see Figure 4a).

Figure 4.

Figure 4

Open in a new tab

(a) Electron diffraction profiles of dibenzopentacene along three reciprocal lattice directions, which are parallel to the a, c, and (a* + c*) directions, due to the orthorhombic crystal symmetry. These data demonstrate that the crystal is of high quality. (b) Electronic excitation spectra (loss function) of dibenzopentacene as measured using EELS in the optical limit (q = 0.1 Å–1) for three momentum vector directions. (c) Wide energy EELS data in the optical limit for momentum directions parallel to the crystal a and c axes. (d) Real part, ϵ1, and imaginary part, ϵ2, of the dielectric function of dibenzopentacene for momentum vectors parallel to the crystal a and c axes as obtained via a Kramers–Kronig analysis. The inset shows a zoomed-in region to denote more features.

With an energy and momentum resolution of about 85 meV and 0.035 Å–1, the measured signal in EELS is proportional to the loss function Im(− 1/ϵ(q, ω)) and can be determined for different momentum transfers q. With increasing the momentum transfer q, the EELS cross section decreases proportionally to 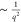Inline graphic.

3. Results and Discussion

3.1. Crystal Structure

The color of the crystal is light pink, compared to the dark burgundy-red of the source material (see Figure 1a). DBP grows in flakelike crystals in the crystal ac plane. In crystals of our desired thickness (50–200 nm for EELS measurements), they tend to roll up or stick to each other. The process of rolling up seems uncontrollable. X-ray diffraction (XRD) measurements revealed the crystal structure for the first time. The crystal system is orthorhombic with the space group P21212 and the crystal axis having the length a = 7.48 Å, b = 36.38 Å, and c = 6.72 Å. The unit cell contains 4 molecules; two molecules are pi-stacked with an small angle (see Figure 1d and e) in the ac plane, similar to the typical herringbone packing of pentacene.50 Both of these pairs connect to each other on the long molecular axis under an angle (see Figure 1d and f) in the b direction. The two phenyl rings at both ends of the molecule have a dihedral angle of ∼4°. According to previous data on nonplanarity, this behavior is not rare in the family of oligoacenes50 (see Figure 1c). The complete crystal structure data are given in the Supporting Information.

Figure 1.

Figure 1

Open in a new tab

(a) Optical picture of the grown dibenzopentacene crystal. (b) Dibenzopentacene molecule drawing at 30% ellipsoid probability. Color code: gray for carbon and white for hydrogen. (c) Dibenzopentacene molecule from the side to show the dihedral angle (nonplanar molecular structure). (d) Molecular packing of the single crystal in the ab plane. (e) Molecular packing in the ac plane. (f) Molecular packing in the bc plane. To guide the vision, one layer of the molecules is highlighted with red and the unit cell borders are lined in blue.

For further crystal characterization, we performed IR and Raman spectroscopy on the dibenzopentacene crystal. The IR data are presented in Figure 2a and consist of the IR spectra in the two lattice directions a and c and a nonpolarized powder spectra. The Raman data are given in Figure 2b and show two curves with different polarizations of the incoming beam (z(yx)z and z(xx)z) and a third curve that is averaged over all angles and therefore nonpolarized (isotropic). Both data sets are strongly polarization-dependent, as can be seen in detail in the figure’s inset. This strong polarization dependence demonstrates that our crystals are of high quality.

Figure 2.

Figure 2

Open in a new tab

(a) IR spectra of the dibenzopentacene crystal with a polarization of the incoming light according to the crystal’s a and c axes and with a powder spectra in comparison. The inset shows a zoomed-in region to display the strong polarization dependence. (b) Raman spectra with two polarization directions of the incoming beam, an averaged isotropic curve, and an inset with an example region to demonstrate the differences of the spectra.

3.2. Electronic Excitations in the Optical Limit

Dibenzopentacene molecules were dissolved and diluted in toluene until the absorption spectra showed no sign of intermolecular excitations. Figure 3a shows the measured spectra. The (0–0) excitation at 2.34 eV is followed by a vibronic progression. The data indicate that this progression is composed of two vibrational modes, as is visible at the (0–1) and (0–2) peaks. The main mode has a vibrational energy of ∼178 meV, while the second mode, visible in (0–1) as a shoulder, has a slightly reduced energy of ∼145 meV. This is in accordance with earlier measurements on solution-phase dibenzopentacene.51 The appearance of vibrational satellites is a well-known feature in the excitation spectra of organic semiconductor molecules; see, for instance, the corresponding data for pentacene and tetracene in solution.27,35

Figure 3.

Figure 3

Open in a new tab

Optical absorption spectra of dibenzopentacene molecules in toluene solution (a) in comparison to the polarization-dependent optical absorption spectra of a dibenzopentacene single crystal (b). The crystal data reveal a strong anisotropy of the absorption as a function of light polarization.

Upon crystallization the spectra change strongly, as shown in Figure 3b. Three curves are shown, measured with linearly polarized light at 77 K. The blue curve shows the spectra with a light polarization in the direction of the crystal a axis, the orange curve is in the direction of the c axis, and the green curve was measured at 45° between these axes to clarify the change between the two spectra. The crystal structure has 4 molecules in the unit cell, which are arranged in two very similar herringbone-like planes, tilted slightly to each other in the b direction. We therefore note that measurements in the ac plane always represent both planes in the unit cell. Due to the P21212 space group, which corresponds to D2 point symmetry, we would expect two Davydov components in the ac plane polarized along the two axes.

The peaks in the absorption data for light polarization parallel to the a and c directions are labeled with A1, A2, and A3 and C1, C2, and C3. At first sight, the polarization-dependent absorption data are strongly anisotropic and undergo a strong red-shift compared to the solution-phase data due to solid-state polarization effects.52 The feature A1 has a peak energy of 2.09 eV. We ascribe the broad appearance of feature A1 to the fact that the transmittivity of a parallel-sided plane (our crystal) is determined by the interplay of transmission and multiple reflections.53−55 Peak A2 at 2.3 eV is the first peak of the vibronic progression. The following peak A3 at 2.39 eV, however, cannot be associated with a vibronic satellite because its energy position does not agree. We instead conclude that it is of electronic origin.

Turning the light polarization by 90°, the spectrum changes dramatically. Peak A1 vanishes completely, and instead peak C1 at 2.2 eV arises. This peak is the second Davydov component and therefore defines the Davydov splitting (DS) as 110 meV, which is a bit lower than that in the close relative pentacene of 120 meV at a similar sample temperature.35,56 Similar to A3, peaks C2 and C3 cannot be associated with simple vibronic satellites.

Compared to single-crystal data from tetracene57 and pentacene,35,56 tetracene shows a regular vibronic progression, while the pentacene spectra show an irregular satellite region when compared to the solution data. For pentacene, it has been shown that the entire excitation region can be well-described by a substantial coupling of molecular Frenkel and CT excitons within a multiparticle basis set in addition to the vibronic coupling.34,35 For dibenzopentacene we expect a similar behavior, particularly regarding the satellite region above 2.3 eV in both directions. This will be further discussed later. The electronic excitation spectra of dibenzopentacene crystals have also been probed using EELS for momentum vectors in the ac plane of the crystal. The corresponding data have been taken at 20 K. The momentum vector has been aligned to the respective crystal directions with the help of the electron diffraction profiles measured in situ in our spectrometer. Figure 4a depicts the electron diffraction profiles along selected reciprocal directions. The data reveal the corresponding Bragg diffraction features and document the single-crystalline nature of our samples.

In Figure 4b we present the electronic excitation spectra at a small momentum value of 0.1 Å–1, which represents the optical limit, as well as spectra for momentum vectors aligned parallel to the a and c crystal directions and the (a* + c*) reciprocal crystal direction. The data are in good agreement with those from optical absorption (see earlier) but do not show the fine structure due to a lower energy resolution. The data can also be compared to thin-film data,37 which show a similar energy onset but not the angle dependence of the single crystals. In detail, the data for a momentum vector parallel to the a axis are characterized by an onset at ∼2 eV and a strong excitation at 2.1 eV (A1). Excitation A2 is seen as a shoulder at 2.3 eV only, while excitation A3 still is represented by a clear maximum at 2.4 eV. For momentum vectors parallel to the crystal c axis, the first spectral structure C1 appears at 2.2 eV followed by a broader feature at 2.4 eV being composed of features C2 and C3 as seen in the optical absorption.

As our EELS spectrometer allows measurements in a large energy range, it is possible to determine the loss function (Im(−1/ϵ(q, ω))) related to all valence excitations. In Figure 4c we show such data for a small momentum-transfer value along the two crystal directions a and c. The two curves are dominated by a broad maximum between 20 and 24 eV, which can be ascribed to the so-called valence band plasmon. This plasmon is due to a collective excitation of all valence electrons. The energy position at which it is observed is typical for π-conjugated solids.58−60 The real and imaginary parts of the dielectric function, ϵ1 and ϵ2, can be derived via a Kramers–Kronig analysis of the loss function after subtraction of the elastic line.48 We have used the oscillator sum rule to normalize the Kramers–Kronig analysis. In Figure 4d we present the results for ϵ1 and ϵ2 in a wide energy range with an inset that shows the energy window of the lowest excitations. The obtained values for ϵ1(0) reveal the anisotropic refractive index 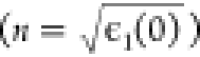Inline graphic for dibenzopentacene in the ac plane: na = 1.96 and nc = 1.52.

3.3. Exciton Dispersion

The evolutions of the excitation spectra for increasing momentum parallel to the a and c axes are depicted in parts a and b of Figure 5, respectively. These data clearly demonstrate a significant momentum dependence of the spectra. We first concentrate on the energy position of the lowest excitation (A1 and C1), which provides the exciton dispersion or exciton band structure of the lowest singlet exciton in dibenzopentacene. For momentum vectors parallel to the a axis, we observe a clear up-shift of the exciton energy. The spectral width of the exciton feature remains rather constant. For momentum vectors parallel to the c axis, a significant down-shift (negative) dispersion is seen, and the exciton feature below 2.2 eV again is a well-defined, symmetric spectral feature, independent of the momentum value.

Figure 5.

Figure 5

Open in a new tab

Electronic excitation spectra of dibenzopentacene crystals measured using EELS as a function of increasing momentum parallel to the crystal a (a) and c axes (b). Data curves are smoothed to obtain better clarity (see the Supporting Information).

The data in parts a and b of Figure 5 are very similar to what has been observed for the exciton dispersion in tetracene61,62 and especially in pentacene single crystals.29,63 This is not surprising in view of the similarities in the molecular-packing habits in the crystals. In Figure 6a, we show a summary of the exciton dispersion in dibenzopentacene, whereas the peak positions in parts a and b of Figure 5 have been determined by fitting the peak with a Gaussian function. To underline the close similarity of the exciton dispersion to pentacene, we have taken the peak centers of the two Davydov components of pentacene (data taken from paper by Roth et al.63) and show it in a side-by-side comparison in Figure 6b.

Figure 6.

Figure 6

Open in a new tab

Dispersion of the lowest singlet excitons in dibenzopentacene and pentacene (data taken from paper by Roth et al.63) for momentum transfers parallel to the a and c axes of the dibenzopentacene crystal and the a and b axes of pentacene, respectively. The solid lines represent the results of the dispersion analysis using a one-dimensional model proposed by Hestand et al.35 (see text).

The exciton behavior and wave function in pentacene were analyzed in detail by Spano and co-workers,35 and they have provided detailed insight into the origin and the nature of the respective spectral features. Furthermore, they have provided a simplified one-dimensional model for the exciton dispersion, which covers the essential information on the exciton band structure arising from the mixing between Frenkel and charge-transfer excitons while the Coulomb coupling is negligible. Within this effective exciton model, the dispersion is governed by the electron and hole hopping integrals to the nearest neighbor, te and th:35

3.3. 1
3.3. 2
3.3. 3

In this model, ω0–0 represents the energy for the first molecular Frenkel exciton, and the parameter ECT stands for the energy difference of the charge transfer and the molecular Frenkel excitation. Importantly, the relative sign of te and th determines the band curvature in the exciton dispersion.

We have applied this simplified model in order to obtain a more quantitative insight into the exciton dispersion and thus also te and th in dibenzopentacene, in comparison to those in pentacene. To do so, we have taken into account the different lattice constants (r = a, b, or c) and replaced the argument in the cosine function in eqs 2 and 3 with 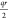Inline graphic. Furthermore, the energy of the charge-transfer excitation ECT in pentacene can be estimated to be ∼0.2 eV, as indicated by electro-absorption measurements22 and detailed theoretical analysis of the pentacene absorption spectra.35 For dibenzopentacene, we assume the same value because the crystal-packing habit is very similar to that for pentacene. The molecular excitation energy ω0–0 can be estimated by taking the energy of the optical absorption in solution and an additional energy shift to lower energies due to crystal formation (i.e., polarization screening of the lowest excitation35,52). We took these into account by setting an upper limit for ω0–0 of 2.24 eV for dibenzopentacene and 2.01 eV for pentacene.

With these values, our data on the exciton dispersion in dibenzopentacene and pentacene can be successfully fitted with these equations. The fit was done with te = th and te ≠ th; the results were virtually independent, and we only show those for te = th in Table 1, as both fits resulted in the same values.

Table 1. Results of the Fit of the Exciton Dispersion, As Described in the Text (See Also Figure 6).

  ω0–0 (eV) te (eV) th (eV)
dibenzopentacene 2.20 0.050 0.050
pentacene 1.99 0.077 0.077
Open in a new tab

The results of our fit confirm what is seen in Figure 6. ω0–0 is larger for dibenzopentacene, in agreement with the larger absorption energy of the solution data. In both materials, te and th have the same sign and are of virtually the same value. In other words, the exciton behaviors in the two compounds are also very similar. The absolute values of te and th are ∼36% smaller in dibenzopentacene compared to pentacene, which results in a smaller exciton bandwidth. Further, this also indicates that electron and hole mobilities may be somewhat smaller in dibenzopentacene.

3.4. Spectral Weight Analysis

As mentioned earlier, parts a and b of Figure 5 demonstrate significant momentum-dependent variation of the spectral shape or the intensity distribution among the various spectral features. We emphasize that the spectral shape is somehow irregular as compared to the well-known appearance of vibronic satellites in the absorption spectra of individual organic semiconductor molecules (e.g., in solution, as shown for dibenzopentacene earlier). Thus, the excitation spectra of dibenzopentacene (and also of pentacene) cannot be rationalized upon coupling to molecular vibrations only. Indeed, the detailed theoretical analysis of the pentacene spectra by Spano and co-workers34,35 has shown that the complete excitation region can be well-understood by a substantial coupling of molecular Frenkel and CT excitons within a multiparticle basis set in addition to the vibronic coupling, and this coupling also determines the exciton dispersion (see earlier). We analyzed the spectral weight distribution of the lowest excitations as a function of momentum parallel to the lattice directions a and c in dibenzopentacene. The same analysis was carried out for the data that were obtained for pentacene earlier.63 (Note that the respective lattice directions in pentacene are denoted as a and b axes.) For our analysis, the measured EELS data were multiplied by the excitation energy to obtain data sets that are proportional to [ω × Im(−1/ϵ(ω))] because this function represents the oscillator sum rule.64 Further, we determined the total spectra weight (Itotal) by integrating these data in an energy window from 1.96 to 3 eV for dibenzopentacene and from 1.64 to 2.9 eV for pentacene. Finally, the spectral weight of the lowest, well-defined exciton (Iexciton) has been derived by fitting a Gaussian function to this lowest-energy region. This allows the determination of the intensity ratio of the lowest exciton feature and the following satellite region:

3.4. 4

Figure 7 shows the results of this analysis. It reveals that the spectral weight distribution between the lowest exciton and the satellite region is significantly momentum- and direction-dependent. For both dibenzopentacene and pentacene and for small momentum transfer, Iexciton represents a quite large portion of the total spectral weight for momenta along the a direction, but it is much smaller for a momentum parallel to the c axis in dibenzopentacene and the b axis in pentacene. This is in very good agreement with the optical measurements of dibenzopentacene and pentacene35,56 as a function of polarization. According to Hestand et al.35 the spectral weight distribution is a direct consequence of the exciton coupling and the admixture of Frenkel and CT excitons and the vibrations. In the optical limit, the dominating exciton coupling is provided by CT coupling, i.e., by electron- and hole-transfer processes, and the resulting exciton spectral weight distribution sensitively depends on the relative signs of the electron- and hole-transfer integrals (te and th), which connect the differently oriented molecules in the unit cell.35

Figure 7.

Figure 7

Open in a new tab

Relative spectral weight of the lowest exciton feature and the following satellite region in the excitation spectra of dibenzopentacene and pentacene as a function of momentum transfer and direction. The dashed lines are included as a guide to the eye.

Electron- and hole-transfer integrals, te and th, in dibenzopentacene and pentacene have the same sign (see paper by Hestand et al.35 and our dispersion analysis earlier); therefore, the coupling near q = 0 is large and results in a charge-transfer J-aggregate-like behavior of the excitons for q (or polarization) parallel to the a axis. It has also been pointed out that the coupling of Frenkel and CT excitons is momentum-dependent. Coupling of Frenkel and CT excitons is provided by a charge separation, and the corresponding matrix element is proportional to |te + th exp(iq̃)| (q̃ is the momentum relative to the reciprocal lattice constants).36 Thus, provided that te and th are of similar absolute value, the Frenkel–CT coupling almost cancels for large q vectors parallel to a. As a consequence, the spectral redistribution at large q approaches that of the vibronic progression seen for individual molecules (see earlier). For momenta along the c direction (for pentacene, b), the Frenkel–CT coupling is very small at low q, i.e., the opposite trend is observed for the spectral weight distribution. For pentacene this has been calculated in detail previously.35 These results clearly support the microscopic theoretical description of the excitation spectrum in pentacene by Spano and co-workers,35 and they demonstrate the close similarity of the exciton behaviors in pentacene and dibenzopentacene.

4. Conclusion

We have grown high-quality single crystals of the organic semiconductor (1,2;8,9)-dibenzopentacene using physical vapor deposition. The crystals were then characterized with XRD; they crystallized in an orthorhombic crystal system with 4 molecules in the unit cell. Furthermore, these crystals grew in thin flakes in the crystal ac plane. IR and Raman measurements showed a strong polarization-dependence. The optical absorption was determined as a function of light polarization in the ac plane of the crystals. These measurements revealed a strong anisotropy and a Davydov splitting of ∼110 meV. Momentum-dependent EELS measurements were performed for momentum vectors parallel to the a and c axes. The first excitations were characterized by a clear exciton dispersion, similar to what has been reported and theoretically analyzed for pentacene and tetracene.29,34,35,61−63 The dispersion was analyzed using a one-dimensional model proposed by Hestand et al.35 In comparison to pentacene, this analysis revealed that electron- and hole-transfer integrals in dibenzopentacene were smaller (by ∼36%) than in the close relative pentacene, which indicated a smaller charge carrier mobility. Finally, a spectral weight analysis of the EELS data of dibenzopentacene and pentacene demonstrated a significant momentum dependence of the irregular satellite region, which was due to strong coupling of molecular Frenkel excitons and charge-transfer excitons.35

Acknowledgments

Diffraction data were collected on BL14.2 at the BESSY II electron storage ring operated by the Helmholtz-Zentrum Berlin. We appreciate the help and support of Dr. Manfred Weiss and his team during the experiments at BESSY II. We are grateful to R. Hübel and F. Thunig for technical assistance. Financial support by the Deutsche Forschungsgemeinschaft within Project nos. KN393/25, KN393/26, KR4364/4, and PO1602/5 is gratefully acknowledged. The publication of this article was funded by the Open Access Fund of the Leibniz Association.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.2c01987.

  • XRD data, more VIS data, and unsmoothed EELS dispersion data (PDF)

The authors declare no competing financial interest.

Supplementary Material

ao2c01987_si_001.pdf (311.7KB, pdf)

References

  1. Kepler R. G. Charge Carrier Production and Mobility in Anthracene Crystals. Phys. Rev. 1960, 119, 1226–1229. 10.1103/PhysRev.119.1226. [DOI] [Google Scholar]
  2. Aleshin A. N.; Lee J. Y.; Chu S. W.; Kim J. S.; Park Y. W. Mobility studies of field-effect transistor structures basedon anthracene single crystals. Appl. Phys. Lett. 2004, 84, 5383–5385. 10.1063/1.1767282. [DOI] [Google Scholar]
  3. de Boer R. W. I.; Klapwijk T. M.; Morpurgo A. F. Field-effect transistors on tetracene single crystals. Appl. Phys. Lett. 2003, 83, 4345–4347. 10.1063/1.1629144. [DOI] [Google Scholar]
  4. Jurchescu O. D.; Baas J.; Palstra T. T. M. Effect of impurities on the mobility of single crystal pentacene. Appl. Phys. Lett. 2004, 84, 3061–3063. 10.1063/1.1704874. [DOI] [Google Scholar]
  5. Kitamura M.; Arakawa Y. Pentacene-based organic field-effect transistors. J. Phys.: Condens. Matter 2008, 20, 184011. [Google Scholar]
  6. Chu C.-W.; Shao Y.; Shrotriya V.; Yang Y. Efficient photovoltaic energy conversion in tetracene-C60 based heterojunctions. Appl. Phys. Lett. 2005, 86, 243506. 10.1063/1.1946184. [DOI] [Google Scholar]
  7. Kim Y.-H.; Jeong H.-C.; Kim S.-H.; Yang K.; Kwon S.-K. High-Purity-Blue and High-Efficiency Electroluminescent Devices Based on Anthracene. Adv. Funct. Mater. 2005, 15, 1799–1805. 10.1002/adfm.200500051. [DOI] [Google Scholar]
  8. Hepp A.; Heil H.; Weise W.; Ahles M.; Schmechel R.; von Seggern H. Light-Emitting Field-Effect Transistor Based on a Tetracene Thin Film. Phys. Rev. Lett. 2003, 91, 157406. 10.1103/PhysRevLett.91.157406. [DOI] [PubMed] [Google Scholar]
  9. Karl N. Charge carrier transport in organic semiconductors. Synth. Met. 2003, 133, 649–657. 10.1016/S0379-6779(02)00398-3. [DOI] [Google Scholar]
  10. Gershenson M.; Podzorov V.; Morpurgo A. Colloquium: Electronic transport in single-crystal organic transistors. RMP 2006, 78, 973. 10.1103/RevModPhys.78.973. [DOI] [Google Scholar]
  11. Kera S.; Yamane H.; Ueno N. First-principles measurements of charge mobility in organic semiconductors: Valence hole–vibration coupling in organic ultrathin films. Prog. Surf. Sci. 2009, 84, 135–154. 10.1016/j.progsurf.2009.03.002. [DOI] [Google Scholar]
  12. Burdett J. J.; Müller A. M.; Gosztola D.; Bardeen C. J. Excited state dynamics in solid and monomeric tetracene: The roles of superradiance and exciton fission. J. Chem. Phys. 2010, 133, 144506. 10.1063/1.3495764. [DOI] [PubMed] [Google Scholar]
  13. Troisi A. Charge transport in high mobility molecular semiconductors: classical models and new theories. Chem. Soc. Rev. 2011, 40, 2347–2358. 10.1039/c0cs00198h. [DOI] [PubMed] [Google Scholar]
  14. Burdett J. J.; Bardeen C. J. The dynamics of singlet fission in crystalline tetracene and covalent analogs. Acc. Chem. Res. 2013, 46, 1312–1320. 10.1021/ar300191w. [DOI] [PubMed] [Google Scholar]
  15. Wilson M. W.; Rao A.; Ehrler B.; Friend R. H. Singlet exciton fission in polycrystalline pentacene: from photophysics toward devices. Acc. Chem. Res. 2013, 46, 1330–1338. 10.1021/ar300345h. [DOI] [PubMed] [Google Scholar]
  16. Cudazzo P.; Sottile F.; Rubio A.; Gatti M. Exciton dispersion in molecular solids. J. Phys.: Condens. Matter 2015, 27, 113204. [DOI] [PubMed] [Google Scholar]
  17. Hestand N. J.; Spano F. C. Expanded theory of H-and J-molecular aggregates: the effects of vibronic coupling and intermolecular charge transfer. Chem. Rev. 2018, 118, 7069–7163. 10.1021/acs.chemrev.7b00581. [DOI] [PubMed] [Google Scholar]
  18. Broch K.; Dieterle J.; Branchi F.; Hestand N. J.; Olivier Y.; Tamura H.; Cruz C.; Nichols V. M.; Hinderhofer A.; Beljonne D.; Spano F. C.; Cerullo G.; Bardeen C. J.; Schreiber F. Robust singlet fission in pentacene thin films with tuned charge transfer interactions. Nat. Commun. 2018, 9, 954. 10.1038/s41467-018-03300-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Davydov A. S. the Theory of Molecular Excitons. SOV PHYS USPEKHI 1964, 7, 145–178. 10.1070/PU1964v007n02ABEH003659. [DOI] [Google Scholar]
  20. Schlosser D. W.; Philpott M. R. Singlet excitons in crystalline naphthalene, antracene, tetracene and pentacene. Chem. Phys. 1980, 49, 181–199. 10.1016/0301-0104(80)85256-6. [DOI] [Google Scholar]
  21. Bounds P. J.; Siebrand W. Charge-transfer excitons in anthracene crystals and their role in optical charge carrier generation. Chem. Phys. Lett. 1980, 75, 414–418. 10.1016/0009-2614(80)80545-8. [DOI] [Google Scholar]
  22. Sebastian L.; Weiser G.; Bässler H. Charge transfer transitions in solid tetracene and pentacene studied by electroabsorption. J. Chem. Phys. 1981, 61, 125–135. 10.1016/0301-0104(81)85055-0. [DOI] [Google Scholar]
  23. Petelenz B.; Petelenz P.; Shurvell H. F.; Smith V. H. Reconsideration of the electroabsorption spectra of the tetracene and pentacene crystals. Chem. Phys. 1988, 119, 25–39. 10.1016/0301-0104(88)80003-X. [DOI] [Google Scholar]
  24. Slawik M.; Petelenz P. Theoretical interpretation of the electroabsorption spectra of polyacene crystals. II. Charge-transfer states. J. Chem. Phys. 1999, 111, 7576–7582. 10.1063/1.480084. [DOI] [Google Scholar]
  25. Petelenz P.; Slawik M.; Yokoi K.; Zgierski M. Z. Theoretical calculation of the electroabsorption spectra of polyacene crystals. J. Chem. Phys. 1996, 105, 4427–4440. 10.1063/1.472295. [DOI] [Google Scholar]
  26. Tiago M. L.; Northrup J. E.; Louie S. G. Ab initio calculation of the electronic and optical properties of solid pentacene. Phys. Rev. B 2003, 67, 115212. 10.1103/PhysRevB.67.115212. [DOI] [Google Scholar]
  27. Lim S.-H.; Bjorklund T. G.; Spano F. C.; Bardeen C. J. Exciton Delocalization and Superradiance in Tetracene Thin Films and Nanoaggregates. Phys. Rev. Lett. 2004, 92, 107402. 10.1103/PhysRevLett.92.107402. [DOI] [PubMed] [Google Scholar]
  28. Hummer K.; Ambrosch-Draxl C. Electronic properties of oligoacenes from first principles. Phys. Rev. B 2005, 72, 205205. 10.1103/PhysRevB.72.205205. [DOI] [Google Scholar]
  29. Schuster R.; Knupfer M.; Berger H. Exciton band structure of pentacene molecular solids: Breakdown of the Frenkel exciton model. Phys. Rev. Lett. 2007, 98, 037402. 10.1103/PhysRevLett.98.037402. [DOI] [PubMed] [Google Scholar]
  30. Gisslén L.; Scholz R. Crystallochromy of perylene pigments: Interference between Frenkel excitons and charge-transfer states. Phys. Rev. B 2009, 80, 115309. 10.1103/PhysRevB.80.115309. [DOI] [Google Scholar]
  31. Gisslén L.; Scholz R. Crystallochromy of perylene pigments: Influence of an enlarged polyaromatic core region. Phys. Rev. B 2011, 83, 155311. 10.1103/PhysRevB.83.155311. [DOI] [Google Scholar]
  32. Mazur G.; Petelenz P.; Slawik M. Transition dipole moments of charge transfer excitations in one-component molecular crystals. Chem. Phys. 2012, 397, 92–97. 10.1016/j.chemphys.2012.01.012. [DOI] [Google Scholar]
  33. Stradomska A.; Kulig W.; Slawik M.; Petelenz P. Excited-state polarizability in crystalline sexithiophene: Charge-transfer and vibronic effects. Chem. Phys. Lett. 2012, 529, 27–30. 10.1016/j.cplett.2012.01.038. [DOI] [Google Scholar]
  34. Yamagata H.; Norton J.; Hontz E.; Olivier Y.; Beljonne D.; Brédas J.-L.; Silbey R.; Spano F. The nature of singlet excitons in oligoacene molecular crystals. J. Chem. Phys. 2011, 134, 204703. 10.1063/1.3590871. [DOI] [PubMed] [Google Scholar]
  35. Hestand N. J.; Yamagata H.; Xu B.; Sun D.; Zhong Y.; Harutyunyan A. R.; Chen G.; Dai H. L.; Rao Y.; Spano F. C. Polarized absorption in crystalline pentacene: Theory vs experiment. J. Phys. Chem. C 2015, 119, 22137–22147. 10.1021/acs.jpcc.5b07163. [DOI] [Google Scholar]
  36. Hestand N. J.; Spano F. C. Molecular Aggregate Photophysics beyond the Kasha Model: Novel Design Principles for Organic Materials. Acc. Chem. Res. 2017, 50, 341–350. 10.1021/acs.accounts.6b00576. [DOI] [PubMed] [Google Scholar]
  37. Mahns B.; Roth F.; König A.; Grobosch M.; Knupfer M.; Hahn T. Electronic properties of 1,2;8,9-dibenzopentacene thin films: A joint experimental and theoretical study. Phys. Rev. B 2012, 86, 035209. 10.1103/PhysRevB.86.035209. [DOI] [Google Scholar]
  38. Otto F.; Huempfner T.; Schaal M.; Udhardt C.; Vorbrink L.; Schroeter B.; Forker R.; Fritz T. Ordered Growth and Electronic Properties of 1,2:8,9-Dibenzopentacene (trans-DBPen) on Ag(111). J. Phys. Chem. C 2018, 122, 8348–8355. 10.1021/acs.jpcc.8b00095. [DOI] [Google Scholar]
  39. Tovstopyat A.; Zojer E.; Leising G. Electronic Properties of 1,2;8,9-Dibenzopentacene in Solutions, Solid Matrices, and Thin Films. J. Appl. Spectrosc. 2016, 83, 20–26. 10.1007/s10812-016-0236-y. [DOI] [Google Scholar]
  40. Xue M.; Cao T.; Wang D.; Wu Y.; Yang H.; Dong X.; He J.; Li F.; Chen G. F. Superconductivity above 30 K in alkali-metal-doped hydrocarbon. Sci. Rep. 2012, 2, 389. 10.1038/srep00389. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Zhong G.-H.; Zhang C.; Yan X.; Li X.; Du Z.; Jing G.; Ma C. Structural and electronic properties of potassium-doped 1,2;8,9-dibenzopentacene superconductor: comparing with doped [7]phenacenes. Mol. Phys. 2017, 115, 472–483. 10.1080/00268976.2016.1274439. [DOI] [Google Scholar]
  42. Roth F.; König A.; Mahns B.; Büchner B.; Knupfer M. Evidence for phase formation in potassium intercalated 1,2;8,9- dibenzopentacene. Eur. Phys. J. B 2012, 85, 242. 10.1140/epjb/e2012-30247-3. [DOI] [Google Scholar]
  43. Laudise R. A.; Kloc C.; Simpkins P. G.; Siegrist T. Physical vapor growth of organic semiconductors. J. Cryst. Growth 1998, 187, 449–454. 10.1016/S0022-0248(98)00034-7. [DOI] [Google Scholar]
  44. Mueller U.; Förster R.; Hellmig M.; Huschmann F. U.; Kastner A.; Malecki P.; Pühringer S.; Röwer M.; Sparta K.; Steffien M.; Ühlein M.; Wilk P.; Weiss M. S. The macromolecular crystallography beamlines at BESSY II of the Helmholtz-Zentrum Berlin: Current status and perspectives. Eur. Phys. J. Plus 2015, 130, 141. 10.1140/epjp/i2015-15141-2. [DOI] [Google Scholar]
  45. Sparta K. M.; Krug M.; Heinemann U.; Mueller U.; Weiss M. S. Xdsapp2.0. J. Appl. Crystallogr. 2016, 49, 1085–1092. 10.1107/S1600576716004416. [DOI] [Google Scholar]
  46. Kabsch W. XDS. Acta Crystallogr. D 2010, 66, 125–132. 10.1107/S0907444909047337. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Sheldrick G. M. Crystal structure refinement with SHELXL. Acta Crystallogr. C 2015, 71, 3–8. 10.1107/S2053229614024218. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Fink J. In Recent Developments in Energy-Loss Spectroscopy; Hawkes P. W., Ed.; Advances in Electronics and Electron Physics; Academic Press: 1989; Vol. 75, pp 121–232. [Google Scholar]
  49. Roth F.; König A.; Fink J.; Büchner B.; Knupfer M. Electron Energy-Loss Spectroscopy: A versatile tool for the investigations of plasmonic excitations. J. Electron Spectrosc. 2014, 195, 85–95. 10.1016/j.elspec.2014.05.007. [DOI] [Google Scholar]
  50. Holmes D.; Kumaraswamy S.; Matzger A. J.; Vollhardt K. P. C. On the Nature of Nonplanarity in the [N]Phenylenes. Chem. Eur. J. 1999, 5, 3399–3412. . [DOI] [Google Scholar]
  51. Perkampus H. H.; Pohl L. Zur Davidov-Aufspaltung in den Absorptionsspektren dünner Filme einiger aromatischer Kohlenwasscrstoffe. Theor. Chem. Acc. 1963, 1, 116–123. 10.1007/BF00529393. [DOI] [Google Scholar]
  52. Köhler A.; Bässler H.. Electronic Processes in Organic Semiconductors: An Introduction; Wiley: 2015; pp 1–405. [Google Scholar]
  53. Fox M.Optical properties of solids; Oxford University Press: 2002. [Google Scholar]
  54. Puschnig P.; Ambrosch-Draxl C. Atomistic modeling of optical properties of thin films. Adv. Eng. Mater. 2006, 8, 1151–1155. 10.1002/adem.200600128. [DOI] [Google Scholar]
  55. Puschnig P.; Ambrosch-Draxl C. First-principles approach to the understanding of π-conjugated organic semiconductors. Monatsh. Chem. 2008, 139, 389–399. 10.1007/s00706-007-0779-y. [DOI] [Google Scholar]
  56. Faltermeier D.; Gompf B.; Dressel M.; Tripathi A. K.; Pflaum J. Optical properties of pentacene thin films and single crystals. Phys. Rev. B 2006, 74, 125416. 10.1103/PhysRevB.74.125416. [DOI] [Google Scholar]
  57. Bree A.; Lyons L. 1002. The intensity of ultraviolet-light absorption by monocrystals. Part IV. Absorption by naphthacene of plane-polarized light. J. Chem. Soc. 1960, 5206–5212. 10.1039/jr9600005206. [DOI] [Google Scholar]
  58. Knupfer M.; Fink J.; Armbruster J. F.; Romberg H. A. Preparation and electronic structure of phase pure K3C60. Z. Phys. B 1995, 98, 9–15. 10.1007/BF01318272. [DOI] [Google Scholar]
  59. Grobosch M.; Schuster R.; Pichler T.; Knupfer M.; Berger H. Analysis of the anisotropy of excitons in pentacene single crystals using reflectivity measurements and electron energy-loss spectroscopy. Phys. Rev. B 2006, 74, 155202. 10.1103/PhysRevB.74.155202. [DOI] [Google Scholar]
  60. Flatz K.; Grobosch M.; Knupfer M. The electronic excitation spectrum of CuPcF16 films. Appl. Phys. A: Mater. Sci. Process. 2009, 94, 179–183. 10.1007/s00339-008-4730-9. [DOI] [Google Scholar]
  61. Roth F.; Nohr M.; Hampel S.; Knupfer M. Low-energy exciton pocket at finite momentum in tetracene molecular solids. EPL 2015, 112, 37004. 10.1209/0295-5075/112/37004. [DOI] [Google Scholar]
  62. Roth F.; Cudazzo P.; Mahns B.; Gatti M.; Bauer J.; Hampel S.; Nohr M.; Berger H.; Knupfer M.; Rubio A. Loss spectroscopy of molecular solids: combining experiment and theory. New J. Phys. 2013, 15, 125024. 10.1088/1367-2630/15/12/125024. [DOI] [Google Scholar]
  63. Roth F.; Schuster R.; König A.; Knupfer M.; Berger H. Momentum dependence of the excitons in pentacene. J. Chem. Phys. 2012, 136, 204708. 10.1063/1.4723812. [DOI] [PubMed] [Google Scholar]
  64. Dressel M.; Grüner G.. Electrodynamics of solids: optical properties of electrons in matter; Cambridge University Press: 2002. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao2c01987_si_001.pdf (311.7KB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES