Hemodynamics of Cerebral Aneurysms: Connecting Medical Imaging and Biomechanical Analysis

Abstract

In the last two decades, numerous studies have conducted patient-specific computations of blood flow dynamics in cerebral aneurysms and reported correlations between various hemodynamic metrics and aneurysmal disease progression or treatment outcomes. Nevertheless, intra-aneurysmal flow analysis has not been adopted in current clinical practice, and hemodynamic factors usually are not considered in clinical decision making. This review presents the state of the art in cerebral aneurysm imaging and image-based modeling, discussing the advantages and limitations of each approach and focusing on the translational value of hemodynamic analysis. Combining imaging and modeling data obtained from different flow modalities can improve the accuracy and fidelity of resulting velocity fields and flow-derived factors that are thought to affect aneurysmal disease progression. It is expected that predictive models utilizing hemodynamic factors in combination with patient medical history and morphological data will outperform current risk scores and treatment guidelines. Possible future directions include novel approaches enabling data assimilation and multimodality analysis of cerebral aneurysm hemodynamics.

1. CEREBRAL ANEURYSM PATHOPHYSIOLOGY, DIAGNOSTICS, AND TREATMENT

Cerebral aneurysms are local dilations of cerebral arteries that are estimated to affect from 2% to 5% of the adult population worldwide (1, 2). Most aneurysms occur within the circle of Willis (CoW) or the vessels immediately distal or proximal to it. Depending on their shape, aneurysms can be described as either saccular or fusiform. A saccular aneurysm is a bulge on one side of an artery, while a fusiform aneurysm incorporates the circumference of the vessel. Saccular and fusiform aneurysms have distinctive pathogeneses; thus, their clinical management is also different (3). Saccular aneurysms, also called berry aneurysms, are more common than their fusiform counterparts (4) and occur predominantly in the anterior circulation of the CoW (5). Common locations include the distal internal carotid artery (ICA), anterior communicating artery, and bifurcations of the middle cerebral artery. Posterior circulation aneurysms are commonly located at the basilar artery bifurcation or on the basilar artery branches, namely the posterior inferior, anterior inferior, and superior cerebellar arteries (5).

A number of hereditary and environmental factors are associated with a risk of cerebral aneurysm formation, including hypertension and smoking history as well as genetic predisposition, vessel wall degradation, inflammation, and hemodynamic conditions (6). However, the exact mechanisms underlying aneurysm progression are still not completely understood (7, 8). Cerebral aneurysms are three times more likely to occur in women than in men (5, 8). Approximately 20–30% of patients have multiple aneurysms (9). Aneurysm rupture leads to subarachnoid hemorrhage (SAH), with high rates of mortality and a morbidity rate of 50% for survivors (10, 11). A growing aneurysm may cause a mass effect due to impingement on brain tissue or cranial nerves; thrombotic aneurysms may also cause distal thromboemboli. Cerebral aneurysms are often asymptomatic (12); moreover, the majority of aneurysms remain stable, with longitudinal studies of large cohorts showing that only 10–15% of aneurysms grow over a timeline of years (13, 14).

1.1. Diagnostics and Clinical Management

Aneurysms are often discovered incidentally, except when they are impinging on cranial nerves, causing a mass effect or hemorrhage. Management of unruptured intracranial aneurysms (UIAs) is challenging because the risk of rupture must be weighed against the risk of intervention (8, 15, 16). Most patients are offered treatment due to the grave consequences of a rupture (4). A number of risk factors are considered in making a clinical decision, including the aneurysm’s size, location, and morphology and the patient’s medical history. Aneurysm size is considered one of the most important risk factors; aneurysms larger than 7 mm are likely to be treated, while giant aneurysms greater than 25 mm have a particularly poor prognosis if left untreated (17–19). Aneurysms smaller than 3 mm typically do not cause symptoms and are managed conservatively (20). Aneurysms in the so-called gray zone, between 3 and 7 mm, may still rupture, and treatment should be individualized. The International Study of Unruptured Intracranial Aneurysms (ISUIA) showed that the annual rupture risk for aneurysms less than 10 mm in diameter is 0.05% for patients without a history of SAH and 0.5% for those with a previous SAH (21). Irregular aneurysm shape (e.g., with multiple lobes or with blebs/daughter aneurysms) can indicate an unstable lesion (22). Aneurysm growth is a critical factor in predicting rupture (13); a growing UIA is associated with a >30-fold-higher risk of rupture than a stable one (23). Risk stratification guidelines for UIAs that have been developed in large clinical studies include those by ISUIA and UCAS (Unruptured Cerebral Aneurysm Study) as well as the PHASES (population, hypertension, age, size, earlier subarachnoid hemorrhage, site) score; the UIATS (unruptured intracranial aneurysm treatment score); and the ELAPSS (earlier subarachnoid hemorrhage, location of aneurysm, age, population, size, and shape) score (7, 21, 24–26), resulting in risk calculators in which all clinical or morphological factors are added to create a certain score. The accuracy of these scores in predicting unstable aneurysms has been suboptimal (13), potentially due to the lack of quantitative factors related to intra-aneurysmal blood flow dynamics and wall biomechanics.

The decision regarding which treatment and follow-up option are best for a patient can be challenging. Surgical clipping is the original treatment method for cerebral aneurysms; however, the number of aneurysms treated using endovascular options such as coiling or stenting is increasing (15, 16, 27). At the same time, endovascular treatment does not always result in complete aneurysm occlusion and may fail for wide-necked or thrombosed aneurysms (28). Commonly, microsurgery results in ligation of the aneurysm neck and is sometimes combined with a bypass for supplying distal vasculature or, in rare cases, aneurysm resection and microsurgical vessel reconstruction (4). Microsurgical treatment of aneurysms of the basilar artery is particularly challenging because it is critical to preserve perforators supplying the brain stem and cerebellum as well as cranial nerves (28). Advantages of endovascular treatment include minimal invasion, reduced interventional and anesthesia time, and possible treatment of multiple aneurysm sites during the same procedure (29). Endovascular aneurysm repair is commonly performed using detachable platinum coils. The coils are deployed into the aneurysm from a catheter in order to obstruct the flow and induce aneurysm embolization. Multiple coils of various lengths and stiffnesses are subsequently deployed to completely pack the aneurysmal sac and obliterate the flow. The International Subarachnoid Aneurysm Trial, involving 2,143 patients with ruptured intracranial aneurysms repaired by coiling or microsurgical clipping, demonstrated significantly better outcomes for endovascular coiling (30). Nevertheless, aneurysm recurrence or recanalization was reported for a significant percentage of coiled aneurysms, ranging from single digits to more than 30% (31), particularly for complex and large lesions. Stent-assisted coiling can be used for complex and wide-neck aneurysms to ensure that the coils remain in the lesion while preserving the patency of the parent artery (32–34).

Complex cerebral aneurysms not amenable to coiling or clipping, such as fusiform, wide-neck, or dissecting aneurysms as well as aneurysms involving vital side branches, are increasingly repaired by deploying flow diverter devices (FDs) (35–38). These devices are also known as flow diverter stents, pipeline embolization devices, silk flow diverters, and surpass flow diverters. In these procedures, aneurysm thrombosis is induced by reducing the flow into the lesion while preserving the flow to side branches and distal vasculature. The tightly woven mesh of the FD provides resistance to the flow across the surface of the device, thus guiding the flow along the parent artery and away from the aneurysmal sac. Importantly, the FD acts as a scaffold for the endothelium that will form a new blood channel following the endovascular repair. A meta-analysis by Ye et al. (39) of multiple clinical studies involving 2,508 patients with 2,826 aneurysm cases demonstrated that FDs are safe and effective for cerebral aneurysm treatment, with an occlusion rate of 78.8% for an average of 6.3 months of follow-up and neurological morbidity and mortality rates of 9.8 and 3.8%, respectively, following the procedure. Given the range of available options for cerebral aneurysm repair, treatment decisions are often based on a neurosurgeon’s preference and intuition, without considering quantitative data regarding preoperative or postoperative hemodynamic conditions.

1.2. Imaging Cerebral Aneurysms

In this section, we describe the imaging modalities used in diagnostics, evaluation, and treatment of cerebral aneurysms and discuss the relative advantages and shortcomings of each. We focus on imaging methods capable of providing functional data, such as flow dynamics, in addition to the anatomical structure of the aneurysms and the surrounding cerebral vasculature.

The imaging modality most commonly used in clinical practice for both diagnosis and treatment of cerebral aneurysms is digital subtraction angiography (DSA; also called X-ray angiography), which is based on X-ray imaging of the flow of an iodine-based contrast agent injected into the vessel of interest from a catheter (40, 41). The images obtained prior to contrast arrival are digitally subtracted from those with contrast-enhanced vessels, thus removing all other background tissues from the image. The standard technique acquires a planar, projection view of the imaged vasculature. A sequence of acquired X-ray images shows the propagation of the injected contrast, enabling not only visualization of the anatomy but also assessment of the regions with obstructed or stagnant flow. These dynamic data also have high spatial resolution, allowing for the imaging of submillimeter blood vessels. The acquisition traces the contrast flow through the arteries, capillary beds, and the venous side of the circulation. These images identify distal vascular territory supplied by the injected vessel, thus indicating feeding and draining blood vessels for a lesion and allowing for surgical planning. By varying the position of the imaging C-arm, the operator can obtain projection images from different perspectives. Rotating the C-arm during the acquisition allows for the combination of multiple projections to form volume-rendered three-dimensional (3D) images of blood vessels, termed 3D rotational angiography (3DRA). Most importantly, DSA is the modality used for image-guided interventions, as it allows the operator to visualize the placement of endovascular devices such as stents and coils and assess their efficiency in altering blood flow dynamics during the procedure. While invaluable for endovascular procedures, DSA has limitations as a diagnostic modality, as it requires patient catheterization and radiation exposure. Even though DSA provides time-resolved data with excellent spatial resolution, obtaining quantitative measurements of the underlying flow fields is quite challenging, as the standard two-dimensional (2D) projections of the vasculature result in intersection of blood vessels located in different planes as well as foreshortening of vessels crossing the field of view at oblique angles (42). Injection of the contrast agent mixture may alter the flow in distal vessels and even cause a retrograde flow through the collateral arteries. Also, a steady injection is superimposed on the pulsatile blood flow, further altering the native hemodynamic conditions. Strother et al. (43) proposed the use of color-coded DSA to visualize flow patterns and quantify contrast arrival times. While the time interval between contrast arrival and departure calculated from the images may not objectively measure flow residence time, color-coded DSA may detect intra-aneurysmal regions prone to thrombus deposition.

Computed tomography angiography (CTA) is also a clinical standard of care, providing tomographic images of the cerebral vessels. A large field of view covering the entire cerebral circulation, starting from the aortic arch, can be obtained in seconds, which is an important advantage in detecting a bleeding aneurysm relative to other modalities. The images of the vascular anatomy can be enhanced by contrast injection. Previous studies suggested that the sensitivity and specificity of CTA in cerebral aneurysm diagnostics are comparable to those of DSA (44, 45); however, a recent report by Philipp et al. (46) showed that CTA has lower sensitivity for detecting aneurysms less than 5 mm in size. Although it delivers 3D images with submillimeter spatial resolution, CTA is not resolved in time, thus providing no data on flow conditions. This modality also requires radiation exposure, making it less than ideal for longitudinal studies monitoring aneurysm progression over time.

Magnetic resonance angiography (MRA) allows for noninvasive 3D imaging of vascular anatomy without ionizing radiation. Time-of-flight (TOF) MRA is a technique based on saturating a region of interest with repeated radio-frequency pulses, thus obtaining a signal from unsaturated blood flowing into this region from the proximal arteries (47, 48). TOF does not require a contrast agent; thus, it is entirely noninvasive. It provides submillimeter resolution sufficient to image the CoW and its distal arteries. The drawback of TOF MRA is that it can be affected by signal loss due to saturation in regions of slow flow. This may cause artifacts in imaging of large aneurysms with regions of flow recirculation, which appear as low-intensity regions. This issue can be resolved by an intravenous injection of gadolinium to increase the T1 contrast within the arteries relative to surrounding tissues (49, 50). Gadolinium-enhanced or contrast-enhanced MRA (CE-MRA) is well suited for monitoring aneurysms with longitudinal studies in order to detect growth (Figure 1c). In such studies, aneurysmal geometries imaged at the baseline are coregistered with those imaged at the follow-up study, thus enabling visualization of aneurysm progression as well as calculation of volumetric change that occurred between the studies (51).

Figure 1.

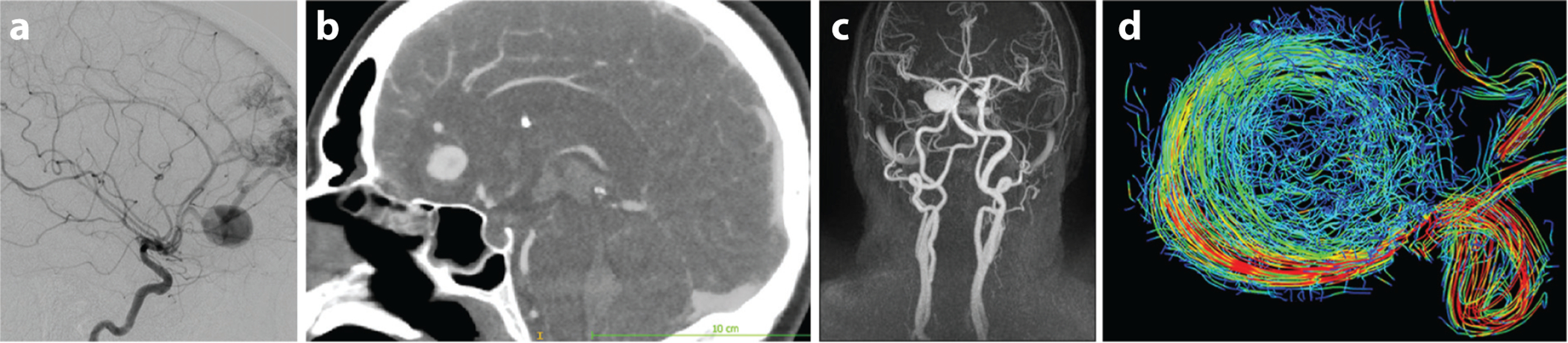
Imaging cerebral aneurysm anatomy and hemodynamics. (a) DSA image. (b) CTA image. (c) CE-MRA maximum-intensity projection for an ICA aneurysm. (d) 4D flow MRI streamlines for an ICA aneurysm. Abbreviations: CE-MRA, contrast-enhanced magnetic resonance angiography; CTA, computed tomography angiography; DSA, digital subtraction angiography; ICA, internal carotid artery; MRI, magnetic resonance imaging. Panel c courtesy of Dr. David Saloner. Panel d courtesy of Dr. Susanne Schnell.

In addition to imaging the lumen, magnetic resonance imaging (MRI) is capable of visualizing and characterizing the arterial wall with associated pathologies. Vessel wall imaging protocol includes a black-blood MR sequence, suppressing the signal from adjacent tissue and blood to enhance the wall. This MRI technique is invaluable for imaging various wall components, visualizing intra-aneurysmal thrombus, and detecting wall inflammation, thus providing insight into aneurysm stability (52, 53). Imaging the arterial walls of intracranial vessels is challenging due to their tortuosity and low wall thickness, thus requiring spatial resolution delivered by high-field-strength MR scanners. Recent imaging studies revealed that unstable cerebral aneurysms are frequently characterized by vessel wall enhancement (54). Zhu et al. (55) conducted high-resolution MRI in 88 asymptomatic aneurysms and showed that the degree of arterial enhancement is associated with traditional aneurysm rupture risk factors calculated by UCAS and PHASES scores.

Blood flow velocities are commonly measured with Doppler ultrasound; however, the skull prevents the use of this modality for quantifying flow in most intracranial blood vessels. The only imaging modality that can provide time-resolved measurements of intracranial flow velocities is phase-contrast MRI (PC-MRI) (56, 57). The phase of the magnetization vector is proportional to flow velocity, allowing velocity encoding with appropriate gradients of the magnetic field (58). 2D PC-MRI acquisition is based on encoding velocities in one direction, thus obtaining either through-plane or in-plane measurements. Three-directional velocity encoding synchronized with an electrocardiogram signal, named four-dimensional (4D) flow MRI, provides time-resolved, 3D velocity fields (59–61). Recent studies demonstrated the capabilities of 4D flow MRI for capturing complex flow patterns in the major vessels of the CoW (62–64). The accuracy of 4D flow MRI is affected by limited spatiotemporal resolution and velocity dynamic range, as well as by image artifacts and noise. 4D flow MRI in cerebral aneurysms is particularly challenging, since their relatively small size and complex flow patterns may result in underresolved or erroneous velocity measurements. These errors are further amplified in calculations of velocity-derived hemodynamic forces (62, 65–67). Enhancing 4D flow imaging of cerebral circulation and reducing imaging time are currently an active area of research (68).

In order to obtain comprehensive information about a cerebral aneurysm, it is often necessary to use different imaging modalities (Figure 1) to combine angiographic images showing vascular anatomy with dynamic data that characterize the flow of a contrast agent or, ideally, measure intra-aneurysmal velocities. In addition, vessel wall imaging is crucial for detecting intra-aneurysmal thrombus, atherosclerotic deposits, and local inflammation of the arterial wall.

2. IMAGE-BASED MODELS OF CEREBRAL ANEURYSM HEMODYNAMICS

Local hemodynamics is key in the initiation, progression, and rupture of cerebral aneurysms (69–74); however, multiple studies investigating the exact relationship between the flow factors and aneurysmal disease have provided controversial results (75–77). In the last two decades, numerous research groups have developed modeling pipelines generating patient-specific models of the flow in cerebral aneurysms based on medical imaging data. Steinman & Pereira (78) recently investigated the sources of error and variability of state-of-the-art computational fluid dynamics (CFD) models of the flow in cerebral aneurysms. Several CFD challenge studies were conducted in which the same aneurysms were modeled by multiple research teams (79–83). The results were highly variable, showing that computed flow fields and hemodynamic forces depend on the modeling methods and assumptions used by the modelers. In this section, we describe the key steps in conducting image-based flow simulations for cerebral aneurysms, discuss modeling assumptions and sources of error, and demonstrate clinical applications of CFD models.

2.1. Patient-Specific Modeling Pipeline

In order to simulate flow and determine hemodynamic metrics related to aneurysm progression, patient-specific models are generated from medical imaging data. While a variety of modeling methods and tools can be used for this purpose, the modeling pipeline typically starts from segmentation of medical image data and construction of 3D vascular geometries. The flow is then either simulated by solving the governing Navier–Stokes equations or measured in experiments conducted in patient-specific flow phantoms. For both approaches, it is essential to ensure that the flow conditions at the inlets and outlets of the model represent the flow in an actual patient. Once the velocity distribution is either computed or measured, various flow-derived metrics can be calculated and analyzed.

2.1.1. Image segmentation.

The first step in generating an aneurysm model is to segment image data in order to obtain a 3D geometry of the aneurysm with its proximal and distal vessels. The segmentation process depends on the imaging modality, with 3DRA typically considered the gold standard due to its high spatial resolution (78, 84). Importantly, because 3DRA is a standard of care, 3DRA data are available for large cohorts of patients, thus allowing CFD studies to be conducted for a statistically significant number of aneurysms (69, 85). Alternatively, aneurysmal geometries can be obtained from CTA or MRA data. Geers et al. (86) reported significant differences in aneurysm necks reconstructed from CTA versus those obtained from 3DRA, which were explained by the difference in imaging resolution. Ramachandran et al. (87) assessed the sensitivity of resulting geometries to imaging modality by using imaging data with comparable spatial resolutions. A comparison of morphological metrics for models generated from in vitro and in vivo imaging with 3DRA, CTA, TOF-MRA, and CE-MRA found consistency across the resulting geometries. As described above, while 3DRA and CTA provide only vascular anatomy, MRI studies can incorporate PC-MRI velocity measurements, thus providing patient-specific flow conditions (88, 89). Image resolution and quality, as well as segmentation approaches, are considered to be major sources of variability for patient-specific modeling (78, 82). The finite size of image voxels results in a partial volume effect, that is, an approximation of a continuous smooth vessel wall by rectangular voxels. Image artifacts and noise often require manual adjustment of the segmented surfaces, thus making modeling results dependent on operator experience and intuition. Once the 3D vascular geometries are obtained, the region to be modeled, typically involving the aneurysm with the vessels immediately proximal and distal to it, has to be selected.

The CFD challenges demonstrated variability in segmenting the same image data sets among participating research groups (79, 82). Several studies investigated the effect of the proximal vessel geometry on the flow in cerebral aneurysms, demonstrating that maintaining long segments of the arteries feeding the aneurysm is crucial for matching patient-specific flow conditions (90–92). Finally, some degree of smoothing is usually applied to ensure that there are no discontinuities or sharp edges in the resulting surface of the model, which could affect the quality of the computational mesh. It is important to ensure that surface smoothing does not alter the size of modeled vessels, which would affect the computed velocity fields.

2.1.2. Numerical solution of the Navier–Stokes equations.

The flow in major cerebral arteries is highly three dimensional and is characterized by intermediate Reynolds and Womersley numbers, thus requiring a numerical solution of the unsteady Navier–Stokes equations. Various solvers, using a finite-volume, finite-difference, or finite-element approach, are used to obtain a numerical solution for velocity and pressure fields. Botti et al. (93) compared the accuracy of finite-volume and finite-element CFD solvers in modeling intracranial aneurysm flow and concluded that both solvers converge to the same numerical solution provided sufficient refinement of the computational mesh. The CFD challenges showed the variety of numerical solvers used by different research groups, with some teams combining commercial modeling packages with in-house scripts and other groups relying on software they developed specifically for modeling hemodynamics. There are a couple of open-source platforms providing tools for the entire modeling pipeline, from image processing to flow visualization and analysis (94, 95). These platforms, based on a finite-element flow solver, provide unique capabilities for specifying inlet and outlet boundary conditions, as described below. A computational mesh is generated on the domain in order to discretize the governing flow equations. An unstructured mesh is commonly used due to the complexity of the vascular geometries. It is crucial to ensure mesh independence of the numerical solution, that is, to establish that the spatial resolution of the computational mesh is adequate for resolving flow features in the region of interest. An important paper by Valen-Sendstad & Steinman (96) considered the effect of increased spatial and temporal resolution of CFD simulations on various hemodynamic parameters. Both high- and normal-resolution simulations were carried out for the same group of aneurysms by using quadratic versus linear mesh elements in the numerical discretization and increasing the number of time steps per cardiac cycle by an order of magnitude. The results showed that numerical discretization used in state-of-the-art simulations may underresolve flow fields in cerebral aneurysms, thus not detecting unstable or turbulent flow and dynamic changes of wall shear stress (WSS) over the cardiac cycle. Nevertheless, time-averaged WSS distributions were similar for both normal- and high-resolution computations. The time steps used in a numerical simulation should be sufficiently small to resolve temporal changes of the flow. Recent high-resolution CFD studies revealed flow instabilities and intermittent structures in cerebral aneurysms that were not detected in simulations with default solving settings and underresolved meshes (97–99).

2.1.3. Modeling assumptions and flow boundary conditions.

CFD modeling of flow in cerebral aneurysms requires assumptions regarding the flow regime, blood rheology, arterial wall compliance, and, most importantly, flow boundary conditions at the inlets and outlets of the model. We address each of these assumptions, as they contribute to variability of patient-specific CFD modeling.

Flow in cerebral arteries is commonly assumed to be laminar, as the Reynolds numbers are in the range of several hundred; however, pulsatile flow in stenotic or aneurysmal vessels may have unsteady shear layers, which lead to transitional flow, as described in the previous section (97–99). Appropriate flow regime remains an open question, particularly since state-of-the-art in vivo flow measurements in cerebral aneurysms lack the temporal resolution required to detect transitional flow. Several studies have addressed non-Newtonian blood behavior and its effect on intra-aneurysmal flow (100, 101). The shear thinning and yield stress properties of blood caused by the interaction among red blood cells (RBCs) can be accounted for by various non-Newtonian viscosity models. Several reports suggested that non-Newtonian viscosity can influence WSS and intra-aneurysmal thrombus deposition in cerebral aneurysms; however, the non-Newtonian blood behavior is currently thought to have a secondary effect on the flow (78). The non-Newtonian blood behavior is significant in flow with shear rates below 100 per second, which is usually below the range observed in cerebral aneurysms. Moreover, while RBC aggregation may take several cardiac cycles, such aggregations break apart in higher-shear-rate regions practically instantaneously.

Accounting for arterial wall compliance requires conducting fluid–structure interaction simulations in which the flow dynamics equations are coupled with solid mechanics equations. In addition to increased computational cost and complexity, this approach is challenging due to the lack of information on vessel wall geometry and material properties available from imaging data. A nonuniform wall thickness and the variability of the structural components that constitute the aneurysmal wall may cause drastic differences in stress distribution. While advanced MRI techniques such as black blood (52) may eventually be able to provide such data, incorrect assumptions may lead to numerical results that would be inferior to those obtained assuming a rigid wall (84). In addition, aneurysmal disease is characterized by loss of elastic lamina and overextension of the collagen fibers, resulting in reduced wall compliance (102).

The remaining assumption, inflow and outflow conditions, is perhaps the most disputed part of image-based CFD modeling. A computational model represents only a small part of the circulation and therefore requires information on the flow in the vessels proximal and distal to the modeled region. The only modality capable of in vivo flow measurements is 4D flow MRI; however, at present it is used for imaging cerebral aneurysms at only a few research centers. Moreover, as discussed above, the limited spatiotemporal resolution and image noise may affect the accuracy of 4D flow data, often resulting in a discrepancy between the inlet and outlet flow rates, thus contradicting the principle of mass conservation. Regardless of these shortcomings, obtaining at least 2D PC-MRI measurements can improve the fidelity of CFD simulations (78, 84). In the absence of patient-specific flow data, the velocity and pressure values at the inlets and outlets must be either prescribed from published data or calculated from reduced-order models. The inlet flow waveforms obtained from the literature can be scaled for a patient-specific vessel size on the basis of the optimal WSS values observed in healthy arteries.

There is a general consensus that assigning zero pressure at all outlets should be avoided, as it is not based on physiology (84). Outflow boundary conditions can be prescribed using Murray’s law. This law, based on kinetic energy minimization, assumes that the flow division is proportional to the cube of the vessel radius. While this assumption is based solely on the geometry of the branches immediately distal to the model, it may be fairly accurate, as blood vessels remodel according to their flow rate in order to maintain an optimal WSS (103). The state-of-the-art approach is based on coupling the 3D CFD domain with reduced-order models of the surrounding vasculature (104, 105). In the open-source modeling platforms developed for patient-specific hemodynamic simulations, distal and proximal vascular territories are modeled using lumped parameter networks coupled with a finite-element solver (94, 95, 104). Alternatively, one-dimensional Navier–Stokes solutions based on flow variables averaged over vessel cross sections can be coupled to full 3D equations (106, 107). An important advantage of the reduced-order models is their ability to simulate flow alterations caused by vascular interventions. Surgical clipping of a vessel or adding a bypass can be modeled by adjusting the resistance and capacitance of the corresponding segments of the equivalent network model.

2.1.4. Computing clinically relevant metrics.

The numerical solution of the Navier–Stokes equations provides velocity and pressure distributions that can be used to calculate flow-derived variables thought to be related to arterial wall remodeling. Multiple flow metrics based on intra-aneurysmal flow characteristics (e.g., velocity, vorticity, flow rates, and residence time), WSS (e.g., time-averaged WSS, oscillatory shear index, WSS spatial gradient, and area of low or high WSS), pressure difference (temporal and spatial), and energy (e.g., kinetic energy and viscous dissipation) are used to find correlations between hemodynamic forces and aneurysm progression. A couple of papers provide comprehensive lists of hemodynamic variables correlated to aneurysm rupture (108, 109). While intra-aneurysmal flow fields can markedly vary over cardiac cycle, there is evidence that time-averaged flow metrics are equally effective in aneurysm risk stratification (109). CFD challenge studies (79, 83) showed that normalizing flow metrics computed in the aneurysm to some reference values, such as those computed at the parent vessel, improved the agreement and consistency of CFD results obtained by different modeling teams. This finding suggests that patient-specific CFD results should be considered not as absolute and fixed values but rather as relative distributions that could be affected by changes in physiological activity or stress level. CFD data allow for colorful visualization of the flow fields and corresponding distributions of the flow-derived parameters (Figure 2), with some critics referring to CFD as “colors for doctors.” It is challenging, however, to distill this abundant information into a few specific indices that clinicians can use for therapeutic decision making. Establishing relevant hemodynamic factors and determining their uncertainty are the focus of current research in cerebral aneurysm modeling.

Figure 2.

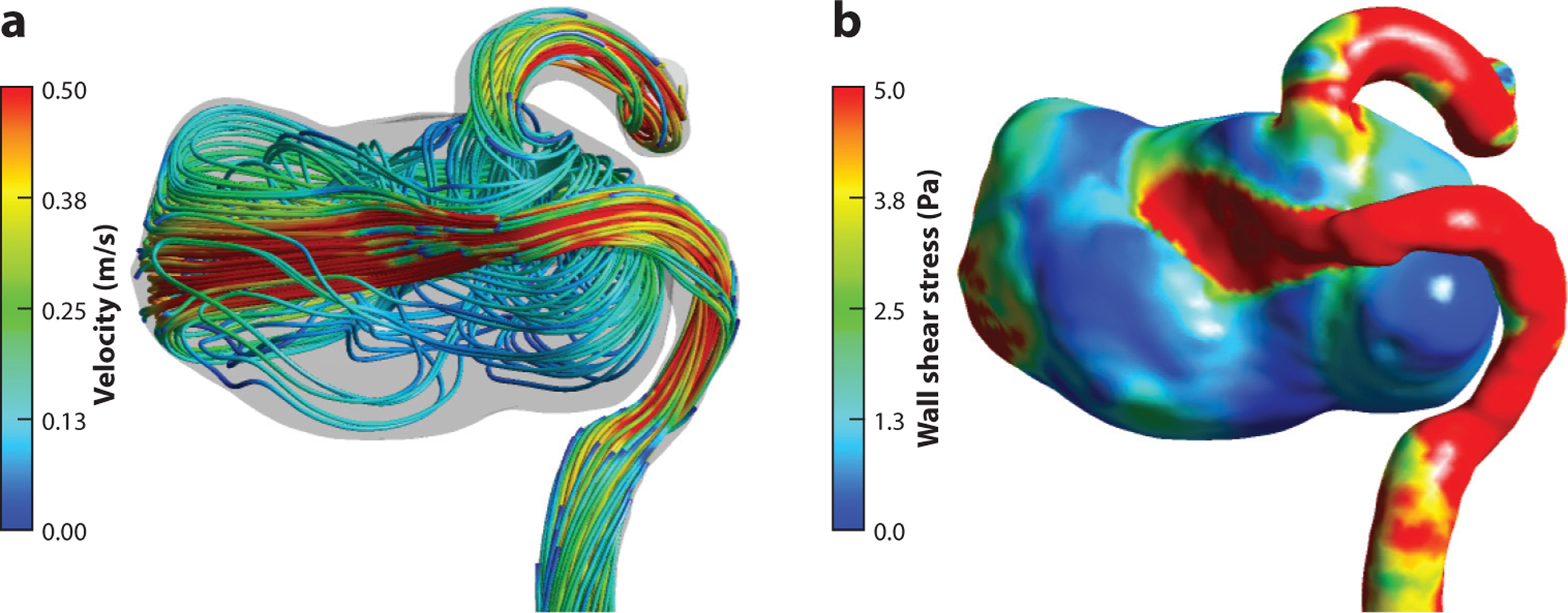
Numerical simulations of blood flow in an internal carotid artery aneurysm. (a) Flow streamlines. (b) Wall shear stress distribution. The computational model is generated from magnetic resonance imaging/magnetic resonance angiography data obtained at San Francisco VA Medical Center.

2.2. Experimental Flow Models

While the vast majority of patient-specific models of cerebral aneurysms use the computational approach, in vitro flow measurements provide valuable insights into intra-aneurysmal hemodynamics and can serve as benchmark data for CFD validation. Vascular geometries obtained from imaging data, as described in Section 2.1.1, are used to fabricate flow phantoms with 3D printing (110, 111). The phantoms are then connected to a flow loop with a blood-mimicking fluid, typically a mixture of glycerol and water. Two primary methods used for experimental flow measurements in cerebral aneurysm models are particle image velocimetry (PIV) and in vitro 4D flow MRI. In order to conduct PIV measurements, the flow is seeded with fluorescent particles, a 2D plane or a volume is illuminated by a flashing laser, and particle motion is recorded with high-speed cameras. This approach can provide spatiotemporal resolution comparable to that of CFD models. Most PIV studies in cerebral aneurysms have measured the flow in a cross-sectional plane due to challenges in obtaining volumetric data in complex and tortuous geometries. The Lieber group (112, 113) carried out pioneering studies on flow diverters placed in aneurysm models and found a strong correlation between PIV measurements and X-ray angiography data. A comparison of CFD simulations and PIV measurements conducted by Ford et al. (114) in replicas of two cerebral aneurysms with matching boundary conditions demonstrated good overall agreement of the velocity fields. Raschi et al. (115) compared PIV and CFD results in models of a growing aneurysm constructed from imaging data acquired at three time points during the aneurysm evolution. The measured and computed velocities were found to be in good qualitative and quantitative agreement, except for some discrepancies in the near-wall regions.

High-resolution data obtained in CFD and PIV models can be used to assess the accuracy of 4D flow MRI. van Ooij et al. (66) compared CFD and 2D PIV results with in vitro 4D flow MRI measurements in a cerebral aneurysm phantom, showing reasonable qualitative and quantitative agreement of both modeling modalities with MRI data under steady and pulsatile flow conditions. The root-mean-square errors of the velocity magnitude in the CFD and MRI comparison (4–5% of the maximum PC-MRI velocity) were smaller than those for the PIV and PC-MRI comparison (10–12% of the maximum PC-MRI velocity), which could be explained by the experimental setup. An instructive study by Roloff et al. (116) compared several flow quantification techniques, including CFD; in vitro PC-MRI; and standard, stereoscopic, and tomographic PIV. Steady flow fields acquired with multiple modalities in a silicone model of an ICA aneurysm were compared using a similarity index that accounted for velocity vector direction and magnitude. The quantitative agreement between CFD and all PIV methods was high; however, PC-MRI data had inferior agreement with the other modalities due to this technique’s lower resolution.

The resolution of imaged velocity fields can be increased by scaling flow phantoms, as long as the Reynolds and Womersley numbers of the experimental and in vivo flow fields are maintained the same. In a comprehensive analysis, Amili et al. (117) investigated various flow metrics measured with 4D flow MRI in a scaled aneurysm phantom and compared the results with numerical simulations reported for the same aneurysm in the 2012 CFD challenge (81). Good agreement was found for cycle-averaged quantities; however, significant discrepancies between MRI and CFD were present at peak systole. Increased spatial and temporal resolution of in vitro measurements allowed for meaningful comparison of the main flow statistics and demonstrated the potential of 4D flow MRI in capturing intra-aneurysmal hemodynamics, which may eventually be attainable in vivo. Although they provided cross-validation for both numerical and experimental approaches, these studies did not compare modeling results with in vivo velocity data. A comparison of in vivo 4D flow MRI measurements with both CFD and PIV models was recently conducted by Brindise et al. (118). While the general velocity features acquired with different modalities were similar, substantial discrepancies were found in distributions of WSS, oscillatory shear index (OSI), and relative residence time (RRT). Since the same algorithms were used to compute these flow-derived variables from velocities obtained with all modalities, the observed differences should be attributed to the specific assumptions and uncertainty of each flow quantification approach.

2.3. Image-Based Computational Fluid Dynamics Models in Unruptured Intracranial Aneurysm Risk Stratification and Interventional Planning

As patient-specific modeling tools became more sophisticated and the time required to carry out flow analysis decreases, a few research teams collaborated with clinicians to conduct modeling studies for relatively large cohorts of cerebral aneurysm patients. These studies aimed to provide guidance either in risk stratification of UIAs or in planning surgical or endovascular interventions. Below, we discuss some of the successful studies that demonstrated the potential value of hemodynamic modeling for assessment of aneurysm stability or for predicting interventional outcomes. Note that while these models provided valuable results, they have not necessarily affected clinical decisions regarding treatment options for these patients.

2.3.1. Predicting cerebral aneurysm growth and rupture.

Despite numerous studies on the subject, assessing the risk of aneurysm rupture remains a clinical challenge. As discussed in Section 1.1, most UIAs remain stable, with approximately 10–15% showing growth in longitudinal studies (13, 14), but since an aneurysm rupture leads to high mortality and morbidity rates (10, 11), most UIAs are currently treated even if the probability of rupture may be negligible. Risk stratification scores such as those from the ISUIA and UCAS and PHASES, UIATS, and ELAPSS, mentioned above (7, 21, 24–26), are based on a combination of aneurysm location (e.g., posterior or anterior), morphology (e.g., size, shape), and clinical factors (e.g., comorbidities, age, gender, smoking status, family history). These scores do not account for local hemodynamic factors, which require either patient-specific modeling or in vivo imaging of the flow. At the same time, deterministic CFD models in which aneurysm stability is predicted solely by hemodynamic factors are oblivious to clinical data. There is a general consensus that a comprehensive clinical tool predicting a risk of aneurysm rupture has to incorporate clinical, morphological, and biomechanical factors and deliver a probabilistic risk assessment rather than a deterministic answer on a patient-specific basis. A small number of studies performed statistical analyses that combined hemodynamic indices with aneurysm location and morphology (14, 62, 69, 70, 108, 119). In a prospective longitudinal study of almost 200 UIAs, Ramachandran et al. (14) compared aneurysm geometry (size and shape), multiple hemodynamic metrics, and pressure-induced wall tension computed from image-based models and found that image-derived biomechanical factors were not significant in differentiating stable and unstable aneurysm populations. In a couple of studies featuring sufficiently large cohorts of stable and unstable aneurysms, statistical methods ranging from regression analysis to deep learning algorithms were trained on these comprehensive data sets (69, 108). The largest of these studies, by Detmer et al. (108), considered 1,631 aneurysms in 1,061 patients with 492 aneurysms ruptured. Following an evaluation of the contributions of 22 hemodynamic and 25 morphological parameters, the final statistical model retained 11 hemodynamic and 12 morphological variables as well as aneurysm location and patient age and gender. This model was then tested on a subset of aneurysms excluded from the training data and was shown to discriminate between ruptured and unruptured aneurysms with an AUC (area under the curve) of 86%. These impressive results illustrate the potential of image-based CFD models in risk stratification of cerebral aneurysms; however, a limitation of this study is that it was based on single-time-point data rather than longitudinal studies of cerebral aneurysms. The aneurysms considered stable at the time of the study may have ruptured later on, potentially affecting the predictive capabilities of the statistical model. Note that a longitudinal study of UIAs has an intrinsic selection bias since high-risk aneurysms are always treated rather than monitored, with the exception of cases when intervention is not feasible or is rejected by the patient.

2.3.2. Modeling postoperative flow dynamics in cerebral aneurysms.

In addition to elucidating the role of biomechanical factors in aneurysmal disease initiation and progression, patient-specific modeling provides a unique framework for analysis of postoperative hemodynamic conditions, which cannot be imaged a priori. A few studies have modeled the postoperative flow fields that would result from surgical treatment of complex cerebral aneurysms (42, 89, 120, 121). In this framework, preoperative image data are used to construct a patient-specific CFD model that is then modified according to the proposed intervention. Some of these studies considered indirect surgical clipping of fusiform aneurysms of the basilar artery, which are not amenable to direct clipping or coiling due to possible occlusion of pontine perforators or distal branches (28). The surgeries aimed to reduce the flow through the basilar trunk, thus decreasing hemodynamic forces acting on the aneurysmal wall and inducing intra-aneurysmal thrombus layering, in the hope that this may prevent aneurysm rupture. The flow was reduced by surgical clipping of a supplying vertebral artery or proximal basilar trunk, accompanied by a middle cerebral to posterior cerebral artery bypass to ensure retrograde filling of the distal basilar territory (122). Alternative surgical scenarios were simulated for a small group of patients in order to predict intra-aneurysmal regions prone to postoperative thrombus deposition, thereby indicating interventional options likely to cause complications (42, 89, 120, 121). Even though only one of the simulated surgical scenarios could be implemented, in most cases CFD-predicted regions of thrombus deposition matched those observed following the procedure. The limitation of this modeling approach was the inability to account for altered cerebral flow distribution following the intervention.

Image-based CFD models have been demonstrated to predict flow fields resulting from endovascular interventions such as aneurysm coiling and deployment of FDs. CFD modeling of the flow following coiling or FD placement involves modeling these devices in addition to the flow. A realistic finite-element model of embolic coils developed by Babiker et al. (123) showed that posttreatment flow conditions depend on variations in packing density and the shape of the coils. In addition to drastically increased computational cost due to resolving endovascular device geometries and surrounding boundary layers, numerical simulations depend on reliable prediction of the device position and orientation relative to the vascular geometries. A virtual deployment of coils and FDs can be simulated prior to flow modeling (124–129); alternatively, these devices could be modeled using a porous medium approach (130, 131). In the virtual stenting approach, a generic FD mesh generated along a vessel centerline is computationally expanded until it reaches the luminal surface; the wires of an FD are then constructed on the resulting surfaces (126). The porous medium approach reduces computational cost and generally agrees with simulations resolving device geometries, as well as with postoperative clinical data; however, the key limitation is that permeability variations caused by bending and interaction with arterial walls cannot be inferred without modeling or imaging patient-specific device orientation (131).

In order to assess the efficacy of the FD treatment, intra-aneurysmal hemodynamic conditions prior to and following the procedure must be compared. Changes in the intra-aneurysmal velocities, flow rates, and viscous energy dissipation, as well as a decrease in WSS and an increase in flow residence time, provide quantitative measures that predict the likelihood of successful aneurysm embolization following FD placement. Cebral et al. (132) indicated that an increase in intra-aneurysmal pressure following FD treatment may cause aneurysm rupture. Paliwal et al. (133) simulated preoperative and postoperative flow fields in 15 cerebral aneurysms and compared the hemodynamic changes resulting from FD treatment with observed clinical outcomes. The results computed for successful and unsuccessful embolization cases (Figure 3) showed a similar 50% reduction in intra-aneurysmal velocities; however, the reduction in vortex core lines and the energy loss were 38.2% and 42.9%, respectively, for successful cases and approximately 10% each for unsuccessful cases. A detailed CFD study by Mut et al. (134) investigated the relation between flow changes and posttreatment occlusion time in 23 aneurysms. A statistical analysis of multiple flow metrics found significant differences in postoperative velocities, inflow rates, and shear rates between aneurysms that were completely occluded 3 months after treatment and those that remained partially patent 6 months after treatment. Interestingly, this study showed that aneurysm occlusion time is determined by postoperative flow conditions immediately after FD placement, rather than by the difference between the pre- and posttreatment flows in the same lesion. Modeling flow alterations resulting from FD deployment can assist surgical planning by providing information on the appropriate length and positioning of the device, evaluating whether a nested FD construct is needed to increase resistance to the flow, and predicting the outcome of the procedure. Moreover, CFD simulations enable evaluation and optimization of the design of novel FDs (128, 135).

Figure 3.

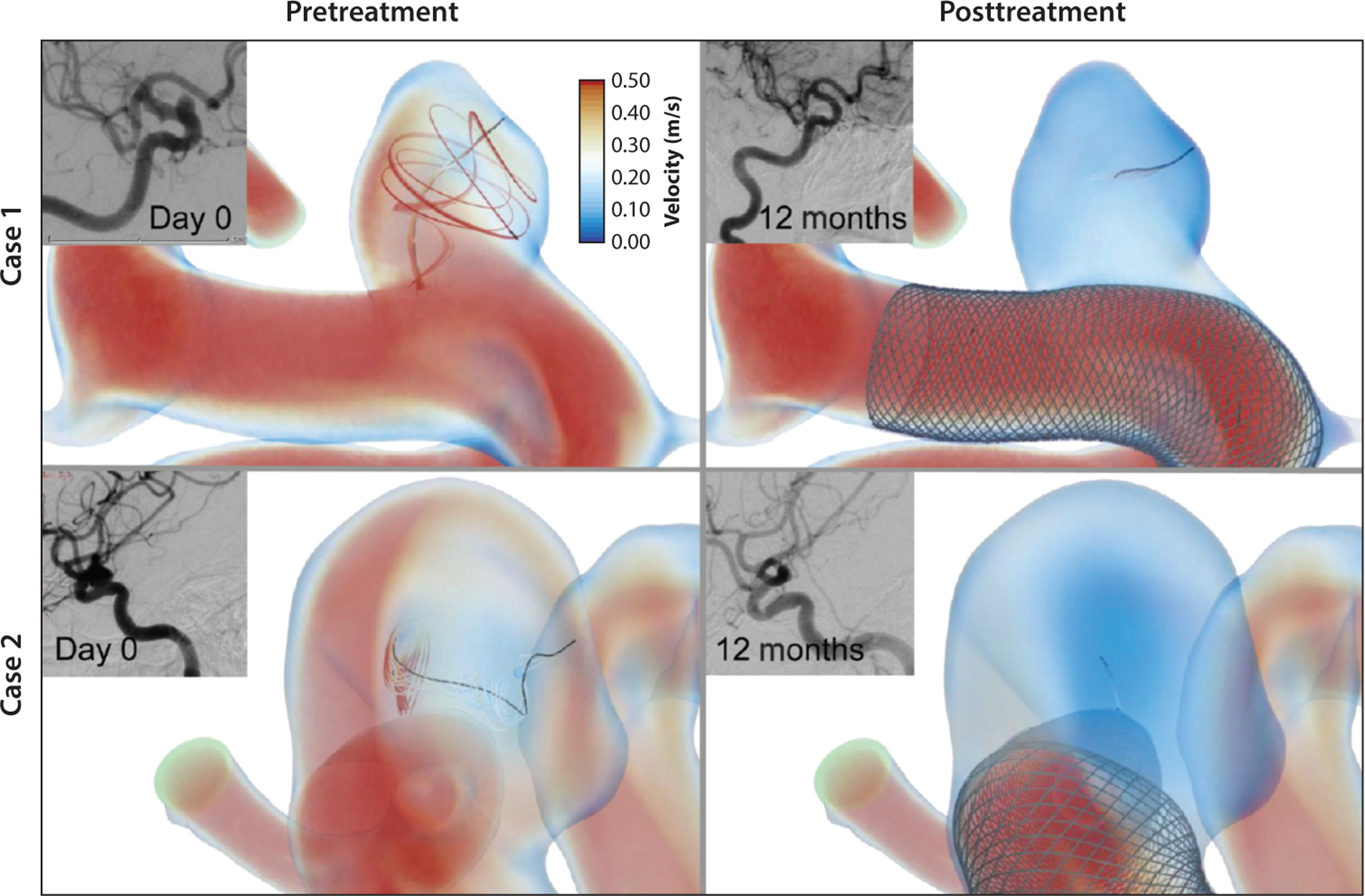
Local hemodynamics before and after flow diverter device treatment in a representative successful case, along with clinical images before treatment and at 12-month follow-up. Figure adapted from Reference 133, courtesy of Dr. Hui Meng.

3. BRIDGING THE GAP BETWEEN CLINICAL PRACTICE AND PATIENT-SPECIFIC MODELS

Although image-based models are capable of providing expansive data quantifying patient-specific hemodynamic conditions and forces, cerebral aneurysm modeling remains a research approach rather than a clinical tool for evaluation and treatment of these lesions. While numerous reports on CFD modeling conducted for large cohorts of patients have been published in biomedical, imaging, and clinical journals and presented at scientific meetings, the translational value of these studies remains controversial. Among the various reasons why the quantitative approach is not readily adopted by clinical community, the following are the most important in our opinion: the challenges in conducting state-of-the-art modeling in clinical settings, the quantification of uncertainty of the modeling results, the controversy regarding exact mechanisms linking local hemodynamics and aneurysm vascular biology, and, finally, the lack of clearly defined indices that could be used for making clinical decisions. We address each of these shortcomings in the subsections below.

3.1. Conducting Modeling Studies in a Clinical Setting

The first challenge is that patient-specific modeling requires highly specialized software tools for medical image processing, 3D modeling of vascular anatomy, numerical solutions of the governing equations, and postprocessing of the results. As described above, few open-source platforms have been designed specifically for comprehensive image-based flow analysis (94, 95); thus, many research teams are either developing their own modeling tools or using various combinations of in-house scripts and commercial software packages. Regardless of the modeling approach, generating image-based CFD models and analyzing the resulting data require highly proficient researchers specifically trained in this interdisciplinary field. We note that it typically takes a couple of years for biomedical graduate students to reach the level of expertise required to conduct reliable CFD simulations of cerebral aneurysm hemodynamics. While rapid progress in machine learning algorithms is posed to automate image segmentation (136, 137) and dramatically reduce modeling time and cost, knowledge of flow physics and cardiovascular mechanics will likely remain necessary for patient-specific hemodynamic analysis. Since it is impractical to train medical practitioners in advanced CFD modeling and implausible that each medical center will keep on staff a modeling expert, the remaining alternative is to use cloud-based computing to conduct flow analysis at dedicated centers. In this paradigm, implemented by HeartFlow, Inc. (138), medical imaging data acquired for a patient are securely transferred to a dedicated server, at which point a team of modeling experts carries out numerical simulations. A report summarizing the computational results is then returned to the clinic. In order to conduct studies on large cohorts of patients, it is crucial to develop fully automated methods for converting imaging data to geometric models for CFD simulations. Seo et al. (139) developed a highly automated modeling framework based on a level-set segmentation of 3D angiograms and an immersed boundary CFD solver and used it to compute the flow in several cerebral aneurysms. Cartesian grids allowed these authors to avoid meshing luminal surfaces and could be easily refined to improve the resolution in smaller vessels. Adopting deep learning algorithms for image segmentation will allow further reduction of the modeling time and automated elimination of image artifacts, as evidenced by innovative studies applying neural networks to CTA data and 3D angiograms of cerebral arteries (136, 137, 140).

3.2. Uncertainty Quantification of Image-Based Computational Fluid Dynamics

The second challenge is quantifying the uncertainty of the hemodynamic metrics predicted by numerical simulations. The sources of error are described above in Section 2.1; here, we reiterate that even though typical CFD data contain specific values, it is crucial to determine the uncertainty of these results and treat them as a sample taken from a range of possible values. Uncertainty quantification (UQ) for patient-specific flow simulations is at the cutting edge of cardiovascular modeling research, with recent studies considering UQ for CFD models of different vascular territories (141–144). As mentioned above, several CFD challenge studies have investigated the variability of image-based CFD models in cerebral aneurysms and provided the groundwork for developing future modeling guidelines (79, 81–83). Two comprehensive recent reviews specifically evaluated state-of-the-art CFD modeling practices applied to cerebral aneurysms and provided recommendations for reliable simulations of intra-aneurysmal hemodynamics (78, 84). In addition to uncertainty due to medical image resolution and noise, modeling assumptions, and numerical approximations, there are confounding factors such as patient genetics and clinical history that are typically not accounted for in the computational analysis but could affect an outcome predicted by a model. Another important consideration is the variability of cardiovascular pressure and flow rates, which depends on the patient’s physical activity, level of stress, and even position during imaging. Flow measured while the patient is resting in a supine position in an MRI scanner can differ substantially from flow measured during exercise or emotional stress.

3.3. Arterial Wall Mechanics and Structure: The Missing Link

A key consideration in the assessment of cerebral aneurysm stability is that while hemodynamic forces can cause arterial wall remodeling, it is ultimately the wall itself that bulges and eventually ruptures due to adverse biomechanical or physiological factors. It is known that blood vessels adjust to flow rate by maintaining an optimal value of WSS (103, 145). Nevertheless, prediction of disease progression based solely on flow factors is an indirect approach to cerebral aneurysm risk assessment. As stated above, very limited information on arterial wall structure and properties can be obtained from noninvasive in vivo studies, inhibiting patient-specific arterial wall analysis. Even so, computational studies based on ex vivo data provide invaluable information on aneurysmal wall structure and function, which may be the missing link in understanding the mechanisms of cerebral aneurysm growth and rupture. Pioneering research by Robertson and colleagues (71, 102) elucidated the complex interplay among hemodynamics, inflammation, and wall remodeling in aneurysmal disease. The mechanical strength of the arterial wall is due to elastic laminae and collagen fibers of the medial and adventitial layers (71). The aneurysmal wall does not passively bulge out under stress, since the distensibility of collagen fibers is limited; rather, it actively grows through collagen remodeling and muscle cell proliferation. This pathological growth and remodeling process is affected by blood flow and inflammation. The aneurysmal wall is characterized by a loss of elastic laminae, resulting in excessive loading of the collagen fibers and increased wall stiffness (102). The remodeling of collagen fibers during the aneurysm enlargement process alters their orientation and, subsequently, the wall strength, and thus is a key factor in the aneurysm’s vulnerability to rupture under intramural pressure (71). By testing the mechanical integrity of wall tissue harvested from UIAs and normal cerebral arteries and analyzing the corresponding collagen fiber architecture with multiphoton microscopy, Robertson et al. (102) discovered that aneurysms with reduced wall strength are characterized by impaired architecture of the fiber layers. This measure can identify UIAs with increased risk of rupture; however, at present there are no imaging tools that can noninvasively assess wall integrity in vivo.

Due to the variability in intra-aneurysmal hemodynamics and the mechanical properties of the aneurysm wall, a meaningful correlation requires precise mapping of the local flow variables and wall characteristics. Cebral et al. (146) developed a unique methodology for coregistration of image-based CFD data with resected aneurysm specimens using in vivo marking of the tissue with a surgical pen and subsequent alignment with 3D-printed models. This framework allowed integration of multiple imaging and modeling modalities, including the mapping of computed WSS distribution to intraoperative video and multiphoton microscopy data showing local collagen fiber architecture (147). The most recent research by Cebral et al. (73, 147) reports on the relationship between several hemodynamic metrics and focal wall characteristics observed intraoperatively in 65 cerebral aneurysms. The regions exposed to recirculating flow with low WSS and increased flow residence time were characterized by atherosclerotic and hyperplastic changes, while inflow jets and high WSS corresponded to local thinning of the wall (73, 147). These findings provide evidence for the theory linking both abnormally low and high WSS to aneurysmal disease progression.

Recent aneurysm models in rodents elucidated the role of transmural macrophage infiltration in disruption of wall elastic lamina and collagen, causing aneurysm formation (71). Subsequent aneurysm growth is also influenced by a combination of abnormal WSS and continuous inflammation. These results suggest that anti-inflammatory drugs may be capable of inhibiting aneurysm progression. Once the exact relationship between hemodynamic forces and aneurysmal wall remodeling is understood, patient-specific CFD models can be used to predict the risk of aneurysm growth and rupture (71).

3.4. Translational Value of Hemodynamic Data

Finally, we consider the challenge of establishing clinically relevant hemodynamic indices and their specific thresholds that could be used for cerebral aneurysm management in a clinical setting. A well-known controversy in cerebral aneurysm modeling resulted from two competing theories stating that aneurysm growth and rupture are caused by either a high or low WSS. Flow simulations conducted for large cohorts of ruptured and unruptured aneurysms determined a correlation between regions of elevated WSS and aneurysm rupture (72, 85, 148). The prevalence of aneurysms in patients with arteriovenous malformations that cause abnormally high flow rates, as well as aneurysm formation in animals following carotid ligation, confirms that elevated WSS is the culprit in aneurysm initiation (71). At the same time, several studies have indicated that aneurysm progression was observed in regions where the aneurysmal wall was exposed to abnormally low WSS (70, 149–152). The correlation detected between averaged WSS and the rupture or growth status determined in these studies did not explain the underlying mechanisms causing disease progression in regions characterized by abnormal WSS values. These confusing reports triggered a publication (153) questioning the potential clinical value of CFD, which it spelled out as “confounding factor dissemination,” due to modeling simplifications, a growing number of confusing hemodynamic indices proposed as risk indicators, and the small number of cases considered in different studies. There is a consensus that bridging the gap between numerical analysis and clinical practice will require multicenter studies of large patient cohorts using standardized modeling framework and multivariate statistical analyses (76, 154). It is crucial to recognize biological processes driving aneurysm growth and repair that can confound biomechanical analysis. Meng et al. (77) proposed a unifying theory, noting that high WSS combined with a positive WSS gradient leads to growth and rupture of small or secondary bleb aneurysms, while low WSS and high OSI lead to growth and rupture of large atherosclerotic aneurysms. Current studies involving hundreds of patients in which CFD results are combined with morphological data and medical history are leading to the development of clinical tools for aneurysm risk stratification (69, 108, 155).

4. FUTURE DIRECTIONS

Enhancing the resolution of medical imaging while reducing the acquisition time will allow quantification of aneurysmal flow and wall mechanics in a clinical setting (67, 68). At the same time, patient-specific models will continue to deliver superior accuracy and, most importantly, capabilities to predict postinterventional conditions on a patient basis. Recent developments in data science provide an opportunity to combine imaging and modeling approaches in order to attain superior fidelity and accuracy of the resulting quantitative data. In this framework, computational results would complement clinical measurements by eliminating noise and image artifacts and increasing the spatiotemporal resolution of the acquired data. Results predicted by computational models would be corrected by in vivo measurements, thereby ensuring that the combined output data represent the actual patient-specific conditions with high fidelity. When applied to cerebral aneurysm hemodynamics, this data fusion approach could enable merging of 4D flow MRI and CFD data in order to improve flow quantification. As discussed in the previous sections, the accuracy of 4D flow MRI measurements in cerebral vessels is affected by limited spatiotemporal resolution, the dynamic range of measured velocities, and image noise. Concurrently, CFD results can be affected by image quality and segmentation, assumptions about the proximal/distal flow conditions, wall compliance and blood viscosity, and numerical schemes used to solve the governing equations (78). The main challenge in eliminating the errors of either modality is in that there is no gold standard or true velocity distribution that can be used to correct the imaging or modeling results. However, these modalities have different sources of error, so it should be possible to reconstruct the underlying velocity field by maintaining the flow features that are common to both data sets.

Data assimilation algorithms and methods are an active area of research. Rispoli et al. (156) proposed using 4D flow MRI data as a regularization step in a CFD solver to correct the numerical solution. An established method of blending modeling predictions and actual measurements for a process evolving in time is the Kalman filter. Ensemble Kalman filtering has been demonstrated to improve patient-specific CFD simulations by calibrating outflow conditions prescribed to numerical solvers (157, 158). Alternatively, modal flow analysis can be used to eliminate image noise and increase the spatial resolution of measured velocities (159). An approach based on common mode decomposition can be applied to combine velocity fields obtained from multiple modalities, such as 4D flow MRI, CFD, and PIV. The modes that are common across these modalities are used for flow reconstruction, while the mismatched modes are assumed to represent errors due to assigned boundary conditions or image noise. Alternatively, the flow fields obtained from different modalities can be combined on the basis of estimates of the local uncertainty of each data set, yielding improved velocity distributions that can then be used to calculate relevant hemodynamic metrics.

A fashionable wave of deep learning approaches is not likely to entirely replace computational modeling; however, in addition to recognized capabilities in automatic generation of image-based geometries, deep learning has the potential to optimize patient-specific input parameters required for flow solvers. In such an approach, neural networks would process a large set of parameters in order to minimize the discrepancy between the numerical solution and available imaging data. Moreover, underresolved flow measurements obtained in vivo could be enhanced with Navier–Stokes-informed deep learning algorithms. Prior knowledge of the underlying principles of flow physics, such as the conservation of mass, momentum, and energy, can be used as a regularization in the training of deep learning networks, allowing them to be applied even if the quantity of training data is limited (160, 161). This novel approach may enable accurate flow reconstruction based on in vivo imaging, thus providing tools for reliable assessment of patient-specific hemodynamic metrics.

5. CONCLUSIONS

State-of-the-art medical imaging and modeling methods enable patient-specific flow quantification in cerebral aneurysms; however, the translational value of acquired hemodynamic data remains limited. Data assimilation techniques offer capabilities for merging in vivo imaging and numerical modeling data or reconstructing imaging data to enhance the resulting flow fields and ensure their adherence to underlying flow physics. Developing image-based models accounting for complex interplay of hemodynamics, arterial wall mechanics, and vascular biology and distilling modeling data into clinically relevant indices will facilitate the application of quantitative analysis to diagnostics and treatment of cerebral aneurysms. Multicenter longitudinal studies in which multivariate statistical analyses are based on aneurysm location and morphology, hemodynamic factors, imaged wall inflammation, and patient medical history are required to develop comprehensive predictive models for UIA risk assessment.