QM/MM Investigation of the Spectroscopic Properties of the Fluorophore of Bacterial Luciferase

Abstract

We employ replica-exchange molecular dynamics (REMD) and a hybrid ab initio multiconfigurational quantum mechanics/molecular mechanics (QM/MM) approach to model the absorption and fluorescence properties of bacterial luciferin-luciferase. Specifically, we employ complete active space perturbation theory (CASPT2) and study the effect of active space, basis set, and IPEA shift on the computed energies. We discuss the effect of the protein environment on the fluorophore’s excited-state potential energy surface and the role that the protein plays in enhancing the fluorescence quantum yield in bacterial bioluminescence.

Graphical Abstract

Bioluminescent enzymes such as bacterial luciferases are used as gene reporters in cell culture and small-animal imaging.¹ They have also become important tools for life science research and drug discovery.² Bacterial luciferases are found naturally in bioluminescent bacteria.³ Their fluorescence wavelength is typically in the range 460–500 nm, with a peak near 490 nm⁴ and a fluorescent quantum yield ranging from 0.1 to 0.3.⁵ There is strong experimental⁶ and computational⁷ evidence implicating the excited state of intermediate 2 (see Scheme 1) in the fluorescence.

Scheme 1. Structure of the Isoalloxazine Moiety in FMNH₂ (1), FMNHOH (2), and FMN (3); (B) Proposed Mechanism of Bioluminescence in Bacterial Luciferase^a.

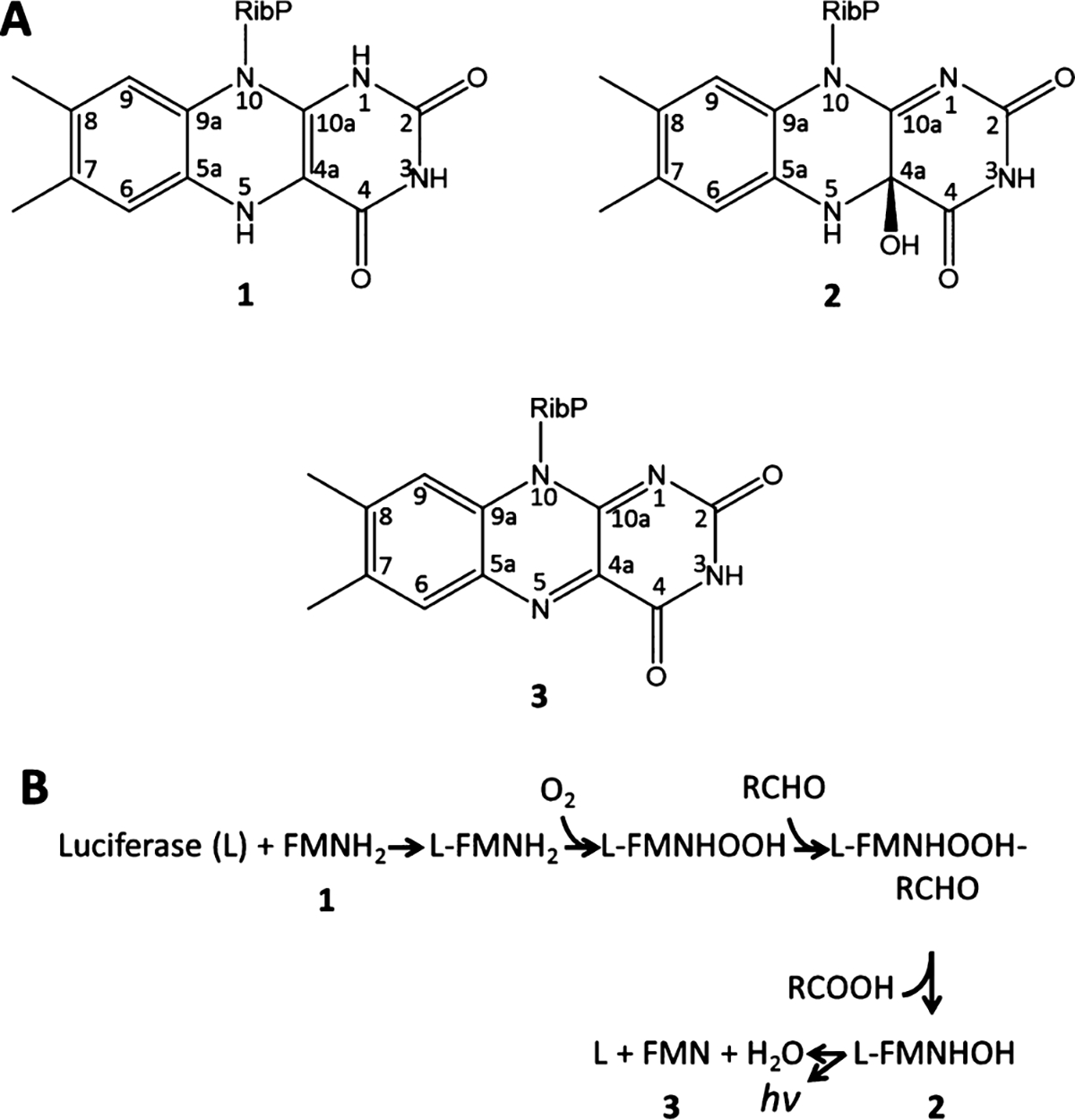
. (A) ^aAdapted with permission from ref 9. Copyright 2004 American Chemical Society.

Bacterial luciferases generate bioluminescence by catalyzing a reaction involving the reduced flavin mononucleotide (FMNH₂; 1 in Scheme 1), O₂, and an aliphatic aldehyde. The reaction produces the corresponding aliphatic carboxylic acid, flavin mononucleotide (FMN, 3), and blue-green light (~490 nm). As reported in Scheme 1B, the reaction proceeds via three intermediates formed by flavin derivatives inside the luciferase binding pocket. First, the bacterial luciferase apoprotein binds with FMNH₂ (1), which rapidly reacts with atmospheric oxygen to give the corresponding oxidized intermediate (FMNHOOH). Another reductive enzyme then provides a long-chain aldehyde (by reducing a carboxylic acid)⁸ which reacts with FMNHOOH to give a peroxyhemiacetal intermediate. This intermediate decomposes to generate the 4a-hydroxy flavin intermediate FMNHOH (2 in Scheme 1A) in an electronically excited state. Finally, 2 undergoes radiative decay to the ground state, yielding FMN (3) as a final product.

Although intermediate 2 displays weak fluorescence in solution,¹⁰ it exhibits strong fluorescence when bound to the enzymatic binding pocket.¹¹ We previously investigated the fluorescence properties of the N(5)-alkylated derivative of 2 in a joint computational and experimental study.¹² The results (see Figure S1 in the Supporting Information) indicated that a large distortion of the terminal pyrimidine ring of the molecule leads to an excited-state deactivation via a conical intersection (CI)-mediated internal conversion. When the geometric deformation of the molecule was inhibited by some constraint (e.g., in a frozen solvent that restrains the pyrimidine ring distortion), an enhanced fluorescence emission was observed. It is assumed that the surrounding environment within the enzymatic binding pocket can behave in the same manner as a frozen solvent. In fact, the crystal structure of the Vibrio harveyi luciferase FMN complex (PDB ID: 3FGC)¹³ reveals that the fluorophore is hosted in a tight protein cavity.

To investigate the fluorescent properties of this system, we employ a hybrid quantum mechanical/molecular mechanical (QM/MM) model constructed from the crystal structure.

METHODOLOGY

Preparing the Protein Model.

The crystal structure of the luciferase/FMN complex (PDB ID 3FGC) was used as a starting point for the simulations.¹³ Specifically, we started with the coordinates of heterodimer 2, since the mobile loop from heterodimer 2 had stronger electron density and therefore higher resolution.

Bacterial luciferase comprises two homologous subunits, designated α and β, both of which assume the TIM barrel fold.¹⁴ Although the β-subunit is required for activity, the catalytic site resides exclusively in the α-subunit.¹⁵ The crystallographic structure of the complex contains these two β/α-heterodimers,¹³ with the α-subunit binding the FMN. The primary difference between the two subunits corresponds to a secondary structural element comprising two antiparallel β-strands near the interface with the β-subunit.¹⁶ For computational efficiency, only the α-chain was included in the simulations. The residues between sequence positions 283 and 291 not observed in the crystal structure were added using homology-based loop modeling (ModLoop).¹⁷ This disordered segment (residues 283–291) is directly adjacent to the FMN-binding cavity, so to build an accurate QM/MM model would require this segment to be modeled carefully. Indeed, as observed by Campbell et al.,¹⁸ the presence of the fluorophore has a significant influence on the conformation of this loop. Therefore, we chose to model these large loop movements in the α-subunit in the presence of the fluorophore (2) within the catalytic binding site.

To generate a model of the fluorophore-bound luciferase, we first perform a gas-phase energy minimization of 2 in the trans configuration.^7a Next, FMN from the crystal structure was replaced by this optimized structure of 2. The entire system was then solvated with explicit water molecules and energy minimized. The movements of residues within the subunit interface were weakly constrained using a harmonic potential to prevent complete unfolding of the α-subunit over the course of simulation. No constraints were applied to the FMNHOH or the mobile loop.

Replica-Exchange Molecular Dynamics (REMD).

REMD differs from standard molecular dynamics (MD) due to the parallel nature of the simulation.¹⁹ Instead of a single simulation at a single temperature, multiple parallel simulations are conducted over a range of temperatures. Periodically, conformations of simulation replicas running at different temperatures are exchanged according to a Monte Carlo procedure. As a result, the conformational space sampled over the simulation is substantially increased. We employed REMD simulations to obtain better sampling of loop conformations. MD and REMD simulations were executed using the GROMACS 4.6.3 program²⁰ using the AMBER99SB force field.²¹ The loop and all atoms within 6 Å of any atom of the loop were allowed to move during REMD, while the rest was kept fixed. The trajectories obtained and the operative conditions are reported in the Supporting Information.

The cluster analysis was accomplished using the single linkage algorithm as implemented in the GROMACS 4.6.3²⁰ g_cluster routine. The five most populated clusters (Figure 1) were obtained by statistical analysis of the REMD trajectory. The setup of the procedure employed 0.1 nm as the RMSD cutoff option to obtain similar structures within the ensembles, and subsequently, the structure with the smallest average distance from the others in each cluster (populated by a minimum of 500 different states) was selected.

Figure 1.

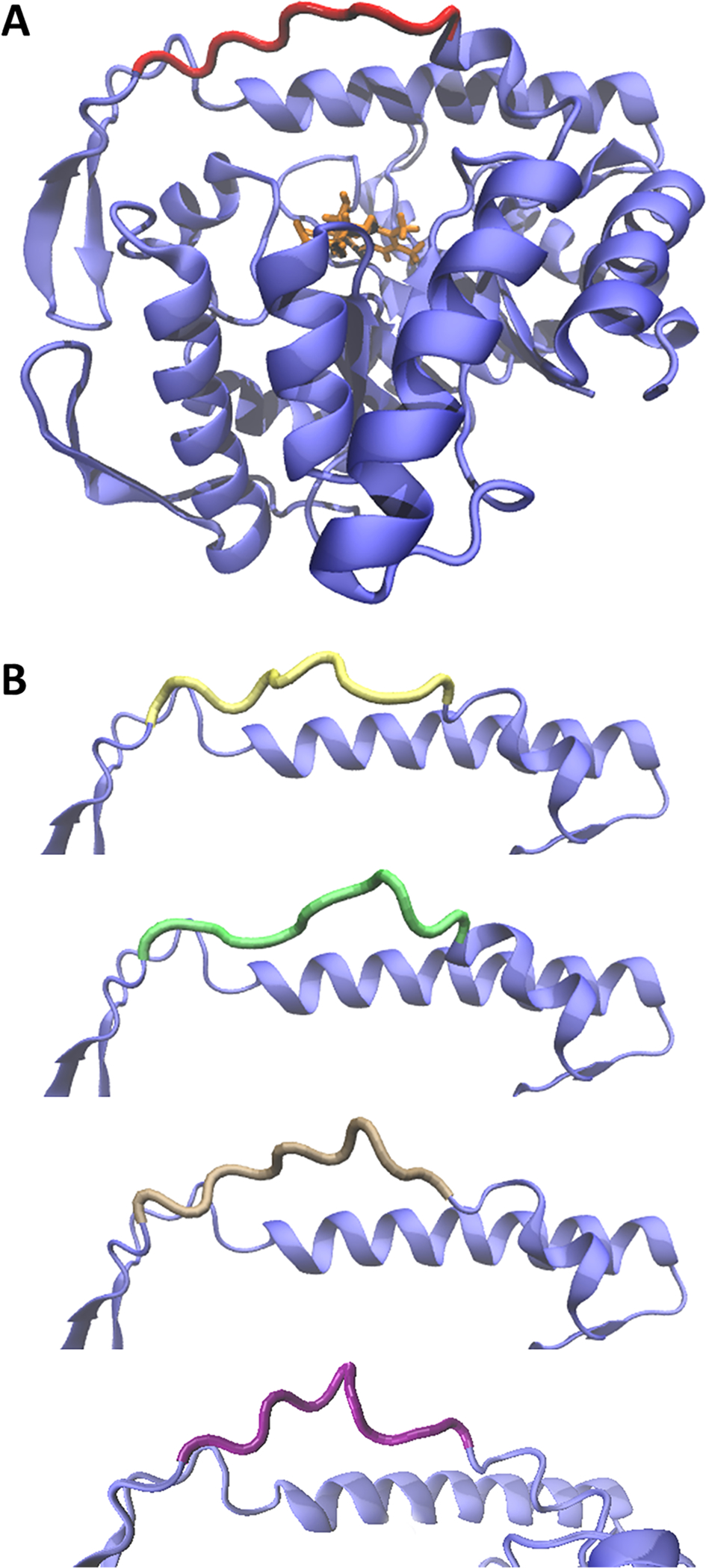
(A) The structure obtained from REMD simulations of the α-subunit of bacterial luciferase in the presence of the emitting intermediate FMNHOH (2, in orange). The structure of the proximal mobile loop was extrapolated from the cluster analysis (in red). (B) Comparison of the conformations of the mobile loops obtained from the other four most populated clusters.

In Figure 1A, the entire α-subunit/FMNHOH complex is shown. The final structure of the mobile loop (in red), which was subsequently used for QM/MM calculations, was chosen as the average of the most populated cluster. In Figure 1B, the structures of the other four major configurations obtained by the clustering analysis are displayed in different colors. Each one of those configurations was extrapolated from a cluster of structures collected in the presence of the ligand. A comparison of the RMSD values for each representation suggests that the closed conformation of the mobile loop is predominant within the ensembles.

QM/MM Calculations.

Simulating the spectroscopy of luciferin-luciferase requires the use of a quantum chemical method capable of describing both the ground and excited states of FMNHOH on an equal footing. This means having a balanced description of static and dynamical electron correlation for both states. We employ the complete active space self-consistent field (CASSCF)²² for geometry optimizations and complete active space second order perturbation theory (CASPT2)²³ for correcting the electronic energies of the CASSCF-optimized structures.

This CASPT2//CASSCF protocol is well-established for photochemistry and photobiology.²⁴ However, while it has been widely used for rhodopsins and other photoreceptor proteins, far fewer studies have applied it to model bacterial luciferase fluorescence. It is therefore not immediately clear which active space and basis set to use. Similarly, an ionization potential electron affinity (IPEA) shift of 0.25 is often applied to improve CASPT2 excitation energy calculations,²⁵ but the use of IPEA and the magnitude of the IPEA shift that should be used has been discussed multiple times in the literature.²⁶ We therefore compute the absorption wavelength and fluorescence wavelength of FMNHOH using several different active spaces, basis sets, and testing both IPEA = 0 and IPEA = 0.25.

Note that the full π active space of 2 would comprise 18 electrons in 15 orbitals. However, we might expect that a reasonable reduction in active space would be the removal of two π and π* orbitals from the active space, resulting in a 14-electron, 11-orbital active space. This is the active space used in our reference solvent-phase study.¹²

While relative energies (e.g., across a series of similar structures or protein mutants) are typically not very sensitive to the details of the CASPT2//CASSCF method used, absolute energy differences(such as computed absorption and fluorescence wavelengths) are sensitive to details such as the active space, basis set, and IPEA shift.²⁴ We will test both the 18,15 and 14,11 active spaces. We will also test the effect of using single-state vs multistate CASPT2, the effect of the IPEA shift set to 0 vs 0.25, and the effect of increasing the basis set from 6–31G* to ANO-L-VTZP.

Finally, we note that there is a cysteine (Cys106) residue that is near the pyrimidine ring of the fluorophore (within ca. 2.7 Å). This cysteine is highly conserved in many proteins associated with the bacterial luciferase-like superfamily.²⁷ Site-directed mutagenesis studies of the luciferase have shown that mutation of the polar thiol group of cysteine to the nonpolar isopropyl side chain of valine destabilizes the FMNHOH emitting intermediate,²⁸ indicating that the electrostatic effect of cysteine may also be important for modulating the emission of the fluorophore. Therefore, we have generated two QM/MM models: one where the −CH₂SH atoms of Cys106 are treated at the QM level of theory (Figure 2) and one where the Cys106 is entirely treated at the MM level of theory.

Figure 2.

Schematic representation of the QM/MM setup including Cys106 in the QM subsection. The colored ball-and-stick model represents the QM subsystem, containing the lumiflavin group of FMNHOH (2) and the −CH₂SH part of Cys106. The gray ribbons in the background represent the protein environment. The hydrogen link atoms, which cap the vacancies at the frontier of QM/MM regions, are highlighted in pink. Another model, that places the entirety of Cys106 in the MM region, is otherwise identical.

Optimizations and minimum energy path (MEP) calculations for FMNHOH were performed at the three-root state-averaged CASSCF level of theory²² with a 14,11 active space and 6–31G* basis set (see the Supporting Information for more details on the active space). The MEPs both with and without the cysteine in the QM subsystem were computed with the intrinsic reaction coordinate method employing a step constraint of 0.03 b·amu^1/2 for the first eight steps, followed by 0.05 b·amu^1/2 for the remainder of the MEP. Single-point CASPT2 calculations²³ were then performed for stationary points and for each point along the MEP path. The Mulliken charges and oscillator strengths reported are computed at the CASPT2 level of theory. All QM and QM/MM calculations were performed with Molcas 7.8 interfaced with Tinker.²⁹ MM atoms were treated using the AMBER99SB force field.²¹ More details regarding the computational protocol and the QM/MM model are provided in the Supporting Information.

RESULTS AND DISCUSSION

Luciferase-bound FMNHOH (2) was first optimized in the ground state (GS). The structure and relevant bond lengths and dihedrals are shown in Figure 3, top left. We also optimized the structure on the first singlet excited state, to obtain the excited-state minimum (EM) from which fluorescence occurs.

Figure 3.

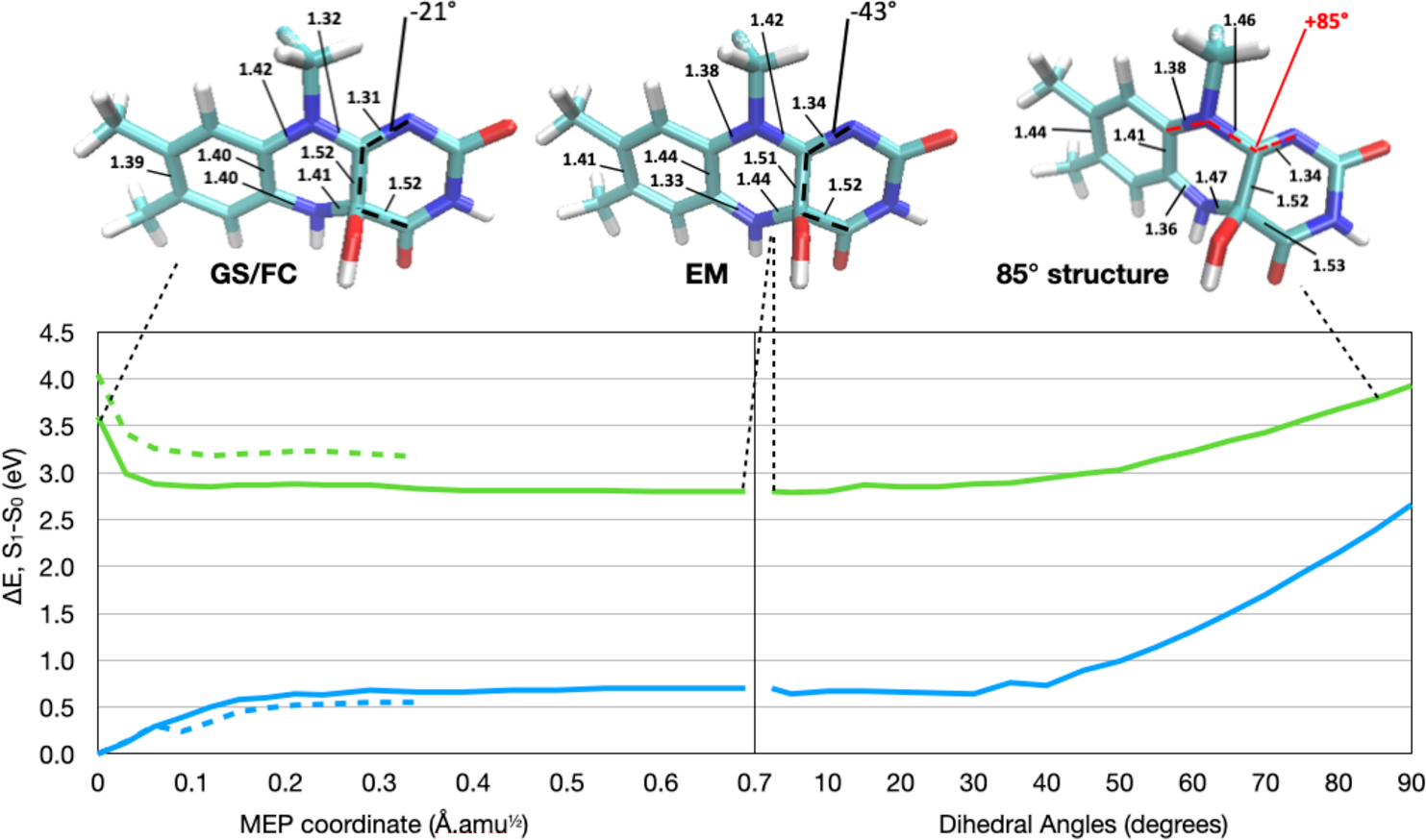
Left: CASPT2//CASSCF S₀ (blue) and S1 (green) energy profiles along the MEP connecting the FC to the energy minimum (EM). Calculations obtained with Cys106 in the QM region are shown as solid lines, while calculations with Cys106 in the MM region are shown as dashed lines. Right: The results of the C9a–N10–C10a–N1 dihedral relaxed scan, performed in intervals of 5° starting from the EM. The energy gap between S₀ and S₁ decreases from 2.1 eV at the EM to 1.3 eV at 90°. Top: Structures of the GS/FC, EM, and 85° constrained structure. All bond lengths that change by more than 0.02 Å during the MEP are labeled for the structures. We also indicate the C4–C4a bond length, which changes minimally. Moreover, we label the C4–C4a–C10a–N1 dihedral, representing out-of-plane distortion of the fluorophore. For clarity, the Cys106 side chain is not included in the structure representations.

At the GS and EM structures, respectively, we computed the vertical excitation wavelength (λ_abs) and fluorescence wavelength (λ_em) using different CASPT2 approaches. The data is shown in Table 1.

Table 1.

Computed Absorption and Emission Wavelengths with Different CASPT2 Methods and Basis Sets

SS or MS	active space	IPEA	basis set	λabs, eV (nm)	λem, eV (nm)
SS	14,11	0	6–31G*	3.67 (338)	2.20 (564)
MS	14,11	0	6–31G*	3.71 (334)	2.34 (530)
SS	14,11	0.25	6–31G*	4.13 (300)	2.54 (488)
MS	14,11	0.25	6–31G*	4.16 (298)	2.67 (464)
SS	14,11	0	ANO-L-VDZP	3.50 (354)	2.06 (603)
MS	14,11	0	ANO-L-VDZP	3.57 (347)	2.29 (542)
SS	14,11	0.25	ANO-L-VDZP	4.00 (310)	2.43 (511)
MS	14,11	0.25	ANO-L-VDZP	4.05 (306)	2.62 (474)
SS	14,11	0	ANO-L-VTZP	3.42 (362)	2.01 (616)
MS	14,11	0	ANO-L-VTZP	3.49 (355)	2.27 (547)
SS	14,11	0.25	ANO-L-VTZP	3.94 (314)	2.40 (517)
MS	14,11	0.25	ANO-L-VTZP	3.99 (311)	2.60 (476)
SS	18,15	0	6–31G*	3.93 (316)	2.08 (595)
MS	18,15	0	6–31G*	3.36 (369)	2.08 (597)
SS	18,15	0.25	6–31G*	4.35 (285)	2.37 (524)
MS	18,15	0.25	6–31G*	3.87 (321)	2.36 (525)
SS	18,15	0	ANO-L-VDZP	3.74(331)a	1.95(636)a
MS	18,15	0	ANO-L-VDZP	3.12(398)a	1.94(638)a
SS	18,15	0.25	ANO-L-VDZP	4.21(295)a	2.25(551)a
MS	18,15	0.25	ANO-L-VDZP	3.68(337)a	2.25(551)a
MS	18,15	0.25	ANO-L-VTZP	3.62(342)b	2.24(554)b
Experiment				(∼360)b	(∼490)d

^aThis calculation was performed with Cholesky decomposition to reduce computational cost.³⁰

^bThis data is obtained using an extrapolation from the effect of triple-ζ relative to double-ζ for the 14,11 active space result.

^cReference 4.

^dReference 9.

A number of trends are clear in the computed wavelengths. Specifically, we find the following:

• The IPEA shift of 0.25 invariably blue-shifts the absorption and fluorescence wavelengths (by up to 100 nm). The IPEA shift has originally been introduced to remedy a systematic underestimation of excitation energies computed using the CASPT2 method,²⁵ and here, we find that the IPEA shift has a similar effect as its originally intended use. For instance, in rhodopsin models, it has been shown that using no IPEA shift benefits from a cancelation of errors in combination with smaller basis sets and that IPEA = 0.25 works well in combination with large basis sets.^26a More recently, Gonzalez and co-workers indicated that the IPEA shift simply is a way to recover missing dynamical electron correlation.^26b Therefore, in this case, the IPEA shift may be considered a computationally inexpensive way to approximately account for missing dynamical electron correlation.

• Increasing the basis set invariably red-shifts the absorption and fluorescence wavelengths. The change from 6–31G* to ANO-L-VDZP is usually more substantial (8–39 nm, depending on method) than the change from ANO-L-VDZP to ANO-L-VTZP (2–13 nm). Again, this is consistent with results found for rhodopsin models^26a and is likely due to the excited state being more diffuse than the ground state.

• The red-shift from the basis set increase is not enough to offset the effect of the blue-shift from the IPEA shift. Therefore, unlike for other biological chromophores where this method provides a favorable cancelation of errors,^26a the IPEA = 0 and 6–31G* basis set combination does not provide quantitative results in this system.

• It is difficult to predict the effect of moving from single-state (SS) CASPT2 to multistate (MS) CASPT2. This sometimes has no effect at all and sometimes may have a large effect (as large as 67 nm). Interestingly, with the 14,11 active space, the absorption changes only slightly while the fluorescence wavelength changes a lot more when using SS vs MS CASPT2. However, with the 18,15 active space, the opposite is observed; the SS and MS CASPT2 are in good agreement for the fluorescence, while they are very different for the absorption. This, likely, stems from state crossing occurring between higher states that may change the character of the third excited state used in state averaging. Indeed, SS and MS CASPT2 do suffer from artifacts near state crossings (see refs 26a and 31). Methods to address this have been recently developed but have not been tested in this work.

Due to the computational cost of running MS-CASPT2-(18,15) with the ANO-L-VTZP, we obtained an estimate by extrapolating other data. Specifically, the basis set effect of moving from ANO-L-VDZP to ANO-L-VTZP for MS-CASPT2(14,11)/ IPEA = 0.25 was used to correct the MS-CASPT2(18,15)/IPEA = 0.25 ANO-L-VDZP data. These resulting computed vertical absorption and emission wavelengths are not in quantitative agreement with experiment, but they are within 0.3 eV. Specifically, the vertical emission wavelength computed at the EM (2.24 eV, or 554 nm) is red-shifted with respect to the experimentally observed wavelength in the luciferase of Vibrio harveyi (2.53 eV, 490 nm),⁹ while, the computed absorption wavelength (3.62 eV, 342 nm) is blue-shifted relative to the experimentally determined absorption spectrum in Vibrio harveyi (360 nm).⁴ Our results are similar to calculations by Luo et al. for this system.^7b We also note that calculations of the absorption and emission maxima of reduced flavin have also been red-shifted to a similar extent.³² Indeed, in both oxidized and reduced flavins, it has also been shown that vertical excitation and emission energies are often shifted with respect to experiments, with ref 32 in particular pointing to the need for computing adiabatic excitation energies and Franck–Condon factors to get a better agreement between computations and experimental λ_max for these systems. Our computed adiabatic excitation energy at the MS-CASPT2(18,15)/IPEA = 0.25/ANO-L-VDZP level of theory is 2.82 eV (440 nm). Notice that the experimental absorption and emission wavelengths lie somewhere between the computed vertical and adiabatic excitation energies. We also cannot rule out that other details of the QM/MM model, such as the polarizability of the MM subsystem, may be important to take into account.³³

The oscillator strength at the GS structure is 0.8. At the EM, it decreases to 0.6. Both strengths are indicative of strong absorption and fluorescence intensities, consistent with a strong radiative S₁ → S₀ decay (i.e., fluorescence). The radiative lifetime can be roughly estimated from the oscillator strength (in the absence of competing photophysical processes) using a simplified version of the Strickler–Berg equation³⁴

$${1/{\tau }^0}_{\text{f}}\approx {0.7{\tilde{v}}_0}^{2}f$$

where τ⁰_f is the fluorescence lifetime, v₀ is the adiabatic excitation in units of cm⁻¹, and f is the oscillator strength. If we assume that the adiabatic absorption corresponds to a wavelength of ~500 nm, this yields a fluorescence lifetime of ~6 ns, in good agreement with the measured fluorescence lifetime of ~10 ns.³⁵ This indicates that competing processes that may quench fluorescence, such as internal conversion or intersystem crossing, are minimized in the protein, which is different from the behavior of the same system in solution where internal conversion is efficient.¹²

Next, we connect the vertical excited GS structure, corresponding to the Franck–Condon (FC) point, to the EM, as done in ref 12. This is done using a minimum energy path (MEP) starting from the FC structure. The S₀ and S₁ energy profiles along the MEP are shown in Figure 3. The purpose of the MEP is to explore the excited-state potential energy surface of FMNHOH near the FC and EM region and to compare with the potential energy surface in Figure S1 from the Supporting Information.¹²

Mutagenesis studies on bacterial luciferase have shown that mutation of Cys106 destabilizes the FMNHOH emitting intermediate.²⁸ Therefore, to investigate a possible role of the Cys106 side chain, we compute this MEP both in the presence and absence of the cysteine in the QM region. Structures along the MEP were obtained by CASSCF geometry optimization, while their single-point energies were computed at the CASPT2 level of theory. In both MEP calculations (with and without the QM Cys106), we use SS-CASPT2(14,11)/IPEA = 0/6–31G*, since this method benefits from some cancelation of error, is affordable, and still gives us an idea about the potential energy surface and the modes involved in reaching the EM.

Both the calculations with and without the Cys106 in the QM region indicate that there is no CI in the vicinity of the FC and EM regions of the S1 potential energy surface. Indeed, at the EM, the S₀–S₁ energy gap is over 2 eV. This is in contrast to calculations on the same fluorophore in solution, where the MEP calculations lead to a CI instead of an EM, indicating relatively efficient internal conversion in solution (ref 12 and Figure S1). The following changes upon including Cys106 in the QM region (see Figure 3 left):

• The first singlet excited state decreases in energy relative to the ground state.

• The excited-state potential becomes slightly flatter. Indeed, while the MEP with Cys106 in the QM region shows a decrease in energy of 0.81 eV between the FC and EM points on the excited state, the calculation with Cys106 in the MM region shows a larger decrease, of 0.87 eV. It also takes additional MEP points for the Cys106 in QM calculation to reach the EM.

The second point indicates that the Cys106 may play a role in modifying the shape of the S₁ potential energy surface. We speculate that this affects vibronic coupling between the S₁ and S₀ states and may explain why mutation of Cys106 affects the fluorescence of bacterial luciferase.²⁸

We also note that including Cys106 in the QM region further worsens the agreement of the absorption and fluorescence wavelengths with experiment. However, including only one polarizing amino acid in the QM region without including other polar amino acids in different positions is biasing the calculation, which may explain the bad agreement (almost 100 nm red-shifted) with respect to the experiment.

The analysis of the MEP (Figure 3) shows that 2 follows multiple molecular relaxation modes to reach the EM. First, a bond length alternation (BLA) inversion occurs within the isoalloxazine ring, where alternating double and single bonds become elongated and shortened, respectively. Specifically, the N10–C10a bond evolves from having double bond character (1.32 Å) on S₀ to a single bond (1.42 Å) on S₁. On the other hand, the adjacent N10–C9a bond changes from a single bond on S₀ (1.42 Å) to gain double-bond character (1.38 Å). This is a fast relaxation typically associated with the π,π* excitation of π-conjugated systems.³⁶ A similar excited-state relaxation was reported for lumiflavin using computations of comparable quality.³⁷ At the same time, since the out-of-plane deformation of the pyrimidine ring with respect to the original flavin plane does not occur in the protein, a different geometrical distortion becomes more prominent here instead. More specifically, following the S₁ energy profile reported in Figure 3, we note an increase in the pyramidalization of carbon C4a indicating an increased tendency to adopt a tetrahedral geometry. Note that C4a is originally sp2-hybridized in FMN but is sp3-hybridized in FMNHOH, where the C4a–OH bond in FMNHOH is nearly perpendicular to the isoalloxazine plane. According to these observations, the calculations revealed a change of the N1–C10a–C4a–C4 dihedral angle from −21° at the FC structure to −43° at the energy minimum on S₁.

Other changes in bond lengths are directly consistent with the BLA previously described;¹² the C4a–N5 bond becomes more elongated (1.41 to 1.44 Å), while the adjacent N5–C5a reduces its length (1.40 to 1.33 Å). These bond stretching modes are coupled with the pyramidalization at C4a. As a result of these structural changes, part of the electronic charge on N5 is transferred to the contiguous benzene ring, resulting in a shorter N5–C5a bond. The N5 lone pair electrons do not conjugate with the aromatic ring because they still lie in an orthogonal plane (Figure S7 of the Supporting Information).

Such a coupling between the charge transfer and excited-state distortion is similar to that observed in other π-conjugated biological chromophores, such as the retinal protonated Schiff base.³⁶ One explanation for the increased pyramidalization of C4a is the propensity of the fluorophore to distort out of plane, as observed in our previous study for the isolated fluorophore.¹² In the protein cavity, since the large out-of-plane distortion is prevented by the tight protein binding cavity, the molecule instead relaxes through a localized pyramidalization.

An analysis of the Mulliken charges along the MEP is reported in the Supporting Information. As anticipated earlier, a charge transfer process accompanies the S₁ geometrical relaxation of 2. The S₀ → S₁ vertical excitation gives a small charge transfer of ca. −0.1 e⁻ from the benzene and pyrazine rings to the pyrimidine ring, but as the molecule relaxes on the excited state, this charge transfer magnitude increases to −0.3 e⁻.

To better understand the photophysics and spectroscopy of this bacterial luciferase, it is important to analyze both the steric and electrostatic effects of the protein on the FMNHOH fluorophore. A Poisson–Boltzmann analysis³⁸ that was performed during the PROPKA (pH 7) determination of side-chain ionization states indicates that the cavity region near the pyrimidine moiety has a negative electrostatic potential. These electrostatic effects have differential effects on the different states and geometries of FMNHOH. For example, since excitation is accompanied by a transfer of negative charge to the pyrimidine ring (fast BLA relaxation), the electrostatics of the proximal residues would play a relevant role to stabilize the emitting state of the intermediate, therefore increasing both the S₁ lifetime and fluorescence quantum yield.

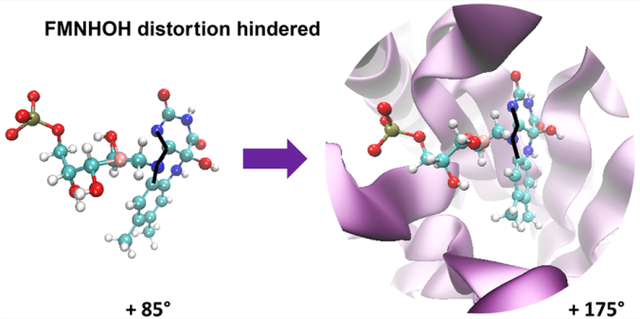
Since the fluorescence of FMNHOH is bright and long-lived, that means that the CI observed in the gas-phase study¹² (reached by distortion of the C9a–N10–C10a–N1 dihedral in Figure S1) must be inaccessible in the protein. In an attempt to map the energy profile connecting the EM to the CI in the protein, we performed a relaxed scan to mimic the same geometrical distortion within the protein binding pocket by constraining the C9a–N10–C10a–N1 up to a 90° out-of-plane distortion. The resulting potential energy scan (shown on the right side of Figure 3) has a very different shape compared to the gas-phase calculation.¹² Specifically, as expected, the geometrical distortions result in an increase rather than a decrease in the potential energy in the presence of the protein. No CI is observed in the protein, even when the pyrimidine ring is constrained to be 90° with respect to the rest of the fluorophore. This is in contrast to the solution phase where the same deformation results in easy access to a low-lying CI. The same CI in the protein is sloped and must be at least 1 eV above the EM (Figure 3, right). This is largely due to the steric effect of the binding pocket, as hypothesized in ref 12, which constrains the fluorophore in a planar configuration and maximizes the fluorescent quantum yield of the EM.

In conclusion, this work computationally investigates the spectroscopy and photophysics of the FMNHOH fluorophore of bacterial luciferase. It is found that the protein blocks an internal conversion channel that was accessible in solution by significantly modifying the shape of the excited-state potential energy surface of the fluorophore. By comparing different QM methods, we test the ability of CASPT2//CASSCF to model the spectroscopic properties of the protein-bound flavin derivative and provide additional insight into the effect of the protein on the fluorophore’s energetics. These effects stabilize the emitting state of the fluorophore to maximize its fluorescence. We hypothesize that steric effects play the main role in enhancing fluorescence by keeping the chromophore in its planar fluorescent state. We have also studied the effect of placing one of the nearby cysteine side chains, Cys106, in the QM region. This test indicates that it is unlikely that the Cys106 plays a role in controlling access to the CI, but it may play a role in modulating the curvature of the excited-state potential energy surface. Further studies are needed to understand how the electrostatic environment around the fluorophore modulates its fluorescence properties.

The investigations of the effect of protein environment on the fluorescent properties of FMNHOH may lead to the further development of FMNHOH as a tool to probe dynamics or rigidity of protein active sites during processes such as catalysis, similar to studies with FMN.³⁹ Furthermore, the insight revealed in this work may aid in the synthesis of novel flavin adducts as novel fluorescent probes.⁴⁰