SUMMARY
Gastrulation movements in all animal embryos start with regulated deformations of patterned epithelial sheets, which are driven by cell divisions, cell shape changes, and cell intercalations. Each of these behaviors has been associated with distinct aspects of gastrulation1–4 and has been a subject of intense research using genetic, cell biological, and more recently, biophysical approaches.5–14 Most of these studies, however, focus either on cellular processes driving gastrulation or on large-scale tissue deformations.15–23 Recent advances in microscopy and image processing create a unique opportunity for integrating these complementary viewpoints.24–28 Here, we take a step toward bridging these complementary strategies and deconstruct the early stages of gastrulation in the entire Drosophila embryo. Our approach relies on an integrated computational framework for cell segmentation and tracking and on efficient algorithms for event detection. The detected events are then mapped back onto the blastoderm shell, providing an intuitive visual means to examine complex cellular activity patterns within the context of their initial anatomic domains. By analyzing these maps, we identified that the loss of nearly half of surface cells to invaginations is compensated primarily by transient mitotic rounding. In addition, by analyzing mapped cell intercalation events, we derived direct quantitative relations between intercalation frequency and the rate of axis elongation. This work is setting the stage for systems-level dissection of a pivotal step in animal development.
In brief
Stern et al. present the first whole-embryo single-cell morphogenetic atlas of cell behaviors driving Drosophila gastrulation. Its analysis reveals that the massive loss of surface epithelium to invaginations is compensated mainly by transient mitotic rounding. Direct relations between intercalation frequency and tissue elongation are quantified.
RESULTS AND DISCUSSION
Description of algorithms for whole-embryo cell segmentation and tracking and cell invagination mapping
Our strategy for deconstructing gastrulation has two main ingredients. The first ingredient is an accurate and efficient approach to segmentation and tracking of cells located on the external surface of the embryo (Figure 1A; Videos S1, S2, and S3). This process starts by forming a two-dimensional (2D) Mercator projection of the apical side of the epithelium sheet for each time point.29 Next, the cells in the projection of the first time point are segmented and assigned unique track ID.30 Cell boundaries and track IDs are then propagated iteratively and automatically over time. This is done by first deforming each projected image to accurately match the position of each cell with the same cell at the next time point, using Maxwell’s Demons algorithm.31 Once cell positions are matched, cell boundaries and track IDs are copied to the next time point, and then fine-tuned using the watershed transformation.32 Lastly, the segmented and tracked 2D projection at each time point is used to generate a 3D polygonal mesh that reveals the apical surfaces of the cells and provides an in toto map of cell-cell adjacencies.33 We optimized each step of this pipeline, enabling it to carry out ~1 million reliable single-cell segmentations in a typical light-sheet imaging dataset from a gastrulating embryo (Figures S1A–S1G).
Figure 1. A pipeline for whole-embryo cell segmentation and tracking and cell invagination mapping.
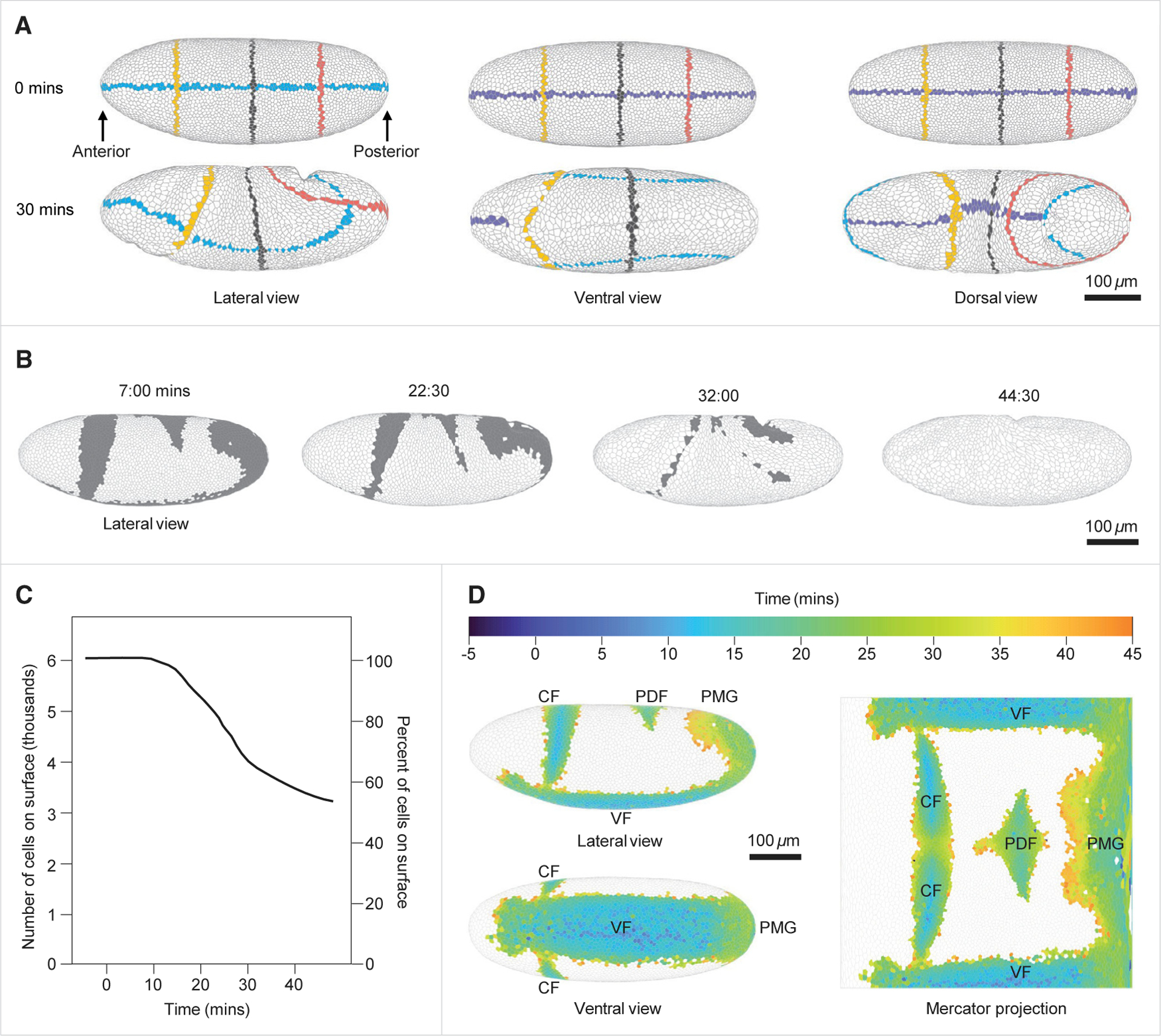
(A) Demonstration of whole-embryo single-cell segmentation and tracking. Lateral, ventral, and dorsal views of the 3D polygonal mesh at 0 and 30 min. Cells intersecting with the mid-coronal plane, the mid-sagittal plane, and three transverse planes have been distinctly colored to demonstrate cell tracking and to reveal how the embryo deforms over time.
(B) Lateral view of the embryo at four time points showing cells that will have invaginated by the end of the movie (gray) and cells that remain on the surface through this time period (white).
(C) Quantification of the number and percent of cells (left and right vertical axes, respectively) remaining on the surface of the embryo over time.
(D) Left: projection of cells undergoing invagination during the first 45 min of gastrulation over the 3D blastoderm shell in lateral and ventral views. Right: Mercator projection of the invagination sites. Each cell is color-coded for the first time point in which it is no longer visible from the outside of the embryo. t = 0 was set as the beginning of apical constriction in the invaginating mesodermal cells.
CF, cephalic furrow; VF, ventral furrow; PDF, posterior dorsal fold; PMG, posterior midgut. Data are derived from embryo #1. See also Figures S1 and S4 and Videos S1, S2, and S3.
Automated detection of dynamic behaviors of single cells and cell groups is the second key ingredient of our strategy for deconstructing gastrulation. Given accurate information of cell volumes and areas, detection of single-cell behaviors (division, internalization, and columnar-to-squamous transition) is relatively straightforward. Large-scale detection of events involving cell groups, such as cell intercalations, is more demanding, both algorithmically and computationally. We used our recently published algorithm for searching dynamic cell behaviors, which is based on optimized graph exploration and multivariable time series matching.34 To illustrate the scale of detected events, in one of the analyzed live imaging datasets from an embryo that started with 6,085 cells in the blastoderm, we detected 2,808 cell invaginations, out of which 1,153 were in the ventral furrow, 582 in the cephalic furrow, 728 in the posterior midgut, and 345 in the posterior dorsal fold. In addition, we detected 1,110 cell divisions, 1,881 cell intercalations, and 176 columnar-to-squamous cell shape changes. The ability to extract all the events from the same embryo allowed us to generate a coherent description of the developmental process. To demonstrate this point, most of the results presented in the main text are based on data from one embryo, with the exception of cell divisions. Analysis of cell divisions was done on an embryo imaged at a later time period, to provide a broader description of mitotic cycle 14. Data from additional embryos are presented in Figures S2 and S3.
We illustrate our approach by focusing on one of the most striking aspects of Drosophila gastrulation. Specifically, spatially patterned cell invaginations result in progressive loss of almost 50% of all cells originally present on the surface of the blastoderm (Figures 1B and 1C). Accurate tracking allows us to map the participating cells to the early blastoderm, thereby providing a fate map for cell invagination (Figure 1D). This type of retrospective mapping will also be essential for analyzing how cell behaviors in the remaining regions of the embryo contribute to large-scale tissue deformations and compensate for cell invagination through spatially controlled intercalations, shape changes, and divisions.
Analysis of cell intercalation dynamics during germband extension
We start by focusing on the germband (GB), a domain of the embryo that converges and extends as a consequence of multiple cell intercalations. Most of these events involve cell quartets and proceed through the so-called T1 transition, in which two nonadjacent cells come together and split the “orthogonal” cell pair (Figure 2A).35 Another intercalary event involves more than four cells, and proceeds through a configuration where several contracting interfaces generate a so-called rosette state.36 We mapped the two bilaterally symmetric blastoderm primordia for the GB using our event detection algorithm to identify all T1s and rosettes during the first 45 min of gastrulation (Figures 2B and 2C).
Figure 2. Cell intercalation distribution and quantitative relation to axis elongation.
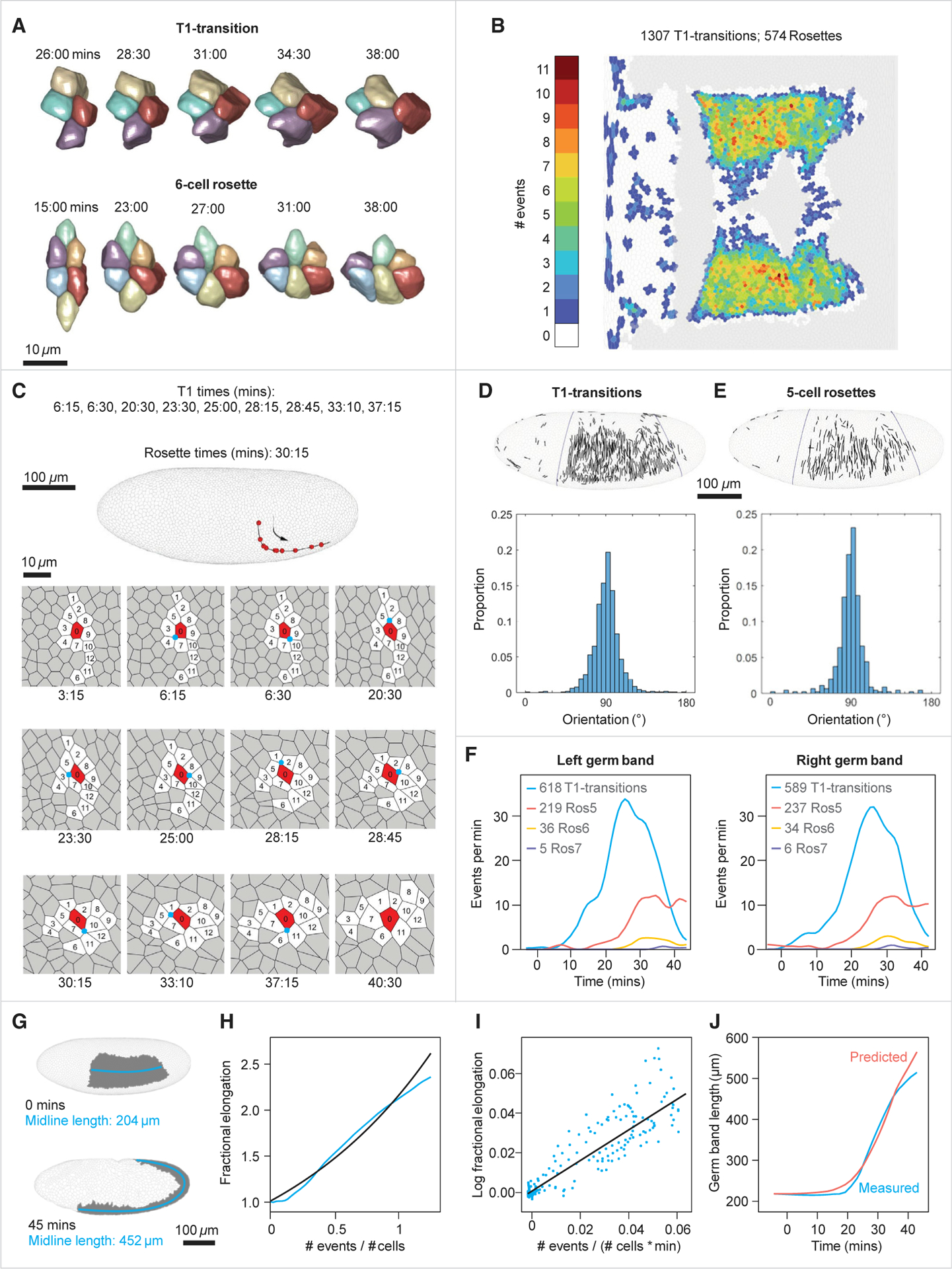
(A) Three-dimensional reconstructions of a representative T1-transition and a 6-cell rosette.
(B) Mercator projection showing the number of intercalary events in which a cell participates over the first 45 min of gastrulation (both T1s and rosettes).
(C) Top: a lateral view of the embryo showing the trajectory of a single cell that participates in 10 sequential intercalation events. Each red dot marks the position of the cell at the moment of an event. Bottom: segmented view of this cell with its neighbors throughout tissue elongation. The central vertex at each intercalation is marked by a cyan circle, and numbers indicate cell identities.
(D) Top: cells participating in each T1-transition have been mapped to the blastoderm and the centers of the two approaching cells joined by a straight line. Bottom: the distribution function of the angles made by these lines and the ventral midline of the embryo (blue; average ± SD = 91.3° ± 14.7°, n = 1,178).
(E) Top: cells participating in each 5-cell rosette have been mapped to the blastoderm, and the centers of the two most distant cells joined by a straight line. Bottom: the distribution function of the angles made by these lines and the ventral midline of the embryo (average ± SD = 89.81° ± 14.8°, n = 455).
(F) Comparison of the temporal frequencies of T1 transitions and 5-, 6-, and 7-cell rosettes between left and right sides of the embryo.
(G) Lateral view of the 3D surface of the embryo at 0 and 45 min, demonstrating convergence and extension of the germband (gray). The length of the germband is measured as the length of the midline (cyan).
(H) Comparison between the actual fractional elongation of the germband plotted as a function of the normalized cumulative number of events (cyan), and fractional elongation predicted by the model (black; see text).
(I) Linear regression of the mean-field model (black). Each dot (cyan) is the log fractional elongation of the germband over 1 min as a function of the normalized cumulative number of events during the same time period.
(J) Parametric plot of the time dependent germband length constructed based on the mean-field model and measured number of intercalary events. Blue, measured; red, predicted.
Data are derived from embryo #1. Data for three additional embryos are supplied in Figures S3C–S3F. See also Figures S1H–S1J.
Individual intercalary events will produce global changes in the shape of a primordium only if they share a common orientation. Oriented intercalations have been documented in small regions of the embryo,37 but previous studies could not track all events, especially as the extending GB rounds the posterior pole of the embryo. To examine orientational order, we mapped intercalary events back to blastoderm surface and represented their orientations as lines joining the centers of cells that are brought into contact by an intercalation event (Figures 2D, 2E, S1H–S1J, and S3C–S3F). Although individual intercalations within the GB occur at different times and in different positions, all are aligned with the overall convergence of the tissue and the dorsal ventral axis of the embryo. This global alignment argues that directionality of intercalary events is set already at the blastoderm stage.
Two different cells within the GB can undergo very different numbers of intercalary events; the number can be as low as one and as high as eleven (average ± SD = 4.18 ± 2.15; Figure 2C). In spite of this high variability at the single-cell level, the total numbers of events are very similar on the two sides of the same embryo (Figure 2F). This observation prompted us examine the dependence between the number of intercalations and global tissue elongation. By plotting the fractional tissue elongation versus the number of intercalations that have occurred by time t, we found a surprisingly simple dependence (Figures 2G and 2H). This behavior can be rationalized using a mean-field model whereby each neighbor exchange, a T1-transition or a rosette, has the same effect on tissue elongation, based on the fact that all events show directionality. Furthermore, we assume that events happening in different time intervals are independent of each other. Such memoryless and additive model gives rise to an exponential dependence between the number of events and elongation: L(t)/L(0) = exp(αE(t)/C), where E(t) is the cumulative number of events by time t, C is the total number of cells in the primordium, and α is a proportionality factor. This model provides a direct connection between oriented cell intercalations and global deformation. Fitting the model to data (Figures 2I and 2J; α = 0.762; R2 = 0.758) reveals that in a tissue with C cells, 0:91C events would double its length. Future work is needed to understand the close match between the number of events and tissue elongation. The total area occupied by the GB increases only by 1.46-fold during the elongation process. We found that this increase is due to an increase in the surface area occupied by individual cells (see below; Figures S4A–S4D).
Analysis of division orientation and tissue deformation in early mitotic domains
To test whether cell proliferation might provide an alternate strategy compensating for cell loss due to invagination, we identified and followed all dividing cells during early gastrulation. In Drosophila, post-blastoderm mitoses can be assigned to 25 domains defined by patterned expression of a mitosis-promoting protein phosphatase.2,38 We constructed a spatiotemporal map of these mitoses, recovering all of the previously described mitotic domains, along with the intra-domain mitotic waves (Figures 3A and S2). Consistent with the classic study by Victoria Foe,10 the vast majority (96%) of cell divisions during this period occur outside the GB. Using our 3D segmentation and tracking pipeline, we then followed single-cell dynamics of all dividing cells. During the course of each division (Figure 3B), cells round up but conserve volume, such that the two daughter cells have a combined volume equal that of the parent cell (Figures 3C, S4E, and S4F). Cell rounding does however cause a transient increase in apical area, coupled with a similarly transient apico-basal shortening (Figures 3E and 3F). Given the large number of divisions at any moment, these transient increases add up to a2.43-fold increase in the area occupied by all dividing cells (Figure 3D) and provide a significant compensation for cell loss during gastrulation.
Figure 3. Shape dynamics of dividing cells and the transformations of mitotic domains.
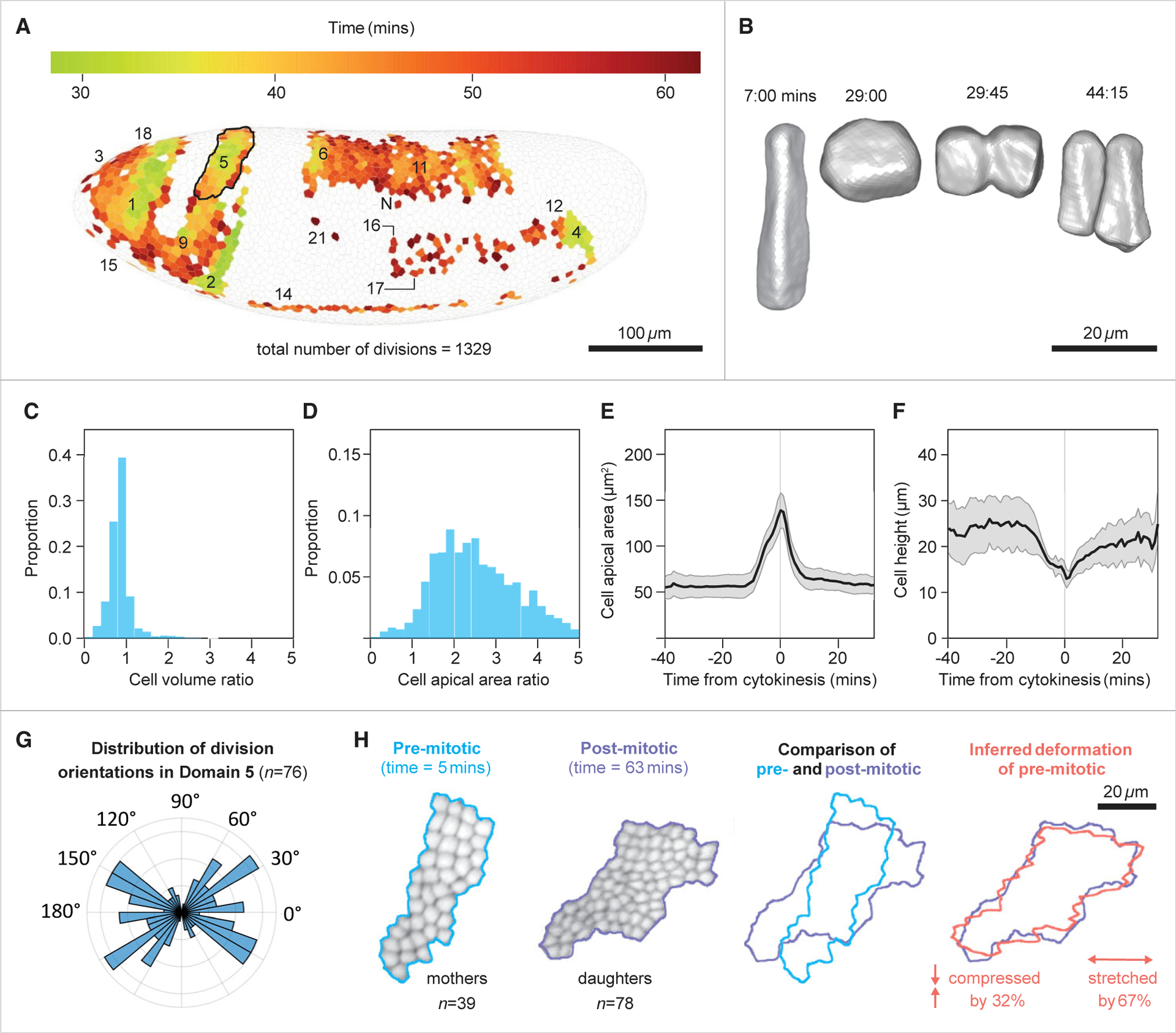
(A) Spatial map of divisions, with dividing cells shown in their original positions at the blastoderm stage, and color indicating their time of completion of their division. Mitotic domains indicated by the nomenclature proposed by Victoria Foe.2
(B) Three-dimensional reconstruction of a dividing cell, showing transient increase in apical area upon rounding up.
(C and D) Histograms of the ratios of final to initial cell volume (C) and final to initial cell apical area (D) in dividing cells. In both histograms tfinal = 43:00. For cell areas tinitial = 0:00 and for cell volumes it is the time at which cellularization is completed in the entire embryo (tinitial = 17:00).
(E) Average and SD of apical area from domain #1. Values represent the apical area of the mother cell and the summed apical areas of both daughter cells. The sharp increase in area toward t = 0 is followed by decrease to approximately pre-division levels, demonstrating that cell divisions have a significant, yet transient contribution to tissue expansion.
(F) Average and SD of apico-basal cell height from domain #1.
(G) Polar histogram of the distribution of division orientations within the domain relative to the DV-AP axes of the embryo at the time of the event (90° = dorsal; average = 4.5°, order parameter = 0.31, n = 76; p = 0.004, Rayleigh test for circular uniformity).
(H) (Left to right) Shapes of the domain before and after the completion of divisions, and their overlay demonstrates their initial dissimilarity. Overlay of the premitotic domain following a simple area-preserving linear transformation which includes a stretch and a compression factor, and the postmitotic domain, demonstrating a good approximation (right most).
Data in (A) and (D) are derived from embryo #2 and in (B) and (C) from embryo #1. See also Figures S1H–S1J, S2, S3A, and S3B.
We found that that several mitotic domains (1, 4, 5, 6, 14, 15, 16, and 18) are characterized by aligned divisions and are, as a consequence, stretched in the direction of common cell division and compressed in the orthogonal direction (Figures 3G, S3A, and S3B). Such reshaping is a direct consequence of the fact that, after the described overshoot, the apical area of an approximately hexagonal parent cell is distributed between two smaller adjacent hexagonal daughter cells. The postmitotic shapes of several domains are indeed consistent with this type of area-preserving transformation (Figure 3H), showing that patterned epithelial domains can be reshaped not only by directed cell intercalations, but also by directed divisions. A similar observation has been made before for domain 4;39 our analysis indicates that this phenomenon is more general.
Quantification of the relative contribution of different cellular processes to epithelial expansion
Another reshaping operation is based on anisotropic cell shape changes, even in the absence of cell intercalations and divisions (Figure 4A). This strategy is followed by the amnioserosa primordium, a narrow band of cells on the dorsal side of the embryo. In response to several locally expressed transcription factors and signaling molecules, cells within the amnioserosa primordium change their shapes from columnar to squamous, expanding their projected apical area by 3.10-fold, with minimal changes in cell volume (Figures 4B, 4C, and S4; Video S4).3,40
Figure 4. Cell flattening and relative contribution of the three different processes to epithelial expansion.
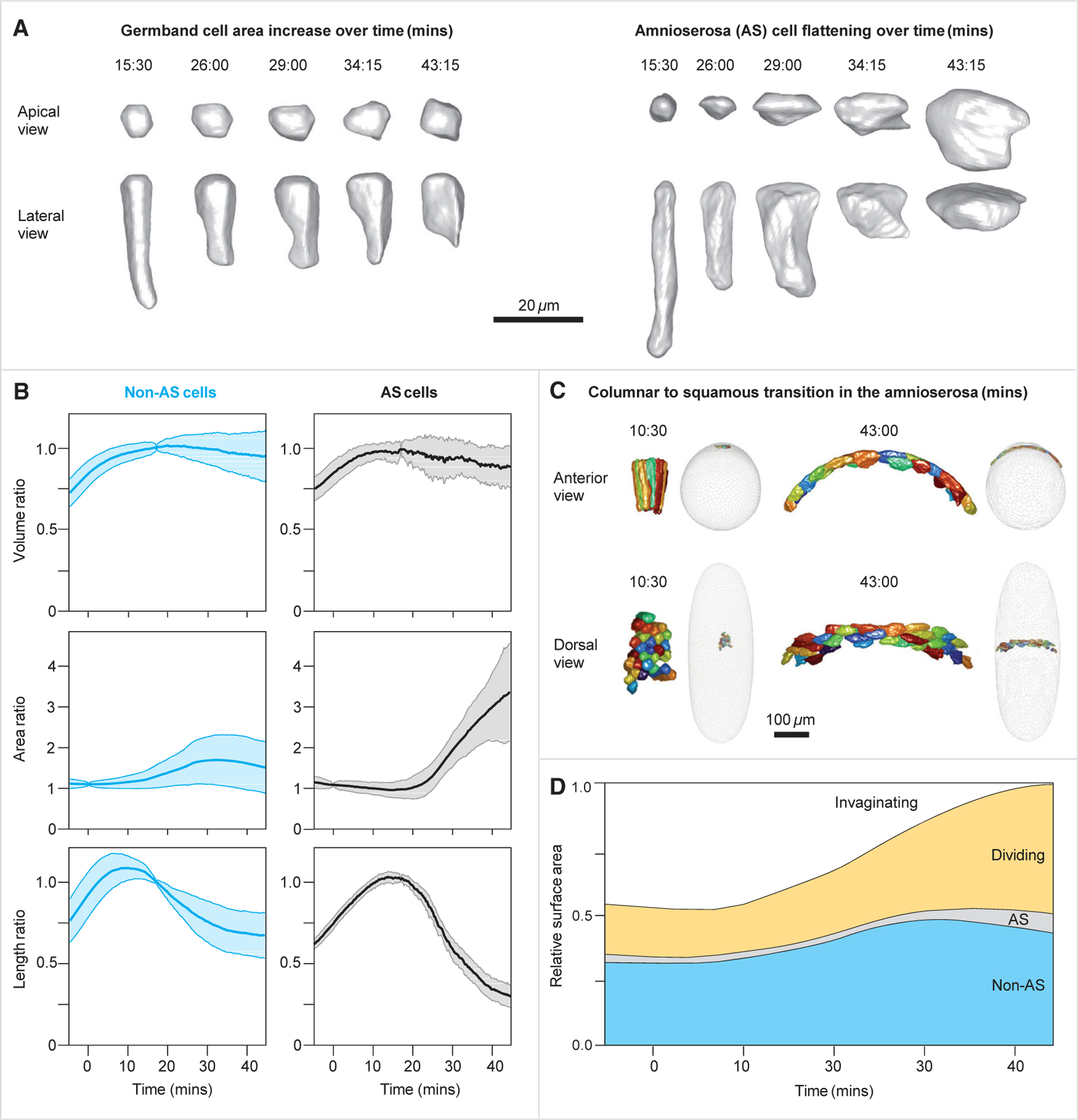
(A) Three-dimensional reconstruction of the geometric transformations of cells from the germband (left) and from the amnioserosa (right).
(B) Dynamics of the volume ratios, area ratios, and apico-basal length in non-AS (left) and AS (right) cells. Blue and black lines are averages, and shaded colors are the SDs over time. The completion of cellularization in the non-AS cells (approximately 8 min) and in the AS cells (approximately 11 min) is indicated by peak in the cell length. At that point, volumes remain relatively constant, and apical surface areas begin to increase.
(C) Three-dimensional reconstruction of AS cells before and late in the columnar-to-squamous transition, shown as anterior (top) and dorsal (bottom) views. In the gray whole-embryo views, the locations of the colored AS cells are shown viewed from the anterior end (upper images) or from the dorsal side (lower images).
(D) The fraction of embryo surface occupied by cells undergoing each of the four behaviors over time, demonstrating the compensation of area loss due to cell invagination.
In (B) and (D), the numbers of invaginating cells is 2,808, the number of dividing cells is 1,110, and the numbers of non-AS and AS cells are 1,991 and 176, respectively. Data are derived from embryo #1. See also Figure S4 and Video S4.
Detection of all instances of cell intercalation, division, and columnar-to-squamous transition allowed us to determine how each of these cell-level events contribute to the large-scale areal expansion that compensates for the loss of invaginating cells (Figure 4D). Although the cells of amnioserosa undergo the largest relative expansion of their apical area, the fraction of the amnioserosa primordium that remains on the surface is small and contributes only 5% to covering the 46% area deficit. The majority of the deficit (30% out of 46%) is compensated by the dividing cells, which can increase their areas quite significantly during individual division events. The residual nondividing regions of the blastoderm, including the previously described germband, undergoes an average 1.35-fold expansion of apical surface area, covering the remaining 11% of the area debt.
Conclusions
Our study demonstrates how recent advances in microscopy, image processing, and machine learning can be used to deconstruct gastrulation in the whole embryo into behaviors of individual cells and cell groups. As a first illustration of this approach, we characterized the large-scale areal expansion that accompanies well-characterized processes of epithelial invagination and germband expansion. Each of the constituent behaviors is a complex regulatory module, reflecting the action of transcriptional, signaling, and cytoskeletal circuits. Our approach bridges the gap between molecular and cellular studies and biophysical models that view epithelium within the continuum mechanics framework where the main players are no longer individual cells, but coarse-grained fields of deformations and forces.10 Moreover, our high-throughput algorithmic pipeline opens the possibility to study developmental variation throughout gastrulation at the whole-embryo level. Having access to cell behaviors throughout embryo promises to provide the much-needed boundary conditions and constitutive laws for these models. The early Drosophila embryo is ideally positioned for making this connection, but we expect that other developmental models will soon follow suit.
STAR★METHODS
RESOURCE AVAILABILITY
Lead contact
Further information and requests for resources should be directed to and will be fulfilled by the lead contact, Eric Wieschaus (efw@princeton.edu).
Materials availability
This study did not generate new unique materials.
Data and code availability
Whole embryo segmentation, tracking, cell lineages, cell intercalation events and various cell geometry attributes used for the main text figures have been deposited at the figshare repository and are publicly available as of the date of publication. The DOI is listed in the key resources table.
All original code has been deposited at the figshare and repository and is publicly available as of the date of publication. The DOI is listed in the key resources table.
Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Deposited data | ||
| Whole embryo cell segmentation and tracking of embryos #1,2 (used in the main text), including cell lineage, cell geometry properties, and extracted intercalations used in the main text. | This study | https://doi.org/10.6084/m9.figshare.18551420.v2 |
| Experimental models: Organisms/strains | ||
| D. melanogaster: Gap43::mCherry/TM3 | Martin et al.41 | N/A |
| D. melanogaster: Tub67a<CAAX-mCherry<sqh3’UTR.attp2./TM3,Sb | Wieschaus Lab | N/A |
| Software and algorithms | ||
| ImageJ 1.53f51 | Schindelin et al.42 | https://imagej.nih.gov/ij/; RRID: SCR_003070 |
| Ilastik 1.3.3post3 | Sommer et al.30 | https://www.ilastik.org/; RRID: SCR_015246 |
| Imsane | Heemskerk and Streichan29 | https://idseheemskerk.com/software/ |
| CellPose | Stringer et al.33 | https://www.cellpose.org/ |
| Algorithm for generating all subgraph induced connected components | Karakashian et al.43 | N/A |
| CircStat | Berens44 | https://www.jstatsoft.org/article/view/v031i10; RRID: SCR 01665 |
| Algorithms for whole embryo cell segmentation, tracking, polygonization, and division detection, including sample raw data for testing the code. | This study | https://doi.org/10.6084/m9.figshare.18551420.v3 |
| Algorithms for handling, visualizing, manipulating, and extracting various features from the deposited whole embryo cell segmentation and tracking data. | This study | https://doi.org/10.6084/m9.figshare.18551420.v3 |
EXPERIMENTAL MODEL AND SUBJECT DETAILS
Fly stocks
We used a total of 4 embryos, marked embryo #1, #2, #3, and #4. Embryo #2 was used for analysis of cell divisions (Figure 3), and was obtained from a Gap43::mCherry/TM341 female. Embryo #1 was used for all other analyses, and was from a Tub67a < CAAX – mCherry < sqh 3’ UTR. attp 2. / TM3, Sb female. Additional analyses in the supplementary material use both these genotypes. Both stocks express a membrane cherry marker which served for cell segmentation. All embryos used in this study were grown at either 18 or 25°C.
Embryo preparation and mounting
Prior to mounting, embryos were collected using apple juice agar plates and dechorionated for 1–2 min in a fresh 50% bleach solution. Embryos were mounted in an agarose gel inside a glass micropipette. We used 1% low-melting agarose (StarPure Low Melt Agarose, cat. no. N3103-0100, StarLab GmbH), which was dissolved in a phosphate buffered saline (PBS) solution at 80 °C on a magnetic stirrer for 6 h.
METHOD DETAILS
A pipeline for cell segmentation, tracking, division detection and polygonization
Input
A series of 3D volumes of an entire fly embryo, reconstructed at isotropic voxel size of dxyz=0.2619 and with temporal intervals of dt seconds (15 ≤ dt ≤ 75).
Output
A series of T polygonal meshes, wherein the polygons of mesh 1 ≤ t ≤ T accurately overlap with the cell membranes in the input volume at time t, approximately 5 microns underneath the apical end of the cells. Two polygons at two different time points have the same polygon index if and only if they represent the same biological cell.
Detection of cell apical surface in 3D volumes
(Figure S1A) We begin by extracting from each 3D volume a 2D surface that is located 5 microns beneath the apical tip of the cells. We selected the −5 microns plane since it presented the highest contrast of the membrane marker. To extract this plane, we use the “Autocontext” module from the freely available image processing software Ilastik30 to train a binary classifier that accurately separates the embryo (labeled “1”; including cells and yolk) from the background (labeled “0”). Lastly, we use morphological erosion by 19 pixels (~4.98 microns) to bring the surface of the binary mask into alignment with the −5 microns surface of the embryo.
Calculation of Mercator projections from cell apical surface simplifies cell segmentation
(Figure S1B) The apical surface of the cells is a 2D surface embedded within a 3D Euclidean space. We first converted it into a standard (flat) 2D images, as more segmentation and tracking tools are available for such data. To do so, we used the ImSAnE algorithm.29 Given a 2D surface embedded within a 3D Euclidean space, ImSAnE divides the surface into four anatomically overlapping regions: Anterior, Posterior, Dorsal and Ventral. Then, it defines a coordinate system covering the surface of interest (SOI). The intensity value at each point on the SOI can then be mapped and displayed in the reference of the coordinate system, resulting in a 2D presentation of the fluorescence data. We will use the following notation for the transformation of a pixel, e.g., from the anterior region of the embryo, from the original 3D embedding space into the flattened space: TFanterior (x,y,z) = (u,v). Notably, ImSAnE also provides us with the inverse of the transformation: . We use ImSAnE to transform the surface defined by the boundaries of the binary object we described in the previous section into four overlapping 2D images, to which we will refer as “pullbacks”.
Segmentation of first time point
(Figure S1C) Our strategy for segmentation and tracking is through watershed seed propagation.45 In our data, this strategy begins by segmenting the four pullbacks of the first time point, based solely on the pixel content of these images. This is followed by iteratively propagating the segmented cells to the next time points using non-rigid image registration. To segment the pullbacks of the first time point we used the Autocontext module in Ilastik, which calculates the probability of each pixel to represent a cell membrane, as the basis for seeded watershed segmentation (pixel connectivity = 4). During this process, each cell (i.e., a connected component of pixels) at each pullback is assigned a unique index from 1 to the number of cells within that pullback.
Assignment of coherent cell indices between pullbacks
Proper cell tracking requires that each biological cell will have a unique and distinct cell index throughout the entire time-lapse. Arbitrary cell indexing, as described in the previous section, is guaranteed not to meet the required criterion. For instance, if a cell located in the overlap region of the dorsal and the ventral pullbacks, it is highly unlikely that by mere chance it will be given the same cell index. Therefore, we identify all the appearances of each of the ~6000 biological cells in all four pullbacks of the first time point and assign all appearances the same unique cell index. The decision of whether two cells in two different pullbacks represent the same biological cell is done based on the level of their overlap in the original 3D embedding space (i.e., before flattening the apical surface).
Segmentation propagation and tracking
Having the four pullbacks of the first time point properly segmented and indexed, we are now ready to describe the propagation step of the segmentation from time point t to t + 1. At this point we have the four unsegmented pullbacks at time point t, the segmentations of these pullbacks, and four additional unsegmented pullbacks at time point t + 1. First, we apply the non-rigid registration method Demon’s algorithm31 to estimate the displacement field of each of the four unsegmented pullbacks at time t to the corresponding pullback at t + 1. To this end, we used MatLab’s implementation - imregdemons, using 8 pyramid levels, 1000 iterations per level, accumulated field smoothing of 2.5, and an initial subsampling of both source and target images by a factor of 2 in both X and Y axes. We use the calculated displacement field , which displaces a pullback of size M * N at time point t to that at time point t + 1, to propagate the segmentation of this pullback using nearest neighbor interpolation. This provides us an approximation to the segmentation of the pullback at time point t + 1. To refine the propagated segmentation, we first apply morphological erosion to remove the three outer layers of pixels from each cell, then use the remaining pixels as seeds for watershed segmentation. Lastly, to guarantee that the indexing of the cells has not changed as a result of the applied watershed, we update the index of each resulting cell to that of its seed.
Detection of cell division events
(Figure S1D) The watershed seed propagation approach provides highly accurate cell segmentation for live movies of membrane labeled tissues, and it has the advantage of tracking the cells at the same time. However, it has the inherent limitation of being unable to detect the presence of a new cells not propagated from the previous time point, such as the two daughter cells following a division event. To overcome this limitation, we integrated into our platform the deep learning segmentation algorithm “CellPose.”33 CellPose has the advantage of segmenting each image independently and can therefore identify the two daughter cells following division. To use CellPose for division detection, we follow the registration-based segmentation of the pullback with a segmentation using CellPose. Then, for each cell segmented by the watershed seed propagation approach (Cws) we declare it as a cell division event, if there are two segmented cells in the CellPose segmentation (CCP1,CCP2), such that:
Area (CCP1) ≥ 35 μm2 and also Area (CCP2) ≥ 35 μm2.
0.5 ≤ (Area(CCP1) /Area(CCP2)) ≤ 2.
At least 85% of the area of Cws is covered by CCP1 and CCP2.
At least 85% of the area of each of CCP1 and CCP2 is covered by Cws.
- (OuterIntensity + InnerIntensity /2) ≤ InterfaceIntensity, where (see Figure S1D):
- OuterIntensity is the median pixel intensity at the non-interfacing membranes.
- InnerIntensity is the 5th percentile intensity inside the two cells.
- InterfaceIntensity is the median pixel intensity at the interfacing membranes.
Once all criteria are met, we replace Cws with CCP1 and CCP2 and assign each daughter cell a new and unique cell index.
So far, our pipeline results in the segmentation, tracking and detection of divisions of the entire time-lapse, where each time point is represented as four pullbacks. Next, we will describe how we reintegrate the four pullbacks at each time point back into the initial 3D configuration.
Projection of segmented cells onto triangle mesh
(Figure S1E) We begin by generating a triangle mesh at −5 microns beneath the apical surface of the cells. Let TriMesh = (F, V) be the triangle mesh, where F = {i, j, k)}, 1 ≤ i < j < k ≤ |V| is the set faces, which contains all triplets of vertex indices composing each face, and V = {(xi, yi, zi)}, is the set of vertices, which contains all 3D coordinate triplets of the vertices composing the triangles. This was done by smoothing the binary mask (generated in the beginning of the pipeline) through convolution with a 3D gaussian kernel that has a standard deviation of 3 voxels (0.7857 μm), followed by calculating the iso-surface of the smoothed mask at iso-value 0.5. Our goal now is to index each triangle face f = (i, j, k) ∈ F according to the cell to which it belongs, based on the segmentations of the pullbacks. Assume that f is located at the anterior pole of the embryo. The geometric centroid of f is the average coordinate of its three vertices. We define the index of f to be the index assigned to the pixel p = (u, v) from the segmentation of a pullback which minimizes: . Simply put, we search for the pixel within the pullback, which has the minimal Euclidean distance to f within the original 3D (embedding) space. For instance, if f is located at the tip of the anterior pole of the embryo, then the matching pixel will be the pixel located in the exact center of the anterior pullback.
As long as the triangles in the mesh are sufficiently small, this procedure is valid by itself. However, a face located at the longitudinal center of the embryo can potentially be matched with a pixel from any of the four pullbacks, due to the significant overlap between the pullbacks. If the quality of the segmentation at a given position in all pullbacks is equal, it makes no practical difference to which pullback the nearest pixel belongs. However, from a mathematical perspective, pullbacks are bound to present some spatial distortions which reduce the quality of segmentation. For instance, the anterior pullback appears less distorted at the center of the image, which corresponds to the apical pole of the embryo, and more distorted the farther we are from the center. Therefore, we prefer to limit the matching of f to the pullback that is least distorted in the vicinity of f, and is therefore likely to have the most accurate segmentation there. To identify that pullback, we search the nearest pixel to f according to the following criteria:
If fcentroid is in the 20% anterior most region of the embryo, search only in the anterior pullback.
If fcentroid is in the 20% posterior most region of the embryo, search only in the posterior pullback.
If fcentroid is within the 20–80% along the AP axis and in the dorsal half of the embryo, search only in the dorsal pullback.
Otherwise, search only in the ventral pullback.
Conversion of triangle mesh to polygonal mesh
(Figure S1E) At this point, each of the several thousand cells at each time point is represented by an average of several hundreds of mesh triangles, which would lead to high time and memory consumption in downstream analyses. Therefore, our last step is to convert the triangle mesh into a polygonal mesh, wherein each cell is represented by a single polygon, and each interface between neighboring cells will be represented by a single edge. The set of vertices of cell c in the polygonal mesh is the subset of vertices of cell c in the triangle mesh which are in contact with at least two additional cells (i.e., they are at the meeting point of three cells or more). In addition, an edge exists between two vertices in the polygonal mesh, if and only if both vertices are in contact with at least two mutual cells.
3D Segmentation and tracking of external cells
(Figure S1F) Having the apical surface of the cells segmented and tracked allows us to segment and track the cells in three-dimensions with minimal efforts. To this end, we used CellPose to segment the raw 3D volumes. Improving the performances of the default neural network used by CellPose on our images requires training it on examples of accurately segmented 2D images from our dataset (Note: CellPose has the advantage of using 2D examples to train segmentation of both 2D and 3D data). Fortunately, the generation of such examples close to the apical end of the cells is already an inherent part of our pipeline for 2D segmentation, thereby requiring preparation of 2D examples only close to the basal end, where imaging contrast is inferior due to unavoidable scattering. For this purpose, we used Ilastik to accurately segment one cross-sectional and one longitudinal section, at the first, middle, and last time points of three different embryo datasets, totaling in 18 slides. This relatively small training set was sufficient for achieving reliable segmentation owing to the superb generalization capacity of CellPose and the contribution of additional 329 segmentation examples of the apical end of the cells. Once the training of the network and the segmentation of all volumes is completed, we are left with the task of tracking the segmented cells over time. To this end, we rely on the fact that at a given time point, the 2D polygon of a cell from the 2D segmentation is entirely, or mostly, contained within the volume of the same cell in the 3D segmentation. To update the indices of all 3D segmented cells, we follow the following routine: for each 2D polygon, identify the cell in the 3D image that contains the centroid of the polygon, and update the index of the 3D cell to the index of the polygon. In case a 3D cell is not re-indexed throughout this procedure (i.e., it is not in overlap with the centroid of any polygon), or is re-indexed multiple times (i.e., it is in overlap with centroids of multiple polygons), we remove it from the image by zeroing all its voxels.
Method limitations
Our mechanism for detecting an event of cell division is based on a hard-coded set of parameterized thresholds. To estimate the accuracy of this approach, following segmentation we examined the identified division events and the corresponding unsegmented image in all five analyzed images. We found the false positive rate to be between 5–10%, and of false negative rate between 0–10%. Reducing the error level to 0% requires within the order of 2–3 hours of manual curation per time lapse. While we find the required manual efforts to be well within reason, given the intense labor associated with generating a single high-quality 3D time lapse at cell resolution, streamlining the generation of processed data may require a more adaptive approach with tolerable error rates.
The second and main limitation of our method stems from its inability to identify new cells appearing on the surface of the embryo. To detect cell division events, we integrated the CellPose33 segmentation algorithm into our pipeline and relied on a series of clear visual criteria as further validation. However, in addition to cell division, cells that invaginate to the inside of the embryo can potentially come back out to the surface at a later time, like cells in the cephalic furrow do at ~45 minutes. Since none of our analyses involve “reappearing” cells, in this work we chose to ignore this limitation. However, it is clear that to have a complete representation of all surface cells at later time periods our algorithm will need to be upgraded. One way to do so is by manually marking a watershed seeding point inside each reappearing cell upon its return to the outer surface. Once a cell has been marked, it will continue to be segmented and tracked automatically by the registration-based segmentation mechanism. Another plausible direction, which can be achieved with minor adjustments to the implementation, is to execute our algorithm on the same dataset a second time, after inverting the temporal order of the volumes. When time is reversed, reappearing cells will be segmented and tracked as invaginating cells are in the normal temporal sequence.
Detection of cell intercalations
T1-transitions (a.k.a 4-cell rosettes) were detected according to our previously developed high accuracy algorithm for template-based mapping of dynamic motifs in tissue morphogenesis.34 For high order rosettes we updated our algorithm so that a rosette must meet all following criteria:
Topological criteria:
Every cell from the rosette has at least two neighbors from within the rosette.
Every cell from the rosette must have at least one neighbor that is not from the rosette.
There is no connected component of cells that do not belong to the rosette and that is surrounded only by cells from the rosette.
There is no cell from the rosette whose removal from the rosette disconnects two other cells from the rosette (i.e. the removal of that cell leaves no path between two other cells in the rosette that passes only through the remaining cells of the rosette).
During invagination, cells from the two sides of a furrow (e.g. the ventral furrow) may appear in the polygonal mesh as undergoing intercalation, although biologically this is not the case. To identify and discard such pseudo-intercalations, assume an intercalation event at time point t = T that includes n cells. For each pair of cells (ci ,cj), we find the all the cells along the shortest path from ci to cj at time t = 0. If any of the cells along this path will invaginate before time point T, we conclude that this intercalation is a result of invagination rather than active intercalation. While intercalations do occur in the mesoderm,15 their detection relies on manual observation.
Geometric criteria:
The maximal apical area of a cell from a rosette is no more than 10 times the minimal apical area.
The maximal pairwise Euclidean distance between the boundaries of a pair of cells from the rosette is (n−2) microns, where n is the number of cells within the rosette.
We define an internal interface to be an interface of the rosette if all the cells that meet at its two vertices belong to the rosette. An external interface is an interface between two cells of the rosette that is not an internal interface. We require that the sum of lengths of all internal interfaces in a rosette will be larger than one third the median length of external interfaces.
Overlap and duplications criteria:
If the cells of an intercalary event “A” are a subset of another intercalary event “B”, and the time difference between the two events is no more than 5 minutes, we remove event “A”.
If a group of n cells meet all described criteria at more than one time point, we keep only the event at the time point in which the maximal pairwise Euclidean distance between cell boundaries is minimal.
We remove intercalations that include a dividing cell. Since a dividing cell can exert significant mechanical force onto its neighbors and lead to cell intercalation, we remove any intercalation in which one of the cells is dividing in the interval between 2 minutes before and 8 minutes after the intercalation event. In the embryo used for presenting intercalation analysis (Figure 2), this step has led to the removal of 94 T1-transitions and 95, 3, and 1 rosettes with 5, 6, and 7 cells, respectively.
Lastly, since our previous benchmark for the algorithm was done only on simulated data and on the extending germ, all detected intercalations outside of the germ-bands were validated manually.
Calculation of intercalation and division orientations
(Figures S1H–S1J and S3)
Generation of the ventral midline
We define the ventral midline as the line on the 3D surface of the embryo that passes in the middle of the domain that will later invaginate as a part of the ventral furrow. To accurately mark the ventral midline, we rely on the 2D Mercator projection of cell invagination map (Figure 1D in the main body of the manuscript), by calculating a distance transform for pixels in the invaginating regions to reach pixels in the non-invaginating regions. The distance transform highlights the ridge of pixels that are farthest from the non-invaginating parts of the embryo, which the user marks with a straight line. Lastly, we transform the points on the marked line back to the original 3D embedding space of the embryo, which will serve us as the ventral midline.
Calculation of DV orientation at a point
Given a point (xvm, yvm, zvm) on the ventral midline, we construct a plane P that is orthogonal to the ventral midline at that point. The intersection of P with the surface of the blastoderm has a ring-like shape which corresponds to a cross-section of the embryo. The DV orientation at a point (xIL, yIL, zIL) on the intersection line is the orientation of the tangent to the intersection line at that point.
Calculation of event orientation
The blastoderm projection of a T1-transition in which the cells cA and cP are at the two ends of the contracting interface, is defined as the line between the centroids of cells cA and cP: (xA, yA, zA) and (xP,yP,zP), respectively, at time t=0. We calculate the orientation of this line as the angle it makes with the DV axis. For rosettes (i.e., events with 5 or more cells), the corresponding line connects the two cells that are most distant at time t=0. The calculation of cell division orientation is similar to this of T1 T1-transitions, with cA and cP representing the two daughter cells at the first time point following cytokinesis.
Manual labeling of mitotic domains
(Figures S2A and S2B) Identification of the set of cells belonging to each mitotic domain was done manually by comparison of the anatomical distribution and temporal dynamics shown in our cell division maps (Figure 3A) to these reported by Foe.2 Domains 3, 8, 15, 18 and 19 did not manifest clear characteristics and were therefore marked with limited confidence. Otherwise, the temporal and geometric characteristics of the identified domains were in strong agreement with Foe.
Quantification of cell geometry attributes
(Figures S4A–S4C and S4E) Cell volume at a given time point was calculated from the image of 3D segmentation as the total number of voxels assigned with the index of that cell × voxel volume (0.2619 μm3). Cell apical area was calculated based on the segmented triangle mesh (i.e., prior to its conversion to a polygonal mesh) by summing the areas of triangles assigned with the index of that cell. To calculate cell length along the apico-basal axis we first calculated an apico-basal (AB) axis. We define the AB axis as the line that is normal to the polygon representation of the cell in the 2D segmentation and passes through the centroid of the polygon. Then, we projected the 3D coordinates of all voxels of the cell from the 3D segmentation onto the normal line. The AB length of the cell was then calculated as the Euclidean distance between the projected voxels at the 1st and 99th percentiles along the line. Analyses of volumes and lengths were validated manually.
Quantification of ratios of cell geometry attributes
(Figures S4D and S4F) For the calculation of ratio between final and initial cell apical area, apico-basal length, and volume, we used t=45 minutes as the final time point since this is when some invaginated cells start coming back out. For apical area ratio we used the last time point before gastrulation movements begin for the initial value (t=0 minutes). For volume and length ratios we used the time at which cellularization over the entire embryo completes as the first time point (t=17 minutes).
Calculation of germ-band length dynamics
Our strategy is to identify in the blastoderm a line of cells that spans the entire AP axis of the germ-band and is located at mid DV length (see Figure 2G). The length of the germ-band at any time point throughout the development of this embryo is defined as the arc-length of a smoothed line that passes in proximity to the centroids of these cells. Our empirically validated assumption is that the identified line of cells will span along the entire germ-band at its mid-height at all later time points as well, which allows the calculation of length to be carried automatically from the second time point onward. Method: first, the blastoderm projected map of the number of intercalations per cell is presented, on which the user marks the cells passing in the middle of the germ-band (see Figure 2B). Although any line that passes through the centroids of the midline cells will approximate the midline of the germ-band, it will most likely zigzag between the centroids of neighboring cells and therefore overestimate the length of the germ-band. Instead, we fit a three-dimensional smoothing spline curve through the centroids. Lastly, we estimate the length of the spline using linear fragmentation.
Live imaging
Fluorescence live imaging of membrane labeled Drosophila embryos relied on the custom built Multi View Selective Plain Illumination Microscope (MuVI SPIM),46 with scatter reducing imaging mode.47 For detection this setup uses a pair of facing 25x Nikon NA 1.1 APO LWD lenses. For excitation it employs a pair of 10 x Nikon NA 0.3 CFI Plan Fluor facing each other. Sample illumination is achieved via continuous OBIS LX laser lines from Coherent, emitting at 488 nm, 561 nm, and 660 nm, respectively. Light sheet was generated using a galvanometric mirror from Cambridge technology and a scan lens from Sill Optics, together with a tube lens. Fluorescence signal from the detection objective passes a filter wheel with Semrock filters (FF01 - 542/27-25, FF01-609/62-25, BLP01-568R-25, BLP01-664R-25), and collected using an sCMOS ORCA-Flash 4.0x V3 camera from Hamamatsu. Sample sectioning is controlled electronically involving controllers and stages from Phyisk Instrumente, specifically a linear piezo stage P-629.1CD with E-753 controller, a rotational stage U-628.03 with C-867 controller, and a linear actuator M-231.17 with C-863 controller. Sequence acquisition was controlled via micro manager.48 Embryos were imaged at rate ranging from frame per 15 to per 75 seconds. In all movies reconstruction resulted in an isotropic voxel dimensions of 0.2619 microns.
Hardware
Code for the described pipeline was developed on a Dell PowerEdge R930 server carrying four Intel(R) Xeon(R) CPU E7-4850 v4 @ 2.10GHz with 16 cores each and 2TB RAM, with RedHat OS. Cell and nucleus segmentation and tracking, and all the analyses of the extracted motifs were done on Intel(R) Xeon(R) CPU E5-1620 v4 @ 3.5GHz, with 32GB memory and Windows 10 64 bits OS. 3D segmentation using the algorithm CellPose was done on a Nvidia P100 GPU with 16 GB memory.
QUANTIFICATION AND STATISTICAL ANALYSIS
Regression analysis
The goal of our model is to connect the relative elongation of the germ-band over a given time period with the density of intercalary events occurring over the same period: (L(t1) /L(t0)) = exp(α(E(t1) −E(t0) /C)), where L(t)and E(t) are the length of the tissue and the accumulated number of events at time t, C is the total number of cells in the primordium, and α is a dimensionless proportionality factor. Our decision of describing these relations as exponential is inspired by the following argument: assume an isolated event of a T1-transition constructed from four perfect hexagons, wherein the initial distance between the centroids of the two parting cells (i.e., the cells that will lose a shared interface) is d. It can be shown from the geometry of the cells and their organization that the application of a T1-transition will increase the distance between the parting cells by to . Similarly, given a tissue with C cells, the application of T1-transitions on all vertical interfaces will increase the distance between all pairs of parting cells by , and as a result, the length of the entire tissue by (supported by simulation of Siang et al.8). To estimate the number of vertical interfaces in a tissue with C cells, we approximate the tissue using a perfect hexagonal grid of the same size. In this grid, the number of vertical interfaces is similar to the number of cells, since every cell can be uniquely coupled with the vertical interface on its right. Therefore, the number of T1-transitions required to elongate a tissue with C cells by is approximately C. Lastly, since these relations do not depend on the initial length of the tissue, we reason that a repeated application of set of C intercalations would lead to the following geometric sequence of tissue elongation: , , ,… This suggests that the relations between intercalation density and fractional tissue elongation for any number of intercalations is also exponential.
The value of α can be estimated using linear regression by applying a ln(x) function on both sides: ln(L(t1) /L(t0)) = α(E(t1) − E(t0) /C)). To generate sample data, we manually marked the right and the left germ-bands in two selected embryos based on the Mercator projection showing the number of intercalations per cell (Figure 2B), resulting in four quantified germ-bands. In each germ-band the fractional elongation of the tissue as well as intercalation density (# intercalations / # cells within the germ-band) were calculated in one-minute intervals, providing a total of 172 data points. Regression was then done using MatLab’s “regress” function. The estimated α and the R2 can be found in the main text.
Circular statistics of division orientations
The average orientation of divisions in a mitotic domain with angles {αj} was calculated using the angle doubling method49 as: . Average orientation of intercalations was calculated similarly. Standard deviation (S.D.) was calculated as: , where r is the mean resultant length of this angle sample. Order parameter (O.P.) in each domain was calculated as: . Testing for non-uniformity in orientation was done using Rayleigh test44 with Bonferroni correction for multiple hypothesis testing. Angle doubling transformation was performed prior to Rayleigh test, as it greatly improves the performances of the test.50 N values (cells), averages, S.D. and O.P. values can be found in the main text, in the legends of Figures 2D, 2E, 3G, and S3B–S3F.
Software
Basic image processing tasks such as rotation, ROI cropping and format conversion was done using Fiji.42 Image segmentation and object classification in 2D for the first time point in each embryo were done using Ilastik.30 Unrolling of the apical surface of the embryo was done using ImSAnE.29 3D segmentation and tracking of cells relied on the deep-learning algorithm CellPose.33 Implementation of the algorithm for generating subgraph induced connected components of size k was done in c language by Shant Karakash and Berthe Choueiry (University of Nebraska-Lincoln, NE, USA) and used under their permission.43 Calculations of circular statistics relied on the circular statistics toolbox.44 All remaining parts of the pipeline were developed in MatLab 2020b.
Supplementary Material
Highlights.
Whole-embryo single-cell morphogenetic atlas of fly gastrulation is presented
Projection of cell behaviors onto blastoderm simplifies visualization and analysis
Surface epithelium loss to invaginations is compensated by transient mitotic rounding
Relation between germband elongation and intercalation density is modeled
ACKNOWLEDGMENTS
We are grateful to Lucy Reading-Ikkanda for graphic design of the figures; Lisa Brown (Simons Foundation) for fruitful discussions on image processing; Trudi Schüpbach, Matej Krajnc (Jožef Stefan Institute), David Denberg, Tal Galili, and Yosi Keller (Bar-Ilan University) for fruitful discussions; Benny Shilo (Weiz-mann Institute of Science) for comments on the manuscript; Matthew Cahn (Princeton University) and the IT of Simons Foundation for technical support with computing resources; Reba Samantha and Laisa Eimont for bureaucratic assistance and Heping Jiang for stock maintenance; and lastly the Wieschaus and Shvartsman lab members for continuous support. The research was supported by the European Molecular Biology Organization long-term fellowship ALTF 215-2017 to T.S., the MCB 1516970 award from the NSF to S.Y.S., and the Howard Hughes Medical Institute to E.F.W.
Footnotes
SUPPLEMENTAL INFORMATION
Supplemental information can be found online at https://doi.org/10.1016/j.cub.2022.02.059.
DECLARATION OF INTERESTS
The authors declare no competing interests.
REFERENCES
- 1.Irvine KD, and Wieschaus E (1994). Cell intercalation during Drosophila germband extension and its regulation by pair-rule segmentation genes. Development 120, 827–841. [DOI] [PubMed] [Google Scholar]
- 2.Foe VE (1989). Mitotic domains reveal early commitment of cells in Drosophila embryos. Trends Genet. 5, 322. [PubMed] [Google Scholar]
- 3.Pope KL, and Harris TJC (2008). Control of cell flattening and junctional remodelling during squamous epithelial morphogenesis in Drosophila. Development 135, 2227–2238. [DOI] [PubMed] [Google Scholar]
- 4.Sweeton D, Parks S, Costa M, and Wieschaus E (1991). Gastrulation in Drosophila: the formation of the ventral furrow and posterior midgut invaginations. Development 112, 775–789. [DOI] [PubMed] [Google Scholar]
- 5.Paré AC, Vichas A, Fincher CT, Mirman Z, Farrell DL, Mainieri A, and Zallen JA (2014). A positional Toll receptor code directs convergent extension in Drosophila. Nature 515, 523–527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Momen-Roknabadi A, Di Talia S, and Wieschaus E (2016). Transcriptional timers regulating mitosis in early Drosophila embryos. Cell Rep. 16, 2793–2801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Lacy ME, and Hutson MS (2016). Amnioserosa development and function in Drosophila embryogenesis: critical mechanical roles for an extra-embryonic tissue. Dev. Dyn 245, 558–568. [DOI] [PubMed] [Google Scholar]
- 8.Siang LC, Fernandez-Gonzalez R, and Feng JJ (2018). Modeling cell intercalation during Drosophila germband extension. Phys. Biol 15, 066008. [DOI] [PubMed] [Google Scholar]
- 9.Etournay R, Merkel M, Popović M, Brandl H, Dye NA, Aigouy B, Salbreux G, Eaton S, and Jülicher F (2016). TissueMiner: a multiscale analysis toolkit to quantify how cellular processes create tissue dynamics. eLife 5, e14334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Streichan SJ, Lefebvre MF, Noll N, Wieschaus EF, and Shraiman BI (2018). Global morphogenetic flow is accurately predicted by the spatial distribution of myosin motors. eLife 7, e27454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Martin AC, Kaschube M, and Wieschaus EF (2009). Pulsed contractions of an actin-myosin network drive apical constriction. Nature 457, 495–499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Bailles A, Collinet C, Philippe JM, Lenne PF, Munro E, and Lecuit T (2019). Genetic induction and mechanochemical propagation of a morphogenetic wave. Nature 572, 467–473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kong D, Wolf F, and Großhans J (2017). Forces directing germ-band extension in Drosophila embryos. Mech. Dev 144, 11–22. [DOI] [PubMed] [Google Scholar]
- 14.Krajnc M, Stern T, and Zankoc C (2021). Active instability of cell-cell junctions at the onset of tissue fluidity. Preprint at arXiv. 10.48550/arXiv.2101.07058. [DOI] [PubMed] [Google Scholar]
- 15.John A, and Rauzi M (2021). A two-tier junctional mechanism drives simultaneous tissue folding and extension. Dev. Cell 56, 1469–1483.e5. [DOI] [PubMed] [Google Scholar]
- 16.Wang X, Merkel M, Sutter LB, Erdemci-Tandogan G, Manning ML, and Kasza KE (2020). Anisotropy links cell shapes to tissue flow during convergent extension. Proc. Natl. Acad. Sci. USA 117, 13541–13551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Huebner RJ, and Wallingford JB (2018). Coming to consensus: a unifying model emerges for convergent extension. Dev. Cell 46, 389–396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Tetley RJ, Blanchard GB, Fletcher AG, Adams RJ, and Sanson B (2016). Unipolar distributions of junctional myosin II identify cell stripe boundaries that drive cell intercalation throughout Drosophila axis extension. eLife 5, 1–35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Solnica-Krezel L, and Sepich DS (2012). Gastrulation: making and shaping germ layers. Annu. Rev. Cell Dev. Biol 28, 687–717. [DOI] [PubMed] [Google Scholar]
- 20.Schauer A, and Heisenberg CP (2021). Reassembling gastrulation. Dev. Biol 474, 71–81. [DOI] [PubMed] [Google Scholar]
- 21.Petridou NI, Corominas-Murtra B, Heisenberg CP, and Hannezo E (2021). Rigidity percolation uncovers a structural basis for embryonic tissue phase transitions. Cell 184, 1914–1928.e19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Kasza KE, and Zallen JA (2011). Dynamics and regulation of contractile actin-myosin networks in morphogenesis. Curr. Opin. Cell Biol 23, 30–38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Khairy K, Lemon W, Amat F, and Keller PJ (2018). A preferred curvature-based continuum mechanics framework for modeling embryogenesis. Biophys. J 114, 267–277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Stegmaier J, Amat F, Lemon WC, McDole K, Wan Y, Teodoro G, Mikut R, and Keller PJ (2016). Real-time three-dimensional cell segmentation in large-scale microscopy data of developing embryos. Dev. Cell 36, 225–240. [DOI] [PubMed] [Google Scholar]
- 25.Xiong F, Ma W, Hiscock TW, Mosaliganti KR, Tentner AR, Brakke KA, Rannou N, Gelas A, Souhait L, Swinburne IA, et al. (2014). Interplay of cell shape and division orientation promotes robust morphogenesis of developing epithelia. Cell 159, 415–427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Liu Z, and Keller PJ (2016). Emerging imaging and genomic tools for developmental systems biology. Dev. Cell 36, 597–610. [DOI] [PubMed] [Google Scholar]
- 27.Megason SG, and Fraser SE (2007). Imaging in systems biology. Cell 130, 784–795. [DOI] [PubMed] [Google Scholar]
- 28.Rauzi M, Krzic U, Saunders TE, Krajnc M, Ziherl P, Hufnagel L, and Leptin M (2015). Embryo-scale tissue mechanics during Drosophila gastrulation movements. Nat. Commun 6, 8677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Heemskerk I, and Streichan SJ (2015). Tissue cartography: compressing bio-image data by dimensional reduction. Nat. Methods 12, 1139–1142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Sommer C, Straehle C, Kothe U, and Hamprecht FA (2011). Ilastik: interactive learning and segmentation toolkit. In 2011 IEEE International Symposium on Biomedical Imaging: From Nano to Macro (IEEE), pp. 230–233. [Google Scholar]
- 31.Thirion JP (1996). Non-rigid matching using demons. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition (IEEE), pp. 245–251. [Google Scholar]
- 32.Meyer F (1994). Topographic distance and watershed lines. Signal Process. 38, 113–125. [Google Scholar]
- 33.Stringer C, Wang T, Michaelos M, and Pachitariu M (2021). Cellpose: a generalist algorithm for cellular segmentation. Nat. Methods 18, 100–106. [DOI] [PubMed] [Google Scholar]
- 34.Stern T, Shvartsman SY, and Wieschaus EF (2020). Template-based mapping of dynamic motifs in tissue morphogenesis. PLoS Comput. Biol 16, e1008049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Bertet C, Sulak L, and Lecuit T (2004). Myosin-dependent junction remodelling controls planar cell intercalation and axis elongation. Nature 429, 667–671. [DOI] [PubMed] [Google Scholar]
- 36.Blankenship JT, Backovic ST, Sanny JSSP, Weitz O, and Zallen JA (2006). Multicellular rosette formation links planar cell polarity to tissue morphogenesis. Dev. Cell 11, 459–470. [DOI] [PubMed] [Google Scholar]
- 37.Rauzi M, Verant P, Lecuit T, and Lenne PF (2008). Nature and anisotropy of cortical forces orienting Drosophila tissue morphogenesis. Nat. Cell Biol 10, 1401–1410. [DOI] [PubMed] [Google Scholar]
- 38.Edgar BA, Lehman DA, and O’Farrell PH (1994). Transcriptional regulation of string (cdc25): a link between developmental programming and the cell cycle. Development 120, 3131–3143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.da Silva SM, and Vincent JP (2007). Oriented cell divisions in the extending germband of Drosophila. Development 134, 3049–3054. [DOI] [PubMed] [Google Scholar]
- 40.Caroti F, González Avalos E, Noeske V, González Avalos P, Kromm D, Wosch M, Schütz L, Hufnagel L, and Lemke S (2018). Decoupling from yolk sac is required for extraembryonic tissue spreading in the scuttle fly megaselia abdita. eLife 7, e34616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Martin AC, Gelbart M, Fernandez-Gonzalez R, Kaschube M, and Wieschaus EF (2010). Integration of contractile forces during tissue invagination. J. Cell Biol 188, 735–749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Schindelin J, Arganda-Carreras I, Frise E, Kaynig V, Longair M, Pietzsch T, Preibisch S, Rueden C, Saalfeld S, Schmid B, et al. (2012). Fiji: an open-source platform for biological-image analysis. Nat. Methods 9, 676–682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Karakashian S, Choueiry BY, and Hartke SG (2013). An algorithm for generating all connected subgraphs with k vertices of a graph. Lincoln, NE 10, 1–37. [Google Scholar]
- 44.Berens P (2009). CircStat: a MATLAB toolbox for circular statistics. J. Stat. Softw 31, e1008049. [Google Scholar]
- 45.Pinidiyaarachchi A, and Wählby C (2005). Seeded watersheds for combined segmentation and tracking of cells. In Lecture Notes in Computer Science Proceedings of the International Conference Image Analysis and Processing (ICIAP) (Springer), pp. 336–343. [Google Scholar]
- 46.Krzic U, Gunther S, Saunders TE, Streichan SJ, and Hufnagel L (2012). Multiview light-sheet microscope for rapid in toto imaging. Nat. Methods 9, 730–733. [DOI] [PubMed] [Google Scholar]
- 47.Medeiros G. De, Norlin, Gunther S, Albert M, Panavaite L, Fiuza UM, Peri F, Hiiragi T, Krzic U, and Hufnagel L (2015). Confocal multi-view light-sheet microscopy. Nat. Commun 6, 8881. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Edelstein AD, Tsuchida MA, Amodaj N, Pinkard H, Vale RD, and Stuurman N (2014). Advanced methods of microscope control using μManager software. J. Biol. Methods 1, e10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Gill C, and Batschelet E (1983). Circular statistics in biology. J. R. Stat. Soc. A 146, 91. [Google Scholar]
- 50.Landler L, Ruxton GD, and Malkemper EP (2018). Circular data in biology: advice for effectively implementing statistical procedures. Behav. Ecol. Sociobiol 72, 128. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Whole embryo segmentation, tracking, cell lineages, cell intercalation events and various cell geometry attributes used for the main text figures have been deposited at the figshare repository and are publicly available as of the date of publication. The DOI is listed in the key resources table.
All original code has been deposited at the figshare and repository and is publicly available as of the date of publication. The DOI is listed in the key resources table.
Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Deposited data | ||
| Whole embryo cell segmentation and tracking of embryos #1,2 (used in the main text), including cell lineage, cell geometry properties, and extracted intercalations used in the main text. | This study | https://doi.org/10.6084/m9.figshare.18551420.v2 |
| Experimental models: Organisms/strains | ||
| D. melanogaster: Gap43::mCherry/TM3 | Martin et al.41 | N/A |
| D. melanogaster: Tub67a<CAAX-mCherry<sqh3’UTR.attp2./TM3,Sb | Wieschaus Lab | N/A |
| Software and algorithms | ||
| ImageJ 1.53f51 | Schindelin et al.42 | https://imagej.nih.gov/ij/; RRID: SCR_003070 |
| Ilastik 1.3.3post3 | Sommer et al.30 | https://www.ilastik.org/; RRID: SCR_015246 |
| Imsane | Heemskerk and Streichan29 | https://idseheemskerk.com/software/ |
| CellPose | Stringer et al.33 | https://www.cellpose.org/ |
| Algorithm for generating all subgraph induced connected components | Karakashian et al.43 | N/A |
| CircStat | Berens44 | https://www.jstatsoft.org/article/view/v031i10; RRID: SCR 01665 |
| Algorithms for whole embryo cell segmentation, tracking, polygonization, and division detection, including sample raw data for testing the code. | This study | https://doi.org/10.6084/m9.figshare.18551420.v3 |
| Algorithms for handling, visualizing, manipulating, and extracting various features from the deposited whole embryo cell segmentation and tracking data. | This study | https://doi.org/10.6084/m9.figshare.18551420.v3 |


