A MULTIPLE IMPUTATION PROCEDURE FOR RECORD LINKAGE AND CAUSAL INFERENCE TO ESTIMATE THE EFFECTS OF HOME-DELIVERED MEALS

Abstract

Causal analysis of observational studies requires data that comprise of a set of covariates, a treatment assignment indicator, and the observed outcomes. However, data confidentiality restrictions or the nature of data collection may distribute these variables across two or more datasets. In the absence of unique identifiers to link records across files, probabilistic record linkage algorithms can be leveraged to merge the datasets. Current applications of record linkage are concerned with estimation of associations between variables that are exclusive to one file and not causal relationships. We propose a Bayesian framework for record linkage and causal inference where one file comprises all the covariate and observed outcome information, and the second file consists of a list of all individuals who receive the active treatment. Under certain ignorability assumptions, the procedure properly propagates the error in the record linkage process, resulting in valid statistical inferences. To estimate the causal effects, we devise a two-stage procedure. The first stage of the procedure performs Bayesian record linkage to multiply impute the treatment assignment for all individuals in the first file, while adjustments for covariates’ imbalance and imputation of missing potential outcomes are performed in the second stage. This procedure is used to evaluate the effect of Meals on Wheels services on mortality and healthcare utilization among homebound older adults in Rhode Island. In addition, an interpretable sensitivity analysis is developed to assess potential violations of the ignorability assumptions.

1. Introduction.

Meals on Wheels (MOW) programs are community-based social service organizations that provide home-delivered meals to homebound older adults in order to reduce hunger and food insecurity, promote socialization, and promote community independence. Providing home-delivered meals to these populations is associated with beneficial nutritional outcomes, decreased risk of falls, and improved mental health (Thomas and Mor (2013), Campbell et al. (2015), Thomas, Akobundu and Dosa (2015), Thomas et al. (2018a), Thomas et al. (2018b), Thomas et al. (2018c)). However, healthcare payers, providers, and policy makers are also interested in the effects of community based organizations, like MOW, on pre-mature mortality and healthcare utilization, such as hospitalizations, emergency department visits, and nursing home placement.

One major challenge to performing such research is that MOW, by the nature of the services provided, do not submit medical claims or maintain clients’ health records. Medicare enrollment records and claims data contain comprehensive information on patients’ demographics, diagnoses, healthcare utilization, and long-term health outcomes, but exclude information about receipt of social services, such as MOW. In order to estimate the effects of MOW services on the healthcare utilization of its clients, linkage of Medicare claims data to MOW client data is required. However, data confidentiality restrictions prevent unique identifiers to be available for linking.

Many studies seek to draw causal conclusions about the impact of an intervention. Randomized experiments are the gold standard for inferring causality; however, they are sometimes infeasible because of logistical, ethical, or financial considerations. In these instances, researchers are limited to use non-randomized observational studies to estimate the causal effects. Causal analysis of observational studies requires data that comprise a set of covariates, a treatment assignment indicator, and the observed outcome (Rubin (1973a), Rubin (1973b), Rubin (1978), Rubin (1979)). In some studies, because of confidentiality restrictions or the nature of the data collection, the covariates, treatment assignment, and outcome information are distributed across two or more data sources without unique identifiers to link records that belong to the same entity. One way to overcome this limitation is to incorporate an initial record linkage step in the design phase of the study.

Record linkage is a set of statistical procedures that identifies individuals or entities that are shared across datasets (Jaro (1989), Winkler (1993)). Record linkage techniques can be classified into two broad classes: deterministic and probabilistic. Deterministic record linkage methods identify records that represent the same entity based on deterministic agreement functions between data elements common to both records. Probabilistic methods calculate probabilities or weights that a pair of records represents the same entity. The Fellegi-Sunter procedure estimates the probabilities of observed agreement patterns of data elements between a pair of records if these records were true links or false links (Fellegi and Sunter (1969)). These probabilities are commonly used in an iterative algorithm that classifies the pair of records with the highest probability as a link, and then removes these records from the pool of possible links. This process continues until a certain threshold is reached (Larsen and Rubin (2001)). The remaining records are either sent for clerical review or are declared non-links. Deterministic methods are used widely in practice and are reported to yield a higher proportion of true links than probabilistic methods (Gomatam et al. (2002), Campbell, Deck and Krupski (2008)). However, when the data elements are subject to variations in spelling, data entry inaccuracies, or incompleteness, deterministic methods may miss more true links than probabilistic linking methods (Gomatam et al. (2002), Campbell, Deck and Krupski (2008)). In applications involving large public health datasets, these missed links may limit the practicality of deterministic linking methods (Newman et al. (2009)). Probabilistic linkage methods are less sensitive to errors among the identifying fields, and some of these methods such as hit-miss models can account for measurement error or missingness within records (Copas and Hilton (1990)).

Both probabilistic and deterministic methods may suffer from incorrectly linked entities. Neter, Maynes and Ramanathan (1965) noted that in finite population sampling, a small amount of incorrectly linked records can lead to biased regression estimates and inflated variances. Multiple methods have been developed to reduce bias and propagate linkage errors using linear and generalized linear models (Scheuren and Winkler (1993), Scheuren and Winkler (1997), Lahiri and Larsen (2005), Chambers et al. (2009), Hof and Zwinderman (2012)). However, these methods are model specific and assume that the linkage probabilities are known or estimable. Further, all of these methods rely on the non-informative linkage assumption, which states that the outcome of interest is conditionally independent from the linkage process given the variables that appear in both files.

Bayesian file linkage procedures are probabilistic record linkage techniques that were proposed as possible solutions to overcome some of these limitations (Fortini, Liseo and Nuccitelli (2001), Larsen (2005), Tancredi and Liseo (2011), Gutman, Afendulis and Zaslavsky (2013), Steorts (2015), Steorts, Hall and Fienberg (2016), Sadinle (2017)). These methods introduce a latent structure indicating the pairing of records from one file with records from another file. By generating multiple samples from the posterior distribution of the latent linking structure, Bayesian record linkage procedures account for the uncertainty in the linkage process.

The objective of the previously mentioned Bayesian and Frequentist methods is to estimate marginal and conditional associations and not causal effects. Wortman and Reiter (2018) proposed a method for estimating causal effects using linked observational data sources and described the possible effects of errors in linkage when estimating causal effects. The proposed method incorporates record pair selection strategies that can improve treatment effect estimation when using propensity score subclassification. However, this method does not adjust for error in the linkage process, is limited to the application of propensity score subclassification, and only applies to settings in which the treatment assignment and covariates are in one file and the outcomes are in another.

Based on the potential outcome framework originally proposed by Neyman (1923) in the context of randomization-based inference in randomized experiments and generalized to other settings in Rubin (1978), we propose a joint Bayesian framework for record linkage and causal inference where one file comprises all of the covariates and observed outcome information, and the second file consists of a list of all individuals who receive the active treatment. To estimate the causal effects, we propose a computationally efficient two-stage procedure that accounts for the uncertainty in the linkage process and the unobserved potential outcomes under certain ignorability assumptions. Bayesian record linkage is performed in the first stage to inform the treatment assignment for all units in the first file. Adjustments for covariates’ imbalance and imputation of the unobserved potential outcomes are performed in the second stage. In addition, we develop a procedure to examine the sensitivity of our results to the ignorability assumptions. We apply this procedure to estimate the effect of MOW services on mortality and healthcare utilization among homebound older adults in Rhode Island, and find that MOW receipt does not have a significant effect on 30 day hospitalization rates or nursing home stays.

2. Framework.

2.1. Notation.

The potential outcomes framework posits that for a population of size $\mathcal{N}$, where $\mathcal{N}$ can be infinite, the effect of a binary treatment W on outcome Y for unit i $(i=1,\dots ,\mathcal{N})$ is the comparison of two “potential” outcomes, Y_i(0) and Y_i(1), which correspond to the two possible levels of W: W_i = 1 indicates the receipt of the active level of the treatment, and W_i = 0 indicates the receipt of the control level. We assume the stable unit treatment value assumption (SUTVA) (Rubin (1980), Rubin (1990)), so that this notation is functionally well defined. For each unit i, there is also a vector of P covariates that are unaffected by W_i, X_i = (X_i1,…, X_iP).

We assume that the observed data is distributed across two files: A and B, which comprise n_A and n_B records, respectively. The P covariates are partitioned into P₁ covariates that only appear in file A, X_A = (X₁,…, X_P1), P₂ covariates that only appear in file B, X_B = (X_P1+1,…, X_P1+P2), and P₃ covariates that appear in both files and can be used as semi-identifying information Z_A = Z_B = (X_P1+P2+1,…, X_P), where P₁ + P₂ + P₃ = P. Record l ∈ {1,…,n_A} in file A comprise X_Al, Z_Al, and the observed outcome $Y_l^{obs}$. Record j ∈ {1,…, n_B} in file B comprise X_Bj and Z_Bj. We further assume that file B represents a list of records that all receive the active treatment, such that W_j = 1, ∀j = 1 … , n_B, and that all records receiving the active treatment in file A also appear in file B, or {l ∈ A : W_l = 1} ∈ B.

We introduce a latent structure C = (C₁,…, C_nA), which represents the link designations in file B for each record in file A:

$$C_l=\{\begin{array}{cc}j\hfill & \text{if record}l\in \mathbf{A}\text{is linked with record}j\in \mathbf{B}\hfill \\ 0\hfill & \text{if record}l\in \mathbf{A}\text{is not linked with any record from file}\mathbf{B}.\hfill \end{array}\phantom{\}}$$ (1)

An immediate consequence of this definition is that all records in A with C_l > 0 receive the active treatment (W_l = 1), and the remaining records with C_l = 0 receive the control treatment (W_l = 0). The observed potential outcomes are defined as ${\mathbf{Y}}^{obs}=\{Y_l^{obs}\}$, where $Y_l^{obs}=1(C_l>0)Y_l(1)+1(C_l=0)Y_l(0)$. Note that the information in X_B for the units with C_l = 0 is missing. We define ${\mathbf{X}}_B=({\mathbf{X}}_B^{obs},{\mathbf{X}}_B^{mis})$, where ${\mathbf{X}}_B^{obs}$ represents the observed information for records in A with C_l > 0 and the records in B with j ∉ C that do not link with any record in A, and ${\mathbf{X}}_B^{mis}$ represents the unobserved information for records in A with C_l = 0 that do not link with any record in B.

To summarize, X_A, Z_A, and Y^obs are observed in A, and X_B, Z_B, and W are observed in B. The additional unobserved variables are C and ${\mathbf{Y}}^{mis}=\{Y_l^{mis}\}$, where $Y_l^{mis}=1(C_l=0)Y_l(1)+1(C_l>0)Y_l(0)$. The joint distribution of the observed and unobserved data across both files is

$$\begin{gathered} f({\mathbf{X}}_A,{\mathbf{X}}_B,{\mathbf{Z}}_A,{\mathbf{Z}}_B,\mathbf{Y}(0),\mathbf{Y}(1),\mathbf{C},\mathbf{W})= \\ f({\mathbf{X}}_A,{\mathbf{X}}_B,{\mathbf{Z}}_A,{\mathbf{Z}}_B)f(\mathbf{Y}(0),\mathbf{Y}(1)\mid {\mathbf{X}}_A,{\mathbf{X}}_B,{\mathbf{Z}}_A,{\mathbf{Z}}_B)\times \\ f(\mathbf{C}\mid {\mathbf{X}}_A,{\mathbf{X}}_B,{\mathbf{Z}}_A,{\mathbf{Z}}_B,\mathbf{Y}(0),\mathbf{Y}(1))f(\mathbf{W}\mid {\mathbf{X}}_A,{\mathbf{X}}_B,{\mathbf{Z}}_A,{\mathbf{Z}}_B,\mathbf{Y}(0),\mathbf{Y}(1),\mathbf{C}). \end{gathered}$$ (2)

2.2. Causal Estimand.

Causal treatment effects are commonly summarized by estimands, τ = τ(Y(0), Y(1), W) = τ(Y^obs, Y^mis, W), which are functions of the unit level potential outcomes of all units, on a common subset of $\mathcal{N}$ units (Rubin (1978)). A Bayesian inference for the effects of an exposure using linked data source considers the observed values X_A, ${\mathbf{X}}_B^{obs}$, Z_B, Z_A and Y^obs as a realization of random variables, and ${\mathbf{X}}_B^{mis}$, Y^mis, C, and W to be unobserved random variables. This perspective explicitly confronts the observed and missing random variables by conditioning on the observed variables in A and sampling from the posterior distribution of τ:

$$\begin{gathered} f(\tau \mid {\mathbf{X}}_A,{\mathbf{X}}_B^{obs},{\mathbf{Z}}_A,{\mathbf{Z}}_B,{\mathbf{Y}}^{obs})= \\ \int f(\tau \mid {\mathbf{X}}_A,{\mathbf{X}}_B,{\mathbf{Z}}_A,{\mathbf{Z}}_B,{\mathbf{Y}}^{obs},{\mathbf{Y}}^{mis},\mathbf{C},\mathbf{W})\times \\ f({\mathbf{X}}_B^{mis},{\mathbf{Y}}^{mis},\mathbf{C},\mathbf{W}\mid {\mathbf{X}}_A,{\mathbf{X}}_B^{obs},{\mathbf{Z}}_A,{\mathbf{Z}}_B,{\mathbf{Y}}^{obs})d({\mathbf{X}}_B^{mis},{\mathbf{Y}}^{mis},\mathbf{C},\mathbf{W}) \end{gathered}$$ (3)

Equation (3) shows that obtaining the posterior distribution of τ involves integrating over

$$\begin{gathered} f({\mathbf{X}}_B^{mis},{\mathbf{Y}}^{mis},\mathbf{C},\mathbf{W}\mid {\mathbf{X}}_A,{\mathbf{X}}_B^{obs},{\mathbf{Z}}_A,{\mathbf{Z}}_B)= \\ \frac{f({\mathbf{X}}_A,{\mathbf{X}}_B,{\mathbf{Z}}_A,{\mathbf{Z}}_B,\mathbf{Y}(0),\mathbf{Y}(1),\mathbf{C},\mathbf{W})}{\int f({\mathbf{X}}_A,{\mathbf{X}}_B,{\mathbf{Z}}_A,{\mathbf{Z}}_B,\mathbf{Y}(0),\mathbf{Y}(1),\mathbf{C},\mathbf{W})d({\mathbf{X}}_B^{mis},{\mathbf{Y}}^{mis},\mathbf{C},\mathbf{W})}. \end{gathered}$$ (4)

2.3. Simplifying Assumptions.

To perform the integration in Equation (3), we make the following simplifying assumptions. Some of these assumptions are made explicitly in many applications and some are made implicitly.

Assumption 1. The covariates that are unique to file B are independent from the potential outcomes given X_A and Z_A. Formally,

$$f(\mathbf{Y}(0),\mathbf{Y}(1),{\mathbf{X}}_B,{\mathbf{Z}}_B\mid {\mathbf{X}}_A,{\mathbf{Z}}_A)=f(\mathbf{Y}(0),\mathbf{Y}(1)\mid {\mathbf{X}}_A,{\mathbf{Z}}_A)f({\mathbf{X}}_B,{\mathbf{Z}}_B\mid {\mathbf{X}}_A,{\mathbf{Z}}_A)$$ (5)

This assumption implies that only the covariates in A are required to predict the potential outcomes, and that X_B and Z_B may only be informative for the linkage process. This assumption is valid in our application, because Z_B represents the same covariates as Z_A, and X_B is only composed of administrative variables that are not influencing the health outcomes given the clinical and demographic covariates defined in X_A. It is possible to incorporate additional covariate information in X_B by using values of ${\mathbf{X}}_B^{obs}$ for linked records in A with C_l > 0 and imputing ${\mathbf{X}}_B^{mis}$ for records with C_l = 0.

Assumption 2. The treatment assignment mechanism is a deterministic function of the linkage structure.

Because file B comprise of all units that received the active treatment, the treatment assignment for units l ∈ A can be derived as a deterministic function of their linkage status, W_l = g(C_l), where

$$W_l=\{\begin{array}{cc}1\hfill & \text{if}{C}_l>0\hfill \\ 0\hfill & \text{if}{C}_l=0.\hfill \end{array}\phantom{\}}$$ (6)

This implies that f(W∣X_A, X_B, Z_A, Z_B, Y(0), Y(1), C) is a degenerate distribution that is completely defined by C, and that τ = τ(Y(0), Y(1), W) = τ(Y^obs, Y^mis, C).

Assumption 3. The linkage is strongly non-informative.

This assumption states that C is conditionally independent from the potential outcomes and any unobserved data components. Formally,

$$f(\mathbf{C}\mid {\mathbf{X}}_A,{\mathbf{X}}_B,{\mathbf{Z}}_A,{\mathbf{Z}}_B,\mathbf{Y}(0),\mathbf{Y}(1))=f(\mathbf{C}\mid {\mathbf{X}}_A,{\mathbf{X}}_B^{obs},{\mathbf{Z}}_A,{\mathbf{Z}}_B).$$ (7)

This is a modified version of the non-informative linkage assumption commonly made when estimating non-causal associations using linked data. The implicit non-informative linkage assumption in the Fellegi-Sunter record linkage model implies that the linkage structure is conditionally independent from Y^obs, X_A, and X_B given Z_A and Z_B (Harron, Goldstein and Dibben (2015)). Equation (7) also implies that the treatment assignment is unconfounded (Rubin (1990)).

By combining Assumptions 1-3, Equation (2) can be expressed as:

$$\begin{gathered} f({\mathbf{X}}_A,{\mathbf{X}}_B,{\mathbf{Z}}_A,{\mathbf{Z}}_B,\mathbf{Y}(0),\mathbf{Y}(1),\mathbf{C},\mathbf{W})= \\ f({\mathbf{X}}_A,{\mathbf{X}}_B,{\mathbf{Z}}_A,{\mathbf{Z}}_B)f(\mathbf{Y}(0),\mathbf{Y}(1)\mid {\mathbf{X}}_A,{\mathbf{Z}}_A)f(\mathbf{C}\mid {\mathbf{X}}_A,{\mathbf{X}}_B^{obs},{\mathbf{Z}}_A,{\mathbf{Z}}_B). \end{gathered}$$ (8)

These assumptions simplify Equation (3) to:

$$\begin{gathered} f(\tau \mid {\mathbf{X}}_A,{\mathbf{X}}_B^{obs},{\mathbf{Z}}_A,{\mathbf{Z}}_B,{\mathbf{Y}}^{obs})= \\ \int f(\tau \mid {\mathbf{Y}}^{obs},{\mathbf{Y}}^{mis},\mathbf{C}),f({\mathbf{Y}}^{mis},\mathbf{C}\mid {\mathbf{X}}_A,{\mathbf{X}}_B^{obs},{\mathbf{Z}}_A,{\mathbf{Z}}_B,{\mathbf{Y}}^{obs})d({\mathbf{Y}}^{mis},\mathbf{C}). \end{gathered}$$ (9)

2.4. Parametric Models.

Given the linkage structure C, we can assume the distributions of X_Al, X_Bl, Z_Al, Z_Bl, Y_l(0), and Y_l(1) are row exchangeable. Using de-Finetti’s theorem, Equation (8) can be written as a product of independent random variables given the parameters Θ = (θ_X, θ_Y·X, θ_C) where θ_X = (θ_XA, θ_XB, θ_ZA, θ_ZB), θ_Y·X = (θ_Y1·X, θ_Y0·X), and θ_C = (θ_CM, θ_CU). When the parameters θ_X, θ_Y·X, and θ_C are a-priori independent with prior distribution p(Θ) = p(θ_X)p(θ_Y·X)p(θ_C), Equation (8) for linked and unlinked data can be expressed as:

$$\begin{gathered} f({\mathbf{X}}_A,{\mathbf{X}}_B,{\mathbf{Z}}_A,{\mathbf{Z}}_B,\mathbf{Y}(0),\mathbf{Y}(1),\mathbf{C},\mathbf{W}) \\ =\int \left[\prod _{l:C_l>0}f({\mathbf{X}}_{Al},{\mathbf{X}}_{Bl}^{obs},{\mathbf{Z}}_{Al},{\mathbf{Z}}_{Bl}\mid {\theta }_X)f(Y_l(0),Y_l(1)\mid {\mathbf{X}}_{Al},{\mathbf{Z}}_{Al},{\theta }_{Y\cdot X})\right] \\ \times \left[\prod _{l:C_l=0}f({\mathbf{X}}_{Al},{\mathbf{X}}_{Bl}^{mis},{\mathbf{Z}}_{Al},{\mathbf{Z}}_{Bl}\mid {\theta }_X)f(Y_l(0),Y_l(1)\mid {\mathbf{X}}_{Al},{\mathbf{Z}}_{Al},{\theta }_{Y\cdot X})\right] \\ \times \left[\prod _{j:j\notin \mathbf{C}}f({\mathbf{X}}_{Bj}^{obs},{\mathbf{Z}}_{Bj}\mid {\theta }_{XB},{\theta }_{ZB})\right]\times f(\mathbf{C},{\theta }_C\mid {\mathbf{X}}_A,{\mathbf{X}}_B^{obs},{\mathbf{Z}}_A,{\mathbf{Z}}_B)p({\theta }_X,{\theta }_{Y\cdot X})d\Theta . \end{gathered}$$ (10)

The information in the second line in Equation (10) represents the data components for linked records in A, the third line reflects the information for unlinked records in A, and the last product represents the unlinked records in B. The integrals over θ_X pass through the distributions for Y_l(0), Y_l(1), and C such that the marginal distribution f(X_A, X_B, Z_A, Z_B) is irrelevant for θ_Y·X and θ_C.

We will make the assumption of no contamination of imputation across treatments (Rubin (2007)):

Assumption 4. The conditional distribution of potential outcomes for the exposed and unexposed units are independent given baseline covariates, and the parameters governing their distributions are a-priori independent.

$$\begin{gathered} f(Y_l(0),Y_l(1)\mid {\mathbf{X}}_{Al},{\mathbf{Z}}_{Al},{\theta }_{Y\cdot X})=f(Y_l(0)\mid {\mathbf{X}}_{Al},{\mathbf{Z}}_{Al},{\theta }_{Y0\cdot X})f(Y_l(1)\mid {\mathbf{X}}_{Al},{\mathbf{Z}}_{Al},{\theta }_{Y1\cdot X}) \\ p({\theta }_{Y\cdot X})=p({\theta }_{Y0\cdot X})p({\theta }_{Y1\cdot X}). \end{gathered}$$ (11)

Based on this assumption, the conditional distribution for the potential outcomes is:

$$f(\mathbf{Y}(0),\mathbf{Y}(1)\mid {\mathbf{X}}_A,{\mathbf{Z}}_A)=\int \prod _{l=1}^{n_A}f(Y_l(0),Y_l(1)\mid {\mathbf{X}}_{Al},{\mathbf{Z}}_{Al},{\theta }_{Y\cdot X})p({\theta }_{Y\cdot X})d{\theta }_{Y\cdot X}$$ (12a)

$$=\int \prod _{l:C_l>0}f(Y_l(0)\mid {\mathbf{X}}_{Al},{\mathbf{Z}}_{Al},{\theta }_{Y0\cdot X})\prod _{l:C_l=0}f(Y_l(0)\mid {\mathbf{X}}_{Al},{\mathbf{Z}}_{Al},{\theta }_{Y0\cdot X})p({\theta }_{Y0\cdot X})d{\theta }_{Y0\cdot X}$$ (12b)

$$\times \int \prod _{l:C_l=0}f(Y_l(1)\mid {\mathbf{X}}_{Al},{\mathbf{Z}}_{Al},{\theta }_{Y1\cdot X})\prod _{l:C_l>0}f(Y_l(1)\mid {\mathbf{X}}_{Al},{\mathbf{Z}}_{Al},{\theta }_{Y1\cdot X})p({\theta }_{Y1\cdot X})d{\theta }_{Y1\cdot X}$$ (12c)

$$\propto \int f(\mathbf{Y}(0{)}^{mis}\mid {\mathbf{X}}_A,{\mathbf{Z}}_A,{\theta }_{Y0\cdot X})p({\theta }_{Y0\cdot X}\mid {\mathbf{X}}_A,{\mathbf{Z}}_A,\mathbf{Y}(0{)}^{obs})d{\theta }_{Y0\cdot X}$$ (12d)

$$\times \int f(\mathbf{Y}(1{)}^{mis}\mid {\mathbf{X}}_A,{\mathbf{Z}}_A,{\theta }_{Y1\cdot X})f({\theta }_{Y1\cdot X}\mid {\mathbf{X}}_A,{\mathbf{Z}}_A,\mathbf{Y}(1{)}^{obs})d{\theta }_{Y1\cdot X}.$$ (12e)

The first factor in Equation (12d) and the first factor in Equation (12e) are the posterior predictive distributions of the unobserved potential outcomes and the remaining terms in each line are the posterior distributions of θ_Y0·X and θ_Y1·X, respectively.

By combining Equation (9) with Equation (10-12), the causal estimand is:

$$\begin{gathered} f(\tau \mid {\mathbf{X}}_A,{\mathbf{X}}_B^{obs},{\mathbf{Z}}_A,{\mathbf{Z}}_B,{\mathbf{Y}}^{obs}) \\ =\int f(\tau \mid {\mathbf{Y}}^{obs},{\mathbf{Y}}^{mis},\mathbf{C})f(\mathbf{Y}(0{)}^{mis}\mid {\mathbf{X}}_A,{\mathbf{Z}}_A,{\theta }_{Y0\cdot X})p({\theta }_{Y0\cdot X}\mid {\mathbf{X}}_A,{\mathbf{Z}}_A,\mathbf{Y}(0{)}^{obs}) \\ \times f(\mathbf{Y}(1{)}^{mis}\mid {\mathbf{X}}_A,{\mathbf{Z}}_A,{\theta }_{Y1\cdot X})p({\theta }_{Y1\cdot X}\mid {\mathbf{X}}_A,{\mathbf{Z}}_A,\mathbf{Y}(1{)}^{obs}) \\ \times f(\mathbf{C},{\theta }_C\mid {\mathbf{X}}_A,{\mathbf{X}}_B^{obs},{\mathbf{Z}}_A,{\mathbf{Z}}_B)d({\theta }_C,\mathbf{C},{\theta }_{Y0\cdot X},{\theta }_{Y1\cdot X},\mathbf{Y}(0{)}^{mis},\mathbf{Y}(1{)}^{mis}). \end{gathered}$$ (13)

2.5. Record Linkage Models.

To model f(C, θ_C∣X_A, ${\mathbf{X}}_B^{obs}$, Z_A, Z_B), we will rely on the record linkage framework initially proposed by Fellegi and Sunter (1969). This framework considers the set of all possible n_A×n_B pairs of records from A and B as the union of two disjoint sets of links M = {(l, j) : l ∈ A, j ∈ B, C_l = j} and non-links U = {(l, j) : l ∈ A, j ∈ B, C_l ≠ j}. Without a loss of generality, assume n_A ≥ n_B. To ensure that each record in file A is linked to at most one record in file B and vice versa, we introduce the following constraint on $\mathbf{C}:{\sum }_{l=1}^{n_A}1\{C_l=j\}\le 1$, ∀ j = 1,…, n_B (Larsen (2005), Sadinle (2017)).

For records l ∈ A and j ∈ B, let Γ(Z_Al, Z_Bj) = (γ_lj1,…,γ_ljP3) be an agreement vector for the k = 1,…, P₃ identifying variables that exist in both files. The agreement of field k between two values can be evaluated on an ordinal scale with r_k = 1,…, R_k levels, where 1 represents complete disagreement, and R_k represents complete agreement (Winkler (1990), Sadinle (2017)). Let θ_CM = {θ_CMk} and θ_CU = {θ_CUk} represent the parameters governing the distributions of the comparison functions for record pairs in M and U, respectively, such that θ_CMk = {θ_CMkr}, where θ_CMkr = Pr(γ_ljk = r∣C_l = j) for k = 1,…,P₃ and r = 1,…,R_k, and similarly, θ_CUk = {θ_CUkr} and θ_CUkr = Pr(γ_ljk = r∣C_l ≡ j).

Mixture models have been proposed to estimate θ_CM, θ_CU, and C based on Γ(Z_Al, Z_Bj) (Jaro (1989), Larsen and Rubin (2001)):

$$\begin{gathered} \Gamma ({\mathbf{Z}}_{Al},{\mathbf{Z}}_{Bj})\mid C_l=j\sim f(\Gamma ({\mathbf{Z}}_{Al},{\mathbf{Z}}_{Bj})\mid {\theta }_{CM}) \\ \Gamma ({\mathbf{Z}}_{Al},{\mathbf{Z}}_{Bj})\mid C_l\ne j\sim f(\Gamma ({\mathbf{Z}}_{Al},{\mathbf{Z}}_{Bj})\mid {\theta }_{CU}) \\ \mathbf{C}\sim p(\mathbf{C},n_m) \end{gathered}$$ (14)

where $n_m={\sum }_{l=1}^{n_A}{\sum }_{j=1}^{n_B}1(C_l=j)$ represents the number of true links.

Let π represent the expected proportion of records that represent the same entities in both files, such that n_m ~ Binomial(n_B, π) and π ~ Beta(α_π, β_π) a-priori. Sadinle (2017) proposes a Beta-Binomial prior for C and n_m that marginalizes over π:

$$p(\mathbf{C},n_m\mid {\alpha }_{\pi },{\beta }_{\pi })=\frac{(n_A-n_m)!}{n_A!}\frac{\Gamma ({\alpha }_{\pi }+{\beta }_{\pi })}{\Gamma ({\alpha }_{\pi })\Gamma ({\beta }_{\pi })}\frac{\Gamma (n_m+{\alpha }_{\pi })\Gamma (n_B-n_m+{\beta }_{\pi })}{\Gamma (n_m+{\alpha }_{\pi })}.$$ (15)

A simplifying assumption that is frequently made in the Fellegi and Sunter record linkage model is that each of the comparison functions are conditionally independent given C (Winkler (1988), Jaro (1989)). Under this assumption, the likelihood for C, θ_CM, θ_CU is

$$\mathcal{L}(\mathbf{C},{\theta }_{CM},{\theta }_{CU}\mid {\mathbf{Z}}_A,{\mathbf{Z}}_B)=\prod _{l=1}^{n_A}\prod _{j=1}^{n_B}\prod _{k=1}^K\prod _{r_k=1}^{R_k}{\left[{\theta }_{CMkr}^{1({\gamma }_{ljk}=r)}\right]}^{1(C_l=j)}{\left[{\theta }_{CUkr}^{1({\gamma }_{ljk}\ne r)}\right]}^{1(C_l\ne j)}$$ (16)

Independent conjugate priors θ_CMk ~ Dirichlet(α_Mk1,…, α_MkRk) and θ_CUk ~ Dirichlet(α_Uk1,…, α_UkRk) for k = 1,…, K can be specified to complete the Bayesian model.

To sample from $f(\mathbf{C},{\theta }_C\mid {\mathbf{Z}}_A,{\mathbf{Z}}_B)\propto p(\mathbf{C})p({\theta }_C)\mathcal{L}(\mathbf{C},{\theta }_C\mid \mathbf{Z})$, we will use the data augmentation algorithm (Tanner and Wong (1987)). The I-Step involves drawing C^[t+1] from $f(\mathbf{C}\mid {\mathbf{Z}}_A,{\mathbf{Z}}_B,{\theta }_C^{[t]})$ and the P-step will update values of ${\theta }_C^{[t+1]}$ from f(θ_C∣Z_A, Z_B, C^[t+1]) (see Appendix A for a detailed description).

2.6. Causal Treatment Effect Estimation.

The record linkage facilitates the identification of the exposed and unexposed units, but it does not guarantee that units are similar across treatment groups. When the distribution of covariates between the treatment and control groups are different, simple comparison of the two groups may result in biased estimates of the treatment effect (Rubin (1973a), Rubin (1973b)). Several types of procedures have been proposed to address this issue when the treatment effect is unconfounded (Imbens and Rubin (2015), Gutman and Rubin (2017)).

Matching is a design phase causal estimation technique that reduces bias by identifying units with similar covariate values between the two treatment groups (Stuart (2010)). With a single covariate, it is often easy to identify a match. This task is more complicated with multiple covariates (Stuart (2010)). Matching on the propensity score (Rosenbaum and Rubin (1983)), which is the probability of W_l = 1 given the covariates, was proposed as a possible solution. Formally, the propensity score for unit l is defined as e(X_Al, Z_Al) ≡ f(W_l∣X_Al, Z_Al, ϕ), where ϕ are the parameters governing this distribution. Point estimates of τ using matching have been shown to be consistent, but may underestimate its sampling variance when ignoring the variability in the matching procedure (Abadie and Imbens (2011), Gutman and Rubin (2017)). In addition, because matching on e(X_Al, Z_Al) is not exact, some covariates may still suffer from minor imbalances, which is often addressed using regression adjustments (Imbens and Rubin (2015)).

A different approach to estimate τ is to combine matching with a Bayesian imputation framework (Rubin (2007), Gutman and Rubin (2013), Gutman and Rubin (2015)). This combination reduces the bias resulting from minor covariate imbalances and increases precision by using modeling to impute Y^mis. Under the Bayesian causal inference framework, the missing potential outcomes are taken to be unobserved random variables that can be sampled from their posterior predictive distribution. Because sampling from a posterior distribution is complex, we use a multiple imputation procedure as an approximation of the posterior distribution of Y^mis (Gutman and Rubin (2013), Gutman and Rubin (2015)).

2.7. Two-Stage Multiple Imputation Estimation Procedure.

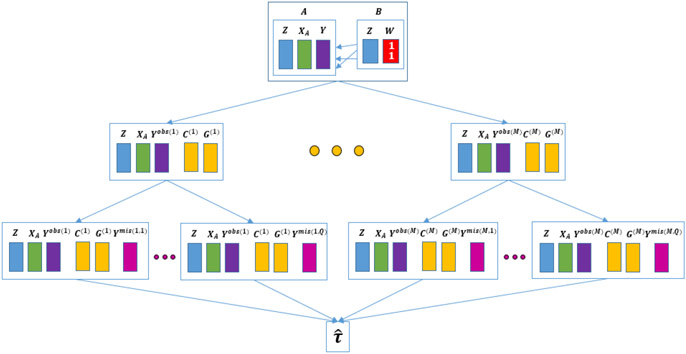
Equation (13) suggests a two-step estimation procedure. In the first step, the record linkage structure is sampled. Using this linkage structure, the potential outcomes are imputed in the second step.

We now explicate and summarize this two stage multiple imputation approach (Shen (2000), Rubin (2003)) to estimate τ

1. Sample C^(m) from f(C, θ_C∣X_A, ${\mathbf{X}}_B^{obs}$, Z_A, Z_B) for m = 1,…,M random draws (Appendix A).

2. For C^(m), m = 1,…,M,

   1. Perform nearest neighbor matching using the estimated the propensity score $\widehat{e}({\mathbf{X}}_A,{\mathbf{Z}}_A{)}^{(m)}$ to obtain a sample of exposed and unexposed units with similar covariate distributions. Let G^(m) = 1 represent the units in this matched sample.
   2. For the units with ${\mathbf{G}}_l^{(m)}=1$, partition Y(0), Y(1) into Y^obs(m) and Y^mis(m).
   3. Sample ${\theta }_{Y0\cdot X}^{(m,q)}$, q = 1,…, Q, from p(θ_Y0·X∣X_A, Z_A, Y(0)^obs(m), G^(m) = 1) and ${\theta }_{Y1\cdot X}^{(m,q)}$ from p(θ_Y1·X∣X_A, Z_A, Y(1)^obs(m), G^(m) = 1).
   4. For each q = 1,…, Q, use ${\theta }_{Y0\cdot X}^{(m,q)}$ and ${\theta }_{Y1\cdot X}^{(m,q)}$ to independently impute the missing potential outcomes for each unit in G^(m) = 1 from the posterior predictive distributions $f(\mathbf{Y}(0{)}^{mis}\mid {\mathbf{X}}_A,{\mathbf{Z}}_A,{\mathbf{G}}^{(m)}=1,{\theta }_{Y0\cdot X}^{(m,q)})$ and $f(\mathbf{Y}(1{)}^{mis}\mid {\mathbf{X}}_A,{\mathbf{Z}}_A,{\mathbf{G}}^{(m)}=1,{\theta }_{Y1\cdot X}^{(m,q)})$. This will result in Q datasets with imputed Y(0)^mis and Y(1)^mis for the matched units.

3. For each of the M×Q imputations, estimate the treatment effect ${\widehat{\tau }}^{(m,q)}$ and the within imputation sampling variance, U^(m,q).

4. The point estimate of the treatment effect τ is calculated as $\widehat{\tau }=\frac{1}{MQ}{\sum }_{m=1}^M{\sum }_{q=1}^Q{\widehat{\tau }}^{(m,q)}$. The total variance can be derived according to Shen (2000) as $T=\widehat{U}+(1+M^{-1})B+(1-Q^{-1})W$, where $\widehat{U}=\frac{1}{MQ}{\sum }_{m=1}^M{\sum }_{q=1}^Q{U}^{(m,q)}$, $B=\frac{1}{M-1}{\sum }_{m=1}^M({\overline{\tau }}^{(m.)}-\widehat{\tau }{)}^2$, and $W=\frac{1}{M}{\sum }_{m=1}^M\frac{1}{Q-1}{\sum }_{q=1}^Q({\widehat{\tau }}^{(m,q)}-{\overline{\tau }}^{(m.)}{)}^2$. Inference for $\widehat{\tau }$ is based on a t-distribution $(\tau -\widehat{\tau })∕\sqrt{T}\sim t_{\nu }$ with ${\nu }^{-1}=\frac{1}{M-1}{\left(\frac{(1+1∕M)B}{T}\right)}^2+\frac{1}{M(Q-1)}{\left(\frac{(1-1∕Q)W}{T}\right)}^2$.

An illustration of this two-stage multiple imputation procedure is presented in Figure 1.

Fig 1.

Two Stage Multiple Imputation Procedure

3. Application to Meals on Wheels Data.

We applied the proposed procedure to estimate the effects of Meals on Wheels (MOW) programs on mortality and healthcare utilization among Medicare beneficiaries. We compared the difference in mortality rate after 30 days of initiating meal delivery service, and the difference in the frequency of acute inpatient, emergency department (ED), and nursing home (NH) events between MOW recipients and non-recipients who were alive after 30 days of enrollment in both the observed treatment and predicted control arms. Because we do not expect MOW receipt to influence mortality, identification of such an effect may indicate potential violations of the unconfoundedness assumption.

3.1. Data Description.

A comprehensive list of all clients who received home-delivered meals between January 1, 2010 and December 31, 2013 was submitted by Meals on Wheels Rhode Island (MOWRI), which serves the entire state of Rhode Island. This list contained information on each client’s sex, date of birth, start and end date of service, and the 9-digit ZIP code corresponding to the address where their meal was delivered. While MOW serves clients of a variety of ages, we restricted the analysis only to individuals older than 65 at enrollment in MOW, because only those individuals are expected to be enrolled in Medicare. This resulted in a total of n_B = 3,916 MOW recipients.

The Medicare Master Beneficiary Summary File (MBSF) is a comprehensive database that contains demographic information on all Medicare enrollees including gender, date of birth, date of death, and the 9-digit ZIP code corresponding to their mailing address. In addition, the MBSF identifies pre-existing chronic medical conditions including congestive heart failure, kidney failure, diabetes, pelvic fracture, stroke, dementia or Alzheimer’s disease, chronic obstructive pulmonary disease, coronary artery disease, and various types of cancer. Using unique identifiers, the MBSF is linked to Medicare inpatient, outpatient, skilled nursing facility, and home health claims as well as the nursing home Minimum Data Set (MDS) between calendar years 2009 and 2014. These claims and assessment data were used to calculate the frequency and cost of inpatient events, emergency department visits, nursing home stays, and home health utilization in the 30, 90, and 180 days prior to enrollment in MOW, as well as the frequency of acute inpatient, ED, and NH events 30 days following MOW enrollment. A total of n_A = 179,269 Medicare beneficiaries over the age of 65 resided in the 5-digit ZIP codes serviced by MOWRI.

3.2. Record Linkage of MOW and Medicare Data.

Comparison of all possible record pairs, where one record appears in the MOW file and another record in the Medicare file would result in over 700 million possible record pairs. “Blocking” is a common record linkage to reduce the computational complexity by only considering record pairs that agree on specific blocking fields (Newcombe et al. (1959), Newcombe (1988)). We generated blocks based on 5-digit ZIP codes and gender (Herzog, Scheuren and Winkler (2007)). We assumed that θ_CM and θ_CU do not differ across blocks, and we restricted record pairs such that the MOW enrollment date precedes the date of death in the Medicare file. These criteria reduced the total number of possible record pairs to 13,786,172. A sensitivity analysis of our results to this blocking criteria is provided in Appendix D.

A recipient’s date of birth (DOB) and 9-digit ZIP code were used as linking variables to classify record pairs into links and non-links. Ordinal agreement patterns were used for both linking variables, whose levels of agreement are described in Table 1. In addition, we modeled the interaction between agreement on DOB and ZIP code (Winkler (1989)). The resulting record linkage likelihood is

$$\begin{gathered} \mathcal{L}(\mathbf{C},{\theta }_{CM},{\theta }_{CU}\mid \Gamma ({\mathbf{Z}}_A,{\mathbf{Z}}_B))= \\ \prod _{l=1}^{n_A}\prod _{j=1}^{n_B}\prod _{r_D=1}^4\prod _{r_Z=1}^5{\left[{\theta }_{CMD{r}_D}^{1({\gamma }_{ljD}=r_D)}{\theta }_{CMZ{r}_Z\mid r_D}^{1({\gamma }_{ljZ}=r_Z,{\gamma }_{ljD}=r_D)}\right]}^{1(C_l=j)1(B_{lj}=1)} \\ \times {\left[{\theta }_{CUD{r}_D}^{1({\gamma }_{ljD}=r_D)}{\theta }_{CUZ{r}_Z\mid r_D}^{1({\gamma }_{ljZ}=r_Z,{\gamma }_{ljD}=r_D)}\right]}^{1(C_l\ne j)1(B_{lj}=1)} \end{gathered}$$ (17)

where B_lj is an indicator that record pair (l, j) was successfully blocked and met the MOW enrollment date constraint, and θ_CM = {θ_CMD, θ_CMZ} and θ_CU = {θ_CUD, θ_CUZ} are the parameters governing the distribution of agreement functions, such that θ_CMD = {θ_CMDrD}, θ_CMZ = {θ_CMZrZ∣rD}, θ_CUD = {θ_CUDrD}, θ_CUZ = {θ_CUZrZ∣rD}. Each θ_CMDrD = Pr(γ_ljD = r_D∣C_l = j, B_lj = 1), θ_CMZrZ∣rD = Pr(γ_ljZ = r_Z∣γ_ljD = r_D, C_l = j, B_lj = 1), θ_CUDrD = Pr(γ_ljD = r_D∣C_l ≠ j, B_lj = 1), and θ_CUZrZ∣rD = Pr(γ_ljZ = r_Z∣γ_ljD = r_D, C_l ≠ j, B_lj = 1) for r_D = 1,…,4 and r_Z = 1,…,5. A total of M = 100 different linkage structures were imputed from the linkage algorithm.

Table 1.

Linking Variable Description and Agreement Level

Agreement Type	Level
Disagreement on DOB	rD = 1
Agree on DOB Year only	rD = 2
Agree on DOB Year and Month only	rD = 3
Agree on DOB Year, Month, and Day	rD = 4
Agree on first 5 digits of ZIP code only	rZ = 1
Agree on first 6 digits of ZIP code only	rZ = 2
Agree on first 7 digits of ZIP code only	rZ = 3
Agree on first 8 digits of ZIP code only	rZ = 4
Agree on all 9 digits of ZIP code	rZ = 5

3.3. Propensity Score Matching.

Each of the m = 1,…, M linked datasets identifies Medicare beneficiaries who received MOW and those who did not. Prior research suggested that MOW programs target older adults who have higher social and economic needs and are at higher risk for institutional care (Lloyd and Wellman (2015), Lee, Shannon and Brown (2015)). Thus, enrollment in MOW programs may be confounded with pre-existing health conditions or prior healthcare utilization. To reduce covariates’ imbalances, matching on the estimated propensity score was performed.

Prior to matching, all linked individuals who were enrolled in a Medicare Advantage (MA) program in the six months prior to receiving MOW, or were enrolled in MA during the month they began MOW, were removed. This truncation was implemented because MA plans are not required to submit claims, and it was not possible to fully observe the prior history of chronic conditions or healthcare utilization for these individuals. A start date for individuals who are not enrolled in MOW programs is not available. Instead, for individuals who were not linked to MOW records, we calculated the medical history and prior healthcare utilization at the start of each quarter for every year in our study period. This resulted in sixteen sets of pre-treatment covariates calculated at different potential enrollment dates for each unlinked individual.

Matching was implemented by enforcing exact agreement on patients’ gender, race, age categories, and whether the patients had any inpatient, ER, or SNF claim in the 90 days prior to enrollment. The remaining covariates were balanced using propensity score models that included pre-existing medical conditions, prior healthcare utilization frequency, and prior healthcare costs. We selected nearest pair matches without replacement based on the propensity score within each quarter (Stuart (2010)). This process was replicated on each of the M = 100 linked datasets to identify beneficiaries that resemble MOW recipients, but did not enroll in the program.

3.4. Imputation of Unobserved Outcomes.

To assess the impact of MOW on mortality, we examine the average treatment effect on the treated (ATT) among linked MOW clients who are matched to a control individual. Let D_l(1) and D_l(0) represent the potential 30 day mortality for individual l had they received meals or not, respectively. The estimand of interest is τ_ATT = E(D(1) − D(0)∣W = 1, G = 1), which can be estimated within each imputation as

$${\widehat{\tau }}_{ATT}^{(m,q)}=\frac{1}{n_G^{(m)}}\sum _{l:C_l^{(m)}>0,G_l^{(m)}=1}(D_l(1{)}^{(m)}-D_l(0{)}^{(m,q)}),$$ (18)

where $n_G^{(m)}$ represents the number of linked MOW clients matched with a control. To predict the unobserved 30 day mortality for MOW clients had they not received meals, we used a Bayesian logistic regression model that included the covariates used in matching, X_Al1, … X_AlP1, and all of their two-way interactions:

$$logit(P(D_l(0)=1))={\beta }_0+\sum _{p=1}^{P_1}{\beta }_p{X}_{Alp}+\sum _{p=1}^{P_1}\sum _{s=1}^{p-1}{\delta }_{ps}{X}_{Alp}{X}_{Als}.$$ (19)

A one-level hierarchical Normal-Gamma shrinkage prior (Griffin and Brown (2017)) was constructed for the coefficients of the main effect and interaction terms such that ${\beta }_p\stackrel{\text{iid}}{\sim }N(0,{\Phi }_1)$, Φ₁ ~ Gamma(1, 1), ${\delta }_{ps}\stackrel{\text{iid}}{\sim }N(0,{\Phi }_2)$, and Φ₂ ~ Gamma(1, 2). These prior distributions attenuate interaction terms more aggressively. We also assumed that β₀ ~ N(0, 10000).

To examine the impact of MOW on healthcare utilization, we estimate the survivor average treatment effect on the treated (SATT), which compares the effect of MOW receipt among MOWRI clients who would be alive 30 days after their enrollment date irrespective of whether they received services from MOW or not (Frangakis and Rubin (2002), Rubin (2006), Frangakis et al. (2007)). The SATT is defined as τ_SATT = E(H(1) − H(0)∣W = 1, D(0) = D(1) = 0, G = 1), where H(1) and H(0) denote the potential utilization frequency among MOW clients and controls, respectively. An estimate for the SATT within each imputation is estimated as

$${\widehat{\tau }}_{SATT}^{(m,q)}=\frac{1}{n_S^{(m,q)}}\sum _{\begin{array}{c}\hfill l:C_l^{\left(m\right)}>0,G_l^{\left(m\right)}=1\hfill \\ \hfill D_l(1{)}^{\left(m\right)}=D_l(0{)}^{(m,q)}=0\hfill \end{array}}(H_l(1{)}^{\left(m\right)}-H_l(0{)}^{(m,q)})$$ (20)

where $n_S^{(m,q)}$ is the number of linked individuals that were matched to a control and who are alive after 30 days following enrollment according to their observed and predicted mortality status.

Bayesian zero-inflated negative binomial models were fitted to impute the frequency of inpatient admissions, emergency department visits, and nursing home stays among MOW clients had they not received meals within each imputed linkage structure. The zero-inflated negative binomial distribution for count response H_l(0) is given by

$$P(H_l(0)=h)=\{\begin{array}{cc}{\pi }_l+(1-{\pi }_l){\left(\frac{\alpha }{{\mu }_l+\alpha }\right)}^{\alpha }\hfill & H_l(0)=0\hfill \\ (1-{\pi }_l)\frac{\Gamma (H_l(0)+\alpha )}{\Gamma (H_l(0)+1)\Gamma (\alpha )}{\left(\frac{{\mu }_l}{{\mu }_l+\alpha }\right)}^{H_l(0)}{\left(\frac{\tau }{{\mu }_l+\alpha }\right)}^{\alpha }\hfill & H_l(0)>0.\hfill \end{array}\phantom{\}}$$ (21)

where α represents the shape parameter,

$$log({\mu }_l)={\zeta }_0+\sum _{p=1}^{P_1}{\zeta }_p{X}_{Alp}+\sum _{p=1}^{P_1}\sum _{s=1}^{p-1}{\eta }_{ps}{X}_{Alp}{X}_{Als}.$$ (22)

and

$$logit({\pi }_l)={\psi }_0+\sum _{p=1}^{P_1}{\psi }_p{X}_{Alp}+\sum _{p=1}^{P_1}\sum _{s=1}^{p-1}{\xi }_{ps}{X}_{Alp}{X}_{Als},$$ (23)

The negative binomial component is modeled in Equation (22) and Equation (23) models the zero-inflation. To complete the Bayesian model, we assumed that ${\zeta }_p\stackrel{\text{iid}}{\sim }N(0,{\Phi }_3)$, Φ₃ ~ Gamma(1, 1), ${\eta }_{ps}\stackrel{\text{iid}}{\sim }N(0,{\Phi }_4)$, Φ₄ ~ Gamma(1, 2), ${\psi }_p\stackrel{\text{iid}}{\sim }N(0,{\Phi }_5)$, Φ₅ ~ Gamma(1, 1), ${\xi }_{ps}\stackrel{\text{iid}}{\sim }N(0,{\Phi }_6)$, and Φ₆ ~ Gamma(1, 2). Lastly, τ ~ U(0, 1000), ζ₀ ~ N(0, 10000) and ψ₀ ~ N(0, 10000). All models were fit using Rstan version 2.17.2 (Stan Development Team (2018)). All outcomes were imputed for 100 datasets within each of the 100 linked datasets, resulting in M × Q = 10,000 complete datasets.

4. Results.

Of the n_B = 3916 MOW clients eligible for linkage to Medicare data, an average of ${\overline{n}}_m=3608.02$ records (95% CI: 3570.91, 3645.14) were linked over M = 100 imputations. Among the Medicare beneficiaries that were linked to MOW clients, an average of 1748.35 (95% CI: 1735.28, 1761.44) individuals had at least 1 month of MA coverage in the 6 months prior to enrollment and were excluded from our analysis. Of the remaining linked individuals, an average of 1859.67 (95% CI: 1835.63, 1883.70) treated units were matched to a control unit that did not receive meals.

Figure 2 displays the median and range of absolute standardized differences for each of the pre-treatment variables between the MOW and control samples before and after matching for the M = 100 linked datasets. The absolute standardized difference exceeded 0.25 in 22 out of the 40 covariates prior to matching. After matching, all absolute standardized differences are less than 0.25 for all covariates, which suggests that the covariates are adequately balanced (Rosenbaum and Rubin (1985), Imbens and Rubin (2015)).

Fig 2.

Covariate balance before and after propensity score matching for M = 100 linked data sets. The points represent the median absolute standardized differences, while the horizontal lines represent the range between the minimum and maximum absolute standardized difference for each covariate.

The observed and imputed potential outcomes for MOW clients, and the estimated treatment effects are provided in Table 1. The estimated ATT on mortality using our two-stage multiple imputation procedure is 0.008 (95% CI: −0.067, 0.083). This indicates that there is no significant difference between the observed and predicted mortality rate among the linked and matched MOW clients. An average of 51.21 individuals died within 30 days of their MOW enrollment or were predicted to die within 30 days without MOW services. This results in an average of 1808.46 individuals who are alive whether they received MOW or not across imputations. Among these individuals, the estimated SATTs are 0.010 (95% CI: −0.174, 0.194) on inpatient acute admissions, −0.013 (95% CI: −0.236, 0.209) on ED visits, and 0.003 (95% CI: −0.268, 0.274) for NH stays. This suggests that among MOW recipients who would be alive 30 days after enrollment irrespective of whether they received MOW or not, no significant differences in the number of acute inpatient admissions, ED visits, or NH stays are detected.

5. Sensitivity Analysis.

5.1. Sensitivity of the Strongly Non-Informative Linkage Assumption.

We examine the sensitivity of our results to the strongly non-informative linkage assumption (Assumption 3). Under Assumption 3, errors in the linkage only depend on comparisons of semi-identifying information that exists in both files. Thus, the probability of record l ∈ A forming a link with record j ∈ B given C(_−l) = (C_l′ : l′ ≠ l} is (see Appendix B for additional details)

$$P(C_l=j\mid \Gamma ({\mathbf{Z}}_{Al},{\mathbf{Z}}_{Bj}),{\theta }_{CM},{\theta }_{CU},{\mathbf{C}}_{(-l)})\propto \frac{f(\Gamma ({\mathbf{Z}}_{Al},{\mathbf{Z}}_{Bj})\mid {\theta }_{CM})}{f(\Gamma ({\mathbf{Z}}_{Al},{\mathbf{Z}}_{Bj})\mid {\theta }_{CU})}1(j\notin {\mathbf{C}}_{(-l)}).$$ (24)

To examine the impact of potential violations of the strongly non-informative linkage assumption on the estimation of the treatment effect, we assume that the errors in the linkage model depend on 30-day mortality status. Let $D_{lj}^{obs}$ be an indicator that is equal to 1 if individual l ∈ A died within 30 days of the start date indicated by record j ∈ B. Let λ_M and λ_U represent parameters governing the distribution of $D_{lj}^{obs}$ for links and non-links, respectively. We assume that the distribution of $D_{lj}^{obs}$ is

$$f(D_{lj}^{obs}\mid C_l,{\lambda }_M,{\lambda }_U)=\{\begin{array}{cc}{\lambda }_M^{D_{lj}^{obs}}\hfill & \text{if}{C}_l=j\hfill \\ {\lambda }_U^{D_{lj}^{obs}}\hfill & \text{if}{C}_l\ne j.\hfill \end{array}\phantom{\}}$$

The posterior probability of individual l ∈ A linking with individual j ∈ B given C_(−l) will then take the form

$$\begin{gathered} P(C_l=j\mid \Gamma ({\mathbf{Z}}_{Al},{\mathbf{Z}}_{Bj}),D_{lj}^{obs},{\theta }_{CM},{\theta }_{CU},{\lambda }_M,{\lambda }_U,{\mathbf{C}}_{(-l)})\propto \\ \frac{f(\Gamma ({\mathbf{Z}}_{Al},{\mathbf{Z}}_{Bj})\mid {\theta }_{CM})}{f(\Gamma ({\mathbf{Z}}_{Al},{\mathbf{Z}}_{Bj})\mid {\theta }_{CU})}\frac{f(D_{lj}^{obs}\mid {\lambda }_M)}{f(D_{lj}^{obs}\mid {\lambda }_U)}1(j\notin {\mathbf{C}}_{(-l)}). \end{gathered}$$ (25)

A violation of the strongly non-informative linkage assumption influences the likelihood of record pairs by a sensitivity factor of $\Delta ={\left(\frac{{\lambda }_M}{{\lambda }_U}\right)}^{D_{lj}^{obs}}$. When Δ = 0, Assumption 3 is valid. Values of Δ > 1 suggest that MOWRI was more likely to enroll individuals who may die shortly after enrollment. Values of Δ < 1 represent scenarios where MOWRI may have selectively avoided enrolling individuals who may die shortly after enrollment.

To estimate the effect of the sensitivity parameter on the outcomes, we implement the algorithm in Section 2.7 after replacing f(C, θ_C∣X_A, ${\mathbf{X}}_B^{obs}$, Z_A, Z_B) in Step 1 with Equation (25).

5.2. Sensitivity Analysis Results.

The average number of records linked for different values of Δ is presented in Table 3. Because a small proportion of the linked individuals die within 30 days after enrollment when Δ = 1, decreasing the sensitivity parameter does not yield significantly lower amounts of linked records. However, increasing the sensitivity parameter significantly increases the number of linked records, specifically record pairs that indicate death within 30 days of enrollment. At Δ = 100, the narrow confidence interval indicates the linkage algorithm links almost all of the MOW records to the Medicare enrollment file.

Table 3.

Sensitivity Analysis Linkage Results

Δ	${\overline{n}}_m$	95% CI
1/100	3566.74	(3521.15, 3612.33)
1/50	3571.50	(3529.74, 3613.26)
1/10	3580.75	(3537.22, 3624.29)
1/5	3589.74	(3549.78, 3629.70)
1/2	3607.69	(3563.14, 3652.24)
1	3608.02	(3570.91, 3645.14)
2	3610.76	(3575.98, 3645.54)
5	3662.55	(3621.70, 3703.40)
10	3714.30	(3677.96, 3750.64)
50	3844.21	(3821.23, 3867.19)
100	3874.40	(3860.50, 3888.31)

The difference in 30-day mortality rate and inpatient acute utilization rate for the various sensitivity levels are presented in Table 4. The estimated mortality difference is similar for values of Δ ≤ 1. While the difference in mortality between MOW clients and controls is negative when Δ = 1/100, this effect is small and insignificant. When Δ ≥ 50, the mortality difference is significant and MOW is estimated to increase mortality among their clients. This results from clients who die within 30 days being added to the linked sample, and subsequently being removed from the potential control cohort to be matched. When Δ = 100, the sensitivity parameter trumps the linkage likelihood such that many MOW clients are linked to Medicare records indicating 30 day mortality despite major disagreements between the linking information in Z_A and Z_B. Assuming that MOW beneficiaries are 50-100 times more likely to die within 30 days of enrollment is highly implausible. The SATT of MOW on inpatient acute admission frequency does not significantly differ across the sensitivity scenarios. These results imply that our analysis is robust to the strongly non-informative linkage assumption with regards to mortality. Similar results were observed for inpatient acute hospitalization (data not shown).

Table 4.

Sensitivity Analysis Causal Treatment Effect Estimates

	30 Day Mortality		30 Day Inpatient Acute
Δ	${\widehat{\tau }}_{ATT}$	95% CI	${\widehat{\tau }}_{SATT}$	95% CI
1/100	−0.006	(−0.055, 0.044)	0.006	(−0.125, 0.137)
1/50	0.004	(−0.070, 0.078)	0.009	(−0.178, 0.197)
1/10	0.005	(−0.070, 0.081)	0.009	(−0.178, 0.195)
1/5	0.006	(−0.068, 0.081)	0.009	(−0.177, 0.196)
1/2	0.007	(−0.067, 0.082)	0.010	(−0.178, 0.197)
1	0.008	(−0.067, 0.083)	0.010	(−0.176, 0.196)
2	0.010	(−0.066, 0.086)	0.010	(−0.174, 0.194)
5	0.016	(−0.059, 0.092)	0.010	(−0.173, 0.193)
10	0.025	(−0.052, 0.102)	0.010	(−0.175, 0.194)
50	0.086	(0.002, 0.170)	0.014	(−0.170, 0.198)
100	0.549	(0.412, 0.686)	0.079	(−0.120, 0.277)

6. Discussion.

We have proposed a novel Bayesian framework to estimate causal treatment effects using linked data sources. We examine a linkage scenario that combines covariate information and outcome information from one file with the treatment assignment defined by a second file. Under a series of conditional independence and ignorability assumptions, we provide a two-stage multiple imputation procedure to obtain statistically valid treatment effect point and interval estimates. This procedure accounts for both the errors in the linkage and the unobserved outcomes. The first stage of the procedure imputes the linkage structure, and the missing potential outcomes are imputed in the second stage. Because the strong non-informative linkage assumption cannot be examined using observed data, we developed a sensitivity analysis to assess its violations.

In the linkage setting that we considered, all of the records in file B receive the active treatment. This allows us to derive the treatment assignment as a deterministic function of the linkage status for records in file A. More research and possibly stronger assumptions are required to estimate treatment effects in different linkage scenarios, such as when one file contains the treatment assignment and some of the covariates, while the other file includes the rest of the covariates and the observed outcomes. In addition, the proposed linkage algorithm is based on the Fellegi-Sunter framework, which does not account for relationships between variables that are exclusive to one file. A possible extension would be to incorporate such relationships as described in Gutman, Afendulis and Zaslavsky (2013). The modularity of our procedure allows for adjustment of the record linkage algorithm without the need to adjust the causal inference component.

We applied our framework to estimate the effect of receiving services from a MOW program in Rhode Island on mortality and healthcare utilization for its clients. Our analysis suggested that MOW does not have a significant impact on reducing 30 day mortality among its clients. Furthermore, among clients who would be alive after 30 days irrespective of MOW services, no significant differences in the frequency of acute inpatient admissions, ED visits, or NH stays are observed. A sensitivity analysis that examined the strong non-informative linkage assumption showed that our analysis is robust against potential violations of this assumption. However, this assumption may not be valid in different applications, and designing procedures that relax this assumption is an area for future research.

A major limitation of Bayesian record linkage procedures is that they are computationally intensive, and commonly require specialized programming that most non-technical researchers cannot implement. We have addressed these issues by utilizing two-stage multiple imputation and blocking. Both of these techniques reduce the computational complexity and enable nontechnical researchers to perform the causal inference analyses while scaling down the record linkage complexity. Multiple imputation has been widely used in other missing data applications, and was shown to provide valid inferences (Rubin (1996)). We have examined the performance of our proposed two-stage imputation in simulation analyses (Appendix C). The results show that the procedure provides valid statistical inference, but that the coverage is higher than nominal. This implies that the proposed procedure may overestimate the sampling variance. Increased efficiency of such procedures is a future area of research.

Using blocking increases the computational efficiency and scalability of the record linkage procedure. However, it may exclude true links and influence subsequent inferences (Murray (2015)). We have examined the performance of our two-stage procedure with stricter and looser blocking criteria (Appendix D). Using a single CPU, the current runtime of our linkage algorithm was approximately 18 days. Loosening the blocking criteria such that the number of record pairs was more than 4 times larger resulted in a runtime of approximately 30 days. The point estimates were relatively similar for the strict and loosened blocking criteria, but the stricter criteria had larger sampling variance because less record pairs were linked. This shows that our algorithm is relatively efficient and that inferences were robust to blocking. Use of parallel computing, more efficient programming languages, and improvement of the MCMC sampling procedure based on ideas proposed by Zanella (2019) may improve the scaling of the proposed algorithm to even larger settings.

In conclusion, this manuscript describes a statistical framework to estimate causal effects using linked datasets where one file contains the covariates and the observed outcome and the second file contains the treatment assignment. Under the strongly non-informative linkage assumption we develop a two stage multiple imputation procedure that provides statistically valid treatment effect estimates, and we describe a sensitivity analysis for this assumption.

Table 2.

Estimated Causal Treatment Effects on MOW Recipients.

30 Day Outcome	${\overline{n}}_G$	$\overline{\mathbf{D}}(1)$	$\overline{\mathbf{D}}(0)$	${\widehat{\tau }}_{ATT}$	95% CI
Mortality	1859.67	0.023(0.001)	0.015(0.004)	0.008	(−0.067, 0.083)
30 Day Outcome	${\overline{n}}_S$	$\overline{\mathbf{H}}(1)$	$\overline{\mathbf{H}}(0)$	${\widehat{\tau }}_{SATT}$	95% CI
Inpatient Acute	1808.46	0.085(0.002)	0.075(0.010)	0.010	(−0.174, 0.194)
Emergency Care	1808.46	0.073(0.002)	0.088(0.012)	−0.013	(−0.236, 0.209)
Nursing Home	1808.46	0.078(0.003)	0.075(0.015)	0.003	(−0.268, 0.274)

${\overline{n}}_G$ is the average sample size of MOW individuals linked and matched to a control individual across M = 100 imputations. ${\overline{n}}_S$ is the average number of linked and matched MOW individuals who are observed and predicted to be alive irrespective of their treatment, across M × Q = 10,000 imputations. $\overline{\mathbf{D}}(1)$ and $\overline{\mathbf{D}}(0)$ represent the mortality rates for linked and matched MOW individuals if they received MOW or not, respectively. $\overline{\mathbf{H}}(1)$ and $\overline{\mathbf{H}}(0)$ are the estimated healthcare utilization rates for linked and matched individuals who are alive for 30 days irrespective of whether they received MOW or not, respectively. ${\widehat{\tau }}_{ATT}$ is the estimated average treatment effect on the treated and ${\widehat{\tau }}_{SATT}$ is the survivor average treatment effect on the treated

APPENDIX A: RECORD LINKAGE GIBBS SAMPLING ALGORITHM

A Gibbs sampling algorithm proposed by Sadinle (2017) can be used to iterate between sampling the posterior distributions of the linking parameters and the linking configuration given the observed data. Starting with initial values for C, we sample from f(C, θ_C∣X_A, ${\mathbf{X}}_B^{obs}$, Z_A, Z_B) using the following procedure:

1. Sample new values of ${\theta }_{CMk}^{[t+1]}$ from

   $$\begin{gathered} {\theta }_{CMk}^{[t+1]}\mid {\mathbf{C}}^{[t]},\Gamma ({\mathbf{Z}}_{Alk},{\mathbf{Z}}_{Bjk})\sim Dirichlet({\alpha }_{Mk1}+\sum _{l=1}^{n_A}\sum _{j=1}^{n_B}1(C_l=j)1({\gamma }_{ljk}=1),\dots ,\phantom{)} \\ \phantom{(}{\alpha }_{Mk{R}_k}+\sum _{l=1}^{n_A}\sum _{j=1}^{n_B}1(C_l=j)1({\gamma }_{ljk}=R_k)) \end{gathered}$$ (26)

   and ${\theta }_{CUk}^{[t+1]}$ from

   $$\begin{gathered} {\theta }_{CUk}^{[t+1]}\mid {\mathbf{C}}^{[t]},\Gamma ({\mathbf{Z}}_{Alk},{\mathbf{Z}}_{Bjk})\sim Dirichlet({\alpha }_{Uk1}+\sum _{l=1}^{n_A}\sum _{j=1}^{n_B}1(C_l\ne j)1({\gamma }_{ljk}=1),\dots ,\phantom{)} \\ \phantom{(}{\alpha }_{Uk{L}_k}+\sum _{l=1}^{n_A}\sum _{j=1}^{n_B}1(C_l\ne j)1({\gamma }_{ljk}=R_k)). \end{gathered}$$ (27)
2. Sample a new state of C^[t+1] by iterating through each entry and proposing updates one entry at a time. Define ${\mathbf{C}}_{(-l)}^{[t+1]}=(C_1^{[t+1]},\dots ,C_{l-1}^{[t+1]},C_{l+1}^{[t+1]},\dots ,C_{n_A}^{[t+1]})$ as the collection of link designations without the l^th entry, and let $n_{m(-l)}^{[t+1]}={\sum }_{j=1}^{n_B}1(j\in {\mathbf{C}}_{(-l)}^{[t+1]})$ be the number of designated links at iteration [t + 1] excluding the l^th entry. The posterior distribution of C_l given C_(−l) is a multinomial distribution where the labels are {j : j ∉ C, 0}. The probability for l ∈ A to pair with the unlinked record j ∈ B and increase the total number of links by 1 is

   $$\begin{gathered} P(C_l^{[t+1]}=j\mid \Gamma ({\mathbf{Z}}_A,{\mathbf{Z}}_B),{\theta }_{CM}^{[t+1]},{\theta }_{CU}^{[t+1]},{\mathbf{C}}_{(-l)})= \\ \frac{\frac{f(\Gamma ({\mathbf{Z}}_{Al},{\mathbf{Z}}_{Bj})\mid {\theta }_{CM}^{[t+1]})}{f(\Gamma ({\mathbf{Z}}_{Al},{\mathbf{Z}}_{Bj})\mid {\theta }_{CU}^{[t+1]})}1(j\notin {\mathbf{C}}_{(-l)}^{[t+1]})}{\sum _{j^{\prime }=1}^{n_B}\frac{f(\Gamma ({\mathbf{Z}}_l,{\mathbf{Z}}_{j^{\prime }})\mid {\theta }_{CM}^{[t+1]})}{f(\Gamma ({\mathbf{Z}}_l,{\mathbf{Z}}_{j^{\prime }})\mid {\theta }_{CU}^{[t+1]})}1(j^{\prime }\notin {\mathbf{C}}_{(-l)}^{[t+1]})+\frac{(n_A-n_{m(-l)})(n_B-n_{m(-l)}+{\beta }_{\pi }-1)}{n_{m(-l)}+{\alpha }_{\pi }}}. \end{gathered}$$ (28)

   Similarly, the probability for l ∈ A not pairing with any record from B and $n_m^{[t+1]}=n_{m(-l)}^{[t+1]}$ is

   $$\begin{gathered} P(C_l^{[t+1]}=0\mid \Gamma ({\mathbf{Z}}_A,{\mathbf{Z}}_B),{\theta }_{CM}^{[t+1]},{\theta }_{CU}^{[t+1]},{\mathbf{C}}_{(-l)})= \\ \frac{\frac{(n_A-n_{m(-l)})(n_B-n_{m(-l)}+{\beta }_{\pi }-1)}{n_{m(-l)}+{\alpha }_{\pi }}}{\sum _{j^{\prime }=1}^{n_B}\frac{f(\Gamma ({\mathbf{Z}}_{Al},{\mathbf{Z}}_{B{j}^{\prime }})\mid {\theta }_{CM}^{[t+1]})}{f(\Gamma ({\mathbf{Z}}_{Al},{\mathbf{Z}}_{B{j}^{\prime }})\mid {\theta }_{CU}^{[t+1]})}1(j^{\prime }\notin {\mathbf{C}}_{-l}^{[t+1]})+\frac{n_A-n_{m(-l)})(n_B-n_{m(-l)}+{\beta }_{\pi }-1)}{n_{m(-l)}+{\alpha }_{\pi }}}. \end{gathered}$$ (29)

APPENDIX B: DERIVATION OF POSTERIOR LINKAGE PROBABILITIES

The posterior distribution of C_l and n_m given the remaining link designations C_(−l) is

$$\begin{gathered} f(C_l,n_m\mid \Gamma ({\mathbf{Z}}_A,{\mathbf{Z}}_B),{\theta }_{CM},{\theta }_{CU},{\mathbf{C}}_{(-l)})\propto = \\ p(\mathbf{C},n_m)\prod _{j=1}^{n_B}f(\Gamma ({\mathbf{Z}}_{Al},{\mathbf{Z}}_{Bj})\mid {\theta }_{CM}{)}^{1(C_l=j)}1({\mathbf{C}}_{(-l)}\ne j)f(\Gamma ({\mathbf{Z}}_{Al},{\mathbf{Z}}_{Bj})\mid {\theta }_{CU}{)}^{1(C_l\ne j)}, \end{gathered}$$ (30)

where p(C, n_m) takes the form of Equation (15).

The marginal posterior probability for record l ∈ A to form a true link with j ∈ B given C_(−l) is

$$\begin{gathered} P(C_l=j\mid \Gamma ({\mathbf{Z}}_A,{\mathbf{Z}}_B),{\theta }_{CM},{\theta }_{CU},{\mathbf{C}}_{(-l)})= \\ \frac{f(C_l=j,n_m=n_{m(-l)}+1\mid \Gamma ({\mathbf{Z}}_A,{\mathbf{Z}}_B),{\theta }_{CM},{\theta }_{CU},{\mathbf{C}}_{(-l)})}{{\sum }_{j=1}^{n_B}f(C_l=j,n_m=n_{m(-l)}+1\mid \Gamma ({\mathbf{Z}}_A,{\mathbf{Z}}_B),{\theta }_{CM},{\theta }_{CU},{\mathbf{C}}_{(-l)})+f(C_l=0,n_m=n_{m(-l)}\mid \Gamma ({\mathbf{Z}}_A,{\mathbf{Z}}_B),{\theta }_{CM},{\theta }_{CU},{\mathbf{C}}_{(-l)})} \end{gathered}$$ (31)

and the marginal posterior probability for record l ∈ A to remain unlinked given C_(−l) is

$$\begin{gathered} P(C_l=0\mid \Gamma ({\mathbf{Z}}_A,{\mathbf{Z}}_B),{\theta }_{CM},{\theta }_{CU},{\mathbf{C}}_{(-l)})= \\ \frac{f(C_l=0,n_m=n_{m(-l)}\mid \Gamma ({\mathbf{Z}}_A,{\mathbf{Z}}_B),{\theta }_{CM},{\theta }_{CU},{\mathbf{C}}_{(-l)})}{{\sum }_{j=1}^{n_B}f(C_l=j,n_m=n_{m(-l)}+1\mid \Gamma ({\mathbf{Z}}_A,{\mathbf{Z}}_B),{\theta }_{CM},{\theta }_{CU},{\mathbf{C}}_{(-l)})+f(C_l=0,n_m=n_{m(-l)}\mid \Gamma ({\mathbf{Z}}_A,{\mathbf{Z}}_B),{\theta }_{CM},{\theta }_{CU},{\mathbf{C}}_{(-l)})}. \end{gathered}$$ (32)

Dividing the numerator and denominator of Equation (31) by

$$p(\mathbf{C},n_m=n_{m(-i)}+1)\prod _{j=1}^{n_B}f(\Gamma ({\mathbf{Z}}_{Al},{\mathbf{Z}}_{B{j}^{\prime }})\mid {\theta }_{CU})$$ (33)

results in Equation (28). Similarly, dividing the numerator and denominator of Equation (32) by Equation (34) results in Equation (29). Therefore, we see that

$$P(C_l=j\mid \Gamma ({\mathbf{Z}}_A,{\mathbf{Z}}_B),{\theta }_{CM},{\theta }_{CU},{\mathbf{C}}_{(-l)})\propto \frac{f(\Gamma ({\mathbf{Z}}_{Al},{\mathbf{Z}}_{Bj})\mid {\theta }_{CM})}{f(\Gamma ({\mathbf{Z}}_{Al},{\mathbf{Z}}_{Bj})\mid {\theta }_{CU})}1(j\notin {\mathbf{C}}_{(-l)}).$$

and

$$P(C_l=0\mid \Gamma ({\mathbf{Z}}_A,{\mathbf{Z}}_B),{\theta }_{CM},{\theta }_{CU},{\mathbf{C}}_{(-l)})\propto \frac{(n_A-n_{m(-l)})(n_B-n_{m(-l)}+{\beta }_{\pi }-1)}{n_{m(-l)}+{\alpha }_{\pi }}.$$

APPENDIX C: SIMULATION STUDY FOR TWO-STAGE MULTIPLE IMPUTATION PROCEDURE

We examine the operating characteristics of a t-distribution approximation for inference of the treatment effect in our two-stage multiple imputation procedure described in Section 2.7 using a simulation study. We consider a simulation setting with n_A = 20,000 records in file A, n_B = 2,000 records in file B, and n_m = 1,600 true links between both files. The treatment effect is simulated for continuous, count, and binary outcomes. Appendix Table 5 depicts the linking variables, covariates, and response surfaces used to generate the simulations. Linking variables for true-links were simulated according to f(Z_A). No errors were simulated among the linking variables, such that Z_A and Z_B took the same values among true-links in both files. When the intervention has no effect, we assumed that f(Y(0)∣X_A, Z_A) = f(Y(1)∣X_A, Z_A). When the treatment effect exists, we assumed that it is constant on the linear, logarithm, or logistic scale for continuous, binary, and count outcomes. The response surfaces were calibrated such that E(Y(0)) is equal to 10 for the continuous outcome, 2 for the count outcome, and 0.3 for the binary outcome. A total of 100 simulated sets of data were generated from this simulation configuration.

Table 5.

Simulated Linking Variables, Covariates, and Outcomes

Linking Variables		f(ZA)	f(ZB)
Age		N(50,52)	N(45, 102)
Gender		Bernoulli(0.5)	Bernoulli(0.5)
ZIP Code		1st Digit ~Discrete Uniform(6)	1st Digit ~Discrete Uniform(6)
		2nd Digit ~Discrete Uniform(7)	2nd Digit ~Discrete Uniform(7)
		3rd Digit ~Discrete Uniform(7)	3rd Digit ~Discrete Uniform(7)
		4th Digit ~Discrete Uniform(7)	4th Digit ~Discrete Uniform(7)
f(XA)		l : Cl > 0	l : Cl = 0
Prior Hospitalization		Poisson(1)	Poisson(0.75)
Prior Log-Healthcare Cost		N(10,32)	N(6,42)
Outcome Type	τ ATT	f(Y(1)∣XA, ZA)
Continuous	0	N(7.95-0.7*Gender+0.4*PriorHosp+.2*PriorCost, 0.1)
Continuous	0.05	N(8.00-0.7*Gender+0.4*PriorHosp+.2*PriorCost, 0.1)
Continuous	0.10	N(8.05-0.7*Gender+0.4*PriorHosp+.2*PriorCost, 0.1)
Count	0	Poisson(exp(0.3431-0.7*Gender+0.2*PriorHosp+0.05*PriorCost))
Count	0.15	Poisson(exp(0.4155-0.7*Gender+0.2*PriorHosp+0.05*PriorCost))
Count	0.20	Poisson(exp(0.4384-0.7*Gender+0.2*PriorHosp+0.05*PriorCost))
Binary	0	Bernoulli(expit(−1.1973-0.7*Gender+0.2*PriorHosp+0.05*PriorCost))
Binary	0.04	Bernoulli(expit(−1.0132-0.7*Gender+0.2*PriorHosp+0.05*PriorCost))
Binary	0.08	Bernoulli(expit(−0.8395-0.7*Gender+0.2*PriorHosp+0.05*PriorCost))

To conduct record linkage of the pairs of simulated files, an individual’s continuous age values were converted to a date of birth (DOB) with a year, month, and day value. Four levels of similarity are used to compare the elements of DOB: no agreement on DOB year, agreement on DOB year only, agreement on DOB year and month only, and agreement on all elements of DOB. Five levels of similarity are used to compare ZIP codes: disagreement on the first ZIP digit, agreement on the first ZIP digit only, agreement on the first and second ZIP digits only, agreement on the first through third ZIP digits only, and agreement on all ZIP digits. Exact agreement is used to compare values of gender. Conditional independence is assumed between agreement on the three linking variables, and Equation (16) is used as the record linkage likelihood. Independent Dirichlet(1, …, 1) prior distributions are used for each θ_CM and θ_CU. M = 100 imputations of the linkage structure was taken for each simulated dataset.

Propensity score models were fitted on linked and unlinked records in A using patients’ age, gender, prior hospitalization, and prior log-healthcare cost. Nearest neighbor matching without replacement was performed based on the propensity score to identify a set of controls with similar covariate distributions as the linked records. We calculated the average treatment effect on the treated for the continuous, count, and binary outcomes by fitting Bayesian linear, Poisson, and logistic regression models using the set of matched records. Each Bayesian model contained the covariates used in matching and all of their two-way interactions similar to the model specified in Equation (19). This results in all of the imputation models being misspecified, but there is no unmeasured confounding. Non-informative prior distributions were placed on all of the parameters in each model.

Appendix Table 6 displays the $\overline{\tau }$, $\overline{Bias}$, $\overline{SE}$, and Coverage over the 100 simulated datasets for the different types of outcomes and treatment effect sizes. In settings where ${\overline{n}}_m$ and ${\overline{n}}_G$ are approximately 1,600, our proposed two-stage procedure can accurately estimate linear, count, and binary treatment effects with minimal bias. Interval estimates according to a t-distribution approximation provides nominal type 1 error and valid statistical inference for true treatment effect for all three types of outcomes and across different treatment effect sizes. However, these intervals seem to be too wide, because the coverage probabilities are close to 1 and are not around the expected nominal coverage of 0.95.

Table 6.

Average bias, SE, coverage, and type I error or power for different outcome distributions and treatment effect sizes.

Outcome Type	τ ATT	$\overline{Estimate}$	$\overline{SE}$	$\overline{Bias}$	Coverage
Linear	0	0.0006	0.0041	0.0006	1
	0.05	0.0695	0.0102	0.0195	1
	0.10	0.1187	0.0102	0.0187	1
Count	0	0.0296	0.0608	0.0296	1
	0.15	0.1688	0.0606	0.0188	1
	0.20	0.2608	0.0611	0.0608	1
Binary	0	0.0005	0.0182	0.0005	1
	0.04	0.0410	0.0182	0.0010	1
	0.08	0.0784	0.0182	−0.0016	1

APPENDIX D: SENSITIVITY ANALYSIS OF BLOCKING CRITERIA

In our linkage of MOW clients to Medicare enrollment records, blocks were generated based on clients’ gender and the first 5 digits of ZIP code to reduce the number of possible record pairs and increase the efficiency of the linkage procedure. Sadinle and Fienberg (2013) demonstrates that blocking can significantly increase the accuracy of the linkage and subsequent inference even when record linkage is computationally feasible without blocking, especially when the linking variables are limited or prone to error. However, Murray (2015) notes that blocking on variables that may be recorded with error can exclude true matches and influence the subsequent inference on the linked data. We examine the sensitivity of our results to different blocking criteria based on ZIP code digits.

Let n_Z represent the number of ZIP code digits used in the blocking criteria, where n_Z = 5 in our application. To examine the potential impact of different blocking restraints on the estimation of the causal treatment effect, we consider different values of n_Z = (4, 6, 7). Altering the blocking criteria shifts the number of ZIP code digits available as linking variables. The record linkage likelihood in Equation (17) can be re-expressed in terms of n_Z as

$$\begin{gathered} \mathcal{L}(\mathbf{C},{\theta }_{CM},{\theta }_{CU}\mid \Gamma ({\mathbf{Z}}_A,{\mathbf{Z}}_B))= \\ \prod _{l=1}^{n_A}\prod _{j=1}^{n_B}\prod _{r_D=1}^4\prod _{r_Z=1}^{9-n_Z+1}{\left[{\theta }_{CMD{r}_D}^{1({\gamma }_{ljD}=r_D)}{\theta }_{CMZ{r}_Z\mid r_D}^{1({\gamma }_{ljZ}=r_Z,{\gamma }_{ljD}=r_D)}\right]}^{1(C_l=j)1(B_{lj}=1)} \\ \times {\left[{\theta }_{CUD{r}_D}^{1({\gamma }_{ljD}=r_D)}{\theta }_{CUZ{r}_Z\mid r_D}^{1({\gamma }_{ljZ}=r_Z,{\gamma }_{ljD}=r_D)}\right]}^{1(C_l\ne j)1(B_{lj}=1)}. \end{gathered}$$ (34)

Treatment effects were estimated according to the algorithm in Section 2.7 after replacing the record linkage likelihood under each blocking scenario with Equation (34).

D.1. Sensitivity Analysis Results.

A comparison of the computational complexity of the linkage for different blocking scenarios and the linkage results are shown in Table 7. While increasing the number of ZIP digits used for blocking significantly reduces the computational complexity, there is also a significant decrease in the number of records that are linked. This is likely due to potential errors or discrepancies in how the 6-9 ZIP code digits are recorded across both files. When blocking on these error-prone ZIP code digits, many true links are classified as non-links. Increasing the blocking constraints also reduces the number of available linking variables, which increases the efficiency of the computation as well. Loosening the blocking criteria to the first 4 ZIP code digits results in more than a 4-fold increase in the number of possible record pairs, as well as an increase in the number of records linked.

The estimates of the causal treatment effects for mortality and acute inpatient admissions for different blocking criteria are presented in Appendix Table 8. Overall, we see that the use of blocking on the first 5 ZIP code digits in our application provides similar results compared to less strict blocking criteria. Gender and the first 5 digits are ZIP code are well defined and unlikely to be reported with errors, which would not result in biased point estimates or suboptimal interval estimates if used as blocking criteria. Using stricter blocking criteria generally results in fewer false links but possibly more true links missed. The point estimates for the stricter criteria were practically the same, but the interval estimates were larger because of the smaller number of true links that were identified.

Table 7. Blocking Sensitivity Analysis Linkage Complexity and Results.

n_A represents the number of unique records in the Medicare data, n_An_B represents the total number of possible record pairs that are partitioned into a gender and ZIP code block, n_m represents the average number of linked records over M = 100 imputations, and run time reflects the approximate time in days our Bayesian record linkage algorithm required to complete 500 iterations using a single CPU core on a Linux system.

Blocking Criteria	nA	nAnB	${\overline{n}}_m$	95% CI	Run time
4 digit ZIP	251,285	56,706,359	3829.67	(3814.40, 3844.94)	30 days
5 digit ZIP	247,724	13,786,172	3608.02	(3570.91, 3645.14)	18 days
6 digit ZIP	234,331	2,666,450	2807.21	(2728.63, 2885.79)	2 days
7 digit ZIP	144,230	436,049	2767.80	(2543.67, 2991.93)	< 1 day

Table 8.

Blocking sensitivity analysis causal treatment effect estimates

	30 Day Mortality		30 Day Inpatient Acute
Blocking Criteria	${\widehat{\tau }}_{ATT}$	95% CI	${\widehat{\tau }}_{SATT}$	95% CI
First 4 digits	0.005	(−0.067, 0.077)	0.007	(−0.168, 0.182)
First 5 digits	0.008	(−0.067, 0.083)	0.010	(−0.174, 0.194)
First 6 digits	0.010	(−0.074, 0.094)	0.016	(−0.180, 0.213)
First 7 digits	0.007	(−0.083, 0.096)	0.009	(−0.203, 0.222)