Mathematical Analysis of Growth and Interaction Dynamics of Streptomycetes and a Bacteriophage in Soil

Abstract

We observed the infection cycle of the temperate actinophage KC301 in relation to the growth of its host Streptomyces lividans TK24 in sterile soil microcosms. Despite a large increase in phage population following germination of host spores, there was no observable impact on host population numbers as measured by direct plate counts. The only change in the host population following infection was the establishment of a small subpopulation of KC301 lysogens. The interaction of S. lividans and KC301 in soil was analyzed with a population-dynamic mathematical model to determine the underlying mechanisms of this low susceptibility to phage attack relative to aquatic environments. This analysis suggests that the soil environment is a highly significant component of the phage-host interaction, an idea consistent with earlier observations on the importance of the environment in determining host growth and phage-host dynamics. Our results demonstrate that the accepted phage-host interaction and host life cycle, as determined from agar plate studies and liquid culture, is sufficient for quantitative agreement with observations in soil, using soil-determined rates. There are four significant effects of the soil environment: (i) newly germinated spores are more susceptible to phage lysis than are hyphae of developed mycelia, (ii) substrate mycelia in mature colonies adsorb about 98% of the total phage protecting susceptible young hyphae from infection, (iii) the burst size of KC301 is large in soil (>150, 90% confidence) relative to that observed in liquid culture (120, standard error of the mean [SEM], 6), and (iv) there is no measurable impact on the host in terms of reduced growth by the phage. We hypothesize that spatial heterogeneity is the principal cause of these effects and is the primary determinant in bacterial escape of phage lysis in soil.

The filamentous nature of streptomycetes causes two problems for their quantification in soil and interaction with phage. First, the identification of a lysable unit during phage infection as a proportion of a hypha is unclear; second, the rate of phage adsorption to hyphae is dependent upon the age of the hyphae (11, 22, 30). Phage interaction, therefore, changes over time as a function of colony heterogeneity. The effects of this heterogeneity are greatest in undisturbed colonies where interactions are dependent on diffusion. Growth on agar is limited to the boundary of the colony by the diffusion of nutrients and staling compounds (33). In contrast, colonies grown in liquid culture have little spatial heterogeneity since diffusion is rapid, and the uniform exposure of host to phage can result in efficient phage lysis (4). The effects of diffusion in soil are expected to be informed by, but distinct from, both of these cases and possibly underlies the environmental dependence observed in a number of systems (15, 17, 28).

Our objective in this study was to use population-dynamic modeling of the phage-streptomycete interaction to quantify and characterize the growth of streptomycetes and the efficiency of phage infection in soil. We examined whether specific growth and interaction characteristics were attributable to the soil environment.

THEORY

The streptomycete life cycle includes germination, colony formation, and development (vegetative growth), and sporulation (7, 18). In brief, spores germinate via a primary germ tube that undergoes branching after a period of linear extension and nucleoid replication. In Streptomyces coelicolor, mature colonies grow exponentially (as measured by DNA content) through linear (apical) extension of individual hyphae with an exponential increase in the number of branches (2). Exponential growth continues until limited through depletion of an essential nutrient, occupancy of all spatial niches, or the accumulation of staling compounds (3). The nature of growth limitation in soil is unclear. Sporulation occurs following the formation of aerial mycelia.

Phage can be extracted from the soil environment, with viability decaying at the rate of 0.1 day⁻¹ (10). Phage survival therefore requires either continuous production (virulence) or latency (lysogeny). Phage adsorb to mycelia in a two-step process (1): a process specific to the phage receptor and a nonspecific process caused by hydrophobic and electrostatic forces. Specific adsorption may lead to infection and either lysis or lysogeny. The susceptibility of streptomycetes to phage infection varies with the age of the mycelia, with older mycelia being more resistant than young tips (11, 22, 30). This variation may be due to higher rates of DNA synthesis in hyphal-tip proximal regions (14) or to differences in the density of, or area covered by, surface receptor molecules (6, 12). The replication rate of phage therefore depends on the rate of adsorption to, and infection of, susceptible hosts, transportation processes such as rates of diffusion of phage, and the burst size of the virus. The burst size may be affected by the environment (15), presumably through the nutritional status of the host.

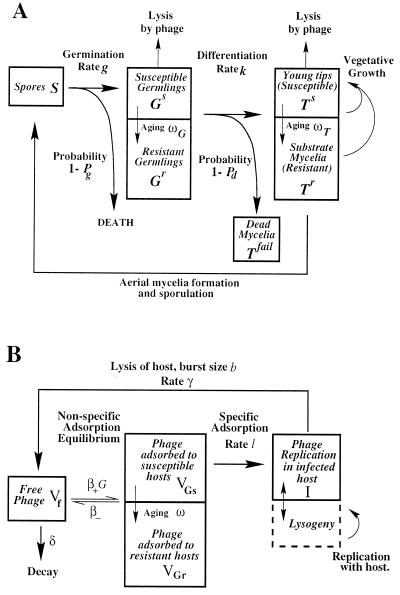
We constructed a model of the lifecycle of the host and phage (Fig. 1) based on mass action adsorption effects. Colony heterogeneity was modeled by separate compartments for spores, germlings, and substrate mycelia. A germling is an intermediate between the spore and the exponentially growing colony and is physically identifiable as the germ tube and initial branchings (when growth is linear) prior to the exponential growth in the number of branches. The relatively slow growth of the germling (compared to the exponential growth of the colony) means that the germling can be treated as a nongrowing state. Viable propagules can be lost when germination fails or when germlings fail to differentiate into viable substrate mycelia. We defined the probabilities P_g and P_d for successful germination and differentiation, respectively (Fig. 1). After differentiation, exponential growth of the substrate mycelia commences and ends with saturation of an unknown resource at the “vegetative capacity,” denoted by K, intrinsic to the soil and conditions. K is less than the final soil capacity because mycelial growth ceases at saturation, while sporulation continues. The growth rate was modeled with a standard logistic form μ(1 − [M/K]), i.e., the growth rate decreases linearly from a maximum value μ to zero as the total mycelial mass M approaches the vegetative capacity K. The germlings and substrate mycelia are divided into susceptible and resistant compartments, designated G^s, G^r, T^s, and T^r, respectively. Germlings and young tips are initially susceptible and acquire resistance to phage lysis as they age (Fig. 1).

FIG. 1.

(A) Schematic representation of the host dynamics. Germlings and young tips are initially susceptible to phage lysis (compartments G^s and T^s) but acquire resistance as they age at rates ω_G and ω_T, respectively (resistant compartments G^r and T^r). After germination, germlings differentiate into exponentially growing substrate mycelium at rate k. Germlings are viable with probability P_g and are successful in forming colonies with probability P_d. If either probability is <1, then a drop in total propagules occurs after germination, which can alternatively be described as death rates g(1 − P_g) and k(1 − P_d) of spores and germlings, respectively. Germlings that die still adsorb phage nonspecifically (T^fail). In the basic model P_g is 1 and ω_T is large so that young tips are effectively resistant. (B) Schematic representation of the phage dynamics interacting with germlings. Interaction with substrate is similar, with T replacing G. Phage adsorbs to mycelia in a two-step process: nonspecific reversible adsorption (forward rate β₊ × mycelium density G, reverse rate β₋) producing phage V_Gs and V_Gr adsorbed to susceptible and resistant germlings, respectively, and specific adsorption leading to host lysis, which is modeled as an infection event (rate l) after nonspecific adsorption. This produces a replicating phage state in an infected host I. Lysis occurs at a rate γ, releasing b free-phage particles. In a model extension, lysogeny is also included as an outcome of infection. Host aging and differentiation transfer adsorbed phage between compartments following host changes. Thus, resistance can be acquired before infection by nonspecific adsorbed phage.

The heterogeneity of the colony structure was also reflected in the phage dynamics. Phage occurred in six states: a free state V_f, replicating phage within an infected host propagule I, or adsorbed on the surface of the available hyphae, i.e., adsorbed to susceptible and resistant substrate mycelium (V_Ts and V_Tr) and susceptible and resistant germlings (V_Gs and V_Gr) (Fig. 1). We excluded lysogeny because its low frequency in our experiments implies lysogeny does not have a significant affect on the growth cycle dynamics.

Experimentally, we measured the number of viable spores, total propagules (T), and free phage (V_f). Spores, germlings, and substrate mycelia were assumed to contribute equally to the propagule count, and phage lysis was assumed to remove a propagule. A model with differential contributions of spores and mycelia to the total propagule assay also was examined to see if this assumption affected the fit to the data.

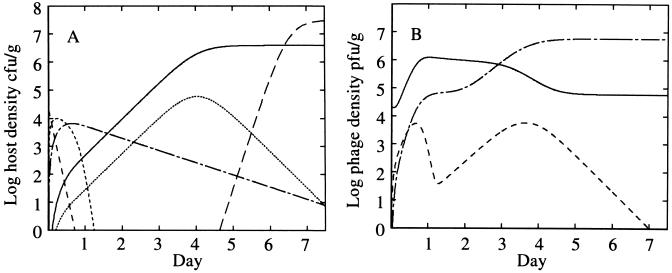
A simulation of the mathematical model is shown in Fig. 2 that demonstrates four key features of the model. (i) Phage growth depends on susceptible propagule numbers. Phage growth is initially rapid since susceptible germling density is high after spore germination, but it declines as resistance is acquired. A second phase of phage growth can occur if the host produces a high density of susceptible tips, T^s, on day 3 of the stimulation, as indicated by the rise in phage adsorbed to susceptible hosts. (ii) Phage adsorption to substrate mycelia protects young tips from infection. Nonspecific adsorption of phage during the vegetative phase produces a decline in the free phage density (Fig. 2, day 3) even though the total phage level increases through the lysis of substrate mycelia. Free-phage density reduction protects young hyphae from infection since phage adsorbed to resistant mycelia are not infectious unless they reenter the free-phage pool by desorption (Fig. 1). This explains why although susceptible hosts (young tips) are in a 10-fold-higher density at day 4 than at day 0 they do not induce significant phage growth. (iii) Temporary cessation of growth occurs when the vegetative capacity is achieved. The increase in total propagule numbers temporarily ceases (Fig. 2, days 5 and 6) prior to the appearance of spores. Growth cessation has been observed experimentally (13, 26). (iv) Differentiation of germlings into substrate mycelium does not correlate with resistance acquisition. In this simulation, differentiation of germlings is slow, whereas the acquisition of resistance by germlings is rapid. Our data suggest that these time scales are in fact similar, a result that is not due to the linking of these effects in the model.

FIG. 2.

Model simulation. (A) Host dynamics: spores (————), susceptible germlings G^s (-----), susceptible mycelia T^s (·······), resistant germlings G^r (–·–·–) and resistant mycelia T^r (———). (B) Phage dynamics: free phage V_f (———); phage adsorbed to susceptible hosts, V_s = V_Gs + V_Ts (––––); and phage adsorbed to resistant hosts, V_r = V_Gr + V_Tr (—-—-—). A sporulation cycle is included to demonstrate the increase in total propagule number after the cessation of exponential growth of the mycelia. Sporulation is modeled as a timed event from germination (18). The parameters in this simulation were chosen to emphasize the model properties discussed in the text: μ = 3 day⁻¹, K = 4 × 10⁶ CFU g⁻¹, k = 1 day⁻¹, P_d = 0.01, b = 300, β₊ = 100 day⁻¹ CFU⁻¹ g, β₋ = 1 day⁻¹, l = 2 day⁻¹, ω_G = 50 day⁻¹, ω_T = 2 day⁻¹, γ = 25 day⁻¹, δ = 0.12 day⁻¹, and g = 6 day⁻¹.

MATERIALS AND METHODS

Sterile, unamended Warwick soil (32) was inoculated with Streptomyces lividans spores (TK24) and phage (KC301) in two protocols. In experiment 1, 1.6 × 10⁶ CFU of TK24 g⁻¹ and various amounts KC301 were used as follows: microcosm 1A, 1.3 × 10⁴ PFU g⁻¹; microcosm 1B, 1.3 × 10³ PFU g⁻¹; microcosm 1C, 1.3 × 10² PFU g⁻¹; microcosm 1D, 1.3 × 10¹ PFU g⁻¹; and microcosm 1F without KC301. In experiment 2, 2.0 × 10⁴ PFU of KC301 g⁻¹ and various amounts of TK24 were used as follows: microcosm 2A, 2.0 CFU g⁻¹; microcosm 2B, 2.0 × 10¹ CFU g⁻¹; microcosm 2C, 2.0 × 10² CFU g⁻¹; microcosm 2D, 2.0 × 10³ CFU g⁻¹; microcosm 2E, 2.0 × 10⁴ CFU g⁻¹; microcosm 2F, 2.0 × 10⁵ CFU g⁻¹; and microcosm 2G without TK24. KC301 is a derivative of φC31 and contains a thiostrepton resistance gene (8).

Sterile soil was prepared by autoclaving twice at 121°C for 15 min and then checked for sterility prior to use by plating on nutrient agar (Oxoid) for 30 days at 28°C. Inoculants were mixed with sterile distilled water to obtain −67-kPa matrix potential. The microcosms were incubated at 22°C for up to 15 days with loosened lids to facilitate gas exchange. No detectable moisture loss occurred during this period.

Measurements (destructive sampling) of total streptomycete propagules (16), spores (16), free phage (21), lysogens, and lysogenic spores were obtained 0, 1, 2, 5, and 15 days after inoculation. Lysogens were detected via thiostrepton resistance. Separate microcosms were prepared for each sampling day and for each extraction type. The microcosms consisted of 20 g of soil for the phage assay, 10 g of soil for assaying total propagules, and 100 g of soil for assaying spores. Triplicate platings were taken from two microcosms for spore measurement and from three microcosms for total propagule and phage assay. The lower limits for detection of phage and total propagules were 13 PFU and 20 CFU/g of soil, respectively. Two experimental protocols were used, varying either the phage inocula or the spore inocula (see above). These experiments were performed at different times of the year, with different phage, spore, and soil batches, although all batches originated from the same phage, spore, and soil stocks. These data have been partially discussed previously (25), and the extraction methods are also discussed elsewhere (23).

The burst size and rise time were determined by performing one-step growth experiments according to the method of Lomovskaya et al. (22). In brief, phage lysate was added at a multiplicity of infection of 0.1 to a suspension of TK24 and incubated at 30°C for 30 min (to achieve maximum phage adsorption). Antiserum was added to neutralize the phage, and the suspension was diluted by a factor of 1,000 and assayed for PFU at specified times.

Statistical significance is based on analysis-of-variance and Student t tests.

RESULTS

Streptomycete growth dynamics.

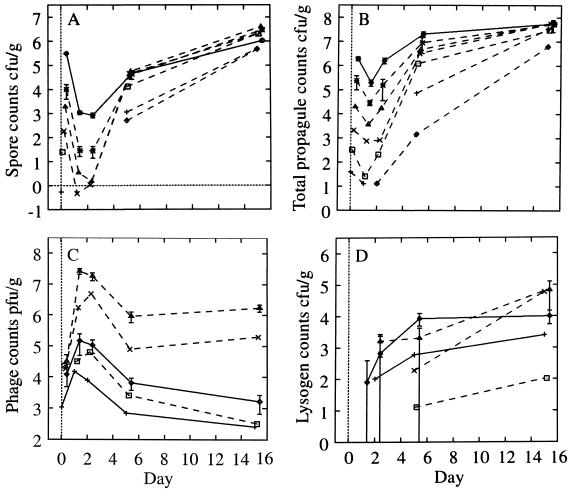
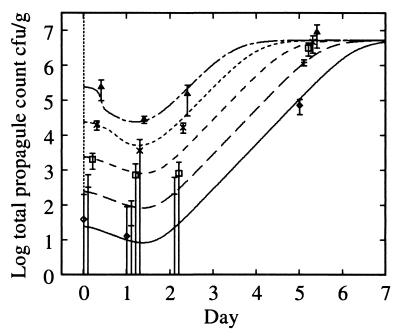
We monitored a single streptomycete growth cycle (Fig. 3). Germination was complete by day 1, vegetative (exponential) growth occurred during days 2 to 5. Sporulation began during days 2 to 5, and by day 15 the growth cycle was complete. The final total propagule counts of microcosms 2B to 2F were 3 × 10⁷ to 6 × 10⁷ CFU g⁻¹; microcosms 2D, 2E, and 2F were not significantly different (P > 25%), as were microcosms 2B and 2C (P > 10%). The total propagule count decreased significantly at day 1 (P < 1%) to approximately 10% of the initial value, with significant growth in the next 24 h (P < 1%). This fall occurred in the absence of phage (microcosm 1F).

FIG. 3.

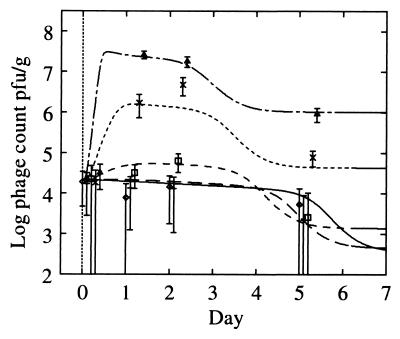
Growth curves (log₁₀) for experiment 1 (solid lines) and experiment 2 (dashed lines). (A) Spore counts. (B) Total propagules. (C) Phage counts (microcosms 2A, 2B, and 2C have less growth than microcosm 2D and are omitted for clarity). (D) Lysogen counts. For experiment 1, an average over microcosms is shown for spore and total propagules since streptomycete growth is identical across microcosms (P > 1% for microcosms 1A, 1B, and 1D). Typical error bars (95%) are shown as indicated, displaced to the right for clarity. Their skewed appearance is due to the logarithmic scale; the confidence intervals were computed based on the absolute values. Symbols (A and B): 2A, ◊; 2B, +; 2C, □; 2D, ×; 2E, ▵; 2F, ∗ with a dashed line; experiment 1 (average over microcosms), solid line. Symbols (C and D): 1A, ◊; 1B, + (experiment 1, solid line); 2D, □; 2E, ×; 2F, ▵ (experiment 2, dashed line). Data are reprinted from Gene Transfers and Environment (25) with permission from the publisher.

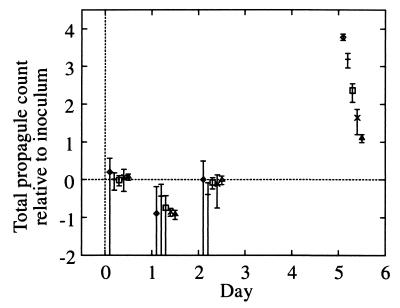
All microcosms (Fig. 4) showed identical relative growth following inoculation at days 1 and 2 (P > 5%), even though the phage count varied by 3 logs (Fig. 4). Thus, S. lividans growth is independent of the phage at these inoculation densities, and the decrease in the total propagule count over the first 24 h cannot be attributed to either phage lysis or to a crowding effect (31). At day 5, the relative growth was significantly different between microcosms (P < 10⁻¹⁴; microcosms 2D, 2E, and 2F), although the total propagule counts were not identical either (P = 3 × 10⁻⁶). The relative differences were significantly reduced by day 5 from an initial scaling of 10 between microcosms 2C, 2D, 2E, and 2F to 1.3, standard deviation [SD], 0.02 (best fit), indicating that exponential growth had ceased by this time. Thus, there is a weak dependence on the initial inoculation density in the total propagule count at day 5. However, microcosms 2D, 2E, and 2F were in an identical state of sporulation by day 5 (P > 20%). We attribute differences in growth between microcosms over the first 48 h solely to different inoculum levels, but during the subsequent 3 days of vegetative growth the microcosms all reached the same density and stage in the growth cycle to a fair approximation.

FIG. 4.

Plot of total propagule growth relative to the inoculum against time on a log₁₀ scale. Microcosms 2C to 2F and an average over microcosms for experiment 1 (adjusted for the difference in extraction efficiency) are shown. Symbols: 2C, ◊; 2D, +; 2E, □; 2F, ×; experiment 1, ▵.

The total propagule count increased over days 5 to 15 by three- to eightfold (Table 1). This increase is caused by the increase in the spore count. In experiment 2, spores contributed 11% of the total propagule count at day 5 and 93% on day 15 (Table 1). In experiment 1, the spore contribution to the total propagule count at day 15 was low (12%), perhaps due to a crowding effect suggested by the poor gain in spores during the growth cycle (Table 1).

TABLE 1.

Growth and assay characteristics^a

Parameter	Results (SD) from:
	Expt 1	Expt 2
Extraction efficiency
Total propagules	1.3 (0.03)	1.2 (0.11)
Spores	0.20 (0.01)	0.079 (0.008)
Phage	0.88 (0.07)	1.1 (0.07)
Soil capacity, CFU/g (total propagules)	5.7 × 107 (2.9 × 106)	4.6 × 107 (2.3 × 106)
Spore gain at:
Day 1 (S1/S0)	0.0035 (0.0004)	0.0020 (0.0003)
Day 15 (S15/S0)	3.4 (0.3)	>70
Spores as fraction of soil capacityb at:
Day 5	0.014 (0.002)	0.11 (0.02)
Day 15	0.12 (0.01)	0.93 (0.16)
Total propagule count relative to soil capacity at day 5 (T5/T15)	0.37 (0.03)	0.12 (0.014)

^aS_k and T_k refer to spore and total propagule measurements on day k. 

^bCorrected for extraction efficiencies of spores and total propagules, i.e., S_k/T₁₅ × ratio of the extraction efficiencies. 

Since the microcosms all reached the same state of growth at day 5, the exponential growth phase ended by reaching a saturation capacity prior to day 5. This saturation capacity is the vegetative capacity (K) of the mathematical model.

Phage growth dynamics.

Phage growth was dependent on the state of S. lividans. During the first 24 h, a large increase in phage density occurred for the higher streptomycete inoculum microcosms (Fig. 3C), was constant for 24 h, and then decreased dramatically in all microcosms between days 2 and 5. Day 5 and 15 counts were equal, indicating that the interaction was complete and that spores were not interacting with phage. Phage growth during the first 24 h in experiment 1 was poor compared to that expected from the trends in experiment 2 (Fig. 3C). In the absence of host, the phage count gradually declined as phage particles were inactivated or became unavailable for detection by the assay (not shown). These data suggest that phage may be adsorbed by the mycelia, similar to the adsorption observed in liquid culture (22, 30). The phage assay detects only unadsorbed phage because of the gentle extraction process (23). Therefore, phage adsorption caused the dramatic decrease in phage count over days 2 to 5 correlating with the increase in mycelial density.

Since the increase in phage numbers occurs within 24 h of inoculation the number of germinated spores lost through lysis can be estimated as (V_i − V₀)/b for a burst size b, where V_i denotes free phage density at day i. The loss of host propagules can be compared directly to the number of available host propagules at day 0, S_inoc, the inoculation density. For a burst size of 120 (see below), effectively all propagules would be lysed for microcosms 2E and 2F ([V_i − V₀]/bS_inoc values estimated as 71%, SD 21% and 110%, SD 12%, respectively). Such high losses through phage lysis would dramatically affect host growth and should produce effects similar to those seen in liquid culture, where the bacteria can be eliminated (4). However, the growth of the host was unaffected by the presence of phage (Fig. 4), suggesting that phage growth resulted from lysis of only a small fraction of the host propagules.

Lysogeny.

Throughout these experiments the lysogen counts were low, indicating that lysogens were a minority (<1% of host population) and that lysis was the more common outcome of infection.

Liquid culture.

The burst size for KC301 on TK24 hosts was 120, standard error of the mean (SEM) 6. This is comparable to φC31 and φA7 with burst sizes of 10 to 80 (22, 23) and 70 to 100 (11), respectively. The rise time (i.e., the time from addition of antiserum to the end of phage increase) was 60 min.

MODEL APPLICATION

Basic model.

We estimated the growth and interaction parameters for the model schematically described in Fig. 1. Sporulation was excluded because we could not estimate the rate of this process from the data set. This restricts analysis to days 0 to 5, which are independent of the sporulation cycle. We initially restricted modeling to microcosms 2B to 2F. Microcosm 2A was removed because of its very low inoculum level. The number of datum points per microcosm is low (measurements were only made at days 0, 1, 2, and 5), but these data are sufficient since the doubling time of the streptomycetes is expected to be 6 to 16 h, although rapid changes in the first 24 h may have been missed. The availability of multiple microcosms with various inoculation conditions ensures model validity over a wide range of initial conditions.

We first developed a “basic model” that (i) ignored lysogeny, (ii) assumed that substrate mycelia were resistant to phage lysis (11), and (iii) assumed that the decrease in the propagule count at 24 h resulted from a failure of germlings to differentiate successfully. Modifications and extensions to this model were then examined.

Determination of parameters.

Extraction efficiencies were estimated from day 0 measurements (Table 1). Three parameters—the germination rate (g = 6.0 day⁻¹), the lysis rate of infected host propagules (γ = 1.0 h⁻¹), and the decay rate of free phage in soil (δ = 0.12 day⁻¹)—were estimated directly because they determine an effect that is either very rapid or very slow and therefore they are not significantly correlated with the other parameters (verified by alteration of these values over reasonable ranges [data not shown]). The germination rate was estimated by comparing the spore counts on day 1 with those on day 0 by the formula g = −log_e (S₁/S₀) (Table 1), which models germination as a probabilistic event with an exponential distribution. The decay of free phage was estimated from microcosm 2G (data not shown), and the lytic time period was estimated from the liquid culture.

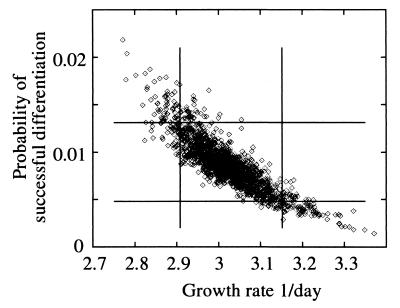
The nine remaining parameters were estimated by optimizing the fit of the model to the data using a sum-of-squares statistic denoted “SS” (see Appendix and reference 29). This method uses the 29 datum points (day 1, 2, and 5 measurements) to simultaneously estimate all nine parameters. The SS was minimized in the nine-dimensional parameter space, i.e., the total error between observed and model predictions of the total propagule and free phage counts summed over days 1 to 5 was minimized. The incline of SS away from that minimum determines the parameter confidence intervals. The burst size b was treated separately from the other parameters (see below). The best fit of the basic model to experiment 2 is shown in Fig. 5 and 6, with the parameter estimates in Table 2. The only strong correlations in the parameters (correlations with b were not determined; see below) were between μ, and P_d (r = −0.869) (Fig. 7), between ω_G with β₊ (r = 0.633), and between ω_G and l (r = 0.581). All other parameters were weakly correlated (r < 0.35). The parameters are discussed in turn below.

FIG. 5.

Fit of basic model to total propagule data of experiment 2, microcosms 2B to 2F. The data are time displaced for clarity. Error bars are 95%. The parameters are given in Table 3. Note the uniformity in the growth over the first 3 days, which reproduces the scaling behavior of Fig. 4. Symbols: 2B, ◊ (———); 2C, + (————); 2D, □ (–––––); 2E, × (-----); 2F, ▵, (—-—-—).

FIG. 6.

Fit of model to phage data for microcosms 2B to 2F. Symbols: 2B, ◊ (———); 2C, + (————); 2D, □ (––––); 2E, × (------); 2F, ▵ (—-—-—).

TABLE 2.

Fitted parameters for basic model (data sets 2B to 2F)

Symbol	Parameter	Estimate	90% CIa
SS	Sum of squares statistic (20 degrees of freedom)	51	<65
μ	Substrate mycelial basic growth rate	3.0 day−1	2.8–3.3
K	Vegetative capacity	4.5 × 106 CFU g−1	2.8–6.8 (×106)
k	Rate of differentiation of germlings to substrate mycelia	1.1 day−1	0.65–1.6
Pd	Success probability of germling differentiation	0.0083	0.0025–0.019
b	Burst size	300	>150
β+b	Adsorption rate of phage to mycelia	β+K = 99 day−1	23–440
β−c	Rate of release of phage from mycelia	β−/β+K = 0.033	0.019–0.052
l	Infection rate (rate of adsorbed phage entering host)	1.9 day−1	0.66–16
ωG	Rate germlings become resistant to phage attack	1.3 day−1	0.6–6.2
ωT	Rate mature mycelia become resistant to phage attack		>29 day−1

^aCI, confidence interval. 

^bThe rate β₊K is estimated normalizing adsorption to a mycelial mat at density K. 

^cThe ratio β₋/(β₊K) is estimated since this determines the equilibrium state. 

FIG. 7.

Correlation between parameters P_d, the probability of a germling differentiating successfully, and μ, the mycelium growth rate. The results are based on 2,000 Monte Carlo simulations. The 90% confidence intervals of the projected distributions are shown. The joint 90% confidence interval calculated from the SS lies inside these separate confidence intervals.

Burst size (b).

A good upper bound for the burst size could not be determined from this data set because streptomycete growth was independent of phage density. Thus, although SS decreases as b increases from 100 to 300, it plateaus over the range b = 300 to 1,000, where SS would normally have a valley. This prevents traditional estimation of b. We fixed the burst size at b = 300, a value equal to that in the first minimum, and derived estimates and confidence intervals of the other parameters subject to this constraint. A lower confidence bound for the burst size was then determined: b > 150 (90% confidence; see Appendix for details). Liquid culture measurements suggest that the burst size is 120; however, a burst size this low is inconsistent with our data set (Table 2).

Colony formation (μ, K, P_d, k, and ω_G).

The vegetative capacity estimate agrees with the day 5 total propagule count for microcosms 2D, 2E, and 2F. We predict that at this time these microcosms had ceased growth. The growth rate μ corresponds to a doubling rate of 5.5 h. The probability P_d of a germling forming a colony was less than 1%, i.e., most of the germlings failed to produce successful colonies. Resistance to phage lysis was attained at the same rate as differentiation, ω_G ∼ k, suggesting that acquisition of resistance might be associated with exponential growth and changes in the early colony structure. This similarity of time scale means that most germlings were available for lysis, and only later did a proportion (of those that escape lysis) successfully form colonies. The ability of the model to satisfy the lack of an impact of the phage on the host population is particularly apparent in microcosm 2F, where ca. 50% of the inoculum was lysed, and 1% of those remaining developed into colonies. In the absence of phage, the total propagule counts would have doubled at days 1 and 2, a change that could not be detected given the measurement errors.

Phage infection (β_± and l).

The rate-limiting step for phage infection (two-step process [1]) changed with the host density from adsorbtion to phage entry. Adsorption to mycelia was rate limiting for total propagule densities of <10⁵ CFU g⁻¹, 3% (ratio l/β₊) of the vegetative capacity K (microcosms 2A to 2E). In microcosm 2F the rate of phage infection was primarily limited by phage entry after adsorption to the surface (Fig. 1). Liquid culture estimates of the adsorption constant β₊ are 2 × 10⁻¹⁰ to 8 × 10⁻¹⁰ ml min⁻¹ (1, 11, 22). By converting to an effective volume of water (equating −67-kPa matrix potential with 15% volume to weight), we calculated β₊ to be 2 × 10⁻⁹ ml min⁻¹ from our data. The similarity of these values is consistent with our interpretation of the phage-host interaction.

The SS for this basic model has a probability of about 0.01%. This low value was caused by high contributions to SS from two points: microcosm 2B (phage on day 1) and microcosm 2E (phage on day 2), suggesting that these data are outliers. Excluding microcosm 2B or 2E reduced the SS to 30 (P = 1.2%) and 31 (P = 0.9%), respectively; removal of both gave an SS of 13 (P > 16%).

Variations on the basic model.

We analyzed four extensions of the basic model in which some of our original assumptions are relaxed.

(i) Modification of saturation dynamics.

In the basic model, growth rate saturation was modeled as logistic, μ[1 − (M/K)], which can be interpreted as inhibition of growth by mass action effects, e.g., secretion of an inhibitor with high diffusivity and inhibition proportional to the local concentration of the inhibitor. However, growth is probably correlated over a colony, suggesting inhibition of a more general form, μ[1 − (M/K)^η]. As discussed in Results, the vegetative capacity also may depend on inoculum through a scaling behavior K ∼ AS₀^ν (Fig. 3B). These modifications lead to a (nonsignificant) reduction of SS to 46 (with a best fit for η = 3, ν = 0.05). Thus, the exact form of the host growth dynamics is not critical in modeling these data.

We analyzed data from both experiments together with these modifications, attributing differences in phage dynamics between experiments to a difference in burst size and differences in vegetative capacities to a weak dependence on the initial inoculum. The fit was very poor (P = 10⁻⁸, SS = 115 with a contribution of 80 from experiment 2, 38 degrees of freedom), suggesting that the model can adequately describe either data set alone but cannot explain both data sets with all parameters identical except for burst size. We hypothesize that differences between these experiments are due to differences in phage adsorption rates and infection cycle dynamics.

(ii) Substrate mycelium susceptibility.

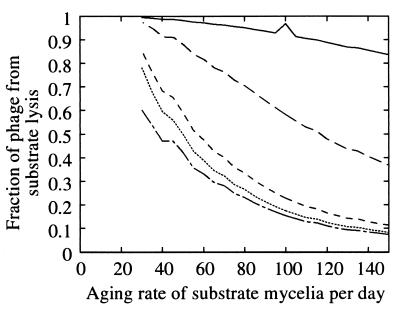
In the basic model, germlings could age but substrate mycelia were assumed to be resistant to phage lysis even though hyphal tips are probably susceptible to some extent (11, 22, 30). We added a parameter, ω_T, for the rate of resistance acquisition by substrate mycelia and estimated the 10 parameters of Table 2 as before. Germlings became resistant at rate 1.3 day⁻¹, independent of the value of ω_T. For a ω_T value as low as 50 day⁻¹ there was no appreciable change in the goodness of fit (SS = 54). Below this value, lysis of substrate mycelium and total phage in the system increase as the ω_T decreases. For a ω_T value of >50 day⁻¹, the phage lysis of germlings dominated. Lysis of substrate mycelia became important as the ω_T decreased to 30 to 50 day⁻¹ (Fig. 8). For a ω_T value of >80 day⁻¹, the free phage at day 5 constituted 2.5% of the total phage, whereas at ω_T = 25 this fraction was 1%. Thus, phage derived from the lysis of substrate mycelia were adsorbed, while the quantity of phage produced by germling lysis remained relatively constant. A lower confidence limit on ω_T (90%) was 29 day⁻¹, corresponding to a susceptible half-life of 35 min. The important parameter for measuring susceptibility of hyphae to phage lysis is the ratio of half-lives ω_T/ω_G, estimated to be >30 at a 90% confidence level. This result suggests that the phage-hypha interaction depends on the state of the colony. Identical results were obtained by varying the rate constant l, i.e., substrate hypha exposure ω_T⁻¹l_T was at least 30 times less than the germling exposure ω_G⁻¹l_G (90% confidence).

FIG. 8.

The proportion of phage that originated from lysis of substrate mycelia as a function of the aging rate ω_T in units per day. Microcosms 2B to 2F are shown in decreasing sequence, i.e., 2B (———), 2C (————), 2D (––––), 2E (·······), and 2F (-—-—-). Germlings acquired resistance at a rate ω_G that remained approximately constant at 1.3 day⁻¹. In microcosm 2B, the phage growth was so low that changes in numerical accuracy of simulation are apparent at a ω_T of 100 day⁻¹ compared to surrounding points.

For a ω_T value of 50 day⁻¹, a hyphal tip is susceptible for only about 20 min compared to 18 h for germlings. During exponential growth, the fraction of the colony that was susceptible is μ/ω_T, with a value of ca. 6%.

(iii) Lysogeny.

We assumed a constant probability of lysogeny per infection, a spontaneous reversal rate of zero, and that the extraction efficiency for the lysogens was the same as that of the total propagules. Under these assumptions the probability of lysogeny was 2 × 10⁻⁴, with a 90% upper confidence limit of 5 × 10⁻⁴ compared to a frequency of lysogeny of φC31 observed in liquid culture of 30 to 40% (22). The low frequency of multiple infection of hyphae predicted by the model for these soil experiments probably explains this difference and is consistent with an environmental dependence of the lysis-lysogeny switch (17).

(iv) Models for propagule loss after germination.

In the basic model, the decrease in total propagule count during the first 24 h was attributed to germlings failing to form colonies. Two alternative hypotheses are that not all spores form viable germlings (P_g < 1; Fig. 1) or that spores, germlings, and substrate mycelia contribute unequally to the total propagule count. We quantified the second alternative as:

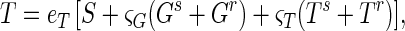where e_T is the assay efficiency (as measured on spores at day 0) and ς_G and ς_T are the relative assay efficiencies for germlings and total propagules, respectively.

The statistic SS indicates that these two models are not significantly better at describing the data (SS = 51 and 49, respectively). Again significant contributions to SS came from two or three outliers. The SS plateaued in burst size at 400 and 200 for the two models, respectively. Parameters that could be suitably compared lay within the confidence intervals of Table 2. Therefore, our estimates are robust against the as-yet-unknown process causing total propagule loss during the first 24 h. Possible explanations are a 99% failure of germlings to differentiate into viable mycelia, failure of 55% of spores to establish a colony on germination, or a 5:2 efficiency ratio for detection by the assay for spores and mycelia (or germlings).

DISCUSSION

Our three main observations were a large burst size (Table 2), a lack of impact of the phage on host growth (Fig. 4), and a high susceptibility to infection of germlings relative to young substrate mycelium (Table 2 and Fig. 8). The difference in the burst size estimates relative to liquid culture can be explained by environmental dependence (28), and molecular explanations for differing susceptibilities and adsorption have been proposed (6, 12). However, these factors also can be explained by spatial effects: spatial colony heterogeneity, localized modification of the environment by hyphae (19), and the spatial distribution-correlation of phage and hosts throughout the microcosm. Liquid culture destroys these spatial effects because of high diffusion and mixing, while growth on agar reduces these effects by restricting growth to the colony boundary. At the molecular level, phage adsorption may be affected by spore and hyphal modification of their local environment. For example, water absorption by the spore could localize phage to germlings, and slow diffusion of phage relative to colony growth will produce high local concentrations of phage after lysis and reduce the effect of phage relative to the total amount of phage present. Local adsorption of phage by substrate mycelia protects substrate hyphal tips more than it does germlings and could partially explain the increased susceptibility of germlings to phage lysis relative to the substrate mycelium.

There are two biological uncertainties in this system: the identity of the adsorbing material and the quantification of mycelial propagules. Because of the physical separation of the aerial mycelium from the substrate mycelium, the substrate mycelium is likely to be the adsorbing material (32), as assumed in the model. However, since adsorption is only important as the mycelial mat matures, the dynamics would be mathematically similar and the exact identity of the adsorbing material is not crucial for parameter estimation. The mycelial nature of streptomycetes is potentially problematic, principally because 1 CFU need not be a lytic unit. However, this problem does not affect parameter estimation since phage growth is restricted to the first 24 h and the streptomycetes are in discrete lysable units during this time because of the absence of septa (20). Further, differential contributions of spores and mycelia to the total propagule assay cannot explain the data any better than can alternative models.

Our analysis implies that the qualitative form of the streptomycete growth cycle and phage-streptomycete interactions observed in liquid (11) and agar plates (7, 18) can explain the dynamics in soil but that both the soil environment and colony heterogeneity are important variables. We note, specifically, the following points. (i) Vegetative exponential growth stops after reaching a vegetative soil capacity, at approximately 10% of the final soil capacity, prior to the sporulation cycle. (ii) Phage do not significantly affect streptomycete growth. (iii) Phage propagation on germlings is more successful than on developed colonies. Thus, mycelial susceptibility to phage lysis varies with age (11, 22, 30). (iv) Adsorption of phage to mycelia significantly reduces the density of free phage. Adsorption dominates the phage dynamics during the vegetative phase of the host, reducing free-phage density by a factor of 50 relative to the total phage in the system. (v) There is a phage-independent growth pause of the host during the first 24 h and a significant decrease in the total propagule count at 24 h. This decrease can be explained by either a failure of 55% of spores to establish a colony on germination, 99% of germlings failing to produce viable mycelia, or a 5:2 efficiency ratio for detection of spores and mycelia (and germlings), respectively, in the total propagule assay. (vi) The burst size is large, with a b of >150 (90% confidence) and a best estimate of b of 300 (germling differentiation failure model).

These results emphasize the role of the environment in the growth and interaction characteristics of streptomycetes and phage. However, in contrast to previous work highlighting the importance of the environment in affecting burst size (15, 28) and the lysis-lysogeny switch (17), which can be explained through the nutrient status of the host, our analysis suggests that physical processes within the environment (e.g., diffusion) significantly affect ecosystem dynamics. Further experimental work is required to clarify the contribution of the environment to the dynamics with regard to physical processes and nutrient status. Experiments incorporating in situ monitoring of DNA for phage (9) and streptomycetes would also enhance the analysis and contribute to model development. In particular, these methods could be used to test model predictions, for instance, the ratio of free phage to total phage in the microcosm at day 15 (estimated to be 1 to 3%) and the rate of decline of free phage over the vegetative phase, predicted by our models to be equal to the growth rate of the adsorbing medium.

Appendix

Mathematical model. The basic model schematically represented in Fig. 1 consists of 14 coupled ordinary differential equations. The model parameters are listed in Table 2.

Susceptible G^s and resistant G^r germlings have dynamics described by:

A1

and

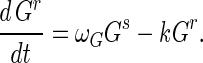A2

In equation A1 the terms are the creation of susceptible germlings by germination (rate g), differentiation into substrate mycelia at rate k, infection by adsorbed phage V_Gs, and acquisition of resistance at rate ω_G, corresponding to the first term of equation A2. Resistant germlings differentiate at rate k, the second term in equation A2. Germination reduces spore numbers as e^−gt. Germination is successful with probability P_g.

Substrate mycelia occur in four states: susceptible mycelia (T^s), resistant mycelia (T^r), an intermediate state (Tⁱ; not shown in Fig. 1), and nonviable mycelia (T^fail). The last two states are introduced to ensure that germling differentiation and aging are independent processes (i.e., to prevent parameter correlations) and to prevent adsorbed phage release to the environment on differentiation failure, respectively. The intermediate state Tⁱ is differentiated (giving rise to growing tips) but acquires resistance on a germling time scale ω_G. T^fail models the fact that failed germlings present an adsorbing surface for a period of time. Decay of this adsorbing surface is not included since the surface area is insignificant once exponential growth is underway, i.e., within 24 h. The substrate mycelium dynamics are as follows:

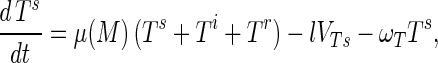A3

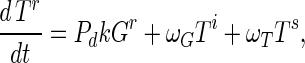A4

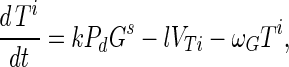A5

and

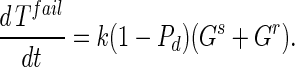A6

Here M = T^s + T^r + Tⁱ is the total growing mycelia with a growth rate μ(M) = μ(1 − M/K). The terms in equation A3 are the production of susceptible mycelia by growth, the loss by infection by adsorbed phage V_Ts, and the acquisition of resistance at rate ω_T. For resistant mycelia, equation A4, the terms are differentiation from resistant germlings and the acquisition of resistance by the intermediate state and susceptible mycelia. Similarly, equations A5 and A6 record the production and loss of Tⁱ and T^fail.

The phage compartments consist of free phage V_f, replicating phage in an infected host I, and phage adsorbed to the host compartments above, denoted V_Gs, V_Gr, V_Ts, V_Tr, V_Ti, and V_fail. The phage dynamics are as follows:

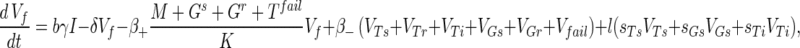A7

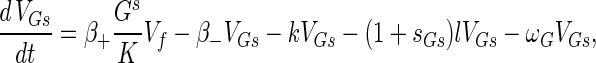A8

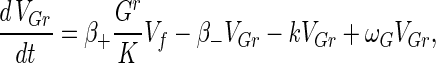A9

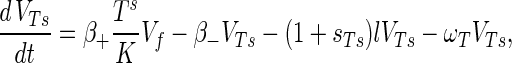A10

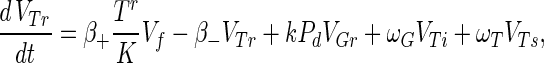A11

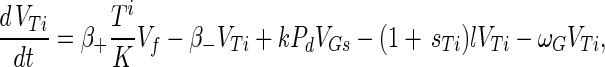A12

and

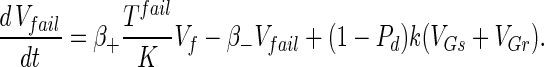A13

Phage adsorption kinetics are based on mass action. The first two terms in equations A8 to A13 represent adsorption and desorption and correspond to the third and fourth terms of equation A7. Adsorbed phage compartments mirror aging, differentiation, and infection of the underlying host equation, except for an extra term at infection that models the additional phage adsorbed to the surface of the hypha at infection. The number of additional particles adsorbed per propagule upon infection is given by s_Gs = V_Gs/G^s and s_Ts = V_Ts/T^s from Poisson statistics for germlings and susceptible substrate mycelia, respectively. These phage particles are released to the free compartment upon infection. Under our experimental conditions this refinement is not important since infected propagules tend to have very few adsorbed phage.

An infection event results in concurrent loss of a host propagule (e.g., the third term in equation A1), the loss of an adsorbed phage particle, and the creation of an infected host I, as follows:

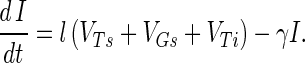A14

Phage replication produces b free-phage particles per infection event on lysis of the infected host at rate γ, the first term of equation A7.

Lysogeny can be added by introducing a probability of an infection event leading to lysogeny. This gives rise to a lysogen compartment L and adsorbed phage V_L.

Alternative growth models for filamentous organisms can be found in references 27 and 34.

Initial conditions. All germling and substrate mycelium compartments are initially empty. The growth process is initiated by germination from spores as calculated in equation A1. Initially, free phage is set to the inoculum level, and all other phage compartments are empty.

Parameter estimation. We use a standard sum-of-squares statistic (SS) for estimation of the model parameters, summing over the observables (phage, total propagules, and lysogens [optional]); over microcosms; and over days 1, 2, and 5. The time points are independent because of destructive sampling. The measurement errors are estimated for each time point from multiple measurements and are likely to be normal (deriving from Poisson statistics for plate counts). Thus, SS is χ²(n − m) distributed (n datum points and m estimated parameters). Parameters δ, γ, and g are fixed as discussed in the text, and SS is minimized to estimate all of the remaining parameters concurrently. These parameters are initially set randomly, and repeat runs are performed from different random initial values to locate the global minimum. For the models considered, the SS has a minimum value of about 51 (experiment 2), which corresponds to P ≈ 0.018%. We consider such values acceptable since the SS is the same order as the 1% significance value of 38 on 20 degrees of freedom. This is justified because there is evidence of outliers, and SS is sensitive to measurement error underestimation that may derive from variation between microcosms.

The nonlinearity of the model requires that SS be calibrated for estimating parameter confidence limits. This is done through Monte Carlo simulation (29). The 90% confidence intervals calculated in Table 2 are performed on a Monte Carlo simulation of 2,000 points. This is sufficient, as shown in Fig. 7, since the points are well distributed across the confidence intervals. The 90% level for the SS statistic is consistent with the approximation χ_α²(m) (confidence 1 − α, estimating m parameters) for nonlinear models not far from linearity (5). For eight parameters χ_0.1²(8) = 13.4, while numerically we obtained 12.0. Throughout, significance intervals are projected onto the corresponding coordinate, i.e., the 90% significance value surface of the SS is identified and the lowest and highest values of the various parameters for that surface are used as the confidence intervals in Table 2. This is conservative given the high dimension of parameter space and ignores all correlations between the parameters (Fig. 7). Multiparameter significance intervals will be narrower than the single-parameter estimates. For parameters that are only constrained by the data in one direction, e.g., the burst size, we fix these parameters at a suitable minimum and calculate the SS statistic probability levels under these constraints. To obtain the appropriate SS statistic for the full parameter space, we use the χ² distribution to adjust for a change in the degrees of freedom, i.e., we normalize the SS to 93.1% on eight variables for 90% confidence on nine. These probability levels are reasonable approximations for the full unconstrained probability distribution since χ_α²(m) was a reasonable approximation to the SS. This is equivalent to imposing a weak prior on b.