Algorithm for Determination of Thresholds of Significant Coherence in Time-Frequency Analysis

Abstract

A quantitative assessment of the level of coherence between two signals is important in many applications. Two biomedically relevant cases are Transfer Function Analysis (TFA) of Cerebral Autoregulation (CA) and Coherent Hemodynamics Spectroscopy (CHS), where the first signal is Arterial Blood Pressure (ABP) and the second signal is either cerebral Blood Flow Velocity (BFV) or cerebral hemoglobin concentration. To determine the time intervals and frequency bands in which the signals are significantly coherent, a coherence threshold is required. This threshold of significant coherence can be found using multiple samples of surrogate data to generate a distribution of coherence. Then the 95^th percentile of the distribution can be used as the threshold corresponding to a significance level α = 0.05. However, storing the entire coherence distribution uses a large amount of computer memory. To address this problem, we have developed an algorithm to determine the coherence threshold with little memory usage. A subfield of data streaming algorithms is devoted to finding quantiles using little memory. This work does not aim to find a new streaming algorithm but rather to develop an algorithm that can be tailored to the needs of applications such as TFA and CHS. The algorithm presented here identifies the coherence thresholds for a wavelet scaleogram using much less memory then what would be required to store the entire coherence distribution.

1. Introduction

Methods based on Transfer Function Analysis (TFA) rely on a high level of coherence between signals considered as input and output of a linear system. A high coherence between input and output signals supports the assumption of a linear, univariate relationship between input and output signals. A key question tackled in this work is: “how can one efficiently determine a threshold value of significant coherence for the specific signals and experimental conditions of a given measurement protocol?”

We consider the cases of TFA of Cerebral Autoregulation (CA) [1] and Coherent Hemodynamics Spectroscopy (CHS) [2]. In TFA of CA, one measures Arterial Blood Pressure (ABP) and Blood Flow Velocity (BFV) in the middle cerebral artery (with transcranial Doppler ultrasound) and describes CA in terms of a high-pass transfer function [3]. In CHS, one measures cerebral hemodynamics (typically the cerebral concentrations of Oxy-Hemoglobin, [HbO₂], and deoxy-Hemoglobin, [Hb], with Near-InfraRed Spectroscopy (NIRS)) that are coherent with a specific physiological signal, most commonly ABP [4,5]. The goal of CHS is to translate cerebral NIRS measurements into physiologically relevant information on cerebral perfusion, including CA [6,7] and Cerebral Blood Flow (CBF) [8].

A key requirement of the TFA and CHS methods is the determination of time intervals and frequency bands that feature significant coherence between the measured signals (i.e. BFV, [HbO₂], [Hb]) and ABP [5], by also considering multiple coherence functions when additional physiological effects beyond ABP must be taken into account [9]. An additional difficulty of CHS, and of any time-varying process, are non-stationary conditions, for which the identification of short-lived the coherent periods require a time resolved signal processing technique. To determine time periods and frequency bands of significant coherence, a coherence threshold must be found for each time-frequency point. This work focuses on an algorithm for the determination of this threshold for use in non-stationary TFA, CHS, and similar techniques.

In non-stationary TFA and CHS, one is interested in identifying time intervals and frequency bands that feature significant coherence and then analyzing the phase and gain relationships of these coherent signals. While various signal processing methods can be used, this work will focus on wavelet analysis. Using the analytic Morlet mother wavelet, the wavelet coherence scalogram and wavelet transfer function scalogram are found for pairs of signals. The wavelet coherence calculated from experimental data is compared against a threshold of coherence (obtained from surrogate data) to determine times and frequencies of significant coherence, and then only those regions in the time-frequency space are analyzed. This workflow relies on the predetermination of a coherence threshold map in time-frequency space. Such coherence thresholds are obtained by generating multiple (100 − 10,000) surrogate data signals with Gaussian Random Number (GRN) to create a distribution of coherence [5,10–14]. The 95^th percentile corresponding to a significance level α = 0.05 of these distributions is then taken as the coherence threshold. However, some studies in the literature used a higher number of iterations to find a single coherence threshold that was then applied to the entire time-frequency space or as a function of frequency but not time [5,10,11,14]. Additionally, cases with large amount or surrogate data (~10,000) limited their sample length to 512 [11]. In principle, each time-frequency point should have its own coherence threshold since the coherence distribution changes with frequency and proximity to the temporal edges of the time-frequency map. This process of finding coherence thresholds for each pixel can be very expensive in terms of memory usage due to the requirement to store the entire distribution of coherence values.

The problem of determining the desired percentile of a large distribution of data with limited memory can be classified as a streaming problem, for which a variety of techniques has been proposed [15–18]. The goal of this work is not to devise a conceptually novel streaming algorithm, but rather to develop an efficient method suited for the specific needs of TFA and CHS to determine a wavelet coherence threshold from GRN surrogate data. We describe an approach to determine wavelet coherence thresholds with little memory usage. The algorithm is tailored to the MATrix LABoratory language (MathWorks MATLAB, Natick, MA, USA) and takes advantage of the native matrix operations since the desired result is a map (two-Dimensional (2D) array) of thresholds in the time-frequency space.

2. Methods

2.1. Random Surrogate Data Method

One method for estimating thresholds of significant coherence in signal analysis is the random surrogate data method [10], which has been applied to TFA of CA [11] and CHS [5]. In this method, GRNs are used to populate two signals in time. These random time signals are then analyzed with whatever coherence analysis is desired, and the coherence of the GRN signals found. GRN signals are generated over many iterations (typically 100) to create a distribution of coherence values for these surrogate data [5,10]. There have been cases where large numbers of iterations have been reported (15,000), but this was done for a single threshold value and not a map [11]. Other methods exist such as scrambling a real signal either in time domain or frequency domain [10]; however, all surrogate data methods result in distributions of coherence. Although 100 iterations have been used in the past, 1,000 − 10,000 or greater iterations are desirable for more accurate threshold estimates since threshold maps show heterogeneity when too few iterations are performed. An example of this heterogeneity will be shown in section 3.2. A threshold of significance is defined as a given percentile of the coherence distribution for surrogate data, with the 95^th percentile being a typical choice (α = 0.05).

2.2. Simple Threshold Determination

The simplest method for determination of the desired threshold corresponding to a given percentile involves storing the entire coherence distribution in memory over the multiple iterations of GRN signals. Once all coherence values in the distribution have been populated, the values are sorted and the one corresponding to the desired percentile accessed. The main disadvantage of this method is the need for large amounts of memory. Since many signal processing techniques create time-frequency maps of coherence, each iteration will create a 2D array (rows and columns representing time and frequency, respectively) of coherence values. This means that the distribution of coherence values will be stored in a three-Dimensional (3D) array (rows by columns by pages) with the samples indexed along the page dimension. In an example where we have a time signal made of 10,000 points and the signal analysis method will produce 200 frequencies (reasonable for wavelet analysis), we will have a 10,000 × 200 × n array of type double (8 Bytes) where n is the number of surrogate data samples. For typical n values of 100 one requires 1.6 GB for this one variable. However, if we consider more desirable values for n of 1,000 − 10,000 we find the need for 16 − 160 GB, matching or exceeding the full capacity of memory of most desktop computers today. This large memory requirement likely has led to either few iterations being chosen [5,10] or a single threshold (instead of a map) being estimated [11]. Therefore, this simple method of threshold determination is not practical when a threshold map is desired.

2.3. Efficient Algorithm for Coherence Threshold Determination

2.3.1. Summary

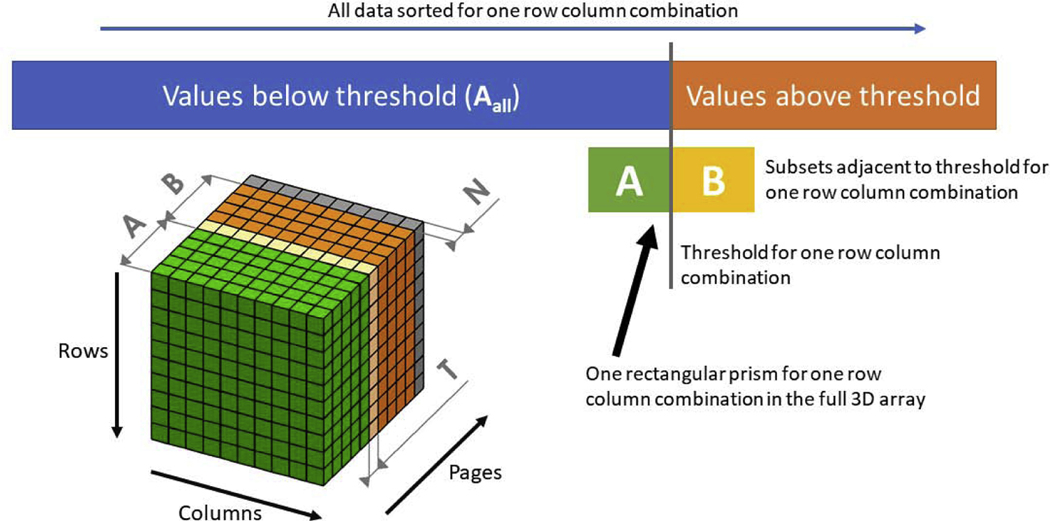
Here we present a method to estimate the ((1 − α) × 100)^th percentile and associated coherence threshold without having to store the entire coherence distribution in memory. The algorithm is summarized below and will be described in detail in the following sections. To estimate the desired percentile with less memory, we start with an initial step that requires building the coherence distribution for several surrogate data samples (2m~100) that is much smaller than the desired value of n (1,000 − 10,000 or greater) but similar to the lesser number of sample iterations used in the past [5,10]. Throughout each iterative step of the proposed algorithm, which processes a new sample of the coherence distribution, the approach is to retain only coherence values that are close to the current threshold estimate (Figure 1). For this purpose, a 3D array (ABN) (time by frequency by surrogate sample index) is built. The notations ABN follows from the fact that this 3D array is made of three subarrays A, B, and N; however, these sub arrays are never separated in memory and always stored as the combination ABN. ABN consists of a total 2m + 1 pages, where each page is a 2D time-frequency array: the first m pages contain coherence values below the desired percentile (3D subarray A); the next m pages contain coherence values above the desired percentile (3D subarray B); the last page is used in the algorithm to accept a new coherence sample in each iteration (2D array N). The first page of B is named T, which is a 2D array containing the coherence threshold estimates for each time and frequency. First, the algorithm initializes the first 2m pages (AB) by populating them with the first n_f × n_t × 2m coherence samples and, after ordering the samples along the page dimension at each time-frequency pixel, estimates the threshold (Figure 2a–c). Here, n_f and n_t are the number of frequency samples and the number of time samples, respectively. Next, a loop is entered, where a new coherence sample is taken at each iteration. In the loop, the new 2D array of coherence samples is first added to ABN (in the last page, N) and then the elements of ABN are properly shifted in the page dimension to keep the coherence threshold array T at the same page index. Note that during this rearrangement some coherence values that were present in the ABN array will be discarded and will be substituted by some elements of the new coherent sample. The method to shift the elements of ABN is controlled by a 2D array, n_Aall, which contains the total number of samples (updated at each iterative step) that are below threshold at each time-frequency pixel. n_Aall is named such since it represents the length of the conceptual set A_all which contains all the samples below the threshold estimate ever extracted until that step of the loop (including samples that were extracted and are no more in the array ABN). In the example where a 10,000 × 200 time-frequency array of thresholds is desired; each page would take 16 MB of memory. For m = 50 (i.e. if A and B are each 50 pages deep), the 3D array ABN would consist of 101 pages. This is 1.6 GB of memory, reasonable for most desktop computers today, but allowing for an arbitrary n of 1,000 − 10,000 or greater. Notice that if we compare this amount of memory to the examples where all coherence samples were saved, the memory usage is equivalent to n = 100 for all samples saved. This is the key advantage of the algorithm, namely the ability to consider an arbitrarily large number of samples with memory usage as if n = 2m + 1 and all samples were saved. Below, we describe in detail the three steps of the algorithm: initialization, adding samples, and shifting elements.

Figure 1:

Structure of the 3D array ABN used in the efficient threshold algorithm. Each voxel contains a coherence value and the values are increasing in the direction of increasing page number. All coherence values below the threshold make up the conceptual array A_all, this array is never stored in its entirety, but only its subset A. The 2D array n_Aall is stored and contains the length of the conceptual A_all for each row and column combination. A and B contain the coherence sample subsets adjacent to the desired percentile. The threshold 2D array (T) is the first element in the sorted B set. The cube shows the implementation of the A, B, and N sets in a 3D array. The rows and columns are the time and frequency dimensions while the page dimension is coherence value samples. The last page of ABN is a null page (N) that contains a new coherence sample at each iterative step of the proposed algorithm.

Figure 2:

[a-c Initialization] a) ABN Array is initialized with 2m samples and sorted. At the end of this phase the thresholds will be at page at index ⌊2m(1 − 𝛼) + 1⌉. b) In order to shift the threshold page (T) to the first page of B, elements too small to be in A (which belong to its first ⌊m(1 − 2𝛼)⌉ pages) are set to the large dummy value (NaN in MATLAB). c) ABNis sorted, and the thresholds are set in the correct page, T. [d-f Adding Samples] d) 2D array of new coherence samples is placed in N replacing what was there. Then the ABN is sorted. Note that the figure does not show an example of first iteration, thus various dummy values are already present. e) For row and columns combinations where the new element was less than or equal to the last threshold estimate, the first page of the array is set to the large dummy value. f) Array is sorted. [g-I Shifting Elements] g) Based on the value of the new samples it is calculated whether they belonged to the A set or the B set and whether the sets are the right size for the desired threshold to be at their boundary. Now it can be seen that the current threshold estimate is scattered in the page dimension and the pages must be shifted for each row and column combination. h) For row and column combinations for which set A is now too large, a large dummy value is placed in the first page of the array. For cases where the A set is now too small, a small dummy value (-Inf in MATLAB) is placed in the last page of the array. i) Again, ABN is sorted setting the thresholds to be in the correct page, T. [Definitions] A: Set below threshold, B: Set above threshold, T: Page corresponding to threshold estimate, N: Extra null page. Blue: Number, Light Blue: Number belonging to threshold estimate, Yellow: Lower dummy value (-Inf in MATLAB), Red: Upper dummy value (NaN in MATLAB).

2.3.2. Initialization

First, the initial 2m values of coherence obtained from GRN data are used to populate the first 2m pages of the ABN. Those values are sorted in the page dimension (Figure 2a) so that T is easily identified. For example, in the case of A and B having 50 pages each (m = 50) and α = 0.05, the coherence thresholds will be at page 96 of ABN. Second, we shift the coherence thresholds to the first element of the B subarray (or page m + 1, page 51 in this example, of the ABN array); to do this, the pages with the smallest ⌊m(1 − 2α)⌉ values in the A subarray (i.e. in the first 45 pages in this example with m = 50 and α = 0.05) are redefined to the large dummy value (in the case of MATLAB implementation, NaN) (Figure 2b). Third, the ABN array is again sorted in the page dimension, thus placing the page T at the first page of the B subarray (Figure 2c), or at page 51 of the ABN array. At this stage, the 3D array ABN has the first m = 50 pages with coherence values under threshold (A array), the 5 following pages (the first 5 pages of B) with coherence value equal or above threshold (first page of B), and all the remaining pages of the B and N subarrays are filled with the large dummy value (NaN in MATLAB). T is accessed to obtain the current coherence threshold estimates. A 2D array is created (n_Aall) where each element contains the number of samples below the threshold estimate for each time-frequency pixel. Per the ((1 − α) × 100)^tℎ percentile, all elements of this array are initialized to the same value ((1 − α) × 100 = 95 in this example). Because of this initialization, most of the B array is set to the large dummy value and the values in the ABN array are sorted in the page dimension.

2.3.3. Adding Samples

The first step taken during each iteration of the threshold updating loop is to obtain a new 2D array of coherence value samples. This 2D array fills the last page, N, of the ABN array (Figure 1), replacing its current values. For each row and column combination, if the new coherence sample is below the current threshold estimate, n_Aall is incremented by one; otherwise n_Aall is unchanged. Then the ABN array is sorted in the page dimension (Figure 2d), moving the new coherence samples into A if they are below the threshold estimate, or into B if they are above the threshold estimate. As a result, one may end up with some coherence values below the current threshold estimate that are in B (this happens if there is at least one element in N below threshold). To shift these elements into A (where they belong), we set the corresponding elements of the first page of ABN to the large dummy value (NaN in MATLAB; Figure 2e). After re-sorting the array ABN, all the elements of ABN below the threshold estimate will be in A.

2.3.4. Shifting Elements

The second step taken during each iteration loop is to determine the new threshold estimate. This step is based on a comparison between the current values in each row and column combination of n_Aall and the expected value of i(1 − α) where i is the iteration number including the 2m initialization samplings. This is because the initialization of the algorithm is considered to take 2m iterations so that the iteration number i is representative of the total number of samples taken thus far. We describe the performed comparisons following MATLAB notation where arrays can be compared to scalars resulting in Boolean arrays: if n_Aall < i(1 − 𝛼), elements must be taken from B and added to A (at those time-frequency pixels of the Boolean array where there is a True); if n_Aall > i(1 − α), (this statement generates an almost complementary Boolean array to the previous one) an element must be taken from A and added to B; no action is needed if n_Aall = i(1 − α). Thus, the row and column combinations that require their elements shifted are found (Figure 2g). In cases where pixels must be shifted to lower-index pages (from B to A), a large dummy value replaces the first page of ABN. In cases where pixels must be shifted to larger-index pages (from A to B), a small dummy value (in the case of MATLAB implementation, -Inf) replaces the last page of ABN (Figure 2h). n_Aall values are incremented by one if a sample was moved from B to A, and decremented by one in the opposite case. Finally, the ABN array is sorted for the last time placing the updated threshold estimates at the T page, the first page of the B array. The T page is accessed to extract the new threshold estimate. Because of this step, the ABN array is sorted, n_Aall and T are updated, and the ABN array is ready for the new loop iteration.

3. Results

3.1. Testing with Constructed Distributions

To validate the results of the algorithm, its output was compared to the true percentile given by a data set consisting of 20,000 samples. The test set was not a coherence distribution, but rather a constructed distribution. In addition, this test was carried out for one threshold value, equivalent to one pixel in a real coherence map. In this example, we take m = 50 to be consistent with the previous sections. The test data resulted from two random Gaussian distributions, one with mean 0 and standard deviation 0.2, and the other with mean 0.5 and standard deviation 0.5. Each of the 20,000 samples had an equal likelihood of coming from either of the Gaussian distributions. The test values of these distributions were limited to the range 0 − 1 inclusive. The purpose of creating this test data set was to create a bag of numbers to test the algorithm against, any bag of numbers constructed in various ways could have been used.

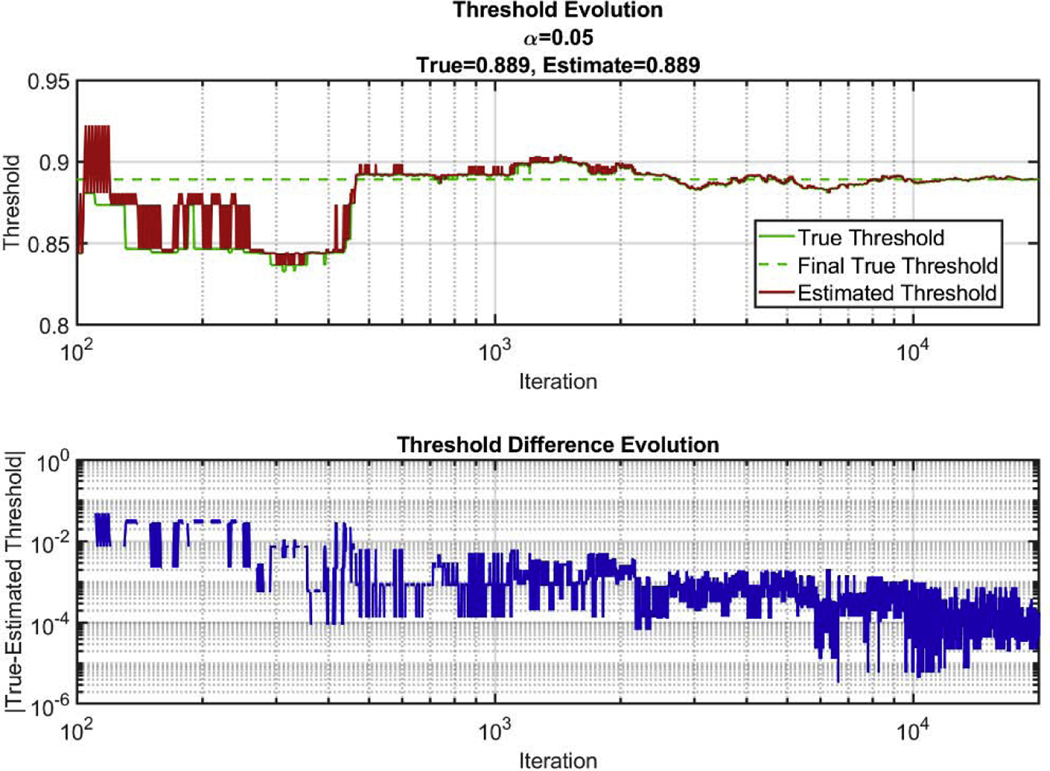
The algorithm was run pulling samples from this test data set to construct its estimate of the 95^th percentile. All the samples from the distribution were saved, and the true 95^th percentile for all the data samples pulled thus far was calculated for each iteration of the loop. The algorithm was run for all n = 20,000 samples and did not show a difference from the true 95^th percentile within the third significant digit (Figure 3). The true final percentile value was determined by finding the 95^th percentile from the whole sample distribution.

Figure 3:

Comparison of true 95^th percentile and estimated 95^th percentile of a test distribution. Top) True threshold over all iterations compared to estimated threshold. Bottom) Absolute value of the difference between the estimated threshold and the true threshold over all iterations. Note that the iteration axis starts at 100, since 100 samples were taken during initialization of the algorithm.

3.2. Application of Wavelet Coherence Analysis

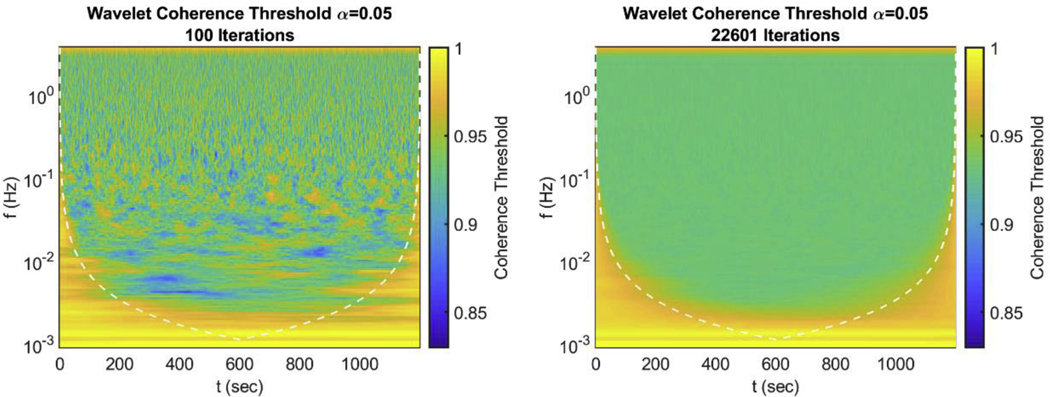
One intended application of this algorithm is to find thresholds for significant coherence in wavelet signal analysis. Using a map of coherence thresholds, one can determine which points in frequency and time are significantly coherent for a given pair of signals. The computation of coherence threshold as a function of time and frequency can be a computationally demanding task for more data samples (longer time acquisitions assuming a fixed sampling frequency). To evaluate the capabilities of the algorithm presented here, we used it to generate coherence thresholds for the coherence calculated by the MATLAB wcoherence function, which was modified to remove smoothing in frequency (Figure 4). The threshold map presented in the right panel of Figure 4 was given a limit of 24 hr to run the algorithm on a typical desktop computer. The algorithm completed 22601 iterations in that time on a 9375 × 145 map of coherence (1,359,375 indivisual cohereance thresholds). This map represented thresholds for a 20 min long signal acquired at a sample rate of 7.8125 Hz with analyzed frequencies from 0.001 to 3.730 Hz. The left panel of Figure 4 shows the initialization of the algorithm (thresholds from 100 iterations). Comparing the 100 iteration map to the 22,601 iteration map, 100 iterations yield a much greater heterogeneity compared to 22,601 iterations. This is representative of thresholds generated for a real experimental protocol on actual distributions of coherence (instead of a single constructed distribution as in the previous section). It is worth noting that if this map was generated by storing the entire coherence distributions 246 GB of memory would have been required, compared to the 1 GB used by the ABN array in the algorithm.

Figure 4:

Example map of coherence thresholds generated by the algorithm with size 9375 × 145 (1,359,375 pixels). Map confidence threshold for a 20 min long signal sampled at 7.8125 Hz with a frequency range from 0.001 to 3.730 Hz. Coherence was found using the MATLAB wcoherence function, modified to remove smoothing in frequency. Left) Thresholds generated form 100 iterations using the entire coherence distribution (initialization of the algorithm). Right) Thresholds generated using the algorithm in 24hr with 22601 iterations on a typical desktop computer.

4. Discussion

4.1. Values of n and m

The main aim of the algorithm is to estimate threshold maps with large n (iterations) without large memory usage. Previous works have either used small n or not generated full threshold maps (but rather just one threshold value) [5,10,11]. From Figure 3 and Figure 4 it can be seen that 100 samples are not enough to get a good estimate of the threshold [5,10]. The threshold map shown in the left panel of Figure 4 shows a visible heterogeneity in the time-frequency map of the threshold. This example, generated from 100 samples, shows that some regions may feature significant coherence when a more accurate threshold estimate would not. Thus, more coherence samples are required (1,000 − 10,000 or greater) but, as discussed in section 2.2, a simple threshold determination would require too much memory to generate a threshold map. Thus, a single threshold estimate (not a map) with a large n has been used [11]. But from the right panel of Figure 4 the threshold map does not contain a constant value as the threshold depends on frequency and temporal proximity to the edge. Therefore, we need a method to estimate entire threshold maps using large n but little memory, the algorithm presented here achieves this goal.

The value chosen for m (size of A and B along the page dimension) has some effect on the algorithm. In principle, it should be set as large as possible without using too much memory or reducing computation time. Here, m = 50 was chosen since it was found to be large enough without using unreasonable amounts of memory. m can also be chosen to be too small. If this is the case, there is a risk of the dummy values appearing in the threshold estimate array, this is further discussed in section 4.3.

4.2. Applicability of the Algorithm

A method that can easily and accurately generate threshold maps is important because a different map may be needed for different experimental protocols. Different experimental protocols may last different durations in time. The data could be collected at different sampling rates. In addition, different experiments may require different coherent analysis parameters (smoothing in wavelet for example). These differences across experimental protocols require coherence maps to be generated frequently without the need for a specialized computer. The algorithm presented here is capable of this, since it does not have large memory requirements, and most desktop computers can be used to generate thresholds. This leads to the possibility of generating thresholds for an experiment overnight on one’s computer and then being able to complete the turnaround on coherence analysis within one day of a new experiment.

The algorithm was developed for and inspired by the need for significant coherence in TFA and CHS. However, its use is not limited to these modalities. In principle it could be applied to any application that needs percentile estimates of many samples with little memory usage. This is the subfield of quantile estimation in the field of streaming algorithms. This work does not aim to develop a new streaming algorithm but rather to create a specific implementation that has been optimized for MATLAB and importantly for estimation of 2D arrays of percentiles. Note that this algorithm is implemented without for loops to index the arrays, but uses instead native array operations in MATLAB, an important consideration when optimizing for MATLAB. This suggests that the algorithm may to applicable to modalities outside TFA and CHS.

Finally, there is a possibility for this algorithm to be implemented in other languages. Despite it being optimized for MATLAB by using the native array operations, MATLAB has disadvantages. First, development in MATLAB requires expensive licenses making it inaccessible to some. Second, MATLAB is inherently not as fast as other languages since it is designed for data analysis and visualization, not writing and compiling standalone programs. Due to these disadvantages it may be desirable to implement the algorithm in another language. There is nothing about the algorithm that would prevent this. Array operations could be implemented in nested for loops and large positive and negative numbers could be used for the dummy values, thus lending to the possible applicability of the algorithm outside MATLAB.

4.3. Considerations and Limitations of the Algorithm

The primary problem that can arise running this algorithm is dummy values showing up in the T page and ruining the estimation of the threshold. It is recommended that a check for dummy values be implemented at every iteration of the threshold estimates, and to disregard them. For these cases, either the previous iteration estimate, or the max sample value (at a time-frequency pixel where a dummy value is present in T) may be used as the updated estimate. The latter is more conservative, possibly overestimating the coherence threshold. Such conservative estimates are sometimes desirable in determining thresholds. In this conservative spirit, we used the first page of B as the threshold instead of the average of the last page of A and the first page of B.

It is also worth noting that three sorting operations are required for each iteration of this algorithm. Sorting operations are one of the more computationally expensive operations in terms of processing time. Considering the sort operations, the cost of the algorithm is ℴ(6 n n_f n_t m log₂(2m)) since MATLAB uses quick sort on the 2m + 1 values in ABN. This sort must be repeated three times for every iteration (n), frequency row (n_f), and time column (n_t). Thus, it may be said that this algorithm reduces memory cost at the expense of an increased processing cost. Parallelism may be a way to alleviate the cost of sorting; because the sort is done for row-column combinations across pages of a 3D array, the sorts of each row and column could be done in parallel, reducing the dependence on n_f and n_t. Of course, there may be further opportunities to improve the algorithm through parallelism. However, the time-frequency analysis of the random signals that must be done at every iteration dominates the processing time in each step and may overshadow the cost of sorting.

The efficacy of the algorithm maybe further improved to reduce computation cost or better take advantage of parallelization. One such improvement may involve changing the way new data is added. Instead of adding one sample at a time, new data may be added in blocks of multiple surrogate data samples (like repeating the initialization step in the iterations). This may require fewer sorting operations but would be more costly in terms of memory and further thought would need to be put into the strategy to add the blocks of data in the ABN array.

5. Conclusions

We presented an algorithm designed to calculate threshold values of significant coherence. The algorithm was designed with the specific objective of calculating time-frequency maps of coherence thresholds for wavelet analysis, but it could be used for any application that requires the estimation of a desired percentile of a sampled distribution. The algorithm allows the calculation of thresholds from large number of samples without requiring large amounts of computer memory. This is because the proposed method employs only the distribution values that fall within a region around an iteratively updated threshold. With this method, the limitation in the number of samples is determined by available computing time, since the memory that the algorithm requires does not increase as more and more samples are acquired. The algorithm will allow for the accurate estimation of coherence thresholds when analyzing pairs of signals. Biomedically relevant signals include ABP and either BFV or [HbO₂], and [Hb] which are relevant for TFA of CA and CHS.