Handling missing data in a composite outcome with partially observed components: simulation study based on clustered paediatric routine data

Abstract

Composite scores are useful in providing insights and trends about complex and multidimensional quality of care processes. However, missing data in subcomponents may hinder the overall reliability of a composite measure. In this study, strategies for handling missing data in Paediatric Admission Quality of Care (PAQC) score, an ordinal composite outcome, were explored through a simulation study. Specifically, the implications of the conventional method employed in addressing missing PAQC score subcomponents, consisting of scoring missing PAQC score components with a zero, and a multiple imputation (MI)-based strategy, were assessed. The latent normal joint modelling MI approach was used for the latter. Across simulation scenarios, MI of missing PAQC score elements at item level produced minimally biased estimates compared to the conventional method. Moreover, regression coefficients were more prone to bias compared to standards errors. Magnitude of bias was dependent on the proportion of missingness and the missing data generating mechanism. Therefore, incomplete composite outcome subcomponents should be handled carefully to alleviate potential for biased estimates and misleading inferences. Further research on other strategies of imputing at the component and composite outcome level and imputing compatibly with the substantive model in this setting, is needed.

Introduction

Composite measures combine information from multiple measures into a single summary score [11,29,37,20,8,6]. In health care settings, composite measures are used as scorecards to measure and benchmark performance and quality of care in neonates [30] and cardiovascular care among adults, [8,6,12,14]. In 2010, Profit et al. [30] presented a conceptual framework on composite indicator development in paediatrics care. More recently, Opondo et al. [25] developed and validated the Paediatric Admission Quality of Care (PAQC) score; a 7-point composite score aimed at benchmarking processes of care among children admitted with common childhood illnesses in low-income settings. In the validation study, PAQC score was shown to be a good proxy for outcome of care [26].

Besides gain in statistical efficiency, composite scores reduce the amount of data processed thus providing global insights and trends about complex and multidimensional quality of care processes [29,37,14]. In addition, the issue of multiple testing is avoided [31,15]. Although composite outcomes complement single measures, weak theoretical and statistical assumptions may undermine the overall reliability [6,30]. For instance, use of inappropriate methods to deal with partially observed subcomponents may impede the validity and reliability of the composite measure in subsequent analyses and inferences [29,20,6,14,10].

In the literature, multiple imputation (MI), proposed by Rubin [36], offers a good, often best practice, solution in dealing with partially observed outcomes and covariates [22,39,7,13]. In particular, handling missing data in single outcomes (with no subcomponents) is straight forward because the imputation model is usually equivalent to the analyst’s model [18]. On the other hand, dealing with missing data in composite outcome context has not received the same level of attention with no consensus on whether to impute at the composite score level or at the missing components level [20,38].

For instance, in a previous analysis of routine paediatric data with PAQC score as the outcome of interest [16], unobserved quality of care indicators (subcomponents) across three domains of care (i.e. assessment, diagnosis and treatment domain) were treated in the conventional approach described in the subsequent section. In another study, MI at item level was used to handle missing PAQC score subcomponents in the treatment domain [17]. Although the proportion of missingness was small, a comparison of the two study results showed notable differences in parameter estimates.

Through a range of simulation conditions, that is, three missing data rates under two missing data mechanisms, we sought to assess the implications of the missing data method (MI versus the conventional method) employed in addressing missing PAQC score subcomponents. Specifically, the amount of bias in regression coefficients and corresponding standard errors attributable to missing PAQC score subcomponents across the simulation scenarios was obtained and compared between MI and the conventional method.

Relevant data

In previous studies mentioned above, routine pneumonia data collected in a cluster-randomized trial in 12 Kenyan hospitals between March and November 2016 [2] were analysed. In total, 2127 pneumonia patients aged 2–59 months were admitted by 378 clinicians across the 12 hospitals. The composite outcome of interest (PAQC score) was adjusted from its original form to encompass the new pneumonia treatment guidelines recommended by the World Health Organization in the year 2013 [27].

In these studies, PAQC score was constructed using 12 pneumonia care indicators using the conventional approach presented in Table 1. The 12 indicators comprised of 9 signs and symptoms in the assessment domain, 1 indicator in the diagnosis and classification domain and 2 indicators in the treatment domain. Specifically, 6 binary indicators were created with 1 representing adherence to recommended childhood pneumonia guidelines and 0 representing inappropriate care. The binary indicators were then summed across domains of care to obtain an ordinal PAQC score ranging between 0 and 6. Variation on the 7-point scale was due to missing data and/or inappropriate care across the three domains of care. That is, missing data in patient’s weight, oral amoxicillin dose, and/or frequency of drug administration among oral amoxicillin recipients. In this study, inappropriate care refers to undocumented primary and secondary signs and symptoms in the assessment domain, incorrect severity classification, undocumented oral amoxicillin prescription or prescription of the drug in the wrong dose or frequency [25].

Table 1.

Pneumonia care indicators used in PAQC score construction.

PAQCa score domain	Pneumonia care indicators	Binary indicators
1. Assessment Primary signs and symptoms (S&S)	Cough, difficult breathing	1: if both primary S&S are documented 0: if at least one is not documented
Secondary S&S	Oxygen saturation, AVPUb, ability to drink, central cyanosis, grunting, respiratory rate and lower chest wall indrawing	1: if all secondary S&S are documented 0: if at least one is not documented
Complete assessment	All primary and secondary S&S	1: if all are documented 0: if at least one S&S is not documented
2. Diagnosis and classification	Pneumonia diagnosis and classification	1: for correct diagnosis classification 0: incorrect diagnosis classification
3. Treatment	Amoxicillin prescription	1: if oral amoxicillin was prescribed 0: if amoxicillin was not prescribed or prescription is missing
	Amoxicillin dosage	1: for correct dose, (i.e. if dose ranges between 32 and 48 (IU/Kg) every 12 h). 0: if dose is missing or < 32 IU/Kg (under dose) or >48 IU/Kg (overdose) or wrong frequency or missing frequency of administration or missing patient’s weight.

^aPaediatric Admission Quality of Care.

^bA for Alert, V for Verbal response, P for pain, U for unresponsive.

The predictor variables of interest included an interaction between the intervention arm and follow up time (in months), hospital-level factors (i.e. malaria prevalence status and paediatric admission workload), clinician level factors (i.e. gender and cadre). At patient level, gender, age and the number of comorbid illnesses were considered [16].

Methods

Simulation study

The aim of this study was to simulate data mimicking the observed pneumonia trial data set. However, simulating a standard data set based on model parameters while preserving the correlation structure was a challenge due to the complex multilevel structure of the trial data set. This was in addition to mixed variable types in covariates and outcome subcomponents in the observed trial data set. To circumvent this challenge, missing data were generated in a complete subset of pneumonia trial data.

Specifically, the simulation study targeted subcomponents in the treatment domain namely patient’s weight, oral amoxicillin dose prescribed and frequency of oral amoxicillin administration. The three pneumonia care indicators are required in the calculation of correctness of the prescribed oral amoxicillin dose. To create a subset of pneumonia trial data, complete in the treatment domain subcomponents of interest, we excluded 65/2127 (3.1%) case records with missing oral amoxicillin prescription. Of the remaining 2062 (96.9%) pneumonia case records, 1036 (50.2%) were prescribed oral amoxicillin while 1026 (49.8%) pneumonia cases were not. Amongst patients prescribed oral amoxicillin, we further excluded 61/1036 (5.9%) cases for whom weight (n=30), amoxicillin dose (n = 4) or frequency of amoxicillin administration (n = 27) were missing.

Therefore, the base data set used in the simulation study consisted of 2001(94.1%) pneumonia patients nested within 372 admitting clinicians in 12 hospitals. Although the data set was complete in the outcome subcomponents of interest, one patient and two clinician level covariates still had missing data. Specifically, patients’ gender was missing in <1% of the case records while clinicians’ cadre and gender were missing in 22.3% (83/372) and 25.1% (82/372) cases, respectively.

Standard parameter estimates

The base data set was used to estimate standard parameter estimates as follows. First, pneumonia PACQ score was constructed for each patient using the procedure described above. Thereafter, missing covariates were imputed 10 times using the latent normal approach within multilevel joint model imputation framework [7,33]. A two-level imputation model for the $i\text{th}$, ( $i=1,\dots ,2127$) patient nested within the $j\text{th,}(j=1,\dots ,378)$ clinician in hospital $l,(\text{l}=1,\dots ,12)$ was defined by

$$\begin{array}{rl}{Y}_{ijl}^{(1)}& =X_{ijl}^{(1)}{\beta }^{(1)}+b_{jl}^{(1)}+e_{ijl}^{(1)}\end{array}$$ (1)

$$\begin{array}{rl}{Y}_{jl}^{(2)}& =X_{jl}^{(2)}{\beta }^{(2)}+b_{jl}^{(2)}\end{array}$$

$$\begin{array}{rl}{e}_{ijl}^{(1)}& \sim N(0,{\sigma }_e^2),||and||(b_{jl}^{(1)},b_{jl}^{(2)})\sim N(0,{\mathrm{\Sigma }}_b),\end{array}$$

where ${\mathit{Y}}_{\mathit{i}\mathit{j}\mathit{l}}^{(1)}$ and ${\mathit{Y}}_{\mathit{j}\mathit{l}}^{(2)}$ are vectors of partially observed level 1 covariates (patient’s sex) and level 2 covariates (clinician’s sex and cadre), respectively. Level 1 predictors ( ${\mathit{X}}_{\mathit{i}\mathit{j}\mathit{l}}^{(1)}$) included fully observed covariates (i.e. an interaction term between follow-up time and intervention arm, hospital workload and malaria prevalence status, patient’s age and number of comorbid illnesses) and PAQC score. The corresponding level 2 predictor variables denoted by ${\mathit{X}}_{\mathit{j}\mathit{l}}^{(2)}$ included an interaction between follow-up time and intervention arm, hospital workload and malaria prevalence status. A clinician random intercept $(b_{jl})$ was included to account for clustering at clinicians’ level and to ensure compatibility with substantive models of interests. MI was conducted using jomo [32] package in R version 3.5.4. Imputed data set were then analysed using proportional odds random intercepts model implemented in R’s Ordinal package [9]. The model corresponded to

$$\begin{array}{rl}& logit[P(Y_{(PAQC|Score;|ijl)}\le k)]\\ & ={\alpha }_k+{\beta }_1{x}_{(age|group;|ijl)}+{\beta }_2{x}_{(patient|sex;|ijl)}\\ & +{\beta }_3{x}_{(comorbidity=0;|ijl)}+{\beta }_4{x}_{(comorbidity=1;|ijl)}+{\beta }_5{x}_{(comorbidity=2;|ijl)}\\ & +{\beta }_6{x}_{(clinician|cadre;|jl)}+{\beta }_7{x}_{(clinician|sex;|jl)}+{\beta }_8{x}_{(admission|workload;|l)}\\ & +{\beta }_9{x}_{(malaria|prevalence;|l)}+{\beta }_{10}{x}_{(time|in|months;|l)}\ast x_{(trial|arm;|l)}+b_{jl}\end{array}$$ (2)

where ${\alpha }_k$, k=1, … ,6 are PAQC score specific intercepts, $\beta$ are estimated regression coefficients and $b_{jl}$ are clinician’s random intercepts. Final parameter estimates were pooled according to Rubin’s rules [35]. The pooled estimates henceforth referred to as standard estimates and denoted by $({\beta }_{MI}^{\ast })$were used as reference estimates against which results from different simulation scenarios were benchmarked.

Simulation scheme

As earlier mentioned, missing data were induced in the base data set targeting three outcome subcomponents in the treatment domain, that is, patient’s weight, oral amoxicillin dose prescribed and frequency of oral amoxicillin administration. Missingness was generated assuming missing completely at random (MCAR) and missing at random (MAR) mechanisms respectively. Binary missing data indicators were generated by sampling random numbers from a random binomial distribution with success probability rates of 3%, 10% and 40%. A 3% missing data rate was selected to evaluate the impact of low proportion of missingness while 10% and 40% were chosen to assess the extent of bias in moderate to high rates of missingness.

Under MCAR mechanism, missing values in the target treatment domain subcomponents were induced independent of other variables in the base data set, that is, covariates and outcome subcomponents in the assessment and clinical diagnosis domains. For the MAR condition, probabilities of missing data were conditionally dependent on variables associated with probability of missingness in the three variables of interest (based on the observed trial data set) (Supplementary Table A1). In both MAR and MCAR, missing data in the target variables were induced independently of each other, such that either one, two or all three variables were missing for any given patient. Each scenario was simulated 1000 times. Random number generators (seeds) were chosen and maintained for different scenarios to ensure reproducibility of results.

Thereafter, two approaches were used to handle missing data in each simulated data set. In the first approach, missing covariates were handled using MI (Equation (1)) while induced missing values in patient’s weight, amoxicillin dose and frequency of administration (outcome subcomponents within treatment domain) were handled using the conventional approach. Undocumented signs and symptoms in the assessment domain were also handled using the conventional approach where they were score with value 0 at PAQC score construction stage described in Table 1. In the first approach, PAQC score was constructed prior to MI of missing covariates and hence included in the imputation model as a one of the predictor variables.

In the second approach, MI was used to handle partially observed covariates and missing treatment domain subcomponents. Outcome subcomponents in the assessment and diagnosis domains were included in the imputation model as predictor variables. In this approach, PAQC score was constructed after MI of incomplete subcomponents in the treatment domain. Variation on the 7-point scale was attributed to inappropriate pneumonia care which encompassed; lack of documentation of all primary sign and symptom, lack of documentation of all secondary signs and symptoms (assessment domain), misdiagnosis or misclassification of disease severity, failure to prescribe oral amoxicillin drug or prescription of the drug in the wrong dose or wrong frequency of amoxicillin administration [25].

Notation

A proportional odds random intercepts model (Equation (2)) was fitted to each imputed data set to obtain imputation-specific parameter estimates. Imputation-specific estimates were pooled using Rubin’s rules [35] to produce a single estimate $({\hat{\beta }}_{i,MI})$ for the $i\text{th}$ simulation. This procedure was repeated in all the scenarios.

Bias in regression coefficients was calculated as the differences between estimates (log odds) averaged over 1000 simulated data sets $({\overline{\hat{\beta }}}_{MI}=\sum _{i=1}^N({\hat{\beta }}_{i,MI})/N)$and estimated (log odd) $({\beta }_{MI}^{\ast })$ from the base data set. That is,

$$Bias={\overline{\hat{\beta }}}_{MI}-{\beta }_{MI}^{\ast }.$$ (3)

To assess accuracy, model-based standard errors calculated as the average of the estimated within simulation standard errors were used. That is,

$$\text{Model based }SE(\hat{\beta })=\sum _{i=1}^{N}SE({\hat{\beta }}_{i,MI})/N.$$ (4)

The model-based standard errors were compared with empirical standard errors calculated as the standard deviation of the estimates of interest [5] across the 1000 data sets, that is,

$$EmpircalSE(\hat{\beta })=\sqrt{1/(N-1)\sum _{i=1}^N{({\hat{\beta }}_{i,MI}-{\overline{\hat{\beta }}}_{i,MI})}^2},$$ (5)

where N denotes the number of simulations, ${\hat{\beta }}_{i,MI}$ is the coefficient estimated in the $i\text{th}$ simulation and ${\overline{\hat{\beta }}}_{i,MI}$ is estimator’s average over 1000 simulations. The mean square error (MSE) which incorporates both measures of bias and variability [13,5,19] was calculated for the regression coefficients as

$$MSE=Bia{s}^2+(EmpiricalSE(\hat{\beta }){)}^2.$$ (6)

Bias and accuracy of the corresponding standard errors were assessed in a similar manner. Coverage probability of the 95% confidence intervals were not applicable in this simulation study because missing data were simulated on the same subset of the pneumonia trial data set.

To assess variability due to finite number of simulations [23], Monte-Carlo standard errors for estimated bias in regression parameters were calculated using

$$\text{Monte-Carlo }SE(\beta )=\sqrt{\begin{array}{cc}\frac{1}{N(N-1)}& \sum _{i=1}^N{({\hat{\beta }}_{i,MI}-{\overline{\hat{\beta }}}_{MI})}^2\end{array}}.$$ (7)

Computation time was also used to assess performance of the two strategies employed in handling missing PAQC score subcomponents. Simulations were carried out using a server with the following specification: 40 GB memory, Intel Xeon E5-4650 (2.70 GHz) processor (12 cores/24 threads), Gnu/Linux Ubuntu 14.04 OS, and R (version 3.4.4) programming language.

Results

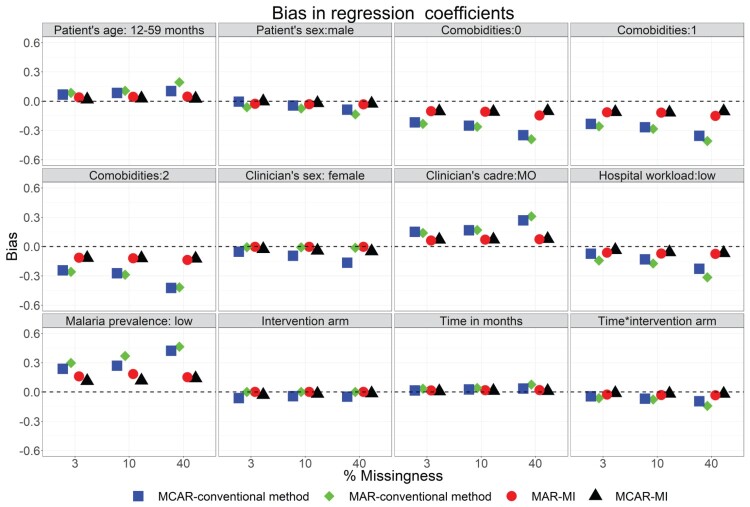
Figures 1 and 2, respectively, present bias estimated in regression coefficients and standard errors under the conventional and MI approaches across 6-simulation scenarios (i.e. 3 missing data rates of 3%, 10% and 40% and 2 missing data mechanisms namely MAR and MCAR).

Figure 1.

Bias in regression coefficients under the conventional approach of handling missing PAQC score subcomponents and after MI of missing PAQC score subcomponents in the treatment domain and missing covariates imputed across missing data rates and missing data mechanisms.

Figure 2.

Bias in standard errors under the conventional approach of handling missing PAQC score subcomponents and after MI of missing PAQC score subcomponents in the treatment domain and missing covariates imputed across missing data rates and missing data mechanisms.

Results for specific scenarios with regard to estimated bias, empirical standard errors, model-based standard errors and MSE for regression coefficients and corresponding standard errors are presented in Tables 2 and 3, and supplementary Tables A2–A7. Monte-Carlo standard errors and confidence interval around bias for regression parameters across simulation scenarios are presented in Supplementary Tables A8–A9.

Table 2.

Performance measures of regression coefficients after MI of covariates and PACQ score subcomponents in the treatment domain: MAR mechanism.

	Proportion missing
		3%				10%				40%
Effect	True esta	Bias	Model-based SE	Emp SEb	MSEc	Bias	Model-based SE	Emp SE	MSE	Bias	Model-based SE	Emp SE	MSE
PAQC score intercept 1	−7.825	0.018	0.015	0.017	0.005	0.021	0.023	0.024	0.001	0.022	0.036	0.036	0.002
PAQC score intercept 2	−2.253	−0.616	0.030	0.030	0.380	−0.707	0.449	0.450	0.701	−0.739	0.153	0.154	0.569
PAQC score intercept 3	−1.189	−0.327	0.080	0.080	0.113	−0.375	0.319	0.321	0.242	−0.392	0.414	0.414	0.325
PAQC score intercept 4	0.083	−0.241	0.582	0.583	0.400	−0.277	0.186	0.188	0.111	−0.289	0.142	0.143	0.104
PAQC score intercept 5	1.371	−0.264	0.237	0.237	0.126	−0.303	0.373	0.374	0.231	−0.317	0.249	0.249	0.162
PAQC score intercept 6	2.246	−0.041	0.131	0.135	0.020	−0.047	0.203	0.203	0.043	−0.049	0.229	0.228	0.055
Age-group:12-59	0.154	0.038	0.083	0.088	0.008	0.044	0.147	0.148	0.023	0.046	0.170	0.172	0.032
Child sex: males	−0.046	−0.027	0.216	0.216	0.047	−0.031	0.259	0.260	0.068	−0.032	0.276	0.277	0.078
Comorbidities: 0	0.474	−0.130	0.228	0.230	0.069	−0.149	0.014	0.015	0.022	−0.156	0.070	0.071	0.029
Comorbidities: 1	0.309	−0.134	0.330	0.333	0.129	−0.154	0.557	0.558	0.334	−0.161	0.644	0.645	0.442
Comorbidities: 2	0.335	−0.111	0.384	0.386	0.163	−0.127	0.570	0.570	0.341	−0.133	0.643	0.644	0.431
Clinicians’ sex: female	0.337	−0.030	0.020	0.020	0.002	−0.050	0.027	0.019	0.002	−0.080	0.016	0.018	0.003
Clinicians’ cadre: MOd	0.038	0.062	0.155	0.156	0.028	0.071	0.054	0.055	0.008	0.074	0.014	0.016	0.006
Hospital workload: low	−0.367	−0.063	0.147	0.150	0.025	−0.072	0.250	0.252	0.068	−0.075	0.290	0.292	0.090
Malaria prevalence: low	−0.189	0.159	0.306	0.302	0.119	0.183	0.170	0.171	0.063	0.191	0.275	0.276	0.112
Enhanced A&Fe	−0.002	−0.065	0.192	0.193	0.041	−0.053	0.189	0.190	0.038	−0.060	0.180	0.182	0.036
Time (months)	−1.754	0.015	0.720	0.721	0.518	0.017	0.696	0.698	0.484	0.018	0.686	0.687	0.470
Time× Enhanced A&F	0.226	−0.028	0.160	0.163	0.026	−0.032	0.106	0.108	0.012	−0.034	0.126	0.126	0.017

^aTrue estimate.

^bEmpirical standard error.

^cMean square error.

^dMedical Officer.

^eAudit and feedback.

Table 3.

Performance measures of regression coefficients after MI of missing covariates and conventional method in handling missing PAQC score subcomponents in the treatment domain: MAR mechanism.

	Proportion missing
		3%				10%				40%
Effect	True esta	Bias	Model-based SE	Emp SEb	MSEc	Bias	Model-based SE	Emp SE	MSE	Bias	Model-based SE	Emp SE	MSE
PAQC score intercept 1	−7.825	0.141	0.015	0.016	0.020	0.171	0.023	0.024	0.03	0.484	0.036	0.037	0.236
PAQC score intercept 2	−2.253	−0.386	0.031	0.031	0.150	−0.697	0.450	0.451	0.688	−0.808	0.154	0.154	0.677
PAQC score intercept 3	−1.189	−0.736	0.080	0.081	0.548	−0.801	0.322	0.323	0.743	−0.900	0.414	0.415	0.982
PAQC score intercept 4	0.083	−0.542	0.584	0.586	0.637	−0.665	0.187	0.188	0.477	−0.798	0.143	0.145	0.657
PAQC score intercept 5	1.371	−0.594	0.236	0.238	0.409	−0.727	0.370	0.374	0.669	−0.805	0.254	0.255	0.710
PAQC score intercept 6	2.246	−0.092	0.135	0.136	0.027	−0.113	0.204	0.205	0.054	−0.186	0.232	0.233	0.088
Age-group:12-59	0.154	0.086	0.084	0.085	0.015	0.106	0.146	0.148	0.033	0.175	0.173	0.173	0.061
Child sex: males	−0.046	−0.061	0.216	0.217	0.051	−0.074	0.260	0.261	0.074	−0.122	0.278	0.279	0.092
Comorbidities: 0	0.474	−0.293	0.230	0.230	0.139	−0.358	0.015	0.017	0.128	−0.593	0.071	0.071	0.357
Comorbidities: 1	0.309	−0.302	0.334	0.335	0.203	−0.370	0.557	0.558	0.448	−0.612	0.643	0.646	0.791
Comorbidities: 2	0.335	−0.250	0.389	0.390	0.215	−0.305	0.571	0.571	0.419	−0.505	0.642	0.644	0.670
Clinicians’ sex: female	0.337	−0.007	0.021	0.022	0.001	−0.007	0.017	0.018	0.011	−0.011	0.017	0.018	0.001
Clinicians’ cadre: MOd	0.038	0.140	0.156	0.157	0.044	0.170	0.055	0.056	0.032	0.281	0.015	0.016	0.079
Hospital workload: low	−0.367	−0.142	0.148	0.149	0.042	−0.173	0.251	0.252	0.093	−0.285	0.291	0.292	0.166
Malaria prevalence: low	−0.189	0.358	0.307	0.307	0.222	0.439	0.172	0.172	0.222	0.726	0.276	0.277	0.603
Enhanced A&Fe	−0.002	−0.005	0.193	0.194	0.038	−0.008	0.189	0.190	0.036	−0.017	0.181	0.182	0.033
Time (months)	−1.754	0.034	0.720	0.721	0.521	0.041	0.696	0.697	0.488	0.068	0.687	0.688	0.477
Time× Enhanced A&F	0.226	−0.063	0.161	0.162	0.030	−0.077	0.110	0.111	0.017	−0.129	0.127	0.127	0.033

^aTrue estimate.

^bEmpirical standard error.

^cMean square error.

^dMedical Officer.

^eAudit and feedback.

Across 6-simulation scenarios, the regression coefficients either underestimated (negative bias) or overestimated (positive bias) the standard estimates (Figure 1). Moreover, the magnitude of bias varied across variables and tended to increase with an increase in the proportion of missingness. However, the bias was much smaller when MI was used to handle incomplete treatment subcomponents compared to the conventional approach (Figures 1).

On the other hand, the standard errors tended to overestimate the standard errors of the base data set resulting to positive bias across simulation scenarios (Figure 2). It was further observed that for individual variables, the standard errors were less prone to bias compared to regression coefficients. These observations were made within and across simulation scenarios. Moreover, simulation results exhibited larger bias when missingness in treatment domain subcomponents were generated under MAR mechanism compared MCAR mechanism.

Across simulation scenarios, the estimated empirical standard errors were close to the estimated model-based standard errors (Table 2, Table 3 and Supplementary Tables A2–A7). In addition, the magnitude of both measures of accuracy tended to increase with an increase in the proportion of missing data in PAQC score components. The results further showed that MSEs were slightly larger under the conventional approach compared to MI approach and were somewhat larger under MAR mechanism compared with MCAR mechanism (Table 2, Table 3 and Supplementary Tables A2–A7).

Across simulation scenarios that is, missing data mechanisms and rates of missingness, Monte-Carlo standard errors of estimated bias in regression parameters ranged between 0.001 and 0.04 (Supplementary Tables A8–A9). The corresponding 95% confidence intervals around bias in the parameters of interest were narrow across simulation settings.

Finally, the simulation process was on average more time-intensive under MI strategy compared to the conventional approach. Furthermore, the computational time increased with an increase in the proportion of missing data irrespective of the mechanism used to generate missing data.

Discussion and conclusions

In this study, bias in regression coefficients and corresponding standard errors attributable to missing PAQC score subcomponents were examined through a range of simulation scenarios. The study results demonstrated superiority of MI as a strategy for dealing with partially observed PAQC score domain subcomponents over the conventional method. Nevertheless, MI approach led to some level of bias in the regression coefficients. These observations could be due to lack of compatibility between the imputation model and the analysis model considering that PAQC score was not included in the imputation model. To be specific, incomplete subcomponents in the treatment domain were include in the imputation model as target variables while subcomponents in the assessment and diagnosis domains were included as predictors variables. In this case, the composite outcome was constructed after MI step. Therefore, further research is needed to compare the performance of the proposed MI method with that of MI including the composite outcome, possibly adapting substantive model compatible MI approaches [3] to this setting, in order to guarantee that the relation between subcomponent and composite outcome is preserved [34].

Simulation results further showed that regression coefficients were more prone to bias compared to standard errors across simulation scenarios. A possible explanation for these results is that case records with missing PAQC score subcomponents in the treatment domain were not discarded in both conventional approach and MI approach and hence no major impact on the estimation of standard errors.

Previously, MI has been used to address missing data at component level in composite scores assessing quality of patient’s care [28,4]. Elsewhere, Simon et al., [38] proposed MI at index level particularly for smaller samples. In the case of PAQC score, there are no possibilities of missing PAQC score at aggregate level (the only possibilities are values between 0 and 6). Therefore, MI can only be implemented at subcomponents level.

In this study, MI was used to handle missing treatment domain subcomponents while undocumented pneumonia signs and symptoms in the assessment domain were regarded as inappropriate care and hence scored 0 in the binary indicators at PAQC score construction stage. This was in consideration of the trial’s inclusion criterion which required recruitment of patients with syndromic pneumonia. That is, patients with at least one of the two primary pneumonia signs and symptoms (the presence of cough or difficult breathing) in addition to at least one secondary sign and symptom necessary for pneumonia severity classification [27,1]. As such, imputation of undocumented signs and symptoms was not expected to have any meaningful impact on simulation study based on pneumonia trial data. However, it should be noted that MI can be extended to handle missing PAQC score subcomponents in other domains of routine care in studies without such restrictive inclusion criteria. Moreover, analyses and MI procedure proposed in this study can be extended to other MI techniques [21,24] in order to examine performance in terms of computational cost, bias and measures of accuracy as appropriate.

In conclusion, MI produce minimally biased estimates in comparison with conventional method. However, the regression coefficients are more prone to bias compared to standards errors more so when the underlying mechanism is MAR. Besides, bias tended to increase with an increase in proportion of missing variable in the outcome subcomponents. Therefore, missing data in subcomponents composite measures should be addressed carefully to alleviate potential for biased estimates and misleading inferences.

Funding Statement

This work was supported through the DELTAS Africa Initiative grant number 107754/Z/15/Z-DELTAS Africa SSACAB. The DELTAS Africa Initiative is an independent funding scheme of the African Academy of Sciences (AAS)’s Alliance for Accelerating Excellence in Science in Africa (AESA) and supported by the New Partnership for Africa’s Development Planning and Coordinating Agency (NEPAD Agency) with funding from the Wellcome Trust [grant number 107754/Z/15/Z] and the UK government. The views expressed in this publication are those of the author(s) and not necessarily those of AAS, NEPAD Agency, Wellcome Trust or the UK government. Funds from the Wellcome Trust [grant number 207522] awarded to Prof. Mike English as a senior Fellowship together with additional funds from a Wellcome Trust core grant awarded to the KEMRI-Wellcome Trust Research Programme [grant number 092654] supported CIN data collection.

Disclosure statement

No potential conflict of interest was reported by the author(s).