Negligible interaction test for continuous predictors

Abstract

Behavioral science researchers are often interested in whether there is negligible interaction among continuous predictors of an outcome variable. For example, a researcher might be interested in demonstrating that the effect of perfectionism on depression is very consistent across age. In this case, the researcher is interested in assessing whether the interaction between the predictors is too small to be meaningful. Unfortunately, most researchers address the above research question using a traditional association-based null hypothesis test (e.g. regression) where their goal is to fail to reject the null hypothesis of no interaction. Common problems with traditional tests are their sensitivity to sample size and their opposite (and hence inappropriate) hypothesis setup for finding a negligible interaction effect. In this study, we investigated a method for testing for negligible interaction between continuous predictors using unstandardized and standardized regression-based models and equivalence testing. A Monte Carlo study provides evidence for the effectiveness of the equivalence-based test relative to traditional approaches.

Negligible interaction test for continuous predictors

An interaction effect between two predictors occurs when the relationship between one predictor and an outcome depends on the level of a second predictor. A negligible interaction is defined as an interaction effect so small that it has no practical significance (importance) within the context of the research; zero interaction (i.e. a population interaction coefficient of exactly 0) would be the smallest magnitude example of a negligible interaction. In this case, the relationship between one predictor and an outcome would not depend on the level of the second predictor, or minimally depend on the level of the second predictor. Detecting a negligible interaction among two or more predictor variables on an outcome variable is of interest to many researchers in the behavioral sciences. For example, negligible interaction might be the primary hypothesis of a study or it might be a necessary requirement in order to drop a higher order interaction term from a model. Applying traditional null hypothesis tests (i.e. tests where the goal is to detect the presence of an association, such as an interaction, among variables) in order to assess whether there is negligible interaction has been a common approach among researchers, even though these tests are not appropriate for assessing a lack of relationship (e.g. [23,29]). More specifically, it is not suitable to use non-significance of the interaction term from a traditional (association-based) null hypothesis significance test as evidence of a lack of interaction.

In this paper, a method based on an equivalence testing framework was proposed for testing negligible interaction among continuous predictors using standardized regression-based models. Previously, Cribbie, Ragoonanan, and Counsell [10] addressed a lack of interaction when predictors are categorical, while in this paper, we address this issue when the predictors are continuous. Cribbie et al. [10] proposed an unstandardized bootstrap-based intersection-union test [5] for 2 × 2 and, in general, a × b designs to assess a negligible interaction among categorical predictors and explained the problems of utilizing factorial analysis of variance test (ANOVA) for this matter. In contrast to categorical variables, selecting an appropriate equivalence interval with continuous predictors is more entailed. Moreover, there are important issues that arise with continuous predictors because of the various scaling.

The order of the paper is as follows. First, the paper introduces the benefits of equivalence tests and methodological difficulties of traditional (association-based) null hypothesis significance tests for detecting negligible interaction. Following that, the paradigm of the proposed test for negligible interaction is outlined. Lastly, a simulation study was used to compare the proposed equivalence-based test of negligible interaction with the inappropriate, but popular, strategy of utilizing a non-significant interaction effect from a traditional regression model (which focuses on detecting the presence of an interaction) to demonstrate negligible interaction.

Introduction to equivalence testing

Traditional null hypothesis significance tests, for example the two independent-samples t-test with null hypothesis H₀: µ₁ = µ₂, can be used to assess whether there is an association among the predictor variable(s) and outcome variable(s) (in this case whether the two populations have different means). It should be evident that increasing the sample size with a traditional test causes an increase in power for detecting an association among the predictor and outcome. In this case, even a small association among the variables may be statistically significant. Moreover, since not rejecting H₀ does not prove that H₀ is true, traditional null hypothesis testing is not useful for research questions regarding a lack of association [11,23].

When the research hypothesis relates to a lack of association among variables, equivalence testing is the recommended approach. In the example from the paragraph above, equivalence testing would be valuable if a researcher was interested in demonstrating that the difference in means across two independent groups was too small to be of any importance. The goal of equivalence tests is not to demonstrate that variables are completely unrelated (e.g. that population means are identical), but instead that the association (in this case difference in means) is too small to be considered meaningful. For example, imagine that a researcher wants to demonstrate that treating an illness with a generic drug is similar to treating the illness with a brand name drug. In this example, showing that the two types of treatments are exactly equivalent (H₀: µ₁= µ₂) would not be the interest of the researcher, but showing that the differences in the treatment results are small enough to be considered negligible would be of interest to the researcher. The null hypothesis in this case could be expressed as: H₀: µ_{1 –} µ₂ ≥ ε | µ_{1 –} µ₂ ≤ −ε, where ε represents the smallest difference in means that is practically significant (| is the ‘or’ operator). Note that the null hypothesis in this case is specifying the presence of a non-negligible mean difference, where traditional null hypotheses specify a lack of association. Rejecting H₀ would provide evidence that the difference in means is negligible (i.e. −ε < µ₁ – µ₂ < ε).

Equivalence tests, which have been popular in biopharmaceutical and bio-statistical studies for decades, are now being used in behavioral science research for determining whether two means are equivalent (e.g. [11,23]), whether there is lack of association among two variables (e.g. [13,17,22,32], for evaluating measurement invariance [31,9], etc. Numerous different types of equivalence-based tests have been proposed (e.g. [2,24,26,28,29,30]). However, the two one-sided tests (TOST) approach of Schuirmann [26] is one of the most popular methods, and important articles by Rogers et al. [23] and Seaman and Serlin [27], which both focused on the TOST approach, introduced equivalence testing to the behavioral sciences. The two one-sided tests approach specifies that a researcher conduct two separate tests, one for each potential direction of an effect. For example, we could rewrite the null hypothesis above as: H₀₁: µ₁ – µ₂ ≥ ε; H₀₂: µ₁ – µ₂ ≤ −ε. The first null hypothesis specifies that the difference in population means is greater than ε, while the second specifies that the difference in population means is less than –ε. Both null hypotheses would need to be rejected in order to conclude that the population mean difference falls between −ε and ε.

In this study, we explore an equivalence-based test for evaluating whether an interaction among two continuous variables is too small to be considered meaningful. As the TOST is the dominant and most straightforward method for conducting equivalence testing, the proposed negligible interaction test is developed using the logic of the TOST procedure.

Traditional linear model test for interaction

We are interested in linear models where the primary focus is on whether there is an interaction among continuous predictors. The traditional general linear model (regression) approach can be written as

$$y_i=b_0+b_1{x}_{1i}+b_2{x}_{2i}+b_3{x}_{1i}{x}_{2i}+{\delta }_i,$$

where y_i is the score on the response variable for subject i, x_1i, x_2i are respectively the scores for the ith subject on the first and second predictors_, and x_1ix_2i represents the interaction among the predictors and is discussed in more detail below. $b_0$ represents the intercept, $b$₁ and $b_2$ are the regression coefficients (slopes) for the predictors, and $b_3$ is the coefficient for the interaction. δ_i represents the error in predicting the outcome score for subject i, and the δ values across all i = 1, … , n subjects are assumed to be independent and normally distributed. With traditional (association-based) null hypothesis testing, if the research hypothesis relates to the interaction then the goal is to reject H₀: $b_3^{\ast }=0$, where $b_3^{\ast }$ represents the population regression coefficient for the interaction, and thus provide support for the alternative hypothesis that there is an interaction (H₁: $b_3^{\ast }\ne 0)$. The (two-tail) null hypothesis is rejected if:

$$\frac{|b_3|}{SE(b_3)}\ge t_{\alpha /2,n-k,}$$

where SE(b₃) represents the standard error associated with b₃, α is the nominal Type I error rate, and k is the number of predictors (in this case k = 3). When a research hypothesis concerns the detection of an interaction, the main goal is to reject the null hypothesis of no interaction. However, when the researcher attempts to establish negligible interaction, they often do so (inappropriately) by attempting to fail to reject the null hypothesis of no interaction. However, this approach is problematic for (at least) two reasons. First, failing to reject the null hypothesis of zero interaction (H₀: $b_3^{\ast }$ = 0) does not imply that $b_3^{\ast }$ = 0; as discussed by Altman and Bland [1], absence of evidence is not evidence of absence. Therefore, any conclusion regarding the null hypothesis, when the null hypothesis of zero interaction is not rejected, cannot be supported because of lack of statistical evidence [7]. Second, when using a test of the traditional null hypothesis to test for a lack of interaction, a decrease in sample size actually increases the probability of concluding that there is no interaction. This runs counter to the more desirable (and scientifically-based) notion that a decrease in sample size should be accompanied by a decrease in one’s ability to detect the actual state of affairs – in this case, interaction. Thus, smaller sample sizes lack power for rejecting H₀: $b_3^{\ast }$ = 0 and have inflated power for finding a lack of interaction. However, when the sample size increases, H₀: $b_3^{\ast }$ = 0 will almost always be rejected and thus it will be almost impossible to ever conclude that there is a negligible interaction effect even if the effect is in fact trivial. This undesirable property of traditional tests, i.e. ample power for finding a negligible interaction with small sample sizes but minimal power for finding a negligible interaction with large sample sizes, is a very important issue that should be addressed under the equivalence-testing framework.

Assessing negligible interaction via equivalence testing

Since a complete lack of association among variables (i.e. population coefficient, such as $b_3^{\ast }$, of exactly 0) is unrealistic, the goal of equivalence tests is not to demonstrate that there is no relationship among variables, but to show that any relationship between the variables is too small to be meaningful (i.e. negligible). Defining how small of a relationship can be considered meaningful is both important and difficult [25]. Let the absolute value of the smallest interaction effect that is still meaningful be ε, which is defined a priori as an equivalence interval [i.e. EI = {−ε, ε}]. Measuring whether the interaction effect ( $b_3^{\ast }$) falls within the pre-specified interval (e.g. −ε < $b_3^{\ast }$ < ε) is the purpose of the proposed equivalence test.

As introduced above, a subjective yet challenging feature of equivalence testing is determining the threshold values based on the experimenters’ goals. There are very few rules to aid behavioral science researchers in choosing these threshold values based on their field of study and expertise [23,25]. This subjective choice requires an understanding of what constitute a minimum meaningful interaction in the research area of interest; for instance, a researcher may find 10% of the standard deviation an appropriate choice, but another researcher may not find it suitable for their particular study.

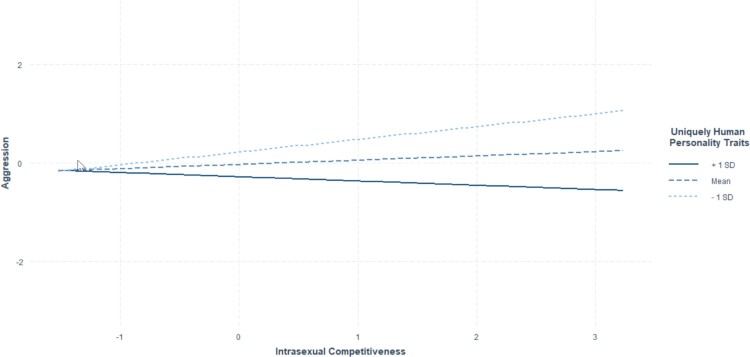
As an example, we discuss a study by Arnocky et al. [3]. The data from the study is accessible at https://osf.io/jqug4/. One the primary hypotheses of Arnocky et al. [3] was the interaction of uniquely human personality traits (comprised of openness and conscientiousness personality items) and individual differences in intrasexual competitiveness on aggression. If this researcher is interested in testing for negligible interaction, then the researcher needs to determine the smallest meaningful interaction effect (i.e. the smallest difference in slopes that would be meaningful for a one unit change in the predictor, recalling that the variables are standardized so a one unit change is a one standard deviation change). Although the decision is highly subjective and dependent on the context of the research, we can use general guidelines as a starting point. Cohen [8] suggested that standardized coefficients of .1 might represent a small relationship and .3 might represent a moderate relationship. Thus, in this study, we adopted values for ε of .1 and .3 to represent conservative and liberal equivalence thresholds (for models including standardized variables). In other words, the associated equivalence intervals would be EI_conservative = {−.1, .1} and EI_liberal = {−.3, .3}. Note that what is being specified, at the conservative level, is that for the effect of uniquely human personality traits a .1 difference in the slopes for a one standard deviation difference in intrasexual competitiveness would be minimally meaningful. Returning to the example, a multiple regression on the standardized variables returns an interaction effect of b_int = −.17, and the interaction is plotted in Figure 1. According to the criteria above, the interaction effect would be considered negligible according to our liberal bounds, but non-negligible according to our conservative bounds. However, no actual hypothesis testing has been conducted so we now outline non-standardized and standardized approaches for testing for negligible interaction.

Figure 1.

Plot of the interaction between intrasexual competitiveness and uniquely human personality traits on aggression.

Non-standardized equivalence-based approach for testing negligible interaction

Under the described model with normally distributed errors, the TOST approach can be used for hypothesis testing. Noting that the following approach could be easily extended to the higher dimensional cases, we focus our attention on the case where there are two predictors (plus the interaction, i.e. k = 3) in our (repeated from earlier) model:

$$y_i=b_0+b_1{x}_{1i}+b_2{x}_{2i}+b_3{x}_{1i}{x}_{2i}+{\delta }_i.$$

In this case, the null hypothesis can be written as H₀: $b_3^{\ast }$ ≥ ε | $b_3^{\ast }$ ≤ −ε and the alternate hypothesis can be written as H₁: −ε < $b_3^{\ast }$ < ε. Unlike traditional association-based hypothesis testing, where the null hypothesis states that b₃* exactly equals zero, in this new proposed method $b_3^{\ast }$ accepts a range of values under the null and alternate hypotheses. The null hypothesis is rejected if:

$$t_1=\frac{b_3-(-\epsilon )}{SE(b_3)}\ge t_{1-\alpha ,n-k}\mathrm{\&}{t}_2=\frac{b_3-\epsilon }{SE(b_3)}\le t_{\alpha ,n-k},$$

where $t_{\alpha ,n-k}i$s $\alpha$ quantile of a t-distribution with n-k degrees of freedom. Equivalently, H₀ is rejected if the (1-2α)% confidence interval for $b_3$ is contained within the equivalence interval [27].

Standardized equivalence-based approach for testing negligible interaction

In some instances, it might be difficult to select an appropriate equivalence interval because the predictor and/or outcome variables are measured on an arbitrary scale. To make the threshold interval unit-invariant, one possibility is to standardize the response variable and predictors before applying the regression analysis; hence the coefficients refer to the number of standard deviation changes in the response or outcome variable per standard deviation increase in the predictor variable [19].

Even though standardizing the variables is convenient, and the recommended approach for standardization, it should be considered that the standard error will not be correct for the standardized coefficients. The standard errors of standardized parameters are not a simple rescaling of the standard errors of the original parameter estimates [14], and will be both biased and inconsistent [15]. In the current study, we adjusted the standard error of the interaction coefficient with the delta method due to Jones and Waller. The delta method, unlike standard methods for computing confidence intervals with standardized variables, accounts for the sampling variability of the criterion standard deviation.

Regardless of the unit invariant property inherited from standardization, there is still much subjectivity in determining an appropriate equivalence interval. In this study, as discussed earlier, we use suggested small and medium thresholds for standardized regression coefficients [8], specifically .1 and .3, respectively. However, researchers are encouraged to consider what the smallest meaningful standardized coefficient might be for their particular research study by considering the context of the work.

Given a sample of n observations, we test the null hypothesis H₀: ${\beta }_3^{\ast }$ ≥ ε | ${\beta }_3^{\ast }$ ≤ −ε by applying the following steps (note that β represents the standardized coefficient, and β* represents the population standardized coefficient). First, standardize the response variable and each of the predictors. Second, create the interaction term as the product of the standardized predictor variables (instead of standardizing the product of the raw predictor variables; see [20]). Third, regress the standardized outcome variable on the standardized predictor and interaction variables. Finally, reject the null hypothesis H₀: ${\beta }_3^{\ast }$ ≥ ε | ${\beta }_3^{\ast }$ ≤ −ε if:

$$t_1=\frac{{\beta }_3-(-\epsilon )}{SE({\beta }_3)}\ge t_{1-\alpha ,n-k}\mathrm{\&}{t}_2=\frac{{\beta }_3-\epsilon }{SE({\beta }_3)}\le t_{\alpha ,n-k},$$

and retain it otherwise. An equivalent alternative is to reject the null hypothesis if the 1 – 2α confidence interval for ${\beta }_3$ falls completely within the equivalence interval { $-\epsilon$, $\epsilon$}. Recall that $SE({\beta }_3)$ is computed via the delta method [15].

To follow up on the Arnocky et al. [3] example, let’s apply the standardized equivalence-based approach for testing for negligible interaction. To recall, the outcome variable is aggression, and the predictors are uniquely human personality traits, individual differences in intrasexual competitiveness, and the interaction among these two predictors. The null hypothesis being evaluated is H₀: ${\beta }_3^{\ast }$ ≥ ε | ${\beta }_3^{\ast }$ ≤ −ε, where in this case ${\beta }_3^{\ast }$ represents the population standardized interaction effect between uniquely human personality traits and individual differences in intrasexual competitiveness. We will use, arbitrarily, α = .05 and the conservative standardized bounds ({ $-\epsilon$, $\epsilon$} = {−.1, .1}). First, we will convert all of our variables (outcome and predictors) to standardized variables. Next, we will compute the interaction term as the product of the standardized predictors. We then use the seBeta function from the fungible package in R to compute the 1 – 2α confidence intervals. The estimated standardized interaction effect is −.191, with a 1 – 2α = 1–2(.05) = .90 (90%) confidence interval of {−0.378, −0.003}. Since the confidence interval does not fall completely within the equivalence interval, {−.1, .1}, we do not reject the null hypothesis. In other words, we cannot conclude that the interaction between uniquely human personality traits and individual differences in intrasexual competitiveness is negligible. To assist readers, we have made the full R code for this example available at: osf.io/?

Method

A simulation study was conducted using R [21] to investigate the efficiency of the proposed negligible interaction test and the traditional association-based test for detecting negligible interaction (i.e. in this latter case, inappropriately concluding negligible interaction from a non-significant test of the interaction). The application of the traditional association-based test is inappropriate for testing for a lack of interaction regardless of the results of the simulation study. However, by providing empirical results, we aim to help the reader better understand the inaccurate use of non-rejection of the null hypothesis of no interaction in a traditional association-based test for detecting a lack of interaction and provide evidence to support the use of the proposed equivalence-based test of negligible interaction.

Ten thousand simulations were conducted for each condition using a nominal significance level of α = .05. Manipulated variables included sample size (N = 25, 50, 100, 1000, 5000), standardized equivalence interval ( ${\epsilon }_{high}=-{\epsilon }_{low}=.1\text{and}.3$) and interaction coefficients ( $b_3^{\ast }$/ ${\beta }_3^{\ast }$). Note that different coefficients are used for evaluating Type I error ( ${\beta }_3^{\ast }$ falls outside of the equivalence interval), maximum Type I error ( ${\beta }_3^{\ast }$ falls on the border of the equivalence interval) and power ( ${\beta }_3^{\ast }$ falls within the equivalence interval). With regard to the maximum Type I error rate, recall that with equivalence testing there is not a point null (e.g. H₀: ${\beta }_3^{\ast }$ = 0), and therefore many mean differences qualify as Type I error conditions. For example, if ${\epsilon }_{high}$ = .1, then rejecting Ho when ${\beta }_3^{\ast }$ = .2 is a Type I error, rejecting Ho when ${\beta }_3^{\ast }$ = .5 is a Type I error, etc. However, the MAXIMUM Type I error rate is achieved when ${\beta }_3^{\ast }$ = .1 (the minimum effect that qualifies as a Type I error). Also note that when referring to the equivalence interval (e.g. ${\epsilon }_{high}=-{\epsilon }_{low}=.1$) below we often just use the short-form ε = .1 (since all of the simulations focus on positive values for $b_3^{\ast }$/ ${\beta }_3^{\ast }$). The specific conditions used in the study can be found in Table 1.

Table 1.

Simulation study conditions.

$ϵ$	Type I Error	Max Type I Error	Power (1)	Power (2)
$0.1$	$b_3^{\ast }$ = 0.08	$b_3^{\ast }$ = 0.02021	$b_3^{\ast }$ = 0	$b_3^{\ast }$ = 0.01
$0.3$	$b_3^{\ast }$ = 0.2	$b_3^{\ast }$ = 0.06290	$b_3^{\ast }$ = 0	$b_3^{\ast }$ = 0.03

Note: ε represents the equivalence bounds [recall that the equivalence interval is (−ε, ε)], $b_3^{\ast }$ represents the unstandardized interaction regression coefficient (which has an associated ${\beta }_3^{\ast }$ coefficient), and Max Type I error represents the case where the standardized interaction coefficient is on the edge of the equivalence interval (i.e. ${\beta }_3^{\ast }$ = ε). Power (1) and Power (2) represent two different conditions in which ${\beta }_3^{\ast }$ falls within the equivalence interval. Each case of $b_3^{\ast }$ represents a distinct condition, so there are eight different conditions. Note that each condition was repeated for each of the sample size conditions.

For each simulation, a sample of size n for $x_1$ and $x_2$ was drawn independently from distributions $N(0,{\sigma }_{x1})$ and $(0,{\sigma }_{x2})$, respectively. A full factorial model was utilized to generate the outcome variable: $y_i=b_0+b_1{x}_{1,i}+b_2{x}_{2,i}+b_3{x}_{1,i}{x}_{2,i}+{\delta }_i,$ where b₁ and b₂ were fixed at 0, δ_i was from the normal distribution N (0, σ²) and $b_3^{\ast }$ was set at the values in Table 1. The next step was to standardize the outcome variable and each of the predictors and generate the interaction term as the product of the standardized predictor variables.

The proposed equivalence-based test was evaluated by exploring Type I error rates and power. In addition, the traditional (association-based) hypothesis testing approach for interactions was utilized where the inappropriate use of a non-significant interaction test was used as evidence of a lack of interaction (and the definitions of Type I error and power are in many cases unique from those of equivalence testing). In other words, since the null and alternate hypotheses are different under these two tests, Type I error and power have different meanings. To relate this back to the Arnocky et al. [3] example, where the null hypothesis was that the interaction was non-negligible, a Type I error would be rejecting the null hypothesis and concluding that the interaction was negligible when in fact in the population it was non-negligible.

For the proposed equivalence-based procedure, when | ${\beta }_3^{\ast }$|≥ ε, Type I error rates were investigated. For example, when $b_3^{\ast }$ = 0.02021 and ε = .1, ${\beta }_3^{\ast }$= ε and Type I error rates are expected to be at the maximum rate. Recall that ${\beta }_3^{\ast }$ represents the population standardized interaction coefficient, and $b_3^{\ast }$ represents the population unstandardized interaction coefficient. Larger values of $b_3^{\ast }$ also fall under the label of Type I error conditions but the expected Type I error rate is expected to be lower since it is less likely to falsely reject the null hypothesis with a large value for $b_3^{\ast }$/ ${\beta }_3^{\ast }$. When |β₃*| < ε power rates were investigated. For example, when $b_3^{\ast }$ = 0 or .01 and ε = .1, ${\beta }_3^{\ast }$ < ε and thus this is a power condition. Type I error rates for the proposed test were considered acceptable if they fell within Bradley’s [6] liberal limits, α ± .5α, which for our study equates to .025–.075.

For the traditional null hypothesis testing procedure, when | ${\beta }_3^{\ast }$| > 0 this would be a power condition, whereas when ${\beta }_3^{\ast }$ = 0 this would be a Type I error condition; however, in this study we are recording when a lack of interaction is concluded (i.e. nonrejection of the traditional null hypothesis) and therefore whenever | ${\beta }_3^{\ast }$| > 0 the recorded rates (i.e. conclusions of lack of interaction) are actually Type II errors, whereas whenever ${\beta }_3^{\ast }$ = 0 the recorded rates are correct decisions. The traditional test is included as a comparison in order to demonstrate to researchers that it is not acceptable to use a non-significant test of interaction as proof of a negligible interaction effect.

Results

Figures 2 and 3 display the proportion of lack of interaction conclusions for the proposed and traditional tests. Figure 2 displays the results for the conservative equivalence interval ( ${\epsilon }_{high}=-{\epsilon }_{low}=0.$1) and Figure 3 displays the results for the liberal equivalence interval ( ${\epsilon }_{high}=-{\epsilon }_{low}=0.3$).

Figure 2.

Rate of detecting negligible interaction between continuous predictors in traditional test and proposed test with the equivalence interval of ${ϵ}_{high}=-{ϵ}_{low}=0.1$. TNI = proposed test of negligible interaction; Trad = traditional interaction test. $b_3^{\ast }$= 0.02021 is an example of an estimated interaction coefficient on the edge of interval, $b_3^{\ast }$ = 0.08 is an example of a non-negligible interaction (ε.), and $b_3^{\ast }$ = 0.01 is an example of a non-zero negligible interaction (−ε < ${\beta }_3^{\ast }$ < ε).

Figure 3.

Rate of detecting negligible interaction between continuous predictors in traditional test and proposed test with the equivalence interval of ${ϵ}_{high}=-{ϵ}_{low}=0.3$. TNI = proposed test of negligible interaction; Trad = traditional interaction test. $b_3^{\ast }$= 0.0629 is an example of an estimated interaction coefficient on the edge of interval, $b_3^{\ast }$ = 0.2 is an example of a non-negligible interaction (ε.), and $b_3^{\ast }$ = 0.03 is an example of a non-zero negligible interaction (−ε < ${\beta }_3^{\ast }$ < ε).

Type I error conditions for the proposed equivalence-based test

The further the interaction coefficient is from the equivalence interval, the more conservative the Type I error rate. Thus, in order to understand the behavior of the upper bound of the Type I error (maximum Type I error rate) as a function of sample size, we consider the interaction coefficient that falls on the edge of the equivalence interval after standardization. In other words, when ${\beta }_3^{\ast }$ is equal to ε this is a Type I error condition for the proposed test (but a power condition for the traditional test, i.e. as discussed, the reported rates are the proportion of Type II errors). Note that $b_3^{\ast }$= .02021 for ε = .1 and $b_3^{\ast }$= .06290 for ε = .3 are the required coefficients for simulating a Type I error condition because the partial standardized coefficient for $b_3^{\ast }$= .02021 is ${\beta }_3^{\ast }$= .1 and the partial standardized coefficient for $b_3^{\ast }$= .06290 is ${\beta }_3^{\ast }$= .3.

When ε = .3, the Type I error results were approximately equal to α at all sample sizes (i.e. within Bradley’s limit). However, when ε = .1, the rates of Type I error were approximately equal to α only for n > 100 and conservative otherwise.

Recalling that the null hypothesis of the proposed test holds whenever the interaction coefficient (after standardization) falls outside of the equivalence interval, in order to simulate Type I error conditions we can choose infinitely many values for the interaction term (i.e. any ${\beta }_3^{\ast }$ ≥ ε | ${\beta }_3^{\ast }$ ≤ −ε). For the cases where we have a non-negligible interaction effect (i.e. $b_3^{\ast }$ = .08 for ε = .1, $b_3^{\ast }$ = .20 for ε = .3), both the traditional test and the proposed test rates of detecting no interaction, as expected, approach zero as the sample size increases. The most important difference is that the proposed test never results in a conclusion of negligible interaction, whereas the traditional null hypothesis test incorrectly concludes a lack of interaction more than 50% of the time at n = 25 and more than 25% of the time at n = 50.

Power conditions for the proposed equivalence-based test

When the partial standardized population interaction coefficient ( ${\beta }_3^{\ast }$) falls within the equivalence interval this is a power condition for the equivalence-based test and our interest is in the power of the proposed test to reject the null (i.e. detect a negligible interaction effect). In addition to $b_3^{\ast }$ = 0, $b_3^{\ast }$= 0.01 and $b_3^{\ast }$= 0.03 are examples of non-zero negligible interaction effects (−ε < ${\beta }_3^{\ast }$ < ε) used in the simulation study for $\epsilon =-{\epsilon }_{low}=0.$1 and ${\epsilon }_{high}=-{\epsilon }_{low}=0.$3, respectively. For the traditional test, however, when $b_3^{\ast }$ = 0 what is being recorded is the inverse of the Type I error rate (i.e. we expect the rates to be equal to 1 – α), whereas when $b_3^{\ast }$ > 0 we are again recording the Type II error rates.

For both ε = .1 and ε = .3, the power of the proposed negligible interaction test increased from 0 to 1 as n increased. The power of the proposed test is close to zero for n < 100 for ${\epsilon }_{high}=-{\epsilon }_{low}=0.1$ and n = 25 for ${\epsilon }_{high}=-{\epsilon }_{low}=0.3$. This was expected, as we do not have enough evidence to reject the null hypothesis of existence of non-negligible interaction with a small number of cases. As sample size grows, we have more statistical power for rejecting H₀: ${\beta }_3^{\ast }$ ≥ ε | ${\beta }_3^{\ast }$ ≤ −ε. For the non-zero interaction coefficient and narrower equivalence interval, as expected, the power of the proposed test is lower.

The traditional null hypothesis test results for $b_3^{\ast }$ = 0 are, as expected, approximately equal to 1 – α. For the cases where we have a non-zero negligible interaction, the traditional test will often conclude no interaction with a small sample size because of a lack of statistical power, but rarely or never find a lack of interaction with a large sample size.

Discussion

Two methods for detecting a negligible interaction effect were compared in this study: The traditional association-based null hypothesis testing method (which is actually testing for the presence of a non-zero interaction effect and relies on a non-significant coefficient for the interaction) and a proposed equivalence-testing based method, which was introduced in this study. Detecting a negligible interaction is the interest of many researchers and consequently the availability of an appropriate test for assessing a negligible interaction effect is crucial. The traditional association-based approach for assessing a lack of interaction has some known issues and is not recommended for the purpose of detecting negligible interaction.

The proposed test introduced in this study, unlike the traditional approach mentioned above, has statistical properties that are in line with the research hypothesis of the study. More specifically, the null hypothesis of the proposed equivalence-based test specifies a non-negligible interaction effect and the goal is to be able to reject this hypothesis and conclude that there is evidence for a negligible interaction effect. A procedure similar in terms of the objective of the study was previously proposed by Cribbie et al. [10] on inappropriately utilizing factorial analysis of variance test (ANOVA) to assess a lack of interaction with categorical predictors. However, the approach proposed in that work involved an unstandardized bootstrap-based intersection-union test for categorical variables in a x b designs. Such an approach is not necessary in the continuous predictor setting because there is a single coefficient representing the interaction term (rather than, for example, multiple interaction contrast dummy variables). In addition to the nature of the test, the procedure, including scaling, equivalence interval construction, interpretation, etc. are very different from the proposed testing procedure of this study for assessing negligible interaction among continuous predictors using standardized regression-based models. Below we discuss the results of the simulation study, and it is important to remember that the definitions of Type I error and power differ for the negligible interaction and traditional hypothesis testing approaches.

Type I error rates for the proposed test of negligible interaction when ${\beta }_3^{\ast }$ = ε = .1, were acceptable only when the sample size reached N = 1000. However, when ${\beta }_3^{\ast }$ = ε = .3, Type I error rates of the proposed test were acceptable at all sample sizes. As was discussed above, there is much subjectivity in setting an appropriate equivalence interval, and our results highlight that when the equivalence interval is very narrow, results can be overly conservative. To clarify, we are not suggesting that researchers increase the width of the equivalence interval in order to achieve appropriate Type I error rates; what we are proposing is that researchers take very seriously the selection of an appropriate equivalence interval for each negligible interaction problem see [4]. What degree of interaction is deemed negligible in one setting may not be deemed negligible in another. As expected, rates of Type I error were zero in all conditions when ${\beta }_3^{\ast }$ > ε. This is a desirable property of the test in that it does not permit any Type I errors when the coefficient falls beyond the border of the equivalence interval.

In the proposed test, when ${\beta }_3^{\ast }$ < ε and ε = .3, power rates reached 100% for both $b_3^{\ast }$= 0 and $b_3^{\ast }$= .03 when sample sizes were equal to 1000. With the conservative interval, ε = .1, when ${\beta }_3^{\ast }$ < ε, power rates reached 100% for sample sizes equal to 5000. Power rates for ε = .1 were nil until N = 500, however ε = .3 increased fairly steadily from the smallest to largest sample size. This is a key point; as introduced at the start of the paper, detecting negligible interaction is an important goal for many researchers. It is possible to declare negligible interaction with a theoretically appropriate method as long as the equivalence interval is not overly narrow or the sample size is large.

To summarize, since the null hypothesis of the proposed test matches the research hypothesis, as the sample size increases the proposed test’s rate of detecting negligible interaction will approach 100% when the interaction term (after standardization) falls within the equivalence interval and reaches zero when the interaction term (after standardization) falls outside the equivalence interval (and approximates α if the interaction term after standardization falls on the edge of the equivalence interval).

The results for the traditional test when ${\beta }_3^{\ast }$ > 0 are Type II errors and thus approach zero as the sample size increases. However, when sample sizes were small the traditional test often concluded a lack of interaction even when the interaction effect was non-zero. It is important to recognize the importance of this result; when working with the proposed test, with small or large sample sizes, interaction coefficients beyond the bounds of the equivalence interval were never declared negligible. However, with the traditional test, even interaction coefficients beyond the bounds of the equivalence interval can lead to a conclusion of no interaction without large sample sizes. These results highlight why it is not appropriate to use non-rejection of a traditional test as evidence of negligible interaction; with null hypothesis significance testing, it is important that power for investigating the research hypothesis increases, not decreases, with sample size.

For the cases with a small sample size and a negligible interaction effect, the traditional test appears to perform better than the proposed test. However, as described above, this apparent superior performance is a result of how the null hypotheses are defined for the traditional test and the proposed test. For small sample sizes, with a traditional test and a small to moderate effect there is a lack of evidence for rejection of the null. In other words, there is not sufficient power for being able to detect the interaction effect. However, it is still inappropriate to prefer the traditional test in this situation since a lack of power for detecting an interaction is not an appropriate test for detecting a lack of interaction. Further, when appropriate, larger values of ε provide good power and maintain the testing within the recommended equivalence testing framework.

What do all of these results mean for applied researchers? If a researcher is attempting to demonstrate that a negligible interaction effect exists between two predictors on an outcome, using a traditional (association-based) null hypothesis significance test might provide more power for concluding that negligible interaction exists with small sample sizes, however that is at the expense of also often declaring that negligible interaction occurs when, in fact, a non-negligible interaction is present. Further, with a large sample size, even very small (i.e. negligible) interactions may be declared statistically significant even if they have little practical significance. These results occur because the hypothesis testing procedure is backwards; the research hypothesis is aligned with the null, not the alternate, hypothesis. The equivalence-testing based approach proposed in this study aligns the research hypothesis (negligible interaction) with the alternate hypothesis, and thus the statistical results are as desired (i.e. power for detecting negligible interaction increases as sample size increases, and Type I error rates are minimal for non-negligible interactions).

As with all simulation studies, the results and conclusions are limited to the conditions we investigated in this study. Our focus was on linear models with two continuous independent variables and all assumptions were met. Future research may expand this methodology to higher order designs, such as three-way interactions, or assessing the effect of assumption violations on lack of interaction tests.

An alternative to the proposed approach is the use of Bayesian methods (e.g. [33]). For example, Bayesian highest density intervals on the interaction effect can be applied in a similar method to that of the methods proposed in this paper (and will yield similar results unless the sample size is small and a precise prior is adopted, see [16]). Bayes factors can also be applied, wherein the researcher is comparing the relative likelihood of the null and alternative hypotheses. It is important in these settings that an interval-based null hypothesis is adopted in order to be able to incorporate the equivalence interval (Hoyda, Counsell, & Cribbie; [18]). Another alternative is to simply explore the effect size for the interaction, however, hypothesis testing adds important information regarding the magnitude of the effect relative to the error [12].

To summarize, although much care is required when setting an appropriate equivalence interval, researchers investigating negligible interaction among continuous predictors are encouraged to utilize an equivalence-testing based approach.

Funding Statement

This work was supported by Social Sciences and Humanities Research Council of Canada: [Grant Number 435-2016-1057].

Disclosure statement

No potential conflict of interest was reported by the author(s).