Abstract
Industrial statistics plays a major role in the areas of both quality management and innovation. However, existing methodologies must be integrated with the latest tools from the field of Artificial Intelligence. To this end, a background on the joint application of Design of Experiments (DOE) and Machine Learning (ML) methodologies in industrial settings is presented here, along with a case study from the chemical industry. A DOE study is used to collect data, and two ML models are applied to predict responses which performance show an advantage over the traditional modeling approach. Emphasis is placed on causal investigation and quantification of prediction uncertainty, as these are crucial for an assessment of the goodness and robustness of the models developed. Within the scope of the case study, the models learned can be implemented in a semi-automatic system that can assist practitioners who are inexperienced in data analysis in the process of new product development.
Keywords: Experimental design, artificial neural networks, random forests, R&D, product development
1. Introduction
In today's competitive environment, quality management and innovation are among the main drivers for value creation and business excellence [52]. Moreover, several studies exist that establish the positive impact of quality management on innovation processes [36,64] and identify quality engineering as one of the promoters of innovation [7]. Strong ties link quality and innovation. In this scenario, industrial statistics plays a major and dual role: on the one hand, it has always contributed greatly to quality improvement in the context of operations; on the other, statistical thinking is needed to enable innovation.
Many statistical methods are used for quality improvement, e.g. data sampling strategies, measurement system analysis, hypothesis testing, statistical process control, Design of Experiments (DOE) and more. Since the 1980s, Six Sigma strategies have demonstrated how a structured application of statistical methods can improve existing processes by reducing costs and eliminating waste. More recently, there has been an expansion of the role of industrial statisticians working in quality to embrace a view more oriented towards innovation. Bisgaard [4] even proposed reframing the perspective of the quality profession as systematic innovation. Hockman and Jensen [30] recognize quality and innovation as two critical elements for business superiority, defining them as the two ‘Pillars of Excellence’. Moreover, the authors [30] acknowledge the primary role of statistics in both fields, and they believe that statisticians can lead not only quality improvement but also innovation. Among others, the tendency to drive decisions based on data and the sequential knowledge gain that comes from the use of the scientific method that characterize statistics are distinctive traits that put statisticians in a leading position.
Undoubtedly, to cope with their prominent role in innovation, statisticians need to expand the classic toolset of methods used in industrial statistics by modifying the existing methodologies and integrating new tools, including those from different fields of research, to create new solutions that can be applied to a broad range of problems [34]. One of the most promising fields in this sense is that of Artificial Intelligence, which indicates the broad set of techniques that simulate human analytical skills for problem solving, including Machine Learning (ML) and deep learning. As a result of recent technological developments and the decreasing cost of computing hardware, ML is now being applied to the most disparate of contexts at a hitherto unprecedented scale, to a point that it is now undertaking tasks that were previously domains of humans. Consequently, Artificial Intelligence and ML are regarded as innovations that in the near future will have the greatest impact on our methods of work and organization [18]. ML is usually applied in settings in which data is abundant and, by leveraging the correlations present in such large data sets, the algorithms are capable of finding the underlying patterns or trends that describe the phenomenon under study, thus making associations between the related variables. This task is usually referred to as the ‘learning’ or ‘training’ phase of the algorithm. Clearly, such an approach is mainly or solely empirical, and the robustness and validity of the results obtained is directly dependent upon the exhaustiveness of the data set selected to train the algorithms. Given the impossibility of obtaining a complete and thorough data set for any physical phenomenon as well as developing a perfect and exact model that explains the said phenomenon, some methods are needed to at least provide some insights into the causative relationships that control it. Moreover, a further obstacle to interpretation is the fact that ML algorithms tend to function as black boxes, making it even more difficult for the analyst to grasp the rationale behind the algorithms and therefore to justify the results of the trained models. For such reasons, we believe that purely empirical approaches may have little value if interest lies in not only obtaining accurate predictions but also in making inferences concerning data.
We agree with Box and Liu [6] that industrial innovation comes as a result of a process of investigation, therefore, at least to some extent, insights about causation are needed to pursue true innovation in the industrial environment. Referring to the traditional methods used in industrial statistics, DOE has proved to be one of the most effective when dealing with innovation, especially in product development and product improvement [30,44]. This is the field studied in this paper. One of the key characteristics of DOE is that it is suitable in situations in which a phenomenon under study has one or more input variables that determine one or more response variables and some of the input variables can be controlled by the experimenter. The strategy of experimentation, based on the ability to control the input variables, allows the analyst to establish causal claims.
In this article, the potential advantages of using a combined approach of DOE and ML modeling will be discussed with reference to an R&D setting. A case study from within the chemical industry will be analyzed and presented as the driver for this work.
2. Design of experiments and machine learning
Taken separately, DOE and ML lines of research are both extensive and intensively investigated. Literature on DOE dates back to the early decades of the twentieth century, and the methodology has been widely applied in many different industries for a long time. Likewise, ML, although it can be regarded as the younger of the two, is rather mature as a research field. However, considering the vastness of the two topics, not many papers have been published that discuss the two methodologies jointly. In this section, (i) a background of previous works on the joint adoption of DOE and ML will be presented and (ii) some related gaps will be pointed out.
2.1. Background on the joint application of DOE and ML
Two main currents have been found in the literature that discuss the joint application of DOE and ML, one concerning the use of DOE as a means to optimize the process of training ML algorithms and one concerning the application of ML for the analysis of DOE data. This second branch will be discussed more extensively since the principal interest of this paper regards the investigation of DOE and ML in R&D settings.
For what concerns the first current, numerous contributions address the use of DOE as a systematic approach to select the best combination of hyperparameters for ML models. The use of DOE facilitates the interpretation of the effect of each parameter on the performances of the algorithms, thus potentially speeding up the process of training the models. Some examples of such applications of DOE in different ML algorithms can be found in [38,41,57].
For what concerns the second current, several studies cover the application of ML methodologies to data collected through experimental design strategies, mainly in R&D settings. In general, ML algorithms are used because of their innovativeness and potentially high predictive power when compared with the most common Response Surface Methodology (RSM) based on quadratic regression with interactions that is employed to model relationships of DOE data. In recent years, the approach of combining DOE data with ML models has found application in diverse fields such as manufacturing, maintenance, supply chain, additive manufacturing, chemical, mechanical and pharmaceutical industries. The most common choice of predictive algorithm is based on Artificial Neural Networks (ANNs) or their modifications [1,8,11,17,19,25,26,28,29,31,32,35,39,48,51,54,61], on support vector machines (SVM) or their adaptations [8,10,12,26,39,60] and a few also employ tree-based methods [8,49,51]. When optimization is one of the study's objectives, a genetic algorithm is often applied [12,14,25,26]. Many of the papers test different ML methods and carry out a comparison of the resulting predictive performance, and some also compare the algorithms with the polynomial model obtained using the RSM approach [1,11,12,17,19,28,35,39,54,60]. In general, employment of ML models slightly improves the predictions, but due to the peculiarities of each case, no algorithm could be regarded as unquestionably superior to the others or to the RSM approach. The typical outcome is that quadratic regression performs better than some of the algorithms and worse than others. For this reason, it is worth continuing the investigation, perhaps also analyzing those methodologies that have only been seldom employed.
2.2. Some critical aspects of the application of ML for the analysis of DOE data
The exploration of the literature on the joint application of DOE and ML leads to the identification of some critical gaps.
A first gap concerns the scarce attention put on quantification of uncertainty. Apart from a few examples [29,39,63], in almost all papers, the role of prediction uncertainty is under-emphasized both for ML and RSM-based applications. This is by no means an uncommon situation, since prediction uncertainty is frequently overlooked in both DOE and ML literatures. However, we believe that some sort of uncertainty quantification should be reported not only for RSM but also for ML models; this is crucial, especially in R&D environments, to obtain a more thorough sense of the goodness and more importantly of the robustness of the models since no real industrial phenomenon can be considered deterministic.
Another critical point emerging from the literature is the lack of causal investigation when dealing with ML predictive algorithms. ML algorithms are not easy to interpret, and the relationships uncovered in the training data are often burdensome to explain. Nonetheless, some insight into causation is needed as proof of the physical significance of the model or for extrapolation of knowledge about the phenomenon. This task is addressed mainly by plotting the results in the form of surface or contour plots, at least to explain bi-variate associations of predictors with the response [14,19,26,28,32,35,39,61]. Although this approach is certainly valid, we believe that further information could be encompassed, e.g. by assessing the relative importance of predictors with respect to the response.
Another point is that for the most part, the papers cited above combine DOE and ML solely for the resolution of the specific problem under investigation. Most of the papers proceed with a direct application of the algorithms on the experimental data, very rarely introducing any consideration of the possible advantages, disadvantages or implications of such a choice. Some discussion of this topic can be found in [10,12,51]. Only recently a paper focusing on a comprehensive discussion of the implications of ML for DOE and how the two methodologies can be applied was proposed by Freiesleben et al. [20]. In their work the authors [20] identify the similarities and differences between DOE and ML and then debate how one can be beneficial to the other. They differentiate between the human-based and software-based parts of the two methodologies and assess how ML can facilitate an automation of the human-based parts of DOE. The authors focus mainly on the production setting in which online monitoring based on sensors and real-time data can potentially provide the ML system with all the information needed to generate a perfect knowledge of the production plant and associated quality problems. In this scenario of data abundance DOE could become obsolete since choice of factors and levels for process investigation would no longer be required.
However, to reach a stage at which DOE is replaced by ML-based systems, some limitations need to be overcome, the most obvious of which relates to data availability. To achieve the extensive knowledge needed for the ML system to supplant DOE, a large-scale structure for continuous monitoring of real-time production data needs to be put in place. Such a system could only be installed if a massive amount of data is already produced and only needs to be captured. While this is certainly the case with production lines, the situation is different in R&D, where a major effort is made in relation to the investigation of a phenomenon and often data is not only to be captured but also generated. In such situations, we believe that a complete substitution of DOE with ML is more difficult or at least less imminent. Another issue that should not be ignored is that even if ‘big data’ are available, exclusively relying on observational data presents some risks and the size of data does not erase the need for appropriate study design and statistical analysis [13].
The remainder of this article will look at a case study concerning the application of ML methodologies to DOE data in an R&D environment. To address the critical points that have emerged from the literature, the focus will be on algorithms that could provide an assessment of the uncertainty of predictions. Emphasis will also be placed on strategies that could shed light on the black box and provide some understanding of the rationale which drives the algorithms. Given that data fed into the algorithms will not purely be observational, but rather generated via an experimental design, some insights into causation can be given as well. The algorithms will be trained on a rather small data set when compared to the usual application of ML on ‘big data’ and the performances will be compared to the ones obtained using the RSM approach which is considered as a baseline for comparison.
3. Case study in the chemical industry
The case study concerns the initial phases of development of a new detergent. At this stage, the main focus is to discover and characterize the relationships existing among the components of detergent's formula and the washing performance on three different types of stain. Such relationships must be formalized in a model, one for each response, and such model must be appropriate in terms of prediction accuracy as well as interpretability. This section is organized as follows: (i) the experiment will be described into details, (ii) the structure of data and some diagnostic information about the data set will be presented, (iii) the ML models employed for data analysis will be discussed and (iv) the results will be shown.
3.1. Description of the experiment
Using the historical data available, nine chemical components of the formula were identified as potentially having an impact on the washing performance. DOE was selected as the appropriate methodology for data collection, and Box–Behnken Design (BBD) [5] was the experimental design of choice. A BBD was preferred for two main reasons, namely the design's relatively high efficiency, and the lack of corner points in the design space. For experimental designs, the efficiency is defined in terms of the ratio between the number of coefficients that could be estimated by the model (RSM) and the number of experiments; BBD has higher efficiency than other competitive designs, such as the Central Composite Design (CCD) or full factorial designs [40]. Moreover, BBD does not include combinations for which all the factors are at their highest or lowest levels; such extreme conditions were not desirable and also not feasible in production. When planning an experimental design, a crucial task concerns the identification of the range over which each factor will be varied: historical data and chemical analysis of the products on the market have been used to identify the relevant range for each component. For the purposes of confidentiality, the names of the chemicals used to define the formulae as well as the names of the stains have been amended.
The BBD with 9 factors resulted in a total of 120 spherical points [43], to which 10 center points have been added. Due to resource constraints, the design with 130 points was computer-optimized using the D-optimality criterion and consequently 70 runs were obtained. This design was then replicated, and the final design with 140 runs was employed for experimentation in the laboratory. Each experimental trial consisted in a full washing cycle carried out using household washing machines. The experiments were conducted in parallel, and several washing machines of the same made were used. For each replication of the same treatment a different washing machine unit was employed. Given that the interest is solely in the performance of the detergents, the type of washing cycle and water temperature were fixed. In each washing cycle, multiple standard soiled fabric samples were employed, with three identified reproducible stain types of interest. The washing performance on each stain type was assessed by means of a reflectance spectrophotometer that performs a colorimetric evaluation in accordance with the CIELAB system and outputs a percentage value that is indicative of the effectiveness of the wash, with 100% indicating perfect stain removal [3,42].
The experimental procedure appropriately simulates the actual process as experienced by consumers, thus it is characterized by high and rather unpredictable variability because washing performance is highly dependent on laundry distribution during the washing cycle. With the aim of assessing the impact of such variability, in each trial the same response was collected from two different samples of fabric – even with the same stain type, the washing cycle may not be equally effective. Considering the replication, this means that for the same experimental conditions four values of each response were registered. Accordingly, the final data set includes 280 data points.
3.2. Description of the structure of experimental data
A model for the variance structure valid for each observation of each response variable is described in Equation (1):
| (1) |
where
is the washing performance observed on the kth sample of fabric (k = 1, 2) from the jth replication of the experiment (j = 1, 2) on which the ith treatment is applied ( ).
μ is the overall mean.
is the fixed effect of the ith treatment, that is the ith formulation of the detergent. Each treatment is determined by the combination of the amounts of the different chemicals in the formula.
is the random effect of the jth replicate of the ith treatment, with . This effect is imputable to the use of different units of washing machine of the same made in the experiments. The effect of the replicate is nested in the treatment, meaning that each replicate, i.e. each washing cycle, should be uniquely identified only with reference to a specific treatment as, for example, it is of interest to differentiate between treatment 1, replicate 1 from treatment 1, replicate 2 but not treatment 1, replicate 1 from treatment 2, replicate 2.
is the random residual, with .
The two variance components from the model in Equation (1) are estimated employing ANOVA-type estimation [53] and reported in Table 1 to 3 for the three response variables ( , , ). The estimates show that is affected by largest variance of the random effects and error ( ), while a smaller impact is found for ( ) and ( ). Another interesting result shows that while for the greatest part of variance is imputable to the variability between replicates ( ), for and majority of variance is found within replicates ( ). This means that, when considering all responses at the same time, both the differences that arise between replicates of the washing cycles and the intrinsic volatility which exists within the same washing cycle play a relevant role. Thus in an ideal scenario a large number of replicates executed on different washing machines and a large number of repetitions of the measurement within the same experimental trial should be conducted for this type of problems.
Table 1.
Estimation of the variance components for the stain .
| Name | DF | Total [%] | σ | CV [%] | |
|---|---|---|---|---|---|
| total | 89.96 | 19.55 | 100 | 4.42 | 6.34 |
| treatment:replicate | 70 | 14.77 | 75.57 | 3.84 | 5.51 |
| error | 140 | 4.77 | 24.43 | 2.19 | 3.13 |
| Mean: 69.72 (N = 280) |
Table 2.
Estimation of the variance components for the stain .
| Name | DF | Total [%] | σ | CV [%] | |
|---|---|---|---|---|---|
| total | 139.76 | 4.33 | 100 | 2.08 | 4.21 |
| treatment:replicate | 70 | 1.45 | 33.50 | 1.20 | 2.43 |
| error | 140 | 2.88 | 66.50 | 1.70 | 3.43 |
| Mean: 49.48 (N = 280) |
Table 3.
Estimation of the variance components for the stain .
| Name | DF | Total [%] | σ | CV [%] | |
|---|---|---|---|---|---|
| total | 138.68 | 3.50 | 100 | 1.87 | 3.27 |
| treatment:replicate | 70 | 1.20 | 34.28 | 1.09 | 1.91 |
| error | 140 | 2.30 | 65.72 | 1.52 | 2.65 |
| Mean: 57.16 (N = 280) |
The coefficient of variation (CV) of each component of variance is also calculated which shows the impact of the variability of the random effects and error on the mean response.
If normality and linearity are assumed, a model for the prediction of the washing performance coherent with the description in Equation 1 is a linear mixed model (LMM)[58] in the form:
| (2) |
where is the vector of the response observations, is the design matrix of fixed effects levels (i.e. the chemical components of the formulation), is the vector of fixed effects parameters, is the design matrix of random effects levels, is the vector of the random effects parameters and is the vector of the random error. Mixed models are conditional models [58], meaning that the observations are conditional on the random model effects, that is . This implies that for a conditional prediction of the response, which is a prediction that takes into account dependencies embedded in the structure of clustered data, the levels of the random effects must be known. Unfortunately this does not apply to our case, since the objective of the study is to develop models that, once put into production, can predict the washing performance of a certain detergent when solely the components of the formula are known, and no information is given about the random effects levels (i.e. replication on a certain washing machine unit). At this point, the only option would be to set and use a marginal model for prediction, that is a model which only includes the fixed effects. If this is the case, the advantage of training a conditional model while only a marginal model can be used for prediction is not expected to be substantial. The LMM in Equation (2) can be extended to the Generalized Linear Mixed Model (GLMM) case that can manage responses which follow a generic distribution from the exponential family and can accommodate non-linear link functions [58]. Furthermore, although the inclusion of random effects in ML models is an open problem in the literature, some methods have been proposed that mix ML algorithms with GLMM for an estimation of both fixed and random effects [27,55,56], leveraging the ability of complex ML algorithms to model highly non-linear data. However, also in these cases [27,55] no substantial advantage in terms of prediction accuracy is found when no information about the random effects level is included in the test data, since the contribution of the ML model is solely in the estimation of the fixed effects.
All of this considered, in these situations the most appropriate strategy is to collapse the contribution of the random effects. Consequently, to proceed with the case study the repeated measures registered for each replicate are collapsed, meaning that the means are calculated and the models will be fit to these values, instead of taking into consideration the individual observations carried out on each single sample of fabric. Accordingly, the data set used hereinafter includes 140 observations. In this way, the random effect is absorbed by the error term , and only fixed effects (plus the random error) are left in the data structure (Equation 1).
Figure 1 shows a variability chart after computation of the averages of repeated measures. The points are obtained as the ratio between the standard deviation between replicates (after computation of the averages of repeated measures) and the mean response value within each replicate. This source of variability is here called ‘latent experimental variability’, which is basically residual noise intrinsic to data after the random effects have been absorbed by the error terms. The crosses are obtained as the ratio between the standard deviation of all DOE data for each stain and the response value for each treatment and replicate after having computed the averages of the repeated measures. This source of variability is here called ‘DOE variability’.
Figure 1.
Visualization of the ‘latent experimental variability’ (points) and ‘DOE variability’ (crosses) across the range of treatments for (a), (b) and (c). In red the cases when ‘latent experimental variability’ is larger than ‘DOE variability’. For confidentiality purposes, the name of the responses has been amended.
A different behavior of the three responses is exhibited by the plots. In particular, for and it can be noted that in several occasions the two values of ‘latent experimental variability’ and ‘DOE variability. are very close, and in red are reported the cases when the ‘latent experimental variability’ is even larger than ‘DOE variability’. This condition is verified 22.86% of times for , only 1.43% of times for and 0% of times for . This result was expected, since was affected by the largest contribution of the random effects (Table 1), which is now absorbed by the random error, hence introducing additional noise into the data. Clearly, when the variability which is not attributable to the factors levels combination (‘latent experimental variability’) is larger than the variability due to the contribution of all the factors and their levels (‘DOE variability’), a proper prediction of the response is burdensome.
Figure 2 shows the box-plots of the distributions which are obtained after computation of the differences between ‘DOE variability’ and ‘latent experimental variability’ for each replicate of each treatment and Figure 3 shows the same data across the range of each response. The box-plots offer a synthetic visualization of the different situation for the three responses and shows that while for the ‘DOE variability’ is consistently larger than the ‘latent experimental variability’, for this difference is narrower and for this difference can often be also negative. Figure 3 reveals that as the responses increase, the impact of the ‘latent experimental variability’ increases, since there is a negative correlation between the difference of ‘DOE variability’ and ‘latent experimental variability’ with each response, although strong statistical significance of this is found only for and . However, it should be noted that the impact of the ‘latent experimental variability’ on , for which the correlation is the strongest, is rather small in absolute terms since the values are consistently positive.
Figure 2.
Box-plots of the difference between ‘DOE variability’ and ‘latent experimental variability’ across the range of treatments for the three responses.
Figure 3.
Scatter plots of the difference between ‘DOE variability’ and ‘latent experimental variability’ across the range of treatments vs the range of the responses: (a), (b) and (c). The coefficient of correlation is calculated and reported together with related p-value.
3.3. Machine learning models
The main goal of the study consists in the development of regression models capable of performing an analytical prediction of the washing performance of a given detergent formula. Emphasis must also be placed on the uncertainty of predictions and on the characterization of the relationships between each factor and the responses. Two ML models are chosen as candidates, namely Random Forests (RFs) and Artificial Neural Networks (ANNs); the results are compared with the ones of a quadratic model with interactions which is typical of the Response Surface Methodology (RSM) to model DOE data.
RFs are an ensemble learning method based on simple decision trees [9]. In the classical implementation of RFs, multiple trees are trained on bootstrap samples of the initial data set and the final prediction is given by the average of the predictions of each tree in the forest. More recent modifications of the algorithm include additional randomization by training the trees on the whole training sample and splitting nodes by choosing cut-points fully at random [24]. Using the arithmetic average of the predictions of the base learners, RFs reduce the variance of results and are therefore able to provide more accurate predictions than single decision trees. Moreover, when growing the trees, RFs perform a random selection of the candidate variables for splitting, thus obtaining a collection of de-correlated trees that makes the algorithm even less sensitive to changes in the training data, meaning that the variance of predictions is further reduced [21].
One of the advantages of RFs is that they natively provide estimates of variable importance, thus making the algorithm fairly interpretable even when many trees are grown and a direct investigation of each one to understand the underlying process becomes infeasible. Breiman [9] proposes two measures for quantification of variable importance, one based on Gini importance and one based on a permutation approach. The first method measures the decrease of the Gini index (impurity) after a node split and uses it as an indicator of feature importance. The larger the decrease in the Gini index, the more relevant the input variable used in that split. The second method measures the increase in the error rate when one predictor variable is randomly permuted. The idea is that, for non-relevant variables there will be no substantial worsening in prediction accuracy while for relevant variables a decrease in accuracy is expected, thus resulting in a positive importance measure.
Like many other ML methods, RFs do not automatically provide an estimation of prediction uncertainty. However, over the years different authors have proposed new formulations for a quantification of RF predictions. In this paper, we refer to the work of Wager et al. [59]. The authors in [59] propose two formulations for an unbiased estimation of variance of RF predictions by expanding on the techniques of jackknife-after-bootstrap [15] and infinitesimal jackknife [16] for bagging. A desirable property of such variance estimates is that, they substantially do not require additional computational effort other than for training the RF. Jackknife, like bootstrap, is a resampling technique. However, instead of drawing from the training set a given number of times with replacement, as done by bootstrap, jackknife leaves just one observation out of the training data thus establishing n−1 distinct sets of data where n is the number of samples in the training data. The jackknife estimator of a parameter proceeds by calculating the parameter on each set of data and then computes the average of such values. The infinitesimal jackknife [33] is a modification of the jackknife where, instead of removing one observation at a time, it iteratively assigns to the observation only slightly less weight than the others. For prediction variance quantification, Wager et al. [59] propose selecting from a trained RF all those trees that were trained on a bootstrap sample that did not contain a certain observation, and repeating the procedure for all the observations in the original training data. As such, multiple small RFs are obtained, and the predictions of each is compared to the prediction of the original RF. Unfortunately this procedure introduces a bias, that is then removed using bias-corrected versions of the variance estimates. When this procedure is completed, some latent upward sampling bias is left for the jackknife-after-bootstrap estimate and some downward bias is left for the infinitesimal jackknife approach. Thus the authors in [59] suggest taking the arithmetic mean as an unbiased estimate of the prediction variance.
ANNs are flexible and powerful ML models that have been applied to solving complex tasks in engineering and science. Similarly to the biological brain, ANNs are made up of a multitude of neurons, also called nodes, which are interconnected by means of weights that perform a function similar to the synapses in the biological brain, thus transferring the impulse from one neuron to the other. The nodes are organized in layers; each layer, together with the constituting nodes and interconnections form the network structure. The higher the number of layers, the higher the potential for ANNs to learn complex functions. For this reason, multi-layered ANNs have recently been applied vastly, to the extent that they have become a separate branch in the field of Artificial Intelligence known as deep learning. The learning procedure of ANNs is based on the iterative adjustment of the connection weights with the aim of reflecting the patterns observed in the training data. A backpropagation algorithm is often applied as a training method and it consists in many cycles (a.k.a. epochs) of forward and backward phases [50]. In the forward phase, the input is passed through the network, the output is computed and compared with the observed output. As such an error is calculated, and it is decomposed in the backward phase and assigned to each weight in a proportion corresponding to the contribution of each weight to the error. The next step consists in the adjustment of the weights by gradient descent thus in a reduction of the error. This procedure is employed iteratively until the algorithm converges to a minimum of the loss function or until a maximum number of epochs is reached. In this process several hyperparameters, such as learning rate and weight decay, can be employed to set the pace of the procedure and to reduce the risk of the model overfitting the data.
When performing the first iteration of training the ANN, the initial weights need to be set, and the most common choice is to randomly initialize each weight. However, the initialization of weights can play a relevant role in the final prediction accuracy of the model given that depending on the initial state of the algorithm, the learning procedure could reach a local minimum or the global minimum of the loss function. One way to deal with this stochastic behavior of ANNs is to employ an ensemble averaging strategy. Similarly to RFs, ensemble averaging in ANNs consists in training several models on the same initial data with the objective of reducing the variance while not increasing the bias of the final model. The extent of the final model's variance reduction is proportional to the degree of independence of the base learners, and by random initialization of the weights, a certain level of independence is already achieved [45]. Thus, by averaging the results of an ensemble of neural networks trained starting from different initial conditions, more robust and more accurate results can be achieved.
ANNs do not natively provide an estimation of variable importance. However, examples are present in the literature that propose methods for an estimation of feature importance in ANNs, based on qualitative and quantitative tools [23,46,47]. Olden et al. [46] propose a flexible method that assesses variable importance by calculation of the summed product of input-hidden and hidden-output weights between input and output nodes. The rationale is that the contribution of the predictors on the response mainly depends upon the magnitude and direction of the connection weights in the ANN. The advantages of this approach include the possibility to extend it to ANNs with multiple hidden layers and the ability to capture both positive and negative effects of the inputs. The importance measures are reported in the same units as the summed products of the connection weights.
Like RFs, ANNs also provide point predictions without estimation of uncertainty. Recently, methods based on Bayesian neural networks have been used because they can provide a measure of uncertainty since a probability distribution is assigned to each weight in the network [22]. Other probabilistic approaches exist, and have shown very good performance for uncertainty estimation, that leverage the advantages of ANN ensembles [37]. Such methods, however, refer to the deep learning setting, in which many hidden layers are added to the network. Considering the relatively small size of data, in this paper we opt for one-hidden-layer feed-forward neural networks trained by backpropagation, therefore such methods do not really apply to our case. However, since the importance of an estimation of prediction uncertainty is stressed, an estimation of uncertainty will be provided by levering the ensemble averaging approach. Since in ensemble averaging many ANNs are trained from different initial conditions, each of these networks will provide a point estimation for a new test instance. As such, all the predictions can be saved and relevant percentiles can be calculated and used to determine an empirical estimate of prediction uncertainty. The same idea can be applied to get an estimate of uncertainty of variable importance measures [2].
3.4. Case study: results
In this section, the details of the data analytical phase of the study are presented. The practicalities of how the models are trained and applied will be discussed and the results will be shown. As explained in Section 3.2, after computation of the means for the repeated measures 140 data points are left from the initial DOE data. This data set is randomly partitioned into 75% for training and 25% for testing. Furthermore, fivefold cross-validation is employed on the training data to tune the models and select the optimal combination of hyperparameters through grid search.
In each RF, the predictions of 2000 trees are averaged to obtain the final prediction. Node splitting is performed either by the principle of minimization of the variance of child nodes or at random, and the number of candidate nodes for splitting is selected as the value that minimizes mean absolute error (MAE) in cross-validation [62]. Variable importance is assessed using the permutation method, and uncertainty of predictions is quantified by summing and subtracting the average of the bias corrected variance estimates, obtained with the jackknife-after-bootstrap and infinitesimal jackknife approaches, to and from the point prediction as suggested in [59].
To predict washing performance on each stain, 100 ANNs are combined using the ensemble averaging strategy. One-layer feed-forward ANNs with logistic activation function are used and the number of nodes in the layer (from 1 to 10) together with weight decay (from 0 to 0.5) are hyperparameters that are optimized with cross-validation. Prior to model fitting, inputs and outputs are standardized and normalized. Independent variables are standardized to z-scores:
| (3) |
where is the standardized value of the n-th observation, is the observed value for the n-th observation, is the mean of variable x, and is the standard deviation of variable x. Dependent variables are normalized to 0−1:
| (4) |
where is the normalized value of the nth observation, is the observed value for the nth observation, and and are the maximum and minimum values of the response y respectively. For each ANN, variable importance is quantified according to Olden et al. [46]. To provide an assessment of the overall importance of each variable in the ensemble, the average of the 100 importance measures is calculated and the 5% and 95% percentiles are included as a quantification of uncertainty of this measure. Similarly, prediction uncertainty is estimated as 5% and 95% percentiles of the predictions of the ANN in the ensemble. The relevance of the application of the ensemble averaging strategy is shown in Figure 4 that displays the box-plots of the distribution of MAE on the five folds of cross-validation data for each model that makes the ensemble for the response : the choice of different initialization weights may significantly impact the final performance of the models, thus an ensemble strategy provides more robust results.
Figure 4.
Box-plots of MAE for the 100 ANNs in the ensemble for the prediction of . The red line connects the average cross-validation errors for each model. Results are similar for and .
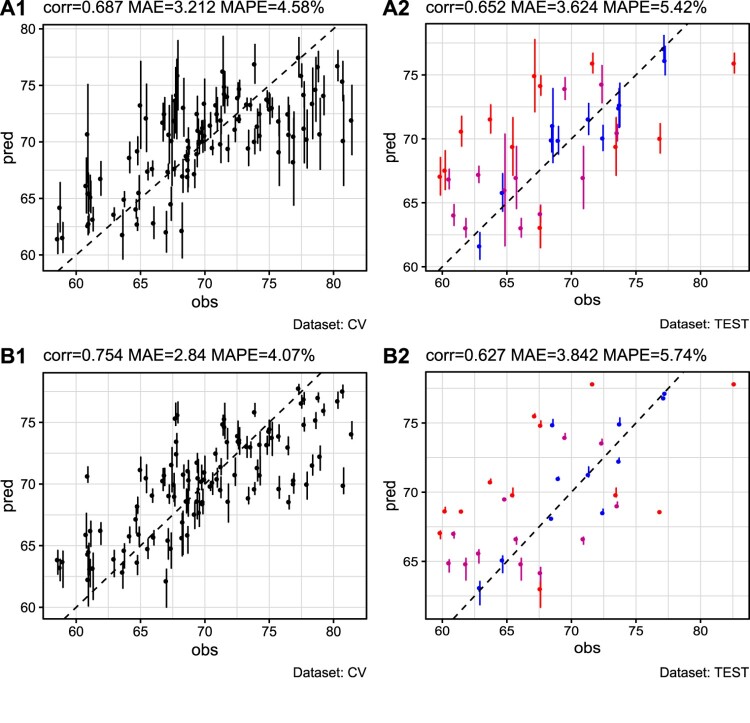
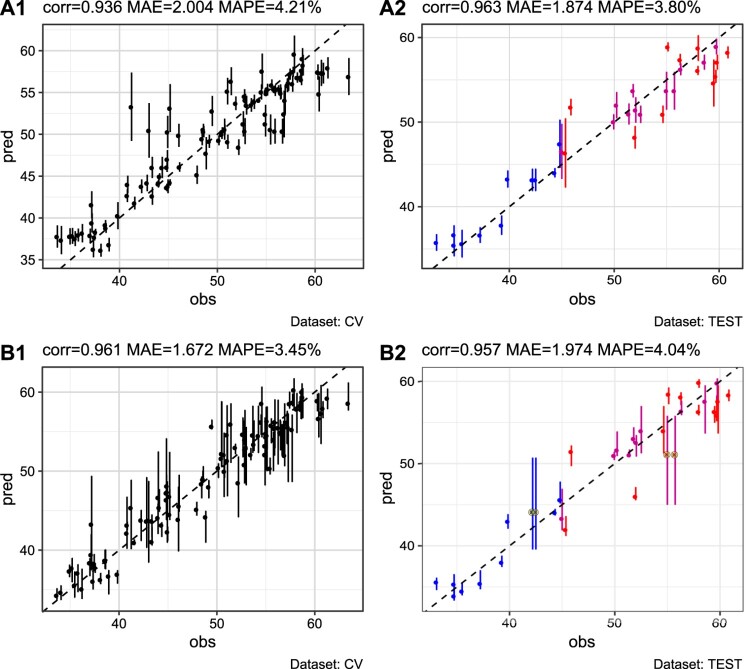
Figure 5 shows the variable importance plots of RF models for stains , and . Figures 6– 8 show diagnostic information about ANNs in the ensemble and variable importance plots for ANN ensemble averaging models of responses , and respectively. After training the models, predictions are carried out on test data. Figures 9– 11 show the predictive performance of the models for the responses, considering both cross-validation on training data and test data. The errors are quantified in terms of correlation between observed and predicted data, MAE and mean absolute percentage error (MAPE). Error bars are included as an estimation of uncertainty, and a color gradient is used which links the predictive performance with the structure of variability displayed in Figures 1 and 2. In particular, a color is assigned to each observation according to the magnitude of the difference between ‘DOE variability’ and ‘latent experimental variability’ of Figure 1. Such values (also plotted in Figure 2) are ordered from the smallest to the largest, and then divided into three equally spaced parts. The color red is assigned to the observations up to the first quantile, fuchsia to observations from the first up to the second quantile and blue to observations from the second quantile up to the maximum. Therefore, shifting from red to blue the plot shows the treatments which are progressively less affected by the presence of random variability which cannot be explained by the factors levels combination.
Figure 5.
Variable importance plots of RF models for (a), (b) and (c).
Figure 6.
Response : the top panels provide information on the optimal number of nodes, and weight decay of each ANN in the ensemble. The bottom panel shows the variable importance plot of the ANN ensemble averaging model.
Figure 8.
Response : the top panels provide information on the optimal number of nodes, and weight decay of each ANN in the ensemble. The bottom panel shows the variable importance plot of the ANN ensemble averaging model.
Figure 9.
Response : plots of observed vs. predicted values of RF (A1, A2) and ANN ensemble (B1, B2) models. The column on the left shows the predictions on the training data (cross-validation), and the column on the right shows the predictions on the test set. The color gradient indicates the impact of ‘latent experimental variability for each observation from small (blue), to large (red). A 45 line is displayed.
Figure 11.
Response : plots of observed vs. predicted values of RF (A1, A2) and ANN ensemble (B1, B2) models. The column on the left shows the predictions on the training data (cross-validation), and the column on the right shows the predictions on the test set. The color gradient indicates the impact of ‘latent experimental variability’ for each observation from small (blue), to large (red). A 45 line is displayed.
Table 4 compares the results of the two ML algorithms with what is obtained by fitting a quadratic regression model with interactions, typical of the RSM approach, which takes the form:
| (5) |
where , , and are the regression coefficients with and , are the k input variables.
Table 4.
Values of MAE on the test set obtained for RF, ANN ensemble and quadratic regression with interactions (RSM) models. The smallest errors are reported in bold, and the reduction (in percentage) of the MAE obtained for the best model vs. the RSM approach is reported as well (Δ).
| Name | RF | ANN ensemble | RSM | Δ [%] |
|---|---|---|---|---|
| 3.624 | 3.842 | 4.553 | 20.40 | |
| 1.874 | 1.974 | 2.449 | 23.48 | |
| 1.921 | 1.697 | 2.376 | 28.56 |
4. Discussion
This section discusses the results and the developed models. In general, the results of the analysis appear to be satisfactory, however some specific observations can be made for each case.
With regard to , both models agree in identifying as being the main contributor in the determination of response, followed in the ranking by and (Figure 5(a), Figure 6). A rather large consensus also exists for the ANNs in the ensemble since almost 75% of the models share the same architecture; some residual uncertainty is however still present for what concerns the variable importance measures, but none of the error bars cross zero, confirming an high agreement between the base models Figure 6. Figure 9 shows the performance of the algorithms in terms of prediction accuracy. The best model in terms of cross-validation error is the ANN ensemble, but the RF achieves a lower error on the test set, indicating a noticeable (but not alarming) overfitting of the ANN ensemble model. For a significant number of instances in the test data, the ANN ensemble fails to assess uncertainty of predictions: this behavior is attributable to the large homogeneity of the ANNs in the ensemble meaning that many of the base learners provide the same point estimation.
A common consensus is also shown for stain in the variable importance plots, since and have the largest contribution in both models (Figure 5(b), Figure 7). In this case the structure of the ANN ensemble is heterogeneous between ANNs with 3, 5 and 10 nodes in the hidden layer. This is an indication that multiple ANN structures can achieve good predictions of the response, and confirms the relevance of an ensemble approach with different initialization of the weights. Both models show good performance on training and test data, displaying correlations between observed and predicted close to the optimum, with a small advantage of the RF on the test set (Figure 10). Despite the goodness of fit, in some cases the ANN ensemble shows rather large error bars. This is the case of the four predictions highlighted near (42.5, 45) and (55, 50) (Figure 10(B2)). Upon closer investigation, the two observations on the left are found to be associated to the same input conditions (treatment 32), similarly to the two observations on the right, which are found to be associated to equal input conditions (treatment 35). In both cases, no instance on which the same treatment was applied is present in the training data, thus the four data points are completely new to the algorithms, and a less certain prediction is expected. However, it is worth noting that in both cases the error bars cross the 45 line, meaning that the predicted values include the observed ones. A comparison with the results obtained by the RF confirms the superiority of this algorithm as for the same test instances the RF provides predictions that are better both in terms of prediction accuracy and uncertainty quantification, since the error bars are much narrower but still include the observed value. Considerations similar to the one above are very valuable for the selection of the best model, and can only be performed if an estimation of uncertainty is associated to point predictions, aspect which is stressed in this paper but is unfortunately very often overlooked in other practical applications of ML.
Figure 7.
Response : the top panels provide information on the optimal number of nodes, and weight decay of each ANN in the ensemble. The bottom panel shows the variable importance plot of the ANN ensemble averaging model.
Figure 10.
Response : plots of observed vs. predicted values of RF (A1, A2) and ANN ensemble (B1, B2) models. The column on the left shows the predictions on the training data (cross-validation), and the column on the right shows the predictions on the test set. The color gradient indicates the impact of ‘latent experimental variability’ for each observation from small (blue), to large (red). A 45 line is displayed.
The variables that most greatly impact the washing performance of stain are , , and , but the ranking of the variables is different for the different models (Figure 5(c), Figure 8). Moreover, the uncertainty associated with the variable importance measures of the ANN ensemble is large and the error bars cross zero in all cases but for , and . This, together with the information about the size of the hidden layer, shows that some relevant heterogeneity exists in the ensemble since the base models tend to develop a rather different logic to explain the relationships that govern the variables. This heterogeneity seems to be beneficial to the model, since the ANN ensemble provides the lowest error on the test data (Figure 11). In general, good performances are achieved by both the models, with a correlation between observed and predicted which is over 85%.
The results discussed in this section are in line with what was expected from Figures 1, 2 and 3: for the impact of the ‘latent experimental variability’ was very relevant, and the models showed some difficulties in unfolding the function underlying data, as confirmed by the values of correlation, MAE and MAPE. For and the impact of ‘latent experimental variability’ was smaller, thus the models were able to achieve better performances. Furthermore, the color gradient assigned to the points in Figures 9 to 11 show that better predictions are achieved for instances with a smaller impact of ‘latent experimental variability’, since, in general, red points are further away from the 45 line. In the case of response , for which the impact of ‘latent experimental variability’ is never excessively large, this effect is partially masked by the strong correlation existing with the goodness of the cleaning performance (Figure 3(b)), but is still noticeable in the upper-right part of the plots (Figure 10(A2,B2)). This behavior confirms that in all cases the algorithms are able to properly capture the effect on the response caused by the factors levels combination, and only the ‘latent experimental variability’ remains partially unexplained.
Apart from some case specific behaviors which depend upon the response considered, we can state that both RF and ANN ensemble models perform in a similar way, leading to good results also considering the substantial residual noise present in the data. Furthermore, in all cases both ML models produce consistently better predictions than the RSM approach, with advantages which range between 20.40% and 28.56% (Table 4). This shows that in this study the adoption of relatively sophisticated ML techniques is justified over the second order polynomial model. This is particularly true because we have shown that some important features of parametric methods such as quantification of variable importance and estimation of uncertainty of predictions is still possible with ML models.
The approach adopted in this paper, although based mainly on ML models, could not be defined as solely empirical or derived from purely black-box algorithms. By using tools already available in the literature, the black-box is illuminated and information is provided about the importance of each variable in the models. Moreover, the fact that the models tend to rank the variables in an identical or very similar way is further information that can be supplied to the process experts and could reinforce their conclusions about the relationships governing the phenomenon. Furthermore, it should not be forgotten that the data used to develop the models is the result of a procedure of experimentation, therefore the relationships uncovered by the models, albeit based on correlations, can also provide strong insights into causation, meaning that not only prediction, but also inference, can be accomplished by the models.
5. Conclusion
In this paper, the application of DOE and ML algorithms was discussed in a product development setting. First a background of the joint application of the two methodologies was presented, then a case study in the chemical industry was conducted.
In the R&D environment, in which the exercise consists in a process of investigation of a phenomenon, the first step is data collection. Then a model needs to be developed to unveil the relationships in data and to predict a response of interest. The data set collected from the experiment showed some problems in terms of dependency occurring between and within replicates of the same treatment, but the nature of the case study required to carry out predictions solely based on the formulations of the detergents, since the random effects levels cannot be known on new data.
We have shown that if the objective is to generate strong conclusions for innovation in R&D, the models should not only provide accurate predictions, but should also provide insights into causation and an estimation of uncertainty – points that, as evinced from the literature, are often under-emphasized in this context. In these cases a sequential approach of DOE and data analysis through ML techniques can be employed since on one hand the quality of DOE data and the experimental setting can provide robust foundations for inference, and on the other hand the advantages of ML such as its ability to model complex relationships and the few assumptions required about data can be leveraged.
Furthermore, if appropriate algorithms are chosen, ML methods can be applied to DOE data that can achieve better predictive performance without necessarily losing much in terms of interpretability with respect to the parametric approaches. Accordingly, in the case study two ML models were developed for the prediction of washing performance, and the results were satisfactory in terms of accuracy, interpretability, and quantification of uncertainty. Considering all the responses, neither RF nor ANN ensemble proved to be unquestionably superior, but they both performed consistently better than quadratic regression with interactions of RSM.
At this point, the ML models learned can be implemented in a semi-automatic system for prediction of the washing performance of new formulations of detergent that can be employed by practitioners who do not have a profound expertise in data analysis and thus facilitate the process of new product development.
Acknowledgments
The paper has been developed by Rosa Arboretti, Riccardo Ceccato, Luca Pegoraro and Luigi Salmaso. Chris Housmekerides, Luca Spadoni, Elisabetta Pierangelo, Sara Quaggia, Catherine Tveit and Sebastiano Vianello contributed in providing the initial idea for the case study and the experimental data.
Disclosure statement
No potential conflict of interest was reported by the author(s).
References
- 1.Bagci E. and Işık B., Investigation of surface roughness in turning unidirectional gfrp composites by using rs methodology and ann, Int. J. Adv. Manuf. Technol. 31 (2006), pp. 10–17. [Google Scholar]
- 2.Beck M.W., Neuralnettools: visualization and analysis tools for neural networks, J. Stat. Softw. 85 (2018), pp. 1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Biranje S.S., Nathany A., Mehra N. and Adivarekar R., Optimisation of detergent ingredients for stain removal using statistical modelling, J. Surfactants. Deterg. 18 (2015), pp. 949–956. [Google Scholar]
- 4.Bisgaard S., The future of quality technology: from a manufacturing to a knowledge economy & from defects to innovations, Qual. Eng. 24 (2012), pp. 30–36. [Google Scholar]
- 5.Box G.E.P. and Behnken D.W., Some new three level designs for the study of quantitative variables, Technometrics 2 (1960), pp. 455–475. [Google Scholar]
- 6.Box G.E.P. and Liu P.Y.T., Statistics as a catalyst to learning by scientific method part i–an example, J. Quality Technol. 31 (1999), pp. 1–15. [Google Scholar]
- 7.Box G.E. and Woodall W.H., Innovation, quality engineering, and statistics, Qual. Eng. 24 (2012), pp. 20–29. [Google Scholar]
- 8.Brecher C., Obdenbusch M. and Buchsbaum M., Optimized state estimation by application of machine learning, Prod. Eng. 11 (2017), pp. 133–143. [Google Scholar]
- 9.Breiman L., Random forests, Mach. Learn. 45 (2001), pp. 5–32. [Google Scholar]
- 10.Cao B., Adutwum L.A., Oliynyk A.O., Luber E.J., Olsen B.C., Mar A. and Buriak J.M., How to optimize materials and devices via design of experiments and machine learning: demonstration using organic photovoltaics, ACS. Nano. 12 (2018), pp. 7434–7444. [DOI] [PubMed] [Google Scholar]
- 11.Çaydaş U. and Hascalık A., A study on surface roughness in abrasive waterjet machining process using artificial neural networks and regression analysis method, J. Mater. Process. Technol. 202 (2008), pp. 574–582. [Google Scholar]
- 12.Chi H.-M., Ersoy O.K., Moskowitz H. and Ward J., Modeling and optimizing a vendor managed replenishment system using machine learning and genetic algorithms, Eur. J. Oper. Res. 180 (2007), pp. 174–193. [Google Scholar]
- 13.Cox D., Kartsonaki C. and Keogh R.H., Big data: some statistical issues, Stat. Probab. Lett. 136 (2018), pp. 111–115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Domagalski N.R., Mack B.C. and Tabora J.E., Analysis of design of experiments with dynamic responses, Org. Process. Res. Dev. 19 (2015), pp. 1667–1682. [Google Scholar]
- 15.Efron B., Jackknife-after-bootstrap standard errors and influence functions, J. R. Stat. Soc.: Ser. B (Methodological) 54 (1992), pp. 83–111. [Google Scholar]
- 16.Efron B., Estimation and accuracy after model selection, J. Am. Stat. Assoc. 109 (2014), pp. 991–1007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Erzurumlu T. and Oktem H., Comparison of response surface model with neural network in determining the surface quality of moulded parts, Mater. Des. 28 (2007), pp. 459–465. [Google Scholar]
- 18.Faraj S., Pachidi S. and Sayegh K., Working and organizing in the age of the learning algorithm, Information and Organization 28 (2018), pp. 62–70. [Google Scholar]
- 19.Fredj N.B. and Amamou R., Ground surface roughness prediction based upon experimental design and neural network models, Int. J. Adv. Manuf. Technol. 31 (2006), pp. 24–36. [Google Scholar]
- 20.Freiesleben J., Keim J. and Grutsch M., Machine learning and design of experiments: alternative approaches or complementary methodologies for quality improvement?, Quality and Reliab. Eng. Int. 36 (2020), pp. 1837–1848. [Google Scholar]
- 21.Friedman J., Hastie T. and Tibshirani R., The elements of statistical learning, Vol. 1, Springer Series in Statistics, New York, 2001. [Google Scholar]
- 22.Gal Y. and Ghahramani Z., Dropout as a bayesian approximation: Representing model uncertainty in deep learning, international conference on machine learning, 2016. pp. 1050–1059.
- 23.Garson G.D., Interpreting neural-network connection weights, AI Expert 6 (Apr. 1991), pp. 46–51. [Google Scholar]
- 24.Geurts P., Ernst D. and Wehenkel L., Extremely randomized trees, Mach. Learn. 63 (2006), pp. 3–42. [Google Scholar]
- 25.Ghalandari M., Ziamolki A., Mosavi A., Shamshirband S., Chau K.-W. and Bornassi S., Aeromechanical optimization of first row compressor test stand blades using a hybrid machine learning model of genetic algorithm, artificial neural networks and design of experiments, Eng.g Appl. Comput. Fluid Mech. 13 (2019), pp. 892–904. [Google Scholar]
- 26.Golkarnarenji G., Naebe M., Badii K., Milani A.S., Jazar R.N. and Khayyam H., A machine learning case study with limited data for prediction of carbon fiber mechanical properties, Computers Indust. 105 (2019), pp. 123–132. [Google Scholar]
- 27.Hajjem A., Bellavance F. and Larocque D., Mixed-effects random forest for clustered data, J. Stat. Comput. Simul. 84 (2014), pp. 1313–1328. [Google Scholar]
- 28.Hassanin H., Alkendi Y., Elsayed M., Essa K. and Zweiri Y., Controlling the properties of additively manufactured cellular structures using machine learning approaches, Adv. Eng. Mater. 22 (2020), pp. 1901338. [Google Scholar]
- 29.Hertlein N., Deshpande S., Venugopal V., Kumar M. and Anand S., Prediction of selective laser melting part quality using hybrid bayesian network, Additive Manufacturing 32 (2020), pp. 101089. [Google Scholar]
- 30.Hockman K.K. and Jensen W.A., Statisticians as innovation leaders, Qual. Eng. 28 (2016), pp. 165–174. [Google Scholar]
- 31.Ibrić S., Djuriš J., Parojčić J. and Djurić Z., Artificial neural networks in evaluation and optimization of modified release solid dosage forms, Pharmaceutics 4 (2012), pp. 531–550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Ivić B., Ibrić S., Cvetković N., Petrović A., Trajković S. and Djurić Z., Application of design of experiments and multilayer perceptrons neural network in the optimization of diclofenac sodium extended release tablets with carbopol 71g, Chemical and Pharmaceutical Bulletin 58 (2010), pp. 947–949. [DOI] [PubMed] [Google Scholar]
- 33.Jaeckel L.A., The infinitesimal jackknife. Bell Telephone Laboratories, 1972.
- 34.Jensen W.A., Montgomery D.C., Tsung F. and Vining G.G., 50 years of the journal of quality technology, J. Quality Technol. 50 (2018), pp. 2–16. [Google Scholar]
- 35.Karazi S., Issa A. and Brabazon D., Comparison of ann and doe for the prediction of laser-machined micro-channel dimensions, Opt. Lasers. Eng. 47 (2009), pp. 956–964. [Google Scholar]
- 36.Kim D.-Y., Kumar V. and Kumar U., Relationship between quality management practices and innovation, J. Oper. Manag. 30 (2012), pp. 295–315. [Google Scholar]
- 37.Lakshminarayanan B., Pritzel A. and Blundell C.. Simple and scalable predictive uncertainty estimation using deep ensembles, Advances in neural information processing systems, 2017. pp. 6402–6413.
- 38.Lasheras F.S., Vilán J.V., Nieto P.G. and del Coz Díaz J., The use of design of experiments to improve a neural network model in order to predict the thickness of the chromium layer in a hard chromium plating process, Math. Comput. Model. 52 (2010), pp. 1169–1176. [Google Scholar]
- 39.Lou H., Chung J.I., Kiang Y.-H., Xiao L.-Y. and Hageman M.J., The application of machine learning algorithms in understanding the effect of core/shell technique on improving powder compactability, Int. J. Pharm. 555 (2019), pp. 368–379. [DOI] [PubMed] [Google Scholar]
- 40.Lucas J.M., Which response surface design is best: A performance comparison of several types of quadratic response surface designs in symmetric regions, Technometrics 18 (1976), pp. 411–417. [Google Scholar]
- 41.Lujan-Moreno G.A., Howard P.R., Rojas O.G. and Montgomery D.C., Design of experiments and response surface methodology to tune machine learning hyperparameters, with a random forest case-study, Expert. Syst. Appl. 109 (2018), pp. 195–205. [Google Scholar]
- 42.Luo M.R., CIELAB, Springer Berlin Heidelberg, Berlin, Heidelberg, 2015. pp. 1–7. [Google Scholar]
- 43.Mee R.W., Optimal three-level designs for response surfaces in spherical experimental regions, J. Quality Technol. 39 (2007), pp. 340–354. [Google Scholar]
- 44.Montgomery D.C., Experimental design for product and process design and development, J. R. Stat. Soc.: Ser. D (The Stat.) 48 (1999), pp. 159–177. [Google Scholar]
- 45.Naftaly U., Intrator N. and Horn D., Optimal ensemble averaging of neural networks, Netw.: Comput. Neural Syst. 8 (1997), pp. 283–296. [Google Scholar]
- 46.Olden J.D., Joy M.K. and Death R.G., An accurate comparison of methods for quantifying variable importance in artificial neural networks using simulated data, Ecol. Modell. 178 (2004), pp. 389–397. [Google Scholar]
- 47.Özesmi S.L. and Özesmi U., An artificial neural network approach to spatial habitat modelling with interspecific interaction, Ecol. Modell. 116 (1999), pp. 15–31. [Google Scholar]
- 48.Quaglio M., Roberts L., Jaapar M.S.B., Fraga E.S., Dua V. and Galvanin F., An artificial neural network approach to recognise kinetic models from experimental data, Comput. Chem. Eng. 135 (2020), pp. 106759. [Google Scholar]
- 49.Radetzky M., Rosebrock C. and Bracke S., Approach to adapt manufacturing process parameters systematically based on machine learning algorithms, IFAC-PapersOnLine 52 (2019), pp. 1773–1778. [Google Scholar]
- 50.Rumelhart D.E., Hinton G.E. and Williams R.J., Learning representations by back-propagating errors, Nature 323 (1986), pp. 533–536. [Google Scholar]
- 51.Salmaso L., Pegoraro L., Giancristofaro R.A., Ceccato R., Bianchi A., Restello S. and Scarabottolo D., Design of experiments and machine learning to improve robustness of predictive maintenance with application to a real case study, Commun. Stat.–Simul. Comput. (2019), pp. 1–13. [Google Scholar]
- 52.Santos G., Gomes S., Braga V., Braga A., Lima V., Teixeira P. and Sá J.C., Value creation through quality and innovation–a case study on portugal, The TQM J. (2019). [Google Scholar]
- 53.Schuetzenmeister A. and Dufey F., VCA: Variance Component Analysis, 2020. R package version 1.4.3.
- 54.Spedding T.A. and Wang Z., Study on modeling of wire edm process, J. Mater. Process. Technol. 69 (1997), pp. 18–28. [Google Scholar]
- 55.Speiser J.L., Wolf B.J., Chung D., Karvellas C.J., Koch D.G. and Durkalski V.L., Bimm forest: A random forest method for modeling clustered and longitudinal binary outcomes, Chemometr. Intell. Lab. Syst. 185 (2019), pp. 122–134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Speiser J.L., Wolf B.J., Chung D., Karvellas C.J., Koch D.G. and Durkalski V.L., Bimm tree: a decision tree method for modeling clustered and longitudinal binary outcomes, Commun. Stat. – Simul. Comput. 49 (2020), pp. 1004–1023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Staelin C.. Parameter selection for support vector machines, Hewlett-Packard Company, Tech. Rep. HPL-2002-354R1, 1, 2003.
- 58.Stroup W.W.. Generalized Linear Mixed Models: Modern Concepts, Methods and Applications, CRC press, Boca Raton, 2012. [Google Scholar]
- 59.Wager S., Hastie T. and Efron B., Confidence intervals for random forests: the jackknife and the infinitesimal jackknife, J. Machine Learning Res. 15 (2014), pp. 1625–1651. [PMC free article] [PubMed] [Google Scholar]
- 60.Wang C., Yang Q., Wang J., Zhao J., Wan X., Guo Z. and Yang Y., Application of support vector machine on controlling the silanol groups of silica xerogel with the aid of segmented continuous flow reactor, Chem. Eng. Sci. 199 (2019), pp. 486–495. [Google Scholar]
- 61.Wong P.K., Gao X.H., Wong K.I. and Vong C.M., Efficient point-by-point engine calibration using machine learning and sequential design of experiment strategies, J. Franklin. Inst. 355 (2018), pp. 1517–1538. [Google Scholar]
- 62.Wright M.N. and Ziegler A., ranger: A fast implementation of random forests for high dimensional data in C++ and R, J. Stat. Softw. 77 (2017), pp. 1–17. [Google Scholar]
- 63.Yan W., Guo Z., Jia X., Kariwala V., Chen T. and Yang Y., Model-aided optimization and analysis of multi-component catalysts: application to selective hydrogenation of cinnamaldehyde, Chem. Eng. Sci. 76 (2012), pp. 26–36. [Google Scholar]
- 64.Yusr M.M., Innovation capability and its role in enhancing the relationship between tqm practices and innovation performance, Journal of Open Innovation: Technology, Market, and Complexity 2 (2016), pp. 6. [Google Scholar]