Microscopic Simulations of Electrochemical Double-Layer Capacitors

Abstract

Electrochemical double-layer capacitors (EDLCs) are devices allowing the storage or production of electricity. They function through the adsorption of ions from an electrolyte on high-surface-area electrodes and are characterized by short charging/discharging times and long cycle-life compared to batteries. Microscopic simulations are now widely used to characterize the structural, dynamical, and adsorption properties of these devices, complementing electrochemical experiments and in situ spectroscopic analyses. In this review, we discuss the main families of simulation methods that have been developed and their application to the main family of EDLCs, which include nanoporous carbon electrodes. We focus on the adsorption of organic ions for electricity storage applications as well as aqueous systems in the context of blue energy harvesting and desalination. We finally provide perspectives for further improvement of the predictive power of simulations, in particular for future devices with complex electrode compositions.

1. Introduction

Spurred by the need for mobile electric power sources, electrochemical energy storage devices have become increasingly important over the past decades. They were required for the development of portable electronics (smartphones, laptops, etc.) and are now expected to play a pivotal role in the energy transition. By efficiently powering electric vehicles they mitigate the use of gasoline. They may also be used in stationary applications, by buffering the integration of renewable electricity sources, which are intermittent by nature, in the power grid. The most important family of devices is the Li-ion battery, which is now produced in large quantities in gigafactories. Then come electrochemical double-layer capacitors (EDLCs), or supercapacitors, which play a complementary role to batteries. They are involved in applications requiring high power deliveries and extremely long cycle-lifes¹ (defined as the number of complete charge/discharge cycles that the device can support before the amount of stored energy becomes insufficient).

Capacitors are systems in which the charge is stored at the surface of electrodes. Among this family, supercapacitors differ markedly from conventional capacitors in the energy storage mechanism and consequently in the performance. Conventional capacitors involve two metallic plates facing each other and separated by a dielectric medium. Opposite charges are accumulated on the two electrodes, and the energy stored is proportional to its capacitance C, which follows the relation

1

where Q is the charge on the positive electrode, V the applied potential difference, ϵ₀ the vacuum permittivity, and ϵ_r the dielectric constant of the medium between the two electrodes; A and d account for the electrodes’ surface area and the distance between them, respectively. There are therefore three parameters that can be tuned to optimize their performance, but the amount of stored energy is generally limited by the geometrical constraint of the two plates facing each other.

In supercapacitors, the dielectric medium is replaced by an ionic electrolyte, as presented in Figure 1. The presence of mobile charges allows local screening of the charge accumulated at the surface of the electrode upon charging the device. In the majority of cases, the electrolyte is liquid, and the region of the interface in which the charge distribution differs from the bulk is called the “electric double layer” (EDL) for historical reasons. While apparently simple, this change induces very different properties. A supercapacitor can be seen as two conventional capacitors (one for each electrode) in series, with a resistance (the bulk electrolyte) in between. However, eq 1 cannot be used because ϵ_r, A, and d become ill-defined and/or impossible to measure. The main advantages of supercapacitors are that the distance between the two charged layers becomes microscopic and that the electrode does not need to be planar anymore; its surface area can be greatly increased through the use of porous materials.² The dielectric constant, or rather its local equivalent at the microscopic scale, was shown to be much lower than that of the bulk in the case of liquids (and it is also affected by confinement³), but this detrimental effect is largely overcome by the other advantages.

Figure 1.

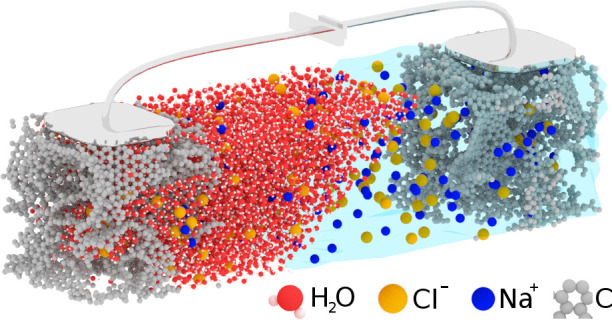
Artistic view of a supercapacitor made of nanoporous carbon electrodes and an aqueous sodium chloride electrolyte. The carbon, chlorine, and sodium atoms are shown in gray, yellow, and blue, respectively; water is shown as a transparent fluid on the right-hand side and as explicit molecules (red, oxygen, white, hydrogen) on the left-hand side.

These capacitive effects can be used beyond electricity storage. For example, by harvesting the free energy lost during the mixing of rivers with seawater (which arises from the salinity gradient between them), it should be possible to generate large amounts of electricity.⁴⁻⁷ Several technologies exploit the osmotic pressure difference between the two water sources through the use of membranes.⁸ Recent developments include single nanotubes through membranes, which create a giant osmotic energy conversion,⁹ but the feasibility of capacitive mixing, from cycling charge/discharge of a supercapacitor at high/low salinity, has also been recently demonstrated.¹⁰ Such capacitors would largely differ from energy storage devices in terms of size, operating conditions, etc., but the underlying physical phenomena are similar.

Supercapacitors have only two main components: the electrode and the electrolyte, but many choices for both are available. Concerning the electrode materials, they need to have good electronic conductivity and large surface area in order to maximize contact with the electrolyte.¹¹ Most commercial devices employ porous carbon materials.¹² For decades, the focus was limited to activated carbons, but the synthesis of new carbon materials with well-controlled porosities¹³ had a deep impact on the field.¹⁴ Materials such as carbon nanotubes¹⁵ or graphene¹⁶ are also full of promise for the possibility to fine-tune more and more efficiently the properties of the devices. Beyond carbon, it is also possible to build supercapacitors involving metallic oxides¹⁷⁻²⁰ such as MnO₂, RuO₂, or Nb₂O₅. In addition to these two main families of materials, other conductive systems were used for supercapacitor electrodes, such as MXenes,²¹⁻²³ nitrides,²⁴ metal organic frameworks,^25,26 or polymers.^27,28

On the other side of the interface, the electrolyte generally consists of a liquid phase containing a solvent, ionic species, and possible additives that are used to tune the physical properties.²⁹ The solvent is either water or an organic molecule such as acetonitrile or propylene carbonate, although new families of electrolytes based on adiponitrile³⁰ or azepanium³¹ have recently been proposed. A notable exception is the family of ionic liquids,^32,33 which are solvent-free electrolytes. The ionic species and the additives depend strongly on the nature of the solvent; it is necessary to use salts with high solubility, and the choice of the ions is generally made in order to optimize the energy density of the device without sacrificing the power density.³⁴ An alternative to liquid electrolytes is the use of ionogels,³⁵ which have been suggested for the development of all-solid state supercapacitors,³⁶ for example, for wearable applications.

Depending on the electrode/electrolyte combination, different charge storage mechanisms may occur.³⁷ The two limiting cases are, on the one hand, double-layer capacitance whereby the charge is stored by the separation of charge at the interface, and, on the other hand, pseudocapacitance achieved by Faradaic electron transfer (redox reactions) between the electrolyte and electrode surface atoms. In the former mechanism, which is expected to occur for electrodes with no redox sites (such as carbon), the charge builds up uniformly at the surface. The associated cyclic voltammogram presents a perfectly rectangular shape, i.e., the current remains constant among the whole range of applied potentials. In the case of pseudocapacitors, because of the Faradaic origin of the charge storage mechanism, the corresponding devices are more difficult to differentiate from batteries. They correspond to cases where the redox reaction takes place only at the surface of the material; hence, the charging rate is not limited by the diffusion of species inside the electrode, and no phase transition occurs in the bulk material. A typical example is MnO₂, although materials such as Ni(OH)₂ and cobalt oxides are erroneously described as pseudocapacitive.³⁸ In such pseudocapacitive materials, the potential at which the reaction occurs depends on the redox state of the surrounding surface atoms, so that the electrochemical signature of pseudocapacitors can be decomposed in a series of successive oxidation/reduction waves that overlap. The resulting shape is rectangular and thus very similar to that of double-layer capacitors. Because of this resemblance, it is often difficult to assess whether a material behaves as a double-layer capacitor or as a pseudocapacitor. Note that another type of pseudocapacitive behavior, based on an intercalation mechanism, has been evidenced in materials such as Nb₂O₅;^19,39 in such cases the electrochemical signature is much more battery-like. However, the distinction with the latter can easily be made by exploring the charging rate limitations of the systems.¹⁹

The difficulty in establishing the storage mechanisms in supercapacitors is due to the fact that most electrochemical techniques provide only a macroscopic perspective. However, the development of spectroscopic analysis tools and computational techniques over the past two decades has allowed for a much better understanding of the microscopic phenomena at play.

From the theoretical point of view, the historical picture of Gouy, Chapman, and Stern⁴⁰ (GCS) based on the Poisson–Boltzmann method is not suited for supercapacitors: such mean field theories become inadequate when the electrostatic correlations between ions and excluded volume effects can no longer be neglected.^41,42 This is the case for supercapacitors because of the high concentrations, confinement effects, and high applied potentials. In this review we focus on the results provided by microscopic simulations, and we provide comparison to existing theories and experimental observations when they are available. Note that we limit the scope to the case of idealized electrode structure and carbon materials on which most of the simulation studies have been conducted to date. It is complementary to previous reviews on this topic, which rather focused on electrostatic models for the simulation of electrode–solution interfaces⁴³ or the use of mean-field theories.⁴⁴ Another review was devoted to the molecular simulations of capacitive energy storage devices.⁴⁵ However, the field has remained very active during the past five years, and the present review also accounts for these latest developments.

We first discuss in section 2 the technical hurdles for the accurate molecular simulations of supercapacitors, which are numerous. In short, the objective of these simulations is to compute structural, thermodynamic, and transport properties using the principles of statistical mechanics. It is necessary to correctly sample the various configurations of the systems at finite temperature and consequently to know their chemical composition and to choose correctly the initial structure. We then describe the principles of classical density functional theory, an alternative method that does not require sampling of the configurations but readily provides average properties. In a nutshell, the electrolyte is now described by density fields and the thermodynamic properties of the system are obtained by minimizing a functional depending on those fields. Having a realistic description of the electrode structure is key to carry out reliable calculations, and we discuss how experimental information was compulsory by focusing on structural models for porous carbon materials. Another difficulty in the simulation of supercapacitors resides in the potential difference applied between the electrode, and we review the various approaches introduced to account for it.

We then focus in section 3 on the use of molecular simulations to understand supercapacitors for energy storage applications. First, we discuss the simple case of planar interfaces and in particular why the canonical Gouy–Chapman–Stern theory of the double layer does not apply due to the use of highly concentrated electrolytes. The interfacial structure is instead characterized by the formation of multilayers, which could be investigated using a wide range of experimental techniques in parallel with simulation studies. In addition, some systems display signs of interfacial ordering in the first adsorbed layer, which can lead to slow dynamics and hysteresis effects in electrochemistry experiments.

Section 4 details the structural features which are induced by the confinement in nanometric-sized pores. We discuss simulation studies performed on model porous geometries, such as carbon nanotubes or slit pores, as well as on much more complex carbon structures. Among the various effects revealed over the past decade, some play a key role for increasing the capacitance of devices. For example, the desolvation of ions in nanopores, which strongly depends on the degree of confinement of the ions, may lead to an increased packing of counter-charges.^46,47 Strong features of concentrated liquids also vanish, such as Coulombic ordering, with the formation of a superionic state. We also detail the main charging mechanisms, such as voltage-induced ion exchange between the porous structure and the bulk electrolyte.

Section 5 is dedicated to the study of capacitors for blue energy harvesting and water desalination (which is the reverse phenomenon). After introducing the capacitive mixing and capacitive deionization processes, we discuss the challenges for modeling before turning to the contributions of molecular simulations and classical density functional theory in these contexts.

Section 6 addresses some dynamic aspects associated with supercapacitors and blue energy/desalination devices. In particular, we review how the confinement inside porous materials can lead to important effects on the microscopic (diffusion coefficients) as well as the macroscopic (charging time) transport properties.

Finally, we provide concluding remarks in which we discuss future directions in the field, both for enhanced studies of carbon-based supercapacitors as well as for an accurate modeling of more complex electrode materials and reactive electrolytes.

2. Molecular-Scale Simulation Methods for Capacitors

Compared to batteries, in which it mostly serves as a lithium charge carrier between the electrodes, the electrolyte plays a much more active role in supercapacitors. Most simulation works reported to date targeted liquid electrolytes, for which many atomic configurations can be adopted at the molecular scale; therefore, the simulations required appropriate methods to sample the phase space. Three main approaches are used to model the systems at the molecular scale. In the following we introduce these methods, splitting them into two categories: on the one hand molecular dynamics and conventional Monte Carlo, which are based on an explicit sampling of the phase space, and on the other hand classical density functional theory in which thermodynamic properties of the system are computed by functional minimization. We then discuss the difficulties in obtaining correct electrode structures in the case of complex nanoporous carbon materials. Finally, we discuss the technical aspects involved in the simulations of supercapacitors due to the need to consider electrochemical conditions.

2.1. Sampling Efficiently the Phase Space with Explicit Molecules

The first method, and by far the most used, is molecular dynamics (MD). All the atoms are generally included explicitly, even though an alternative consists in coarse-graining them in order to decrease the computational cost of the simulations.⁴⁸⁻⁵⁰ The trajectories of these atoms are computed by integration of Newton’s equations of motion, so that the main ingredient of the simulations is the interaction potential between the atoms, from which the forces are derived. The reason for the popularity of molecular dynamics for simulating supercapacitors mainly lies in its practicality (many codes are freely available and well-documented) and its efficiency. From the trajectories of the atoms, it is possible to extract many structural, thermodynamic, and dynamical features of the system using the tools of statistical mechanics. In its simplest implementation, MD samples the microcanonical ensemble in which the number of atoms (N), the volume (V), and the total energy (E) of the system are fixed (the microcanonical ensemble is often called the NVE ensemble). However, for most practical applications it is necessary to fix the temperature (T), which is made by coupling the molecular system with a thermostat. Energy exchanges occur, so that E is not conserved anymore, leading to the canonical ensemble (NVT). In many other MD applications, it is also compulsory to fix the pressure of the system, which leads to volume fluctuations. In the present case, this is rendered difficult by the geometry of the electrochemical cell, so that simulations in this NPT ensemble are very scarce for capacitors.

The second approach to sample phase space is classical Monte Carlo (MC), in which the central quantity is the potential energy of the system. The most widely used algorithm is the one of Metropolis et al.,⁵¹ in which a new atomic configuration is generated randomly from the previous one and is then accepted if the new energy is lower or with a probability equal to exp(−ΔE/k_BT) where ΔE is the energy difference between the two configurations instead (and k_B the Boltzmann constant). Any type of moves may be performed to generate new configurations, but it is generally not necessary to go beyond the translation of an atom or of a molecule and the rotation of a molecule. Because of the use of a fixed T to define the probability of acceptance of the moves, it is not possible to sample the NVE ensemble and simulations are generally performed in the NVT ensemble. MC shares most of its analysis tools with MD, the only difference being that they are used on a series of configurations that do not correspond to a trajectory because there is no notion of time. A consequence is that dynamical properties such as diffusion coefficients or adsorption lifetimes cannot directly be determined in MC. However, this comes with an advantage: there is no need of continuity in the presence of the atoms, so it is possible to perform additional MC moves in which specific atoms or molecules may be removed from/added to the simulation cell. It is thus possible to fix the chemical potential of the concerned species (instead of their number) by exchanging the molecules with another cell in which this quantity is known, which allows sampling the grand canonical ensemble (μVT).⁵² Such simulations are termed grand canonical Monte Carlo and are widely used to study the adsorption properties of fluids.^53,54 This method is therefore appealing for the study of the adsorption of electrolytes within porous materials, but these liquids are generally very dense and display specific interactions; this means the rate of acceptance of insertion moves becomes too small and more complex biasing techniques have to be used.⁵⁵

2.2. Classical Density Functional Theory for the EDL

Because MD and MC simulations require an extensive sampling to properly describe the equilibrium properties of the simulated system, they are computationally intensive. Classical density functional theory (cDFT) can be a numerically efficient alternative that allows circumventing these problems. cDFT is naturally formulated in the grand canonical ensemble,^56,57 and despite some attempts to do canonical calculations,⁵⁸ the vast majority of cDFT studies are grand canonical. In the context of EDLs, cDFT describes each ionic species i by a density field ρ_i(r). The solvent can be represented either implicitly as a dielectric medium or explicitly by introducing an additional density field.

The efficiency of cDFT results from the following ansatz:^56,57 (1) For any external perturbation, there exists a unique functional of the densities. In the scope of supercapacitor studies, the external perturbation is due to the electrodes. (2) The ionic and solvent densities minimizing this functional are the (3D) equilibrium ones. (3) At its minimum, the functional is equal to the grand potential of the system (the thermodynamic potential in the grand canonical ensemble).

The free energy and the equilibrium density profiles at any point of the system can be obtained by functional optimization instead of an expensive sampling of the phase space. However, while the theory guarantees the existence of the functional, its expression remains unknown. Prior to any calculation, one therefore needs to choose an approximate functional. We describe here the functional form that is the most commonly employed to study EDL capacitors. It is a common practice to start by splitting the functional as^57,59

2

where {ρ_i} = {ρ₁, ..., ρ_N} is the set of densities of the N considered species, with N = 2 for cations and anions in an implicit dielectric solvent and N = 3 when the solvent is accounted for explicitly. The first term of the right-hand side of eq 2 is an entropic contribution, while the second one accounts for the external perturbation created by the electrodes, described by a classical force field. Both terms can be computed exactly and efficiently. The last term of eq 2 is the excess functional that accounts for the interactions between particles constituting the electrolytic solution. There is no known practical expression for the exact excess functional, and various approximations have been proposed to study ionic systems. Because we are dealing with charged particles, it is convenient to separate the electrostatic mean-field Coulomb contribution from the remainder:^60,61

3

Note that if the electrodes bear charges, their electrostatic contribution is already taken into account in the external term in eq 2. The second term in the right-hand side of eq 3, F^cor[{ρ_i}], describes correlation effects. When this term is omitted, one recovers Poisson–Boltzmann theory.

In order to go beyond mean-field, an approximation should be proposed for F^cor. Since the early 1980s⁶⁰ many studies have been carried out to address this issue. In most of these works, ions are described as charged hard spheres in which the correlations are due to both packing effects and electrostatics. Rosenfeld proposed an extremely precise density functional for the hard sphere fluid, the so-called fundamental measure theory (FMT).⁶² Alternative⁶³ or more accurate⁶⁴ formulations have been proposed, but we will not distinguish between the hard sphere functionals which will all be referred to as FMT in the present work. Because of the quality of the FMT functional, most of the studies dedicated to EDL systems with cDFT decompose the correlation part of eq 3 as the sum of a hard-sphere term modeled by FMT and one that is due to electrostatic correlations:

4

Essentially, studies of EDL using DFT differ by their choice to describe the electrostatic correlation F_ES^cor. The objective of this section is to give an introduction to classical DFT for the study of EDL systems to nonspecialists; a more detailed description of the several existing approximations of F_ES would be too technical to be included here. We refer interested readers to two recent publications comparing the performance of various electrostatic excess free-energy functionals against reference MC simulations.^65,66 Since the early 1980s⁶⁰ a considerable number of studies has been dedicated to electrolytic solution using cDFT either with an explicit description of the solvent⁶⁷⁻⁷¹ or modeling it by a dielectric continuum.^72,73 Most of these studies focused on predictions of the EDL structure⁷²⁻⁷⁶ or on the impact of the ions on the wetting properties of the solvent.^70,71 In the following, we focus on studies using cDFT to investigate electrochemical capacitors and particularly their capacitive properties.

The principal advantage of cDFT over MD and MC simulations is its computational efficiency. It allows carrying out systematic investigations that would be out of reach of molecular simulations. This is however at the cost of using basic models for both the electrode and the electrolyte. Because the functional in eq 3 is unknown, it also requires using approximations as opposed to MD which is essentially exact (provided of course that proper sampling can be achieved).

2.3. Force Fields for Supercapacitor Electrolytes

The force fields describing the potential energy of the system as well as the forces that act on all the atoms are generally well-established for the liquids relevant to supercapacitors. Most of the studies involve all-atom models, which account for intramolecular terms including bonding, bending, and torsion potentials, while the intermolecular term includes the Coulombic interactions (through the use of partial charges located on the atoms) supplemented by Lennard-Jones potentials. In general, many different force fields were already available in the literature for solvents, such as water, acetonitrile, or propylene carbonate, and simple inorganic ions. The different families (such as OPLS,⁷⁷ CHARMM,⁷⁸ AMBER,⁷⁹ COMPASS,⁸⁰etc.) differ through their analytical expression and/or their parametrization. Among the items in this list, OPLS is often selected for supercapacitor simulations because it was designed more specifically for liquids, while the other force fields are more oriented toward biological applications. However, a majority of works involved ionic liquids as electrolytes, for which a specific force field (CL&P) was developed by Canongia Lopes and Pádua^81,82 based on the OPLS analytical form.

Over the past decade, more advanced force fields including explicit polarization effects have increasingly been used.^50,83 In contrast to previous models, these models include explicit dipoles to account for polarization effects, while nonpolarizable force fields generally deal with them implicitly via the attractive term of the Lennard-Jones potentials or the charge-scaling approach.⁸⁴ In MD simulations, a generic option to handle the polarization of the molecules is to use core–shell models.⁸⁵ The most popular one is the Drude oscillator, in which the atoms bear two charges: The first one is located at the atomic position, while the second one is mobile and tethered to the other site by a harmonic potential. These models, often termed “charge-on-a-spring”, are very popular for the study of biomolecular systems,⁸⁶ but also for electrolytes such as ionic liquids.^87,88 A second approach consists of using explicit induced dipoles, which are treated as additional degrees of freedom of the system.⁸⁶ They are located on the atomic site and are usually determined self-consistently using an iterative procedure. This approach is more difficult to implement in MD codes because it requires using an Ewald summation for calculating the various terms up to the dipole–dipole interaction, but it can be generalized to higher-order multipoles if necessary.⁸⁹

The main difficulty with using such polarizable force fields is that there are very few parameters available in the literature, and the parametrization from ab initio calculations may be very time-consuming⁹⁰ in comparison to simpler systems such as molten salts.⁹¹ Goloviznina et al. recently proposed a solution by developing a simple procedure for parametrizing the Drude oscillator-based polarizable force field for any ionic species provided that CL&P parameters are already available, leading to the new CL&Pol force fields.^92,93 In a nutshell, quantum chemistry calculations are performed to calculate atomic polarizabilities,⁹⁴ atomic dipoles, and energy decompositions between fragments. This allows parametrizing the Drude oscillator strength and the Lennard-Jones parameters of the force field.

Even though the increase in computational resources now allows the routine use of such costly polarizable force fields, initial studies on supercapacitors were more limited in system sizes and simulation durations. To overcome this limitation, many studies employed coarse-grained force fields instead of all-atom ones.⁹⁵ In such representations, several atoms are grouped together in a single interaction site, as shown in Figure 2 for a typical ionic liquid. The computational cost may be reduced by 1 order of magnitude at the expense of losing atomic resolution for the study of adsorption mechanisms.

Figure 2.

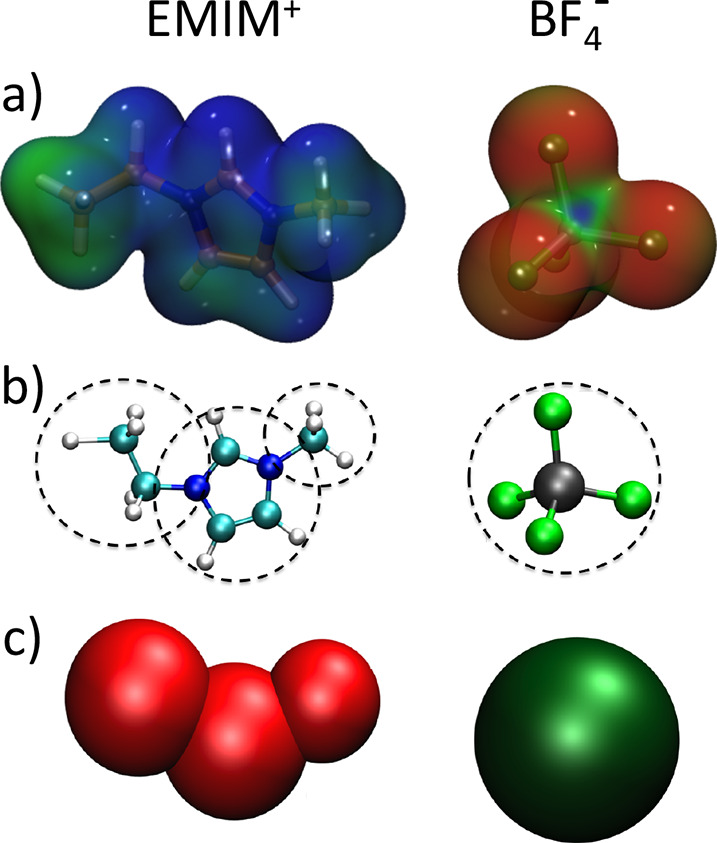
Coarse-graining of the EMIM⁺-BF₄^– ionic liquid. (a) Electron density isosurface mapped with the corresponding electrostatic potential. (b) All-atom representation of the ionic liquid. (c) Coarse-grained representation. Reproduced with permission from ref (50). Copyright 2015 PCCP Owner Societies.

2.4. Modeling the Correct Electrode Structure

In contrast to crystalline materials, which have a well-characterized structure, porous carbons are much less easily defined. They are generally ordered at the local scale only; each carbon atom adopts either sp² or sp³ hybridization, with a ratio depending on the synthesis pathway. Many porous carbons formed in the Earth crust, such as kerogen,⁹⁶ display a large amount of sp³ carbon atoms, but the materials used in supercapacitors need to have good electrical conductivity, which is achieved only with sufficiently high sp² proportion.¹⁴ This leads to the formation of locally planar, graphene-like sheets. However, the size, arrangement, and packing of these sheets is very disordered and thus difficult to describe in atomistic models. The challenge to obtain a correct structure is reminiscent of the case of glasses. Inspired by earlier studies performed on such disordered systems, two main approaches can be adopted.

First, one can use reverse MC, by moving the atoms with a MC procedure in which the cost function is the difference between calculations and experimental data such as X-ray or neutron diffraction patterns.⁹⁷ However, it is necessary to introduce structural constraints in order to enhance the efficiency of the algorithm. A first example was proposed by Pikunic et al., who constrained the bond angle distribution and the average carbon coordination number.⁹⁸ Their obtained disordered porous structures of saccharose-based carbon are in good agreement with experiments, both for the target diffraction data but also with transmission electron microscopy images. The protocol was further enhanced by using hybrid reverse MC, in which an energy penalty term is introduced in the acceptance criteria. This energy is calculated based on an interaction potential between the carbon atoms, namely, the reactive empirical bond order potential⁹⁹ in ref (100) (which again focused on saccharose-based porous carbons). It was then applied to a typical supercapacitor electrode material, carbide-derived carbons (CDCs, see below),¹³ leading to highly amorphous structures mostly made of twisted graphene sheets.¹⁰¹ Recently, another stochastic approach involving dynamic reactive transformations, global optimization, and an extensive set of descriptors¹⁰² showed very promising results for predicting the morphology of carbonaceous materials for arbitrary densities.

The second main approach consists of quenching liquid carbon using molecular dynamics simulations. This necessitates using an accurate and transferable interaction potential for carbon and correctly choosing the cooling rate. These two constraints lead to very high computational costs. Shi proposed using the reaction state scheme,¹⁰³ in which there is no explicit reactivity but each chemical state of the system is modeled separately. The composition of the system evolves by minimizing a weight function, which was chosen to direct the system toward the formation of sp² carbon atoms.¹⁰⁴ The quenching rate then determines the number of nonhexagonal rings, leading to carbon with various densities, pore size distributions, pore connectivities, etc. The procedure developed by Shi was then extended to the case of CDCs.¹⁰⁵ The latter are synthesized by high-temperature chlorination of metallic carbides such as TiC.¹³ In experiments, the temperature was shown to be the key parameter for controlling the average pore size. Surprisingly, simulations showed that varying the quenching rate led to similar differences in the final structure, allowing systematic studies of these materials to be carried out. Finally, it is worth mentioning that a hybrid method combining hybrid reverse MC with MD simulations was also proposed, leading to the accurate prediction of activated sucrose coke¹⁰⁶ and kerogen⁹⁶ structures.

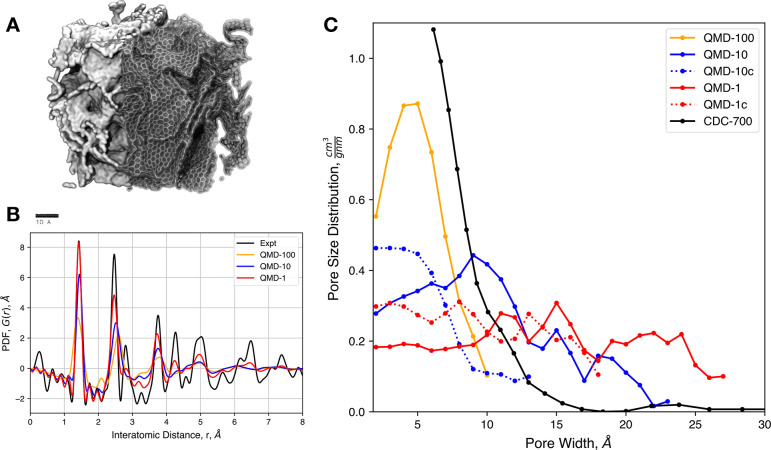
The increase in the performance of MD software and of available computational resources have allowed for the use of more involved carbon interaction potentials. For example, Thompson et al. were able to obtain very large CDC models (of more than 20 000 atoms) using a reactive force field¹⁰⁷ (ReaxFF) specifically designed for carbon materials.¹⁰⁸ An example of such carbon structures is shown in Figure 3A, together with a comparison of the pair distribution function of several structures with typical experimental data and the pore size distributions obtained for different quenching rates. Another study employed the environment-dependent interatomic potential,¹⁰⁹ resulting in similar agreement with the structural data.¹¹⁰ Further improvement in the quality of the generated nanoporous carbon structures can be expected in the future through the use of highly accurate machine-learning potentials.¹¹¹

Figure 3.

Molecular models for complex nanoporous carbons. (A) Typical CDC structure generated from quenched molecular dynamics using the ReaxFF force field. (B) Comparison of the simulated pair distribution functions for various quench rates with experimental data. (C) Pore size distributions obtained for various quench rates. Reproduced from ref (107). Copyright 2017 MDPI under CC BY 4.0 (https://creativecommons.org/licenses/by/4.0/).

To conclude this section, we note that in cotnrast to MD and MC studies, the importance of a realistic representation of the structure is often overlooked in cDFT studies, in which electrodes are usually modeled by ideal geometries such as planar walls, cylinders, or spheres.¹¹²

2.5. Simulating Systems under Electrochemical Conditions

The simulation techniques described above (MD, MC, and cDFT) are very well-established for a large variety of chemical systems ranging from biology to material science. However, the case of capacitors is peculiar due to two main technical difficulties: first, electrochemical boundary conditions should be introduced for the electrodes; second, the interactions at the interface between the electrode and the electrolyte (Figure 4C) need special care.

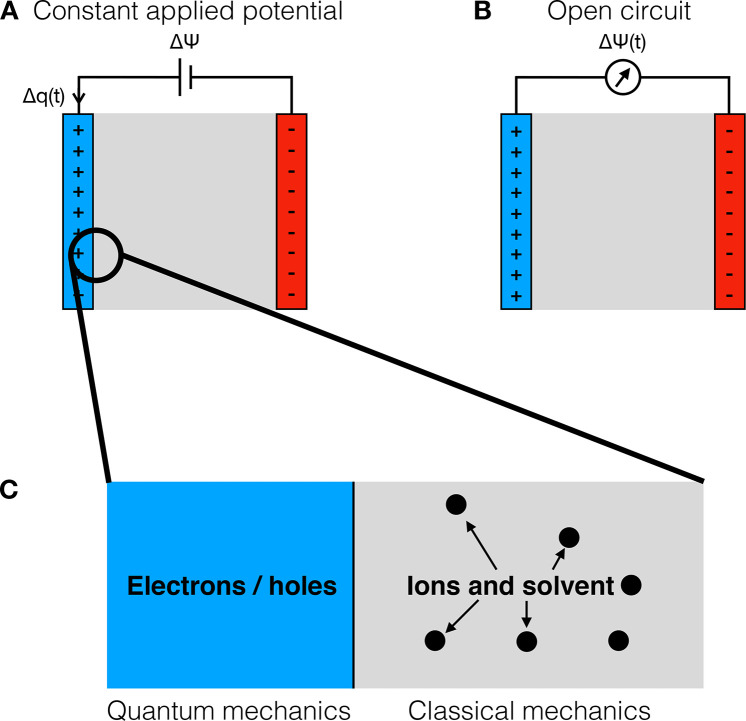
Figure 4.

Schematic illustration of electrochemical boundary conditions. (A) Electrochemical system under constant applied voltage. The two electrodes are allowed to exchange charge in order to maintain the potential difference between them at a fixed value. (B) Electrochemical system under open-circuit conditions. The electrodes cannot exchange charge so the potential difference between them fluctuates over time. (C) Cartoon of the electrode/electrolyte interface: On the electrode side, the charge carriers are electrons and/or holes, in which the main physical effects occur at the quantum level, while on the electrolyte side the dynamics of the ions and of the solvent molecules are mainly described using classical physics and statistical mechanics.

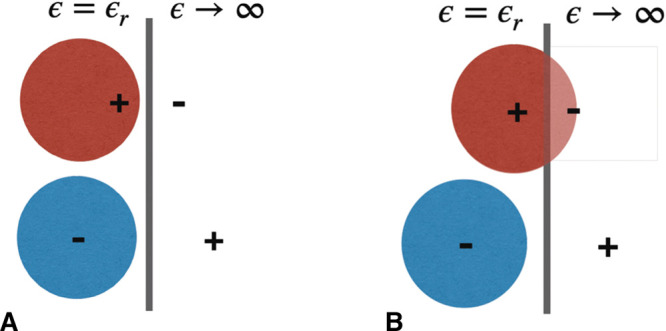
As schematized in Figure 4A,B, the electrochemical boundary conditions can be cast into two categories. On the one hand, if a voltage is applied between the two electrodes, there exists a current in the external circuit and the two electrodes continuously exchange electrons. On the other hand, if the electrical circuit is open, the total charge of each electrode remains constant (but not necessary null) and the potential difference between the electrodes now fluctuates. When introducing the various methods we will discuss how such conditions can possibly be enforced.

From the point of view of intermolecular interactions, even though the carbon force fields mentioned above predict accurately the (meta)stability of the electrode materials, they do not account explicitly for their metallic character; the electron sharing effects are included in the bonded terms of the interaction potential. Similar conclusions may be drawn for other metals, which are well-simulated using bond order potentials that do not include electrostatic effects. This becomes problematic when these metals are put in contact with an electrolyte, because the ions and the solvent molecules exert an external perturbation to the electronic distribution. In principle, such effects would be better taken into account in electronic structure calculations, which is generally done at the DFT level in many fields, such as the study of catalytic effects on chemical reactions occurring at metallic surfaces.^113,114 However, in the present case, the liquid properties need to be properly sampled, which leads to system sizes and simulation times that are almost out of reach of DFT-based ab initio MD. As an illustration, in a recent study devoted to the graphene–ionic liquid interface which provided interesting results on the structure and the polarization of the surface, the simulation time was less than 10 ps,¹¹⁵i.e., 3 orders of magnitude smaller than what is usually done in classical MD simulations. To circumvent this problem, many strategies were proposed in the literature. In the following we provide the generic ideas behind these approaches.

A first method was proposed by Price and Halley.¹¹⁶ In order to keep an explicit representation of the electronic structure, they proposed a quantum mechanics/molecular mechanics (QM/MM) approach, as illustrated in Figure 5A. The main difficulty with such models is that they require a very careful parametrization; therefore, the method was applied only to the study of the interaction between copper and an aqueous electrolyte¹¹⁹ and was not further used for the study of complex capacitors. On the other side of the difficulty/accuracy spectrum, a second approach is based on the use of so-called image charges^120,121 (Figure 5C). The latter depend on the mismatch between the dielectric constants of the two phases which are put into contact. In the particular case of electrochemical cells, the dielectric constant is almost infinite for the metal, so in practice the image charges have the same magnitude as the “real” charge carried by the electrolyte atoms but an opposite sign. Although this formulation accounts for the polarization of the electrode due to the liquid, it initially lacked three key ingredients: (i) at a given time, this polarization should depend on the position of all the charges in a nonlinear way; (ii) the necessity to apply a voltage between the electrodes; and (iii) it cannot treat electrodes with nonplanar geometries. The two former items were overcome to simulate electrochemical systems through the introduction of additional uniform charges to the electrodes¹²² and more recently by systematically controlling the effect of surface, solvent, and solute polarization.¹²³ However, the third ingredient is an intrinsic limitation of the method which cannot be overcome with current algorithms.

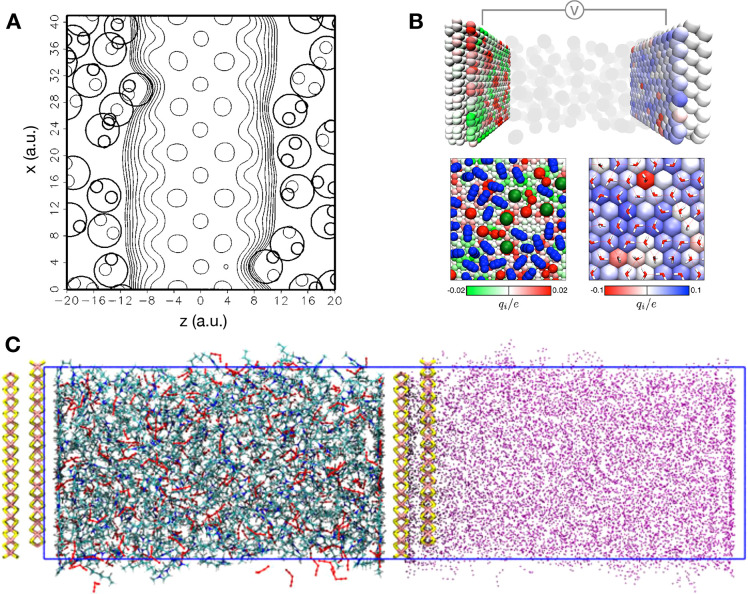
Figure 5.

Snapshots illustrating some of the simulation techniques. (A) Contour plot of the electron density of a copper electrode in contact with water molecules (the latter are shown with large or small circles corresponding to the oxygen and hydrogen atoms, respectively). Reproduced with permission from ref (116). Copyright 1995 AIP Publishing. (B) Induced atomic charges at the surface of typical electrodes. Left: graphite in contact with an organic electrolyte (represented using a coarse-grained model; blue spheres, acetonitrile molecules; red spheres, 1-butyl-3-methylimidazolium (BMIM⁺) cations; and green spheres, hexafluorophosphate (PF₆^–) anions). Right: platinum in contact with pure water (red and white sticks: O–H bonds). Reproduced with permission from ref (117). Copyright 2013 the American Physical Society. (C) Simulation setup for image charge simulations of an ionic liquid (green, red, and blue sticks) between two MoS₂ electrodes (pink and yellow sticks). The purple points are the image charges. Reproduced with permission from ref (118). Copyright 2021 AIP Publishing.

A more complex family of methods was introduced by Siepmann and Sprik in another context, to investigate the influence of surface topology and electrostatic potential when an atomic force microscopy probe is put in contact with liquid water.¹²⁴ Inspired by the Car–Parrinello method for DFT-based MD,¹²⁵ they introduced an extended Lagrangian in which the metal atomic charges are considered as additional degrees of freedom and are therefore allowed to fluctuate. Each electrode atom carries a Gaussian charge distribution (in contrast to the electrolyte, which is usually represented using point charges) and obeys a constraint of fixed electrostatic potential, allowing simulation of systems under applied potential very naturally. The method was further adapted to systems with electrochemical cell geometries.¹²⁶ The fluctuating charges (as shown in Figure 5B) resemble image charges and are sometimes referred to in this way, but they are not strictly equivalent. They result from the solution of the many-body electrostatic problem and should therefore represent more accurately the response of the electronic structure of the metal to the perturbation induced by the electrolyte.

Note that in this approach, the mathematical problem that is solved to obtain the partial charges is similar to the case of the charge equilibration method proposed for molecular systems by Rappé and Goddard.¹²⁷ As recently discussed in ref (128), the difference lies in the definition of the parameters, which are the atomic species’ chemical potential and hardness in one case and the electrode potential and the Gaussian charge width in the other. Despite the similar expressions, the underlying models are different because the charge equilibration parameters are determined from the electronic affinity and ionization energy which are characteristic properties of atoms or molecules,¹²⁹ rather than that of bulk materials such as the ones constituting the electrodes (in addition, using Gaussian charges does not have the same effect as simply introducing a hardness because their width also impacts all the electrostatic interactions involving electrode atoms; consequently the two models are not mathematically equivalent).

Recently, we proposed an extension of the Siepmann–Sprik model by introducing a computational Thomas–Fermi electrode.¹³⁰ The model is based on a reformulation of the Thomas–Fermi model^131,132 based on a set of atomic charges instead of the electronic density. It accounts for the screening of the electrostatic potential through the introduction of an additional term involving a characteristic screening length as a parameter. This model should be more appropriate for systems such as carbon materials because their electronic structure deviates noticeably from the ones of typical metals. Another approach has also been proposed, which consists of using a “virtual” Thomas–Fermi fluid of charged particles to account for the screening.¹³³ It is also possible to go further in that direction by treating the electrode materials using the tight binding model,^134,135 in which the electronic band structure is approximated using atomic wave functions. However, these enhanced electrode models have not yet been used to simulate supercapacitor devices with complex material structures.

The fluctuating charge models can also differ in some technical aspects. For example, the computation of electrostatic interactions has to include long-range effects due to the analytical expression of the Coulomb interaction potential. In MD and MC, this is generally made based on the Ewald summation technique,¹³⁶ but many different flavors have been introduced over the decades. In the specific case of electrochemical cells, it is necessary to adopt either a 2D¹²⁶ or pseudo-2D¹³⁷ formulation. The latter corresponds to the conventional 3D case to which a vacuum slab is added between the two electrodes in the region with no electrolyte atoms; corrections to the energy and its derivative then need to be added,¹³⁸ although a recent approach combining finite fields with fluctuating charges allowed for the use of a 3D cell geometry with results similar to those of the 2D case for planar electrodes.^139,140 The handling of the long-range part can also be formulated in different ways depending on the use of explicit reciprocal-space vectors¹²⁶ or of a particle–particle particle-mesh solver.¹³⁷

The fluctuating charges can also be determined using different methods. While the initial approach of Siepmann and Sprik¹²⁴ was based on the Car–Parrinello algorithm,¹²⁵ in which the additional degrees of freedom are attributed well-chosen fictitious masses, the majority of subsequent studies used a Born–Oppenheimer approach in which the set of self-consistent equations is solved at each time step of the simulation. The problem can be solved through many conventional techniques such as conjugate gradients or matrix inversion, the latter being much more efficient computationally if the electrode atoms do not move. A reformulation of the problem using constrained molecular dynamics¹⁴¹ was also recently shown to be efficient and computationally stable.

Another option is to avoid the use of fluctuating charges. As discussed above for the electrolyte force fields, in MD simulations, the most generic option to handle the polarization of the molecules is to use Drude oscillators. This method is implemented in many MD simulation packages, so it was naturally used to account for the polarization in metallic systems.¹⁴² An alternative to the spring was proposed in which the mobile charge rotates at a fixed distance around the atom.¹⁴³ It was used, for example, to study the solvation of nanoparticles in ionic liquids.¹⁴⁴ These approaches, however, do not allow charge to be transferred from one atom to another inside the electrode or between the two electrodes. They are therefore not well-suited for the study of supercapacitors.

Alternative approaches based on an explicit solution of the Poisson equation have also been proposed. In such cases, the charges are no longer placed on the electrode atomic sites, but rather on a grid. This method was introduced to compute induced charges on arbitrary dielectric boundaries through the introduction of a space-dependent dielectric constant for the dielectric medium.^145,146 In another implementation, the electrode surface is modeled as an equi-potential smooth surface with a net charge.¹⁴⁷ The surface of the electrode acts as a metallic foil which separates the charges of the electrolyte (both from the solvent and from the ionic species) and a set of fixed charges located inside the electrode. In the latter approach, a voltage is applied by solving an auxiliary Laplace equation, following a method proposed by Raghunathan and Aluru.¹⁴⁸

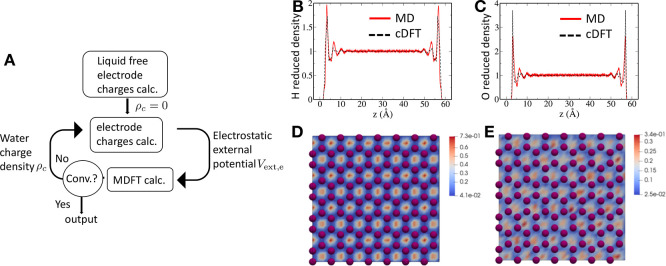
Most of the developments introduced above were done for MD and MC simulations, and their application to cDFT is much more recent. Because cDFT aims solely at computing the equilibrium properties and the electrode models considered are ideal geometric objects, the problem is considerably simplified. Applying a constant potential as in Figure 4A simply requires the use of appropriate boundary conditions when solving the Poisson equation, while open-circuit conditions as in Figure 4B require the imposition of a uniform charge density on each electrode. The electrode polarizability is often neglected, but some studies account for it using mirror charges.¹⁴⁹ We implemented the Siepmann and Sprik¹²⁴ description of polarizability in our cDFT study of a water–graphene capacitor.¹⁵⁰ The algorithm used to self-consistently optimize the electrode charges and the water density is schematically represented in Figure 6A. The predicted densities are in quantitative agreement with MD simulations, as shown in Figure 6B–E.

Figure 6.

Constant potential classical DFT simulations. (A) Workflow to compute the equilibrium solvent density and the charge distribution within the electrodes under a fixed potential difference. In-plane averaged equilibrium densities of H (B) and O (C) of water along the direction perpendicular to the graphene planes. Slices of oxygen density computed by cDFT (D) and MD (E) in a plane parallel to the graphene at a distance of 2.5 Å; the purple balls represent the graphene carbon atoms. Reproduced with permission from ref (150). Copyright 2019 AIP Publishing.

It is worth noting that all the methods described above aim at simulating a system under constant applied potential, i.e., the situation shown in Figure 4A only. However, in the field of electronic density functional theory, the possibility of simulating systems under open-circuit conditions (Figure 4B) has long been realized through the use of the electric displacement as a control variable.¹⁵¹ This gap has recently been filled in classical MD by using the same methodology.¹⁵² The main feature of the new approach is to replace the two-dimensional two-electrode setup with a single electrode in contact with a liquid on its two sides (and thus applying 3D periodic boundary conditions). This electrode is held at constant potential, and the whole system is subject to either a fixed electric field, which mimics the constant applied potential situation,¹³⁹ or a fixed electric displacement, which corresponds to fixing the total charge of the electrode, thus open-circuit conditions.¹⁴⁰ It is then even possible to apply an electric displacement ramp in order to reproduce typical amperometry experiments. Although the proof of concept was validated, the method has not been applied to the case of supercapacitors yet.

In addition to electrostatics, the interaction between the electrodes and the electrolyte should also include short-range repulsion and dispersion effects. They are typically accounted for using Lennard-Jones potentials similar to the ones between the electrolyte atoms. Several parameters are available for typical materials, such as carbon,^153,154 gold,^142,155 platinum,¹⁵⁵etc. However, most of these force fields were parametrized without considering in detail the above-mentioned metallicity of the materials, so cancellation errors have to be expected. We therefore expect that future works will focus on more accurate representations of the nonelectrostatic interactions. A major difficulty is the lack of experimental data focused on the interface at the molecular scale, and the difficulty of performing ab initio simulations on these systems. For example, in a recent study on the adsorption of water molecules on carbon surfaces, adsorption energies calculated at the DFT level showed a wide discrepancy.^156,157 It is then necessary to use more accurate quantum chemistry methods, such as quantum Monte Carlo,¹⁵⁸ in order to obtain reliable results, but their high computational cost prohibits their systematic use to investigate a large variety of systems. Finally, from the modeling point of view, chemisorption effects are much more challenging to describe than nonbonding interactions and require, for example, resorting to reactive force fields. Fortunately, chemisorption generally does not play an important role in supercapacitors because it is avoided in order to maximize the performance in terms of power.

2.6. Interfacial Capacitance

As will be discussed in the next sections, molecular simulations provide important information on the structure and dynamics of electrolytes at electrochemical interfaces. Such quantities are rather standard to calculate as they are not specific to the case of supercapacitors. From the thermodynamic point of view, the main target quantity is the interfacial capacitance. The total capacitance of the interface (C_tot) is generally obtained by considering the EDL (C_EDL) and quantum (C_Q) capacitances in series¹⁵⁹ as

5

The EDL capacitance is the contribution due to the formation of the double layer at the surface of the electrode. It is worth noting that two definitions are encountered in the literature. On the one hand, the integral capacitance (C_int) is defined as

6

where ⟨Q₊⟩ is the average charge on the positive electrode and ΔΨ the potential difference. One can calculate the integral capacitance for the whole electrochemical cell, in which case ΔΨ is the applied voltage, or for a specific electrode if it is possible to determine the potential difference between the latter and the electrolyte. This is generally feasible for planar electrodes only.¹⁶⁰

On the other hand, the differential capacitance (C_diff) is defined as

7

It is complementary to the integral capacitance, because its variations often are signatures of the physical chemistry processes occurring at the interface.¹⁶¹ It is often obtained by computing ⟨Q₊⟩ for several applied voltages and then differentiating an interpolated curve. However, a fluctuation–dissipation was recently derived, which expresses the differential capacitance from the fluctuations of the charge of the electrode.^43,117 It is then possible to use histogram reweighting techniques^117,162,163 to investigate correlations in the double layer and their impact on the charge accumulated at the interface over the whole range of interesting applied potentials with a limited set of simulations.

The quantum capacitance is an intrinsic property of the electrode. In computer simulations, it is generally calculated using electronic DFT from the density of state of the material around the Fermi level.^164−166 It is important to account for this contribution for materials such as graphene, for which it dominates the total capacitance in the vicinity of the point of zero charge.¹⁶⁷ The introduction of the Thomas–Fermi electrode model (see section 2.5) provides a convenient approximation to include this contribution within classical MD simulations, but a wide majority of the studies discussed in the following either neglect the quantum capacitance (which is a good approximation for electrodes with a large number of electronic states available near the Fermi level) or simply add it to the EDL capacitance a posteriori. For simplicity, we will generally designate C_EDL as the capacitance in the remainder of the review.

3. The Electrochemical Double Layer beyond Dilute Electrolytes

3.1. The Kornyshev Paradigm Shift

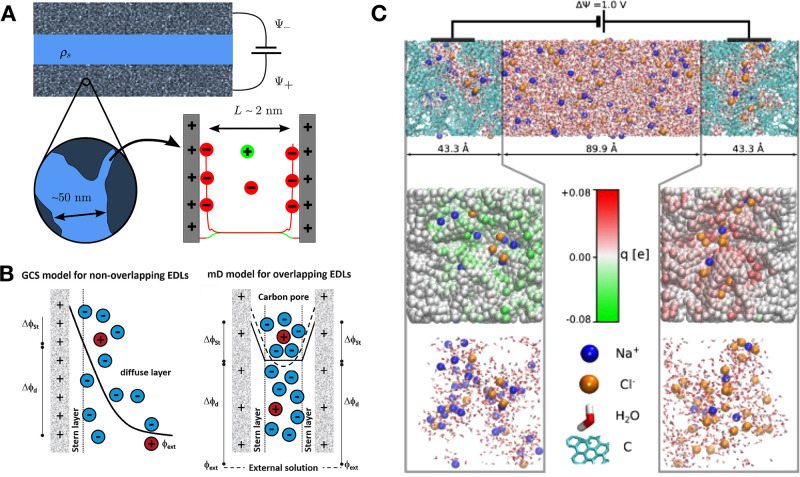
Before focusing on the case of porous electrodes, which is the most relevant for applications in capacitive devices, it is important to discuss first the structure and the properties of the electrochemical double layer formed at planar electrode surfaces. The name “double layer” is a legacy from early theories aiming at depicting this interface. The first layer, called the Helmholtz layer, contains strongly adsorbed ions. The second one is a diffuse layer whose concentration decreases away from the surface of the electrode, as introduced in the works of Gouy and Chapman. A schematic representation of this GCS model is displayed in Figure 7. The distribution of ions and the electrostatic potential profile in this diffuse layer can be described using Poisson–Boltzmann (PB) theory. The linearized version of this theory (Debye–Hückel) predicts an exponential decay of ionic and potential profiles, with a characteristic decay length called the Debye length that decreases with increasing concentration of the electrolyte. This theory is for example able to predict the minimum capacitance at the point of zero charge for simple salts in aqueous solution.

Figure 7.

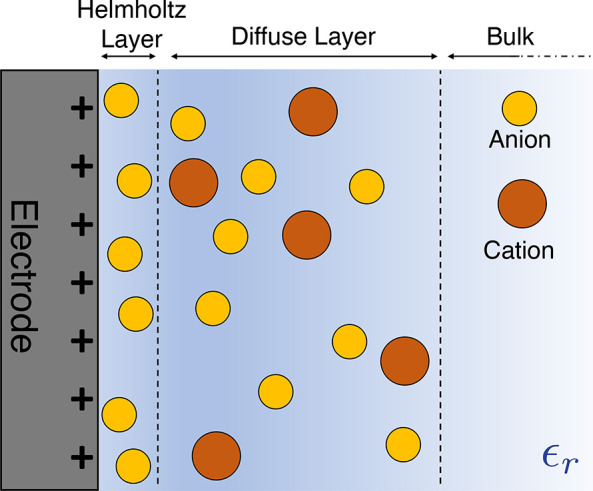
Schematic representation of the electrical double layer at a planar electrode according to the GCS model. Anions are displayed in yellow, and cations are in orange. They are immersed in a dielectric continuum of relative permittivity ϵ_r.

However, within PB theory ions interact with each other at the mean field level only and there is no limit for their concentration at the interface. Consequently, this theory is appropriate for dilute electrolytes only. In capacitive devices, the electrolytes display much larger ionic concentrations, typically above 1 mol/L. At such concentrations, the hypotheses underlying PB theory do not hold anymore—in particular in the case of ionic liquids in which ion–ion correlations dominate the physicochemical properties of the system. Despite these limitations, very few studies have aimed at improving the simulation and the theory of capacitors for many years. The situation changed following the publication of a series of seminal works by Kornyshev, who introduced important additional ingredients to the Gouy–Chapman theory, such as the existence of a maximal ionic concentration at the interface¹⁶¹ (which lead to the prediction of a transition from “bell-shape” to “camel-shape” for the evolution of the capacitance with applied voltage), the existence of overscreening effects,¹⁶⁸ and even of short-range correlations.¹⁶⁹ Interestingly, after these publications, many experimental studies reported large deviations from Gouy–Chapman theory, showing a large variety of nontrivial capacitive behaviors.

3.2. From a Double-Layer to a Multilayer Picture

In parallel to these theoretical and experimental works, many MD simulation studies were also conducted. Note that at that time, most studies did not use a realistic metallic model for the electrodes but relied on simpler constant uniform charge distributions instead.¹⁷⁰ However, much of the structural results should not have been impacted by this choice.¹⁷¹ These studies provided qualitatively similar results, indicating the formation of a layered structure for the liquid at the interface. Such a result is in fact very generic and has been consistently reported in numerous other studies involving interfaces of liquids in contact with vapor, biological systems, or solid materials. The definition of the “layers” is rather broad; in fact, this term is used whenever successive regions of high and low densities (with respect to the bulk) are observed.

In the specific case of ionic liquids in contact with charged surfaces, strong layering was also observed in surface-sensitive experiments. For example, in atomic force microscopy performed on metallic surfaces or in a surface force apparatus which uses charged mica surfaces, experiments performed with ionic liquids display similar patterns, with the presence of oscillations between repulsive and attractive forces up to as much as 10 nm away from the surface, with the period of the oscillations showing some commensurability with the dimensions of the ions.^172−177 Another proof of the layered structure was provided by high-energy X-ray reflectivity experiments, which were able also to discriminate the presence of cations and anions in the various layers.^178,179 Finally, it is worth noting that the structure inside the first adsorbed layer was shown to differ from the one in the bulk. In particular, using sum-frequency generation spectroscopy, Baldelli and co-workers were able to demonstrate the existence of specific orientational effects.^180−182

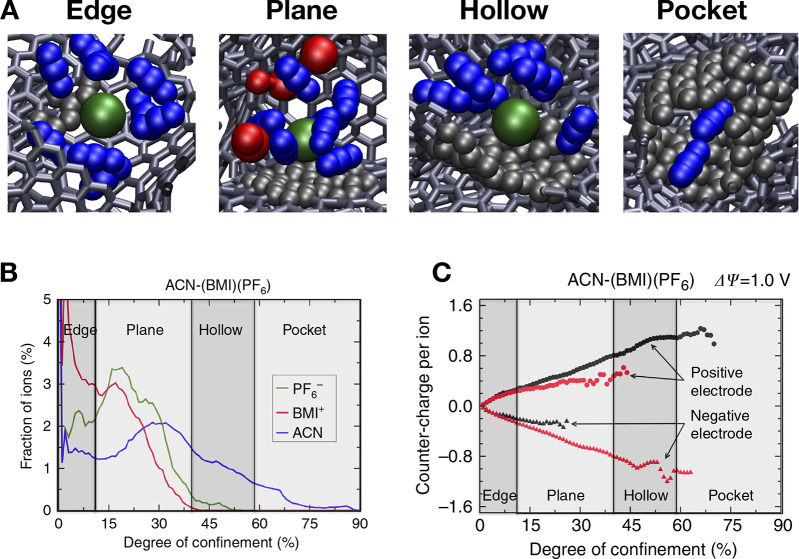
Going back to the simulation studies, the first important result with respect to the Gouy–Chapman theory was that the layering extends over a length scale noticeably larger than the Debye length. This is easily explained by the fact that the Debye length is shorter than the size of ions for the large ionic concentrations used in supercapacitors. The nature of the species involved in the adsorbed layers varies according to the presence/absence of solvent in the electrolyte. In ionic liquids, close to the point of zero charge (PZC), the layers contain equimolar concentrations of both ions. The PZC is defined as the electrode potential for which the electrode is neutral. In simulations, for symmetry reasons, this is the case when no potential difference is applied between two identical electrodes. Note that when the electrolyte is dissolved in an organic solvent, such as acetonitrile, solvent molecules can also be present in the adsorbed layers.¹⁸³

When a finite voltage is applied between the two electrodes, the latter accumulate a net charge. This is accompanied by a reorganization of the adsorbed liquid. In the absence of collective ordering transitions (see below), the main effect is the exchange of anions/cations between the first adsorbed layer and the following ones.^184−188 For small voltages, as predicted in theoretical works from Kornyshev and co-workers,^161,168 overscreening effects are observed: The charge in the first layer of liquid is larger than the electrode charge, so that it has to be compensated in the second layer, and the effect sometimes extends over several layers. On the basis of this observation, Feng et al. proposed a counter-charge layer framework to analyze the structure of adsorbed liquids.¹⁸⁹ Upon increasing the potential, the overscreening effects vanish and they are replaced by lattice saturation.¹⁹⁰ The first adsorbed layer saturates in counterions, and the following layers start to exchange ions with the bulk. However, it is not clear whether these effects really occur in experiments because the corresponding potentials may be outside the electrochemical window of the systems, i.e., the electric potential range over which none of the components of the electrolyte are neither oxidized nor reduced. This is true even in ionic liquids that generally display larger windows than organic solvents. In parallel to these concentration changes, the orientation of the ionic species with respect to the surface was also shown to vary with the applied potential.

The multilayered structure may however be less pronounced if the surface of the electrode is not completely flat. By simulating the atomically corrugated prismatic face of graphite, Vatamanu et al. showed a qualitatively different packing of the electrolyte, accompanied by changes in the differential capacitance, compared to the case where the graphite is facing the liquid through its basal plane.¹⁹¹ By using ideal structures, they were able to further study the effect of the surface roughness and concluded on a noticeable improvement in the stored energy in the double layer when its typical length matched the ionic dimensions,¹⁹² an effect which is reminiscent of the case of nanoporous carbons (see the next section). The curvature effect was also investigated by simulating interfaces of carbon nanotubes^193,194 or onion-like carbons¹⁹⁵ with ionic liquids. For such systems, a systematic increase of the capacitance was observed. The authors proposed to include the effect by introducing the radius of the electrode in analytical models.

Flat surfaces were also extensively investigated using cDFT. Jiang et al. were able to reproduce some results of Kornyshev.¹⁹⁶ In this work, the electrolyte is described by the so-called restricted primitive model (RPM), in which cations and anions are identical hard spheres of opposite charge immersed in a solvent described as a continuum dielectric medium. Electrodes are described as ideal hard walls bearing a homogeneous surface charge density. Thus, the molecular nature of the solvent and the complex structure of the electrodes are ignored. In this study, the electrostatic correlations of eq 4 are approximated using a Taylor expansion up to second order around the one of the homogeneous fluid.^72,197 The second-order direct correlation of the homogeneous fluid required to express the quadratic term is computed using the mean spherical approximation (MSA), for which analytical expressions are available in the case of the primitive model.¹⁹⁸ Jiang et al. computed the differential capacitance as a function of the applied surface potential for electrolytes with bulk packing fraction ranging from 0.01 to 0.5 and recovered the transition from camel shape to bell shape as predicted by Kornyshev.¹⁶¹ They also compared cationic and anionic density profiles at high (0.5) and low (0.01) packing fractions for different values of the applied potential. At high concentration, they observed a strong oscillatory ordering for both ion profiles as in various MD simulations. At high potential they also observed the overscreening effect where the electrode charge is overcompensated by the adsorbed ions. When the curve is bell-shaped, the potential at which the capacitance reaches a maximum is shifted toward the positive potentials when cations have radii larger than anions. This can be explained by noting the “camel shape” curves at high density become asymmetric, with a large peak at positive potentials and a small one at negative potentials, a behavior that was also predicted by Kornyshev.¹⁶¹

The primitive model is known to freeze at low temperature for realistic IL densities,¹⁹⁹ so that the liquid state behavior reported in ref (196) in fact corresponds to a metastable state. Lu et al. proposed using a more realistic model in ref (200). The model is asymmetric because the charges are displaced from the center of the hard spheres. Electrodes are still described as infinite flat walls bearing a uniform charge, but the polarization is accounted for using mirror charges. The predicted differential capacitance and density profiles are in qualitative agreement with MC simulations and the “camel-shape” of the capacitance is also properly described. This group also investigated the effect of ion pairing and clustering using the same ionic liquid models.^201,202 To do so, they described the solution as a mixture of free ions, ion pairs, and clusters with a fixed ratio between the species. They found that while the short-ranged structure adjacent to surfaces is almost unaffected by the degree of ion association, this is not the case for the differential capacitance. According to cDFT predictions, clustering reduces the differential capacitance, especially at low potential. Cluster dissociation could thus be an explanation for the experimentally observed increase of capacitance at higher temperature.

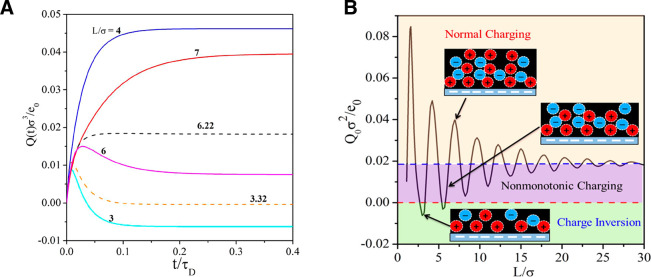
3.3. Two-Dimensional Structural Transitions

Among the studied electrolytes, some ionic liquids may also display intriguing results at planar interfaces.²⁰⁴ In nonelectrochemical contexts, several experimental studies showed the formation of one or several ordered layers of ions at the liquid/vapor interface²⁰⁵ or upon adsorption on ionic surfaces such as mica.²⁰⁶ In the case of electrochemical interfaces, in situ scanning tunneling microscopy investigations of the adsorption of an ionic liquid on a planar gold electrode displayed the formation of an ordered AlCl₄^– adlayer.²⁰⁷ Using a chloroaluminate ionic liquid also led to the observation of moiré-like patterns at potentials in a specific potential range, which were attributed to the formation of a two-dimensionally ordered adlayer of PF₆^– anions²⁰⁸ with a 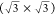structure. In a further study, the formation of ordered layers of butylmethylimidazolium cations was correlated with the presence of a sharp peak in the capacitance–voltage curve.²⁰⁹

Tracking these structural transitions using molecular simulations is not an easy task. They are collective transformations by nature, and one often needs to involve complex reaction coordinates and/or resort to improved sampling techniques in order to simulate them. However, in the case of the electrochemical double layer, several two-dimensional transitions could be observed using MD simulations. A first example was obtained in the case of a high-temperature molten salt (LiCl) in contact with an aluminum electrode.^210,211 Depending on the nature of the surface and on the applied potential, the liquid adopts different ordered/disordered structures. When a potential-induced transition occurs, it is accompanied by a jump in the electrode surface charge,²¹¹ which should be reflected in a peak of the differential capacitance. However, the latter could not be characterized in the study because of sampling difficulties.

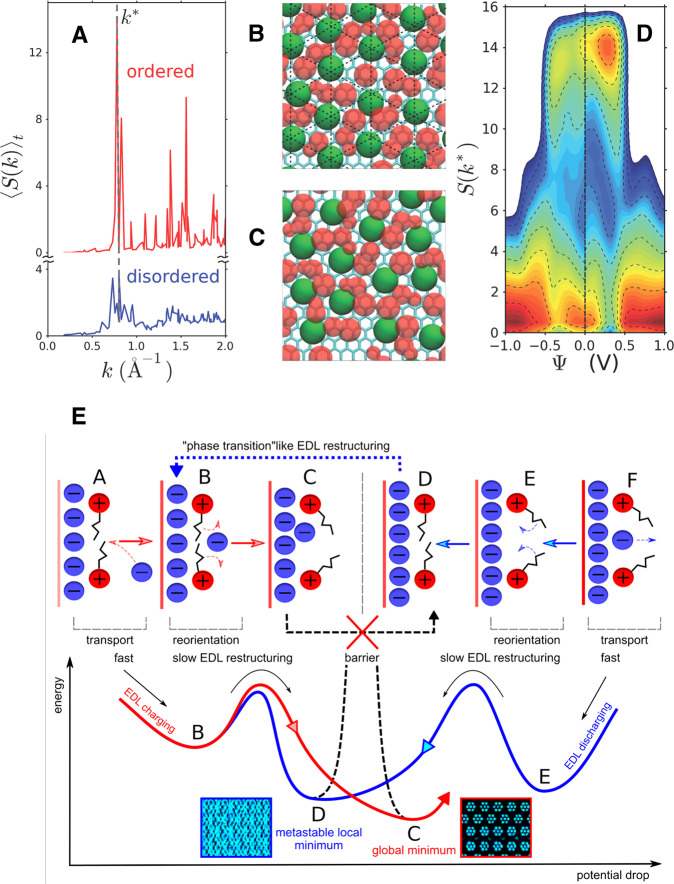
It was later noted that the differential capacitance can be determined from the fluctuations of the total charge of an electrode in constant applied potential simulations¹¹⁷ (a result which was further refined to account for the global electroneutrality constraint²¹²) and that these fluctuations (among others) can be efficiently sampled using importance sampling methods, considering voltage itself as a bias which can be unbiased using, for example, histogram reweighting. This was used in a study of the adsorption of 1-ethyl-3-methylimidazolium (EMIM)-PF₆ ionic liquid on carbon electrodes, which was already known to adopt an ordered structure.^95,213 By determining quantities such as an in-plane structure factor, the orientation, and the number of ions in the first adsorbed layer, the existence of an order–disorder transition was evidenced.¹⁶²Figure 8A shows typical anion–anion structure factors for the ordered and disordered structures, while the corresponding snapshots illustrating such structures are displayed in panels B and C of Figure 8, respectively. In the ordered structure, the anion–anion structure factor reaches a maximum at a wave vector denoted by k* evidenced by the vertical dashed line in Figure 8A. In Figure 8D is displayed the probability distribution of the anion–anion structure factor at the maximum, S(k*), as a function of the applied voltage. Large values of S(k*) indicate an ordered structure, while low values reflect disordered structures. The left (right) side of the figure corresponds to negative (positive) potentials. Red and blue areas correspond to basins of stability and energy barriers, respectively. Close to zero applied potential, the disordered structure is the most stable. When the potential is increased around 0.25 V, an ordered structure becomes stable at the anode before becoming unstable again as the potential is further increased. This transition results in an anomalous response in the charging induced on the electrode surface as evidenced by the presence of a peak in the differential capacitance similar to the experimental results reported by Su et al.²⁰⁹

Figure 8.

Two-dimensional structural transitions at the surface of planar electrodes. (A) Average anion–anion structure factor in the first adsorbed layer of BMIM-PF₆ ionic liquid adsorbed on graphite electrodes, as a function of the norm of the in-plane wave vector, for a null applied voltage. (B) Representative snapshot of the adsorbed layer in the ordered phase (a coarse-grained model is used; green spheres, (PF₆^–) anions; red spheres, (BMIM⁺) cations). (C) Representative snapshot of the adsorbed layer in the disordered state. (D) Probability distribution of the anion–anion structure factor at the maximum S(k*) in the first adsorbed layer on the electrodes, as a function of the electrode voltage. The probability is reported on a logarithmic scale, with lines separated by a difference of 0.5. Three distinct basins emerge from the analysis. Reproduced with permission from ref (162). Copyright 2014 American Chemical Society. (E) Schematic overview of the anion and cation reorganizations within the adsorbed layer during the surface discharging/charging. The energy diagram shows the activation barriers involved during these processes. Reproduced with permission from ref (203). Copyright 2020 American Chemical Society.

The presence of ordered structures was further established in other simulation studies. For example, when changing the electrode charge density in constant-charge simulations, a transition toward a surface-frozen monolayer of densely packed counterions, with a moiré-like structure, was established.²¹⁴ At very high charge density the second layer was also shown to adopt a layered structure, yielding a herringbone structure (i.e., the superposition of two ordered monolayers). It is interesting that such a structure was also observed in experiments performed on gold, but in that case, it is the electrode materials which underwent structural transitions at the surface.^215,216 Concomitant structural changes on the two sides of the solid–liquid interfaces still remain to be studied from computer simulations; such studies should in particular involve reactive force fields for the metallic or carbonaceous species, which are difficult to parametrize in this context.

Collective transitions in liquid are often associated with high free energy barriers, which result in slow kinetics (and strong finite-size effects in molecular simulations). Although such a link could not be made because of the lack of available structural data on the interface, many experimental studies pointed to the existence of slow capacitive processes when performing impedance spectroscopy^216−218 and of strong hysteresis effects in cyclic voltammetry studies,^219,220 which would not be expected from a simple limitation due to diffusion effects.¹⁴⁰ It is only very recently that the hysteresis could be reproduced in simulations by simulating a system over the two potential scan directions for a system made of 1-butyl-3-methylimidazolium (BMIM), hexafluorophosphate (PF₆), and a Au(111) electrode.²⁰³ The presence of two long-lived interfacial structures led to marked differences in the capacitive response of the system as schematized in Figure 8E. Further investigation of the complex interplay between the dynamics, the thermodynamics, and the structure would be necessary, but these analyses are difficult because they involve understanding finite-size effects and the impact of the scan rate on the kinetics of barrier crossing.

Using cDFT with two modified primitive models shown schematically in Figure 9A,B, Lu et al. were able to predict a structural phase transition.^149,200 For both models, the anion is modeled by a negatively charged hard sphere. The first model is called aspherical because the cation charge is offset from the center of the hard sphere, while the second model is defined as “wall-penetrating” as the cationic charge is allowed to come closer than one ionic radius from the electrode. The phase transition originates from the ability of the cationic charge to approach the electrode interface closer than the anionic one, and it is accompanied by a divergence of the differential capacitance at the potential where the two phases coexist. It should be noted that because the calculation is pseudo-1D in the sense that it is invariant by translation parallel to the electrode plane, the lateral correlations between charges are ignored. This phase transition is not two-dimensional but rather corresponds to two different layerings of the cations and anions. With such limitations, it is hard to link this theoretical model with experimental work.

Figure 9.

Modified primitive models. (A) Aspherical primitive model. (B) Wall-penetrating primitive model. Reproduced from ref (149). Copyright 2021 Royal Society of Chemistry under CC BY 3.0 (https://creativecommons.org/licenses/by/3.0/).

4. Molecular Origin(s) of Supercapacitive Effects

4.1. An Anomalous Increase of the Capacitance

Porous carbon materials have long been established as the materials with the best overall properties for the development of supercapacitor devices.² Decades of intense experimental research lead to important improvements in the synthesis of such carbons and in the use of dopants or surface modifications to improve their properties.¹¹ In the absence of Faradaic effects, it clearly appeared that activated carbon offered excellent performance, in particular when combined with organic electrolytes.²²¹

The rise of nanomaterials provided new directions for improvement to the field. Several groups started to investigate the impact of the nanotexture of the materials on the performance²²² or to use better-defined carbon structures such as carbon nanotubes.^28,223 However, materials displaying porosity at the nanoscale are more difficult to characterize using standard gas adsorption techniques. For example, analyses based on the Brunauer–Emmett–Teller theory²²⁴ cannot access the pore size distribution.²²⁵ Indeed, in a nanopore the confinement effects become very important and the liquids may not adopt their traditional layered structure, contrary to the case of mesopores. In addition, simple estimates based on the size of the solvated ions suggested that they would not be able to enter into nanometric pores.

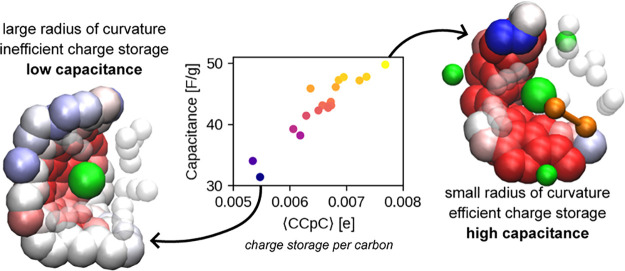
The use of CDCs, for which a typical structure is shown in Figure 3, as electrode materials drastically changed the situation. Because of their high tunability (through the use of different synthesis temperatures), they allowed for the efficient study of the link between the pore size and ion dimension, leading to the conclusion that the two had to match in order to obtain maximized performances in organic electrolytes.⁴⁶ This increase in capacitance for pores smaller than 1 nm was originally called “anomalous” because it challenged the consensus at the time that pores smaller than the size of solvated electrolyte could not contribute to charge storage. The superior performance of nanopores for capacitance was also established in the case of aqueous electrolytes.²²⁶ Using different ionic species,²²⁷ it was shown that, contrary to the case of mesopores in which the structure of the liquid remains mostly intact, in nanopores the ions tend to (at least partially) desolvate, resulting in a smaller effective radius. This interpretation was also supported by earlier extended X-ray absorption fine structure (EXAFS) results on the adsorption of aqueous Rb⁺ ions in nanopores,²²⁸ for which a decrease in the coordination number was observed compared to the bulk. The importance of matching the average pore size with the ionic dimensions was further demonstrated in ionic liquid electrolytes.²²⁹

These results had a deep impact on the field.³⁷ Going beyond electrochemical measurements, the structure of electrolytes in nanopores was studied by a huge variety of analysis and spectroscopy techniques, such as X-ray scattering,^230−237 neutron scattering,^238−240 nuclear magnetic resonance (NMR),^47,241−247 electrochemical quartz crystal microbalance (EQCM),^248−250 infrared (IR),^251,252etc. They have also triggered a large number of simulation studies, which are much better suited to the case of nanopores rather than mesopores. Indeed, their main practical limitations are either the number of molecules that can be put in a simulation cell in MD and MC or the number of grid points to be included in cDFT. These numbers typically correspond to dimensions smaller than 10 nm. In parallel with the many intriguing results obtained on planar electrodes, it quickly appeared that characterizing the adsorption of the ions, their solvation under confinement, and the interplay of these structural characteristics with the capacitance of the electrodes would bring important benefits to the understanding of supercapacitors.

4.2. Ion Layering Inside Nanotubes and Nanometric Slit-Pores and Curvature Effects

The first simulation studies aiming at understanding the anomalous increase of the capacitance in nanopores focused on simple electrode geometries, such as carbon nanotubes, considering the adsorption of the ions both outside²⁵³ and inside.²⁵⁴ In the first case (ions outside the tubes), the simulated system consisted of a single nanotube immersed in the electrolyte, but the porosity was introduced by varying the size of the simulation cell. Because of the use of periodic boundary conditions, the liquid was thus confined between successive nanotubes as illustrated in Figure 10A. The liquid structure was characterized by strong adsorption peaks, relatively similar to the ones obtained on planar electrodes, and the simulations yielded capacitances in qualitative agreement with the experiments, although the structure of the simulated electrode was much more ordered than the experimental one. In the second case (ions inside the tubes), by varying the size of the nanotubes, Shim and Kim showed that the ions transition from a structure in which both counterions and co-ions adsorbed together in multilayers in the largest ones to a situation where the tubes are filled with aligned counterions only under stronger confinement,²⁵⁴ as shown in Figure 10B. The capacitance reaches a maximum for nanotubes of diameter ∼1 nm, which is also the diameter where the structural transition occurs. This is similar to the maximum of capacitance experimentally measured in CDC with pore sizes comparable to ionic diameters.⁴⁶ However, the computed capacitances were substantially smaller. This can be attributed to the limitations of studying a single pore while the experimental carbons have a much denser structure characterized by multiple connected pores.

Figure 10.

Ionic liquid adsorption in confined materials. (A) Typical snapshot showing the adsorption of tetraethylammonium (blue balls) and tetrafluoroborate (BF₄^–, green balls) dissolved in propylene carbonate (sticks) within a carbon nanotube forest (turquoise balls). R represents the pore radius. Reproduced with permission from ref (253). Copyright 2009 American Chemical Society. (B) Typical snapshots of the adsorption of EMIM-BF₄ ionic liquid (red balls, EMIM⁺ center of mass; blue balls, BF₄^– center of mass) within the interior of carbon nanotubes in (n, n) armchair configurations (sticks). The corresponding n values are associated with each snapshot. Reproduced with permission from ref (254). Copyright 2010 American Chemical Society.

Switching from a one-dimensional to a bidimensional structure, numerous simulation studies considered slit pores.^255−258 Compared to nanotubes, they are likely to be more representative of the structure of complex porous carbons, and they should in principle suffer less strongly from crowding effects on the dynamics. In particular, Feng and Cummings simulated such nanopores ranging in size from 0.67 to 1.8 nm.²⁵⁹ Their result was even more complex than the picture drawn from experiments, because they showed an oscillatory behavior characterized by two maxima of the capacitance instead of one. Although the first maximum was easily attributed to the formation of a monolayer, the second one arose in the regime where the ions form multiple layers. The authors therefore interpreted this effect by the formation of wave interference, that is, the superposition of the adsorption peaks from the two electrode walls that are either constructive or destructive. Because of the computational cost of MD simulations, it was not possible to go beyond 1.8 nm in this study, but similar systems were also investigated with cDFT, leading to a generalization of the oscillatory behavior of the capacitance with the slit pore size.

For instance, Jiang et al. carried out a systematic study of the influence of the pore width on the capacitance, from 2 to 30 ionic diameters.^260,261 The pore was modeled by two symmetric hard walls of equal surface charge. The capacitance oscillates with an overall decaying envelope. This oscillatory behavior is explained by a constructive superposition of the ionic densities in the EDL on both walls. Interestingly, when the solvent is explicitly modeled by a hard-sphere dimer of opposite charges, this oscillatory behavior of the capacitance vanishes.^261,262 Examining the density profiles, the authors indeed observed a desolvation of counterion concomitant with the capacitance peak.

Lian et al. analyzed the effect of the pore curvature on the capacitance of an ionic liquid-based supercapacitor.²⁶³ The electrodes are now represented as two spherical surfaces sharing the same center, as illustrated in Figure 11A. The inner sphere radius is labeled R, while the pore width is labeled D; thus, the outer sphere has a radius R + D. The ionic liquid, modeled with the restricted primitive model, can access the volume depicted in white in Figure 11A, comprised between the small sphere and the large one. The electrode potential is held constant at the same value for the inner and outer surfaces of the shell. The authors observed an oscillatory behavior of the integral capacitance with the pore width as in the case of the slit pore²⁶⁰ (see Figure 11C,D). While the capacitance at the concave interface is comparable to the slit pore one, the capacitance at the convex interface is increased by up to 50% for the smallest pore (R = 1 nm). This can be rationalized by considering the effect of the curvature on the charge density at each surface of the shell presented in Figure 11B. When the inner radius increases, the charge on the concave surface increases greatly while that of the convex surface remains almost unchanged.

Figure 11.

Electrode curvature effects on IL-based supercapacitor performance. (A) Schematic setup for a supercapacitor with two identical porous electrodes and the spherical shell model that is used in cDFT to study the effect of curvature. (B) Charge density on the concave (outer) and convex (inner) surfaces as a function of the inner radius of the spherical shell obtained with a pore thickness D = 4.0 nm at a surface potential Ψ = 1.5 V. (C) Integral capacitance of the convex surface as a function of the pore width D for different values of the inner radius R. (D) Same as panel C for the concave surface. Reproduced with permission from ref (263). Copyright 2016 American Chemical Society.

Another group studied three different electrode geometries using cDFT:¹¹² the first one is an infinite wall, while the two others separately display spherical and cylindrical shapes. On the basis of polymer DFT, they developed an ionic liquid model²⁶⁴ that is more realistic than the frequently used RPM. Here, organic anions are described by tangentially connected hard beads as illustrated in Figure 12. Some beads are charged while others are neutral, and the electrode bears a constant charge. For a given electrolyte, the larger the curvature, the higher and “flatter” the capacitance; that is, the capacitance increases when passing from planar to a cylinder and then to a sphere. Regarding the influence of the alkyl chain of the cation, a longer hydrocarbon chain also gives rise to a lower magnitude for the differential capacitance because the neutral beads diminish the ability to screen the surface charge.

Figure 12.

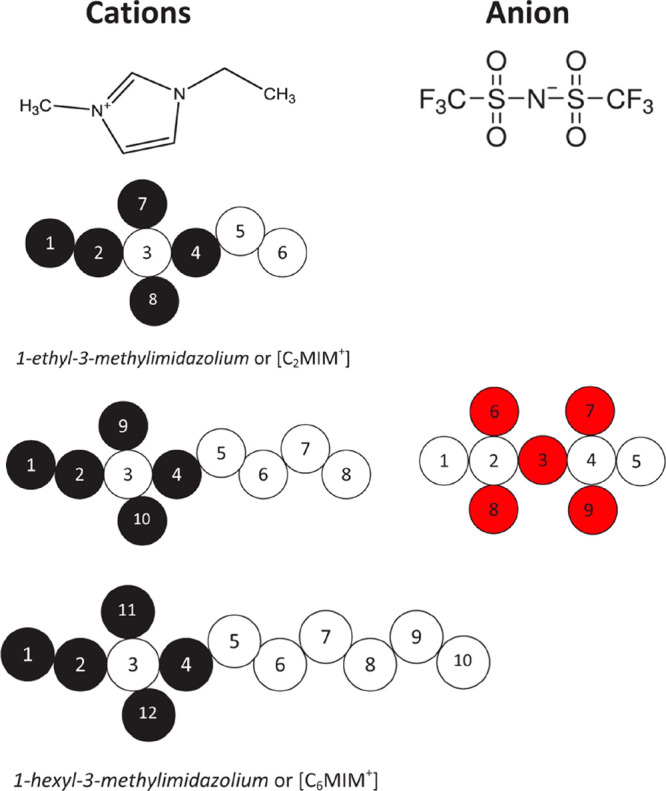
Coarse-grained models of ionic liquids describing a series of 1-alkyl-3-methyl imidazoliums (C_nMIM⁺) cations and bis(trifluoromethylsulfonyl)imide (TFSI) anion. Colored spheres are charged, blank ones are neutrals. Reproduced with permission from ref (112). Copyright 2014 American Chemical Society.

4.3. Mechanisms for Charging Nanopores

In bulk liquids, ions of the same sign strongly repel each other, which results in well-established Coulomb ordering effects. Thus, the structures formed inside carbon nanotubes of small dimensions, i.e., a single line of similarly charged ions as obtained in the study of Shim and Kim²⁵⁴ (Figure 10B), are intriguing. This result was rationalized using a mean-field theory,²⁶⁵ which was further confirmed using MC simulations,²⁶⁶ through the formation of a so-called “superionic state”. This is due to the opposite charges which are induced at the electrode surface. They screen the repulsive electrostatic interactions between ions of the same sign inside the pore. In their mean-field theory, Kondrat and Kornyshev also observed that the transition from an anion-rich regime to a cation-rich one by lowering voltage could lead to a peak of the capacitance as a function of voltage.

The question then arose of whether such a superionic state could be formed only under specific geometries such as nanotubes or slit pores. By performing MD simulations on a realistic system made of a BMIM-PF₆ ionic liquid and nanoporous CDC electrodes, the formation of like ion pairs was shown to be a generic effect inside electrified nanopores.²⁶⁷ In this study, large capacitances in agreement with experimental works were further obtained, showing the importance of the superionic effect on the performance of the devices. It was only several years later that an experimental confirmation was provided. By performing X-ray scattering experiments to determine the structure of the EMIM–bis(trifluoromethane)sulfonimide (TFSI) ionic liquid inside CDC structures, Futamura et al. observed a reduction of the Coulombic ordering, only for pore sizes that could accommodate no more than a single layer of ions.²³⁷ Furthermore, the proportion of equally charged ion pairs was shown to increase when a potential was applied to the electrodes because of the induction of a surface charge of opposite sign in the carbon pore walls. The presence of a superionic state under strong confinement only was further analyzed by computing the induced surface charge under two conditions, corresponding to monolayer and bilayer ionic liquid structures. In the monolayer case, the highly charged domains are more extended and more correlated. From the energetic point of view, the confined structure is more stabilized because of an enhancement of the ion–electrode Coulombic interactions.²³⁷

Another important piece of information was obtained from both computational and in situ spectroscopic studies, namely, that in generic electrolytes, nanopores are initially filled by the liquid at null applied voltage. The electrode surface does not have any net charge, which implies that as many cations as anions are adsorbed in order to maintain the electroneutrality. This rules out charging mechanisms based on counterion adsorption only (unless specific ionophobic effects could be induced as discussed below) and opens the possibility for ion exchange as well as co-ion desorption to occur when a voltage is applied between the electrodes, as summarized in Figure 13. In a perspective article, Forse et al. therefore introduced a charging mechanism parameter in order to discriminate the various effects.⁴⁷ By analyzing data from MD,^257,267,268 NMR,^243,246,269 X-ray,²³¹ EQCM^249,270 and IR,²⁷¹ they concluded that ion exchange is the dominant mechanism, even though depending on the conditions the other effects can become important.

Figure 13.

Schematics of the various possible charging mechanisms in a carbon nanopore (black surface, carbon nanopore; blue circles, anions; red circles, cations; green circles, solvent molecules). At 0 V, the pore is already filled with electrolyte, and electroneutrality is conserved. Upon application of a non-null voltage, three mechanisms can occur: counterion adsorption, ion exchange, or co-ion desorption. A charging mechanism parameter was introduced to discriminate between the three based on simulation and/or in situ experimental techniques. Reproduced with permission from ref (47). Copyright 2016 American Chemical Society.

4.4. Ionic Interactions Across Pores

Although most of these studies focused on single slit pores, it is also important to investigate the impact of adjacent pores inside the electrode. In practice, for a slit geometry this corresponds to the case of graphene-based capacitors, which have also been studied experimentally despite the difficulty of obtaining a dense structure without restacking the graphene planes together.^16,272−274 Several cases of graphene “transparency” were reported in the literature. For example, when a metallic or a semiconductor substrate is coated with thin layers of graphene (below 6 planes), the intrinsic wettability of the assembly is not significantly modified with respect to that of the initial substrate.²⁷⁵ A similar observation was made when nucleating ZnO nanocrystals on a surface coated with graphene. The structure of the synthesized crystals was similar to that of the substrate located on the other side of the graphene.²⁷⁶ It is therefore of interest to check whether such effects may occur in the case of graphene-based supercapacitors.

Unfortunately, it is difficult to find an experimental observable allowing for the detection of such an effect. MD simulations were therefore performed on electrode materials made of perforated graphene sheets.²⁷⁷ The spacing between the graphene planes was fixed to a series of values corresponding to either monolayer or bilayer adsorption, as discussed previously. When the liquid adopts a monolayer structure, ions of the same sign tend to adsorb in front of each other on the two sides of the graphene plane. This was attributed to the polarization of the surface. Because of the adsorption of the first ion, the neighboring carbon atoms tend to adopt opposite charges which then attract a second ion of the same sign on the other side. In these simulations, the effect was more pronounced for PF₆^– anions than for BMIM⁺ cations, which was attributed to the more widespread charge of the latter. In the case of a bilayer of liquid, a very different situation is observed. The correlations between like and unlike ions from one pore to another almost completely vanish. It is not easy to determine whether this observation is due to a lesser localization of the surface charge of the electrode or to the formation of a structure which minimizes the overall Coulombic interactions by optimizing the packing of the ions.

Although these results were obtained using a coarse-grained model for the ionic liquid, they were then confirmed in all-atom simulations of the (2-methoxyethyl)triethylphosphonium TFSI ionic liquid in aligned graphene slit pores.²⁷⁸ The use of classical MD could also be a source of error in such a case involving very specifically the local response of the metallic electrode. Nevertheless, an electronic DFT study of the adsorption of lithium ions on the two sides of carbon nanotubes confirmed this picture. The electronic structure calculations showed that the carbon surface screens the electrostatic interaction between the ions and that the presence of an ion inside the nanotube favored the adsorption of the second ion outside.²⁷⁹

The effect of this new type of ion ordering on the electrode capacitance was investigated in more detail by combining a mean-field theory with MC simulations.²⁸⁰ By introducing a coupling constant that could be either positive or negative, the authors showed that important variations of the amount of energy stored could occur. The interpore thickness may therefore be another important parameter that needs to be tuned to design efficient capacitors.

4.5. Beyond Pore Size Effects

The formation of a liquid monolayer, in which a superionic state is induced by the screening of the Coulombic interaction because of the charge of the electrode surface, gives an almost complete picture of the origin of supercapacitance in simple nanoporous carbon geometries. However, as discussed previously, the materials employed in most experiments as well as in commercial devices are much more disordered. By performing MD simulations of realistic supercapacitors, it was possible to provide a detailed analysis of the various environments experienced by the ions.²⁶⁸ Four different adsorption types were identified, as shown on Figure 14A. They are labeled as edge, planar, hollow, and pocket sites and correspond to situations in which the coordination of the ions by carbon surface atoms increases. The concentration of the ions in each of the adsorption sites was determined (Figure 14B), demonstrating a positive correlation between the local charge stored on the electrode and the degree of confinement (Figure 14C). This led to the conclusion that concave structural motifs were necessary to increase the performance of the device. This conclusion was further confirmed in an aqueous electrolyte through the use of in situ X-ray scattering analyzed by a reverse MC approach.²³³

Figure 14.

Adsorption of a typical electrolyte in CDC-based supercapacitors. (A) Typical snapshots of the four different adsorption modes identified in CDC electrodes (gray sticks, C–C bonds; red spheres, BMIM⁺ cations; green spheres, PF₆^– anions; blue spheres, acetonitrile molecules; gray spheres, C atoms which are in the coordination sphere of the central molecule). (B) Concentration of the various species in the four different adsorption modes at null voltage. (C) Counter-charge accumulated at the surface of the electrode (per ion) as a function of the degree of confinement of the ion for an applied voltage of 1 V. Reproduced with permission from ref (268). Copyright 2013 Nature Publishing Group.

The interplay between the local structure and the capacitance of the material was further studied using a library of zeolite-templated carbons, which are ordered nanoporous materials.²⁸¹ Because of their well-defined pore shape, it was possible to study the impact of various geometrical descriptors. Even though the average degree of confinement was not a good indicator of the performance of the overall material, the authors confirmed the importance of the local charge. As shown in Figure 15, a small radius of curvature in the carbon surface resulted in a larger amount of charge stored per carbon atom and a larger capacitance.

Figure 15.

Simulated capacitance with respect to the charge storage per carbon atom descriptor for a series of carbons with regular pore geometry. Typical snapshots for two of the structures are also shown. Carbon atoms are colored according to their charge, with blue indicating negative and red indicating positive charge, scaled from −0.01e to 0.01e. The green sphere corresponds to the BF₄^– anions, and the orange spheres correspond to the BMIM cations; the transparent linear molecules are the solvent. Reproduced with permission from ref (281). Copyright 2019 American Chemical Society.

As mentioned previously, graphene-based materials have attracted a lot of interest from the community because they should in principle allow for the precise control of the pore size distribution. However, in such a structure only planar adsorption sites will be present. In order to test whether graphene-based supercapacitors could enhance the capacitance of the devices, MD simulations were performed using the same BMIM-PF₆ electrolyte model as for realistic CDC structures.²⁸² Although the simulations confirmed the better performance of monolayer over bilayer adsorption, it was shown that whatever the proposed metric (i.e., expressing the capacitance normalized by the mass or by the volume of the electrode), the graphene-based materials yielded lower performance than the CDCs. This was attributed to a beneficial effect of having pores of different sizes in the structure. In CDCs, the small pores accommodate the counterions as discussed before, but the few larger pores also play an important role by allowing co-ions to adopt positions far from the surface in order to maximize the capacitance. This conclusion differs from the results of an earlier work focusing on the effect of pore size and dispersity on the stored energy,²⁸³ which is likely due to the use of too crude hypotheses in the theory used in the latter study. In particular, the peculiar ionic adsorption structure in larger pores, with co-ions sitting in the middle and counterions closer to the surface, could not be included.

A recent study went further in analyzing the effects of interpore connectivity in complex nanoporous carbon structures.²⁸⁴ The latter were modeled using the method of Gaussian random fields, in order to mimic the structure of various CDCs and activated carbons. A probe-specific effective porosity was introduced in order to account for the ion sizes. It was shown that reduced percolation effects could lead to a substantial decrease of the stored energy density, which highlights the importance of optimizing the pore connectivity when developing new electrode materials.

Finally, an interesting feature of simulations is that they allow for the investigation of situations that have not been previously explored experimentally. In this respect, a series of works suggested tuning the wettability of the pores, introducing in particular the concept of “ionophobic” pores^285−287 in analogy to the well-known hydrophobic effect. It is based on the fact that beyond a given voltage, pores may be filled with counterions only. Charging becomes more difficult, resulting in a fading of the capacitance, which is detrimental in terms of energy density. By using ionophobic pores, which would charge only when the driving force (the voltage) is large enough to overcome the repulsion between the electrode and the pore, it would therefore be possible to significantly enhance the energy density.²⁸⁶ However, to date, the concept remains to be realized experimentally.

4.6. Effect of the Electrolyte on the Capacitance

Compared to batteries, in which the electrolyte plays the passive role of a Li⁺ ion charge carrier, in supercapacitors it becomes an essential ingredient. Three main families of liquid electrolytes are usually considered in the literature: ionic liquids, aqueous electrolytes, and organic electrolytes, the latter being mainly based on acetonitrile or on propylene carbonate.²⁸⁸ The major bulk properties differing strongly from one family to another are the electrochemical window, which limits the operating voltage of the device and thus its specific energy, and the ionic conductivity, which directly impacts the power that can be delivered. The electrochemical window increases when passing from water to organic solvents and then to ionic liquids, while the trend is the opposite concerning the conductivity. Organic solvents are also relatively cheap, and they enable long cycle-life; therefore, they are traditionally chosen for commercial applications, but ionic liquids have attracted a lot of attention because of their high versatility.²⁹ Consequently, most molecular simulation studies have focused on these two families of electrolytes, but aqueous systems were nevertheless studied in the framework of blue energy and water desalination, as discussed in section 5.

Although some variations in the interfacial capacitance were observed in molecular simulations when changing the nature of the ions and/or of the solvents, no real trend could be extracted from the various simulation studies. In fact, most of the differences very likely arise from the use of different methods for treating the electrodes (geometry, use of electrochemical conditions) as well as the electrolyte (choice of coarse-grained models vs all-atom ones, parametrization of the force field), etc. In this subsection we will therefore focus on dedicated studies in which several electrolytes were studied using a common framework to allow for proper comparisons.

A first important question is whether ionic liquids and organic solvents should display different capacitances. This was expected with the rise of ionic liquids for energy applications because they should allow for the accumulation of more ions at the interface.^32,289 However, no such effect was observed in the literature, so a combined experimental/simulation technique was performed to specifically address this point.²⁹⁰ To this end, supercapacitors based on a generic CDC electrode and a series of electrolytes composed of a 1-ethyl-3-methylimidazolium tetrafluoroborate (EMIM-BF₄) mixed with acetonitrile at mass fractions ranging from 0% to 67% were studied using cyclic voltammetry and MD. Despite the large variations in the number of adsorbed ions inside the electrodes at null potential, the capacitance was shown to vary only slightly: A smaller capacitance was obtained in experiments for the pure ionic liquid, but this was attributed to the much more sluggish dynamics of this system at room temperature (preventing thermodynamic equilibrium for being reached). This constant trend was attributed to an increasing difficulty of separating oppositely charged ions as they become more concentrated. In the organic solvent, this separation is facilitated because of the screening of the Coulombic interactions. The charging mechanism parameter introduced above (Figure 13) was also calculated. In the dilute electrolyte, the smaller concentration of ions leads to a mechanism dominated by counterion adsorption; ion exchanges then become progressively more important when the composition tends toward the pure ionic liquid.

Systematically comparing several solvents by MD is a complex multidimensional problem, which can be drastically simplified using cDFT. Jiang et al. studied the role of the solvent²⁹¹ by systematically varying its polarity between 0.85 and 4.5 D. For a low-polarity solvent (≤1.7 D), the capacitance exhibits oscillations as a function of the pore size, similar to the case of pure ionic liquids.²⁶⁰ For an intermediate polarity solvent, one recovers the behavior previously reported in ref (260), with a damping of the oscillations after the first peak. Highly polar solvents (4.5 D) exhibit another behavior with the appearance of a second maximum at three ionic diameters, which is actually larger than the first peak occurring at a distance corresponding to one ionic diameter. Examining the density profiles, the authors propose that this new behavior might be due to the presence of antialigned dipoles. Finally, plotting the value of the capacitance in a 4 nm pore as a function of the solvent polarity, a volcano-shape trend is observed, where the capacitance increases with the polarity until it reaches a maximum at around 4 D before decreasing.

The same group also studied with cDFT the impact of impurities on the performance of the supercapacitor.²⁹² The electrolyte is still modeled by a restricted primitive model, and 1% impurity is added. The impurities are neutral hard spheres with radii identical to that of the ions, r = 5 Å. Their interaction with the narrow slit pore of width H = 6 Å is modeled by a square potential of depth ω. If ω > 0, the pore tends to repel the impurities from the surface, while if ω < 0, impurity adsorption is favored. Within this model, the capacitance and the energy stored by the device remain unchanged when the impurities are not attracted by the pore (ω > 0). However, when ω < 0, the capacitance versus potential curve changes from bell shape to camel shape, and the more the impurities are attracted by the pore, the more energy is stored by the capacitor. These effects are rationalized by looking at the density profiles. When the impurities have no affinities with the pore (ω ≥ 0), the charging mechanism solely consists of co-ion/counterion exchange as in the absence of impurities. The more ω is negative, the more the pore is filled by impurities at null potential. At very negative ω, the charging mechanism involves replacement of neutral impurities by counterions. At intermediate values of ω the mechanism consists of both co-ion–counterion exchange and counterion insertion.

Since Fedorov et al. initially related the camel shape of the capacitance to the presence of neutral tails of ions in ionic liquids,¹⁸⁶ Wu et al. explored the effect of the asphericity of ions²⁹³ by modeling the cation as a dimer made of one charged and one neutral sphere. Using MD simulations, they found that the shape of the differential capacitance transforms continuously from a double hump to a single hump as the electrolyte concentration is increased for both the spherical and nonspherical cations. They concluded that the transition from bell shape to camel shape is thus mainly due to concentration effects.

Finally, Neal et al.(294) studied with cDFT the properties of a double-layer capacitor filled with mixtures of two ionic liquids, namely, a symmetric salt in which both ions have the same diameter (0.5 nm) and an asymmetric one made of the same cation and a smaller anion (0.3 nm). They computed the capacitance as a function of the molar fractions of the ionic liquid for different values of the applied potential. The capacitance of the asymmetric salt is larger than the symmetric one. More interestingly, the capacitance reaches a maximum when the ionic liquid is a mixture of both anion sizes. The electrolyte composition corresponding to the maximum capacitance varies with the surface potential. The increased capacitance is attributed to an optimal ion packing near the charged surface: the small anions intercalate into the layer-by-layer structure formed between the larger cations and anions.

5. Blue Energy Harvesting and Water Desalination Using Capacitors

As mentioned in the Introduction, capacitive effects can be exploited in thermodynamic cycles to harvest (so-called “osmotic” or “blue”) energy from salinity gradients or conversely to desalinate water. The potential of salinity gradients as energy sources was recognized almost 70 years ago.⁴ The mixing free energy of salty seawater with fresh river water, which can be estimated from the ideal, entropic contribution, is of the order of 2.8 kJ/L of each solution (equivalent to the change in potential energy through a 280 m waterfall), and it is estimated that a power of ∼1 TW could be harnessed on the global scale.²⁹⁵ However, recovering this yet untapped energy source remains a great challenge for membrane-based technologies, which dissipate a large fraction of the potentially extractable energy (conversely, membrane-based technologies to desalinate water are energy intensive), and many efforts have been dedicated to improving their efficiency. Alternative approaches, based on nanofluidics in 1D nanotubes or 2D materials, have demonstrated the possibility of achieving much larger powers than with conventional membrane-based technologies.^9,296 Porous carbon electrodes such as the one used in supercapacitors for energy storage may contribute to the development of these new approaches to convert ionic currents in the device to electronic ones usable in an electric circuit. Here, we focus instead on another strategy to extract blue energy using a capacitor (capacitive mixing, CapMix^10,297,298), or conversely to desalinate water (capacitive deionization, CDI^299−301). After describing the basic principle of these processes, we highlight some challenges for modeling and the insights gained from molecular simulations and DFT.

5.1. Capacitive Mixing and Capacitive Deionization

The principle of the CapMix cycle, proposed by Brogioli in 2009,¹⁰ is shown in Figure 16A. It consists of four steps, involving the charge/discharge of a capacitor consisting of (porous carbon) electrodes and an electrolyte with high/low salt concentration: (1) The capacitor is charged with the high-concentration electrolyte. (2) The circuit is open, and the capacitor is flushed with the low-concentration electrolyte. (3) The capacitor is discharged. (4) The circuit is open and the capacitor is flushed with the high-concentration electrolyte. During this cycle, the charge accumulated on the electrodes and the potential difference between them change, as shown schematically in Figure 16B. The area enclosed within the loop is equal to the energy that can theoretically be extracted per cycle and is equal to

8

where C₁ and C₂ are the capacitances in the presence of the high/low salt concentration electrolyte and ΔΨ is the voltage between the electrodes at the end of steps 1 and 3. Other thermodynamic cycles have been proposed,^302,303 but in all cases the process crucially relies on the fact that the capacitance depends on the concentration of the electrolyte. In CDI, the cycle is reversed and the corresponding energy must be spent to desalinate water. In order to optimize both processes, many efforts on the theoretical side have been devoted to the prediction of the capacitance as a function of salt concentration (in the range of a few 10 mM typical of fresh river water to a few 100 mM typical of salty seawater) and of the nature of the electrode (porosity, pore size, chemical defects, etc.).

Figure 16.

Illustration of the capacitive mixing (CapMix) concept. (A) Illustration of the steps of the CapMix cycle, described in the text. (B) Illustration of the CapMix cycle in the charge/voltage plane. The area of the closed dashed region is equal to the energy than can theoretically be extracted per cycle. Adapted with permission from ref (298). Copyright 2012 Royal Society of Chemistry under CC BY 3.0 (https://creativecommons.org/licenses/by/3.0/).

5.2. Challenges for Modeling

As for energy storage applications, the challenges for modeling are numerous, and various strategies have been proposed to predict the capacitance and the salt adsorption capacity (mass of salt adsorbed inside the electrode per unit mass of electrode, which is more important for CDI than for CapMix). Figure 17A illustrates the concept underlying most theoretical approaches: A potential difference is imposed between two macroscopic porous electrodes separated by a bulk electrolyte, which acts as a salt reservoir exchanging ions with the fluid confined inside each electrode. The ion exchange occurs mainly in the nanopores, whose surfaces are maintained at the same potential (one value for each electrode). At equilibrium, the chemical potential of each species is equal in all “phases”, and one can deduce properties inside the pore from that of the reservoir and from the potential difference between the electrodes. The properties of the whole device are computed from predictions at the pore level and from global structural properties, such as the porosity and the specific surface area.

Figure 17.

Models for CapMix devices. (A) A full device consists of two macroscopic porous electrodes maintained at different potentials. Inside each electrode, the confined fluid can exchange particles with the bulk electrolyte reservoir, and the exchange of ions leading to charge storage occurs mainly in nanopores. Reproduced with permission from ref (304). Copyright 2015 IOP Publishing. (B) Two standard approaches used in the contexts of CapMix and CDI (see text for more details): GCS theory and modified Donnan (mD) model, thought to apply better in the limits of nonoverlapping and overlapping electric double layer regimes, respectively. The lines represent the potential distribution at the interface or inside the pore. cDFT can provide a more accurate description of the ionic and potential distribution in the same model geometries, including at larger concentrations. Adapted with permission from ref (299). Copyright 2015 Royal Society of Chemistry under CC BY 3.0 (https://creativecommons.org/licenses/by/3.0/). (C) Molecular simulation of a capacitor consisting of two nanoporous carbon electrodes maintained at a constant potential difference and a 1 M aqueous NaCl solution (top). The charge of each electrode atom fluctuates (color scale in the middle part of the panel) in response to the instantaneous microscopic configuration of the electrolyte (bottom). Reproduced with permission from ref (305). Copyright 2018 American Physical Society under CC BY 4.0 (https://creativecommons.org/licenses/by/4.0/).

Molecular-scale information on the confined electrolyte can be obtained from in situ X-ray and neutron experiments.^233,306 On the theoretical side, pore-level predictions are typically obtained from a simplified description of the interface using Poisson–Boltzmann (GCS) theory, possibly also introducing excluded volume effects or using cDFT. For nanoporous materials, an alternative approach successfully used to model experimental data in the context of CDI, the so-called modified Donnan (mD) model, considers instead the equilibrium between ions inside the micropore treated as homogeneous (beyond ions adsorbed in a Stern layer) and the bulk reservoir.³⁰⁷ The mD model requires introducing parameters such as an attractive chemical potential or a Stern layer capacitance; the resulting expressions are rather simple, and the parameters can be fitted to successfully describe experimental results. The PB/GCS and mD approaches are generally thought to better apply in the limits of nonoverlapping and overlapping EDLs, respectively. They are illustrated in Figure 17B, which shows schematized potential profiles at the interface and within the pore in relation to the distribution of ions.

cDFT provides a more accurate theory valid not only in both limit cases but also in intermediate regimes and at higher concentrations thanks to a better account of excluded volume effects. Some results will be presented in section 5.4. In order to go beyond the idealized slit pore geometry typically considered in PB or cDFT studies, it is possible to use constant-potential molecular simulations with a realistic pore structure, as illustrated in Figure 17C. While MD simulations provide in principle the most accurate description of the molecular interactions among ions, solvent molecules, and electrodes, their computational cost prevents their systematic use to make predictions. In particular, the system sizes that can be simulated are small, and concentrations lower than 0.1 M are difficult to handle because the corresponding number of ions in the simulation box is too small to obtain statistically converged results within typical simulation times. This is obviously an issue to make direct predictions for the low-concentration electrolyte involved in CapMix or CDI, typically on the order of a few tens of mM.

5.3. Molecular Dynamics

The possibility to use nanoporous carbon electrodes (such as the CDCs used with organic electrolytes and ionic liquids in supercapacitors) for CapMix or CDI^308−310 and the known limitations of PB-like approaches to predict their properties due to the breakdown of the underlying approximations in such materials, together with the previous success of constant-potential MD simulations for supercapacitors, motivated Simoncelli et al. to investigate the predictive power of this latter approach with aqueous electrolytes.³⁰⁵ The setup used in these simulations is shown in Figure 17C. Compared to previous work on supercapacitors using coarse-grained models of ionic liquids dissolved in acetonitrile,²⁶⁸ the use of an all-atom model for water was necessary, which together with the smaller size of water molecules resulted in a significant increase in the total number of atoms.

MD simulations were performed for one CDC structure and for two concentrations, 0.5 and 1 M, i.e., only in the high-concentration regime for CapMix and CDI. The predicted capacitances, on the order of ∼110–120 F·g^–1, were in good agreement with experiments, and their slight increase with concentration was correctly captured. As expected (because the corresponding representation of the interface is too simple when the molecular nature of the ions and the solvent play an essential role), this was not the case with Debye–Hückel or PB theory, even when introducing a modified solvent permittivity due to confinement^311−315 or a maximum ion concentration to account for excluded volume effects.^{161,168,316,317} Using parameters from the literature, fitted to experimental data for similar materials (at lower salt concentrations),^308,318 the modified Donnan model underestimated the order of magnitude of the capacitance but correctly predicted a slight increase with concentration.

In order to make predictions for lower concentrations relevant for CapMix and CDI, for which it was not possible to perform MD simulations, Simoncelli et al. parametrized a modified Donnan model on their simulation results at high concentrations. The values of the capacitance extrapolated at lower concentration using this model were in relatively good agreement with the experiments, available down to 50 mM. The mD model parametrized to reproduce the MD capacitance at high concentration also allowed for the consideration of the salt adsorption capacity (relevant for CDI) over the whole concentration range, after checking that it reasonably predicted the ones determined from the MD simulations at high concentration.

MD simulations further provide microscopic insights into the structure of the electrolyte inside the nanopores. It was found in ref (305) that the desolvation of the ions was quite limited compared to observations with organic ions dissolved in acetonitrile.²⁶⁸ The same conclusion was reached in a later study by Ganfoud et al., who observed that only ∼10% of Na⁺ cations lose 1 molecule of their first solvation shell inside the nanopores of CDC, while desolvation is more pronounced with Cl^– anions, which may lose 1–2 molecules in order to make direct contact with the carbon surface.³¹⁹ Such a desolvation was found to be even more limited on graphite surfaces, which can serve as model of carbon materials with wider pores.^282,319

Overall, the results from these studies confirmed both the potential of CDC electrodes for CapMix and CDI applications and that of classical MD to investigate aqueous electrolytes in these materials. Because the electrolyte (sea or river water) cannot be changed as for energy storage applications, it might be useful to study the influence on other parameters, e.g., the role of surface functionalization³²⁰ to optimize the performance of the processes. However, as mentioned above, the computational cost of such MD simulations prevents their use for systematic studies or to make predictions at low concentrations. In order to go beyond the parametrization of a modified Donnan on MD at high concentration to extrapolate to the low concentration regime relevant for CapMix and CDI, one needs descriptions capturing the molecular details of the electrolyte and its interactions with the disordered nanoporous electrodes. As in the previously discussed case of supercapacitors, cDFT proves to be an appropriate alternative.

5.4. Density Functional Theory

The first investigation of the CapMix process with cDFT was carried out by Boon and van Roij, using a simple functional with a mean-field treatment of electrostatics and a lattice-gas-like treatment of the steric effects,³⁰² a level of theory equivalent to the modified PB method.¹⁶¹ The porous electrode is modeled by two parallel walls bearing the same uniform charge density, and the gap between them is filled by the inhomogeneous electrolyte immersed in an implicit dielectric solvent (see Figure 17A). As described previously, taking into account the steric effect corrects some known defects of the GC model. For example, at high surface charge density it prevents the too large condensation of counterions, and the surface potential increases much more strongly with the surface charge density than the logarithmic behavior predicted by the GC model.

Using thermodynamic arguments, they draw an analogy between the electrical work produced by the EDL capacitors and the mechanical work produced by a heat engine. With this analogy in mind, they proposed that a Carnot-like cycle would be more efficient than the one proposed by Brogioli, producing more work per ion exchanged from the sea to the river. This cycle consists of replacing branches 2 and 4 of the original cycle displayed in Figure 16B, which are flushing of the solution at a constant electrode charge, with the same operations at a constant number of ions. They then carried out a detailed study of the energetic performance of the Brogioli and of the Carnot-like cycles using cDFT, considering high and low salt concentrations of 0.6 and 0.024 M, respectively, and several pairs of high and low surface charge. Note that such a dilute concentration is out of reach for MD and MC simulation. The analysis confirms that the Carnot-like cycle provides more work per exchanged ion than the original Brogioli cycle, even though the latter offers more work per cycle. It is however difficult to make quantitative comparisons because at comparable electrostatic potentials, the charge density in Brogioli’s experiments is almost 2 orders of magnitude smaller than the theoretical estimates.

Härtel et al. studied the same system with a more evolved functional for the restricted primitive model,³⁰⁴i.e., identical charged hard spheres of opposite charge immersed in a dielectric medium. The excess functional now takes the form of eqs 3 and 4 with the electrostatic correlations described using the solution of the Ornstein–Zernike equation supplemented with the mean spherical approximation (MSA) closure.^72,197 A detailed comparison of the performance of this functional with respect to Brownian dynamics in the context of electrode/electrolyte interfaces can be found in ref (321). The electrode potential is imposed as a boundary condition for the Poisson equation, which is solved alongside functional minimization to determine the ionic density profiles and the electrode charge.

The voltage rise at fixed electrode charge, ΔΨ(Q), between the dilute and the concentrated electrolytes for a given electrode charge Q is directly related to the amount of blue energy that can be harvested. This quantity reaches a plateau at high electrode charge density for the two pore sizes investigated, 2 and 8 Å. This plateau is properly captured by all the different level of theories considered in this study, ranging from PB to cDFT with MSA treatment of electrostatic correlations. When steric effects are included, the value of the plateau rises by 30%. Interestingly, when the dependency of the solvent dielectric constant on the salt concentration is taken into account, the evolution of the voltage rise with the electrode charge is no longer monotonic and a maximum is reached at intermediate charges. In the context of CapMix or CDI, this means that devices could be optimized by an adequate choice of the operating voltage.

Another direction is to exploit the effect of temperature. Van Roij et al. explored this idea in a series of publications combining thermodynamic considerations and cDFT calculations.^322−324 These studies predict in particular³¹⁴ an increase by a factor of 2 of the energy extracted by the CapMix device if the dilute source is heated from 10 to 50 °C. The authors therefore proposed to take advantage of this effect to build a heat-to-current converter to harvest waste energy.³²³ As opposed to CapMix, in such a process it is no longer necessary to change the solution filling the cell and the same sealed device is charged and discharged at different temperatures.

Kong et al. also used cDFT to describe the CapMix device, considering a smooth hard slit pore of width H filled by an electrolyte modeled by the primitive model.³²⁵ The functional includes correlation through FMT to describe the steric effect and MSA to account for the electrostatic correlations.³²⁶ In this study, the effects of the pore size H and the charging potential Ψ on the extracted energy per cycle and per exchanged ion are investigated systematically. The predictions of Gouy–Chapman and cDFT agree well for large pores, but it is no longer the case when the width of the pore becomes smaller than 2 nm. The discrepancy increases with the applied potential. Interestingly, the efficiency and the extracted energy predicted by cDFT reaches a maximum at intermediate applied potential values for pores smaller than ∼2 nm. For a given pore size, the potential maximizing the extracted energy per ion exchanged and the one maximizing the extracted energy per cycle differ. These optimal charging potentials are also very sensitive to the pore size. For this system, the optimal pore size is around 2 nm because the overall maximum value of the extracted energy per cycle is reached for this width.

Lian et al. analyzed the effect of the electrode hydrophilicity on the CapMix cycle using the same functional in ref (327). The hydrophilicity of the electrode surface is accounted for by modifying the dielectric constant in the vicinity of the electrode³¹⁴ as

9

where z is the distance to the closest electrode plane and z^DDS = 0.5σ or 0.52σ for a hydrophilic or hydrophobic surface, respectively, with σ the ion diameter (the DDS superscript refers to dielectric dividing surface³¹⁴). The predicted surface charge as a function of the applied potential is reduced when the electrode becomes more hydrophobic. Regarding the differential capacitance, the predicted shapes are the same regardless of the hydrophilicity of the electrode, but the magnitude is reduced in the case of the hydrophobic surface. The same trend is observed for the work extracted by the CapMix cycle as a function of the electrode charge. The curves have the same shape with a maximum located at the same position, but hydrophilic electrodes allow for the extraction of more energy than the hydrophobic ones. This is in agreement with experiments³²⁸ and a possible route for optimizing the process.

The same group investigated the capacitive energy extraction using electrodes consisting of several (from 1 to 6) layers of graphene.³²⁹ The graphene electrodes are still modeled by hard slit pores, and their molecular nature is fully neglected, while the ions are described as charged hard spheres and the solvent as an explicit dipolar hard dimer,³³⁰ using the MSA functional to capture electrostatic correlations. In addition, a quantum calculation is done alongside the cDFT one, using an implicit solvation model to estimate the quantum capacitance of the electrodes.³³¹ The charge on the electrode is fixed, and two independent calculations are performed: cDFT to obtain the potential drop across the EDL and electronic DFT to obtain the one due to the quantum capacitance. The total capacitance of the interface, C_tot, is then obtained according to eq 5. The EDL capacitance is not affected by the number of layers of graphene, while the quantum capacitance increases with the number of layers. This results in a change of the shape of the differential capacitance as a function of the charging potential when the number of layers of graphene increases. For the single-layer graphene, C_Q is small compared to C_EDL, so that the total capacitance resembles the quantum one and the profile is “V-shaped”. When the number of graphene layers increases, C_Q becomes larger than C_EDL, and the total capacitance resembles the latter, leading to a camel shape. Overall the total capacitance increases with the number of layers and tends to converge beyond 4–5 layers. The potential rise when salty water is replaced by dilute water reaches a maximum for an optimal value of applied voltage whatever the number of graphene layers. The maximum value of potential rise hardly depends on this number, but the applied potential at which it is reached does. Adding layers decreases the optimal potential, again with a convergence with 4–5 layers. Similar conclusions are drawn for the amount of extracted energy: it reaches a maximum at intermediate charging potential, and the corresponding potential decreases when the number of layers increases. More interestingly, the maximum value of the extracted work increases by 60% when the number of graphene layers increases from 1 to 6.

6. Dynamical Processes in Supercapacitors

Because the main advantage of supercapacitors compared to batteries is their ability to deliver large power and their corresponding fast charge/discharge,³⁴ several theoretical strategies have also been developed to understand the dynamical processes occurring inside the electrodes. As for thermodynamic and structural properties, these approaches include continuous models, cDFT, and molecular simulations so as to cover the relevant range of length and time scales. In order to make the link with electrochemical experiments, usually quantified by the electrochemical impedance of the cell as a function of frequency, Z(ω), several studies also tried to bridge scales by devising equivalent circuit models from their results at a given scale and level of description.

6.1. Continuous Models

The dynamics of EDLs in capacitors can be described at the mean-field level within the framework of Poisson–Nernst–Planck (PNP) theory. This description couples the Poisson equation for the electric potential ψ:

10

with ρ_el = ∑_iz_ieρ_i the local charge density, expressed here from the concentrations ρ_i of the ionic species with valencies z_i, and ϵ_r the dielectric constant of the solvent, with a conservation law for the ionic species, taking into account their diffusion due to local concentration gradients and their migration under the effect of the local electric field:

11

with D_i the ionic diffusion coefficients. At equilibrium, this reduces to PB theory. Bazant, Thornton, and Ajdari provided in ref (332) a thorough discussion of the diffuse-charge dynamics in parallel-plate capacitors based on the above PNP equations, including a historical review and the link with equivalent circuit models—in particular, the RC circuit with capacitors describing the EDL in series with a resistance describing the bulk electrolyte. They emphasized in particular the role of the characteristic time 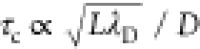, with L the distance between the electrodes, λ_D the Debye screening length, and D the ionic diffusivity, which corresponds to the RC charging time in the limit of thin EDLs, and they provided a correction to this limit expression valid in the linear response regime (i.e., small applied voltages). They further discussed nonlinear effects and set directions beyond the assumptions considered in their work, namely, 1D geometry, binary symmetric electrolytes with identical diffusivities, and no Faradaic reactions at the surface of the electrodes. The effect of curvature was recently investigated at the same level of description by Janssen in ref (333), who considered spherical and cylindrical electrodes and showed in particular that the ionic relaxation time scales depend explicitly on the radii of both electrodes and not only on their difference.

The case of porous electrodes, relevant for supercapacitors as well as for blue energy and desalination, was investigated under the assumption of thin double layers compared to the pore size by Biesheuvel and Bazant in ref (334). This assumption allows for a simplified treatment of transport inside the pores, where the thin layers are introduced as boundary terms for the mass and charge fluxes inside the pores (again in the case of binary symmetric electrolytes with identical diffusivities and no Faradaic reactions), supplemented by a GCS model of the double layer and overall mass and charge conservation equations. The authors evidenced two limiting regimes associated with different time scales. On the one hand, for small voltages and/or early times, they discuss a so-called “supercapacitor” regime, in which charge evolves diffusively and can be described by the transmission line model (TLM) often used to model charge dynamics in porous media,^2,335 with a corresponding rescaled RC time. On the other hand, for large voltages and long times, a so-called “desalination” regime is used, where the salt concentration within the porous medium deviates significantly from its initial value. Recently, the link between electrolyte dynamics in porous media and the TLM has also been investigated in simplified 1D geometries by Janssen, who considered the effect of the finite length of the pore,³³⁶ and by Lian et al., who explicitly considered stacks of slabs with finite width.³³⁷ This last study found for example that at high voltage, the charging slows down and deviates from the TLM (which describes well the behavior at low voltage), with two relaxation time scales: one is related to the RC time and the number of stacked electrodes, and the other is related to the diffusive adsorption of salt from the bulk electrolyte to the porous electrodes.

The work of Biesheuvel and Bazant³³⁴ inspired various extensions coupling conservation equations and constitutive equations corresponding, e.g., to the modified Donnan model presented in section 5 for the exchange of ions between micropores and larger pores acting as reservoirs. This simplified description of the system pragmatically captures the essential features and can be parametrized to reproduce in particular the evolution of the adsorbed salt and the electrode charge during CDI as a function of the half-cycle time.^307,339,340 The theory can also take into account electrochemical reactions at the surface of the electrodes and their kinetics via the Frumkin–Butler–Volmer equation.^341,342 The flexibility of this approach offers a convenient framework to analyze experimental data in complex processes such as CDI beyond the traditional equivalent circuit models such as the TLM used for supercapacitors, even though such models remain an important component even in the context of CDI.²⁹⁹

While the PNP equations neglect the coupling with the solvent dynamics, which results in so-called electrokinetic effects, such coupling can be captured at the same level of theory by coupling the PNP equations, including an advection term ρ_ku, with u the local velocity of the fluid, in the ionic fluxes and describing the evolution of u via the Navier–Stokes equation, including the local electric force density −ρ_el∇ψ. This PNP–Stokes framework is the cornerstone for the study of electrokinetic effects such as electro-osmosis, i.e., the fluid flow induced by an applied electric field due to the net charge within EDLs, which develops even in charge-neutral regions far from the surfaces because of momentum diffusion. Fluid flow usually does not play a major role in the charge/discharge of capacitors because of the geometry of electrochemical cells, with electrodes imposing a vanishing normal component of the fluid velocity at their surface. In more complex geometries, electrokinetic effects in capacitors can be investigated by solving the PNP–Stokes equations numerically or by using other numerical approaches, such as lattice Boltzmann simulations capturing electrokinetic couplings as well as other phenomena such as adsorption/desorption on surfaces.^343−349 A recent study by Asta et al. introduced a modification of the electrostatic boundary conditions in such lattice Boltzmann electrokinetics simulations to investigate the charging dynamics in nanoscale capacitors in various geometries, as well as electro-osmotic flows induced by additional applied electric fields parallel to the electrode surfaces in charged capacitors.³⁵⁰ Such an approach is in fact not limited, at least in principle, to the PNP–Stokes description of the electrolyte solution, because it relies on a more general nonequilibrium thermodynamics formulation of the evolution of the composition due to local thermodynamic gradients, which we now describe briefly to illustrate its applications to the charging dynamics in supercapacitors.

6.2. Time-Dependent cDFT

cDFT, already presented in the previous sections for the study of structural and thermodynamic properties, can also be extended to describe the evolution of the density fields. Such a time-dependent cDFT (TDcDFT) is generally expressed in the simple form of a conservation equation:³⁵¹

12

where M_i is the mobility of species i and the functional derivative on the right-hand side expresses the local chemical potential μ_i(r), which can be computed for a given choice of the free energy functional. For sufficiently dilute solutions, the mobility can be taken as M_i = D_i/k_BT, with D_i the diffusion coefficient, and the free energy functional can be limited to the ideal and mean-field electrostatic contributions. Equation 12 then reduces to the PNP eqs 10 and 11. TDcDFT provides a generic framework to go beyond this simple approximation by introducing more physical ingredients, such as excluded volume, via the free energy functional—and in principle also in the mobility, even though this other aspect is typically less explored.

Jiang et al.(338) used TDcDFT to investigate the charging properties of RTIL-based parallel plate capacitors with various interelectrode distances, ranging from a few to a few tens of molecular diameters. Using a functional for restricted primitive models, the authors studied the evolution of the electrode charge in response to an applied voltage, as well as the corresponding evolution of the ionic density profiles. They found the charging dynamics to be highly sensitive to the interelectrode distance: The evolution of the charge can be monotonic as for the usual equivalent RC circuit model, but also non-monotonic, reaching a maximum before decaying exponentially toward the equilibrium value. More surprisingly, in some cases, the ionic density profiles lead to an effective surface charge density with a sign opposite to the one expected from the applied voltage. The different behaviors are illustrated in Figure 18A. A systematic analysis of the influence of the interelectrode distance L showed that the type of charging dynamics can be correlated with the value of the steady-state surface charge density (i.e., after the transient regime), Q_L, with respect to the one for an infinite separation, Q_∞, represented as a dotted blue line in Figure 18B. The charging dynamics is monotonic when Q_L > Q_∞ and is nonmonotonic otherwise.

Figure 18.

Charging dynamics of parallel plate EDLCs. (A) Evolution of surface charge density with time for different cell widths. Blue, red, and black curves correspond to the normal charging scenario; the purple and yellow curves exhibit a non-monotonic charging, whereas there is a charge inversion for the cyan curve. (B) Equilibrium surface charge density versus the cell width predicted by TDcDFT. The blue dotted line is the asymptotic limit of the effective surface charge density at infinite electrode separation. Adapted with permission from ref (338). Copyright 2014 American Chemical Society.

The same group also studied the effect of dispersion interactions for sufficiently large pores (20 ionic diameters) to avoid the above-mentioned effect of the interelectrode distance.³⁵² In this regime, the charging dynamics are monotonic in the absence of dispersion. Including dispersion interactions between ions leads to a nonmonotonic charging dynamics, with a quick rise to a maximum followed by an exponential decay toward the equilibrium value. In contrast, dispersion interactions between ions and the electrode walls do not alter the monotonic nature of the charging dynamics (at least over the range of considered values).

Finally, the potential profiles obtained from cDFT can also be combined with the Stokes equation to predict the stationary electro-osmotic flow in simple geometries and then be introduced in an effective medium approximation to capture the effects of the pore size distribution and network connectivity. In agreement with earlier work by Obliger et al. based on lattice Boltzmann simulations corresponding to the PNP–Stokes description of the fluid (see section 6.1) combined by a pore network model approach,³⁴⁸ the cDFT-Stokes study of Lian et al.(353) emphasized the difference between the transport through a single pore and that between a porous network. Even though this possibility has not been explored in the context of supercapacitors, one can go beyond such a coupling between cDFT (for the ionic and potential profiles) and Stokes equation (for hydrodynamics) to treat both consistently at the level of kinetic theory (and corresponding implementation in lattice Boltzmann algorithms).^354,355

6.3. Molecular Dynamics

Mean-field and cDFT-based techniques thus provide most of the key dynamic properties of EDLCs and blue energy/desalination devices for generic electrolytes and well-controlled (simplified) electrode geometries. However, they cannot capture molecular-scale effects occurring when the ionic adsorption properties and their interplay with diffusion become dominant, which is typically the case in complex nanoporous carbons. Yet, compared to the structural observables, dynamical ones are much more difficult to compute using classical MD (and impossible in the case of MC because of the absence of time). It typically requires much longer sampling times to obtain converged properties. In addition, compared to bulk liquids in which it is possible to efficiently compute properties such as the diffusion coefficient, the electrical conductivity, or the viscosity from equilibrium simulations using suitable time-correlation functions (e.g., via Green–Kubo relations), in EDLC simulations the presence of the two phases and of interfaces makes such approaches much more difficult.

As a consequence of these difficulties, the earliest MD studies on the dynamics of liquids inside nanoporous electrodes employed primitive or coarse-grained models for the ions in order to reduce the simulation times and obtain longer trajectories.^285,357 It is first interesting to focus on the case of slit-like pores. Kondrat et al. observed drastic variations in the composition (and thus in the structure) of the liquid depending on the applied voltage.²⁸⁵ At both null and large potentials, the ions tend to order inside the pore, which results in very slow dynamics, while for intermediate voltages, the structure is fluid-like. Intriguingly, the diffusion coefficients could then reach values larger (by 1 order of magnitude) than in the bulk electrolyte, because of the drastic change in the ionic concentrations. In addition to these structural changes, dynamical properties are affected by collective effects, such as overfilling/defilling events. This behavior was further confirmed by performing computer simulations of cyclic voltammetry experiments.³⁵⁸ In this study, in which a coarse-grained model was used for the ionic liquid instead of a primitive one, it was shown that charge storage at high scan rates is dominated by counterions while the contribution by co-ions is marginal or negative because of crowding effects. At low scan rates, the charging mechanism is less affected, resulting in a larger charge accumulated at the surface of the electrode.

In a further study focusing on the effect of the slit-pore length on the structure of the adsorbed fluid, the latter was shown to depend on the charging method in MD simulations.³⁵⁹ Applying abruptly a voltage or increasing its value linearly did not lead to the same charging dynamics. Indeed, the first case resulted in large amounts of co-ions trapped at the entrance of the pore, an effect prevented when the voltage changes more smoothly. This approach was investigated further, and an optimal voltage sweep was deduced, resulting in an overall much faster charging dynamics for the system.³⁶⁰ This effect is not reversible because in the case of the discharge, an abrupt change of potential resulted in faster dynamics. This approach was verified experimentally.³⁶¹ Finally, these authors proposed the use of nonlinear voltage sweeps to further increase the power density of the devices.

The importance of the rate at which the voltage is increased was also confirmed using a more elaborate atomistic model for the ionic liquid EMIM-BF₄.³⁶² Again in a slit-shape porous structure, Pak and Hwang have indeed shown by adjusting the voltage scan rate that the final amount of accumulated charge depends on the extent of crowding effects. In particular, upon rapid charging, the formation of a dense neutral region at the entrance of the pore hinders the fast accumulation of counterions.

We next move on to the case of complex nanoporous electrodes, for which the variations are much less pronounced, probably because of the disorder of the structure. In a first study performed on three different CDC structures,¹⁰⁵ highly heterogeneous charging dynamics were observed, with some pores charging very quickly and others much more progressively.³⁵⁷ The variation of the charge with time was used to parametrize an equivalent circuit model using four physical parameters, namely, the resistivity in the bulk liquid and inside the pores and the capacitance of two successive layers of the porous electrodes (see a simulation snapshot and the corresponding circuit in Figure 19A). This approach allowed for extrapolation of the molecular simulation results to macroscale devices, yielding charging times of the order of a second for a typical electrode width of 100 μm. Although in good agreement with experiments, this comparison remained indirect, so that further simulations were performed on a system in parallel to experiments.³⁶³ In-pore diffusivities were computed for the ions, from which the resistivity of the liquid was determined (and not fitted as in the equivalent circuit model mentioned above). The latter was directly compared to results extracted from electrochemical impedance measurements, yielding almost quantitative agreement. When injecting back the calculated parameters into the equivalent circuit model, the latter showed very good agreement with previous charging simulations in which the potential was abruptly turned on to a finite value as shown in Figure 19B, further confirming the validity of the corresponding model.³⁵⁶

Figure 19.

Equivalent circuit models. (A) Typical snapshot of a simulation cell, with the corresponding equivalent circuit model. Blue, acetonitrile molecules; red, BMIM⁺ cations; green, PF₆^– anions; and turquoise, carbon electrodes. In the equivalent circuit model, R_bulk is the resistance of the electrolyte in the bulk region, while R_l and C_l are the resistance and the capacitance inside the electrodes, respectively. (B) Total charge accumulated on the positive electrode during a charge–discharge–charge cycle obtained directly from MD simulations (black) and using the equivalent circuit model (red). Reproduced with permission from ref (356). Copyright 2016 Elsevier.

The analysis of charging mechanisms then showed that it was characterized by a hierarchy of time scales arising from ion confinement, solvation, and electrosorption effects. For the adsorption, the importance of the nature of the electrolyte (organic vs ionic liquid) and of the local confinement of the ions on the carbon structure was also investigated by computing site-dependent adsorption lifetimes.³⁶⁴

7. Concluding Remarks

The scientific approach to studying EDLCs has greatly evolved over the past decades. Although materials synthesis and electrochemical characterization remain at the core of this research field, they are now complemented by a wide range of in situ spectroscopic techniques as well as theoretical and simulation methods. This combination has led to a much better understanding of the physical phenomena at play and thus to the selection of systems with more efficient storage mechanisms.³⁷ This review focused on microscopic-scale descriptions, for which the most used techniques are molecular dynamics and Monte Carlo simulations and classical density functional theory. A large body of work was dedicated over the years to adapt these techniques to the case of electrochemical interfaces. They now allow much structural, dynamical, and thermodynamical information to be obtained. Some properties, such as the interfacial capacitance, are directly comparable to experiments, but some are otherwise inaccessible to most experimental techniques.

Comparison with experiments allows for the (in)validation of theoretical approaches. In most cases, the agreement is at least qualitative, thus validating the choice of the models and of the underlying approximations or assumptions. Quantitative agreement could even be obtained in some studies. This requires a careful parametrization of the simulations and entails a high computational cost. The main added-value of the simulations is to provide an accurate picture of the microscopic structure of the liquid adsorbed at the surface and its link with the charge accumulated on the electrode. Simulations have thus not only allowed for the rationalization of previous experimental results, such as the increase of the capacitance in nanoporous carbons,⁴⁶ but also suggested conditions to optimize the performance, such as the choice of particular pore geometries,²⁶⁸ the use of ionophobic pores,²⁸⁵ or the application of different charging protocols.³⁶¹ Although these suggestions may not easily be realized experimentally, they provide interesting methods for future improvements.

Despite theses successes, many challenges are still ahead for a complete modeling of EDLC devices in future years. In the case of carbon-based EDLCs, the accessible system size does not allow for the simulation of many experimental structures. Enhancing the cDFT models based on MD studies could provide a strategy to bridge this dimensional gap. In practice, there are two difficulties to address. First, the current functionals allow simulating generic electrolytes because they are mainly based on the primitive model. In order to gain more insight into specific effects linked to the chemical nature of the ions, additional molecular ingredients need to be included in the functionals. Second, from a technical point of view, the main difficulty for simulating extended systems (such as the realistic structures of nanoporous carbons shown above) will be the reduction of the memory. In contrast to MD, which involves large CPU resources but for which software is now tuned to reduce the memory footprint, cDFT is a grid-based method, so this is currently a strong bottleneck.

In the case of MD, even though significant effort has been devoted to accurately simulating the electrodes, some limitations remain. For example, better accounting for the electronic structure would certainly yield improved capacitance prediction, while introducing the flexibility of the bonds in electrode models would enable the study of mechanical aspects involved during the charge/discharge of the devices. The advanced models based on the Thomas–Fermi representation^130,133 or on the tight-binding approximation^134,135 provide promising leads in that direction, but to date, very little progress has been made in order to parametrize accurate van der Waals interactions in force fields for the electrodes. On the liquid side, the models were enhanced over the years, shifting from coarse-grained or simplified force fields to polarizable ones. In the case where the polarization is handled using induced dipoles, there is a need for accessible MD software allowing the coupling between the self-consistent calculation of the dipoles of the liquid and the fluctuating charge models for the electrodes. Finally, even though very few chemical reactions are supposed to occur in EDLCs, they can be at the origin of the capacitance fading over time, but modeling them is completely beyond the range of current methods. Many studies are currently devoted to the modeling of the formation of the solid electrolyte interphase at the surface of battery electrodes.^366,367 Research on supercapacitors can benefit from these advances by adapting the approach to the typical electrolytes involved in such devices.

However, the main challenges concern the simulation of more complex materials, which generally display pseudocapacitive signatures.³⁶⁸ Although this review focused on the study of carbon-based systems, a few recent studies have already considered other nanoporous materials, such as metal–organic frameworks³⁶⁹ or other 2D materials such as MoS₂.³⁷⁰ Among the new families of materials, MXenes appear to be very promising because of their excellent electrochemical properties.³⁷¹ Many different compounds may be obtained by changing the synthesis method. Besides the change of composition, it is for example possible to tune the surface chemistry³⁷² by changing the surface elements, as shown in Figure 20. Nevertheless, simulations on such multicomponent compounds employed so far similar methods as the ones presented here for carbon materials. The peculiar effects due to the different chemical nature of the atoms were not taken into account explicitly; therefore, further model refinements would certainly lead to improved accuracy. Taking the simple example of MoS₂, the partial charges carried by the Mo and S atoms, as well as their ability to fluctuate to maintain the constant potential, should be different in order to reproduce correctly the interactions with the liquid electrolyte. In the case of metal–organic frameworks or MXenes, some atomic species should even not participate in the metallic character, which renders the adaptation of constant potential methods even more challenging.

Figure 20.

Electrolytes and electrode structures investigated in a recent study of MXene-based supercapacitors. In particular, the surface termination of the electrode material (with F, O, or OH groups) may impact the energy storage properties. Reproduced with permission from ref (365). Copyright 2020 Elsevier.

Even more complex is the case of transition metal oxides (MnO₂, RuO₂) because they employ aqueous electrolytes and their redox properties are strongly affected by proton transfer reactions occurring at the surface. For such systems, classical MD is probably not well-adapted and it is necessary to use more involved methods such as DFT-based MD (in which the atomic forces are obtained from a DFT calculation at each time step). First steps were made in that direction.^373−375 In these calculations, the interface is polarized using the same finite-field method mentioned above for controlling the potential of classical electrodes using three-dimensional periodic boundary conditions.^139,140 However, the size of the systems will again be a strongly limiting factor because DFT-based MD can be used only for systems of a few hundred atoms (i.e., a few thousand electrons), which is much smaller than the dimensions of the classical MD cells employed to simulate supercapacitors. A possibility to overcome this difficulty could be the use of machine-learned force fields with DFT accuracy for the electrolytes, but these are still in their infancy.³⁷⁶

Recent experimental improvements have also been reported on the electrolyte side. For example, the introduction of water-in-salts,³⁷⁷ which are highly concentrated aqueous electrolytes, opens the way toward aqueous devices with better performance. They are characterized by the formation of complex nanostructures in the liquid state,^378,379 and an interesting interplay between these structures and the porosity of EDLC electrodes has been observed experimentally,³⁸⁰ which remains to be investigated using molecular simulations. Biredox ionic liquids also are a promising lead for devices with increased energy densities.³⁸¹ In such systems, the difficulty for simulations is to consider explicitly the redox reactions³⁸² and to simulate the oxidized and reduced species of the couple with similar accuracy.³⁸³ Conventional MD methods do not allow accounting for such reactive events easily, so that approaches based on the surface-hopping methodology have been proposed to tackle this problem.^384,385 In conclusion, the study of EDLCs will certainly remain an exciting field with significant room for methological developments of microscopic simulations over the next decade.

Glossary

Abbreviations

EDL

electric double layer

EDLC

electrochemical double-layer capacitor

CDC

carbide-derived carbon

cDFT

classical density functional theory

FMT

fundamental measure theory

CapMix

capacitive mixing

CDI

capacitive deionization

MF

mean field

GCS

Gouy–Chapman-Stern

MD

molecular dynamics

MC

Monte Carlo

PB

Poisson–Boltzmann

RPM

restricted primitive model

MSA

mean spherical approximation

NMR

nuclear magnetic resonance

EQCM

electrochemical quartz crystal microbalance

IR

infrared

mD

modified Donnan

PNP

Poisson–Nernst–Planck

TLM

transmission line model

TDcDFT

time-dependent classical density functional theory

Biographies

Guillaume Jeanmairet is a CNRS researcher at Sorbonne University (Paris). He graduated in Chemistry from the École Normale Supérieure in 2011 and received his Ph.D. in 2014 from the Université Pierre et Marie Curie (now Sorbonne University). He then spent two years as a postdoctoral researcher at the Max Planck Institute FKF (Stuttgart) with Ali Alavi before joining Sorbonne University for another postdoctoral contract after which he became a CNRS researcher. His research focuses on developing classical density functional theory to study solvation in molecular solvents and especially water. Lately, his interest shifted to the development of functionals able to describe aqueous electrolytes to study electrochemical devices.

Benjamin Rotenberg is a CNRS senior researcher at Sorbonne University (Paris). He graduated in Chemistry from the Ecole Normale Supérieure in 2004 and received his Ph.D. in 2007 from the Université Pierre et Marie Curie. He then joined the FOM Institute for Atomic and Molecular Physics (Amsterdam) as a postdoctoral fellow before starting as a CNRS researcher in 2008. He was a visiting professor/scholar at the Universities of Barcelona, Berkeley, and Freiburg, as well as in the Helmholtz Zentrum Berlin. He has received several awards, including the Grand Prix MG Schlumberger from the French Academy of Sciences in 2013, the Bronze medal of CNRS in 2015, and a Bessel research award from the Alexander von Humboldt foundation in 2017. His research focuses on multiscale modeling of charged interfaces, in particular in the fields of energy and the environment, as well as methodological developments for numerical simulations.

Mathieu Salanne is professor at Sorbonne University (Paris) and a junior member of the Institut Universitaire de France (2020–2025). He graduated in chemical engineering from Chimie ParisTech in 2004. He obtained his Ph.D. in 2006 at Sorbonne University, under the supervision of Pierre Turq and in strong collaboration with Paul Madden (University of Oxford). His research focuses on the molecular simulation of electrochemical systems. These are typically molten salts in the framework of their use in the future generation of nuclear reactors or supercapacitors which are high-power energy storage devices. To this end, he develops methods to allow realistic simulations of the systems, and he is the main developer of the molecular dynamics software MetalWalls.

The authors declare no competing financial interest.