Abstract
Adaptive measurement of change (AMC) is a psychometric method for measuring intra-individual change on one or more latent traits across testing occasions. Three hypothesis tests—a Z test, likelihood ratio test, and score ratio index—have demonstrated desirable statistical properties in this context, including low false positive rates and high true positive rates. However, the extant AMC research has assumed that the item parameter values in the simulated item banks were devoid of estimation error. This assumption is unrealistic for applied testing settings, where item parameters are estimated from a calibration sample before test administration. Using Monte Carlo simulation, this study evaluated the robustness of the common AMC hypothesis tests to the presence of item parameter estimation error when measuring omnibus change across four testing occasions. Results indicated that item parameter estimation error had at most a small effect on false positive rates and latent trait change recovery, and these effects were largely explained by the computerized adaptive testing item bank information functions. Differences in AMC performance as a function of item parameter estimation error and choice of hypothesis test were generally limited to simulees with particularly low or high latent trait values, where the item bank provided relatively lower information. These simulations highlight how AMC can accurately measure intra-individual change in the presence of item parameter estimation error when paired with an informative item bank. Limitations and future directions for AMC research are discussed.
Keywords: adaptive measurement of change, item parameter estimation error, computerized adaptive testing
Researchers and practitioners in the social sciences often seek to measure intra-individual change across multiple occasions. For example, a teacher might track whether students’ math or reading ability improved after a semester course, or a medical clinician might want to determine whether significant change in a patient’s reported symptoms has occurred following treatment. Traditional methods for measuring change, largely based on classical test theory (CTT), are commonly used in applied research, yet can be psychometrically flawed (Cronbach & Furby, 1970; Finkelman et al., 2010; O’Connor, 1972; Wang et al., 2020). For example, proposed change statistics like the reliable change index (Jacobson et al., 1984; Jacobson & Truax, 1991) generally depend upon the sample composition and reliability, and are thus unable to adequately identify significant intra-individual change between test administrations that is independent of the group in which an individual is embedded (Finkelman et al., 2010; Kim-Kang & Weiss, 2007, 2008; Wang et al., 2020). More modern methods to identify longitudinal individual change (e.g., Embretson’s, 1991, multidimensional Rasch model for learning and change) are also limited by restrictive item parameter assumptions and insufficient generalizability (Finkelman et al., 2010).
A viable psychometric alternative is adaptive measurement of change (AMC; Kim-Kang & Weiss, 2007, 2008; Weiss & Kingsbury, 1984), which determines whether a single individual has significantly changed on one or more latent traits across testing occasions. To achieve this goal, AMC uses the principles of item response theory (IRT) and computerized adaptive testing (CAT; Weiss, 1982). CAT tailors a test to an individual’s unique ability, and there is evidence (e.g., Weiss, 1982, 2004; Weiss & Kingsbury, 1984) that this method facilitates more efficient and precise measurements of the intended latent trait. CAT can either provide a latent trait ( ) point estimate, or can classify individuals into discrete categories (e.g., Pass/Fail). In particular, AMC uses a classification procedure wherein an individual’s trait estimates ( ) are compared across testing occasions, and the individual is categorized based on whether the differences among their estimates are “psychometrically significant.” 1 AMC first functions as an omnibus test, classifying whether individuals have changed across the full set of testing occasions. If significant change is indicated, post hoc analyses are necessary to pinpoint between which testing occasions the change occurred.
The efficacy of AMC thus largely depends upon the method’s ability to accurately determine if, and when, an individual’s has substantially changed. The extant literature on AMC implements null hypothesis significance testing methods to make these individual classifications. Specifically, for t testing occasions measuring the same , the null hypothesis denotes no differences among an individual’s estimates from these t test occasions. Then, the alternative hypothesis denotes a nonzero difference between at least two of the estimates (Finkelman et al., 2010; Wang & Weiss, 2018; Wang et al., 2020). Researchers have proposed several statistical tests to address these hypotheses, including variants of a Z test, a likelihood ratio test (LRT; Finkelman et al., 2010; Phadke, 2017; Wang & Weiss, 2018), and a score ratio index (SRI; Lee, 2015; Phadke, 2017; Wang & Weiss, 2018). Previous simulation studies provide evidence that these significance tests exhibit strong statistical properties across a variety of CAT applications, including the unidimensional two-occasion (Finkelman et al., 2010; Lee, 2015) and multi-occasion (Phadke, 2017) testing scenarios. 2
However, a significant limitation of these simulations is that all have assumed that the item parameter values in the examined item banks do not contain estimation error (Wang et al., 2020). Specifically, these studies designed their item banks by generating item parameters (e.g., difficulty, discrimination) with values drawn directly from a specified population distribution. This process strongly contrasts with CAT development in applied settings, where the test developers do not know the true parameter values. Instead, item banks are typically created by (a) developing a large set of items, (b) administering these items to a calibration sample, and (c) using the responses to then estimate the item parameter values (Embretson & Reise, 2000). This estimation process inherently adds error to the item bank. Thus, assuming that item banks contain true rather than estimated item parameter values limits the generalizability of previous AMC hypothesis test research.
Item parameter estimation error can be particularly problematic for ensuring adequate measurement quality in adaptive testing. There is compelling evidence, both in adaptive (e.g., Patton et al., 2013; van der Linden & Glas, 2000) and nonadaptive testing contexts (e.g., Cheng & Yuan, 2010; Hambleton & Jones, 1994), that higher degrees of item parameter estimation error are associated with negatively biased standard errors. Consequently, spuriously small standard errors might lead researchers to overestimate both the accuracy of the estimates and the corresponding test information functions (Hambleton et al., 1993; Olea et al., 2012; Patton et al., 2013; van der Linden & Glas, 2000). Moreover, when the CAT termination criterion depends on the standard errors (e.g., the test terminates when the confidence interval is of a certain width), standard error deflation can cause variable-length CATs to stop prematurely (Patton et al., 2013). Importantly, the effects of item parameter estimation error are often exacerbated as the item bank’s calibration sample size decreases (e.g., Drasgow, 1989; Feuerstahler, 2018; Hambleton & Jones, 1994; Li & Lissitz, 2004; Swaminathan et al., 2003; Weiss & Von Minden, 2012; Yoes, 1995).
As noted above, the extant AMC literature has largely ignored the presence of estimation error when designing CAT item banks. However, because AMC hypothesis tests generally involve estimating and the associated standard error, it is plausible that item parameter estimation error could influence the performance of these hypothesis tests (Wang et al., 2020). For example, the Z-test statistic is based on the ratio of the difference between two estimates and the pooled standard error. Larger estimation error might spuriously increase the magnitude of this test statistic, leading to higher false positive rates. Understanding the relationship between item parameter estimation error and AMC hypothesis test performance will expand the efficacy and accurate implementation of this method across a broader range of test settings. Moreover, identifying the degree to which AMC hypothesis tests are robust to estimation error will highlight the necessary calibration sample sizes for facilitating quality measurement of intra-individual change.
Purpose
The present study addressed this gap in the AMC research by testing the robustness of three omnibus AMC hypothesis tests—the Z test, LRT, and SRI—to the presence of item parameter estimation error. Across a variety of testing conditions with four CAT administrations, two related research questions were examined. First, to what extent do errors in item parameter estimates affect the ability of the three AMC hypothesis tests to detect psychometrically significant individual change? Second, if item parameter estimation error influences the results of the hypothesis tests, what calibration sample size is necessary for accurately measuring intra-individual change with AMC?
Method
Omnibus AMC hypothesis test performance in the presence of item parameter estimation error was examined using three Monte Carlo simulations, with CATs administered at four testing occasions. Specifically, the simulations measured false and true positive rates, average test length, and change recovery when manipulating three design factors: (a) amount of item parameter estimation error, (b) magnitude of change between true values at each testing occasion, and (c) AMC hypothesis test.
The primary simulation, referred to as Simulation 1, introduced item parameter estimation error by estimating item parameters from an “error-free” item bank with calibration samples of varying sizes. Two additional simulations were conducted to examine the generalizability of the results from Simulation 1. Specifically, these simulations either modified the “error-free” (EF) item bank (Simulation 2) or the method of introducing estimation error (Simulation 3).
Simulation 1
Item Parameter Generation
The Simulation 1 item bank was generated with 300 dichotomous items from the unidimensional three-parameter logistic model (3PLM; Birnbaum, 1986) with . The item parameters—discrimination (a), difficulty (b), and pseudo-guessing (c)—were randomly drawn from specified distributions to construct an item bank with a moderately high and relatively flat bank information function. The a parameters were drawn from a truncated N(1.25, 0.25) distribution with bounds at 0.50 and 2.0. A truncated normal distribution was used to mirror a typical CAT bank, where items with extremely small or large discriminations are often removed (Crichton, 1981). The b parameters were drawn from a sequence of uniform distributions ranging from −3.0 to 3.0. This sequence was segmented into 12 intervals of width 0.50 (i.e., [−3.0, −2.5], [−2.5, −2.0], . . . , [2.0, 2.5], [2.5, 3.0]). Within each interval, 25 realizations of a uniform distribution with the corresponding bounds were generated (Finkelman et al., 2010). The c parameters were realizations of a U[0.00, 0.25] distribution (Sahin & Weiss, 2015). In this EF item bank consisting of the 300 true (i.e., not estimated) item parameters, the means and standard deviations for the a, b, and c parameters were 1.21 (0.40), 0.00 (1.73), and 0.12 (0.07), respectively.
Item Parameter Estimation
Using the EF item bank, varying degrees of estimation error were generated in Simulation 1 by systematically decreasing the calibration sample size for each estimated item bank. This method of incorporating item parameter estimation error has been commonly used in previous research (e.g., Cheng & Yuan, 2010; Feuerstahler, 2018; Kaskowitz & De Ayala, 2001; Patton et al., 2014). Four calibration sample sizes were selected, comprising either 500, 750, 1,000, or 2,500 simulees. Based on common guidelines for accurate 3PLM item parameter estimation (e.g., De Ayala, 2013; Hulin et al., 1982; Lord, 1968; Sahin & Anil, 2017), these sample sizes were chosen to construct a range of simulees from arguably too small (N = 500) to sufficiently large (N = 2,500).
To create each estimated item bank, response vectors based on the true item and person parameter values were first generated. The values for simulees in the calibration samples were random realizations of the standard normal distribution. The calibration samples were independent, such that a new set of simulees was generated for each calibration sample rather than selecting simulees from one large sample. To generate each item response, the probability of a simulee’s correct response to the given item, , was calculated using the 3PLM with the simulee’s true θ value and the true item parameters (i.e., from the EF item bank). A single realization of the U[0,1] distribution was subsequently generated; a simulee was considered to have a correct response (denoted 1) if was greater than the randomly generated number, and a score of 0 was assigned otherwise. Note that although the true item parameter values were used to simulate the item responses, the estimated item parameters were used for subsequent CAT item selection, estimation, and AMC hypothesis testing.
Using the simulated response vectors for each calibration sample, the three item parameter values (a, b, and c) were estimated for each of the 300 items. Item parameter estimation was completed using an expectation-maximization (EM) algorithm (Bock & Aitkin, 1981) with 62 quadrature points and the nlminb optimizer (as implemented in the R package mirt; Chalmers, 2012). Parameter bounds were used for the intercept and slope values (−4 < d < 4 and 0.5 < a < 2.5, respectively) to facilitate convergence. Note that mirt by default uses the slope-intercept parameterization; these parameters were converted to the traditional IRT parameterization (a, b, and c) prior to subsequent analyses. Parameter bounds also helped produce more realistic item banks, with estimated parameter values that better align with those seen in practice (e.g., Reise, 2014).
Table 1 presents the item parameter recovery statistics within each estimated item bank in Simulation 1. Supporting past research on item parameter estimation error (e.g., Drasgow, 1989; Patton et al., 2013, 2014; Swaminathan et al., 2003; Weiss & Von Minden, 2012; Yoes, 1995), the bias and root mean-square error (RMSE) for all three parameters decreased as the calibration sample size increased. For example, the RMSE for a decreased from 0.399 to 0.176 as the calibration sample size increased from 500 to 2,500 simulees. Furthermore, the correlations between the true and estimated item parameters increased for larger calibration sample sizes. Although some of the recovery statistics indicated relatively poorer item parameter recovery than in other simulation studies, the estimated item banks were sufficient for addressing the primary research aim: examining AMC’s performance in the presence of item parameter estimation error.
Table 1.
Item Parameter Recovery Statistics for Item Banks Estimated With Varying Degrees of Item Parameter Estimation Error.
| Item bank | Bias | RMSE | Correlations | ||||||
|---|---|---|---|---|---|---|---|---|---|
| a | b | c | a | b | c | a | b | c | |
| Simulation 1 | |||||||||
| 500 | 0.131 | 0.147 | 0.058 | 0.399 | 0.751 | 0.177 | 0.668 | 0.912 | 0.250 |
| 750 | 0.071 | 0.139 | 0.044 | 0.335 | 0.543 | 0.162 | 0.737 | 0.953 | 0.280 |
| 1,000 | 0.092 | 0.138 | 0.069 | 0.289 | 0.537 | 0.177 | 0.798 | 0.954 | 0.266 |
| 2,500 | 0.053 | 0.102 | 0.039 | 0.176 | 0.363 | 0.122 | 0.911 | 0.980 | 0.475 |
| Simulation 2 | |||||||||
| 500 | 0.118 | 0.501 | 0.114 | 0.588 | 1.325 | 0.294 | 0.158 | 0.896 | — |
| 750 | 0.097 | 0.575 | 0.121 | 0.507 | 1.283 | 0.282 | 0.180 | 0.909 | — |
| 1,000 | 0.047 | 0.475 | 0.104 | 0.425 | 1.144 | 0.254 | 0.306 | 0.929 | — |
| 2,500 | 0.037 | 0.356 | 0.091 | 0.308 | 0.946 | 0.234 | 0.371 | 0.945 | — |
| Simulation 3 | |||||||||
| Moderate | 0.012 | 0.008 | 0.085 | 0.500 | 0.297 | 0.169 | 0.382 | 0.986 | 0.213 |
| Large | 0.028 | 0.008 | 0.153 | 0.562 | 0.533 | 0.244 | 0.264 | 0.954 | 0.223 |
Note. Correlations between true and estimated c parameters in Simulation 2 are not available because the true parameter value was 0.20 for all items.
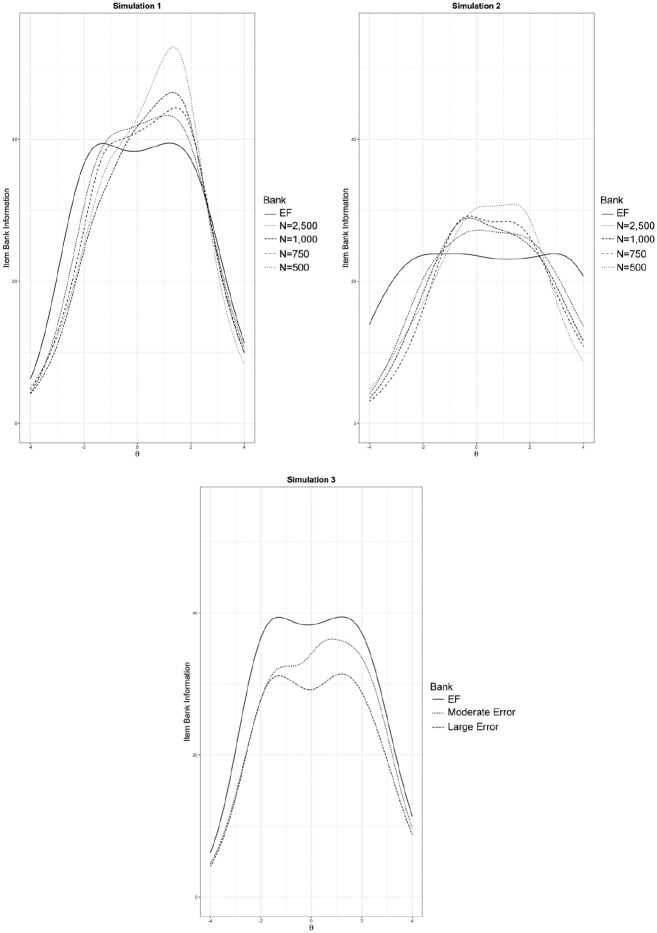
Corresponding item bank information functions (BIFs) are presented in Figure 1. All item banks provided decreasing information as θ became increasingly negative or positive. For , the error-laden item banks provided more information than the EF item bank (e.g., Hambleton et al., 1993; van der Linden & Glas, 2000). The EF BIF was similar to simulated item banks used in previous AMC research (Finkelman et al., 2010). Moreover, the EF BIF corresponded to a standard error of measurement (SEM) below 0.25 for the range of latent trait values examined in the subsequent simulations (i.e., ).
Figure 1.
Item bank information functions for Simulations 1, 2, and 3.
AMC Hypothesis Tests
The simulation compared three common AMC hypothesis tests: the Z test, the likelihood ratio test, and the score ratio index. All three hypothesis tests have demonstrated desirable statistical properties in previous AMC research (e.g., Finkelman et al., 2010; Lee, 2015; Phadke, 2017; Wang et al., 2020). In a typical AMC procedure, each hypothesis test is conducted after an examinee responds to an administered item (assuming that one or more CATs have preceded the given test, to appropriately compare the estimates). This iterative process continues until either (a) the method determines that psychometrically significant intra-individual change has occurred or (b) a maximum number of items has been administered without a significant change determination.
Z test
The omnibus Z test (Phadke, 2017) compares the standardized differences among estimates at three or more testing occasions. The omnibus test requires the computation of Z indices between all unique pairs of testing occasions; with t testing occasions, there will be unique Z indices (Phadke, 2017). For the kth unique Z index between testing occasions i (Ti) and j (Tj), the Z index is
| (1) |
where and are the estimated trait values at Tj and Ti, respectively, is the estimated across all items administered at both testing occasions, and and are the expected test information values computed at for items administered at Tj and Ti, respectively (Finkelman et al., 2010). The expected test information was used in this context to avoid the possibility of negative information values with the 3PLM (Bradlow, 1996). It merits comment that the Z test incorporates different information functions (and therefore different likelihood functions), each which correspond to the specified set of items. However, all estimates remain on a common scale because the test uses a common item bank.
The statistic in Equation 1 quantifies the difference in estimates between any two testing occasions. For the multiple-occasion context, a statistic is computed for all possible pairs of testing occasions. Then, the omnibus index is computed as (Phadke, 2017)
| (2) |
where the null hypothesis for the omnibus test indicates no difference between the values across the t testing occasions (i.e., ). Because is compared with quantiles from the standard normal distribution (Finkelman et al., 2010), is compared with a chi-square distribution with k degrees of freedom to determine significance (Phadke, 2017).
Likelihood ratio test
The second hypothesis test examined was a likelihood ratio test (LRT), which compares the likelihood function evaluated at the maximum likelihood estimate (MLE) under the null hypothesis with the likelihood function evaluated at the MLE with no restrictions (Agresti, 2007). In the AMC context, (calculated across t testing occasions) is the MLE under . Given no parameter restrictions, the likelihood function across all testing occasions is the product of the separate likelihoods evaluated at the corresponding estimate (Finkelman et al., 2010; Phadke, 2017). Thus, the omnibus likelihood ratio for t testing occasions is
| (3) |
where L(·) is the likelihood function for the 3PLM evaluated at a given value, is the response vector for Ti (i = 1, . . . , t), and is the response vector across all testing occasions. The LRT index is then computed as . Under the null hypothesis, this statistic follows a chi-square distribution with degrees of freedom (Phadke, 2017).
Score ratio index
The third hypothesis test examined in these simulations was the score ratio index (SRI), first proposed for the AMC domain with two testing occasions by Lee (2015, pp. 19-21), and then extended to the multi-occasion scenario by Phadke (2017). The SRI is based on the score test statistic, defined as
| (4) |
where is the first derivative (with respect to ) of the log-likelihood function for the response vector evaluated at (also referred to as the score function), and is the test information evaluated at (Lee, 2015). Across t testing occasions, the SRI for AMC is constructed as
| (5) |
where is again calculated using the response pattern across all t testing occasions. Under the null hypothesis of no change, follows a chi-square distribution with degrees of freedom (Phadke, 2017).
Critical values for variable-length tests
For all three AMC hypothesis tests, critical values are chosen to maintain nominal error rates (e.g., ). As noted above, asymptotic distributions have been derived for each of the aforementioned hypothesis tests (see Finkelman et al., 2010; Lee, 2015; Phadke, 2017). Yet in variable-length CAT, the hypothesis tests are conducted after each item administration, so choosing critical values without accounting for multiple testing issues can inflate false positive rates. To adjust for the potential inflation in false positive rates, a preliminary simulation was conducted to select sets of empirically derived critical values that would maintain the desired error rates. Specifically, a procedure outlined by Finkelman et al. (2010), and later replicated by Lee (2015), was used. Three sets of critical values were chosen to correspond to each of the three omnibus hypothesis tests when using the EF item banks; these selected critical values were then used for the remaining conditions with the four estimated item banks.
Simulated CAT Administration
The aim of the omnibus AMC procedure is to determine whether intra-individual change had occurred across four testing occasions. Therefore, four CAT administrations were simulated, with AMC applied only at the fourth testing occasion. At each of the four testing occasions, a set of item responses was generated for a CAT measuring one latent trait. The true values at the first testing occasion ( ) again comprised 11 discrete values ranging from −2.5 to 2.5 (Finkelman et al., 2010) with 1,000 replications of simulees at each of the possible values. As shown in Table 2, 10 change trajectories for were examined, including one linear trajectory (where increased by 0.25 at each testing occasion), eight nonlinear trajectories, and one “No Change” condition where remained constant across all four testing occasions. The nonlinear trajectories were selected to mimic change patterns seen in longitudinal health data (Wang et al., 2020).
Table 2.
Change Trajectory Patterns Analyzed Across Four Simulated Testing Occasions.
| Pattern | |||
|---|---|---|---|
| Linear | +0.25 | +0.25 | +0.25 |
| Nonlinear 1 | +0.50 | +0.25 | +0.00 |
| Nonlinear 2 | +0.75 | +0.00 | +0.00 |
| Nonlinear 3 | +0.75 | −0.25 | −0.25 |
| Nonlinear 4 | +0.50 | +0.25 | −0.50 |
| Nonlinear 5 | +0.00 | +0.00 | +0.50 |
| Nonlinear 6 | +0.00 | +0.00 | +0.75 |
| Nonlinear 7 | –0.50 | −0.25 | +0.00 |
| Nonlinear 8 | +0.00 | −0.50 | +0.00 |
| No change | +0.00 | +0.00 | +0.00 |
Note. was set as a sequence of values from −2.5 to 2.5 with a step size of 0.5, and 1,000 simulees were assigned to each value in the sequence.
All four simulated tests were fixed-length CATs with 50 items. The starting values for the first testing occasion (T1) were set to 0 (the average true ), and the starting values for subsequent CAT administrations were set to the final estimates from the previous test administration. For example, the starting values at T3 were the final values. To measure the performance of the three AMC hypothesis tests as termination criteria, a post hoc analysis was conducted using the response data from the T4 CAT. This analysis implemented the AMC termination indices as if the T4 administration was a variable-length test. This approach was used to directly compare the performance of the three AMC hypothesis tests on the same data sets.
Rather than simulate three fixed-length tests and a final variable-length test, variable-length CATs could have been simulated at all testing occasions. In practice, variable-length CATs are commonly used, based on improved test efficiency and accuracy compared with using a fixed-length termination criterion (Choi et al., 2011; Wang et al., 2019). However, recall that AMC was applied in the current study to identify omnibus change across all four testing occasions. Using only one variable-length CAT (at T4) provided a clearer picture of AMC’s performance as a termination criterion (rather than comparing AMC results across two or more testing occasions). Given that the primary focus of the analyses was on the fourth testing occasion, the first three testing occasions used a fixed-length termination criterion to better standardize the AMC process.
In the post hoc, variable-length CAT for T4, the minimum and maximum test lengths were set to 10 and 50, respectively. For each simulee and each AMC hypothesis test, a sequence of test statistics was computed, corresponding to Items 10 through 50. This sequence of statistics was used to identify the item after which the T4 CAT would have terminated in a variable-length administration (note that these statistics were computed only after all four CATs were administered). Based on this stopping point, the corresponding item response pattern was used to evaluate the hypothesis test performance (described below). In this context, termination for the omnibus AMC method was based on whether psychometrically significant change had occurred (a dichotomous “yes” or “no”) across all four testing occasions. In this study, no post hoc analyses were conducted to identify between which specific test occasions the change had occurred.
In these simulated CAT administrations, each value was estimated using maximum likelihood estimation. When a simulee did not have a mixed response vector (i.e., the simulee answered all items correctly or incorrectly, typically occurring only in the early stages of a CAT), was estimated using maximum a posteriori estimation with a standard normal prior distribution. Moreover, at each stage of the CAT, items were chosen to maximize the expected Fisher information at the current latent trait estimate (Embretson & Reise, 2000). It merits comment that within each condition, items were drawn from the same item bank at each testing occasion. In this way, simulees could answer a given item multiple times across the four simulated CAT administrations.
Dependent Variables
In summary, Simulation 1 comprised a Monte Carlo simulation with four CAT administrations to examine AMC performance when varying three design factors: (a) item bank calibration sample size, (b) magnitude and pattern of change between true s at each testing occasion, and (c) AMC hypothesis test. Results were compared across 150 conditions (5 levels of item parameter estimation error × 10 change trajectories × 3 omnibus hypothesis tests) at 11 starting levels with 1,000 simulees (i.e., replications) per level. Because AMC examines psychometric change at the individual level, each simulation condition was essentially replicated 1,000 times at each level.
Using the post hoc analysis results to simulate a variable-length CAT at T4, AMC performance was evaluated using false positive rates (FPRs)—the proportion of simulees identified as demonstrating psychometrically significant change when their s did not change across testing occasions—and true positive rates (TPRs)—the proportion of simulees identified as demonstrating psychometrically significant change when their s did indeed change across testing occasions. Next, the average test length (ATL) at T4 was computed when employing each of the hypothesis tests (Finkelman et al., 2010).
It also was of interest to examine the extent to which the estimated change between the initial and final testing occasions mirrored the true change in . To quantify this (omnibus) intra-individual change recovery, a “change recovery index” was calculated as
| (6) |
where and ( ) are the true and estimated latent trait values, respectively, at the first or fourth testing occasion, averaged across all 1,000 replicated simulees in a given condition with the same at T1. In Equation 6, the first quantity represents the true difference between the final and initial . The second quantity represents the corresponding estimated change, using the estimates from the first fixed-length CAT administrations (T1) and the final, variable-length AMC administration (T4).
The above dependent variables were compared among the simulation conditions in three ways. First, a series of two-way analyses of variance 3 (ANOVAs) were fit to describe the relative effects of the three design factors (amount of item parameter estimation error, change pattern, and AMC hypothesis test) on each termination index. The true value at the first testing occasion ( ) was also included as a predictor in the ANOVAs to examine differences across the trait continuum. Classical effect sizes were computed as
| (7) |
where SS denotes the sum-of-squares from the ANOVA computation. Separate ANOVAs were run for each dependent variable (e.g., FPRs, ATL). Second, using the nonnegligible effect sizes as guidance for subsequent interpretation ( ), each dependent variable was examined when averaging across all s. Finally, results were analyzed when conditioning on .
Simulations 2 and 3
A common question with any CAT-based simulation concerns the extent to which results are driven by such factors as the choice of item bank or estimation procedure, rather than reflective of underlying trends in CAT performance. To better evaluate the generalizability of the results from the present study, Simulation 1 was reproduced in two ways. These additional simulations differed from Simulation 1 primarily in the methods used for item bank generation. All other procedures from Simulation 1 (i.e., CAT administration, estimation, post hoc analyses for AMC test performance) were replicated in Simulations 2 and 3.
In Simulation 2, a different EF item bank was constructed with a new set of item parameters. Specifically, 300 items were generated following a unidimensional 3PLM model with , with bounds at 0.5 and 2.0, and for all items (Lee, 2015). Compared with the item parameter distributions in Simulation 1, the new item bank in Simulation 2 included a widened difficulty distribution, relatively smaller variance for the discrimination parameter, and a constant (rather than uniformly distributed) pseudo-guessing parameter. As in Simulation 1, item parameters for four item banks were then estimated using an EM algorithm (Bock & Aitkin, 1981) in mirt (Chalmers, 2012) with the aforementioned calibration sample sizes.
The item parameter recovery statistics for this set of item banks are provided in Table 1, and the corresponding BIFs are presented in Figure 1. Compared with Simulation 1, both the EF and error-laden item banks in Simulation 2 provided relatively less information across much of the continuum. The low information in the Simulation 2 EF item bank was largely due to the relatively low discrimination values. Indeed, the BIF in Figure 1 aligns with the information function from a “low-discrimination” condition in Lee (2015). Although arguably providing less information than some banks used in practice with CAT, the EF item bank in Simulation 2 facilitated a clear comparison of AMC’s performance in the presence of item parameter estimation error as a function of bank information (i.e., when comparing between Simulations 1 and 2). Moreover, note that even with the relatively low information, the SEM for the EF item bank in Simulation 2 was still less than approximately 0.25 across the range of values examined in the current study (i.e., ).
In Simulation 3, rather than estimating item parameters with calibration samples of varying sizes, item parameter estimation error was introduced by adding a residual term of a given magnitude to each true item parameter value. Numerous researchers (e.g., Crichton, 1981; Huang, 2018; Patton et al., 2013; Sun et al., 2020) have used such a method to simulate calibration error in the item parameters. Following procedures from Crichton (1981), the estimated parameter values were computed as
| (8) |
where is the estimated item parameter value, is the true item parameter value, and . The true parameter values ( ) were the EF item parameter values used in Simulation 1. The degree of item parameter estimation error was systematically increased by modifying the value of , which were based on common RMSE values for the three item parameters in 3PLM research. Using values reported in Crichton (1981), two item banks with estimation error were created, comprising either a moderate or large amount of added error. In the moderate-error item bank, the values for the discrimination, difficulty, and pseudo-guessing parameters were 0.4, 0.1, and 0.04, respectively. Similarly, in the large-error item bank, the values were 0.6, 0.3, and 0.08, respectively (Crichton, 1981). In both item banks with error, the error-laden item parameter values were bounded such that , , and .
Again, the item parameter recovery statistics for the three item banks in Simulation 3 are presented in Table 1. As shown in Figure 1, whereas the incorporation of item parameter estimation inflated the BIFs for some values in Simulations 1 and 2 (e.g., Hambleton et al., 1993; van der Linden & Glas, 2000), item parameter estimation error in Simulation 3 was associated with uniformly lower bank information across the continuum.
Software
All simulations were conducted using R statistical software (R Core Team, 2021). Item parameter and estimation were completed using the mirt (Chalmers, 2012) and catIrt (Nydick, 2014) libraries, respectively. Figures were created using ggplot2 (Wickham, 2016). All other analyses (e.g., simulated CAT administrations) used author-written functions. The code for these analyses is available on request.
Results
Simulation 1
Although AMC was only applied at T4, the AMC hypothesis tests incorporate the latent trait estimates from previous testing occasions. Therefore, the observed SEMs for through were first examined to ensure sufficient estimation accuracy. Averaging the SEM values across the 1,000 simulees in each ( size trajectory) condition, the median SEM for all three latent trait estimates was 0.222, with corresponding interquartile ranges of 0.215 to 0.232 for all three testing occasions. Note that the median and interquartile range were reported here due to positive skew in the SEM distributions. A relatively small proportion of conditions (less than 0.03) for a given testing occasion produced SEM values greater than 0.30, all of which corresponded to simulees with .
Results of the two-way ANOVA examining the effects of four factors—calibration sample size, change trajectory, value at the first testing occasion ( ), and AMC hypothesis test—on each of the dependent variables of interest are presented in Table 3. The change pattern produced the largest effect across all dependent variables, with greater than 0.79 for TPRs and ATL. The starting value demonstrated moderate effects, both on its own and in conjunction with the true change trajectory. The calibration sample size and choice of AMC hypothesis test had negligible effects on ATL and change recovery, but these factors accounted for larger proportions of variance in FPRs (Table 3). The AMC hypothesis test choice had a small effect on TPRs. Moreover, the interactions between and calibration sample size had nontrivial effects on FPRs, and to a lesser extent change recovery, with of 0.216 and 0.032, respectively. However, the interactions between calibration sample size and AMC hypothesis test did not strongly influence the examined dependent variables.
Table 3.
Classical Effect Sizes (η2) From a Two-Way Analysis of Variance (ANOVA) on False Positive Rates, True Positive Rates, Average Test Length, and Change Recovery.
| Factor | η 2 | Sum of squares | df |
|---|---|---|---|
| False positive rates | |||
| Starting (Trait) | 0.300 | 0.019 | 10 |
| Calibration size (Size) | 0.170 | 0.011 | 4 |
| AMC hypothesis test (Test) | 0.152 | 0.010 | 2 |
| Trait × Size | 0.216 | 0.014 | 40 |
| Trait × Test | 0.124 | 0.008 | 20 |
| Size × Test | 0.006 | 0.000 | 8 |
| Residuals | — | 0.002 | 80 |
| True positive rates | |||
| Starting (Trait) | 0.060 | 1.082 | 10 |
| Calibration size (Size) | 0.001 | 0.017 | 4 |
| AMC hypothesis test (Test) | 0.021 | 0.372 | 2 |
| True change (Change) | 0.793 | 14.206 | 8 |
| Trait × Size | 0.023 | 0.415 | 40 |
| Trait × Test | 0.013 | 0.230 | 20 |
| Trait × Change | 0.049 | 0.879 | 80 |
| Size × Test | 0.000 | 0.001 | 8 |
| Size × Change | 0.004 | 0.072 | 32 |
| Test × Change | 0.002 | 0.035 | 16 |
| Residuals | NA | 0.599 | 1264 |
| Average test length | |||
| Starting (Trait) | 0.038 | 1605.090 | 10 |
| Calibration size (Size) | 0.002 | 78.258 | 4 |
| AMC hypothesis test (Test) | 0.002 | 89.332 | 2 |
| True change (Change) | 0.847 | 35872.322 | 9 |
| Trait × Size | 0.014 | 585.960 | 40 |
| Trait × Test | 0.022 | 936.969 | 20 |
| Trait × Change | 0.023 | 992.919 | 90 |
| Size × Test | 0.000 | 8.490 | 8 |
| Size × Change | 0.004 | 156.991 | 36 |
| Test × Change | 0.012 | 528.193 | 18 |
| Residuals | NA | 1498.775 | 1412 |
| Change recovery index | |||
| Starting (Trait) | 0.170 | 3.189 | 10 |
| Calibration size (Size) | 0.012 | 0.219 | 4 |
| AMC hypothesis test (Test) | 0.002 | 0.040 | 2 |
| True change (Change) | 0.307 | 5.744 | 9 |
| Trait × Size | 0.032 | 0.608 | 40 |
| Trait × Test | 0.048 | 0.901 | 20 |
| Trait × Change | 0.277 | 5.185 | 90 |
| Size × Test | 0.001 | 0.023 | 8 |
| Size × Change | 0.016 | 0.303 | 36 |
| Test × Change | 0.011 | 0.202 | 18 |
| Residuals | NA | 2.296 | 1412 |
Note. Classical effect sizes greater than or equal to 0.02 have been bolded. AMC = Adaptive measurement of change.
False Positive Rates
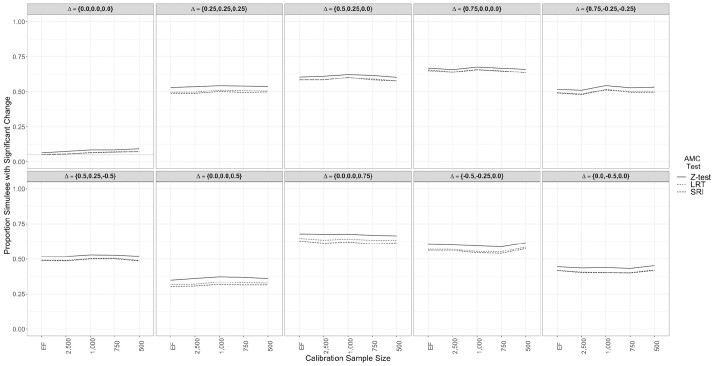
Marginalizing across the continuum, there was evidence of a small negative relationship between item parameter estimation error and FPRs for all three AMC hypothesis tests. As shown in the first panel of Figure 2, under the condition of “no change,” the FPRs slightly increased as the calibration sample size decreased to 500 examinees. This relationship reflects the moderate effect size from the ANOVA ( ). Still, the FPRs among the item banks never differed by more than 0.03, and thus, these results might not reflect a practically significant relationship between calibration sample size and FPRs.
Figure 2.
False positive rates (Panel 1) and true positive rates (Panels 2-10) for three adaptive measurement of change (AMC) hypothesis tests at the fourth testing occasion across 10 change trajectories conditioning on calibration sample size.
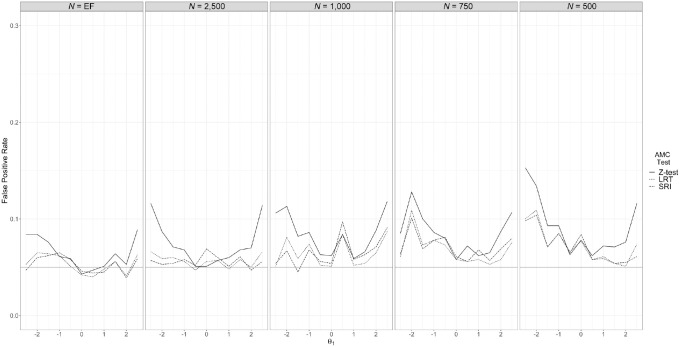
Figure 3 presents the FPRs conditional on the simulees’ values. As the calibration sample size decreased, there was greater variation in FPRs across the continuum, with FPRs reaching or exceeding 0.10 in some cases. The conditional analyses also highlight the possibility of differential FPRs among the three hypothesis tests for particularly high-performing ( ) and low-performing ( ) simulees. Specifically, the Z test consistently produced higher FPRs than the LRT or SRI for these extreme values. Still, the differences in FPRs among the hypothesis tests were small, and reanalyzing the data using only simulees with did not substantially change the average FPRs for each of the three hypothesis tests across the calibration sample sizes.
Figure 3.
False positive rates for three adaptive measurement of change (AMC) hypothesis tests across decreasing calibration sample sizes when conditioning on .
True Positive Rates
The remaining panels in Figure 2 present the TPRs for each AMC hypothesis test among the nine linear and nonlinear change patterns. These results suggest negligible differences in TPRs as the degree of item parameter estimation error increased (reflecting the very small effect size of ). Specifically, across the examined change and AMC hypothesis test conditions, using an item bank calibrated with 500 examinees produced TPRs that were roughly equivalent to those produced when using an item bank with the true EF parameter values. There was evidence of slight differences in TPRs as a function of calibration sample size for a handful of change trajectories (e.g., Panels 4 and 8 of Figure 2), but the total magnitude of differences never exceeded 0.05. Rather, the largest determinant of differences in TPRs was the true change trajectory ( ), with certain nonlinear trajectories (e.g., a moderate increase between the final two testing administrations, as in Panel 7 of Figure 2) resulting in lower TPRs across the examined item banks.
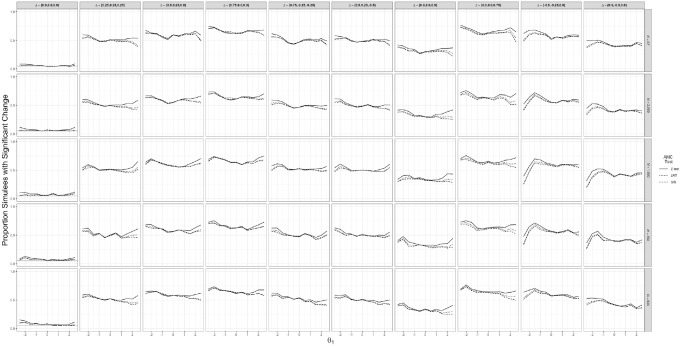
Examining the TPR patterns across the continuum, there was also little evidence of a relationship between calibration sample size and TPRs conditional on . As shown in Figure 4, any differences that occurred among the varying calibration sample sizes were generally limited to simulees with extremely small or large values. Across the TPR analyses, there were also few meaningful differences in TPRs when comparing among the AMC hypothesis tests. Only for extreme values did there appear evidence of relatively small differences among the hypothesis tests.
Figure 4.
False positive rates (Panel 1) and true positive rates (Panels 2-10) for three adaptive measurement of change (AMC) hypothesis tests across 10 change trajectories when conditioning on .
Average Test Length
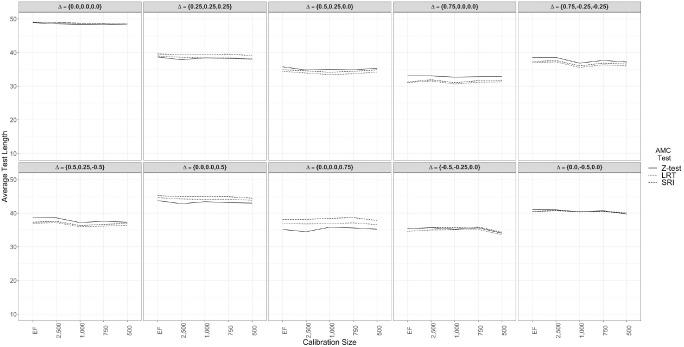
Simulation 1 results did not provide compelling evidence that using an item bank with higher levels of item parameter estimation error substantially influenced the ATL of a variable-length CAT at the final testing occasion. As seen in Figure 5, the change trajectory was the strongest driver of differences in ATL among the examined testing conditions ( ). In the “no change” condition (Panel 1), all three hypothesis tests required close to the maximum number of items (50 items) to terminate the test. Importantly, comparing among the AMC hypothesis tests, the ATL differences never exceeded three to four items.
Figure 5.
Average test length for three adaptive measurement of change (AMC) hypothesis tests at the fourth testing occasion across 10 change trajectories conditioning on calibration sample size.
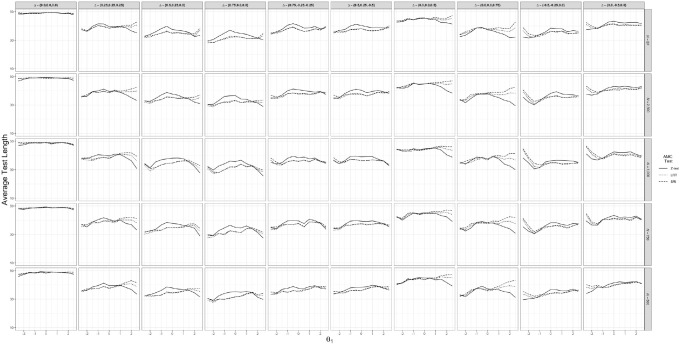
Like the TPR analyses, the ATL patterns conditional on (see Figure 6) also demonstrated a negligible relationship between calibration sample sizes and variable-length CAT test length ( ). Across the examined change conditions, ATL was often smaller among values for which the hypothesis tests demonstrated higher TPRs. The conditional ATL analyses further highlight that the largest differences in ATL among the hypothesis tests generally occurred for simulees with large or small . In particular, in many contexts where , the Z test required fewer items than the LRT or SRI to determine whether psychometrically significant change had occurred (e.g., Columns 2 and 7 of Figure 6). There were also some conditions wherein the Z test required more items for simulees with midrange values, but the number of items only differed by approximately five.
Figure 6.
Average test length for three adaptive measurement of change (AMC) hypothesis tests across 10 trajectories when conditioning on .
Change Recovery
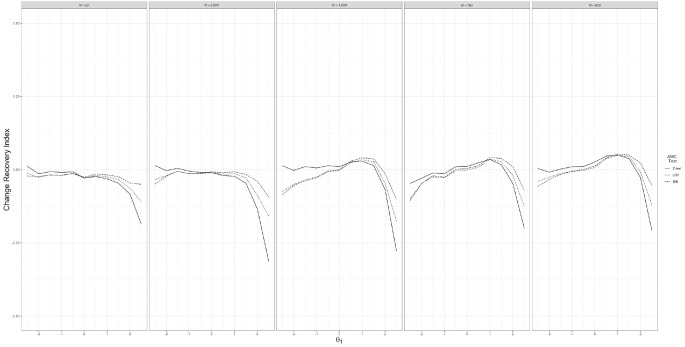
The final dependent variable examined in Simulation 1 was change recovery, quantified as the difference between the true and estimated change between the first and fourth testing occasions. The results (Figure 7) indicated no strong evidence that AMC’s ability to recover the true change was affected by the introduction of item parameter estimation error. Marginalizing across all other design factors, the average change magnitudes never differed by more than 0.04 among the examined calibration sample sizes, and the standard deviations increased by at most 0.05 between the error-free and error-laden item banks.
Figure 7.
Change recovery index for three adaptive measurement of change (AMC) hypothesis tests across decreasing calibration sample sizes when conditioning on .
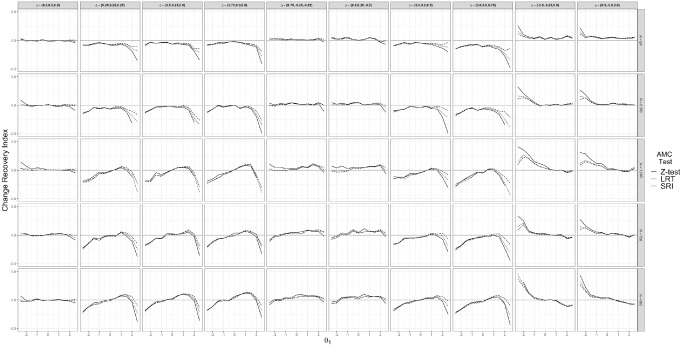
Unsurprisingly, the largest determinant of change recovery was the true change trajectory (Figure 8). Specifically, the variability in change recovery increased for change trajectories with larger true differences between the initial and final . For instance, with all other factors held constant, the standard deviations for the change recovery index were approximately 0.11 or 0.12 for trajectories with a true change magnitude of . On the contrary, the standard deviations were 0.04 for both trajectories with a true change magnitude of . In other words, for simulees with larger change in values, AMC was more likely to either under- or overestimate the change magnitude.
Figure 8.
Change recovery index for three adaptive measurement of change (AMC) hypothesis tests across 10 trajectories when conditioning on .
The change recovery analyses conditional on the value, shown in Figure 8, again indicated few differences as a function of calibration sample size. Rather, differences in change recovery were largely driven by the value. As shown in Figure 8, for many change trajectories, AMC tended to overestimate the change magnitude (translating to a more negative change recovery index value) as increased past 1.5. The conditional analyses also highlight how, compared with the other two hypothesis tests, the Z test suffered the greatest declines in change recovery among particularly high- or low-performing simulees. For example, note how in Figure 8 (Columns 1, 9, and 10) the Z test tended to underestimate change for . Although not always to the same extent as the Z test, the LRT and SRI similarly demonstrated slightly worse change recovery for simulees with extreme values.
Simulations 2 and 3
Simulation 2
Again, the fixed-length CATs for the first three testing occasions demonstrated reasonable observed SEM values for the latent trait estimates. Specifically, averaged across the 1,000 simulees in each condition (i.e., size trajectory), the median SEM values and corresponding interquartile ranges for , , and were 0.267 (0.255–0.285), 0.264 (0.255–0.284), and 0.264 (0.255–0.284), respectively. Average SEM values greater than 0.30 were limited to simulees with .
The results from Simulation 2, using a different EF item bank, corroborated certain trends that were observed in Simulation 1. For example, the Simulation 2 results also demonstrated a small negative relationship between calibration sample size and FPRs (with differences in FPRs between item banks at most 0.02). Additionally, calibration sample size had a negligible effect on TPRs and ATL. The ANOVA results for Simulation 2 are presented in Table S1 (available online). Additionally, Figures S1 to S7 (available online) replicate Figures 2 to 8 using the data from Simulation 2.
However, the Simulation 2 results contrasted with those from Simulation 1 in two important ways. First, the calibration sample size had a larger effect on the change recovery index ( in Simulation 2 compared with in Simulation 1). Importantly, this relationship was significantly moderated by ( ), the change trajectory ( ), and the choice of AMC hypothesis test ( ). Figure S6 (available online) shows that when marginalizing across the change trajectory conditions, the LRT and SRI tended to underestimate change for simulees with high positive values as the calibration sample size decreased. The Z test, however, showed an opposing trend. Specifically, the Z test tended to underestimate change for simulees with high negative values as calibration sample size decreased. For simulees with high positive values (e.g., ), the Z test tended to overestimate change, even using the EF item bank.
Figure S7 (available online) presents the change recovery across both the continuum and examined change trajectories. This figure highlights that across the continuum, the LRT and SRI showed relatively little bias in omnibus change recovery with calibration sample sizes of approximately 1,000 or higher. Even with smaller calibration sample sizes, the change recovery index never exceeded 0.25 for either the LRT or SRI when measuring simulees with extreme values. In the majority of change trajectories, however, the Z test demonstrated a notable dip in change recovery when , indicating a tendency to overestimate the magnitude of change between the first and final testing occasion.
These trends in the change recovery index further illustrate the second major difference in results between Simulations 1 and 2. Namely, the choice of AMC hypothesis test had a larger effect on all examined dependent variables in Simulation 2 ( , , , and ). The analyses conditional on indicated that similar to the aforementioned change recovery results, these effect sizes were largely driven by the Z test’s performance among simulees with high positive values, even when using the EF item bank. For example, as shown in Figures S2 and S5 (available online), using AMC with the Z test tended to produce higher FPRs and required fewer items for this range of simulees. Importantly, for simulees in the middle range of the continuum, the Simulation 2 results again indicated few substantial differences as a function of AMC hypothesis test.
Simulation 3
In the third simulation, item parameter estimation error was introduced by adding normally distributed residual terms to each item parameter value (using the true item parameters from the EF item bank in Simulation 1). This simulation examined AMC performance across three item banks, with either no, moderate, or large levels of estimation error. The median observed SEM values and corresponding interquartile ranges were 0.233 (0.227–0.240) for all three testing occasions. Again, average SEM values exceeding 0.30 were limited to simulees with values less than −2.0.
Table S2 (available online) and Figures S8 to S14 (available online) present the results from this set of analyses. Simulation 3 again indicated a positive relationship between item parameter estimation error and FPRs. Additionally, the relationships among the examined design factors and the dependent variables largely depended on simulees’ values, with greater variation among simulees with particularly large positive or negative values. However, in contrast to Simulations 1 and 2, the effect of the degree of item parameter estimation error on all dependent variables was substantially larger in Simulation 3 ( , , , and ). For example, the differences in FPRs between the item banks with and without error reached a magnitude of 0.19 (recall that in Simulations 1 and 2, the FPRs differed by at most 0.03). In contrast to Simulations 1 and 2, the dependent variables in Simulation 3 tended to change as the degree of item parameter estimation error increased for simulees with midrange ability levels. For example, Figure S13 (available online) shows that across the continuum, the change recovery index became more negative (implying a tendency to overestimate omnibus change) for item banks with more estimation error.
Discussion
The results from three Monte Carlo simulations suggest that item parameter estimation error plays at most a small role in AMC performance. Specifically, when averaging across all values, increasing the degree of item parameter estimation error (either through reducing the calibration sample size or adding normally distributed error terms) was associated with a modest increase in FPRs. Item parameter estimation error, when introduced using varying calibration sample sizes, had negligible effects on TPRs or ATL, and at most a small effect on change recovery. Analyses conditional on the initial estimate revealed that differences in the four examined dependent variables—FPRs, TPRs, ATL, and change recovery—as a function of item parameter estimation error and hypothesis test choice were mainly driven by differences among particularly low- and high-θ examinees (i.e., ). For example, AMC was more likely to under- or overestimate the change between the first and final testing occasions for simulees with large positive or negative values. Focusing on the middle range of the continuum (i.e., ), only Simulation 3 revealed noticeable differences in AMC performance, specifically related to FPRs and omnibus change recovery, as a function of item parameter estimation error (introduced using normally distributed residual terms).
Across all analyses, examinee played an important role in AMC performance. A consistent trend emerged wherein the greatest differences in the dependent variables occurred for simulees with particularly extreme values, both when averaging across and comparing among the three hypothesis tests. The BIFs provide some insight into this trend. For example, Figures 1 and 3 together highlight how values with relatively lower bank information were associated with greater variation in the FPRs. Interestingly, although error-laden item banks demonstrated inflated information for certain ranges of simulees (e.g., in Simulations 1 and 2), a trend that corroborates past research (see, Hambleton et al., 1993; van der Linden & Glas, 2000), these changes in information did not noticeably translate to stronger effects on AMC performance in terms of the examined dependent variables. The one exception was for the change recovery index, which was relatively higher (indicating a tendency to underestimate change) at values with inflated BIFs.
Relatedly, even though the BIFs substantially decreased in magnitude at both extremes of the continuum, the AMC methods tended to perform more poorly for simulees with large, positive values than simulees with large, negative values. For example, in Simulation 1, all three AMC hypothesis tests demonstrated notable dips in the change recovery index for , but not to the same extent for (see Figure 7). To explain this phenomenon, recall that seven of the 10 latent trait change trajectories had a positive omnibus change from to . In these cases, simulees with large positive values had even more extreme values when AMC was applied at the fourth testing occasion. The AMC procedure may have therefore demonstrated a ceiling effect at these high values. On the contrary, simulees with large negative values were more likely to have midrange values at the fourth testing occasion, among which AMC tended to show better performance. In summary, these results strongly suggest that researchers and practitioners should use caution when applying AMC to measure high-ability individuals, particularly, when coupled with item banks providing relatively little information at these values.
When controlling for simulees’ values, the overall level of information provided by the item bank appeared to moderate the relationship between AMC change recovery and item parameter estimation error. Recall that the error-free BIF for Simulation 2 provided substantially less information across the continuum than in Simulation 1. Comparing the results between the first two simulations, the calibration sample size had a larger effect on the change recovery index when using the lower information BIF. Moreover, even when not accounting for the amount of item parameter estimation error present in the bank, the lower BIF in Simulation 2 was associated with lower FPRs and TPRs, as well as higher ATLs, than in Simulation 1. Taken together, these results highlight the importance of using an item bank with sufficient information at the desired latent trait levels when implementing AMC.
Figure 1 also helps to explain the stronger effects of item parameter estimation error that were revealed in Simulation 3. Namely, the differences in BIFs between each of the generated item banks were exacerbated in Simulation 3 as compared with Simulations 1 and 2. Incorporating item parameter estimation error in Simulation 3 reduced bank information along a larger proportion of the continuum, which might explain why Simulation 3, but not Simulations 1 and 2, revealed a stronger negative relationship between item parameter estimation error and change recovery among simulees with midrange θ levels. Whereas both estimation error methods (i.e., using calibration samples in Simulations 1 and 2, or adding normally distributed error terms in Simulation 3) introduced sampling error, using a calibration sample introduced additional variability due to the chosen estimation method (e.g., an EM algorithm with a specified number of quadrature points and other software options). Using calibration sizes less than 1,000 likely also introduced additional instability in the item parameter estimates. For Simulations 1 and 2, the increased estimation variability might have minimized the differences in item parameter recovery and BIFs among the error-laden item banks, precluding the stronger relationships revealed in Simulation 3. These results highlight how the method of incorporating item parameter estimation error plays an important role in simulation studies focused on item parameter recovery and CAT item bank structures. Given that calibration samples are used to generate item banks in applied test settings, future research in this area should further compare AMC’s performance across item banks using different implementations of the EM algorithm, or alternative item parameter estimation methods.
Furthermore, the present study revealed noticeable differences among the three AMC hypothesis tests. In particular, the Z test tended to perform worse than the LRT or SRI, as evidenced by higher FPRs and less accurate omnibus change recovery. This trend was largely among simulees with extreme values, and often evident even when using an EF item bank. It is possible that the AMC hypothesis tests were differentially influenced by the lower bank information at these values. Specifically, the AMC hypothesis test had the strongest effect on all four dependent variables in Simulation 2, which had the lowest BIFs. This reduced information might have exacerbated differences between the Z test and the LRT or SRI.
The present study highlights important considerations for designing a testing protocol using AMC. First, these simulations provide evidence that AMC is relatively robust to the presence of item parameter estimation error as long as the item bank provides sufficient information for the intended examinee levels. For example, Simulations 1 and 2 indicated that given adequate information, AMC could provide relatively accurate identification of psychometrically significant change for many examinees with a calibration sample size of only 500 examinees. Therefore, researchers implementing AMC should prioritize constructing an item bank with an information function that closely corresponds to their measurement goals (i.e., with high information across the range of hypothesized values). Still, when the goal is to accurately measure intra-individual change for individuals with particularly low and high values, the current findings suggest that researchers would be wise to use a calibration sample size of at least 1,000 examinees in conjunction with a carefully constructed, high-information item bank. Finally, given the differential performance of the three AMC hypothesis tests in the present study, test administrators should consider using the SRI or LRT with a minimum calibration sample size of 1,000 examinees for the best combination of low error, high power, and accurate change estimation. If the Z test is to be used, then the item bank should provide high information across the range of intended levels. Still, more research replicating these effects is necessary to provide widespread recommendations for AMC’s practical use.
Despite the relationships between item parameter estimation error and AMC performance revealed in these simulations, it is important to again stress that differences among item banks and among AMC hypothesis tests were often trivial in magnitude. For instance, it is an open question as to whether an average increase of 0.03 in FPRs across item banks with varying calibration sample sizes is practically significant. Additionally, item parameter estimation error did not strongly influence TPRs or ATL. As previously noted, it is possible that the small effects revealed in Simulations 1 and 2 might be a result of the small differences in BIFs.
Furthermore, these trends were highly dependent upon underlying latent trait change patterns, which are unknown in applied test settings. For example, the true change trajectories produced the largest effect sizes across the examined dependent variables, with in some cases. This finding is not particularly surprising, and aligns with previous AMC research (e.g., Finkelman et al., 2010; Wang et al., 2020) showing that the power to detect true change is dependent upon the given change trajectory. However, these results suggest that item parameter estimation error does not substantially influence AMC’s performance either above and beyond, or as a function of, the true latent trait change trajectory. Future AMC research would benefit from a more nuanced exploration of the method’s performance across a broader range of plausible change trajectories.
It also merits comment that the TPRs in these analyses were relatively small, ranging between approximately 0.30 and 0.70. The small TPRs likely stem from the combination of (a) relatively small omnibus changes in between the first and fourth testing occasions ( ), and (b) relatively small item discriminations. Indeed, the TPR range in the current study agrees with previous results at similar change magnitudes with error-free item banks (Finkelman et al., 2010; Phadke, 2017; Wang et al., 2020). Previous research demonstrates that with item banks consisting of higher discriminations, higher power, and simulees with larger changes between testing occasions, AMC’s power often exceeds 0.80 (Finkelman et al., 2010; Lee, 2015; Phadke, 2017; Wang et al., 2020).
Limitations
This study is the first to test the AMC method in conditions that incorporate item parameter estimation error. It is thus important to emphasize additional limitations in the study design to facilitate future research in this area. For one, as with any set of simulations, these findings can only be generalized to testing scenarios that match the examined conditions. Although the aforementioned results were replicated with more than one item bank and more than one method of introducing item parameter estimation error, the studied conditions clearly do not extend to all possible testing scenarios. Future studies should further explore the influence of item parameter estimation error on AMC performance by (a) expanding the range of calibration sample sizes, (b) generating item banks with different sets of parameter distributions (particularly with higher discrimination values), (c) modifying the number of testing occasions, and (d) incorporating conditions of model misspecification, such as when dimensionality or other model assumptions are violated. Two of the current authors are also developing a new stochastic curtailment termination criterion for AMC, designed to terminate an AMC CAT when significant change is not detected. This new method should be compared with the current AMC hypothesis tests in conditions of item parameter estimation error.
On the topic of item bank generation, the item parameter recovery statistics in these studies demonstrated poorer recovery than might be expected in practice with the 3PLM. One factor underlying these results might have been the relatively small calibration sizes (De Ayala, 2013). Indeed, in a study examining the effects of item calibration error on CAT performance, Patton et al. (2013) chose to introduce error by adding normally distributed residual terms to facilitate convergence with a 400-item bank and calibration sizes of only 500 examinees. The relatively low item bank information in Simulation 2 might have also led to the higher bias and RMSE values for the item parameter estimates as compared with Simulation 1. Finally, the relatively poor item parameter recovery could also be the result of the estimation software used, and corresponding options selected when implementing the estimation. Regardless of the source of the less-than-optimal recovery, the focus of Simulations 1 and 2 was on the effect of magnitudes of error that resulted from item parameter estimation. Therefore, the source of item parameter estimation error (and its comparisons to previous studies) was not of relative importance for addressing the primary research aim.
Still, in future AMC research, a wider range of item banks should be examined to gauge the generalizability of the current findings. In addition, different estimation methods for calibrating item banks should be compared. In the present study, the item banks were appropriate for examining AMC’s performance in the presence of item parameter estimation error. Interestingly, negligible to small effects were found even with item banks that demonstrated relatively poor item parameter recovery. This finding suggests that item parameter estimation error could have an even smaller effect on AMC’s performance when using (potentially more realistic) item banks with better parameter recovery.
Moreover, in any longitudinal study, it is important to establish measurement invariance for the latent trait of interest. In other words, do the values measured at each testing occasion represent the same underlying construct (Meredith, 1993; Millsap, 1997; Widaman & Reise, 1997)? Although the present study assumed measurement invariance across the four testing occasions (an assumption made in previous AMC research; Wang et al., 2020; Wang & Weiss, 2018), applied testing contexts should explicitly evaluate this assumption.
As currently implemented, AMC functioned as an omnibus test, indicating whether psychometrically significantly change occurred at any point across the four testing occasions. Because AMC uses estimates across numerous testing occasions, AMC’s performance is arguably contingent upon the accuracy of these estimates. The three examined AMC hypothesis tests account for the uncertainty of these estimates by incorporating the previous values and associated standard errors. The observed SEM values for through were relatively reasonable given the amount of information in the corresponding item banks. Still, future researchers and practitioners seeking to use AMC should be cognizant of, and routinely verify, the accuracy of the estimates across all testing occasions prior to AMC’s implementation.
Two additional suggestions for future research in this area merit comment. First, it would be beneficial to examine the performance of post hoc hypothesis tests to pinpoint the particular testing occasions between which significant change occurred. The majority of the extant AMC research has focused on the omnibus method, leaving open numerous avenues for future research into the efficacy of these post hoc methods. Finally, as previously mentioned, the current study used fixed-length CATs for the first three testing occasions. Future research should therefore replicate these analyses using variable-length CATs (e.g., with a stopping rule based on the standard error of measurement; Choi et al., 2011; Wang et al., 2019).
Conclusions
In summary, these simulations are the first to highlight the functioning of AMC, in terms of decision accuracy and change recovery, in the presence of item parameter estimation error. These results add to a growing body of literature (e.g., Finkelman et al., 2010; Phadke, 2017; Wang & Weiss, 2018; Wang et al., 2020) supporting AMC as a psychometrically rigorous and practical method for understanding latent trait change at the individual level. Integrating the extant research, this method provides promise for the accurate and effective implementation of a person-centered approach to the measurement of change. Still, a plethora of future work remains to better understand the nuanced applications of AMC to psychological and educational testing.
Supplemental Material
Supplemental material, sj-pdf-1-epm-10.1177_00131644211033902 for Robustness of Adaptive Measurement of Change to Item Parameter Estimation Error by Allison W. Cooperman, David J. Weiss and Chun Wang in Educational and Psychological Measurement
In this context, “psychometrically significant” change refers to evaluating differences in trait estimates at the individual level based on psychometric error theory. In contrast, “statistically significant” change refers to evaluating trait differences at the group (i.e., sample) level using statistical sampling theory (Wang et al., 2020).
Although this study focuses exclusively on the unidimensional testing scenario, AMC has also been recently extended to the multidimensional two-occasion (Wang & Weiss, 2018) and multi-occasion testing scenarios (Wang et al., 2020).
A two-way ANOVA was conducted here because with the number of simulation condition combinations, a three-way ANOVA resulted in a fully saturated model and precluded the computation of effect sizes.
Footnotes
Authors’ Note: Preliminary results were presented at the 32nd Annual Convention of the Association for Psychological Science in May 2020.
Declaration of Conflicting Interests: The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Funding: The author(s) received no financial support for the research, authorship, and/or publication of this article.
ORCID iD: Allison W. Cooperman  https://orcid.org/0000-0002-7759-3831
https://orcid.org/0000-0002-7759-3831
Supplemental Material: Supplemental material for this article is available online.
References
- Agresti A. (2007). An introduction to categorical data analysis. John Wiley. 10.1002/0470114754 [DOI] [Google Scholar]
- Birnbaum A. (1986). Some latent trait models and their use in inferring an examinee’s ability. In Lord F. M., Novick M. R. (Eds.), Statistical theories of mental test scores (pp. 397-479). Addison-Wesley. [Google Scholar]
- Bock R. D., Aitkin M. (1981). Marginal maximum likelihood estimation of item parameters: Application of an EM algorithm. Psychometrika, 46(4), 443-459. 10.1007/BF02293801 [DOI] [Google Scholar]
- Bradlow E. T. (1996). Teacher’s corner: Negative information and the three-parameter logistic model. Journal of Educational and Behavioral Statistics, 21(2), 179-185. 10.3102/10769986021002179 [DOI] [Google Scholar]
- Chalmers R. P. (2012). mirt: A multidimensional item response theory package for the R environment. Journal of Statistical Software, 48(6). 10.18637/jss.v048.i06 [DOI] [Google Scholar]
- Cheng Y., Yuan K.-H. (2010). The impact of fallible item parameter estimates on latent trait recovery. Psychometrika, 75(2), 280-291. 10.1007/s11336-009-9144-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choi S. W., Grady M. W., Dodd B. G. (2011). A new stopping rule for computerized adaptive testing. Educational and Psychological Measurement, 71(1), 37-53. 10.1177/0013164410387338 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crichton L. I. (1981). Effect of error in item parameter estimates on adaptive testing [Unpublished doctoral dissertation]. University of Minnesota. [Google Scholar]
- Cronbach L. J., Furby L. (1970). How we should measure “change”: Or should we? Psychological Bulletin, 74(1), 68-80. 10.1037/h0029382 [DOI] [Google Scholar]
- De Ayala R. J. (2013). The theory and practice of item response theory. Guilford. [Google Scholar]
- Drasgow F. (1989). An evaluation of marginal maximum likelihood estimation for the two-parameter logistic model. Applied Psychological Measurement, 13(1), 77-90. 10.1177/014662168901300108 [DOI] [Google Scholar]
- Embretson S. E. (1991). A multidimensional latent trait model for measuring learning and change. Psychometrika, 56(3), 495-515. 10.1007/BF02294487 [DOI] [Google Scholar]
- Embretson S. E., Reise S. P. (2000). Item response theory for psychologists. Lawrence Erlbaum. [Google Scholar]
- Feuerstahler L. M. (2018). Sources of error in IRT trait estimation. Applied Psychological Measurement, 42(5), 359-375. 10.1177/0146621617733955 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Finkelman M. D., Weiss D. J., Kim-Kang G. (2010). Item selection and hypothesis testing for the adaptive measurement of change. Applied Psychological Measurement, 34(4), 238-254. 10.1177/0146621609344844 [DOI] [Google Scholar]
- Hambleton R. K., Jones R. W. (1994). Item parameter estimation errors and their influence on test information functions. Applied Measurement in Education, 7(3), 171-186. 10.1207/s15324818ame0703_1 [DOI] [Google Scholar]
- Hambleton R. K., Jones R. W., Rogers H. J. (1993). Influence of item parameter estimation errors in test development. Journal of Educational Measurement, 30(2), 143-155. 10.1111/j.1745-3984.1993.tb01071.x [DOI] [Google Scholar]
- Huang H.-Y. (2018). Effects of item calibration errors on computerized adaptive testing under cognitive diagnosis models. Journal of Classification, 35(3), 437-465. 10.1007/s00357-018-9265-y [DOI] [Google Scholar]
- Hulin C. L., Lissak R. I., Drasgow F. (1982). Recovery of two- and three-parameter logistic item characteristic curves: A Monte Carlo study. Applied Psychological Measurement, 6(3), 249-260. 10.1177/014662168200600301 [DOI] [Google Scholar]
- Jacobson N. S., Follette W. C., Revenstorf D. (1984). Psychotherapy outcome research: Methods for reporting variability and evaluating clinical significance. Behavior Therapy, 15(4), 336-352. 10.1016/S0005-7894(84)80002-7 [DOI] [Google Scholar]
- Jacobson N. S., Truax P. (1991). Clinical significance: A statistical approach to defining meaningful change in psychotherapy research. Journal of Consulting and Clinical Psychology, 59(1), 12-19. 10.1037/0022-006X.59.1.12 [DOI] [PubMed] [Google Scholar]
- Kaskowitz G. S., De Ayala R. J. (2001). The effect of error in item parameter estimates on the test response function method of linking. Applied Psychological Measurement, 25(1), 39-52. 10.1177/01466216010251003 [DOI] [Google Scholar]
- Kim-Kang G., Weiss D. J. (2007). Comparison of computerized adaptive testing and classical methods for measuring individual change. Paper presented at the Proceedings of the 2007. GMAC Conference on Computerized Adaptive Testing. https://www.psych.umn.edu/psylabs/CATCentral/
- Kim-Kang G., Weiss D. J. (2008). Adaptive measurement of individual change. Zeitschrift Für Psychologie/Journal of Psychology, 216(1), 49-58. 10.1027/0044-3409.216.1.49 [DOI] [Google Scholar]
- Lee J. E. (2015). Hypothesis testing for adaptive measurement of individual change [Unpublished doctoral dissertation]. University of Minnesota. [Google Scholar]
- Li Y. H., Lissitz R. W. (2004). Applications of the analytically derived asymptotic standard errors of item response theory item parameter estimates. Journal of Educational Measurement, 41(2), 85-117. 10.1111/j.1745-3984.2004.tb01109.x [DOI] [Google Scholar]
- Lord F. M. (1968). An analysis of the verbal scholastic aptitude test using Birnbaum’s three-parameter logistic model. Educational and Psychological Measurement, 28(4), 989-1020. 10.1177/001316446802800401 [DOI] [Google Scholar]
- Meredith W. (1993). Measurement invariance, factor analysis and factorial invariance. Psychometrika, 58(4), 525-543. 10.1007/BF02294825 [DOI] [Google Scholar]
- Millsap R. E. (1997). Invariance in measurement and prediction: Their relationship in the single-factor case. Psychological Methods, 2(3), 248-260. 10.1037/1082-989X.2.3.248 [DOI] [Google Scholar]
- Nydick S. (2014). catIrt: An R package for simulating IRT-based computerized adaptive tests (Version 0.50-0). https://cran.r-project.org/package=catIrt
- O’Connor E. F. (1972). Extending classical test theory to the measurement of change. Review of Educational Research, 42(1), 73-97. 10.3102/00346543042001073 [DOI] [Google Scholar]
- Olea J., Barrada J. R., Abad F. J., Ponsoda V., Cuevas L. (2012). Computerized adaptive testing: The capitalization on chance problem. Spanish Journal of Psychology, 15(1), 424-441. 10.5209/rev_SJOP.2012.v15.n1.37348 [DOI] [PubMed] [Google Scholar]
- Patton J. M., Cheng Y., Yuan K.-H., Diao Q. (2013). The influence of item calibration error on variable-length computerized adaptive testing. Applied Psychological Measurement, 37(1), 24-40. 10.1177/0146621612461727 [DOI] [Google Scholar]
- Patton J. M., Cheng Y., Yuan K.-H., Diao Q. (2014). Bootstrap standard errors for maximum likelihood ability estimates when item parameters are unknown. Educational and Psychological Measurement, 74(4), 697-712. 10.1177/0013164413511083 [DOI] [Google Scholar]
- Phadke C. (2017). Measuring intra-individual change at two or more occasions with hypothesis testing methods [Unpublished doctoral dissertation]. University of Minnesota. [Google Scholar]
- R Core Team. (2021). R: A language and environment for statistical computing. https://www.R-project.org/
- Reise S. P. (2014). Item response theory. In Cautin R. L., Lilienfeld S. O. (Eds.), Encyclopedia of clinical psychology (pp. 1-10). John Wiley. 10.1002/9781118625392.wbecp357 [DOI] [Google Scholar]
- Sahin A., Anil D. (2017). The effects of test length and sample size on item parameters in item response theory. Educational Sciences: Theory & Practice, 17(1), 321-335. 10.12738/estp.2017.1.0270 [DOI] [Google Scholar]
- Sahin A., Weiss D. J. (2015). Effects of calibration sample size and item bank size on ability estimation in computerized adaptive testing. Educational Sciences: Theory & Practice, 15(6), 1585-1595. 10.12738/estp.2015.6.0102 [DOI] [Google Scholar]
- Sun X., Liu Y., Xin T., Song N. (2020). The impact of item calibration error on variable-length cognitive diagnostic computerized adaptive testing. Frontiers in Psychology, 11, Article 575141. 10.3389/fpsyg.2020.575141 [DOI] [PMC free article] [PubMed]
- Swaminathan H., Hambleton R. K., Sireci S. G., Xing D., Rizavi S. M. (2003). Small sample estimation in dichotomous item response models: Effect of priors based on judgmental information on the accuracy of item parameter estimates. Applied Psychological Measurement, 27(1), 27-51. 10.1177/0146621602239475 [DOI] [Google Scholar]
- van der Linden W. J., Glas C. A. W. (2000). Capitalization on item calibration error in adaptive testing. Applied Measurement in Education, 13(1), 35-53. 10.1207/s15324818ame1301_2 [DOI] [Google Scholar]
- Wang C., Weiss D. J. (2018). Multivariate hypothesis testing methods for evaluating significant individual change. Applied Psychological Measurement, 42(3), 221-239. 10.1177/0146621617726787 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang C., Weiss D. J., Shang Z. (2019). Variable-length stopping rules for multidimensional computerized adaptive testing. Psychometrika, 84(3), 749-771. 10.1007/s11336-018-9644-7 [DOI] [PubMed] [Google Scholar]
- Wang C., Weiss D. J., Suen K. Y. (2020). Hypothesis testing methods for multivariate multi-occasion intra-individual change. Multivariate Behavioral Research. Advance online publication. 10.1080/00273171.2020.1730739 [DOI] [PubMed]
- Weiss D. J. (1982). Improving measurement quality and efficiency with adaptive testing. Applied Psychological Measurement, 6(4), 473-492. 10.1177/014662168200600408 [DOI] [Google Scholar]
- Weiss D. J. (2004). Computerized adaptive testing for effective and efficient measurement in counseling and education. Measurement and Evaluation in Counseling and Development, 37(2), 70-84. 10.1080/07481756.2004.11909751 [DOI] [Google Scholar]
- Weiss D. J., Kingsbury G. G. (1984). Application of computerized adaptive testing to educational problems. Journal of Educational Measurement, 21(4), 361-375. 10.1111/j.1745-3984.1984.tb01040.x [DOI] [Google Scholar]
- Weiss D. J., Von Minden S. (2012). A comparison of item parameter estimates from Xcalibre 4.1 and Bilog-MG. Assessment Systems. [Google Scholar]
- Wickham H. (2016). ggplot2: Elegant graphics for data analysis (2nd ed.). Springer International. 10.1007/978-3-319-24277-4 [DOI] [Google Scholar]
- Widaman K. F., Reise S. P. (1997). Exploring the measurement invariance of psychological instruments: Applications in the substance use domain. In Bryant K. J., Windle M., West S. G. (Eds.), The science of prevention: Methodological advances from alcohol and substance abuse research (pp. 281-324). American Psychological Association. 10.1037/10222-009 [DOI] [Google Scholar]
- Yoes M. (1995). An updated comparison of micro-computer based item parameter estimation procedures used with the 3-parameter IRT model. Assessment Systems. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplemental material, sj-pdf-1-epm-10.1177_00131644211033902 for Robustness of Adaptive Measurement of Change to Item Parameter Estimation Error by Allison W. Cooperman, David J. Weiss and Chun Wang in Educational and Psychological Measurement