Non-pharmaceutical interventions and mortality in U.S. cities during the great influenza pandemic, 1918–1919

Abstract

A key issue for the ongoing COVID-19 pandemic is whether non-pharmaceutical public-health interventions (NPIs) retard death rates. Good information about causal effects from NPIs comes from flu-related excess deaths in large U.S. cities during the second wave of the Great Influenza Pandemic, September 1918-February 1919. The measured NPIs are in three categories: school closings, prohibitions of public gatherings, and quarantine/isolation. Although an increase in NPIs flattened the curve in the sense of reducing the ratio of peak to overall flu-related excess death rates, the estimated effect on overall deaths is small and statistically insignificant. These findings differ from those associated with COVID-19 in the sense that facemask mandates and usage seem to reduce COVID-related cases.

The mortality experienced during the Great Influenza Pandemic of 1918–1920 likely provides a useful guide for outcomes under the COVID-19 pandemic. An important issue is how mortality responds to non-pharmaceutical interventions (NPIs), which in 1918–1920 emphasized school closings, prohibitions of public gatherings, and quarantine/isolation. A difficulty in finding causal effects of NPIs during the COVID-19 Pandemic is reverse causality; that is, U.S. state and city governments clearly reacted to numbers on mortality, hospitalizations, and cases by adjusting the extent of interventions. Specifically, when the extent of disease increased, governments were more likely to mandate closing of non-essential businesses and wearing of facemasks. This endogenous reaction makes it difficult to assess the effects of NPIs on health outcomes.

For scientific purposes, the ideal setting would be controlled experiments, whereby NPIs were adjusted randomly across governmental jurisdictions. This kind of experimentation did not arise during the Great Influenza or COVID-19 Pandemic.1 However, the nature of the evolution of the Great Influenza across U.S. cities offers the potential to assess causal effects of NPIs on death rates. Specifically, the flu spread gradually across locations from its origin point in Boston, and the distance from Boston provides a reasonable instrumental variable for the intensity of NPIs. The subsequent analysis lays out this methodology and considers possible concerns about this identification strategy.

1. Non-Pharmaceutical interventions and flu-related death rates

Epidemiologists, notably Markel et al. (2007); Hatchett et al. (2007); and Bootsma and Ferguson (2007), have studied effects of non-pharmaceutical public-health interventions (NPIs) on flu-related excess deaths in large U.S. cities over the 24-week period corresponding to the peak of the Great Influenza Pandemic, September 1918-February 1919. The weekly data on flu-related excess death rates come from U.S. Census Bureau, Weekly Health Index, reproduced in Collins et al. (1930, Appendix, Table B). Continuous weekly data over the study period are available for 45 of the 50 largest U.S. cities, where this group of 50 corresponds to a central-city population in the 1910 U.S. Census of at least 100,000.1 Monthly data on flu-related excess deaths are available for these cities back to 1910 (Collins, Appendix Table A).

Markel et al. (2007, Table 1 and supplemental figures) collected data on NPIs from September 1918 to February 1919 for 43 of the 45 cities that have full weekly data on flu-related excess mortality. Atlanta and Detroit were excluded, but the current study adds these cities to the sample. The data on NPIs were organized by Markel et al. (2007) into the three broad categories of school closings, prohibitions of public gatherings, and quarantine/isolation. Hatchett et al. (2007) consider many more categories of NPIs but analyze only 17 of the 43 cities considered by Markel et al. (2007).2 Mask ordinances, prominent recently in the context of COVID-19, are indicated by Hatchett et al. (2007, Table 1) as applying in only 2 of their 17 cities.

Table 1.

Descriptive Statistics.

Variable:	NPI	School closings	Public gatherings	Quarantine	PHRT	Excess flu-related death rate 9/18–2/19	Relative peak excess flu-related death rate 9/18–2/19
Units	years	years	years	years	years	% of population per year	number
Mean	0.24	0.10	0.09	0.05	0.02	1.12	4.6
Median	0.18	0.08	0.08	0	0.02	1.15	4.4
Std dev.	0.13	0.06	0.05	0.07	0.02	1.32	1.3
Max	0.47	0.29	0.22	0.26	0.10	1.78	7.9
Min	0.08	0	0	0	−0.03	0.47	2.8

Variable:	Flu-related death rate 1910–1916, winter	Excess flu-related death rate 1/18–4/18	Excess all-cause death rate 9/18–2/19	Relative peak all-cause excess death rate 9/18–2/19	Distance from Boston	Population 1910	Area
Units	% of population per year	% of population per year	% of population per year	number	1000 miles	1000s	square miles
Mean	0.172	0.34	0.98	3.4	1.01	434	49.7
Median	0.172	0.27	0.99	2.9	0.83	224	37.0
Std dev.	0.046	0.35	0.45	1.3	0.92	760	53.4
Max	0.294	1.51	2.87	6.3	3.10	4768	286.8
Min	0.080	−0.35	0.21	1.9	0	100	6.3

Note: These statistics apply to variables defined and shown in Appendix Table A1.

The underlying information on NPIs in Markel et al. (2007) comes from articles in two newspapers in each city, along with other sources. The main data were reported as number of days in which NPIs of each type were in effect, with a focus on a variable that considers the presence of any type of NPI. For example, when school closings and prohibitions of public gatherings prevail on the same day, the variable records two days’ worth of NPI.3 Barry (2007) raises objections to the NPI data collected for New York City, and these objections are discussed below. Business closings, emphasized in the context of the ongoing coronavirus pandemic, were not implemented in broad form during the Great Influenza, although staggering of business hours was common.4 Likely because of the absence of substantial business closings, Markel et al. (2007) did not focus on this category of NPI. However, the variable for prohibitions of public gatherings includes closings of theatres, bars, entertainment and sporting events, and so on.

The present analysis considers two characteristics of each city's flu-related excess death rates: first, the cumulative flu-related excess death rate out of the total population over the full 24-week study period, and second, the ratio of the peak weekly excess death rate during the period to the overall death rate. (All death rates are expressed at annual rates.) A lower cumulative death rate is a reasonable gauge of the ultimate success of the NPIs. In contrast, a lower relative peak implies a smoother pattern, often described as a “flattening of the curve,” which can be desirable from the standpoint of easing burdens on the healthcare system, possibly leading thereby to fewer cumulative deaths. However, for a given overall excess death rate, if an NPI lowers the relative peak, the implication is that the intervention delays deaths but does not ultimately avoid them.

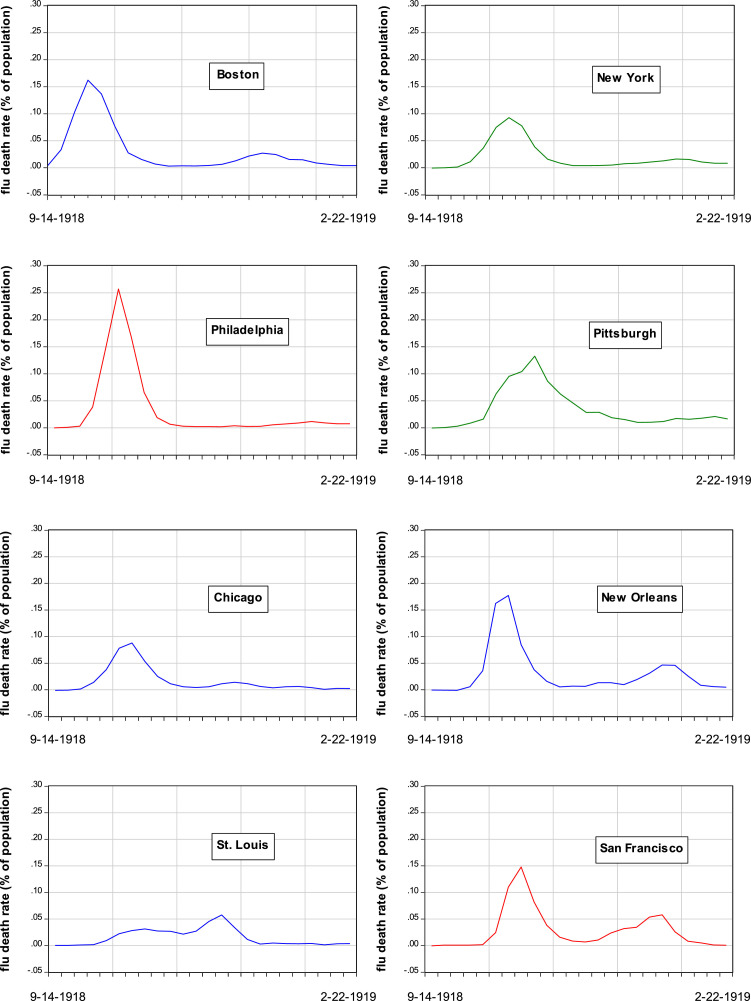
For illustrative purposes, Fig. 1 shows the weekly evolution of flu-related excess death rates from September 1918 to February 1919 in 8 of the 45 cities studied: Boston, New York, Philadelphia, Pittsburgh, Chicago, New Orleans, St. Louis, and San Francisco. The typical pattern is that the excess death rate starts around zero, rises to a sharp peak, then falls rapidly and remains positive for several more weeks. For example, Boston and especially Philadelphia have pronounced peaks in early to mid-October 1918. Pittsburgh has a smaller peak but high death rates over a longer period around the peak. New York and Chicago have smaller peaks and a milder overall experience. New Orleans and San Francisco show second peaks in early 1919. St. Louis has the mildest outcomes overall without a pronounced peak.

Fig. 1.

Evolution of Flu-Related Excess Death Rates in Selected Cities September 1918-February 1919. Note: The graphs show the evolution of the weekly flu-related excess death rate (percent of city population) for each city from the week ending September 14, 1918 to that ending February 22, 1919. Data are from Collins et al. (1930, Appendix Table B).

The epidemiologists used standard epidemiological models to study the dynamics of flu-related excess deaths during the Great Influenza Pandemic, as illustrated by Fig. 1. The present analysis focuses instead on two measures of overall outcomes—the cumulative flu-related excess death rate over the study period (which corresponds to the areas under the curves in Fig. 1) and the peak weekly excess death rate measured relative to the overall rate.

As already mentioned, there is concern that NPIs—measured, say, by length of time in force—and flu-related death rates are simultaneously determined at the level of cities. On the one hand, the basic hypothesis is that more NPIs reduce death rates. On the other hand, NPIs implemented by city governments are likely to respond to death rates in terms of numbers realized or anticipated. The implicit assumption in the statistical analysis by the epidemiologists is that NPIs are determined exogenously; that is, shifts in actual or anticipated flu-related excess death rates do not impact the chosen NPIs. Bootsma and Ferguson (p. 7592) recognize the endogeneity problem—“Causality will never be proven, because, unsurprisingly, control measures were nearly always introduced as case incidence was increasing and removed after it had peaked”—but did not deal with it. The present research attempts to account for the potential endogeneity of NPIs by employing an instrumental-variable approach.

Appendix Table A1 shows the data used for the 45 large U.S. cities in the sample. The variables include measures of death rates, measures of non-pharmaceutical interventions (NPIs), and other variables. Table 1 has descriptive statistics for the variables detailed in Appendix Table A1.

2. Regression analysis

In the parts of their analysis that assess overall outcomes for flu-related death rates, the epidemiologists rely on an array of pair-wise correlations involving NPIs, flu-related excess death rates, and other variables. One shortcoming of this approach is that it does not account for relations with variables outside of each pair—for example, in assessing the connection between NPIs and flu-related excess death rates, there is no consideration of overall health status or other variables. In addition, as already noted, the approach does not attempt to establish causation between the two variables in each pair—is it NPIs that affect death rates or vice versa or both?

The present analysis deals with these issues by employing the multivariate-regression framework familiar to economists. This analysis includes an instrumental-variable approach to attempt to isolate causal effects of NPIs on flu-related excess death rates.

2.1. First-Stage regression for NPIs

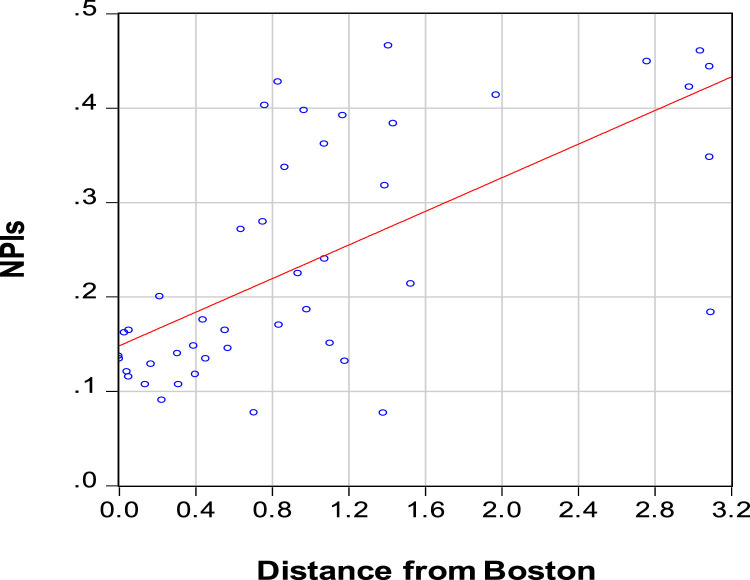
An important consideration is that the second wave of the Great Influenza began in the United States by late August 1918, likely coming from Europe and then appearing around Boston at the army base Fort Devens and the Navy's Commonwealth Pier facility.5 Shortly thereafter, sailors leaving Boston on ships spread the flu to Philadelphia and New Orleans, leading subsequently to spread to other places. From this perspective, distance from Boston (shown in Appendix Table A1, column 9) may serve as an exogenous measure of how early the Influenza Pandemic tended to reach each city in the sample. Specifically, cities further from Boston typically had more time to prepare and were, therefore, more likely to react in terms of the implementation of NPIs.6 Empirically, distance from Boston, entered in a quadratic form, has considerable explanatory power for the NPI variable. The pair-wide relationship between distance and overall NPIs, shown in Fig. 2 , is positive with a simple correlation coefficient of 0.65. (The NPI variable is in Appendix Table A1, column 3.)

Fig. 2.

Relationship between Distance from Boston (thousands of miles) and NPIs (years of implementation). Note: The sample is for 45 U.S. cities. Distance from Boston is the minimum distance shown by Google Maps. Non-Pharmaceutical Interventions (NPIs) from September 1918 to February 1919 are from Markel et al. (2007, Table 1), updated to include Atlanta and Detroit. NPIs are days in effect (in units of years) for school closings, prohibitions of public gatherings, and quarantine/isolation. See Appendix Table A1.

Although distance from Boston is clearly exogenous, the distance-from-Boston variable might be problematic for instrumental estimation if this variable affects flu-related deaths directly (or is correlated with other variables that relate to these deaths). That is, the effects of distance on mortality may not work solely through the channel of influencing choices of NPIs. This issue is taken up in the subsequent discussion.

A first-stage OLS regression for NPIs across 45 cities for September 1918-February 1919 is:

$$\begin{array}{ccc}& & \text{NPI}=0.{107}^{***}+0.{190}^{***}·\left(\text{distance}\text{Boston}\right)-0.{033}^{**}·{\left(\text{distance}\text{Boston}\right)}^2,\hfill \\ & & \left(0.029\right)\left(0.053\right)\left(0.016\right)\hfill \end{array}$$ (1)

where R² = 0.47, mean of dependent variable = 0.24 (years), standard error of regression = 0.094, standard errors of coefficients are in parentheses, and the statistical significance of each coefficient is denoted by *** at 1% and ** at 5%. The F-Statistic for the two distance variables jointly is 18.8. Eq. (1) implies that the estimated marginal effect of distance on NPIs is positive for most of the sample and is roughly zero at the furthest away cities on the west coast, for which the distance variable is around 3 (in thousands of miles).

Eq. (1) matches up with second-stage regressions for the relative peak death rate, as discussed in the next section. The F-Statistic for the two distance variables jointly of 18.8 is well above the critical value of 10 favored by Stock and Yogo (2005), so that a weak-instrument problem should not apply, and two-stage-least-squares estimates should be satisfactory. The next section also considers second-stage regressions for excess flu-related death rates, and these specifications include an additional explanatory variable that is regarded as exogenous: the flu-related gross death rate for 1910–1916 (for September-February periods). If this variable is added to Eq. (1), the F-Statistic for the two distance variables jointly becomes 10.5.

2.2. Second-State regressions for flu-related excess death rates

Effects of NPIs on cumulative excess death rates and relative peak excess death rates.Table 2 has second-stage regressions applying to the 45 U.S. cities for weeks ending from September 8, 1918 to February 22, 1919. The analysis considers two dependent variables: the cumulative flu-related excess death rate and the relative peak flu-related excess death rate (the peak weekly excess death rate divided by the overall rate, with all rates expressed on an annual basis). These data are in Appendix Table A1, columns 1 and 2.

Table 2.

Effects from Non-Pharmaceutical Interventions (NPIs) 45 U.S. Cities, September 1918-February 1919.

Dependent variable:	Flu-Related Excess Death Rate		Relative Peak Excess Death Rate
	(1)	(2)	(3)	(4)
Method:	OLS	TSLS	OLS	TSLS
Constant	0.48** (0.24)	0.33 (0.34)	5.96*** (0.36)	6.60*** (0.51)
Non-pharmaceutical interventions, NPI	−0.02 (0.37)	0.31 (0.64)	−5.86*** (1.32)	−8.55*** (2.01)
Flu-related gross death rate 1910–1916	3.76*** (1.03)	4.21*** (1.26)	–	–
R-squared	0.30	0.29	0.31	0.25
Standard error of regression	0.27	0.27	1.11	1.16
Number of observations	45	45	45	45

Dependent variable:	Excess Death Rate		Relative Peak Death Rate
	(5)	(6)	(7)	(8)
Method:	OLS	TSLS	OLS	TSLS
Constant	0.47** (0.23)	0.40 (0.33)	5.86*** (0.39)	6.51*** (0.56)
School closings	1.60* (0.83)	1.70* (0.90)	−6.72* (3.58)	−8.31** (3.86)
Prohibitions of public gatherings	−2.43** (1.01)	−2.24* (1.20)	−3.21 (4.44)	−7.42 (5.26)
Quarantine/isolation	0.47 (0.60)	0.62 (0.79)	−7.12*** (2.34)	−9.39*** (2.79)
p-value, 3 NPIs same coefficients	0.05	0.06	0.74	0.90
p-value, 3 NPI coefficients=0	0.10	0.11	0.001	0.002
Flu-related gross death rate 1910–16	4.07*** (0.99)	4.27*** (1.21)	–	–
R-squared	0.40	0.40	0.32	0.26
Standard error of regression	0.26	0.26	1.13	1.18
Number of observations	45	45	45	45

Dependent variable:	Overall Flu-Related Excess Death Rate		Relative Peak Death Rate
	(9)	(10)	(11)	(12)
Method:	OLS	TSLS	OLS	TSLS
Constant	0.14 (0.30)	−0.20 (0.53)	6.69*** (0.51)	7.40*** (0.73)
Non-pharmaceutical interventions, NPI	0.51 (0.47)	1.13 (0.91)	−7.46*** (1.52)	−9.79*** (2.29)
Public-health response time, PHRT	4.29* (2.40)	6.33* (3.54)	−17.7* (9.0)	−25.2** (10.7)
p-value, NPI & PHRT jointly	0.22	0.19	0.000	0.000
Flu-related gross death rate 1910–1916	4.53*** (1.09)	5.42*** (1.57)	–	–
R-squared	0.35	0.33	0.37	0.34
Standard error of regression	0.262	0.267	1.07	1.10
Number of observations	45	45	45	45

***Significant at 1% level.

**Significant at 5% level.

*Significant at 10% level.

Notes to Table 2.

The sample applies to 45 large U.S. cities observed from week ending September 14, 1918 to that ending February 22, 1919. The dependent variable in columns 1, 2, 5, 6, 9, and 10 is the cumulative flu-related excess death rate, given in Appendix Table A1, column 1. The dependent variable in columns 3, 4, 7, 8, 11, and 12 is the relative peak death rate, given in Appendix Table A1, column 2. Standard errors of coefficients are in parentheses. OLS is ordinary least-squares. TSLS is two-stage least-squares. In column 2, the instrumental variables are the distance from Boston and its square and the flu-related gross mortality rate for the September-February periods of 1910–1916. In column 4, the instrumental variables are the distance from Boston and its square. In columns 6 and 8, the instrument lists include also the difference between school closings and prohibitions of public gatherings and between school closings and quarantine. In columns 11 and 12, the instrument lists include also the PHRT variable. All variables are shown in Appendix Table A1.

The main analysis uses information on deaths ascribed to influenza and pneumonia. This concept, used by the epidemiologists and reported for the relevant period for the 45 cities on a weekly basis in Collins et al. (1930), is expressed as flu-related excess death rates. Specifically, for each city, the average gross flu-related death rates for 1910-1916 are subtracted from the gross flu-related death rates during the 24-week study period.

An alternative concept considers all-cause excess mortality rates. This measure is available for the relevant period for the 45 cities on a monthly basis from Mortality Statistics 1918 and Mortality Statistics 1919 (U.S. Department of Commerce, Bureau of the Census, 1920 and 1921). An advantage of this concept is that it does not depend on diagnoses of causes of death, specifically of deaths due to influenza and pneumonia. A disadvantage is that it includes deaths from non-flu-related causes, which are not the focus of the study; that is, overall excess mortality adds a lot of noise to the dependent variable. Another problem is that the lack of weekly data on all-cause excess morality makes it difficult to pinpoint the peak death rate. The present analysis focuses on the flu-related concept, but the results using all-cause excess mortality turn out to yield similar results.

Aside from NPIs, the cumulative flu-related excess death rate in each city likely depends on age structure and other demographic characteristics and would depend on the nature of healthcare facilities to the extent that these were effective in curbing mortality. To take account of these effects, the regressions for cumulative flu-related excess death rates include as an explanatory variable the flu-related gross mortality rate from a prior period7 —specifically, the median rate for 1910–1916, corresponding to the months, September-February, used for the dependent variable. This variable, shown in Appendix Table A1, column 8, is calculated from information in Collins et al. (1930, appendix Table A). The idea is that this measure would reflect city characteristics such as demographics and healthcare facilities to the extent that they influence flu-related deaths in general and, therefore, likely also the flu-related excess deaths experienced during the 1918-1919 period.

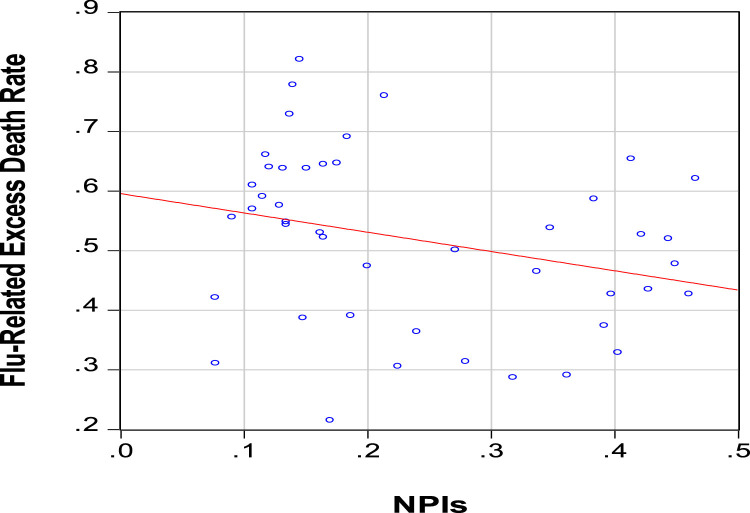
The pair-wise association between NPIs and cumulative flu-related excess death rates during the study period is in Fig. 3 . This relationship is negative, as expected (simple correlation coefficient equals −0.28). Regression results in columns 1 and 2 of Table 2 show the estimated effects of NPIs on the cumulative flu-related excess death rate (holding constant flu-related mortality for 1910–1916). For the OLS regression in column 1, the estimated coefficient on NPI is close to zero and insignificantly different from zero at the 10% level. In the two-stage least-squares (TSLS) regression in column 2,8 the estimated coefficient on NPI has the “wrong” sign (positive) and is still insignificantly different from zero at the 10% level. Therefore, there is no evidence that the variations in cumulative flu-related excess death rates across cities reflect variations in NPIs.9

Fig. 3.

Relationship between NPIs and Cumulative Flu-Related Excess Death Rate. Note: The sample is for 45 U.S. cities. NPIs from September 1918 to February 1919 is from Markel et al. (2007, Table 1), updated to include Atlanta and Detroit. The cumulative flu-related excess death rate for September 1918 to February 1919 is calculated from Collins et al. (1930, Appendix, Table B). NPIs are days in effect (in units of years) for school closings, prohibitions of public gatherings, and quarantine/isolation. See Appendix Table A1.

The estimated coefficient of the flu-related gross death rate for 1910–1916 is positive and statistically significant at the 1% level in columns 1 and 2. As mentioned, these coefficients likely pick up effects from demographics and healthcare facilities.

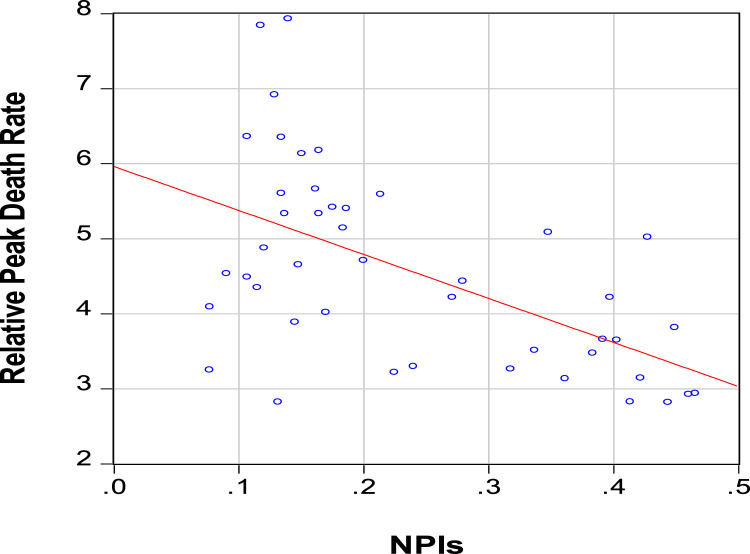
The pairwise association between NPIs and the relative peak flu-related excess death rate is in Fig. 4 . This relationship is negative, as expected, with a simple correlation coefficient of −0.56. Regression results in columns 3 and 4 of Table 2 show the estimated effects of NPIs on the relative peak death rate. The estimated coefficients on the NPI variable are −5.9 (s.e.=1.3) in column 3 (OLS) and −8.5 (s.e.=2.0) in column 4 (TSLS). Hence, the coefficients are negative and highly statistically significant, with the coefficient under TSLS notably larger in magnitude.10 A larger magnitude under TSLS makes sense because a higher relative peak death rate likely encouraged the enactment of NPIs with longer duration. That is, this reverse causation likely resulted in an upward bias (less negative) in the OLS coefficient. In terms of magnitudes, the point estimate of the coefficient on the NPI variable of −8.6 in column 4 implies that a one-standard-deviation change in NPI (by 0.13 in Table 2) implies a change in the relative peak death rate by 1.1, compared to the respective mean and standard deviation of 4.6 and 1.3 (as shown in Table 2). Hence, the variations in NPI likely account for a substantial part of the observed variations in relative peak death rates.11

Fig. 4.

Relationship between NPIs and Relative Peak Death Rate. Note: The sample is for 45 U.S. cities. NPIs from September 1918 to February 1919 is from Markel et al. (2007, Table 1), updated to include Atlanta and Detroit. The relative peak death rate, defined as the ratio of the peak weekly flu-related excess death rate to the overall flu-related excess death rate, is calculated from Collins et al. (1930, Appendix, Table B). NPIs are days in effect (in units of years) for school closings, prohibitions of public gatherings, and quarantine/isolation. See Appendix Table A1.

Overall, there is clear evidence that an increase in NPIs flattens the pattern of flu-related excess death rates, gauged by the drop in the ratio of the peak weekly flu-related excess death rate to the overall rate. This result indicates that NPIs, as measured, do matter for flu-related mortality. But this influence shows up in the relative peak death rate, not in the overall rate.

Columns 5–8 of Table 2 consider the separate roles of the three types of NPIs—school closings, prohibitions of public gatherings, and quarantine/isolation (shown in Appendix Table A1, columns 4–6). There are insufficient instruments to allow for endogeneity of all three types of NPI individually. However, it seems plausible that, while the overall duration of NPIs is endogenous with respect to flu-related excess death rates, the distribution among the three types would be exogenous. Therefore, the TSLS estimation in columns 6 and 8 includes on the instrument list the variables used before in columns 2 and 4, respectively, along with the differences between the durations of the various NPIs (school closings minus prohibitions of public gatherings and school closings minus quarantine/isolation).

For the cumulative flu-related excess death rate, the OLS results are in column 5 and the TSLS results in column 6. The only coefficients related to NPIs that are statistically significant at the 5% level are the negative ones on prohibitions of public gatherings. The results in columns 5 and 6 accept the hypothesis with p-values of 0.10 and 0.11, respectively, that the coefficients of the three NPI variables are all zero. Therefore, there is still little evidence that longer-duration NPIs reduce overall flu-related excess death rates.

For the relative peak flu-related excess death rate, the OLS results are in column 7 and the TSLS results in column 8. As in columns 3 and 4, the allowance for endogeneity of overall NPIs makes a substantial difference, with the magnitudes of the estimated coefficients notably larger under TSLS (column 8) compared to those under OLS (column 7). The results accept the hypothesis that the coefficients of each form of NPI are equal, with a p-value of 0.74 for OLS and 0.90 for TSLS. Thus, it is satisfactory to combine the three types of NPIs into a single additive form, as in columns 3 and 4.

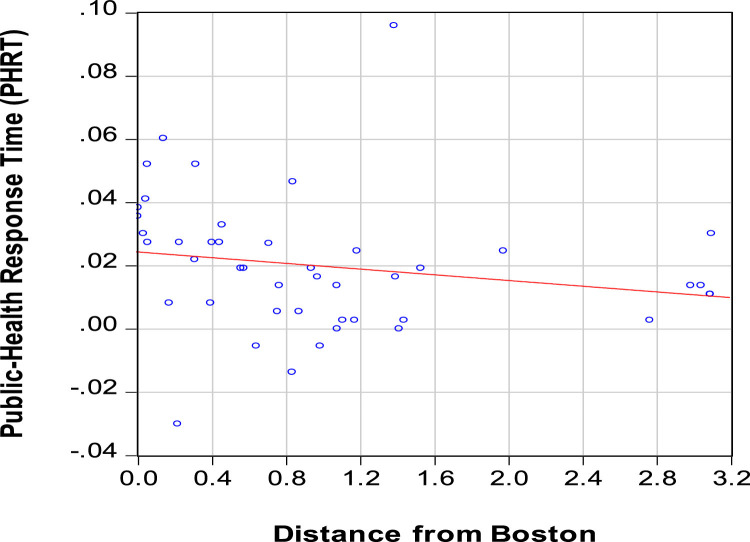
Effects from public-health response time. Columns 9–12 of Table 2 consider another measure of how NPIs were implemented—the public-health response time or PHRT constructed by Markel et al. (2007, Table 1) and shown in Appendix Table A1, column 7.12 The idea is that a higher PHRT indicates more delay in a city implementing the first intervention intended to retard flu-related deaths. Fig. 5 shows from the pair-wise relationship that the PHRT variable is negatively but weakly associated with distance from Boston, with a simple correlation coefficient of -0.20. Thus, while being further from Boston clearly raises the number of NPIs employed (Fig. 2), it has a weaker association with acting quickly to install some form of NPI. The PHRT also has positive but small simple correlation coefficients with the cumulative flu-related excess death rate (0.17) and the relative peak death rate (0.10).

Fig. 5.

Relationship between Distance from Boston (thousands of miles) and Public-Health Response Time (PHRT in years). Note: The sample is for 45 U.S. cities. Distance from Boston is the minimum distance shown by Google Maps. The public-health response time or PHRT is from Markel et al. (2007, Table 1), updated to include Atlanta and Detroit. See Appendix Table A1.

The available instruments are insufficient to distinguish the effects from the NPI and PHRT variables—moreover, the first-stage regression for PHRT analogous to Eq. (1) has an F-Statistic of only 1.9. For this reason, the TSLS results shown in Table 2, columns 10 and 12, include as instruments the variables discussed before related to NPI along with the PHRT variable itself.

For the cumulative flu-related excess death rate, when the PHRT variable is included in columns 9 and 10, the only coefficients related to NPIs that are statistically significant are the positive ones on PHRT. A positive value here suggests that a longer delay in implementing some form of intervention leads to a higher death rate. However, these coefficients differ significantly from zero only at the 10% level, and the coefficients for NPI and PHRT jointly differ insignificantly from zero at the 10% level. Thus, the inclusion of the PHRT variable still does not provide much statistical support for the hypothesis that NPIs influence cumulative flu-related excess death rates.

For the relative peak death rate, in columns 11 and 12, the regressions still show significantly negative effects from the NPI variable. The results also show, surprisingly, negative estimated coefficients on the PHRT variable; that is, a longer delay is estimated to reduce the relative peak death rate. The estimated coefficient is significant at the 10% level in the case of OLS (column 11) and at the 5% level for TSLS (column 12). These results reflect interactions between PHRT and NPI—these two forms of interventions are inversely related (simple correlation coefficient of -0.54), meaning that places with more NPIs tended to respond with a shorter delay. Therefore, the simple correlation (0.10) between PHRT and the relative peak death rate reflects partly a proxying of larger PHRT for lower NPI (which has a substantially positive estimated effect on the relative peak death rate). Once the NPI variable is held fixed, as in columns 11 and 12, the coefficient on PHRT becomes negative.

To interpret these results, imagine that an NPI is put into place with a duration of 30 days. If PHRT=0, the NPI is present from a point near the beginning of the epidemic. In contrast, if the start of the NPI is delayed by a week, so that PHRT=0.02 years, the NPI is still in effect for 30 days but begins one week later and lasts one week further into the future. The results indicate that this rise in PHRT reduces the relative peak death rate. This effect likely arises because, with a higher PHRT (up to a point), the NPIs in place match up better with the highest death rates.

Additional effects of distance from Boston. A concern with the TSLS results in Table 2 is that greater distance from Boston may impact cumulative flu-related deaths directly, not just through influencing choices of NPIs. One idea is that cities further from Boston, for which the Great Influenza tended to arrive later, have fewer weeks in the study period from the local onset of the Great Influenza until the fixed end point, which is the week ending February 24, 1919. For that reason, there could be a mechanical inverse relation between distance from Boston and the cumulative flu-related excess death rate. In fact, as is clear from Fig. 1, the mortality rates experienced in each city in the later weeks of the study period are all negligible compared to those from the peak weeks. This point is even stronger if the study period is extended out to the week ending May 31, 1919 (in which case the magnitudes in the later weeks are not only small but many appear as negative excess death rates). Thus, this mechanical effect of distance from Boston on excess death rates turns out to be unimportant.

Other concerns involve effects on mortality from a city's having more time to prepare for the disease. Since development of medical treatments (including a vaccine that turned out to be ineffective) would not have been relevant, the main possibility here is through preparation of healthcare facilities.13 However, it is unclear in 1918–1919 that better healthcare facilities mattered a lot for flu-related mortality. Thus, this form of benefit from delaying the onset of disease may have been unimportant.

Another conjecture is that cities further from Boston tended to be those that suffered more from the first wave of the Great Influenza—roughly January to April 1918—and, thereby, had more immunity against the second wave.14 This idea can be checked by using the flu-related excess mortality rate for each city from January to April 1918 (available from Collins, et al. [1930, Appendix Table A] and shown in appendix table A1, column 13). The correlation of this excess death rate with distance from Boston turns out to be weakly negative, -0.12, not positive as conjectured. The excess death rate for January to April 1918 can be added to the regressions in Table 2, columns 1 and 2, for explaining the cumulative flu-related excess death rate from September 1918 to February 1919. The estimated coefficients on the January-April 1918 variable are 0.40 (s.e.=0.68) for column 1 (OLS) and 0.47 (0.70) for column 2 (TSLS); that is, the coefficients differ insignificantly from zero. Hence, there is no evidence at the level of cities that greater exposure to the flu in the first wave diminished mortality rates in the second wave. (Note that these regressions hold fixed the flu-related gross mortality rate for the September-to-February periods of 1910–1916.)

Measured quarantine in New York City. As mentioned before, Barry (2007) has raised objections to the NPI data constructed by Markel et al. (2007) for New York City.15 The Markel data (supplement, slide 30) show that New York imposed a mandatory quarantine starting September 26, 1918, effective for 73 days. There were no school closings and no prohibitions of public gatherings. Barry (2007) argues that the quarantine, while announced, was likely never seriously implemented, in which case it would be appropriate to treat New York as having an NPI of zero. However, Aimone's (2010) discussion indicates that some aspects of a quarantine did operate in New York. Given these uncertainties, it seems appropriate to compare the initial results, with New York's NPI data reflecting a quarantine, with those modified to have no quarantine operating in New York.

The regressions in Table 2, cols. 1–8, were redone after modifying the NPI variable and the quarantine/isolation component for New York to equal 0, rather than the 0.2 years used before. This modification has minor effects on all of the results. In Table 2, columns 1 and 2, the estimated effects of the NPI variable on cumulative flu-related excess death rates remain statistically insignificantly different from zero. In columns 3 and 4, the estimated effects of the NPI variable on the relative peak death rate are still negative and highly statistically significant. The estimated coefficient falls in magnitude from -5.9 (s.e.=1.3) to −5.5 (1.3) in column 3 and from -8.5 (2.0) to −8.2 (1.9) in column 4. Similarly, in columns 5–8, the results change only in minor ways with the revised treatment of New York.16 Thus, the inference is that, even if Barry (2007)’s criticism of the measurement of quarantine in New York City is valid, a modification to account for this objection leaves the main findings intact.

3. Effects of NPIs during the COVID-19 pandemic

NPIs have also been used during the COVID-19 Pandemic. Specifically, mandated wearing of facemasks has been used extensively to attempt to reduce cases and deaths.

Herby et al. (2022) carried out a meta-analysis of 24 studies of the effects of facemask mandates on COVID-19 mortality. These studies applied across a large group of countries, within Europe, or within the United States. Their overall conclusion is “lockdowns have had little to no effect on COVID-19 mortality” (op. cit., Abstract). However, many of the studies considered lack clear causal evidence. Moreover, some studies with convincing methods of identification were excluded and seem to provide more support for the efficacy of facemasks.

Probably the most convincing analysis of the effects of facemask usage on COVID-related outcomes comes from the large-scale randomized control trial carried out from November 2020 to April 2021 in rural Bangladesh by Abaluck, et al. (2022). This study covered 342,000 adults from 600 villages, which were randomly assigned between an intervention group (178,000 persons) and a control group (164,000 persons). The intervention group “received free masks, information on the importance of masking, role modeling by community leaders, and in-person reminders for 8 weeks” (op. cit., Summary). The frequency of proper mask wearing observed in the treatment group was much higher, 42.3%, than that in the control, 13.3%. That is, the interventions raised substantially the usage of facemasks.

The fraction of persons reporting COVID-like symptoms was 7.6% in the treatment group, compared to 8.6% in the control; that is, the difference was 11.6%, which is highly statistically significant. Somewhat weaker results applied to results from blood tests on symptomatic persons (although only 40% of these persons consented to having the tests). Overall, the findings reveal clear negative causal effects of facemask usage on COVID-related cases. However, the study did not cover mortality.

Two observational studies for the United States seem to provide convincing identification of the effects of facemask mandates or usage on COVID-19 outcomes. First, Hansen and Mano (2021) used a regression-discontinuity design applied to U.S. counties across state borders to assess the effects of facemask mandates on mortality.17 They found a significantly negative effect, although Barro (2022, pp. 7–8) observes that this effect is quantitatively much weaker than that from vaccinations.

Second, Welsch (2020) relied on instrumental estimation, using the Republican share of voting in each state in the 2016 U.S. Presidential election as an instrument for facemask usage. This usage was measured in July 2020 in a large survey conducted by The New York Times. Welsch found that facemask usage had a significantly negative effect on COVID-19 mortality. Moreover, consistent with the findings in Herby et al. (2022), this relationship did not show up in OLS regressions. That is, estimation that did not allow for the endogeneity of facemask usage found little impact of facemasks on COVID-related deaths.

4. Concluding observations

The main results for the Great Influenza Pandemic applied to 45 large U.S. cities during the peak of the Pandemic from September 1918 to February 1919. The regressions demonstrate that NPIs—in the forms of school closings, restrictions of public gatherings, and quarantine/isolation—had large and statistically significant negative effects on relative peak flu-related excess death rates; that is, more interventions clearly flattened the curve for mortality. However, the impacts on cumulative flu-related excess death rates were statistically insignificantly different from zero. That is, the NPIs delayed deaths but did not ultimately avoid them.

One possible explanation for the results is that the NPIs were not maintained long enough to have a clear negative effect on cumulative deaths.18 Table 1 shows that the mean durations of school closings and prohibitions of public gatherings were only 36 days (0.10 years), whereas that for quarantine/isolation was even shorter, 18 days (0.05 years). In this view, NPIs maintained for longer periods would have had more payoff in terms of avoiding overall deaths.

In contrast to the results from the Great Influenza, NPIs in the form of facemask mandates and usage seem to have negative impacts on cases and deaths during the COVID-19 pandemic. One possible reason for the different results is that COVID-era NPIs in the form of facemask mandates and usage are more effective than the NPIs employed during the Great Influenza. The present study emphasized school closings, prohibitions of public gatherings, and quarantine/isolation. Facemasks were, in fact, used extensively during the Great Influenza, although they were not typically mandated. However, as argued by Barry (2004, especially pp. 374–375), these facemasks were constructed from gauze and were ineffective.

This last result is analogous to findings about vaccines. As argued in Barro (2022), vaccinations have been highly effective against COVID-related mortality. In contrast, vaccines against the Great Influenza, while widely developed and used, proved to be useless (see Barry [2004, especially pp. 356–358]).

Declaration of Competing Interest

There are no conflicts of interest involved in this research.

Appendix

 

Table A1.

Data Used in Regressions.

City	(1)	(2)	(3)	(4)	(5)
	Flu-related excess death rate 9/18–2/19	Relative peak flu-related excess death rate	NPI	School closings	Public gatherings
Albany	1.25	6.92	0.129	0.090	0.038
Atlanta	0.79	3.30	0.240	0.112	0.049
Baltimore	1.43	7.84	0.118	0.071	0.047
Birmingham	1.38	2.82	0.132	0.071	0.060
Boston	1.58	5.33	0.137	0.071	0.066
Buffalo	1.19	6.35	0.134	0.077	0.058
Cambridge	1.18	5.60	0.134	0.071	0.063
Chicago	0.85	5.40	0.186	0.000	0.107
Cincinnati	1.01	3.51	0.337	0.173	0.164
Cleveland	1.09	4.22	0.271	0.063	0.077
Columbus	0.71	3.65	0.403	0.186	0.216
Dayton	0.94	5.02	0.427	0.093	0.222
Denver	1.42	2.83	0.414	0.219	0.093
Detroit	0.67	4.09	0.077	0.030	0.047
Fall River	1.40	6.18	0.164	0.088	0.077
Grand Rapids	0.47	4.02	0.170	0.044	0.077
Indianapolis	0.66	3.22	0.225	0.104	0.066
Kansas City MO	1.35	2.94	0.466	0.205	0.115
Los Angeles	1.14	3.14	0.422	0.290	0.132
Louisville	0.93	4.22	0.397	0.162	0.162
Lowell	1.15	5.66	0.162	0.082	0.079
Milwaukee	0.63	3.13	0.362	0.107	0.148
Minneapolis	0.62	3.26	0.318	0.156	0.148
Nashville	1.38	6.13	0.151	0.071	0.079
New Haven	1.32	4.49	0.107	0.000	0.107
New Orleans	1.65	5.59	0.214	0.112	0.101
New York	1.03	4.71	0.200	0.000	0.000
Newark	1.20	4.53	0.090	0.052	0.038
Oakland	1.17	5.09	0.348	0.110	0.088
Omaha	1.27	3.48	0.384	0.077	0.118
Philadelphia	1.69	7.93	0.140	0.077	0.063
Pittsburgh	1.78	3.89	0.145	0.068	0.077
Portland OR	1.13	2.82	0.444	0.101	0.096
Providence	1.28	4.35	0.115	0.060	0.055
Richmond	1.13	5.33	0.164	0.082	0.082
Rochester	0.84	4.65	0.148	0.074	0.074
San Francisco	1.50	5.14	0.184	0.101	0.082
Seattle	0.93	2.92	0.460	0.099	0.101
Spokane	1.04	3.82	0.449	0.189	0.181
St. Louis	0.81	3.66	0.392	0.200	0.192
St. Paul	0.91	3.25	0.077	0.033	0.044
Syracuse	1.24	6.36	0.107	0.058	0.049
Toledo	0.68	4.43	0.279	0.142	0.137
Washington DC	1.40	5.42	0.175	0.088	0.088
Worcester	1.39	4.88	0.121	0.060	0.060

	(6)	(7)	(8)	(9)	(10)
City	Quarantine	Public-health response time, PHRT	Flu-related gross death rate, Sep-Feb 1910–16	Distance from Boston	Population 1910
Albany	0.000	0.008	0.186	0.169	100.3
Atlanta	0.079	0.000	0.208	1.076	154.8
Baltimore	0.000	0.027	0.230	0.401	558.5
Birmingham	0.000	0.025	0.220	1.182	132.7
Boston	0.000	0.036	0.220	0.000	670.6
Buffalo	0.000	0.033	0.160	0.455	423.7
Cambridge	0.000	0.038	0.196	0.003	104.8
Chicago	0.079	−0.005	0.222	0.983	2185.3
Cincinnati	0.000	0.005	0.182	0.869	363.6
Cleveland	0.132	−0.005	0.134	0.640	560.7
Columbus	0.000	0.014	0.148	0.763	181.5
Dayton	0.112	−0.014	0.156	0.833	116.6
Denver	0.101	0.025	0.172	1.972	213.4
Detroit	0.000	0.027	0.166	0.707	465.8
Fall River	0.000	0.027	0.216	0.053	119.3
Grand Rapids	0.049	0.047	0.090	0.837	112.6
Indianapolis	0.055	0.019	0.152	0.936	233.6
Kansas City MO	0.145	0.000	0.162	1.410	248.4
Los Angeles	0.000	0.014	0.120	2.983	319.2
Louisville	0.074	0.016	0.166	0.969	223.9
Lowell	0.000	0.030	0.194	0.030	106.3
Milwaukee	0.107	0.014	0.132	1.074	373.9
Minneapolis	0.014	0.016	0.134	1.391	301.4
Nashville	0.000	0.003	0.244	1.105	110.4
New Haven	0.000	0.060	0.238	0.138	133.6
New Orleans	0.000	0.019	0.228	1.526	339.1
New York	0.200	−0.030	0.206	0.215	4767.9
Newark	0.000	0.027	0.176	0.225	347.5
Oakland	0.151	0.011	0.128	3.089	150.2
Omaha	0.189	0.003	0.146	1.435	124.1
Philadelphia	0.000	0.022	0.182	0.308	1549.0
Pittsburgh	0.000	0.019	0.294	0.572	533.9
Portland OR	0.247	0.011	0.090	3.088	207.2
Providence	0.000	0.052	0.198	0.051	224.3
Richmond	0.000	0.019	0.216	0.556	127.6
Rochester NY	0.000	0.008	0.146	0.392	218.1
San Francisco	0.000	0.030	0.148	3.095	416.9
Seattle	0.260	0.014	0.080	3.039	237.2
Spokane	0.079	0.003	0.110	2.762	104.4
St. Louis	0.000	0.003	0.196	1.171	687.0
St. Paul	0.000	0.096	0.106	1.383	214.7
Syracuse	0.000	0.052	0.154	0.312	137.2
Toledo	0.000	0.005	0.132	0.754	168.5
Washington DC	0.000	0.027	0.172	0.440	331.1
Worcester	0.000	0.041	0.192	0.043	146.0

	(11)	(12)	(13)	(14)	(15)
City	Area	Population Density 1910	Flu-related excess death rate 1/18–4/18	All-cause excess death rate 9/18–2/19	Relative peak all-cause excess death rate 9/18–2/19
Albany	10.8	9.29	−0.03	0.83	6.26
Atlanta	25.7	6.02	0.61	0.43	2.90
Baltimore	30.1	18.55	0.43	0.98	5.75
Birmingham	48.3	2.75	1.42	1.00	2.18
Boston	41.1	16.32	0.42	1.39	2.68
Buffalo	38.7	10.95	0.27	1.10	4.28
Cambridge	6.3	16.63	0.35	1.24	2.58
Chicago	185.1	11.81	−0.22	0.65	4.79
Cincinnati	49.8	7.30	0.39	0.88	2.62
Cleveland	45.6	12.30	0.37	1.11	2.06
Columbus	20.3	8.94	0.22	0.59	2.30
Dayton	15.7	7.43	0.12	0.62	5.07
Denver	57.9	3.69	0.27	1.20	2.25
Detroit	40.8	11.42	0.31	0.47	2.66
Fall River	33.9	3.52	−0.35	1.33	4.98
Grand Rapids	16.8	6.70	0.16	0.21	5.40
Indianapolis	33.0	7.08	0.38	0.39	3.00
Kansas City MO	58.5	4.25	0.76	1.08	2.09
Los Angeles	99.2	3.22	−0.06	0.91	1.95
Louisville	20.7	10.82	0.78	1.01	2.93
Lowell	13.0	8.18	0.54	1.03	4.35
Milwaukee	22.8	16.40	0.26	0.46	3.41
Minneapolis	50.1	6.02	0.19	0.52	2.21
Nashville	17.1	6.46	1.09	1.33	4.24
New Haven	17.9	7.46	0.09	1.02	4.12
New Orleans	196.0	1.73	0.17	1.33	3.85
New York	286.8	16.62	0.32	0.75	4.35
Newark	23.2	14.98	0.44	0.99	4.16
Oakland	45.7	3.29	0.27	1.00	2.17
Omaha	24.1	5.15	0.23	2.87	1.87
Philadelphia	130.2	11.90	0.60	1.46	5.51
Pittsburgh	41.4	12.90	1.51	1.90	2.69
Portland OR	48.4	4.28	0.16	1.09	1.99
Providence	17.7	12.67	0.24	1.26	3.54
Richmond	10.0	12.76	−0.04	0.68	4.99
Rochester NY	20.1	10.85	0.25	1.40	2.63
San Francisco	46.5	8.97	0.19	1.30	2.41
Seattle	55.9	4.24	0.17	0.86	1.86
Spokane	36.8	2.84	0.16	0.84	2.42
St. Louis	61.4	11.19	0.44	0.58	2.87
St. Paul	52.2	4.11	0.14	0.76	2.76
Syracuse	17.3	7.93	0.39	0.79	5.75
Toledo	25.0	6.74	0.25	0.45	3.10
Washington DC	60.0	5.52	0.52	0.92	4.60
Worcester	37.0	3.95	0.28	1.18	3.89

Notes to Table A1.

The sample comprises 45 of the 50 U.S. cities with center-city populations in 1910 above 100,000. These 45 have weekly data on flu-related excess death rates over the second and most deadly wave of the Great Influenza Pandemic: the 24 weeks from week ending September 14, 1918 to week ending February 22, 1919. The remaining 5 large cities lack parts of the weekly data over this period.

Flu-related excess death rates, including deaths attributed to pneumonia, are calculated as percent of city population and expressed at an annual rate. The cumulative flu-related excess death rate 9/18–2/19 refers to the 24-week sample from the week ending September 14, 1918 to the week ending February 22, 1919. These values are calculated from the weekly data given in Collins et al. (1930, Appendix Table B). (A typo in the data for Pittsburgh for November 23, 1918 was corrected based on the information in Davis, 1918). The flu-related excess death rate is calculated by Collins, op.cit., as the difference between the flu-related gross death rate for each city and week and the median of the flu-related gross death rates for the corresponding city and week for 1910–1916. The relative peak death rate is the ratio of the highest weekly flu-related excess death rate in the 24-week sample to the overall flu-related excess death rate.

The flu-related gross death rate for 1910–1916 is calculated from the median values shown for the September-February months in Collins et al. (1930, Appendix Table A). Excess death rate 1/18-4/18 is the cumulative flu-related excess death rate from January 1918 to April 1918, calculated from the monthly data given in Collins et al. (1930, Appendix Table A). The all-cause excess mortality rate is the gross death rate for all causes from September 1918 to February 1919 from U.S. Department of Commerce, 1920 and 1921 (Mortality Statistics 1918, pp. 123–132; Mortality Statistics 1919, pp. 109–118), less the average of the gross death rate for all causes for 1910–1916 (Mortality Statistics 1919, pp. 12–13). The relative peak all-cause death rate uses the peak monthly death rate from September 1918 to February 1919 from the same sources.

NPI is the duration in years of three forms of non-pharmaceutical interventions—school closings, prohibitions of public gatherings, and quarantine/isolation—over the 24-week sample, as estimated by Markel et al. (2007, Table 1 and supplemental figures). Data on NPIs for Atlanta and Detroit were obtained from information in, respectively, The Atlanta Constitution and The Detroit Free Press, Public Health Reports for the two cities, and the Influenza Encyclopedia, available at influenzaarchive.org. The three forms of NPIs are shown separately, and NPI is the sum of these three. The public-health response time or PHRT, defined in Markel et al. (2007, Table 1), is the difference in years between the date of the first NPI implementation and the time when the weekly flu-related excess death rate reached twice the median gross death rate applicable to the corresponding month in 1910–1916.

Distance from Boston is the minimum distance in thousands of miles from Google Maps. Population 1910 (in thousands) and area (in square miles) are for central cities from 1910 U.S. Census. Population density is the ratio of population to area.