Background selection under evolving recombination rates

Abstract

Background selection (BGS), the effect that purifying selection exerts on sites linked to deleterious alleles, is expected to be ubiquitous across eukaryotic genomes. The effects of BGS reflect the interplay of the rates and fitness effects of deleterious mutations with recombination. A fundamental assumption of BGS models is that recombination rates are invariant over time. However, in some lineages, recombination rates evolve rapidly, violating this central assumption. Here, we investigate how recombination rate evolution affects genetic variation under BGS. We show that recombination rate evolution modifies the effects of BGS in a manner similar to a localized change in the effective population size, potentially leading to underestimation or overestimation of the genome-wide effects of selection. Furthermore, we find evidence that recombination rate evolution in the ancestors of modern house mice may have impacted inferences of the genome-wide effects of selection in that species.

1. Introduction

Different modes of selection (e.g. positive, purifying and balancing) all affect genetic variation at sites linked to the actual targets of selection (reviewed in [1]). In the case of purifying selection, the removal of deleterious mutations causes linked neutral variants to be lost along with them through a process referred to as background selection (BGS; [2]). Of the mutations that affect fitness in natural populations, the vast majority are likely deleterious, with a comparatively small proportion of beneficial mutations [3]. For those reasons, it has been proposed that BGS is ubiquitous across eukaryotic genomes and should be incorporated into null models for population genomics [4,5]. Indeed, recent studies have used BGS to set baseline patterns for identifying the locations and effects of positively selected mutations [6,7] and understanding Lewontin's paradox of genetic diversity [8]. Interpreting genome-wide patterns of genetic diversity in terms of BGS, however, requires accurate estimates of population genetic parameters, particularly recombination rates.

In many species, the recombination rate per base pair (r) varies across the genome both between and within chromosomes [9]. For example, in the house mouse (Mus musculus), the average r for chromosome 19 (the shortest chromosome) is around 60% higher than for chromosome 1 (the longest chromosome; [10]). The requirement of at least one crossover per chromosome per meiosis in mammals causes shorter chromosomes to recombine at a higher average rate than longer ones [11–13]. Local recombination rates can vary substantially across chromosomes as well, and, in some cases, this variation is predicted by gross features of chromosome architecture such as the locations of centromeres and telomeres [14]. In mice, the majority of crossovers occur in a minority of the genome, in narrow windows (in the order of 1 to 5 kbp) referred to as hotspots [14]. The positions of recombination hotspots in mice and, in some other vertebrates, are determined by the binding of a protein encoded by the PRDM9 gene to specific DNA motifs [15,16], although hotspots are still observed in PRDM9 knockout lines and in dogs, which lack a functional copy of PRDM9 [17,18].

Estimates of r can be obtained empirically by examining the inheritance of genetic markers through controlled crosses or through pedigrees, or by comparing an individual's genome to that of its gametes (e.g. [19]). Both methods reconstruct recombination events over one or a few generations and thus provide estimates of r for contemporary populations. Alternatively, estimates of r can be obtained indirectly by analysing patterns of linkage disequilibrium across the genome (e.g. [20]), in which case estimates reflect both recent and ancestral recombination events. Whether recombination rates are estimated from marker transmission or population genetics, using such estimates when analysing variation across the genome in terms of BGS implicitly assumes that the recombination landscape has not changed over the time in which patterns of diversity have been established. However, recombination rate landscapes can evolve rapidly in some lineages. For example, owing to the relationship between chromosome size and average r, changes in chromosome length (i.e. karyotype evolution) may induce changes in r. The lineage leading to Mus musculus (2n = 40) has experienced large chromosomal rearrangements since it shared a common ancestor with Mus pahari (2n = 48) 3–5 million years ago [21]. Moreover, populations of Mus musculus domesticus harbouring different karyotypes exhibit different genomic landscapes of recombination [22]. Chromosomal fusions can exhibit meiotic drive [23] so new karyotypes may spread to fixation very rapidly. Even mice with the same karyotype vary in regional recombination rate across substantial proportions of the genome [24,25] and in total number of crossovers [26,27], both within and between sub-species. There is also evidence that PRDM9, the gene that encodes the protein that dictates the locations of recombination events, has undergone recurrent bouts of positive selection in mice [28], and wild-derived lines of M. musculus spp. possess various PRDM9 alleles corresponding to different suites of recombination hotspots [29]. Overall, there is clear evidence from mice that recombination rates can evolve rapidly on broad and fine scales.

Changes in the recombination rate over time may influence patterns of genetic variation across the genome [4,30]. For example, chromosomal fusions would decrease recombination rates experienced by individual nucleotides in the fused chromosomes and thus increase the effects of BGS and other processes mediated by recombination. Consistent with this hypothesis, Cicconardi et al. [31] found evidence suggesting that chromosomes that underwent fusions in the ancestors of extant Heliconius butterfly species now exhibit reduced recombination rates and nucleotide diversity (π), presumably owing to amplified BGS effects. Following the evolution of the recombination rate landscape, there will be a lag period wherein patterns of genetic variation more closely reflect ancestral recombination rates than derived rates. Furthermore, the fixation of recombination modifiers may be associated with demographic effects. For example, the fixation of a new chromosomal variant would resemble a localized population bottleneck. Over time, as new deleterious mutations arise and cause BGS, patterns of genetic variation will come to reflect derived recombination rates. Depending on the extent and pace of recombination rate evolution, effects of BGS may be obscured in lineages that are still within the lag period. In this paper, we examine how patterns of neutral genetic variation under BGS respond to evolution of the recombination rate and describe how this could affect analyses that are used to identify the effects of selection on a genome-wide scale.

2. Results

(a) . Background selection under evolving recombination rates

The effects of BGS reflect the interplay of purifying selection and recombination [32], so changes to the recombination rate will influence the effects of BGS. Under strong purifying selection, BGS resembles a localized reduction in the effective population size (N_e). N₀ is used to denote the hypothetical effective population size that would be expected in the absence of all linked selection effects. It is difficult to estimate N₀ from empirical data [33], but in some species N₀ may be approximated by examining genomic regions that are expected to be only weakly affected by BGS [5]. An increase in the recombination rate between neutral sites and sites subject to purifying selection will decrease the effect of BGS (bringing N_e closer to N₀) and vice versa for a decrease in the recombination rate. At a neutral locus v, coalescence times under BGS ($T_{\mathrm{BGS},\nu }$) are shorter than those expected in the absence of linked selection (T₀) [32] and the effect of BGS is often expressed as $B_{\nu }=T_{\mathrm{BGS},\nu }/T_0=N_{\mathrm{e},\nu }/N_0$ (e.g. [32]). Consider a population that underwent a change in the recombination rate such that v experiences a BGS effect of $B_{\nu }^{\mathrm{\prime }}$ under the derived recombination rate regime. Even with instantaneous changes in the recombination rate, genetic variation at v would not reflect $B_{\nu }^{\mathrm{\prime }}$ immediately, as there would be a lag period after recombination rate change wherein coalescence times (and patterns of genetic variation) would more closely reflect B_v.

If BGS resembles a localized reduction in N_e under strong purifying selection, the period of lag after a change in the recombination rate may resemble the change in coalescence times following a change in the population size. If the recombination rate changed at time t in the past (measured in 2N₀ generations), then BGS under the new recombination rate can be described with

$$B_{\nu ,t}=B_{\nu }\left(1+\left({\displaystyle \frac{B_{\nu }}{B_{\nu }^{\mathrm{\prime }}}-1}\right){\mathrm{e}}^{-t}\right).$$ 2.1

We obtained equation (2.1) by modifying an expression that describes coalescence times after an instantaneous change in the population size from Johri et al. [5]. Note that Pool & Nielsen [34] provided similar expressions to those given by Johri et al. [5].

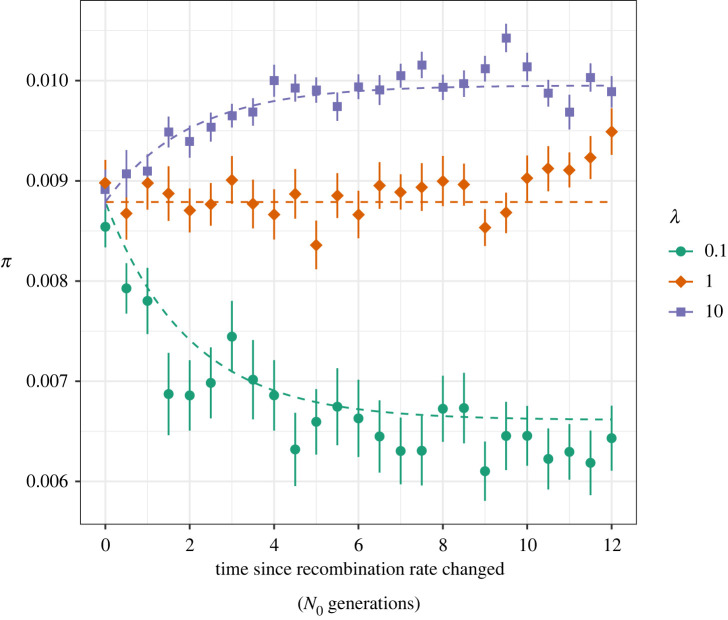
We modelled deleterious mutations occurring in a single functional element (e.g. a protein-coding exon) and examined π for neutral mutations in and around this region after an instantaneous change in the recombination rate (electronic supplementary material, figure S1). The value of π gradually departed from the expectations based on the ancestral recombination rate over 4N₀ generations, when it finally aligned to the expectation under the derived recombination rate (figure 1; electronic supplementary material, figure S2). Up to approximately 2N₀ generations after a change in the recombination rate, π more closely resembled the expectation under the ancestral recombination rate than it did under the derived rate (figure 1; electronic supplementary material, figure S2). After around 4N₀ generations, coalescence times closely reflected those expected under BGS given the derived recombination rate, as measured by π (figure 1; electronic supplementary material, figure S2). However, it is important to note that when deleterious mutations have nearly neutral deleterious effects, equation (2.1) may not predict changes in nucleotide diversity particularly well because in such cases BGS does not resemble a simple reduction in N_e [35,36].

Figure 1.

The effect of BGS on nucleotide diversity (π) over time after recombination rates change by a factor λ. The dashed lines were calculated using equation (2.1) and formulae from Nordborg et al. [32]. Points indicate the mean from 50 replicate simulations. Nucleotide diversity was calculated for neutral sites 10 000 bp away from sites subject to purifying selection. Points are shown with error bars indicating ± 1 standard error. (Online version in colour.)

In the case of a population that has recently undergone shifts in the recombination rate landscape (i.e. fewer than 2N₀ generations ago), estimates of r would likely reflect contemporary recombination rates regardless of how they were obtained. Estimates of r from patterns of marker inheritance in crosses or pedigrees always reflect contemporary rates, and our results suggest that population genetic estimates (i.e. obtained from patterns of linkage disequilibrium (LD)) may reflect contemporary recombination rates within 0.5N₀ generations of an increase or decrease in r (electronic supplementary material, figure S3). However, LD-based estimates of the recombination rate are downwardly biased by the effects of BGS (electronic supplementary material, figure S3).

Depending on the direction and magnitude of recombination rate change, population genomic analyses that compare features of genetic variation with estimates of r could underestimate or overestimate the effects of BGS (and other forms of selection) on patterns of genetic variation. For example, LD-based estimates of r (in units 4N_er) have been compared with estimates of nucleotide diversity, which, for neutral sites, approximates 4N_eμ, to investigate the relative role of recombination and mutation in shaping patterns of linked selection (e.g. [37]). Applying such an analysis to lineages that have recently undergone evolution of the recombination map may overestimate or underestimate the effects of BGS, depending on how recombination rates have changed.

(b) . Patterns of genetic variation after evolution of the recombination landscape

To understand how population genomic analyses may be affected by changes in r, we simulated two scenarios of BGS under evolving recombination rates. In the first, the broad-scale landscape of r was rearranged (electronic supplementary material, figure S4A). In the second, the locations of recombination hotspots were shifted, as if a new PRDM9 allele had fixed in a population (electronic supplementary material, figure S4B). In both scenarios, deleterious mutations occurred at random across the genome, generating widespread BGS such that there was a positive correlation between π and r at equilibrium (figure 2). For the sake of simplicity, our analyses assumed that recombination rate is invariant among individuals, even as heritable variation in recombination rates has been reported in several species (reviewed in [9]).

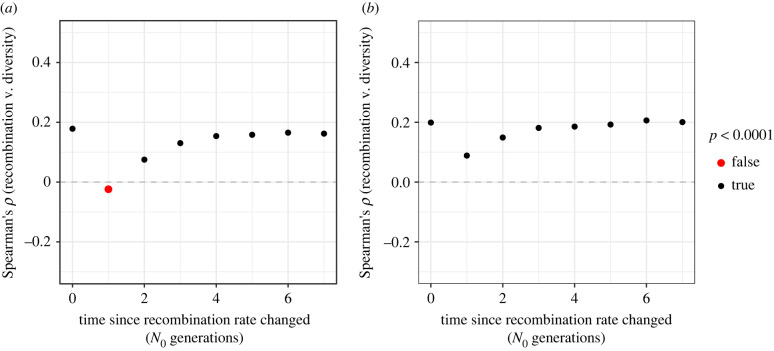
Figure 2.

Spearman's correlation between nucleotide diversity (π) and recombination rate (r) over time after recombination rates evolve; (a) shows results for a broad-scale shift in the recombination landscape and (b) shows results for recombination rate evolution by the movement of hotspots. Results are shown for 10 kbp analysis windows. (Online version in colour.)

A positive correlation between π and r is a hallmark of selection at linked sites across a genome [38], but the evolution of the recombination rate may obscure this pattern. In both the scenarios we simulated, changes in r did not influence the average nucleotide diversity across simulated chromosomes (electronic supplementary material, figure S5), because, under the models of recombination rate evolution we implemented, the average map length was constant over time. However, before the change in the recombination rate, there was a positive correlation between π and r in both scenarios that was detectable when examining 10 kbp, 100 kbp and 1 Mbp analysis windows (figure 2; electronic supplementary material, figure S6). Following changes in the recombination rate landscape under the model of broad-scale recombination rate variation, the correlation between π and r was either absent or misleading (figure 2a; electronic supplementary material, figure S6A). Under the model of recombination hotspot evolution, the correlation between π and r was weakened by change in the landscape of hotspots (figure 2b). In both cases we simulated, after about 4N₀ generations a positive correlation between π and derived r was restored to levels similar to what had been observed before the recombination maps changed (figure 2; electronic supplementary material, figure S6). Figure 2 shows results for 10 000 bp analysis windows; similar results were found when examining larger windows (electronic supplementary material, figure S5).

Both scenarios we simulated are hypothetical, but they demonstrate that recombination rate evolution can readily obscure population genomic analyses aimed at understanding genome-wide processes. In the case of the broad-scale map, we simulated a quite extreme scenario that caused the correlation between π and r to change sign (figure 2a). While this scenario may be unrealistic in nature, it serves to demonstrate the effects that recombination rate evolution could exert on patterns of diversity. The simulations modelling hotspot evolution were more realistic, as we based the length, number and intensity of recombination hotspots on results for mice. Given the extensive evidence of recombination hotspot evolution in mice, the simulations we performed demonstrate that evolution of hotspots could indeed weaken genome-wide patterns such as the relationship between π and r (figure 2b).

(c) . Rapid recombination rate evolution in house mice

Rapid evolution of recombination rates in Mus musculus may have influenced our ability to identify the effects of selection across that species' genome. Kartje et al. [39] recently demonstrated that natural populations of M. m. domesticus exhibit a very weak correlation between π and r (when examining analysis windows of various widths) and concluded that selection at linked sites exerted only modest effects on genetic variation throughout the genome. This is notable because wild mice are thought to have large effective population sizes for mammals [40] and genome-wide effects of selection are thought to be more pronounced in species with large N_e [38]. As discussed in the Introduction, there is evidence that mice have undergone rapid evolution of the recombination rate. For example, around 3–5 Ma, the lineage leading to M. musculus experienced a burst of karyotype evolution [21]. If that burst of karyotype evolution affected recombination rates and ancestral mouse populations were very large, then contemporary mice may still be within the lag period described by equation (2.1). Patterns of genetic diversity in mice may still be adjusting to historical changes in the recombination rate, and we may see a stronger correlation between π and r in genomic regions that have not undergone dramatic changes in the recombination rate.

Using an alignment of genomes from closely related species, Thybert et al. [21] distinguished chromosomes in the M. musculus genome that have undergone dramatic rearrangements in the last 5 million years from those that have not. We re-analysed data from Kartje et al. [39] and found that the correlation coefficient between π and r was more positive on chromosomes that have not undergone large-scale rearrangements in the last 3–5 million years (table 1) for M. m. domesticus individuals from France and Germany. This pattern holds when looking at analysis windows of 5 kbp and 1 Mbp (table 1). No substantial correlations were found for mice from Gough Island in any comparison. M. m. domesticus are believed to have colonized Gough Island in the nineteenth century and to have experienced a severe population bottleneck [41], a demographic history that could have further obscured the correlation between nucleotide diversity and recombination rate in that population.

Table 1.

The correlation between nucleotide diversity (π) and recombination rate (r) for three populations of house mice (Mus musculus domesticus) calculated from all autosomes, conserved chromosomes that exhibit no syntenic breaks between M. musculus and M. pahari, and chromosomes that experienced large-scale rearrangements as identified by Thybert et al. [21]. Correlations with p-values less than 0.00056 (a Dunn–Šidák corrected ɑ = 0.01) are highlighted in italics.

window size	population	whole genome		conserved chromosomes		rearranged chromosomes
		Spearman's ρ	p-value	Spearman's ρ	p-value	Spearman's ρ	p-value
5 kbp	Gough Island	0.00767 [0.00340–0.0113]	4.28 × 10−5	0.00880 [0.00208–0.0155]	0.0102	0.00486 [0.000466–0.00925]	0.0302
5 kbp	France	0.00408 [0.000407–0.00775]	0.0295	0.0403 [0.0336–0.0470]	6.10 × 10−32	−0.0107 [−0.0151 – −0.00632]	1.76 × 10−6
5 kbp	Germany	0.00752 [0.00385–0.0112]	6.05 × 10−5	0.0152 [0.00844–0.0219]	9.63 × 10−6	0.00386 [−0.00053–0.00825]	0.0849
1 Mbp	Gough Island	0.0536 [0.0131–0.0938]	0.009 46	0.0588 [−0.0162–0.1332]	0.124	0.0437 [−0.00438–0.0916]	0.0748
1 Mbp	France	0.0450 [0.00452–0.0853]	0.0294	0.135 [0.0606–0.208]	0.000 400	0.00999 [−0.0381–0.0580]	0.684
1 Mbp	Germany	0.0535 [0.0131–0.0938]	0.00953	0.0775 [0.0025–0.0152]	0.0428	0.0426 [−0.00554–0.0905]	0.0828

3. Discussion

The evolution of the recombination rate will influence the effects of selection at linked sites (e.g. BGS and selective sweeps) and thus influence patterns of genetic variability. Estimates of the recombination rate made from contemporary populations may not adequately predict genetic variability up to 2N₀ generations following evolution of the recombination rate landscape (figures 1 and 2). Our re-analysis of the Kartje et al. [39] data suggests that mice are still within the lag period after evolution of the recombination rate, such that π in M. m. domesticus does not fully reflect contemporary recombination rates in M. musculus. By contrast, the ancestors of Heliconius butterflies also underwent large-scale karyotype evolution, but gross patterns of π versus chromosome length in those species suggest that patterns of variation have largely re-equilibrated after changes in r [31].

While our re-analysis of the data from Kartje et al. [39] suggests that recombination rate evolution in the ancestors of mice obscures the evidence for natural selection across the genome, the overall correlations between π and r were still fairly weak on the conserved chromosomes (table 1). The largest rank correlation coefficient we found was 0.135 for the sample of M. m. domesticus from France (1 Mbp windows; table 1). By contrast, Spearman's rank correlation between nucleotide diversity and recombination rate in humans has been reported to be 0.219 for 400 kbp analysis windows [42]. The variance in recombination rates across the M. musculus genome is less than half of that reported for humans [43], so perhaps the effects of BGS across the genome are more homogeneous in M. musculus than they are in humans, contributing to the weak correlations between π and r shown in table 1. Beyond the pulse of karyotype evolution reported by Thybert et al. [21], there is clear evidence of recent and likely ongoing evolution of the recombination rate in M. musculus (see Introduction), which may further obscure genome-wide evidence for the effects of natural selection. For example, there is evidence that the landscape of recombination hotspots in the M. musculus genome has evolved rapidly among sub-species and populations [29]. Our simulations suggest that even a single change to the locations of hotspots can substantially weaken the correlation between π and r (figure 2; electronic supplementary material, figure S6). Of course, there are reasons why species may not exhibit a strong positive correlation between π and r that have nothing to do with recombination rate evolution [38]. For example, wild rice and domesticated rice (Oryza spp.) exhibit negative correlations between π and r, but in those species, there is a strong positive correlation between the density of functional sites (i.e. sites subject to purifying selection) and the recombination rate [44]. In such a case, the effects of BGS are primarily occurring in regions of high recombination.

In the model we used in this study, we assumed that recombination rate modifiers fix instantaneously. While instantaneous change is unlikely, there is reason to expect that recombination rate evolution may occur rapidly. For example, in the case of karyotype evolution, derived chromosomal variants may exhibit meiotic drive [23] and rapidly spread to fixation. In addition, the spread of some kinds of recombination modifiers may mimic demographic effects. For example, the fixation of a derived chromosomal variant would generate the effect of a localized population size bottleneck followed by an expansion, changes that can interact with BGS [4,5,45,46]. BGS acting during the course of a bottleneck + expansion scenario leads to levels of nucleotide diversity that deviate from standard BGS predictions [46]. The interaction between recombination rate evolution and demography in the context of BGS is an area for further research.

This paper should add to the growing appreciation of recombination as an evolutionarily labile trait. As pointed out by Smukowski Heil et al. [47], Comeron [4], and Pettie et al. [30], information on recombination rates in outgroup species is an important covariate when performing population genomic analyses. In some lineages, recombination rates may evolve slowly. Birds, for example, have highly conserved karyotypes and in some cases highly conserved recombination landscapes [48,49]. Evolution of the recombination rate is one of many possible reasons why one might not be able to adequately identify the effects of BGS (or natural selection more broadly) from population genomic data (see reviews in [38] and [4]), but conservation of recombination landscapes will likely make comparative population genomics more straightforward [30].

4. Methods

(a) . Model

BGS has been modelled as the reduction in effective population size (N_e) at a neutral site due to the removal of linked deleterious variants. The effects of BGS are often expressed as $B=N_{\mathrm{e}}/N_0,$ where N_e is the effective population size and N₀ is the expected population size under strict neutrality. In a non-recombining genome, B is proportional to the ratio of the deleterious mutation rate to the strength of selection acting on harmful mutations [2]. For a neutral site present on a recombining chromosome, the effects of BGS depend on the density of functional sites (i.e. those that can mutate to deleterious alleles), the strength of selection at functional sites, the mutation rate at functional sites and the recombination rate between the neutral site and the functional sites [32,50,51]. For a neutral locus v linked to x functional sites, the reduction in N_e has been described with the following equation:

$$B_{\nu }={\displaystyle \frac{N_{\mathrm{e}}}{N_0}=\exp \left[-\sum _x{\displaystyle \frac{u_x}{t{(1+(1-t)r_{x,v}/t)}^2}}\right],}$$

where u_x is the deleterious mutation rate at functional site x, t is the heterozygous fitness effect of a deleterious mutation (i.e. 0.5s in the case of semi-dominance) and r_x,v is the recombination map distance between the neutral locus and functional site x. In the above equation, deleterious mutations have fixed effects, but it is straightforward to incorporate a distribution of fitness effects [32]. The above equation holds when selection is sufficiently strong that random drift does not overwhelm selection $(N_{\mathrm{e}}s>1)$ [35].

(b) . Simulations

We simulated BGS under recombination rate evolution using two types of simulations in SLiM v. 3.2 [52]. We simulated diploid populations of N_e = 5000 individuals. In all cases, we scaled mutation, recombination and the strength of selection to approximate evolution in a large population.

The first set of simulations was designed to examine how long it takes for patterns of neutral diversity under BGS to equilibrate after the recombination rate evolves. In these simulations, the genome was 25 kbp long with a 5 kbp functional element in the centre. Mutations occurred in the functional element at rate $\mu =5\times {10}^{-7}$ and had semi-dominant fitness effects with a fixed selection coefficient of $s=-0.01$. Recombination occurred at a uniform rate of r = 5 × 10⁻⁷ across the chromosome. After 80 000 generations (16N_e generations), we simulated an instantaneous change in the recombination rate, multiplying r by λ, giving $r=5\times {10}^{-7}\lambda$. We simulated cases with λ = 0.1, 1.0 and 10.0. Simulated populations were sampled every 2500 generations after the recombination rate changed and we performed 200 replicates for each set of parameters tested. Note that these simulations were not designed to be particularly realistic, but to provide clear-cut patterns to test the theoretical predictions.

The second set of simulations was designed to examine how patterns of π versus r varied over time when recombination rates evolved at fine and/or broad scales. For these simulations, we modelled chromosomes that were 10 Mbp long. Neutral mutations occurred at random across the length of the sequence at a rate of 5 × 10⁻⁷ (such that expected nucleotide diversity was 0.01). Deleterious mutations occurred at random across the length of the sequence at a rate of 5 × 10⁻⁸ with semi-dominant fitness effects drawn from a gamma distribution with a mean ($\overline{s}$) of −0.1 and a shape parameter of 0.1. The deleterious mutation rate was chosen so that 10% of the genome was subject to purifying selection. Populations evolved under BGS for 80 000 generations (i.e. 16N_e generation). In generation 80 000, there was instantaneous evolution of the recombination landscape, after which we recorded the tree-sequence of the population every 5000 generations for a further 40 000 generations. We incorporated two models of recombination rate variation and evolution of the recombination map as follows.

(1) We modelled recombination rate evolution at broad scales by rearrangement of the recombination landscape. Recombination rates vary across the genome [9]. For example, recombination rates vary by a factor of 3 across chromosome 1 in mice. In these simulations, recombination varied from r = 2.08 × 10⁻⁷ to r = 6.24 × 10⁻⁷ across the simulated chromosome (electronic supplementary material, figure S4A). When the recombination landscape evolved, we reversed the order of recombination rates across the genome (electronic supplementary material, figure S4A).

(2) We modelled evolution of the recombination map by the movement of hotspots. Recombination occurred at a uniform rate of r = 6 × 10⁻⁸, except in 5 kbp hotspots, where it occurred at a rate of r = 6 × 10⁻⁶. At the beginning of a simulation, a Poisson number of hotspots was sampled with an expectation of 120. Hotspots were placed at random across the simulated chromosome. When the recombination landscape evolved, we resampled the locations of hotspots (electronic supplementary material, figure S4B).

In both cases, rates were chosen such that the total map length was similar to one that recombined at a constant rate of $4N_{\mathrm{e}}r=0.008$, the value reported for wild mice [53]. For both models of recombination rate map evolution, we performed 20 simulation replicates, giving a total of 200 Mbp-worth of simulated data, similar to the length of chromosome 1 in mice.

For all simulations, we used the tree-sequence recording option in SLiM and neutral mutations were added to the resulting tree-sequences at a rate of 5 × 10⁻⁷ using PySLiM and msprime [54,55]. Nucleotide diversity (π) was calculated in windows of varying size using sci-kit-allel. We used the program PyRho [20] to estimate recombination rates from samples of 10 diploid individuals from 20 replicate simulations. Spearman's ρ between π and r was calculated using R [56] . All figures were made using ggplot2. All simulation scripts and analysis and plotting scripts are deposited at https://github.com/TBooker/BGS_RecombinationRateEvolution.

Data accessibility

All simulation scripts and analysis and plotting scripts are deposited at https://github.com/TBooker/BGS_RecombinationRateEvolution.

Authors' contributions

T.R.B.: conceptualization, formal analysis, investigation, methodology, writing—original draft, and writing—review and editing; B.A.P.: conceptualization, resources, and writing—review and editing; A.T.: conceptualization, and writing—review and editing.

All authors gave final approval for publication and agreed to be held accountable for the work performed herein.

Conflict of interest declaration

We declare we have no competing interests.

Funding

T.R.B. was funded by a Bioinformatics Fellowship awarded by the Biodiversity Research Centre at the University of British Columbia. B.A.P. was supported by NIH R35 GM139412.