Mathematics of a single-locus model for assessing the impacts of pyrethroid resistance and temperature on population abundance of malaria mosquitoes

Abstract

This study presents a genetic-ecology modeling framework for assessing the combined impacts of insecticide resistance, temperature variability, and insecticide-based interventions on the population abundance and control of malaria mosquitoes by genotype. Rigorous analyses of the model we developed reveal that the boundary equilibrium with only mosquitoes of homozygous sensitive (resistant) genotype is locally-asymptotically stable whenever a certain ecological threshold, denoted by ${\mathcal{R}}_0^{SS}({\mathcal{R}}_0^{RR})$, is less than one. Furthermore, genotype i drives genotype j to extinction whenever ${\mathcal{R}}_0^j>1$ and ${\mathcal{R}}_0^i<1$ (where i, j = SS or RR, with i ≠ j). The model exhibits the phenomenon of bistability when both thresholds are less than one. In such a bistable situation, convergence to any of the two boundary equilibria depends on the initial allele distribution in the state variables of the model. Furthermore, in this bistable case, where $\max \{{\mathcal{R}}_0^{SS},{\mathcal{R}}_0^{RR}\}<1$, the basin of attraction of the boundary equilibrium of the mosquito genotype with lower value of the ecological threshold is larger. Specifically, the basin of attraction of the boundary equilibrium for genotype i is larger than that of genotype j if ${\mathcal{R}}_0^i<{\mathcal{R}}_0^j<1$. When both ecological thresholds exceed one $(\mathrm{m}\mathrm{i}\mathrm{n}\{{\mathcal{R}}_0^{SS},{\mathcal{R}}_0^{RR}\}>1)$, the two boundary equilibria lose their stability, and a coexistence equilibrium (where all three mosquito genotypes coexist) becomes locally-asymptotically stable. Global sensitivity analysis shows that the key parameters that greatly influence the dynamics and population abundance of resistant mosquitoes include the proportion of new adult mosquitoes that are females, the insecticide-induced mortality rate of adult female mosquitoes, the coverage level and efficacy of adulticides used in the community, the oviposition rates for eggs of heterozygous and homozygous resistant genotypes, and the modification parameter accounting for the reduction in insecticide-induced mortality due to resistance. Numerical simulations show that the adult mosquito population increases with increasing temperature until a peak is reached at 31 °C, and declines thereafter. Simulating the model for moderate and high adulticide coverage, together with varying fitness costs of resistance, shows a switch in the dominant genotype at equilibrium as temperature is varied. In other words, this study shows that, for certain combinations of adulticide coverage and fitness costs of insecticide resistance, increases in temperature could result in effective management of resistance (by causing the switch from a stable resistant-only boundary equilibrium (at 18 °C) to a stable sensitive-only boundary equilibrium (at 25 °C)). Finally, this study shows that, for moderate fitness costs of resistance, density-dependent larval mortality suppresses the total population of adult mosquitoes with the resistant allele for all temperature values in the range [18 °C–36 °C].

1. Introduction

Malaria, a parasitic infection transmitted between humans via the bite of infected adult female Anopheles mosquitoes, is one of the deadliest infectious diseases that has been plaguing mankind for tens of thousands of years (World Health Organization, 2021a, World Health Organization, 2021b, World Health Organization, 2021c). Over 2.5 billion people live in geographies that permit the transmission of P. falciparum, the protozoan parasite species responsible for over 90% of malaria-related deaths (with most of the deaths occurring in children under the age of five (Taylor et al., 2019; World Health Organization, 2020a, World Health Organization, 2020b; World Health Organization, 2021a, World Health Organization, 2021b, World Health Organization, 2021c. Data from the 2021 Malaria Report of the World Health Organization shows that malaria accounted for over 241 million confirmed cases and 627,000 deaths across 85 malaria-endemic countries in 2020 (World Health Organization, 2021a, World Health Organization, 2021b, World Health Organization, 2021c).

Control measures against malaria are primarily focused on the use of insecticide-based interventions based on killing mosquitoes or preventing mosquitoes from biting humans. Specifically, the main control interventions are based on using insecticide-treated bednets (ITNs; later replaced by long-lasting insecticidal nets (LLINs)) and indoor residual spraying (IRS). Five classes of chemical insecticides, namely carbamates, neonicotinoids, organochlorines, organophosphates, and pyrethroids are currently used for mosquito control (Mohammed-Awel, Iboi, & Gumel, 2020). While all five are used in IRS, only pyrethroids are approved for use in bednets (owing to their speed, high efficacy at low doses, and low human toxicity (Zaim, Aitio, & Nakashima, 2000)). Bacterial larvicides (such as Bacillus thuringiensis subsp. israelensis, or Bti) may be used to supplement bednets and IRS if vector breeding sites are fixed, identifiable, and few enough that the resources used can be justified (World Health Organization, 2013). The widescale use of these insecticide-based interventions over the period between 2000 and 2015 has resulted in a dramatic reduction in malaria mortality and morbidity in malaria-endemic areas, prompting a renewed quest to eradicate malaria (World Health Organization, 2021a, World Health Organization, 2021b, World Health Organization, 2021c). Much of this success has been attributed LLINs (Bhatt et al., 2015); once coverage is sufficiently high, mosquito populations (and subsequently malaria transmission) are lowered to the point that those without bednets are also protected (Huijben & Krijn, 2018; Killeen & Smith, 2007; Levitz et al., 2018; Okumu & Moore, 2011). These efforts include the ZeroX40 initiative, a collaboration between agriculture companies, the Bill and Melinda Gates Foundation, and the Innovative Vector Control Consortium aiming to eradicate malaria by 2040 (Innovative Vector Control Consortium, 2022), and the Global Technical Strategy for Malaria, which aims to reduce malaria cases and deaths by 90% by 2030 (World Health Organization, 2021a, World Health Organization, 2021b, World Health Organization, 2021c). Unfortunately, however, such widespread and wide-scale use of the insecticides has resulted in Anopheles resistance to all the chemicals currently used in LLINs and IRS (World Health Organization, 2021a, World Health Organization, 2021b, World Health Organization, 2021c; Ranson & Lissenden, 2016; Corbel et al., 2007; N’Guessan, Vincent, Akogbéto, & Rowland, 2007; Innovative Vector Control Consortium, 2022). Mosquitoes who are no longer able to be killed by a standard dose of an insecticide are said to be resistant to that insecticide (Innovative Vector Control Consortium, 2022).

Although a number of approaches to overcome insecticide resistance have been implemented, such as the use of synergists (such as piperonyl butoxide (PBO)) in bednets to improve the ability of the net to kill insecticide-resistant mosquitoes (World Health Organization, 2020a, World Health Organization, 2020b), the precise impact of insecticide resistance on malaria transmission and incidence remains unknown due to the possible heterogeneities or fitness costs induced by resistance (Alout et al., 2016; Alout, Roche, Kounbobr Dabiré, & Anna, 2017; Djogbénou, Noel, & Agnew, 2010; Platt et al., 2015). Specifically, numerous entomological features, such as vector competence, biting behavior, fecundity, mating success, and natural mortality of mosquitoes, have been shown to be affected by insecticide resistance, and subsequently may influence malaria epidemiology (Alout et al., 2016; Alout et al., 2017; Djogbénou, Noel, & Agnew, 2010; Platt et al., 2015). Owing to the fact that the development period for effective insecticides for mosquito control is long (taking 10–12 years at a cost of $250 million (Innovative Vector Control Consortium, 2022; Sparks, 2013)), it is imperative to understand how to best use currently available insecticides to achieve the dual objective of minimizing malaria burden (measured in terms of new cases and mortality) while effectively managing insecticide resistance in a changing climate (Eikenberry & Gumel, 2018).

A number of mathematical models have been designed and used to study the impact of insecticide resistance on malaria mosquitoes and diseases. For instance, Barbosa et al. (Barbosa & Hastings, 2012) developed a one-locus sex-structured genetics model that explored the spread of insecticide resistance in different niche environments, ranging from insecticide-free households to homes with ITNs treated with synergists. Their study showed that overall selection pressure for resistance may increase if a synergist reduces selection for resistance in one niche but subsequently increases selection in others (Barbosa & Hastings, 2012). In particular, the study highlighted that the evaluation of insecticide resistance cannot be restricted to selection pressures via bednet use or IRS deployment, but must also account for the use of insecticides in agriculture (Barbosa & Hastings, 2012; Mouhamadou et al., 2019). In another study, Barbosa et al. (Barbosa, Kay, Chitnis, & Hastings, 2018) used a difference equation model to assess the impact of insecticide-based interventions on resistance and malaria transmission. This study showed that the spread of resistance increases if larvicides are used, although this intervention was the most effective at reducing the overall adult population (Barbosa et al., 2018).

Levick et al. (Levick, South, & Hastings, 2017) developed a two-locus model which allowed for heterogeneity in mosquito encounters with insecticides (such as differences in selection pressures and encounter rates), and used the model to assess the impacts of various insecticide deployment strategies. Their study suggested the deployment of two insecticides at once if few mosquitoes encounter the insecticide and the insecticides are highly effective against fully susceptible mosquitoes (Levick, South, & Hastings, 2017). Using a novel population genetics model, Mohammed-Awel and Gumel (Mohammed-Awel & Gumel, 2019) showed that high coverage of ITNs and IRS may effectively control malaria but fail to manage insecticide resistance. Furthermore, they showed that managing insecticide resistance is dependent on the level of dominance of the resistance allele, as well as the fitness costs due to resistance (Mohammed-Awel & Gumel, 2019). Mohammed-Awel et al. (Mohammed-Awel et al., 2020) showed that the size of the effective control window (where malaria is effectively controlled while resistance is effectively managed), in LLINs-IRS parameter space, was dependent on larvicide coverage, the sex ratio of new adult mosquitoes, and the initial frequency of the resistance allele (Mohammed-Awel et al., 2020). Churcher et al. (Churcher, Lissenden, Griffin, Worrall, & Ranson, 2016) conducted detailed meta-analyses of bioassay studies and experimental hut trials to characterise how pyrethroid resistance changes the efficacy of standard bednets, and those containing the synergist piperonyl butoxide (PBO), and assess its impact on malaria control.

The objective of the current study is to extend the aforementioned prior work to assess the combined impacts of insecticide resistance, Anopheles sex structure, and climate change (as measured in terms of local fluctuation in climatic variables, notably temperature) on the population genetics and abundance of malaria mosquitoes. Our study will allow for the exploration of scenarios that may result in the persistence or extinction of resistance genes in the gene pool, in addition to quantifying the impact of fitness costs due to resistance on mosquito abundance and how temperature variability affects the fitness costs as well as mosquito ecology. The paper is organized as follows. The model is formulated, and its basic qualitative properties explored, in Section 2. Specifically, the model describes the temporal dynamics of the Anopheles mosquito population by genotype. In addition to incorporating the population genetics of the mosquito, the model stratifies the mosquito population by sex (male and female) and incorporates the effect of temperature variability on the population dynamics of the (immature and adult) malaria mosquito. In this study, insecticide resistance in the mosquito population is assumed to be biallelic on a single locus, with a mosquito's phenotype determined by the presence or absence of insecticide-resistant (R) and insecticide-sensitive (S) alleles (Mohammed-Awel et al., 2020). Consequently, the mosquito population is stratified according to the following genotypes: homozygous sensitive (genotype SS), heterozygous (genotype RS), and homozygous resistant (genotype RR). The total population of mosquitoes of each genotype at time t is then split into mutually-exclusive compartments according to lifecycle stage (egg, larva, pupa, and adult). The model is rigorously analysed, with respect to the existence and asymptotic stability of equilibria, in Section 3. Global sensitivity analysis is also carried out in this section. Numerical simulations are carried out to evaluate the effect of temperature and the use of insecticides-based interventions on mosquito population by genotype in Section 4.

2. Formulation of mathematical model

The model to be formulated in this study monitors the temporal dynamics of the state variables associated with the immature and adult mosquitoes, as described below.

2.1. State variables of the model by genotype

It is convenient to let E(t), L(t), and P(t) represent the total number of eggs, larvae and pupae at time t, respectively. The population at the egg stage is further classified as those of insecticide-sensitive genotype (E_SS), insecticide-resistant genotype (E_RR), and heterozygous genotype (E_RS). Similarly, the population at the larval (pupal) stage is further classified as those of insecticide-sensitive genotype L_SS(P_SS), insecticide-resistant genotype L_RR(P_RR) and heterozygous genotype L_RS(P_RS). Thus,

$$E(t)=E_{SS}(t)+E_{RS}(t)+E_{RR}(t),L(t)=L_{SS}(t)+L_{RS}(t)+L_{RR}(t),\text{and}P(t)=P_{SS}(t)+P_{RS}(t)+P_{RR}(t).$$

Similarly, let M^f(t) and M^m(t) respectively represent the total number of adult female and male mosquitoes by genotype at time t. Furthermore, let $M_{SS}^f$($M_{SS}^m$) be the total female (male) population of SS genotype, $M_{RS}^f$($M_{RS}^m$) be the total female (male) population of RS genotype and $M_{RR}^f$($M_{RR}^m$) be the total female (male) population of RR genotype. Hence,

$$M^f(t)=M_{SS}^f(t)+M_{RS}^f(t)+M_{RR}^f(t)\text{and}{M}^m(t)=M_{SS}^m(t)+M_{RS}^m(t)+M_{RR}^m(t).$$

2.2. Random mating process

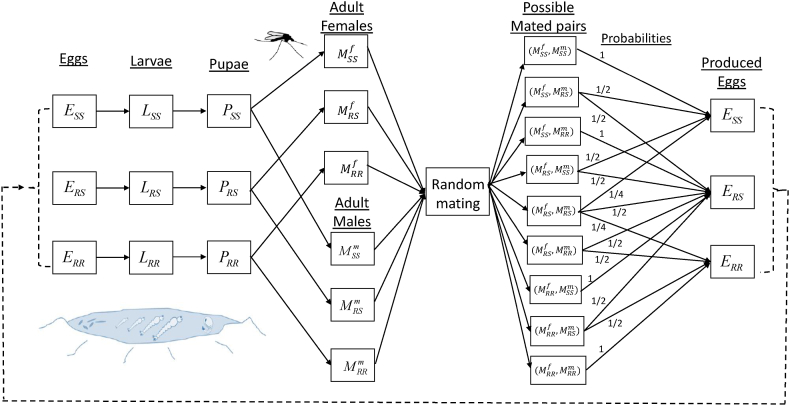
In this study, it is assumed that adult mosquitoes mate with other adult mosquitoes of the opposite sex at random, regardless of genotype (Kuniyoshi & dos Santos, 2017; Mohammed-Awel et al., 2020). In other words, it is assumed that all adult mosquitoes, regardless of genotype, have the same chance of finding a mating partner (of the opposite sex) and reproducing (i.e., we assume that insecticide resistance does not inflict any fitness costs with respect to mating). This assumption is made for mathematical tractability.

Following (Hastings, 2013; Kuniyoshi & dos Santos, 2017; Mohammed-Awel & Gumel, 2019; Mohammed-Awel et al., 2020), we define the frequency of the resistant (R) and sensitive (S) allele as follows (it is assumed that M^f(t) > 0 and M^m(t) > 0 for all t, so that the probabilities p_k and q_k, with k = {f, m}, are defined):

$$\begin{array}{cccc}{q}_f\left(t\right)& =\frac{M_{SS}^f\left(t\right)+\frac{1}{2}{M}_{RS}^f\left(t\right)}{M^f\left(t\right)},& p_f\left(t\right)=\frac{M_{RR}^f\left(t\right)+\frac{1}{2}{M}_{RS}^f\left(t\right)}{M^f\left(t\right)}& ,\\ q_m\left(t\right)& =\frac{M_{SS}^m\left(t\right)+\frac{1}{2}{M}_{RS}^m\left(t\right)}{M^m\left(t\right)},& p_m\left(t\right)=\frac{M_{RR}^m\left(t\right)+\frac{1}{2}{M}_{RS}^m\left(t\right)}{M^m\left(t\right)}& ,\end{array}$$ (2.1)

where $\left(0\le q_f(t),q_m(t)\right)\le 1$ represents the frequency of the sensitive allele (S) in adult female (male) mosquitoes at time t, and 0 ≤ p_f(t), p_m(t) ≤ 1 represents the frequency of the resistant allele (R) in adult female (male) mosquitoes at time t.

Recalling the assumption that insecticide resistance is determined by the combination of two alleles at a single locus, and that each mosquito in a mating pair contributes one allele, it then follows from (2.1) that the probability of the formation of eggs of SS genotype is q_f(t) × q_m(t). Similarly, the probability of the formation of eggs of RR genotype is p_f(t) × p_m(t). Finally, the probability of the formation of eggs of RS genotype is q_f(t) × p_m(t) + p_f(t) × q_m(t). This accounts for the case where a female contributes a sensitive (S) allele and a male contributes a resistant (R) allele, and the case where a female contributes a resistant (R) allele and a male contributes a sensitive (S) allele. Hence, q_f(t) × q_m(t), q_f(t) × p_m(t) + p_f(t) × q_m(t), and p_f(t) × p_m(t) represent the proportion of eggs of genotype SS, RS, and RR in the next generation, respectively (Hastings, 2013; Kuniyoshi & dos Santos, 2017; Mohammed-Awel & Gumel, 2019; Mohammed-Awel et al., 2020).

It should be observed that q_f(t) + p_f(t) = 1, q_m(t) + p_m(t) = 1, and $q_f(t)q_m(t)+\left(q_f(t)p_m(t)+p_f(t)q_m(t)\right)+p_f(t)p_m(t)=1$, which is the Hardy-Weinberg condition in population genetics (Hastings, 2013; Kuniyoshi & dos Santos, 2017).

Fig. 1 depicts the mosquito random mating process by genotype as well as possible mating outcomes.

Fig. 1.

Flow diagram of the model {(2.2)–(2.6)}, depicting the random mating process described in Section 2.2.

2.3. Equations of mathematical model

The model to be developed in this study consists of equations for the temporal dynamics of the immature and adult Anopheles mosquitoes by genotype. In addition to adding sex structure and population genetics of immature and adult mosquitoes, a notable feature of the model to be developed is that it incorporates the impact of temperature variability on the population dynamics of the mosquito, owing to the fact that the entire lifecycle of both the malaria vector and parasites are greatly dependent on temperature and other climatic variables (Bayoh, 2001; Bayoh & Lindsay, 2003, 2004; Eikenberry & Gumel, 2018; Lyimo, Takken, & Koella, 1992).

2.3.1. Immature mosquitoes

The equations for the dynamics of the immature mosquitoes by genotype are given by the following deterministic system of nonlinear differential equations:

2.3.1.1. Egg stage

$$\begin{array}{ll}\frac{d{E}_{SS}}{dt}& ={\alpha }^{SS}{q}_f\left(t\right)q_m\left(t\right){\left(1-\frac{E}{K_E}\right)}_{+}{M}^f-[{\sigma }_E^{SS}\left(T_W\right)+{\mu }_E^{SS}\left(T_W\right)]E_{SS},\\ \frac{d{E}_{RS}}{dt}& ={\alpha }^{RS}\left[p_f\left(t\right)q_m\left(t\right)+p_m\left(t\right)q_f\left(t\right)\right]{\left(1-\frac{E}{K_E}\right)}_{+}{M}^f-[{\sigma }_E^{RS}\left(T_W\right)+{\mu }_E^{RS}\left(T_W\right)]E_{RS},\\ \frac{d{E}_{RR}}{dt}& ={\alpha }^{RR}{p}_f\left(t\right)p_m\left(t\right){\left(1-\frac{E}{K_E}\right)}_{+}{M}^f-[{\sigma }_E^{RR}\left(T_W\right)+{\mu }_E^{RR}\left(T_W\right)]E_{RR},\end{array}$$ (2.2)

2.3.1.2. Larval stage

$$\begin{array}{ll}\frac{d{L}_{SS}}{dt}& ={\sigma }_E^{SS}\left(T_W\right)E_{SS}-[{\sigma }_L^{SS}\left(T_W\right)+{\epsilon }_L\left(T_W\right)C_L{\delta }_L+{\Psi }_L^{SS}L+{\mu }_L^{SS}\left(T_W\right)]L_{SS},\\ \frac{d{L}_{RS}}{dt}& ={\sigma }_E^{RS}\left(T_W\right)E_{RS}-[{\sigma }_L^{RS}\left(T_W\right)+{\epsilon }_L\left(T_W\right)C_L(1-h_L{k}_L){\delta }_L+{\Psi }_L^{RS}L+{\mu }_L^{RS}\left(T_W\right)]L_{RS},\\ \frac{d{L}_{RR}}{dt}& ={\sigma }_E^{RR}\left(T_W\right)E_{RR}-[{\sigma }_L^{RR}\left(T_W\right)+{\epsilon }_L\left(T_W\right)C_L(1-k_L){\delta }_L+{\Psi }_L^{RR}L+{\mu }_L^{RR}\left(T_W\right)]L_{RR},\end{array}$$ (2.3)

2.3.1.3. Pupal stage

$$\begin{array}{ll}\frac{d{P}_{SS}}{dt}& ={\sigma }_L^{SS}\left(T_W\right)L_{SS}-[{\sigma }_P^{SS}\left(T_W\right)+{\epsilon }_P\left(T_W\right)C_P{\delta }_P+{\mu }_P^{SS}\left(T_W\right)]P_{SS},\\ \frac{d{P}_{RS}}{dt}& ={\sigma }_L^{RS}\left(T_W\right)L_{RS}-[{\sigma }_P^{RS}\left(T_W\right)+{\epsilon }_P\left(T_W\right)C_P(1-h_P{k}_P){\delta }_P+{\mu }_P^{RS}\left(T_W\right)]P_{RS},\\ \frac{d{P}_{RR}}{dt}& ={\sigma }_L^{RR}\left(T_W\right)L_{RR}-[{\sigma }_P^{RR}\left(T_W\right)+{\epsilon }_P\left(T_W\right)C_P(1-k_P){\delta }_P+{\mu }_P^{RR}\left(T_W\right)]P_{RR},\end{array}$$ (2.4)

where T_A(t) and T_W(t) represent ambient air and water temperature, respectively (Okuneye, Eikenberry, & Gumel, 2019).

In (2.2), αⁱ (with i = {SS, RS, RR}) represents the rate at which eggs of genotype i are laid by adult female mosquitoes, q_f(t)q_m(t) is the probability of the formation of eggs of genotype SS, and K_E ≥ E(t) for all t is the environmental carrying capacity of eggs. Following (Okuneye, Eikenberry, & Gumel, 2019), we use the notation ${(X)}_{+}=\max \left\{0,X\right\}$ to ensure the non-negativity of the oviposition term. Since air and water temperatures are known to impact mosquito development rates and survival at all lifecycle stages (Bayoh, 2001; Bayoh & Lindsay, 2003, 2004; Lyimo et al., 1992), the natural genotype-specific development rate of immature mosquitoes (denoted by ${\sigma }_j^i\left(T_W\right)$, i = {SS, RS, RR}, j = {E, L, P}) is defined as a function of water temperature. Similarly, the natural mortality rate for immature stages is water temperature-dependent, and is represented by ${\mu }_j^i\left(T_W\right)$, i = {SS, RS, RR}, j = {E, L, P}. The parameter ${\Psi }_L^i$, i = {SS, RS, RR} represents the density-dependent mortality rate of larvae by genotype. The temperature-dependent efficacy of larvicides and pupacides is denoted by 0 ≤ ε_L(T_W) ≤ 1 and 0 ≤ ε_P(T_W) ≤ 1 (Glunt, Oliver, Hunt, & Paaijmans, 2018), respectively, and the coverage of these insecticides is denoted C_L and C_P, respectively (with 0 ≤ C_L, C_P ≤ 1).

The parameters δ_L and δ_P represent the insecticide-induced mortality rate for larvae and pupae of genotype SS, respectively, and these rates are assumed to depend on the concentration of the larvicide (Mohammed-Awel et al., 2020). The fractions 0 ≤ k_L ≤ 1 and 0 ≤ k_P ≤ 1 are modification parameters that account for the assumed reduction in mortality due to insecticides for larvae and pupae of genotype RR (in comparison to larvae and pupae of SS genotype), respectively. Furthermore, the proportions 0 ≤ h_L ≤ 1 and 0 ≤ h_P ≤ 1 represent the measure of dominance of the resistance allele, in comparison to the sensitive allele, in heterozygous immature mosquitoes at the larval and pupal stages, respectively. That is, h_L = h_P = 1 represents the case where the insecticide-resistant gene is dominant in heterozygous larvae and pupae. In this case, the heterozygous (RS genotype) immature mosquitoes are equally as resistant as homozygous resistant (RR genotype) immature mosquitoes. Similarly, h_L = h_P = 0 represents the case where the resistance gene is recessive, and heterozygous immature mosquitoes are killed by larvicides and pupacides at the same rate as insecticide-sensitive (SS genotype) immature mosquitoes.

2.3.2. Adult mosquitoes by genotype

The equations for the dynamics of adult mosquitoes, stratified by sex and genotype, are given by following deterministic system of nonlinear differential equations:

2.3.2.1. Adult females

$$\begin{array}{ll}\frac{d{M}_{SS}^f}{dt}& ={\nu }_f{\sigma }_P^{SS}\left(T_W\right)P_{SS}-[{\epsilon }_M\left(T_A\right)C_M{\delta }_{M_f}+{\mu }_{M_f}^{SS}\left(T_A\right)]M_{SS}^f,\\ \frac{d{M}_{RS}^f}{dt}& ={\nu }_f{\sigma }_P^{RS}\left(T_W\right)P_{RS}-[{\epsilon }_M\left(T_A\right)C_M(1-h_M{k}_M){\delta }_{M_f}+{\mu }_{M_f}^{RS}\left(T_A\right)]M_{RS}^f,\\ \frac{d{M}_{RR}^f}{dt}& ={\nu }_f{\sigma }_P^{RR}\left(T_W\right)P_{RR}-[{\epsilon }_M\left(T_A\right)C_M(1-k_M){\delta }_{M_f}+{\mu }_{M_f}^{RR}\left(T_A\right)]M_{RR}^f,\end{array}$$ (2.5)

2.3.2.2. Adult males

$$\begin{array}{ll}\frac{d{M}_{SS}^m}{dt}& =(1-{\nu }_f){\sigma }_P^{SS}\left(T_W\right)P_{SS}-[{\epsilon }_M\left(T_A\right)C_M{\delta }_{M_m}+{\mu }_{M_m}^{SS}\left(T_A\right)]M_{SS}^m,\\ \frac{d{M}_{RS}^m}{dt}& =(1-{\nu }_f){\sigma }_P^{RS}\left(T_W\right)P_{RS}-[{\epsilon }_M\left(T_A\right)C_M(1-h_M{k}_M){\delta }_{M_m}+{\mu }_{M_m}^{RS}\left(T_A\right)]M_{RS}^m,\\ \frac{d{M}_{RR}^m}{dt}& =(1-{\nu }_f){\sigma }_P^{RR}\left(T_W\right)P_{RR}-[{\epsilon }_M\left(T_A\right)C_M(1-k_M){\delta }_{M_m}+{\mu }_{M_m}^{RR}\left(T_A\right)]M_{RR}^m.\end{array}$$ (2.6)

In {(2.5), (2.6)}, 0 < ν_f < 1 is the proportion of new adult mosquitoes that are females. Furthermore, ${\mu }_{M_f}^i\left(T_A\right)$ and ${\mu }_{M_m}^i\left(T_A\right)$ denote, respectively, the genotype-specific natural death rate of adult females and males as a function of air temperature for i = {SS, RS, RR}. The temperature-dependent efficacy and coverage of adulticides is given by 0 ≤ ε_M(T_A) ≤ 1 and 0 ≤ C_M ≤ 1, respectively. The concentration-dependent insecticide mortality rate for adults of genotype SS is denoted by ${\delta }_{M_f}$ for females and ${\delta }_{M_m}$ for males. The modification parameter for the assumed reduction in insecticide-induced mortality is given by 0 ≤ k_M ≤ 1. Finally, 0 ≤ h_M ≤ 1 represents a measure of the dominance of the resistance allele, in comparison to the sensitive allele, in heterozygous adult mosquitoes.

The genotypes and state variables of the model {(2.2)–(2.6)} are described in Table 1. Furthermore, the parameters of the model are described in Table 2, and the associated functional forms of the temperature-dependent parameters are formulated (based on field and lab entomological data) in Section 2.4.

Table 1.

Description of mosquito genotypes and state variables of the model {(2.2)–(2.6)}, where i = {SS, RS, RR}.

Mosquito genotype	Description	Genotype-specific populations
SS	Homozygous insecticide-sensitive genotype	$(E_{SS},L_{SS},P_{SS},M_{SS}^f,M_{SS}^m)$
RS	Heterozygous genotype	$(E_{RS},L_{RS},P_{RS},M_{RS}^f,M_{RS}^m)$
RR	Homozygous insecticide-resistant genotype	$(E_{RR},L_{RR},P_{RR},M_{RR}^f,M_{RR}^m)$

State variable	Description
Ei = Ei(t)	Population of eggs of genotype i at time t
Li = Li(t)	Population of larvae of genotype i at time t
Pi = Pi(t)	Population of pupae of genotype i at time t
$M_i^f=M_i^f(t)$	Population of adult female mosquitoes of genotype i at time t
$M_i^m=M_i^m(t)$	Population of adult male mosquitoes of genotype i at time t

Table 2.

Description of the parameters of the model {(2.2)–(2.6)}. Notation: T_W (T_A) represents local water (air) temperature at time t.

Parameter	Description (i = {SS, RS, RR}, j = {E, L, P})
αi	Rate at which eggs of genotype i are laid by adult female mosquitoes
KE	Environmental carrying capacity of eggs
${\sigma }_j^i(T_W)$	Development rate of immature mosquitoes by genotype
${\mu }_j^i(T_A)$	Natural mortality rate of immature mosquitoes by genotype
${\mu }_{M_f}^i(T_A)({\mu }_{M_m}^i(T_A))$	Natural mortality of adult female (male) mosquitoes by genotype
${\Psi }_L^i$	Density-dependent larval mortality rate by genotype
0 < νf < 1	Proportion of adult mosquitoes that are female
0 ≤ CL(CP) ≤ 1	Coverage of larvicide (pupacide)
0 ≤ CM ≤ 1	Coverage of adulticide
0 < εL(TW) (εP(TW)) ≤ 1	Efficacy of larvicide (pupacide)
0 < εM(TA) ≤ 1	Efficacy of adulticide
δj	Insecticide-induced mortality rate for immature mosquitoes of genotype SS
${\delta }_{M_f}({\delta }_{M_m})$	Insecticide-induced mortality rate for adult female (male) mosquitoes of genotype SS
0 ≤ kL(kP) ≤ 1	Modification parameter for the reduction in larval (pupal) mortality
	due to insecticide resistance
0 ≤ kM ≤ 1	Modification parameter for the assumed reduction in adult mosquito mortality
	due to insecticide resistance
0 ≤ hL(hP) ≤ 1	Measure of dominance of resistance allele, over sensitive allele, in heterozygous
	mosquitoes at the larval (pupal) lifecycle stage
0 ≤ hM ≤ 1	Measure of dominance of resistance allele, over sensitive allele, in heterozygous
	adult mosquitoes
ξRS > 1	Fitness factor due to resistance for mosquitoes of RS genotype
ξRR > 1	Fitness factor due to resistance for mosquitoes of RR genotype

The 15-dimensional model {(2.2)–(2.6)} is an extension of numerous population biology models for malaria mosquitoes or disease, such as those in [6, 26, 28–30], by inter alia.

• (a)Explicitly incorporating the effect of changes in local climatic variables (notably temperature) on the population ecology of the immature and adult Anopheles mosquito by genotype (the effect of changes in local climatic variables are not accounted for in (Barbosa et al., 2018; Barbosa & Hastings, 2012; Levick et al., 2017; Mohammed-Awel & Gumel, 2019; Mohammed-Awel et al., 2020)). Adding this important feature allows us to evaluate the genotype-specific impact of local climate change on the evolution of insecticide resistance in the community.
• (b)Allowing for heterogeneity, by mosquito lifecycle stage, in the level of dominance of the resistant allele in heterozygous mosquitoes. That is, we allowed the dominance of the resistant allele in the larval (h_L), pupal (h_P), and adult (h_M) stages to be different (owing to the fact that larvicides, pupacides, and adulticides are different chemicals and may have different modes of action or exposure rates at each life stage). We consider resistance at one site although mutations at other/multiple sites may affect resistance (Levick et al., 2017). For example, a mutation at the site in question may confer a high level of resistance to larvicides, but heterozygous adults may still be sensitive to adulticides (Tikar et al., 2011). The dominance of the resistant allele in heterozygous mosquitoes is represented using the same parameter (h) at each lifecycle stage in (Mohammed-Awel & Gumel, 2019; Mohammed-Awel et al., 2020).
• (c)Allowing for heterogeneity, by mosquito lifecycle stage, in the reduction in insecticide-induced mortality due to insecticide resistance. In particular, we used parameters k_L, k_P, and k_M (with 0 < k_L, k_P, k_M < 1) to represent the reduction in the insecticide-induced mortality due to resistance in the larval, pupal, and adult stage, respectively. Again, this accounts for a mutation at the site in question conferring differing levels of resistance to the chemicals used in larvicides, pupacides, and adulticides (Tikar et al., 2011).
• (d)Allowing for heterogeneity in eggs oviposition rate by genotype (represented by αⁱ; with i = {SS, RS, RR}). This heterogeneity is not accounted for in (Mohammed-Awel et al., 2020) (but was accounted for in (Mohammed-Awel & Gumel, 2019)).
• (e)Explicitly distinguishing the implementation of pupacides (as measured by the parameter k_P) and larviciding (as measured by k_L), since the two chemicals may be different. This heterogeneity is not accounted in (Mohammed-Awel et al., 2020) (where it is assumed that larvicides kill pupae at the same rate as larvae). Since pupacides are not commonly used, our formulation allows us to capture this fact (by setting this parameter to, or close to, zero).
• (f)Accounting for the possible heterogeneity in encounters with insecticides among males and females (Barbosa & Hastings, 2012; Birget & Koella, 2015; Levick et al., 2017). Since only adult female mosquitoes bite humans, female mosquitoes may have higher exposures to insecticides (and thus, different mortality rates) than male mosquitoes. Hence, we use ${\delta }_{M_f}$ and ${\delta }_{M_m}$ to differentiate these values.
• (g)Incorporating the effect of temperature on insecticides. Glunt et al. (Glunt et al., 2018) found that increasing temperature reduces toxicity of deltamethrin in susceptible Anopheles arabiensis females, while resistant female Anopheles arabiensis had higher mortality at low (18 °C) and high (30 °C) temperatures, and increased survival under standard insectary temperatures of 25 °C. These findings are encompassed the insecticide efficacy parameters ε_L(T_W), ε_P(T_W), and ε_M(T_A).

2.4. Temperature-dependent parameters

The functional forms for the temperature-dependent parameters of the model {(2.2)–(2.6)} are taken from (Iboi et al., 2020a; Okuneye et al., 2019), which fitted data to laboratory results (Bayoh & Lindsay, 2003, 2004). Furthermore, the functional forms of parameters of the model that are genotype-specific are obtained from the relationships described in (Mohammed-Awel et al., 2020). The formulation of the functional forms of each temperature-dependent parameter of the model are described below.

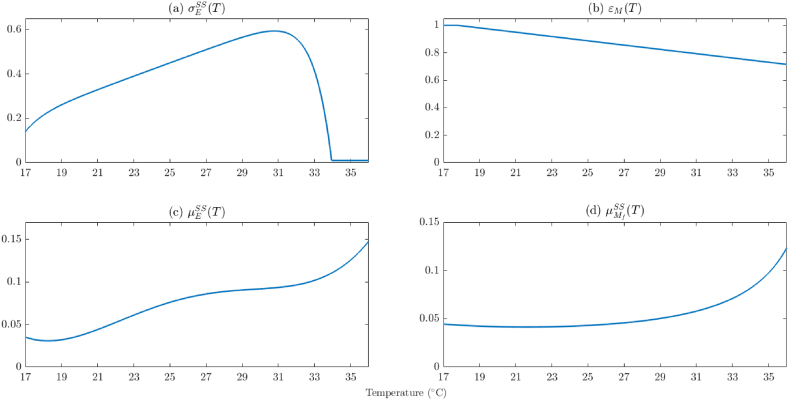
The laboratory data for larval survival times reported by Bayoh and Lindsay (Bayoh & Lindsay, 2004) are used to determine the functional forms for the natural mortality rate for eggs, larvae, and pupae (Iboi et al., 2020a; Okuneye et al., 2019). Specifically, the per capita natural death rate for immature mosquitoes of genotype SS, as a function of water temperature (T_W), is given by (Bayoh & Lindsay, 2004; Okuneye et al., 2019):

$${\mu }_i^{SS}\left(T_W\right)=\left(8.929\times 10^{-6}\right)T_W^4-\left(9.271\times 10^{-4}\right)T_W^3+\left(3.536\times 10^{-2}\right)T_W^2-0.5814T_W+3.509,$$

for i = {E, L, P}. To account for the fitness costs of resistance with respect to natural mortality and development (Alout et al., 2016; Alout et al., 2017; Djogbénou, Noel, & Agnew, 2010; Platt et al., 2015), we introduce the genotype-specific quantities ξ^RS > 1 and ξ^RR > ξ^RS > 1, which modifies the development and natural mortality rates of mosquitoes of RS genotype and RR genotype, in relation to those of SS genotype. Specifically, we define the natural mortality rates for immature mosquitoes of RS genotype and RR genotype to be:

$${\mu }_i^{RS}\left(T_W\right)={\xi }^{RS}\times {\mu }_i^{SS}\left(T_W\right)\text{and}{\mu }_i^{RR}\left(T_W\right)={\xi }^{RR}\times {\mu }_i^{SS}\left(T_W\right),\text{with}i=\{E,L,P\},\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e}\mathrm{l}\mathrm{y}.$$

Hence, in this study, we assume (due to fitness costs of insecticide resistance) that the genotype-specific and temperature-dependent natural mortality rates for heterozygous and homozygous resistant mosquitoes (both immature and adult) are higher than those for homozygous sensitive mosquitoes (in line with (Alout et al., 2016; Alout et al., 2017; Djogbénou, Noel, & Agnew, 2010; Platt et al., 2015)).

Following Okuneye et al. (Okuneye et al., 2019), the temperature-dependent natural mortality rates for adult female mosquitoes is estimated using mean mosquito survival times at 60% relative humidity from (Bayoh, 2001) (with the survival curve estimated in (Okuneye et al., 2019)). Hence, the functional form of the temperature-dependent parameter for the survival of an adult female mosquito of genotype SS is given by:

$${\mu }_{M_f}^{SS}(T_A)=\max \left\{{\left(-11.8239+3.3292T_A-0.0771T_A^2\right)}^{-1},0.01\right\}.$$

Although male Anopheles mosquitoes can survive in a laboratory setting for 20 days or longer, adult males in the wild tend to survive for 5–10 days (Bayoh, 2001; Howell & Knols, 2009). Hence, the functional form describing adult male survival of genotype SS is taken as half of the natural mortality for adult females of genotype SS, and is given by:

$${\mu }_{M_m}^{SS}(T_A)=\max \left\{{\left(-5.9112+1.6646T_A-0.0386T_A^2\right)}^{-1},0.01\right\},$$

Again following (Mohammed-Awel et al., 2020), the survival times for females of genotype RS and RR are given, respectively, by:

$${\mu }_{M_f}^{RS}\left(T_A\right)={\xi }^{RS}\times {\mu }_{M_f}^{SS}\left(T_A\right),{\mu }_{M_f}^{RR}\left(T_A\right)={\xi }^{RR}\times {\mu }_{M_f}^{SS}\left(T_A\right),$$

while survival times for males of genotype RS and RR are respectively given by:

$${\mu }_{M_m}^{RS}\left(T_A\right)={\xi }^{RS}\times {\mu }_{M_m}^{SS}\left(T_A\right),{\mu }_{M_m}^{RR}\left(T_A\right)={\xi }^{RR}\times {\mu }_{M_m}^{SS}\left(T_A\right).$$

The development rate of immature mosquitoes of genotype SS is adopted from the relationship between water temperature and development time from egg to adult described by Bayoh and Lindsay (Bayoh & Lindsay, 2003), and is given by (Okuneye et al., 2019):

$$\ell (T_W)={\left(a+b{T}_W+c{e}^{T_W}+d{e}^{-T_W}\right)}^{-1},$$

where a = −0.05, b = 0.005, c = −2.139 × 10⁻¹⁶, and d = −2.81357 × 10⁵ (Iboi et al., 2020a; Okuneye et al., 2019). Iboi et al. (Iboi et al., 2020a) and Okuneye et al. (Okuneye et al., 2019) used this relationship when calculating the overall development time for eggs, four larval instars, and pupae, assuming that each of these six stages have the same duration. Although larval instars are not accounted for explicitly in this model, we follow a similar formulation as (Iboi et al., 2020a; Okuneye et al., 2019), so that:

$$\frac{1}{{\sigma }_E^{SS}(T_W)}=\frac{1}{6}\ell (T_W),\frac{1}{{\sigma }_L^{SS}(T_W)}=\frac{4}{6}\ell (T_W),\frac{1}{{\sigma }_P^{SS}(T_W)}=\frac{1}{6}\ell (T_W).$$

It should be observed that $1/{\sigma }_E^{SS}(T_W)+1/{\sigma }_L^{SS}(T_W)+1/{\sigma }_P^{SS}(T_W)=\ell (T_W)$. Again, following (Mohammed-Awel et al., 2020), the development rates for eggs, larvae, and pupae of genotype RS are, respectively, given by:

$${\sigma }_E^{RS}(T_W)=\frac{1}{{\xi }^{RS}}{\sigma }_E^{SS}(T_W),{\sigma }_L^{RS}(T_W)=\frac{1}{{\xi }^{RS}}{\sigma }_L^{SS}(T_W),{\sigma }_P^{RS}(T_W)=\frac{1}{{\xi }^{RS}}{\sigma }_P^{SS}(T_W),$$

while the development rates for eggs, larvae, and pupae of genotype RR are given by:

$${\sigma }_E^{RR}(T_W)=\frac{1}{{\xi }^{RR}}{\sigma }_E^{SS}(T_W),{\sigma }_L^{RR}(T_W)=\frac{1}{{\xi }^{RR}}{\sigma }_L^{SS}(T_W),{\sigma }_P^{RR}(T_W)=\frac{1}{{\xi }^{RR}}{\sigma }_P^{SS}(T_W).$$

Because of the assumption that ξ^RR > ξ^RS > 1, the development rates for mosquitoes of genotype RS and RR are slower than those of genotype SS (due to the assumption for the fitness disadvantages associated with insecticide resistance).

The parameter values for insecticide efficacy (0 ≤ ε_j ≤ 1, j = {L, P, M}) and reduction in insecticide-induced mortality (0 ≤ k_j ≤ 1, j = {L, P, M}) are derived from Glunt et al. (Glunt et al., 2018), where the authors studied insecticide effectiveness (measured by mortality percentage) on insecticide-sensitive (SENN) and insecticide-resistant (SENN-DDT) Anopheles females at 18 °C, 25 °C, and 30 °C. Insecticide-induced mortality was shown to decrease as temperature increased in insecticide-sensitive females, while mortality in insecticide-resistant females was lowest at 25 °C but highest at 18 °C and 30 °C. The estimated mortality percentages for the given temperatures (and hence overall insecticide efficacies) are listed in Table 3. For the purposes of this model, insecticide efficacy as a function of temperature (ε_M(T_A)) for adult mosquitoes of genotype SS and genotype RR are derived from the estimated efficacies for SENN and SENN-DDT mosquitoes, respectively. A linear model is fit to the SENN mortality data in Table 3 to allow for simulations of the model {(2.2)–(2.6)} at various temperatures. The relationship between air temperature and insecticide efficacy on adult mosquitoes is given by:

$${\epsilon }_M(T_A)=\mathrm{m}\mathrm{i}\mathrm{n}\{-0.0156T_A+1.2773,1\}.$$

Table 3.

Estimated efficacy of insecticides (measured by percent killed by the insecticide deltamethrin), as a function of temperature, taken from Fig. 1 of Glunt et al. (Glunt et al., 2018). SENN denotes an insecticide-sensitive anopheline strain, while SENN-DDT denotes an insecticide-resistant anopheline strain.

SENN		SENN-DDT
18 °C	0.99	18 °C	0.7
25 °C	0.9	25 °C	0.45
30 °C	0.8	30 °C	0.55

We further assume that ε_L(T_W) = ε_P(T_W) = ε_M(T_A).

It is worth recalling that, in the model {(2.2)–(2.6)}, the overall insecticide efficacy for an adult mosquito of genotype SS is given by ε_M(T_A), while the overall insecticide efficacy for an adult mosquito of genotype RR is given by ε_M(T_A)(1 − k_M). It follows, using the values listed in Table 3, that the estimated efficacy of the chemical insecticide at 18 °C is given by:

$$0.99(1-k_M)=0.7,$$

which yields the value of k_M to be k_M ≈ 0.2930. Similarly, following the same approach for other temperature values, we determined that the values of k_M at 25 °C and 30 °C are k_M ≈ 0.45 and k_M ≈ 0.3125, respectively. We assume that k_M takes the average of these three values, giving k_M ≈ 0.37. We also assume, for simplicity, that k_L = k_P = k_M.

Finally, it is worth stating that, although the model {(2.2)–(2.6)} was formulated as a non-autonomous system of differential equations (owing to the fact that some of the parameters of the model are temperature-dependent, hence, time-dependent), the simulations to be carried out will be for the case where air and water temperature are fixed. Hence, although non-autonomous by formulation, the model {(2.2)–(2.6)} is autonomous in practice. Furthermore, for simplicity, it will be assumed that, near the surface of water, air and water temperature are approximately the same. That is, we assume that T_A(t) = T_W(t) = T for all time t (Iboi et al., 2020a).

It should be mentioned that in all the numerical simulations to be carried out in this study, the aforementioned temperature-dependent parameters of the model {(2.2)–(2.6)} will be evaluated at temperature values ranging from 17 °C to 36 °C (this is a typical temperature range for malaria transmission in endemic areas (Eikenberry & Gumel, 2018; Iboi et al., 2020a; Mordecai et al., 2013; Okuneye & Gumel, 2017; Okuneye et al., 2019)). For temperature values in this range, all the aforementioned temperature-dependent parameters of the model are positive, continuous, and bounded (see Figure A1 in Appendix A for depiction of the profiles of some of the temperature-dependent parameters of the model). It should be stated that for temperatures below or above this range, the mosquito population significantly decreases (hence, the burden (i.e., mortality and morbidity) of the diseases they cause also decreases) (Abdelrazec & Gumel, 2017; Craig, Snow, & le Sueur, 1999; Eikenberry & Gumel, 2018; Okuneye & Gumel, 2017; Okuneye, Abdelrazec, & Gumel, 2018; Okuneye et al., 2019; Snow, Craig, Deichmann, & Marsh, 1999). For instance, in the context of malaria disease, Plasmodium falciparum (the malaria parasite responsible for most severe form of the disease and deaths) cannot complete its maturation (sporogonic cycle) in the Anopheles mosquito at temperatures below 20 °C (Centers for Disease Control and Prevention, 2022). Furthermore, temperatures above 32 °C are correlated with reduced vector fitness and increased vector mortality (Craig et al., 1999).

The basic qualitative properties of the model {(2.2)–(2.6)} will now be explored below.

2.5. Basic qualitative properties of the model

Since the model {(2.2)–(2.6)} monitors the temporal dynamics of mosquito populations, all its state variables and parameters are non-negative. Furthermore, parameters related to natural mortality at each life-stage (${\mu }_E^i$, ${\mu }_L^i$, ${\mu }_P^i$, ${\mu }_{M_f}^i$, and ${\mu }_{M_m}^i$, i = {SS, RS, RR}) and the environmental carrying capacity (K_E) are positive and finite. It is convenient to group the state variables of the model {(2.2)–(2.6)} according to lifecycle stage and/or genotype (in line with (Mohammed-Awel et al., 2020)). Specifically, let:

$$\begin{array}{cc}& {\mathcal{B}}_1=\left(E_{SS},L_{SS},P_{SS},E_{RS},L_{RS},P_{RS},E_{RR},L_{RR},P_{RR}\right),\\ {\mathcal{B}}_2& =\left(M_{SS}^f,M_{SS}^m\right),{\mathcal{B}}_3=\left(M_{RS}^f,M_{RS}^m\right),{\mathcal{B}}_4=\left(M_{RR}^f,M_{RR}^m\right).\end{array}$$ (2.7)

Following (Okuneye et al., 2019), we define the following quantities for the temperature-dependent parameters of the model {(2.2)–(2.6)}:

$$x^{\ast }={\sup }_{t\ge 0}x(t),x_{\ast }={\inf }_{t\ge 0}x(t).$$

Using these definitions, it can be seen from the first equation of (2.3) that (noting that L = L_SS + L_RS + L_RR):

$$\begin{gathered} \begin{array}{cc}\frac{d{L}_{SS}}{dt}& ={\sigma }_E^{SS}\left(t\right)E_{SS}-[{\sigma }_L^{SS}\left(t\right)+{\epsilon }_L\left(t\right)C_L{\delta }_L+{\Psi }_L^{SS}L+{\mu }_L^{SS}\left(t\right)]L_{SS},\\ & \le {\sigma }_E^{SS}\left(t\right)K_E-[{\sigma }_L^{SS}\left(t\right)+{\epsilon }_L\left(t\right)C_L{\delta }_L+{\Psi }_L^{SS}L+{\mu }_L^{SS}\left(t\right)]L_{SS},\end{array} \\ \le {\sigma }_E^{SS\ast }{K}_E-[{\sigma }_{L\ast }^{SS}+{\epsilon }_{L\ast }{C}_L{\delta }_L+{\mu }_{L\ast }^{SS}]L_{SS} \end{gathered}$$

from which it follows (by the Gronwall inequality (Gronwall, 1919)):

$${\mathrm{lim\; sup}}_{t\to \infty }{L}_{SS}(t)\le \frac{{\sigma }_E^{SS\ast }{K}_E}{{\sigma }_{L\ast }^{SS}+{\epsilon }_{L\ast }{C}_L{\delta }_L+{\mu }_{L\ast }^{SS}}=L_{SS}^{\diamond }.$$ (2.8)

Similarly, it can be shown that

$${\mathrm{lim\; sup}}_{t\to \infty }{L}_{RS}(t)\le \frac{{\sigma }_E^{RS\ast }{K}_E}{{\sigma }_{L\ast }^{RS}+(1-h_L{k}_L){\epsilon }_{L\ast }{C}_L{\delta }_L+{\mu }_{L\ast }^{RS}}=L_{RS}^{\diamond }$$ (2.9)

and,

$${\mathrm{lim\; sup}}_{t\to \infty }{L}_{RR}(t)\le \frac{{\sigma }_E^{RR\ast }{K}_E}{{\sigma }_{L\ast }^{RR}+(1-k_L){\epsilon }_{L\ast }{C}_L{\delta }_L+{\mu }_{L\ast }^{RR}}=L_{RR}^{\diamond }.$$ (2.10)

Furthermore, using the bounds (2.8)–(2.10) in the equations in (2.4), shows that:

$${\mathrm{lim\; sup}}_{t\to \infty }{P}_{SS}(t)\le \frac{{\sigma }_L^{SS\ast }{L}_{SS}^{\diamond }}{{\sigma }_{P\ast }^{SS}+{\epsilon }_{P\ast }{C}_P{\delta }_P+{\mu }_{P\ast }^{SS}}=P_{SS}^{\diamond },$$ (2.11)

$${\mathrm{lim\; sup}}_{t\to \infty }{P}_{RS}(t)\le \frac{{\sigma }_L^{RS\ast }{L}_{RS}^{\diamond }}{{\sigma }_{P\ast }^{RS}+(1-h_p{k}_P){\epsilon }_{P\ast }{C}_P{\delta }_P+{\mu }_{P\ast }^{RS}}=P_{RS}^{\diamond },$$ (2.12)

and,

$${\mathrm{lim\; sup}}_{t\to \infty }{P}_{RR}(t)\le \frac{{\sigma }_L^{RR\ast }{L}_{RR}^{\diamond }}{{\sigma }_{P\ast }^{RR}+(1-k_P){\epsilon }_{P\ast }{C}_P{\delta }_P+{\mu }_{P\ast }^{RR}}=P_{RR}^{\diamond }.$$ (2.13)

The following bounds for the adult female mosquito populations can also be established:

$${\mathrm{lim\; sup}}_{t\to \infty }{M}_{SS}^f(t)\le \frac{{\sigma }_P^{SS\ast }{P}_{SS}^{\diamond }}{{\epsilon }_{M\ast }{C}_M{\delta }_{M_f}+{\mu }_{M_f\ast }^{SS}}=M_{SS}^{f\diamond },$$ (2.14)

$${\mathrm{lim\; sup}}_{t\to \infty }{M}_{RS}^f(t)\le \frac{{\sigma }_P^{RS\ast }{P}_{RS}^{\diamond }}{(1-h_M{k}_M){\epsilon }_{M\ast }{C}_M{\delta }_{M_f}+{\mu }_{M_f\ast }^{RS}}=M_{RS}^{f\diamond },$$ (2.15)

and,

$${\mathrm{lim\; sup}}_{t\to \infty }{M}_{RR}^f(t)\le \frac{{\sigma }_P^{RR\ast }{P}_{RR}^{\diamond }}{(1-k_M){\epsilon }_{M\ast }{C}_M{\delta }_{M_f}+{\mu }_{M_f\ast }^{RR}}=M_{RR}^{f\diamond }.$$ (2.16)

Finally, the following inequalities also hold for the adult male mosquito populations:

$${\mathrm{lim\; sup}}_{t\to \infty }{M}_{SS}^m(t)\le \frac{{\sigma }_P^{SS\ast }{P}_{SS}^{\diamond }}{{\epsilon }_{M\ast }{C}_M{\delta }_{M_m}+{\mu }_{M_m\ast }^{SS}}=M_{SS}^{m\diamond },$$ (2.17)

$${\mathrm{lim\; sup}}_{t\to \infty }{M}_{RS}^m(t)\le \frac{{\sigma }_P^{RS\ast }{P}_{RS}^{\diamond }}{(1-h_M{k}_M){\epsilon }_{M\ast }{C}_M{\delta }_{M_m}+{\mu }_{M_f\ast }^{RS}}=M_{RS}^{m\diamond },$$ (2.18)

and,

$${\mathrm{lim\; sup}}_{t\to \infty }{M}_{RR}^m(t)\le \frac{{\sigma }_P^{RR\ast }{P}_{RR}^{\diamond }}{(1-k_M){\epsilon }_{M\ast }{C}_M{\delta }_{M_m}+{\mu }_{M_m\ast }^{RR}}=M_{RR}^{m\diamond }.$$ (2.19)

Having established the bounds above, we can now seek to prove the non-negativity and boundedness of the solutions of the model. Consider, next, the following ecologically-feasible region for the model {(2.2)–(2.6)}:

$$\mathrm{\Omega }={\mathrm{\Omega }}_1\cup {\mathrm{\Omega }}_2\cup {\mathrm{\Omega }}_3\cup {\mathrm{\Omega }}_4,$$

where,

$$\begin{array}{cc}{\mathrm{\Omega }}_1=& \left\{{\mathcal{B}}_1\in {\mathbb{R}}_{+}^9:E_{SS}\le K_E,L_{SS}\le L_{SS}^{\diamond },P_{SS}\le P_{SS}^{\diamond },\right)\\ & E_{RS}\le K_E,L_{RS}\le L_{RS}^{\diamond },P_{RS}\le P_{RS}^{\diamond },\\ & \left(E_{RR}\le K_E,L_{RR}\le L_{RR}^{\diamond },P_{RR}\le P_{RR}^{\diamond }\right\},\\ {\mathrm{\Omega }}_2=& \left\{{\mathcal{B}}_2\in {\mathbb{R}}_{+}^2:M_{SS}^f\le M_{SS}^{f\diamond },M_{SS}^m\le M_{SS}^{m\diamond }\right\},\\ {\mathrm{\Omega }}_3=& \left\{{\mathcal{B}}_3\in {\mathbb{R}}_{+}^2:M_{RS}^f\le M_{RS}^{f\diamond },M_{RS}^m\le M_{RS}^{m\diamond }\right\},\\ {\mathrm{\Omega }}_4=& \left\{{\mathcal{B}}_4\in {\mathbb{R}}_{+}^2:M_{RR}^f\le M_{RR}^{f\diamond },M_{RR}^m\le M_{RR}^{m\diamond }\right\}.\end{array}$$

We claim the following result:

Lemma 2.1

All solutions of the model {(2.2)–(2.6)} with non-negative initial data remain non-negative and bounded for all t > 0.

Proof. The right-hand side of the equations of the model {(2.2)–(2.6)} are continuously-differentiable and locally-Lipschitz at t = 0. Thus, it follows, by the Picard-Lindelöf theorem, that a unique solution of the model with non-negative initial conditions exists in Ω for all time t > 0 (see also (Iboi et al., 2020a; Mohammed-Awel et al., 2020; Okuneye et al., 2019)). It should be recalled that since it was assumed that ${\left(1-\frac{E}{K_E}\right)}_{+}\ge 0$ for all t ≥ 0, then E(t) ≤ K_E for all t ≥ 0. Therefore, E_SS(t) ≤ K_E, E_RS(t) ≤ K_E, and E_RR(t) ≤ K_E for all t ≥ 0. Furthermore, it can be seen from equations (2.8), (2.19) that the solutions of the other state variables of the model {(2.2)–(2.6)} are bounded. Hence, the solutions of the model {(2.2)–(2.6)} are bounded.

Theorem 2.1

The region Ω is positively-invariant and attracts all solutions of the model {(2.2)–(2.6)}.

Proof. This result follows from Lemma 2.1. The invariance of Ω₁ is established from the fact that if E(t) > K_E, then $\frac{dE(t)}{dt}<0$. Furthermore, $\frac{d{L}_i(t)}{dt}<0$ whenever $L_i(t)>L_i^{\diamond }(t)$ and $\frac{d{P}_i(t)}{dt}<0$ whenever $P_i(t)>P_i^{\diamond }(t)$, for i = {SS, RS, RR}. Similarly, $\frac{d{M}_i^j(t)}{dt}<0$ whenever $M_i^j(t)>M_i^{j\diamond }(t)$, for j = {f, m}. Hence, the region Ω is positively-invariant and attracts all solutions of the model {(2.2)–(2.6)}, and it is sufficient to study the dynamics of the model within this region.

In the following section, the existence and asymptotic stability of the trivial and boundary equilibria of the model {(2.2)–(2.6)} will be explored.

3. Existence and asymptotic stability of equilibria of the model

As stated earlier, the model {(2.2)–(2.6)} is autonomous (since all the temperature-dependent parameters of the model are evaluated at fixed temperature values, making them to be constants). It is convenient to define the following entomological quantities:

$${\mathcal{R}}_{SS}=\frac{{\sigma }_E^{SS}{\sigma }_L^{SS}{\sigma }_P^{SS}{\nu }_f{\alpha }^{SS}}{K_1{K}_4{K}_7{K}_{10}},{\mathcal{R}}_{RS}=\frac{{\sigma }_E^{RS}{\sigma }_L^{RS}{\sigma }_P^{RS}{\nu }_f{\alpha }^{RS}}{K_2{K}_5{K}_8{K}_{11}}\text{and}{\mathcal{R}}_{RR}=\frac{{\sigma }_E^{RR}{\sigma }_L^{RR}{\sigma }_P^{RR}{\nu }_f{\alpha }^{RR}}{K_3{K}_6{K}_9{K}_{12}},$$ (3.1)

where,

$$\begin{array}{cccccc}& K_1={\sigma }_E^{SS}+{\mu }_E^{SS}& & K_2={\sigma }_E^{RS}+{\mu }_E^{RS},& & K_3={\sigma }_E^{RR}+{\mu }_E^{RR},\\ K_4& ={\sigma }_L^{SS}+{\epsilon }_L{C}_L{\delta }_L+{\mu }_L^{SS},& & K_5={\sigma }_L^{RS}+(1-h_L{k}_L){\epsilon }_L{C}_L{\delta }_L+{\mu }_L^{RS},& & K_6={\sigma }_L^{RR}+(1-k_L){\epsilon }_L{C}_L{\delta }_L+{\mu }_L^{RR},\\ K_7& ={\sigma }_P^{SS}+{\epsilon }_P{C}_P{\delta }_P+{\mu }_P^{SS},& & K_8={\sigma }_P^{RS}+{\epsilon }_P{C}_P(1-h_P{k}_P){\delta }_P+{\mu }_P^{RS},& & K_9={\sigma }_P^{RR}+{\epsilon }_P{C}_P(1-k_P){\delta }_P+{\mu }_P^{RR},\\ K_{10}& ={\epsilon }_M{C}_M{\delta }_{M_f}+{\mu }_{M_f}^{SS},& & K_{11}={\epsilon }_M{C}_M(1-h_M{k}_M){\delta }_{M_f}+{\mu }_{M_f}^{RS},& & K_{12}={\epsilon }_M{C}_M(1-k_M){\delta }_{M_f}+{\mu }_{M_f}^{RR}.\end{array}$$

The threshold quantities ${\mathcal{R}}_i$ (with i = {SS, RS, RR}) are the net production numbers for mosquitoes of genotype i (Veprauskas & Cushing, 2016). Specifically, ${\mathcal{R}}_i$ measures the average rate at which new adult female mosquitoes of genotype i are produced. For instance, the threshold quantity ${\mathcal{R}}_{SS}$, given in (3.1), can be interpreted entomologically as follows: it is the product of the rate at which eggs of SS genotype are laid by adult female mosquitoes (α^SS), the probability that these eggs survived and hatch into larvae of SS genotype $\left(\frac{{\sigma }_E^{SS}}{K_1}\right)$, the probability that the larvae survived and mature into pupae of the same genotype $\left(\frac{{\sigma }_L^{SS}}{K_4}\right)$, the probability that pupae metamorphose into adult female mosquitoes of SS genotype $\left(\frac{{\nu }_f{\sigma }_P^{SS}}{K_7}\right)$ and the average lifespan of an adult female mosquito of SS genotype $\left(\frac{1}{K_{10}}\right)$. The net production numbers, ${\mathcal{R}}_{RS}$ and ${\mathcal{R}}_{RR}$, for genotype RS and RR, respectively, can be entomologically interpreted similarly. Let,

$$K_{13}={\epsilon }_M{C}_M{\delta }_{M_m}+{\mu }_{M_m}^{SS},K_{14}={\epsilon }_M{C}_M(1-h_M{k}_M){\delta }_{M_m}+{\mu }_{M_m}^{RS},K_{15}={\epsilon }_M{C}_M(1-k_M){\delta }_{M_m}+{\mu }_{M_m}^{RR}.$$

The analysis in this section, for the existence and asymptotic stability of the model {(2.2)–(2.6)}, will be carried out for the special case of the model in the absence of density-dependent larval mortality (i.e., we will analyse the model {(2.2)–(2.6)} with ${\Psi }_L^i=0$, for i = {SS, RS, RR}). Specifically, we let:

$$X=\left(E_{SS}^{\ast },E_{RS}^{\ast },E_{RR}^{\ast },L_{SS}^{\ast },L_{RS}^{\ast },L_{RR}^{\ast },P_{SS}^{\ast },P_{RS}^{\ast },P_{RR}^{\ast },M_{SS}^{f\ast },M_{RS}^{f\ast },M_{RR}^{f\ast },M_{SS}^{m\ast },M_{RS}^{m\ast },M_{RR}^{m\ast }\right)$$

represent the components of any arbitrary equilibrium of the autonomous model {(2.2)–(2.6)} with ${\Psi }_L^i=0$ (i = {SS, RS, RR}). It can be seen that the model {(2.2)–(2.6)} with ${\Psi }_L^i=0$ (i = {SS, RS, RR}) has the following equilibria:

• (i).A trivial mosquito-free equilibrium, given by:

$${\mathcal{T}}_1=(0,0,0,0,0,0,0,0,0,0,0,0,0,0,0).$$

• (ii).A boundary equilibrium with only insecticide-sensitive mosquitoes (referred to as SS-only boundary equilibrium), given by:

$${\mathcal{T}}_2=\left(E_{SS}^{\ast },0,0,L_{SS}^{\ast },0,0,P_{SS}^{\ast },0,0,M_{SS}^{f\ast },0,0,M_{SS}^{m\ast },0,0\right),$$

where $E_{SS}^{\ast }=\frac{K_E}{{\mathcal{R}}_{SS}}\left({\mathcal{R}}_{SS}-1\right)$, $L_{SS}^{\ast }=\frac{{\sigma }_E^{SS}{E}_{SS}^{\ast }}{K_4}$, $P_{SS}^{\ast }=\frac{{\sigma }_L^{SS}{L}_{SS}^{\ast }}{K_7}$, $M_{SS}^{f\ast }=\frac{{\nu }_f{\sigma }_P^{SS}{P}_{SS}^{\ast }}{K_{10}}$, and $M_{SS}^{m\ast }=\frac{(1-{\nu }_f){\sigma }_P^{SS}{P}_{SS}^{\ast }}{K_{13}}$.

• (iii).A boundary equilibrium with only insecticide-resistant mosquitoes (referred to as RR-only boundary equilibrium), given by:

$${\mathcal{T}}_3=\left(0,0,E_{RR}^{\ast \ast },0,0,L_{RR}^{\ast \ast },0,0,P_{RR}^{\ast \ast },0,0,M_{RR}^{f\ast \ast },0,0,M_{RR}^{m\ast \ast }\right),$$

where $E_{RR}^{\ast }=\frac{K_E}{{\mathcal{R}}_{RR}}\left({\mathcal{R}}_{RR}-1\right)$, $L_{RR}^{\ast }=\frac{{\sigma }_E^{RR}{E}_{RR}^{\ast }}{K_6}$, $P_{RR}^{\ast }=\frac{{\sigma }_L^{RR}{L}_{RR}^{\ast }}{K_9}$, $M_{RR}^{f\ast }=\frac{{\nu }_f{\sigma }_P^{RR}{P}_{RR}^{\ast }}{K_{12}}$, and $M_{RR}^{m\ast }=\frac{(1-{\nu }_f){\sigma }_P^{RR}{P}_{RR}^{\ast }}{K_{15}}$.

Furthermore, let

$${\mathcal{T}}_4=\left(E_{SS}^{\ast \ast \ast },E_{RS}^{\ast \ast \ast },E_{RR}^{\ast \ast \ast },L_{SS}^{\ast \ast \ast },L_{RS}^{\ast \ast \ast },L_{RR}^{\ast \ast \ast },P_{SS}^{\ast \ast \ast },P_{RS}^{\ast \ast \ast },P_{RR}^{\ast \ast \ast },M_{SS}^{f\ast \ast \ast },M_{RS}^{f\ast \ast \ast },M_{RR}^{f\ast \ast \ast },M_{SS}^{m\ast \ast \ast },M_{RS}^{m\ast \ast \ast },M_{RR}^{m\ast \ast \ast }\right),$$ (3.2)

represent an arbitrary coexistence equilibrium (i.e., an equilibrium where the component of each state variable of the model {(2.2)–(2.6)} is nonzero). It can be shown, from the equations of the {(2.2)–(2.6)} (with ${\Psi }_L^i=0$) at an arbitrary coexistence equilibrium, that:

$$\begin{array}{cccccc}{E}_{SS}^{\ast \ast \ast }& =\frac{K_2{K}_3{K}_E{q}_f^{\ast \ast \ast }{q}_m^{\ast \ast \ast }{\alpha }^{SS}\left({\mathcal{R}}_C-1\right)}{{\mathcal{R}}_C^{\ast }{\mathcal{R}}_C},& & E_{RS}^{\ast \ast \ast }=\frac{{\alpha }^{RS}{K}_1}{{\alpha }^{SS}{K}_2}\left(\frac{p_f^{\ast \ast \ast }}{q_f^{\ast \ast \ast }}+\frac{p_m^{\ast \ast \ast }}{q_m^{\ast \ast \ast }}\right)E_{SS}^{\ast \ast \ast },& & E_{RR}^{\ast \ast \ast }=\frac{{\alpha }^{RR}{K}_1}{{\alpha }^{SS}{K}_3}\frac{p_f^{\ast \ast \ast }{p}_m^{\ast \ast \ast }}{q_f^{\ast \ast \ast }{q}_m^{\ast \ast \ast }}{E}_{SS}^{\ast \ast \ast },\\ & L_{SS}^{\ast \ast \ast }=\frac{{\sigma }_E^{SS}}{K_4}{E}_{SS}^{\ast \ast \ast },& & L_{RS}^{\ast \ast \ast }=\frac{{\sigma }_E^{RS}}{K_5}{E}_{RS}^{\ast \ast \ast },& & L_{RR}^{\ast \ast \ast }=\frac{{\sigma }_E^{RR}}{K_6}{E}_{RR}^{\ast \ast \ast },\\ & P_{SS}^{\ast \ast \ast }=\frac{{\sigma }_L^{SS}}{K_7}{L}_{SS}^{\ast \ast \ast },& & P_{RS}^{\ast \ast \ast }=\frac{{\sigma }_L^{RS}}{K_8}{L}_{RS}^{\ast \ast \ast },& & P_{RR}^{\ast \ast \ast }=\frac{{\sigma }_L^{RR}}{K_9}{L}_{RR}^{\ast \ast \ast },\end{array}$$ (3.3)

with,

$$\begin{array}{cc}& {\mathcal{R}}_C=\left(q_f^{\ast \ast \ast }{q}_m^{\ast \ast \ast }\right){\mathcal{R}}_{SS}+\left(p_f^{\ast \ast \ast }{q}_m^{\ast \ast \ast }+p_m^{\ast \ast \ast }{q}_f^{\ast \ast \ast }\right){\mathcal{R}}_{RS}+\left(p_f^{\ast \ast \ast }{p}_m^{\ast \ast \ast }\right){\mathcal{R}}_{RR},\\ {\mathcal{R}}_C^{\ast }& =K_2{K}_3\left(q_f^{\ast \ast \ast }{q}_m^{\ast \ast \ast }\right){\alpha }^{SS}+K_1{K}_3\left(p_f^{\ast \ast \ast }{q}_m^{\ast \ast \ast }+p_m^{\ast \ast \ast }{q}_f^{\ast \ast \ast }\right){\alpha }^{RS}+K_1{K}_2\left(p_f^{\ast \ast \ast }{p}_m^{\ast \ast \ast }\right){\alpha }^{RR},\\ & q_f^{\ast \ast \ast }=\frac{M_{SS}^{f\ast \ast \ast }+\frac{1}{2}{M}_{RS}^{f\ast \ast \ast }}{M^{f\ast \ast \ast }},q_m^{\ast \ast \ast }=\frac{M_{SS}^{m\ast \ast \ast }+\frac{1}{2}{M}_{RS}^{m\ast \ast \ast }}{M^{m\ast \ast \ast }},\\ & p_f^{\ast \ast \ast }=\frac{M_{RR}^{f\ast \ast \ast }+\frac{1}{2}{M}_{RS}^{f\ast \ast \ast }}{M^{f\ast \ast \ast }},p_m^{\ast \ast \ast }=\frac{M_{RR}^{m\ast \ast \ast }+\frac{1}{2}{M}_{RS}^{m\ast \ast \ast }}{M^{m\ast \ast \ast }},\end{array}$$ (3.4)

where,

$$M^{f\ast \ast \ast }=M_{SS}^{f\ast \ast \ast }+M_{RS}^{f\ast \ast \ast }+M_{RR}^{f\ast \ast \ast }\text{and}{M}^{m\ast \ast \ast }=M_{SS}^{m\ast \ast \ast }+M_{RS}^{m\ast \ast \ast }+M_{RR}^{m\ast \ast \ast }.$$ (3.5)

It can be seen from (3.4) that $q_f^{\ast \ast \ast }{q}_m^{\ast \ast \ast }+(p_f^{\ast \ast \ast }{q}_m^{\ast \ast \ast }+p_m^{\ast \ast \ast }{q}_f^{\ast \ast \ast })+p_f^{\ast \ast \ast }{p}_m^{\ast \ast \ast }=1$, which is the Hardy-Weinberg condition in population genetics (Hastings, 2013; Kuniyoshi & dos Santos, 2017). It follows, from the expressions in (3.3) with (3.4), (3.5), that, the model {(2.2)–(2.6)} with $M_i^{f\ast \ast \ast }>0$, $M_i^{m\ast \ast \ast }>0$ and ${\Psi }_L^i=0$ $(i=\left\{SS,RS,RR\right\})$ has a coexistence equilibrium whenever ${\mathcal{R}}_C>1$ (Mohammed-Awel et al., 2020). It should be noted that a boundary equilibrium with only heterozygous mosquitoes (genotype RS) does not exist due to the random mating process. These results are summarized in the theorem below.

Theorem 3.1

The model {(2.2)–(2.6)} with ${\Psi }_L^i=0$ (i = {SS, RS, RR}) has:

• (i)a trivial mosquito-free equilibrium (denoted by${\mathcal{T}}_1$),
• (ii)an insecticide-sensitive-only boundary equilibrium (denoted by${\mathcal{T}}_2$) if and only if${\mathcal{R}}_{SS}>1$,
• (iii)an insecticide-resistant-only boundary equilibrium (denoted by${\mathcal{T}}_3$) if and only if${\mathcal{R}}_{RR}>1$,
• (iv)a coexistence equilibrium (denoted by${\mathcal{T}}_4$) if and only if$M_i^{f\ast \ast \ast }>0$,$M_i^{m\ast \ast \ast }>0$(with$i=\left\{SS,RS,RR\right\}$) and${\mathcal{R}}_C>1$.

3.1. Asymptotic stability of the boundary equilibria of the model

Since the trivial mosquito-free equilibrium $({\mathcal{T}}_1)$ is ecologically unrealistic, we focus instead on the asymptotic stability of the boundary (${\mathcal{T}}_2$ and ${\mathcal{T}}_3$) and coexistence $({\mathcal{T}}_4)$ equilibria. This is explored below.

3.1.1. Asymptotic stability of the sensitive-only boundary equilibrium

Let ${\mathcal{J}}_{{\mathcal{T}}_2}$ denotes the Jacobian of the model {(2.2)–(2.6)} with ${\Psi }_L^i=0$ (i = {SS, RS, RR}) evaluated at the insecticide-susceptible-only equilibrium ${\mathcal{T}}_2$. It can be shown that its associated characteristic polynomial is given by:

$$p(x)=(x+K_3)(x+K_6)(x+K_9)(x+K_{12})(x+K_{13})(x+K_{15})p_4(x)p_5(x),$$ (3.6)

where,

$$\begin{array}{cc}& p_4\left(x\right)=x^4+a_1{x}^3+a_2{x}^2+a_{3}x+a_4,\\ & p_5\left(x\right)=x^5+b_1{x}^4+b_2{x}^3+b_3{x}^2+b_{4}x+b_5,\end{array}$$ (3.7)

with,

$$\begin{array}{cc}& a_1=\frac{K_E(K_1+K_4+K_7+K_{10})+{\alpha }^{SS}{M}_{SS}^{f\ast }}{K_E},\\ & a_2=\frac{K_E(K_1{K}_4+K_1{K}_7+K_1{K}_{10}+K_{10}{K}_4+K_{10}{K}_7+K_4{K}_7)+{\alpha }^{SS}{M}_{SS}^{f\ast }(K_4+K_7+K_{10})}{K_E},\\ & a_3=\frac{K_E(K_1{K}_4{K}_{10}+K_1{K}_7{K}_{10}+K_1{K}_4{K}_7+K_4{K}_7{K}_{10})+{\alpha }^{SS}{M}_{SS}^{f\ast }(K_4{K}_{10}+K_7{K}_{10}+K_4{K}_7)}{K_E},\\ & a_4=\frac{K_4{K}_7{K}_{10}{\alpha }^{SS}{M}_{SS}^{f\ast }}{K_E},\\ & b_1=K_2+K_5+K_8+K_{11}+K_{14},\\ & b_2=K_{11}(K_2+K_5+K_8+K_{14})+K_{14}(K_2+K_5+K_8)+K_8(K_2+K_5)+K_2{K}_5,\\ & b_3=K_{11}[K_{14}(K_2+K_5+K_8)+K_8(K_2+K_5)+K_2{K}_5]+K_{14}[K_8(K_2+K_5)+K_2{K}_5]+K_2{K}_5{K}_8,\\ & b_4=\left(K_{14}\{K_{11}[K_8(K_2+K_5)+K_2{K}_5]+K_2{K}_5{K}_8\}+K_2{K}_5{K}_8{K}_{11}\right)\left(1-{\mathcal{R}}_{0_1}^{SS}\right),\\ & b_5=K_2{K}_5{K}_8{K}_{11}{K}_{14}\left(1-{\mathcal{R}}_{0_2}^{SS}\right),\end{array}$$

and,

$$\begin{array}{cc}& {\mathcal{R}}_{0_1}^{SS}=\left(\frac{K_2{K}_5{K}_8{K}_{11}}{K_{14}\{K_{11}[K_8(K_2+K_5)+K_2{K}_5]+K_2{K}_5{K}_8\}+K_2{K}_5{K}_8{K}_{11}}\right)\frac{{\mathcal{R}}_{RS}}{2{\mathcal{R}}_{SS}}\left(1+\frac{(1-{\nu }_f)M_{SS}^{f\ast }}{{\nu }_f{M}_{SS}^{m\ast }}\right),\\ & {\mathcal{R}}_{0_2}^{SS}=\frac{{\mathcal{R}}_{RS}}{2{\mathcal{R}}_{SS}}\left(1+\frac{(1-{\nu }_f)K_{11}{M}_{SS}^{f\ast }}{{\nu }_f{K}_{14}{M}_{SS}^{m\ast }}\right).\end{array}$$ (3.8)

It is convenient to define the threshold quantity:

$${\mathcal{R}}_0^{SS}=\max \left\{{\mathcal{R}}_{0_1}^{SS},{\mathcal{R}}_{0_2}^{SS}\right\}.$$ (3.9)

It follows from (3.6) that the roots of the characteristic polynomial p(x) are given by six negative real roots (namely − K₃, − K₆, − K₉, − K₁₂, − K₁₃ and − K₁₅) and the roots of the fourth and fifth degree polynomials, p₄(x) and p₅(x), respectively. It can be seen that all the coefficients of the fourth degree polynomial p₄(x) are positive and satisfy the inequality $a_1{a}_2{a}_3>a_3^2+a_1^2{a}_4$ (see B). That is, the associated Routh-Hutwitz criterion for a quartic to have roots with negative real parts are satisfied (Martcheva, 2015). Hence, all roots of p₄(x) are negative or have negative real part (Martcheva, 2015).

Similarly, it follows from (3.7) that if ${\mathcal{R}}_0^{SS}<1$, then all the coefficients of p₅(x) are positive. Further, it can be shown that the inequalities $b_1{b}_2{b}_3>b_3^2+b_1^2{b}_4$ and $(b_1{b}_4-b_5)(b_1{b}_2{b}_3-b_3^2-b_1^2{b}_4)>b_5{(b_1{b}_2-b_3)}^2+b_1{b}_5^2$ are satisfied (see the B). Hence, by Routh-Hurwitz criterion for a quintic, all roots of p₅(x) have negative real parts if and only if ${\mathcal{R}}_0^{SS}<1$. Thus, it can be concluded that all roots of the characteristic polynomial p(x) have negative real parts if ${\mathcal{R}}_0^{SS}<1$. Consequently, the sensitive-only boundary equilibrium $({\mathcal{T}}_2)$ is locally-asymptotically stable whenever ${\mathcal{R}}_0^{SS}<1$, and is unstable if ${\mathcal{R}}_0^{SS}>1$. This result is summarized below.

Theorem 3.2

The sensitive-only boundary equilibrium$({\mathcal{T}}_2)$of the model {(2.2)–(2.6)} with ${\Psi }_L^i=0$ (i = {SS, RS, RR}), which exists only if ${\mathcal{R}}_{SS}>1$, is locally-asymptotically stable if ${\mathcal{R}}_0^{SS}<1$, and unstable if ${\mathcal{R}}_0^{SS}>1$.

The ecological implication of Theorem 3.2 is if the initial number of the insecticide-resistance {(2.2)–(2.6)} with Ψ_i = 0 (i = {SS, RS, RR}) and ${\mathcal{R}}_{SS}>1$ is as follows: if the initial number of the insecticide-sensitive mosquitoes in the community falls within the basin of attraction of ${\mathcal{T}}_2$, the insecticide-sensitive mosquito population will persist in the community (with the other genotypes going extinct) provided the threshold quantity ${\mathcal{R}}_0^{SS}$ can be brought to (and maintained at) a value less than one. It can be seen from the expression of the reproduction threshold ${\mathcal{R}}_0^{SS}$ that, for the sensitive-only boundary equilibrium to be asymptotically-stable (i.e., in order for ${\mathcal{R}}_0^{SS}$ to be less than unity), the rate at which new adult female mosquitoes of genotype SS are produced $({\mathcal{R}}_{SS})$ must be sufficiently larger than the rate at which new adult females of genotype RS are produced $({\mathcal{R}}_{RS})$. This is due to the fact that heterozygous mosquitoes also contribute to the production of new adult mosquitoes of RS and RR genotypes.

3.1.2. Asymptotic stability of the resistant-only boundary equilibrium

Similarly, let ${\mathcal{J}}_{{\mathcal{T}}_3}$ denote the Jacobian of the model {(2.2)–(2.6)} with ${\Psi }_L^i=0$ (for i = {SS, RS, RR}) evaluated at the resistant-only boundary equilibrium ${\mathcal{T}}_3$. It can be shown that characteristic polynomial associated with ${\mathcal{J}}_{{\mathcal{T}}_3}$ is given by:

$$q(x)=(x+K_1)(x+K_4)(x+K_7)(x+K_{10})(x+K_{13})(x+K_{15})q_4(x)q_5(x),$$ (3.10)

where,

$$\begin{array}{cc}& q_4\left(x\right)=x^4+c_1{x}^3+c_2{x}^2+c_{3}x+c_4,\\ & q_5\left(x\right)=x^5+d_1{x}^4+d_2{x}^3+d_3{x}^2+d_{4}x+d_5,\end{array}$$ (3.11)

with,

$$\begin{array}{cc}& c_1=\frac{K_E(K_3+K_6+K_9+K_{12})+{\alpha }^{RR}{M}_{RR}^{f\ast \ast }}{K_E},\\ & c_2=\frac{K_E(K_3{K}_6+K_3{K}_9+K_3{K}_{12}+K_{12}{K}_6+K_{12}{K}_9+K_6{K}_9)+{\alpha }^{RR}{M}_{RR}^{f\ast \ast }(K_6+K_9+K_{12})}{K_E},\\ & c_3=\frac{K_E(K_3{K}_6{K}_{12}+K_3{K}_9{K}_{12}+K_3{K}_6{K}_9+K_6{K}_9{K}_{12})+{\alpha }^{RR}{M}_{RR}^{f\ast \ast }(K_6{K}_{12}+K_9{K}_{12}+K_6{K}_9)}{K_E},\\ & c_4=\frac{K_6{K}_9{K}_{12}{\alpha }^{RR}{M}_{RR}^{f\ast \ast }}{K_E},\\ & d_1=K_2+K_5+K_8+K_{11}+K_{14},\\ & d_2=K_{11}(K_2+K_5+K_8+K_{14})+K_{14}(K_2+K_5+K_8)+K_8(K_2+K_5)+K_2{K}_5,\\ & d_3=K_{11}[K_{14}(K_2+K_5+K_8)+K_8(K_2+K_5)+K_2{K}_5]+K_{14}[K_8(K_2+K_5)+K_2{K}_5]+K_2{K}_5{K}_8,\\ & d_4=\left(K_{14}\{K_{11}[K_8(K_2+K_5)+K_2{K}_5]+K_2{K}_5{K}_8\}+K_2{K}_5{K}_8{K}_{11}\right)\left(1-{\mathcal{R}}_{0_1}^{RR}\right),\\ & d_5=K_2{K}_5{K}_8{K}_{11}{K}_{14}\left(1-{\mathcal{R}}_{0_2}^{RR}\right),\end{array}$$

$${\mathcal{R}}_{0_1}^{RR}=\left(\frac{K_2{K}_5{K}_8{K}_{11}}{K_{14}\{K_{11}[K_8(K_2+K_5)+K_2{K}_5]+K_2{K}_5{K}_8\}+K_2{K}_5{K}_8{K}_{11}}\right)\frac{{\mathcal{R}}_{RS}}{2{\mathcal{R}}_{RR}}\left(1+\frac{(1-{\nu }_f)M_{RR}^{f\ast \ast }}{{\nu }_f{M}_{RR}^{m\ast \ast }}\right),$$ (3.12)

and,

$${\mathcal{R}}_{0_2}^{RR}=\frac{{\mathcal{R}}_{RS}}{2{\mathcal{R}}_{RR}}\left(1+\frac{(1-{\nu }_f)K_{11}{M}_{RR}^{f\ast \ast }}{{\nu }_f{K}_{14}{M}_{RR}^{m\ast \ast }}\right).$$ (3.13)

Here, too, it is convenient to define the following threshold quantity:

$${\mathcal{R}}_0^{RR}=\max \left\{{\mathcal{R}}_{0_1}^{RR},{\mathcal{R}}_{0_2}^{RR}\right\}.$$ (3.14)

Using similar algebraic computations and manipulations as in Section 3.1.1, it can be shown that all roots of the characteristic polynomial q(x) are negative or have negative real part if and only if ${\mathcal{R}}_0^{RR}<1$. Consequently, the resistant-only equilibrium $({\mathcal{T}}_3)$ of the model {(2.2)–(2.6)} is locally-asymptotically stable if ${\mathcal{R}}_0^{RR}<1$, and unstable if ${\mathcal{R}}_0^{RR}>1$. Hence, we have established the following result.

Theorem 3.3

The insecticide-resistant-only boundary equilibrium ($({\mathcal{T}}_3)$of the special case of the model {(2.2)–(2.6)} with ${\Psi }_L^i=0$ (for i = {SS, RS, RR}), which exists only if ${\mathcal{R}}_{RR}>1$, is locally-asymptotically stable if ${\mathcal{R}}_0^{RR}<1$, and unstable if ${\mathcal{R}}_0^{RR}>1$.

Here, too, the implication of Theorem 3.3 is that initial conditions in the basin of attraction of the resistant-only boundary equilibrium $({\mathcal{T}}_3)$ will converge to ${\mathcal{T}}_3$ if the threshold quantity ${\mathcal{R}}_0^{RR}$ is less than one. Furthermore, to ensure that ${\mathcal{R}}_0^{RR}<1$ (so that the asymptotic stability of the RR-only boundary equilibrium can be achieved), it is necessary that the rate at which new adult female mosquitoes of genotype RR are produced $({\mathcal{R}}_{RR})$ must be sufficiently larger than the rate at which new adult females of genotype RS are produced $({\mathcal{R}}_{RS})$. This is due to the fact that heterozygous mosquitoes also contribute to the production of new adult mosquitoes of SS and RR genotypes.

It can be shown from (3.12) that the following inequalities hold:

$$\frac{K_2{K}_5{K}_8{K}_{11}}{K_{14}\{K_{11}[K_8(K_2+K_5)+K_2{K}_5]+K_2{K}_5{K}_8\}+K_2{K}_5{K}_8{K}_{11}}\le 1,$$ (3.15)

and,

$$\frac{K_2{K}_5{K}_8{K}_{11}}{K_{14}\{K_{11}[K_8(K_2+K_5)+K_2{K}_5]+K_2{K}_5{K}_8\}+K_2{K}_5{K}_8{K}_{11}}\le \frac{K_{11}}{K_{14}}.$$ (3.16)

It follows from (3.15) that if K₁₁ ≥ K₁₄, then

$${\mathcal{R}}_{0_1}^{RR}\le \frac{{\mathcal{R}}_{RS}}{2{\mathcal{R}}_{RR}}\left(1+\frac{(1-{\nu }_f)M_{RR}^{f\ast \ast }}{{\nu }_f{M}_{RR}^{m\ast \ast }}\right)\le \frac{{\mathcal{R}}_{RS}}{2{\mathcal{R}}_{RR}}\left(1+\frac{(1-{\nu }_f)K_{11}{M}_{RR}^{f\ast \ast }}{{\nu }_f{K}_{14}{M}_{RR}^{m\ast \ast }}\right)={\mathcal{R}}_{0_2}^{RR}.$$

Furthermore, it follows from (3.16) that if K₁₁ ≤ K₁₄, then

$${\mathcal{R}}_{0_1}^{RR}\le \frac{K_{11}}{K_{14}}\frac{{\mathcal{R}}_{RS}}{2{\mathcal{R}}_{RR}}\left(1+\frac{(1-{\nu }_f)M_{RR}^{f\ast \ast }}{{\nu }_f{M}_{RR}^{m\ast \ast }}\right)\le \frac{{\mathcal{R}}_{RS}}{2{\mathcal{R}}_{RR}}\left(1+\frac{(1-{\nu }_f)K_{11}{M}_{RR}^{f\ast \ast }}{{\nu }_f{K}_{14}{M}_{RR}^{m\ast \ast }}\right)={\mathcal{R}}_{0_2}^{RR}.$$

Therefore,

$${\mathcal{R}}_{0_1}^{RR}\le {\mathcal{R}}_{0_2}^{RR}\text{and}{\mathcal{R}}_0^{RR}=\max \left\{{\mathcal{R}}_{0_1}^{RR},{\mathcal{R}}_{0_2}^{RR}\right\}={\mathcal{R}}_{0_2}^{RR}.$$ (3.17)

In other words, the above analyses show that the threshold quantity, ${\mathcal{R}}_0^{RR}$, which governs the asymptotic stability of the resistant-only boundary equilibrium of the model {(2.2)–(2.6)}, reduces to (or is precisely given by) ${\mathcal{R}}_{0_2}^{RR}$. Hence, if ${\mathcal{R}}_{0_2}^{RR}<1$, then all the coefficients of q₅(x) (and thus of q(x)) are positive, and it can be verified that the Routh-Hurwitz criteria for quartic and quintic polynomials are satisfied (see Appendix B) (Martcheva, 2015). Similarly, it can be shown that

$${\mathcal{R}}_{0_1}^{SS}\le {\mathcal{R}}_{0_2}^{SS}\text{and}{\mathcal{R}}_0^{SS}=\max \left\{{\mathcal{R}}_{0_1}^{SS},{\mathcal{R}}_{0_2}^{SS}\right\}={\mathcal{R}}_{0_2}^{SS}.$$ (3.18)

3.2. Asymptotic stability of coexistence equilibrium

Extensive numerical simulations of the model {(2.2)–(2.6)} with ${\Psi }_L^i=0$ suggest that initial solutions converge to a coexistence equilibrium (of the form ${\mathcal{T}}_4$) whenever the asymptotic stability conditions for the sensitive-only and resistant-only boundary equilibria (stated in Theorems 3.2 and 3.3) are violated. This suggests the conjecture below.

Conjecture 3.1A coexistence equilibrium of the model {(2.2)–(2.6)} with ${\Psi }_L^i=0$ (i = {SS, RS, RR}) and ${\mathcal{R}}_C>1$ (of the form ${\mathcal{T}}_4$), which exists when $M_i^{f\ast \ast \ast }>0$ and $M_i^{m\ast \ast \ast \ast }>0$, is locally-asymptotically stable whenever $\mathrm{m}\mathrm{i}\mathrm{n}\left\{{\mathcal{R}}_{SS},{\mathcal{R}}_{RR}\right\}>1$.

The theoretical results given in Theorems 3.2, 3.3, and Conjecture 3.1 are numerically-illustrated in Section 3.3.

3.3. Numerical illustration of theoretical results

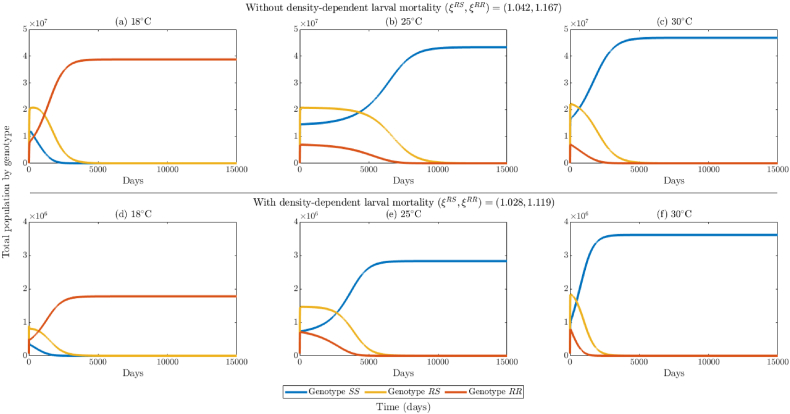
In this section, numerical simulations will be carried out to illustrate the asymptotic stability results derived in Section 3 for the model {(2.2)–(2.6)}. Since the analyses in Section 3 were conducted for the special case of the model in the absence of density-dependent larval mortality, we will set the density-dependent larval mortality parameters, ${\Psi }_L^i$ (i = {SS, RS, RR}), to zero in the numerical simulations here (this will be relaxed in some of the numerical simulations to be carried out in Section 4 for assessing the impact of density-dependent larval mortality on the population abundance of mosquitoes). The simulations in this section are carried out using 1000 randomly-generated initial conditions in the interval [0, 3 × 10⁷]. Specifically, 250 initial conditions are chosen such that all three genotypes initially exist, and another set of 250 initial conditions were chosen for the case where there are no mosquitoes of SS, RS and RR genotype in the population, respectively (this is to ensure that we generate results that fill up the entire allele frequency spectrum of 0 < p, q ≤ 1 such that p + q = 1). Values of the parameters of the model are randomly chosen so that the reproduction thresholds, ${\mathcal{R}}_0^{SS}$ and ${\mathcal{R}}_0^{RR}$, take values below or above one, in line with the hypotheses of Theorems 3.2 and 3.3 and Conjecture 3.1 (i.e., the parameter values are chosen for illustrative purposes, and may not be realistic ecologically).

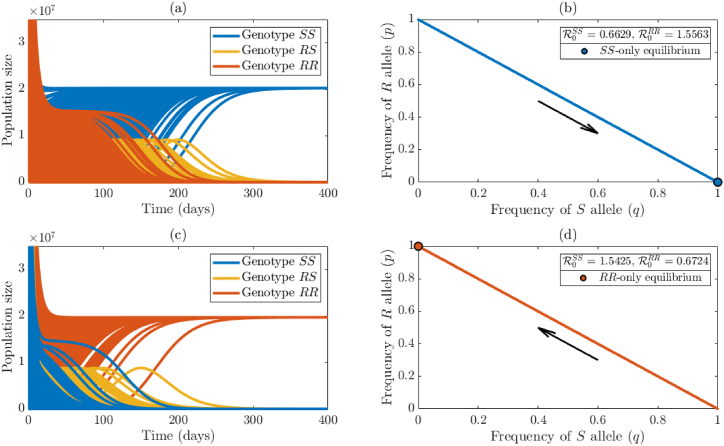
The simulation results obtained, for the case where the values of the parameters of the model are chosen such that ${\mathcal{R}}_0^{SS}\approx 0.6629<1$ and ${\mathcal{R}}_0^{RR}\approx 1.5563>1$, depicted in Fig. 2(a), show convergence of initial solutions to the sensitive-only boundary equilibrium, ${\mathcal{T}}_2$ (where mosquitoes of RS and RR genotype become extinct, while those of SS genotype persist in the population). Furthermore, in this case, for any allele distribution in which the initial frequency of the sensitive allele is nonzero, trajectories converge to the sensitive-only boundary equilibrium (Theorem 3.2(b)), where only sensitive mosquitoes are present in the population (for this case, q(t) → 1 and p(t) → 0, at t → ∞). These simulation results are in line with Theorem 3.2.

Fig. 2.

Numerical illustration of the theoretical results given in Theorems 3.2 and 3.3. Simulations of the model {(2.2)–(2.6)} with ${\Psi }_L^i=0$, i = {SS, RS, RR}. (a) Time series of total population of mosquitoes of SS genotype (blue curves), RS genotype (gold curves), and RR genotype (orange curves), generated using various initial conditions and parameter values chosen such that ${\mathcal{R}}_0^{SS}\approx 0.6629<1$ and ${\mathcal{R}}_0^{RR}\approx 1.5563>1$, as a function of time. (b) Plot of frequencies of sensitive (q) versus resistant (p) alleles, over time, for the case when ${\mathcal{R}}_0^{SS}\approx 0.6629<1$ and ${\mathcal{R}}_0^{RR}\approx 1.5563>1$. (c) Time-series of total population of mosquitoes of SS genotype (blue curves), RS genotype (gold curves), and RR genotype (orange curves), generated using various initial conditions and parameter values chosen such that ${\mathcal{R}}_0^{SS}\approx 1.5425>1$ and ${\mathcal{R}}_0^{RR}\approx 0.6724<1$. (d) Plot of frequencies of sensitive (q) versus resistant (p) alleles, over time, for each initial condition, when ${\mathcal{R}}_0^{SS}\approx 1.5425>1$ and ${\mathcal{R}}_0^{RR}\approx 0.6724<1$. Orange and blue dots indicate the average allele frequency at steady-state, and black arrows point in the direction of the trajectories in the phase portraits.

On the other hand, if parameter values are chosen such that ${\mathcal{R}}_0^{RR}\approx 0.6724<1$ and ${\mathcal{R}}_0^{SS}\approx 1.5425>1$, our simulations show convergence of initial solutions to the resistant-only boundary equilibrium, ${\mathcal{T}}_3$ (Fig. 2(c); where mosquitoes of SS and RS genotype go extinct, while those of RR genotype persist in the population). Here, too, the allele distribution shows that all mosquitoes are homozygous resistant as long as the initial frequency of the resistance allele is nonzero (Fig. 2(d); specifically, p(t) → 1 and q(t) → 0, at t → ∞). These simulation results are in line with Theorem 3.3.

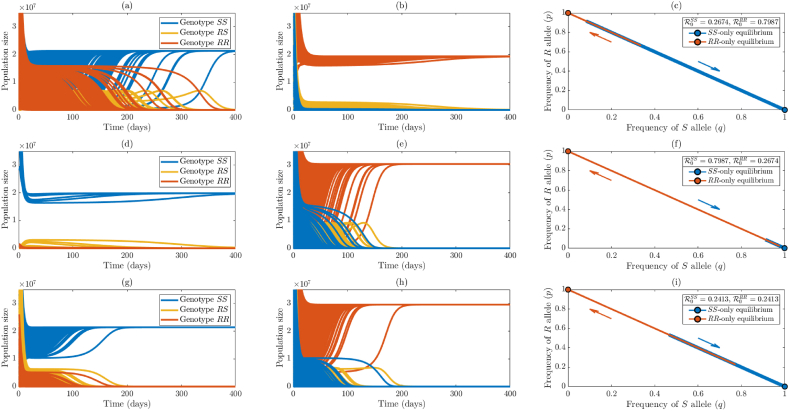
We simulated the case where the values of the parameters of the model are chosen such that each of the two reproduction thresholds is less than one (so that, by Theorems 3.2 and 3.3, both boundary equilibria, ${\mathcal{T}}_2$ and ${\mathcal{T}}_3$, are locally-asymptotically stable). The simulation results obtained, for the case where $0<{\mathcal{R}}_0^{SS}\approx 0.2674<{\mathcal{R}}_0^{RR}\approx 0.7987$, show that while some initial conditions converged to the sensitive-only boundary equilibrium (Fig. 3(a)), others converged to the resistant-only boundary equilibrium (Fig. 3(b)). In other words, for the case when each of the two reproduction thresholds is less than one, the model exhibits the phenomenon of bistability, where convergence to any of the two stable boundary equilibria depends on the initial conditions used in the simulations. The bistability phenomenon is also illustrated in terms of distribution of alleles in the population. Specifically, it is shown that, for this case (where both reproduction thresholds are less than one), some initial allele frequencies converged to the sensitive-only equilibrium, while others converged to the resistant-only boundary equilibrium (Fig. 3(c)). This figure shows a wider range of initial allele frequencies that converge to the sensitive-only boundary equilibrium (in comparison to those that converge to the resistant-only boundary equilibrium). For this case, the sensitive-only boundary equilibrium $({\mathcal{T}}_2)$ has a larger basin of attraction than the resistant-only boundary equilibrium $({\mathcal{T}}_3)$.

Fig. 3.

Numerical illustration of the theoretical results given in Conjecture 3.1. Simulations of the model {(2.2)–(2.6)} with ${\Psi }_L^i=0$, i = {SS, RS, RR}, for various initial conditions, showing bistability when $\mathrm{m}\mathrm{a}\mathrm{x}\{{\mathcal{R}}_0^{SS},{\mathcal{R}}_0^{RR}\}<1$. Top row: numerical simulations for the case where the parameter values are chosen such that ${\mathcal{R}}_0^{SS}\approx 0.2674<1$ and ${\mathcal{R}}_0^{RR}\approx 0.7987<1$. Middle row: numerical simulations for the case where the parameter values are chosen such that ${\mathcal{R}}_0^{SS}\approx 0.7987<1$ and ${\mathcal{R}}_0^{RR}\approx 0.2674<1$. Bottom row: numerical simulations for the case where the parameter values are chosen such that ${\mathcal{R}}_0^{SS}\approx 0.2413<1$ and ${\mathcal{R}}_0^{RR}\approx 0.2413<1$. Left column: simulations where initial solutions converge to the insecticide-sensitive-only boundary equilibrium (for ${\mathcal{R}}_0^{SS}<1$ and ${\mathcal{R}}_0^{RR}<1$). Middle column: simulations where initial solutions converge to the insecticide-resistant-only boundary equilibrium (for ${\mathcal{R}}_0^{SS}<1$ and ${\mathcal{R}}_0^{RR}<1$). Right column: plot of frequency of sensitive allele (q) versus frequency of resistant allele (p) in the population, showing allele frequencies over time for each initial condition (and for the given values of ${\mathcal{R}}_0^{SS}<1$ and ${\mathcal{R}}_0^{RR}<1$). In the left and middle columns, mosquito populations of genotype SS are indicated by blue curves, mosquito populations of genotype RS are indicated by gold curves, and mosquito populations of genotype RR are indicated by orange curves. In the right column, trajectories whose final state is the insecticide-sensitive-only equilibrium are shown in blue, and trajectories whose final state is the insecticide-resistant-only equilibrium are shown in orange. Arrows indicate the direction of the allele frequencies (with the same color scheme).

It can be observed from Fig. 3(a) and (b) that the majority of the initial conditions tend to converge to the sensitivity-only boundary equilibrium. This is due to the fact that the value of the reproduction threshold for the sensitive-only equilibrium $({\mathcal{R}}_0^{SS}\approx 0.2674)$ is less than that of the resistant-only boundary equilibrium $({\mathcal{R}}_0^{RR}\approx 0.7987)$. This fact is further highlighted by simulating the case when both reproduction thresholds are less than one, but that of the resistant-only boundary equilibrium is lower. Specifically, we plotted the case where $0<{\mathcal{R}}_0^{RR}\approx 0.2674<{\mathcal{R}}_0^{SS}\approx 0.7987$. The results obtained again show bistability, with some of the trajectories converging to the sensitive-only boundary equilibrium (Fig. 3(d)), while others (constituting majority of the trajectories) converged to the resistant-only boundary equilibrium (Fig. 3(e)). This result is also illustrated in terms of the allele frequency distribution (Fig. 3(f)), showing a wider range of initial allele distributions that converge to the resistant-only boundary equilibrium (in comparison to those that converged to the sensitive-only boundary equilibrium). In this case, the resistant-only boundary equilibrium has a larger basin of attraction than the sensitive-only boundary equilibrium.

Finally, we simulated the case where both reproduction thresholds are less than one but nearly equal (specifically, ${\mathcal{R}}_0^{SS}\approx {\mathcal{R}}_0^{RR}\approx 0.2413$). These numerical results (shown in Fig. 3(g) and (h)) again exhibit the bistability phenomenon. Depending on the initial conditions, trajectories could converge to the sensitive-only equilibrium (Fig. 3(g)) or to the resistant-only equilibrium (Fig. 3(h)). The allele frequency distribution (shown in Fig. 3(i)) highlights this occurrence, depicting a wide range of allele frequencies in which trajectories converge to either boundary equilibrium (although there is a slight asymmetry with more trajectories heading to the RR-only equilibrium, likely due to the parameter values used).

It is worth mentioning that the bistability phenomenon illustrated in Fig. 2, Fig. 3 does not occur if the mosquito population is not stratified according to genotype. In other words, the model {(2.2)–(2.6)} with ${\Psi }_L^i=0\left(i=\{SS,RS,RR\}\right)$ will not exhibit bistability if mosquito population genetics is not taken into account (see, for example the models in (Abdelrazec & Gumel, 2017; Lutambi, Penny, Smith, & Chitnis, 2013; Ngwa, Niger, & Gumel, 2010; Okuneye et al., 2018), which did not stratify mosquitoes by genotype). Thus, this study shows that mosquito population genetics (i.e., stratifying the mosquito population according to genotype) causes the phenomenon of bistability in the population dynamics of the mosquito. Ecologically-speaking, this bistability phenomenon implies that, if the initial mosquito population lies in the basin of attraction for the homozygous resistant boundary equilibrium, only resistant mosquitoes will persist in the community at equilibrium (since mosquitoes of the other genotypes will become extinct in this case). This could result in the failure of insecticide-based public health interventions implemented in the community. However, if the total population of RR genotype mosquitoes that are persisting in this case is small enough (so that malaria can be effectively controlled in the community), then this bistability scenario can be considered a public health success (in terms of effectively controlling malaria), but, on the other hand, a failure to effectively manage insecticide resistance (since, at equilibrium, all mosquitoes in the community only carry the resistant allele in this case). Conversely, the other bistability scenario where initial solutions converge to the homozygous sensitive boundary equilibrium may be considered a success in terms of effective management of insecticide resistance (since the mosquitoes of resistant genotype die out asymptotically), but could be a public health failure if the total population of the insecticide-sensitive mosquitoes that are now persisting under this bistability scenario is high enough to sustain increased malaria transmission in the community.

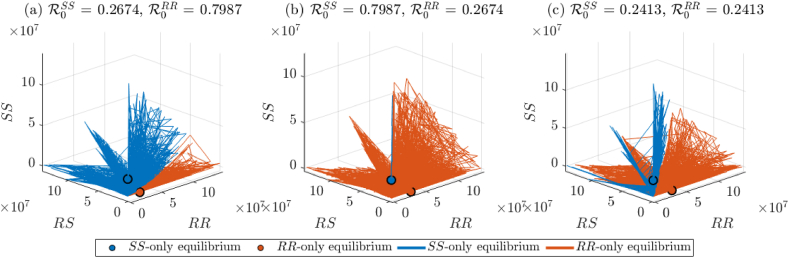
The simulation results in Fig. 3 are further illustrated using three-dimensional plots (Fig. 4) to enhance the clarity of the associated basin of attraction of the boundary equilibria. In particular, the three-dimensional plots allow for the analysis of the overlapping regions in Fig. 3(c),(f), and (i) that indicate initial allele frequencies converging to either of the two boundary equilibria. Fig. 4(a) shows that, for the case $0<{\mathcal{R}}_0^{SS}<{\mathcal{R}}_0^{RR}<1$, most solution trajectories converge to the sensitive-only boundary equilibrium (shaded blue region). However, given a sufficiently large population of mosquitoes of genotype RS and RR (relative to the population of mosquitoes of genotype SS), some solution trajectories will also converge to the RR-only boundary equilibrium (shaded orange region of Fig. 4(a)) under this condition. Similarly, for the case when $0<{\mathcal{R}}_0^{RR}<{\mathcal{R}}_0^{SS}<1$, most solution trajectories converge to the resistant-only boundary equilibrium (Fig. 4(b), shaded orange region), with very few solutions converging to the sensitive-only boundary equilibrium (Fig. 4(b), shaded blue region). Finally, the case where $0<{\mathcal{R}}_0^{RR}\approx {\mathcal{R}}_0^{SS}<1$ is depicted in Fig. 4(c), showing majority of trajectories converging to the resistant-only boundary equilibrium (shaded orange region); this asymmetry is likely due to the parameter values chosen for exploratory purposes.

Fig. 4.

Three-dimensional depiction of the bistability property of the model {2.2–2.6} with ${\Psi }_L^i=0$ (i = {SS, RS, RR}) in the SS- vs. RS- vs. RR-genotype plane, for various initial conditions and parameter values chosen such that $\mathrm{m}\mathrm{a}\mathrm{x}\{{\mathcal{R}}_0^{SS},{\mathcal{R}}_0^{RR}\}<1$. (a) Solution trajectories for the case ${\mathcal{R}}_0^{SS}<{\mathcal{R}}_0^{RR}<1$. (b) Solution trajectories for the case ${\mathcal{R}}_0^{RR}<{\mathcal{R}}_0^{SS}<1$. (c) Solution trajectories for the case ${\mathcal{R}}_0^{SS}\approx {\mathcal{R}}_0^{RR}<1$. Notation: solution trajectories whose final state is the sensitive-only boundary equilibrium are shown in blue, while those whose final state is the resistant-only boundary equilibrium are shown in orange.

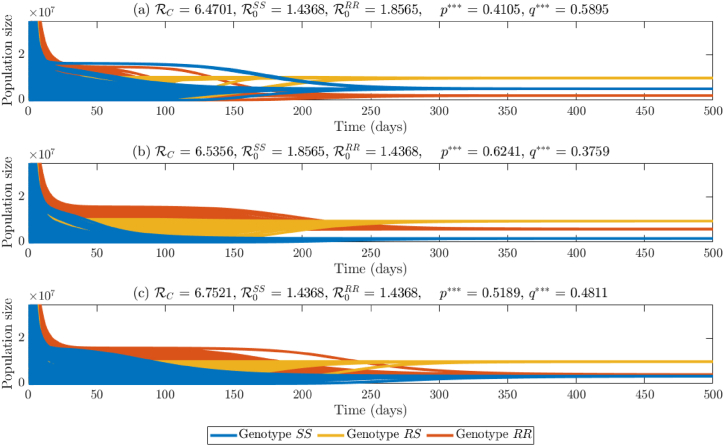
Finally, we now consider the case where the values of the parameters of the model {(2.2)–(2.6)} with ${\Psi }_L^i=0$ are chosen such that both reproduction thresholds exceed unity (i.e., $\mathrm{m}\mathrm{i}\mathrm{n}\{{\mathcal{R}}_0^{SS},{\mathcal{R}}_0^{RR}\}>1$). For this case, the two boundary equilibria are unstable (see Theorems 3.2 and 3.3) and Conjecture 3.1 hypothesizes that a coexistence equilibrium is asymptotically stable. Simulating the model with parameter values such that ${\mathcal{R}}_0^{SS}\approx 1.4368$ and ${\mathcal{R}}_0^{RR}\approx 1.8565$ shows convergence of initial conditions to all three genotypes (Fig. 5(a)). In this figure, the population of heterozygous mosquitoes (Fig. 5(a), gold curves) dominate those for the homozygous-sensitive (Fig. 5(a), blue curves) and the homozygous-resistant (Fig. 5(a), red curves), in this order. The dominance of mosquitoes with the SS genotype over those with the RR genotype in this figure is due to the fact that the value of the reproduction threshold for the SS genotype $({\mathcal{R}}_0^{SS})$ is lower than that of the RR genotype $({\mathcal{R}}_0^{RR})$ in this case. Further, for this scenario, the frequency of the sensitive allele at steady-state (q∗∗∗) is approximately 0.5895, while that of the resistant allele (p∗∗∗) is approximately 0.4105 (note that q∗∗∗ + p∗∗∗ = 1).

Fig. 5.

Numerical simulations of the model {2.2–2.6} with ${\Psi }_L^i=0$, i = {SS, RS, RR} for various values of ${\mathcal{R}}_0^{SS}>1$ and ${\mathcal{R}}_0^{RR}>1$. (a) Time series of mosquito populations when $1<{\mathcal{R}}_0^{SS}<{\mathcal{R}}_0^{RR}$. (b) Time series of mosquito populations when $1<{\mathcal{R}}_0^{RR}<{\mathcal{R}}_0^{SS}$. (c) Time series of mosquito populations when $1<{\mathcal{R}}_0^{SS}\approx {\mathcal{R}}_0^{RR}$. Allele frequencies at steady-state are shown in the title of each plot. Mosquitoes of genotype SS are shown in blue, mosquitoes of genotype RS are shown in gold, and mosquitoes of genotype RR are shown in orange.

The case where the reproduction threshold for the RR genotype is lower than that of the SS genotype (but both greater than unity) is depicted Fig. 5(b). This figure shows that, although mosquitoes with heterozygous genotype are the most abundant, mosquitoes with RR genotype dominate those with SS genotype. Here, p∗∗∗∗ ≈0.6251 and q∗∗∗ ≈0.3759. Finally, the case where both reproduction thresholds are equal is depicted in Fig. 5(c), showing, once again, the dominance of the RS genotype mosquitoes over the other two genotypes, but, in this case, the populations of the homozygous SS and RR genotype are approximately the same at steady-state. For this case, the frequency of resistant allele is p∗∗∗ ≈0.5189 and that of the sensitive allele is q∗∗∗ ≈0.4811. It is worth mentioning that in the simulations described above, mosquitoes of RS genotype always have higher relative abundance compared to mosquitoes of SS or RR genotypes. This is due to the values of the parameters used in the simulations. In general, extensive numerical simulations of the model show that mosquitoes of homozygous genotype with the lower reproduction threshold (which is above unity) is always more abundant than mosquitoes of the other homozygous genotype. The results of the simulations carried out to generate Fig. 5 are summarized in the remark below.

Remark 3.1

Consider the model {(2.2)–(2.6)} with ${\Psi }_L^i=0$ (i = {SS, RS, RR}) and $\mathrm{m}\mathrm{i}\mathrm{n}\{{\mathcal{R}}_0^{SS},{\mathcal{R}}_0^{RR}\}>1$.

• (i)If $1<{\mathcal{R}}_0^{SS}<{\mathcal{R}}_0^{RR}$, then mosquitoes of genotype SS will dominate (i.e., be more abundant than) mosquitoes of genotype RR at steady-state. Hence, the frequency of the sensitive allele at steady-state will exceed that of the resistant allele.
• (ii)If $1<{\mathcal{R}}_0^{RR}<{\mathcal{R}}_0^{SS}$, then mosquitoes of genotype RR will dominate mosquitoes of genotype SS at steady-state. In this case, the frequency of the resistant allele will exceed that of the sensitive allele at steady-state.
• (iii)If $1<{\mathcal{R}}_0^{RR}\approx {\mathcal{R}}_0^{SS}$, then the population abundance of mosquitoes of genotypes RR and SS will be nearly the same. Similarly, the frequency of the resistant and sensitive alleles at steady-state will be nearly identical.

(iv) Although, based on the parameter values used in the above simulations, mosquitoes of RS genotypes always dominate those of SS and RR genotypes whenever $\min \{{\mathcal{R}}_0^{SS},{\mathcal{R}}_0^{RR}\}>1$ (resulting in the coexistence of the three genotypes at steady-state), mosquitoes of homozygous genotype (i.e., SS or RR) with smaller reproduction threshold greater (which is than unity) are more abundant than mosquitoes of the other homozygous genotype with higher reproduction threshold (again greater than one).

3.4. Sensitivity analysis

The model {(2.2)–(2.6)} contains numerous parameters, and uncertainties in the estimate of the values of the parameters used in the numerical simulation of the model are bound to occur. It is, therefore, instructive to carry out global uncertainty and sensitivity analysis of the model, to determine the parameters that have the most influence on a chosen response function (associated with the dynamics and population abundance of the mosquito by genotype). Specifically, we will implore a global sensitivity analysis, using Latin Hypercube Sampling (LHS) and Partial Rank Correlation Coefficients (PRCC), to quantify the impact of the variations or sensitivity of each parameter of the model on the response function, and, consequently, on the associated numerical simulations carried out (Blower & Dowlatabadi, 1994; Gomero, 2012; Marino, Hogue, Ray, & Kirschner, 2008; McKay, Beckman, & Conover, 1979).

While PRCC values, which range from −1 to +1, provide a measure of the monotonicity after the removal of the linear effects of all but one variable (Blower & Dowlatabadi, 1994), LHS, a stratified sampling without replacement technique, enables for the assessment of parameter variations across simultaneous uncertainty ranges in each parameter of the model (McKay et al., 1979). A parameter with a PRCC value greater than 0.5 in magnitude (and correspondingly small p-value $(<0.05)$) indicate that the chosen response function is highly sensitive to the parameter (Blower & Dowlatabadi, 1994; Gomero, 2012; Marino et al., 2008). A PRCC value closer to +1 or −1 indicates a stronger influence, with the negative sign indicating that the parameter is inversely proportional to the response function (Blower & Dowlatabadi, 1994; Gomero, 2012; Marino et al., 2008). Furthermore, the response function is sensitive to parameters with small p-values even when the corresponding PRCC is low (Blower & Dowlatabadi, 1994; Gomero, 2012; Marino et al., 2008).

Since our emphasis is on minimizing the population abundance of resistant mosquitoes, we choose the sum of the net production thresholds for adult female mosquitoes with RS and RR genotype $({\mathcal{R}}_{RS}+{\mathcal{R}}_{RR})$ as the response function. The baseline values and ranges of the parameters used in the sensitivity analysis are tabulated in Table 4. Given that insecticide-resistant mosquitoes have been found in the wild (Ranson & Lissenden, 2016; Corbel et al., 2007; N’Guessan et al., 2007), in this analysis we use the fitness factor pair (ξ^RS, ξ^RR) = (1.01, 1.15) since, for these parameter values, solutions of the model {(2.2)–(2.6)} tend toward the coexistence equilibrium (although other fitness factor pairs which lead to coexistence were tested for various temperatures, the overall results did not change). Each parameter in the response function is assumed to obey a uniform distribution (Gomero, 2012; Marino et al., 2008) and ranges from 80% to 120% of the baseline value (although it should be mentioned that since pupacides are not currently used in malaria-endemic areas, pupacide-related parameters are excluded from the sensitivity analysis). We generate (sample) 1000 runs of the response function $({\mathcal{R}}_{RS}+{\mathcal{R}}_{RR})$. The sensitivity analysis was performed for temperature fixed at T = 25 °C (although similar results were obtained when temperature was fixed at T = 18 °C or T = 30 °C).

Table 4.

Global sensitivity analysis for the model {(2.2)–(2.6)}, giving PRCCs and p-values for the chosen response function, ${\mathcal{R}}_{RS}+{\mathcal{R}}_{RR}$. Parameters of the model are assumed to be uniformly distributed within the ranges indicated. Temperature-dependent parameters of the model are evaluated at 25 °C, and parameter values are chosen such that the fitness factors, ξ^RS and ξ^RR, take the values ξ^RS = 1.01 and ξ^RR = 1.15, respectively. Significant parameters (i.e., parameters with a PRCC value greater or equal to 0.5 in magnitude) are highlighted in bold font.

Parameter	Baseline	Range	PRCC	p-value
αRS	64.3564	51.4851–77.22768	0.7777	<0.01
αRR	50	40–60	0.7941	<0.01
${\sigma }_E^{RS}$	0.4454	0.3563–0.5345	0.2096	<0.01
${\sigma }_E^{RR}$	0.3461	0.2769–0.4153	0.2176	<0.01
${\mathit{\sigma }}_{\mathit{L}}^{\mathit{R}\mathit{S}}$	0.1114	0.0891–0.1337	0.5380	<0.01
${\mathit{\sigma }}_{\mathit{L}}^{\mathit{R}\mathit{R}}$	0.0865	0.0692–0.1038	0.5945	<0.01
${\sigma }_P^{RS}$	0.4454	0.3563–0.5345	0.2366	<0.01
${\sigma }_P^{RR}$	0.3461	0.2769–0.4153	0.2178	<0.01
${\mu }_E^{RS}$	0.0767	0.0614–0.0920	−0.1038	<0.01
${\mu }_E^{RR}$	0.0987	0.0790–0.1184	−0.2140	<0.01
${\mu }_L^{RS}$	0.0767	0.0614–0.0920	−0.3346	<0.01
${\mu }_L^{RR}$	0.0987	0.0790–0.1184	−0.4327	<0.01
${\mu }_P^{RS}$	0.0767	0.0614–0.0920	−0.1896	<0.01
${\mu }_P^{RR}$	0.0987	0.0790–0.1184	−0.2655	<0.01
${\mu }_{M_f}^{RS}$	0.0435	0.0348–0.0522	−0.0937	<0.01
${\mu }_{M_f}^{RR}$	0.0560	0.0448–0.0672	−0.2352	<0.01
νf	0.5	0.4–0.6	0.9308	<0.01
hL	0.25	0.2–0.3	0.0559	0.0813
hM	0.25	0.2–0.3	0.1319	<0.01
kL	0.37	0.2960–0.4440	0.1147	<0.01
kM	0.37	0.2960–0.4440	0.5609	<0.01
δL	0.84	0.6720–1.0080	−0.4922	<0.01
${\mathit{\delta }}_{{\mathit{M}}_{\mathit{f}}}$	0.84	0.6720–1.0080	−0.9023	<0.01
εL	0.8873	0.7098–1	−0.4223	<0.01
εM	0.8873	0.7098–1	−0.8753	<0.01
CL	0.1	0.08–0.12	−0.4834	<0.01
CM	0.5	0.4–0.6	−0.9019	<0.01

It can be seen from the PRCC values tabulated in Table 4 that the top parameters of the model {(2.2)–(2.6)} (contained in the expressions for ${\mathcal{R}}_{RS}$ and ${\mathcal{R}}_{RR}$) that have the highest influence on the response function $({\mathcal{R}}_{RS}+{\mathcal{R}}_{RR})$ are, in descending order of magnitude, the proportion of new adult mosquitoes that are female (ν_f, PRCC = 0.9308), the insecticide-induced mortality rate of adult female mosquitoes (${\delta }_{M_f}$, PRCC = −0.9023), the coverage level of adulticide (C_M, PRCC = −0.9019), the efficacy of adulticide (ε_M, PRCC = −0.8753), the rate at which eggs of genotypes RS (α^RS, PRCC = 0.7777) and RR (α^RR, PRCC = 0.7941) are laid, and the modification parameter for the reduction in insecticide-induced mortality due to insecticide resistance (k_M, PRCC = 0.5609).

Since the parameters ν_f, α^RS, α^RR and k_M have positive PRCC values, it follows that any increase (decrease) in the values of these parameters will increase (decrease) the size of the response function $({\mathcal{R}}_{RS}+{\mathcal{R}}_{RR})$. Furthermore, since the response function denotes the average rate at which new adult female mosquitoes of genotype RS and RR are produced in the community, a mosquito control strategy that decreases the values of these four parameters will reduce the response function and, consequently, lead to the reduction in the population of adult female mosquitoes of the two (heterozygous and homozygous-resistant) genotypes.

Similarly, since the parameters ${\delta }_{M_f}$, C_M, and ε_M have negative PRCC values, any increase (decrease) in their values will lead to a decrease (increase) in the value of the response function. Thus, mosquito control strategies that increase the values of these parameters will decrease the response function, resulting in a reduction in the population abundance of the heterozygous and homozygous-resistant adult female mosquitoes in the community.

It follows from the sensitivity analysis in this section that mosquito control strategies that increase the values of the parameters ${\delta }_{M_f}$, C_M, and ε_M, and/or decrease the values of the parameters ν_f, α^RS, α^RR, and k_M will lead to the effective control of the population abundance of adult female mosquitoes that carry the resistant allele in the population. The parameters ${\delta }_{M_f}$ and ε_M can be increased through the development of new, more highly efficacious insecticides, or the rotation of insecticides to a chemical to which mosquitoes are not resistant. The parameter denoting the reduction in insecticide-induced mortality for homozygous resistant mosquitoes k_M (further modified by the measure of dominance h_M in heterozygous mosquitoes), can be increased through the use of synergists (such as PBO (World Health Organization, 2020a, World Health Organization, 2020b)) in order to overcome resistance (World Health Organization, 2020a, World Health Organization, 2020b). The adulticide coverage level can be increased by distributing more bednets or more widely deploying IRS. However, as explored in the following sections, increasing these parameters may select for resistance (increasing the relative abundance of heterozygous and homozygous resistant mosquitoes compared to homozygous sensitive mosquitoes) although overall resistant mosquito populations are reduced. The sex ratio parameter ν_f can be decreased through gene editing; for example, through the use of a sex-distorter gene drive which could reduce the female population without selecting for resistance (Simoni et al., 2020). Furthermore, α^RS, α^RR can be decreased through habitat destruction (i.e., the removal of oviposition sites) or sterile insect technology (i.e., the release of sterile males into the wild so that females who mate with these males do not produce offspring) (Alphey et al., 2010).

It should be recalled that the theoretical analysis conducted in Section 3 was for the special case of the model {(2.2)–(2.6)} without density-dependent larval mortality. Hence, the parameter of the model {(2.2)–(2.6)} related to density-dependent larval mortality $({\Psi }_L^i)$ does not appear in the expressions for the response function ${\mathcal{R}}_{RS}+{\mathcal{R}}_{RR}$. This explains why ${\Psi }_L^i$ does not appear in the PRCC table (i.e., ${\Psi }_L^i$ is not one of the parameters that influences the response function).

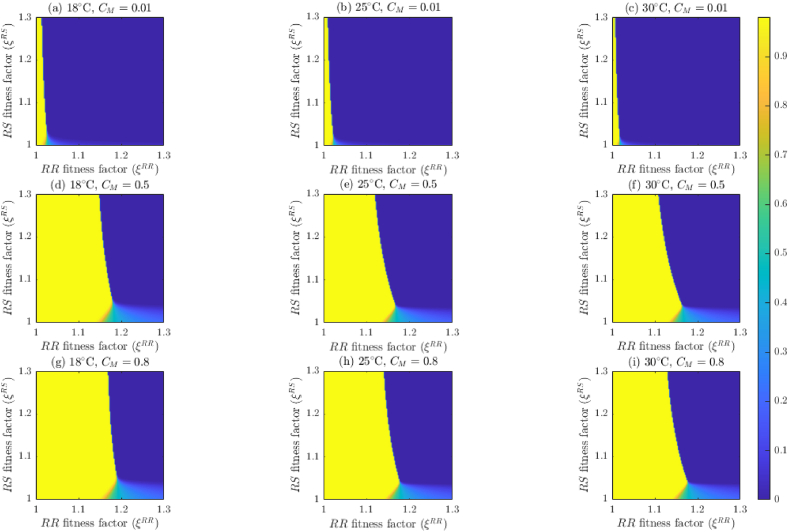
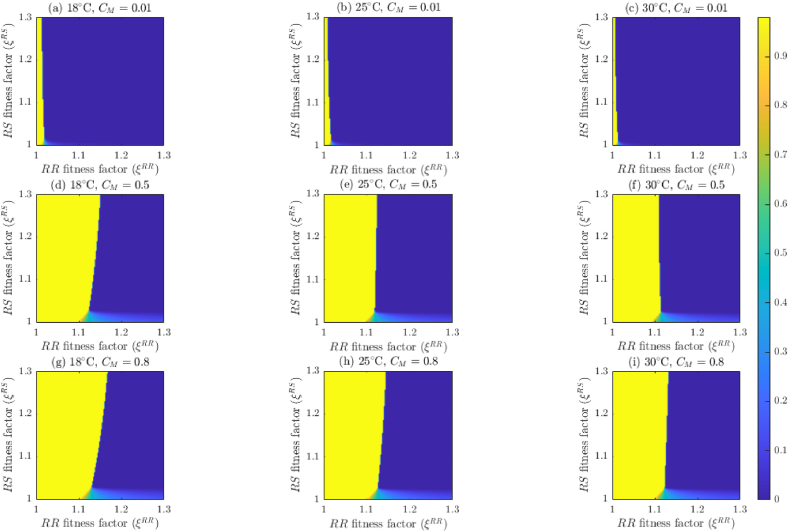
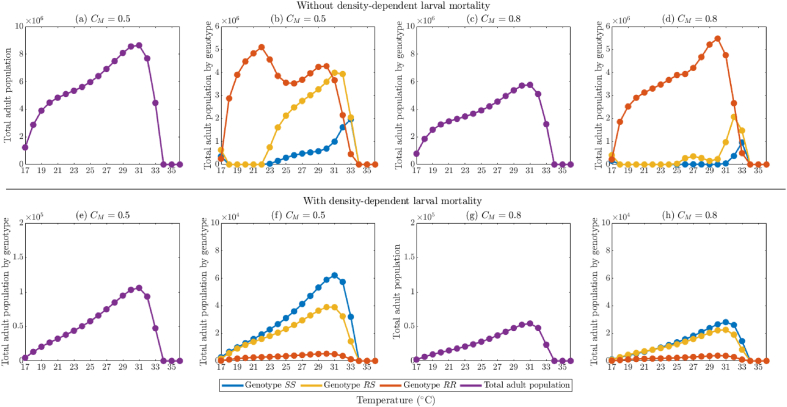
4. Effect of temperature on mosquito abundance and insecticide effectiveness

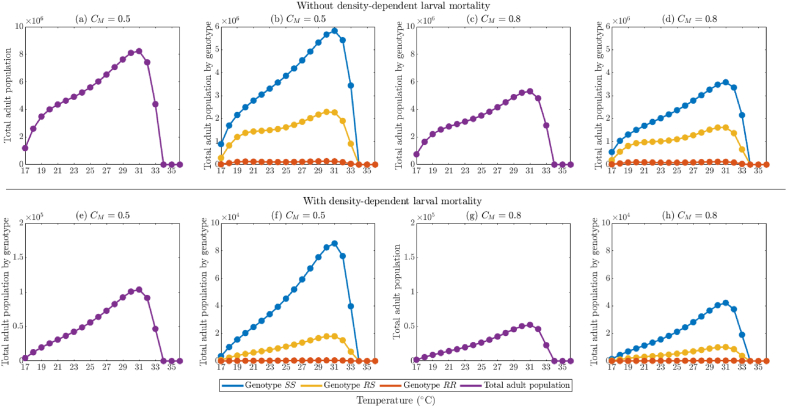
In this section, the model {(2.2)–(2.6)} will be simulated, using the baseline parameter values in Table 5, Table 6 (unless otherwise stated), to assess the impact of temperature variability on mosquito abundance by genotype and on the effectiveness of insecticide-based mosquito control interventions considered in this study (in particular, adulticides) and fitness costs of resistance. Although the dependence of mosquito dynamics on temperature has been well-established in the literature (see, for instance, (Abdelrazec & Gumel, 2017; Bayoh, 2001; Bayoh & Lindsay, 2003; Bayoh & Lindsay, 2004; Iboi et al., 2020a; Lyimo et al., 1992; Okuneye et al., 2019), this, to our knowledge, has not been established for the case where the mosquito population is stratified by genotype.

Table 5.

Insecticide-independent parameters of the model {(2.2)–(2.6)}. The derivation of functional forms for temperature-dependent parameters is described in Section 2.4. Temperature-dependent parameters were evaluated at 25 °C to obtain the values listed. Units are day⁻¹ unless otherwise noted.

Parameter	Baseline (day−1)	Reference
Immature mosquitoes
TW(TA)	25 °C	Mordecai et al. (2013)
KE	107 (dimensionless)	Mohammed-Awel and Gumel, 2019, Mohammed-Awel et al., 2020
αSS	65	Iboi et al. (2020a)
αRS	$\frac{1}{{\xi }^{RS}}\times {\alpha }^{SS}$	Iboi et al., 2020a, Mohammed-Awel et al., 2020
αRR	$\frac{1}{{\xi }^{RR}}\times {\alpha }^{SS}$	Iboi et al., 2020a, Mohammed-Awel et al., 2020
${\sigma }_E^{SS}$	0.4499	Iboi et al., 2020a, Mohammed-Awel et al., 2020, Okuneye, Eikenberry, & Gumel, 2019
${\sigma }_E^{RS}$	$\frac{1}{{\xi }^{RS}}\times {\sigma }_E^{SS}$	Iboi et al., 2020a, Mohammed-Awel et al., 2020, Okuneye, Eikenberry, & Gumel, 2019
${\sigma }_E^{RR}$	$\frac{1}{{\xi }^{RR}}\times {\sigma }_E^{SS}$	Iboi et al., 2020a, Mohammed-Awel et al., 2020, Okuneye, Eikenberry, & Gumel, 2019
${\sigma }_L^{SS}$	0.1125	Iboi et al., 2020a, Mohammed-Awel et al., 2020, Okuneye, Eikenberry, & Gumel, 2019
${\sigma }_L^{RS}$	$\frac{1}{{\xi }^{RS}}\times {\sigma }_L^{SS}$	Iboi et al., 2020a, Mohammed-Awel et al., 2020, Okuneye, Eikenberry, & Gumel, 2019
${\sigma }_L^{RR}$	$\frac{1}{{\xi }^{RR}}\times {\sigma }_L^{SS}$	Iboi et al., 2020a, Mohammed-Awel et al., 2020, Okuneye, Eikenberry, & Gumel, 2019
${\sigma }_P^{SS}$	0.4499	Iboi et al., 2020a, Mohammed-Awel et al., 2020, Okuneye, Eikenberry, & Gumel, 2019
${\sigma }_P^{RS}$	$\frac{1}{{\xi }^{RS}}\times {\sigma }_P^{SS}$	Iboi et al., 2020a, Mohammed-Awel et al., 2020, Okuneye, Eikenberry, & Gumel, 2019
${\sigma }_P^{RR}$	$\frac{1}{{\xi }^{RR}}\times {\sigma }_P^{SS}$	Iboi et al., 2020a, Mohammed-Awel et al., 2020, Okuneye, Eikenberry, & Gumel, 2019
${\mu }_E^{SS}$	0.0760	Iboi et al., 2020a, Mohammed-Awel et al., 2020, Okuneye, Eikenberry, & Gumel, 2019
${\mu }_E^{RS}$	${\xi }^{RS}\times {\mu }_E^{SS}$	Iboi et al., 2020a, Mohammed-Awel et al., 2020, Okuneye, Eikenberry, & Gumel, 2019
${\mu }_E^{RR}$	${\xi }^{RR}\times {\mu }_E^{SS}$	Iboi et al., 2020a, Mohammed-Awel et al., 2020, Okuneye, Eikenberry, & Gumel, 2019
${\mu }_L^{SS}$	0.0760	Iboi et al., 2020a, Mohammed-Awel et al., 2020, Okuneye, Eikenberry, & Gumel, 2019
${\mu }_L^{RS}$	${\xi }^{RS}\times {\mu }_L^{SS}$	Iboi et al., 2020a, Mohammed-Awel et al., 2020, Okuneye, Eikenberry, & Gumel, 2019
${\mu }_L^{RR}$	${\xi }^{RR}\times {\mu }_L^{SS}$	Iboi et al., 2020a, Mohammed-Awel et al., 2020, Okuneye, Eikenberry, & Gumel, 2019
${\mu }_P^{SS}$	0.0760	Iboi et al., 2020a, Mohammed-Awel et al., 2020, Okuneye, Eikenberry, & Gumel, 2019
${\mu }_P^{RS}$	${\xi }^{RS}\times {\mu }_P^{SS}$	Iboi et al., 2020a, Mohammed-Awel et al., 2020, Okuneye, Eikenberry, & Gumel, 2019
${\mu }_P^{RR}$	${\xi }^{RR}\times {\mu }_P^{SS}$	Iboi et al., 2020a, Mohammed-Awel et al., 2020, Okuneye, Eikenberry, & Gumel, 2019
${\Psi }_L^{SS}$	0.00002 larvae−1 day−1	Iboi et al., 2020a, Okuneye, Eikenberry, & Gumel, 2019
${\Psi }_L^{RS}$	${\xi }^{RS}\times {\Psi }_L^{SS}$ larvae−1 day−1	Iboi et al., 2020a, Mohammed-Awel et al., 2020, Okuneye, Eikenberry, & Gumel, 2019
${\Psi }_L^{RR}$	${\xi }^{RR}\times {\Psi }_L^{SS}$ larvae−1 day−1	Iboi et al., 2020a, Mohammed-Awel et al., 2020, Okuneye, Eikenberry, & Gumel, 2019
Adult mosquitoes
νf	0.5 (dimensionless)	Mohammed-Awel et al., 2020, Okuneye, Eikenberry, & Gumel, 2019
${\mu }_{M_f}^{SS}$	0.0431	Iboi et al., 2020a, Okuneye, Eikenberry, & Gumel, 2019
${\mu }_{M_f}^{SS}$	${\xi }^{RS}\times {\mu }_{M_f}^{SS}$	Iboi et al., 2020a, Mohammed-Awel et al., 2020, Okuneye, Eikenberry, & Gumel, 2019
${\mu }_{M_f}^{SS}$	${\xi }^{RR}\times {\mu }_{M_f}^{SS}$	Iboi et al., 2020a, Mohammed-Awel et al., 2020, Okuneye, Eikenberry, & Gumel, 2019
${\mu }_{M_m}^{SS}$	0.0215	Bayoh, 2001, Howell & Knols, 2009
${\mu }_{M_m}^{RS}$	${\xi }^{RS}\times {\mu }_{M_m}^{SS}$	Mohammed-Awel et al., 2020, Okuneye, Eikenberry, & Gumel, 2019
${\mu }_{M_m}^{RR}$	${\xi }^{RR}\times {\mu }_{M_m}^{SS}$	Mohammed-Awel et al., 2020, Okuneye, Eikenberry, & Gumel, 2019

Table 6.

Insecticide-related parameters of the model {(2.2)–(2.6)}. The derivation of functional forms for temperature-dependent parameters is described in Section 2.4. Temperature-dependent parameters were evaluated at 25 °C to obtain the values listed. Units are day⁻¹ unless otherwise noted.

Parameter	Baseline (day−1)	Reference
Immature mosquitoes
CL	0 (dimensionless)	Assumed
CP	0 (dimensionless)	Assumed
εL	0.8873 (dimensionless)	Derived from (Glunt et al., 2018)
εP	0.8873 (dimensionless)	Derived from (Glunt et al., 2018)
δE	0.84	Mohammed-Awel et al. (2020)
δL	0.84	Mohammed-Awel et al. (2020)
δP	0.84	Mohammed-Awel et al. (2020)
kL	0.37 (dimensionless)	Derived from (Glunt et al., 2018)
kP	0.37 (dimensionless)	Derived from (Glunt et al., 2018)
hL	0.25 (dimensionless)	Mohammed-Awel et al. (2020)
hP	0.25 (dimensionless)	Mohammed-Awel et al. (2020)
Adult mosquitoes
CM	Varied (dimensionless)	Assumed
εM	0.8873 (dimensionless)	Derived from (Glunt et al., 2018)
${\delta }_{M_f}$	0.84	Mohammed-Awel et al. (2020)
${\delta }_{M_m}$	0.84	Mohammed-Awel et al. (2020)
kM	0.37 (dimensionless)	Derived from (Glunt et al., 2018)
hM	0.25 (dimensionless)	Mohammed-Awel et al. (2020)

For simulation purposes, the initial conditions are chosen such that half of the mosquitoes initially carry the insecticide-resistant gene, while the remaining half carry the sensitive gene. Specifically, we choose the following initial sizes of the state variables of the model (Mohammed-Awel et al., 2020):

$$\begin{array}{cccccc}& E_{SS}\left(0\right)=25,000,& & E_{RS}\left(0\right)=25,000,& & E_{RR}\left(0\right)=25,000,\\ & L_{SS}\left(0\right)=21,200,& & L_{RS}\left(0\right)=21,200,& & L_{RR}\left(0\right)=21,200,\\ & P_{SS}\left(0\right)=18,000,& & P_{RS}\left(0\right)=18,000,& & P_{RR}\left(0\right)=18,000,\\ & M_{SS}^f\left(0\right)=1,750,& & M_{RS}^f\left(0\right)=1,750,& & M_{RR}^f\left(0\right)=1,750,\\ & M_{SS}^m\left(0\right)=1,750,& & M_{RS}^m\left(0\right)=1,750,& & M_{RR}^m\left(0\right)=1,750.\end{array}$$

In the following numerical simulations, the temperature-dependent parameters of the model (described in Section 2.4) are evaluated at fixed temperature values in the range 17 °C–36 °C (since malaria transmission in most malaria-endemic settings occurs for temperatures in this range (Mordecai et al., 2013)). Furthermore, although the model {(2.2)–(2.6)} (and all subsequent rigorous analyses) was robust enough to allow for the assessment of all mosquito interventions (larvicides, pupacides, and adulticides), we will consider only adulticide-based interventions in the numerical simulations in this section. This is because larvicides are only recommended in special cases and pupacides are not currently used (World Health Organization, 2013). Consequently, we set the coverage for larvicides and pupacides to zero (i.e., we set C_L = C_P = 0) in the simulations in this section. Additionally, since pesticides are used in agricultural contexts in malaria-endemic settings (and these pesticides sometimes include pyrethroids (Mouhamadou et al., 2019)), we set a baseline coverage of adulticide to C_M = 0.01 to account for the background level of adulticide that may be encountered by a mosquito (even when indoor residual spraying is not implemented in the community). Following (Mohammed-Awel et al., 2020), we set C_M = 0.5 to represent a moderate level of adulticide coverage in the community. Furthermore, we set C_M = 0.8 to represent the highest possible coverage level of adulticide (World Health Organization, 2019).

4.1. Impacts of insecticide coverage and fitness costs of resistance on mosquito abundance

In this section, the model {(2.2)–(2.6)} is simulated using the baseline values of the parameters in Table 5, Table 6, for the case with and without density-dependent larval mortality $({\Psi }_L^i;i=\{SS,RS,RR\})$, to assess the impact of fitness costs of insecticide resistance (as measured by the fitness factors ξ^RS and ξ^RR, defined in Section 2.4) on the frequency of sensitive and resistant alleles in the population.

Fig. 6 depicts the frequency of the sensitive and resistant alleles in the total mosquito population across all life stages, as a function of the fitness factors for the heterozygous (ξ^RS) and homozygous resistant (ξ^RR) mosquitoes, for various fixed temperature values and adulticide coverage (C_M) for the case of the model with no density-dependent larval mortality (i.e., ${\Psi }_L^i=0$). This figure shows that, for low adulticide coverage, if the fitness of the homozygous resistant mosquitoes exceed a certain threshold (ξ^RR > 1.05), only mosquitoes of genotype SS persist in the population (dark blue shaded region of Fig. 6(a)), regardless of the level of the fitness costs of the RS mosquitoes. For very low fitness factor of the homozygous resistant mosquitoes (e.g., ξ^RR < 1.02), only mosquitoes of RR genotype persist in the population (yellow shaded region of Fig. 6(a)). This figure further shows a very small window where the three genotypes coexist (depicted by the light green-bluish triangular region at the bottom of Fig. 6(a)). The same pattern is observed, for this low adulticide coverage level, at higher temperatures, such as 25 °C (Fig. 6(b)) and 30 °C (Fig. 6(c)).

Fig. 6.

Contour plots of the frequency of the R allele in the total mosquito population using the model {(2.2)–(2.6)} without density-dependent larval mortality (i.e. ${\Psi }_L^i=0$, i = {SS, RS, RR}). Each column contains results for a given temperature (18 °C, 25 °C, and 30 °C); the top row contains results for low adulticide coverage (C_M = 0.01), the middle row contains results for moderate adulticide coverage (C_M = 0.5), and the bottom row contains results for high adulticide coverage (C_M = 0.8). Baseline parameter values are listed in Table 5, Table 6. Functional forms for temperature-dependent parameters are described in Section 2.4.

When adulticide coverage is increased to a moderate level (i.e., C_M = 0.5) and temperature kept at 18 °C, the region for the existence of mosquitoes of SS genotype only occurs when the fitness factor pair (ξ^RR, ξ^RS) lie in the region in the (ξ^RR − ξ^RS)-plane where ξ^RR > 1.17 and ξ^RS > 1.04 (Fig. 6(d)). This figure also shows a marked reduction in the region where only mosquitoes of SS genotype exist in the population (and a corresponding marked increase in the region where mosquitoes of RR genotype only exist), in comparison to the case where low adulticide coverage is used (compare shaded dark blue and yellow regions in Fig. 6(a) with those in Fig. 6(d)). Here, the window for the coexistence of all three genotypes is larger in comparison to the case where the adulticide coverage is low (compare light green-bluish region in Fig. 6(a) with that in Fig. 6(d)). For this case, the window for the coexistence of the three genotypes appears at the bottom right corner of the (ξ^RR − ξ^RS)-plane, where the fitness cost factor of the RS genotype (ξ^RS) is low and that of the RR genotype (ξ^RR) is high. In this case, the higher adulticide coverage and high fitness cost of the RR genotype cause the populations of mosquitoes with RR and SS genotype to be significantly diminished (this is because moderate coverage significantly reduces the SS population, while higher value of ξ^RR reduces the size of the population of mosquitoes with the RR genotype). At this adulticide coverage and fitness cost, the mosquitoes with RS genotype will not be as affected in comparison to the RR and SS mosquitoes. Consequently, this enhances the survival and abundance of mosquitoes with the RS genotype, thereby causing the coexistence of mosquitoes of all three genotypes due to random mating (recall that the random mating between RS and RS mosquitoes produces offspring with (1/4)th of them of RR, (1/4)th of SS and the remaining (1/2) of RS genotype). Similar general pattern is observed at higher temperatures (Fig. 6(e) and (f)), although the size of the region where only SS genotype mosquitoes exist increases (in relation to the corresponding size in Fig. 6(d)). This change is illustrated in Figure C1, which depicts the time-series of the total mosquito population at all life-stages, as a function of time, for moderate adulticide coverage and fitness factor pair (ξ^RS, ξ^RR) = (1.042, 1.167). Under this parameterization, the populations of homozygous sensitive and heterozygous mosquitoes go extinct, while that of the homozygous resistant mosquitoes persists, at 18 °C (Figure C1(a)). For the same parameterization, but with temperature now increased to 25 °C, the heterozygous and homozygous resistant populations become extinct, while the homozygous sensitive population now persists (Figure C1(b)), showing the switch in genotype persistence as temperature increases. The trend in Figure Figure C1(b)) is observed if temperature is further increased to 30 °C (Figure C1(c))). Similar results are obtained when density-dependent larval mortality is incorporated in the model (Figures C1(d)–(f)).

Finally, for high adulticide coverage (i.e., C_M = 0.8) and temperature fixed at 18 °C, our simulations (depicted in Fig. 6(g)) show that the region for the existence of only mosquitoes with SS genotype is achieved at essentially the same window as the corresponding one for C_M = 0.5 (Fig. 6(d)). This figure further shows that the size of the blue shaded region is slightly smaller in comparison to the corresponding size in Fig. 6(d). Furthermore, this figure shows that the window for the coexistence of the three genotypes is essentially the same as that for the corresponding case with moderate adulticide coverage (shown in Fig. 6(d)). Similar pattern is observed at higher temperatures (Fig. 6(h) and (i)). It is, however, notable that the size of the window where only mosquitoes with the RR genotype exist reduces as temperature increases from 18 °C to 25 °C (compare the sizes of the shaded yellow regions in Fig. 6(a),(d) and (g) with those in Fig. 6(b),(e) and (h)). The reduction increases with increasing adulticide coverage. However, the size of this region does not significantly change as temperature is increased from 25 °C to 30 °C (compare the sizes of shaded yellow regions in Fig. 6(e)–(f) with those in Fig. 6(h)-(i)).

In summary, the simulation results depicted in Fig. 6 show that, in the absence of density-dependent larval mortality, the size of the window in the (ξ^RR − ξ^RS)-plane where only mosquitoes of SS genotype exist decreases with increasing adulticide coverage (C_M). Similarly, the size of the window where all three genotypes coexist increases with increasing adulticide coverage from low to moderate (the size remains the same as adulticide coverage is increased from moderate to high, as shown in (Fig. 6). This phenomenon is observed for the three temperature values we considered in this study. It is seen that, for a given adulticide coverage (low, moderate or high) and temperature values increasing from 18 °C to 25 °C, the size of the window in the (ξ^RR − ξ^RS)-plane where only mosquitoes of RR genotype persist reduces with increasing values of the fitness factor of the RS mosquitoes (ξ^RS). The size of this reduction is more pronounced for the case where moderate and high adulticide coverage are used.

For the case where density-dependent larval mortality is maintained at its baseline level, our simulations show that, for the case where temperature is fixed at 18 °C and adulticide coverage is low (i.e., C_M = 0.01), only mosquitoes of SS genotype exist in the population if the fitness factor for resistant mosquitoes (ξ^RR) exceed ξ^RR = 1.04 (see dark blue shaded region in Fig. 7(a)). The size of this region remains the same at higher temperatures (Fig. 7(b) and (c)). The size of the window for the coexistence of the three genotypes significantly decreases, in comparison to the case without density-dependent larval mortality (compare the light green-bluish shaded regions in Fig. 7(a)–(c) with those in Fig. 6(a)-(c)). Here, too, the size of the window for the existence of mosquitoes of SS genotype only decreases as adulticide coverage is increased to moderate level (7(d)-(f)). However, in this case, the size of the window for the coexistence of the three genotypes significantly decreases, in comparison to the case without density-dependent larval mortality (compare the light green-bluish shaded regions in Fig. 7(d)–(f) with those in Fig. 6(d)-(f)). For the case when the adulticide coverage is increased to a high level (i.e., C_M = 0.8), our simulation results show that the size of the window for the existence of mosquitoes of SS genotype further decreases (with corresponding increase in the size of the window for the existence of mosquitoes of RR genotype). This can be seen by comparing the shaded dark blue and yellow regions in Fig. 7(g)–(i) with the corresponding plots in Fig. 6(g)–(i). Furthermore, it can be seen from Fig. 7 (g)–(i) that the size of the window, in the (ξ^RR − ξ^RS)-plane, for the coexistence of all three genotypes remains essentially the same as the corresponding size for the case where adulticide coverage is moderate (compare shaded green-bluish regions in Fig. 7(g)–(i) with those in Fig. 7(d)-(f)). However, it is evident from Fig. 7 that the size of the window for the coexistence of the three genotypes decreases in comparison to the case when density-dependent larval mortality is not taken into account (compare the size of the light green-bluish shaded regions in Fig. 7 with the corresponding regions in Fig. 6). Here, too, it is shown that, for a given adulticide coverage level (low, moderate and high) and temperature increasing from 18 °C to 25 °C, the size of the region where mosquitoes of SS genotype persists decreases with increasing values of ξ^RS. This decrease is more pronounced for moderate and high coverage levels of adulticide (and no significant change in the size of the region is observed if temperature is increased from 25 °C to 30 °C). This decrease is illustrated by simulating the model {(2.2)–(2.6)} with moderate adulticide coverage and fitness factor pair (ξ^RS, ξ^RR) = (1.028, 1.119). The results obtained show that, for this parameterization and temperature fixed at 18 °C, the mosquitoes of RR genotype persist in the population, while those of genotype RS and SS die out (Figure C1(d)). However, for the same parameterization but with temperature now increased to 25 °C, mosquitoes of RS and RR genotypes die out, while those of SS genotype now persist in the population (Figure C1(e)). This result clearly shows the effect of increasing temperature values on the survival of the mosquitoes with resistant genotypes (when the fitness factors are chosen within a certain range). Similar results (not shown) are observed when temperature fixed at 30 °C.

Fig. 7.

Contour plots of the frequency of the R allele in the total mosquito population using the model {(2.2)–(2.6)} with density-dependent larval mortality (i.e. ${\Psi }_L^i\ne 0$, i = {SS, RS, RR}). Each column contains results for a given temperature (18 °C, 25 °C, and 30 °C); the top row contains results for low adulticide coverage (C_M = 0.01), the middle row contains results for moderate adulticide coverage (C_M = 0.5), and the bottom row contains results for high adulticide coverage (C_M = 0.8). Baseline parameter values are listed in Table 5, Table 6. Functional forms for temperature-dependent parameters are described in Section 2.4.

In conclusion, Fig. 6, Fig. 7 show that, although the simulation results for the cases with and without density-dependent larval mortality are qualitatively similar (with respect to the impacts of the fitness factor, adulticide coverage, and temperature variability on mosquito abundance), density-dependent larval mortality causes important quantitative differences with respect to the relative size of the regions, in the (ξ^RS-ξ^RR)-plane, where mosquitoes of certain or all genotypes exist (as adulticide coverage and temperature are varied). Specifically, density-dependent larval mortality reduces the size of the windows where only mosquitoes of RR genotype exist or mosquitoes of all three genotypes coexist (for ξ^RS values in the range 0 ≤ ξ^RS ≤ 1.02), in comparison to the case where density-dependent larval mortality is not accounted for (compare Fig. 6, Fig. 7). Furthermore, unlike in the case without density-dependence where the window for the existence of mosquitoes of SS genotype decreases with increasing level of the fitness factor for heterozygous mosquitoes (ξ^RS), the size of this window actually increases when density-dependent larval mortality is allowed (and this phenomenon is more pronounced when moderate and high coverage levels of adulticide are used). In other words, Fig. 6, Fig. 7 show that density-dependent larval mortality causes the following effects:

• (a)For any given combination of temperature and adulticide coverage, density-dependent larval mortality increases (reduces) the size of the window for existence of mosquitoes of SS(RR) genotype. The size of this increase (reduction) is more pronounced for the case where moderate and high levels of adulticide coverage are used.
• (b)For any given combination of temperature and adulticide coverage, density-dependent larval mortality reduces the size of the window for the coexistence of mosquitoes of all three genotypes, with coexistence requiring lower fitness costs relative to the case without density-dependent larval mortality. Here, too, the level of reduction is more pronounced for the case where moderate and high adulticide coverage are used.
• (c)In the presence of density-dependent larval mortality, the size of the window for the existence of only SS(RR) genotype mosquitoes decreases (increases) with increasing level of the fitness factor for heterozygous mosquitoes (ξ^RS). However, in the absence of density-dependent larval mortality, the size of the window for the existence of SS(RR) genotype mosquitoes increases (decreases) with increasing levels of ξ^RS. These observations are more pronounced for the case where moderate and high adulticide coverage are used.

4.2. Effect of temperature on mosquito abundance

The model {(2.2)–(2.6)} is now simulated to assess the impact of temperature variability on the abundance of mosquitoes in the population. Because malaria transmission in endemic areas occurs in the range 17 °C–36 °C (Mordecai et al., 2013), simulations will be done for fixed temperatures in the range 17 °C–36 °C. These simulations will be carried out for various values of the adulticide coverage parameter (C_M) and in the presence and absence of density-dependent larval mortality $({\Psi }_L^i,i=\{SS,RS,RR\})$. Furthermore, these simulations will be carried out for the following levels of the fitness cost parameters, ξ^RS and ξ^RR (in the absence of lab data for quantifying these costs, we choose these scenarios based on the results shown in Section 4.1):

• (i)Moderate fitness cost scenario: for this scenario, we assume that mosquitoes with RS (RR) genotype have a 1% (15%) lower development rate and 1% (15%) higher natural mortality rate, in comparison to SS genotype mosquitoes. That is, for the moderate fitness cost scenario, we set (ξ^RS, ξ^RR) = (1.01, 1.15).
• (ii)High fitness cost scenario: for the high fitness cost scenario, we assume that mosquitoes with RS(RR) genotype have a 1% (23%) lower development rate and 1% (30%) higher natural mortality rate, in comparison to SS genotype mosquitoes. That is, we set (ξ^RS, ξ^RR) = (1.01, 1.3) for this fitness cost scenario.

4.2.1. Simulations for moderate fitness costs of insecticide resistance

In this section, the model {(2.2)–(2.6)} will be simulated to assess the impacts of moderate fitness cost due to resistance (as measured by the fitness factors, ξ^RS and ξ^RR, defined in Section 4.2), adulticide coverage (C_M) and density-dependent larval mortality $({\Psi }_L^i,i=\{SS,RS,RR\})$, for various temperature values, on the mosquito population. The objective is to determine how all these factors affect the each genotype in the mosquito population. We consider the following scenarios.

4.2.1.1. Moderate fitness costs and adulticide coverage without density-dependent larval mortality

We first simulate the model {(2.2)–(2.6)} for the case without density-dependent larval mortality (i.e., we set ${\Psi }_L^i=0;i=\{SS,RS,RR\}$ and with moderate fitness costs (i.e.,(ξ^RS, ξ^RR) = (1.01, 1.15)) and moderate adulticide coverage (i.e., C_M = 0.5). The simulation results obtained show that the population of adult mosquitoes at equilibrium increases with increasing temperature values from 17 °C until a peak is reached at around 31 °C (Fig. 8(a)). The adult mosquito population decreases rapidly for temperatures above 31 °C and becomes extinct at 34 °C). Thus, Fig. 8(a) shows that, for the baseline parameter values used in our simulations, the optimal temperature for maximum abundance of adult mosquitoes is 31 °C. This result is in line with previous studies (Beck-Johnson et al., 2013; Iboi et al., 2020a; Mordecai et al., 2013; Okuneye et al., 2019) that estimate maximum mosquito abundance between 20 and 30 °C (with a sharp decline after 32 °C (Beck-Johnson et al., 2013; Mordecai et al., 2013)), but higher than the 26 °C hypothesized for optimal malaria transmission (possibly due to the malaria parasite affecting the vector's survival at increased temperatures) (Murdock, Sternberg, & Thomas, 2016; Shapiro, Whitehead, & Thomas, 2017).

Fig. 8.

Simulation of the model {(2.2)–(2.6)}, showing the profile of total adult mosquito population at steady-state, as a function of temperature, for the case with moderate fitness costs (ξ^RS = 1.01, ξ^RR = 1.15) and various levels of adulticide coverage (C_M). (a)–(d) Simulations carried out in the absence of density-dependent larval mortality (i.e. ${\Psi }_L^i=0$, i = {SS, RS, RR}). (e)–(h) Simulation carried out in the presence of density-dependent larval mortality (i.e. ${\Psi }_L^i\ne 0$, i = {SS, RS, RR}). Other parameter values used in the simulations are as given by the baseline values in Table 5, Table 6 The functional forms of the temperature-dependent parameters of the model are described in Section 2.4, and are evaluated at fixed temperatures ranging from 17 °C to 36 °C.

Simulations for the effect of temperature on adult mosquito abundance by genotype, for this case with moderate fitness costs and adulticide coverage, show that the population of adult homozygous resistant mosquitoes rapidly increases with increasing temperature and reaches a peak at 22 °C. The extinction of the heterozygous and homozygous sensitive mosquito population is likely due to the high efficacy of insecticides at lower temperatures (Glunt et al., 2018), resulting in selection for homozygous insecticide resistance. This population then decreases until the temperature reaches 25 °C, and then increases again to a local maximum at 30 °C. It finally decreases sharply (and becomes extinct) at 34 °C (Fig. 8(b), orange curve). Similarly, the population of adult heterozygous mosquitoes initially was extinct for temperatures above 18 °C until a temperature of about 23 °C is reached, and increases slowly thereafter and reaches its maximum at 31 °C. The population then drops quickly (and becomes extinct) at 34 °C (Fig. 8(b), gold curve). The population of adult homozygous sensitive mosquitoes, which was also initially extinct for temperatures 18 °C or higher until a temperature of 23 °C is reached, increases slowly (for temperatures greater than 23 °C) and reaches its maximum at 33 °C. This population then declines rapidly (and becomes extinct) when temperature slightly increases to 34 °C (Fig. 8(b), blue curve).

It is worth noting from Fig. 8(b) that, for temperatures in the range [18, 22] °C, only homozygous resistant mosquitoes exist at equilibrium (the heterozygous and homozygous sensitive are extinct for temperatures in this range). Furthermore, this figure shows that all three adult mosquito genotypes coexist at equilibrium for temperatures in the range [23, 33] °C (this result is consistent with the result of the coexistence region reported in Fig. 6(e)–(f)). Homozygous resistant mosquitoes have the highest relative abundance (followed by heterozygous then homozygous sensitive mosquitoes) for temperatures in [23, 30] °C, with heterozygous mosquitoes surpassing the homozygous resistant population at 31 °C. At 33 °C, heterozygous and homozygous sensitive mosquitoes have comparable relative abundances, with homozygous resistant mosquitoes maintained at low levels.

4.2.1.2. Moderate fitness costs with high adulticide coverage and no density-dependent larval mortality

Simulations for the case with moderate fitness cost but with adulticide coverage increased from moderate to high (i.e., (ξ^RS, ξ^RR) = (1.01, 1.15) and C_M = 0.8) show that the total adult mosquito population at equilibrium increases with increasing temperature until a peak is attained at 31 °C, and decreases thereafter (Fig. 8(c)). It can be seen, by comparing Fig. 8(a) and (c), that the size of the total adult mosquito population at equilibrium for the case with high adulticide coverage is approximately 33% lower than that for the case where adulticide coverage is moderate. For this scenario (with moderate fitness cost but high adulticide coverage), our simulations show that the population of adult mosquitoes with RR genotype increases with increasing temperature, until a peak is reached at 30 °C, and decreases thereafter (Fig. 8(d), red curve). Furthermore, the population of the adult mosquitoes with the RS genotype decreases from its initial size to zero for temperatures in the range [18, 24] °C. This population remains at zero until temperature reaches 25 °C, and increases slowly until temperature reaches 27 °C. It decreases, then increases sharply and reaches a peak at 32 °C before quickly decreasing to extinction at 34° (Fig. 8(d), gold curve). The population of adult mosquitoes with the SS genotype at equilibrium decreases quickly to zero for temperatures in the range [18, 24] °C, and remains at zero until the temperature reaches 25 °C. This population then increases slightly, and then decreases to extinction at 34 °C (Fig. 8(d), blue curve).

In conclusion, the simulations depicted in Fig. 8(d) show that only mosquitoes of RR genotype exist in the population at equilibrium when temperature lies in the range [18, 24] °C. Adult mosquitoes of all genotypes coexist if the temperature lies in the range [25, 34)°C, with the homozygous resistant population being significantly more abundant than the other two (RS and SS genotype) populations.

4.2.1.3. Moderate fitness costs and adulticide coverage with density-dependent larval mortality

We carried additional simulations for the case with moderate fitness costs and adulticide coverage (ξ^RS, ξ^RR) = (1.01, 1.15) and C_M = 0.5) but with density-dependent larval mortality $({\Psi }_L^i;i=\{SS,RS,RR\})$ set at its baseline value in order assess the impact of density-dependent larval mortality for this setting. The simulation results obtained show that the total adult mosquito population at equilibrium increases with increasing temperature until a maximum is attained at 31 °C, with the population decreasing thereafter and reaching extinction at 34 °C (Fig. 8(e)). In this case, the total population of adult mosquitoes is significantly reduced, in comparison to the case without density-dependent larval mortality (compare Fig. 8(a) and (e)).

Furthermore, our simulations show that the population of RR genotype mosquitoes is maintained at low size for all temperature values below 34 °C (Fig. 8(f)), which differs from the result obtained for the case with no density-dependent larval mortality (depicted in Fig. 8(b)), where the population of RR genotype mosquitoes is very high (and much higher than the steady-state populations for the SS and RS mosquitoes). Furthermore, while the relative abundance of mosquitoes with the SS genotype is higher than the comparable case without density-dependent larval mortality for temperatures in the range [17, 33] °C, the population of mosquitoes with the RS genotype is lower than its corresponding population for the case without density-dependent larval mortality for temperatures below 34 °C (but with a higher relative abundance for temperatures in the range [17, 25)°C) (Fig. 8(f)). Thus, it follows, by comparing Fig. 8(f) and (b), that density-dependent larval mortality dramatically reduces the relative population abundance of mosquitoes with the RR and RS genotypes, while significantly increasing the relative population abundance of mosquitoes with the SS genotype for temperatures in the range [17, 34] °C).

Fig. 8(f) further shows that the populations of the SS and RS genotype mosquitoes increase with increasing temperature until their peaks are attained at 31 °C, and then decrease to extinction at 34 °C. However, the population of the SS genotype mosquitoes is higher than the populations of the RS and RR genotype mosquitoes (compare blue curve with gold and red curves in Fig. 8(f)).

4.2.1.4. Moderate fitness costs with high adulticide coverage and density-dependent larval mortality

The simulations carried out above (for moderate fitness costs and adulticide coverage, and baseline density-dependent larval mortality) are extended to the case with high adulticide coverage. The results obtained, depicted in Fig. 8(g), show a further reduction in the total mosquito population at equilibrium, in comparison to the case with moderate adulticide coverage (shown in Fig. 8(c)). The populations of adult mosquitoes with the SS and RS genotypes, which coincide for all temperature values, increase with increasing temperatures until a peak is reached at 31 °C. This population then declines thereafter and reaches zero at 34 °C (Fig. 8(h)). Furthermore, the population of adult mosquitoes with the RR genotype remains consistently very low for all temperature values (Fig. 8(h)). Here, too, this result differs from the corresponding result without density-dependent larval mortality (depicted in Fig. 8(d)), where the population of adult mosquitoes with the RR genotype is very high both in magnitude and relative abundance. Overall, the simulations in Fig. 8(h) show that the combination of density-dependent larval mortality and high coverage of adulticide dramatically reduces the mosquito population of all genotypes (this is evident by comparing Fig. 8(h) and (b)).

In summary, our simulations for the moderate fitness costs and adulticide coverage scenario show that adding density-dependent larval mortality led to a dramatic reduction in the total adult mosquito population at equilibrium (compare Fig. 8(a) and (f)). Although this reduction is also achieved if density-dependent mortality is not accounted for when adulticide coverage is high, the level of reduction in adult mosquito abundance is much higher if density-dependent larval mortality is accounted for (compare Fig. 8(c) and (g)). In both scenarios (without and with density-dependent larval mortality), the total adult mosquito population increases with increasing temperature until a peak is reached and 31 °C, and then decreases thereafter (reaching extinction at 34 °C). Furthermore, while the equilibrium population of adult mosquitoes with the RR genotype is predominantly higher than that of the other two genotypes when density-dependent larval mortality is not accounted for (Fig. 8(b) and (f)), this population is exceedingly low at equilibrium when density-dependent larval mortality is accounted for (compare Fig. 8(b) and (f))). This phenomenon is also observed when adulticide coverage is increased to a high level (see Fig. 8(d) and (h)); however, increasing adulticide coverage in the presence of density-dependent larval mortality selects for resistance (as measured by the relative abundance of mosquitoes carrying the resistance allele).

4.2.2. Simulations for high fitness costs of insecticide resistance

In this section, the model {(2.2)–(2.6)} will be simulated to assess the impact of high fitness cost of insecticide resistance, for the case with moderate or high adulticide coverage and in the absence or presence of density-dependent larval mortality (for various temperature values), as described below.

4.2.2.1. (E): high fitness cost with moderate/high adulticide coverage and no density-dependent larval mortality

Simulations of the model {(2.2)–(2.6)} for the case with high fitness costs of resistance ((ξ^RS, ξ^RR) = (1.01, 1.3)), moderate adulticide coverage (C_M = 0.5), and no density-dependent larval mortality $({\Psi }_L^i=0)$ show an increase in the adult mosquito population at steady-state for increasing temperature until a peak is reached at 31 °C, and decreases thereafter (Fig. 9(a)). These simulations show a dramatic reduction in the populations of mosquitoes with the RR and RS genotypes, in comparison to the case with moderate fitness costs of resistance (compare Fig. 9(b) with Fig. 8(b)). In fact, the population of the heterozygous resistant adult mosquitoes at steady-state is essentially suppressed (9(b)). Furthermore, this figure shows a dramatic increase in the population of mosquitoes with SS genotype (in comparison to the corresponding case with moderate fitness costs) with increasing temperature, until a peak is attained at 31 °C.

Fig. 9.

Simulation of the model {(2.2)–(2.6)}, showing the profile of total adult mosquito population at steady-state, as a function of temperature, for the case with high fitness costs (ξ^RS = 1.01, ξ^RR = 1.30) and various levels of adulticide coverage (C_M). (a)–(d) Simulations carried out in the absence of density-dependent larval mortality (i.e. ${\Psi }_L^i=0$, i = {SS, RS, RR}). (e)–(h) Simulation carried out in the presence of density-dependent larval mortality (i.e. ${\Psi }_L^i\ne 0$, i = {SS, RS, RR}). Other parameter values used in the simulations are as given by the baseline values in Table 5, Table 6 The functional forms of the temperature-dependent parameters of the model are described in Section 2.4, and are evaluated at fixed temperatures ranging from 17 °C to 36 °C.

Similar trend is observed when the adulticide coverage is increased to high level (i.e., C_M = 0.8), but with the size of the adult mosquito population dramatically reduced in comparison to the case with moderate adulticide coverage (compare Fig. 9(c) and (d) with Fig. 9(a) and (b)).

4.2.2.2. (F): high fitness costs with moderate/high adulticide coverage and density-dependent larval mortality

Simulations of our model with high fitness costs combined with moderate adulticide coverage and density-dependent larval mortality show a significant reduction $(\approx 98\%)$ in the total adult mosquito at steady-state, in comparison to the case without density-dependent larval mortality (compare Fig. 9(e) with Fig. 9(a)). However, a far more dramatic reduction in the total adult mosquito population with RS genotype is recorded, in comparison to the case without density-dependent larval mortality (compare gold curves in Fig. 9(f) and (b))). Here,too, a dramatic increase in the relative abundance of the SS genotype is recorded, in comparison to the case without density-dependent larval mortality (compare Fig. 9(e) with Fig. 8(b) or (f)).

Further dramatic reduction in the adult mosquito population (collectively and by genotype) is recorded when the adulticide coverage is increased to high level, in comparison to the case where the coverage is moderate (compare Fig. 9(g) and (h) with Fig. 9(e) and (f)). Furthermore, for this case with high adulticide coverage and density-dependent larval mortality, the steady-state populations of mosquitoes with the RS and SS genotypes is significantly lower than their corresponding populations for the case without density-dependent larval mortality (compare Fig. 9(g) and (h) with Fig. 8(e) and (f)). In all the simulations of the model with high fitness costs of resistance, the population of mosquitoes with the RR genotype is suppressed.

In summary, when fitness costs are high, the total adult mosquito population increases with increasing temperature until a maximum is attained at 31 °C. Regardless of the inclusion of density-dependent larval mortality, homozygous sensitive mosquitoes have the highest relative abundance across all temperatures and insecticide coverage scenarios considered. While increasing adulticide coverage suppresses the overall adult population, the genotype SS population sees the largest reduction (hence selecting for resistance). Furthermore, it is clear that inclusion (or exclusion) of density-dependent larval mortality has a significant impact on the mosquito population (also found in (Beck-Johnson et al., 2013)), notably in its suppression of mosquitoes who carry the resistance allele. Laboratory studies (Nkahe et al., 2020; Osoro et al., 2021) have hypothesized that the fitness costs associated with resistance (specifically, the longer development time for insecticide-resistant larvae) may make the resistant larvae more susceptible to habitat destruction and, in this case, density-dependent mortality.

5. Discussion

The mosquito (Spanish and Portuguese for “little fly”) is the greatest killer of mankind among animals. Each year, diseases caused by mosquitoes (and spread between humans via the bite of disease-carrying female mosquito during the process of questing for bloodmeals needed for egg development), account for over 700 million infections and 1 million deaths globally. Malaria, a parasitic infection transmitted to humans through the bite of an infectious female Anopheles mosquito, was responsible for 241 million cases and 627,000 deaths in malaria-endemic areas (World Health Organization, 2021a, World Health Organization, 2021b, World Health Organization, 2021c). Motivated by the fact that deep understanding of the population abundance of mosquitoes is crucial to gaining realistic insight into the dynamics and burden of the diseases they cause, this study focused on modeling the population dynamics and control of malaria mosquitoes (Anopheles) in malaria-endemic settings, with emphasis on quantifying the combined impacts of insecticide resistance and temperature variability on the mosquito population.

The wide-scale use of insecticide-based malaria control interventions, notably indoor residual spraying (IRS), larvicides, and the use of pyrethroid-based insecticide-treated bednets (ITNs, later replaced by long-lasting insecticidal nets (LLINs)), during the period 2000 to 2020, has resulted in a dramatic reduction in malaria burden (data from the World Health Organization shows that over 10.6 million malaria deaths may have been averted during this period (World Health Organization, 2021a, World Health Organization, 2021b, World Health Organization, 2021c)), prompting renewed efforts, such as Zero by 40 (an initiative of five chemical companies with the support of the Bill and Melinda Gates Foundation and the Innovative Vector Control Consortium (Innovative Vector Control Consortium, 2022)) and The Global Technical Strategy for Malaria 2016–2030 initiative (approved by the World Health Assembly in May 2015 (World Health Organization, 2021a, World Health Organization, 2021b, World Health Organization, 2021c)). Specifically, the wide-scale use of insecticide-based interventions (in particular, LLINs (Bhatt et al., 2015)) had a major role in averting 10.6 million deaths (largely in the WHO African Region) from 2000 to 2020 (World Health Organization, 2021a, World Health Organization, 2021b, World Health Organization, 2021c). Unfortunately, despite these successes, malaria remains a major public health problem for about half of the world's population (who live in geographies that permit the local transmission of Plasmodium falciparum, the parasite responsible for the most life-threatening form of malaria (Gething et al., 2011)). This is due to a number of factors, including Anopheles resistance to all chemical agents currently used in IRS, larvicides, and LLINs (World Health Organization, 2021a, World Health Organization, 2021b, World Health Organization, 2021c; Ranson & Lissenden, 2016; Corbel et al., 2007; N’Guessan et al., 2007), climate change (Bayoh, 2001; Bayoh & Lindsay, 2003, 2004; Eikenberry & Gumel, 2018; Mordecai et al., 2013; Okuneye & Gumel, 2017; Okuneye et al., 2018), Plasmodium resistance to drug therapy (World Health Organization, 2021a, World Health Organization, 2021b, World Health Organization, 2021c), etc. Mosquitoes are said to be resistant to an insecticide if the insecticide's ability to kill the mosquitoes upon contact with the insecticide is either greatly reduced or eliminated altogether (Innovative Vector Control Consortium, 2022). Furthermore, insecticide resistance inflicts fitness costs for these mosquitoes (e.g., with respect to survival, development, fecundity, host-seeking, biting etc.) (Alout et al., 2016; Alout et al., 2017; Djogbénou et al., 2010; Platt et al., 2015), making it critical to investigate the balance between controlling the abundance of the mosquito population using insecticide-based interventions, and effectively managing the evolution and spread of insecticide resistance in the mosquito population. This formed the objective of this study.

We developed a novel mathematical model for studying the temporal dynamics of malaria mosquitoes in a population. Some of the notable features of the model included stratifying the mosquito population by genotype (resistant or sensitive to insecticides), incorporating the entire immature and adult mosquito lifecycles, sex structure, density-dependent larval mortality, and the effect of temperature on mosquito dynamics. The model also included the wide-scale use of insecticide-based mosquito control interventions; specifically, larvicides, pupacides, and adulticides (this allowed for the assessment of the impact of their use on the spread of insecticide resistance in the mosquito population; albeit we focused on the use of adulticides, due to the limited nature of the use of larvicides and pupacides in malaria-endemic areas (World Health Organization, 2013)). Furthermore, the fitness costs associated with insecticide resistance were also explicitly incorporated into the model. Specifically, the costs were incorporated in the form of heterogeneities in fecundity, development rates, and natural mortality rates.

The resulting mathematical model, which was of the form of a 15-dimensional deterministic system of nonlinear differential equations, was rigorously analysed to show its well-posedness mathematically and ecologically. Further, conditions for the existence and asymptotic stability of the associated boundary equilibria (where only mosquitoes of one genotype exist in the community) were obtained analytically for the special case with no density-dependent larval mortality. It was shown that the dynamics of the mosquito population by genotype is governed by the size of certain ecological thresholds, namely ${\mathcal{R}}_0^{SS}$ and ${\mathcal{R}}_0^{RR}$, for the adult mosquitoes homozygous in carrying the sensitive and resistant alleles, respectively. Specifically, it was illustrated that initial solutions will converge locally to the sensitive-only (resistant-only) boundary equilibrium if its associated ecological threshold, ${\mathcal{R}}_0^{SS}$ $({\mathcal{R}}_0^{RR})$, is less than one (note that, in both of these cases, heterozygous mosquitoes do not exist at equilibrium). Further, when both ${\mathcal{R}}_0^{SS}$ and ${\mathcal{R}}_0^{RR}$ are less than one, the model (in the absence of density-dependent larval mortality) exhibits the phenomenon of bistability, where each of the two boundary equilibria is locally-asymptotically stable and convergence to either of the two equilibria depends on the initial size of each of the state variables of the model. However, the bistability phenomenon implies that, if the initial distribution of the mosquito population is within the basin of attraction of the RR genotype-only boundary equilibrium, only homozygous resistant mosquitoes will exist (which could drastically impact public health interventions reliant on insecticide-based control measures). However, if the deployment of insecticides still reduces the vector population enough for the control (or ideally, eradication) of malaria, this may be considered a success from a public health perspective (although a failure in terms of resistance management). On the contrary, if insecticide use is limited (to avoid selecting for resistance), an over-abundance of insecticide-sensitive mosquitoes will be counter-productive in terms of disease control, both in their high population and increased vectorial capacity. For the case where each of the reproduction thresholds (${\mathcal{R}}_0^{SS}$ and ${\mathcal{R}}_0^{RR}$) is greater than unity, we showed (via numerical simulations) that mosquitoes of all three genotypes coexist in the population, and the homozygous mosquito genotype with reproduction threshold greater than unity but lower than that of the other homozygous mosquito genotype is more abundant (at equilibrium), in comparison to the population size of the homozygous mosquito genotype with larger reproduction threshold.

To account for the impact of uncertainties in the estimate of parameter values used in our numerical simulations, we carried out a global sensitivity analysis with the sum of the net production rates of adult female heterozygous and homozygous resistant mosquitoes $({\mathcal{R}}_{RS}+{\mathcal{R}}_{RR})$ as the response function. Based on these analyses, our study identified a number of parameters of the model that have the highest influence on the response function. These parameters include the proportion of new adult mosquitoes that are female, the insecticide-induced mortality rate of adult female mosquitoes, the coverage level and efficacy of adulticide in the community, the oviposition rates for eggs of genotypes RS and RR, and the modification parameter accounting for the assumed reduction in insecticide-induced mortality due to resistance. While the sex ratio of emerging adult mosquitoes could be altered using, for instance, gene editing techniques to produce more male mosquitoes, rather than female mosquitoes, in the community (Simoni et al., 2020; Iboi et al., 2020b), the genotype-specific egg oviposition rates can be reduced through habitat destruction or the use of sterile insect technology (Alphey et al., 2010; Iboi et al., 2020b). Although increasing the levels of insecticide-related parameters (e.g., coverage and efficacy of insecticides) will reduce the overall mosquito population (including mosquitoes who carry the resistance allele), increases in the values of these parameters may result in selection for resistance (i.e., deploying highly efficacious insecticides at high coverage levels may result in increasing the population abundance of resistant mosquitoes in the community). Mohammed-Awel and Gumel (Mohammed-Awel & Gumel, 2019; Mohammed-Awel et al., 2020) also identified parameters related to insecticide coverage, efficacy, and fitness costs of insecticide resistance as influential to the population abundance of insecticide-resistant mosquitoes in a malaria-endemic setting.

The combined impacts of temperature, fitness costs of insecticide resistance (as measured in terms of the values of the fitness factors, ξ^RS and ξ^RR, defined in Section 4.2) and adulticide coverage on the frequency of the sensitive and resistant alleles in the population (or, equivalently, the distribution of the mosquito population by genotype) were assessed. In the absence of density-dependent larval mortality, the size of the window in the (ξ^RR − ξ^RS)-plane where all three genotypes coexist increases with increasing adulticide coverage from low to moderate (the size remains the same as adulticide coverage is increased from moderate to high), and is not significantly impacted by temperature. However, in the presence of density-dependent mortality, the window for coexistence in the (ξ^RR − ξ^RS)-plane is considerably smaller and requires that the resistance allele induce lower fitness costs (i.e., insecticide-resistant mosquitoes must compete with but not out-compete insecticide-sensitive mosquitoes)

Extensive numerical simulations were carried out to assess the impact of temperature variability (within the range [17, 36]°C on the population abundance of the malaria mosquito. The simulations showed that mosquito population increases with increasing temperature until a peak is attained at 31 °C, and declines thereafter. This result is consistent with some earlier studies, such as those in (Beck-Johnson et al., 2013; Iboi et al., 2020a; Mordecai et al., 2013; Okuneye et al., 2019), which estimates the temperature for maximum abundance of potentially-infectious malaria mosquitoes to lie in the range 20–30 °C (with the mosquito population declining sharply after 32 °C, also shown in (Beck-Johnson et al., 2013)). One of the key features of our model is that it allowed for the assessment of the impact of temperature variability on mosquito abundance by genotype (to the authors’ knowledge, this study is the first to provide such genotype-specific result). In particular, our study showed that homozygous sensitive mosquitoes were the most impacted by temperature when density-dependent larval mortality is incorporated into the model and/or fitness costs associated with insecticide resistance are high. Under these scenarios, heterozygous and homozygous resistant mosquitoes were the next most impacted by temperature, with heterozygous mosquitoes sustained at moderate levels and homozygous resistant mosquitoes persisting at low levels in the population. Given that mosquitoes of genotype RS were the second most abundant genotype in our simulation results depicting the impact of temperature on the mosquito population (Fig. 8, Fig. 9), our study highlights the need to conduct lab and field experiments to generate data needed to realistically quantify the impact of this (dominance of resistance allele in heterozygous mosquito population) parameter (since this parameter determines the survival or death of mosquitoes of RS genotype when exposed to chemical insecticides). The importance of this parameter on the abundance of mosquitoes in population has also been emphasized in earlier studies, such as those in (Mohammed-Awel & Gumel, 2019; Mohammed-Awel, Agusto, Mickens, & Gumel, 2018; Mohammed-Awel et al., 2020). Furthermore, our study clearly highlights density-dependent larval mortality as a key mechanism in suppressing insecticide-resistant mosquito populations, particularly when fitness costs due to insecticide resistance are moderate (which has also been found in (Beck-Johnson et al., 2013)). In particular, it has been hypothesized that the fitness costs associated with insecticide resistance in the larval stages (specifically fitness costs pertaining to the longer development times in insecticide resistant mosquitoes, in comparison to sensitive mosquitoes) imply that resistant larvae may be more susceptible to habitat destruction and density-dependent mortality in (Nkahe et al., 2020; Mohammed-Awel & Gumel, 2019; Mohammed-Awel et al., 2020; Osoro et al., 2021). This mechanism (of increased susceptibility of resistant larvae to habitat destruction and density-dependent larval mortality due to fitness cost-induced longer duration of maturation to pupae) is of major ecological significance, since it inhibits larvae of all genotypes from maturing to pupae (thereby reducing the overall mosquito population), while not selecting for insecticide resistance (because the fitness cost of increasing mortality in resistant immature and adult mosquitoes is independent of insecticide use in the community). The fitness factors used in our study captured or reflected the aforementioned hypothesis (of longer development duration and higher insecticide-induced mortality of resistant mosquitoes, in comparison to sensitive mosquitoes).

In conclusion, the results from the extensive numerical simulations presented in this study showed that, for moderate fitness costs of insecticide resistance, adding density-dependent larval mortality suppressed the total population of adult mosquitoes with the resistant genotype for each of the three temperature values considered in this study (18 °C, 25 °C and 30 °C). This result suggests that any mosquito control mechanism that reduces the mosquito population at the larval stage (without selecting for resistance) can potentially help to effectively manage insecticide resistance in the community. Furthermore, the simulations showed that a high fitness cost of insecticide resistance can greatly reduce the size of the mosquito population with the resistant genotype (which is a highly desirable result in the effort to eradicate malaria). This study has provided a novel ecology-genetic modeling framework for theoretically assessing the combined impacts of insecticide resistance, adulticide coverage and temperature variability on the population biology of malaria mosquitoes.

Some limitations of the study include the absence of lab or field data to quantify the parameters related to fitness costs of insecticide resistance and the dominance of the resistant allele in heterozygous mosquitoes. Spatial heterogeneity is also important in the context of malaria transmission dynamics. For instance, accounting for the mobility of insecticide-resistant mosquitoes from neighboring patches or communities (that are malaria-endemic) where insecticide-based interventions (or pesticides for agricultural purposes) were heavily used (resulting in the abundance of resistant mosquitoes that may migrate to neighboring patches that may, hitherto, only have small or no population of resistant mosquitoes). Similarly, the spatial heterogeneity of the human host is also very important (accounting for the mobility of humans from one patch to another). Furthermore, this study does not explicitly account for background exposure of mosquitoes to insecticides via their usage in agricultural practices (Barbosa & Hastings, 2012; Mouhamadou et al., 2019), nor does it account for possible heterogeneities in mating (in our study, we assumed random mating, and no possible mating preferences by genotype) (Alout et al., 2016; Alout et al., 2017; Djogbénou et al., 2010; Githinji et al., 2020; Platt et al., 2015). The authors plan to address these challenges in future studies (for instance, we will explore the important issue of spatial heterogeneity (for both the aforementioned spread of resistance between patches and human mobility) in the context of malaria disease, by extending our modeling framework to include humans and the spread of malaria in both the vector and human host populations, in a future study).

Ultimately, our study has highlighted the complex interactions between the use of insecticides in mosquito control, the emergence and spread of insecticide resistance (and the associated fitness costs of resistance), and temperature variability. We highlighted the fact that the likelihood of effectively managing insecticide resistance in the mosquito population is highly-dependent on the fitness costs associated with insecticide resistance and the level of density-dependent larval mortality. Our study also showed that the prospects of effectively controlling the population abundance of malaria mosquitoes of all three genotypes (and, consequently, malaria disease) in malaria-endemic settings are promising especially if integrated vector control measures that enhance the mortality of mosquitoes (of all genotypes) at the larval stage (in particular, measures that enhance density-dependent larval mortality), increase the fitness costs of insecticide resistance in mosquitoes, and deploy adulticides with high efficacy and coverage are implemented in the community.

Declaration of competing interest

None.

Handling Editor: Dr HE DAIHAI HE

Appendix A. Profile of Selected Temperature-Dependent Parameters

Fig. A.1.

Profile of selected temperature-dependent parameters of the model {(2.2)–(2.6)}, as described in Section 2.4.

Appendix B. Routh-Hurwitz Conditions for Stability of Boundary Equilibria

We prove the asymptotic stability of the insecticide-sensitive-only boundary equilibrium $({\mathcal{T}}_2)$ using the Routh-Hurwitz criterion (Martcheva, 2015). The proof for the asymptotic stability of the insecticide-resistant-only equilibrium $({\mathcal{T}}_3)$ is analogous (hence, will not be repeated here). We require that $0<R_{0_1}^{SS}<1$ and $0<R_{0_2}^{SS}<1$. Furthermore, recall that $R_{0_1}^{SS}<R_{0_2}^{SS}$ and all coefficients of the fourth-degree polynomial p₄(x) (3.7) have been shown to be positive. We now need to verify the condition $a_1{a}_2{a}_3>a_3^2+a_1^2{a}_4$ (Martcheva, 2015).

For computational convenience, we show that $a_1{a}_2{a}_3-(a_3^2+a_1^2{a}_4)>0$. Note that

$$\begin{array}{cc}& a_1{a}_2{a}_3=\left(\frac{K_E(K_1+K_4+K_7+K_{10})+{\alpha }^{SS}{M}_{SS}^{f\ast }}{K_E}\right)\\ & \cdot \left(\frac{K_E(K_1{K}_4+K_1{K}_7+K_1{K}_{10}+K_{10}{K}_4+K_{10}{K}_7+K_4{K}_7)+{\alpha }^{SS}{M}_{SS}^{f\ast }(K_4+K_7+K_{10})}{K_E}\right)\\ & \cdot \left(\frac{K_E(K_1{K}_4{K}_{10}+K_1{K}_7{K}_{10}+K_1{K}_4{K}_7+K_4{K}_7{K}_{10})+{\alpha }^{SS}{M}_{SS}^{f\ast }(K_4{K}_{10}+K_7{K}_{10}+K_4{K}_7)}{K_E}\right)\end{array}$$

and,

$$\begin{array}{cc}& a_3^2+a_1^2{a}_4=\frac{1}{K_E^3}\left[K_4{K}_7{K}_{10}{M}_{SS}^{f\ast }{\alpha }^{SS}{\left(K_E(K_1+K_4+K_7+K_{10})+M_{SS}^{f\ast }{\alpha }^{SS}\right)}^2\right]\\ & +{\left(K_1{K}_4{K}_{10}+K_4{K}_7{K}_{10}+K_1{K}_7(K_4+K_{10})+\frac{(K_4{K}_7+K_{10}(K_4+K_7))M_{SS}^{f\ast }{\alpha }^{SS}}{K_E}\right)}^2.\end{array}$$

Then,

$$a_1{a}_2{a}_3-(a_3^2+a_1^2{a}_4)=z_0+\frac{z_1}{K_E}+\frac{z_2}{K_E^2}+\frac{z_3}{K_E^3},$$

where,

$$\begin{array}{cc}& z_0=(K_1{K}_4{K}_{10}+K_4{K}_7{K}_{10}+K_1{K}_7(K_{10}+K_4))\\ & \cdot \left[(K_4+K_{10})(K_7+K_{10})(K_4+K_7)+K_1^2(K_{10}+K_4+K_7)+K_1{(K_{10}+K_4+K_7)}^2\right],\\ z_1=& (K_4+K_{10})(K_7+K_{10})(K_4+K_7)(K_4{K}_7+K_{10}(K_4+K_7))M_{SS}^{f\ast }{\alpha }^{SS}\\ & +2K_1{(K_{10}+K_4+K_7)}^2(K_4{K}_7+K_{10}(K_4+K_7))M_{SS}^{f\ast }{\alpha }^{SS}\\ & +K_1^2\left[3K_{10}^2(K_4+K_7)+3K_4{K}_7(K_4+K_7)+K_{10}\left(3K_4^2+8K_4{K}_7+3K_7^2\right)\right]M_{SS}^{f\ast }{\alpha }^{SS},\\ z_2=& (K_{10}+K_4)(K_{10}+K_7)(K_4+K_7)\left(K_{10}+K_4+K_7\right){\left(M_{SS}^{f\ast }{\alpha }^{SS}\right)}^2\\ & +K_1\left(3K_{10}^2(K_4+K_7)+3K_4{K}_7(K_4+K_7)+K_{10}\left(3K_4^2+7K_4{K}_7+3K_7^2\right)\right){\left(M_{SS}^{f\ast }{\alpha }^{SS}\right)}^2,\\ z_3=& (K_4+K_{10})(K_7+K_{10})(K_4+K_7){\left(M_{SS}^{f\ast }{\alpha }^{SS}\right)}^3.\end{array}$$

Since z₀ > 0, z₁ > 0, z₂ > 0, and z₃ > 0, this implies that $a_1{a}_2{a}_3>a_3^2+a_1^2{a}_4$, as desired.

Furthermore, recall that all the coefficients of the fifth-degree polynomial p₅(x) (3.7) have been shown to be positive if ${\mathcal{R}}_0^{SS}<1$. First, we verify that $b_1{b}_2{b}_3>b_3^2+b_1^2{b}_4$. Observe that

$$\begin{array}{cc}& b_1{b}_2{b}_3=(K_{11}+K_{14}+K_2+K_5+K_8)\\ & \cdot \left[K_2{K}_5+(K_2+K_5)K_8+K_{14}(K_2+K_5+K_8)+K_{11}(K_{14}+K_2+K_5+K_8)\right]\\ & \cdot \left[K_{14}{K}_2{K}_5+K_2{K}_5{K}_8+K_{14}(K_2+K_5)K_8+K_{11}(K_2{K}_5+(K_2+K_5)K_8+K_{14}(K_2+K_5+K_8))\right],\end{array}$$

and,

$$\begin{array}{cc}& b_3^2+b_1^2{b}_4={(K_{14}{K}_2{K}_5+K_2{K}_5{K}_8+K_{14}(K_2+K_5)K_8+K_{11}(K_2{K}_5+(K_2+K_5)K_8+K_{14}(K_2+K_5+K_8)))}^2\\ & +{(K_{11}+K_{14}+K_2+K_5+K_8)}^2\cdot (K_{14}{K}_2{K}_5{K}_8+K_{11}(K_{14}{K}_2{K}_5+K_2{K}_5{K}_8+K_{14}(K_2+K_5)K_8))(1-{\mathcal{R}}_{0_1}^{SS}).\end{array}$$

From here, it can be shown that $b_1{b}_2{b}_3-(b_3^2+b_1^2{b}_4)>0$. The left-hand side of the inequality becomes

$$b_1{b}_2{b}_3-(b_3^2+b_1^2{b}_4)=z_0+z_1{K}_{11}+z_2{K}_{11}^2+z_3{K}_{11}^3,$$

with,

$$\begin{array}{cc}& z_0=(K_{14}+K_2)(K_{14}+K_5)(K_2+K_5)(K_{14}+K_8)(K_2+K_8)(K_5+K_8)+K_{14}{K}_2{K}_5{K}_8{(K_{14}+K_2+K_5+K_8)}^2{\mathcal{R}}_{0_1}^{SS},\\ & z_1=(K_2+K_5)(K_2+K_8)(K_5+K_8)(K_5{K}_8+K_2(K_5+K_8))+K_2{K}_5{K}_8{(K_2+K_5+K_8)}^2{\mathcal{R}}_{0_1}^{SS}\\ & +K_{14}^3({(K_2+K_5+K_8)}^2+K_5{K}_8{\mathcal{R}}_{0_1}^{SS}+K_2(K_5+K_8){\mathcal{R}}_{0_1}^{SS})+K_{14}(K_2+K_5+K_8)\left(K_2^2(K_5+K_8)(2+{\mathcal{R}}_{0_1}^{SS})\right)\\ & \left(+K_5{K}_8(K_5+K_8)(2+{\mathcal{R}}_{0_1}^{SS})+K_2(K_5^2(2+{\mathcal{R}}_{0_1}^{SS})+K_8^2(2+{\mathcal{R}}_{0_1}^{SS})+K_5{K}_8(3+7{\mathcal{R}}_{0_1}^{SS}))\right)\\ & +K_{14}^2\left(K_2^3+2K_2^2(K_5+K_8)(2+{\mathcal{R}}_{0_1}^{SS})+(K_5+K_8)(K_5^2+K_8^2+K_5{K}_8(3+2{\mathcal{R}}_{0_1}^{SS}))+K_2\left(2K_5^2(2+{\mathcal{R}}_{0_1}^{SS})\right)\right)\\ & \left(\left(+2K_8^2(2+{\mathcal{R}}_{0_1}^{SS})+K_5{K}_8(7+9{\mathcal{R}}_{0_1}^{SS})\right)\right),\\ z_2=& K_{14}^3(K_2+K_5+K_8)+(K_2+K_5+K_8)((K_2+K_5)(K_2+K_8)(K_5+K_8)+2K_2{K}_5{K}_8{\mathcal{R}}_{0_1}^{SS})\\ & +2K_{14}^2({(K_2+K_5+K_8)}^2+K_5{K}_8{\mathcal{R}}_{0_1}^{SS}+K_2(K_5+K_8){\mathcal{R}}_{0_1}^{SS})+K_{14}\left(K_2^3+2K_2^2(K_5+K_8)(2+{\mathcal{R}}_{0_1}^{SS})\right)\\ & \left(+(K_5+K_8)(K_5^2+K_8^2+K_5{K}_8(3+2{\mathcal{R}}_{0_1}^{SS}))+K_2(2K_5^2(2+{\mathcal{R}}_{0_1}^{SS})+2K_8^2(2+{\mathcal{R}}_{0_1}^{SS})+K_5{K}_8(7+9{\mathcal{R}}_{0_1}^{SS}))\right),\\ z_3=& (K_2+K_5)(K_2+K_8)(K_5+K_8)+K_{14}^2(K_2+K_5+K_8)+K_2{K}_5{K}_8{\mathcal{R}}_{0_1}^{SS}+K_{14}\left({(K_2+K_5+K_8)}^2\right)\\ & \left(+K_5{K}_8{\mathcal{R}}_{0_1}^{SS}+K_2(K_5+K_8){\mathcal{R}}_{0_1}^{SS}\right)\end{array}$$

Since z₀ > 0, z₁ > 0, z₂ > 0, and z₃ > 0, it follows that $b_1{b}_2{b}_3>b_3^2+b_1^2{b}_4$.

We now verify that

$$\left(b_1{b}_4-b_5\right)\left(b_1{b}_2{b}_3-b_3^2-b_1^2{b}_4\right)>b_5{\left(b_1{b}_2-b_3\right)}^2+b_1{b}_5^2,$$

or, alternatively, that $\left(b_1{b}_4-b_5\right)\left(b_1{b}_2{b}_3-b_3^2-b_1^2{b}_4\right)-b_5{\left(b_1{b}_2-b_3\right)}^2-b_1{b}_5^2>0$. The expression on the left-hand side can be written in the form

$$-\left(K_2+K_5+K_8+K_{11}+K_{14}\right)\left[Q_4{K}_{11}^4+Q_3{K}_{11}^3+Q_2{K}_{11}^2+Q_1{K}_{11}+Q_0\right],$$ (B.1)

where Q_i(i = {1, 2, 3, 4, 5}) are as shown (and color-coded) in the Supplementary Material. Hence, to show that (B.1) is positive (and, thus, show that the sensitive-only-equilibrium is locally-asymptotically stable), it is sufficient to show that Q₀, Q₁, Q₂, Q₃, and Q₄ are negative. The negativity of Q_i(i = {1, 2, 3, 4, 5}) can be established by showing that the following expressions are negative (and noting that $0<R_{0_1}^{SS}<R_{0_2}^{SS}<1$):

• (i)${\mathcal{R}}_{0_1}^{SS}-\frac{1}{3}{\mathcal{R}}_{0_2}^{SS}-\frac{2}{3}$; it follows that

$${\mathcal{R}}_{0_1}^{SS}-\frac{1}{3}{\mathcal{R}}_{0_2}^{SS}-\frac{2}{3}<{\mathcal{R}}_{0_2}^{SS}-\frac{1}{3}{\mathcal{R}}_{0_2}^{SS}-\frac{2}{3}<0.$$

• (ii)${\left({\mathcal{R}}_{0_1}^{SS}\right)}^2+2{\mathcal{R}}_{0_1}^{SS}-{\mathcal{R}}_{0_2}^{SS}-2$; then,

$${\left({\mathcal{R}}_{0_1}^{SS}\right)}^2+2{\mathcal{R}}_{0_1}^{SS}-{\mathcal{R}}_{0_2}^{SS}-2<{\left({\mathcal{R}}_{0_2}^{SS}\right)}^2+{\mathcal{R}}_{0_2}^{SS}-2<0.$$

• (iii)${\left({\mathcal{R}}_{0_1}^{SS}\right)}^2+\frac{3}{2}{\mathcal{R}}_{0_1}^{SS}-{\mathcal{R}}_{0_2}^{SS}-\frac{3}{2}$; hence,

$${\left({\mathcal{R}}_{0_1}^{SS}\right)}^2+\frac{3}{2}{\mathcal{R}}_{0_1}^{SS}-{\mathcal{R}}_{0_2}^{SS}-\frac{3}{2}<{\left({\mathcal{R}}_{0_2}^{SS}\right)}^2+\frac{1}{2}{\mathcal{R}}_{0_2}^{SS}-\frac{3}{2}<0.$$

• (iv)${\left({\mathcal{R}}_{0_1}^{SS}\right)}^2+\left(-\frac{1}{14}{\mathcal{R}}_{0_2}^{SS}+\frac{2}{7}\right){\mathcal{R}}_{0_1}^{SS}-\frac{4}{7}{\mathcal{R}}_{0_2}^{SS}-\frac{9}{14}$; which implies

$${\left({\mathcal{R}}_{0_1}^{SS}\right)}^2+\left(-\frac{1}{14}{\mathcal{R}}_{0_2}^{SS}+\frac{2}{7}\right){\mathcal{R}}_{0_1}^{SS}-\frac{4}{7}{\mathcal{R}}_{0_2}^{SS}-\frac{9}{14}<{\left({\mathcal{R}}_{0_2}^{SS}\right)}^2+\left(-\frac{1}{14}{\mathcal{R}}_{0_2}^{SS}+\frac{2}{7}\right){\mathcal{R}}_{0_2}^{SS}-\frac{4}{7}{\mathcal{R}}_{0_2}^{SS}-\frac{9}{14}.$$

The right-hand side can be rewritten in the form $\frac{1}{14}\left({\mathcal{R}}_{0_2}^{SS}-1\right)\left(13{\mathcal{R}}_{0_2}^{SS}+9\right)<0$ since ${\mathcal{R}}_{0_2}^{SS}<1$.

• (v)${\left({\mathcal{R}}_{0_1}^{SS}\right)}^2+\left(-\frac{1}{16}{\mathcal{R}}_{0_2}^{SS}+\frac{3}{8}\right){\mathcal{R}}_{0_1}^{SS}-\frac{1}{2}{\mathcal{R}}_{0_2}^{SS}-\frac{13}{16}$; using a similar strategy as (iv), we have

$$\frac{1}{16}\left({\mathcal{R}}_{0_2}^{SS}-1\right)\left(15{\mathcal{R}}_{0_2}^{SS}+13\right)<0.$$

• (vi)${\left({\mathcal{R}}_{0_1}^{SS}\right)}^2+\frac{5}{4}{\mathcal{R}}_{0_1}^{SS}-\frac{3}{4}{\mathcal{R}}_{0_2}^{SS}-\frac{3}{2}$; thus,

$${\left({\mathcal{R}}_{0_1}^{SS}\right)}^2+\frac{5}{4}{\mathcal{R}}_{0_1}^{SS}-\frac{3}{4}{\mathcal{R}}_{0_2}^{SS}-\frac{3}{2}<{\left({\mathcal{R}}_{0_2}^{SS}\right)}^2+\frac{5}{4}{\mathcal{R}}_{0_2}^{SS}-\frac{3}{4}{\mathcal{R}}_{0_2}^{SS}-\frac{3}{2}.$$

This can be rewritten ${\left({\mathcal{R}}_{0_2}^{SS}\right)}^2+\frac{1}{2}{\mathcal{R}}_{0_2}^{SS}-\frac{3}{2}$, which is less than zero.

• (vii)${\left({\mathcal{R}}_{0_1}^{SS}\right)}^2+\left(-\frac{1}{9}{\mathcal{R}}_{0_2}^{SS}-\frac{1}{9}\right){\mathcal{R}}_{0_1}^{SS}+\frac{1}{45}{\left({\mathcal{R}}_{0_2}^{SS}\right)}^2-\frac{17}{45}{\mathcal{R}}_{0_2}^{SS}-\frac{19}{45}$; using the fact that $0<R_{0_1}^{SS}<R_{0_2}^{SS}<1$, this implies

$$\begin{array}{cc}& {\left({\mathcal{R}}_{0_1}^{SS}\right)}^2+\left(-\frac{1}{9}{\mathcal{R}}_{0_2}^{SS}-\frac{1}{9}\right){\mathcal{R}}_{0_1}^{SS}+\frac{1}{45}{\left({\mathcal{R}}_{0_2}^{SS}\right)}^2-\frac{17}{45}{\mathcal{R}}_{0_2}^{SS}-\frac{19}{45}\\ & <{\left({\mathcal{R}}_{0_2}^{SS}\right)}^2+\left(-\frac{1}{9}{\mathcal{R}}_{0_2}^{SS}-\frac{1}{9}\right){\mathcal{R}}_{0_2}^{SS}+\frac{1}{45}{\left({\mathcal{R}}_{0_2}^{SS}\right)}^2-\frac{17}{45}{\mathcal{R}}_{0_2}^{SS}-\frac{19}{45},\end{array}$$

which is equivalent to $\frac{1}{45}\left({\mathcal{R}}_{0_2}^{SS}-1\right)\left(41{\mathcal{R}}_{0_2}^{SS}+19\right)<0$.

• (viii)${\left({\mathcal{R}}_{0_1}^{SS}\right)}^2+\left(-\frac{1}{14}{\mathcal{R}}_{0_2}^{SS}+\frac{1}{7}\right){\mathcal{R}}_{0_1}^{SS}-\frac{3}{7}{\mathcal{R}}_{0_2}^{SS}-\frac{9}{14}$; the negativity of this expression follows from (iv).

Since these eight expressions are negative, Q₀, Q₁, Q₂, Q₃, and Q₄ are negative. Thus,

$$-\left(K_2+K_5+K_8+K_{11}+K_{14}\right)\left[Q_4{K}_{11}^4+Q_3{K}_{11}^3+Q_2{K}_{11}^2+Q_1{K}_{11}+Q_0\right]>0.$$

Because all conditions of the Routh-Hurwitz criterion are satisfied (Martcheva, 2015), the insecticide-sensitive-only equilibrium is locally-asymptotically stable when $R_0^{SS}=\max \left\{{\mathcal{R}}_{0_1}^{SS},{\mathcal{R}}_{0_2}^{SS}\right\}<1$, and unstable when $R_0^{SS}>1$.

The proof for the local asymptotic stability of the insecticide-resistant-only boundary equilibrium can be obtained by making the following substitutions:

• (i)K₃ for K₁, K₆ for K₄, K₉ for K₇, and K₁₂ for K₁₀;
• (ii)$M_{RR}^{f\ast \ast }$ for $M_{SS}^{f\ast }$, and α^RR for α^SS;
• (iii)${\mathcal{R}}_{0_1}^{RR}$ for ${\mathcal{R}}_{0_1}^{SS}$, and ${\mathcal{R}}_{0_2}^{RR}$ for ${\mathcal{R}}_{0_2}^{SS}$.

Appendix C. Effect of Temperature on Stability of Boundary Equilibria

Fig. C.1.

Numerical simulations of the model {(2.2)–(2.6)} showing the mosquito population, as a function of time, for the indicated temperature values and fitness factor pair (ξ^RS, ξ^RR) where adulticide coverage is moderate (C_M = 0.5) and no larvicides or pupacides are used (C_L = C_P = 0). (a)–(c): without density-dependent larval mortality. (d)–(f): with density-dependent larval mortality. The baseline values of the parameter values listed in Table 5, Table 6 are used in the simulations. The functional forms of the temperature-dependent parameters are described in Section 2.4.

Appendix A. Supplementary data

The following is the Supplementary data to this article: