Two-step Aberration Correction: application to Transcranial Histotripsy

Abstract

Objective:

Phase aberration correction is essential in transcranial histotripsy to compensate for focal distortion caused by the heterogeneity of the intact skull bone. This paper improves the 2-step aberration correction (AC) method that has been previously presented and develops an AC workflow that fits in the clinical environment, in which the computed tomography (CT)-based analytical approach was first implemented, followed by a cavitation-based approach using the shockwaves from the acoustic cavitation emission (ACE).

Approach:

A 700 kHz, 360-element hemispherical transducer array capable of transmit-and-receive on all channels was used to transcranially generate histotripsy-induced cavitation and acquire ACE shockwaves. For CT-AC, two ray-tracing models were investigated: a forward ray-tracing model (transducer-to-focus) in the open-source software Kranion, and an in-house backward ray-tracing model (focus-to-transducer) accounting for refraction and the sound speed variation in skulls. Co-registration was achieved by aligning the skull CT data to the skull surface map reconstructed using the acoustic pulse-echo method. For ACE-AC, the ACE signals from the collapses of generated bubbles were aligned by cross-correlation to estimate the corresponding time delays.

Main results:

The performance of the 2-step method was tested with 3 excised human calvariums placed at 2 different locations in the transducer array. Results showed that the 2-step AC achieved 90±7% peak focal pressure compared to the gold standard hydrophone correction. It also reduced the focal shift from 0.84 to 0.30 mm and the focal volume from 10.6 to 2.0 mm³ on average compared to the no AC cases.

Significance:

The 2-step AC yielded better refocusing compared to either CT-AC or ACE-AC alone and can be implemented in real-time for transcranial histotripsy brain therapy.

1. Introduction

Histotripsy is a non-invasive ultrasound therapy modality that liquefies targeted tissue into acellular debris via acoustic cavitation generated using high-pressure (peak negative pressure P_> 15 MPa), short duration (several μs) ultrasound pulses (Xu et al. 2004; Parsons et al. 2006; Maxwell et al. 2013; Vlaisavljevich et al. 2014). Unlike high-intensity focused ultrasound (HIFU) which relies on thermal effects produced by continuous sonication, histotripsy mechanically breaks down soft tissue into acellular debris via the localized strain from the rapid expansion and collapse of the cavitation bubbles (Vlaisavljevich et al. 2016). Previously, transcranial histotripsy has been shown to be effective for ex vivo treatment through an excised human skull (Kim et al. 2014; Sukovich et al. 2016). Transcranial histotripsy treatment guided by magnetic resonance imaging (MRI) demonstrated successful ablation in the intact porcine brain in vivo through an excised human skull without excessive brain edema or hemorrhage outside of the target volume in an acute study (Lu et al. 2021; Lu et al. 2022). Another in vivo study showed that cerebral lesions generated by craniotomy histotripsy in the normal pig brain induced minimal bleeding in the acute and subacute phases after treatment (Sukovich et al. 2019). With a very low duty cycle (< 0.1%), transcranial histotripsy can treat a wide range of locations and volumes through the skull while minimizing the unwanted skull heating (Constans et al. 2018; Gerhardson et al. 2017a; Schwartz et al. 2018). These preliminary results suggested the potential of using transcranial histotripsy for non-invasive brain therapy.

The heterogeneity of the intact skull poses a major challenge for transcranial histotripsy (Fry and Barger 1978; Tanter et al. 1998). Variations in composition, density, thickness, and sound speed of the skull distort the shape of the pressure field and decrease its amplitude at the target location, reducing the targeting accuracy, treatment efficacy, and efficiency. Pressure loss is particularly concerning for histotripsy because very high pressure is required to nucleate the bubbles responsible for the treatment. Extensive studies have been conducted on aberration correction for focused ultrasound to estimate the phase shifts induced by the skull bone (Jones and Hynynen 2015; Kyriakou et al. 2014; Leung et al. 2019). The “gold standard" approach for aberration correction is to place a hydrophone at the target location to directly measure the phase lags of the arrival time from transducer elements comprising a phased array and use them as offsets for optimal focusing (Gerhardson et al. 2017b; Hynynen and Jolesz 1998; Pernot et al. 2007). However, hydrophone implantation would be highly invasive and thus not clinically favorable for most brain applications. Because the skull thickness and speed of sound may be estimated from the pre-treatment CT scans of the patient's head, full-wave acoustic simulations can be performed based on CT data to determine the propagation delays of ultrasound through this heterogeneous path a priori (Aubry et al. 2003; Hughes et al. 2016; Marquet et al. 2009; Mcdannold et al. 2019; Pichardo et al. 2010; Pinton et al. 2012; Robertson et al. 2017; Top et al. 2016). These image-based simulation methods typically use finite difference time domain (FDTD) or pseudo-spectral time-domain (PSTD) models, which often require hours of computation time to complete even when implemented on high-performance computing clusters. An alternative CT-based approach that has been widely used in commercial HIFU systems is an image-based ray tracing method, where rays are traced from each transducer element to the target location, and the tissue profile along the rays is used to calculate the phase shifts (Chang et al. 2016; Clement and Hynynen 2002; Sammartino et al. 2019). In practice, the performance of these CT-analytical methods is limited by variations in the relationship between CT Hounsfield Units (HU) and acoustic properties of the skull because such correlation changes with photon energy and reconstruction methods for the CT scans so that the speed of sound may not be accurately estimated by HU (Webb et al. 2018). Besides, the clinical CT resolution may fail to resolve micro-structural information that could have a large impact on absorption and attenuation in the skullbone. Recently, MR acoustic radiation force imaging (MR-ARFI) has been investigated for energy-based adaptive focusing. MR-ARFI applies motion-sensitive encoding MR gradients to measure the local static tissue displacement induced by focused ultrasound waves, which can be used to estimate acoustic intensity at the target location non-invasively (McDannold and Maier 2008). A set of spatially encoded ultrasound pulses are transmitted and the resulting local displacements are estimated with MR-ARFI, from which phase aberration can be extracted using a non-iterative inversion process (Kaye et al. 2012; Liu et al. 2015; Marsac et al. 2012). Nevertheless, this method requires the therapeutic procedure to be performed in an MRI scanner with MR-compatible equipment that meets the high requirement of MR-ARFI sensitivity. Recent clinical studies have also shown the feasibility of aberration correction using echos from low-power pulsed sonications of intravascular ultrasound contrast agent microbubbles in transcranial MR-guided focused ultrasound (TcMRgFUS) thalamotomy (Jones et al. 2020), offering better focal quality provided by existing CT-based focusing methods. However, the associated risks of intravenous microbubbles during ultrasound exposures to the brain are still a concern.

When active cavitation bubbles can be nucleated near the desired target, the acoustic cavitation emission (ACE) shockwaves from these bubbles can be used as a point source around the target location to resolve the phase aberration in soft tissue (Macoskey et al. 2018). This technique is straightforward and fast as it can directly measure the relative delays in travel time from the cavitation spot to the receive-capable array elements, and only requires the generation of a single initial cavitation event to accomplish. Two major questions remain to be investigated in terms of implementing ACE-based aberration correction for transcranial applications. First, the intact skull bone induces more prominent aberration and attenuation compared to soft tissue, which decreases the spatial range where the initial cavitation can be generated without any prior knowledge of the phase delays, thus limiting the viable range for this method. Second, ACE-based aberration correction in the previous study relied on cavitation generated without prior aberration correction and thus only corrected for aberrations at the location where the cavitation event was generated, but could not correct for targeting aberrations. Though this is not likely to introduce any major complication for large volume treatment targets where debulking is the therapeutic goal, it could result in undesired damage during targeting that requires very high precision like transcranial histotripsy for brain surgery.

In this paper, we proposed a 2-step aberration correction approach, where the CT analytical method is implemented as the first step and followed by the ACE-based aberration correction. The CT analytical method is first used for aberration correction and targeting to minimize the spatial shift of the focus induced by aberrations and to enable the initial cavitation events in a wider range of locations by recovering some pressure loss. Then the ACE-based aberration correction is used as a second step to achieve maximal focal pressure recovery. The concept of 2-step aberration correction was previously demonstrated by Gâteau et al., in which a 3-D finite-difference simulation based on CT was used first, followed by cavitation-based correction for transcranial HIFU. In this study, the simulation-based correction was replaced with the ray-tracing-based analytical model to substantially reduce the computation time so that it can be applied almost in real-time (within minutes). In addition, a histotripsy array with transmit-and-receive capability was used herein to generate the cavitation event as the point source, allowing the shockwaves from the cavitation nucleation and collapse to be resolved accurately and independently. We hypothesize that these improvements can enable the 2-step AC to fit in well with the current clinical procedure for histotripsy treatment and provide better refocusing for transcranial histotripsy brain therapy.

This paper first demonstrates the feasibility and performance of transcranial aberration correction using a CT-based ray-tracing analytical method and an ACE-based method separately. An acoustic-based co-registration technique using the pulse-echo method is developed to reduce the need for the stereotactic frame in CT-based correction. Next, the workflow of 2-step aberration correction is presented. Finally, the performance and efficacy of the 2-step aberration correction approach are evaluated through ex vivo human skulls and compared to each step alone.

2. Materials and Methods

2.1. Transmit-Receive-Capable Histotripsy System

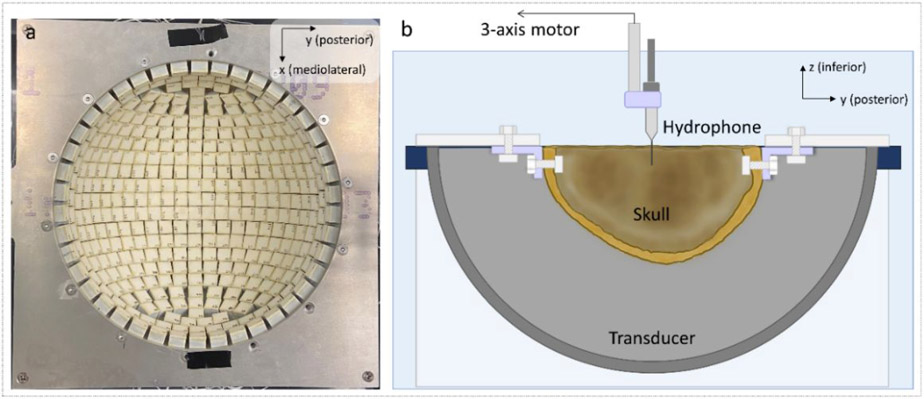
Experiments were conducted using a 700 kHz, 360-element hemispherical phased array with a radius of 15 cm built in-house (Fig. 1a). The array consists of 17-mm square transducer elements constructed with flat piezo ceramic material (PZ36, Ferroperm, Kvistgaard, Denmark, −6 dB frequency range = 0.5 – 1.0 MHz) and 3D-printed housing and matching layers. The elements were patterned to optimize their packing within the hemisphere scaffold, resulting in a packing density of 73.6%. A custom-built, high-voltage pulsing system that generated 1-cycle pulses was used to drive the transmit portion of the histotripsy array with 10-ns timing precision. At a peak drive voltage of 3 kV, a single module can generate a peak-negative pressure of 1.6 MPa at a distance of 150 mm in the free field. Received signals were digitized with an analog front-end integrated circuit containing a 12-bit digitizer (AFE5801, Texas Instruments, Dallas, TX) and a programmable variable gain amplifier (VGA). System-on-a-chip (SoC) FPGA devices were used to control the transducer and acquire signals.

Figure 1.

Top view of the transducer array (a) and the experimental setup (b) used in this study. During the experiments, each skull was mounted to a plastic frame and secured in the transducer array. The whole setup was submerged in degassed de-ionized water. Measurements were acquired with hydrophones affixed to a motorized 3-axis positioning system.

2.2. Skull preparation

Three embalmed cadaver heads were acquired from the Anatomical Donation Program at our institution. The heads were cut from ear to ear along the circumference and de-fleshed to extract the calvarium (the domelike superior portion of the skull). The skulls were CT-scanned (Discovery CT750 HD, GE Healthcare, USA) at a voltage of 120 kVp, with an in-plane resolution of 0.488 × 0.488 mm², and a 1.25 mm slice thickness (reconstructed to 0.625 mm) along the inferior-superior axis. A built-in reconstruction kernel “BONE+” provided by the GE CT scanner was used for image reconstruction. This kernel has been approved by the InSightec patient screening imaging protocol (Leung et al. 2021). These skulls vary in shape, dimensions, and thicknesses, as summarized in Table 1 and shown in Fig.7. The skulls were stored in refrigerated de-ionized water and degassed for at least 12 hours in a vacuum chamber before all experiments to minimize gas in the cancellous bone.

Table 1.

Measurements of the calvariums used in experiments

Skull No.	Major dimensions1 (mm)			Thickness1 (mm)			Skull Density Ratio (SDR)2
	AP	ML	SI	Max	Min	Mean
1	180.8	148.1	87.8	17.3	1.9	8.7	0.43
2	196.5	147.0	104.3	16.7	2.2	6.9	0.54
3	170.3	134.5	106.2	21.0	1.9	8.7	0.48

¹Measurements of the calvariums’ dimensions were obtained from CT scans of their volumes (AP = anterior-to-posterior; ML = mediolateral; SI = superior-to-inferior).

²Calculated as the global average of the ratio between the radiodensity in CT Hounsfield units of cancellous to the cortical bone within the skull (Chang et al. 2016).

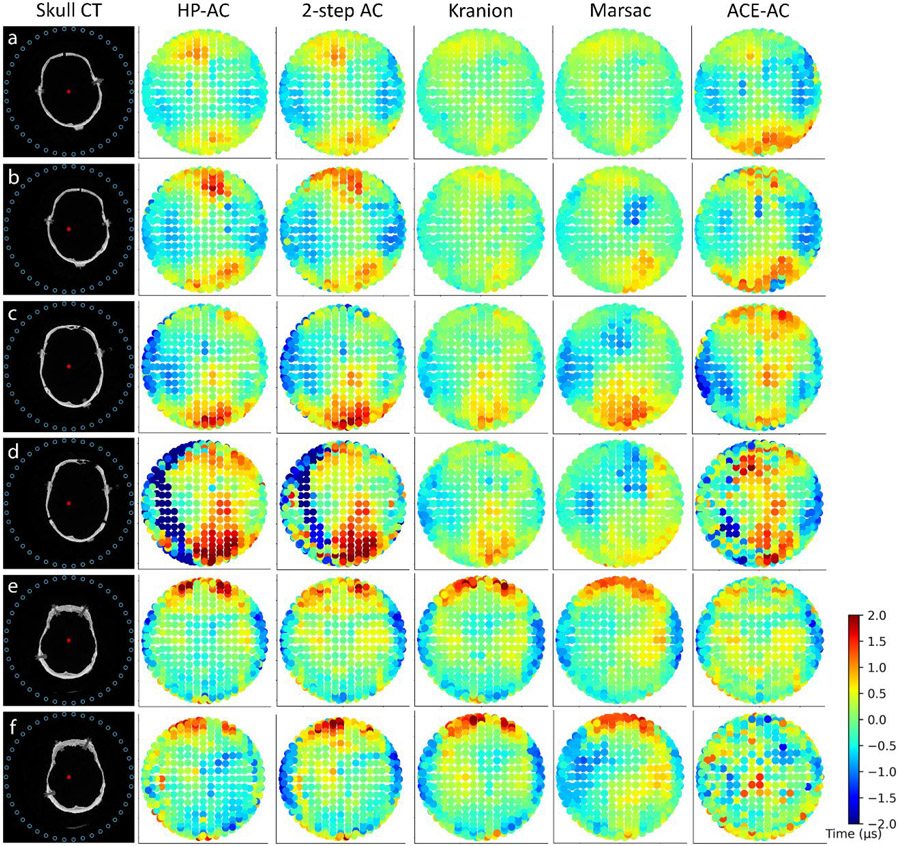
Figure 7.

The co-registered skull locations in the transducer array and their corresponding computed time delays for each experiment. Column 1: Cross-section of the skull CT data co-registered to the array (elements on the top ring labeled as blue circles). a,b: Skull #1; c,d: Skull#2; e,f: Skull#3. a,c,e: the first location tested for each skull; b,d, f: the second location tested for each skull. The geometric focus of the array is labeled as a red asterisk. Columns 2–6: Time delays calculated projected on the surface of the transducer for HP-AC, 2-step AC, CT-AC(Kranion), CT-AC (Marsac), and ACE-AC, respectively. Each dot represents one transducer element.

During experiments, each skull was mounted on a rigid plastic frame via L-brackets and nylon screws and positioned in the transducer array. Each skull was placed at two different locations in the transducer. For the first location, the skull was well-centered in the array with the geometric focus of the array close to the midline of the skull. For the second location, the skull was translated laterally 15 to 20 mm away with no rotational changes. The second location allowed us to assess the efficacy of the 2-step aberration correction method for a focal location closer to the skull, motivated by transcranial applications such as brain tumors.

2.3. Acoustic-based co-registration

The CT data were segmented by intensity thresholding using open-source software, Invesalius (https://invesalius.github.io/, intensity threshold = [226, max(intensity)] for each skull), resulting in a skull defined in 3D by a series of vertices and faces. The skull outer surface was then extracted by selecting the vertices clusters on the outer surface using a 3D mesh processing software MeshLab (https://www.meshlab.net/) and downsampled to reduce the computation complexity for co-registration.

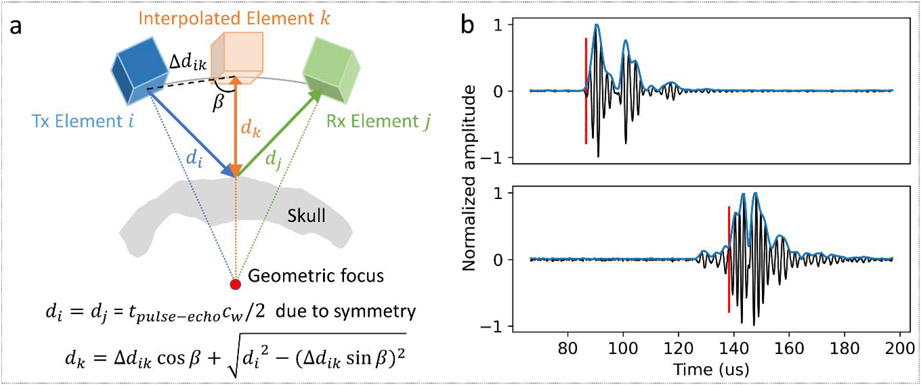
Instead of using fiducial markers on a stereotactic frame to register the skull with the histotripsy device, a skull surface map was also generated using acoustic pulse-echo methods for each trial and co-registered to the skull CT scan as follows. Each transducer element was pulsed individually while a set of the 9 closest elements (including the pulsed element itself) received the echoes from the reflection off of the skull outer surface. For each transmitter-receiver pair, a synthetic element was defined to lie at the mid-point of the chord connecting them, as illustrated in Fig. 2a. Duplicate synthetic elements were excluded, resulting in 1889 unique synthetic elements for the skull surface mapping. The time-of-arrival t_k of the acoustic pulse reflected off of the skull surface at the receiving element of the pair was determined by identifying the rising edge of the acquired signal. To achieve this, the Hilbert transform was taken and digitally filtered with a third-order Butterworth lowpass filter (2 MHz) to extract the signal envelope. The envelope signal was cropped temporally to exclude the firing signal and signals associated with any second reflection on each channel. The rising edge of the signal envelope was then determined by the first local maximum of the envelope derivative. The motivation for interpolating the array was that the sharpness of the rising edges showed significant differences across transducer elements as shown in Fig. 2b, which posed a challenge to estimating the time-of-arrival accurately on channels with less sharp rising edges. Interpolating the array to generate more sampling points would improve the robustness of the overall estimation as well as provide finer resolution for the skull surface map. The distance d_k from each element to the skull surface was calculated as d_k = 2c_wt_k, assuming the spherical spreading of wavefronts from the transducer elements. The sound speed in water c_w was calculated at the measured temperature for each experiment using the waterSoundSpeed function in the k-Wave Toolbox (Treeby and Cox 2010). These distances were projected along beam paths from each synthetic element to the geometric focus (the directivity of each transducer) to find the collision points which define the skull outer surface.

Figure 2.

Skull surface mapping using pulse-echo data. (a) Example pair of transmit (Tx)-receive (Rx) elements and the corresponding interpolated element. (b) Example echo waveforms (black: raw signal; blue: envelope) from skull surface reflection on two different transducers showing significant differences in the sharpness of the rising edge. The red vertical line denotes the identified time-of-arrival.

Co-registration was achieved by aligning the CT-reconstructed skull surface to the acoustic-based surface map. The CT-reconstructed surface was first rotated to bring it into rough alignment with the array coordinate space as an initial transform estimate. Then, an iterative closest point (ICP) algorithm (Besl and McKay 1992) was implemented to calculate the transformation matrix by minimizing the total distance between the corresponding closest points from two point clouds using an open-source Python library, Trimesh (https://trimsh.org/index.html). The maximum number of iterations was set to 200 to guarantee convergence. At the end of iterations, the average distance for each pair of points was observed to be less than 2.5 mm for all experiments (more details in the Discussion section).

2.4. CT-based analytical aberration correction (CT-AC)

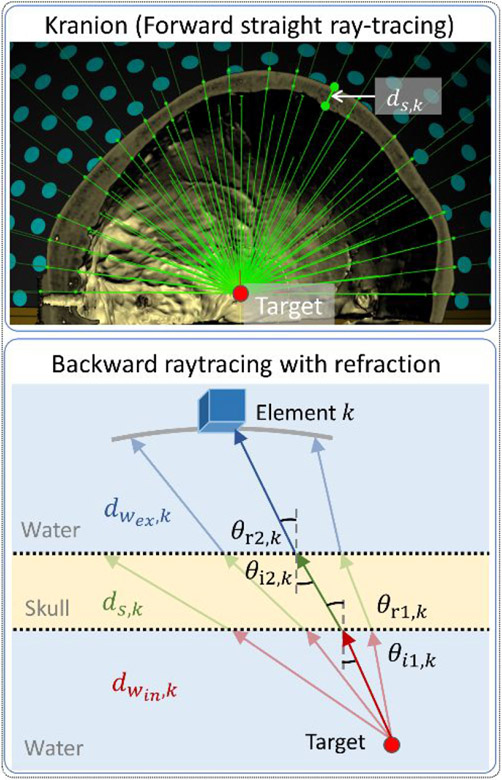
We investigated two ray-tracing approaches for CT-based analytical aberration correction. Ray-tracing was chosen over a full propagation simulation for computational efficiency and recent literature has shown that the ray-tracing approach can yield comparable accuracy to a full propagation simulation at 660kHz (Bancel et al. 2021). The first approach was a forward ray-tracing model in Kranion (Jin et al. 2020; Sammartino et al. 2019), an open-source phase correction toolkit for transcranial focused ultrasound in the clinical environment. Although Kranion was capable of ray-tracing with refraction, we noticed that the time delays from Kranion with refraction seemed to be less accurate than those using straight ray-tracing during experiments, which was likely because the refracted rays in the forward model do not necessarily focus constructively on the target location. As a result, rather than using Kranion to calculate the full ray-traced propagation delays of the acoustic pulses, it was instead used to measure the thickness of the bone lying along the straight line between each array element and the transducer focus as shown in Fig.3, from which the relative time delays Δt_{CT − Kranion} induced by the skull for each element were then calculated by

$$t_{CT-Kranion,k}={}^{(R-d_{s,k})}∕_{c_w}+{}^{d_{s,k}}∕_{\overline{c_s}}$$ (1)

$$\Delta t_{CT-Kranion,k}=t_{CT-Kranion,k}-\underset{k}{min}\left(t_{CT-Kranion,k}\right)$$ (2)

where d_s,k denotes the propagation path length in the skull, R denotes the array radius, and the averaged skull sound speed c_s was set to 2300 m/s based on empirical measurements from the skulls used in this study.

Figure 3.

Two ray-tracing models used in CT-AC. Top: A screenshot of Kranion demonstrates the straight ray-tracing based on forward propagation from the transducers (sea green) to the target (red) with collision points (lime) on skull surfaces. Bottom: A diagram illustrates the backward ray tracing from the target (red dot) to the one transducer (blue cube) with refraction at the water-to-skull and skull-to-water boundaries. The ray intersecting the transducer closest to the center of each array element was highlighted. Normal vectors (gray dash line), incident angles (black arc), and refracted angles (black arc) were labeled at boundaries.

The second approach was a backward ray-tracing model developed in-house to account for the path length difference in both skull and water due to the refraction. 3960 rays were projected from the geometric focus of the array outward with uniform angular spacing (spacing = 3°, azimuth range = [−180°, 180°], elevation range = [−90°, 9°]). Refraction on both inner and outer skull surfaces (reconstructed from CT data) was calculated using Snell’s law with the sound speed of cortical bone set to 2300 m/s. The ray intersecting the transducer closest to the center of each array element was used as the propagation trajectory for that transducer, as shown in Fig.3. The maximum distance allowed between the intersection and center of the transducer was set to 8.5 mm (i.e., half the length of the transducer elements). For elements with corresponding distances larger than this value, the time delays calculated for the nearest neighboring elements were used instead. Multiple methods have been previously developed to compensate for the heterogeneity of sound speed in skull bone based on CT data. Bancel et al. compared the performance of 3 different mappings between HU and the longitudinal speed of sound inside the skull and showed that the Marsac mapping (Marsac et al. 2017) restored the most pressure for a full-wave simulation. Therefore, we used the Marsac mapping to estimate the skull sound speed from the co-registered CT data and applied the average speed on each beam c_s,k for element k. The relative time delays Δt_{CT − Marsac} were defined as the differences of time-of-flight t_{CT − Marsac}, given by:

$$t_{CT-Marsac,k}={}^{d_{s,k}}∕_{c_{s,k}}+{}^{(d_{w_{in},k}+d_{w_{ex},k})}∕_{c_w}$$ (3)

$$\Delta t_{CT-Marsac,k}=t_{CT-Marsac,k}-\underset{k}{min}\left(t_{CT-Marsac,k}\right)$$ (4)

where d_win,k and d_wex,k denote the propagation path length in water from target to skull inner surface and from skull outer surface to the transducer, respectively. The time delays were inverted and applied as offsets to the elements’ firing time to align the pulses at the geometric focus (i.e., the target location in this study) based on the principle of time-reversal (Tanter et al. 2000).

2.5. ACE-based aberration correction (ACE-AC)

The transducer array was excited at an output power above the cavitation threshold to generate cavitation in water through the calvariums targeting the geometric focus with a pulse repetition frequency (PRF) of 1 Hz. In theory, only one cavitation event is needed to perform ACE-AC. Here 10 cavitation events were generated and the shockwave that gave the best SNR was used for analysis. Previous studies used shockwave emissions from the cavitation bubble expansion to correct for phase aberration because this signal has a high amplitude detectable with a limited sensitivity receiver (Macoskey et al. 2018). The system used for the present study has significantly improved sensitivity allowing for high SNR resolution of the cavitation emission associated with the bubble collapse. These collapse signals were found to have a significantly shorter duration, which was assumed to yield improved delay estimates. The round-trip time for sound to travel from the array to the focus and back was approximately 200μs and cavitation bubbles collapsed within 100μs after the expansion using the chosen input acoustic pulsing parameters. Therefore, received signals were recorded for each element of the array over a time window from 195 to 300μs after firing the array to capture the ACE collapse shockwaves. The signals were recorded at a sampling frequency of 12.5 MHz. Waveforms from two array firings were subtracted from each other to remove signals associated with reflections and reverberations from the calvariums and the water surface in the received signals. The ACE collapse signals were identified within a cropped time window of 6μs and cross-correlated with a reference signal consisting of the channel that gave the highest amplitude. Due to inherent pulse-to-pulse variabilities in cavitation collapse times, 2 temporally separated collapse shockwaves were expected after subtraction, and the stronger one was selected by windowing to apply the cross-correlation. Time delays Δt_ACE were defined as the relative temporal lags that gave the maximal correlations. Since the time delays on neighboring transducers should have relatively small differences, values outside the range of the median ± 1.6 times the standard deviation of delays from 4 neighboring elements were identified as outliers, and the median of delays from these neighboring elements was assigned for the outlier channels. The time delays were inverted and applied as offsets to the elements’ firing times for aberration correction at the geometric focus.

2.6. Two-step Aberration Correction (2-step AC)

In the 2-step AC, we first applied CT-AC as an initial estimate of the time delays. For the second step, 10 cavitation events were generated with these estimated time delays, and the ACE shockwaves with the best SNR were used to refine the time delays through ACE-AC. The implementation details of CT-AC and ACE-AC were kept identical as discussed in sections 2.3 and 2.4. Since two approaches were investigated for CT-AC, the one that gave higher pressure recovery was selected for 2-step AC in each experiment to achieve optimal refocusing.

2.7. Experiments and Performance Assessment

For all 6 experiments (3 skulls × 2 locations per skull), the target was defined as the geometric focus of the array. The 2D pressure beam profiles in the transverse (X-Y) and coronal (X-Z) planes around the focal zone were acquired by a needle hydrophone (Müller-Platte Needle Probe, Dr. Müller Instruments, Oberursel, Germany) at low pressure (i.e., < 2 MPa) in free field with all transducer elements pulsed simultaneously. The position of the geometric focus in water was localized by finding the position with maximum P – in the beam profiles. Following insertion and positioning of the skull, the needle hydrophone was re-placed at the geometric focus to acquire waveforms with each transducer element fired individually. The time delays for hydrophone-based aberration correction (HP-AC) Δ t_HP were calculated by cross-correlating the hydrophone signals in the same way as described in section 2.4 and used as the ground truth to compare with time delay estimates from other methods. In total, 5 cases were considered for performance evaluation and analysis: no aberration correction (N-AC), CT-AC, ACE-AC, 2-step AC, and HP-AC. For all cases, transmit amplitude for all elements was held constant, even for elements with large incident angles upon the skull.

The following metrics were used to evaluate the performance of the aberration correction methods in this study. The P – at the geometric focus and at the spatial location where it gave the largest peak pressure were directly measured using a calibrated fiber-optic hydrophone (HFO-690, ONDA, Sunnyvale, CA, USA) up to 10 MPa with all elements pulsed simultaneously (averaged across 100 pulses). The spatial shift of the location of maximum pressure with respect to the geometric focus was defined as the Euclidean distance between the two locations for each AC method. To characterize the main lobe and side lobes of the refocused pressure field, 2D cross-sections of the pressure field on transverse (X-Y) and coronal (X-Z) planes were acquired using the same needle hydrophone as mentioned above at low pressure (i.e., < 2 MPa) over a range of ±5 mm (0.25-mm step size) centered the peak location for each method. The focal volume V was defined as the product of the full width at half-maximum (FWHM) identified on 3 axes on the pressure field maps with ellipsoidal approximation, i.e., V = FWHM_x · FWHM_y · FWHM_z · π/6.

3. Results

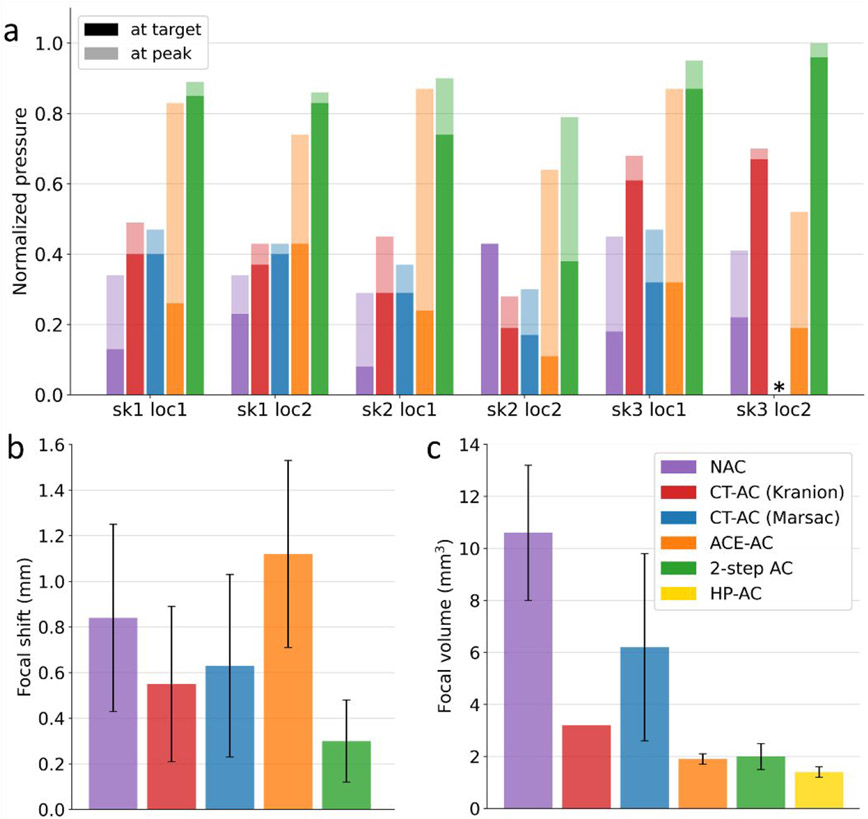
Fig. 5 and Table 2 show the metric measurements for various aberration correction methods. All pressure measurements were normalized to the HP-AC method. All the correction methods except HP-AC yielded a spatial shift in the location of peak pressure, therefore, results were recorded for both the geometric focus and the observed spatial peak.

Figure 5.

Quantitative metrics used to evaluate the phase correction methods. Corresponding numerical data are presented in Supplementary Tables. (a) Pressure at the geometric focus and the spatial peak location normalized to HP-AC for all 6 experiments. Two pressure measurements for each method in each experiment are stacked together. Bars with opaque colors represent pressures at the geometric focus; bars with transparent colors represent pressures at the peak location. The experiment with skull 1 at the first location is noted as “sk1 loc1”. Two pressure measurements for each method in each experiment are stacked together. The pressures from HP-AC are not displayed as they are 1 after normalization for all cases. *Results from Marsac ray-tracing were not acquired for skull#3 at the second location. (b) Spatial peak focal shift. (c) Focal volume. **Only one data point was available for calculating focal volume from Kranion ray-tracing, so the error bar is not presented for this case.

Table 2.

Summary of results (mean ± standard deviation) for the metrics used to evaluate AC methods.

	N-AC	CT-AC (Kranion)	CT-AC (Marsac)	ACE-AC	2-step AC	HP-AC
Normalized target pressure	0.21±0.11	0.42±0.17	0.32±0.08	0.26±0.10	0.77±0.19	1.00±0.00
Normalized peak pressure	0.38±0.06	0.51±0.15	0.41±0.07	0.75±0.13	0.90±0.07	1.00±0.00
Focal shift (mm)	0.84±0.41	0.55±0.34	0.63±0.40	1.12±0.41	0.30±0.18	0.00±0.00
Focal volume (mm3)	10.6±2.6	3.2±0.0	6.2±3.6	1.9±0.2	2.0±0.5	1.4±0.2

3.1. CT-AC

As summarized in Table 2, the CT-based aberration correction using either Kranion or the backward ray-tracing modestly increased the peak pressure location at or near the geometric focus. At the geometric focus, CT-AC provided normalized pressures of 0.42±0.17 and 0.32±0.08 compared to HP-AC using Kranion and the backward ray-tracing models, respectively, whereas at the peak location the two models yielded normalized pressures of 0.51±0.15 and 0.41±0.07 compared to HP-AC respectively. Though the statistical significance of the CT-AC improvements was low when normalized to the hydrophone correction and aggregated, CT-AC yielded pressure recovery for 5 of 6 experiments as shown in Fig.5a.

With no aberration correction, the focal spot was displaced from the geometric focus and defocused into multiple side lobes as shown in Fig.6. CT-AC reduced the mean focal shifts to 0.55 and 0.63 mm using the two ray-tracing models, respectively (Fig.5b). The focal volume was reduced to 3.2 and 6.2 mm³ on average respectively (Fig.5c), with the side lobes prominently suppressed on the transverse plane (x- and y-axis).

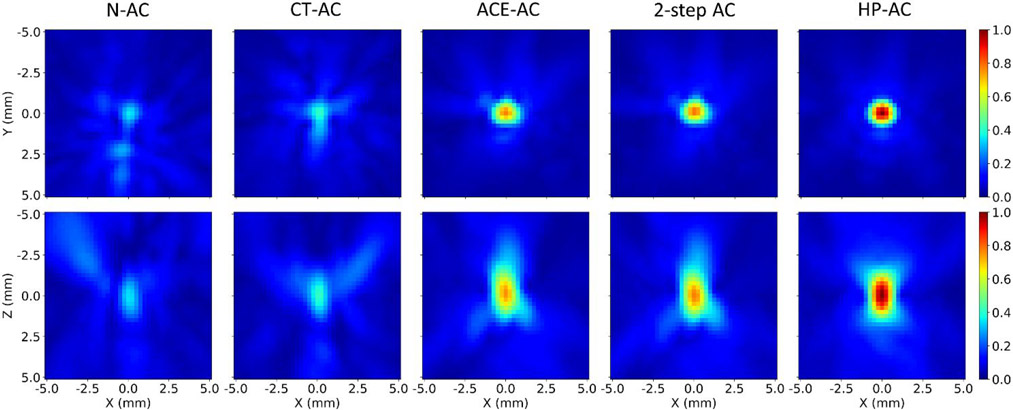
Figure 6.

Pressure field maps centered at the spatial peak location of each correction method for skull#1 at the first location. Top row: pressure field maps in the transverse (x-y) plane. Bottom row: pressure field maps in the coronal (x-z) plane where the z-axis is the beam propagation direction. The pressure amplitudes of all maps were normalized to the amplitude at the geometric focus with HP-AC.

3.2. ACE-AC

ACE-AC yielded a 0.75±0.13 peak pressure normalized to HP-AC and a 0.26±0.10 normalized pressure at the geometric focus. In two experiments (second location for skull#2 and skull#3), the pressure at the geometric focus decreased with ACE-AC compared to N-AC, however, pressure at the corresponding peak location increased significantly. For all 3 skulls, the pressure recovery by ACE-AC was observed to be higher at the first skull location (central) than those at the second location (close to the skull), suggesting that the performance of ACE-AC degraded when the target was located closer to the skull.

The focal shift for ACE-AC was observed to be 1.12±0.41 mm, larger than the shifts for CT-AC but comparable to N-AC (Fig.5b). The peak locations for ACE-AC and N-AC were observed to be very close in each experiment because the cavitation events were most likely to originate at the peak location without correction. The focal shifts did not show any notable difference between the first and second locations for each skull but did vary between skulls. Overall, the focal shifts for different skulls, ranked in descending order, are as follows: skull#2 > skull#3 > skull#1, which correlated well with the variance of time delays from the skulls as shown in Fig.7.

ACE-AC significantly reduced the focal volume to 1.9±0.2 mm³ (Fig. 5c). Pressure field maps (Fig.6) demonstrated smaller focal zone widths and reduced side lobes on all 3 axes for ACE-AC compared to N-AC, suggesting successful refocusing of the pressure field.

3.3. Two-step Aberration Correction

The 2-step method outperformed CT-AC and ACE-AC at both the geometric focus and peak location for all experiments, yielding a normalized peak pressure of 0.90±0.07 and a normalized target pressure of 0.77 ±0.19 compared to HP-AC (Fig.5a). Notably, for the second location of skull#3, 2-step AC achieved identical pressure as HP-AC at the peak location.

The 2-step AC resulted in a focal shift of 0.30 ± 0.18 mm (Fig.5b), successfully reducing the shift compared to N-AC for all experiments except for the second location of skull#2, where 2-step AC produced a focal shift of 0.67 mm whereas no focal shift was observed for N-AC. The focal volume was decreased to 2.0 ± 0.5 mm³ by 2-step AC. This was comparable to the focal volume for ACE-AC as we expected because both methods compute the time delays based on shockwaves from the acoustic cavitation bubbles, which have finite sizes rather than being a perfect “point source” with negligible dimensions.

4. Discussion

In this study, we investigated three methods of phase aberration correction for transcranial histotripsy: CT-AC, ACE-AC, and 2-step AC combining the CT and ACE methods sequentially. For all AC methods, the pressure increases at the peak locations were larger than those at the geometric focus. This was expected because the defocused spot could be biased spatially but still preserve a substantial amount of pressure at the location where the pulses add constructively (i.e., the peak location). Overall, the 2-step AC outperformed CT-AC and ACE-AC, achieving close results compared to HP-AC. This is also supported by the calculated time delays displayed in Fig.7. The 2-step AC successfully captured the spatial variation features and trends in the time delay distributions over the array and produced decent estimates for time delays on most of the transducer elements.

Traditionally, the CT-analytical method relies on stereotactic registration with rigid frames and fiducial markers in position for the preoperative CT. This article demonstrates, to our knowledge, the first CT-analytical aberration correction with acoustic-based co-registration using the echoes from skull surface reflection, without dependence on other equipment. In a clinical environment, such acoustic-based co-registration would allow the CT to be taken well in advance of the intervention for treatment planning purposes.

One limitation of this study is the lack of CT scans with a stereotactic frame as the “ground truth” to analyze the co-registration accuracy using the acoustic-based approach. Nevertheless, the residual error from the ICP algorithm (i.e., the average distance for each pair of points) was observed to be less than 2.5 mm, which can be used as an estimation for the registration accuracy. This was less favorable compared to the accuracy of stereotactic registration which has been reported to be less than 1 mm in literature (Leung et al. 2019; O’Reilly et al. 2016), but on the same order as the acoustic-based skull localization accuracy (1.9 mm/ 2.0°) presented by Calum Crake et al. This suggests that the performance of CT-AC in this paper may have been limited by registration error. With a customized high-frequency array (center frequency of 11 MHz), O’Reilly et al. achieved accuracy on the order of 1 mm/ 1° using a similar approach, suggesting the acoustic-based co-registration described herein can be further improved. Part of the registration bias might be attributable to errors in the estimation of the arrival time t_k. For elements near the cut plane of the skull, scattering from the water surface or the L-bracket attached to the skull sometimes led to an artificially shortened t_k. Some elements were also observed to produce low signal amplitude due to non-normal incident angles on the skull, which resulted in the sound being reflected away to elements that were out of the neighboring subset. Therefore, it may be beneficial to select the elements providing the best fit to the skull surface before evaluating the cost function at each iteration during co-registration. An additional limitation of this study is that only the calvariums without scalp were used. Although the scalp is not expected to affect the CT segmentation given the high contrast between bone and soft tissue, the signal processing algorithm used to identify the skull echo may require modification.

Two ray-tracing models were used in this paper for CT-AC. Theoretically, the backward ray-tracer with Marsac mapping should provide better modeling of the wave propagation through the skull as compared to Kranion, because it was designed to compensate for not only the path length difference in the skull but also in water with optimal focusing on the target. In addition, it also enabled assigning different skull sound speeds for individual elements using the acoustic parameters derived from HU in CT data for each skull, whereas Kranion (at the time this study was performed) applied only a user-defined average sound speed on all elements uniformly. However, overall, the results did not exhibit any notable difference between the two ray-tracing methods. The performance of these two models seemed to vary case-by-case depending on which skull was used. This might be attributed to two reasons. First, the sound speed in cortical bone was manually set to 2300 m/s to calculate the refraction in the backward ray-tracing model, and it was not guaranteed to be the optimal cortical bone speed for every skull. Second, large incident angles (θ_i > 20°), which have been shown to degrade the performance of the ray-tracing models (Bancel et al. 2021), were observed for more than 10% of the elements in all experiments. Shear-wave propagation is known to play a significant role for incident angles higher than 20° at the bone surfaces and can influence the phase aberration (Hayner and Hynynen 2001). Both ray-tracing models tested in this study were based on a fluid model and did not consider the mode conversions at the bone surfaces. Algorithms to find the optimal cortical bone speed for refraction and to compensate for shear-wave propagation inside the skull will be investigated in future studies.

For ACE-AC, cavitation needs to be generated first. Though we expect the intrinsic threshold pressure to be about 26 MPa to generate cavitation in brain tissue using 1-cycle pulses, the acoustic power needed for the transducer may vary for different patients and different focal locations due to the attenuation and aberration. For in vivo implementation, source power could be ramped up until cavitation is observed. This process would avoid uncontrolled cavitation outside the targeted region since the cavitation threshold would only be exceeded slightly.

In this study, the array was able to generate cavitation even without aberration correction for all experiments. However, when the target location is close to the skull, there could be cases for which the maximum power output of the array is not sufficient to create the initial cavitation events without aberration correction. In a clinical environment, applying ACE-AC directly may only be possible in a limited range of locations for a limited selection of patients. In such cases, implementing CT-AC as a first step can recover pressure to enable cavitation generation in the target zone, thus enlarging the spatial range that is viable for ACE-AC and histotripsy treatment.

Even when cavitation can be generated with no aberration correction, the 2-step approach is still advantageous over ACE-AC alone in two aspects. First, ACE-AC resulted in a notable focal shift because cavitation emissions originated from bubbles at the peak location rather than the target location, raising concern for potential off-target damage. It is challenging to estimate this shift before the treatment because the peak location may be biased in different directions depending on the geometry of the skull. Although transcranial cavitation localization using ACE shockwaves could be incorporated to monitor the location of the cavitation events (Sukovich et al. 2020) and correct for the focal shift adaptively, the precision of refocusing would still be limited by the resolution of cavitation localization. For 2-step AC, however, the spatial shift of the focus can be minimized by applying CT-AC first, thus improving the targeting precision. Second, the 2-step AC effectively aggregated the pressure recovery from both CT-AC and ACE-AC, thus yielding higher pressure recovery compared to ACE-AC alone for all experiments in this study. This suggests that 2-step AC may provide larger acoustic headroom and promote treatment efficiency.

In the previous 2-step AC study presented by Gâteau et al., the spectrum of the generated pulse had to be investigated to determine whether a cavitation event was induced with limited receiving capability on the transducers. Besides, due to the complex dynamics of the microbubbles, it also remained unknown whether the recorded signal comes from the expansion or the collapse of the bubble, or acoustic scattering off the bubble. In this study, the shockwaves from the cavitation nucleation and collapse can be resolved accurately and independently in the time domain thanks to the histotripsy array with full transmit-and-receive capability. As we have observed during the experiments, the expansion shockwave signals often spanned several microseconds in duration because each bubble in the cloud emits its own shockwave upon nucleation. However, the collapse of a cloud appears to produce only a small number and frequently only one shockwave, thus the collapse shockwave signals were generally singular and compact regardless of the cloud initial size. The difference in the behaviors of expansion versus collapse shockwaves and the robustness of using collapse signal for AC are currently under investigation and will be addressed in different papers.

Though this study only presented the feasibility and performance of aberration correction at a single focus, aberration correction with electronic focal steering is possible. The efficacy and efficiency of a 2-step correction with electronic focal steering for transcranial histotripsy should be addressed in future studies.

5. Conclusion

This paper presented a 2-step aberration correction method with a CT-based analytical approach as the first step followed by a cavitation-based approach using acoustic emission signals from histotripsy. Compared to CT-AC and ACE-AC individually, the 2-step AC recovered more pressure at both the peak location and the target location and resulted in a smaller focal shift and smaller focal volume, yielding comparable performance to hydrophone aberration correction. These results suggested that 2-step AC has promising potential in improving the precision and efficiency of transcranial histotripsy treatment. It may also enable a larger subset of the patient population to receive treatment and a larger range of cerebral locations that are viable for treatment. These improvements would be relevant and beneficial for all cavitation-based focused ultrasound applications for brain therapy beyond transcranial histotripsy.

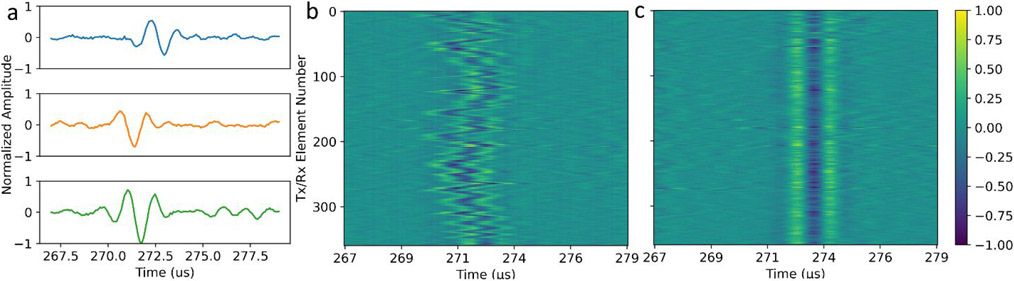
Figure 4.

ACE shockwave waveforms after the two-firing subtraction. (a) Examples of received signals from one cavitation collapse on three different elements (blue: Element 32; orange: Element 154; green: Element 272) normalized to the largest amplitude channel (Element 272). (b) Unaligned waveforms from one cavitation collapse on all channels showing a pattern of phase aberration through the calvarium. (c) Re-aligned waveforms based on cross-correlation peaks.