The annotation and analysis of complex 3D plant organs using 3DCoordX

Abstract

A fundamental question in biology concerns how molecular and cellular processes become integrated during morphogenesis. In plants, characterization of 3D digital representations of organs at single-cell resolution represents a promising approach to addressing this problem. A major challenge is to provide organ-centric spatial context to cells of an organ. We developed several general rules for the annotation of cell position and embodied them in 3DCoordX, a user-interactive computer toolbox implemented in the open-source software MorphoGraphX. 3DCoordX enables rapid spatial annotation of cells even in highly curved biological shapes. Using 3DCoordX, we analyzed cellular growth patterns in organs of several species. For example, the data indicated the presence of a basal cell proliferation zone in the ovule primordium of Arabidopsis (Arabidopsis thaliana). Proof-of-concept analyses suggested a preferential increase in cell length associated with neck elongation in the archegonium of Marchantia (Marchantia polymorpha) and variations in cell volume linked to central morphogenetic features of a trap of the carnivorous plant Utricularia (Utricularia gibba). Our work demonstrates the broad applicability of the developed strategies as they provide organ-centric spatial context to cellular features in plant organs of diverse shape complexity.

Spatial context is essential to draw biological insight from 3D image data, and 3DCoordX is an intuitive, open-source computational tool that provides this context for plant organs with complex shapes.

Introduction

It remains a salient challenge to understand the generation of biological shape. Gaining comprehensive insight into the multi-scale processes underlying morphogenesis critically depends on the quantitative description of molecular, cellular, and tissue-level parameters, such as gene and protein expression, cell geometry, and cell topology

(Boutros et al., 2015; Hong et al., 2018; Jackson et al., 2019; Kierzkowski et al., 2019; Kierzkowski and Routier-Kierzkowska, 2019; Sapala et al., 2019). Moreover, as prominently proposed by D’Arcy Thompson, the generation of shape can be achieved by growth that is oriented relative to a coordinate system imposed on the organ (Thompson, 1942). Thus, insight into tissue morphogenesis further relies on putting cellular data into context by placing them within an organ-related frame of reference (Hejnowicz, 1984; Schmidt et al., 2014; Montenegro-Johnson et al., 2015; Strauss et al., 2021 (preprint)).

Realistic 3D digital organs with cellular resolution have become indispensable tools for the study of morphogenesis. They can be obtained by deep imaging of fluorescently marked specimens using for example confocal laser scanning microscopy or light sheet fluorescence microscopy followed by 3D cell segmentation of the obtained z-stacks of optical sections with the help of constantly improving software (Fernandez et al., 2010; Lowekamp et al., 2013; Barbier de Reuille et al., 2015; Stegmaier et al., 2016; Eschweiler et al., 2019; Wolny et al., 2020; Strauss et al., 2021 (preprint)). Tissues and organs of model plants are particularly well suited for the generation of such 3D digital representations. Plant cells are immobile simplifying the detection of cellular growth patterns associated with tissue formation. In addition, plant tissues are characterized by a small number of different cell types and often exhibit a well-structured, layered organization. Thus, they usually feature a cellular anatomy of manageable complexity. Accordingly, a growing number of realistic 3D digital tissues with cellular resolution are being generated, mainly in the model plant Arabidopsis (Arabidopsis thaliana; Bassel et al., 2014; Schmidt et al., 2014; Yoshida et al., 2014; Montenegro-Johnson et al., 2015, 2019; Lora et al., 2017; Pasternak et al., 2017; Fridman et al., 2021; Graeff et al., 2021; Hernandez-Lagana et al., 2021; Refahi et al., 2021; Vijayan et al., 2021; Silveira et al., 2022).

With the help of 3D digital organs quantitative information about geometric and molecular parameters of up to thousands of cells can readily be obtained using open-source software, such as MorphoGraphX (Barbier de Reuille et al., 2015; Strauss et al., 2021 (preprint)). However, meaningful exploration of such complex data sets remains challenging. In particular, it is important to provide spatial context by placing the cell’s data within an organ-related frame of reference (Hejnowicz, 1984). Several computational pipelines have been established that provide such a tissue-level frame of reference and allow the semi-automatic annotation of 3D cellular properties in a plant tissue context with cellular resolution: iRoCS (Schmidt et al., 2014), 3DCellAtlas (Montenegro-Johnson et al., 2015), and 3DCellAtlas Meristem (Montenegro-Johnson et al., 2019). These computational pipelines have been applied very successfully for the annotation of cells and tissues in the main root and the hypocotyl, radially symmetric organs with limited curvature, or the shoot apical meristem (SAM), a dome-shaped structure exhibiting an anatomy of moderate complexity. However, not all plant organs fall into these simple morphogenetic categories. For example, strong curvature caused by developmentally regulated differential growth limits the usefulness of the implemented analytical strategies in iRoCS and 3DCellAtlas, particularly for indexing the axial position of a cell and determining its absolute distance to a reference. Yet, curvature represents a central element of the morphogenesis of plant organs with complex 3D shapes (Whitewoods and Coen, 2017). Many plant organs exhibit varying degrees of curvature, for example, the apical hook of seedlings, leaves, or floral organs, such as sepals or petals. The ovule, the major female reproductive organ in seed plants, constitutes a particularly prominent example. Ovules are characterized by complex anatomy consisting of a central “trunk,” made up of several functionally distinct tissues stacked on top of each other, and by one or two laterally attached integuments, determinate planar tissues that eventually develop into the seed coat (Bouman, 1984). Moreover, most angiosperm ovules exhibit an extreme curvature due to asymmetric growth of the integuments (Endress, 2011).

Here, we developed generic strategies that allow the straightforward establishment of intrinsic coordinate systems in organs of simple or elaborate shape. We implemented those strategies in 3DCoordX, a module of MorphoGraphX. In 3DCoordX the annotation of cell position is guided by intrinsic, tissue-specific developmental axes. To work out the formal strategies we took advantage of a recently generated digital 3D reference atlas of ovule development in Arabidopsis (Vijayan et al., 2021). We illustrate how such a coordinate system enables rapid annotation of cell identity and cell position in 3D and greatly facilitates the quantitative analysis of cellular features. We applied our strategies to an investigation of cell proliferation patterns in the ovule primordium and the cellular basis of differential integument growth. Finally, we demonstrate the broad applicability of the introduced concepts by providing proof-of-concept analysis for selected parameters in different plant organs of varying shape complexity.

Results

Curvature-related complications in the assignment of axial position

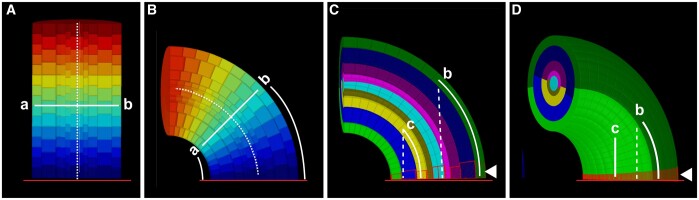
The analytical strategies for the positional annotation of individual cells relative to tissue organization depend on the structure under study. For example, the straightforward approaches employed in iRoCS and 3DCellAtlas involve cylinder coordinates and work very well for indexing axial position of cells relative to a reference in the root or hypocotyl, structures exhibiting limited curvature (Figure 1A). However, asymmetric growth caused by differential cell proliferation and/or cell expansion can result in slanted or highly curved organs. In these instances, such approaches may lead to cells of the same indexed position having different absolute axial distances to a common reference (Figure 1B). Thus, we devised a different strategy to minimize such axial distance errors when assigning 3D positional annotation to cells of organs that exhibit complex shapes. Our approach takes cues from central patterning events that frequently occur during early plant organogenesis, in particular the distinction of radial layers, the subdivision into anterior–posterior domains, and the establishment of a proximal–distal (axial) distance field (Figure 1, C and D). The proximal–distal distance of a cell relative to a user-defined reference is estimated by finding the shortest path through the cell centroids. Importantly, the search is confined to a given tissue layer and may not cross the anterior–posterior domain. The restriction to a tissue layer removes a large part of the axial distance error as the shortest path through the tissue layers cannot extend through interior tissues (Figure 1C). On top of this restriction, prohibiting the shortest path from passing the anterior–posterior boundary further minimizes the error (Figure 1D).

Figure 1.

Axial cell distance determination in curved tissue. A, Section through an artificial template of a tube-like and straight tissue consisting of multiple concentric cell layers. The heatmap indicates distance from the reference (line at bottom). The dashed line outlines the central axis. Note that the two cells (a and b) at the same cell index position also show the same absolute axial distance to the origin (B) Same structure as in (A) but curved. Note that cells a and b differ in their axial distances to the reference. C, Same structure as in (B). The separate cell layers are distinguished by their different colors. Two cells in different layers are highlighted (c and b). Dashed lines indicate shortest distances to the reference ignoring tissue layers. Solid lines mark the shortest distances to the reference that are restricted to tissue layers. Confining the shortest distance to a given layer reduces axial distance errors. The line at the bottom highlights the reference. The arrowhead marks origin cells. Origin cells exhibit a close distance in 3D to the reference (5–15 µm). D, 3D representation of (C) revealing how the anterior–posterior boundary further minimizes the axial distance error for a cell in the posterior half of the structure.

Developmental axes of the ovule

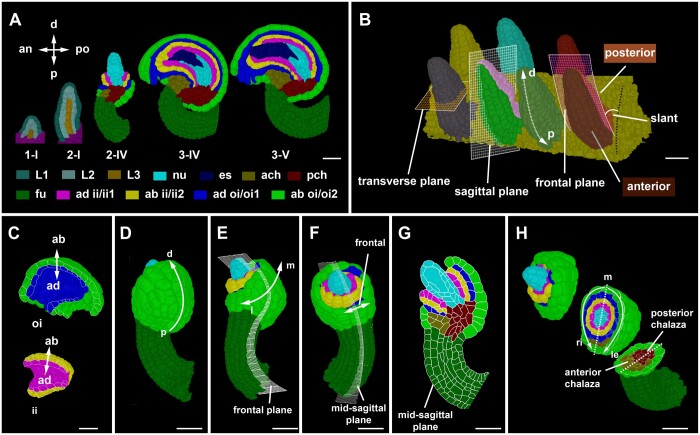
The need to assign spatial context to cellular features was sparked by our interest in the cellular basis of ovule development in Arabidopsis, an elaborately curved structure (Figure 2A; Supplemental Figure S1; Supplemental Text S1). Moreover, in order to orient a 3D coordinate system along internal patterning processes our design of 3DCoordX was guided by intrinsic developmental axes of the developing ovule. Ovule development in Arabidopsis is well described (Robinson-Beers et al., 1992; Schneitz et al., 1995; Hernandez-Lagana et al., 2021; Vijayan et al., 2021; Supplemental Figure S1; staging according to Schneitz et al. (1995) and Vijayan et al. (2021). Here, we shortly summarize the different developmental axes that become apparent during its complex development (Figure 2).

Figure 2.

Developmental axes in ovule development. A, Mid-sagittal sections through 3D digital ovules of representative stages. The individual images were digitally extracted for comparison. The different tissues are indicated as are the anterior–posterior and proximal–distal axes, respectively. Staging according to Schneitz et al. (1995) and Vijayan et al. (2021). B, 3D rendering of a placenta area carrying seven wild-type Stage 2-I ovules. The anterior–posterior and proximal–distal axes are marked. The sagittal, transverse, and frontal planes are marked by grids on the primordia. The frontal plane separates the anterior and posterior halves of the organ. The sagittal plane separates the left and right half of the organ. The dashed white arrow indicates the proximal–distal axis. Anterior and posterior side of the organ is highlighted with different colors in two of the representative ovules showing the sagittal and the frontal grid. Black dotted line indicates the placental surface to which the posterior side of the ovule is slanted with a small angle. C, Outer and inner integument tissues extracted from the 3D mesh for visualizing the abaxial–adaxial polarity. Tilted view of mid-sagittal sections through the outer and inner integument, respectively, of a Stage 3-IV 3D digital ovule. The arrows highlight the adaxial–abaxial axes of each integument. D–H, Visualization of different tissues in a Stage 2-V Arabidopsis ovules at different orientations of the organ. D, Posterior view of the ovule with the proximal–distal axis of the outer integument marked. E, Side view (left) and anterior view (right). Grid represents the frontal plane. The medio-lateral axis is indicated. F, Anterior view of the ovule visualizing the frontal region. The grid represents the mid-sagittal plane. G, A mid-sagittal section view of the ovule in (F) visualizing the maximal proximal–distal extension of the integuments. H, A 3D clipped view of the 3D digital ovule is displayed. It is oriented with the posterior side to the right. The 3D view allows the discrimination of the left-right sides of the 3D digital ovule. The dashed line indicates the medial line. an, anterior; ab, abaxial; ad, adaxial; ach, anterior chalaza; ch, chalaza; d, distal; ii, inner integument; es, embryo sac; fu, funiculus; l, lateral; le, left; m, medial; nu, nucellus; oi, outer integument; p, proximal; pch, posterior chalaza; po, posterior; ri, right. Scale bars: 20 µm.

The ovule primordium exhibits the typical radial organization into the L1, L2, and L3 cell layers (Satina et al., 1940; Jenik and Irish, 2000; Figure 2A). In addition, the distal nucellus, central chalaza, and proximal funiculus represent three proximal–distal pattern elements along the trunk of the developing ovule. Gene expression patterns underlying the proximal–distal organization of the primordium are relatively well understood (Reiser et al., 1995; Gross-Hardt et al., 2002; Vijayan et al., 2021). The anterior–posterior axis is initially characterized by a primordial slant relative to the placenta surface, with the small angle of the slant facing the septum (Figure 2B). The anterior–posterior axis persists in the main trunk in later stages as indicated by the organization of the embryo sac, the posterior initiation of the outer integument, the placement of the phloem in the funiculus, and the overall curvature (Vijayan et al., 2021). The anterior–posterior axis is further supported by differential expression of genes, such as the class III HD-ZIP gene PHABULOSA (Sieber et al., 2004) or the KANADI family member KAN1 (Supplemental Figure S2). The two integuments are characterized by their own intrinsic developmental axes (Figure 2, C–H). A distinct adaxial–abaxial (dorso-ventral) axis is prominent as the individual cell layers of each integument differ in cellular morphology and gene expression patterns (Schneitz et al., 1995; Villanueva et al., 1999; Sieber et al., 2004; McAbee et al., 2006; Kelley et al., 2009; Figure 2C). Both integuments also feature their own proximal–distal axes (Figure 2D;Supplemental Figure S1). Related to its hood-like shape the outer integument flanks a frontal section and features a medio-lateral axis (Figure 2, E and F). As a rule, we position the ovule with the anterior domain and the micropyle pointing to the left and the proximal end of the funiculus pointing toward the bottom right. Based on this arrangement we define the left and right lateral sides of the medio-lateral axis (Figure 2H).

Primordium: cell layer detection, individual organ separation, and anterior–posterior domain annotation in 3D

The annotation of cell position in 3D in the slanted ovule primordium required the application of the general principles outlined above. To be able to do so in a fast and robust manner we devised a method for radial tissue labeling. Current pipelines, such as 3DCellAtlas and 3DCellAtlas Meristem, invoke a surface mesh as a central tool for cell and tissue annotation in the root, hypocotyl, and the SAM (Montenegro-Johnson et al., 2015, 2019). However, establishing a surface mesh does not work well in situations where organs are in close contact with each other as is often the case for young ovule primordia attached to the placenta (Figure 3A). The resulting individual surface meshes fail to outline the surfaces of the cells in contact and it is labor intensive to recreate a surface mesh in such instances.

Figure 3.

Ovule primordium tissue detection and coordinate system. A, 3D segmented cell mesh view of a pistil fragment with four ovules of late Stage 2-I. B–D, Layer detection using the outside wall area ratio. B, Zoomed view of a sagittal section displaying the heatmap of outside wall area ratio. Threshold selection of outer surface cells based on the heatmap of outside wall area ratio. C, Heatmap indicates cell index, the number of cells an individual cell is separated from the selected outer surface cells marked in red. D, Heatmaps of cell distances in (C) were converted to integer values representing the tissue identity labels L1, L2, and L3. E, Same method applied to the entire 3D mesh shown in (A). F, 3D Mesh view of the specimens shown in (A) with the distal most cell selected for organ separation. G, Colors on individual ovule primordia represent the results of organ separation after selecting the distal most cell and clustering the cell connectivity network. Result of the combination of L1, L2, and L3 label and organ separated labels annotated for the ovules shown in (A). H, Transverse section of (G) displaying the L1, L2, and L3 labels for different ovules in different colors. I–J, Anterior (an) and posterior (po) labels added to the tissue-annotated ovule primordia 3D cell meshes. I, Surface view. J, Mid-sagittal section. K–L, Heatmap of distance coordinates from the point-like origin at the distal end of the organ (white arrow). Heat values indicate the distance in micrometer from individual cells centroid to the Bezier ring (indicated by white arrow) of the coordinates in a tissue restricted manner. K, 3D view. L, Sagittal section view. M and N, Heatmap of cell number coordinates instead of distance coordinates as in (K and L). Heat values indicate how many cells apart is a cell of interest from the origin of the coordinates through tissue-restricted manner. M, 3D view. N, Sagittal section view. Scale bars: 20 µm.

To address this problem, we developed a strategy to perform automatic layer detection that groups cells into L1, L2, and L3 without a need for a surface mesh (Figure 3, A–D). In a first step L1, cells are clustered on the basis of a cell at the outer surface of the organ not being flanked by a neighboring cell at their outer surface. This feature is captured by defining the ratio of unshared wall area to shared wall area of individual cells (outside wall area ratio). Once L1 cells are clustered, L2 and L3 cells are found by their relative distances to the L1 cells. To this end, a network of cell centroids is established and the shortest number of centroids a cell must cross to reach to the nearest L1 cell is determined. The corresponding result essentially reveals how many cells separate the cell of interest from the L1. The information can be directly used to cluster cells into L2 and L3 as L2 cells are direct neighbors of L1 cells and L3 cells are separated from the L1 by more than one cell. The strategy does not completely solve the issue when surface cells of neighboring organs are in full contact. However, the process works well when there is partial contact that still leaves behind a substantial outside unshared cell wall area. This approach successfully annotated the radial tissue layers in ovule primordia of all stages. As examples, cell layer detection is shown for Stage 2-I ovule primordia (Figure 3, A–D) and the SAM (Supplemental Figure S3).

Another problem relates to the separation of the multiple ovule primordia attached to the placenta into distinct units to allow ovule-specific analyses. We devised a method that takes advantage of the cell connectivity graph (Figure 3, F–H). From a selected cell at the distal end on each different ovule, distances to all other cells on the cell connectivity graph are computed. Cells are then assigned a label based on their nearest selected cell on that graph. A further parameter sets a maximum size of the ovules (in number of cells from the selected cells) to separate the ovules from their surrounding tissue. To facilitate downstream analysis, different labeling types, such as the cell layers and the ovule labels, are combined to create a unique label for each layer in every ovule.

In the last step, cells of anterior and posterior domains of similar dimensions are obtained by manual selection (Figure 3, I and J). For the funiculus we also devised a semi-automatic method to distinguish the anterior and posterior domains (Supplemental Figure S4). In summary, the outlined approaches enable the generation of 3D digital ovule primordia of separate identities and near-perfect radial and anterior–posterior tissue annotation with minimal user input.

Primordium: assignment of proximal–distal position to individual cells in 3D

To determine the proximal–distal (axial) position of an ovule primordium cell we generated a method that applies to 3D digital ovules for which radial cell layers and the anterior–posterior domains have already been annotated. The proximal–distal position of each cell is calculated, either in terms of cell index or absolute or relative distance to a reference, in a two-step procedure (Figure 3, K–N). In the first step, a Bezier ring (a mathematically defined curved line) will serve as reference for the proximal–distal distance field and is placed at one end of the tissue. In the case of the cone-shaped ovule primordium a small, near point-size Bezier ring is positioned at the distal tip of the primordium. Positioning the Bezier ring at the distal tip corresponds to a biologically relevant maximum of the phytohormone auxin at the tip as inferred from the expression of the auxin response reporter pDR5::GFP (Benková et al., 2003), the spatial signal of the auxin sensor R2D2 (ratiometric version of two DIIs; Liao et al., 2015; Kawamoto et al., 2020), and the finding that polar auxin transport mediated by PINFORMED1 is required for ovule primordium formation (Bencivenga et al., 2012; Galbiati et al., 2013). In case of the mature funiculus that is close in shape to a curved cylinder, a larger Bezier ring is placed at its proximal end. Origin cells are then defined by their close distance in 3D (usually 5–15 µm) to the user-specified Bezier ring (Figure 1, C and D). They act as seeds for the distance coordinates of the remaining cells of the tissue that are obtained by searching for the shortest path through the cell centroids to the centroid of an origin cell. The search is restricted to a radial layer and by the anterior–posterior boundary. It should be noted that with this approach small axial distance errors still occur within the anterior or posterior domains depending on the number of laterally arranged cell files within these areas. The remaining errors are typically in the range of a few microns, but can be eliminated when taking individual cell files into account. This is possible within the software, however, the procedure involves cumbersome manual annotation of all cell files for each cell layer. Moreover, the gain of resolution is minimal.

A coordinate system for integuments

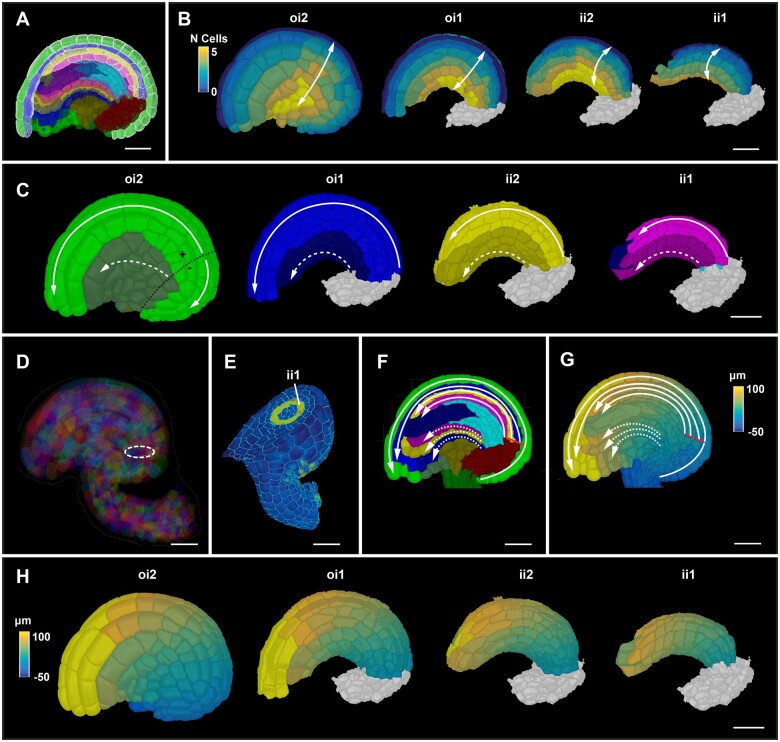
We successfully applied to the integuments some of the same formal strategies as described for the primordium or funiculus. In an initial step, the integumentary adaxial–abaxial cell layers are labeled manually. In a subsequent step, medio-lateral coordinates of all cells of a given integument layer are established relative to a file of posterior midline cells (Figure 4A). Cell distance is computed in terms of how many cells separate a given cell from the midline (Figure 4B). Cells along the medio-lateral axis can be grouped further into median and lateral subdomains that occupy about half the width of an integument layer. For example, for the outer layer of the outer integument we grouped cells that are located three cells to the left or right of the posterior midline cells into the median domain. The remaining cells are classified as lateral cells (Figure 4C). In the following step, proximal–distal distance coordinates are assigned for all integument cells. A Bezier ring is first placed at the proximal end of the inner side of the outer integument (next to its inner layer) facing the outer layer of the inner integument (Figure 4D). The circular origin is in the same plane as the ring-shaped expression pattern of a reporter for CUP-SHAPED COTYLEDON3 (pCUC3::CFP) which marks the proximal base of the two innermost layers of the inner integument, respectively (Figure 4E). Members of the CUC gene family are generally required for primordium initiation and organ boundary formation (Aida et al., 1997; Ishida et al., 2000; Takada et al., 2001; Breuil-Broyer et al., 2004; Sieber et al., 2007; Galbiati et al., 2013; Gonçalves et al., 2015). Origin cells are then defined by their close user-specified distance to the Bezier ring in 3D (∼5–15 µm). As a direct result of the placement of the Bezier ring, cells of the outer layer of the outer integument that are in direct contact with the subepidermal proximal chalaza are assigned a negative value for the proximal–distal position (Figure 4, F and G). This feature can be used to separately cluster and analyze those cells. Finally, proximal–distal distance coordinates of the integument cells are obtained by searching for the shortest path through the cell centroids to the centroid of an origin cell (Figure 4, F–H). The search is again restricted to a given tissue layer and may not cross the medio-lateral boundary. Taken together, the procedure assigns medio-lateral and proximal–distal positions for all cells of the integuments.

Figure 4.

Integument coordinate system. A, Mid-sagittal section highlighting the selected medial cells on the posterior side of the four layers of integument tissues for medio-lateral coordinate annotation. Colors represent tissue annotations similar to Figure 1B. A Stage 3-IV ovule is shown as an example. B, Heatmap of medio-lateral cell coordinates. Heat values indicate the lateral position in terms of the number of cells from the median file of cells. Different integument tissues are digitally extracted from the 3D mesh to display the medio-lateral coordinates at their respective tissue surfaces. C, 3D surface view of integument tissues similar to (B). Medial and lateral cells are distinguished. Solid line represents the tissue restricted coordinate direction along the medial group of cells. Dashed line represents the tissue restricted coordinate direction along the lateral group of cells. Black dotted line on oi2 represents the coordinate origin projected on the surface which separates the proximal oi2 cells with negative coordinate values (D) semi-transparent view of a mature 3D ovule displaying the coordinate origin as a ring inside the organ. E, 3D clipping view of a transverse section of an ovule highlighting the ring-like expression of the pCUC3::CFP reporter in yellow. F, Sagittal section of a mature ovule displaying the coordinate directions of the medial and lateral group of cells in solid and white lines, respectively. Solid red line indicates the origin of the coordinate system. G, Sagittal section as in (F) displaying the heatmap of distance coordinates. Solid red line indicates the origin of the coordinate system. H, 3D surface view of integument tissues similar to (B) displaying the distance coordinates at the surface of internal tissues. ii1, inner layer of inner integument; ii2, outer layer of inner integument; oi1, inner layer of outer integument; oi2, outer layer of outer integument. Scale bars: 20 µm.

Differential distribution of cellular growth patterns during early ovule development

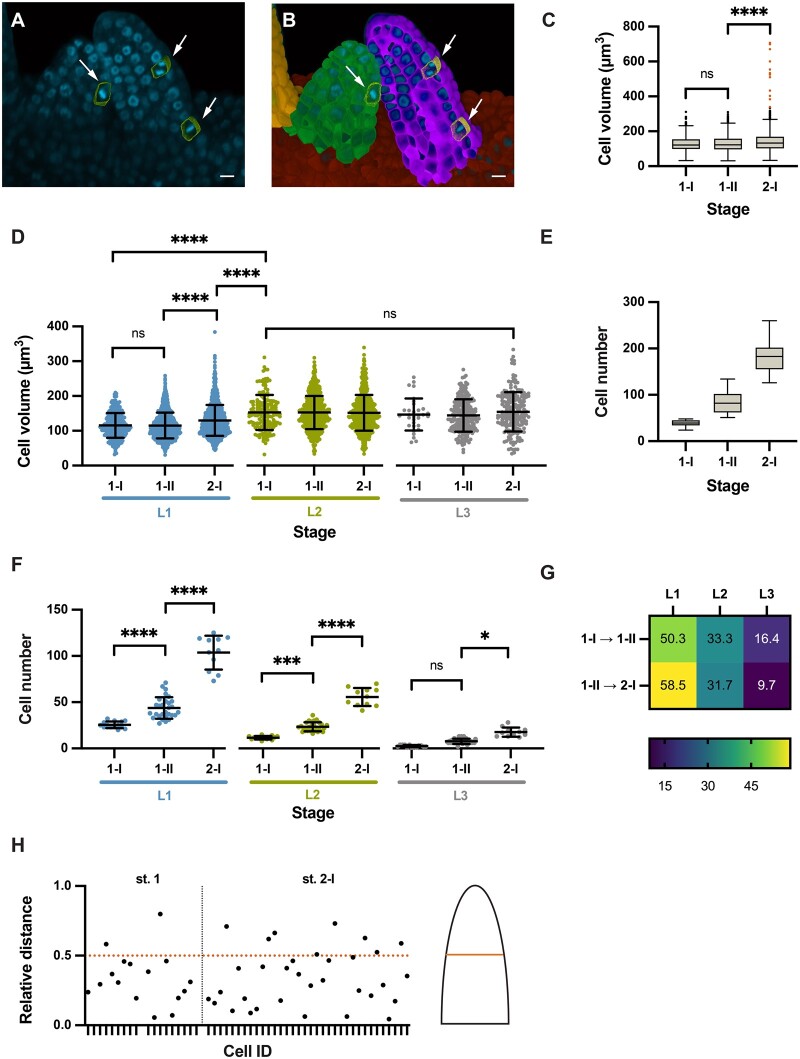
To provide proof of concept for the usefulness of our computational tools in the quantitative analysis of cellular patterns in a 3D context we assessed spatial growth patterns in selected aspects of ovule development. To this end, we made use of a previously published dataset of wild-type 3D digital ovules of the Col-0 accession (Vijayan et al., 2021). We first focused on primordium outgrowth. It was previously shown that ovule primordia grow in a continuous fashion based on an analysis of the total number of cells and the increase of organ volume from Stages 1-I to 2-I (Hernandez-Lagana et al., 2021; Vijayan et al., 2021). However, it remained unclear how cell numbers and cell volumes of the radial layers compare to each other. In addition, it was not known if mitoses are randomly distributed along the proximal–distal axis or if they preferentially occur in specific domains. To address these questions, we analyzed 53 3D digital wild-type ovule primordia that encompassed Stages 1-I to 2-I (Figure 5, A and B).

Figure 5.

Cellular growth patterns in the ovule primordium. Different stages of wild-type (Col-0) ovule primordia are analyzed. A, 3D frontal plane view of ovule primordia displaying the To-PRO-3 nuclear stain. Cells undergoing mitosis are outlined and marked by arrows. B, Same section in (A) with an overlay of 3D labeled meshes. Arrows indicate mitotic figures (C) Comparison of cell volumes. Box and whiskers plots are shown. Number of cells scored: Stage 1-I: n = 554, Stage 1-II: n = 2071, Stage 2-I: n = 1957. D, Comparison of cell volume between radial layers of different stages. Number of cells scored: Stage 1-I: n = 554, Stage 1-II: n = 2071, Stage 2-I: n = 1946. E, Comparison of cell numbers. Box and whiskers plots are shown. Number of ovules scored: Stage 1-I: n = 23, Stage 1-II: n = 66, Stage 2-I: n = 49. Dataset of 138 ovules as described in Vijayan et al. (2021). F, Comparison of cell numbers between radial layers of different stages. Number of ovules scored: Stage 1-I: n = 14, Stage 1-II: n = 28, Stage 2-I: n = 11. G, Heatmap of percentage increase in number of cells per tissue compared to overall increase in number of cells. H, Plot showing the relative distance along the proximal–distal axis of mitotic cells in a primordium. Relative distance was calculated by the following formula: reldist = 1−distance coordinate/mean length. Total number of ovules scored: 53. Total number of ovules containing at least one mitotic cell: 26. Total number of mitotic cells: 52. Ovules covered Stages 1-I to 2-I. Statistics: (C and E) Box and whiskers plots: the box extends from the 25th to the 75th percentiles. The horizontal line in the box is plotted at the median. Whiskers extend to 1.5× the interquartile range from the 25 or 75 percentile, respectively (Tukey). Data points lying outside of the range indicated by the box and whiskers are represented as individual dots. D and F, Data are mean ± sd. Significances: ****P < 0.0001; ***P < 0.0004; *P < 0.02. Ordinary one-way ANOVA followed by Tukey’s multiple comparison test. Scale bars: 20 µm.

We initially undertook a comparison of cell volumes between stages (Figure 5C) and radial layers (Figure 5D; Table 1). In this dataset, the L2-derived megaspore mother cells (MMCs) at Stage 2-I feature an average cell volume of 543.3 ± 120.6 µm³ (mean ± sd) with a minimal volume of 335 µm³ (Vijayan et al., 2021). Thus, the volume of the MMCs is beyond the largest cell volumes observed for other cells (Figure 5C). We therefore eliminated the MMCs from this analysis to eliminate skewing of the results due to their out-of-range size. We observed that the average volume of L1 cells slightly increased during development while the average volume of L2/L3 cells stayed about constant (Figure 5D;Table 1). The results further indicated that with the exception of the MMCs the L2 and L3 feature cells of about similar cell volumes while the L1 is composed of smaller cells.

Table 1.

Layer-specific cellular growth characteristics in the ovule primordium

Cell Layer	Stagea
	I-I			1-II			2-I
	Cell number	Cell volumeb	Percentage mitotic cellsc	Cell number	Cell volumeb	Percentage mitotic cellsc	Cell number	Cell volumeb	Percentage mitotic cellsc
L1	25.6 ± 3.7	115.6 ± 35.7	2.46	43.8 ± 11.6	115.2 ± 36.8	1.70	103.6 ± 18.4	129.9 ± 44.5	1.84
L2	11.6 ± 1.9	152.8 ± 50.3	1.41	23.4 ± 4.9	152.7 ± 47.6	2.47	55.6 ± 9.7	158.5 ± 74.2	1.96
L3	2.5 ± 1.2	146.8 ± 45.9	0	7.7 ± 2.8	144.1 ± 46.6	0	17.6 ± 5.0	154.7 ± 56.5	0.52

^a Number of 3D digital ovules scored: 14 (Stage 1-I), 28 (Stage 1-II), 11 (Stage 2-I).

^b Volumes are given in cubic micrometer.

^c Number of observed mitotic cells: Stages 1-I: 7 (L1), 2 (L2), 0 (L3), number of ovules with at least one mitotic cell: 9; Stages 1-II 5 (L1), 4 (L2), 0 (L3), number of ovules with at least one mitotic cell: 6; Stages 2-I: 21 (L1), 12 (L2), 1 (L3), number of ovules with at least one mitotic cell: 11. Percentage was calculated using the average cell number per layer and stage of only the ovules that showed at least one mitotic cell. Values represent mean ± sd.

We then compared cell numbers between stages (Figure 5E) and radial layers (Figure 5F;Table 1). Overall, we observed a steady increase in cell numbers during primordium outgrowth (Figure 5E). The L1 covers a larger surface of the primordium than the L2 or L3. Considering this aspect and given the smaller cell volume of L1 cells in comparison to L2/L3 cells, we hypothesized that the L1 consists of more cells than the L2 and L3. This assumption was supported by layer-specific cell counts (Figure 5F;Table 1). We also determined that the L1 showed the largest percentage increase in cell numbers, while the L3 showed the least percentage increase in cell numbers (Figure 5G).

Next, we assessed the spatial distribution of mitoses. To this end we manually labeled cells that exhibit mitotic figures (Figure 5, A and B) (see “Materials and methods”). In our dataset of 53 3D digital ovule primordial, we identified 26 specimens with at least one mitotic cell. Overall, we detected 52 mitotic cells distributed across those 26 specimens. We first asked if there were differences in the number of mitoses between the cell layers. We found 33 mitotic cells in the L1, 18 in the L2, and 1 in the L3. We also calculated the layer-specific fraction of cells in mitosis for Stages 1-I, 1-II, and 2-I (Table 1). For the L1 and L2, the values may point to differential dynamics in cell proliferation between the two layers during primordium formation. The determined mitotic index for the L3 is very likely an underestimate as the number of L3 cells and sampled ovules are small in this proof-of-concept analysis. We then investigated if there was a difference between the number of mitotic cells in the anterior and posterior L1. We found 23 and 10 mitoses in the anterior and posterior L1, respectively, indicating that more cell divisions occur in the anterior L1 domain. Finally, we took advantage of the 3DCoordX coordinates and analyzed the overall distribution of mitotic cells along the proximal–distal axis from Stages 1-I to 2-I. We found that ∼80%–85% of scored mitotic cells were located in the proximal half of the developing primordium (Figure 5H).

Taken together, our data indicate that primordium outgrowth is preferentially driven by an increase in cell number, not cell volume. In addition, they suggest unequal spatial distribution of mitoses between cell layers and along the anterior–posterior and proximal–distal axes. A higher number of mitoses in the anterior domain might explain primordium slanting. The data further indicate that a cell proliferation zone located in the bottom half of the developing primordium contributes substantially to its outgrowth.

Funiculus curvature corresponds to differences in cell number and cell volume along the anterior–posterior and proximal–distal axes

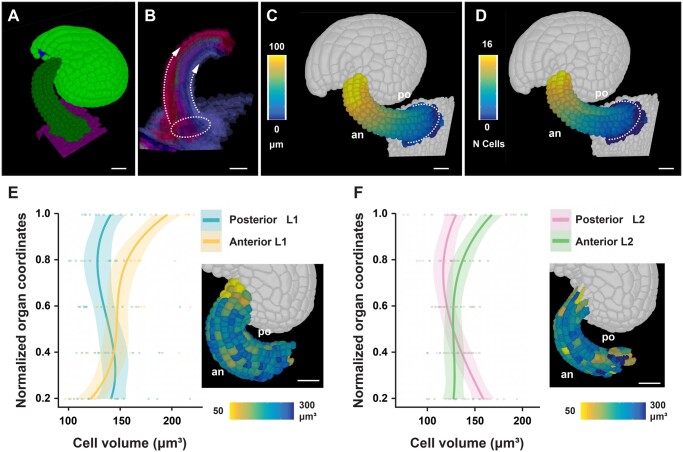
To obtain insight into the cellular processes underlying funiculus curvature, we performed an initial analysis of its cellular characteristics using 14 3D digital ovules of Stage 3-IV (Figure 6, A–F). By this stage growth of the funiculus has ceased (Vijayan et al., 2021). We focused on the L1 and L2 layers. To investigate cellular features of the L2, we digitally removed the L1 from the 3D digital funiculi. First, we assessed the proximal–distal distance and cell number along the L1 midlines of the anterior and posterior domains, respectively (Figure 6, A–F). We observed that the anterior midline was longer and characterized by a higher number of cells in comparison to the posterior midline. To directly compare volumes of anterior and posterior cells we converted the cells’ coordinates into relative proximal–distal positions (Zhang et al., 2020). There we noticed a gradient in the volume of anterior L1 and L2 cells with the distal-most cells featuring nearly 1.5–2 times the volume of cells located at the proximal end (Figure 6, E and F). We did not detect a noticeable volume increase in the posterior cells.

Figure 6.

Cellular features of funiculus curvature. Wild-type (Col-0) ovules of Stage 3-IV are analyzed. A, Tilted side-view of a 3D cell mesh. B, Semi-transparent 3D mesh view of funiculus extracted from the 3D mesh of the organ. The Bezier ring serving as origin is placed at the proximal base of the funiculus. The dashed arrow lines indicate the coordinate direction along the anterior and posterior midlines. C and D, Same specimen as in (A). The anterior (an) and posterior (po) sides are marked. C, Heatmap of cell distances along the proximal–distal axis of the funiculus. D, Heatmap of cell numbers along the proximal–distal axis of the funiculus. White dotted line indicates the coordinate origin as a ring. E, Graph depicting cell volumes of anterior and posterior L1 cells in relation to the normalized proximal–distal position. The inset in the bottom right corner shows a heat map of cell volume in the L1 of the funiculus. Fourteen 3D digital ovules were analyzed. Regression curves are cubic polynomials with 95% confidence intervals (shaded regions). Number of cells: 1,568 ≤ n ≤ 1,768. F, Similar graph as in (E) revealing cell volumes of anterior and posterior L2 cells. Number of cells: 1,175 ≤ n ≤ 1,352. Scale bars: 20 µm.

In summary, our data suggest that a combination of differential cell proliferation along the anterior–posterior axis and unequal cell growth along the proximal–distal axis of the anterior domain contributes to the curvature of the funiculus.

Proximal–distal growth gradient in Arabidopsis integuments

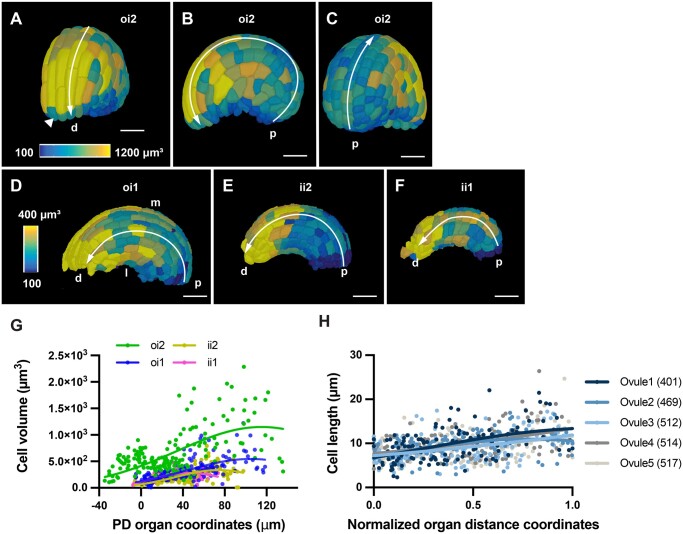
Genetic data indicated that asymmetric growth of the outer integument is instrumental for the anatropous shape of the ovule (Baker et al., 1997; Schneitz et al., 1997; Vijayan et al., 2021). However, the 3D architecture of integument cells in relation to their position within the tissue remained unknown. Thus, to provide proof of concept we undertook a first analysis of the 3D geometry of integument cells in 3D digital ovules of Stage 3-IV. We used 3DCoordX to measure cell volumes of the outer layer of the outer integument along the proximal–distal axis. We found a gradient in cell volume along this axis. We observed that proximal cells exhibited small cell volumes while, with the exception of small cells at the tip of the integument, distal cells were characterized by larger sizes (Figure 7A). Next, we expanded the 3D cellular analysis to all cells of the integuments. In a typical Stage 3-IV 3D digital ovule, we found a proximal–distal gradient of cell volumes in cells of the other layers, but at a smaller scale compared to the outer layer of the outer integument (Figure 7, A–G). We then compared cell length to cell position along the proximal–distal axis in the medial domain of the inner layer of the outer integument across five different specimens. We found that cell length increased along the proximal–distal axis (Figure 7H).

Figure 7.

3D geometry of integument cells. Wild-type (Col-0) ovules of Stage 3-IV are analyzed. A–C, Heatmap of oi2 cell volumes. The proximal–distal axis is indicated. A, Tilted frontal view. The arrowhead marks a small tip cell. B, Side view. C, Tilted back view. D–F, Side views of the same specimen as in (A) showing the 3D surface view of internal tissues. Heatmaps of the oi1, ii2, and ii1 layers, respectively. D, oi1. E, ii2. F, ii1 (C). G, Graph showing cell volume in relation to proximal–distal distance for the four integument layers of a representative ovule. The respective nonlinear Gaussian regression curves are indicated. 95 ≤ n ≤ 172. H, Cell lengths in relation to normalized proximal–distal distance. Cells in the median oi1 layer of five ovules were analyzed. The respective nonlinear Gaussian regression curves are indicated. 126 ≤ n ≤ 133. Note the increase in cell length toward the distal end. d, distal; ii1, inner layer of inner integument; ii2, outer layer of inner integument; l, lateral; m, medial; oi1, inner layer of outer integument; oi2, outer layer of outer integument; p, proximal; PD, proximal–distal. Scale bars: (A–F) 20 µm.

Taken together, our data suggest that preferential cell elongation along the proximal–distal axis may be an important factor underlying differential growth of the outer integument and ovule curvature.

Application to other plant organs

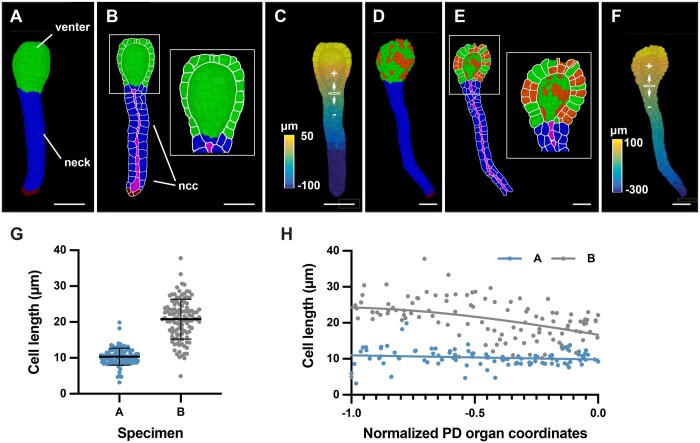
Finally, we explored if our approach for an organ-intrinsic coordinate system was useful beyond the Arabidopsis ovule and could be of value to provide spatial context to cellular growth patterns in different organs of various plant species. To this end, we investigated 3D digital plant organs of diverse morphological complexity. We first inspected the archegonium of the liverwort genetic model system Marchantia (Marchantia polymorpha). The archegonium is an organ of simple morphology consisting of two main tissues: the spherical venter harboring the egg cell and the elongated neck through which the sperm cell reaches the egg cell (Shimamura, 2016). We generated two 3D digital archegonia: a younger specimen A and an older specimen B. Both archegonia were imaged, 3D segmented, and cells of the neck, neck canal, venter, and venter canal were identified and labeled manually. We removed the egg and canal cells from our analysis and focused on the venters and the necks of the two 3D digital archegonia (Figure 8, A–F). A first inspection already revealed differences between the two specimens. We observed that the venter of specimen A possessed only one cell layer with no obvious signs of periclinal cell division. In contrast, we found that a scattered pattern of periclinal cell divisions had occurred in the venter of specimen B associated with the formation of a second cell layer (Figure 8, D and E; Shimamura, 2016). This observation indicated temporal and spatial asynchrony in the control of these periclinal cell divisions.

Figure 8.

Cellular analysis of 3D digital archegonia from Marchantia. A–C and D–F, 3D cell meshes of two different-stage archegonia are depicted. A, Specimen A. The venter and neck are indicated. B, An about mid-sagittal section through the venter. A view of the sectioned cells and the interior of one half of the venter is depicted. The outlines of the sectioned cells are indicated in white. The neck canal cells are highlighted in purple. C, Distance values along the central axis. The Bezier ring at the venter-neck boundary, which serves as the origin of the coordinate system, is indicated (B). D, Specimen B. Cells having undergone periclinal cell divisions are marked in orange. E, Highlighted white box represents the zoom view of the venter. The neck canal cells are highlighted in purple. F, Distance values along the central axis. The Bezier ring at the venter-neck boundary, which serves as the origin of the coordinate system, is indicated. G, Graph depicting the cell lengths of all neck cells of specimens (A) and (B). The mean ± sd is indicated. Specimen A: n = 98. Specimen B: n = 114. H, Graph showing cell length of individual neck cells of the two specimens shown in (C) in relation to their normalized position along the long axis of the neck. The tip of the neck is oriented to the left (0.0 corresponds to the ring position, the tip of the neck is at position −1.0, compare with Figure 8B). Abbreviations: ncc, neck canal cells; PD, proximal-distal. Scale bars: (A–F) 50 µm.

A monolayer of cells formed the necks of both specimens. We implemented an organ coordinate system to enable a spatial analysis of some basic cellular parameters along the long axes of the two specimens. We placed a Bezier ring at the boundary between the venter and neck cells (Figure 8, C and F). The placement of the ring resulted in the assignment of positive and negative organ coordinate values for the venter and neck cells, respectively. We then assessed the basis of the differences in neck lengths between the two specimens. Measuring neck length along the main central axis revealed that the neck of specimen B was about 2 times longer than specimen A (329 µm versus 160 µm). We then asked if the length disparity between the necks of the two specimens was due to a difference in cell numbers and/or cell elongation. We determined 98 and 114 neck cells for specimens A and B, respectively, indicating a minor difference in neck cell numbers. Next, we quantified cell length along the central organ axis for all neck cells. We observed that the neck cells of specimen A had an average length of 10.3 ± 2.4 µm and exhibited a relatively uniform cell length (Figure 8G). Neck cells of specimen B showed a more heterogeneous distribution of cell length and were noticeably more elongated with an average cell length of 20.8 ± 5.6 µm. Moreover, cell elongation increased toward the tip of the neck in specimen B while no such increase was observed for specimen A (Figure 8H). The results indicated that enhanced cell elongation along the central axis of the neck was mainly associated with the increase in neck length in specimen B in comparison to specimen A.

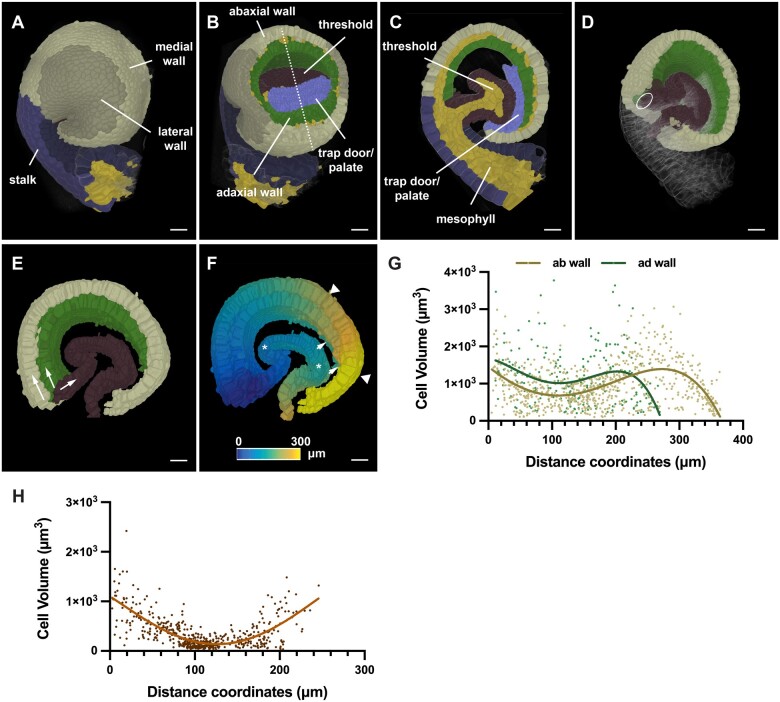
Finally, we turned our attention to a plant organ of complex 3D morphology. The cup-shaped trap of the aquatic carnivorous plant Utricularia (Utricularia gibba) represents a highly curved 3D leaf form (Reifenrath et al., 2006; Płachno et al., 2015). Quantitative growth analysis at the tissue level combined with computer modeling indicated that the complex shape transformations occurring during trap development are associated with differential rates and orientations of growth (Lee et al., 2019; Whitewoods et al., 2020). However, a quantitative analysis of 3D cellular parameters had not been performed. To obtain insight into the cellular basis of the growth patterns shaping the Utricularia trap we generated a 3D digital representation with cellular resolution of an intermediate-stage trap collected 6 d after initiation (Lee et al., 2019). By this stage, an invagination in the near-spherical young trap had occurred, followed by the formation of further folds and tissue broadening, and resulting in the emergence of the interior trap door and threshold (Figure 9, A–C). We manually labeled the various tissues, including the abaxial and adaxial cells of the wall, the threshold, and the combined trap door/palate domain, and distinguished between medial and lateral domains of the adaxial and abaxial wall, respectively. To define an origin of the distance coordinate system we placed an ellipsoid Bezier ring at the boundary between the base of the threshold and the wall of the trap (Figure 9D). We then asked if there were position-related differences in cell volume in the epidermal layers of the wall and threshold by analyzing epidermal cells located along the respective midlines of the tissues (Figure 9, E–H). We observed that cell volume varied along the measured distances. For example, we noticed a sudden increase in cell volume in an interval from 240 to 320 µm for cells of the abaxial wall (Figure 9G). This region precedes a prominent kink in the abaxial wall (Figure 9, E and F). In contrast, cell volumes of the adaxial wall dropped toward the end. The decrease in cell volume was likely associated with the tapering of the adaxial wall that could be observed in this area. Volumes of threshold cells positioned within a range of 80 µm to about 150 µm from the origin showed relatively small volumes in comparison to the cells flanking this interval (Figure 9H). The 80–150 µm zone corresponded to a section of the threshold which was only moderately curved and provided a large surface exposed to the lumen of the trap (Figure 9, E and F). Taken together, the data revealed spatial differences in cell volume for all three examined tissues of this specimen and support the notion that differential cell growth contributes to the morphogenesis of the Utricularia trap.

Figure 9.

3D digital Utricularia trap. A specimen 6 d after initiation is shown. A, Side view of the 3D cell mesh with annotation of various tissues. B, Tilted view of (A) with part of the wall removed by a tangential clipping plane. The dashed line indicates the mid-sagittal section shown in (C). C, Mid-sagittal section. D, Slanted 3D view of (A) with half of the trap cut off at the mid-sagittal plane shown in (B). The trap door and palate domain were removed. The position of the Bezier ellipsoid is indicated. E, Arrows indicate the direction of the distance coordinates through the epidermis of the abaxial and adaxial tissue of the wall and the threshold, respectively. F, Heat map indicating distances. Wall and threshold are treated separately. Triangles mark the 240–320 µm interval of the abaxial wall. Arrows highlight the tapering end of the adaxial wall. Asterisks indicate the 80- to 150-µm interval of the threshold. G, Graph displaying cell volume of epidermal trap cells in relation to their position. Values for the abaxial (ab) and adaxial (ad) wall are superimposed. The respective nonlinear regression curves fitting a fourth order polynomial function are indicated. ab wall: n = 786, ad wall: n = 231. H, Graph displaying cell volume of threshold cells in relation to their position. The line marks a nonlinear regression curve. n = 533. Scale bars: 20 µm.

Discussion

The generation of biological form can be explained in terms of growth oriented relative to an organ-centric coordinate system (Thompson, 1942; Coen and Rebocho, 2016; Whitewoods and Coen, 2017). To understand tissue morphogenesis, it is therefore essential to provide spatial context to the quantitative analysis of the molecular and cellular networks that underlie the development of tissues and organs. It requires robust methods that enable the objective assignment of position to individual cells in a rapid and reliable manner. Here, we developed 3DCoordX, a collection of computational tools that enable the assignment of organ-centric coordinate systems to several different plant organs with complex shapes that were not accessible with previous methods. By applying mathematically defined criteria for the annotation of cell position in 3D the tools largely eliminate user-derived ambiguities in the cell annotation process. 3DCoordX is implemented as an add-on to the open-source software MorphoGraphX (Barbier de Reuille et al., 2015; Strauss et al., 2021 (preprint)). A detailed user guide can be found in the Supplement Text S2. 3DCoordX enables quantitative analyses of cellular features in their spatial context, in a rapid manner, and on a large scale.

We took advantage of the recently made available 3D digital reference atlas of the Arabidopsis ovule to develop generic conceptual and computational approaches that enable the assignment of 3D coordinate systems to organs of simple as well as complex curved morphology. Previous efforts, such as iRoCS (Schmidt et al., 2014) and 3DCellAtlas (Montenegro-Johnson et al., 2015), relied on externally imposed coordinate systems. The design of the strategies for the annotation of cell position presented here are guided by intrinsic patterning processes and assign cell distance in relation to organ-centric developmental axes. Such tissue polarity axes are thought to play a central role in the spatial control of growth (Kennaway et al., 2011; Kuhlemeier and Timmermans, 2016; Whitewoods and Coen, 2017). To accommodate the particular architecture of the ovule we devised two 3D coordinate systems, one for the main “trunk,” the central proximal–distal axis consisting of the nucellus, chalaza, and funiculus, and one for the integuments. Both coordinate systems are based on similar general principles. First, we distinguish between individual cell layers as in the L1–L3 layers of the primordium or the adaxial–abaxial (dorso-ventral) cell layers of the two integuments. Importantly, with the concept of “outside wall area ratio” 3DCoordX embodies a strategy for the classification of the radial layers. It does not rely on a surface mesh for classification and thus is more versatile than other published methods. Second, the cell layers then become subdivided into two domains: the anterior–posterior domains of the trunk and the medio-lateral domains of the integument cell layers. Third, subsequent assignment of a proximal–distal distance value to each cell is constricted by these two prepatterns. For the placement of reference Bezier rings, we took cues from the localization of important developmental regulators, such as the presence of an auxin maximum at the distal tip of the ovule primordium or the CUC3 expression in the chalaza (Benková et al., 2003; Gonçalves et al., 2015; Liao et al., 2015; Kawamoto et al., 2020). As a result of the approach each cell is annotated in 3D with respect to the radial and proximal–distal dimensions as well as to either an anterior–posterior or medio-lateral axis. With the help of 3DCoordX, we readily discovered previously unidentified cellular growth patterns in the primordium and integuments. For example, our data indicate a basal cell proliferation zone in the ovule primordium and suggest that preferential cell proliferation in the anterior domain is important for primordium slanting. Moreover, we obtained evidence that the increase in cell volume along the proximal–distal axis of the outer integument, a tissue without radial symmetry, is mainly explained by an increase in cell length.

Importantly, our work revealed that the respective principles can be successfully applied to the establishment of coordinate systems for organs of varying degrees of morphological complexity and the subsequent quantitative analysis of 3D cellular parameters. We provided evidence for a preferential increase in cell length during axial neck growth of the Marchantia archegonium. Moreover, we identified distinct cellular patterns possibly associated with important morphological features of the intricately folded U. gibba trap. These data reveal that 3DCoordX has broad applicability and eliminates the need to work with multiple different pipelines when analyzing the cellular architecture of organs in 3D. The general strategies and computational methods put forward in this work will greatly reduce the time required for the spatial analysis of cellular parameters so central to various approaches, such as computational modeling of morphogenesis or comparative morphometry of specimens from different genotypes.

Materials and methods

Plant work and lines

Arabidopsis (A. thaliana (L.) Heynh. var. Columbia-0 (Col-0)) was used as a wild-type strain. Plants were grown on soil as described earlier (Fulton et al., 2009). The pKAN1::KAN1:2xGFP construct (Caggiano et al., 2017) and the pCUC3::CFP line (Gonçalves et al., 2015) were gifts from Marcus Heisler and Nicolas Arnaud, respectively. Wild-type plants were transformed with the pKAN1::KAN1:2xGFP construct using Agrobacterium (Agrobacterium tumefaciens) strain GV3101/pMP90 (Koncz and Schell, 1986) and the floral dip method (Clough and Bent, 1998). Transgenic T1 plants were selected on Glufosinate (Basta; 10 μg/mL) plates and transferred to soil for further inspection. Marchantia (M. polymorpha) of the BoGa ecotype was grown on half-strength Gamborg’s B5 medium under long-day conditions (16L:8D) at 22°C. For induction of reproductive structures, plants were grown under 60-µmol white light supplemented with far-red light (730 nm) on half-strength Gamborg’s B5 medium supplemented with 1% (w/v) glucose and 14-g L⁻¹ agarose (Althoff et al., 2014). Gametangiophores appeared after 4–6 weeks.

Clearing and staining of tissue samples

Treatment of ovules of the pKAN1::KAN1:2xGFP and the pCUC3::CFP lines was done as described in (Tofanelli et al., 2019) and (Vijayan et al., 2021). Tissue was fixed in 4% paraformaldehyde in PBS followed by two washes in PBS before transfer into the ClearSee solution (xylitol (10%, w/v), sodium deoxycholate (15%, w/v), urea (25%, w/v), in H₂O; Kurihara et al., 2015). Clearing was done at least overnight or for up to 2–3 d. Cell wall staining with SR2200 (Renaissance Chemicals, Selby, UK) was performed as described in (Musielak et al., 2015). Cleared tissue was washed in PBS and then put into a PBS solution containing 0.1% SR2200 and a 1/1,000 dilution of the nuclear stain TO-PRO-3 iodide (Thermo Fisher Scientific Waltham, MA, USA) for 20 min. Tissue was washed in PBS for 1 min, transferred again to ClearSee for 20 min before mounting in Vectashield antifade agent (Vector Laboratories, Burlingame, CA, USA). Marchantia archegoniophores were fixed for 1 week in 4% paraformaldehyde in PBS followed by two washes in PBS before transfer to ClearSee. Clearing was done for 4–7 d. Cell wall staining and subsequent clearing, washing, and mounting steps were the same as for Arabidopsis ovules. Archegonia were dissected in Vectashield mounting medium (Vector Laboratories, Burlingame, CA, USA).

Microscopy and image acquisition

Confocal laser scanning microscopy of ovules stained with SR2200 and TO-PRO-3 iodide was performed on an upright Leica TCS SP8 X WLL2 HyVolution 2 (Leica Microsystems, Wetzlar, Germany) equipped with GaAsP (HyD) detectors and a 63× glycerol objective (HC PL anterior–posteriorO CS2 63x/1.30 GLYC, CORR CS2). Scan speed was at 400 Hz, the pinhole was set to 0.6 Airy units, line average between 2 and 4, and the digital zoom between 1 and 2. For z-stacks, 12-bit images were captured at a slice interval of 0.24 μm with voxel size of 0.125 × 0.125 × 0.24 μm. Laser power or gain was adjusted for z compensation to obtain an optimal z-stack. Images were adjusted for color and contrast using Adobe Photoshop 2021 (Adobe, San Jose, CA, USA) or MorphographX (Barbier de Reuille et al., 2015) software. Image acquisition parameters for the pKAN1::KAN1:2xGFP line were the following: SR2200; 405 diode laser 0.10%, HyD 420–480 nm, detector gain 10. 2xGFP; 488 nm Argon laser 2%, HyD 525–550 nm, detector gain 100. TO-PRO-3; 642 nm White Laser 2%, HyD 660–720 nm, detector gain 100. In each case, sequential scanning was performed to avoid crosstalk between the spectra. Image acquisition parameters for the pCUC3::CFP line were the following: SR2200; 405 diode laser 0.10%, HyD 420–480 nm, detector gain 10. CFP; 514 nm Argon laser 2%, HyD 525–550 nm, detector gain 100. TO-PRO-3; 642 nm White Laser 2%, HyD 660–720 nm, detector gain 100. In each case, sequential scanning was performed to avoid crosstalk between the spectra. Imaging conditions for the Marchantia archegonia stained with SR2200 and TO-PRO-3 iodide were the same as for the ovules. In the late stage, Marchantia archegonium was imaged using the same 63× glycerol objective and a tilescan of 8 tiles. For z-stacks of the older specimen, 8-bit images were captured at a slice interval of 0.33 μm with voxel size of 0.126 × 0.126 × 0.33 μm; for z-stack of the younger 12-bit images were captured at a slice interval of 0.33 μm with voxel size of 0.127 × 0.127 × 0.33 μm. Tiles were stitched and merged to form the final 3D image stack of the organ in Leica Application Suite X data processing software (LASX version 3.5.7.23225). The early stage archegonium was imaged without tile scan.

Datasets and 3D instance cell segmentation

The dataset encompassing the segmented wild-type 3D digital ovules was described earlier (Vijayan et al., 2021). The two z-stacks of Marchantia archegonia were 3D cell segmented using the PlantSeg pipeline (Wolny et al., 2020). The z-stack of the Utricularia (U. gibba) trap was obtained from a fixed and modified pseudo-Schiff-stained (Truernit et al., 2008) specimen (Lee et al., 2019). 3D cell segmentation was performed using the PlantSeg-MorphoGraphX hybrid method as described in (Vijayan et al., 2021). In all instances, generation of cell surface meshes and cell type labeling was performed with MorphoGraphX. The datasets of this study have been deposited with the BioStudies data repository (https://www.ebi.ac.uk/biostudies) under the accession S-BSST734. Example dataset contains raw cell boundaries, cell boundaries, predictions from PlantSeg, nuclei images, segmented cells as well as the annotated 3D cell meshes, and the associated attribute files in csv format. The 3D meshes used in different manuscript figures are also available for download from the repository. 3D mesh files can be opened in MorphoGraphX.

Software

The MorphographX software was used for the generation of cell surface meshes, cell type labeling, and the analysis of 3D cellular features (Barbier de Reuille et al., 2015). It can be downloaded from its website (https://morphographx.org). The 3DCoordX toolbox is integrated as an add-on in MorphoGraphX version 2.0. A detailed user manual is provided in the supplement (Supplemental Text S2). The PlantSeg pipeline (Wolny et al., 2020) was used for 3D cell boundary prediction and segmentation. The software can be obtained from its Github repository (https://github.com/hci-unihd/plant-seg).

Supplemental data

The following materials are available in the online version of this article.

Supplemental Figure S1. Ovule development in A. thaliana.

Supplemental Figure S2. Expression of KANADI1 in the early ovule primordium.

Supplemental Figure S3. Automatic cell layer detection in the Arabidopsis SAM.

Supplemental Figure S4. Separation of funiculus into radial and anterior and posterior domains.

Supplemental Text S1. Development of the Arabidopsis ovule.

Supplemental Text S2 . User guide for annotation and analysis of complex 3D plant organsusing 3DCoordX.

 

A.V., S.S., R.S.S., and K.S. designed the study. A.V., S.S., R.T., T.A.M., and K.L. performed the experiments. A.V., S.S., R.T., T.A.M., K.L., M.T., R.S.S., and K.S. interpreted the results. M.T., R.S.S., and K.S. secured funding. K.S. wrote the paper with comments from all authors. All authors read and approved the final manuscript.

The author responsible for distribution of materials integral to the findings presented in this article in accordance with the policy described in the Instructions for Authors (https://academic.oup.com/plphys/pages/general-instructions) is Kay Schneitz (kay.schneitz@tum.de).