Evidence of Substantial Carbon Isotope Fractionation among Substrate, Inorganic Carbon, and Biomass during Aerobic Mineralization of 1,2-Dichloroethane by Xanthobacter autotrophicus

Abstract

Carbon isotope fractionation during aerobic mineralization of 1,2-dichloroethane (1,2-DCA) by Xanthobacter autotrophicus GJ10 was investigated. A strong enrichment of ¹³C in residual 1,2-DCA was observed, with a mean fractionation factor α ± standard deviation of 0.968 ± 0.0013 to 0.973 ± 0.0015. In addition, a large carbon isotope fractionation between biomass and inorganic carbon occurred. A mechanistic model that links the fractionation factor α to the rate constants of the first catabolic enzyme was developed. Based on the model, it was concluded that the strong enrichment of ¹³C in 1,2-DCA arises because the first irreversible step of the initial enzymatic transformation of 1,2-DCA consists of an S_N2 nucleophilic substitution. S_N2 reactions are accompanied by a large kinetic isotope effect. The substantial carbon isotope fractionation between biomass and inorganic carbon could be explained by the kinetic isotope effect associated with the initial 1,2-DCA transformation and by the metabolic pathway of 1,2-DCA degradation. Carbon isotope fractionation during 1,2-DCA mineralization leads to 1,2-DCA, inorganic carbon, and biomass with characteristic carbon isotope compositions, which may be used to trace the process in contaminated environments.

1,2-Dichloroethane (1,2-DCA) has been produced in larger quantities than any other chlorinated hydrocarbon (35). This compound is mainly used as a precursor for poly(vinyl chloride) production and as a solvent. 1,2-DCA is frequently detected in the environment and has been classified as a priority pollutant by the United States Environmental Protection Agency. Because of its high aqueous solubility and low sorption coefficient (37), 1,2-DCA is likely to contaminate groundwater if it is released into the environment. Under abiotic conditions, dissolved 1,2-DCA is transformed slowly and toxic products such as vinyl chloride may be formed (26). In contrast, microorganisms can rapidly degrade 1,2-DCA to nontoxic end products. Under anaerobic conditions, ethene is usually the main degradation product (12), but chloroethane and ethane production has also been observed (19). Under aerobic conditions, 1,2-DCA is completely mineralized to CO₂ and Cl⁻ (15, 24, 25, 40, 45). Anaerobic degradation of 1,2-DCA to ethene has been observed at several field sites, while aerobic degradation has been reported less frequently (6, 10, 28, 29). Aerobic biodegradation of 1,2-DCA is more difficult to demonstrate at field sites than anaerobic degradation because the end products of aerobic degradation, inorganic carbon and Cl⁻, often occur at high background concentrations in groundwater while the main end product of aerobic degradation, ethene, is less common.

The use of compound-specific isotope analysis is a promising tool for substantiating intrinsic biodegradation of organic contaminants in groundwater (1, 21, 47). This method relies on the frequent occurrence during abiotic and biotic transformation processes (2, 39) of a kinetic isotope effect, which consists of differences in reaction rates for molecules of a compound containing light (¹²C, H, or ³⁵Cl) and heavy (¹³C, D, or ³⁷Cl) isotopes, respectively. As a result, precursor and products isotope ratios differ; this is called (kinetic) isotope fractionation. Usually the product is depleted of heavy isotopes relative to the precursor and, therefore, the precursor becomes increasingly enriched in heavy isotopes as the reaction proceeds. Large kinetic isotope effects frequently occur with respect to atoms that constitute the bond that is broken or formed during the reaction step (primary isotope effect), while small effects occur with respect to atoms at other positions (secondary isotope effect). The occurrence of kinetic isotope effects has been used extensively in organic chemistry and enzymology to investigate reaction mechanisms and to identify rate-limiting steps in multistep transformation processes (see, e.g., references 9 and 13).

During microbial degradation, an enrichment of heavy isotopes in the remaining substrate is expected if the initial enzymatic transformation step is accompanied by a kinetic isotope effect (17). Such an effect has been observed during reductive dechlorination of tetrachloroethene, trichloroethene, cis-1,2-dichloroethene, and vinyl chloride (4, 21, 38) and oxidation of dichloromethane (18). In contrast, only a small or no carbon isotope fractionation was observed during aerobic or anaerobic degradation of aromatic hydrocarbons (27, 31, 38). Isotope analysis can be used not only to demonstrate that a contaminant is being degraded but also to link nonunique degradation end products, such as ethene, ethane, and dissolved inorganic carbon (DIC), to degrading contaminants. Recent studies (4, 21) have shown that ethene produced by reductive dechlorination of chlorinated ethenes is initially very depleted in ¹³C. In contrast, during biodegradation of hydrocarbons, only a small carbon isotope fractionation between substrate and inorganic carbon has been observed (14, 16). Analysis of ¹³C/¹²C ratios in DIC has been used to distinguish between inorganic carbon produced by contaminant degradation and inorganic carbon resulting from carbonate dissolution (5, 22).

The aim of this study was to investigate and quantify carbon isotope fractionation among substrate, biomass, and inorganic carbon during aerobic mineralization of 1,2-DCA by a pure microbial culture. This study is a first step in the evaluation of the utility of compound-specific isotope analysis in assessment of 1,2-DCA degradation at contaminated sites. Several microorganism, in pure cultures, are known to be capable of aerobic degradation of 1,2-DCA (15, 25, 40, 45). For this study, Xanthobacter autotrophicus GJ10 was chosen since the organism is well characterized (24) and has previously been used to treat contaminated groundwater (41). Furthermore, the reaction mechanism of the enzyme that catalyzes the initial transformation of 1,2-DCA, haloalkane dehalogenase, is thoroughly documented (36, 48). In previous studies of isotope fractionation during biodegradation of organic contaminants, an empirical model was used to quantify isotope fractionation (4, 18, 38). In contrast, in this study we developed a mechanistic model to explain the origin and magnitude of the observed high degree of isotope fractionation. The use of a mechanistic model makes it possible to draw some general conclusions with regard to the occurrence and characteristics of isotope fractionation during contaminant degradation.

MATERIALS AND METHODS

Organism and growth conditions.

X. autotrophicus GJ10 was obtained from D. B. Janssen (Department of Biochemistry, University of Groningen, Groningen, The Netherlands). The organism, originally isolated from a mixture of activated sludge and chemically polluted soils, is capable of growing on 1,2-DCA as a sole carbon and energy source (25). It constitutively produces two different dehalogenases (24): one is specific for halogenated alkanes, while the other is specific for halogenated carboxylic acids. In the initial step, which may cause enrichment of heavy isotopes in the residual substrate, 1,2-DCA is transformed to 2-chloroethanol by hydrolytic dehalogenation (24).

The mineral medium employed was similar to the one used by Janssen and coworkers (25) except that the strength of the phosphate buffer was reduced since lower 1,2-DCA concentrations were used. The medium, which contained (per liter) 3.22 g of Na₂HPO₄ · 12H₂O, 0.81 g of KH₂PO₄, 0.5 g of (NH₄)₂SO₄, 0.2 g of MgSO₄ · 7H₂O, and 0.015 g of CaCl₂ · 2H₂O, was supplemented with 1 ml of trace element solution (42) per liter and adjusted to pH 7.2 before being autoclaved. Afterward, 0.1 ml of a sterile vitamin solution (44) was added per liter of medium. The culture was grown in 250-ml glass bottles which contained 185 ml of medium and were closed with Mininert-Valves (Vici Precision Sampling, Baton Rouge, La.). Before the experiments were begun, the culture was transferred three times. Each subculture received 0.61 mM (60 ppm) of 1,2-DCA at four time points.

Experiments.

For all experiments, 15 ml of the previous subculture was added to bottles containing 170 ml of autoclaved medium. To remove DIC, the medium was purged for 2 h with helium by the use of a sterile stainless steel needle. Afterward, 20 ml of O₂ and 1,2-DCA (99.8% purity; Aldrich, Milwaukee, Wis.) were added and the bottles were placed on a shaker. After 1 h of shaking, samples representing initial concentrations were removed.

In experiment I, 1,2-DCA was added at a concentration of 0.61 mM (60 ppm). The cultures were incubated in duplicate at 10 and 23°C, respectively, and continuously shaken. The concentration and ¹³C/¹²C ratio of 1,2-DCA were determined at various time points during degradation. Furthermore, the concentrations and ¹³C/¹²C ratios of inorganic carbon and biomass were determined at the beginning and the end of the experiment.

In experiment II, 1,2-DCA was added at a concentration of 1.22 mM (120 ppm). A higher concentration than that used in experiment I was chosen in order to obtain inorganic carbon and biomass at concentrations sufficient to determine ¹³C/¹²C ratios at intermediate stages. Six bottles were prepared and incubated at 23°C. The concentration and ¹³C/¹²C ratio of 1,2-DCA in one of the cultures were determined at various times during degradation. The other cultures were stopped at different time points by adding HgCl₂ (25 ppm Hg²⁺), and the concentrations and ¹³C/¹²C ratios of 1,2-DCA, inorganic carbon, and biomass were measured. In addition, the Cl⁻ concentration was measured at the beginning and the end of the experiment to confirm that 1,2-DCA mineralization had reached completion.

Sampling.

For concentration and ¹³C/¹²C ratio analyses of 1,2-DCA, liquid samples (2-ml volume) were taken and preserved with HgCl₂ (25 ppm of Hg²⁺). To determine the concentration and ¹³C/¹²C ratio of CO₂, 0.5 ml of headspace gas was removed and analyzed immediately. For concentration and ¹³C/¹²C ratio analyses of DIC, 2.5-ml volumes of liquid sample were dispensed into helium-filled 10-ml Vacutainer tubes (Becton Dickinson, Franklin Lakes, N.J.), displacing the same volume of helium. Immediately after the sampling, 0.1 ml of 100% H₃PO₄ was added to each sample to stop biological processes and to transform all dissolved inorganic carbonate to carbonic acid and CO₂. To determine optical densities, 1-ml volumes of liquid samples were removed. To analyze chloride concentrations, 2-ml volumes of liquid samples were taken and preserved with sodium azide. In all cases, the removed sample was replaced by a similar volume of helium. The biomass was collected by centrifugation at 12,000 × g for 10 min. For analysis of biomass in intermediate samples, the culture was inactivated by adding HgCl₂ (25 ppm of Hg²⁺) and purged for 3 h with helium to remove volatile compounds before centrifugation. The precipitate was washed twice with 15 mM phosphate buffer and freeze-dried.

Analytical methods.

All stable-isotope analyses were performed in the Environmental Isotope Laboratory of the University of Waterloo. ¹³C/¹²C ratios are reported in the usual delta notation (δ¹³C). The δ¹³C value is defined as δ¹³C = (R_s/R_r − 1) × 1,000, where R_s and R_r are the ¹³C/¹²C ratios of the sample and the international standard Vienna Peedee Belemnite (VPDB), respectively.

The δ¹³C of pure-phase 1,2-DCA was determined as previously described (20). The δ¹³C values of dissolved 1,2-DCA and headspace CO₂ were determined with a gas chromatography-combustion-isotope ratio mass spectrometry (GC-C-IRMS) system. The GC-C-IRMS system consisted of an Agilent (Palo Alto, Calif.) gas chromatograph equipped with a split/splitless injector, a Micromass (Manchester, United Kingdom) combustion interface operated at 850°C, and a Micromass Isochrom isotope-ratio mass spectrometer. For headspace analysis of CO₂, the gas chromatograph was equipped with a GS-GasPro column (J&W Scientific, Folsom, Calif.). The δ¹³C values of dissolved 1,2-DCA were determined by a method based on solid-phase microextraction as described by Hunkeler and Aravena (20). Concentrations of CO₂ and 1,2-DCA were determined based on the peak areas of the mass 44 signal for samples and external standards. The analytical system was verified daily by using reference compounds with known δ¹³C values (20). The standard uncertainty of the δ¹³C measurement was ± 0.5‰ for CO₂ and 1,2-DCA (n = 3). The relative standard uncertainty of the concentration measurement was ± 8% for CO₂ and 1,2-DCA (n = 3).

Carbon isotope ratios and concentrations of DIC were determined with a μGas breath analyzer coupled to a Micromass Isochrom isotope-ratio mass spectrometer (Micromass). External DIC standards were prepared by dissolution of NaHCO₃ with a known δ¹³C in distilled water that had been purged with helium for 0.5 h. Standards and samples were shaken for at least 1 h prior to carbon isotope analysis. DIC concentrations were quantified based on the peak areas of the mass 44-ion trace of samples and external standards. The standard uncertainty of the δ¹³C measurement was ± 0.15‰ for DIC (n = 6). The relative standard uncertainty of the concentration measurement was ± 4% for DIC (n = 6).

Carbon isotope ratios and carbon content of biomass were determined with a CE Instruments (Rodano, Italy) elemental analyzer coupled to a Micromass Isochrom isotope-ratio mass spectrometer. Samples of 1 mg were packed into tin cups and combusted at 1,030°C. The standard uncertainty of the δ¹³C of biomass was ± 0.6‰, while the relative standard uncertainty of the carbon content was ± 10% (n = 4).

Chloride concentrations were analyzed with a Dionex (Sunnyvale, Calif.) ion chromatography system equipped with an AS4A-SC column (Dionex). Optical densities were determined at 600 nm using an Ultraspec Plus UV/visible spectrophotometer (Amersham Pharmacia Biotech).

Calculations.

For 1,2-DCA and inorganic carbon, expected concentrations if the total masses of these compounds were present in the aqueous phase are reported. This allows for easy comparison of 1,2-DCA consumption and production of inorganic carbon, biomass, and Cl⁻. For 1,2-DCA, δ¹³C values determined by solid-phase microextraction of the aqueous phase are given. They correspond to the δ¹³C of the total mass of 1,2-DCA since only a very small carbon isotope fractionation between 1,2-DCA in the aqueous phase and headspace occurs (20) and since the mass of 1,2-DCA in the headspace is small. In contrast, a significant pH-dependent carbon isotope fractionation occurs between headspace CO₂ and DIC. At pH 7.2, CO₂ in the headspace is depleted of ¹³C by 7‰ compared to DIC (8). Therefore, the δ¹³C of the total inorganic carbon was calculated based on concentrations and δ¹³C values of DIC in the aqueous phase and CO₂ in the headspace. The biomass concentration was calculated by multiplying the carbon content by the total mass of freeze-dried biomass and dividing the result by the volume of the aqueous phase. The δ¹³C of the produced biomass was calculated based on the concentrations and δ¹³C values of biomass at the beginning of the experiment and at the time of sampling. The ¹³C-mass balance was calculated by multiplying the concentrations of 1,2-DCA, inorganic carbon, and biomass by their δ¹³C values, adding the contributions, and dividing the sum by the total concentration of these compounds.

Isotope fractionation during biodegradation of 1,2-DCA was quantified using a Rayleigh-type evolution model (7, 8, 30). According to this model, the isotopic composition of the substrate is given by

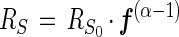1

where ƒ is the fraction of substrate remaining, R_S is the substrate isotope ratio at a remaining fraction ƒ, R_S0 is the initial isotope ratio of the substrate, and α is the fractionation factor. The fractionation factor (30) is defined by

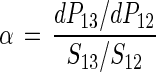2

where dP₁₃ and dP₁₂ are increments of product containing ¹³C and ¹²C, respectively, which appear in an infinitely short period of time (instantaneous product) and S₁₃ and S₁₂ are the concentrations of substrate with ¹³C and ¹²C, respectively.

By using the δ¹³C notation for carbon isotope ratios, equation 1 transforms to

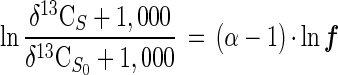3

where δ¹³C_S is the carbon isotope ratio of the substrate at a remaining fraction ƒ and δ¹³C_S0 is the initial carbon isotope ratio of the substrate. The fractionation factor α was quantified on the basis of equation 3 by linear regression.

RESULTS

Concentrations and carbon isotope ratios. (i) Experiment I.

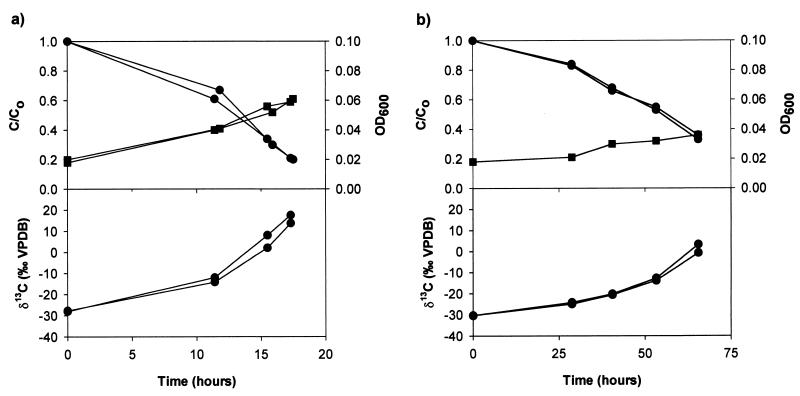
At 23°C, 1,2-DCA (60 ppm) was consumed by X. autotrophicus GJ10 within about 20 h and the optical density increased (Fig. 1a). The δ¹³C of added 1,2-DCA (initial δ¹³C, −30.6‰) increased to values of more than +10‰ during the experiment. Similar concentrations and δ¹³C values were obtained for duplicate batch cultures. The produced inorganic carbon was depleted in ¹³C (δ¹³C = −46.2‰) and the biomass was enriched in ¹³C (δ¹³C = −17.2‰) compared to the initially added 1,2-DCA (δ¹³C = −30.6‰). Degradation of 1,2-DCA took about four times longer at 10°C than at 23°C. Again, a strong increase in the δ¹³C of 1,2-DCA was observed during its biodegradation (Fig. 1b).

FIG. 1.

Experiment I: relative concentration of 1,2-DCA (closed circles, top panel), δ¹³C of 1,2-DCA (closed circles, bottom panel), and optical density (closed squares) in batch cultures of X. autotrophicus GJ10 at 23°C (a) and 10°C (b). The initial concentration of 1,2-DCA was 60 ppm.

(ii) Experiment II.

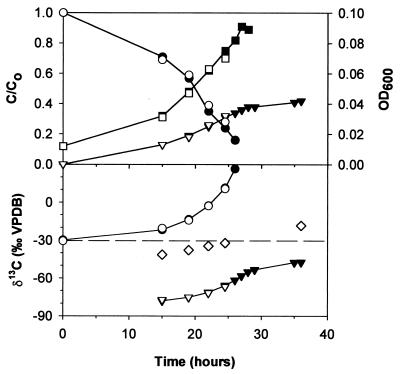
In experiment II, 120 ppm of 1,2-DCA was consumed within about 30 h and the optical density increased (Fig. 2). The amount of inorganic carbon relative to the carbon initially added as 1,2-DCA reached a final value of 0.4 (Fig. 2). The δ¹³C of 1,2-DCA increased from −30.6 to +28.0‰. The δ¹³C of inorganic carbon in the continuous microcosm was −78.0‰ in the first intermediate sample and increased to a final value of −47.4‰ (Fig. 2). Similar concentrations and δ¹³C values were obtained for continuous and sacrificial microcosms at similar points in time (Fig. 2). The yield of inorganic carbon (inorganic carbon production divided by 1,2-DCA consumption in millimolar concentration of C) remained nearly constant throughout the experiment, with an average of 0.42 (Table 1). The δ¹³C of produced biomass was −44.2‰ in the first intermediate sample and increased to −18.3‰ (Table 1; Fig. 2). The concentration and δ¹³C of the sum of 1,2-DCA, inorganic carbon, and biomass in intermediate and final samples corresponded to the initial concentration and δ¹³C of 1,2-DCA (Table 1). This indicates that all products containing carbon were recovered and that accumulation of intermediate degradation products was negligible. The total production of chloride was 2.45 mM, which confirmed that complete degradation of 1,2-DCA took place.

FIG. 2.

Experiment II: relative concentration of 1,2-DCA (closed circles, top panel), yield of DIC (closed inverted triangles, top panel), δ¹³C of 1,2-DCA (closed circles, bottom panel), δ¹³C of inorganic carbon (closed inverted triangles, bottom panel), and optical density (closed squares) in batch culture of X. autotrophicus GJ10 incubated at 23°C. Open symbols are corresponding values in sacrificial batch cultures. The initial concentration of 1,2-DCA was 120 ppm. Open diamond, δ¹³C of biomass in sacrificial batch cultures; dashed line, δ¹³C of added 1,2-DCA.

TABLE 1.

Mass balance and carbon isotope balance for experiment II

Time (h)	Value for:
	1,2-DCA			Inorganic carbon			Biomass		Total Carbon
	Concn (mM C)	δ13C (‰ VPDB)	fdega	Concn (mM C)	δ13C (‰ VPDB)	fICb	Concn (mM C)	δ13C (‰ VPDB)	Concn (mM C)	δ13C (‰ VPDB)
0	2.42	−30.6	0.00						2.42 ± 0.19	−30.6 ± 0.5
15	1.68	−20.5	0.31	0.31	−77.2	0.42	0.29	−44.2	2.28 ± 0.14	−31.3 ± 0.6
19	1.42	−14.3	0.41	0.43	−75.2	0.43	0.60	−37.4	2.45 ± 0.10	−30.6 ± 0.8
22	0.94	−2.9	0.61	0.62	−71.8	0.42	0.68	−34.3	2.23 ± 0.09	−31.5 ± 0.8
24.5	0.67	10.6	0.72	0.77	−66.8	0.44	0.78	−31.8	2.22 ± 0.09	−31.2 ± 0.8
36			1.00	1.01	−47.4	0.42	1.35	−18.3	2.36 ± 0.14	−30.9 ± 0.8

^af_deg, fraction of 1,2-DCA degraded. 

^bf_IC, yield of inorganic carbon. 

Fractionation factors.

To be able to compare the magnitudes of isotope fractionation during the different experiments, fractionation factors were calculated based on equation 3. The regression coefficients are close to 1 (≥0.9878), indicating that the fractionation factor remained essentially constant throughout the experiments (Table 2). Fractionation factors of duplicate experiments agreed closely, and only small differences were observed for different initial concentrations and temperature.

TABLE 2.

Fractionation factors (α) determined by least-squares linear regression based on the Rayleigh equation

Expt (temp, °C)	1,2-DCA concn (ppm)	α	ς	R2	n
I (23)	60	0.973	0.0015	0.9994	4
I (23)	60	0.972	0.0022	0.9878	4
I (10)	60	0.970	0.0014	0.9934	5
I (10)	60	0.971	0.0014	0.9933	5
II (23)	120	0.970	0.0014	0.9930	5
II (23)	120	0.968	0.0013	0.9931	5

DISCUSSION

Aerobic mineralization of 1,2-DCA by X. autotrophicus GJ10 is accompanied by a strong carbon isotope fractionation. The obtained fractionation factors are the largest yet reported for biodegradation of two-carbon organic compounds. Significant carbon isotope fractionation has previously been observed during reductive dechlorination of trichloroethene (0.993 to 0.998 [4, 21, 38]), cis-1,2-dichloroethene (0.985 to 0.988 [4, 21]), and vinyl chloride (0.974 to 0.975 [4, 21]) and during aerobic oxidation of dichloromethane (0.958 [18]). In contrast, during both aerobic and anaerobic degradation of toluene, only a small carbon isotope fractionation occurred (0.997 to 0.998 [31]). As shown in the present study, aerobic oxidation of 1,2-DCA is accompanied not only by a strong enrichment of ¹³C in 1,2-DCA but also by an unusually large fractionation of carbon isotopes between inorganic carbon and biomass.

Carbon isotope fractionation during initial transformation.

The magnitude of the fractionation factor α depends on the magnitude of the isotope fractionation occurring during transport of 1,2-DCA across the cell membrane, the magnitude of the isotope fractionation during its initial transformation, and the relative rates of these two processes. Since the cell membrane of X. autotrophicus GJ10 does not act as a barrier to permeation of 1,2-DCA (46), it can be concluded that the observed fractionation factor mainly reflects isotope fractionation during initial 1,2-DCA transformation. This is consistent with the observation that the magnitude of the fractionation factor α can be explained only by the action of an enzymatic process and not by a transport process. Since the catalytic mechanism of the haloalkane dehalogenase is well understood, it is possible to evaluate in more detail the origin of the large isotope fractionation during the initial transformation of 1,2-DCA. Using basic equations of enzyme kinetics, the fractionation factor α can be linked to parameters that characterize the kinetics of the haloalkane dehalogenase. If substrate with ¹²C and ¹³C at the reactive center is simultaneously available, as in this study, the amount of product with ¹²C, d¹²P, that is formed during an infinitely short time period dt is given by (39, 43)

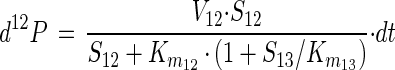4

where V₁₂ is the limiting rate for substrate with ¹²C at the reactive center, S₁₂ and S₁₃ are the concentrations of substrate with ¹²C and ¹³C, respectively, at the reactive center, and K_m12 and K_m are the Michaelis constants for substrate with ¹²C and ¹³C, respectively, at the reactive center.

By inserting equation 4 and an analogous equation for dP₁₃ into equation 2, the following equation for α is obtained:

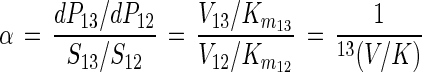5

where ¹³(V/K), defined by

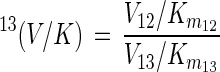is the isotope effect on V/K (32). Thus, biodegradation experiments with isotope ratios at natural abundance levels reflect isotope effects on V/K, analogous to enzyme studies under competitive conditions (labeled and unlabeled substrate simultaneously present [33]). For the haloalkane dehalogenase (Fig. 3), V/K is given by

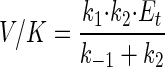6

where k₁ and k₋₁ are the rates of formation and dissociation, respectively, of the substrate enzyme complex, k₂ is the rate of the first irreversible catalytic step, and E_t is the total enzyme concentration. Isotope fractionation during formation and dissociation of the substrate-enzyme complex is small compared to that during irreversible transformation steps and can usually be neglected (34). Under this assumption, the following expression for α in terms of the kinetic constants of the enzyme is obtained by inserting equation 6 into equation 5:

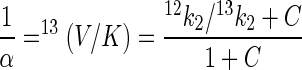7

where C = ¹² k₂/k₋₁; C is usually referred to as commitment to catalysis since it represents the tendency of the enzyme-substrate complex to go forward through catalysis rather than to break down to free enzyme and substrate (32). The ratio ¹²k₂/¹³k₂ is usually denoted as the intrinsic isotope effect since it represents the full isotope effect originating from a single reaction step (32). Several important conclusions can be drawn from equation 7. First, the fractionation factor α is expected to be constant since the right-hand side of equation 7 contains only rate constants. Thus, equation 7 justifies the hypothesis that α is constant, which has been postulated in this and in previous studies (4). Second, the magnitude of α or ¹³(V/K) depends only on the steps up to and including the first irreversible step, as previously observed for isotope effects in enzyme studies under competitive conditions (34, 39). It does not depend on whether the rate-limiting step is accompanied by isotope fractionation. Indeed, for the haloalkane dehalogenase, the slowest step is the release of the Cl⁻ (Fig. 3), which is not accompanied by carbon isotope fractionation. Third, the degree to which the intrinsic isotope effect (¹²k₂/¹³k₂) is detectable depends on the commitment to catalysis. The larger the rate of catalysis (¹²k₂) is, compared to the rate of dissociation of the substrate-enzyme complex (k₋₁), and thus the larger C is, the smaller is ¹³(V/C) for a given value of the intrinsic isotope effect (equation 7). The equations given above are specific for the case discussed in this study. For other enzyme mechanisms (e.g., two substrates), a different expression for C is obtained (33). Furthermore, if the rate of substrate transformation by the first catabolic enzyme is high compared to the rate of substrate export from the cell, a more complex relationship between α and ¹³(V/C) arises.

FIG. 3.

Reaction scheme for dehaloalkane dehalogenase. The rate constants have the following values (means ± standard deviations): k₁ = 9 × 10³ ± 1 × 10⁻³ μM⁻¹ s⁻¹, k₋₁ = 20 ± 5 s⁻¹, k₂ = 50 ± 10 s⁻¹, k₃ = 14 ± 3 s⁻¹, and k₄ = 8 ± 2 s⁻¹ (36). C = k₂/k₋₁ = 2.5.

Based on equation 7, it is possible to relate the magnitude of the fractionation factor α to the intrinsic isotope effect associated with the first irreversible step of 1,2-DCA transformation. For the haloalkane dehalogenase, the first irreversible step consists of an S_N2 nucleophilic substitution ((48)), in which a carboxylate group of a side chain of the enzyme acts as a nucleophile and displaces a chloride ion. From numerous studies in organic chemistry, it is known that S_N2 processes are prone to a large kinetic isotope effect with ¹²k/¹³k ratios of up to 1.080 (13). In the present study, an average fractionation factor of 0.970 was observed, which was measured with respect to both carbon positions of 1,2-DCA. However, in the first irreversible step (S_N2 reaction), only one of the two carbon atoms is involved in the reaction mechanism. Assuming that no significant secondary isotope effect occurs, which is a reasonable assumption for carbon isotopes (23), the fractionation factor with respect to the reactive carbon is 0.940. Using this value and the known value of C (2.5 [Fig. 3]), the magnitude of the intrinsic isotope effect (¹²k₂/¹³k₂) for the S_N2 step of the enzyme can be estimated using equation 7. A value of 1.090 is obtained, which is in the range typical for S_N2 reactions. In summary, the large carbon isotope effect associated with 1,2-DCA transformation by X. autotrophicus GJ10 can be explained by a combination of (i) a large kinetic isotope effect during the first irreversible step of the initial enzymatic transformation (S_N2 reaction), (ii) a relatively small commitment to catalysis leading to a large ¹³(V/K), and (iii) rapid transport of 1,2-DCA into and out of the cell, which makes isotope fractionation detectable outside the cell.

Carbon isotope fractionation between inorganic carbon and biomass.

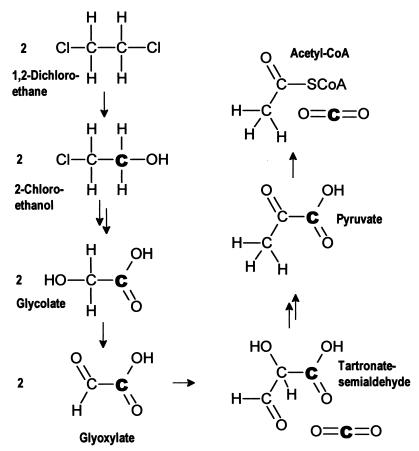
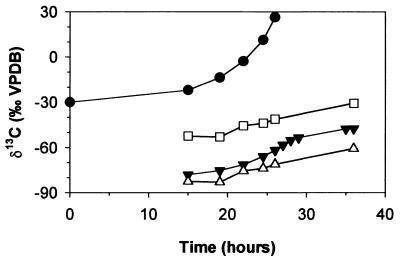
In this study, the inorganic carbon is depleted in ¹³C by 29.1 to 37.8‰ compared to the biomass (Table 1). In previous studies with different substrates, a similar, though much smaller, ¹³C depletion in inorganic carbon has been observed. Inorganic carbon produced by biodegradation of glucose was depleted in ¹³C by 2.8‰ (3), while inorganic carbon from phenol and benzoate mineralization was depleted by up to 8‰ (16). The unusually large carbon isotope fractionation between biomass and inorganic carbon during 1,2-DCA mineralization can be explained based on the metabolic pathway. 1,2-DCA is transformed via 2-chloroethanol, 2-chloroaldehyde, and chloroacetate to glycolate (Fig. 4), which enters the central metabolic pathway (24). Glycolate is usually oxidized to glyoxylate and transformed to acetyl coenzyme A (acetyl-CoA) via the glycerate pathway by bacteria. Two of the reactions on the way to acetyl-CoA, the transformation of two glycoxylate molecules to tartronate semialdehyde and the transformation of pyruvate to acetyl-CoA, involve a decarboxylation step (Fig. 4). In both of them, the liberated CO₂ molecule originates from the carboxyl position of the glycolate (the carbon boldfaced in Fig. 4). In contrast, the carbon in the acetyl-CoA corresponds to the hydroxyl carbon of the glycolate. Given a position-specific α of 0.940 for the initial 1,2-DCA transformation, the carboxyl carbon is expected to be depleted in ¹³C by approximately 60‰ relative to the substrate while the hydroxyl carbon has a δ¹³C similar to that of the concurrent substrate. The δ¹³C of the inorganic carbon depends on the relative amount of inorganic carbon originating from the two decarboxylation steps on the way to and from acetyl-CoA, respectively. In Fig. 5, the calculated average δ¹³C of glycolate and the average δ¹³C of its carboxyl-carbon position are plotted and compared to the δ¹³C of the inorganic carbon. If all inorganic carbon originated from the carboxyl-carbon position, the δ¹³C of the inorganic carbon would correspond to that of the carboxyl position of the glycolate. If carboxyl and hydroxyl positions equally contributed to inorganic carbon production, the δ¹³C of the inorganic carbon should correspond to that of the glycolate. Figure 5 shows that the δ¹³C of the inorganic carbon lies between the two calculated curves, indicating that more inorganic carbon originates from the carboxyl carbon than from the hydroxyl carbon. Correspondingly, a larger fraction of isotopically heavier hydroxyl carbon is incorporated into biomass via acetyl-CoA, glycolate, and/or pyruvate, which leads to an enrichment of ¹³C in biomass compared to inorganic carbon. In addition to this effect associated with position-specific δ¹³C differences in glycolate, isotope fractionation at branch points of the intracellular carbon flow may also contribute to differences between biomass and inorganic carbon δ¹³C values (17). Such an effect is known to occur at the branch point downgradient of pyruvate (11). However, this effect alone cannot explain the large isotope fractionation between biomass and inorganic carbon observed in this study.

FIG. 4.

Metabolic pathway of 1,2-DCA degradation.

FIG. 5.

Experiment II: measured δ¹³C of 1,2-DCA (closed circles), measured δ¹³C of inorganic carbon (closed inverted triangles), calculated average δ¹³C of glycolate (open squares), and calculated average δ¹³C of carboxyl-carbon position of glycolate (open triangles).

Summary and conclusions.

A very large kinetic isotope effect accompanied by an unusually strong carbon isotope fractionation between biomass and inorganic carbon, was observed during aerobic transformation of 1,2-DCA by X. autotrophicus GJ10. These effects led to very characteristic δ¹³C values for 1,2-DCA and inorganic carbon during biodegradation of 1,2-DCA which potentially could be used to monitor intrinsic biodegradation of this compound in the environment. The origin and magnitude of the large kinetic isotope effect during initial substrate transformation were substantiated by using a mechanistic model. The model makes it possible to draw some conclusions concerning the occurrence and predictability of kinetic isotope effects during biodegradation of contaminants. A prerequisite for the occurrence of a detectable carbon isotope fractionation during biodegradation of organic compounds is the occurrence of a significant intrinsic isotope effect during the first irreversible step of the first enzymatic transformation. Whether this effect is detectable depends on several factors, including (i) the number of carbon atoms in the molecule, since the intrinsic isotope effect usually occurs with respect to a specific position in the molecule while the isotope ratio measurement is usually compound specific; (ii) the magnitude of the commitment to catalysis; and (iii) the rate of transport of the substrate into and out of the cell. The large number of factors that affect the magnitude of the observed isotope fractionation makes it difficult to predict isotope fractionation. Not only the degradation mechanism but also the relative rates of the various processes must be known. To determine the effect of factor ii, the rate constants of the enzyme have to be known. The effect of factor iii could be evaluated by comparing isotope fractionation by whole cells with isotope fractionation by cell extracts. Factors i and iii may explain why a large isotope fractionation has been observed for small molecules, as in this study, while only a small isotope effect occurs during degradation of larger molecules. In the context of intrinsic biodegradation, the fate of small mobile molecules is commonly of particular concern. For such molecules, a detectable isotope fractionation is more likely to occur and may be a valuable tool to demonstrate intrinsic biodegradation, as suggested by the first field trials (21). For practical application of the method, more information about variations of fractionation factors between different cultures and under different environmental conditions is required.