Abstract
Purpose:
To compare the efficacy of Kane formula with Sanders Retzlaff Kraff/Theoretical (SRK/T) and Barrett Universal II in predicting intraocular lens (IOL) power in Indian eyes.
Methods:
This retrospective study conducted in a tertiary care eye hospital. Data from patients having uneventful cataract surgery with Tecnis ZCB00 IOL implantation were obtained from Lenstar and electronic medical records. Eyes were divided into subgroups based on axial length (AL) as short (<22.0 mm), medium (22–24 mm), and long (>24 mm). The predicted refractive outcome for each patient was calculated after optimizing the lens constant. Prediction error was calculated by subtracting the predicted spherical equivalent from achieved spherical equivalent 1 week post-surgery. The mean absolute error (MAE) and median absolute error (MedAE) and percentage of eyes within 0.25, 0.5, 1, and 2 D were calculated for each formula. Friedman test, Cochrane Q test were used for statistical analysis.
Results:
Out of the 350 eyes included in the study, we found that without lens constant optimization, Barrett formula performed better than SRK/T and Kane (P < 0.0001). Over the entire range of axial lengths, Kane formula performed slightly inferior compared to Barrett and SRK-T, both of which performed equally well (P = 0.006). On subgroup analysis, Kane formula performed inferiorly for medium eyes as compared to the other two. No significant differences were noted between the formulae for short and long eyes
Conclusion:
Kane formula did not outperform Barrett Universal II and SRK/T in Indian eyes.
Keywords: Indian eyes, Kane formula, SRK/T formula
Cataract surgery has graduated from being only an extraction procedure to a refractive procedure. There is increasing demand for unaided 20/20 vision as well as excellent quality of vision. Accurate biometry and an appropriate intraocular lens (IOL) formula are the main factors for the best visual outcomes post uneventful phacoemulsification surgery.[1]
Accurate biometry can be achieved with the newer biometers. Appropriate IOL formulae will yield precise post-operative results. The newer generation formulae are now freely available online. Newer IOL power formulae take into consideration multiple variables to improve refractive outcome predictions, with Holladay 2 having the maximum number of variables.[2]
Sanders Retzlaff Kraff/Theoretical (SRK/T) formula, developed in 1990 by Retzlaff et al.,[3] represents the combination of linear regression method and a theoretical eye model. The Barrett universal formula, shown to be accurate across a wide range of axial lengths, was designed by Graham Barrett in 1993 and was modified in 2010. In this, a theoretical model is used to determine the relationship between the various parameters of the eye.[4] Kane formula is a newer IOL power formula that combines theoretical optics, thin lens formulae, and big data techniques to make its predictions.[5] It utilizes axial length, keratometry readings, anterior chamber depth, central corneal thickness, lens thickness, and sex of the patient to predict the IOL power.
The aim of our study is to compare the accuracy of Kane formula with SRK/T and Barrett Universal II formula across a range of axial lengths by using Lenstar, online Kane calculator, online Barrett Universal 2 calculator, and optimized A constants. To the best of our knowledge, there is limited work done about the performance of Kane formula on Indian eyes.
Methods
The study was a retrospective chart review comprising data of patients who underwent phacoemulsification cataract surgery with implantation of Tecnis monofocal nontoric IOL ZCB00 IOL (Johnson & Johnson Vision) over a period of 3 years (Jan 2017–Jan 2020). All surgeries were performed by a single surgeon at a large tertiary care center. SRK/T formula was used to calculate the IOL power in all cases irrespective of axial length.
The electronic medical records (EMR) were searched for a period of 3 years, and 350 eyes of 350 patients who met the inclusion criteria were utilized in the study. The inclusion criteria were uneventful phacoemulsification surgery with in-the-bag placement of single-piece monofocal nontoric IOL Tecnis ZCB00 (Johnson & Johnson Vision), patients who have not undergone any previous ocular surgery, and whose 1-week post-operative follow-up data were available.
Exclusion criteria were patients with incomplete biometry, astigmatism more than 1D, additional procedures performed intraoperatively during phacoemulsification surgery, post-operative complications, and post-operative 1-week vision worse than 6/12.
OLCR-based biometer, Lenstar (LS 900), was used to perform biometry, and the following variables used for IOL power calculation were obtained directly from the database of Lenstar: flat keratometry (K1), steep keratometry (K2), anterior chamber depth (ACD), axial length (AL), corneal horizontal white to white diameter (WTW), and lens thickness (LT). The demographics of the patients and the remaining variables were obtained from the EMR. Subjective refraction was performed at 1 week post cataract surgery by a single optometrist. Studies have proven that predicted post-operative spherical equivalent at 1 week post uneventful cataract surgery is reliable and can be prescribed to make spectacles. Thus, only 1-week data were included in our study.[6]
The pre-op data were input into the online calculators of Barrett Universal II available at https://calc.apacrs.org/barrett_universal2105 and Kane online calculator available at https://www.iolformula.com to obtain the predicted spherical equivalent.
The constant for each formula was optimized by zeroing out the arithmetic mean error.[7] The predicted postoperative refraction for each patient was calculated using the optimized IOL constants. The prediction error was then calculated as the actual postoperative refraction minus the refractive result predicted by each formula. A negative prediction error indicated a myopic outcome whereas a positive prediction error indicated a hyperopic outcome. The mean numerical prediction error (ME), mean absolute prediction error (MAE), and median absolute prediction error (MedAE) were calculated for each formula. The percentages of eyes that had a prediction error within ± 0.25, ±0.50, ±1.00, and ± 2.00 D were also calculated for each formula. Subgroup analysis was performed based on the following AL groups: short (<22.0 mm), medium (22.0 to 24 mm), and long (>24.0 mm).
Data were entered in MS Excel 2017 (Microsoft Corporation, Redmond, USA) and analyzed using MedCalc Statistical Software Version 18.6 (MedCalc Software bvba, Ostend, Belgium; http://www.medcalc.org; 2018). The differences in absolute error between formulas were assessed using the Friedman test. Cochrane Q test was used to evaluate whether the percentages of eyes within certain prediction errors were significantly different between formulas.
Results
In all, 350 eyes were included in the study, out of which 29 eyes belonged to the short eyes group (AL <22 mm), 262 eyes belonged to the medium eyes group (AL 22–24 mm), and 59 eyes belonged to long eyes group (AL >24 mm). The mean age was 64. 30 ± 7.97 years. The mean age in the short eyes group was 63.21 years, in the medium eyes group was 64.79 years, and in the long eyes group was 62.63 years. In the short eyes group, there were two males and 27 females; in the medium eyes group, there were 132 males and 130 females; in the long eyes group, there were 42 males and 17 females. The mean axial length and mean IOL power in the short eyes group were 21.62 ± 0.4 mm and 26 ± 1.36, respectively; in the medium eyes group, 23 ± 0.3 mm and 22.74 ± 1.48, respectively; and in the long eyes group, 24.81 ± 0.9 mm and 19 ± 3.15, respectively.
We found that without lens constant optimization, Barrett formula performed statistically significantly better compared to SRK/T and Kane with its median error being closest to zero (P < 0.0001)
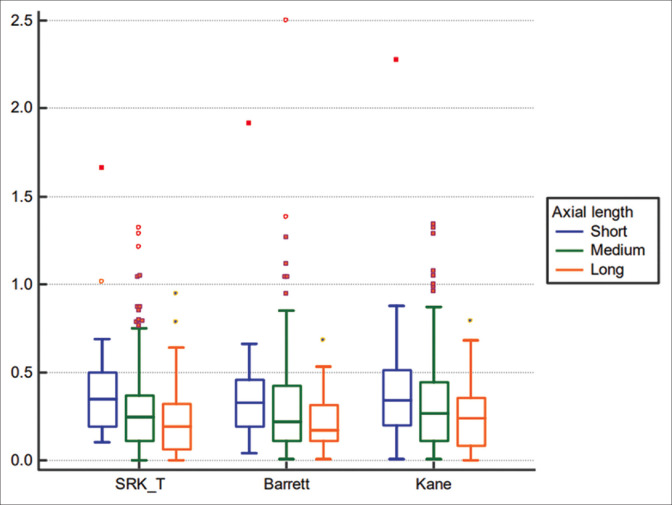
On comparing the three formulae after lens constant optimization, all three formulae performed very well, with MAE and MedAE values within a range of 0.24–0.32 and over 80% eyes within 0.50 D in all three groups. Over the entire range of axial lengths, Kane formula performed slightly inferior as compared to Barrett and SRK-T, both of which performed equally well (P = 0.006) This can be seen by comparing the absolute errors of the three formulae (Freidman test) [Table 1 and Fig. 1]. Also, on comparing the formulae categorically, the Kane formula had fewer percentages of eyes within 0.25 and 0.5 D compared to the other two, although this was not statistically significant [Table 2 and Fig. 2].
Table 1.
Analysis of all eyes
| MAE | SD | MedAE | |
|---|---|---|---|
| SRK/T | 0.28 | 0.24 | 0.24 |
| BARRETT | 0.29 | 0.26 | 0.21 |
| KANE | 0.31* | 0.26 | 0.26* |
P=0.006 (Friedman Test) MAE and MedAE of Kane is significantly higher than Barrett and SRK/T. No significant difference between Barrett and SRK/T
Figure 1.
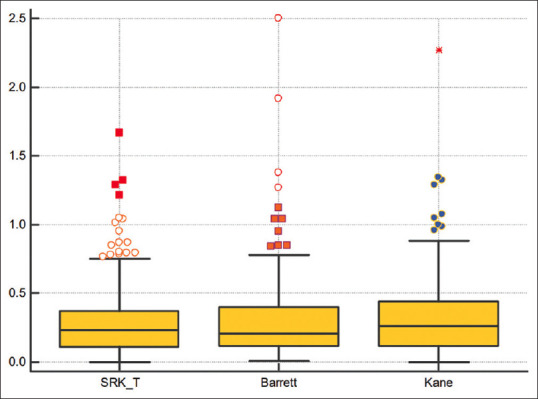
Absolute error of all eyes after lens constant optimization
Table 2.
Percentage of eyes within 0.25, 0.5, 1, and 2 D
| % of eyes within 0.25D | % Of eyes within 0.5D | % Of eyes within 1D | % Of eyes within 2D | |
|---|---|---|---|---|
| SRK/T | 54 | 85 | 98 | 100 |
| BARRETT | 55 | 86 | 98 | 99.71 |
| KANE | 49 | 82 | 98 | 99.71 |
| P (Cochrane Q test) | 0.092 | 0.106 | 0.882 | 0.607 |
Kane formula has a smaller number of eyes within 0.25 and 0.5 D compared to Barrett and SRK/T but not statistically significant
Figure 2.
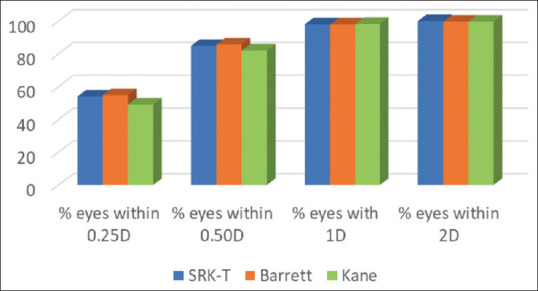
Absolute error of all eyes within 0.25, 0.5, 1, and 2 D
Subgroup analysis
In the short eyes group (AL <22 mm), all three formulae performed almost equally, which can be seen by the almost equal values of MedAE in all three groups (0.35, 0.33, and 0.34). In this group, the percentage of eyes within 0.25 D was more in Kane (41%) compared to that in Barrett (34%) and SRK/T (31%), whereas in the 0.5 D group, it was lower in Kane but not statistically significant.
In the medium eyes group (AL 22–24 mm), Kane performed inferiorly (MedAE 0.26). This finding was statistically significant. There was no significant difference between SRK/T (MedAE 0.25) and Barrett (Med AE 0.22). This finding can be attributed to the fact that the majority of eyes belonged to the medium AL group, thus yielding results similar to the overall sample. The percentage of eyes within 0.25 D in this group was low in Kane (49%), whereas the percentage within 0.5 D was almost the same.
In the long eyes group (AL >24 mm), again, Kane showed higher MedAE (0.24) compared to Barrett (0.17) and SRK/T (0.19), but it was not statistically significant. Among the subjects in this group, the percentage of eyes within 0.25 D was lower in Kane (54%), whereas the percentage within 0.5 D was the same as that of Barrett.
No significant differences were noted between the formulae for short and long eyes. However, this could be due to the much smaller sample set in these groups.
On comparing the formulae across different axial lengths, we found that all three formulae showed a similar trend of improvement in predictability with increasing axial lengths. The lowest MAE and MedAE values were seen in long eyes, followed by medium eyes and then short eyes in all three formulae. However, this trend was significant in SRK-T (P = 0.001; Kruskal–Wallis test) and Barrett formula (P = 0.018; Kruskal–Wallis test) but not so in the Kane formula (P = 0.0537; Kruskal–Wallis test) [Fig. 3].
Figure 3.
Trend of absolute errors of the three formulae across axial lengths
Discussion
Our study was a retrospective chart review performed at a tertiary eye care center in India. In total, 350 subjects were included in the study and were divided into three subgroups depending on the axial lengths. We included patients who had undergone implantation of Tecnis monofocal nontoric IOL ZCB00 IOL (Johnson & Johnson Vision). The outcomes of Tecnis IOL with SRK/T, Barrett, and Kane formula have not yet been reported in any studies.
SRK/T formula is a combination of linear regression methods and a theoretical eye model. Based on the nonlinear terms of the theoretical formulas, the SRK/T also incorporates empirical regression methodology for optimization, resulting in greater accuracy. Studies have shown the high accuracy of SRK/T formula in long eyes.[8,9] However, it does not take into account the effective lens position (ELP), which is an important factor for accurately determining the IOL power.
The Barrett II Universal Formula uses a theoretical model in which the ACD is related to axial length and keratometry, but unlike other formulas, the location of the principal plane of refraction of the IOL is retained as a relevant variable in the formula. Barrett formula also considers the ELP in predicting the IOL power, thus yielding accurate results. This has been consistently proven in various studies.[10,11]
Kane formula was recently developed. It is the only formula that takes into consideration the biological sex of the patient in the calculator. Studies have shown Kane formula to be superior to the majority of the formulae available.[5,12]
We chose these formulae in our study because their principle and the variables taken into account are different from each other. The combination of SRK/T, BUII and Kane formula with OLCR based biometer and Tecnis IOL has not yet been studied. The aforementioned formulae were chosen as they are freely available online which makes them easy to access.
In our study, we found that the mean error of Barrett Universal II is closest to zero among the three formulae, and it was the lowest among the three, showing that it is the most accurate formula in eyes of all axial lengths without lens constant optimization. Similar findings were reported by Khatib et al.[13] in their study.
We also noted that the majority of ME and MedE (median prediction error) showed a myopic trend in all three formulae across all axial lengths. Thus, the recommended lens constant for the Tecnis IOL should be altered for optimization. This finding was opposite to the study by Khatib et al.[13] The purpose of analyzing the outcomes without lens constant optimization was to find the formula that can be used in a scenario when optimization is not possible.
After lens constant optimization, we found that all three formulae performed very well, with MAE and MedAE values within a range of 0.24–0.32 and over 80% eyes within 0.50 D in all three groups. Across the entire range of axial length, Kane formula performed significantly poorly compared to SRK/T and Barrett, whereas Barrett and SRK/T performed equally. This finding was opposite to Connell and Kane[5] who found that Kane was an accurate predictor of IOL power across all axial lengths compared to Barrett. We also found that Kane formula had the lowest percentage of eyes within 0.25 D and 0.5 D compared to the other two, which was again contrary to the finding of Connell and Kane,[5] though the difference was not statistically significant.
On subgroup analysis, we found that in short eyes, the MAE and MedAE of Kane formula were almost equal to that of SRK/T and Barrett, showing that Kane does not outperform SRK/T and Barrett in eyes with axial hyperopia. This finding was again contradictory to the finding of the author of the formula, Kane and Melles.[12] In their study, they found Kane formula having the least MAE compared to Barrett and SRK/T in high hyperopes, thus showing that it is accurate even in small eyes. There was no statistically significant difference between the aforementioned formulae among the short eyes. This finding was consistent with that of Connell and Kane. It can be attributed to the small sample size in this group.
In medium eyes too, Kane performed inferiorly compared to Barrett and SRK/T, with MAE being significantly higher than SRK/T and Barrett. Also, the percentage of eyes within 0.25 D and 0.5 D by Kane was the lowest among the three formulae. This finding can be attributed to the fact that the majority of eyes belonged to the medium AL group, thus yielding results similar to the overall sample. This observation was also opposite to that observed by Connell and Kane.[5] In our study, among the medium eyes, Barrett and SRK/T was almost equal with Barrett being marginally better with MAE and MedAE of Barrett being less than SRK/T. This is consistent with Kane et al.[10] who found that Barrett formula had the lowest MAE compared to the newer generation formulae in all three groups of axial lengths.
As per our study, in long eyes too, the MedAE and MAE of Kane formula are higher than SRK/T and Barrett, indicating that Kane formula is not reliable in eyes with axial myopia. This finding is also against that found by Connell and Kane[5] and Hipólito-Fernandes et al. Hipólito-Fernandes et al.[14] also showed that Kane formula had the lowest MAE among the formulae that they analyzed. There was no significant difference between the three formulae among the axial myopia patients. It could be due to the small sample size in this group.
In our study, the trend analysis of all three formulae in each axial length subgroup showed that all three formulae showed a similar trend of improvement in predictability with increasing axial lengths. The lowest MAE and MedAE values were seen in long eyes, followed by medium eyes and then short eyes in all three formulae. MedAE of SRK/T was significantly different from each other in all three subgroups, the lowest being in the long eyes group. MedAE of Barrett was significantly lower in the long eyes group compared to short and medium eyes, which was almost similar. The MedAE of Kane among the three subgroups was not significantly different.
The limitations of our study could be the relatively small sample size of 350 eyes in contrast to other studies having a sample size of more than 1000 eyes. Probably another subgroup with >26 mm AL may have given interesting results for long eyes as 24–26 mm is sometimes considered in the normal range. Also, we used an OLCR-based biometer, Lenstar (LS 900), for measuring the variables. This device is marginally inferior to SS-OCT-based and PCI-based biometers especially in measuring the axial length.[15] Another limitation could be the use of a single type of IOL. This factor limited our inclusion criteria, especially in the extreme axial lengths. We could not explore the performance of Kane formula by different IOLs owing to the limiting factor of a single IOL. Though our sample size was good enough to meet the aim of our study, a higher sample size could have yielded a better subgroup analysis making the study more powerful.
Conclusion
Kane formula did not outperform Barrett Universal II and SRK/T in Indian eyes. Without lens constant optimization, Barrett formula is the best. With lens constant optimization, all three formulae perform very well, with Barrett and SRK-T being marginally better than Kane. All three formulae show excellent accuracy in long eyes, even better than normal range eyes, which is something that has rarely been reported before. In short eyes, all three perform slightly inferior, which is consistent with the results of previous studies. No one formula seems to be superior to the other in extreme axial lengths. Further studies on Indian eyes exclusively with extreme axial lengths would be helpful to produce significant results.
Financial support and sponsorship
Nil.
Conflicts of interest
There are no conflicts of interest.
References
- 1.Gavin EA, Hammond CJ. Intraocular lens power calculation in short eyes. Eye. 2008;22:935–8. doi: 10.1038/sj.eye.6702774. [DOI] [PubMed] [Google Scholar]
- 2.Kane JX, Van Heerden A, Atik A, Petsoglou C. Intraocular lens power formula accuracy: Comparison of 7 formulas. J Cataract Refract Surg. 2016;42:1490–500. doi: 10.1016/j.jcrs.2016.07.021. [DOI] [PubMed] [Google Scholar]
- 3.Retzlaff J, Sanders DR, Kraff MC. Development of the SRK/T intraocular lens implantation power calculation formula. J Cataract Refract Surg. 1990;16:333–40. doi: 10.1016/s0886-3350(13)80705-5. [DOI] [PubMed] [Google Scholar]
- 4.Kuthirummal N, Vanathi M, Mukhija R, Gupta N, Meel R, Saxena R, et al. Evaluation of Barrett Universal II formula for intraocular lens power calculation in Asian Indian population. Indian J Ophthalmol. 2020;68:59–64. doi: 10.4103/ijo.IJO_600_19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Connell BJ, Kane JX. Comparison of the Kane formula with existing formulas for intraocular lens power selection. BMJ Open Ophthalmol. 2019;4:e000251. doi: 10.1136/bmjophth-2018-000251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Ostri C, Holfort SK, Fich MS, Riise P. Automated refraction is stable 1 week after uncomplicated cataract surgery. Acta Ophthalmol. 2018;96:149–53. doi: 10.1111/aos.13545. [DOI] [PubMed] [Google Scholar]
- 7.Wang L, Koch DD, Hill W, Abulafia A. Pursuing perfection in intraocular lens calculations: III. Criteria for analyzing outcomes. J Cataract Refract Surg. 2017;43:999–1002. doi: 10.1016/j.jcrs.2017.08.003. [DOI] [PubMed] [Google Scholar]
- 8.Chen C, Xu X, Miao Y, Zheng G, Sun Y, Xu X. Accuracy of intraocular lens power formulas involving 148 eyes with long axial lengths: A retrospective chart-review study. J Ophthalmol 2015. 2015 doi: 10.1155/2015/976847. 976847. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Hoffer KJ, Savini G. IOL power calculation in short and long eyes. Asia Pac J Ophthalmol (Phila) 2017;6:330–1. doi: 10.22608/APO.2017338. [DOI] [PubMed] [Google Scholar]
- 10.Kane JX, Van Heerden A, Atik A, Petsoglou C. Accuracy of 3 new methods for intraocular lens power selection. J Cataract Refract Surg. 2017;43:333–9. doi: 10.1016/j.jcrs.2016.12.021. [DOI] [PubMed] [Google Scholar]
- 11.Melles RB, Holladay JT, Chang WJ. Accuracy of intraocular lens calculation formulas. Ophthalmology. 2018;125:169–78. doi: 10.1016/j.ophtha.2017.08.027. [DOI] [PubMed] [Google Scholar]
- 12.Kane JX, Melles RB. Intraocular lens formula comparison in axial hyperopia with a high-power intraocular lens of 30 or more diopters. J Cataract Refract Surg. 2020;46:1236–9. doi: 10.1097/j.jcrs.0000000000000235. [DOI] [PubMed] [Google Scholar]
- 13.Khatib ZI, Haldipurkar SS, Shetty V, Dahake H, Nagvekar P, Kashelkar P. Comparison of three newer generation freely available intraocular lens power calculation formulae across all axial lengths. Indian J Ophthalmol. 2021;69:580–4. doi: 10.4103/ijo.IJO_943_20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Hipólito-Fernandes D, Elisa Luís M, Gil P, Maduro V, Feijão J, Yeo TK, et al. VRF-G, a new intraocular lens power calculation formula: A 13-formulas comparison study. Clin Ophthalmol. 2020;14:4395–402. doi: 10.2147/OPTH.S290125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kane JX, Chang DF. Intraocular lens power formulas, biometry, and intraoperative aberrometry: A review. Ophthalmology. 2021;128:e94–114. doi: 10.1016/j.ophtha.2020.08.010. [DOI] [PubMed] [Google Scholar]