Abstract
Competing and complementary models of resting-state brain dynamics contribute to our phenomenological and mechanistic understanding of whole-brain coordination and communication, and provide potential evidence for differential brain functioning associated with normal and pathological behaviour. These neuroscientific theories stem from the perspectives of physics, engineering, mathematics and psychology and create a complicated landscape of domain-specific terminology and meaning, which, when used outside of that domain, may lead to incorrect assumptions and conclusions within the neuroscience community. Here, we review and clarify the key concepts of connectivity, computation, criticality and coherence—the 4C's—and outline a potential role for metastability as a common denominator across these propositions. We analyse and synthesize whole-brain neuroimaging research, examined through functional magnetic imaging, to demonstrate that complexity science offers a principled and integrated approach to describe, and potentially understand, macroscale spontaneous brain functioning.
Keywords: complexity, connectivity, computation, criticality, metastability, integrated information
1. Introduction
The orchestrated activity of the approximately 100 billion neurons connected via an estimated 200 trillion synapses in the human brain [1] is certainly perplexing, and its explanation has allured scientists for more than 100 years [2]. A popular way to approach this challenge has been to see the brain as a computer, i.e. a physical instantiation of algorithms that works on inputs from various sensory systems in order to generate behaviour [3–6]. The computational view of the brain has introduced important new conceptual resources to neuroscience, providing a (in principle) feasible roadmap of how one could attempt to understand the brain—e.g. through Marr's celebrated ‘three levels of analysis' [7].
While the brain can be seen as a computer, it is first and foremost a living organ driven by metabolic and thermodynamic constraints. In effect, while an uninformed computational view could suggest that the brain is ‘idle’ when not actively engaging with a specific task, early evidence has shown that the brain accounts for 20% of the body's energy consumption while making up just 2% of body weight [8]. In effect, brain functional activity may be spontaneous or evoked with cognitive, behavioural or motor tasks, and the metabolic cost of spontaneous or intrinsic activity far exceeds the costs for evoked activity [9]. Despite this evidence, and the work of notable pioneers such as Freeman [10], neuroimaging data from resting-state conditions did not attract as much attention within the neuroimaging community as data from task-related conditions. Nonetheless, there is nowadays a growing consensus that making sense of spontaneous brain activity is crucial for understanding brain function [11–13].
Among the available neuroimaging techniques, functional magnetic resonance imaging (fMRI) provides a modality to probe resting-state whole-brain activity at a high spatial resolution. Evidence has repeatedly shown that the resulting time series of resting-state experiments are highly structured, in a way that is not easy to explain purely in terms of an input/output information-processing perspective. Here, we argue that complexity science provides an important complement to the computational view for building explanations on the nature of these data.
Complexity science aims to identify common laws that govern complex systems made by multiple interactive elements, bringing together tools from statistical physics, dynamical systems theory (DST), information theory (IT) and other fields [14–16]. Although this multiplicity of approaches brings richness to the research, it can also inadvertently lead to inconsistent use of terminology, misunderstandings, and to potentially inconsistent conclusions. Adding to these problems, neuroscientists face the challenge of translating diverse domain-specific conceptual theories and models into plausible biophysical mechanisms. Acknowledging the magnitude of this challenge, in this paper, we review the notions of connectivity, intrinsic computation, criticality and coherence—the 4C's of the brain at rest—from a complexity science perspective.
2. Background
2.1. Complexity in the brain
Conceptualizing the brain as a complex system is an especially powerful way to investigate the spontaneous ongoing dynamics of the brain [17]. While the exact definition of a complex system is still under debate [17,18], the brain satisfies the four properties all systems characterized as ‘complex’ necessarily share [19]:
-
1.
Multiplicity and interdependence: the brain is made of small subunits that interact with each other through a vast network of local and long-range connections.
-
2.
Nonlinearity: the interactions between neural elements are often nonlinear, giving rise to rich dynamical phenomena.
-
3.
Self-organization: the activity of the multiple brain subunits develops into structured patterns spontaneously, in the absence of any form of centralized control mechanisms.
-
4.
Emergence: the macroscopic behaviour of coordinated brain activity cannot be understood purely in terms of the neuron-to-neuron interactions.
This perspective allows us to bring the sophisticated conceptual machinery of complexity science to the study of the brain, while extending the repertoire of techniques employed in neuroimaging analysis with tools specifically designed to fully exploit the richness of such datasets.
At a high level, we will consider two distinct approaches to brain complexity: one from the perspective of nonlinear DST, and one from the application of IT. In the former, complexity is associated with dynamical instabilities giving rise to pattern formation, self-organization and metastability [20–22]. In the latter, complexity is related to the statistical structure of brain activity, typically quantified with tools derived from entropy or mutual information (MI) [23]. In order to situate our 4C's within these approaches, we provide in the next sections a brief overview of the intuitions and terminologies native to these two approaches.
2.2. Dynamical systems theory
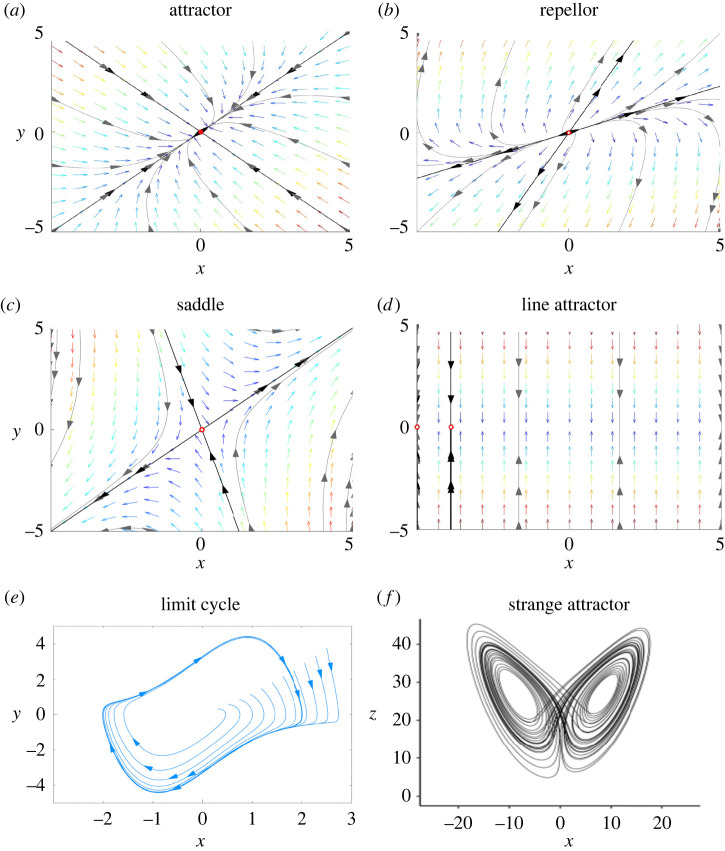
A dynamical system is a system that changes over time in a way that can be described by a single or a set of differential equations [24]. If there are nonlinear interactions among the variables of the system, the system is described by nonlinear equations and is referred to as a nonlinear dynamical system. Given a set of initial conditions, the solution to the differential equation(s) can be plotted in a phase diagram that illustrates the temporal evolution or trajectory of the system. These trajectories exist within an n-dimensional phase space,1 which gives an account of the possible solutions that the system could potentially adopt—with n reflecting the dimensionality of the representation of the system. If a family of trajectories (i.e. solutions of the equations starting from different initial conditions) flows towards a particular region of phase space, that region is known as an attractor. If small perturbations in the system eventually return the system to its current attractor, the attractor (solution) is said to be stable. Conversely, if the trajectories flow away from a region, that region is considered a repellor. If trajectories flow towards an attractor in one dimension, but away from it in another, the region is referred to as a saddle point. Attractors may be fixed points, fixed lines, stable or unstable limit cycles, or when characterized by more complex forms, they are termed strange attractors [24] as illustrated in figure 1.
Figure 1.
Phase portraits—geometrical representations of trajectories in dynamical systems with different attractor types (with or without vector fields). A phase portrait is a plot of the trajectories of a dynamical system. Colour-coded slope or vector fields represent the rate of change of the trajectory at that point with respect to time—deep red indicates high rates of change and dark blue indicates low rates of change. Examples of trajectories for different initial conditions are shown in black. (a–d) Produced with Phase Portrait Plotter [26]. (e) XaosBits at English Wikipedia, CC BY 2.5, https://commons.wikimedia.org/w/index.php?curid=732841. (f) The Lorenz attractor is an example of a strange attractor [27].
Thinking in terms of attractors enables some useful taxonomies for dynamical systems: a multi-stable system is a system with more than one attractor; a metastable system is a system with a saddle which may be linked in sequence with other saddles; and finally, a critical system is a system that has an attractor that responds to small perturbations with long and unstructured excursions [28] (the notion of criticality is developed in a later section).
A system exhibits dynamic stability if it reliably returns to its steady-state attractor after perturbations. A parameter of the system that is capable of driving the system out of dynamic stability is called a control parameter. At a point of instability, a bifurcation often occurs—where a single attractor divides in two or changes shape, and solutions that were previously stable become unstable.
The preceding description adheres to the terminology of mathematics. In statistical physics, a variable in a dynamical system is known as a state variable; and a bifurcation is referred to as a phase transition [29]. Water turning into ice at 0°C is an example of a first-order phase transition where the density of H2O changes abruptly at the freezing point (resulting in the well-known increase in volume). By contrast, an iron magnet changing from being ferromagnetic to paramagnetic at 770oC is an example of a second-order phase transition. The net magnetization does not change abruptly at the Curie temperature; rather, at the critical point there is a divergence of the magnetic susceptibility, resulting in large fluctuations of the magnetization. Hence, first-order phase transitions display a discontinuity on an observable (e.g. density), while second-order transitions display discontinuities in some of their derivatives (e.g. the rate of change of the magnetization with respect to an external field) [30].
2.3. Information theory
In the dynamical systems framework, relationships between variables are typically described in terms of differential equations. A complementary description investigates the interactions between the variables through their statistical interdependencies. These interdependencies may be probed via statistics and probability theory, and more specifically through the framework of information dynamics [31,32], which aims to describe complex dynamical interdependencies via MI [33,34] and related tools.
In general, the (statistical) entropy of a signal measures its degree of variability or diversity. Similarly, the MI between two signals captures their covariation—or more precisely, to what extent the observed values are different from the values from similar but statistically independent signals. Using these basic building blocks, a range of different extended measures of interdependencies can be built. For example, transfer entropy corresponds to how well the future of a ‘target’ signal can be predicted from the past of a ‘source’ signal, over and above how well the target signal predicts itself [35,36]. As another example, there exist various multivariate extensions of the MI that capture high-order (i.e. beyond pairwise) interactions, which can be characterized as assessing different types of covariation [37], or via other mathematical principles such as cohomology [38].
An important feature of information-theoretic tools is their great flexibility: these tools can be applied to ordinal, categorical, and continuous data from linear and nonlinear systems. Their generality and wide range of applicability turns the notion of information into a powerful ‘common currency’, through which interdependencies in different systems can be characterized and compared [31,37,39,40].
It is important to bear in mind that, in these types of applications, information-theoretic quantities are not conceptualized in terms of optimal solutions to engineering problems of data transmission (i.e. Shannon's characterization), but as descriptions of states of incomplete knowledge—following the seminal work of Jaynes [41]. Therefore, measures like statistical entropy, MI, transfer entropy and multivariate information measures are understood not as actual bits being transferred through a communication channel [42], but as inferential statements about the statistical structure of the system of interest [43].
3. The 4C's: conceptual approaches to spontaneous brain dynamics
Building on a view centred on complexity, dynamical systems and IT, the following sections review various approaches to analyse brain activity captured with fMRI at rest from a complexity-science perspective. Furthermore, we discuss recent findings where this approach revealed novel relationships between DST and information dynamics.
3.1. Connectivity: networks and patterns
Experimental evidence accumulated in recent years has revealed that variation in structure and function in the human brain (both for normal development and for disease) tends to be widely distributed, and hence there is often no simple one-to-one mapping between cognitive functions and individual brain regions [44–47]. An important paradigm shift in neuroimaging research was therefore to go beyond mere activation and focus instead on co-activation, i.e. on the interdependency between the activity of multiple regions. The fact that the latter approach is providing rich empirical results is likely related to the anatomical configuration of the central nervous system, which constitutes an organized network of axonal tracts between distinct grey matter regions. This evolving map of structural connections between neuronal elements is known as the (structural) ‘connectome’ [48,49], which can be assessed non-invasively in vivo via probabilistic or deterministic tractography based on diffusion-weighted MRI imaging [48].
Contrasting with structural connectivity (SC), which refers to the physical anatomical connections between regions, functional connectivity (FC) refers to the statistical relationship of coordinated activity in spatially distant regions [50]. Before moving on to more elaborate (and perhaps more principled) approaches to connectivity, we will briefly review the origins of FC. Temporal correlations of slow spontaneous fMRI fluctuations of less than 0.1 Hz between brain regions were initially observed in the early 1990s during task execution [51]. Similar correlations were then observed between the left and right sensorimotor cortices when the brain was at rest [52]. Since then, it has been shown—initially through positron emission tomography, and now more commonly with fMRI—that spontaneous activity reflects sustained functionality in the form of a ‘default mode’ of intrinsic connectivity [53]. Patterns of resting-state temporal correlations have been extracted and documented as resting-state networks (RSNs) [53–55] using a multitude of methods.
Evolving from FC, whether static or time-varying [56], a number of different forms of connectivity have been defined and named to distinguish them from canonical statistical relationships. Effective connectivity, evaluated, for example, via dynamic causal modelling [57,58], aims to infer the causal architecture of dynamical systems. Time-varying or dynamical FC (dFC) has also progressed beyond statistical relationships in temporal correlations. Indeed, dFC has been elucidated with phase relationships [59–61] and information-theoretic measures [62], which are in principle more amenable for investigations in nonlinear dynamical systems [63,64].
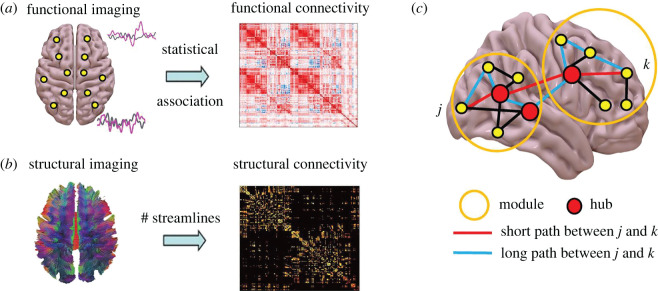
Although the word ‘network’ is usually used to define resting-state FC, the tools of graph theory (such as community structure [65]) can be applied to a range of scenarios. For example, from a complexity science perspective both SC and FC (however defined) can be conceptualized as networks—considering systems of neuronal ensembles or regions to be nodes (or vertices), connected by links (edges) corresponding to either axonal projections (SC) or FC relationships [66,67] (figure 2). As a matter of fact, the broad application of graph theory to a range of aspects of brain imaging data has given birth to the emerging field of network neuroscience [68–71].
Figure 2.
Connectivity in the human brain. (a) Functional connectivity can be quantified from functional MRI, as the linear correlation statistical relationships between BOLD signals. (b) Structural connectivity can be quantified from diffusion-weighted MRI, as the white matter streamlines between regions. (c) Graph theory can characterize local properties of individual nodes (e.g. high-degree nodes or ‘hubs’) but also mesoscopic properties (e.g. modular organization) and macroscale (e.g. average shortest path length in the network).
Studies following this approach have shown that healthy brain SC and FC networks exhibit a host of complex network features, including small-worldness [72,73], short path lengths, high clustering, hubs [66], a rich club [74], a diverse club [75], within a modular and fractal (self-similar) community structure [76–78]. Examples of graph-theoretic metrics that are commonly employed in neuroscience may be found in electronic supplementary material, table S1. The ‘rich club’ of strongly interconnected bi-hemispheric hub regions includes superior parietal and frontal cortices, precuneus, putamen, hippocampus and thalamus, which are considered to be crucial for whole-brain communication [74].
Overall, conceptualizing the brain in terms of structural and functional networks has made it possible to import into neuroscience a number of well-developed mathematical tools from complexity science, providing a much-needed framework to study the brain as the interconnected system it is.
3.2. Computation and information dynamics
3.2.1. Integrated information and partial information decomposition
The great flexibility and interesting interpretability of information-theoretic measures have triggered a large range of investigations of the human brain using such tools. Early efforts in information-theoretic analysis of resting brain activity endeavoured to formalize the notion of ‘dynamical complexity’, understood as the simultaneous occurrence of functional segregation and global integration in the brain [79]. Systems exhibiting both high integration and a high specialization exhibit functional patterns of the highest dynamical complexity. Subsequent work inspired by further developments of these ideas led to a measure of ‘integrated information’, Φ, that quantifies the ability of a system to carry information as a whole beyond what is carried by its parts [80], which leads towards novel and practical measures for data analysis [81,82].
However, the intuition that information can only be transferred or stored between parts of a system fails to capture the full range of possible information dynamics, as noted, for example, by James et al. [42]. Another important extension of classic information-theoretic tools to capture such higher-order interactions is provided by the framework of partial information decomposition (PID) [83].2 PID proposes a formal decomposition of the MI provided by various predictors about a target variable, introducing three fundamentally distinct types of information: redundant, unique and synergistic. Intuitively, unique information refers to information that is provided by one predictor but not the others, redundancy refers to the case where multiple predictors each provide the same information about the target, and synergy refers to predictive information that only becomes available if the predictors are considered together. There is an ongoing discussion on how to best calculate these different types of information in practice, which constitutes an active area of ongoing research. However, despite their technical differences, many of these proposals do not differ much in practical setups [84,85], and have been proven successful in various applications.
This powerful extension of classic IT has already found successful application in neuroscience; for example, PID has been used to assess synergistic information processing in an organotypic culture of spiking neurons [86], to link information storage and information transfer to sub- and supercritical regions of phase transition in a neuronal population oscillator model [87], and to show that rich club neurons perform 160% more computation than non-rich club neurons [88]—providing avenues to combine the information-dynamic and graph-theoretic views of the brain.
3.2.2. Applications of ΦID: integrated information decomposition
However, the framework of information dynamics introduced by PID is restricted to scenarios with a single target variable, being unable to discriminate between different ways in which two or more target variables can be affected collectively. To account for how multiple variables jointly affect one another's temporal evolution, a further generalization is needed. Building on intuitions from both Φ and PID, the framework of integrated information decomposition (ΦID) proposes an encompassing taxonomy for the diverse information dynamics phenomena that can take place in complex stochastic systems [82], [Preprint] [89]. ΦID has two main features: it can be used to decompose and hence better understand existent measures of complexity; and it can provide the fundamental building blocks to tailor new measures that track specific processes of interest. Such new measures have been able to reconcile the dynamical systems and information dynamic views of complexity. As an example of the former, ΦID has been used to show that existing quantifications of integrated information (and related quantities such as ‘causal density’ [90]) are not capturing a unique type of information dynamics, but rather conflating multiple ones. Following this finding, a revised version of Φ—denoted by ΦR—has been proposed, which has been shown to capture various important aspects of a broad range of complex systems [91,92], and be more precise than Φ in finding or detecting specific differences between conscious and unconscious dynamics of the human brain [93].
More broadly, ΦID is enabling novel ways to conceptualize brain function, by providing an information-resolved FC that complements the time-resolved perspective [93]. Empirical analyses based on fMRI data have shown a role for redundancy in ensuring robust input/output communication channels, as is especially prominent in somatomotor and sensory regions. By contrast, synergy is related to efficient communication in high-order association cortices, and supports humans' sophisticated cognitive functions, being more prominent in evolutionarily expanded regions of the cerebral cortex [93]. The further identification of specific molecular, cytoarchitectonic and metabolic profiles suggests that in the close future we may be able to embody information processing properties into tissues’ biophysical properties, a critical step towards supporting the biological plausibility of intrinsic computation in the brain.
Crucially, ΦID also provides a mathematical framework as a basis for formalizing causal emergence. This framework has shown the emergence of motor information from electrocorticography recorded from a macaque's motor cortex, and also that emergent dynamics are more prevalent in healthy controls rather than in subjects with serious brain lesions. Therefore, ΦID provides a way to address two of the key aspects of a complex system outlined in [19] and [17]: namely, multiplicity and emergence.
3.3. Criticality
3.3.1. Origins and meanings
Criticality refers to scenarios where collective properties of a system composed of many parts exhibit an abrupt change—akin to the freezing of water when temperature goes below 0°C. In general, a system is said to undergo a phase transition when a small change in a control parameter (e.g. temperature) causes a large collective change (e.g. freezing). In textbooks, criticality is often illustrated through canonical examples, most prominently the Ising spin model [94], which possesses a well-studied phase transition between disordered and magnetized states. Importantly, besides the abrupt change in the order parameter that defines them, a system that is near a phase transition (or critical point) displays a host of unusual features: long-range correlations, power law (also known as scale-free3) statistics, fractal structure, long transient periods and sensitivity to external perturbations—to name a few [28,30,95]. Furthermore, theoretical and computational work has demonstrated that systems poised near criticality can exhibit several advantageous computational properties, such as an extended range of responses to inputs [96] or increased transfer of information [97]. It is for these reasons that some have suggested the idea of criticality as a universal guiding principle for brain organization [30,98,99].
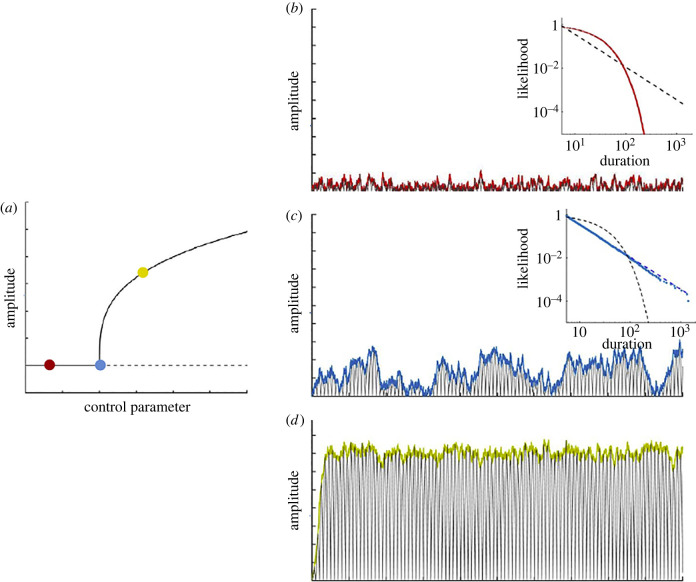
One important distinction is that between statistical criticality, in which a system is in a critical state and follows the statistical patterns discussed above, and dynamical criticality, in which the system is close to a phase transition, or in mathematical terms, lies close to a dynamical bifurcation, where small deviations can lead to an abrupt change in its dynamical behaviour. The position of a system with respect to the bifurcation defines whether it is classified as subcritical (the system has a steady state equilibrium but responds to perturbation with dampened oscillations) and supercritical (where the stability of the steady state equilibrium is lost and oscillations are self-sustained). At the bifurcation point, the equivalent stability of both steady-state and oscillatory equilibria drives large amplitude fluctuations exhibiting statistical patterns of critical systems (figure 3).
Figure 3.
Criticality in a low-dimensional system consisting of a few interacting components. (a) Diagram of a supercritical bifurcation depicting the amplitude of a system's state variable (y-axis) as a function of a control parameter (such as the strength of interactions, x-axis). When the control parameter is increased, the activity of the system switches from subcritical (red circle) to a supercritical regime (yellow circle). The point of change is known as the critical point (blue circle). (b) In the presence of noise, the subcritical system (red circle) systematically returns to the steady state equilibrium with rapidly decaying amplitude. The duration of high amplitude events follows an exponential probability distribution (red dots, inset). (c) At the critical point, the amplitude fluctuations have high variance, rising and falling slowly due to the transient stability of oscillations. The relationship between the duration and the likelihood of high amplitude oscillations follows a power law distribution, corresponding to a linear relationship in double logarithmic coordinates with a slope described by a critical exponent of −3/2 (inset). (d) Beyond the critical point, the system is in a supercritical regime and exhibits sustained oscillations with small amplitude variability. Adapted from [28] with permission from Elsevier.
The idea that critical states are particularly important in nature received further support with the idea of self-organized criticality, which postulates that dynamical systems can self-organize into a critical state spontaneously, without careful fine-tuning of a control parameter [100]. Unfortunately, applying these principles in practical scenarios is a challenging endeavour. In fact, it is known that some systems may display some, but not all, of the properties of the classical critical models; and that exotic phenomena can take place in systems with heterogeneous components, like smeared phase transitions [101] or Griffiths phases [102]. Furthermore, while statistical and dynamical criticality are often related, they can also occur independently of each other [103]. It is for these reasons, among others, that the study of criticality in neural systems is rife with difficulties and misunderstandings.
3.3.2. Criticality in the brain
Despite significant challenges, over the last 20 years scientists have found evidence for multiple signatures of criticality in neural data from multiple modalities. Arguably, the first evidence of this kind was found in human brain oscillations in the large variability, long-range temporal correlations, and power law scaling of electroencephalography (EEG) amplitude fluctuations in the 10–20 Hz frequency range [104]. Mesoscale signatures of criticality were demonstrated in the scale-free power law distribution of size and life-time of neuronal avalanches in mature organotypic cultures and acute slices of rat cortex [105]. These local synchronized activity patterns were confirmed to be scale-free in awake non-human primates [106]; this finding was an important intermediate transition towards demonstration of avalanches in human neuroimaging. Subsequently, scale-free avalanche dynamics were found in resting magnetoencephalography (MEG) [107].
More recently, scale-free avalanche dynamics were found in a combined broadband analysis of MEG and EEG, confirming that broadband resting state activity measured with MEG and EEG can be described as a series of neuronal avalanches [108]. At a larger scale, studies in resting-state fMRI have shown avalanches of activated clusters of voxels using an innovative point-process [109]. Scale-free power law distributions have also been found in the life-time of phase-locked activity between different brain regions in fMRI and MEG [110], although these findings have been contested [109,111]. Returning to long-range temporal correlations, these amplitude correlations in the 10–20 Hz frequency range have been found to correlate with behavioural scaling [112], and to reproduce in broadband signals [108]. In addition to temporal correlations, long-range spatial correlations were found in resting state fMRI using spatial coarse graining [113].
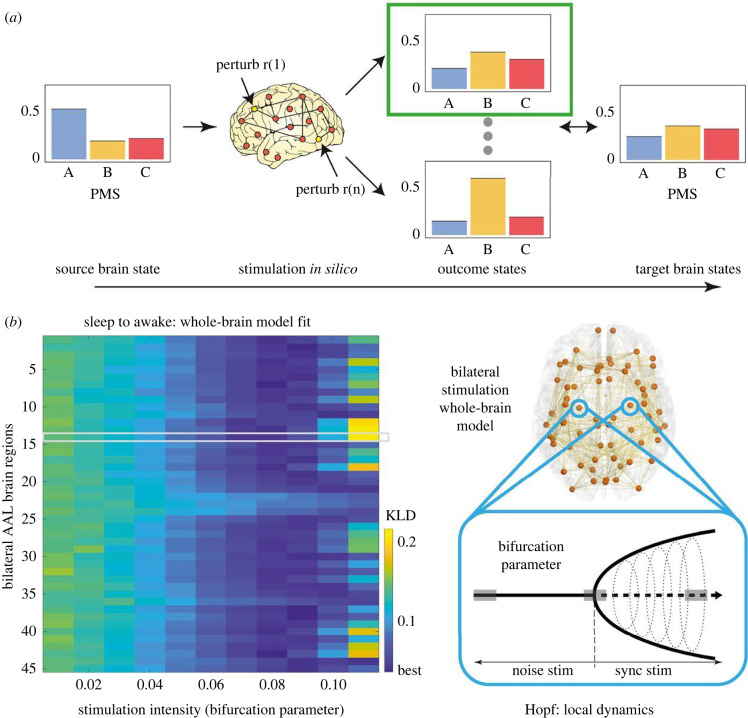
Interestingly, these signatures of criticality seem to be characteristic of healthy, conscious brain dynamics. Deviations from critical dynamics were found in MEG in interictal epileptiform activity in epilepsy patients [114] and disruption of long range temporal correlations has been found in patients with major depressive disorder [115], early-stage Alzheimer's disease [116] and in healthy adults during deep sleep [117]. During loss of consciousness, the long-range amplitude correlations across brain regions disappear [118] and overall the brain appears to move away from dynamical criticality towards greater dynamic stability [119]. By contrast, during consciousness dynamical criticality is maintained as the underlying dynamical modes hover in the vicinity of the critical stability threshold [120]. These findings are consistent with a computational model of the difference in stability between awake and sleep states [121]. The dynamic stability in the sleep state was reflected in a rigidity to external perturbations. By contrast, the awake state was reflected in a longer integration of the perturbations and a slower return to equilibrium dynamics. Building on these findings, a further study showed that shifting certain dynamical modes in the model towards their critical stability threshold through local bifurcation parameter changes, stimulated switching between sleep and awake states [122] as shown in figure 4. Although the studies of Solovey et al. [119] and Deco et al. [121,122] were not related, the results demonstrate the linkages between critical control parameters at the level of individual regions or dynamical modes, and the resulting whole-brain dynamical criticality or stability.
Figure 4.
Schematic of strategy for forcing transition between source and target brain states. (a) The brain regions in the whole-brain model of the source state can be systematically stimulated, and the results can be compared to the target state. Specifically, in the local-region Hopf model, it is easy to perturb the model by simply changing the bifurcation parameter [121]. (b) The stimulation intensity, i.e. the strength of the perturbation, is directly related to the amount of shifting of the local bifurcation parameter [123]. The composite results are shown left of stimulating the whole-brain EC model bilaterally. The KL distance obtained for brain state transition fitting when perturbing separately each of the 45 AAL regions (using bilateral stimulation) with different stimulation intensities in source state (deep sleep) is shown. Here, one region is highlighted in a grey region, which is being stimulated while the other regions are kept at their normal bifurcation parameter. The colour scale for the results shows the level of fitting with the target state (wakefulness), i.e. lower values (deep blue) correspond to the most effective transitions. Hopf model—a computational model that emulates the transition from noisy to oscillatory dynamics as the bifurcation parameter changes; KL, Kullback–Leibler; AAL, automated anatomical labelling [124]. Adapted with permission from [122].
Considering the previous discussion on information dynamics, it is interesting to note the link between neuronal avalanches and computation. In neuronal cultures and non-human primates, a special type of neuronal avalanche called coherence potential was identified when a threshold function was applied to binarize local field potentials [125]. Coherence in this sense refers to the resulting waveform (similarity of local field potentials), and potential reflects their all-or-none behaviour, characteristic of action potentials. These coherence potentials propagate macroscopically keeping their amplitude and waveform, involving both short- and long-range cortical co-activations [125]. The emergence of coherence potentials has been likened to the emergence of gliders in Conway's Game of Life [126], and theorized to play a role in information transfer within the cortex at the network level [127,128]. This hypothesis alludes to a powerful link between criticality and computation, which we believe deserves more investigation.
Nonetheless, the concept of criticality in the brain is not without controversy [129]. This stems from its occasional metaphorical use without robust support of empirical data [98,130], and fundamental challenges to power law statistics and universal scaling as critical phenomena [131]. Moreover, recent proposals suggest that the brain may not be in a critical regime, but rather in a quasi-critical [132] or a slightly subcritical regime [133]. Overall, it is clear that while these difficulties continue to generate heated debate, the theory of dynamical criticality and phase transitions brings extremely useful tools to neuroimaging, which can be used pragmatically to characterize brain dynamics across states.
3.4. Coherence and synchronization in the brain
The concept of coherence is fundamental for investigating fluctuating quantities in many scientific disciplines [134]. Although the term is commonly used in neuroimaging research, the precise meaning and mathematical definition varies across studies. For example, FC has been estimated with time–frequency coherence derived from signal magnitude and phase as a function of time and frequency [60], and with phase coherence derived from instantaneous phase differences as a function of time [123]. For narrow band-pass filtered signals, coherence has been defined as the correlation coefficient between two signals [134], and phase synchrony as the instantaneous phase difference between two signals [135]. Using this definition, Varela proposed that dynamic connections, mediated by synchrony between distributed networks, create transient neuronal assemblies that facilitate large-scale integration of functionally specialized brain regions [135].
To understand synchrony, one must first recognize that neural activity is mainly oscillatory due to nonlinear interactions between neurons, with the resulting aggregation of electrical signals producing rhythmic activity at distinct frequencies. Such activity has been measured in spiking neurons, local field potentials and macroscopically with EEG, MEG and fMRI [1]. Oscillations in the gamma frequency (30–60 Hz) reflect the collective firing of action potentials in pyramidal excitatory neurons, coordinated via the delayed negative feedback of gamma aminobutyric acid (GABA) interneurons [136]. This coupling of pyramidal and GABA neurons is known as the pyramidal interneuronal network gamma (PING) network. GABA interneurons also link PING networks into and across individual cortical columns, creating a mechanism for the spread of rapid synchronization and desynchronization across the cortex [137]. It has been shown in computational and empirical studies that these gamma rhythms generate the slow macroscopic whole-brain dynamics observed in MEG and fMRI [138–140]. Varela proposed that canonical motifs such as the PING network were matched by parallel phase synchrony [135].
To avoid confusion with the terms of coherence, phase coherence and phase synchrony, we prefer to discuss the different phase relationships that may exist between distributed neuronal assemblies, or in the context of whole-brain studies, between distributed brain regions. We will focus on two common and complementary measures of phase relationships (figure 5).
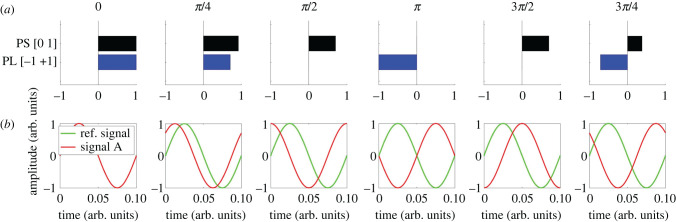
Figure 5.
The phase relationships of phase synchrony and phase-locking. Phase synchrony (PS) reflects the degree of synchronization between the two signals, while phase-locking (PL), evaluated as the cosine of the relative phase, reflects the degree of phase alignment and is sensitive to both in-phase and anti-phase relationships between the two signals. (a) Values of PS and PL for different phase shifts between a reference signal and signal A. (b) Visualization of the reference signal and signal A waveforms over time for different phase shifts.
3.4.1. Phase synchrony and the Kuramoto order parameter
The Kuramoto model of coupled oscillators is a classic model of mathematical physics, being a simple model that is capable of displaying phase transitions and other interesting collective phenomena of great relevance for the study of brain dynamics [141]. The Kuramoto order parameter (KOP) is a metric of instantaneous phase synchrony that encapsulates the collective behaviour of the group of oscillators. Additionally, the time average of this order parameter is a measure of global synchrony, and the variability of the order parameter over time provides a proxy measure of metastability (discussed in detail in the next section). Phase synchrony refers to phase uniformity between neuronal assemblies, being calculated as the magnitude of the average phase. As such, phase synchrony of 1 represents full synchrony while 0 corresponds to complete asynchrony. The KOP has been used to compare global synchrony and metastability in a pharmacological challenge [142], to predict clinical symptoms in schizophrenia [143], and to assess the emergence of cluster synchronization in semi-empirical computational models of coupled oscillators [139].
3.4.2. Phase-locking
Phase-locking refers to a constant relationship between the phases of two neuronal assemblies, commonly calculated as the cosine of the phase difference between two signals. Hence, phase-locking of −1 and +1 represents anti-phase-locking and in-phase-locking, respectively. Phase-locking has been used to identify community structure in fMRI resting state data through dynamic FC [59,144]. Neuronal coherence, measured with phase-locking, underlies the hypothesis that distant neuronal communities do not necessarily need to be synchronized (phase synchrony), since (phase-locked) coherence is sufficient for optimal transfer of spiking-encoded information between the sender and the receiver. Although this communication-through-coherence (CTC) [145–147] hypothesis was proposed for gamma-mediated microscopic neuronal assemblies, the signature of an underlying gamma-band coherence mechanism has been observed in semi-empirical fMRI data [148].
The complementary phase relationships of phase synchrony and phase-locking have recently been investigated in resting state fMRI data. Using a complexity-science approach, a battery of metrics derived from theories of dynamical systems, stochastic processes and information dynamics was developed to characterize resting state dynamics. Novel relationships between the metrics were revealed, allowing a predictive model for ΦR to be constructed using metrics from dynamical systems and IT. Overall, the study showed the complementary utility of phase synchrony and phase-locking, and revealed that the majority of fMRI resting-state characteristics reflected an interrelated dynamical and informational complexity profile [92].
4. Discussion
Viewing the brain as a complex system complements alternative domain-specific models of spontaneous brain activity. With a focus on mesoscale interactions leading to macroscale phenomena, complexity science provides a rich set of concepts, theories and methods from disparate scientific disciplines, which can be used for investigative and explanatory studies of brain dynamics. Complexity in the brain has been associated with dynamic instabilities that give rise to pattern formation and self-organization [22] and with balancing the dialectic dynamics of regional functional segregation with global coherent integration [79]. Taking this into consideration, we have reviewed the key concepts of DST, network science and information dynamics, and illustrated how these notions provide complementary perspectives on the temporal evolution, organization and interactions of macroscopic brain components. We have shown how network science expands on the limitations of canonical FC through identification and quantification of network properties. The notion of criticality was addressed from the perspectives of statistical and dynamical criticality, and the role of perturbation analysis to investigate criticality in both empirical and semi-empirical computational models was discussed [149]. Computation in the absence of tasks, intrinsic computation, was reviewed and shown to be characterized in terms of synergistic and transfer information flows, and quantified by ΦR. Coherence was discussed under its many guises and the complementary nature of phase synchrony and phase-locking was explored. Finally, metastability was introduced as the standard deviation of the Kuramoto order parameter.
Metastability appears to be universal across the 4C's of complex brain dynamics, although it is not yet clear if metastability plays an enabling or a defining role for healthy brain functioning. Metastability expresses a healthy tension between the competition for functional specialization and global coordination in the brain [150]. Indeed, when we review our 4C's we see that for connectivity, metastability was maximized for a community and small-world structure [151], reduced after damage to SC following traumatic brain injury [152], and when at a maximum, revealed a dynamic core in FC [123]. For criticality, statistical indicators of criticality have been observed when metastability was at a maximum [109,110,153]. For computation, global synchronization and ΦR were found to be intimately dependent on metastability [91,92]. Importantly, cluster synchronization, also dependent on metastability, has been shown to drive the transient emergence of collective oscillations, replicating features of resting-state MEG [139]. For coherence, CTC-like routes of communication were found to be optimized when metastability was at a maximum [148].
Metastability has been described as a subtle blend of segregation and integration among brain regions that show tendencies to diverge and function independently, as well as tendencies to converge and function collectively [150]. In dynamical systems, these tendencies occur when a system moves away from a stable equilibrium or attractor and exhibits transient dynamics while remaining away from any attractor of the system [154]. Trajectories in the metastable regime follow a sequence of metastable states or saddle nodes (see §2.2) on a path that joins different equilibrium points, where the unstable dimension of one saddle node is the stable dimension for the following saddle node as illustrated in figure 6 [156]. The system moves between saddle nodes without the need for energy consuming disengagement mechanisms [157], and so freely explores a repertoire of metastable states until changes in the control parameter move the system to a different regime of mono- or multi-stability [157].
Figure 6.
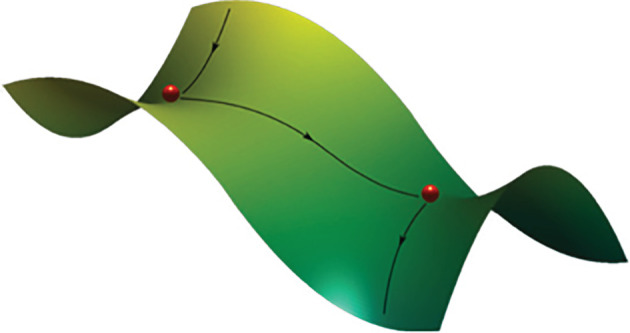
Representation of a path that joins metastable states. In the phase space of a dynamical model, a metastable state is represented by a saddle fixed point. Based on this landscape metaphor, it is easy to see that two saddles can be connected by an unstable one-dimensional saddle. Adapted from [155] with permission from Elsevier.
This highly theoretical conceptualization of metastability has not prevented its investigation in computational and semi-empirical models, and in empirical imaging data. A first quantification of metastability goes back to the late 1990s where it was estimated as the entropy of the spectral density of a time series [158]. However, it was the appearance of the seminal article on the Kuramoto model [141] that led to the now most common quantification of a proxy for metastability as the standard deviation of the KOP4 [138,151,159,160]. Computational models have used this metric of metastability to investigate the relationship between the amplitude modulation envelopes of MEG and the slow fMRI signal [139], to study the effect of lesions on functional brain dynamics [161], to reveal the coincidence of metastability with integrated information [91], and to show that the brain at rest operates at maximum metastability [123]. Furthermore, CTC-like routes of communication, as discussed in §3.4, emerged when metastability was at a maximum in a semi-empirical model of whole-brain dynamic FC [148], putting forward a possible mechanism for flexible communication within a fixed SC.
Studies of metastability have not been confined to computational models. In empirical studies, metastability was shown to be at a maximum when the brain was at rest [162], being reduced during states of unconsciousness [163], and increasing beyond the resting state value during psychedelic states [142,164]. Metastability has also been shown to predict clinical symptoms of schizophrenia [143], reduce progressively for mild cognitive impairment and Alzheimer's disease [165], and be correlated with cognitive flexibility [152] and high-order cognitive ability [166].
In summary, metastability is ubiquitous across diverse models of brain functioning in resting state. Proxy measures of metastability and ΦR provide complementary quantification of complexity, and reveal novel relationships between dynamical and informational complexity [91,92]. It may now be time to better understand the physics behind metastability [167] and so improve the proxies used to measure this universal phenomenon in resting state brain dynamics.
5. Conclusion
Unravelling the mysteries of coordination and communication in RSNs has attracted attention in the scientific disciplines of mathematics, statistical and theoretical physics, network science and IT. This classical leakage of discipline-related methods into neuroimaging research is welcome, despite the resulting introduction of a plethora of terminology and concepts which are not always applied in their strict scientific sense. Under the auspices of complexity science, this review has attempted to disentangle the ‘4C's’ most commonly found in resting-state fMRI literature, locate them in their respective disciplines and conceptualizations, and highlight their complementarities and intersections. The nebulous concept of metastability was shown to be universal across these 4C's and symbiotic with ΦR as a proxy for complexity. Accepting the plausibility and legitimacy of different models of brain functioning, and embracing their eclectic methods and tools, should ultimately lead to improved descriptions, and eventually to understanding and prediction for healthy and disordered brain functioning.
Acknowledgements
The authors would like to acknowledge the use of the following freely available code: Kumar [26].
Footnotes
For historical reasons, the term ‘phase’ here does not refer to the phase of an oscillation, but more in general to the possible phases that any system can explore [25].
The pioneering work from Williams & Beer [83] initiated a subfield of information theory and has been cited in more than 300 peer-reviewed publications.
Scale-free denotes that a system does not possess a characteristic time or length scale. Statistically, the system exhibits a power law probability distribution where the constant exponent k in y ∝ x−k, the critical exponent, is less than 2.
The reasoning behind this proxy is that both extreme values of the KOP (0 and 1) correspond to equilibrium points of the model (desynchronized and hyper-synchronized, respectively). Thus, the standard deviation of the order parameter quantifies how widely it fluctuates between the vicinity of these two equilibrium states.
Data accessibility
This article has no additional data.
Authors' contributions
F.H.: conceptualization, writing—original draft, writing—review and editing; F.E.R.: writing—review and editing; P.A.M.M.: writing—review and editing; A.I.L.: writing—review and editing; J.C.: writing—review and editing; O.D.: writing—review and editing; F.E.T.: conceptualization, supervision, writing—review and editing.
All authors gave final approval for publication and agreed to be held accountable for the work performed therein.
Conflict of interest declaration
We declare we have no competing interests.
Funding
F.H. received no financial support for the research, authorship and/or publication of this article. F.E.R. is supported by the Ad Astra Chandaria foundation. P.A.M.M. is funded by the Wellcome Trust (grant no. 210920/Z/18/Z). A.I.L. is supported by a Gates Cambridge Scholarship (OPP1144). This work was supported by the Alan Turing Institute under EPSRC grant no. EP/N510129/1. J.C. was funded by Portuguese Foundation for Science and Technology (FCT) grant nos. CEECIND/03325/2017, UIDB/50026/2020 and UIDP/50026/2020, Portugal. O.D. is supported by the NIHR Maudsley's Biomedical Research Centre at the South London and Maudsley NHS Trust.
References
- 1.Buzsáki G. 2006. Rhythms of the brain. Oxford, UK: Oxford University Press. See http://www.oxfordscholarship.com/view/10.1093/acprof:oso/9780195301069.001.0001/acprof-9780195301069. [Google Scholar]
- 2.Harlow JM. 1993. Recovery from the passage of an iron bar through the head. Hist. Psychiatry 4, 274-281. ( 10.1177/0957154X9300401407) [DOI] [Google Scholar]
- 3.Myin E, Zahidi K. 2015. Explaining the computational mind, by Marcin Milkowski. Mind 124, 951-954. ( 10.1093/mind/fzv066) [DOI] [Google Scholar]
- 4.Pylyshyn ZW. 1986. Computation and cognition: toward a foundation for cognitive science. Cambridge, MA: The MIT Press. [Google Scholar]
- 5.Rescorla M. 2017. From Ockham to Turing—and back again. In Philosophical explorations of the legacy of Alan Turing (eds Floyd J, Bokulich A). Boston Studies in the Philosophy and History of Science, vol. 324, pp. 279-304. Cham, Switzerland: Springer International Publishing. ( 10.1007/978-3-319-53280-6_12) [DOI] [Google Scholar]
- 6.Richards B. 2018. Yes, the brain is a computer…. Medium. See https://medium.com/the-spike/yes-the-brain-is-a-computer-11f630cad736.
- 7.Marr D. 1982. Vision: a computational approach. San Francisco, CA: Freeman & Co. See https://web.stanford.edu/class/psych209a/ReadingsByDate/01_07/Marr82Philosophy.pdf. [Google Scholar]
- 8.Kety SS, Schmidt CF. 1948. The nitrous oxide method for the quantitative determination of cerebral blood flow in man: theory, procedure and normal values. J. Clin. Invest. 27, 476-483. ( 10.1172/JCI101994) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Raichle ME, Snyder AZ. 2007. A default mode of brain function: a brief history of an evolving idea. Neuroimage 37, 1083-1090. ( 10.1016/j.neuroimage.2007.02.041) [DOI] [PubMed] [Google Scholar]
- 10.Freeman WJ. 2000. Tuning curves to optimize temporal segmentation and parameter evaluation of adaptive filters for neocortical EEG. In Neurodynamics: an exploration in mesoscopic brain dynamics, pp. 313-349. London, UK: Springer. ( 10.1007/978-1-4471-0371-4_14) [DOI] [Google Scholar]
- 11.McCormick DA. 1999. Spontaneous activity: signal or noise? Science 285, 541-543. ( 10.1126/science.285.5427.541) [DOI] [PubMed] [Google Scholar]
- 12.Raichle ME. 2010. Two views of brain function. Trends Cogn. Sci. 14, 180-190. ( 10.1016/j.tics.2010.01.008) [DOI] [PubMed] [Google Scholar]
- 13.Ringach DL. 2009. Spontaneous and driven cortical activity: implications for computation. Curr. Opin. Neurobiol. 19, 439-444. ( 10.1016/j.conb.2009.07.005) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Holland JH. 2014. Complexity: a very short introduction, p. 112. Oxford, UK: Oxford University Press. [Google Scholar]
- 15.Thurner S, Hanel R, Klimek P. 2018. Introduction to the theory of complex systems. Oxford, UK : Oxford University Press. [Google Scholar]
- 16.Waldrop MM. 1993. Complexity: the emerging science at the edge of order and chaos. New York, NY: Pocket Books. [Google Scholar]
- 17.Turkheimer FE, et al. 2021. A complex systems perspective on neuroimaging studies of behavior and its disorders. Neuroscientist. ( 10.1177/1073858421994784) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ladyman J, Lambert J, Wiesner K. 2013. What is a complex system? Eur. J. Phil. Sci. 3, 33-67. ( 10.1007/s13194-012-0056-8) [DOI] [Google Scholar]
- 19.Jensen HJ. 1998. Self-organized criticality: emergent complex behavior in physical and biological systems. Cambridge, UK: Cambridge University Press. See https://www.cambridge.org/core/books/selforganized-criticality/0EE3D52D140A543C2F3A706D18CD4F1A. [Google Scholar]
- 20.Fuchs A, Kelso JAS, Haken H. 1992. Phase transitions in the human brain: spatial mode dynamics. Int. J. Bifurc. Chaos 2, 917-939. ( 10.1142/S0218127492000537) [DOI] [Google Scholar]
- 21.Haken H. 1996. Basic concepts of synergetics. II. Formation of spatio-temporal patterns. In Principles of brain functioning: a synergetic approach to brain activity, behavior and cognition. Springer Series in Synergetics, vol. 67, pp. 149-155. Berlin, Germany: Springer. ( 10.1007/978-3-642-79570-1_11) [DOI] [Google Scholar]
- 22.Kelso JAS. 1995. Dynamic patterns: the self-organization of brain and behavior. Cambridge, MA: The MIT Press. [Google Scholar]
- 23.Cover TM, Thomas JA. 2006. Elements of information theory. Wiley Series in Telecommunications and Signal Processing. New York, NY: Wiley-Interscience. [Google Scholar]
- 24.Strogatz SH. 1994. Nonlinear dynamics and chaos: with applications to physics, biology, chemistry, and engineering. Cambridge, MA: Westview Press. [Google Scholar]
- 25.Nolte DD. 2010. The tangled tale of phase space. Phys. Today 63, 33. ( 10.1063/1.3397041) [DOI] [Google Scholar]
- 26.Kumar M. 2022. Phase Portrait Plotter. See https://www.mathworks.com/matlabcentral/fileexchange/81026-phase-portrait-plotter.
- 27.Keydana S. 2020. RStudio AI Blog: deep attractors: where deep learning meets chaos. See https://blogs.rstudio.com/tensorflow/posts/2020-06-24-deep-attractors/.
- 28.Cocchi L, Gollo LL, Zalesky A, Breakspear M. 2017. Criticality in the brain: a synthesis of neurobiology, models and cognition. Prog. Neurobiol. 158, 132-152. ( 10.1016/j.pneurobio.2017.07.002) [DOI] [PubMed] [Google Scholar]
- 29.Stanley HE. 1971. Introduction to phase transitions and critical phenomena. International Series of Monographs on Physics, vol. 40. Oxford, UK: Oxford University Press. [Google Scholar]
- 30.Chialvo DR. 2010. Emergent complex neural dynamics. Nat. Phys. 6, 744-750. ( 10.1038/nphys1803) [DOI] [Google Scholar]
- 31.Lizier JT. 2013. The local information dynamics of distributed computation in complex systems. Berlin, Germany: Springer. ( 10.1007/978-3-642-32952-4) [DOI] [Google Scholar]
- 32.Lizier JT. 2014. JIDT: an information-theoretic toolkit for studying the dynamics of complex systems. Front. Robot. AI 1. ( 10.3389/frobt.2014.00011) [DOI] [Google Scholar]
- 33.Shannon CE. 1948. A mathematical theory of communication. Bell Syst. Tech. J. 27, 379-473, 623–656. [Google Scholar]
- 34.Shannon CE, Weaver W. 1949. The mathematical theory of communication. Champaign, IL: University of Illinois Press. [Google Scholar]
- 35.Bossomaier T, Barnett L, Harré M, Lizier JT. 2016. An introduction to transfer entropy: information flow in complex systems, pp. 65-95. Cham, Switzerland: Springer International Publishing. ( 10.1007/978-3-319-43222-9_4) [DOI] [Google Scholar]
- 36.Schreiber T. 2000. Measuring information transfer. Phys. Rev. Lett. 85, 461-464. ( 10.1103/PhysRevLett.85.461) [DOI] [PubMed] [Google Scholar]
- 37.Rosas FE, Mediano PAM, Gastpar M, Jensen HJ. 2019. Quantifying high-order interdependencies via multivariate extensions of the mutual information. Phys. Rev. E 100, 032305. ( 10.1103/PhysRevE.100.032305) [DOI] [PubMed] [Google Scholar]
- 38.Baudot P, Tapia M, Bennequin D, Goaillard JM. 2019. Topological information data analysis. Entropy 21, 869. ( 10.3390/e21090869) [DOI] [Google Scholar]
- 39.Crutchfield JP, Feldman DP. 2003. Regularities unseen, randomness observed: levels of entropy convergence. Chaos Interdiscip. J. Nonlinear Sci. 13, 25-54. ( 10.1063/1.1530990) [DOI] [PubMed] [Google Scholar]
- 40.Rosas FE, Ntranos V, Ellison CJ, Pollin S, Verhelst M. 2016. Understanding interdependency through complex information sharing. Entropy 18, 38. ( 10.3390/e18020038) [DOI] [Google Scholar]
- 41.Jaynes ET. 2003. Probability theory: the logic of science. Cambridge, UK: Cambridge University Press. ( 10.1017/CBO9780511790423) [DOI] [Google Scholar]
- 42.James RG, Barnett N, Crutchfield JP. 2016. Information flows? A critique of transfer entropies. Phys. Rev. Lett. 116, 238701. ( 10.1103/PhysRevLett.116.238701) [DOI] [PubMed] [Google Scholar]
- 43.Barnett L, Bossomaier T. 2012. Transfer entropy as a log-likelihood ratio. Phys. Rev. Lett. 109, 138105. ( 10.1103/PhysRevLett.109.138105) [DOI] [PubMed] [Google Scholar]
- 44.Ecker C, et al. 2010. Investigating the predictive value of whole-brain structural MR scans in autism: a pattern classification approach. Neuroimage 49, 44-56. ( 10.1016/j.neuroimage.2009.08.024) [DOI] [PubMed] [Google Scholar]
- 45.Hipólito I. 2022. Cognition without neural representation: dynamics of a complex system. Front. Psychol. 12, 5472. ( 10.3389/fpsyg.2021.643276) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Thompson PM, et al. 2001. Mapping adolescent brain change reveals dynamic wave of accelerated gray matter loss in very early-onset schizophrenia. Proc. Natl Acad. Sci. USA 98, 11 650-11 655. ( 10.1073/pnas.201243998) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Zhuo C, Li G, Lin X, Jiang D, Xu Y, Tian H, Wang W, Song X. 2019. The rise and fall of MRI studies in major depressive disorder. Transl. Psychiatry 9, 335. ( 10.1038/s41398-019-0680-6) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Hagmann P, Cammoun L, Gigandet X, Meuli R, Honey CJ, Wedeen VJ, Sporns O. 2008. Mapping the structural core of human cerebral cortex. PLoS Biol. 6, e159. ( 10.1371/journal.pbio.0060159) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Sporns O, Tononi G, Kötter R. 2005. The human connectome: a structural description of the human brain. PLoS Comput. Biol. 1, e42. ( 10.1371/journal.pcbi.0010042) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Friston KJ. 1994. Functional and effective connectivity in neuroimaging: a synthesis. Hum. Brain Mapp. 2, 56-78. ( 10.1002/hbm.460020107) [DOI] [Google Scholar]
- 51.Bandettini PA, Wong EC, Hinks RS, Tikofsky RS, Hyde JS. 1992. Time course EPI of human brain function during task activation. Magn. Reson. Med. 25, 390-397. ( 10.1002/mrm.1910250220) [DOI] [PubMed] [Google Scholar]
- 52.Biswal B, Yetkin FZ, Haughton VM, Hyde JS. 1995. Functional connectivity in the motor cortex of resting human brain using echo-planar MRI. Magn. Reson. Med. 34, 537-541. ( 10.1002/mrm.1910340409) [DOI] [PubMed] [Google Scholar]
- 53.Raichle ME, MacLeod AM, Snyder AZ, Powers WJ, Gusnard DA, Shulman GL. 2001. A default mode of brain function. Proc. Natl Acad. Sci. USA 98, 676-682. ( 10.1073/pnas.98.2.676) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Damoiseaux JS, Rombouts SARB, Barkhof F, Scheltens P, Stam CJ, Smith SM, Beckmann CF. 2006. Consistent resting-state networks across healthy subjects. Proc. Natl Acad. Sci. USA 103, 13 848-13 853. ( 10.1073/pnas.0601417103) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Fox MD, Snyder AZ, Vincent JL, Corbetta M, Essen DCV, Raichle ME. 2005. The human brain is intrinsically organized into dynamic, anticorrelated functional networks. Proc. Natl Acad. Sci. USA 102, 9673-9678. ( 10.1073/pnas.0504136102) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Lurie DJ, et al. 2020. Questions and controversies in the study of time-varying functional connectivity in resting fMRI. Netw. Neurosci. 4, 30-69. ( 10.1162/netn_a_00116) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Friston KJ. 2009. Causal modelling and brain connectivity in functional magnetic resonance imaging. PLoS Biol. 7, e1000033. ( 10.1371/journal.pbio.1000033) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Zarghami TS, Friston KJ. 2020. Dynamic effective connectivity. Neuroimage 207, 116453. ( 10.1016/j.neuroimage.2019.116453) [DOI] [PubMed] [Google Scholar]
- 59.Cabral J, et al. 2017. Cognitive performance in healthy older adults relates to spontaneous switching between states of functional connectivity during rest. Sci. Rep. 7, 1. ( 10.1038/s41598-016-0028-x) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Chang C, Glover GH. 2010. Time–frequency dynamics of resting-state brain connectivity measured with fMRI. Neuroimage 50, 81-98. ( 10.1016/j.neuroimage.2009.12.011) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Demertzi A, et al. 2019. Human consciousness is supported by dynamic complex patterns of brain signal coordination. Sci Adv. 5, eaat7603. ( 10.1126/sciadv.aat7603) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Ma S, Calhoun VD, Phlypo R, Adalı T. 2014. Dynamic changes of spatial functional network connectivity in healthy individuals and schizophrenia patients using independent vector analysis. Neuroimage 90, 196-206. ( 10.1016/j.neuroimage.2013.12.063) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Pedersen M, Omidvarnia A, Zalesky A, Jackson GD. 2018. On the relationship between instantaneous phase synchrony and correlation-based sliding windows for time-resolved fMRI connectivity analysis. Neuroimage 181, 85-94. ( 10.1016/j.neuroimage.2018.06.020) [DOI] [PubMed] [Google Scholar]
- 64.Quian QR, Kraskov A, Kreuz T, Grassberger P. 2002. Performance of different synchronization measures in real data: a case study on electroencephalographic signals. Phys. Rev. E 65, 041903. ( 10.1103/PhysRevE.65.041903) [DOI] [PubMed] [Google Scholar]
- 65.Newman M. 2010. Networks: an introduction. Oxford, UK: Oxford University Press. See https://oxford.universitypressscholarship.com/10.1093/acprof:oso/9780199206650.001.0001/acprof-9780199206650. [Google Scholar]
- 66.Bullmore E, Sporns O. 2009. Complex brain networks: graph theoretical analysis of structural and functional systems. Nat. Rev. Neurosci. 10, 186-198. ( 10.1038/nrn2575) [DOI] [PubMed] [Google Scholar]
- 67.Cabral J, Kringelbach ML, Deco G. 2012. Functional graph alterations in schizophrenia: a result from a global anatomic decoupling? Pharmacopsychiatry 45(Suppl. 1), S57-S64. [DOI] [PubMed] [Google Scholar]
- 68.Bassett DS, Sporns O. 2017. Network neuroscience. Nat. Neurosci. 20, 353-364. ( 10.1038/nn.4502) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Easley D, Kleinberg J. 2010. Networks, crowds, and markets. Econ. Theory 26, 1-28. ( 10.1017/S0266466609090598) [DOI] [Google Scholar]
- 70.Fornito A, Zalesky A, Breakspear M. 2015. The connectomics of brain disorders. Nat. Rev. Neurosci. 16, 159-172. ( 10.1038/nrn3901) [DOI] [PubMed] [Google Scholar]
- 71.Petersen SE, Sporns O. 2015. Brain networks and cognitive architectures. Neuron 88, 207-219. ( 10.1016/j.neuron.2015.09.027) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Humphries MD, Gurney K. 2008. Network ‘Small-World-Ness’: a quantitative method for determining canonical network equivalence. PLoS ONE 3, e0002051. ( 10.1371/journal.pone.0002051) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Muldoon SF, Bridgeford EW, Bassett DS. 2016. Small-world propensity and weighted brain networks. Sci. Rep. 6, 22057. ( 10.1038/srep22057) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.van den Heuvel MP, Sporns O. 2011. Rich-club organization of the human connectome. J. Neurosci. 31, 15 775-15 786. ( 10.1523/JNEUROSCI.3539-11.2011) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Bertolero MA, Yeo BTT, D'Esposito M. 2017. The diverse club. Nat. Commun. 8, 1277. ( 10.1038/s41467-017-01189-w) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Gallos LK, Makse HA, Sigman M. 2012. A small world of weak ties provides optimal global integration of self-similar modules in functional brain networks. Proc. Natl Acad. Sci. USA 109, 2825-2830. ( 10.1073/pnas.1106612109) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Luppi AI, et al. 2021. Preserved fractal character of structural brain networks is associated with covert consciousness after severe brain injury. NeuroImage Clin. 30, 102682. ( 10.1016/j.nicl.2021.102682) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Varley TF, Craig M, Adapa R, Finoia P, Williams G, Allanson J, Pickard J, Menon DK, Stamatakis EA. 2020. Fractal dimension of cortical functional connectivity networks & severity of disorders of consciousness. PLoS ONE 15, e0223812. ( 10.1371/journal.pone.0223812) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Tononi G, Sporns O, Edelman GM. 1994. A measure for brain complexity: relating functional segregation and integration in the nervous system. Proc. Natl Acad. Sci. USA 91, 5033-5037. ( 10.1073/pnas.91.11.5033) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Balduzzi D, Tononi G. 2008. Integrated information in discrete dynamical systems: motivation and theoretical framework. PLoS Comput. Biol. 4, e1000091. ( 10.1371/journal.pcbi.1000091) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Barrett AB, Seth AK. 2011. Practical measures of integrated information for time-series data. PLoS Comput. Biol. 7, e1001052. ( 10.1371/journal.pcbi.1001052) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Mediano PAM, Seth AK, Barrett AB. 2019. Measuring integrated information: comparison of candidate measures in theory and simulation. Entropy 21, 17. ( 10.3390/e21010017) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Williams PL, Beer RD. 2010. Nonnegative decomposition of multivariate information. (https://arxiv.org/abs/1004.2515)
- 84.Rosas FE, Mediano PAM, Jensen HJ, Seth AK, Barrett AB, Carhart-Harris RL, Bor D. 2020. Reconciling emergences: an information-theoretic approach to identify causal emergence in multivariate data. PLoS Comput. Biol. 16, e1008289. ( 10.1371/journal.pcbi.1008289) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Tax TMS, Mediano PAM, Shanahan M. 2017. The partial information decomposition of generative neural network models. Entropy 19, 474. ( 10.3390/e19090474) [DOI] [Google Scholar]
- 86.Sherrill SP, Timme NM, Beggs JM, Newman EL. 2020. Correlated activity favors synergistic processing in local cortical networks in vitro at synaptically relevant timescales. Netw. Neurosci. 4, 678-697. ( 10.1162/netn_a_00141) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Li M, Han Y, Aburn MJ, Breakspear M, Poldrack RA, Shine JM, Lizier JT. 2019. Transitions in information processing dynamics at the whole-brain network level are driven by alterations in neural gain. PLoS Comput. Biol. 15, e1006957. ( 10.1371/journal.pcbi.1006957) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Faber SP, Timme NM, Beggs JM, Newman EL. 2018. Computation is concentrated in rich clubs of local cortical networks. Netw. Neurosci. 3, 384-404. ( 10.1162/netn_a_00069) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Mediano PAM, et al. 2021. Towards an extended taxonomy of information dynamics via integrated information decomposition. (https://arxiv.org/abs/2109.13186)
- 90.Seth AK, Izhikevich E, Reeke GN, Edelman GM. 2006. Theories and measures of consciousness: an extended framework. Proc. Natl Acad. Sci. USA 103, 10 799-10 804. ( 10.1073/pnas.0604347103) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Mediano PAM, Rosas FE, Farah JC, Shanahan M, Bor D, Barrett AB. 2022. Integrated information as a common signature of dynamical and information-processing complexity. Chaos Interdiscip. J. Nonlinear Sci. 32, 013115. ( 10.1063/5.0063384) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Hancock F, et al. 2022. Metastability, fractal scaling, and synergistic information processing: what phase relationships reveal about intrinsic brain activity. BioRxiv. ( 10.1101/2022.01.17.476583) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Luppi AI, et al. 2022. A synergistic core for human brain evolution and cognition. Nat. Neurosci. 25, 771-782. ( 10.1038/s41593-022-01070-0) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Christensen K, Moloney NR. 2005. Complexity and criticality. Advanced Physics Texts, vol. 1. London, UK: Imperial College Press. See http://www.worldscientific.com/worldscibooks/10.1142/p365. [Google Scholar]
- 95.Werner G. 2010. Fractals in the nervous system: conceptual implications for theoretical neuroscience. Front. Physiol. 1, 15. ( 10.3389/fphys.2010.00015) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Shew WL, Yang H, Petermann T, Roy R, Plenz D. 2009. Neuronal avalanches imply maximum dynamic range in cortical networks at criticality. J. Neurosci. 29, 15 595-15 600. ( 10.1523/JNEUROSCI.3864-09.2009) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Barnett L, Lizier JT, Harré M, Seth AK, Bossomaier T. 2013. Information flow in a kinetic Ising model peaks in the disordered phase. Phys. Rev. Lett. 111, 177203. ( 10.1103/PhysRevLett.111.177203) [DOI] [PubMed] [Google Scholar]
- 98.Mora T, Bialek W. 2011. Are biological systems poised at criticality? J. Stat. Phys. 144, 268-302. ( 10.1007/s10955-011-0229-4) [DOI] [Google Scholar]
- 99.Turing AM. 1950. I.—Computing machinery and intelligence. Mind LIX, 433-460. ( 10.1093/mind/LIX.236.433) [DOI] [Google Scholar]
- 100.Bak P, Paczuski M. 1995. Complexity, contingency, and criticality. Proc. Natl Acad. Sci. USA 92, 6689-6696. ( 10.1073/pnas.92.15.6689) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Vojta T, Hoyos JA. 2010. Smeared quantum phase transition in the dissipative random quantum Ising model. Physica E 42, 383-387. ( 10.1016/j.physe.2009.06.067) [DOI] [Google Scholar]
- 102.Moretti P, Muñoz MA. 2013. Griffiths phases and the stretching of criticality in brain networks. Nat. Commun. 4, 2521. ( 10.1038/ncomms3521) [DOI] [PubMed] [Google Scholar]
- 103.Sorbaro M, Herrmann JM, Hennig M. 2019. Statistical models of neural activity, criticality, and Zipf's law. In The functional role of critical dynamics in neural systems (eds Tomen N, Herrmann JM, Ernst U). Springer Series on Bio- and Neurosystems, vol. 11, pp. 265-287. Cham, Switzerland: Springer International Publishing. ( 10.1007/978-3-030-20965-0_13) [DOI] [Google Scholar]
- 104.Linkenkaer-Hansen K, Nikouline VV, Palva JM, Ilmoniemi RJ. 2001. Long-range temporal correlations and scaling behavior in human brain oscillations. J. Neurosci. 21, 1370-1377. ( 10.1523/JNEUROSCI.21-04-01370.2001) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 105.Beggs JM, Plenz D. 2003. Neuronal avalanches in neocortical circuits. J. Neurosci. 23, 11 167-11 177. ( 10.1523/JNEUROSCI.23-35-11167.2003) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106.Petermann T, Thiagarajan T, Lebedev MA, Nicolelis MA, Chialvo DR, Plenz D. 2009. Spontaneous cortical activity in awake monkeys composed of neuronal avalanches. Proc. Natl Acad. Sci. USA 106, 15 921-15 926. ( 10.1073/pnas.0904089106) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107.Shriki O, Alstott J, Carver F, Holroyd T, Henson RNA, Smith ML, Coppola R, Bullmore E, Plenz D. 2013. Neuronal avalanches in the resting MEG of the human brain. J. Neurosci. 33, 7079-7090. ( 10.1523/JNEUROSCI.4286-12.2013) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Lombardi F, Shriki O, Herrmann HJ, de Arcangelis L.. 2021. Long-range temporal correlations in the broadband resting state activity of the human brain revealed by neuronal avalanches. Neurocomputing 461, 657-666. ( 10.1016/j.neucom.2020.05.126) [DOI] [Google Scholar]
- 109.Tagliazucchi E, Balenzuela P, Fraiman D, Chialvo DR. 2012. Criticality in large-scale brain fMRI dynamics unveiled by a novel point process analysis. Front. Physiol. 3, 15. ( 10.3389/fphys.2012.00015) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 110.Kitzbichler MG, Smith ML, Christensen SR, Bullmore E. 2009. Broadband criticality of human brain network synchronization. PLoS Comput. Biol. 5, e1000314. ( 10.1371/journal.pcbi.1000314) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111.Botcharova M. 2014. Modelling and analysis of amplitude, phase and synchrony in human brain activity patterns. See https://discovery.ucl.ac.uk/id/eprint/1443453/1/M%20Botcharova%20Thesis%20v9_FINAL.pdf.
- 112.Palva JM, Zhigalov A, Hirvonen J, Korhonen O, Linkenkaer-Hansen K, Palva S. 2013. Neuronal long-range temporal correlations and avalanche dynamics are correlated with behavioral scaling laws. Proc. Natl Acad. Sci. USA 110, 3585-3590. ( 10.1073/pnas.1216855110) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 113.Expert P, Lambiotte R, Chialvo DR, Christensen K, Jensen HJ, Sharp DJ, Turkheimer F. 2011. Self-similar correlation function in brain resting-state functional magnetic resonance imaging. J. R. Soc. Interface 8, 472-479. ( 10.1098/rsif.2010.0416) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 114.Arviv O, Medvedovsky M, Sheintuch L, Goldstein A, Shriki O. 2016. Deviations from critical dynamics in interictal epileptiform activity. J. Neurosci. 36, 12 276-12 292. ( 10.1523/JNEUROSCI.0809-16.2016) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 115.Linkenkaer-Hansen K, Monto S, Rytsälä H, Suominen K, Isometsä E, Kähkönen S. 2005. Breakdown of long-range temporal correlations in theta oscillations in patients with major depressive disorder. J. Neurosci. 25, 10 131-10 137. ( 10.1523/JNEUROSCI.3244-05.2005) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 116.Montez T, et al. 2009. Altered temporal correlations in parietal alpha and prefrontal theta oscillations in early-stage Alzheimer disease. Proc. Natl Acad. Sci. USA 106, 1614-1619. ( 10.1073/pnas.0811699106) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 117.Tagliazucchi E, von Wegner F, Morzelewski A, Brodbeck V, Jahnke K, Laufs H.. 2013. Breakdown of long-range temporal dependence in default mode and attention networks during deep sleep. Proc. Natl Acad. Sci. USA 110, 15 419-15 424. ( 10.1073/pnas.1312848110) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 118.Tagliazucchi E, Chialvo DR, Siniatchkin M, Amico E, Brichant JF, Bonhomme V, Noirhomme Q, Laufs H, Laureys S. 2016. Large-scale signatures of unconsciousness are consistent with a departure from critical dynamics. J. R. Soc. Interface 13, 20151027. ( 10.1098/rsif.2015.1027) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 119.Solovey G, Alonso LM, Yanagawa T, Fujii N, Magnasco MO, Cecchi GA, Proekt A. 2015. Loss of consciousness is associated with stabilization of cortical activity. J. Neurosci. 35, 10 866-10 877. ( 10.1523/JNEUROSCI.4895-14.2015) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 120.Alonso LM, Solovey G, Yanagawa T, Proekt A, Cecchi GA, Magnasco MO. 2019. Single-trial classification of awareness state during anesthesia by measuring critical dynamics of global brain activity. Sci. Rep. 9, 4927. ( 10.1038/s41598-019-41345-4) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 121.Deco G, et al. 2018. Perturbation of whole-brain dynamics in silico reveals mechanistic differences between brain states. Neuroimage 169, 46-56. ( 10.1016/j.neuroimage.2017.12.009) [DOI] [PubMed] [Google Scholar]
- 122.Deco G, Cruzat J, Cabral J, Tagliazucchi E, Laufs H, Logothetis NK, Kringelbach ML. 2019. Awakening: predicting external stimulation to force transitions between different brain states. Proc. Natl Acad. Sci. USA 116, 18 088-18 097. ( 10.1073/pnas.1905534116) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 123.Deco G, Kringelbach ML, Jirsa VK, Ritter P. 2017. The dynamics of resting fluctuations in the brain: metastability and its dynamical cortical core. Sci. Rep. 7, 3095. ( 10.1038/s41598-017-03073-5) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 124.Tzourio-Mazoyer N, Landeau B, Papathanassiou D, Crivello F, Etard O, Delcroix N, Mazoyer B, Joliot M. 2002. Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain. Neuroimage 15, 273-289. ( 10.1006/nimg.2001.0978) [DOI] [PubMed] [Google Scholar]
- 125.Thiagarajan TC, Lebedev MA, Nicolelis MA, Plenz D. 2010. Coherence potentials: loss-less, all-or-none network events in the cortex. PLoS Biol. 8, e1000278. ( 10.1371/journal.pbio.1000278) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 126.Gardner M. 1970. Mathematical games. Sci. Am. 223, 120-123. ( 10.1038/scientificamerican1070-120) [DOI] [Google Scholar]
- 127.Plenz D. 2012. Neuronal avalanches and coherence potentials. Eur. Phys. J. Spec. Top. 205, 259-301. ( 10.1140/epjst/e2012-01575-5) [DOI] [Google Scholar]
- 128.Plenz D, Ribeiro TL, Miller SR, Kells PA, Vakili A, Capek EL. 2021. Self-organized criticality in the brain. Front. Phys. 9, 639389. ( 10.3389/fphy.2021.639389) [DOI] [Google Scholar]
- 129.Beggs JM, Timme N. 2012. Being critical of criticality in the brain. Front. Physiol. 3, 163. ( 10.3389/fphys.2012.00163) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 130.Clauset A, Shalizi CR, Newman MEJ. 2009. Power-law distributions in empirical data. SIAM Rev. 51, 661-703. ( 10.1137/070710111) [DOI] [Google Scholar]
- 131.Touboul J, Destexhe A. 2017. Power-law statistics and universal scaling in the absence of criticality. Phys. Rev. E 95, 012413. ( 10.1103/PhysRevE.95.012413) [DOI] [PubMed] [Google Scholar]
- 132.Bonachela JA, Muñoz MA. 2009. Self-organization without conservation: true or just apparent scale-invariance? J. Stat. Mech: Theory Exp. 2009, P09009. ( 10.1088/1742-5468/2009/09/P09009) [DOI] [Google Scholar]
- 133.Priesemann V, et al. 2014. Spike avalanches in vivo suggest a driven, slightly subcritical brain state. Front. Syst. Neurosci. 8, 108. ( 10.3389/fnsys.2014.00108) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 134.Gardner WA. 1992. A unifying view of coherence in signal processing. Signal Process. 29, 113-140. ( 10.1016/0165-1684(92)90015-O) [DOI] [Google Scholar]
- 135.Varela F, Lachaux JP, Rodriguez E, Martinerie J. 2001. The brainweb: phase synchronization and large-scale integration. Nat. Rev. Neurosci. 2, 229-239. ( 10.1038/35067550) [DOI] [PubMed] [Google Scholar]
- 136.Börgers C, Kopell N. 2003. Synchronization in networks of excitatory and inhibitory neurons with sparse, random connectivity. Neural Comput. 15, 509-538. ( 10.1162/089976603321192059) [DOI] [PubMed] [Google Scholar]
- 137.Turkheimer FE, Leech R, Expert P, Lord LD, Vernon AC. 2015. The brain's code and its canonical computational motifs. From sensory cortex to the default mode network: a multi-scale model of brain function in health and disease. Neurosci. Biobehav. Rev. 55, 211-222. ( 10.1016/j.neubiorev.2015.04.014) [DOI] [PubMed] [Google Scholar]
- 138.Cabral J, Hugues E, Sporns O, Deco G. 2011. Role of local network oscillations in resting-state functional connectivity. Neuroimage 57, 130-139. ( 10.1016/j.neuroimage.2011.04.010) [DOI] [PubMed] [Google Scholar]
- 139.Cabral J, Luckhoo H, Woolrich M, Joensson M, Mohseni H, Baker A, Kringelbach ML, Deco G. 2014. Exploring mechanisms of spontaneous functional connectivity in MEG: how delayed network interactions lead to structured amplitude envelopes of band-pass filtered oscillations. Neuroimage 90, 423-435. ( 10.1016/j.neuroimage.2013.11.047) [DOI] [PubMed] [Google Scholar]
- 140.Cabral J, et al. 2022. Synchronization in the connectome: metastable oscillatory modes emerge from interactions in the brain spacetime network. bioRxiv. ( 10.1101/2022.01.06.475196) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 141.Acebrón JA, Bonilla LL, Pérez Vicente CJ, Ritort F, Spigler R. 2005. The Kuramoto model: a simple paradigm for synchronization phenomena. Rev. Mod. Phys. 77, 137-185. ( 10.1103/RevModPhys.77.137) [DOI] [Google Scholar]
- 142.Lord LD, et al. 2019. Dynamical exploration of the repertoire of brain networks at rest is modulated by psilocybin. Neuroimage 199, 127-142. ( 10.1016/j.neuroimage.2019.05.060) [DOI] [PubMed] [Google Scholar]
- 143.Lee WH, Doucet GE, Leibu E, Frangou S. 2018. Resting-state network connectivity and metastability predict clinical symptoms in schizophrenia. Schizophr. Res. 201, 208-216. ( 10.1016/j.schres.2018.04.029) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 144.Vohryzek J, Deco G, Cessac B, Kringelbach ML, Cabral J. 2020. Ghost attractors in spontaneous brain activity: recurrent excursions into functionally-relevant BOLD phase-locking states. Front. Syst. Neurosci. 14, 20. ( 10.3389/fnsys.2020.00020) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 145.Fries P. 2005. A mechanism for cognitive dynamics: neuronal communication through neuronal coherence. Trends Cogn. Sci. 9, 474-480. ( 10.1016/j.tics.2005.08.011) [DOI] [PubMed] [Google Scholar]
- 146.Fries P. 2009. Neuronal gamma-band synchronization as a fundamental process in cortical computation. Annu. Rev. Neurosci. 32, 209-224. ( 10.1146/annurev.neuro.051508.135603) [DOI] [PubMed] [Google Scholar]
- 147.Fries P. 2015. Rhythms for cognition: communication through coherence. Neuron 88, 220-235. ( 10.1016/j.neuron.2015.09.034) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 148.Deco G, Kringelbach ML. 2016. Metastability and coherence: extending the communication through coherence hypothesis using a whole-brain computational perspective. Trends Neurosci. 39, 125-135. ( 10.1016/j.tins.2016.01.001) [DOI] [PubMed] [Google Scholar]
- 149.Kringelbach ML, Deco G. 2020. Brain states and transitions: insights from computational neuroscience. Cell Rep. 32, 108128. ( 10.1016/j.celrep.2020.108128) [DOI] [PubMed] [Google Scholar]
- 150.Tognoli E, Kelso JAS. 2014. The metastable brain. Neuron 81, 35-48. ( 10.1016/j.neuron.2013.12.022) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 151.Wildie M, Shanahan M. 2012. Metastability and chimera states in modular delay and pulse-coupled oscillator networks. Chaos Interdiscip. J. Nonlinear Sci. 22, 043131. ( 10.1063/1.4766592) [DOI] [PubMed] [Google Scholar]
- 152.Hellyer PJ, Scott G, Shanahan M, Sharp DJ, Leech R. 2015. Cognitive flexibility through metastable neural dynamics is disrupted by damage to the structural connectome. J. Neurosci. 35, 9050-9063. ( 10.1523/JNEUROSCI.4648-14.2015) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 153.Haldeman C, Beggs JM. 2005. Critical branching captures activity in living neural networks and maximizes the number of metastable states. Phys. Rev. Lett. 94, 058101. ( 10.1103/PhysRevLett.94.058101) [DOI] [PubMed] [Google Scholar]
- 154.Rabinovich MI, Huerta R, Varona P, Afraimovich VS. 2008. Transient cognitive dynamics, metastability, and decision making. PLoS Comput. Biol. 4, e1000072. ( 10.1371/journal.pcbi.1000072) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 155.Rabinovich MI, Afraimovich VS, Bick C, Varona P. 2012. Information flow dynamics in the brain. Phys. Life Rev. 9, 51-73. ( 10.1016/j.plrev.2011.11.002) [DOI] [PubMed] [Google Scholar]
- 156.Rabinovich MI, Zaks MA, Varona P. 2020. Sequential dynamics of complex networks in mind: consciousness and creativity. Phys. Rep. 883, 1-32. ( 10.1016/j.physrep.2020.08.003) [DOI] [Google Scholar]
- 157.Kelso JAS. 2012. Multistability and metastability: understanding dynamic coordination in the brain. Phil. Trans. R. Soc. B 367, 906-918. ( 10.1098/rstb.2011.0351) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 158.Friston KJ. 1997. Transients, metastability, and neuronal dynamics. Neuroimage 5, 164-171. ( 10.1006/nimg.1997.0259) [DOI] [PubMed] [Google Scholar]
- 159.Ponce-Alvarez A, Deco G, Hagmann P, Romani GL, Mantini D, Corbetta M. 2015. Resting-state temporal synchronization networks emerge from connectivity topology and heterogeneity. PLoS Comput. Biol. 11, e1004100. ( 10.1371/journal.pcbi.1004100) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 160.Shanahan M. 2010. Metastable chimera states in community-structured oscillator networks. Chaos Interdiscip. J. Nonlinear Sci. 20, 013108. ( 10.1063/1.3305451) [DOI] [PubMed] [Google Scholar]
- 161.Váša F, Shanahan M, Hellyer PJ, Scott G, Cabral J, Leech R. 2015. Effects of lesions on synchrony and metastability in cortical networks. Neuroimage 118, 456-467. ( 10.1016/j.neuroimage.2015.05.042) [DOI] [PubMed] [Google Scholar]
- 162.Hellyer PJ, Shanahan M, Scott G, Wise RJS, Sharp DJ, Leech R. 2014. The control of global brain dynamics: opposing actions of frontoparietal control and default mode networks on attention. J. Neurosci. 34, 451-461. ( 10.1523/JNEUROSCI.1853-13.2014) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 163.Jobst BM, Hindriks R, Laufs H, Tagliazucchi E, Hahn G, Ponce-Alvarez A, Stevner ABA, Kringelbach ML, Deco G. 2017. Increased stability and breakdown of brain effective connectivity during slow-wave sleep: mechanistic insights from whole-brain computational modelling. Sci. Rep. 7, 4634. ( 10.1038/s41598-017-04522-x) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 164.Carhart-Harris RL, et al. 2014. The entropic brain: a theory of conscious states informed by neuroimaging research with psychedelic drugs. Front. Hum. Neurosci. 8, 20. ( 10.3389/fnhum.2014.00020) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 165.Córdova-Palomera A, et al. 2017. Disrupted global metastability and static and dynamic brain connectivity across individuals in the Alzheimer's disease continuum. Sci. Rep. 7, 40268. ( 10.1038/srep40268) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 166.Lee WH, Moser DA, Ing A, Doucet GE, Frangou S. 2019. Behavioral and health correlates of resting-state metastability in the human connectome project. Brain Topogr. 32, 80-86. ( 10.1007/s10548-018-0672-5) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 167.Hruby L, Dogra N, Landini M, Donner T, Esslinger T. 2018. Metastability and avalanche dynamics in strongly correlated gases with long-range interactions. Proc. Natl Acad. Sci. USA 115, 3279-3284. ( 10.1073/pnas.1720415115) [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
This article has no additional data.