Abstract

External electric fields can modify binding energies of reactive surface species and enhance catalytic performance of heterogeneously catalyzed reactions. In this work, we used density functional theory (DFT) calculations—assisted and accelerated by a deep learning algorithm—to investigate the extent to which ruthenium-catalyzed ammonia synthesis would benefit from application of such external electric fields. This strategy allows us to determine which electronic properties control a molecule’s degree of interaction with external electric fields. Our results show that (1) field-dependent adsorption/reaction energies are closely correlated to the dipole moments of intermediates over the surface, (2) a positive field promotes ammonia synthesis by lowering the overall energetics and decreasing the activation barriers of the potential rate-limiting steps (e.g., NH2 hydrogenation) over Ru, (3) a positive field (>0.6 V/Å) favors the reaction mechanism by avoiding kinetically unfavorable N≡N bond dissociation over Ru(1013), and (4) local adsorption environments (i.e., dipole moments of the intermediates in the gas phase, surface defects, and surface coverage of intermediates) influence the resulting surface adsorbates’ dipole moments and further modify field-dependent reaction energetics. The deep learning algorithm developed here accelerates field-dependent energy predictions with acceptable accuracies by five orders of magnitudes compared to DFT alone and has the capacity of transferability, which can predict field-dependent energetics of other catalytic surfaces with high-quality performance using little training data.
Keywords: ammonia synthesis, density functional theory, electric field-dipole effects, deep learning
Ammonia is one of the world’s most important and heavily produced inorganic chemicals. It is easily transported and is used widely as fertilizers and energy storage and is also promising as a future zero-carbon fuel.1 160 million tons of ammonia are produced each year, and global demand is expected to grow 1.5% annually until 2050. For the past century, ammonia has been produced by means of the Haber–Bosch process, which is an industrial-scale chemical process that requires both exceedingly high temperature (700 K) and pressure (150 bar).2 To provide the requisite energy, Haber–Bosch consumes 2% of worldwide demand for fossil fuels and releases 420 million tons of CO2 into the atmosphere each year.3 There is thus a critical need to drastically lower these energy requirements (400 K and 1 atm) and generate zero-carbon ammonia (NH3) fuels via an energy-resilient and modular approach using renewable electricity.4,5
Currently, producing ammonia under mild conditions using various catalysts has obtained much progress6−13 but still has the following limitations: (1) electrochemistry yields only trace amounts of ammonia at modest current efficiencies due to the kinetically restricted initial N2 dissociation step at room temperature,1,14−22 (2) biomimetic routes suffer from mass transport limitations,16,23,24 (3) chemical looping is in the exploratory stage,25 and (4) non-thermal plasma suffers from fast energy loss and low energy efficiencies.26,27
A potential strategy to overcome kinetic limitations and enhance energy efficiency of ammonia synthesis in a modular setup is to apply a large electric field, on the order of >0.1 V/Å. Such fields have the potential to rearrange electronic orbitals of reactive intermediates, altering their binding energetics, reaction mechanism, and the catalytic performance (Scheme 1a,b).28,29 Large electric fields can be experimentally generated through three ways: (1) internally on molecular length scales in (metallo)enzyme30−37 and zeolite catalytic38 active sites, on the order of >1.5 V/Å, (2) externally in a gas/solid heterogeneous catalytic system, such as ultra-high vacuum conditions via scanning tunneling microscopy,32,39 field ion/emission microscopy,40−42 on the order of >1.5 V/Å, or flow reactor-type via probe-bed-probe,43−48 dielectric barrier discharge reactors,49 plasma catalysis,27,50−56 coaxial capacitor reactors,57−60 and microwave heating,61−65 and (3) in an interfacial way at gas/liquid/solid triple-phase boundary, on the order of 0.4 V/Å.66−68 More details could be referred to large electric field in experimental setups in the Supporting Information.
Scheme 1. Combined Theoretical and Deep Learning Study of Electric Fields Facilitated Sustainable Ammonia Synthesis; (a) Density Functional Theory (DFT) Calculations of Electric Field Effects on Ammonia Synthesis from Dinitrogen Reduction Over Transition Metal Surfaces; (b) Electric Fields Can Alter Electronic Interactions Over Catalytic Surfaces; Positive Electric Fields Favor the Associative Mechanism (First Hydrogenation of Dinitrogen) rather than the Dissociative Mechanism (Initial Dissociation of N≡N Bonds); and (c) Developed Deep Learning Algorithm, that is, Employing a Graph Neural Network (GNN) to Capture the Relationship Among the configurations of an Adsorbate in the Gas Phase, Pure Catalytic Surface, and Adsorbate Adsorption Over the Catalytic Surface (Total), Followed by a Shared Multiple-Layer Perception (MLP), to Predict Field-Induced Adsorption Energies, Dipole Moments, and Polarizabilities of Reactive Intermediates Over Surfaces for Catalytic Ammonia Synthesis.
For sustainable ammonia synthesis, Sekine and co-workers44−47 used a fixed-bed flow-type reactor and contacted a catalyst bed with two inserted stainless-steel rods as electrodes to induce the strong external electric field effects in ammonia synthesis. They achieved the maximum reaction rate of ammonia synthesis of 30,099 μmol gcat–1 h–1 over a 9.9 wt % Cs/5.0 wt % Ru/SrZrO3 catalyst at a temperature of 634 K, a pressure of 0.9 MPa, and a DC constant current of 6 mA. The energy consumption was very low (only 2.82 W), leading to a high energy efficiency of ammonia production of 36.3 g kW h–1, which is 12-fold higher than that under non-thermal plasma.69 Electric fields also accelerated the reaction rates of ammonia synthesis by up to 10-fold compared to conventional heating.44−46 The Hu and Spencer groups61−63,65,70 reported that microwave heating could induce high electric fields on the catalytic surface and interact with surface species and, consequently, shift equilibrium toward the production of ammonia two-fold higher than that under thermal heating at 473 K and 0.1 MPa.
Compared to experimental studies, theoretical work on electric field effects in catalysis is very limited due to the low efficiency of pure DFT calculations for predicting field-dependent energetics of catalytic reactions.71−73 This has led to an incomplete picture of how electric fields (i.e., field–dipole effects) influence catalytic mechanisms on the atomic scale and hinders the design and optimization of field-induced catalytic technologies.65,74,75 One approach to promote the in-depth understanding and advance the design of field-induced catalysis is to develop a deep learning algorithm to predict the intermediate species’ energetics (e.g., adsorption, reaction, and mechanism) under electric fields and, thus, the field-induced catalytic performance in a short time with acceptable accuracies. Deep learning techniques are being adopted in practical catalyst design,76−83 including predicting binding energy of reactive intermediates,84−88 electronic properties of catalytic materials,89−93 experimental spectroscopy data,94 catalytic kinetic properties,95,96 and so on. However, to the best of our knowledge, the predictions of field-induced catalysis with deep learning techniques are under explored (Scheme 1c).
To address the above gaps, we explored the electric field effects on ammonia synthesis over ruthenium (Ru, Figure S1), answering the following fundamental questions with DFT and deep learning models: (1) What are the key descriptors influencing the activity of field-induced catalytic reactions? (2) Will the electric field change the catalytic reaction mechanism? (3) To what extent does the local surface environment couple with the electric field to further affect catalytic performance? (4) How is the performance of a deep learning algorithm on field-dependent energetics and how much can predictions be accelerated? (5) Can the designed deep learning framework be applicable to other catalysts (e.g., Fe)?
What are the key descriptors influencing the activity of field-induced catalytic reactions? In theory, dipole moments (μ⃗) of surface species should be closely correlated with field-dependent energetics in eq 1.73
| 1 |
where ΔU is field-induced potential energy change and F⃗ is the external electric field.
In this section, we investigate what factors affect the direction and magnitude of μ⃗ and how the field–dipole effect influences the energetics of elementary reactions. We first obtained the first and second most favorable thermodynamic reaction paths for ammonia synthesis over Ru with no fields (Figures S2 and S3 and Scheme 1b). We examined the field effects on the most favorable configurations of reaction intermediates over Ru (Figures S4–S19). Adsorption (reaction) energetics can be expressed using Taylor expansion73 in terms of fields
| 2 |
| 3 |
where Ead(F) and Ead are the adsorption
energies with and without fields. μ⃗ and α are
dipole moment and polarizability for surface adsorbates, respectively.97 When calculating the Ead(F), the electric field effect on the species
in the gas phase was not included (eq S1) because Ead(F) describes
the adsorption of species far away from the surface. ΔHrxn(F) and ΔHrxn are the reaction energies with and without fields.  and Δαrxn are dipole
moment and polarizability change between final and initial states
of an elementary reaction, respectively. In theory, reactions with
larger μ⃗ (
and Δαrxn are dipole
moment and polarizability change between final and initial states
of an elementary reaction, respectively. In theory, reactions with
larger μ⃗ (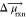 ) will have larger field
effects.
) will have larger field
effects.
The non-polarized species of ammonia synthesis are N2*, H2*, N*, and H*. When these species adsorb over a flat Ru(0001) surface (i.e., the most thermodynamically favorable Ru flat facet), DFT calculations show that the electric field effect on their adsorption energies is negligible with energy changes within ∼0.2 eV (Figure S20). As compared to Ru(0001), the adsorption energies of these non-polarized species over the Ru(1013) step surface (i.e., the most active facet for ammonia synthesis) were more significantly affected by electric fields (besides H2*). This happens because the stepped Ru atoms induce step surface–adsorbate dipole moments (Figures 1a and S21), indicating that the stepped surface might have greater field impacts on the surface reactions. Also, μ⃗ of surface species is not only related to that of the intermediates but also the catalytic surface.
Figure 1.
Field-dipole effects on adsorption energies of reactive intermediates. (a) Investigation of the effective dipole moment (μ⃗) of non-polarized and polarized species over Ru catalytic surfaces and (b) electric field effects on altering the adsorption energies of NH3* over Ru. The inserted picture refers to the corresponding differential charge density (isosurface level = 0.01 e/bohr3) and Bader charge analysis of NH3* over Ru(1013) to illustrate the dipole moment of the species. Green color in the inserted picture represents the stepped Ru atoms and (c) the linear correlations between the system dipole moments and the charge differences between N and H of the reactive intermediates NHx* and N2H* over Ru catalytic surfaces.
The polarized species of ammonia synthesis (Scheme 1b) are NHx* and N2H*. As expected, the electric field affects the adsorption energies of these polarized intermediates much more than it affects the non-polarized ones. For example, when NH3* adsorbs over the Ru surfaces, the μ⃗ of N–H bond dominates its net μ⃗ and aligns with a positive field (Figure 1b). As a result, NH3* should be stabilized when a positive electric field applies. DFT calculations confirm the predictions, with the Ead(F) of NH3* being strengthened as the field increases from negative to positive. In addition, for polarized species, such as NHx* and N2H*, their system dipole moments are linearly correlated to the charge difference between positively charged H and negatively charged N (Figure 1c).
For field–dipole effects on the adsorption energies of ammonia synthesis-related reactive intermediates, we found that (1) field-dependent adsorption energies are closely related to the dipole moments of surface adsorbates (i.e., ΔEad ≈ −μ⃗·F⃗), (2) the direction of μ⃗ of adsorbates is correlated to their adsorption and their charge distribution over the catalytic surface, and (3) the magnitude of μ⃗ increases with increasing reactive intermediates μ⃗ and defects on catalytic surfaces.
We then examined the field-dependent reaction energies of each possible elementary step during ammonia synthesis (Figures S22–S30). Regardless of the electric fields, the elementary steps of bond cleavage during ammonia synthesis are all exothermic and hydrogenation reactions are all endothermic over Ru based on DFT calculations. As compared to the flat Ru(0001) surface, the electric field effects on the stepped Ru(1013) surface are much larger due to the larger changes in their dipole moments (Figure 2a). The reaction energy of bond cleavage steps (i.e., N–N, H–H, and HN–N) for ammonia synthesis becomes less exothermic as the electric fields are increased from −1 to 1 V/Å (Figure 2b).
Figure 2.
DFT calculations of field-induced reaction during ammonia synthesis. (a) Investigation of the effective dipole moment differences (Δμ⃗) of bond cleavage and formation over Ru, (b) electric fields effects on altering the reaction energies of bond cleavage (i.e., H2, N2, and N2H) over Ru, and (c) electric field effects on altering the reaction energies of bond formation (i.e., NH, NH2, NH3, and N2H) over Ru.
Bond forming steps show the opposite trend as compared to bond cleavage ones during ammonia synthesis. Upon increasing the fields from −1 to 1 V/Å, the reaction energies of hydrogenation steps (e.g., thermodynamically, potential rate-determining steps (RDSs)–NH* + H* ↔ NH2* over Ru(0001) and NH2* + H* ↔ NH3* over Ru(1013)) become less endothermic or even exothermic (Figure 2c). The reason is that the direction of the dipole moment changes between the final and initial state (Δμ⃗ = μ⃗FS – μ⃗IS) of hydrogenation steps is opposite to the ones for bond cleavage.
Will the electric field change the catalytic reaction mechanism? Based on the energy diagrams of ammonia synthesis over Ru(0001), regardless of electric fields, the most favorable reaction path follows the decomposition of N2 and hydrogenation of N to NH3 (Figure 3a). One of the potential RDS from thermodynamic energy diagrams could be the hydrogenation of NH to NH2, which has a positive reaction energy of 0.68 eV without electric fields. Positive electric fields make this step more exothermic by ∼0.2 eV. For ammonia synthesis, the overall reaction energy becomes more exothermic by ∼0.5 and ∼1.0 eV when a positive field is used as compared to no field or negative fields, respectively. Thus, a positive field favors the overall thermodynamic energetics of ammonia synthesis over Ru(0001).
Figure 3.
Electric fields shift the most thermodynamically favorable reaction mechanism. (a) Energy diagram of ammonia synthesis over Ru(0001) under different electric fields; the straight line represents the dissociative pathway (N2* ↔ 2N*), while the straight line with a square represents the associative pathway (N2* + H* ↔ N2H*); (b) positive fields favor the associative pathway (N2* + H* ↔ N2H*) by avoiding kinetically unfavorable strong initial N≡N bond dissociation over Ru(1013); (c) over 0.63 V/Å, the most favorable reaction path will change from N2 dissociation to N2H formation over Ru(1013). (d) Activation barrier of NH3 formation from NH2 hydrogenation over Ru(1013) under different electric fields. The inserted pictures are the structures of the initial state (IS), transition state (TS), and final state (FS); (e) forward and backward rate constants for NH2* + H* ↔ NH3* over Ru(1013) under different electric fields at 473 K; and (f) correlations between the dipole moment differences (Δμ = μFS – μIS) of an elementary reaction and its equilibrium constant under electric fields at 473 K. Asterisk (*) represents the empty surface site.
Interestingly, for Ru(1013), DFT results show that a positive electric field (>0.63 V/Å, Figure 3b,c) shifts the reaction coordinate such that hydrogenation of adsorbed N2 occurs before cleavage of the N≡N bond, whose direct cleavage is otherwise kinetically unfavorable. This agrees well with the experiments from the Sekine group,43−46 where they applied in situ diffuse reflectance infrared fourier transform spectroscopy and performed isotope studies to reveal that N2 activation is via proton hopping to form N2H+ at 473 K under a positive field. In addition, compared to no fields, a positive electric field makes the overall reaction energy for NH3* synthesis over Ru(1013) more exothermic by 0.8 eV. Similar findings were reported by Xin and Feng groups’ previous work on ambient ammonia synthesis from N2RR (electroreduction reaction of N2), in which they showed that the Pd hydride formation from proton–electron coupling over Pd lowers the overpotential of N2RR via decreasing the free energy barrier of the possible RDS N2* + H* ↔ N2H*.98
Electric field influences not only the thermodynamic energetics of ammonia synthesis (i.e., adsorption/reaction energies) but also the kinetic properties (i.e., activation barriers and reaction rates). For Ru(0001), the reaction pathway follows the N2 dissociation pathway (Scheme 1b and Figure 3a). Based on literature review,99 one of the potential RDSs during ammonia synthesis over Ru is the N≡N triple bond cleavage. Our results show that the activation barrier of N≡N triple bond cleavage over Ru(0001) under no electric field is 1.01 eV, which is significantly higher than the activation barrier of the same elementary step at the B5 site of Ru(1013) (0.65 eV). This indicates that the B5 site of Ru(1013) is more active for catalyzing ammonia synthesis than that over Ru(0001), consistent with literature reports.99,100
We then calculated the activation barriers of possible elementary steps (Figure 3b and eqs S5–S11) of ammonia synthesis over more kinetically active Ru(1013) surface in the presence and absence of electric fields (Figure S31). Our results show the potential RDS over Ru(1013) is NH3* formation (NH2* + H* ↔ NH3*) because it has the highest activation barrier among all examined steps during the ammonia synthesis, which is consistent with Nakao et al.’s microkinetic model that NH3* formation is the RDS over Ru-based catalysts.101 Importantly, a positive electric field of 1 V/Å significantly lowers the activation barrier of NH3* formation by 0.11 and 0.25 eV as compared to the ones under no electric fields and a negative electric field of −1 V/Å (Figure 3d). This agrees with experimental observation from Manabe et al.,69 where they found that the presence of positive electric fields decreased the apparent activation energy from 121 to 37 kJ/mol.
To estimate the electric field effects on the kinetic properties of ammonia synthesis, we calculated the rate constants (eqs S17 and S18) of NH2* + H* ↔ NH3* at 473 K using the calculated field-dependent activation barrier (ΔG‡(F)) and field-dependent reaction energy (ΔGrxn(F)) (Tables S1 and S2). The result shows that as the electric field increases from −1 to 1 V/Å, the forward rate constant increases, while the backward rate constant decreases (Figure 3e). This suggests that a positive electric field could favor the potential RDS and thus facilitate the reaction rate of ammonia synthesis. In addition, we calculated the equilibrium constants for N2* ↔ 2N*, N2* + H* ↔ N2H*, and NH2* + H* ↔ NH3*. The reason is that these are either the key elementary steps for determining dissociative/associative pathways or the potential RDS of ammonia synthesis over Ru(1013). Our results show that the presence of a positive electric field favors the equilibrium toward ammonia synthesis via the associate reaction pathway. This is because positive field significantly increases the equilibrium constants of N2* + H* ↔ N2H* and NH2* + H* ↔ NH3*, but decreases those of N2* ↔ 2N* as compared to no electric field or with negative field (Figure 3f). More interestingly, our results further show that the field-dependent equilibrium constant is correlated with dipole moment difference between the initial and final states of the examined elementary steps. When the dipole moment difference is negative (e.g., N2* ↔ 2N*), a positive electric field decreases the equilibrium constant, while a positive electric increases the equilibrium constant when the dipole moment difference is positive (e.g., N2* + H* ↔ N2H* and NH2* + H* ↔ NH3*). Overall, a positive electric field could favor the associative pathway and enhance the rate constants and equilibrium constants of the possible RDS and thus promote the overall reaction rates of Ru-catalyzed ammonia synthesis.
To what extent does the local surface environment couple with the electric field to further affect catalytic performance? Under positive electric fields, the rate of ammonia synthesis over Ru could become desorption-limited due to the strong binding energy of NH3* (∼1.60 eV). However, this might be combatted by repulsive interactions with the nearby NH3* at a higher surface coverage. To investigate this, we further increased the surface coverages of NH3*. As the surface coverage increases from 1/16 monolayer (ML) to 4/16 ML, under a positive electric field, its desorption energy decreases greatly from 1.55 eV/NH3* to 1.26 eV/NH3* over Ru(0001) and from 1.62 eV/NH3* to 1.23 eV/NH3* over Ru(1013) (Figure 4a), while its dipole moment decreases from ∼0.48 to 0.33 eÅ over Ru(0001) and from 0.42 to 0.28 eÅ over Ru(1013) (Figure 4b). The reason for the decrease in the overall dipole moment is that charge difference per NH3* between N and H decreases as surface coverage increases (Figures 4b and S32). With the field increasing from −1 to 1 V/Å, at a low surface coverage of 1/16 ML, the desorption energy of NH3* with larger dipole moments increases by 0.95 eV/NH3* over Ru(0001) and 0.83 eV/NH3* over Ru(1013), while at a high coverage of 4/16 ML, the desorption energy of NH3* with smaller dipole moments increases only by 0.66 eV/NH3* over Ru(0001) and 0.53 eV/NH3* over Ru(1013). This indeed shows that field–dipole effects can couple with the local surface environment (i.e., lateral interactions at various surface coverages) to influence catalysis. Similar observations of surface coverage effects on the dipole moments of the intermediates can also be found in the previous literature reports.102,103 In summary, according to the DFT results of field-dependent catalytic performance of Ru-based ammonia synthesis, electric field–dipole effects play an essential role in changing the thermodynamic and kinetic landscape of catalytic reactions, altering the most favorable energy paths, and modulating its potential RDS.
Figure 4.
(a) Lateral interaction effects on the desorption energies (Edes) of NH3 over catalytic Ru surfaces as a function of electric fields and (b) their corresponding dipole moments. The inserted pictures are differential charge density analysis (isosurface level = 0.01 e/bohr3) and Bader charge analysis of NH3* over Ru(1013) from a low surface coverage (1/16 ML) to a high surface coverage (4/16 ML).
How is the performance of a deep learning algorithm in field-dependent energetics and how much can predictions be accelerated? One of the drawbacks in DFT calculations for predicting the heterogeneous catalytic performance is the low efficiency. Thanks to the current deep learning techniques, they have powerful capacities to fit complicated functions and run very fast at the inference stage, although the deep learning model needs relatively long offline training time. The deep learning framework is expected to provide potential good catalyst candidates for field-induced heterogeneous catalysis via prediction of the field-dependent energies in a short time, where the DFT calculations will be further applied to validate these predictions.104,105 By this means, some unacceptable catalyst candidates can be quickly filtered out, thus avoiding unnecessary computations.
To achieve this, we designed a novel deep learning framework for predicting the field-dependent adsorption energies (Scheme 1c and Figure S33). Especially, we employed a Graph Neural Network (GNN) to capture the relationship among the geometries of adsorbates (intermediates during ammonia synthesis) in the gas phase, pure catalytic surface, and adsorbate adsorption over the catalytic surface, where GNN106 is a special deep learning architecture widely used to capture the information exchange among the relational data.
Based on this, we modeled the energies of the adsorbate, surface, and adsorbate adsorption over the surface, followed by a shared MLP for field-induced catalytic reaction prediction. It is worth noting that although there are several pioneering attempts76,77,79,80,84−96 of deep learning techniques in the catalysis field, to our best knowledge, we are the first ones to address the electric field-induced catalytic problem with a newly designed framework. The innovative part of our work is that the designed shared GNN and MLP modules learn a common low-dimensional space among the adsorbate, surface, and adsorbate adsorption over the surface, which facilitates field-dependent adsorption energy (Ead(F)) prediction. Our deep learning model first predicted Ead(F), and then, we did a quadratic fitting of Ead(F) to get adsorption energy under no electric fields Ead, the dipole moment (μ⃗), and the polarizability (α). The training structures are shown in Tables S3 and S4.
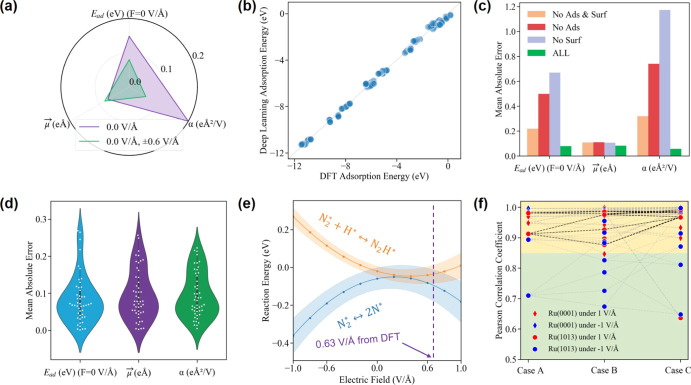
The estimated mean absolute error (MAE) of field-dependent adsorption energies is within 0.15 eV when we input the configurations and the corresponding adsorption energies of no electric field (0.0 V/Å) only. The MAE of our deep learning model is significantly decreased to within 0.08 eV by the additional inputs of configurations and energetics at ±0.6 V/Å (Figure 5a). The deep learning-predictive field-dependent adsorption energies of ammonia synthesis-related intermediates over two Ru surfaces have been strongly correlated with the DFT-calculated energetics (Figure 5b). The results show that our designed deep learning framework provides accurate estimation for the field-dependent adsorption energies of adsorbates over Ru. Moreover, we also demonstrated the ablation study of different components within our framework (Figure 5c). The ablation study is a terminology in computer science, which gradually removes one component of the whole model and tests the performance of different components or their combinations. The input components in our ablation study include under 0.0 V/Å and ±0.6 V/Å, (1) ALL model: adsorbate adsorption over the surface, the adsorbate in the gas phase, and surface geometry and their corresponding energetics, (2) no surf model: without surface geometry and energy from the ALL model, (3) no ads model: without the adsorbate in the gas-phase geometry and energy from the ALL model, and (4) no surf and ads model: adsorbate adsorption over the surface only. Our ablation study shows that the prediction of μ⃗ is not influenced by the above input components, but adsorption energy (Ead) and polarizability (α) predictions are greatly influenced. With the input geometries and energetics of the ALL model at 0.0 and ±0.6 V/Å, our deep learning model gives us the optimal accuracy of field-dependent adsorption energies (Figure 5d). The MAEs of Ead, μ⃗, and α with 5% outliers removed are within 0.08 eV, 0.09 eÅ, and 0.06 eÅ2/V, respectively.
Figure 5.
Performance of the developed deep learning algorithm in field-dependent energetics. (a) Estimated average error of field-dependent adsorption energies, given the configurations and the corresponding adsorption energies at 0.0 and ±0.6 V/Å, respectively, (b) comparison between the DFT adsorption energies and the deep learning-predicted adsorption energies of ammonia synthesis-related intermediates over Ru(0001) and Ru(1013) surfaces, (c) ablation study of different components within our framework (i.e., ALL model: adsorbate adsorption over the surface, the adsorbate in the gas phase, and surface geometry and their corresponding energetics, no surf model: without surface geometry and energy from the ALL model, no ads model: without adsorbate in the gas-phase geometry and energy from the ALL model, and no surf and ads model: adsorbate adsorption over the surface only), (d) with the given the configurations and the corresponding adsorption energies at 0.0 and ±0.6 V/Å, the performance of our deep learning model of electric field effects on the adsorption energies with 5% outliers being removed is within 0.08 eV, 0.09 eÅ, and 0.06 eÅ2/V for Ead (no fields), dipole moments and polarizability, respectively, and (e) deep learning-predicted field-dependent reaction energies of N2 dissociation and N2H formation over Ru(1013). The purple dash refers to the critical electric field from DFT in Figure 3c that changes the pathway. The blue and orange band represents the standard deviation of field-dependent reaction energies of these two elementary steps and (f) Pearson correlation coefficient (r) for the field-dependent energy diagrams of DFT and deep learning results over Ru surfaces with 5% outliers being removed. The yellow area refers to a strong positive relationship with r greater than 0.85. Bold dashes represent the correlations of energy diagrams of two reaction pathways over Ru(1013) under a positive electric field of 1 V/Å.
Our deep learning model could also predict the field-dependent reaction energies and energy diagrams of ammonia synthesis and draw similar conclusions to the DFT calculations. Based on DFT calculations (Figure 3c), a positive electric field greater than 0.63 V/Å may tune the ammonia synthesis mechanism from a dissociative pathway (N2* ↔ 2N*) to an associative pathway (N2* + H* ↔ N2H*) over Ru(1013). We then calculated the field-dependent reaction energies of N≡N bond cleavage and N2H formation for these two pathways with the predicted adsorption energy from our designed deep learning framework (Figure 5e). The result suggests that the deep learning framework has acceptable accuracy and points out the similar conclusion as DFT calculations that a positive electric field of 0.63 V/Å makes it possible to tune the ammonia synthesis mechanism over Ru(1013). In addition, we correlated the field-dependent energy diagrams from DFT (Figure 3a,b) and our deep learning model using Pearson correlation coefficients (r)
| 4 |
where xi and yi represent the values of DFT data and deep learning data. x̅ and y̅ stand for the mean of xi and yi. Specifically, we have presented Pearson correlation coefficients in three scenarios, including (1) the overall field-dependent energy diagram with all elementary steps in Figure 3a,b (case A), (2) the field-dependent energy diagram considering one of two continuous elementary steps as one reaction step (case B); (3) the field-dependent energy diagram considering one of three continuous elementary steps as one reaction step (case C). Overall, our deep learning model provides accurate estimation for energy diagram of ammonia synthesis under electric fields, where the Pearson correlation coefficients for various scenarios (cases A, B, and C) are in the range of 0.62–1 (Figure 5f). In most cases, the coefficients are greater than 0.85, indicating a strong positive relationship between the deep learning-predicted energetics under fields and the DFT-calculated ones. Especially, for ammonia synthesis over Ru(1013) under 1 V/Å (bold dashes in Figure 5f), where we found that a positive electric field shifts the reaction mechanism from dissociative to associate pathways, the Pearson correlation coefficients are greater than 0.88 between deep learning prediction and DFT data, indicating that the similar conclusion of mechanism changes would also be drawn from our deep learning model.
To obtain the electric field effects on the adsorption energies of the reactive intermediates from eq 2, our DFT calculations need at least 11 calculations of adsorbate adsorption over the surface, 11 calculations of the surface, and 1 calculation of adsorbates in the gas phase. The significance of our developed deep learning algorithm is that it could keep acceptable accuracy and reduce the required DFT calculations to three calculations of adsorbate adsorption over the surface, three calculations of surface, and one calculation of adsorbates in the gas phase. On average, to obtain μ⃗ and α of ammonia synthesis-related species, DFT optimization requires ∼205646.4 CPU seconds with 40 CPUs in the supercomputing cluster (i.e., at the Massachusetts Green High-Performance Computing Center), while our developed deep learning algorithm only needs 0.8078 GPU seconds (i.e., with a single NVIDIA GP102 GPU card) for inference. In summary, our deep learning model significantly accelerates field-dependent adsorption energy prediction by five orders of magnitudes than that obtained from DFT calculations. More details are given in the deep learning method in the Supporting Information.
Can the designed deep learning framework be applied to other catalysts? To broaden the impacts of our developed deep learning algorithm, we also demonstrate that our deep learning model has the transferability to predict field-dependent adsorption energies, dipole moments, and polarizabilities of reaction intermediates over other catalytic surfaces, which have not been calculated by DFT. For example, our deep learning algorithm was first trained with the DFT data using the system of electric field-dependent ammonia synthesis over Ru(0001) and Ru(1013). We then applied the Ru-trained deep learning model to predict the energetics of ammonia synthesis over Fe(110) and Fe(111) surfaces under electric fields (Figure S34). The results show that with 10, 20, and 30% training data (Tables S5–S7) of ammonia synthesis-related intermediate adsorption energy over Fe(110) and Fe(111), we can predict the rest adsorption data of field-dependent ammonia synthesis over Fe with the MAE of 0.17, 0.14, and 0.09 eV, respectively. With 30% Fe training data fine tuning the model, our Ru-trained deep learning framework provides accurate estimation for the field-dependent adsorption energies of reaction intermediates over Fe surfaces with very limited data. The MAE for adsorption energy, dipole moment, and polarizability over Fe systems are 0.08 eV, 0.08 eÅ, and 0.07 eÅ2/V, respectively (Figure S35). In addition, we further calculated the Pearson correlation coefficients for the field-dependent energy diagram over Fe(110) and Fe(111) surfaces. Similar to Ru, in most cases, the Pearson correlation coefficients of the Fe system are greater than 0.85, indicating the the deep learning-predicted reaction energies are accurate. Collectively, our deep learning framework has the capacity of transferability, which can be adapted to predict field-dependent energetics of another catalytic surface with high-quality performance using little training data.
To conclude, our work provides fundamental understanding of electric field effects on catalytic reactions, that is, adsorption, reaction, barrier, and mechanism. A high positive electric field will enhance ammonia synthesis through lowering the overall energetics of dinitrogen reduction to ammonia, altering the reaction mechanism via avoiding kinetically restricted N2 triple bond cleavage, decreasing the energy requirements of the potential RDSs of NH3 formation from NH2 hydrogenation, thus enabling more efficient energy utilization and N2 conversion efficiency to NH3 than obtained with conventional heating.
This deep learning-assisted DFT theoretical research for revealing electric field–dipole effects on catalytic ammonia synthesis shows societal impacts from three perspectives: (1) Impacts of modular ammonia synthesis on society. The renewable energy-accelerated ammonia market size will grow to USD 852 million by 2030 (forecasted year) from USD 11 million in 2020 (estimated year), at a compound annual growth rate of 54.9% during the forecast period.107 Electric field-accelerated zero-carbon ammonia synthesis using renewable electricity is an innovative, energy-efficient, modular catalytic technology. Modular ammonia synthesis would mitigate the environmental challenge of global warming and the delivery challenge of non-grid power to operating systems: it can be generated on demand; the input power source can be solar or wind,108 and ammonia can be used in combustion engines109 and fuel cells.110 (2) Impacts of field–dipole interactions in heterogeneous catalysis on society. The DFT simulation in this study provides understanding of field–dipole interactions in heterogeneous catalysis, which is critical to advance the designs of modular catalytic devices, including scanning tunneling microscopes32,39,111−113 or field ion/emission microscopes (FIMs or FEMs),40−42,114,115 flow reactor systems via probe-bed-probe reactors,43−48 coaxial capacitor reactors,57−60 dielectric barrier discharge reactors,49 microwave reactors,61−65 and electrode/electrolyte interfaces, where large electric fields exist. This study also provides the theoretical guidance to the field-induced catalysis that the potential RDS of a reaction with significant dipole changes will be greatly influenced by the strong electric fields. Dynamic electric field-induced resonance effects116,117 could potentially promote the conversion and turnover frequency of heterogeneous catalysis, that is, ammonia synthesis, a topic certainly worthy of detailed investigation in the future. (3) Impacts of deep learning algorithm development on society. The predictions of field-induced catalysis with deep learning techniques are underexplored in the current research field. The deep learning framework in our study provides acceptable predictions on the field-dipole interaction effects on the energetics of heterogeneous catalysis with much cheaper computational costs. Our designed deep learning framework can provide potential good catalyst candidates for field-induced heterogeneous catalysis in a short time, where the DFT calculations will be further applied to validate these predictions. By this means, some unacceptable catalyst candidates can be quickly filtered out, thus avoiding the unnecessary computations. Overall, the deep learning framework will greatly accelerate the cycle time necessary for field-accelerated catalysis experiment designs.
Computational Section
DFT-Based Calculation
DFT calculations were conducted using the Vienna Ab-initio Simulation Package (VASP)118,119 with the Perdew–Burke–Ernzerhof exchange–correlation functional.120−122 The climbing image nudged elastic band (CI-NEB) method123 and the dimer124 method were used to search the transition state. All geometries with and without electric fields were considered optimized when the energy had converged to 10–5 eV and the forces were smaller than 0.03 eV/Å. We inserted a dipole layer with opposite charges on each side in the middle of a vacuum to apply the electric fields.125 More theoretical details can be found in Supporting Information.
GNN-Based Deep Learning
This model employed the GNN to capture the relationship among the geometries of the adsorbate in the gas phase, pure catalytic surface, and adsorbate adsorption over the catalytic surface. MLP was adopted for regression analysis. 10-fold cross-validation was performed at the species level for ammonia synthesis in deep learning experiments. Implementation and deep learning experiment details can be found in Supporting Information.
Acknowledgments
This work was partially supported by the institutional faculty start-up funds and Immersive Scholar program from the University of Massachusetts Lowell. The project undertaken was also partially sponsored by the Department of the Navy, Office of Naval Research, under award no. 1172044/2/93083. The authors acknowledge the computational resources provided by the Massachusetts Green High-Performance Computing Center (MGHPCC). The authors also thank Dr. Gregory Collinge and Prof. Chris (Yuguang) Li for helpful discussions.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacsau.2c00003.
Computational setup, deep learning details, field-induced energetics (adsorption, reaction, and activation barriers) over Ru and Fe, and field-dependent transition-state calculations (PDF)
Author Contributions
M.W. and H.Y. equally contributed to the work. M.W., J.N., and F.C. mainly contributed to DFT calculations, analysis, and article preparation and revision. F.C. supervised the project, conceived the idea of the project, and revised the article. H.Y. and H.L. mainly contributed to deep learning algorithm development, analysis, and article deep learning section writing.
The authors declare no competing financial interest.
Supplementary Material
References
- Nørskov J.; Chen J.; Miranda R.; Fitzsimmons T.; Stack R.. Sustainable Ammonia Synthesis—Exploring the Scientific Challenges Associated with Discovering Alternative, Sustainable Processes for Ammonia Production; US DOE Office of Science, 2016-02-18, 2016.
- Smith C.; Hill A. K.; Torrente-Murciano L. Current and future role of Haber–Bosch ammonia in a carbon-free energy landscape. Energy Environ. Sci. 2020, 13, 331–344. 10.1039/c9ee02873k. [DOI] [Google Scholar]
- Liu X.; Elgowainy A.; Wang M. Life cycle energy use and greenhouse gas emissions of ammonia production from renewable resources and industrial by-products. Green Chem. 2020, 22, 5751–5761. 10.1039/d0gc02301a. [DOI] [Google Scholar]
- Erdemir D.; Dincer I. A perspective on the use of ammonia as a clean fuel: Challenges and solutions. Int. J. Energy Res. 2021, 45, 4827–4834. 10.1002/er.6232. [DOI] [Google Scholar]
- Afif A.; Radenahmad N.; Cheok Q.; Shams S.; Kim J. H.; Azad A. K. Ammonia-fed fuel cells: a comprehensive review. Sustainable Energy Rev. 2016, 60, 822–835. 10.1016/j.rser.2016.01.120. [DOI] [Google Scholar]
- Li K.; Andersen S. Z.; Statt M. J.; Saccoccio M.; Bukas V. J.; Krempl K.; Sažinas R.; Pedersen J. B.; Shadravan V.; Zhou Y.; Chakraborty D.; Kibsgaard J.; Vesborg P. C. K.; Nørskov J. K.; Chorkendorff I. Enhancement of lithium-mediated ammonia synthesis by addition of oxygen. Science 2021, 374, 1593–1597. 10.1126/science.abl4300. [DOI] [PubMed] [Google Scholar]
- Cao N.; Chen Z.; Zang K.; Xu J.; Zhong J.; Luo J.; Xu X.; Zheng G. Doping strain induced bi-Ti(3+) pairs for efficient N2 activation and electrocatalytic fixation. Nat. Commun. 2019, 10, 2877. 10.1038/s41467-019-10888-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song Y.; Johnson D.; Peng R.; Hensley D. K.; Bonnesen P. V.; Liang L.; Huang J.; Yang F.; Zhang F.; Qiao R.; Baddorf A. P.; Tschaplinski T. J.; Engle N. L.; Hatzell M. C.; Wu Z.; Cullen D. A.; Meyer H. M.; Sumpter B. G.; Rondinone A. J. A physical catalyst for the electrolysis of nitrogen to ammonia. Sci. Adv. 2018, 4, e1700336 10.1126/sciadv.1700336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hao Q.; Liu C.; Jia G.; Wang Y.; Arandiyan H.; Wei W.; Ni B.-J. Catalytic reduction of nitrogen to produce ammonia by bismuth-based catalysts: state of the art and future prospects. Mater. Horiz. 2020, 7, 1014–1029. 10.1039/c9mh01668f. [DOI] [Google Scholar]
- Tang S.; Dang Q.; Liu T.; Zhang S.; Zhou Z.; Li X.; Wang X.; Sharman E.; Luo Y.; Jiang J. Realizing a Not-Strong-Not-Weak Polarization Electric Field in Single-Atom Catalysts Sandwiched by Boron Nitride and Graphene Sheets for Efficient Nitrogen Fixation. J. Am. Chem. Soc. 2020, 142, 19308–19315. 10.1021/jacs.0c09527. [DOI] [PubMed] [Google Scholar]
- Chang F.; Tezsevin I.; de Rijk J. W.; Meeldijk J. D.; Hofmann J. P.; Er S.; Ngene P.; de Jongh P. E. Potassium hydride-intercalated graphite as an efficient heterogeneous catalyst for ammonia synthesis. Nat. Catal. 2022, 5, 222. 10.1038/s41929-022-00754-x. [DOI] [Google Scholar]
- Banisalman M. J.; Kim M.-C.; Han S. S. Origin of Enhanced Ammonia Synthesis on Ru–Co Catalysts Unraveled by Density Functional Theory. ACS Catal. 2022, 12, 1090–1097. 10.1021/acscatal.1c05023. [DOI] [Google Scholar]
- Zhang W.; Fu Q.; Luo Q.; Sheng L.; Yang J. Understanding Single-Atom Catalysis in View of Theory. JACS Au 2021, 1, 2130–2145. 10.1021/jacsau.1c00384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vojvodic A.; Medford A. J.; Studt F.; Abild-Pedersen F.; Khan T. S.; Bligaard T.; Nørskov J. K. Exploring the limits: A low-pressure, low-temperature Haber–Bosch process. Chem. Phys. Lett. 2014, 598, 108–112. 10.1016/j.cplett.2014.03.003. [DOI] [Google Scholar]
- Honkala K.; Hellman A.; Remediakis I. N.; Logadottir A.; Carlsson A.; Dahl S.; Christensen C. H.; Nørskov J. K. Ammonia Synthesis from First-Principles Calculations. Science 2005, 307, 555–558. 10.1126/science.1106435. [DOI] [PubMed] [Google Scholar]
- Hellman A.; Baerends E. J.; Biczysko M.; Bligaard T.; Christensen C. H.; Clary D. C.; Dahl S.; van Harrevelt R.; Honkala K.; Jonsson H.; Kroes G. J.; Luppi M.; Manthe U.; Nørskov J. K.; Olsen R. A.; Rossmeisl J.; Skúlason E.; Tautermann C. S.; Varandas A. J. C.; Vincent J. K. Predicting Catalysis: Understanding Ammonia Synthesis from First-Principles Calculations. J. Phys. Chem. B 2006, 110, 17719–17735. 10.1021/jp056982h. [DOI] [PubMed] [Google Scholar]
- Amar I. A.; Lan R.; Petit C. T. G.; Tao S. Solid-state electrochemical synthesis of ammonia: a review. J. Solid State Electrochem. 2011, 15, 1845. 10.1007/s10008-011-1376-x. [DOI] [Google Scholar]
- Kyriakou V.; Garagounis I.; Vasileiou E.; Vourros A.; Stoukides M. Progress in the Electrochemical Synthesis of Ammonia. Catal. Today 2017, 286, 2–13. 10.1016/j.cattod.2016.06.014. [DOI] [Google Scholar]
- Guo X.; Zhu Y.; Ma T. Lowering reaction temperature: Electrochemical ammonia synthesis by coupling various electrolytes and catalysts. J. Energy Chem. 2017, 26, 1107–1116. 10.1016/j.jechem.2017.09.012. [DOI] [Google Scholar]
- Giddey S.; Badwal S. P. S.; Kulkarni A. Review of electrochemical ammonia production technologies and materials. Int. J. Hydrogen Energy 2013, 38, 14576–14594. 10.1016/j.ijhydene.2013.09.054. [DOI] [Google Scholar]
- Licht S.; Cui B.; Wang B.; Li F.-F.; Lau J.; Liu S. Ammonia synthesis by N2 and steam electrolysis in molten hydroxide suspensions of nanoscale Fe2O3. Science 2014, 345, 637–640. 10.1126/science.1254234. [DOI] [PubMed] [Google Scholar]
- Shipman M. A.; Symes M. D. Recent progress towards the electrosynthesis of ammonia from sustainable resources. Catal. Today 2017, 286, 57–68. 10.1016/j.cattod.2016.05.008. [DOI] [Google Scholar]
- Li C.; Wang T.; Gong J. Alternative Strategies Toward Sustainable Ammonia Synthesis. Trans. Tianjin Univ. 2020, 26, 67–91. 10.1007/s12209-020-00243-x. [DOI] [Google Scholar]
- Hao Y.-C.; Guo Y.; Chen L.-W.; Shu M.; Wang X.-Y.; Bu T.-A.; Gao W.-Y.; Zhang N.; Su X.; Feng X.; Zhou J.-W.; Wang B.; Hu C.-W.; Yin A.-X.; Si R.; Zhang Y.-W.; Yan C.-H. Promoting nitrogen electroreduction to ammonia with bismuth nanocrystals and potassium cations in water. Nat. Catal. 2019, 2, 448–456. 10.1038/s41929-019-0241-7. [DOI] [Google Scholar]
- Lan R.; Irvine J. T. S.; Tao S. Synthesis of ammonia directly from air and water at ambient temperature and pressure. Sci. Rep. 2013, 3, 1145. 10.1038/srep01145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Samukawa S.; Hori M.; Rauf S.; Tachibana K.; Bruggeman P.; Kroesen G.; Whitehead J. C.; Murphy A. B.; Gutsol A. F.; Starikovskaia S.; Kortshagen U.; Boeuf J.-P.; Sommerer T. J.; Kushner M. J.; Czarnetzki U.; Mason N. The 2012 Plasma Roadmap. J. Phys. D 2012, 45, 253001. 10.1088/0022-3727/45/25/253001. [DOI] [Google Scholar]
- Patil B. S.; Wang Q.; Hessel V.; Lang J. Plasma N2-fixation: 1900–2014. Catal. Today 2015, 256, 49–66. 10.1016/j.cattod.2015.05.005. [DOI] [Google Scholar]
- Mohsennia M.; Rakhshi M.; Rasa H. A computational study on interactions of Ni- and Pt-doped boron nitride nano tubes with NH 3 in presence and absence of electric fields. Comput. Theor. Chem. 2018, 1136–1137, 1–9. 10.1016/j.comptc.2018.05.013. [DOI] [Google Scholar]
- Zhou M.; Wang H. Optimally Selecting Photo- and Electrocatalysis to Facilitate CH4 Activation on TiO2(110) Surface: Localized Photoexcitation versus Global Electric-Field Polarization. JACS Au 2022, 2, 188–196. 10.1021/jacsau.1c00466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schkolnik G.; Salewski J.; Millo D.; Zebger I.; Franzen S.; Hildebrandt P. Vibrational Stark Effect of the Electric-Field Reporter 4-Mercaptobenzonitrile as a Tool for Investigating Electrostatics at Electrode/SAM/Solution Interfaces. Int. J. Mol. 2012, 13, 7466–7482. 10.3390/ijms13067466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fried S. D.; Bagchi S.; Boxer S. G. Extreme electric fields power catalysis in the active site of ketosteroid isomerase. Science 2014, 346, 1510–1514. 10.1126/science.1259802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shaik S.; Mandal D.; Ramanan R. Oriented electric fields as future smart reagents in chemistry. Nat. Chem. 2016, 8, 1091–1098. 10.1038/nchem.2651. [DOI] [PubMed] [Google Scholar]
- Cassone G.; Pietrucci F.; Saija F.; Guyot F.; Saitta A. M. One-step electric-field driven methane and formaldehyde synthesis from liquid methanol. Chem. Sci. 2017, 8, 2329–2336. 10.1039/c6sc04269d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joy J.; Stuyver T.; Shaik S. Oriented External Electric Fields and Ionic Additives Elicit Catalysis and Mechanistic Crossover in Oxidative Addition Reactions. J. Am. Chem. Soc. 2020, 142, 3836–3850. 10.1021/jacs.9b11507. [DOI] [PubMed] [Google Scholar]
- Shaik S.; Danovich D.; Joy J.; Wang Z.; Stuyver T. Electric-Field Mediated Chemistry: Uncovering and Exploiting the Potential of (Oriented) Electric Fields to Exert Chemical Catalysis and Reaction Control. J. Am. Chem. Soc. 2020, 142, 12551–12562. 10.1021/jacs.0c05128. [DOI] [PubMed] [Google Scholar]
- Ogura K.; Yoshida I. Electrocatalytic reduction of CO2 to methanol: Part 9: Mediation with metal porphyrins. J. Mol. Catal. 1988, 47, 51–57. 10.1016/0304-5102(88)85072-7. [DOI] [Google Scholar]
- Welborn V. V.; Ruiz Pestana L.; Head-Gordon T. Computational optimization of electric fields for better catalysis design. Nat. Catal. 2018, 1, 649–655. 10.1038/s41929-018-0109-2. [DOI] [Google Scholar]
- Liu N.; Zhang R.; Li Y.; Chen B. Local Electric Field Effect of TMI (Fe, Co, Cu)-BEA on N2O Direct Dissociation. J. Phys. Chem. C 2014, 118, 10944–10956. 10.1021/jp5023949. [DOI] [Google Scholar]
- Hofer W. A.; Fisher A. J.; Wolkow R. A.; Grütter P. Surface Relaxations, Current Enhancements, and Absolute Distances in High Resolution Scanning Tunneling Microscopy. Phys. Rev. Lett. 2001, 87, 236104. 10.1103/physrevlett.87.236104. [DOI] [PubMed] [Google Scholar]
- Müller E. W.; Bahadur K. Field Ionization of Gases at a Metal Surface and the Resolution of the Field Ion Microscope. Phys. Rev. 1956, 102, 624–631. 10.1103/physrev.102.624. [DOI] [Google Scholar]
- Müller E. W. Field Ion Microscopy. Science 1965, 149, 591–601. 10.1126/science.149.3684.591. [DOI] [PubMed] [Google Scholar]
- Müller E. W. Work Function of Tungsten Single Crystal Planes Measured by the Field Emission Microscope. J. Appl. Phys. 1955, 26, 732–737. 10.1063/1.1722081. [DOI] [Google Scholar]
- Manabe R.; Nakatsubo H.; Gondo A.; Murakami K.; Ogo S.; Tsuneki H.; Ikeda M.; Ishikawa A.; Nakai H.; Sekine Y. Electrocatalytic synthesis of ammonia by surface proton hopping. Chem. Sci. 2017, 8, 5434–5439. 10.1039/c7sc00840f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gondo A.; Manabe R.; Sakai R.; Murakami K.; Yabe T.; Ogo S.; Ikeda M.; Tsuneki H.; Sekine Y. Ammonia Synthesis Over Co Catalyst in an Electric Field. Catal. Lett. 2018, 148, 1929–1938. 10.1007/s10562-018-2404-6. [DOI] [Google Scholar]
- Murakami K.; Manabe R.; Nakatsubo H.; Yabe T.; Ogo S.; Sekine Y. Elucidation of the role of electric field on low temperature ammonia synthesis using isotopes. Catal. Today 2018, 303, 271–275. 10.1016/j.cattod.2017.08.008. [DOI] [Google Scholar]
- Murakami K.; Tanaka Y.; Hayashi S.; Sakai R.; Hisai Y.; Mizutani Y.; Ishikawa A.; Higo T.; Ogo S.; Seo J. G.; Tsuneki H.; Nakai H.; Sekine Y. Governing factors of supports of ammonia synthesis in an electric field found using density functional theory. J. Chem. Phys. 2019, 151, 064708. 10.1063/1.5111920. [DOI] [Google Scholar]
- Sakai R.; Murakami K.; Mizutani Y.; Tanaka Y.; Hayashi S.; Ishikawa A.; Higo T.; Ogo S.; Tsuneki H.; Nakai H.; Sekine Y. Agglomeration Suppression of a Fe-Supported Catalyst and its Utilization for Low-Temperature Ammonia Synthesis in an Electric Field. ACS Omega 2020, 5, 6846–6851. 10.1021/acsomega.0c00170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Akamatsu M.; Sakai N.; Matile S. Electric-Field-Assisted Anion−π Catalysis. J. Am. Chem. Soc. 2017, 139, 6558–6561. 10.1021/jacs.7b02421. [DOI] [PubMed] [Google Scholar]
- Brandenburg R. Dielectric barrier discharges: progress on plasma sources and on the understanding of regimes and single filaments. Plasma Sources Sci. Technol. 2017, 26, 053001. 10.1088/1361-6595/aa6426. [DOI] [Google Scholar]
- Hong J.; Aramesh M.; Shimoni O.; Seo D. H.; Yick S.; Greig A.; Charles C.; Prawer S.; Murphy A. B. Plasma Catalytic Synthesis of Ammonia Using Functionalized-Carbon Coatings in an Atmospheric-Pressure Non-equilibrium Discharge. Plasma Chem. Plasma Process. 2016, 36, 917–940. 10.1007/s11090-016-9711-8. [DOI] [Google Scholar]
- Hong J.; Prawer S.; Murphy A. B. Plasma Catalysis as an Alternative Route for Ammonia Production: Status, Mechanisms, and Prospects for Progress. ACS Sustainable Chem. 2018, 6, 15–31. 10.1021/acssuschemeng.7b02381. [DOI] [Google Scholar]
- Mehta P.; Barboun P.; Herrera F. A.; Kim J.; Rumbach P.; Go D. B.; Hicks J. C.; Schneider W. F. Overcoming ammonia synthesis scaling relations with plasma-enabled catalysis. Nat. Catal. 2018, 1, 269–275. 10.1038/s41929-018-0045-1. [DOI] [Google Scholar]
- Xie Q.; Zhuge S.; Song X.; Lu M.; Ruan R.; Nie Y.; Ji J. Hydrogenation of plasma-excited nitrogen over an alumina catalyst for ammonia synthesis. Int. J. Hydrogen Energy 2018, 43, 14885–14891. 10.1016/j.ijhydene.2018.06.051. [DOI] [Google Scholar]
- Ben Yaala M.; Saeedi A.; Scherrer D.-F.; Moser L.; Steiner R.; Zutter M.; Oberkofler M.; De Temmerman G.; Marot L.; Meyer E. Plasma-assisted catalytic formation of ammonia in N2–H2 plasma on a tungsten surface. Phys. Chem. Chem. Phys. 2019, 21, 16623–16633. 10.1039/c9cp01139k. [DOI] [PubMed] [Google Scholar]
- Rouwenhorst K. H. R.; Engelmann Y.; van ‘t Veer K.; Postma R. S.; Bogaerts A.; Lefferts L. Plasma-driven catalysis: green ammonia synthesis with intermittent electricity. Green Chem. 2020, 22, 6258–6287. 10.1039/d0gc02058c. [DOI] [Google Scholar]
- Winter L. R.; Ashford B.; Hong J.; Murphy A. B.; Chen J. G. Identifying Surface Reaction Intermediates in Plasma Catalytic Ammonia Synthesis. ACS Catal. 2020, 10, 14763–14774. 10.1021/acscatal.0c03166. [DOI] [Google Scholar]
- Kado S.; Sekine Y.; Nozaki T.; Okazaki K. Diagnosis of atmospheric pressure low temperature plasma and application to high efficient methane conversion. Catal. Today 2004, 89, 47–55. 10.1016/j.cattod.2003.11.036. [DOI] [Google Scholar]
- Wang J.-Y.; Xia G.-G.; Huang A.; Suib S. L.; Hayashi Y.; Matsumoto H. CO2 Decomposition Using Glow Discharge Plasmas. J. Catal. 1999, 185, 152–159. 10.1006/jcat.1999.2499. [DOI] [Google Scholar]
- Yu Q.; Kong M.; Liu T.; Fei J.; Zheng X. Characteristics of the Decomposition of CO2 in a Dielectric Packed-Bed Plasma Reactor. Plasma Chem. Plasma Process. 2012, 32, 153–163. 10.1007/s11090-011-9335-y. [DOI] [Google Scholar]
- Gray J. T.Designing Electric Field Assisted Catalytic Reactors for Hydrogen Production Applications. Ph.D. Thesis, Washington State University, Ann Arbor, 2019. [Google Scholar]
- Bai X.; Tiwari S.; Robinson B.; Killmer C.; Li L.; Hu J. Microwave catalytic synthesis of ammonia from methane and nitrogen. Catal. Sci. Technol. 2018, 8, 6302–6305. 10.1039/c8cy01355a. [DOI] [Google Scholar]
- Bai X.; Robinson B.; Killmer C.; Wang Y.; Li L.; Hu J. Microwave catalytic reactor for upgrading stranded shale gas to aromatics. Fuel 2019, 243, 485–492. 10.1016/j.fuel.2019.01.147. [DOI] [Google Scholar]
- Hu J.; Wildfire C.; Stiegman A. E.; Dagle R. A.; Shekhawat D.; Abdelsayed V.; Bai X.; Tian H.; Bogle M. B.; Hsu C.; Luo Y.; Davidson S. D.; Wang Y. Microwave-driven heterogeneous catalysis for activation of dinitrogen to ammonia under atmospheric pressure. Chem. Eng. J. 2020, 397, 125388. 10.1016/j.cej.2020.125388. [DOI] [Google Scholar]
- Tiwari S.; Caiola A.; Bai X.; Lalsare A.; Hu J. Microwave Plasma-Enhanced and Microwave Heated Chemical Reactions. Plasma Chem. Plasma Process. 2020, 40, 1–23. 10.1007/s11090-019-10040-7. [DOI] [Google Scholar]
- Wildfire C.; Abdelsayed V.; Shekhawat D.; Dagle R. A.; Davidson S. D.; Hu J. Microwave-assisted ammonia synthesis over Ru/MgO catalysts at ambient pressure. Catal. Today 2020, 365, 103–110. [Google Scholar]
- Stuve E. M. Ionization of water in interfacial electric fields: An electrochemical view. Chem. Phys. Lett. 2012, 519–520, 1–17. 10.1016/j.cplett.2011.09.040. [DOI] [Google Scholar]
- Kim C.; Weng L.-C.; Bell A. T. Impact of Pulsed Electrochemical Reduction of CO2 on the Formation of C2+ Products over Cu. ACS Catal. 2020, 10, 12403–12413. 10.1021/acscatal.0c02915. [DOI] [Google Scholar]
- Chen L. D.; Urushihara M.; Chan K.; Nørskov J. K. Electric Field Effects in Electrochemical CO2 Reduction. ACS Catal. 2016, 6, 7133–7139. 10.1021/acscatal.6b02299. [DOI] [Google Scholar]
- Manabe R.; Nakatsubo H.; Gondo A.; Murakami K.; Ogo S.; Tsuneki H.; Ikeda M.; Ishikawa A.; Nakai H.; Sekine Y. Electrocatalytic synthesis of ammonia by surface proton hopping. Chem. Sci. 2017, 8, 5434–5439. 10.1039/c7sc00840f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wildfire C.; Abdelsayed V.; Shekhawat D.; Spencer M. J. Ambient pressure synthesis of ammonia using a microwave reactor. Catal. Commun. 2018, 115, 64–67. 10.1016/j.catcom.2018.07.010. [DOI] [Google Scholar]
- Deshlahra P.; Wolf E. E.; Schneider W. F. A Periodic Density Functional Theory Analysis of CO Chemisorption on Pt(111) in the Presence of Uniform Electric Fields. J. Phys. Chem. A 2009, 113, 4125–4133. 10.1021/jp810518x. [DOI] [PubMed] [Google Scholar]
- McEwen J.-S.; Gaspard P.; Visart de Bocarmé T.; Kruse N. Oscillations and Bistability in the Catalytic Formation of Water on Rhodium in High Electric Fields. J. Phys. Chem. C 2009, 113, 17045–17058. 10.1021/jp901975w. [DOI] [Google Scholar]
- Che F.; Gray J. T.; Ha S.; Kruse N.; Scott S. L.; McEwen J.-S. Elucidating the Roles of Electric Fields in Catalysis: A Perspective. ACS Catal. 2018, 8, 5153–5174. 10.1021/acscatal.7b02899. [DOI] [Google Scholar]
- Kong Y.; Cha C. Y. Reduction of NOx adsorbed on char with microwave energy. Carbon 1996, 34, 1035–1040. 10.1016/0008-6223(96)00051-6. [DOI] [Google Scholar]
- Fried S. D.; Boxer S. G. Electric Fields and Enzyme Catalysis. Annu. Rev. Biochem. 2017, 86, 387–415. 10.1146/annurev-biochem-061516-044432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang S.-H.; Pillai H. S.; Wang S.; Achenie L. E. K.; Xin H. Infusing theory into deep learning for interpretable reactivity prediction. Nat. Commun. 2021, 12, 5288. 10.1038/s41467-021-25639-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhong M.; Tran K.; Min Y.; Wang C.; Wang Z.; Dinh C.-T.; De Luna P.; Yu Z.; Rasouli A. S.; Brodersen P.; Sun S.; Voznyy O.; Tan C.-S.; Askerka M.; Che F.; Liu M.; Seifitokaldani A.; Pang Y.; Lo S.-C.; Ip A.; Ulissi Z.; Sargent E. H. Accelerated discovery of CO 2 electrocatalysts using active machine learning. Nature 2020, 581, 178–183. 10.1038/s41586-020-2242-8. [DOI] [PubMed] [Google Scholar]
- LeCun Y.; Bengio Y.; Hinton G. Deep learning. Nature 2015, 521, 436–444. 10.1038/nature14539. [DOI] [PubMed] [Google Scholar]
- Esterhuizen J. A.; Goldsmith B. R.; Linic S. Theory-Guided Machine Learning Finds Geometric Structure-Property Relationships for Chemisorption on Subsurface Alloys. Chem 2020, 6, 3100–3117. 10.1016/j.chempr.2020.09.001. [DOI] [Google Scholar]
- Tran K.; Ulissi Z. W. Active learning across intermetallics to guide discovery of electrocatalysts for CO2 reduction and H2 evolution. Nat. Catal. 2018, 1, 696–703. 10.1038/s41929-018-0142-1. [DOI] [Google Scholar]
- Shi X.; Lin X.; Luo R.; Wu S.; Li L.; Zhao Z.-J.; Gong J. Dynamics of Heterogeneous Catalytic Processes at Operando Conditions. JACS Au 2021, 1, 2100–2120. 10.1021/jacsau.1c00355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou W.; Yang L.; Wang X.; Zhao W.; Yang J.; Zhai D.; Sun L.; Deng W. In Silico Design of Covalent Organic Framework-Based Electrocatalysts. JACS Au 2021, 1, 1497–1505. 10.1021/jacsau.1c00258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen S.; Jung Y. Deep Retrosynthetic Reaction Prediction using Local Reactivity and Global Attention. JACS Au 2021, 1, 1612–1620. 10.1021/jacsau.1c00246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma X.; Xin H. Orbitalwise coordination number for predicting adsorption properties of metal nanocatalysts. Phys. Rev. Lett. 2017, 118, 036101. 10.1103/PhysRevLett.118.036101. [DOI] [PubMed] [Google Scholar]
- Wang S.; Pillai H. S.; Xin H. Bayesian learning of chemisorption for bridging the complexity of electronic descriptors. Nat. Commun. 2020, 11, 6132. 10.1038/s41467-020-19524-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Back S.; Yoon J.; Tian N.; Zhong W.; Tran K.; Ulissi Z. W. Convolutional neural network of atomic surface structures to predict binding energies for high-throughput screening of catalysts. J. Phys. Chem. Lett. 2019, 10, 4401–4408. 10.1021/acs.jpclett.9b01428. [DOI] [PubMed] [Google Scholar]
- Chowdhury A. J.; Yang W.; Walker E.; Mamun O.; Heyden A.; Terejanu G. A. Prediction of adsorption energies for chemical species on metal catalyst surfaces using machine learning. J. Phys. Chem. C 2018, 122, 28142–28150. 10.1021/acs.jpcc.8b09284. [DOI] [Google Scholar]
- Li Z.; Wang S.; Chin W. S.; Achenie L. E.; Xin H. High-throughput screening of bimetallic catalysts enabled by machine learning. J. Mater. Chem. A 2017, 5, 24131–24138. 10.1039/c7ta01812f. [DOI] [Google Scholar]
- Xie T.; Grossman J. C. Crystal graph convolutional neural networks for an accurate and interpretable prediction of material properties. Phys. Rev. Lett. 2018, 120, 145301. 10.1103/physrevlett.120.145301. [DOI] [PubMed] [Google Scholar]
- Fung V.; Hu G.; Ganesh P.; Sumpter B. G. Machine learned features from density of states for accurate adsorption energy prediction. Nat. Commun. 2021, 12, 88. 10.1038/s41467-020-20342-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weng B.; Song Z.; Zhu R.; Yan Q.; Sun Q.; Grice C. G.; Yan Y.; Yin W.-J. Simple descriptor derived from symbolic regression accelerating the discovery of new perovskite catalysts. Nat. Commun. 2020, 11, 3513. 10.1038/s41467-020-17263-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- García-Muelas R.; López N. Statistical learning goes beyond the d-band model providing the thermochemistry of adsorbates on transition metals. Nat. Commun. 2019, 10, 4687. 10.1038/s41467-019-12709-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Z.; Achenie L. E. K.; Xin H. An adaptive machine learning strategy for accelerating discovery of perovskite electrocatalysts. ACS Catal. 2020, 10, 4377–4384. 10.1021/acscatal.9b05248. [DOI] [Google Scholar]
- Lansford J. L.; Vlachos D. G. Infrared spectroscopy data- and physics-driven machine learning for characterizing surface microstructure of complex materials. Nat. Commun. 2020, 11, 1513. 10.1038/s41467-020-15340-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garrido Torres J. A.; Jennings P. C.; Hansen M. H.; Boes J. R.; Bligaard T. Low-scaling algorithm for nudged elastic band calculations using a surrogate machine learning model. Phys. Rev. Lett. 2019, 122, 156001. 10.1103/physrevlett.122.156001. [DOI] [PubMed] [Google Scholar]
- Peterson A. A. Acceleration of saddle-point searches with machine learning. J. Chem. Phys. 2016, 145, 074106. 10.1063/1.4960708. [DOI] [PubMed] [Google Scholar]
- Deshlahra P.; Wolf E. E.; Schneider W. F. A Periodic Density Functional Theory Analysis of CO Chemisorption on Pt(111) in the Presence of Uniform Electric Fields. J. Phys. Chem. A 2009, 113, 4125–4133. 10.1021/jp810518x. [DOI] [PubMed] [Google Scholar]
- Wang J.; Yu L.; Hu L.; Chen G.; Xin H.; Feng X. Ambient ammonia synthesis via palladium-catalyzed electrohydrogenation of dinitrogen at low overpotential. Nat. Commun. 2018, 9, 1795. 10.1038/s41467-018-04213-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Honkala K.; Hellman A.; Remediakis I. N.; Logadottir A.; Carlsson A.; Dahl S.; Christensen C. H.; Nørskov J. K. Ammonia Synthesis from First-Principles Calculations. Science 2005, 307, 555–558. 10.1126/science.1106435. [DOI] [PubMed] [Google Scholar]
- Ding J.; Wang L.; Wu P.; Li A.; Li W.; Stampfl C.; Liao X.; Haynes B. S.; Han X.; Huang J. Confined Ru Nanocatalysts on Surface to Enhance Ammonia Synthesis: An In situ ETEM Study. ChemCatChem 2020, 13, 534–538. 10.1002/cctc.202001423. [DOI] [Google Scholar]
- Nakao T.; Tada T.; Hosono H. First-Principles and Microkinetic Study on the Mechanism for Ammonia Synthesis Using Ru-Loaded Hydride Catalyst. J. Phys. Chem. C 2019, 124, 2070–2078. 10.1021/acs.jpcc.9b10850. [DOI] [Google Scholar]
- Deshlahra P.Study of Electronic Effects in a Catalytic Diode: Dft Calculations and Meiras Experiments; University of Notre Dame, 2011. [Google Scholar]
- Deshlahra P.; Conway J.; Wolf E. E.; Schneider W. F. Influence of Dipole–Dipole Interactions on Coverage-Dependent Adsorption: CO and NO on Pt(111). Langmuir 2012, 28, 8408–8417. 10.1021/la300975s. [DOI] [PubMed] [Google Scholar]
- Ulissi Z. W.; Medford A. J.; Bligaard T.; Nørskov J. K. To address surface reaction network complexity using scaling relations machine learning and DFT calculations. Nat. Commun. 2017, 8, 14621. 10.1038/ncomms14621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhong M.; Tran K.; Min Y.; Wang C.; Wang Z.; Dinh C.-T.; De Luna P.; Yu Z.; Rasouli A. S.; Brodersen P.; Sun S.; Voznyy O.; Tan C.-S.; Askerka M.; Che F.; Liu M.; Seifitokaldani A.; Pang Y.; Lo S.-C.; Ip A.; Ulissi Z.; Sargent E. H. Accelerated discovery of CO2 electrocatalysts using active machine learning. Nature 2020, 581, 178–183. 10.1038/s41586-020-2242-8. [DOI] [PubMed] [Google Scholar]
- Wu Z.; Pan S.; Chen F.; Long G.; Zhang C.; Yu P. S. A Comprehensive Survey on Graph Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 4–24. 10.1109/tnnls.2020.2978386. [DOI] [PubMed] [Google Scholar]
- Green Ammonia Market Worth $852 Million by 2030—Exclusive Report by MarketsandMarkets. PR Newswire, 2020.
- Winebrake J. J. Energy at the Crossroads. Am. J. Agric. Econ. 2005, 87, 810–812. 10.1111/j.1467-8276.2005.00767_5.x. [DOI] [Google Scholar]
- Erdemir D.; Dincer I. A perspective on the use of ammonia as a clean fuel: Challenges and solutions. Int. J. Hydrogen Energy 2021, 45, 4827–4834. 10.1002/er.6232. [DOI] [Google Scholar]
- Afif A.; Radenahmad N.; Cheok Q.; Shams S.; Kim J. H.; Azad A. K. Ammonia-fed fuel cells: a comprehensive review. Renewable Sustainable Energy Rev. 2016, 60, 822–835. 10.1016/j.rser.2016.01.120. [DOI] [Google Scholar]
- Zang Y.; Zou Q.; Fu T.; Ng F.; Fowler B.; Yang J.; Li H.; Steigerwald M. L.; Nuckolls C.; Venkataraman L. Directing isomerization reactions of cumulenes with electric fields. Nat. Commun. 2019, 10, 4482. 10.1038/s41467-019-12487-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wintterlin J.Scanning tunneling microscopy studies of catalytic reactions. Impact of Surface Science on Catalysis; Advances in Catalysis; Academic Press, 2000; Vol. 45, pp 131–206. [Google Scholar]
- Hofer W. A. Challenges and errors: interpreting high resolution images in scanning tunneling microscopy. Prog. Surf. 2003, 71, 147. 10.1016/s0079-6816(03)00005-4. [DOI] [Google Scholar]
- Block J. H.; Czanderna A. W.. Field ion mass spectrometry applied to surface investigations. Methods of Surface Analysis; Elsevier, 1975; pp 379–446. [Google Scholar]
- Kruse N.; Bocarmé T. V. d.. Heterogeneous Catalysis and High Electric Fields. Handbook of Heterogeneous Catalysis, 2008; pp 870–895. [Google Scholar]
- Wittreich GR; Liu S.; Dauenhauer PJ; Vlachos DG Catalytic resonance of ammonia synthesis by simulated dynamic ruthenium crystal strain. Sci. Adv. 2022, 8, eabl6576 10.1126/sciadv.abl6576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lim C. W.; Hülsey M. J.; Yan N. Non-Faradaic Promotion of Ethylene Hydrogenation under Oscillating Potentials. JACS Au 2021, 1, 536–542. 10.1021/jacsau.1c00044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kresse G.; Hafner J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B: Condens. Matter 1993, 47, 558–561. 10.1103/physrevb.47.558. [DOI] [PubMed] [Google Scholar]
- Kresse G.; Furthmüller J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. 10.1016/0927-0256(96)00008-0. [DOI] [PubMed] [Google Scholar]
- White J. A.; Bird D. M. Implementation of gradient-corrected exchange-correlation potentials in Car-Parrinello total-energy calculations. Phys. Rev. B: Condens. Matter Mater. Phys. 1994, 50, 4954–4957. 10.1103/physrevb.50.4954. [DOI] [PubMed] [Google Scholar]
- Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/physrevlett.77.3865. [DOI] [PubMed] [Google Scholar]
- Perdew J. P.; Wang Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B: Condens. Matter Mater. Phys. 1992, 45, 13244–13249. 10.1103/physrevb.45.13244. [DOI] [PubMed] [Google Scholar]
- Henkelman G.; Uberuaga B. P.; Jónsson H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 2000, 113, 9901–9904. 10.1063/1.1329672. [DOI] [Google Scholar]
- Henkelman G.; Jónsson H. A dimer method for finding saddle points on high dimensional potential surfaces using only first derivatives. J. Chem. Phys. 1999, 111, 7010–7022. 10.1063/1.480097. [DOI] [Google Scholar]
- Neugebauer J.; Scheffler M. Adsorbate-substrate and adsorbate-adsorbate interactions of Na and K adlayers on Al(111). Phys. Rev. B: Condens. Matter 1992, 46, 16067–16080. 10.1103/physrevb.46.16067. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.