Abstract
The highly ramified arbors of neuronal dendrites provide the substrate for the high connectivity and computational power of the brain. Altered dendritic morphology is associated with neuronal diseases. Many molecules have been shown to play crucial roles in shaping and maintaining dendrite morphology. However, the underlying principles by which molecular interactions generate branched morphologies are not understood. To elucidate these principles, we visualized the growth of dendrites throughout larval development of Drosophila sensory neurons and found that the tips of dendrites undergo dynamic instability, transitioning rapidly and stochastically between growing, shrinking, and paused states. By incorporating these measured dynamics into an agent-based computational model, we showed that the complex and highly variable dendritic morphologies of these cells are a consequence of the stochastic dynamics of their dendrite tips. These principles may generalize to branching of other neuronal cell types, as well as to branching at the subcellular and tissue levels.
The complex and highly variable dendritic morphologies emerge from the stochastic dynamics of dendrite tips.
INTRODUCTION
Neurons are polarized cells (1) whose axons and dendrites are often highly branched. Branching provides the surface area necessary for dendrites to receive inputs from thousands of other cells or from the environment (2), and for axons to output signals to multiple cells. In these ways, branching facilitates the high connectivity of the brain (2). Thus, the morphology of the neurons, together with their synaptic connections (3, 4), defines the structure of the nervous system, the connectome, which is viewed as a prerequisite for understanding brain function (5). Whereas much is known about the growth of axons, whose tips, the growth cones, are guided by extracellular signals and guidepost cells (6), the mechanisms underlying the growth and branching of dendrites are poorly understood. Elucidation of these mechanisms is the goal of the present work.
While many molecules have been shown to play crucial roles in shaping dendrites, the underlying rules by which molecular interactions generate branched morphologies are not understood. To investigate these rules, we have focused on dendrite morphogenesis in class IV dendritic arborization neurons in Drosophila, a model system for dendritogenesis (7, 8). These nociceptive neurons form a highly branched meshwork just under the cuticle that senses puncture of the larva by the ovipositor barbs of parasitic wasps and initiates avoidance behaviors (9, 10). Class IV cells are ideal for studying branching morphogenesis because they grow rapidly over 5 days of larval development, their branches are noncrossing due to self-avoidance mediated by the Down’s syndrome cell adhesion molecule (11–13) and other molecules (14, 15), and they can be visualized using cell-specific labeling (7, 16). Many molecules that participate in dendrite morphogenesis have been identified: transcription factors (17); extracellular matrix and integrins (18, 19); actin-associated proteins (20); microtubule motors such as dynein and kinesin (21, 22); microtubule regulators such as spastin (23), katanin (24), and γ-tubulin (25); and microRNAs such as bantam (14). A major difficulty, however, is that it is currently not possible to predict quantitatively how developmental processes occurring at the molecular and subcellular levels determine the morphology of the entire dendritic arbor.
While several theoretical and computational models can produce dendrite-like branched morphologies, they are not grounded in molecular or development data. Early models, designed to describe and classify neurons, reconstituted morphologies based on the statistical properties of the observed arbors themselves (26, 27). Optimization-based models that minimize wiring (i.e., the total lengths of the branches) capture key features of neuronal morphology (28, 29) but lack connection to the cellular processes, as do models based on more abstract processes such as diffusion-limited aggregation (30) and Turing-like pattern formation (31). More realistic models of Drosophila sensory cells, for example, capture important properties of the dendrite morphologies but use hypothetical branching and growth parameters (32, 33). Models of branching morphogenesis in tissues are of limited applicability to dendrites: Models of branching in the lungs (34) and kidneys (35, 36) produce stereotyped morphologies that are distinct from the highly variable morphologies of neurons (37). Stochastic models developed for other tissues, such as the mammary glands, use properties that are specific to these systems, such as tip bifurcation (38). Thus, current computational models fall short in providing a mechanistic understanding of dendrite morphology.
To circumvent these limitations, we have formulated a computational model that is based entirely on experimentally observed properties of dendrites measured over their development. The data-based model takes as input tip growth dynamics, branching rates, and self-avoidance measured using high-resolution, live-cell imaging in the developing animal. The model successfully recapitulates class IV dendrite morphogenesis and shows how the complex and variable morphology of dendritic arbors emerges from the microscopic dynamics of dendrite tips and provides insights into several mutant phenotypes.
RESULTS
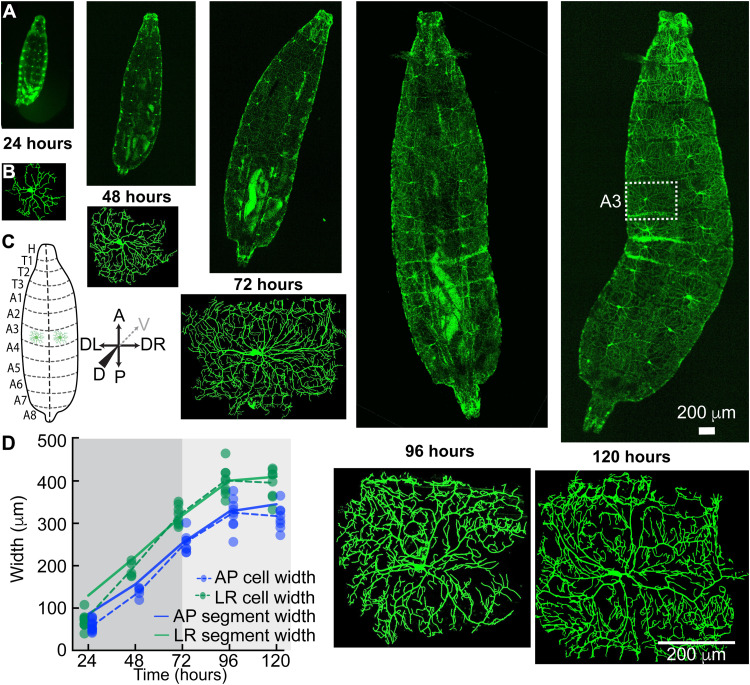
As Drosophila larvae grow (Fig. 1A), the arbors of their class IV dendrites also grow (Fig. 1B). By the end of larval development, the meshwork of branches covers the larval surface like chain mail and the individual dendritic arbors fill the eight abdominal segments with widths up to 500 μm. Each abdominal segment on the dorsal side, on which we focus, has two class IV neurons, one on either side of the dorsal midline (see Fig. 1C and fig. S1A for definitions of the larval axes), and each occupying an approximately rectangular hemisegment. When the first instar larva hatches at 24 hours after egg lay (AEL) (egg lay is defined as time zero), the widths of the dendritic arbors (green and blue points) are smaller than the hemisegments (solid lines), as shown in Fig. 1D (see Materials and Methods for how the sizes of the arbors and segments were calculated). Over the next 24 hours, the arbors grow faster than the segments and reach the edges of the adjacent hemisegments. By 72 hours, the arbor has densely filled the hemisegment (fig. S1B) and thereafter grows with the growing hemisegment in a process called scaling (14). The tiling of the larval surface (39), during which the dendrites do not cross into the adjacent hemisegments, is due to inhibitory interactions between neighboring class IV cells (13) and interactions with the adjacent epithelial cells (14). We sought to understand how the dendrites grow and fill the hemisegments.
Fig. 1. Growth of larvae and class IV neurons over development.
(A) Whole-mount, living larvae imaged by spinning disk confocal microscopy at 24 to 120 hours (egg lay defined as time zero). Class IV neurons are marked with the transmembrane protein CD4 tagged with green fluorescent protein (GFP) (genotype ;;ppkCD4-tdGFP). (B) Individual class IV cells from the A3 or A4 segments. An A3 segment is outlined in (A) (120 hours). (C) Cartoon of larvae as viewed from the dorsal side. The dashed line is dorsal midline. Anterior (A) is up, and posterior (P) is down. Left (DL) and right (DR) are as viewed from the dorsal side (for the sake of simplicity, we will mention DL-DR as LR everywhere in the text and subsequent figures); the gray dashed arrow points at the ventral direction. (D) Growth of class IV arbors compared to their hemisegments. At 24 hours, the cell widths (solid circles with dashed lines through the averages) are smaller than the hemisegment widths (solid lines). In the next 24 hours, they touch the growing segment boundaries, and by 72 hours, they fill the hemisegment and then continue to grow with the hemisegment (light gray). The cell widths along each axis are defined as the sides of the rectangle that contain the same mass of branch skeleton distributed uniformly (see Materials and Methods).
Dendrite growth is not due to elongation of all branches in the arbor
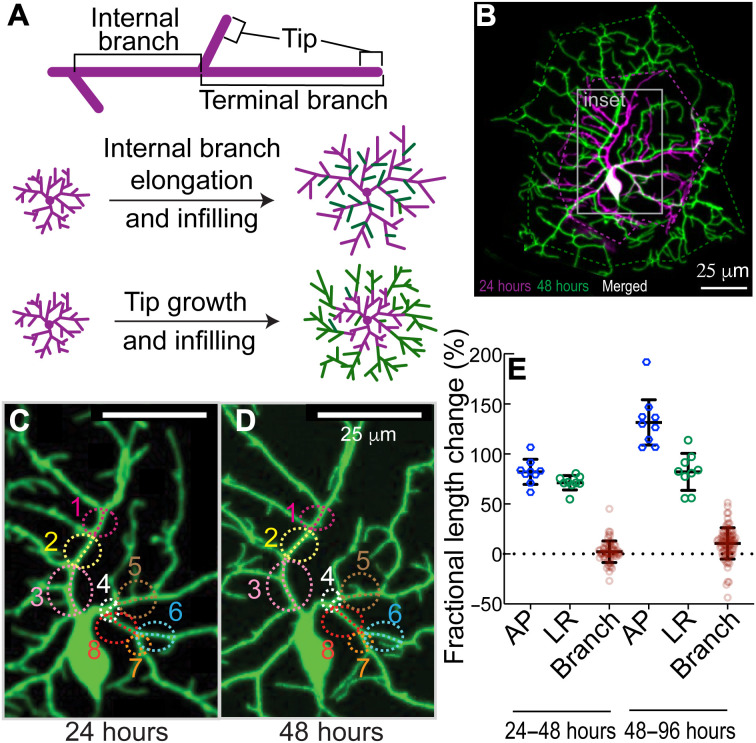
We first asked whether class IV arbors grow through the elongation of all their branches, both internal and terminal (Fig. 2A, top). In other words, the arbor expands uniformly as shown in Fig. 2A (middle), as proposed in (40). Such uniform expansion describes the growth of the overlying epithelial cells, whose number remains constant over larval development (14), and of class I cells, which expand concomitantly with the segments (33, 41). To test the role of branch elongation in arbor expansion, we reimaged the same neurons at discrete times over development, at 24 and 48 hours and at 48 and 96 hours (Fig. 2B). As the arbors grow, there is continuous addition and removal of branches. Nevertheless, it was possible to identify shared structural features of internal branches in the proximal region (Fig. 2, C and D, and Materials and Methods). The fractional increases in lengths of these identified internal branches were considerably less than the fractional increase in length of the hemisegments along the anterior-posterior (AP) and left-right (LR) axes (Fig. 2E), in agreement with earlier measurements (28). Because elongation of internal branches contributes only 3% (24 to 48 hours) to 11% (48 to 96 hours) of the overall growth of the dendrites, other mechanisms must contribute to the bulk of arbor growth. This finding implies that the proximal branches are not rigidly attached to the adjacent epithelium but must slowly slip as the hemisegments grow, an interesting issue that we will not explore further here.
Fig. 2. Branch dilation does not account for dendrite growth.
(A) Top: Internal branches are branches that lie between two branch points, as distinct from terminal branches that end in a tip. Bottom two panels: Two models for dendrite growth. Middle: Elongation of existing branches and infilling with new branches. Bottom: Maintenance of internal branches and growth and infilling with new branches. (B) Maximum projection image of a GFP-labeled class IV neuron cell (genotype ;;ppkCD4-tdGFP) at 24 hours (magenta color) and same cell imaged at 48 hours (green color). Twenty-four– and 48-hour images are combined with a leftward displacement of the latter. The area in the gray boundary (inset) is enlarged in (C) and (D), where conserved internal branches are marked with the same color circle and number (see Materials and Methods). (E) The fractional length changes of the hemisegments along the AP and LR axes were calculated from 24 to 48 hours and from 48 to 96 hours, together with the fractional length changes of the internal branches. Each blue and green circle is a different larva; the red circles correspond to several branch measurements in each of six larvae.
Terminal dendrites grow from their tips and not from their bases
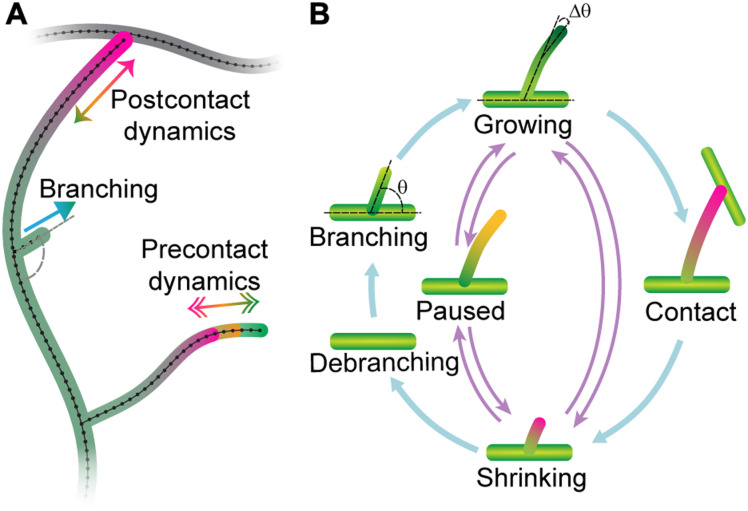
An alternative hypothesis to elongation of internal branches is that the growth of the arbor is due to branching and subsequent lengthening of the newly formed terminal branches (Fig. 2A, bottom). To test this hypothesis, the behavior of terminal dendrites was examined. Following birth by lateral branching from existing branches (42), terminal dendrites can lengthen, shorten spontaneously or following contact with another branch, and pause (Fig. 3A). Time-lapse imaging (movies S1 to S5) suggests that lengthening is due primarily to the addition of material near the tip. For example, the distances between the base of a branch and new branch points or bends do not change, while the distal tips grow and shorten (Fig. 3A, top-left panel, and movies S6 to 10). These observations argue against growth at the base and against uniform elongation along the length of terminal dendrites. Because new branches can form as close as 2 μm to an existing tip, we estimate that growth occurs within ~2 μm of the distal ends. Thus, tip growth, which occurs on time scales of minutes, may contribute to the overall growth of the arbor.
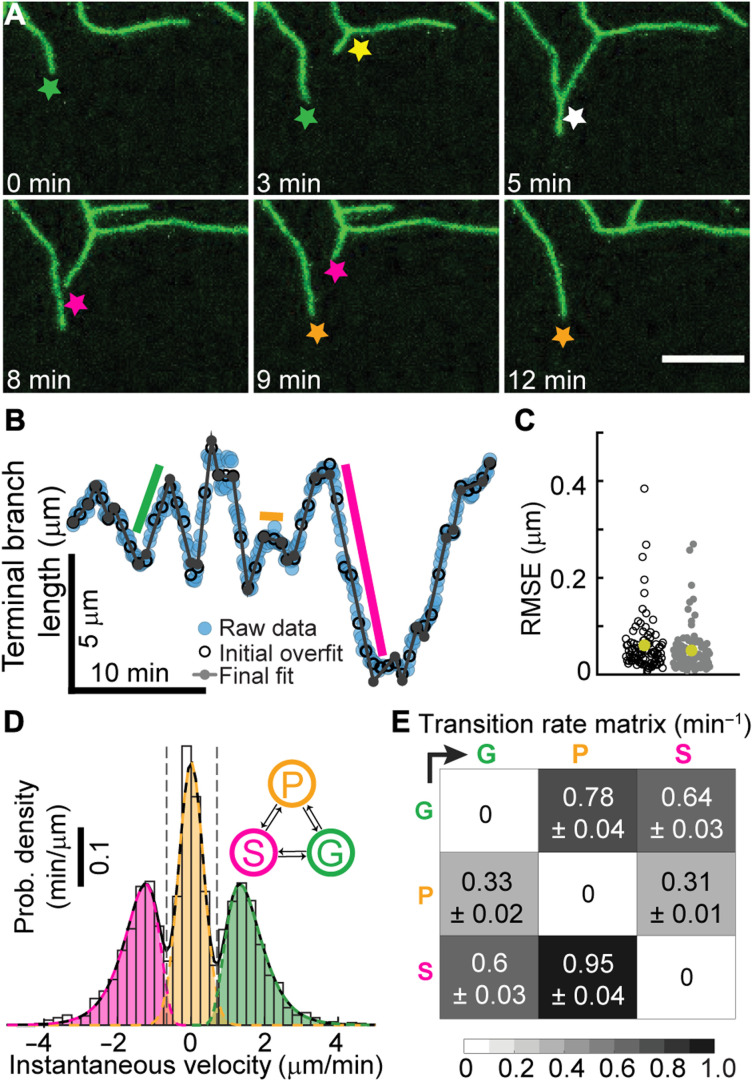
Fig. 3. Dendrite tips transition between growing, shrinking, and paused states.
(A) Class IV dendrites growing (green star), birthing (yellow star), colliding (white star), shrinking (magenta star), and pausing (orange star). Maximum projection spinning disk images of neurons were collected every 5 s for larval stage of 24 hours (genotype ;;ppkCD4-tdGFP). (B) Length of a dendrite as a function of time (see Materials and Methods). The black open circles represent the initial piecewise linear fit using N/6 segments, where N is the total number of frames. The gray dots show the fitting after the iterative merging process (see Materials and Methods). Green, orange, and magenta indicated periods of growth, pausing, and shrinkage, respectively. (C) The root mean square error (RMSE) before (black) and after (gray) merging for 91 trajectories (24 hours). The average error is 50 nm. (D) The velocity distribution shows three distinct peaks representing the growing (G), paused (P), and shrinking (S) states. (E) Transition rates between the three states.
High-resolution tracking shows that tips transition between periods of constant growth velocity
To determine whether tip growth can account for arbor expansion, we tracked the lengths of terminal dendrites over time with an accuracy of ~0.1 μm (Materials and Methods and fig. S2, A to F). To ensure that mounting and imaging larvae did not interfere with growth, we restricted imaging to 20 to 30 min (fig. S1C). Typical trajectories show that dendrite growth is highly dynamic, with large fluctuations in velocity (Fig. 3B and fig. S2, G, I, and K). To analyze tip trajectories, we first considered tip growth as a diffusion-with-drift process, a common way to describe particles moving in a flow. However, we ruled out this description because there were extended times of near-constant velocity: The green, magenta, and orange lines in Fig. 3B (and fig. S2, G, I, and K) indicate periods of elongation, shortening, and stationarity. We therefore fit the trajectories to a piecewise linear continuous function, for which fast algorithms exist (43). This initial segmentation into regions of constant velocity provided a good fit to the tracking data (Fig. 3, B and C, black circles), showing that tip trajectories can be decomposed into sequential periods of linear growth or shrinkage.
Dendrite tips undergo dynamic instability
We then asked the more difficult question of whether tips undergo dynamic transitions between growing (G), shrinking (S), and paused (P) states. In other words, can we classify the regions of constant growth into just three states such that transitions only occur between different states. Such a description is analogous to the dynamic instability of microtubules (44), which transition stochastically between two states: growing and shrinking.
To test whether a three-state dynamic model could account for tip growth, we assigned each region to be in a growing, shrinking, or paused state by fitting the histogram of velocities with a three-peaked distribution, such as shown in Fig. 3D, to define velocity thresholds between growth and pause and shrinkage and pause. We then merged adjacent regions that belonged to the same state. Through an iterative procedure (see Materials and Methods), we segmented the trajectories into growing, shrinking, and paused states, with transitions only between different states. The resulting trajectory (Fig. 3B, gray lines) was an excellent fit to the data: The root mean square error was, on average, ~0.05 μm (Fig. 3C), accounting for 85 to 99% of the variance (fig. S2, H, J, and L). From these data, we calculated (i) the growing and shrinking speeds (Fig. 3D) and (ii) the rates of the transitions between the three states (Fig. 3E). At 24 hours, the growing and shrinking speeds were 1.61 and 1.52 μm/min, respectively, and the transition rates ranged from 0.31 to 0.95/min, corresponding to average lifetimes of individual states between 0.6 and 1.5 min. The net speed of dendrite elongation, ~0.034 μm/min (Table 1A), is much smaller than the average speed in the growing state because the dendrites spend roughly equal times in the growing and shrinking states.
Table 1. Dynamical parameters of dendrite tips at different developmental stages.
Errors are SE.
| A: Precontact tip dynamics parameters | ||||||||||||
| Age (hours) | Tip velocity parameters | Tip transition rates | Corr. | Average tip velocity | ||||||||
|
μG,σG
(μm/min) |
μP,σP
(μm/min) |
μS,σS
(μm/min) |
kGP
(min−1) |
kGS
(min−1) |
kPG
(min−1) |
kPS
(min−1) |
kSG
(min−1) |
kSP
(min−1) |
r and P |
(μm/min) |
(μm/min) |
|
| 18–20 (E) | 0.37, 0.34 VG = 1.53 |
0, 0.36 | 0.43, 0.37 VS = 1.65 |
0.696 | 0.509 | 0.423 | 0.296 | 0.669 | 0.71 | 0.017 0.09 |
0.097 ± 0.0158 |
0.100 ± 0.0151 |
| 24 (L1) | 0.41, 0.36 VG = 1.61 |
0, 0.34 | 0.35, 0.37 VS = 1.52 |
0.784 | 0.64 | 0.335 | 0.314 | 0.598 | 0.946 | 0.008 0.65 |
0.034 ± 0.0196 |
0.038 ± 0.0191 |
| 48 (L2) | 0.40, 0.39 VG = 1.61 |
0, 0.25 | 0.0, 0.41 VS = 1.1 |
0.933 | 0.435 | 0.155 | 0.235 | 0.282 | 1.251 | 0.045 0.24 |
0.020 ± 0.1545 |
0.026 ± 0.0177 |
| 96 (L3) | 0.36, 0.52 VG = 1.64 |
0, 0.25 | 0.19, 0.44 VS = 1.33 |
0.923 | 0.799 | 0.116 | 0.117 | 0.575 | 1.276 | 0.002 0.9 |
0.008 ± 0.0039 |
0.022 ± 0.0177 |
| B: Postcontact tip dynamics parameters | ||||||||||||
| Age (hours) | Tip velocity parameters | Tip transition rates | Corr. | Average tip velocity | ||||||||
|
(μm/min) |
(μm/min) |
(μm/min) |
(min−1) |
(min−1) |
(min−1) |
(min−1) |
(min−1) |
(min−1) |
r and P |
(μm/min) |
(μm/min) |
|
| 18–20 (E) | 0.53, 0.49 |
0, 0.28 | 0.53, 0.54 |
0.635 | 0.992 | 0.263 | 0.401 | 0.469 | 0.593 | 0.07 0.12 |
−0.42 ± 0.07 |
−0.34 ± 0.07 |
| 48 (L2) | 0.40, 0.50 |
0, 0.25 | 0, 0.38 |
1.446 | 1.24 | 0.134 | 0.29 | 0.239 | 0.814 | 0.018 0.76 |
−0.23 ± 0.05 |
−0.19 ± 0.04 |
This analysis shows that the growth trajectories accord with a three-state kinetic scheme, which provides a succinct yet comprehensive description of tip dynamics. This scheme is a generalization of the Dogterom and Leibler model of microtubule dynamic instability (45), with inclusion of a third paused state, and the growing and shrinking states having distributions of speeds.
Dendrite dynamics and branching rates change over development time
Throughout development, the growing and shrinking speeds were roughly unchanged (Table 1A). The main change over development was that the transition rates out of the paused state decreased two- to fourfold and the transition rates into the paused state increased by about 50%. As a result, the dendrites spend more time in the paused state: They become less dynamic.
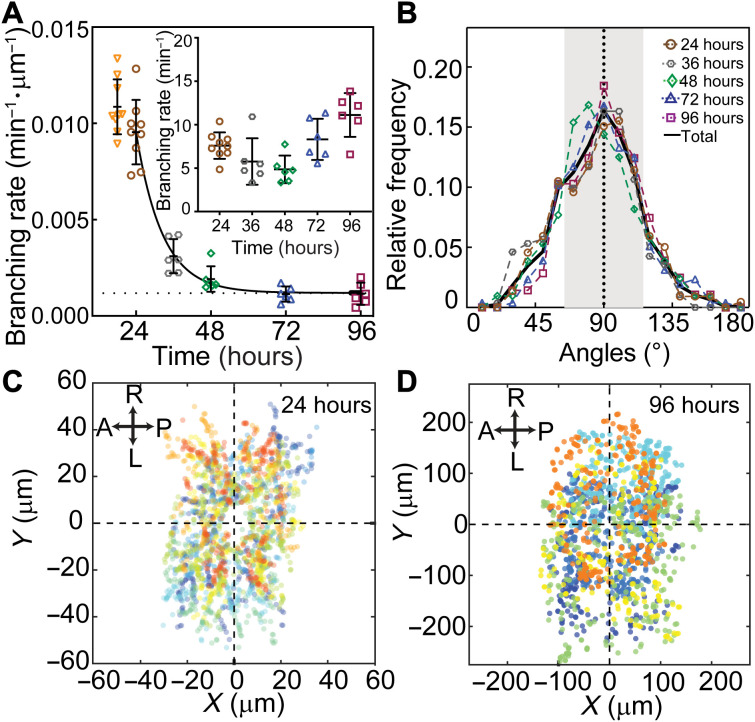
Branching, which always occurs on the sides of existing branches, also slowed down over development. The branching rate per unit dendrite length decreased roughly 10-fold from 24 to 96 hours (Fig. 4A and table S1). This decrease is another manifestation of dendrites becoming less dynamic over time. The geometry of branching, however, remained constant over development: The mean angle of a new (daughter) branch was close to 90° at all developmental stages (Fig. 4B and table S1), and the spatial distribution of branching remained roughly uniform (Fig. 4, C and D). In summary, both growth and branching are highly stochastic throughout development, although the transition and branching rates slow down over time.
Fig. 4. Dendrite branching over development.
(A) The rate of appearance of new branches normalized by the total branch length is plotted against developmental time. Each symbol represents a neuron from a different larva (except at 24 hours where three neurons in each of the three larvae were analyzed). The curve is an exponential fit with an offset (dotted line). Inset: Total branching rate per cell. (B) Distribution of branch angles between daughters at different developmental stages. The angle is zero when the new daughter grows parallel to the mother. Numbers of neurons are the following: six (24 hours), seven (36 hours), four (48 and 96 hours), and five (72 hours). (C) Spatial distribution of branching events at 24 hours (nine neurons from three larvae). (D) Spatial distribution of branching events in 96 hours (six neurons from six larvae). In both (C) and (D), the soma positions are centered at the origin. Different colors represent different cells.
Dendrite tips retain memories: Their dynamics are not Markovian
We tested whether the transitions between growth states are Markovian, meaning that they depend only on their current state, i.e., they do not depend on the history and there is no memory of earlier states. Consistent with a Markov process, the lifetimes of the states were approximately exponential at long times (fig. S3, A to I), and the probability of a transition in the sequence of occupied states (e.g., GPGSPGPSG…) did not depend on the previous state. For example, we found that the likelihood of G→P did not depend on the prior state, that is, SG→P and PG→P were equally likely.
There were several violations of the Markov property, however. First, following contact of a tip with another branch, the growth dynamics change: The rates out of the growing state increase, so the dendrites spend less time growing (Table 1B). Therefore, in addition to contact-induced retraction, there is a long-lasting alteration of the dynamics: The average tip growth rate changes from positive to negative (Table 1), and the postcontact dendrites shrink on average. This alteration implies that there is a long-lasting memory of the collision. Second, we found that the lifetimes of newly born dendrites were longer than expected for a Markov process. Following birth into the growing state, the transition rates, which were measured for older dendrites (>5 min after birth), predict that there will be an initial linear decrease in surviving dendrites because of the chance that a growing dendrite stochastically switches into a shrinking state, which then shortens and disappears. Instead, we found that the survival curve was initially flat, consistent with an initial growing state of 0.3 min (fig. S4A). Such a survival curve is another violation of the Markov process and implies that a newborn dendrite retains a memory of birth. Third, growth and shrinkage events with higher absolute speeds tended to have shorter lifetimes (fig. S3, J and K). Thus, while growth is highly stochastic, it deviates from being Markovian, indicating memory and “hidden variables” that influence the dynamics. These hidden variables are likely to be long-lived biochemical states (e.g., phosphorylation) triggered by dendrite birth or tip contact with other dendrites, which influence the dynamics.
An agent-based model incorporates measured tip properties
To test whether the dynamical properties of the dendrites measured above can account for the observed morphology, we developed an agent-based computational model to predict morphologies based on tip dynamics. The elementary “particle” in the model is the dendrite tip, which serves as the agent (Fig. 5A).
Fig. 5. Schematic of the agent-based computational model.
(A) A cartoon diagram depicted the different components of the model: Tips are born by branching and transition between growing, shrinking, and paused states. Upon contact with another branch, the tips retract. (B) Diagram of the transitions. Parameters are listed in Table 1 and tables S1 and S2.
Tips were simulated using rules that closely followed the experimental measurements (see Fig. 5B and Materials and Methods). Terminal dendrites lengthen and shorten with speeds sampled from the growth and shrinkage distributions (e.g., Fig. 3D). They transition between growing, shrinking, and paused states according to the measured transition rates (Table 1), which were linearly interpolated between different developmental stages. Tip birth occurred randomly in time and space along extant branches with the measured branching rates (Fig. 4A). The nascent daughter branch was assumed to start in a growing state (Fig. 5) with an initial length of 0.5 μm (table S2) and included an initial lag of 0.3 min during which the transition out of the growing state was forbidden, in accordance with our observations. Dendrite death occurred when the last point disappeared during a shrinkage event. Contact, defined as a tip getting closer than 0.15 μm to another branch (roughly the radius of the terminal branch) (46), switched a growing tip to a shrinking one with the postcontact dynamics (Table 1B).
The initial larval morphology at 24 hours was established by (i) growing two to four branches from a point (the origin) using the embryonic growth parameters at 18 to 20 hours and (ii) allowing growth until the total branch length and number reached their values at 24 hours. To model the segment boundary, we assumed that contact with neighboring dendrites induced shrinkage (14). Neighbor interaction was implemented using a periodic boundary condition such that one side of a growing neuron feels its opposite side as if growing on the topological equivalent of a torus. Over time, we gradually increased the size of the boundary according to the measured segment growth rates (Fig. 1D).
Simulated dendritic trees recapitulate coarse-grained features of dendrite morphology
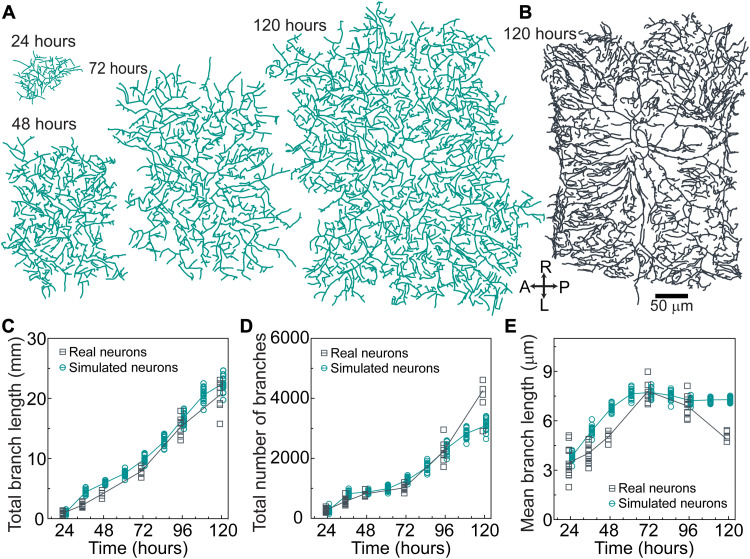
We simulated dendritic trees using the parameters from Table 1 and tables S1 and S2, all of which were measured or tightly constrained by experiments. The simulations (Fig. 6A) recapitulated key properties of real arbors (Fig. 6B).
Fig. 6. The agent-based model accords with overall neuronal growth.
(A) Example of a simulated neuron using the parameters in Table 1 and tables S1 and S2 at different developmental stages. Same scale bar as in (B). (B) Example of the skeleton of a real neuron at 120 hours. (C) Total branch length over development for simulated and real neurons. (D) Total number of branches. (E) Mean branch length (total branch length/total number of branches).
Arbor growth
In the absence of a boundary, the widths of simulated arbors initially grew at 10 μm/hour and then, after 48 to 72 hours, they slowed down to 4 μm/hour (fig. S5, Aii). Thus, the dendrite initially grew faster than the hemisegments (which grow at 4 μm/hour), leading to complete infilling by 72 hours; after 72 hours, arbor growth was just sufficient to keep up with segment growth. Contact-based retraction with the adjacent cell kept the dendrite confined to the hemisegment (i.e., tiling).
Total branch length and number
The simulations predicted the observed increases in total branch length (Fig. 6C) and number (Fig. 6D), as well as the mean branch length (Fig. 6E). The branch length distributions were roughly exponential in the simulations and the data (fig. S6, A to E). An interesting feature of the branch number is the initial burst (24 to 36 hours) and subsequent plateau (36 to 72 hours). The burst is predicted by the model and arises from two features of tip growth: the high initial branching rate (Fig. 4A) and the perseverance of the initial growth of branches (i.e., a delay in transitioning out of the growing state). Without perseverance, which is a memory of birth, the plateau is less pronounced, showing that the initiation of branching is an important determinant of arbor morphology.
There were some discrepancies between the data and the model. For example, the branch number of the simulated arbors saturated at 120 hours, while that of the real arbors continued to increase with an associated late decrease in mean branch length of real arbors. These discrepancies may indicate that dynamical properties change after 96 hours, the last time at which the dynamic parameters were measured (simulations beyond 96 hours are extrapolations). Another possible source of the discrepancy at 120 hours may be due to the high branch density at intersegment boundaries along the AP axis (Fig. 6B, right) arising from close cell-cell interactions, which were not predicted by the model. Nevertheless, we believe that the model is in good agreement with the average properties of the arbors.
Simulated arbors capture the variability of dendrite morphology
In addition to predicting average branch properties, the model also predicted the variation of these features. For example, the measured branch numbers are highly variable, with coefficients of variation (CVs; SD/mean) ranging from 0.11 to 0.22 over development. This CV is even larger than that of a Poisson process, a prototypical random process whose CV equals the inverse square root of the branch number (expected range of 0.02 to 0.06). This comparison to a Poisson process indicates that the branch number is highly variable from arbor to arbor, a manifestation of the stochasticity of the morphology. Total branch length and average branch length were also highly variable. The simulations recapitulated this variability (Fig. 6, C to E). Thus, the model predicted both the average properties and the stochasticity of the branch number and length.
Simulated arbors recapitulate fine-scale properties of dendrite morphology
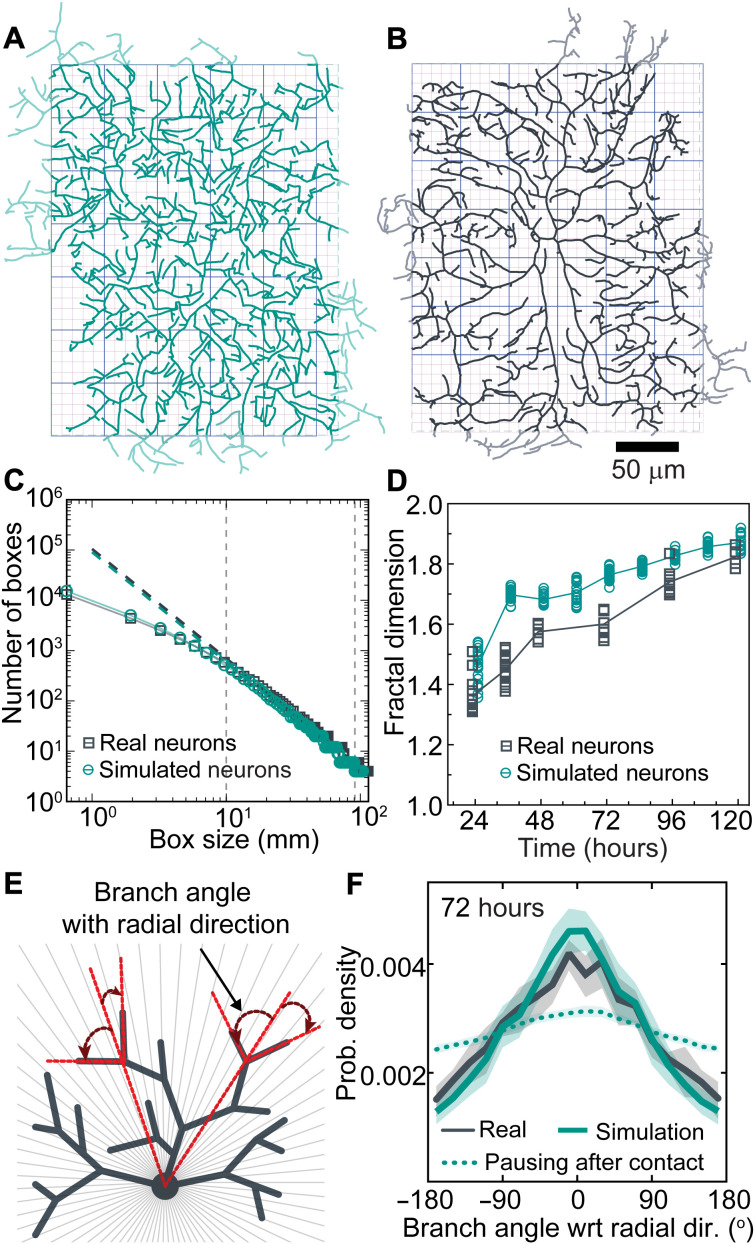
The branches of both the simulated and real arbors formed dense meshworks (Fig. 7, A and B). We estimated the extent to which the branches cover the arbor using the box-counting method (47) in which the number of boxes that contain a branch is plotted against the size of the boxes (Fig. 7C). We found that the logarithm of box number was approximately proportional to the logarithm of box size, indicating that the patterns have scale-free and fractal-like properties. The proportionality breaks down at box sizes below 5 μm, the size of the “holes” in the pattern due to the average branch size. We defined the fractal dimension as the slope of the log-log plot (the power-law exponent) in the central region encompassing the middle 50% of the points (Fig. 7C, dashed lines). The fractal dimension increased from 1.4 to 1.8 from 24 to 120 hours for both the simulated and real arbors (Fig. 7D). Because a region containing a single line has a fractal dimension of 1, whereas a completely filled region has a fractal dimension of 2, the dendritic patterns are of intermediate dimension and, at 120 hours, nearly fill the plane (fractal dimension of 1.8). Although the fractal dimensions of real arbors were consistently lower by about 0.1, we nevertheless conclude that the simulated arbors recapitulate the real arbors in this metric.
Fig. 7. The agent-based model recapitulates the fine-scale patterns of real arbors.
(A) Model arbor at 72 hours. Light green branches indicate the outer 5% of the arbors excluded from the analysis to mitigate against spurious boundary effects (see Materials and Methods). Boxes with two different sizes are shown in the background. (B) Skeletonized real arbor at 72 hours. Light gray branches were excluded from the analysis. (C) The number of boxes that contain a branch (y axis) is plotted against the box size (x axis). The slopes over the central 50% of the data (vertical dashed lines) define the fractal dimensions. (D) Fractal dimensions of real and simulated arbors both increase over development. (E) Diagram defining the radial orientation. (F) Radial orientation of a simulated tree (green solid line) and a real arbor (black) at 72 hours. Green dotted curve: Simulated tree with pausing instead of retraction.
Simulations recapitulate the radial orientation of dendrite branches
We found that class IV cells have an unexpected long-range order: Branches are not randomly oriented but instead tended to be parallel to the radial orientation (Fig. 7, E and F, and fig. S6, F to J). The simulations also displayed radial orientation. Radial orientation is a consequence of contact-based retraction; if contact-based retraction is replaced by contact-based pausing, the radial orientation was greatly reduced (Fig. 7F, dotted curve).
Morphological predictions of the model
The agent-based model allowed us to explore which parameters are most important for arbor growth and mesh size (fig. S5) and provides hypothesis for the phenotypes of mutants. A surprising finding was that branching drives overall arbor growth: Increasing the branching rate not only increased the number and density of branches, as expected, but also increased arbor size (fig. S5B). Setting the average velocity of dendrite extension to zero still resulted in arbor growth, albeit slower (figs. S5E and S7), showing that branching without net tip growth can drive arbor expansion. This is not to imply that the average tip growth rate is unimportant: Doubling the net growth rate doubled the dendrite area (fig. S5D), and halving the net growth rate halved the dendrite area (fig. S5D). The latter finding accounts for the reduced arbors in Katanin (Kat-60L1) mutants, which spend less time in the paused states and more time in the shrinking state (24): The mutant cells will therefore have a reduced net growth rate compared to controls, leading to smaller size (see table S3).
Another surprising finding was that fluctuations in branch length also lead to growth. When the fluctuations were increased (by reducing the tip transition rates), the growth rate increased, and vice versa (fig. S5C). This suggests an unexpected growth mechanism: Length fluctuations are locked in by the formation of new branches, as only terminal branches can shorten and disappear. This stresses the importance of branching in growth.
The branching angle also affected arbor growth: If the branch angle was decreased to 45° (i.e., growth toward the direction of the mother branch), arbor growth increased, showing that outward-growing branches are more likely to survive. The persistence of branch growth after birth was also important.
Our model shows that dendrite density is set by the interplay between branching and self-avoidance. Branching is a form of positive feedback that increases branch density (fig. S5B). Therefore, branching is essential not only for expansion but also for infilling the hemisegment. Self-avoidance is negative feedback: Reducing self-avoidance in the model increases the branch density (table S3), which is observed in studies in which self-avoidance molecules are mutated (11–13, 15).
By performing this variational analysis (e.g., fig. S5), we could identify which of the 67 parameters (see Materials and Methods) are key to overall dendrite growth and morphology. The key parameters are the following: the net growth velocity and its variance together with the net shrinkage following contact (three parameters) and the branching rate (one parameter) and angle (two parameters). In the absence of the boundary, these determine the growth rate, branch number, and length, together with the fine structure (fractal dimension and radial orientation). While the detailed growth and morphology depend on the change of these six parameters over development (and the boundary), these parameters are the fundamental ones that specify growth and morphology.
DISCUSSION
We have found that the tips of Drosophila class IV dendrites transition stochastically between three states—growing, shrinking, and paused. This allows dendrites to explore extracellular space, analogous to the exploration of intracellular space by microtubules undergoing dynamic instability (48). Our modeling shows that these transitions, together with lateral branching and contact-mediated retraction, give rise to the complex and highly variable morphology of the dendritic arbors, allowing them to fulfill their biological functions. The dense, almost unbroken meshwork optimizes detection of the fine ovipositor barbs of parasite wasps (9, 10). In addition, the radial orientation of branches, a form of long-range order that emerges from local interactions (49, 50), in this case, contact-induced retraction, reduces the path distance to the cell body: This minimizes signaling delays and wiring costs (28). Thus, stochastic tip dynamics may partially solve the riddle of how “the morphological features displayed by neurons appear to obey precise rules that are accompanied by useful consequences” (51).
Model limitations
The agent-based model fails to account for some features of class IV cells. For example, the model does not extrapolate well to 120 hours, suggesting that important developmental changes may occur after 96 hours. The model also fails to predict the asymmetry of real arbors, which form close contacts with class IV cells in the adjacent segment along the AP axis but not along the LR axis (Fig. 6, A and B); the model contains no asymmetries. Thus, the interactions between neighbors is more than just the contact-based retractions assumed in the model. Another shortcoming is that many simulated branches have sharp angles, whereas real branches are smoother: This is because, when a mother branch shrinks back to a daughter in the model, the original branch angle is preserved (average of 90°), whereas in the real cells the bend smoothens over time (see an example of this in movie S7). Thus, there are important features of real class IV dendritic arbors that are not accounted for. Other important aspects of dendrite morphology, such as branch diameters (46) and the three-dimensionality of class IV cells (18), have not been included in the model. Moreover, the model does not take into account the guidance of class IV dendrites by external cues such as the cuticular epithelium (14, 52) and other neurons (39), although theoretical tools have recently been developed to incorporate these cues (14, 52). Last, the internal branches in our model are completely immobile, whereas we have observed internal branch movements with respect to the substrate. However, despite these limitations, our model provides a framework on which to build more complex interactions.
Dendrite tips: An intermediate organizational principle of dendrite morphology
Our results strongly support the concept that the dendrite tip is a “branching engine … that initiates, directs, and maintains branch outgrowth during development and regrowth” (53). The dendrite tip, with a diameter of only 0.2 μm (46) and with dynamics on the time scale of ~1 min (the state lifetimes), generates structures up to 500 μm in diameter (>1000 times larger sizes) over 5 days (>1000 times longer times). Tips, therefore, are intermediate in length scale and time scales between molecules (small size and short–time scale motions) and morphology (large size and long–time scale motions).
The concept of the dendrite tip as a branching machine has four important implications. First, if the molecular basis of tip growth and branching can be elucidated, our agent-based model will provide a full connection between genotype and phenotype, with the caveats that morphogenesis is stochastic and some features such as three-dimensionality are not included. Second, altered tip dynamics due to mutations and diseases may underlie altered dendrite morphologies (see Introduction and the “Morphological predictions of the model” section). Third, tip rules may specify neuronal identity, often defined by dendrite morphology (54). Fourth, the stochastic nature of the tip rules may facilitate the evolution of neuronal cell types. This is because developmental stochasticity amplifies genetic variation by allowing a large class of morphologies to be sampled for each genotype. While some morphological outliers may function poorly, others might be beneficial, and genetic and/or epigenetic mechanisms could selectively stabilize these beneficial morphologies.
Potential molecular mechanisms underlying dendrite tip dynamics and branching
Neurite elongation by tip growth also occurs in axons (55) and in other dendrites, such as those in Caenorhabditis elegans PVD neurons (56). An important difference between dendrite tips in class IV cells and the growth cones seen in these other cells is that the tips of class IV dendrites are much smaller. The diameter of class IV terminal dendrites is only ~200 nm (46), as small as a single filopodium, the finest feature of growth cones observed under the light microscope. Thus, tip growth mechanisms in class IV dendrites likely differ from growth cone–based growth. An important open question is how the cytoskeleton and membranes reach the dendrite tips: What are the relative contributions of diffusion, filament polymerization (17, 25, 57), motor-driven transport (58), and motor-driven sliding (59)?
General mechanisms of branching morphogenesis
Dendrite tips share features of branch tips in other systems. Tip cells drive branching in branched tissues such as the mammary glands (53). The growing ends of cytoskeletal filaments, with associated nucleation factors, drive branching of organelles such as the microtubule-based mitotic spindle (60, 61) and the actin-based lamellipodium (62). In all three cases (dendrites, tissues, and cytoskeleton), the tips operate at shorter length scales and time scales than those of the structures they produce. Furthermore, they all respond to external signals: contact-based retraction of dendrite tips, cortex-induced catastrophe of microtubule ends (63), and self-avoidance of mammary gland branches (53). Last, all three are stochastic and generate highly variable morphologies. Given these commonalities, it is likely that the principles that we have elucidated for dendrites generalize to other branched systems.
Branching
Our observation that branching is an intensive property—the total rate of formation of branches is almost independent of arbor size (Fig. 4A, inset)—is evidence that there are only a limited number of “branching factors” being produced in the entire cell per unit time. The uniform distribution of new branches suggests that the branching factors are dispersed throughout the cells, perhaps by molecular motors. Several phenotypes of molecular motor mutants in class IV cells support this hypothesis. The perturbation of molecular motors and their adapter proteins, including dynein (21, 22, 64) and kinesins (21, 65), results in nonuniform branch densities, as expected if the distribution of branching factors was disrupted (see table S3).
Generalization of the agent-based model to other neurons
To explore the generality of our model, we have simulated different neuronal cell types, such as Drosophila class I neurons, mammalian retinal ganglion cells, Purkinje cells, and starburst amacrine cells. By modifying the input parameters, our model was able to successfully capture the key morphological features of these cells, as shown in fig. S8. In class I cells, contact-based tip retraction leads to secondary branches being orthogonal to the primary branch even when the initial branching angles are uniformly distributed (fig. S8A); this confirms the finding in (33) and is related to the radial orientation of class IV cells described above. Contact-based retraction also leads to the radial orientation of retinal ganglion cells (fig. S8B), although we found better agreement using a small branching angle (45° relative to the direction of the mother). To simulate Purkinje cells, we assumed slow tip growth of dendritic tips and complete retraction after contact to recapitulate the locally parallel branch orientations (fig. S8C). To simulate starburst amacrine cells, it was necessary to replace lateral branching with tip bifurcation (fig. S8D). Although our model can recapitulate certain aspects of the morphologies of these cells, these simulations are just predictions based on hypothetical model parameters and need to be tested experimentally. Nevertheless, these examples show that the model is versatile and has predictive potential beyond just Drosophila class IV sensory neurons. If the dendrite branching rules deduced for class IV cells do generalize to other neurons, then they may facilitate mapping connectomes by providing anatomical constraint on connectivity, as well as giving insight into genetic disorders that affect morphology (66–69).
MATERIALS AND METHODS
Fly stocks and maintenance
The fly line ;;ppk-cd4-tdGFP (homozygous) was used to image class IV dendritic arborization neurons and was a gift from C. Han (Cornell University). Fly crosses were maintained in fly chambers at 25°C, 60% humidity in a Darwin chamber with 12-hour light/12-hour dark cycles. An apple agar plate was used to collect the fly embryos, and a big drop of yeast paste was put in the center of the agar plate to induce egg laying.
Apple agar plates were made by mixing 4× apple juice concentrate (355 ml), water (300 ml), dextrose (155 g), and sucrose (80 g). This solution was stirred and heated to dissolve the sugars, and agar (Bacto agar, Becton Dickinson; 60 g) and 1.25 N NaOH (70 ml) were added. The solution was covered loosely with foil and autoclaved in the liquid cycle for 30 min. The plating mixture contained 100 ml of this apple agar concentrate, 197 ml of water, and 3 ml of acid mix A—an equal mixture of propionic acid (100%; 83.6 ml; 16.4 ml of water) and phosphoric acid (100%; 8.3 ml; 91.7 ml of water). For neuron morphometrics, embryos were collected every 15 min and imaged when they reached the appropriate age AEL: 24, 48, 72, 96, and 120 hours.
Sample preparation
For imaging, embryos of appropriate age (18 to 22 hours AEL) were collected from apple agar plates and dechorionated by gently rolling them on a piece of double-sided tape stuck to a glass slide. The dechorionated embryos were then placed with their dorsal side down on a No. 1.5 coverslip, MatTex, with a small drop of halocarbon oil 700. A piece of wet Kimwipes was placed near the embryos to maintain humidity during imaging. No anesthetics were used for embryo imaging. For larvae imaging, larvae of ages 24, 48, 72, 96, and 120 hours were washed with 20 and 5% sucrose solution, anesthetized using FlyNap (Carolina Biologicals, Burlington, NC, USA), and transferred to apple agar plates to recover for 1 to 5 min. After recovery, larvae were gently placed with their dorsal side up on a 1% agar bed adhered to a glass slide and imaged in a drop of 50% phosphate-buffered saline, 50% Halocarbon oil 700 (Sigma-Aldrich). Larvae were further immobilized by gently pressing them with a 22 mm–by–22 mm coverslip lined with Vaseline or vacuum grease.
Imaging
Samples were imaged on a spinning disk microscope: a Yokogawa CSU-W1 disk (pinhole size of 50 μm) built on a fully automated Nikon TI inverted microscope with perfect focus, 488-nm laser illumination at 18 to 21% laser power, either a 40× [1.25 numerical aperture (NA), 0.1615-μm pixel size] or a 60× (1.20 NA, 0.106-μm pixel size) water immersion objective, an sCMOS (scientific Complementary Metal-Oxide-Semiconductor) camera (Zyla 4.2 plus), and Nikon Elements software. The temperature of the sample region was maintained using an objective space heater at 25°C (Okolab stage heater). Samples were manually focused to identify abdominal third and fourth segments (A3 or A4 neurons) before image acquisition. Full-frame movies (2048 pixels by 2048 pixels) containing 6 to 12 1-μm sections were collected every 4 to 6 s. Static images for morphometric studies were acquired using a 60× water immersion objective for 24 hours and 40× objective for later stages. Images were stitched using an in-house code (https://github.com/oliviertrottier/neuron-stitch). Movies were curated for subsequent offline analysis. Image analysis (segmentation, skeletonization, branching analysis, and angle measurements) was done using ImageJ.
Controls for growth
Class IV neurons are susceptible to mechanical pressure, which, if too large, stops growth and causes degeneration. Therefore, embryos were imaged without an overlying coverslip. Larvae were immobilized with minimal pressure under a coverslip and were placed on a 1% agar bed. As a control, we plotted the size of neurons throughout imaging to confirm that they remain on the “standard” growth curve (fig. S1C).
Segment length determination
The Drosophila larval abdomen is divided into eight abdominal segments (Fig. 1C and fig. S1A). Each segment on the dorsal side has two neurons, each occupying a hemisegment (Fig. 1C). Each hemisegment is approximately rectangular with AP and LR axes. The width of the segment along the AP axis was measured as the distance between the cell bodies of the adjacent neurons along the AP axis. The LR width was measured as the distance between cell bodies in adjacent hemisegments across the dorsal midline corrected for the offset of the cell bodies, which are not in the centers of the cells but displaced away from the midline. These segment widths were measured abdominal segments A2 to A5 for three larvae for all the respective stages.
Arbor skeletonization and branch length measurements
Scanning confocal images were maximally projected, and individual dendrites were manually segmented from their neighbors. The segmented neurons were binarized using a custom algorithm and skeletonized using MATLAB’s “bwmorph.” The individual branches were identified by subtracting the branch points identified by bwmorph from the skeleton. The pixel coordinates of the branches were smoothed using a spline before calculating the total length of all branches and their average length.
Dendrite arbor width
The arbors of class IV are approximately rectangular, with axes parallel to the AP and LR axes. If the mass of the dendrite skeleton is uniformly distributed in a rectangle, then the widths, DAP and DLR, are
where Rg is the radius of gyration, N is the total number of occupied pixels in the skeleton, rj is the projection onto the respective axis of the jth occupied pixel, and is the mean projected position of all occupied pixels. Rg is the SD of the dendrite pixels, i.e., their spread from the center. We confirmed that the widths defined in this way were good approximations to the rectangles containing 95% of the skeletal mass.
Analysis of the elongation of internal branches
To study the possible role that the elongation of internal branches in arbor growth, we imaged the same dorsal neurons (A3, A4, and A5) every 24 hours. Larvae were mounted and imaged as described, but without the use of anesthetics. Their movement was minimized by imaging at 4°C for 2 to 5 min. They were then returned to the apple agar plate in the Darwin chamber. The larvae were imaged using 20× and 40× objectives. For image analysis, the same neurons at 24 and 48 hours and 48 and 96 hours were segmented and aligned using ImageJ to identify conserved nonterminal internal branches in the proximal region. The fractional increases in branches and segment lengths were defined as
Branching rate and branch angle
To determine branching events, time-lapse movies of duration 20 to 30 min were analyzed manually using ImageJ. A new protrusion of length >0.25 μm was scored as a new branch. The total branching rate (min−1) was calculated by dividing the total number of branching events by the total time. The specific branching rate (μm−1 min−1) was calculated as the total branching rate divided by the total branch length. The spatial distribution of all branching events was plotted using MATLAB with the soma at the origin (x = 0, y = 0). The angle of new branches was measured using the angle tool of ImageJ (0° defined as in the direction of the mother). The angle distribution graph was plotted using Prism.
Fractal dimension
We used the box-counting method to calculate the fractal dimension. For each box width, W, we measured the number of boxes, N(W), needed to cover all the occupied pixels of the skeleton (Fig. 7, A and B). N(W) is approximately linear on a log-log plot (Fig. 7C), indicative of a power law. The middle 50% of points (between the dashed lines in Fig. 7C) was fit to N(W) = W−Df to obtain the fractal dimension Df.
Tip-tracking algorithm
To quantify the dynamical properties of the tips, we developed an in-house algorithm to track dendritic tips and determine dendrite length-time curves. Time-lapse movies were stabilized and maximum-projected (ImageJ), and terminal dendrites were selected for analysis based on their separation from neighboring dendrites and the signal-to-background ratio. Terminal dendrites were selected throughout the arbor. Examples are shown in Fig. 3A. Extraneous objects were manually deleted.
To track the growing and shrinking tips, the algorithm determined the longitudinal centerline of the terminal dendrite and the location of its end for each frame. The central line was computed by fitting Gaussians to the cross-sectional intensity profiles at regular intervals along the backbone of the dendrite using
(70), where x is the position along a normal to the dendrite, I0 is the peak intensity value, xc is the center of the Gaussian, σ is the SD, and d is the measured camera offset (100) plus the background fluorescence. To compute the location of the tip, (xtip, ytip), we fit a two-dimensional Gaussian function convolved with an error function using (70)
where I0 is the peak intensity, θ is the angular direction of the tip, and σv and σp are the SDs along the orthogonal and parallel directions. The length of the dendrite in each frame was determined by fitting the center line and the tip with a cubic spline. Length-time traces were smoothed with a median filter of size 3 to remove glitches.
To estimate the precision of our tracking algorithm, we used two different approaches. In the first approach, we tracked synthetic images of capped cylindrical tubes of known length and radius with fluorophores placed randomly on their surfaces (10% labeling density) and convolved with a point spread function (350 nm at full width at half maximum). To ensure that our algorithm could perform robustly under a wide range of signal-to-background ratios, we tested the tracking accuracy with decreasing signal-to-background ratios. The typical precision was ≪1 pixel (100 nm) even for low signal-to-background ratios (71). In the second approach, we tracked the position of in vivo dendritic tips that are in long-term paused states and found that the average SD of length was ~0.1 μm (<1 pixel, 0.1615 μm), as shown in fig. S2D. This accuracy is comparable to and, in some cases, better than available software, such as FIESTA (71), JFilament (72), and Simple Neurite Tracer (73). Using a parallelized method, several hundred tips can be tracked simultaneously. A caveat of our method is that it can only track filaments that are reasonably free of extraneous objects and excessive noise and have no breaks, discontinuities, or overlapping segments.
Calculating velocities and transition rates
Fitting piecewise linear functions to the data is an ill-posed problem (74) because a perfect fit can always be achieved with a large enough number of segments (equal to the number of data points minus one). To circumvent this problem, we defined a temporal resolution, T (in frames), that is necessary to distinguish a transition event from the noise in the data. Then, the maximum number of segments in each trajectory was calculated by dividing the total number of data points (total number of frames) by the temporal resolution. We used simulated data to estimate the temporal resolution that performs the best (T = 6, see end of section). We generated Markovian trajectories with known and realistic velocity distribution (±1.5 μm/min) and transition rates (0.5 min−1), similar to those shown in Fig. 3. We then added Gaussian white noise of SD 0.25 μm to the trajectories to mimic the experimental noise. To analyze the trajectories, we used the following steps as shown in fig. S9:
(i) We fit the trajectories with piecewise linear function considering Ndata/T as the initial number of segments (Nseg).
(ii) The velocity distribution (slope of the segments) was fitted to a lognormal-Gaussian-lognormal distribution
where the C’s are the normalization constants, the μ’s are the means, the σ’s are the SDs, and the subscripts P, G, and S stand for paused, growth, and shrinkage states, respectively. The first term is a Gaussian and denotes the paused state, whereas the second and third terms are log-normal distributions representing the growth and shrinkage states.
After fitting the above velocity distribution, the intersections between the paused and growth distribution (IG) and the paused and shrinkage distribution (IS) were calculated, and the segments were labeled using these two velocity thresholds.
(iii) Consecutive segments with similar labels were then merged. This process decreased the number of segments (Nnseg). The trajectories were then refitted with the new number of segments. Steps (ii) and (iii) were repeated until Nnseg stabilized.
(iv) Last, the transition rates were calculated by counting the total number of transitions from one state to another and then dividing that number by the total time spent in that state. For example, if NGP is the total number of transitions from G to P state and TG is the total time spent in the G state, then the transition rate from G to P is .
Figure S9 shows the working protocol along with the validation of our analysis method. To estimate the optimal frame resolution, we plotted the root mean square difference between the input and output transition rates as a function of the frame resolution. Our analysis shows that the temporal resolution of six frames generates the best results for rates of ~0.5/min and noise of ~0.25 μm. We used this frame resolution for all our tip dynamics data analysis.
Average tip velocity and validation of segmentation
The segmentation yields a set of intervals, i, with associated distances, di, durations, ti, and velocities, vi = di/ti. The distribution of velocities is fit to a lognormal-Gaussian-lognormal model p(v) with parameters PG, μG, σG, PP,0, σP, PS, μS, and σS such that
| (1) |
and
| (2) |
where LμG, σG(v) and LμS, σS(v) are the log-normal distributions corresponding to growth and shrinkage and G0, σP(v) is the Gaussian distribution of the paused state. Transitions can only occur between unlike states. This imposes an important structure on the data: There are two threshold velocities v+ and v− such that if the segment velocity vi > v+, then it is assigned to be a growing segment. Likewise, if vi < v−, then it is a shrinking segment. The ones in the middle are paused.
The average velocity is
| (3) |
where is the mean velocity,is the mean time, and rv, t is the Pearson correlation coefficient. We used the definition of the Pearson’s correlation coefficient rx, y = σx, y/σxσy and cross-correlation to calculate Eq. 3. The average velocity vd has two parts: , calculated assuming that ti and vi are independent of each other, and a cross-correlation term, . is given by
| (4) |
where and are the first moments of the lognormal velocity distributions for growth and paused states, and PG and Ps can be calculated from the master equation associated with the transition matrix
| (5) |
| (6) |
| (7) |
where Kij, j ≠ i i, j = {G, P, S} are the transition rates. The steady-state solution, assuming and using Eq. 1, is
| (8) |
| (9) |
| (10) |
where D = KGS ∙ KPG + KGP ∙ KPS + KGS ∙ KPS + KGP ∙ KSG + KGP ∙ KSP + KGS ∙ KSP + KPG ∙ KSG + KPG ∙ KSP + KPS ∙ KSG.
Last, the average velocity is
| (11) |
The average velocity is a key parameter, which controls the growth of the simulated arbor (fig. S5, D and E). The average velocity calculated in this way from the transition matrix agreed with that calculated directly from the raw traces at all developmental stages (Table 1), noting that the Pearson correlation coefficient rv,t = 0 (fig. S3L). This validates of our segmentation scheme.
Computational model
The agent-based two-dimensional computational model of dendritic growth incorporated the fundamental processes that govern the morphogenesis of class IV neurons: (i) branching, (ii) tip dynamics, and (iii) contact-based retraction (nonoverlapping). We started our simulation with randomly oriented two to four branches emanating from the origin (cell body). Each branch is a filament, and points (x, y) are added at 0.1 μm (∆l) intervals as the branch grows. The simulation is divided into 0.1-min time steps (Δt). The details of individual processes are as follows.
Branching
Assuming that the branching is a random process, we visit all the branches randomly and calculated the branching probability Pb = 1 − e−Lbωb∆t, where Lb is the length of the branch and ωb is the branching rate per unit time per unit length (Fig. 4A). Then, a uniformly distributed unit random number R(0,1) is compared to Pb to spawn a nascent branch from a random point on the mother branch. The branching angle is chosen randomly from the measured branch angle distribution, which is distributed normally with a mean of ~90° and SD of ~26°, as shown in Fig. 4B and table S1. Each newly spawned branch is assumed to start in the growing phase with an initial length of 0.5 μm.
Tip dynamics
Each branch with a free end (tip) follows a Markov process (after an initial lag, see below), transitioning between growing (G), paused (P), and shrinking (S) states with measured transition rates (Kij,j≠i i, j = {G, P, S}) and velocities (V{G, P, S}) for free tips (Fig. 3, D and E, and Table 1). The transition dynamics is implemented using a standard “Monte Carlo” method. At each time step, the total probability of transition is calculated using Pi = 1 − e−Ktot ∆t, where Ktot is the sum of the transition rates from one particular state: . For example, the total transition rate from the growth state is Ktot = KGP + KGS. Subsequently, Pi is compared with a uniform random number R(0,1) to implement the transition. If there is a transition, it happens maintaining the ratio Kij/Ktot. After the transition, the tip is assigned with corresponding state velocity, the magnitude of which is randomly chosen from their respective velocity distributions (log normal for growth and shrinkage and normal for paused) (Fig. 3D). The growth process is implemented by adding new points to the existing branch tip at each time step, Δt, as follows
where k is the index of the last point in the previous time step and lp is the persistence length of the branches (set to 150 μm; table S2). In addition, the ∆l value of the last point is adjusted if lG is not an integer multiple of ∆l. Θ is a unit Gaussian variable centered at zero. While shrinking, points from the branches are removed until the shrinking length lS = VSΔt is reached.
Contact-based retraction
It has been shown by several studies that Dscam molecules play an important role in the self-avoidance of dendritic tips in class IV neurons (12, 13). To investigate the phenomenon, we measured the dynamics of the dendritic tips after a collision/contact event has occurred. We observed that the transition rates are altered after contact, as shown in Table 1B, and leads to an overall shrinkage of the dendritic tips. To implement this observation in the model, we assumed that the contact is achieved whenever a tip comes very close (<0.15 μm, ~average radius of branches; table S2) to a nearby branch. Furthermore, we used the altered tip dynamical parameters after a tip makes a contact (postcontact). Because it is difficult to measure how long the tips remain in their postcontact dynamics, we added this as a free parameter in the model (table S2). It was chosen to be longer than the expected lifetimes of postcontact dendrites (10 to 15 min).
Boundary condition
Individual class IV neurons grow within the hemisegments (39). We have experimentally measured the segment sizes in the AP and LR directions at different developmental stages, as shown in Fig. 1D. Linearly fits to the growing region (24 to 96 hours) defined the growth rates of the boundary used in our model. Because there is self-avoidance interaction between the neighboring neurons, we used a periodic boundary condition.
Initial condition
To avoid any ambiguity in the initial time point in the simulation, we divided the simulation process into two halves. We started our simulation at 14 hours with two to four randomly oriented branches of length ~15 μm and allowed them to grow with the 18-hour tip dynamics data (Table 1A) and the 24-hour branching rate. When the dendritic tree reached the measured value of total branch number at 24 hours, we reassigned this time as 24 hours. In this way, we simulated larval morphogenesis.
Initial lag
There is an unexpected paucity of dendrite deaths at short times. To analyze this, we calculated the survival probability of the branches in the following way:
Suppose dendritic tips are born and die throughout the observation period T. Divide T into small equal intervals dt. Let,
f(0) = Number{die in time [0, dt)}/Number{alive at time 0}
f(dt) = Number{die in time [dt,2dt)}/Number{alive at time dt}
f(2dt) = Number{die in time [2dt,3dt)}/Number{alive at time 2dt} …etc.
Then, we can write the survival probability as
The survival probability of the experimentally observed dendritic tips was measured manually and then calculated by using the above formula. This is shown by the solid black line in fig. S4A. The survival curve does not decay exponentially, which led us to conclude that the tips have some initial period of sustained growth that we termed as initial lag τlag. To estimate the amount of initial lag, we simulated 1000 free tips with 48 hours of tip dynamics data (because it is in the middle of the developmental time) and implemented an initial lag (τlag) during which the tips did not switch into the paused or shrinking states (KGP = KGS = 0; t ≤ τlag). We calculated the survival probability by dividing the number of alive branches by the total number of branches. The survival probability increases with the initial lag τlag, as shown by the dotted lines in fig. S4A. The dark blue is the best fit to the real data (τlag = 0.3 min; table S2), and we used this value in our model.
Markovian tests of the tip trajectories
The tip dynamics is not a “Markovian process.” The non-Markovian traits are shown by the presence of initial lag during nascent branch formation (τlag) and the change of dynamics after contact (table S2). However, the dynamics is a first-order process as shown by the single exponential decay of phase durations, as shown in fig. S3 (A to I), which points toward the fact that the dynamics do not have any long-term memory. To confirm this, we calculated the state-state autocorrelation function. The average autocorrelation function quickly becomes uncorrelated, showing the absence of any long-term memory in the states.
Acknowledgments
We thank all members of the Howard laboratory for many helpful discussions and suggestions. We especially thank S. Ganguly, H. Bowne-Anderson and M. Grace for early contributions to this project. We thank A. Arthur for proofreading the manuscript. We also thank H. Cuntz, D. Clark, and J. Carlson for comments on an earlier version of the manuscript, as well as C. Han and the Bloomington Drosophila Stock Center for fly stocks.
Funding: O.T. was supported by the Fonds de Recherché du Quebec–Nature et Technologies. X.L. was supported by the National Natural Science Foundation of China (NSFC grant 31671389) and the Max-Planck Partner Program. J.H. was supported by NIH grants DP1 MH110065 and R01 NS118884. Y.T. is supported by an NIH grant (R35GM131734).
Author contributions: S.Sh., S.Su., and J.H. designed the experiments based on early results by X.L. S.Sh. conducted the experiments and analyzed branching. S.Su., O.T., Y.T., and J.H. conceptualized the models, which were implemented by S.Su., who performed image and tip tracking analysis and wrote the source code for the in silico model, based on earlier work by O.T. S.Sh., S.Su., and J.H. wrote the manuscript.
Competing interests: The authors declare that they have no competing interests.
Data and materials availability: The data used for the analysis have been deposited in Dryad (doi:10.5061/dryad.djh9w0w2r). Simulation code and analysis software are uploaded in Dryad (doi:10.5061/dryad.fbg79cnx9) as well.
Supplementary Materials
This PDF file includes:
Figs. S1 to S9
Tables S1 to S3
References
Other Supplementary Material for this manuscript includes the following:
Movies S1 to S10
REFERENCES AND NOTES
- 1.S. Ramón y Cajal, The structure and connexions of neurons, Nobel Lecture (1906).
- 2.Lefebvre J. L., Sanes J. R., Kay J. N., Development of dendritic form and function. Annu. Rev. Cell Dev. Biol. 31, 741–777 (2013). [DOI] [PubMed] [Google Scholar]
- 3.Fornito A., Zalesky A., Breakspear M., The connectomics of brain disorders. Nat. Rev. Neurosci. 16, 159–172 (2015). [DOI] [PubMed] [Google Scholar]
- 4.Zheng Z., Lauritzen J. S., Perlman E., Robinson C. G., Nichols M., Milkie D., Torrens O., Price J., Fisher C. B., Sharifi N., Calle-Schuler S. A., Kmecova L., Ali I. J., Karsh B., Trautman E. T., Bogovic J. A., Hanslovsky P., Jefferis G. S. X. E., Kazhdan M., Khairy K., Saalfeld S., Fetter R. D., Bock D. D., A complete electron microscopy volume of the brain of adult Drosophila melanogaster. Cell 174, 730–743.e22 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Denk W., Briggman K. L., Helmstaedter M., Structural neurobiology: Missing link to a mechanistic understanding of neural computation. Nat. Rev. Neurosci. 13, 351–358 (2012). [DOI] [PubMed] [Google Scholar]
- 6.Stoeckli E. T., Understanding axon guidance: Are we nearly there yet? Development 145, dev151415 (2018). [DOI] [PubMed] [Google Scholar]
- 7.Jan Y.-N., Jan L. Y., Branching out: Mechanisms of dendritic arborization. Nat. Rev. Neurosci. 11, 316–328 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Singhania A., Grueber W. B., Development of the embryonic and larval peripheral nervous system of Drosophila. Wiley Interdiscip. Rev. Dev. Biol. 3, 193–210 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Basak R., Sutradhar S., Howard J., Focal laser stimulation of fly nociceptors activates distinct axonal and dendritic Ca2+ signals. Biophys. J. 120, 3222–3233 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Robertson J. L., Tsubouchi A., Tracey W. D., Larval defense against attack from parasitoid wasps requires nociceptive neurons. PLOS ONE 8, e78704 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Hughes M. E., Bortnick R., Tsubouchi A., Bäumer P., Kondo M., Uemura T., Schmucker D., Homophilic Dscam interactions control complex dendrite morphogenesis. Neuron 54, 417–427 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Matthews B. J., Kim M. E., Flanagan J. J., Hattori D., Clemens J. C., Zipursky S. L., Grueber W. B., Dendrite self-avoidance is controlled by Dscam. Cell 129, 593–604 (2007). [DOI] [PubMed] [Google Scholar]
- 13.Soba P., Zhu S., Emoto K., Younger S., Yang S.-J., Yu H.-H., Lee T., Jan L. Y., Jan Y.-N., Drosophila sensory neurons require Dscam for dendritic self-avoidance and proper dendritic field organization. Neuron 54, 403–416 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Parrish J. Z., Xu P., Kim C. C., Jan L. Y., Jan Y. N., The microRNA bantam functions in epithelial cells to regulate scaling growth of dendrite arbors in Drosophila sensory neurons. Neuron 63, 788–802 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Emoto K., He Y., Ye B., Grueber W. B., Adler P. N., Jan L. Y., Jan Y.-N., Control of dendritic branching and tiling by the tricornered-kinase/furry signaling pathway in Drosophila sensory neurons. Cell 119, 245–256 (2004). [DOI] [PubMed] [Google Scholar]
- 16.Grueber W. B., Ye B., Moore A. W., Jan L. Y., Jan Y. N., Dendrites of distinct classes of Drosophila sensory neurons show different capacities for homotypic repulsion. Curr. Biol. 13, 618–626 (2003). [DOI] [PubMed] [Google Scholar]
- 17.Jinushi-Nakao S., Arvind R., Amikura R., Kinameri E., Liu A. W., Moore A. W., Knot/collier and cut control different aspects of dendrite cytoskeleton and synergize to define final arbor shape. Neuron 56, 963–978 (2007). [DOI] [PubMed] [Google Scholar]
- 18.Han C., Wang D., Soba P., Zhu S., Lin X., Jan L. Y., Jan Y. N., Integrins regulate repulsion-mediated dendritic patterning of drosophila sensory neurons by restricting dendrites in a 2D space. Neuron 73, 64–78 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Kim M. E., Shrestha B. R., Blazeski R., Mason C. A., Grueber W. B., Integrins establish dendrite-substrate relationships that promote dendritic self-avoidance and patterning in Drosophila sensory neurons. Neuron 73, 79–91 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Stürner T., Tatarnikova A., Mueller J., Schaffran B., Cuntz H., Zhang Y., Nemethova M., Bogdan S., Small V., Tavosanis G., Transient localization of the Arp2/3 complex initiates neuronal dendrite branching in vivo. Development 146, dev171397 (2019). [DOI] [PubMed] [Google Scholar]
- 21.Satoh D., Sato D., Tsuyama T., Saito M., Ohkura H., Rolls M. M., Ishikawa F., Uemura T., Spatial control of branching within dendritic arbors by dynein-dependent transport of Rab5-endosomes. Nat. Cell Biol. 10, 1164–1171 (2008). [DOI] [PubMed] [Google Scholar]
- 22.Zheng Y., Wildonger J., Ye B., Zhang Y., Kita A., Younger S. H., Zimmerman S., Jan L. Y., Jan Y. N., Dynein is required for polarized dendritic transport and uniform microtubule orientation in axons. Nat. Cell Biol. 10, 1172–1180 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Sherwood N. T., Sun Q., Xue M., Zhang B., Zinn K., Drosophila spastin regulates synaptic microtubule networks and is required for normal motor function. PLOS Biol. 2, e429 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Stewart A., Tsubouchi A., Rolls M. M., Tracey W. D., Sherwood N. T., Katanin p60-like1 promotes microtubule growth and terminal dendrite stability in the larval class IV sensory neurons of Drosophila. J. Neurosci. 32, 11631–11642 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ori-McKenney K. M., Jan L. Y., Jan Y.-N., Golgi outposts shape dendrite morphology by functioning as sites of acentrosomal microtubule nucleation in neurons. Neuron 76, 921–930 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ascoli G. A., Krichmar J. L., L-neuron: A modeling tool for the efficient generation and parsimonious description of dendritic morphology. Neurocomputing 32-33, 1003–1011 (2000). [Google Scholar]
- 27.Nanda S., Das R., Bhattacharjee S., Cox D. N., Ascoli G. A., Morphological determinants of dendritic arborization neurons in Drosophila larva. Brain Struct. Funct. 223, 1107–1120 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.L. Baltruschat, G. Tavosanis, H. Cuntz, A developmental stretch-and-fill process that optimises dendritic wiring. bioRxiv 2020.07.07.191064 [Preprint]. 7 July 2022. 10.1101/2020.07.07.191064. [DOI]
- 29.Cuntz H., Forstner F., Borst A., Häusser M., One rule to grow them all: A general theory of neuronal branching and its practical application. PLOS Comput. Biol. 6, e1000877 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Luczak A., Spatial embedding of neuronal trees modeled by diffusive growth. J. Neurosci. Methods 157, 132–141 (2006). [DOI] [PubMed] [Google Scholar]
- 31.Sugimura K., Shimono K., Uemura T., Mochizuki A., Self-organizing mechanism for development of space-filling neuronal dendrites. PLOS Comput. Biol. 3, e212 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.S. Ganguly, O. Trottier, X. Liang, H. Bowne-Anderson, J. Howard, Morphology of fly larval class IV dendrites accords with a random branching and contact based branch deletion model. arXiv: 1611.05918 [q-bio.NC] (17 November 2016).
- 33.Palavalli A., Tizón-Escamilla N., Rupprecht J.-F., Lecuit T., Deterministic and stochastic rules of branching govern dendrite morphogenesis of sensory neurons. Curr. Biol. 31, 459–472.e4 (2021). [DOI] [PubMed] [Google Scholar]
- 34.Metzger R. J., Klein O. D., Martin G. R., Krasnow M. A., The branching programme of mouse lung development. Nature 453, 745–750 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Lefevre J. G., Short K. M., Lamberton T. O., Michos O., Graf D., Smyth I. M., Hamilton N. A., Branching morphogenesis in the developing kidney is governed by rules that pattern the ureteric tree. Development 144, 4377–4385 (2017). [DOI] [PubMed] [Google Scholar]
- 36.Short K. M., Combes A. N., Lefevre J., Ju A. L., Georgas K. M., Lamberton T., Cairncross O., Rumballe B. A., McMahon A. P., Hamilton N. A., Smyth I. M., Little M. H., Global quantification of tissue dynamics in the developing mouse kidney. Dev. Cell 29, 188–202 (2014). [DOI] [PubMed] [Google Scholar]
- 37.Kanari L., Dłotko P., Scolamiero M., Levi R., Shillcock J., Hess K., Markram H., A topological representation of branching neuronal morphologies. Neuroinformatics 16, 3–13 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Hannezo E., Scheele C. L. G. J., Moad M., Drogo N., Heer R., Sampogna R. V., van Rheenen J., Simons B. D., A unifying theory of branching morphogenesis. Cell 171, 242–255.e27 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Grueber W. B., Jan L. Y., Jan Y. N., Tiling of the Drosophila epidermis by multidendritic sensory neurons. Development 129, 2867–2878 (2002). [DOI] [PubMed] [Google Scholar]
- 40.Yang W.-K., Chien C.-T., Beyond being innervated: The epidermis actively shapes sensory dendritic patterning. Open Biol. 9, 180257 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Castro A. F., Baltruschat L., Stürner T., Bahrami A., Jedlicka P., Tavosanis G., Cuntz H., Achieving functional neuronal dendrite structure through sequential stochastic growth and retraction. eLife 9, e60920 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Gao F.-B., Brenman J. E., Jan L. Y., Jan Y. N., Genes regulating dendritic outgrowth, branching, and routing in Drosophila. Gene Dev. 13, 2549–2561 (1999). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.J. D’Errico, SLM-shape language modeling (MathWorks, 2021); www.mathworks.com/matlabcentral/fileexchange/24443-slm-shape-language-modeling.
- 44.Mitchison T., Kirschner M., Dynamic instability of microtubule growth. Nature 312, 237–242 (1984). [DOI] [PubMed] [Google Scholar]
- 45.Dogterom M., Leibler S., Physical aspects of the growth and regulation of microtubule structures. Phys. Rev. Lett. 70, 1347–1350 (1993). [DOI] [PubMed] [Google Scholar]
- 46.Liao M., Liang X., Howard J., The narrowing of dendrite branches across nodes follows a well-defined scaling law. Proc. Natl. Acad. Sci. U.S.A. 118, e2022395118 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.K. Falconer, Fractal Geometry: Mathematical Foundations and Applications (Wiley, ed. 2, 1990). [Google Scholar]
- 48.Kirschner M., Mitchison T., Beyond self-assembly: From microtubules to morphogenesis. Cell 45, 329–342 (1986). [DOI] [PubMed] [Google Scholar]
- 49.Toner J., Tu Y., Long-range order in a two-dimensional dynamical XY model: How birds fly together. Phys. Rev. Lett. 75, 4326–4329 (1995). [DOI] [PubMed] [Google Scholar]
- 50.Vicsek T., Czirók A., Ben-Jacob E., Cohen I., Shochet O., Novel type of phase transition in a system of self-driven particles. Phys. Rev. Lett. 75, 1226–1229 (1995). [DOI] [PubMed] [Google Scholar]
- 51.S. R. Cajal, Histology of the nervous system of man and vertebrates, in History of Neuroscience (Oxford Univ. Press, 1995). [Google Scholar]
- 52.Uçar M. C., Kamenev D., Sunadome K., Fachet D., Lallemend F., Adameyko I., Hadjab S., Hannezo E., Theory of branching morphogenesis by local interactions and global guidance. Nat. Commun. 12, 6830 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Lu P., Werb Z., Patterning mechanisms of branched organs. Science 322, 1506–1509 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.DeFelipe J., López-Cruz P. L., Benavides-Piccione R., Bielza C., Larrañaga P., Anderson S., Burkhalter A., Cauli B., Fairén A., Feldmeyer D., Fishell G., Fitzpatrick D., Freund T. F., González-Burgos G., Hestrin S., Hill S., Hof P. R., Huang J., Jones E. G., Kawaguchi Y., Kisvárday Z., Kubota Y., Lewis D. A., Marín O., Markram H., McBain C. J., Meyer H. S., Monyer H., Nelson S. B., Rockland K., Rossier J., Rubenstein J. L. R., Rudy B., Scanziani M., Shepherd G. M., Sherwood C. C., Staiger J. F., Tamás G., Thomson A., Wang Y., Yuste R., Ascoli G. A., New insights into the classification and nomenclature of cortical GABAergic interneurons. Nat. Rev. Neurosci. 14, 202–216 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Dent E. W., Gupton S. L., Gertler F. B., The growth cone cytoskeleton in axon outgrowth and guidance. Cold Spring Harb. Perspect. Biol. 3, a001800 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Liang X., Kokes M., Fetter R. D., Sallee M. D., Moore A. W., Feldman J. L., Shen K., Growth cone-localized microtubule organizing center establishes microtubule orientation in dendrites. eLife 9, e56547 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Yalgin C., Ebrahimi S., Delandre C., Yoong L. F., Akimoto S., Tran H., Amikura R., Spokony R., Torben-Nielsen B., White K. P., Moore A. W., Centrosomin represses dendrite branching by orienting microtubule nucleation. Nat. Neurosci. 18, 1437–1445 (2015). [DOI] [PubMed] [Google Scholar]
- 58.Weiner A. T., Lanz M. C., Goetschius D. J., Hancock W. O., Rolls M. M., Kinesin-2 and Apc function at dendrite branch points to resolve microtubule collisions. Cytoskeleton 73, 35–44 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Winding M., Kelliher M. T., Lu W., Wildonger J., Gelfand V. I., Role of kinesin-1-based microtubule sliding in Drosophila nervous system development. Proc. Natl. Acad. Sci. U.S.A. 113, E4985–E4994 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Decker F., Oriola D., Dalton B., Brugués J., Autocatalytic microtubule nucleation determines the size and mass of Xenopus laevis egg extract spindles. eLife 7, e31149 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Petry S., Groen A. C., Ishihara K., Mitchison T. J., Vale R. D., Branching microtubule nucleation in Xenopus egg extracts mediated by augmin and TPX2. Cell 152, 768–777 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Pollard T. D., Borisy G. G., Cellular motility driven by assembly and disassembly of actin filaments. Cell 112, 453–465 (2003). [DOI] [PubMed] [Google Scholar]
- 63.Komarova Y. A., Vorobjev I. A., Borisy G. G., Life cycle of MTs: Persistent growth in the cell interior, asymmetric transition frequencies and effects of the cell boundary. J. Cell Sci. 115, 3527–3539 (2002). [DOI] [PubMed] [Google Scholar]
- 64.Arthur A. L., Yang S. Z., Abellaneda A. M., Wildonger J., Dendrite arborization requires the dynein cofactor NudE. J. Cell Sci. 128, 2191–2201 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Kelliher M. T., Yue Y., Ng A., Kamiyama D., Huang B., Verhey K. J., Wildonger J., Autoinhibition of kinesin-1 is essential to the dendrite-specific localization of Golgi outposts. J. Cell Biol. 217, 2531–2547 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Forrest M. P., Parnell E., Penzes P., Dendritic structural plasticity and neuropsychiatric disease. Nat. Rev. Neurosci. 19, 215–234 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Koleske A. J., Molecular mechanisms of dendrite stability. Nat. Rev. Neurosci. 14, 536–550 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Kulkarni V. A., Firestein B. L., The dendritic tree and brain disorders. Mol. Cell. Neurosci. 50, 10–20 (2012). [DOI] [PubMed] [Google Scholar]
- 69.Kapitein L. C., Hoogenraad C. C., Building the neuronal microtubule cytoskeleton. Neuron 87, 492–506 (2015). [DOI] [PubMed] [Google Scholar]
- 70.Demchouk A. O., Gardner M. K., Odde D. J., Microtubule tip tracking and tip structures at the nanometer scale using digital fluorescence microscopy. Cell Mol. Bioeng. 4, 192–204 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Ruhnow F., Zwicker D., Diez S., Tracking single particles and elongated filaments with nanometer precision. Biophys. J. 100, 2820–2828 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Smith M. B., Li H., Shen T., Huang X., Yusuf E., Vavylonis D., Segmentation and tracking of cytoskeletal filaments using open active contours. Cytoskeleton 67, 693–705 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Longair M. H., Baker D. A., Armstrong J. D., Simple Neurite Tracer: Open source software for reconstruction, visualization and analysis of neuronal processes. Bioinformatics 27, 2453–2454 (2011). [DOI] [PubMed] [Google Scholar]
- 74.Hansen P. C., O’Leary D. P., The use of the L-curve in the regularization of discrete Ill-Posed problems. Siam. J. Sci. Comput. 14, 1487–1503 (1993). [Google Scholar]
- 75.Masri R. A., Percival K. A., Koizumi A., Martin P. R., Grünert U., Survey of retinal ganglion cell morphology in marmoset. J. Comp. Neurol. 527, 236–258 (2019). [DOI] [PubMed] [Google Scholar]
- 76.Murru S., Hess S., Barth E., Almajan E. R., Schatton D., Hermans S., Brodesser S., Langer T., Kloppenburg P., Rugarli E. I., Astrocyte-specific deletion of the mitochondrial m-AAA protease reveals glial contribution to neurodegeneration. Glia 67, 1526–1541 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Bloomfield S., Miller R., A functional organization of ON and OFF pathways in the rabbit retina. J. Neurosci. 6, 1–13 (1986). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Liu Z., Steward R., Luo L., Drosophila Lis1 is required for neuroblast proliferation, dendritic elaboration and axonal transport. Nat. Cell Biol. 2, 776–783 (2000). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Figs. S1 to S9
Tables S1 to S3
References
Movies S1 to S10