Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2022 Apr 1;2(3):257–271. doi: 10.1021/acsengineeringau.2c00004

Catalytic Conversion of Alkenes on Acidic Zeolites: Automated Generation of Reaction Mechanisms and Lumping Technique

Elsa Koninckx †, Joseph G Colin ‡, Linda J Broadbelt †, Sergio Vernuccio ‡,*
PMCID: PMC9242524  PMID: 35781936

Abstract

graphic file with name eg2c00004_0019.jpg

Acid-catalyzed hydrocarbon transformations are essential for industrial processes, including oligomerization, cracking, alkylation, and aromatization. However, these chemistries are extremely complex, and computational (automatic) reaction network generation is required to capture these intricacies. The approach relies on the concept that underlying mechanisms for the transformations can be described by a limited number of reaction families applied to various species, with both gaseous and protonated intermediate species tracked. Detailed reaction networks can then be tailored to each industrially relevant process for better understanding or for application in kinetic modeling, which is demonstrated here. However, we show that these networks can grow very large (thousands of species) when they are bound by typical carbon number and rank criteria, and lumping strategies are required to decrease computational expense. For acid-catalyzed hydrocarbon transformations, we propose lumping isomers based on carbon number, branch number, and ion position to reach high carbon limits while maintaining the high resolution of species. Two case studies on propene oligomerization verified the lumping technique in matching a fully detailed model as well as experimental data.

Keywords: reaction mechanism, alkenes, acidic zeolites, automated generation, lumping, kinetic model

1. Introduction

Catalytic conversion of alkenes over acidic zeolites finds application in a wide variety of refining and petrochemical processes including oligomerization, alkylation, and aromatization.1 Acidic zeolites are porous, three-dimensional, aluminosilicate frameworks that contain catalytically active Brønsted acid sites. These active sites catalyze the transformation of hydrocarbons in a confined environment (zeolite pores), which allows for shape-selective effects.2,3 The regular geometry and the microporous structure of acidic zeolites lead to the high selectivity of specific reactants and products as well as impact the stabilization of the reaction intermediates. Furthermore, acidic zeolites are nontoxic and environmentally friendly catalysts compared to homogeneous analogues, with exceptional physical properties such as excellent mechanical and thermal stability.4,5

Acidic zeolite-catalyzed light alkene transformations proceed through extensive and highly interconnected reaction networks. Generally, these transformations can be broadly categorized as:

  • Oligomerization. Oligomerization of light alkenes is an economically beneficial process to produce liquid linear and branched higher alkenes, which provide key intermediates for manufacturing high-octane gasoline and products such as detergents, oil additives, and petrochemicals.6,7 The increased availability in recent years of shale gas resources that contain significant percentages of ethane and propane has directed considerable emphasis on oligomerization over acidic zeolites.8

  • Alkylation. The acid-catalyzed alkylation of alkanes with alkenes is crucial in gasoline reformulation processes where light hydrocarbons obtained from catalytic cracking are converted to a complex mixture of branched alkanes, called alkylate, which is used as a blending component to increase gasoline octane number.9,10

  • Aromatization. The production of aromatics (benzene, toluene, xylenes) from light hydrocarbons is pivotal for the manufacture of fine chemicals and plastics.11 The conversion of alkanes to aromatics over acidic zeolites proceeds through the formation of intermediate alkenes. The addition of a metal promoter to the zeolite favors the dehydrogenation of alkanes into alkenes.12−15

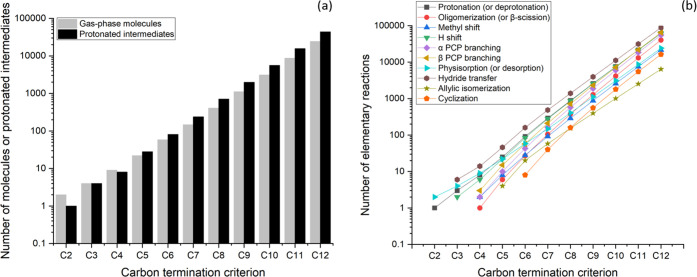
The processes described above typically involve complex feedstocks that consist of several hundreds or thousands of molecular species. Furthermore, the acid-catalyzed chemistry results in the formation of protonated surface species as intermediates that are interconnected by thousands of elementary reactions steps. A mechanistic approach to model the kinetics of these complex reacting systems consists of the automated development of reaction networks and microkinetic models that provide a detailed description of the reaction pathways, including each possible elementary step and reaction intermediate.16 As an example, in an oligomerization network, Table 1 quantifies the potential number of species that are involved in the reaction networks for alkene conversion on acidic zeolites. Networks composed of this level of complexity and specificity of species defy manual construction; rather automated network generation algorithms are necessary computational tools to construct detailed networks and elucidate the complexity of chemical transformations.

Table 1. Number of Gaseous and Protonated Structural Alkene Isomers for a Given Total Carbon Length.

alkene carbon length number of gaseous structural isomers number of protonated structural isomers (no primary)
3 1 1
6 13 9
9 153 122
12 2281 1819
13 5690 4852
14 14 397 11 602
15 36 562 29 623
16 93 646 76 037
Open in a new tab

However, kinetic models must balance the specificity of the species that are included with computational expense; if too large a span of carbon number is covered, the model may be too unwieldy to be solved or used. Returning to Table 1, the possible number of alkene isomers increases exponentially as the carbon number increases. Once a carbon length of C15 is reached, a fully detailed microkinetic model already includes a total of about 60 000 unique gaseous species and about 50 000 unique protonated intermediates, for a total of about 110 000 unique species. Similarly, the hundreds of thousands of reactions between each unique isomer create a system of equations too large and stiff to be solved molecularly that likely includes numerous kinetically insignificant pathways. Rather, lumping similar isomer groups together and assuming each lump is at equilibrium can allow for higher carbon lengths to be reached.

Lumping techniques have been used in the past, and lumps are often a compromise between the capabilities of the experimental analytics to characterize and the computational complexity to replicate.17 For example, one of the first lumped models was proposed by Nace and Weekman in 1971 to model fluid catalytic cracking (FCC) that contained only three lumps corresponding to the three distillation cuts: unreacted gas oil, gasoline, and gas + coke.18 Since then, experimental analytics and computational power have improved, leading to lumping approaches based on carbon number and number of branches or carbon number and number of rings that have been applied by a variety of kinetic modeling endeavors to model catalytic hydrocracking19−21 and catalytic reforming,22 to name a few.17 However, these previous lumping studies mainly focus on lumping based on carbon number alone and are assumed because large groups of intermediates are considered in equilibrium already (such as during hydrocracking). In this work, more detailed kinetic lumping is required for processes like oligomerization, where lumping should depend on not only carbon number but also the degree of branching and the protonated surface intermediates covering the catalyst within the reactor.

In this work, a library of detailed reaction networks was constructed using an automated network generator to describe several industrially relevant alkene transformations over acidic zeolites, namely, light alkene oligomerization, alkylation, and aromatization. The underlying mechanisms for these transformations can be described based on a limited number of reaction families, and the complexity of the reaction mechanisms can be tuned by selecting appropriate termination criteria for the network generation algorithm. We also proposed a lumping strategy based on carbon number, degree of branching, and ion type for gaseous species and protonated intermediates to create kinetic models that can reach high carbon numbers while keeping a high level of mechanistic detail. The proposed reaction networks are sufficiently general to be tailored to the different acidic zeolite frameworks of interest via combination with an appropriate set of kinetic descriptors. The aim of the work is to provide ready-to-use tools for the mechanistic description of alkene transformations on acidic zeolites and the construction of microkinetic models with different degrees of complexities.

The computational details for the automated generation of reaction networks and lumping strategy are presented in Section 2. Section 3 describes the generated reaction networks. Finally, we discuss the proposed lumping strategy based on two case studies applied to propene oligomerization (Section 4).

2. Computational Details

2.1. Automated Network Generation and Visualization

Automated network generators are used to develop networks of elementary reactions with different degrees of complexities depending on the reaction types, or reaction families, and the reaction rules that are defined by the user.16,23

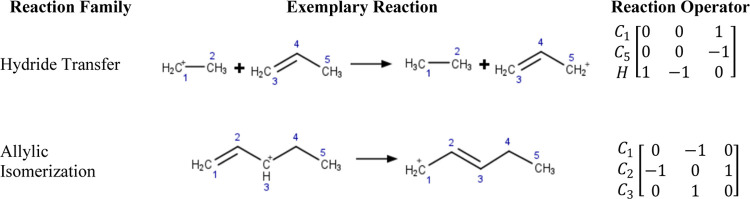
In the present implementation, chemical species are represented using graphs and converted into mathematical expressions using the concept of the bond and electron (BE) matrix.24 The diagonal element [BE]ii of a BE matrix represents the number of free valence electrons of atom i. The off-diagonal element [BE]ij of the BE matrix represents the order of the bond between atoms i and j with [BE]ij = 0 if i and j are not adjacent. Types of chemical reactions are often referred to as reaction families and represent what bonds break and form when a species undergoes a chemical reaction. A reaction family operator can be given as an input to generate a product from a reactant or it can be defined as the difference of the BE matrices that represent the product(s) and the reactant(s) of the chemical transformation. This concept is illustrated in Figure 1 that shows an exemplary oligomerization step between ethene and ethoxy (that is represented for simplicity as a carbenium ion).

Figure 1.

Figure 1

Open in a new tab

Construction of the oligomerization reaction operator. The oligomerization of ethene with ethoxy is chosen as an exemplary reaction step. First, the reactants and products are expressed as BE matrices based on the atom connectivity. Second, the reactant BE matrices are combined, and reduced BE matrices that include only the atoms that are affected by the chemical reaction are identified for both reactant and product. Third, the reaction operator is obtained as a difference of product and reactant BE reduced matrices.

The BE matrices for the reactants ethene and ethoxy are combined into one matrix and permuted to move the atoms that take part in the chemical reaction to the top. This step helps identifying reduced BE matrices that include only atoms for which either bonds break or form. Following this procedure, a reaction operator can be defined for an exemplary elementary reaction of each reaction family.

The same reaction operators can be used to describe multiple unique reactions that belong to the same general family by applying the same reaction operator to a variety of reactant species BE matrices. Moreover, complex networks can be created from a small set of starting species and reaction families by allowing products in one run to be reactants in the next.

The reaction family operators are implemented in NetGen, a software developed by Broadbelt and co-workers.25,26 NetGen automatically generates the reaction products by adding the reaction operators to the reduced BE matrices that represent the reactant species. Graphical networks in this work have been created via Cytoscape 3.9.0 software27 to visualize the reaction mechanisms and their growth as a function of the termination criteria.

2.2. Kinetic Parameters

The kinetic parameters of these models are typically estimated based on a solid theoretical basis, and no a priori assumptions about the rate-determining step(s) are needed.17 As a result of their robust structure, microkinetic models are powerful tools to design industrial processes, optimize the operating conditions of chemical reactors, and inspire novel catalyst development.

The Arrhenius equation was used to calculate rate constants k, where A is the pre-exponential factor, Ea is the activation energy, R is the universal gas constant, and T is the temperature (eq 1).

2.2. 1

Further, Evans–Polanyi relationships28 were used to calculate the activation energies (eq 2)

2.2. 2

where E0 is the intrinsic energy barrier and ΔHR is the enthalpy of the reaction. For all cases, the α transfer coefficient (0 ≤ α ≤ 1) was set to 0.1 and 0.3 for oligomerization and protonation, respectively, and 0.5 for all isomerization reactions.29,30

The enthalpy of reaction is dependent upon ΔHf, which denotes gaseous enthalpy of formation, ΔHphy, which is the physisorption energy for a physisorbed species within a specific framework, Δq, which is the stabilization energy for a protonated intermediate within a specific framework, and υi, which is the species’ stoichiometric coefficient (eq 3).

2.2. 3

The kinetic parameters of kinetic models for acid catalysis are a combination of “kinetic/thermodynamic” and “catalyst” descriptors.31 Kinetic/thermodynamic parameters include gas-phase enthalpies of formation, which are independent of the catalyst. The gas-phase formation enthalpies of the species considered here were calculated using group additivity values based on the formulation by Benson.32 A value of 365.7 kcal/mol was considered for the enthalpy of formation of the proton in the gas phase.33 Catalyst descriptors depend on the specific framework of the zeolite, which account for the impact of the zeolite topology on the kinetics (physisorption enthalpy and stabilization enthalpy). Physisorption enthalpy trends were obtained from hydrocarbon-focused density functional theory (DFT) studies published by De Moor et al.,34−36 as well as Kostetskyy et al.37 In those works, physisorption enthalpies are reported as linear scaling relationships dependent on carbon number. Stabilization energy trends were also taken from DFT studies.38−41 The combination of the contributions from the gas-phase reaction enthalpy with the catalyst descriptors allows the estimation of the reaction enthalpy on the zeolite surface for each of the elementary steps included in the network.

2.3. Carbon and Rank Termination Criteria

The automated generation of a reaction network consists of repeatedly applying the reaction operators to the reactants and their progeny. However, this algorithm results in the possibility of generating an infinite number of reactions and species. To produce a reasonably sized reaction network, a termination criterion can be applied to the generation algorithm. In this work, a “carbon and rank” termination criterion25,42 has been applied, which consists of limiting the maximum carbon number of the species that are allowed to react as well as the rank. The rank of a species reflects its associated order of appearance in the reaction network. Reactants have rank 0. The rank of the products increases by 1 depending on their order of appearance such that primary products are associated with rank 1, secondary products with rank 2, and so forth.42 The increase of the species rank is only associated with the formation of molecules and not with the formation of protonated species. In this work, the criteria used to terminate the network generation algorithm have been indicated using the expression CiRj, where Ci represents the maximum carbon number and Rj represents the maximum rank of the species allowed to react.

2.4. Oligomerization Networks

An acid-catalyzed alkene-oligomerization network converts lower carbon number alkenes to both linear and branched oligomers. The first step of the oligomerization pathway is the activation of the reactant alkene. This consists of the physisorption of the alkene from the gas phase to the pores of the zeolite, followed by protonation to a chemisorbed protonated intermediate.43 The protonated intermediate has been proposed to take the form of either a covalent alkoxide that is connected to an oxygen atom within the zeolite framework or as an ion pair (carbenium ion) with the negatively charged zeolite framework.44 All protonated intermediates are represented in this work as carbenium ions for simplicity.

Deprotonation is the reverse step that regenerates a physisorbed alkene and returns a proton to the zeolite. The number of physisorption and desorption reactions are both equal to the total number of alkenes that are supplied and generated in the network. The protonated species can increase their hydrocarbon chain length through an oligomerization step, representing the addition of a physisorbed molecule to an alkoxide or carbenium ion. The reverse step is β-scission that returns a smaller alkene and a chemisorbed species.

The skeletal rearrangement of the chemisorbed species proceeds through four types of isomerization steps, namely, hydride shift, methyl shift, as well as α- and β-protonated-cyclopropane-mediated (PCP) branching.

The list of reaction families that are involved in the overall oligomerization network and the exemplary elementary steps are listed in Table 2 with the associated reaction operators. To note, this network assumes only alkenes and no alkanes are present. This alkene-oligomerization network can be assumed when only small alkenes are present with few abstractable hydrogens, limiting the hydride-transfer reaction from producing alkane products as well as alkenyl and allylic intermediates. By assuming the network only depends on alkene chemistry, the complexity and size of the network are greatly reduced, which lends to a much more manageable kinetic model. For this reason, it is important to consider if the alkene feedstock and products remain small (<C10) or if operating conditions limit hydride transfer, allowing for the smaller oligomerization set of reaction families to be used. There are several examples in literature of light alkene oligomerization and cracking studies that make such an assumption to focus on alkenes alone.45−47 Networks including alkanes will be discussed in Section 2.5 and are generally much larger than alkene-oligomerization networks of the same initial species, rank, and carbon limit by simply adding two additional reaction families.

Table 2. List of Reaction Families with Exemplary Elementary Steps and Associated Reaction Operators that Are Included in the Alkene-Oligomerization Networka.

2.4.

Open in a new tab
a

The suffixes (g) and (p) represent the gaseous phase and pores of the zeolite, respectively.

2.5. Alkylation Networks

Alkenes and alkanes can kinetically interact by introducing a hydride-transfer step in the list of reaction families. The mechanism of hydride transfer involves the attack of a physisorbed molecular species by a protonated intermediate resulting in the transfer of a hydrogen atom.

The transfer of a hydride from the alkyl group of an alkene to a protonated intermediate forms an alkenyl intermediate, which deprotonates and desorbs as a diene. Similarly, the transfer of a hydride from an alkane to a protonated intermediate that is otherwise saturated results in the formation of a different alkane.

Allylic isomerization was also included in the network to represent the different resonance forms of an allylic ion and the corresponding reaction products, given that charge is associated with a single atom for bookkeeping purposes. The reaction families that complete the list presented in Table 2 to generate the alkylation network are depicted in Table 3.

Table 3. List of Reaction Families with Exemplary Elementary Steps and Associated Reaction Operators to be Added to the List in Table 2 to Generate the Alkylation Network.

2.5.

Open in a new tab

2.6. Cyclization and Aromatization Networks

Cyclization is the transformation of a linear protonated intermediate into a cyclic protonated intermediate. These can either undergo a deprotonation step resulting in the formation of a cycloalkene or a cyclic hydride-transfer step to form a cycloalkane. Four cyclization families that lead to the formation of 1,5 endo, 1,5 exo, 1,6 endo, and 1,6 exo cyclization protonated intermediates were included in this network. Additionally, the reverse reactions of the cyclization steps were included in the network as a form of β-scission. Aromatics can be formed based on a series of deprotonation and hydride-transfer steps applied to a cyclohexene alkoxide or carbenium ion. The reaction families that complete the list presented in Tables 2 and 3 to generate the cyclization and aromatization networks are depicted in Table 4.

Table 4. List of Reaction Families with Exemplary Elementary Steps and Associated Reaction Operators to be Added to the List in Tables 2 and 3 to Generate Cyclization and Aromatization Networks.

2.6.

Open in a new tab

2.7. Lumping Strategy

Lumping involves grouping isomers, which may be done through various means.48 In our case, lumps are based on unique combinations of carbon number, degree of branching, and ion type (primary, secondary, or tertiary) (Figure 2). Within the group of isomers or lump, species are considered to be in thermodynamic equilibrium. In other words, internal isomer reactions that do not change carbon number, degree of branching, nor ion position are assumed to be much faster than reactions that affect the carbon backbone or ion type. This resolution of different ion types advances our lumping technique beyond previously used approaches by retaining the differences in ion stabilities on reaction rates, which can be accounted for with Evans–Polanyi relationships. Pathways between lumps with distinct kinetic parameters are still retained in the model. Each lump is represented by a reference species, which is used to calculate the equilibrium concentrations of all other molecules within the lump. The equilibrium term added to the rate expression is often referred to as a “lumping coefficient” and is determined by thermodynamic properties.

Figure 2.

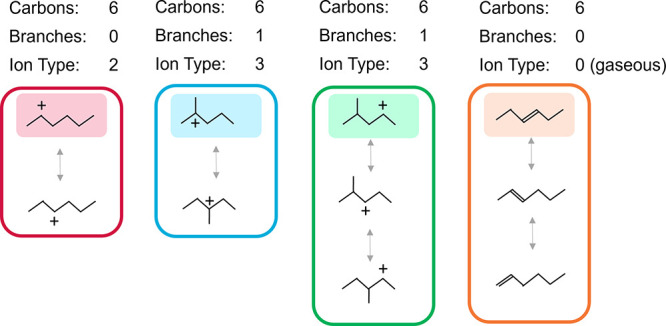
Figure 2

Open in a new tab

Examples of hexene lumped species. Each lumped species has a unique combination of carbon number, branching degree, and ion type. Ion types include primary alkoxide (1), secondary alkoxide (2), tertiary ion (3), or gaseous species (0). Highlighted species represent example reference species for the entire lump.

Lumping is done after network generation to ensure all pathways are still considered and to ensure kinetic rate constants remain specific to the unique reactant. Most often, generating the large network through matrix addition is far easier than modeling kinetics by solving (stiff) differential equations. Moreover, kinetic models must be solved multiple times for optimizations, while the underlying network is only generated once. In other words, network complexity generally impedes developing the kinetic modeling rather than automatic network generation. However, there are works that approach lumped network generation as well when species get very large.20

By applying lumping to an initially fully defined system, the reaction pathways as well as rate constants still retained all specificity of the initial system, prior to lumping, in which all isomers are considered. Only in calculating the concentration of the species, to be multiplied by the rate constant for the final rate calculation, was lumping influential (Figure 3). Concentrations are rewritten assuming equilibrium with respect to a reference species. Species in thermodynamic equilibrium with each other can be simplified into algebraic expressions, effectively reducing the stiffness of the differential equations in the model. Additionally, internal isomerization reactions in which the reactant and product are in the same lump can be removed, further reducing the number of rates.

Figure 3.

Figure 3

Open in a new tab

Schematic exemplifying the reduction realized by lumping of rates and differential equations for flow of gaseous species on the protonation/deprotonation of linear 2- and 3-hexene. In this example, h+ represents a linear C6 protonated intermediate with h+,2 and h+,3 being a secondary or tertiary ion, respectively, which can produce either linear 2-hexene or 3-hexene. H+ represents a proton from the acidic support. Bolded species, h+,2 and 2-hexene, are the reference species for each lump. When lumping, equilibrium (Keq) is assumed within a lump and the concentrations in the rate expression are rewritten based on the lump reference species (C2-hexenelump or Ch+,2,lump). The rate constants, such as pre-exponential factors and activation energies, are not changed and are still calculated specifically for each unique isomer. Isomerization rates within a lump can be removed as the relationship is maintained with an equilibrium expression. Overall, only the reference lump differential flow rates need to be solved, reducing the model stiffness and complexity while maintaining high mechanistic detail.

This type of lumping technique is notably applicable in modeling catalytic reactions in which species can grow in carbon number, and the network could theoretically grow to infinite size. Limiting the model to too few carbon numbers can lead to inaccurate accumulation of species at the carbon limit, and such termination effects have been reported already in previous propene oligomerization models.29 Thus, being able to extend an oligomerization model to lengths past what is experimentally reported is likely necessary to accurately capture kinetics capable of oligomerization.

3. Results and Discussion

This section describes the reaction networks obtained using the methodology presented above. The library of reaction networks described in this section is available on the GitHub repository that is linked to this paper (https://github.com/JosephColin1/supporting-documents). The networks were catalogued based on the carbon and rank termination criteria (indicated as CiRj) that were used for the automated generation process. Each elementary step is associated with a reaction family and assigned a gas-phase reaction enthalpy.

3.1. Oligomerization Networks

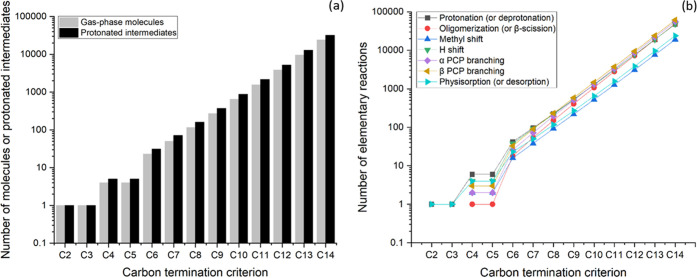
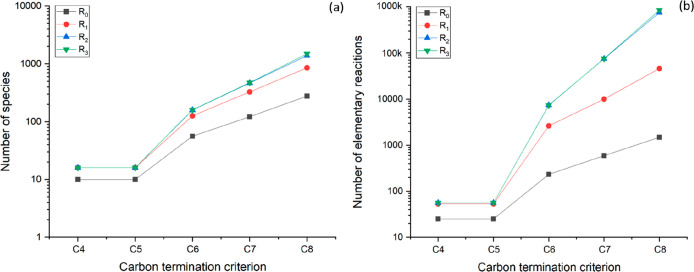
This section presents the networks generated using the reaction families listed in Table 2 by applying the termination criteria CiR0 with i ranging from 2 to 14. The networks were generated by considering ethene and the zeolite proton as the only rank 0 species. However, these can be used to simulate the oligomerization chemistry of any other alkene included in the network. An exponential growth trend was observed for the number of generated alkenes and protonated intermediates (Figure 4a) as well as elementary reactions (Figure 4b) as a function of the carbon termination criterion. The exponential increase of the isomerization reaction steps included in the network corresponds to an increase in the number of possible isomers. This provides a complete description of the chemistry of the process, potentially allowing for a detailed prediction of process performance and distribution of isomers. However, this increased complexity of the reaction network is difficult to handle, and the solution of the associated models is computationally expensive or impossible without the implementation of appropriate reduction techniques, as discussed in Section 4.

Figure 4.

Figure 4

Open in a new tab

Number of (a) molecules and protonated intermediates and (b) elementary reactions included in reaction networks for alkene oligomerization. The networks were generated using ethene as the initial reactant and applying the termination criteria CiR0 with i ranging from 2 to 14.

Figures 5 and 6 show exemplary acid-catalyzed oligomerization networks obtained using ethene as the initial reactant and different termination criteria. Red edges indicate protonation and deprotonation steps, green edges indicate oligomerization and β-scission steps, and blue edges indicate isomerization steps. Black nodes refer to molecular species, and white nodes refer to protonated species. The complete reaction networks including the list of elementary reactions and the Cytoscape files for visualization are available in the section “Oligomerization Networks” of the GitHub repository.

Figure 5.

Figure 5

Open in a new tab

Projected reaction network to describe the acid-catalyzed alkene oligomerization. The network was obtained using ethene (“spe2” highlighted in red) as the initial reactant and the C6R0 termination criterion. Red edges indicate protonation and deprotonation steps, green edges indicate oligomerization and β-scission steps, and blue edges indicate isomerization steps. Black nodes indicate molecular species, and white nodes indicate protonated species. The graphs of molecular and protonated species are listed in Table S1.

Figure 6.

Figure 6

Open in a new tab

Exemplary projected reaction networks that describe the acid-catalyzed alkene oligomerization. The networks were obtained using ethene as the initial reactant and by applying the following termination criteria: (a) C8R0, (b) C9R0, and (c) C10R0. Red edges indicate protonation and deprotonation steps, green edges indicate oligomerization and β-scission steps, and blue edges indicate isomerization steps.

3.2. Alkylation Networks

In this section, we present a library of reaction networks that were generated using the reaction families presented in Tables 2 and 3. The alkylation networks were obtained using the termination criteria CiRj with i ranging from 2 to 12 and j ranging from 0 to 3. The carbon termination criteria were limited to C8 for rank termination criteria Rj > 0. Each network was generated by considering ethene and the zeolite proton as the only rank 0 species. The presence of alkanes in the product mixture is guaranteed by the occurrence of hydride-transfer steps, as previously discussed. Figure 7 shows an exemplary reaction network describing the acid-catalyzed alkylation of isobutane with propene to 2,2-dimethylpentane. Additional alkylation products can be obtained through isomerization and skeletal rearrangements of the C7 protonated intermediate.

Figure 7.

Figure 7

Open in a new tab

Exemplary core catalytic cycle that is part of the reaction network of the acid-catalyzed alkylation of isobutane with propene to 2,2-dimethylpentane.

Figure 8 shows the exponential growth of the number of gas-phase molecules and protonated intermediates (a) and elementary steps (b) included in the networks as a function of the carbon termination criteria for a R0 rank termination criterion. As evident from a comparison between Figures 4 and 8, the inclusion of hydride-transfer steps results in a considerable increase in the size of the reaction network. As an example, for a C12 carbon termination criterion, the inclusion of hydride-transfer steps results in an increase of a factor of 6 in the number of generated species, and of a factor of 8 in the number of generated elementary steps.

Figure 8.

Figure 8

Open in a new tab

Number of molecules and protonated intermediates (a) and elementary reactions (b) included in the reaction networks for alkane/alkene alkylation networks. The networks were generated using ethene as the initial reactant and applying the termination criteria CiR0 with i ranging from 2 to 12.

The generated molecular species include alkanes, alkenes, and dienes with the distribution depicted in Table 5 for a carbon termination criterion ranging from C8 to C12. Figure 9a,b summarizes the results of the network generation procedure, in terms of the number of generated species and elementary steps, for different combinations of the carbon and rank termination criteria. The complete reaction networks described in this section including the list of elementary reactions and the Cytoscape files for visualization are available in the section “Alkylation Networks” of the GitHub repository. The same reaction networks presented in this section can be used to describe the acid-catalyzed cracking process of heavy alkene and alkane feeds.49−51 In these processes, hydride-transfer steps need to be considered because of the presence in the feed of large alkenes with many abstractable hydrogens.

Table 5. Number of Gas-Phase Molecules for the Alkane/Alkene Alkylation Network Obtained by Imposing the Termination Criteria CiR0 with i Ranging from 8 to 12.

  formula C8 C9 C10 C11 C12
alkanes CnH2n+2 39 74 149 308 643
alkenes CnH2n 116 269 646 1560 3841
dienes CnH2n–2 128 390 1138 3232 9112
Open in a new tab

Figure 9.

Figure 9

Open in a new tab

Total number of generated species (a) and elementary steps (b) for the alkane/alkene alkylation network as a function of the carbon (Cj) and rank (Rj) termination criteria. The networks were generated using ethene as the initial reactant.

3.3. Cyclization and Aromatization Networks

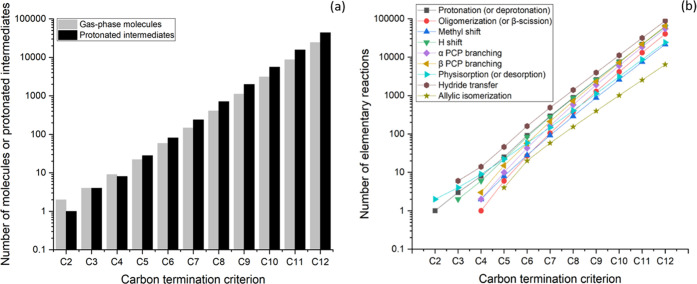
This section presents the reaction networks that were generated based on the complete set of reaction families presented in Tables 2–4. Figure 10 shows the number of generated species (a) and elementary steps (b) as a function of the carbon termination criterion for a R0 rank termination criterion. The species distribution of the networks presented in Figure 10 is highlighted in Table 6, including alkanes, alkenes, dienes, cycloalkanes, and cycloalkenes.

Figure 10.

Figure 10

Open in a new tab

Number of molecules and protonated intermediates (a) and elementary reactions (b) included in cyclization and aromatization networks. The networks were generated using ethene as the initial reactant and applying the termination criteria CiR0 with i ranging from 2 to 12.

Table 6. Number of Gas-Phase Molecules for the Alkane/Alkene Cyclization/Aromatization Network Obtained by Imposing the Termination Criteria CiR0 with i Ranging from 8 to 12.

  formula C8 C9 C10 C11 C12
alkanes CnH2n+2 39 74 149 308 643
alkenes CnH2n 116 269 646 1560 3841
dienes CnH2n–2 128 390 1138 3232 9112
cycloalkanes CnH2n 22 62 173 477 1315
cycloalkenes CnH2n–2 92 309 992 3069 9286
Open in a new tab

The presence of aromatics in the reaction network can be obtained using the same reaction families listed in Tables 2–4 by varying the rank termination criterion. This is exemplified in Figure 11 that shows a possible aromatization pathway of ethene to benzene. First, three molecules of ethene undergo oligomerization to 1,4-hexadiene, which is a rank 2 species. A hydride-transfer step and the following cyclization and deprotonation result in the formation of 1,3-cyclohexadiene as a rank 3 species. Benzene is finally formed from an additional hydride-transfer step followed by deprotonation. Although this is only one possible aromatization path of ethene to benzene, it is worth noting that a rank termination criterion R≥3 is required to generate benzene from ethene. Figure 12 shows the simultaneous impact of the carbon and rank termination criteria on the total number of generated species (a) and elementary steps (b) using ethene as the initial reactant. The presence of branched aromatics heavier than benzene can be obtained by increasing the maximum carbon number of the species that are allowed to react. For example, the termination criterion C7R3 results in the formation of toluene, and the termination criterion C8R3 results in the formation of xylenes.

Figure 11.

Figure 11

Open in a new tab

Aromatization pathway for the formation of benzene from ethene. Ri indicates the rank of the molecular species in the reaction network.

Figure 12.

Figure 12

Open in a new tab

Total number of generated species (a) and elementary steps (b) for the cyclization and aromatization network as a function of the carbon (Cj) and rank (Rj) termination criteria. The networks were generated using ethene as the initial reactant.

The complete reaction networks described in this section including the list of elementary reactions and Cytoscape files for visualization are available in the section “Cyclization and Aromatization Networks” of the GitHub repository.

4. Lumping in Microkinetic Modeling

In the next sections, we use propene oligomerization to test the validity of the lumped modeling technique. The oligomerization network generated using the termination criterion C9R0 and described in Section 3.1 was used to generate both the full model and the lumped model, ensuring both models have the same underlying reaction networks and calculated thermodynamics. The full network is available in the GitHub repository that is linked to the paper, and more details of the model can be found in the Supporting Information.

4.1. Case 1. Full Model vs Lumped Model at Equilibrium

When applying lumping techniques, we assumed that internal isomerization reactions among species with the same carbon number, degree of branching, and ion type occurred very fast and reached thermodynamic equilibrium. To ensure isomer congruity, we compare the lumped isomer (“lump”) and fully defined (“full”) models when isomerization is manually set to be very fast. In the case of fast isomerization reactions, assumed in the lumped model and applied in the full model, both results should converge to similar isomer fractions.

Isomerization reactions were set to be very fast by increasing the pre-exponential factor to 5 × 1012 s–1 and lowering the intrinsic activation energy to 5.0 kcal/mol (Table S3). Product mole fractions with respect to the entire product distribution are compared in Figure 13. A low conversion of about 1% was used in the comparison.

Figure 13.

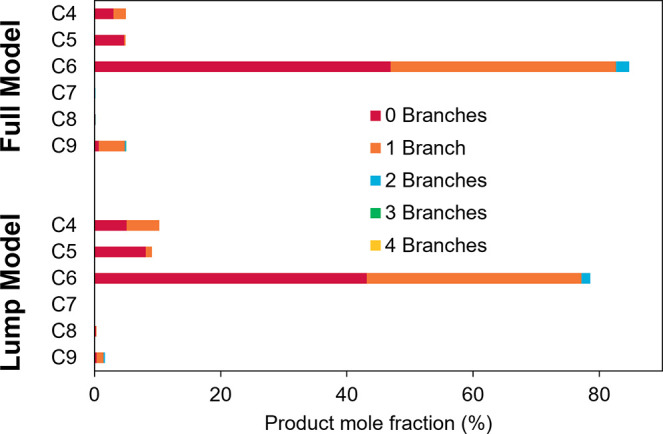
Figure 13

Open in a new tab

Product mole fractions for full and lump model simulations. Fractions were calculated with respect to the entire product distribution (C4–C9). Conversion for both simulations was about 1%.

As expected, both models converge to very similar results, with the minor differences that can be explained by the inherent differences in the model network (irreversible reactions now assumed reversible), tolerances imposed to solve the stiff set of model equations, or reaction path degeneracy. In both cases, the models predict that about 45 mol % of hexenes produced are linear, followed by about 35 mol % methylpentenes, and 2 mol % dimethylbutenes. Isomers of butene are produced in about even amounts (note that mole fractions are calculated across the entire product distribution and not within each carbon number). Overall, isomer fractions between the full and lumped model show similar mole fractions, suggesting that the models converge with fast isomerization or assuming isomerization equilibrium.

4.2. Case 2. Experiments vs Full Model vs Lumped Model

In this section, we compared the results of the fully defined and lumped isomer models against actual experimental data. The experiments were taken from the previously mentioned propene oligomerization study29 and are summarized in Figure 14, and the experimental conversion and selectivities are reported in Table S4.29 Initial time on stream data was used due to catalyst deactivation, and only up to C9 species were measured in the experiments. In this case, we want to show that the lumped model can still match experimental data, even when the ion distribution is not at equilibrium, as assessed by the full model.

Figure 14.

Figure 14

Open in a new tab

Parity plots of conversion and selectivity comparing the full model and the lumped model to propene oligomerization experimental values. Kinetic parameters can be found in Tables S4–S6.

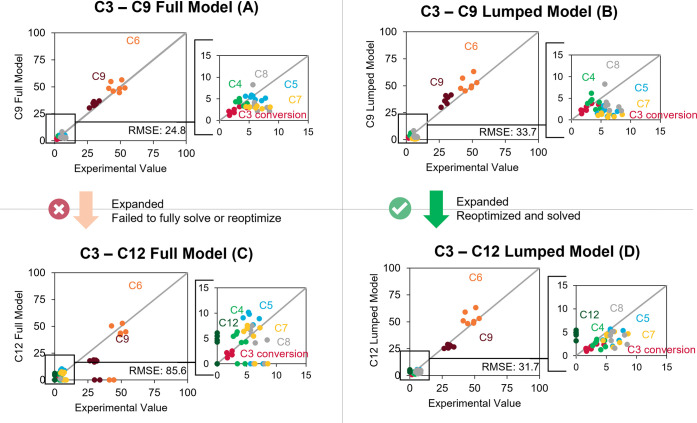
First, a C3–C9 model was developed, following the procedure described elsewhere.29 The fully defined model encompassed 628 species and 2615 reactions. Compared to the experimental data, the full model results in an RMSE value of 24.8 (Figure 14A, kinetic parameters in Table S5). However, the high production and even overproduction of C9, the maximum carbon length, suggest that flux is artificially stuck at this limit as no further oligomerization pathways are present. As a result, C9s accumulate and are forced to crack into smaller products. This, in turn, can lead to incorrect kinetic parameters upon optimization such that the experimental data is captured, which results in a detailed kinetic model with limited utility. The lumped model does sufficiently well in describing the experiments, with an RMSE of 33.7 (Figure 14B, kinetic parameters in Table S6). A significant amount of this error comes from underproducing C5 and C7, which are difficult to produce with a carbon limit of C9, as either butenes (C5 + C4) or ethene (C2 + C7) must be produced, which is often energetically unfavorable.

Comparing kinetic parameters, both the full model and the lumped model share similar rates of protonation and deprotonation, as well as oligomerization and β-scission rate constants. Rate constants for isomerization, specifically for methyl and hydride shift, change more significantly. This difference is most likely due to the lumped model assuming most of these isomerization reactions are in equilibrium as well as the model being less sensitive to changes in isomerization reactions, which are fast, compared to oligomerization, which are slower and often rate-determining. To note, the lumped model is significantly smaller than the full model, containing only 79 reference species and 974 reactions. Although the full model has a lower RMSE compared to the lumped model, the solution of the lumped model is significantly computationally less expensive than the full model.

Next, a C3–C12 model including 8832 species and 42 097 reactions was developed to better describe the experimental data. Due to the extended carbon limit, the solution of this model failed past about 2.8% conversion (Figure 14C). On the other hand, the lumped model was able to be solved and optimized to fit the experimental data. The extended lumped model included 152 species and 4814 reactions and drops the RMSE to 31.7 (Figure 14D, kinetic parameters in Table S7). In this extended lumped model, C12s are being produced and more easily cracked to match the higher selectivities of C5 and C7. The absence of >C9 species in the experimental data does not exclude the formation and accumulation of these heavier species in the pores of the catalyst, causing the reported deactivation. Nevertheless, these heavier species being produced in either the experiments or the model remain relatively low for the mass balances to close ≥ 95%. Additionally, the rate of oligomerization in the C3–C12 model is lower than the C3–C9 model and is likely more accurate. In the previous C3–C9 case, an overestimation of the oligomerization rate would only provide more carbon into the C9 fraction, whereas in this larger C3–C12 model, an overestimation of oligomerization rates will direct carbon away from C9 and into C12.

Despite the RMSE being slightly higher than the full C9 model, the lumped C12 model likely provides a better description of the intrinsic kinetics of the system, without the false accumulation of the maximum carbon species and more viable paths to produce C5 and C7.

One of the benefits of using a mechanistic approach in kinetic modeling is being able to distinguish products of unique carbon number and branch degree. However, many times, experimental analysis only reports groups based on carbon number, such as in these propene experiments. Both the full and lumped models suggest slightly different branching isomer fractions; however, it is impossible to know which is closest to the experimental “truth” until such detailed experiments are carried out. Intriguingly, the availability of models that capture this level of detail as offered in the present work provides impetus for additional experimentation and even provides guidance about what species may dominate to aid the interpretation of complex spectroscopic analyses.

5. Conclusions

Computational automatic network generation is a powerful tool to create large networks encompassing many industrially relevant acid-catalyzed hydrocarbon chemistries including oligomerization, alkylation, and aromatization. These complex chemistries can be summarized in succinct sets of reaction families with chemical species written as a bond and electron matrix. Carbon and rank limits are required to provide bounds and focus on relevant carbon numbers and products. Examples of reaction networks and their reaction families, with Cytoscape visualization, show how these networks grow in complexity and can quickly become extremely extensive. To better utilize extensive kinetic models, lumping is required to reduce model size and computational load. Our lumping approach uniquely uses a combination of carbon number, branching degree, and ion position to retain high product specificity for both gaseous and protonated intermediates. The addition of ion position allows for a better description of the catalytic surface and preserves ion stability differences. This novel lumping technique was explored in three case studies, which confirms congruence with a fully defined kinetic model. Additionally, the application of lumping was confirmed to capture experimental oligomerization kinetics to a high degree of fidelity. Moving forward, this lumping technique could be applied to a wide variety of chemistries allowing for more robust and expansive models in the future.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsengineeringau.2c00004.

  • Graphs of molecular and protonated species represented in the reaction network in Figure 6; experimental conditions (propene conversion and selectivities) used in Section 4.2; kinetic parameters used in modeling the fully defined model, for both networks spanning C3–C9 and C3–C12; the full networks described in Section 3 are available on the GitHub repository that is linked to this paper (https://github.com/JosephColin1/supporting-documents) (PDF)

Financial support for this work is gratefully acknowledged from The National Science Foundation (NSF) Graduate Research Fellowships Program (GRFP) Grant Number DGE-1842165. Support from the NSF under Cooperative Agreement No. EEC-164772 is also acknowledged; any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation. The authors also acknowledge the support of the Belgium American Education Foundation (BAEF) fellowship to E.K. and the support from The Royal Society of Chemistry (RSC) Undergraduate Research Bursary (URB) Application Number: U21-6382489973 to J.G.C.

The authors declare no competing financial interest.

This paper was published on April 1, 2022, with part of the Figure 3 graphic missing. The corrected version was reposted on April 4, 2022.

Supplementary Material

eg2c00004_si_001.pdf (263.9KB, pdf)

References

  1. Weber J. L.; Martínez del Monte D.; Beerthuis R.; Dufour J.; Martos C.; de Jong K. P.; de Jongh P. E. Conversion of Synthesis Gas to Aromatics at Medium Temperature with a Fischer Tropsch and ZSM-5 Dual Catalyst Bed. Catal. Today 2021, 369, 175–183. 10.1016/j.cattod.2020.05.016. [DOI] [Google Scholar]
  2. Lukyanov D. B.; Vazhnova T.; Cherkasov N.; Casci J. L.; Birtill J. J. Insights into Brønsted Acid Sites in the Zeolite Mordenite. J. Phys. Chem. C 2014, 118, 23918–23929. 10.1021/jp5086334. [DOI] [Google Scholar]
  3. Vermeiren W.; Gilson J.-P. Impact of Zeolites on the Petroleum and Petrochemical Industry. Top. Catal. 2009, 52, 1131–1161. 10.1007/s11244-009-9271-8. [DOI] [Google Scholar]
  4. Naqvi S. R.; Uemura Y.; Yusup S.; Sugiur Y.; Nishiyama N.; Naqvi M. The Role of Zeolite Structure and Acidity in Catalytic Deoxygenation of Biomass Pyrolysis Vapors. Energy Procedia 2015, 75, 793–800. 10.1016/j.egypro.2015.07.126. [DOI] [Google Scholar]
  5. Li Y.; Li L.; Yu J. Applications of Zeolites in Sustainable Chemistry. Chem 2017, 3, 928–949. 10.1016/j.chempr.2017.10.009. [DOI] [Google Scholar]
  6. Lallemand M.; Finiels A.; Fajula F.; Hulea V. Catalytic Oligomerization of Ethylene over Ni-Containing Dealuminated Y Zeolites. Appl. Catal., A 2006, 301, 196–201. 10.1016/j.apcata.2005.12.019. [DOI] [Google Scholar]
  7. Monama W.; Mohiuddin E.; Thangaraj B.; Mdleleni M. M.; Key D. Oligomerization of Lower Olefins to Fuel Range Hydrocarbons over Texturally Enhanced ZSM-5 Catalyst. Catal. Today 2020, 342, 167–177. 10.1016/j.cattod.2019.02.061. [DOI] [Google Scholar]
  8. Korpyś M.; Synowiec P.; Wojcik J. Methods for Sweetening Natural and Shale Gas. Chem. Sci. 2014, 68, 213–215. [Google Scholar]
  9. Feller A.; Lercher J. A. Chemistry and Technology of Isobutane/Alkene Alkylation Catalyzed by Liquid and Solid Acids. Adv. Catal. 2004, 48, 229–295. 10.1016/S0360-0564(04)48003-1. [DOI] [Google Scholar]
  10. Ganesh H. S.; Dean D. P.; Vernuccio S.; Edgar T. F.; Baldea M.; Broadbelt L. J.; Stadtherr M. A.; Allen D. T. Product Value Modeling for a Natural Gas Liquid to Liquid Transportation Fuel Process. Ind. Eng. Chem. Res. 2020, 59, 3109–3119. 10.1021/acs.iecr.9b06673. [DOI] [Google Scholar]
  11. Uslamin E. A.; Saito H.; Kosinov N.; Pidko E.; Sekine Y.; Hensen E. J. M. Aromatization of Ethylene over Zeolite-Based Catalysts. Catal. Sci. Technol. 2020, 10, 2774–2785. 10.1039/C9CY02108F. [DOI] [Google Scholar]
  12. Perego C.; Pollesel P.. Advances in Aromatics Processing Using Zeolite Catalysts. In Advances in Nanoporous Materials; Ernst S., Ed.; Elsevier, 2010; pp 97–149. [Google Scholar]
  13. Caeiro G.; Carvalho R. H.; Wang X.; Lemos M. A. N. D. A.; Lemos F.; Guisnet M.; Ramôa Ribeiro F. Activation of C2 -C4 Alkanes over Acid and Bifunctional Zeolite Catalysts. J. Mol. Catal. A 2006, 255, 131–158. 10.1016/j.molcata.2006.03.068. [DOI] [Google Scholar]
  14. Bhan A.; Nicholas Delgass W. Propane Aromatization over HZSM-5 and Ga/HZSM-5 Catalysts. Catal. Rev. 2008, 50, 19–151. 10.1080/01614940701804745. [DOI] [Google Scholar]
  15. Tessonnier J. P.; Louis B.; Rigolet S.; Ledoux M. J.; Pham-Huu C. Methane Dehydro-Aromatization on Mo/ZSM-5: About the Hidden Role of Brønsted Acid Sites. Appl. Catal., A 2008, 336, 79–88. 10.1016/J.APCATA.2007.08.026. [DOI] [Google Scholar]
  16. Vernuccio S.; Broadbelt L. J. Discerning Complex Reaction Networks Using Automated Generators. AIChE J. 2019, 65, e16663 10.1002/aic.16663. [DOI] [Google Scholar]
  17. De Oliveira L. P.; Hudebine D.; Guillaume D.; Verstraete J. J. A Review of Kinetic Modeling Methodologies for Complex Processes. Oil Gas Sci. Technol. 2016, 71, 45 10.2516/ogst/2016011. [DOI] [Google Scholar]
  18. Nace D. M.; Voltz S. E.; Weekman V. W. J. Application of a Kinetic Model for Catalytic Cracking. Ind. Eng. Chem. Process Des. Dev. 1971, 10, 530–538. 10.1021/i260040a018. [DOI] [Google Scholar]
  19. Valéry E.; Guillaume D.; Surla K.; Galtier P.; Verstraete J.; Schweich D. Kinetic Modeling of Acid Catalyzed Hydrocracking of Heavy Molecules: Application to Squalane. Ind. Eng. Chem. Res. 2007, 46, 4755–4763. 10.1021/ie061559w. [DOI] [Google Scholar]
  20. Martens G. G.; Marin G. B. Kinetics for Hydrocracking Based on Structural Classes: Model Development and Application. AIChE J. 2001, 47, 1607–1622. 10.1002/aic.690470713. [DOI] [Google Scholar]
  21. Quintana-Solórzano R.; Thybaut J. W.; Galtier P.; Marin G. B. Simulation of an Industrial Riser for Catalytic Cracking in the Presence of Coking Using Single-Event MicroKinetics. Catal. Today 2010, 150, 319–331. 10.1016/J.CATTOD.2009.07.110. [DOI] [Google Scholar]
  22. Cochegrue H.; Gauthier P.; Verstraete J. J.; Surla K.; Guillaume D.; Galtier P.; Barbier J. Reduction of Single Event Kinetic Models by Rigorous Relumping: Application to Catalytic Reforming. Oil Gas Sci. Technol. 2011, 66, 367–397. 10.2516/ogst/2011122. [DOI] [Google Scholar]
  23. Broadbelt L. J.; Stark S. M.; Klein M. T. Computer Generated Reaction Modelling: Decomposition and Encoding Algorithms for Determining Species Uniqueness. Comput. Chem. Eng. 1996, 20, 113–129. 10.1016/0098-1354(94)00009-D. [DOI] [Google Scholar]
  24. Ugi I.; Bauer J.; Brandt J.; Friedrich J.; Gasteiger J.; Jochum C.; Schubert W. New Applications of Computers in Chemistry. Angew. Chem., Int. Ed. 1979, 18, 111–123. 10.1002/anie.197901111. [DOI] [Google Scholar]
  25. Broadbelt L. J.; Stark S. M.; Klein M. T. Computer Generated Pyrolysis Modeling: On-the-Fly Generation of Species, Reactions, and Rates. Ind. Eng. Chem. Res. 1994, 33, 790–799. 10.1021/ie00028a003. [DOI] [Google Scholar]
  26. Klein M. T.; Hou G.; Bertolacini R. J.; Broadbelt L. J.; Kumar A.. Molecular Modeling in Heavy Hydrocarbon Conversions; CRC Press, 2005. [Google Scholar]
  27. Killcoyne S.; Carter G. W.; Smith J.; Boyle J. Cytoscape: A Community-Based Framework for Network Modeling. Methods Mol. Biol. 2009, 563, 219–239. 10.1007/978-1-60761-175-2_12. [DOI] [PubMed] [Google Scholar]
  28. Evans M. G.; Polanyi M. Inertia and Driving Force of Chemical Reactions. Trans. Faraday Soc. 1938, 34, 11 10.1039/tf9383400011. [DOI] [Google Scholar]
  29. Vernuccio S.; Bickel E. E.; Gounder R.; Broadbelt L. J. Microkinetic Model of Propylene Oligomerization on Brønsted Acidic Zeolites at Low Conversion. ACS Catal. 2019, 9, 8996–9008. 10.1021/acscatal.9b02066. [DOI] [Google Scholar]
  30. Vernuccio S.; Bickel E. E.; Gounder R.; Broadbelt L. J. Propene Oligomerization on Beta Zeolites: Development of a Microkinetic Model and Experimental Validation. J. Catal. 2021, 395, 302–314. 10.1016/j.jcat.2021.01.018. [DOI] [Google Scholar]
  31. Thybaut J. W.; Marin G. B. Single-Event MicroKinetics: Catalyst Design for Complex Reaction Networks. J. Catal. 2013, 308, 352–362. 10.1016/j.jcat.2013.08.013. [DOI] [Google Scholar]
  32. Bjorkman K. R.; Sung C. Y.; Mondor E.; Cheng J. C.; Jan D. Y.; Broadbelt L. J. Group Additivity Determination for Enthalpies of Formation of Carbenium Ions. Ind. Eng. Chem. Res. 2014, 53, 19446–19452. 10.1021/ie503348z. [DOI] [Google Scholar]
  33. Lemmon E. W.; McLinden M. O.; Friend D.. Thermophysical Properties of Fluid Systems. In NIST Chemistry WebBook; Linstrom P. J.; Mallard W. G., Eds.; National Institute of Standards and Technology: Gaithersburg MD, 2014. [Google Scholar]
  34. De Moor B. A.; Reyniers M. F.; Gobin O. C.; Lercher J. A.; Marin G. B. Adsorption of C2-C8 n-Alkanes in Zeolites. J. Phys. Chem. C 2011, 115, 1204–1219. 10.1021/jp106536m. [DOI] [Google Scholar]
  35. De Moor B. A.; Reyniers M. F.; Sierka M.; Sauer J.; Marin G. B. Physisorption and Chemisorption of Hydrocarbons in H-FAU Using QM-Pot(MP2//B3LYP) Calculations. J. Phys. Chem. C 2008, 112, 11796–11812. 10.1021/jp711109m. [DOI] [Google Scholar]
  36. Nguyen C. M.; De Moor B. A.; Reyniers M. F.; Marin G. B. Physisorption and Chemisorption of Linear Alkenes in Zeolites: A Combined QM-Pot(MP2//B3LYP:GULP)-Statistical Thermodynamics Study. J. Phys. Chem. C 2011, 115, 23831–23847. 10.1021/jp2067606. [DOI] [Google Scholar]
  37. Kostetskyy P.; Koninckx E.; Broadbelt L. J. Probing Monomer and Dimer Adsorption Trends in the MFI Framework. J. Phys. Chem. B 2021, 125, 7199–7212. 10.1021/acs.jpcb.1c02929. [DOI] [PubMed] [Google Scholar]
  38. Nguyen C. M.; De Moor B. A.; Reyniers M. F.; Marin G. B. Isobutene Protonation in H-FAU, H-MOR, H-ZSM-5, and H-ZSM-22. J. Phys. Chem. C 2012, 116, 18236–18249. 10.1021/jp304081k. [DOI] [Google Scholar]
  39. Boronat M.; Viruela P. M.; Corma A. Reaction Intermediates in Acid Catalysis by Zeolites: Prediction of the Relative Tendency to Form Alkoxides or Carbocations as a Function of Hydrocarbon Nature and Active Site Structure. J. Am. Chem. Soc. 2004, 126, 3300–3309. 10.1021/ja039432a. [DOI] [PubMed] [Google Scholar]
  40. Boronat M.; Zicovich-Wilson C. M.; Viruela P.; Corma A. Influence of the Local Geometry of Zeolite Active Sites and Olefin Size on the Stability of Alkoxide Intermediates. J. Phys. Chem. B 2001, 105, 11169–11177. 10.1021/jp011481r. [DOI] [Google Scholar]
  41. Rozanska X.; Van Santen R. A.; Demuth T.; Hutschka F.; Hafner J. A Periodic DFT Study of Isobutene Chemisorption in Proton-Exchanged Zeolites: Dependence of Reactivity on the Zeolite Framework Structure. J. Phys. Chem. B 2003, 107, 1309–1315. 10.1021/jp021646b. [DOI] [Google Scholar]
  42. Broadbelt L. J.; Stark S. M.; Klein M. T. Termination of Computer-Generated Reaction Mechanisms: Species Rank-Based Convergence Criterion. Ind. Eng. Chem. Res. 1995, 34, 2566–2573. 10.1021/ie00047a003. [DOI] [Google Scholar]
  43. Overend J. Chemistry of Catalytic Processes. J. Chem. Educ. 1979, 56, A242. 10.1021/ed056pA242.2. [DOI] [Google Scholar]
  44. Cnudde P.; De Wispelaere K.; Van der Mynsbrugge J.; Waroquier M.; Van Speybroeck V. Effect of Temperature and Branching on the Nature and Stability of Alkene Cracking Intermediates in H-ZSM-5. J. Catal. 2017, 345, 53–69. 10.1016/j.jcat.2016.11.010. [DOI] [Google Scholar]
  45. von Aretin T.; Standl S.; Tonigold M.; Hinrichsen O. Optimization of the Product Spectrum for 1-Pentene Cracking on ZSM-5 Using Single-Event Methodology. Part 2: Recycle Reactor. Chem. Eng. J. 2017, 309, 873–885. 10.1016/j.cej.2016.10.103. [DOI] [Google Scholar]
  46. Von Aretin T.; Schallmoser S.; Standl S.; Tonigold M.; Lercher J. A.; Hinrichsen O. Single-Event Kinetic Model for 1-Pentene Cracking on ZSM-5. Ind. Eng. Chem. Res. 2015, 54, 11792–11803. 10.1021/acs.iecr.5b02629. [DOI] [Google Scholar]
  47. Ying L.; Zhu J.; Cheng Y.; Wang L.; Li X. Kinetic Modeling of C2-C7 Olefins Interconversion over ZSM-5 Catalyst. J. Ind. Eng. Chem. 2016, 33, 80–90. 10.1016/j.jiec.2015.09.021. [DOI] [Google Scholar]
  48. Guillaume D. Network Generation of Oligomerization Reactions: Principles. Ind. Eng. Chem. Res. 2006, 45, 4554–4557. 10.1021/ie0510019. [DOI] [Google Scholar]
  49. Park Y.-K.; Lee C. W.; Kang N. Y.; Choi W. C.; Choi S.; Oh S. H.; Park D. S. Catalytic Cracking of Lower-Valued Hydrocarbons for Producing Light Olefins. Catal. Surv. Asia 2010, 14, 75–84. 10.1007/s10563-010-9089-1. [DOI] [Google Scholar]
  50. Rahimi N.; Karimzadeh R. Catalytic Cracking of Hydrocarbons over Modified ZSM-5 Zeolites to Produce Light Olefins: A Review. Appl. Catal., A 2011, 398, 1–17. 10.1016/J.APCATA.2011.03.009. [DOI] [Google Scholar]
  51. Gholami Z.; Gholami F.; Tišler Z.; Tomas M.; Vakili M. A Review on Production of Light Olefins via Fluid Catalytic Cracking. Energies 2021, 14, 1089 10.3390/en14041089. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

eg2c00004_si_001.pdf (263.9KB, pdf)

Articles from ACS Engineering Au are provided here courtesy of American Chemical Society

RESOURCES