Abstract
An accurate record of preindustrial (pre-1900 CE) sea level is necessary to contextualize modern global mean sea level (GMSL) rise with respect to natural variability. Precisely dated phreatic overgrowths on speleothems (POS) provide detailed rates of Late Holocene sea-level rise in Mallorca. Statistical analysis indicates that sea level rose locally by 0.12 to 0.31 m (95% confidence) from 3.26 to 2.84 thousand years (ka) ago (2σ) and remained within 0.08 m (95% confidence) of preindustrial levels from 2.84 ka to 1900 CE. This sea-level history is consistent with glacial isostatic adjustment models adopting relatively weak upper mantle viscosities of ~1020 Pa s. There is virtual certainty (>0.999 probability) that the average GMSL rise since 1900 CE has exceeded even the high average rate of sea-level rise between 3.26 and 2.84 ka inferred from the POS record. We conclude that modern GMSL rise is anomalous relative to any natural variability in ice volumes over the past 4000 years.
Modern global sea-level rise is anomalous relative to any natural variability over the past 4000 years.
INTRODUCTION
Estimates of preindustrial (pre-1900 CE) Holocene global mean sea level (GMSL) variability provide the background state against which changes due to modern greenhouse warming may be calibrated (1, 2). Late Holocene (last 4200 years) sea level reconstructions cover the transition from geological to instrumental records, and, when highly resolved, the former can precisely determine when modern rates of sea-level rise began (3, 4). Probabilistic estimates based on data compilations have resolved centennial-scale variability in GMSL since ~3 thousand years (ka) ago (1, 5). However, large discrepancies in these inferences for prior to 2.5 ka before the present (B.P.), indicate that they are poorly constrained over this earlier period. An accurate, highly resolved estimate of GMSL change that extends across the past 4 ka is thus critical for establishing both the degree of stability of the cryosphere during the relatively equable climate of the Late Holocene and the extent to which sea-level rise over the past century and decades is an anomalous consequence of human-induced global warming (6–8).
GMSL is commonly reconstructed by compiling globally distributed individual relative sea level (RSL) records after consideration for specific local to regional processes including glacial isostatic adjustment (GIA), tectonics, sediment compaction, and mantle dynamic topography (for records extending tens of thousands of years) (3, 9, 10). Even at far-field sites (i.e., those that are located distant from major glaciation centers), the RSL signal is not immune to GIA and may record substantial departures from GMSL (11). Thus, in general, the inference of GMSL from such data is often coupled to assumptions regarding the two primary inputs to GIA models, global ice history and mantle viscosity structure. As we demonstrate herein, Mallorca, an island in the western Mediterranean Sea that has a long history of tectonic stability (the Supplementary Materials and fig. S1A) and hosts many littoral caves containing phreatic overgrowths on speleothems (POS) (12), is a promising location for establishing a high-resolution time series of GMSL throughout the Late Holocene.
RESULTS AND DISCUSSION
POS data and RSL in Mallorca
POS are gaining recognition as precise still-stand sea level gauges that cover up to millennial time scales (13–15). Their morphologies include knob, spindle, or composite and depend on the length of the vadose speleothem upon which they grow (usually stalactites), the duration that it remained immersed in water, and the amplitude of the RSL change (Fig. 1 and the Supplementary Materials). Because they only form within the tidal range (~0.25 m), POS unambiguously capture the vertical extent [i.e., indicative range (IR)] of sea level, and their thickest part corresponds to the reference water level (RWL), which is the position of MSL (Fig. 1A) for the period of POS growth. These two attributes, supplemented with exact location, accurate elevation, and subcentury-scale uranium-series (U-series) chronologies, make POS meaningful sea level index points that allow for accurate and precise (decimeter-scale) RSL reconstructions (see the Supplementary Materials). To date, because of sample-specific vertical and temporal uncertainties, only a handful of other sea level proxies have provided RSL records that capture well-dated, submeter sea level fluctuations (16, 17).
Fig. 1. Holocene POS in Mallorca.
(A) Schematic representation of the indicative meaning of POS. RSL is measured by subtracting POS’s RWL from its elevation relative to modern sea level. IR, indicative range; ht, high tide; lt, low tide. (B) Drawing depicting types of POS growth. 1, Knob-type POS encrusting a stalactite that was too short to allow growth over the full tidal range (i.e., only high-tide growth); 2, spindle-shaped POS precipitated on a column over the entire tidal range as shown in (A) and 2a/b. (C) Composite POS in Coves del Drac formed during sea level still stand no. 1 (2b) and after a sea-level rise to still stand no. 2 (2a). Photo credit: B. P. Onac, University of South Florida.
Our Late Holocene sea level estimates (~3.9 ka B.P. to 1900 CE) are based on 136 new, precise U-series dates of 13 POS samples (table S1) obtained from eight caves along the southern and eastern coastline of the island of Mallorca (fig. S1B). The data show two distinct RSL still-stand intervals in the Late Holocene: approximately −0.25 ± 0.1 m from ~3.89 ± 0.02 to 3.26 ± 0.01 ka (hereafter, ± refers to 2σ unless otherwise specified) and ~0 ± 0.05 m from 2.84 ± 0.02 to 0.03 ± 0.004 ka, both relative to the pre-20th century GMSL (Fig. 2). The composite POS samples from Coves del Drac depict a distinct and relatively rapid sea-level rise of ~0.25 m at ~3 ka, allowing for the direct measurement of the elevation difference between the fossil POS and its modern analog (fig. S2). Thus, they represent an ideal single-site setting for determining the magnitude of RSL change (18). Moreover, most POS are composed of aragonite and can be accurately and precisely dated (14). For example, samples DR-D15b and DR-D18b establish a paleo-RSL position at −0.25 ± 0.1 m from 3.89 to 3.26 ka (the Supplementary Materials, Fig. 2, and figs. S3 and S4).
Fig. 2. Mallorca POS-derived Late Holocene RSL.
A Bayesian statistical analysis (19) of the POS data (green and yellow envelopes denote the 67 and 95% credible intervals, respectively) shows that RSL (uncorrected for GIA) remained still at −0.25 m between ~3.9 and ~3.3 ka and at preindustrial GMSL for the past ~2.8 ka. Blue and red curves show the GMSL with respect to 1900 CE (mean with 1σ uncertainties) in (1) and (8), respectively. Solid circles and open rhombs denote POS analyzed at University of New Mexico and University of Bern, respectively. The inset focuses on the RSL position measured in three caves since 2008. Codes in the legend represent the identifiers of each U-series dated POS as listed in table S1. Vertical uncertainties on the POS data are omitted from the figure but are shown on fig. S18A.
Sample DR-D7b exhibits some minor growth during the period of sea-level rise, but the main overgrowth of this POS formed at the preindustrial level between 2.78 ± 0.19 and 0.50 ± 0.02 ka (fig. S5). Similar conducive conditions for carbonate deposition at sea level (i.e., preexisting vadose speleothems and/or appropriate geochemical conditions) must have existed in other caves on the island (within 50 km of each other; fig. S1) since 73 of the U-series ages of samples from seven caves contribute further evidence of near-modern sea level since 2.84 ka (Fig. 2 and table S1). Because of the POS shape and highly resolved growth rate, we report RSL estimates for each sample data point in the past 2840 years with 0.07-m uncertainty (σRSL-POS; fig. S6).
A Bayesian statistical change-point model (19) applied to our POS data (the Supplementary Materials) estimates a sea-level rise of ~0.20 m (95% credible interval between 0.12 and 0.31 m) from ~3.26 to 2.84 ka B.P. with a mean rate of RSL change of ~0.54 mm year−1 (95% confidence interval between 0.30 and 0.91 mm year−1). Our results show that, after that rise, RSL stayed within 0.08 m (95% confidence interval) of preindustrial levels from 2.84 ka B.P. to 1900 CE (Fig. 2 and tables S2 and S3). Except for the sea-level rise event between 3.26 and 2.84 ka, the aggregated results show only a few short gaps of up to 150 years between sample ages from the past 4000 years. The 0.35-m length of individual POS and their near-continuous growth preclude the possibility of sea level oscillations larger than 0.35 m on centennial time scales (the Supplementary Materials and figs. S5, S7, and S8).
Our POS-derived constraint on RSL over the past 2500 years (RSLPOS) is largely consistent with the submillennial-scale variability in two independent estimates (1, 8) of GMSL (Fig. 2). Although local RSL at Mallorca cannot be directly equated to GMSL, we repeated the probabilistic analysis in (8) and compared the GMSL curve with the local solution at Mallorca estimated in that analysis and found that their amplitude and temporal variability were broadly qualitatively consistent. As we noted earlier, the disagreement in the two GMSL curves before ~2.5 ka in Fig. 2 reflects the relatively weak observational constraints over this period adopted in these analyses, and neither analysis was able to rule out a long-term trend in the estimates. In addition, a recent compilation of Holocene RSL records from the western Mediterranean includes a small number of data from Mallorca (20), which indicate that local sea level remained within ±1 m (2σ) of the present day. The RSLPOS curve falls within the 2σ uncertainty of these and other records to the north along the Balearic Sea and Gulf of Lion mainland coasts (20).
GIA modeling
Mallorca sits in a geologically stable region, away from any of the major tectonic boundaries that exist in the Mediterranean basin. The absence of significant earthquake activity (i.e., M > 3.5) in historical times (21) and minimal vertical motions since the Upper Miocene (the Supplementary Materials) (15, 22, 23), suggest that Mallorca represents one of the most tectonically stable regions in the western Mediterranean Sea. Therefore, we assume that tectonics has had a negligible influence on the Late Holocene RSL evolution, and no correction for vertical displacements is applied to our sea level index points.
We conclude that the relatively rapid ~0.20-m increase in RSL between 3.26 and 2.89 ka resolved by the POS record reflects net melting from ice sheets and glaciers over this period. What were possible sources for this event? Sourcing the event entirely from glacier mass flux is unlikely, given that ~0.20 m of sea-level rise is comparable to the total present-day volume of glaciers outside Antarctica and Greenland (24). We also discount the Greenland Ice Sheet (GrIS) as the significant source, given that sedimentary evidence (25, 26) indicate that the perimeter of the ice sheet has remained close to the present-day extent over the past 4000 years. The potential for relatively rapid instability of ice within the many marine-terminating basins in Antarctica suggests that the associated ice sheet was the most likely source of the 0.20-m sea-level rise in Mallorca. This suggestion is supported by evidence from cosmogenic exposure ages (27, 28) of thinning of some sectors of the West Antarctic Ice Sheet (WAIS) that persisted until at least ~2.5 ka (28, 29) and large-scale ice sheet reconstructions that are characterized by continuing ice mass loss from Antarctica after 4 ka (28, 29).
The question arises: Is there a plausible model of the GIA process since the Last Glacial Maximum that is consistent with the POS-derived RSL history at Mallorca? Across the Late Holocene, departures from GMSL at Mallorca would largely be controlled by two GIA-related processes. (i) Continental levering: Meltwater loading of the Mediterranean that acts to tilt the crust down, and thus raise sea level, offshore of the Spanish coastline, including at Mallorca; and (ii) ocean syphoning: a migration of water away from far field sites, including Mallorca, toward offshore zones at the periphery of former ice cover that are undergoing subsidence, yielding a sea-level fall at such sites (11). In GIA modeling, the net effect of these processes depends on the adopted ice history, mantle viscosity structure, and lithosphere thickness. Previous studies assumed negligible GMSL change across the Late Holocene and predicted a monotonic sea-level rise (and thus a dominance of continental levering effects) near Mallorca of magnitude of ~0.5 to 1.0 m ka−1 (30–32). If these predictions are accurate, then the flat, POS-derived RSL curve (Fig. 2) would require significant growth in ground ice cover across the Late Holocene, which is not supported by existing evidence (16, 17).
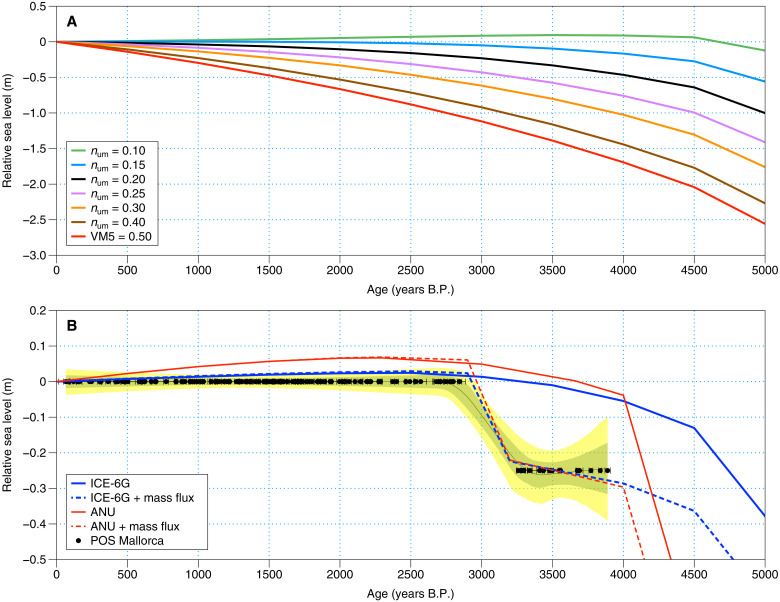
To explore this apparent inconsistency, we have generated a large suite of GIA predictions based on a gravitationally self-consistent sea level theory (Materials and Methods) and a wide range of Earth models in which we varied the lithospheric thickness (LT) and upper (num) and lower (nlm) mantle viscosity. To begin, we adopt the ICE-6G deglaciation history (33). This history is coupled to the VM5 Earth model defined by a LT of 90 km, num = 5 × 1020 Pa s, and nlm that varies with depth from 2 to 3 × 1021 Pa s. A prediction of RSL change at Mallorca based on this GIA model is characterized by a net sea-level rise of ~2 m since 4 ka (Fig. 3A, solid red line), consistent with earlier calculations cited above. Tomographic imaging of mantle seismic structure below Mallorca indicates an extensive region of low shear wave velocities within the upper mantle (34, 35). Under the assumption that these anomalies have a thermal origin, they imply a zone of viscosity beneath the lithosphere that is significantly lower than the VM5 value (fig. S10). To test the implications of this structure, we have repeated the ICE-6G/VM5 calculation with the exception that we adopt a suite of progressively weaker num in the range of 1 to 5 × 1020 Pa s (Fig. 3A).
Fig. 3. Comparison between RSL observations (POS) and predictions from GIA models in Mallorca over the past 5000 years.
(A) Predictions based on the ICE-6G history and the VM5 viscosity model (red line) as well as a series of additional Earth models in which the num of VM5 is progressively reduced from 0.4 × 1021 to 0.1 × 1021 Pa s (num, as labeled, in units of 1021 Pa s). UM, upper mantle. (B) Prediction (solid blue) based on the ICE-6G ice history and the VM5 Earth model with the exception that the num of that model is reduced to 1.3 × 1020 Pa s. The dashed blue line is identical to the solid but augmented to include a linear melt event from WAIS between 3.26 and 2.84 ka equivalent to 0.22-m GMSL, which would be necessary for a ~0.25-m RSL change in Mallorca. To achieve the same sea-level rise at Mallorca from GrIS melt would require a mass flux equivalent to ~0.5 m of the GMSL rise, which is unlikely, given the arguments cited above favoring WAIS as the source. The red lines are analogous to the blue, except that the Australian National University (ANU) ice history is adopted (with the component of melt in that model over the past 4 ka removed) and the adopted Earth model has LT = 60 km, num = 1.5 × 1020 Pa s, and nlm = 2 × 1021 Pa s. Solid black circles (with age uncertainties) represent POS elevations transferred from Fig. 2, the green and yellow shaded envelopes representing 67 and 95% credible intervals, respectively, determined from the Bayesian change point model.
These predictions indicate that a model with num values between 1020 and 1.5 × 1020 Pa s will yield a relatively flat RSL curve since 4 ka. A prediction for the specific case of 1.3 × 1020 Pa s is shown in Fig. 3B (solid blue line). For this case, we also show a second prediction in which the ice history is augmented by rapid mass flux from WAIS between 3.26 and 2.84 ka equivalent to 0.22 m of the GMSL rise (Fig. 3B, dashed blue line). This latter prediction provides an excellent fit to the full POS-derived RSL history over the past 4 ka, including both segments of RSL still stands and the intervening RSL increase of ~0.20 m (the Supplementary Materials).
To test whether our fit to the POS-derived RSL record is sensitive to the adopted ice history, we also considered the global ice history extending over the last glacial cycle described in (29) [henceforth the “ANU” (Australian National University) ice history], which is based on a systematic set of regional GIA studies of RSL records. In contrast to ICE-6G, where no such melting occurs, the ANU reconstruction of ice history permits Antarctic ice mass flux of up to 1 m (GMSL equivalent) from 4 ka to the end of the 19th century. The analysis in (29) derived two classes of preferred Earth model defined by values for LT, num, and nlm. Both favor LT values of 40 to 70 km and upper mantle viscosities of 1 × 1020 to 2 × 1020 Pa s. The two classes differ in their preferred values of lower mantle viscosities, with one group in the range of 7 × 1020 to 4 × 1021 Pa s and the second in the range of 1 × 1022 to 2 × 1023 Pa s. We have adopted Earth models that encompassed an even broader range than these parameters, specifically: LT = 35 to 100 km, num = 1020 to 1021 Pa s, and nlm = 7 × 1020 to 5 × 1022 Pa s. We found no single model capable of fitting the POS-derived RSL curve when we included the 4 ka to recent melting of the ANU ice history. When this mass flux was excluded, however, satisfactory fits were obtained and the prediction that best fit the POS-derived RSL data over the past 2840 years was characterized by values of LT = 60 km, num = 1.5 × 1020 Pa s, and nlm = 2 × 1021 Pa s (Fig. 3B, solid red line). The first two of these values fall in the middle of the preferred ranges cited in (29) for LT and num, while the third is at the center of one of the two classes of preferred lower mantle models. The prediction based on this model, as well as a case in which the model is once again augmented by WAIS melting between 3.26 and 2.84 ka equivalent to 0.22 m of GMSL rise, is shown in Fig. 3B (red lines).
The two Earth models in Fig. 3B that fit the observations are consistent and suggest an num of ~1020 Pa s. These models bring the magnitude of the continental levering-induced sea-level rise at Mallorca into close accord with the ocean syphoning–related sea-level fall; the net effect is an RSL prediction that remains flat over the past 4 ka and within the bound imposed by the POS data when an additional, short-lived melt event at ~3 ka is added to the ice history. These results demonstrate that the POS-derived RSL record does not require continuous ice sheet growth over the Late Holocene. We note that one of our GIA simulations (green curve in Fig. 3A) predict a minor sea level fall over the past 4000 years, and if this was correct, then it would admit the possibility of a low-amplitude, long-term GMSL melt signal across the Late Holocene that nearly precisely cancels out the ongoing GIA effects. In any case, our constraints suggest a net GMSL rise since 4 ka that is intermediate to the ICE-6G history, which is characterized by no GMSL change during this period, and the ANU model, which involves a GMSL rise of 1 m across the same time window.
The negligible contribution of ongoing GIA to RSL at Mallorca across the Late Holocene implies its absence in the 21st century sea-level change. Monitoring of RSL from three caves in Mallorca since 2008 yields an average rise of 2.05 ± 0.58 mm year−1 (Materials and Methods). Models of sea-level change due to recent ice mass loss from the Greenland and Antarctic ice sheets and a global database of glaciers and ice caps predict an average sea-level rise of 1.43 mm year−1 at Mallorca in the period 2002–2019 (Materials and Methods and fig. S11). Any small discrepancy between these two values would likely be due to the contribution of ocean dynamic and steric effects to modern sea-level change (36, 37).
We have inferred a long period of stable RSL across the Late Holocene from the statistical analysis of POS records in Mallorca, except for a relatively rapid increase of ~0.20 m between 3.26 and 2.84 ka (the Supplementary Materials). This inference has important implications for the climate system. For example, the flat RSL history since 2.84 ka coincides with a period of substantial climatic variability, including, for example, the Medieval Warm Period and the Little Ice Age.
The sixth assessment report of the Intergovernmental Panel on Climate Change (IPCC) estimates an average GMSL rise from 1993 to 2018 of 3.25 mm year−1 (95% confidence interval between 2.88 and 3.61) (38). We have estimated an average rate of RSL change at Mallorca of 0.54 mm year−1 (95% confidence interval between 0.30 and 0.91 mm year−1) over the time period from ~3.26 to ~2.84 ka. If the Antarctic Ice Sheet was the source for this sea-level rise, then the average rate of GMSL change over the ~400-year interval would be ~10% less than the Mallorca rise (i.e., 95% confidence interval between 0.27 and 0.83 mm year−1); the inferred GMSL rate would double if the GrIS was the source. In either case, the probability that the rate of GMSL change estimated by the IPCC over the 1993–2018 period is greater than the GMSL rate that would result from the estimated RSL change from our POS record is >0.999, and we conclude that modern global sea-level rise is highly anomalous relative to any natural variability in ice volumes over the past 4000 years.
MATERIALS AND METHODS
Data treatment and statistics
We use a Bayesian hierarchical framework to partition uncertainties among model levels. These uncertainties are estimated through a universal approach (briefly described) and include age and RSL uncertainty inherent in measurement and inference [e.g., (39, 40)]. Geological sea level proxies are derived from sediments, fossils, and geomorphological and archaeological features, the formation of which was controlled by the past position of RSL (18). These sea level proxies have a systematic and quantifiable relationship to elevation with respect to a tidal datum (e.g., MSL). The relationship of a proxy to sea level, known as the proxy’s indicative meaning, is defined by (i) an RWL, which approximates the central tendency (e.g., mean or median) of the proxy with respect to a tidal datum, and (ii) an IR, which describes the vertical distribution of the proxy in relation to its RWL. For POS, the RWL is MSL and therefore corresponds to 0 elevation difference, and the IR is assumed to follow a normal distribution based on the length of the POS. The total uncertainty for each sample is a combination of the IR and measurement uncertainties, which are related to depth (see the Supplementary Materials).
Dated sea level proxies approximate the past position of RSL as RSL = E – RWL, where E is the true (latent) elevation of the proxy record (40). Each sample has unique uncertainty estimates based on measurement error in E, the inferential uncertainty (from IR) and age uncertainty from measurement, and inferential uncertainties associated with the method used to date the sample (e.g., laboratory and calibration uncertainties for radiometrically dated samples). When reconstructing RSL, the IR and elevation uncertainties are assumed to be uncorrelated.
Bayesian change-point analysis was performed in R using Just Another Gibbs Sampler (JAGS) following (19), where we assume that the POS data can be modeled as a piecewise linear continuous function with two change points. The model estimates probabilistic distributions of parameters (including the timing of change points and the rates of change of each linear section), RSL, and rates of RSL change through Markov chain Monte Carlo methods, accounting for uncertainties in the level and age of each sample (tables S2 and S3). More details on model specification, parameter estimates, and statistical results can be found in the Supplementary Materials.
U-series analytical methods
Subsample powders analyzed in the Radiogenic Isotope Laboratory at University of New Mexico were collected by milling of those samples that could easily be drilled, and subsample pieces were extracted from samples too porous to mill. Powder amounts ranged from 10 to 200 mg. Powders and pieces were completely dissolved in 15 N HNO3 in Teflon beakers and spiked with a mixed solution of 229Th, 233U, and 236U tracer. One to two drops of HClO4 were added, and the sample-spike mixture were fluxed for about 2 hours and dried down to assure complete mixing and removal of organic matter in the samples. After cooling, the subsample crust was dissolved in 7 N HNO3 for anion resin (Eichrom 1x8, 200 to 400 mesh, chloride form) columns chemistry. Subsamples were clean in the columns using 7 HNO3 to remove the matrix. The Th fraction was eluted with 6 N HCl and the U using H2O.
U and Th were analyzed separately using a Thermo Scientific Neptune plus multicollector inductively coupled plasma mass spectrometer (ICP-MS) in static mode, because our instrument has enough detectors for all the peaks. The U and Th solutions were introduced using an Aridus II desolvating nebulizer, which enhances signal intensity by about a factor of 4. All isotopes, except 230Th and 234U, were measured on Faraday cups with 1010-, 1011-, and 1012-ohm resistors, depending on signal intensity. 230Th and 234U were measured on the secondary electron multiplier, with a retardation potential that provides low abundance sensitivity (~5 × 10−7). Gain calibration between the Faraday cups and scanning electron microscope was done using the U standard CRM-112 and an in-house 230Th-229Th standard. Dates were calculated using the decay constants in (41).
For the analysis performed at the University of Bern (Switzerland), 0.1 to 0.2 g of sample chip were spiked with a mixed 229Th-236U spike and dissolved in concentrated HNO3 and taken to dryness. Organic material, if present, was attacked with 0.5 ml of H2O2 + HNO3 (concentrated). U and Th were separated on a custom-built polytetrafluoroethylene column using 0.2 ml of UTEVA resin. After evaporation, the fractions were again treated with a cold O2 plasma in a Bio-Rad PT 7100 radio frequency plasma barrel etcher to remove organic remnants from the resin (42).
U and Th mass spectrometry was done on an Nu Instruments multicollector ICP-MS equipped with a wide aperture retardation potential, capable of an abundance sensitivity <0.1 parts per million (ppm). Samples were introduced using an Elemental Scientific, Inc. Apex desolvating system without membrane.
U measurements were done from 0.5 N HNO3 solutions in static mode, whereby masses 236 and 234 were measured in parallel electron multipliers and masses 235 and 238 in Faraday cups. Baselines were taken on either side of peaks and interpolated. The electron multiplier yield was calibrated every four samples by running a NIST U050 solution and found to drift by less than 0.2% per day. The 238U/235U ratio was used for instrumental fractionation correction if the 238U signal was greater than 10−11 A; if smaller, then the fractionation factor was input from bracketing standards. Normal washout time for U between samples was 5 min with 0.5 N HNO3 [< 1 per mil (‰) memory]; longer washout times were used where significant isotope differences between samples were expected. Runs on the NBL-112 standard yielded δ234U = −38.5‰, where the equilibrium ratio is after (41, 43). Th measurements were made from 3 N HCl solutions in a two-cycle multicollector dynamic mode, whereby one electron multiplier fitted with WARP alternatingly measured masses 229 and 230. U standard was added to Th run solutions for two reasons: first, to enable correction for instrumental mass fractionation, and second, to provide a reference isotope (238) to eliminate the effects of plasma flicker in obtaining the 229Th/230Th ratios. Variations of U and Th signals during the run are fully correlated if no organic matter is present. Baselines were measured at masses 229.5 and 230.5 for samples and standards with significant (>10−12A) 232Th. For stalagmites, the baseline was quite flat and measured at mass 230.5. Washout time was 15 min to 1‰ of the Th signal, if the capillary and nebulizer were free of organics. Ages calculations used the decay constants in (41).
U-Th dates were corrected for 230Th that is associated with detrital 232Th using an initial 230Th/232Th activity ratio value. To correct our dates, both laboratories used high values (8.2 ± 4.1 activity ratio or 44 ± 22 ppm atomic ratio) that were previously measured for POS in Mallorca (14) for samples having measured 230Th/232Th activity ratios of >40 and the crustal value (0.82 ± 0.41 activity ratio or 4.4 ± 2.2 ppm atomic ratio) for samples having measured 230Th/232Th activity ratios of <40. The one exception was sample POS GE-D08, a dirty sample that has a measured initial 230Th/232Th activity ratio of 1.48 ± 0.74 or 8.0 ± 4.0 ppm. The lower initial values are only used as supportive results, and those values were not used for estimating the sea level curve in Fig. 2. For the curve, we rejected all age results having uncertainties larger than 250 years.
GIA modeling
Our predictions of RSL change are global in extent and are based on a gravitationally self-consistent sea level theory that accounts for migrating shorelines due to local rise or fall of sea level, the changing perimeter of grounded, marine-based ice sheets, and the impact on sea level of perturbations in Earth’s rotation (44, 45). The calculations adopt the pseudo-spectral sea level algorithm of (44) with a truncation at degree and order 256. As described here, we adopt two ice histories. The first, the ANU model (5), initiates at the end of the Last Interglacial (120 ka), while the second, ICE-6G (7), starts at the Last Glacial Maximum (25 ka). The Earth models considered in the calculations assume one-dimensional, i.e., depth varying structure. The density and elastic profile through the model are prescribed from the seismic Preliminary Reference Earth Model (46). In addition, the viscosity profile is discretized into three layers: the shallowest, the lithosphere, a region of effectively infinite viscosity (i.e., the region acts as an elastic plate), and two isoviscous layers, one extending from the base of the lithosphere to the base of the upper mantle at a depth of 670 km, and the other covering the entire lower mantle. The thickness of the elastic lithosphere and the num and nlm serve as free parameters in the modeling (see GIA modeling section).
Modern sea-level elevation measurements
The modern RSL positions reported in Fig. 2 (inset) were measured irregularly over the past 11 years in two caves. The 2008 and 2010 elevations (the mean of two readings for each year) were referenced to the RWL defined by several spindle POS surrounding PV 1681 that grew from 1801 ± 13 to 313 ± 4 years B.P. at preindustrial sea level in Cova des Pas de Vallgornera (fig. S13). The remaining measurements were made in Cova de Cala Varques A against a well-defined preindustrial POS horizon (fig. S14). Because there are several types of processes with atmospheric and astronomical forcing (e.g., barometric pressure, waves, tides, steric changes, etc.) that result in sea level variability on time scales of hours to several days or years, the in situ cave readings were first corrected for tide and barometric pressure. These values yielded a mean annual sea-level rise of 2.05 ± 0.58 mm year−1 (2σ) for the past 11 years. The Permanent Service for Mean Sea Level reports a long term (1997–2018) rate of 2.18 ± 2.39 mm year−1 for the Palma de Mallorca tide gauge record; the uncertainty would be higher for the rate based on data after 2008 (https://sealevel.info/MSL_graph.php?id=225-011) (47).
Ocean steric and dynamic effects are not captured in our numerically predicted sea-level change of 1.43 mm year−1 for 2008–2019 associated with ice sheet and glacier mass flux (see the “Predicted sea-level change in Mallorca (2002–2019)” section below). To better compare this prediction to the observed value, we can subtract from the latter the sea level increase due to steric effects that was estimated to be 0.47 ± 0.04 mm (48). The new mean annual value (1.58 ± 0.58 mm year−1) is consistent with the predicted ice melt contribution. These values are well below the recently estimated GMSL trend of 3.7 ± 0.3 mm year−1 since 2000 CE (38). The discrepancy between the Mallorca-based sea-level rise and the assessed global trend is not unexpected, given the significant geographic variability that characterizes processes contributing to modern sea-level change.
Predicted sea-level change in Mallorca (2002–2019)
The total sea level prediction, produced by ice mass loss from the Antarctic and Greenland ice sheets and a global database of glaciers and ice caps in the period 2002–2019, yields an average sea-level rise of 1.43 mm year−1 since 2008 (black line in fig. S11). Predictions are based on the same sea level theory used to compute the results in Fig. 3 (described above), with the exception that the Earth model is elastic and a truncation at spherical harmonic degree and order 512 is adopted. Yearly average ice mass changes for the Greenland and Antarctic ice sheets are calculated from Gravity Recovery and Climate Experiment (GRACE) and GRACE-Follow-On–derived mass balance time series given in (49) and are projected across the corresponding drainage basins (50, 51). Tests using a higher spatial resolution–calibrated radar altimetry mass balance dataset for Greenland (52) yielded similar sea level curves to the low–spatial resolution GRACE data shown in fig. S11. Yearly average ice mass changes for a global inventory of glaciers and ice caps are calculated from GRACE and GRACE-Follow-On–derived mass balance data given in (53). We pair these yearly ice mass balances with static glacier outlines from the Randolph Glacier Inventory (54) to establish a complete history of glacier and ice cap evolution.
Acknowledgments
We thank the administration of Coves del Drac and Conselleria de Medi Ambient i Territori (Govern de les Illes Balears) for granting permission to sample the caves and F. Gràcia, J.C. Lázaro, M.À. Perelló, and A. Cirer for providing underwater samples and photographs.
Funding: B.P.O. and V.J.P. were funded by a collaborative NSF grant (AGS 1602670 and 1602685). Additional research costs were covered by an NSF grant (EAR 0326902 to Y.A. and V.J.P.) and Agencia Estatal de Investigación grants (CGL2016-79246-P AEI-FEDER, EU and PID2020-11272GB-100/AEI10.13039/501100011033 to J.J.F.). J.X.M. acknowledges funding from the Star-Friedman Challenge and the John D. and Catherine T. MacArthur Foundation. E.L.A. is supported by NSF grant OCE-2002437. This work is a contribution to IGCP Project 639, INQUA Project CMP1601P “HOLSEA,” and PALSEA3. M.J.H. acknowledges support from the Exploring for the Future research program.
Author contributions: B.P.O., J.G., J.J.F., A.G., and V.J.P. designed the research. B.P.O., J.G., A.G., and J.J.F. measured the POS elevations and collected the samples. U-series ages of POS samples were measured at the University of New Mexico (V.J.P. and Y.A.) and Bern University (P.T., M.S., and I.M.V.). J.X.M. produced the GIA models. E.L.A. developed the statistical model described in Materials and Methods and in the Supplementary Materials. M.J.H. investigated Earth models beneath Mallorca. S.C. computed predictions of sea-level change in Mallorca over the past two decades. B.P.O., J.X.M., Y.A., and V.J.P. drafted and wrote most of the manuscript with input from all authors.
Competing interests: The authors declare that they have no competing interests.
Data and materials availability: All data generated or analyzed during this study are included in this published article and its Supplementary Materials. Full statistical analysis code and results are available at https://doi.org/10.5281/zenodo.6047270.
Supplementary Materials
This PDF file includes:
Supplementary Text
Figs. S1 to S18
Tables S1 to S3
References
REFERENCES AND NOTES
- 1.Kopp R. E., Kemp A. C., Bittermann K., Horton B. P., Donnelly J. P., Gehrels W. R., Hay C. C., Mitrovica J. X., Morrow E. D., Rahmstorf S., Temperature-driven global sea-level variability in the Common Era. Proc. Natl. Acad. Sci. U.S.A. 113, E1434–E1441 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Dutton A., Carlson A. E., Long A. J., Milne G. A., Clark P. U., DeConto R., Horton B. P., Rahmstorf S., Raymo M. E., Sea-level rise due to polar ice-sheet mass loss during past warm periods. Science 349, aaa4019 (2015). [DOI] [PubMed] [Google Scholar]
- 3.Horton B. P., Kopp R. E., Garner A. J., Hay C. C., Khan N. S., Roy K., Shaw T. A., Mapping sea-level change in time, space, and probability. Annu. Rev. Env. Resour. 43, 481–521 (2018). [Google Scholar]
- 4.Walker J. S., Kopp R. E., Little C. M., Horton B. P., Timing of emergence of modern rates of sea-level rise by 1863. Nat. Commun. 13, 966 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Kemp A. C., Wright A. J., Edwards R. J., Barnett R. L., Brain M. J., Kopp R. E., Cahill N., Horton B. P., Charman D. J., Hawkes A. D., Hill T. D., van de Plassche O., Relative sea-level change in Newfoundland, Canada during the past ∼3000 years. Quat. Sci. Rev. 201, 89–110 (2018). [Google Scholar]
- 6.Hay C. C., Morrow E., Kopp R. E., Mitrovica J. X., Probabilistic reanalysis of twentieth-century sea-level rise. Nature 517, 481–484 (2015). [DOI] [PubMed] [Google Scholar]
- 7.Frederikse T., Landerer F., Caron L., Adhikari S., Parkes D., Humphrey V. W., Dangendorf S., Hogarth P., Zanna L., Cheng L., Wu Y.-H., The causes of sea-level rise since 1900. Nature 584, 393–397 (2020). [DOI] [PubMed] [Google Scholar]
- 8.Walker J. S., Kopp R. E., Shaw T. A., Cahill N., Khan N. S., Barber D. C., Ashe E. L., Brain M. J., Clear J. L., Corbett D. R., Horton B. P., Common Era sea-level budgets along the U.S. Atlantic coast. Nat. Commun. 12, 1841 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Austermann J., Mitrovica J. X., Latychev K., Milne G. A., Barbados-based estimate of ice volume at Last Glacial Maximum affected by subducted plate. Nat. Geosci. 6, 553–557 (2013). [Google Scholar]
- 10.Rovere A., Stocchi P., Vacchi M., Eustatic and relative sea level changes. Curr. Clim. Change Rep. 2, 221–231 (2016). [Google Scholar]
- 11.Mitrovica J. X., Milne G. A., On the origin of late Holocene sea-level highstands within equatorial ocean basins. Quat. Sci. Rev. 21, 2179–2190 (2002). [Google Scholar]
- 12.A. Ginés, J. Ginés, L. Pomar, Phreatic speleothems in coastal caves of Majorca (Spain) as indicators of Mediterranean Pleistocene paleolevels, paper presented at the Proceedings of the 8th International Congress of Speleology, July 18 to 24, 1981, Bowling Green, KY (1981).
- 13.Dorale J. A., Onac B. P., Fornós J. J., Ginés J., Ginés A., Tuccimei P., Peate D. W., Sea-level highstand 81,000 years ago in Mallorca. Science 327, 860–863 (2010). [DOI] [PubMed] [Google Scholar]
- 14.Polyak V. J., Onac B. P., Fornós J. J., Hay C., Asmerom Y., Dorale J. A., Ginés J., Tuccimei P., Ginés A., A highly resolved record of relative sea level in the western Mediterranean Sea during the last interglacial period. Nat. Geosci. 11, 860–864 (2018). [Google Scholar]
- 15.Dumitru O. A., Austermann J., Polyak V. J., Fornos J. J., Asmerom Y., Gines J., Gines A., Onac B. P., Constraints on global mean sea level during Pliocene warmth. Nature 574, 233–236 (2019). [DOI] [PubMed] [Google Scholar]
- 16.Kemp A. C., Horton B. P., Donnelly J. P., Mann M. E., Vermeer M., Rahmstorf S., Climate related sea-level variations over the past two millennia. Proc. Natl. Acad. Sci. U.S.A. 108, 11017–11022 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.A. J. Meltzner, C. D. Woodroffe, Coral microatolls, in Handbook of Sea-Level Research, I. Shennan, A. J. Long, B. P. Horton, Eds. (Wiley, 2015), pp. 125–145. [Google Scholar]
- 18.I. Shennan, Handbook of sea-level research: Framing research questions, in Handbook of Sea-Level Research, I. Shennan, A. J. Long, B. P. Horton, Eds. (Wiley, 2015), pp. 3–25. [Google Scholar]
- 19.Cahill N., Rahmstorf S., Parnell A. C., Change points of global temperature. Environ. Res. Lett. 10, 084002 (2015). [Google Scholar]
- 20.Vacchi M., Ghilardi M., Melis R. T., Spada G., Giaime M., Marriner N., Lorscheid T., Morhange C., Burjachs F., Rovere A., New relative sea-level insights into the isostatic history of the Western Mediterranean. Quat. Sci. Rev. 201, 396–408 (2018). [Google Scholar]
- 21.Sánchez-Alzola A., Sánchez C., Giménez J., Alfaro P., Gelabert B., Borque M. J., Gil A. J., Crustal velocity and strain rate fields in the Balearic Islands based on continuous GPS time series from the XGAIB network (2010–2013). J. Geodyn. 82, 78–86 (2014). [Google Scholar]
- 22.Just J., Hübscher C., Betzler C., Lüdmann T., Reicherter K., Erosion of continental margins in the Western Mediterranean due to sea-level stagnancy during the Messinian salinity crisis. Geo-Mar. Lett. 31, 51–64 (2011). [Google Scholar]
- 23.Stocchi P., Vacchi M., Lorscheid T., de Boer B., Simms A. R., van de Wal R. S. W., Vermeersen B. L. A., Pappalardo M., Rovere A., MIS 5e relative sea-level changes in the Mediterranean Sea: Contribution of isostatic disequilibrium. Quat. Sci. Rev. 185, 122–134 (2018). [Google Scholar]
- 24.Farinotti D., Huss M., Fürst J. J., Landmann J., Machguth H., Maussion F., Pandit A., A consensus estimate for the ice thickness distribution of all glaciers on Earth. Nat. Geosci. 12, 168–173 (2019). [Google Scholar]
- 25.Carlson A. E., Winsor K., Ullman D. J., Brook E. J., Rood D. H., Axford Y., LeGrande A. N., Anslow F. S., Sinclair G., Earliest Holocene south Greenland ice sheet retreat within its late Holocene extent. Geophys. Res. Lett. 41, 5514–5521 (2014). [Google Scholar]
- 26.Lesnek A. J., Briner J. P., Young N. E., Cuzzone J. K., Maximum Southwest Greenland Ice Sheet recession in the Early Holocene. Geophys. Res. Lett. 47, e2019GL083164 (2020). [Google Scholar]
- 27.Hein A. S., Marrero S. M., Woodward J., Dunning S. A., Winter K., Westoby M. J., Freeman S. P. H. T., Shanks R. P., Sugden D. E., Mid-Holocene pulse of thinning in the Weddell Sea sector of the West Antarctic ice sheet. Nat. Commun. 7, 12511 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Stone J. O., Balco G. A., Sugden D. E., Caffee M. W., Sass L. C., Cowdery S. G., Siddoway C., Holocene deglaciation of Marie Byrd Land, West Antarctica. Science 299, 99–102 (2003). [DOI] [PubMed] [Google Scholar]
- 29.Lambeck K., Rouby H., Purcell A., Sun Y., Sambridge M., Sea level and global ice volumes from the Last Glacial Maximum to the Holocene. Proc. Natl. Acad. Sci. U.S.A. 111, 15296–15303 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Lambeck K., Purcell A. P., Sea-level change in the Mediterranean Sea since the LGM: Model predictions for tectonically stable areas. Quat. Sci. Rev. 24, 1969–1988 (2005). [Google Scholar]
- 31.Roy K., Peltier W. R., Relative sea level in the Western Mediterranean basin: A regional test of the ICE-7G_NA (VM7) model and a constraint on Late Holocene Antarctic deglaciation. Quat. Sci. Rev. 183, 76–87 (2018). [Google Scholar]
- 32.Stocchi P., Spada G., Influence of glacial isostatic adjustment upon current sea level variations in the Mediterranean. Tectonophysics 474, 56–68 (2009). [Google Scholar]
- 33.Peltier W. R., Argus D. F., Drummond R., Space geodesy constrains ice age terminal deglaciation: The global ICE-6G_C (VM5a) model. J. Geophys. Res. Solid Earth 120, 450–487 (2015). [Google Scholar]
- 34.Zhu H., Bozdağ E., Tromp J., Seismic structure of the European upper mantle based on adjoint tomography. Geophys. J. Int. 201, 18–52 (2015). [Google Scholar]
- 35.Richards F. D., Hoggard M. J., White N., Ghelichkhan S., Quantifying the relationship between short-wavelength dynamic topography and thermomechanical structure of the upper mantle using calibrated parameterization of anelasticity. J. Geophys. Res. Solid Earth 125, e2019JB019062 (2020). [Google Scholar]
- 36.Giese B. S., Seidel H. F., Compo G. P., Sardeshmukh P. D., An ensemble of ocean reanalyses for 1815–2013 with sparse observational input. J. Geophys. Res. Oceans 121, 6891–6910 (2016). [Google Scholar]
- 37.Dangendorf S., Frederikse T., Chafik L., Klinck J. M., Ezer T., Hamlington B. D., Data-driven reconstruction reveals large-scale ocean circulation control on coastal sea level. Nat. Clim. Chang. 11, 514–520 (2021). [Google Scholar]
- 38.B. Fox-Kemper, H. T. Hewitt, C. Xiao, G. Aðalgeirsdóttir, S. S. Drijfhout, T. L. Edwards, N. R. Golledge, M. Hemer, R. E. Kopp, G. Krinner, A. C. Mix, D. Notz, S. Nowicki, I. S. Nurhati, L. Ruiz, J.-B. Sallée, A. B. A. Slangen, Y. Yu, Ocean, cryosphere and sea level change, in Proceedings of the Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change, V. Masson- Delmotte, P. Zhai, A. Pirani, S. L. Connors, C. Péan, S. Berger, N. Caud, Y. Chen, L. Goldfarb, M. I. Gomis, M. Huang, K. Leitzell, E. Lonnoy, J. B. R. Matthews, T. K. Maycock, T. Waterfield, O. Yelekçi, R. Yu, B. Zhou, Eds. (Cambridge Univ. Press, 2021), chap. 9, pp. 9-1 to 9-257. [Google Scholar]
- 39.O. van de Plassche, in Sea-Level Research. A Manual for the Collection and Evaluation of Data (Springer, 1986), pp. 618. [Google Scholar]
- 40.M. P. Hijma, S. E. Engelhart, T. E. Tornqvist, B. P. Horton, P. Hu, D. F. Hill, A protocol for a geological sea-level database, in Handbook of Sea-Level Research, I. Shennan, A. J. Long, B. P. Horton, Eds. (Wiley, 2015), pp. 536–553. [Google Scholar]
- 41.Cheng H., Edwards R. L., Shen C.-C., Polyak V. J., Asmerom Y., Woodhead J., Hellstrom J., Wang Y., Kong X., Spötl C., Improvements in 230Th dating, 230Th and 234U half-life values, and U-Th isotopic measurements by multi-collector inductively coupled plasma mass spectrometry. Earth Planet. Sci. Lett. 371, 82–91 (2013). [Google Scholar]
- 42.Tuccimei P., Soligo M., Ginés J., Ginés A., Fornós J., Kramers J., Villa I. M., Constraining Holocene sea levels using U-Th ages of phreatic overgrowths on speleothems from coastal caves in Mallorca (Western Mediterranean). Earth Surf. Process. Landf. 35, 782–790 (2010). [Google Scholar]
- 43.Cheng H., Edwards R. L., Hoff R. L., Gallup C. D., Richards D. A., Asmerom Y., The half-lives of uranium-234 and thorium-230. Chem. Geol. 169, 17–33 (2000). [Google Scholar]
- 44.Kendall R., Mitrovica J., Milne G., On post-glacial sea level – II. Numerical formulation and comparative results on spherically symmetric models. Geophys. J. Int. 161, 679–706 (2005). [Google Scholar]
- 45.Mitrovica J. X., Hay C. C., Morrow E., Kopp R. E., Dumberry M., Stanley S., Reconciling past changes in Earth’s rotation with 20th century global sea-level rise: Resolving Munk’s enigma. Sci. Adv. 1, e1500679 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Dziewonski A. M., Anderson D. L., Preliminary reference Earth model. Phys. Earth Planet. Inter. 25, 297–356 (1981). [Google Scholar]
- 47.Holgate S., Matthews J. A., Woodworth P., Rickards L. L., Tamisiea J. M., Bradshaw E. E., Foden P., Gordon R. K., Jevrejeva M. S., Pugh J., New data systems and products at the Permanent Service for Mean Sea Level. J. Coastal Res. 29, 493–504 (2013). [Google Scholar]
- 48.Storto A., Bonaduce A., Feng X., Yang C., Steric sea level changes from ocean reanalyses at global and regional scales. Water 11, 1987 (2019). [Google Scholar]
- 49.Velicogna I., Mohajerani Y., A G., Landerer F., Mouginot J., Noel B., Rignot E., Sutterley T., Broeke M., Wessem M., Wiese D., Continuity of ice sheet mass loss in Greenland and Antarctica from the GRACE and GRACE follow-on missions. Geophys. Res. Lett. 47, e2020GL087291 (2020). [Google Scholar]
- 50.Rignot E., Velicogna I., van den Broeke M. R., Monaghan A., Lenaerts J. T. M., Acceleration of the contribution of the Greenland and Antarctic ice sheets to sea level rise. Geophys. Res. Lett. 38, L05503 (2011). [Google Scholar]
- 51.Rignot E., Mouginot J., Scheuchl B., Antarctic grounding line mapping from differential satellite radar interferometry. Geophys. Res. Lett. 38, L10504 (2011). [Google Scholar]
- 52.Simonsen S. B., Barletta V. R., Colgan W. T., Sørensen L. S., Greenland ice sheet mass balance (1992–2020) from calibrated radar altimetry. Geophys. Res. Lett. 48, e2020GL091216 (2021). [Google Scholar]
- 53.Ciracì E., Velicogna I., Swenson S., Continuity of the mass loss of the world’s glaciers and ice caps from the GRACE and GRACE follow-on missions. Geophys. Res. Lett. 47, e2019GL086926 (2020). [Google Scholar]
- 54.RGI Consortium, “Randolph Glacier Inventory – A Dataset of Global Glacier Outlines, Version 6” (Technical Report, Global Land Ice Measurements from Space, 2017); 10.7265/4m1f-gd79. [DOI]
- 55.Faccenna C., Becker T. W., Auer L., Billi A., Boschi L., Brun J. P., Capitanio F. A., Funiciello F., Horvàth F., Jolivet L., Piromallo C., Royden L., Rossetti F., Serpelloni E., Mantle dynamics in the Mediterranean. Rev. Geophys. 52, 283–332 (2014). [Google Scholar]
- 56.Devoti R., Agostino N., Serpelloni E., Pietrantonio G., Riguzzi F., Avallone A., Cavaliere A., Cheloni D., Cecere G., Ambrosio C., Franco L., Selvaggi G., Metois M., Esposito A., Sepe V., Galvani A., Anzidei M., A combined velocity field of the Mediterranean Region. Ann. Geophys. 60, S0217 (2017). [Google Scholar]
- 57.O.-A. Dumitru, J. Austermann, V. J. Polyak, J. J. Fornós, Y. Asmerom, J. Ginés, A. Ginés, B. P. Onac, “Supplement to: Dumitru, O.-A. et al. (2019): Constraints on global mean sea level during Pliocene warmth (Nature)” (PANGAEA, 2019); 10.1594/PANGAEA.905851. [DOI] [PubMed]
- 58.A. Ginés, J. Ginés, F. Gràcia, Cave development and patterns of caves and cave systems in the Eogenetic coastal karst of southern Mallorca (Balearic Islands, Spain), in Coastal Karst Landforms, M. J. Lace, J. E. Mylroie, Eds. (Springer, 2013), pp. 245–260. [Google Scholar]
- 59.Boop L. M., Onac B. P., Wynn J. G., Fornós J. J., Rodríguez-Homar M., Merino A., Groundwater geochemistry observations in littoral caves of Mallorca (western Mediterranean): Implications for deposition of phreatic overgrowths on speleothems. Int. J. Speleol. 43, 193–203 (2014). [Google Scholar]
- 60.J. Ginés, A. Ginés, J. J. Fornós, P. Tuccimei, B. P. Onac, F. Gràcia, Phreatic overgrowths on speleothems (POS) from Mallorca, Spain: Updating forty years of research, in Mallorca. A Mediterranean benchmark for Quaternary Studies, A. Ginés, Ed. (Monografia de la Societat d’Història Natural de les Balears, Societat d’Història Natural de les Balears, 2012), vol. 18, pp. 111–146. [Google Scholar]
- 61.Parnell A. C., Sweeney J., Doan T. K., Salter-Townshend M., Allen J. R. M., Huntley B., Haslett J., Bayesian inference for palaeoclimate with time uncertainty and stochastic volatility. J. R. Stat. Soc. C Appl. Stat. 64, 115–138 (2015). [Google Scholar]
- 62.Ashe E. L., Khan N. S., Toth L. T., Dutton A., Kopp R. E., A statistical framework for integrating nonparametric proxy distributions into geological reconstructions of relative sea level. Adv. Stat. Climatol. Meteorol. Oceanogr. 8, 1–29 (2022). [Google Scholar]
- 63.L. J. Le Roux, L. E. Glendenin, Half-life of 232Th, in Proc. Natl. Conf. Nucl. Energy (Pretoria, 1963), pp. 83–94. [Google Scholar]
- 64.Jaffey A. H., Flynn K. F., Glendenin L. E., Bentley W. C., Essling A. M., Precision measurement of half-lives and specific activities of 235U and 238U. Phys. Rev. C 4, 1889–1906 (1971). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Text
Figs. S1 to S18
Tables S1 to S3
References