A behavioral paradigm for measuring perceptual distances in mice

Summary

Perceptual similarities between a specific stimulus and other stimuli of the same modality provide valuable information about the structure and geometry of sensory spaces. While typically assessed in human behavioral experiments, perceptual similarities—or distances—are rarely measured in other species. However, understanding the neural computations responsible for sensory representations requires the monitoring and often manipulation of neural activity, which is more readily achieved in non-human experimental models. Here, we develop a behavioral paradigm that enables the quantification of perceptual similarity between sensory stimuli using mouse olfaction as a model system.

Graphical abstract

Highlights

• •Mice can learn to indicate the perceptual distance between any two odor stimuli
• •This behavioral paradigm enables high-throughput quantification of perceptual distances
• •Perceptual relationships between sets of odors are conserved across individuals
• •Mapping perceptual space in an animal model can unlock the neural code for odors

Motivation

Understanding the basic principles of sensory information processing requires good knowledge of structure and geometry of perceptual spaces and the ability to place stimuli on a corresponding map of that space. Measuring perceptual distances between multiple pairs of stimuli in animals allows us to reveal the structure of the perceptual space, allowing future measurement and manipulation of neural activity to reveal the neural mechanisms responsible for shaping this space.

Nakayama et al. develop a behavioral paradigm to determine perceptual distances between odorant stimuli in the mouse. These distances form a metric space linking odorant stimuli to odor perception. This method can be coupled with physiological experiments to crack the neural code for mammalian olfaction.

Introduction

Perceptually similar objects are represented by similar patterns of neuronal activity in the brain (Johnson et al., 2002). Thus, for an ensemble of sensory objects, both their relative perceptual distances and the structure of their perceptual space—its dimensionality and topology—should be reflected in the corresponding space of their neural representations. For example, the perceptual proximities between different spectral colors reveals the circular organization of hue in two-dimensional space (Shepard, 1962, 1980), and the perceptual similarity between different sounds underlies the helical organization of musical tone (Shepard, 1965). Such information about perceptual space is indispensable for the understanding of neural-coding mechanisms underlying sensory perception.

However, it is usually difficult to perform both perceptual and neural measurements in the same model organism. Most attempts to measure perceptual similarities between stimuli have been performed in psychophysical studies with either human or non-human primate subjects (but see Ghirlanda et al., 2003; Guttman and Kalish, 1956). Recent technological progress makes the mouse an attractive model for recording (Buzsaki et al., 1996; Svoboda et al., 1997) and manipulating (Chong et al., 2020; Emiliani et al., 2015; Gill et al., 2020; Packer et al., 2015; Zhang et al., 2007) neural activity at different temporal and spatial scales. However, a lack of behavioral methods for measuring perceptual distances prevents the linking of neural activity with perceptual space in the same species.

Here, we develop a robust and high-throughput method for estimating perceptual distances between multiple pairs of sensory stimuli in mice, using olfaction as a model system. The choice of olfaction is dictated by two main factors. First, olfaction is a highly relevant sensory modality for rodents, which makes it easier to train animals on demanding behavioral paradigms. Second, olfaction is one of the least explored primary sensory systems, and our understanding of the structure of olfactory perceptual space is still limited (Gerkin and Castro, 2015; Gerkin, 2021; Mamlouk and Martinetz, 2004; Meister, 2015; Zhou et al., 2018). Individual odorants (chemical molecules) are characterized by thousands of physicochemical features, and the majority of stimuli experienced by animals in the wild are complex odor mixtures. How multidimensional sensory space is represented in the brain remains unknown.

In human psychophysics, odor perceptual space has been characterized using multiple approaches including semantic descriptors (Dravnieks et al., 1985; Koulakov et al., 2011; Wise et al., 2000), analog ratings of perceptual qualities (Keller et al., 2017; Secundo et al., 2015), and analog ratings of perceptual similarity between odor pairs (Snitz et al., 2013). Among them, only similarity ratings between odors can be obtained in non-human model animals including rodents. In rodent experiments, the cross-habituation paradigm has been used to assess if pairs of odors are perceptually similar or not (Cleland et al., 2002). However, the paradigm is low throughput and requires many animals for each odor pair. Due to this limitation, it is challenging to collect sufficient pairwise similarity measurements to recover the structure of perceptual space. If a sufficient volume of similarity measurements could be collected, standard algorithms for embedding such data in low-dimensional perceptual spaces could be applied to recover the structure of olfactory perception.

Results

To overcome this limitation, we designed a behavioral paradigm that allows us to perform high-throughput measurement of perceptual distances across many odor pairs. We used a delayed match-to-sample (DMTS) behavioral paradigm, where mice are trained to respond differently depending on whether two sequentially presented odors are the same or different. The probability that a trained mouse responds as if two presented odors within a trial are the same (or different) is taken to reflect the pairwise perceptual similarities (or distances) of those two odors.

The DMTS paradigm was originally developed for pigeons and monkeys (Etkin and D'Amato, 1969; Grant, 1975) and has been used to study short-term memory in primates and, more recently, visual perception (Koopman et al., 2017). The olfactory DMTS task was initially established for freely moving rodents (Otto and Eichenbaum, 1992) and was recently used with head-fixed rodents to study short-term memory (Liu et al., 2014; Taxidis et al., 2020; Wu et al., 2020). In those olfactory DMTS experiments, only a small number of stimuli (usually two odors) were used. Introducing new odors required new, time-consuming training, and thus testing many odor pairs—a requirement for mapping perceptual space—would be impractically time consuming (Wu et al., 2020).

In contrast to previous studies, we trained mice to perform the task using a general rule that is independent of the specific identity of the odors, thus preventing mice from forming behavioral strategies that are only applied to specific odors. This allows us to use the task for high-throughput measurement of pairwise odor perceptual distances—similar to that undertaken in human studies. We collected behavioral data for 276 odor pairs and demonstrated that these data yielded consistent estimates of perceptual similarity between odors as well as a metric space for odor perception.

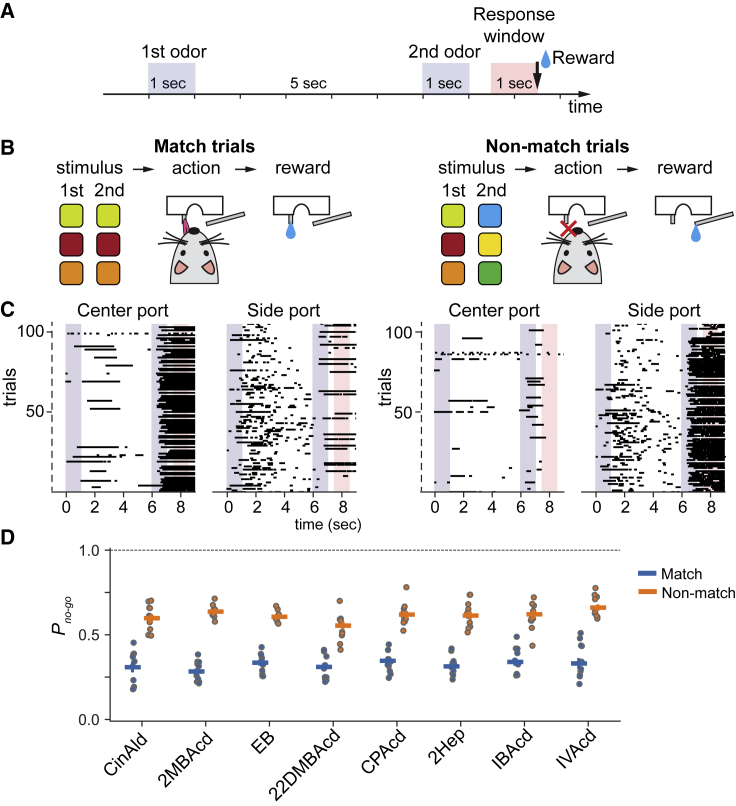
The behavioral paradigm was designed to make animals compare two odors that were presented within the same trial. Head-fixed mice received two sequential odor presentations (1 s duration each, and 5 s inter-stimulus interval) followed by a 1 s response window (Figure 1A and S2). If two odor stimuli were the same (a match trial), mice were rewarded for licking a center water spout during the response time window (go response). If not (a non-match trial), the correct response was to suppress licking (no-go response) (Figure 1B). In non-match trials, mice were rewarded for no-go responses with a drop of water from a side water spout. Although two water spouts were used, licking or not licking the side water spout did not affect the reward contingency.

Figure 1.

Characterization of task performance

(A) The sequence of events in a delayed match-to-sample task trial.

(B) Schematics of two trial types. Left panel: match trials—the correct behavior response is licking a center port (go), followed by a water reward provided from the same port. Right panel: non-match trials—the correct behavior response is not licking the center port (no-go), followed by a reward provided from a side lick port. Licking to the side port during the response window does not affect outcomes.

(C) Lick patterns in example trials for matched (right two columns) and non-matched (left two columns) trials. Lick patterns for individual trials are shown as single rows on both center- and side-port raster plots. Licks are shown as black ticks.

(D) Probability of a no-go choice by odor identity. Trials are assigned to a specific odor identity whether that odor was presented first or second in the trial. Circles correspond to individual mice, and bars are averages across mice (n = 10 mice, 75,195 trials, odor set #1; Table S1).

Odors in each trial were pseudo-randomly chosen from a panel of monomolecular odors and their binary mixtures (Table S1). To discourage mice from comparing two odors based on their intensity, each odor was presented at either a high or low concentration (5-fold difference) randomly selected at each trial.

Trained mice exhibited differential lick responses between match and non-match trials (Figure 1C), with the probability of a no-go response being 0.31 ± 0.02 and 0.65 ± 0.04, respectively (mean ± SD, across all odor identities and all mice) (Figure 1D). (For the effect of odor concentration in match trials, see Figure S2.)

We collected data from 10 mice over 308 sessions (75,195 total trials after excluding the first 5 trials of each session) for a panel of 8 monomolecular odors and 16 binary mixtures (Figure 2A). The probability of an error in non-match trials varied across different odor pairs, and we assumed that the error rate should increase with, and thus be a measure of, odor perceptual similarity. Thus, we propose a distance metric as the probability of correct responses in non-match trials (P_nogo) normalized by the probability of error responses on match trials for identical odors in a way similar to previous work (Shepard, 1987):

$$D\left(A,B\right)=1-\frac{1-P_{nogo}\left(A,B\right)}{\sqrt{\left(1-P_{nogo}\left(A,A\right)\right)\left(1-P_{nogo}\left(B,B\right)\right)}}$$ (Equation 1)

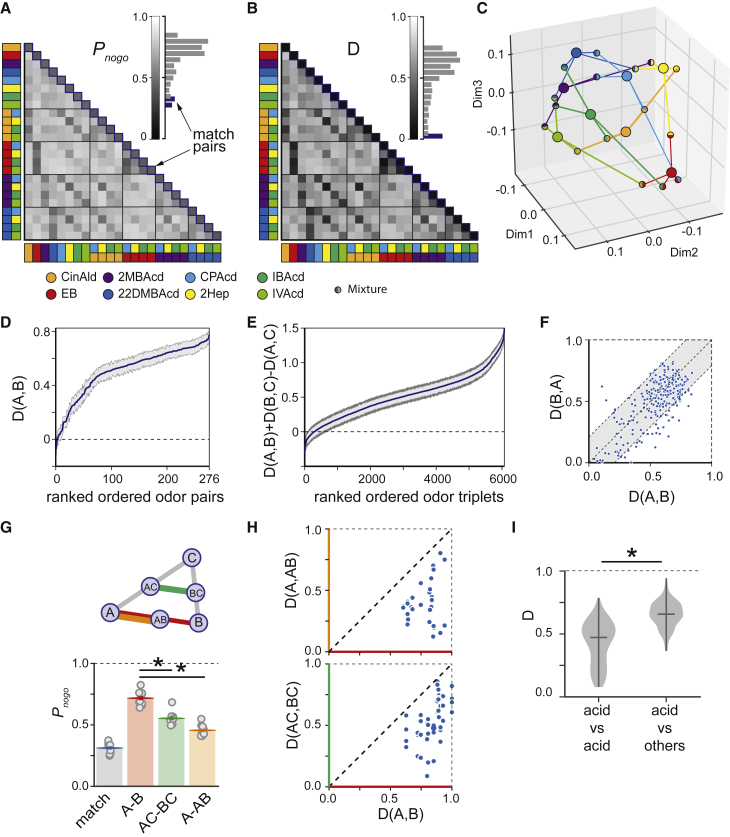
Figure 2.

Validation of the behavioral readout as a measure of a perceptual distance

(A) Matrix and distribution (insert) of probabilities of a no-go choice for each of odor pair.

(B) Perceptual-distance matrix calculated from the matrix in (A).

(C) MDS embedding of odors calculated from the distance matrix in (B).

(D) Non-negativity test: cumulative distribution of estimated perceptual distances for all odor pairs. Gray area is a bootstrap-estimated standard deviation; values >0 are consistent with a metric space.

(E) Triangle inequality test: Cumulative distribution of the expression $D\left(A,B\right)+D\left(B,C\right)-D\left(A,C\right)$ for all odor triplets. Gray area is bootstrap-estimated standard deviation; values >0 are consistent with a metric space.

(F) Symmetry test: raster plot of distances $D\left(A,B\right)$ versus $D\left(B,A\right)$. Gray area reflects the 95% confidence interval for the difference; values inside the gray area are consistent with a metric space.

(G) Top: a schematic illustrating perceptual distances between binary mixtures and their component odors. Bottom: average probabilities of a no-go choice for match trials and three types of non-match trials corresponding to different odor- and binary-mixture trials. (D(A,B)>D(A,AB): p = 0.0039, D(AC,BC)<D(A,B): p = 0.0039, n = 10 mice, Wilcoxon signed-rank test after Bonferroni correction of p values.

(H) Individual odor-pair scatterplots corresponding to the relationship shown in (G), top: D(A, AB) versus D(A, B), bottom: D(AC, BC) versus D(A, B) (n = 10 mice, 75,195 trials).

(I) Distribution of the distances between acids (mean: D_median = 0.47) and between acids and non-acids (mean: D_median = 0.66) (p < 10^-33, Mann-Whitney U-test).

Plots in (B)–(G) are based on raw data presented on a panel: n = 10 mice, 75,195 trials, odor set #1. Plot i is based the same data plus two additional datasets: odor set #2: 6 mice, 24,295 trials, and odor set #3: 12 mice, 58,232 trials (Table S1).

The distance metric is chosen to be equal to zero for identical odors and increases as odors became less similar. The distribution of the distances for all measured odor pairs is presented in Figure 2B. For data-visualization purposes, we applied multidimensional scaling (MDS) (Borg and Groenen, 1997; Kruskal, 1964a, 1964b) to the distance matrix and presented an odor-odor distance graph in the resulting three-dimensional space (Figure 2C).

If the proposed metric is a distance metric in a mathematical sense, it should satisfy several conditions: (1) identity $\left(D\left(A,A\right)=0\right)$, (2) non-negativity $\left(D\left(A,B\right)>0\right)$, (3) triangle inequality $\left(D\left(A,B\right)\le D\left(A,C\right)+D\left(C,B\right)\right)$, and (4) symmetry $\left(D\left(A,B\right)=D\left(B,A\right)\right)$. The identity condition is satisfied by definition (see Equation 1). Using data presented in Figure 2A, we tested both non-negativity for every pair of odors (Figure 2D) and triangle inequality for every triplet of odors (Figure 2E). Both conditions were satisfied for the vast majority of cases. Of the small proportion of cases where distance turned out to be negative (0.7%) and triangle inequality was not satisfied (4.8%), many might be a result of sampling error due to the finite number of trials collected for each odor pair. Confidence intervals constructed using a bootstrap method allowed us to apply a null-hypothesis testing framework to these questions, and indeed, we could only reject the conditions of non-negativity for one odor pair (0.36%) and the triangle inequality for a small fraction (1.7%) of odor triplets.

To test the symmetry condition, we asked how frequently $D\left(A,B\right)$ was significantly different in magnitude from $D\left(B,A\right)$). Under the null hypothesis that they were equal, the observed difference $\Delta =D\left(A,B\right)-D\left(B,A\right)$ should be approximately normally distributed around zero, with variance equal to the twice the variance of the distance. The rejection criterion (for $\alpha =0.05$) was given by the dashed lines in Figure 2F. 17% of odor pairs showed Δ outside this boundary (5% expected by chance), thus while the symmetry condition was well satisfied for majority of odor pairs, it might not hold for all of them.

To further test the assumption that our proposed distance metric reflected a perceptual distance between odors, we performed a series of analyses with binary mixtures. Unlike the tests above, which did not exploit the composition of the stimuli, these analyses assessed relationships between mixtures and their components. For humans, the most common outcome of perceiving a binary mixture is an average of the qualitative odor descriptors for the component molecules (Ferreira, 2012). Thus, we first hypothesized that the distance between two odors should be greater than between one of them and their binary mixture: $D\left(A,AB\right)<D\left(A,B\right)$. Second, we assumed that the distance between two binary mixtures sharing a common component should be less than the distance between odors not sharing a common component: $D\left(AC,BC\right)<D\left(A,B\right)$ (Figure 2G). We found that both of these assumptions were satisfied on average (Figure 2G) and for each odor pair (Figure 2H). ($D\left(A,B\right)>D\left(A,AB\right)$: p = 0.0039, $D\left(AC,BC\right)<D\left(A,B\right)$: p = 0.0039, n = 10 mice, Wilcoxon signed-rank test after Bonferroni correction of p values.)

From human studies, we also know that chemical similarity, on average, correlates with perceptual similarity (Snitz et al., 2013). To test this in our data, we divided odors into two groups: acids and non-acids. The average perceptual distance between acids was significantly smaller than between acids and non-acids (median distance within acids [163 pairs]: 0.47, median distance between acids and non-acids [220 pairs]: 0.66 [p < 10^-33, Mann-Whitney U-test]; Figure 2F).

Our analyses of binary mixtures and odors from different chemical groups provided encouraging evidence that our metric can be used to measure distances in perceptual space. We further performed a series of experiments and analyses to confirm that the behavioral responses primarily depended on odor identity rather than other aspects of the task including an odor concentration, a short-term memory, a long-term drift in performance, and an odor presentation sequence.

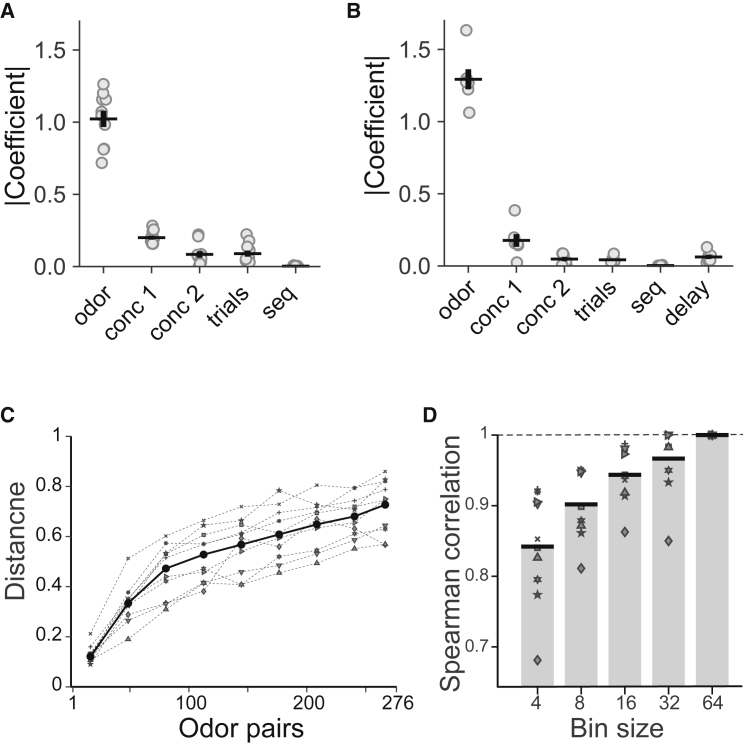
To investigate the influence of different variables on choice behavior, we fitted logistic regression models, which were designed to predict a choice based on the distance metric, $D\left(A,B\right)$, and other behavioral variables such as (1) concentrations of the 1^st and 2^nd odors in the trial: $X_{conc1},X_{conc2}=0\mathit{or}1$ for the low or high concentrations; (2) a phase of data collection, $X_{trials}=0or1$ for the 1^st versus 2^nd half the session; and (3) a sequence of odor presentation, $X_{seq}=-1\mathit{or}1$ for A→B and B→A odor presentations in non-match trials and $X_{seq}=0$ for match trials. To compare the regression coefficients, we normalized the variances and subtracted the means of individual independent variables. The absolute value of the distance metric regression coefficient was ∼5 times higher than that for the concentration of the first odor and at least 10-fold larger than all other regression coefficients, indicating that the distance metric had a much larger influence on choice behavior than other task variables: $D\left(A,B\right)$ versus $X_{conc1}$, p < 0.001; $D\left(A,B\right)$ versus $X_{conc2}$, p < 0.001; $D\left(A,B\right)$ versus $X_{trails}$, p < 0.001; and $D\left(A,B\right)$ versus $X_{seq}$, p < 0.001 (Tukey’s honestly significant difference test) (Figure 3A). As expected from the regression coefficient, logit(p_nogo) (the left-hand side of Equation 2) increased as the distance metric $D\left(A,B\right)$ increased (Figure S3A). In a separate experiment, we varied the delay between odor presentations ($X_{delay}$ = 0 or 1, for 3 and 5 s delays) and repeated the regression analysis for a new dataset adding the additional independent variable $X_{delay}$. Again, we found that the effect of distance metric was significantly larger than that of the delay: $D\left(A,B\right)$ versus $X_{delay}$, p < 0.001 (Figures 3B and S3B).

Figure 3.

Perceptual distances are driven by odor identity and show consistency across individuals

(A) Absolute value of regression coefficients in the logistic regression model (Equation 2) for an odor identity (odor), a concentration of the first (conc 1) and the second (cons 2) presented odors, earlier versus later trials in a session (trials), and a sequence of odor presentation A→B versus B→A (seq) (n = 10 mice, 75,195 trials).

(B) Same as in (A) for regression model including variable delay, 3 versus 5 s (delay) (Equation 3) (n = 6 mice, 24,295 trials, odor set #3, Table S1).

(C) Comparison of perceptual distances across animals. n = 276 odor pairs were ranked based on perceptual distances calculated in Figure 2B (1 is the shortest and 276 is the longest distance), averaged across animals, and binned (bin size - 32 odor pairs). Perceptual distances for the same odorant pairs within each bin averaged for each animal (gray symbols) and across all animals (black dots).

(D) Spearman correlation between perceptual distances (averaged within each bin) calculated for individual animals and averaged across all animals, as a function of bin size (gray symbols, individual mice; black bars, averaged across all mice) (10 mice, 75,195 trials, odor set #1; Table S1).

All experiments indicate that the proposed metric reflects perceptual distance between two odors, similar to what is observed in human experiments that solicit explicit (dis-)similarity judgements. But are these distance relationships conserved across individuals? Potentially, each mouse might exploit different perceptual features or subsets of features to make judgements in the DMTS paradigm. Comparison of distances across individual mice was challenging due to the small number of trials for each individual mouse. To address this, we first ranked all odor pairs based on their perceptual distances averaged across all mice (like in Figure 2D) and binned them with different bin sizes (4, 8, 16, 32, and 64 pairs), such that each bin had a fixed set of odor pairs (the last bin was excluded if the number of odor pairs was less than half of a bin size). We then averaged distances for the odor pairs within each bin for each mouse and examined the agreement across mice. The result for bin size 32 is shown in Figure 3C. As mouse-averaged perceptual distance increases, the perceptual distance for each mouse also increases. For each bin size, we also computed within-bin average distances for each mouse and measured the Spearman correlation coefficients between mice for these bin averages (Figure 3D). As bin size increased, the Spearman correlation also increased, reaching 1 for bin size equal to 64, i.e., all individual mice were in agreement about the relative distance ordering of the four quartiles determined from averaging across mice. This is strong evidence for similarity between perceptual spaces of individual mice, with remaining discrepancies possibly explained by statistical noise and an insufficient number of trials.

While in all our analysis we chose the specific distance metric defined by Equation 1, this choice probably is not unique. Any function that preserves the rank-order relationship from p_nogo (and which ideally includes terms to compensate for possible behavioral biases for each odor) is a candidate for a perceptual distance metric. See results using an alternative distance metric in Figure S4.

Discussion

These experiments indicate that the behavioral readouts are consistent with what is expected from an internal representation of perceptual distance. Notably, we found that perceptual distances largely agree across different animals. This observation, along with the possibility of testing many odors, makes our paradigm a promising tool to investigate olfactory perceptual space. Robust psychophysical measurements of perceptual distances in mice will allow researchers to capitalize on advances in mouse genetics and modern methods for recording and manipulating neural activity. In addition, these methods have a lower implementation threshold in head-fixed animals than alternatives such as cross-habituation in addition to providing higher throughput. We expect that our behavioral paradigm will contribute to the study of the neural coding of olfaction through direct comparison between perceptual representation of odors and corresponding neuronal activity. Beyond research into mouse olfaction, this paradigm allows sensory perception to be studied in generalized settings that have analogs in human psychophysics.

Limitations of the study

Although the behavioral paradigm developed in this paper enabled us to explore perceptual relationship between odors, there are few limitations.

The number of odors used in the study is limited. The behavioral measurements are noisy and require a large number of trails (∼100) per each stimuli pair. The number of trails scales like number of stimuli squared, which makes it difficult to significantly expand the number of odors.

The perceptual-distance measurement is mostly sensitive for similar odors or their mixtures. For majority of pure odor pairs, the distances are large, and the method has poor resolution. This may be solved by measuring distances between binary mixtures with different ratios, rather than pure odorants, which leads to a significant increase of number of trials.

In the current paper, we did not explore three and more component mixtures or natural odors, which significantly complicates the odor-delivery system.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Chemicals, peptides, and recombinant proteins
Cinnamaldehyde	Sigma-Aldrich	C80687-25G
Ethyl butyrate	Sigma-Aldrich	E15701-500ML
2-Methylbutyric acid	Sigma-Aldrich	193,070-25G
2,2-Dimethylbutyric acid	Oakwood Chemical	035,602-5g
Cyclopentanecarboxylic acid	Sigma-Aldrich	537,683-100ML
2-Heptanone	Sigma-Aldrich	537,683-100ML
Isobutyric acid	Sigma-Aldrich	I1754-100ML
Isovaleric acid	Sigma-Aldrich	129,542-100ML
3-Heptanone	TCI	H0038
Methylvalerate	Sigma-Aldrich	277,827-5G
Propionic acid	Sigma-Aldrich	81,910-1L
Butyric acid	Sigma-Aldrich	B103500-100ML
(+)-α-Pinene	Sigma-Aldrich	P45680-100ML
Benzaldehyde	Sigma-Aldrich	B1334-100G
5-Methyl-2-Hexanone	Sigma-Aldrich	537,705-1L
Valeric acid	Sigma-Aldrich	110,140-1L
3-Methylvaleric acid	Sigma-Aldrich	222,453-5G
3,3-Dimethylbutyric acid	Sigma-Aldrich	B88403-25G
4-Methylvaleric acid	Sigma-Aldrich	277,827-5G
Hexanoic acid	Sigma-Aldrich	153,745-2.5G
Experimental models: Organisms/strains
Mouse: C57BL/6J-Tg(Thy1-GCaMP6f)GP5.11Dkim/J	The Jackson Laboratory	Strain #:024,339
Deposited data
Mouse behavioral data	This paper	http://github.com/pyrfume/pyrfume-data
Software and algorithms
Python version 3.8	Python Software Foundation	https://www.python.org
Voeyur software	Smear et al., 2013	https://github.com/olfa-lab/Voyeur
Multidimensional scaling	Borg and Groenen, 1997, Kruskal, 1964a	https://scikit-learn.org/stable/modules/generated/sklearn.manifold.MDS.html
Code for manuscript	http://github.com/olfa-lab/mouse-perceptual-distance	https://doi.org/10.5281/zenodo.6537497
Other
Arduino Mega 2560 microcontroller	Arduino	https://www.arduino.cc
Mass flow controller (0–1000 mL/min)	Alicat	Alicat MC-1SLPM-D/5M/5IN
Mass flow controller (0–100 mL/min)	Alicat	MC-100SCCM-D/5M/5IN
Inline manifold isolation valve	NResearch	225T082
2-way normally closed isolation valve	NResearch	TI1403270
3-way isolation valve	NResearch	SH360T042
Precleaned Volatile Organic Analyte (VOA) Sampling Vials	Restek	21,797
Capacitive touch sensor	Sparkfun	SEN-1024
Pinch valve	Valcor	SV74P61T

Resource availability

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, Dmitry Rinberg (rinberg@nyu.edu).

Materials availability

This study did not generate new unique reagents.

Experimental model and subject details

Animals

Both male and female Thy1-GCaMP6f (GP5.11) mice (Stock No: 024,339) (Jackson laboratories) were used in the task. At the start of behavioral training, mice were at least two months old and had 20 g body weight. Mice were housed under a 12-h inverted light/dark cycle. All procedures were approved under a New York University Langone Health institutional animal care and use committee (IACUC protocol # 16–00,197).

Method details

Animal surgeries

Prior to behavioral training, mice were implanted with a 3D-printed head-bar for head fixation in the behavioral apparatus. Mice were anesthetized with isoflurane (2% for induction, 1.5% during surgery) and placed on a heated floor during surgery. Skin overlying the skull was sterilized with betadine and incised to expose the skull. The periosteum was gently scraped away and the surface of the skull was cleaned with hydrogen peroxide. The head-bar was fixed to the skull using C&B Metabond dental cement (Parkell).

Odor delivery

A two-cassette air-dilution olfactometer was used to prepare and deliver odors with specific concentrations (Figure S1) (Shusterman et al., 2011). Each olfactometer cassette consisted of two mass flow controllers (MFCs): one was used for a clean air line (0–1000 mL/min, Alicat MC-1SLPM-D/5M/5IN) and another was used for odor line (0–100 mL/min, Alicat, MC-100SCCM-D/5M/5IN), four inline Teflon four-valve manifolds, (NReserach, 225T082), one on-off clean-air three port bypass valve (NResearch, TI1403270), and eight odor vials. Odors were diluted in water and stored in amber volatile organic analysis vials (Restek, 21,797). In a default state, both of clean air line MFCs were set at 400 mL/min, and odor line MFCs at 100 mL/min. The air from the odor line MFCs was flowing through the bypass valves, while all odor valves were closed. The combined flow from clean air lines and odor lines (total 1000 mL/min) was going through the final valve (NResearch, SH360T042), to an exhaust. A separate clean air line was setup with a manual flow regulator at 1000 mL/min and delivering a clean air through the final valve to the odor port. To deliver an odor, the bypass valve on one of the cassettes was closed while simultaneously a pair of odor valves was opened. Air flow passed through the valve headspace and merged with the clean air line, thus providing air dilution to odor accumulated in the headspace. To present a binary mixture, both bypass valves were closed and two pairs odor vials from two cassettes were opened simultaneously. Concentrations of an individual odor, or components of an odor mixture, were controlled by changing the flow rate of MFCs in the odor line, while keeping the total flow constant. For example, to deliver a high concentration of odor, an air-line MFC was set at 400 mL/min, and odor line MFCs at 100 mL/min. To present a 5x lower concentration of an odor, flow through the odor line of one of the cassettes was set at 20 mL/min, and the air line of this cassette was set at 480 mL/min. After flow was stabilized (∼1 s), the final valve was switched between odorized flow and clean air flow, and odor was delivered to the odor port with <100 ms latency. At the end of stimulus presentation, the final valve switched back and delivered clean air to the odor port once again.

Odor stimulus

Eight or ten monomolecular odors and their binary mixtures were used for each experiment. Set #1: 1) Cinnamaldehyde (CinAl), 2) Ethyl butyrate (EB), 3) 2-Methylbutyric acid (2MBAcd), 4) 2,2-Dimethylbutyric acid (22DMBAcd), 5) Cyclopentanecarboxylic acid (CPAcd), 6) 2-Heptanone (2Hep), 7) Isobutyric acid (IBAcd), 8) Isovaleric acid (IVAcd); Set #2: 1) 3-Heptanone (3Hep), 2) Methylvalerate (MVT), 3) EB, 4) Propionic acid (PpAcd), 5) Butyric acid (ButAcd), 6) (+)-α-Pinene (Pinene), 7) Benzaldehyde (BzAld), 8) 5-Methyl-2-Hexanone (5M2H); Set #3: 1) 3Hep, 2) EB, 3) Valeric acid (ValAcd), 4) 3-Methylvaleric acid (3MVAcd), 5) 3,3-Dimethylbutyric acid (33DMBAcd), 6) Pinene, 7) BzAld, 8) IVAcd, 9) 4-Methylvaleric acid (4MVAcd), 10) Hexanoic acid (HexAcd). All monomolecular odors were diluted in deionized water and stored in vials during experiments. These odor dilutions were prepared daily and were placed in two different cassettes. Each olfactometer contained four or five odors to enable the generation of binary mixtures by mixing odors from different cassettes. The initial headspace concentration was estimated based on saturated vapor pressure from a given chemical at a specific dilution. Following this, the odor was diluted between 10- and 100-fold using air dilution in the olfactometer. Specific dilutions (v/v) for each experiment are presented in Table S1.

Behavioral setup

Mice were head-fixed and placed on a wheel allowing free running and experienced minimal stress (Figure S1). A mouse snout was placed into a specially designed odor port (made of PTFE). The odor port was connected to the olfactometer, from which odorized air was delivered, and a vacuum line was present to quickly remove the odorized air during inter-stimulus intervals. Mice were trained to register their behavioral judgments by licking water spouts, and licking was detected using a capacitive touch sensor (Sparkfun, SEN-1204). Two water spouts were installed, one in the center and the other to the side of the position of a mouse snout in the odor port. Water delivery was controlled by a pinch valve (Valcor, SV74P61T). All behavioral events (stimulus delivery, water delivery, and lick detection) were monitored and controlled by custom programs written in Python interfacing with a custom behavioral control system (Janelia Research Campus) based on an Arduino Mega 2560 microcontroller.

Behavioral paradigm

The behavioral paradigm aims to train mice to judge whether two odors presented in each trial are the same or not. In each trial, mice were presented with two sequential 1 s odor stimuli, separated by a delay period of 5 s. The odor stimuli were either the same (match trails) or different (non-match trials). Mice were trained with a lick based go-nogo paradigm and instructed to report their behavioral judgment during a 1 s response window, which occurs 0.5–1.5 s after the offset of the second odor presentation in each trial (Figures 1A and 1B). Odor concentration for each presentation was randomized by adjusting the air flow. Only the center water spout was used to evaluate behavioral response, and licking the side water spout had no effect on trial outcome. Mice were trained to lick (go choice) the center water spout in match trials and to suppress licks (no-go choice) in non-match trials. At the end of a response window, correct responses were followed by reward delivery in the center spout (go choice in match trials) or in the side water spout (no-go choice in non-match trials).

Although we used two water spouts, our behavioral paradigm is different from a conventional two-alternative forced choice task (2AFC). In our task animals don’t need to actively lick one of the lick spouts, and can instead passively receive reward after correct no-go responses. This modification makes behavioral training easier in challenging stimulus conditions like our paradigm. Beyond easier training of animals, our paradigm offers better interpretability of behavioral responses compared to conventional go-nogo (GNG) paradigms. In the conventional GNG paradigm, nogo responses are performed both as correct behavioral responses and as a consequence of low task engagement. In our paradigm, however, the passive side-port is placed in a different location and animals often show anticipatory licks before correct non-match trials. Thanks to the anticipatory responses, we can potentially differentiate nogo responses caused by a low level of task engagement from that caused by the correct behavioral response. Since the level of anticipatory lick responses to the passive side port was variable across animals, we leave such analysis for future study. Thus, our paradigm is a hybrid of 2AFC and GNG tasks and facilitates easier training of animals than in 2AFC tasks and better interpretability of behavioral readouts than in GNG tasks.

Behavioral training

The training procedure consisted of multiple steps outlined below:

Water restriction and habituation

During the entire period of behavioral training, mice were kept under water deprivation, which began at least one week after surgery. Mice received a total of 1 mL of water per day either as accumulated rewards for behavioral performance, or supplemented to the full amount at the end of the day. During the initial phase, mice were habituated to the handling by experimenters for 10–15 min per day. Once each mouse could comfortably drink water drops on the glove of experimenter’s hand, it was habituated to the experimental setup. During the habituation to experimental setup, mice were head-fixed on the running wheel and placed in the behavioral box for 10–15 min per day. During this phase, mice were occasionally presented with water through a syringe. Once each mouse showed reliable licking responses to water delivered through a syringe, it began lick training.

Lick training

At this phase mice learned to lick water spouts to obtain a water reward. Mice were given a 1–1.5 ul water drop each time they licked water spouts. Both center and side water spouts were introduced and a water reward was provided alternately from them. In case mice did not lick the water spouts at all, multiple water drops were delivered by experimenters until mice started licking water spouts. Mice proceeded to the next training step if they received 100 water drops within 30 min. Otherwise, lick training was repeated in the following days.

Behavioral shaping step one – Pavlovian shaping

The purpose of this step is to get mice familiarized with the timing of behavioral events and water reward delivery. At each trial, mice were presented with the same odor twice with 3 s delay, which was followed by a 1 s response window (0.2–1.2 s from the second odor offset). At this step, only match trials were presented and two odor presentations in a given trial were always the same. Five ul of water reward were delivered at the end of response window regardless of behavioral responses. Although licking behavior of mice had no consequence on reward delivery, mice started to show anticipatory licking during the response time window. If mice licked during the response window at >80% of trials across 80 trials, mice proceeded to the next step. In shaping steps one to three, all odors in odor set two in Table S1 were used.

Behavioral shaping step two – odor lick association

The purpose of this step was to make mice lick during the response window to receive a water reward. The trial structure was same as in step one, except mice had to lick a water spout during the response window (0.5–1.5 s from the second odor offset) in order to trigger water delivery. No water was delivered if mice did not lick the water spout during the response time interval. If mice received a water reward for >80% of trials across 100 trials, they proceeded to the next step.

Behavioral shaping step three – Full task training

At this step, mice were presented with both match and non-match trials. The timing of the response window was set to 0.5–1.5 s from the second odor offset. The delay duration between two odor presentations was set to 3 s at the first session of this step. The delay duration was increased by 0.5 s if mice achieved 70% or more correct performance in the previous behavioral sessions.

Trial type (match/non-match) for each trial was chosen pseudo-randomly so that mice did not receive rewards from same trial types in four or more consecutive trials. We also implemented a bias correction strategy as described in Behavioral bias correction strategy section. The trial type of the coming trial was chosen so that the biased response would be incorrect, if a choice bias could be predicted from the response history of the past three trials. Otherwise, match and non-match trials were presented with equal probability. At this step, to simplify training, we did not present odor pairs, which were similar and could cause some confusion, such as odor mixtures sharing one of the components, like (A, AB), or (AC, BC). Once mice showed >70% correct performance across 100 trials with 5 s delay, they were ready to be used to test perceptual similarities between odors of interest.

Testing of perceptual similarity

The task was performed as in shaping step three, except that all combinations of first and second odors were used. Delay duration was fixed at 5 s, unless the effect of delay duration was being investigated (Figures 3B, 3 and 5 s). The first five trials of each session were match trials to encourage mice to lick water spouts, and these trials were excluded from all analyses. The number of mice, sessions, and trials of each dataset are summarized in Table S2.

Behavioral bias correction strategy

Occasionally during training an animal exhibited some behavioral bias which affected interpretation of results. We considered the possibility of bias whenever the result of the next trial was related to the history of the previous trials (Tervo et al., 2014). If the bias was detected, the next trial type (match vs non-match) was chosen to be opposite of the one that the bias would have predicted. To detect the bias we searched for different sequences of previously observed trials (for example, a sequence ‘match’-‘no-match’-‘match’ trials), and tested if it predicted a specific response ‘go’ or ‘no-go’. We analyzed 3, two and one trial patterns, using only trial type (‘match’, ‘no-match’), and two and one trail patterns using both trial type and trial outcome (‘rewarded’, ‘non-rewarded’). To minimize random bias detection, we implemented a criterium that if four out of five estimates predicted higher probability for one behavioral response, we flagged the current trial as biased and chose the upcoming trial type so that the other response type is the correct response. The above policy was applied after 40 trials had passed from the start of a session, and used the previous 40 trial window to detect behavioral bias.

Quantification and statistical analysis

Quantification of perceptual distances

The perceptual distance between a pair of odors was calculated based on the fraction of non-match trials where mice gave the correct response (no-go choice). The probability of a no-go choice for a given odor pair was normalized by the lapse rate for individual odors, i.e., the probabilities of a no-go choice for match trails (see Equation 1). For a reliable estimate of perceptual distances, it is desirable to have at least 100 trials for each odor pair. The transformation from no-go probabilities to the distance measure makes all diagonal elements of the distance matrix take a value of 0. Some non-match odor pairs may take a negative value due to a small number of trials. The negative values were replaced by 0.001 to keep all non-match odor pairs distinct from self-comparison (match trials), which correspond to zero distance.

Multidimensional scaling

We used non-classical metric multidimensional scaling (MDS) to calculate a low-dimensional representation of odor perceptual space (Borg and Groenen, 1997; Kruskal, 1964a). MDS was performed using the Python scikit-learn package (sklearn.manifold.MDS). MDS takes a pairwise distance matrix as input and returns coordinates of data points in low dimensional space, such that pairwise distances in the input are maximally conserved. Non-classical metric MDS was applied to the matrix representing pairwise perceptual distances between odor pairs. We used a scaling dimension of three for visualization.

Statistics

Perceptual distances between odor mixtures were compared (Figure 2D) using the Wilcoxon signed-rank test. First, the probability of a no-go choice was calculated for each trial type (match, A-B, AC-BC and A-AB) separately for individual mice. Comparisons were performed for pairs (A-B, AC-BC) and (A-B, A-AB) by treating mice as repeated measures. p values were corrected for multiple comparisons with the Bonferroni method.

For the comparison of distances between acids and those between acids and non-acids (Figure 2F), we first calculated perceptual distances across all odor pairs by pooling trials from all animals. Then, we classified the perceptual distances into two groups: distances between acids, and distances between acids and non-acids. Odor pairs including binary mixtures of both acids and non-acids were excluded from this analysis. The difference between these groups was tested with the Mann-Whitney U test.

To quantify the effects of odor identity and other behavioral variables, we fit a logistic regression model (James et al., 2013):

$$log\left(\frac{p}{1-p}\right)={\beta }_0+{\beta }_{od}D\left(A,B\right)+{\beta }_{conc1}{X}_{conc1}+{\beta }_{conc2}{X}_{conc2}+{\beta }_{trials}{X}_{trials}+{\beta }_{seq}{X}_{seq},$$ (Equation 2)

$$log\left(\frac{p}{1-p}\right)={\beta }_0+{\beta }_{od}D\left(A,B\right)+{\beta }_{conc1}{X}_{conc1}+{\beta }_{conc2}{X}_{conc2}+{\beta }_{trials}{X}_{trials}+{\beta }_{seq}{X}_{seq}+{\beta }_{delay}{X}_{delay},$$ (Equation 3)

where $p$ is probability of no-lick responses; $D\left(A,B\right)$ is the distance between odors A and B defined in (Equation 1), and calculated separately for each mouse; $X_{conc1}$ and $X_{conc2}$ are concentrations of the 1^st and 2^nd odor in the trail: $X_{conc1},X_{conc1}=0or1$ for the low or high concentrations; $X_{trials}$ is a phase of data collection, $X_{trials}=0\text{or}1$ for the 1^st vs 2^nd half of total set of trials in the session; $X_{seq}$ is a sequence of odor presentation, $X_{seq}=-1\text{or}1$ for A- > B and B- > A odor presentations in non-match trials and $X_{seq}=0$ for match trials. Assignment of values of A- > B and B- > A sequences were randomized. $X_{delay}$ is a delay between sequential odor presentation in one trial, $X_{delay}=0\text{or}1$, for 3 and 5 s delays.

To compare the magnitude of different independent variables, these were standardized so that mean and standard deviation of each variable becomes 0 and 1 respectively. We fit these regression models using stats models package in Python (Seabold and Perktold, 2010). We compared the absolute value of regression coefficients using One-way ANOVA and post hoc tests corrected for multiple comparisons (Tukey’s Honestly Significant Difference test).

Published: June 9, 2022

Data and code availability

• •Datasets are deposited into the Pyrfume project for odorant-linked datasets (https://pyrfume.org/) and it can be accessed at http://github.com/pyrfume/pyrfume-data, archive name 'nakayama_2022'.
• •Code for this manuscript can be obtained at http://github.com/olfa-lab/mouse-perceptual-distance
• •Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon reasonable request.