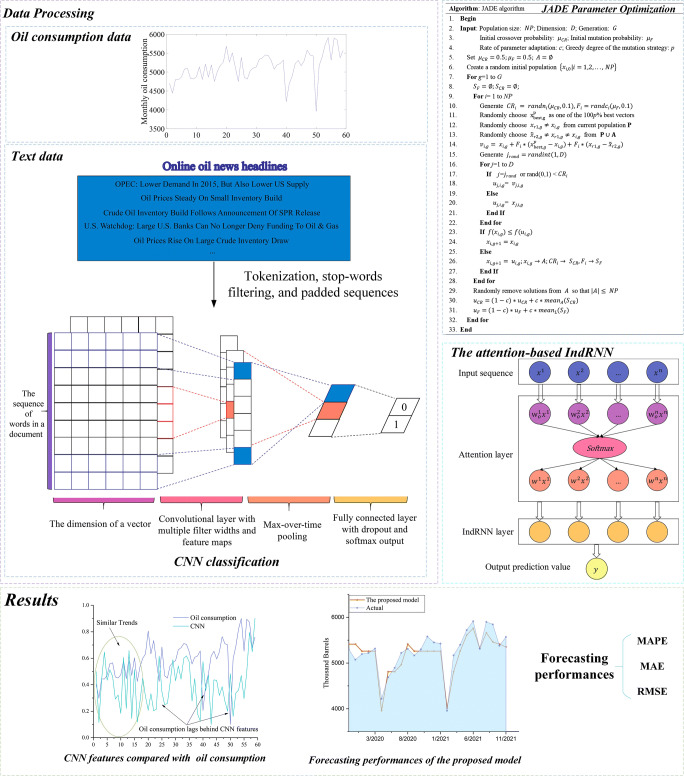
Abstract
Accurate prediction of oil consumption plays a dominant role in oil supply chain management. However, because of the effects of the coronavirus disease 2019 (COVID-19) pandemic, oil consumption has exhibited an uncertain and volatile trend, which leads to a huge challenge to accurate predictions. The rapid development of the Internet provides countless online information (e.g., online news) that can benefit predict oil consumption. This study adopts a novel news-based oil consumption prediction methodology–convolutional neural network (CNN) to fetch online news information automatically, thereby illustrating the contribution of text features for oil consumption prediction. This study also proposes a new approach called attention-based JADE-IndRNN that combines adaptive differential evolution (adaptive differential evolution with optional external archive, JADE) with an attention-based independent recurrent neural network (IndRNN) to forecast monthly oil consumption. Experimental results further indicate that the proposed news-based oil consumption prediction methodology improves on the traditional techniques without online oil news significantly, as the news might contain some explanations of the relevant confinement or reopen policies during the COVID-19 period.
Keywords: Oil consumption forecasting, Online news, Text mining, Deep learning, Independent recurrent neural network, COVID-19 pandemic
Introduction
Research background and motivation
The oil supply chain is of great significance in the global economy, and oil plays a dominant role in energy resources [1–4]. Based on the BP Statistical Review of World Energy 2021, oil is the largest consumed commodity among energy commodities, at about 33.2%, 33.1%, and 31.2% in 2018, 2019, and 2020, respectively. Therefore, exploring the oil supply chain management has had its appeal in the field of theory and application for profit maximization and risk minimization [5]. Accurate prediction of oil consumption can also benefit related companies or countries that develop budget plans and stabilization policies.
The uncertainty of the oil market leads to the difficulty of the forecasting oil market [6]. The error sources of oil consumption forecasting include various unpredictable factors. Oil consumption has remarkable features and various external factors including exogenous factors (e.g., extreme weather, conflicts, war, as well as economic development) and oil market factors (e.g., price and inventory). For example, because of the effects of the coronavirus disease 2019 (COVID-19) pandemic, the oil market has shown volatile trends in many countries.
Thus, modeling diverse factors that affect oil consumption is crucial to oil consumption prediction. The challenging question is how to select the most helpful predictors, some of which are hard to quantify. Fortunately, many novel techniques can be employed to quantify qualitative data [7]. Recently, it becomes a hot spot in converting the qualitative analysis of politics, disasters, and emergencies into quantitative information [8].
The emergence of the Internet provides adequate online media information (e.g., online news) that can show the reasons for driving the oil markets [9]. Online media is a key source, and its analysis can assist political and economic predictions [10]. Furthermore, online news is considered a more comprehensive and adequate information source than other sources, such as Twitter or blogs, because it is more persuasive [11]. Accordingly, oil news is considered as helpful qualitative data that could improve oil consumption prediction.
This study aims to adopt a news-based oil consumption prediction methodology that considers online oil news. To analyze the specific impact of each influencing factor on the oil consumption forecasting, an attention mechanism is introduced to the independent recurrent neural network (IndRNN) in this study. The attention mechanism can assign different weights to different influencing factors of oil consumption, and the model can automatically highlight more critical influencing factors, thereby improving the prediction accuracy of the IndRNN model. In addition, an effective intelligent evolutionary algorithm, namely adaptive differential evolution with optional external archive (JADE) is used to search the hyperparameters of attention-based IndRNN to improve the performance of the oil consumption forecasting model.
Literature review
The majority of studies on forecasting energy consumption have used traditional econometric models, time-series techniques, and emerging intelligent algorithms [12–15]. Emerging artificial intelligence (AI) approaches use powerful self-learning capacities to capture the complex nonlinear features of energy markets [16]. For example, Wei et al. [17] combined an enhanced singular spectrum analysis with long short-term memory (LSTM) to predict daily natural gas consumption. Somu et al. [18] proposed a deep learning framework, namely kCNN-LSTM to forecast building energy consumption. Li et al. [19] studied 26 combination models using the traditional combination method to increase oil forecasting accuracy in China. Compared with the traditional model, their proposed AI combination model can obtain ideal prediction results.
Despite these attempts, the research on forecasting energy consumption remains inadequate. A common shortcoming of the above studies is that oil consumption trends are based on historical statistics. The error in oil consumption forecasting is very large when emergency events have a short-term effect on oil markets. Thus, it is important to consider exogenous factors and oil market factors. Few studies have explored oil consumption forecasting using qualitative information. For example, Yu et al. [1] proposed that using Google Trends is a helpful method to predict oil consumption. They found that Google Trends reflect various related factors according to a mass of search results. However, when irregular events occur, Google Trends appear to be on the rise, regardless of what causes oil consumption to rise or fall. Thus, to develop their study, this study further proposes a text-based approach to predict energy consumption.
The oil markets are heavily influenced by uncertain events, such as political instability, and actionable information can be extracted from text-mining algorithms from online news. Text mining has been widely used in oil price forecasting. For example, Li, Shang, and Wang [20] used oil news to predict WTI oil price, and their results show that oil news contains useful information for predicting oil price. Inspired by previous studies, this study intends to examine whether oil news contributes to the prediction of oil consumption.
Text mining can transform an unstructured format into a structured format to extract information and identify ideas [21, 22]. Hemmatian and Sohrabi [23] conducted aspect extraction, opinion classification, abstract generation, and evaluation on the emerging artificial intelligence technology and proposed an appropriate text mining framework. They believed that the convolutional neural network (CNN) is worth studying and is a potential text mining method. Huang et al. [24] used CNN to extract the features of sentiment from six real cases. The results showed that their proposed CNN model had more effective power than the baseline methods. Based on their study, this study also employs the CNN model to extract text features of oil news.
Suitable forecasting models also determine the performance of oil consumption forecasting except for effective predictors. Oil consumption shows complex nonlinear features and the artificial neural networks (ANNs) with strong nonlinear fitting capability are more suitable to predict oil consumption [25]. Deep learning models with a good ability to fit nonlinear features are suitable for oil consumption forecasting [26].
Deep learning methods (e.g., recurrent neural network), have been applied for time-series forecasting [27, 28]. To overcome gradient vanishing and gradient exploding problems existing in traditional recurrent neural networks (RNNs) [29], Li et al. [30] proposed an independent recurrent neural network (IndRNN), where neurons in the same layer are independent of each other. Compared with the traditional RNN and LSTM, using IndRNNs achieved better performances on various tasks. IndRNN is a new model, few studies are using the deep learning technique. For example, Chu and Yu [31] combined IndRNN with back-propagation neural networks to predict rice yield. They employed IndRNN to learn deep spatial and temporal features and obtained good performance. Thus, this study applies IndRNN for the first time as an effective oil consumption forecasting technique.
Many parameters for IndRNN affect forecasting accuracy. Consequently, an intelligence algorithm can be employed to select the parameters of IndRNN. The adaptive differential evolution with optional external archive (JADE) is competitive in easy implementation and quick convergence, with better robustness than other popular algorithms [32, 33]. Accordingly, this study uses the JADE algorithm to determine the hyperparameters of IndRNN.
The current models based on the neural network use different influencing factors as the input of the prediction model to forecast oil consumption. The analysis of the specific impact of each influencing factor on oil consumption is not sufficient. The calculation of the forecasting model is a black-box process, and it is difficult to assess how the input of the neural network affects the final forecasting value. The attention mechanism can mine the coupling relationship between the input variable and the target variable, explain the influence of the input variable on the target variable, and extract key input variables, thereby improving the performance of prediction [34, 35]. Therefore, different from previous research, this study introduces an attention mechanism to the JADE-IndRNN model. By assigning weight to the input, key input factors can be better selected and the effect of multi-factor forecasting can be improved [36].
Main work and contributions
This study adopts two numerical examples to verify the feasibility of text-based oil consumption forecasting and the proposed attention-based JADE-IndRNN model. The empirical results indicate that oil news text features have considerable effective predictive information. The attention-based JADE-IndRNN model can increase the accuracy of oil consumption prediction as compared with other popular techniques. The main contributions can be described as follows:
An effective and novel forecasting model, namely the attention-based JADE-IndRNN model, is proposed via artificial intelligence (AI) techniques for volatile oil consumption. The proposed forecasting model combines the key information capture ability of the attention mechanism, the intelligent and efficient search parameter ability of JADE, and the accurate prediction ability of IndRNN for time series.
The main finding of this study is that online oil news can facilitate monthly oil consumption forecasting. Online oil news significantly improves the accuracy performance of oil consumption prediction, particularly when oil consumption fluctuates dramatically.
Two real-life oil consumption forecasting cases are applied to verify the performance of the attention-based JADE-IndRNN model. The results show that the performance of the proposed model in the monthly oil consumption forecasting is more effective than that of other popular models.
The rest of the paper is described as follows. Section 2 discusses the methodology, including the attention-based JADE-IndRNN and convolutional neural network. Section 3 presents performance tests of different evolutionary algorithms. Section 4 presents the data descriptions, experimental designs, the results of oil consumption forecasting, and managerial implications. Section 5 describes the conclusion.
Methodology
Figure 1 depicts the general framework of the attention-based JADE-IndRNN model for oil consumption forecasting. This study adopts two numerical examples to verify the feasibility of text-based oil consumption forecasting, namely U.S. oil consumption forecasting, and Indian oil consumption forecasting. From the well-known energy news website “Oilprice.com”, oil news headlines are collected using the keyword “American oil” or “India oil”. The convolutional neural network (CNN) model is adopted to fetch useful text features. Then, the historical oil consumption and CNN features are inputted to the proposed attention-based JADE-IndRNN model. This study refers mainly to three techniques, namely, convolutional neural network, adaptive differential evolution (JADE), and attention-based independent recurrent neural network. The details of these methodologies are described as follows:
Fig. 1.
The general framework of the attention-based JADE-IndRNN model for oil consumption forecasting
Text mining technology: convolutional neural network
The CNN model is employed to extract online news. The CNN model fully utilizes the semantic relationship between oil news modes to help us extract the media’s view of the ups and downs of oil consumption. In this study, The CNN value represents the probability that the text is classified as positive sentiment. Figure 1 shows a complete and concise flowchart designed to help us better understand the CNN algorithm. The outputs of the CNN classification denote the fluctuations of the monthly oil consumption, either decrease or increase. The oil consumption movement 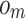 is described as follows:
is described as follows:
| 1 |
where 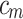 denotes the oil consumption at the end of month m.
denotes the oil consumption at the end of month m.
-
(b)
Adaptive differential evolution
JADE is used to determine the parameters of attention-based IndRNN. The selected parameters are the number of layers, number of time steps, number of units of the single hidden layer, number of batch sizes, and steps of learning rates. JADE is an excellent variant of the DE algorithm, showing excellent results on high-dimensional problems [33]. Compared with basic DE, JADE has three main improvements: a new mutation strategy “DE/current-to-pbest” is implemented; an optional external archiving is added; parameters are updated adaptively. “DE/current-to-pbest” and optional archiving operations diversify the population and improve convergence performance. Parameter adaptation automatically updates the control parameters to appropriate values, which helps to improve the robustness of the algorithm. Figure 1 shows the basic steps of JADE.
-
(c)
Attention-based IndRNN model
An independent recurrent neural network (IndRNN) was proposed to overcome gradient vanishing and gradient exploding problems existing in traditional recurrent neural networks (RNNs) [30]. Neurons in the same layer are not connected but are connected across layers, while IndRNN can easily avoid gradient vanishing and gradient exploding problems. However, IndRNN is slightly insufficient in explaining the relationship between the input and output of the network. To solve this problem, this study introduces an attention mechanism to assign different weights to the features of input influencing factors, which can effectively highlight the factors that affect oil consumption and improve the prediction accuracy. The IndRNN model based on the attention mechanism includes input sequence, attention layer, IndRNN layer, and output prediction value, as shown in Fig. 1.
In the attention layer, the weights are firstly allocated in the input sequence, and then the weights are multiplied by the input sequence to form a new vector. The new vector will be regarded as the input of the IndRNN layer. For the multi-factor time series forecasting problem, suppose the input sequence is 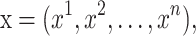 and the corresponding weight is
and the corresponding weight is 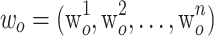 ,
, 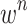 represents the weight of attention,
represents the weight of attention, 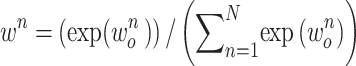 , the Softmax function is to ensure that the sum of all weights is 1, and the input of IndRNN is
, the Softmax function is to ensure that the sum of all weights is 1, and the input of IndRNN is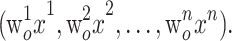
Attention mechanism helps to capture important factors by assigning different weights to the features of the input, especially in multi-factor time forecasting [37]. Thus, this study designed the attention-based JADE-IndRNN which combined the advantages of attention mechanism and JADE-IndRNN.
Performance tests of different evolutionary algorithms
The algorithms were coded using Matlab R2020b and calculations were carried out on a personal computer with an Intel (R) Core (TM) i7-4710MQ, 8 GB RAM, 2.50 GHz CPU, and Windows 10 professional Operational System.
Benchmark functions
The 29 benchmark functions listed in Table 1 are all widely used benchmark functions [38–40]. Functions 1 to 15 (F1 to F15) are unimodal, whereas functions 16 to 29 (F16 to F29) are multimodal. Unimodal functions are easier to find global solutions than multimodal functions. Multimodal function structures are more complex than unimodal functions, with peaks, valleys, channels, and flat hyperplanes of varying heights. Therefore, these functions are suitable for verifying the performance of different evolutionary algorithms.
Table 1.
Details of benchmark functions
| No. | Functions | xi | x∗ | f(x∗) |
|---|---|---|---|---|
| F1 | (–5.12, 5.12) | 0 | 0 | |
| F2 | (–10, 10) | 0 | ||
| F3 | (–1, 1) | 0 | –1 | |
| F4 | (–100, 100) | 0 | 0 | |
| F5 | (–1.28, 1.28) | 0 | 0 | |
| F6 | (–30, 30) | 0 | 1 | |
| F7 | (–100, 100) | 0 | 0 | |
| F8 | f(x) = max(| xi| ) | (–100, 100) | 0 | 0 |
| F9 | (–10, 10) | 0 | 0 | |
| F10 | (–100, 100) | 0 | 0 | |
| F11 | (–100, 100) | 0 | 0 | |
| F12 | (–1, 1) | 0 | 0 | |
| F13 | (–10, 10) | 0 | 0 | |
| F14 | (–100, 100) | 0 | –450 | |
| F15 | (–100, 100) | 0 | –450 | |
| F16 | (–32, 32) | 0 | 0 | |
| F17 | (–10, 10) | 0 | 0 | |
| F18 |
f (x) = f1(x1, x2) + f1(x2, x3) + … + f1(xn, x1) f1(x, y) = (x2 + y2)0.25[sin2(50(x2 + y2)0.1) + 1] |
(–100, 100) | 0 | 0 |
| F19 |
f (x) = f1(x1, x2) + f1(x2, x3) + … + f1(xn, x1)
|
(–100, 100) | 0 | 0 |
| F20 |
yi = 1 + 0.25(xi + 1)
|
(–50, 50) | -1 | 0 |
| F21 | (–600, 600) | 0 | 0 | |
| F22 | (–5, 5) | 0 | 1 − n | |
| F23 | (−n2, n2) | i(n + 1 − i) | ||
| F24 | (–100, 100) | 0 | 0 | |
| F25 | (–5.12, 5.12) | 0 | 0 | |
| F26 |
|
(–5.12, 5.12) | 0 | 0 |
| F27 | (–100, 100) | 0 | 0 | |
| F28 |
α = 0.5, b = 0.3, kmax = 30 |
(–0.5, 0.5) | 0 | 0 |
| F29 |
|
(–100, 100) | 1 | 0 |
Algorithms used for comparison
DE, DE variants, OBPSO, and SCA algorithms with strong robustness and appropriate convergence speeds are used for comparison for the following reasons:
Differential Evolution (DE) is a stochastic model that simulates biological evolution by iterating over and over so that those individuals that adapt to the environment are preserved [41]. The DE algorithm possesses a simple structure, is easy to implement, and has a good convergence speed.
-
Linear Adaptive Differential Evolution (LADE) and S-shaped Adaptive Differential Evolution (SADE) have better convergence speed and stronger global search ability than basic DE. The scaling factor F determines the individual’s variation scale. If F is too small, because the algorithm is premature, and it cannot guarantee that the diversity of the population will easily fall into the local optimal solution; if F is too large, the iteration efficiency of DE will be slow, and the algorithm will be difficult to converge [42]. Therefore, this study selected two mutation strategies to assess the performance of different DE variants. The adaptive functions of LADE and SADE are as follows:
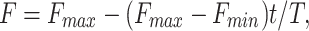
2 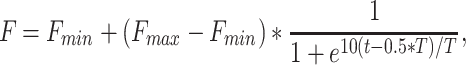
3 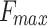 ,
, 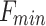 represent the maximum and minimum values of the variation factor, respectively.
represent the maximum and minimum values of the variation factor, respectively. 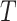 represents the maximum number of iterations, and
represents the maximum number of iterations, and 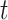 represents the current number of iterations.
represents the current number of iterations.
-
(c)
Adaptive Hybrid Differential Evolution algorithm (AHDE) proposed by Reference [43] combines adaptive dynamic parameter control mechanism and a local random search (LRS) operator to obtain higher robustness and effectiveness.
-
(d)
JADE proposed by Reference [33] is an adaptive differential evolution algorithm with an optional external archive. Their simulation results show that in most cases, the convergence performance of the JADE algorithm is better than other adaptive DE algorithms.
-
(e)
Sine Cosine Algorithm (SCA) proposed by Reference [44] is a novel population-based optimization algorithm. SCA can effectively solve practical problems with constraints and unknown search spaces.
-
(f)
Opposition-based Barebones Particle Swarm Optimization (OBPSO) combines opposition-based learning and barebones particle swarm optimization to improve the quality of solutions. In most cases, CLPSO performs better than basic PSO and other PSO variants [45].
Parameter setting
For a fair comparison, the dimensionality (N) of all algorithms is set to 30, the size of population (sizepop) is set to 30, and the maximum number of iterations (maxgen) is set to 1000.
Based on the suggestion of reference [33] for JADE, the rate of parameter adaptation c is set to 0.1, and the greedy degree p of the mutation strategy is set to 0.05. For DE, LADE, SADE, AHDE, JADE, SCA, and OBPSO, the grid search method is used to select parameters. For DE and its variants, crossover probability (or initial crossover probability) CR is set to 0.5, and mutation probability F (or initial mutation probability = 0.5) is set in the range [0.2, 0.5]. As for SCA, 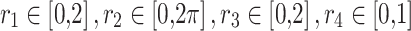 . For OBPSO, the learning rate
. For OBPSO, the learning rate 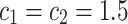 , and the inertia weight
, and the inertia weight 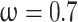 .
.
Results and analysis
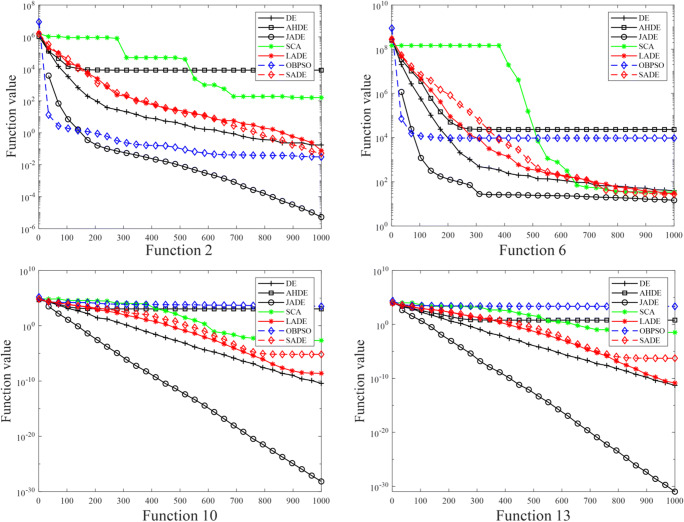
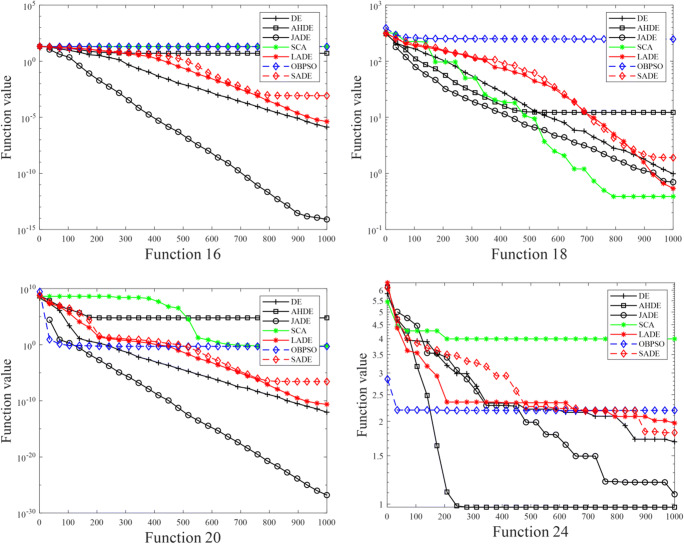
Each benchmark function is tested 30 times for each algorithm, and the final mean and standard deviation are shown in Table 2. Figures 2 and 3 show several average convergence plots for unimodal and multimodal benchmark functions, respectively. The results are analyzed in detail below.
Table 2.
Comparison results between JADE and other evolutionary algorithms
| Function | JADE | AHDE | SADE | LADE | DE | OBPSO | SCA | |
|---|---|---|---|---|---|---|---|---|
| F1 | Mean | 1.65E-22 | 5.501E + 00 (+) | 1.29E-07 (+) | 3.57E-11 (+) | 7.06E-13 (+) | 3.52E + 02 (+) | 7.91E-05 (+) |
| Std. | 9.05E-22 | 8.01E + 00 | 2.92E-07 | 8.32E-11 | 3.75E-13 | 3.81E + 02 | 2.29E-04 | |
| F2 | Mean | 2.29E-02 | 1.70E + 03(+) | 1.02E-01(+) | 2.97E-01(+) | 5.71E-01(+) | 8.45E + 00(+) | 2.79E + 01(+) |
| Std. | 5.72E-02 | 3.24E + 03 | 1.02E-01 | 1.62E + 01 | 3.33E-01 | 2.21E + 01 | 1.16E + 02 | |
| F3 | Mean | -1.00E + 00 | -9.89E-01(+) | -1.00E + 00(≈) | -1.00E + 00(≈) | -1.00E + 00(≈) | -8.66E-01(+) | -1.00E + 00(≈) |
| Std. | 1.08E-05 | 1.47E-02 | 6.06E-10 | 1.13E-13 | 1.37E-15 | 2.15E + 01 | 1.08E-05 | |
| F4 | Mean | 1.39E-20 | 3.06E + 06(+) | 6.70E-03(+) | 4.43E-06(+) | 7.72E-08(+) | 2.87E + 08(+) | 1.44E + 00(+) |
| Std. | 6.68E-20 | 7.13E + 06 | 1.03E-02 | 1.63E-05 | 3.66E-08 | 3.28E + 08 | 4.53E + 00 | |
| F5 | Mean | 3.31E-01 | 1.37E-01(-) | 1.06E-01(-) | 1.07E-01(-) | 3.87E-01(≈) | 1.45E-02(-) | 2.77E-02(-) |
| Std. | 7.75E-02 | 1.73E-01 | 3.62E-02 | 3.75E-02 | 9.21E-02 | 1.78E-02 | 1.79E-02 | |
| F6 | Mean | 1.37E + 01 | 2.31E + 05(+) | 4.71E + 01(+) | 5.12E + 01(+) | 6.25E + 01(+) | 2.13E + 03(+) | 1.11E + 03(+) |
| Std. | 1.17E + 01 | 5.07E + 05 | 2.41E + 01 | 2.37E + 01 | 3.45E + 01 | 7.35E + 03 | 4.45E + 03 | |
| F7 | Mean | 9.94E-03 | 4.94E + 03(+) | 1.41E + 04(+) | 1.36E + 04(+) | 1.32E + 04(+) | 1.02E + 05(+) | 3.35E + 03(+) |
| Std. | 2.79E-02 | 2.50E + 03 | 2.33E + 03 | 2.08E + 03 | 1.78E + 03 | 6.46E + 04 | 2.74E + 03 | |
| F8 | Mean | 2.55E-02 | 4.86E + 01(+) | 5.77E + 00(+) | 4.35E + 00(+) | 3.98E + 00(+) | 1.00E + 02(+) | 1.80E + 01(+) |
| Std. | 2.44E-02 | 8.39E + 00 | 1.01E + 00 | 5.60E-01 | 6.14E-01 | 0.00E + 00 | 1.11E + 01 | |
| F9 | Mean | 1.27E-11 | 1.21E + 00(+) | 3.85E-05(+) | 5.51E-07(+) | 2.93E-07(+) | 6.18E + 01(+) | 1.78E-05(+) |
| Std. | 4.20E-11 | 1.42E + 00 | 2.02E-05 | 1.14E-06 | 6.68E-08 | 2.98E + 01 | 4.41E-05 | |
| F10 | Mean | 1.07E-23 | 3.49E + 02(+) | 7.33E-06(+) | 2.35E-09(+) | 5.20E-11(+) | 2.08E + 04(+) | 4.65E-02(+) |
| Std. | 5.85E-23 | 4.31E + 02 | 9.15E-06 | 5.21E-09 | 2.54E-11 | 1.23E + 04 | 1.62E-01 | |
| F11 | Mean | 1.40E + 00 | 3.05E + 02(+) | 0.00E + 00(-) | 0.00E + 00(-) | 0.00E + 00(-) | 2.42E + 04(+) | 1.00E-01(-) |
| Std. | 4.77E + 00 | 4.60E + 02 | 0.00E + 00 | 0.00E + 00 | 0.00E + 00 | 1.26E + 04 | 4.03E-01 | |
| F12 | Mean | 8.62E-54 | 9.69E-04(+) | 1.11E-33(+) | 2.52E-41(+) | 4.64E-52(+) | 1.44E-13(+) | 3.31E-07(+) |
| Std. | 3.96E-53 | 3.80E-03 | 3.66E-33 | 1.38E-40 | 1.74E-51 | 4.56E-13 | 1.52E-06 | |
| F13 | Mean | 1.58E-26 | 2.67E + 01(+) | 1.06E-06(+) | 2.95E-10(+) | 5.79E-12(+) | 2.42E + 03(+) | 5.21E-03(+) |
| Std. | 7.41E-26 | 2.83E + 01 | 1.19E-06 | 8.34E-10 | 2.69E-12 | 1.32E + 03 | 1.69E-02 | |
| F14 | Mean | -4.50E + 02 | -9.09E + 01(+) | -4.50E + 02(≈) | -4.50E + 02(≈) | -4.50E + 02(≈) | 2.35E + 04(+) | -4.50E + 02(≈) |
| Std. | 5.28E-14 | 4.35E + 02 | 4.78E-05 | 1.30E-08 | 1.89E-11 | 1.08E + 04 | 8.16E-02 | |
| F15 | Mean | -4.50E + 02 | 4.34E + 03(+) | 1.33E + 04(+) | 1.35E + 04(+) | 1.31E + 04(+) | 1.02E + 05(+) | 2.03E + 03(+) |
| Std. | 4.41E-02 | 2.67E + 03 | 1.80E + 03 | 1.96E + 03 | 1.75E + 03 | 5.72E + 04 | 2.15E + 03 | |
| F16 | Mean | 7.57E-02 | 3.64E + 00(+) | 5.82E-04(-) | 6.67E-06(-) | 1.75E-06(-) | 1.99E + 01(+) | 1.39E + 01(+) |
| Std. | 2.93E-01 | 2.10E + 00 | 3.99E-04 | 5.03E-06 | 4.64E-07 | 1.67E-01 | 8.94E + 00 | |
| F17 | Mean | -1.69E + 02 | -1.56E + 02(-) | -1.79E + 02(+) | -1.81E + 02(+) | -1.78E + 02(+) | -7.58E + 02(+) | -1.42E + 02(-) |
| Std. | 1.69E + 00 | 3.18E + 00 | 2.34E + 00 | 2.30E + 00 | 3.05E + 00 | 2.29E + 02 | 4.79E + 00 | |
| F18 | Mean | 3.52E-01 | 4.32E + 01(+) | 1.50E + 00(+) | 4.45E-01(+) | 9.10E-01(+) | 2.47E + 02(+) | 4.71E-01(+) |
| Std. | 8.00E-02 | 1.75E + 01 | 3.13E-01 | 8.00E-02 | 1.35E-01 | 2.34E + 01 | 2.03E-01 | |
| F19 | Mean | 4.47E + 00 | 3.26E + 00(-) | 3.72E + 00(-) | 4.35E + 00(≈) | 4.51E + 00(≈) | 1.28E + 01(+) | 9.00E + 00(+) |
| Std. | 3.54E-01 | 6.32E-01 | 4.47E-01 | 3.75E-01 | 4.02E-01 | 7.41E-01 | 1.27E + 00 | |
| F20 | Mean | 1.90E-12 | 2.18E + 05(+) | 4.52E-07(+) | 1.81E-10(+) | 3.46E-03(+) | 6.10E-01(+) | 4.03E + 03(+) |
| Std. | 1.30E-12 | 6.24E + 05 | 5.49E-07 | 5.31E-10 | 1.89E-02 | 6.99E-01 | 2.05E + 04 | |
| F21 | Mean | 1.15E-03 | 4.14E + 00(+) | 5.76E-05(-) | 8.91E-08(-) | 3.38E-09(-) | 2.33E + 02(+) | 2.84E-01(+) |
| Std. | 3.02E-03 | 3.61E + 00 | 8.92E-05 | 2.91E-07 | 8.05E-09 | 9.66E + 01 | 2.73E-01 | |
| F22 | Mean | -2.55E + 01 | -2.13E + 01(+) | -2.17E + 01(+) | -2.07E + 01(+) | -2.04E + 01(+) | -6.27E + 00(+) | -2.16E + 01(+) |
| Std. | 5.19E + 00 | 7.51E-01 | 6.74E-01 | 5.17E-01 | 6.27E-01 | 1.76E + 00 | 5.04E-01 | |
| F23 | Mean | -4.59E + 03 | 3.71E + 04(+) | 5.10E + 04(+) | 5.08E + 04(+) | 2.75E + 04(+) | 2.17E + 03(+) | 8.83E + 03(+) |
| Std. | 2.48E + 02 | 4.49E + 04 | 1.57E + 04 | 1.54E + 04 | 9.88E + 03 | 6.25E + 03 | 2.46E + 04 | |
| F24 | Mean | 1.27E + 00 | 1.35E + 00(≈) | 1.86E + 00(+) | 1.85E + 00(+) | 1.82E + 00(+) | 1.70E + 00(+) | 4.00E + 00(+) |
| Std. | 2.89E-01 | 2.00E-01 | 1.77E-01 | 1.58E-01 | 1.49E-01 | 8.57E-01 | 2.21E-01 | |
| F25 | Mean | 1.35E-02 | 3.03E + 01(+) | 3.94E-01(+) | 6.78E-01(+) | 6.06E + 00(+) | 2.31E + 02(+) | 1.86E + 01(+) |
| Std. | 3.59E-02 | 9.46E + 00 | 4.32E-01 | 3.64E-01 | 4.42E + 00 | 4.26E + 01 | 2.45E + 01 | |
| F26 | Mean | 6.26E + 00 | 3.37E + 01(+) | 1.07E + 00(-) | 2.20E + 00(-) | 1.68E + 01(+) | 2.65E + 02(+) | 5.57E + 01(+) |
| Std. | 2.49E + 00 | 6.63E + 00 | 1.23E + 00 | 8.28E-01 | 1.24E + 00 | 6.18E + 01 | 3.01E + 01 | |
| F27 | Mean | 8.04E-09 | 1.44E-08(+) | 1.04E-08(+) | 9.88E-09(+) | 5.74E-09(-) | 0.00E + 00(-) | 1.09E-08(+) |
| Std. | 1.25E-08 | 2.93E-08 | 2.26E-08 | 2.51E-08 | 8.60E-09 | 0.00E + 00 | 1.35E-08 | |
| F28 | Mean | -3.95E + 01 | -3.88E + 01(-) | -3.95E + 01(-) | -3.94E + 01(-) | -3.91E + 01(-) | -3.51E + 01(-) | -2.49E + 01(-) |
| Std. | 1.49E-02 | 4.68E-01 | 3.38E-03 | 2.21E-02 | 2.23E-01 | 3.27E + 00 | 9.86E-01 | |
| F29 | Mean | 2.39E + 01 | 1.14E + 14(+) | 2.78E + 02 (+) | 9.89E + 01(+) | 9.02E + 01(+) | 2.10E + 08(+) | 2.92E + 12(+) |
| Std. | 2.93E + 01 | 2.41E + 14 | 5.62E + 01 | 1.15E + 02 | 1.54E + 02 | 8.98E + 08 | 1.16E + 13 | |
| +(JADE is significantly better) | 24 | 19 | 20 | 20 | 26 | 23 | ||
| -(JADE is significantly worse) | 4 | 8 | 6 | 5 | 3 | 4 | ||
| ≈ | 1 | 2 | 3 | 4 | 0 | 2 | ||
Note: Bold values indicate the best performance
Fig. 2.
Convergence graphs for several unimodal benchmark functions
Fig. 3.
Convergence graphs for several multimodal benchmark functions
As shown in Table 2, JADE outperforms other algorithms for F1, F2, F4, F6 to F10, F12, F13, F15, F18, F20, F22 to F25, and F29, indicating that JADE has a better structure to avoid falling into local optima.
As shown in Table 2, for most benchmark functions, the standard deviation of JADE is lower than that of other algorithms, indicating that JADE is more computationally stable and more robust than other algorithms.
It can be seen from Figs. 2 and 3 that, in most cases, the iteration speed and accuracy of JADE are better than other algorithms, indicating that JADE has an efficient global search capability.
The results of the Wilcoxon test at a 5% significance level are shown in Table 2. The JADE algorithm is significantly different from other algorithms and outperforms other algorithms in at least 19 benchmark algorithms.
Therefore, JADE has good potential in solving practical problems, and this study uses JADE to optimize the parameters of IndRNN.
Numerical examples and results
In this section, two actual examples were applied to verify the feasibility and superiority of the proposed text-based forecasting method. Based on the BP Statistical Review of World Energy 2021, the world’s top three oil-consuming countries are the United States, China, and India, with 17,178 thousand barrels daily, 14,225 thousand barrels daily, and 4669 thousand barrels daily in 2020, respectively. But there is no official data on China’s monthly oil consumption, so this study only used the data from the United States and India for the experiments. All techniques are implemented using Python 3.8. Deep learning networks, such as LSTM, RNN, and CNN models, are built by a Python library, TensorFlow.
Example 1: U.S. oil consumption forecasting
Data descriptions and experimental designs
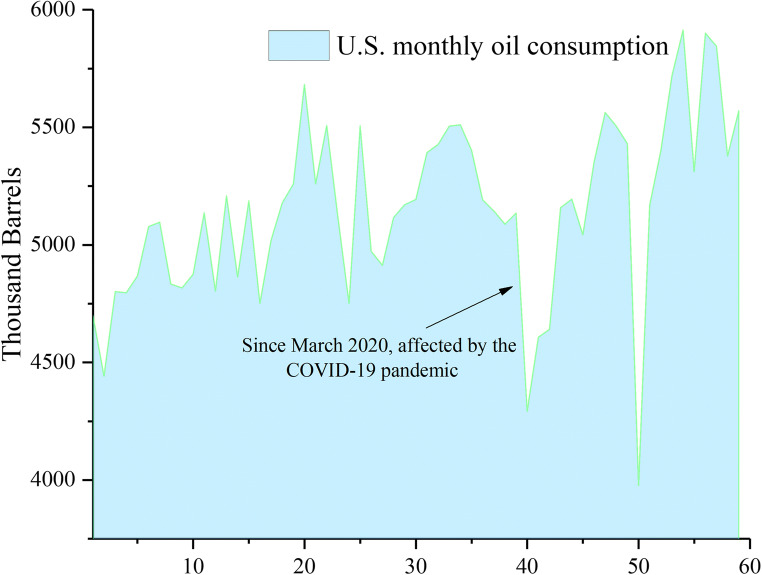
This study used monthly oil consumption as our forecast variables. The monthly oil consumption data by the industrial sector were selected from the US EIA (http://www.eia.gov) and covered the period from January 2017 to November 2021, with a total of 59 observations as shown in Fig. 4. As shown in Fig. 4, during the COVID-19 pandemic, oil consumption has exhibited an uncertain and volatile trend. That is, since March 2020, to cope with the COVID-19, confinement policies and measures were implemented by the US government. Affected by the confinement policy, from March 2020 to April 2020, US industrial oil consumption went down 842.151 thousand barrels per day, which represents a total reduction of 16.40%. With reopening policies, oil consumption had a significant increase between May 2020 to Dec 2020.
Fig. 4.
U.S. monthly oil consumption
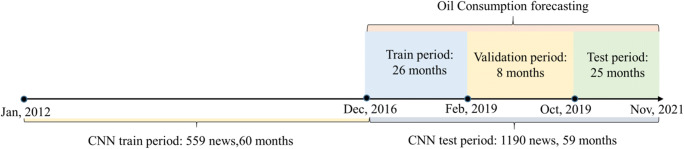
From the section “Crude oil news” of the well-known energy news website “Oilprice.com”, oil news headlines were collected using the keyword “American oil”. “Oilprice.com” partners with some of the most prominent companies in the financial news space. “Oilprice.com” is a suitable source for collecting helpful data to predict oil consumption. This study chose the headline rather than the full article because the headline is the essence of the content.
The historical oil consumption is selected to cover the period from December 2016 to October 2021, with a total of 59 observations. This study collected 1749 oil news headlines from January 2012 to November 2021. Online news is spliced into a sample for every month.
Figure 5 shows that in the CNN model, the training period is January 2012–December 2016, covering 559 news headlines and 60 monthly records. The test set begins from January 2017–to November 2021, covering 1190 news headlines and 59 monthly collections. Given that the input variables of oil consumption prediction use CNN models, the CNN test period is used to determine the training and testing periods for the oil consumption forecasting model. The training period for the oil consumption forecasting model is January 2017–February 2019 and consists of 26 monthly records. The validation set is March 2019–October 2019, including eight monthly records. By contrast, the testing set is from November 2019 to November 2021 and consists of 25 monthly records. The oil consumption prediction models are estimated and tested using rolling windows. When testing with the testing set, the training set, and the validation set constitute a new training set to train the prediction model.
Fig. 5.
Training, validation, and testing period of oil consumption prediction model
Text mining of online news
Figure 6 shows the top 100 words cloud with the largest term frequency-inverse document frequency (TF–IDF) weightings. The top 20 words are “crude,” “API,” “report,” “build,” “inventory,” “price,” “U(USA),” “draw,” “Venezuela,” “gas,” “energy,” “gasoline,” “sanction,” “pipeline,” “Iran,” “oil,” “export,” “surprise,” “production,” “major,” “Saudi”. Figure 6 also shows “crude,” “oil,” “energy”, “gasoline,” and “gas” represent a close relationship with oil. At the same time, “production,” “build,” “inventory,” “export,” and “price” may suggest the oil supply, oil inventory, and oil price, which are related closely to the fluctuation of oil consumption. Furthermore, “the USA,” “Iran,” “Venezuela,” and “Saudi,” reflect political events. News headlines cover a variety of factors that affect oil consumption. For instance, the COVID-19 pandemic over the USA has had a considerable effect on the movement of oil consumption. Especially at the beginning of COVID-19, the news media became pessimistic about the subsequent oil consumption, and the subsequent oil consumption did decline rapidly. Therefore, analyzing the semantic relations hidden in online news modes will facilitate oil consumption forecasting.
Fig. 6.
Top 100 words cloud
CNN is used to classify text, and the CNN value represents the probability that the text is classified as positive sentiment. Using the grid search, after a series of experiences, the satisfactory parameters of the CNN model are batch size = 50, the number of filters = 128, filter size = 2,3,4, and embedding dimension = 100. The other parameters of CNN are set in reference to previous studies [46]: l2 regulation = 0; Drop out probability = 0.5; The max sequence lengths = 150.
Four criteria, namely accuracy, precision, recall, and F-measure are employed to test the performance of CNN models. The four criteria are described as follows:
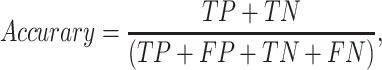 |
4 |
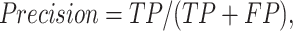 |
5 |
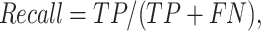 |
6 |
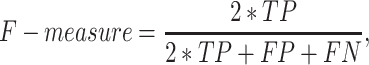 |
7 |
where 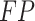 is the number of true positive samples categorized as negative,
is the number of true positive samples categorized as negative, 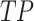 is the number of true positive samples classified as positive,
is the number of true positive samples classified as positive, 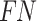 is the number of true positive samples categorized as negative, and
is the number of true positive samples categorized as negative, and 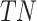 is the number of true negative samples classified as negative.
is the number of true negative samples classified as negative.
The results of CNN model are accuracy = 0.63, precision = 0.63; recall = 0.63; F-measure = 0.63. These results suggest that news headlines contain considerable oil supply and demand information leading to oil consumption movements.
The CNN values and oil consumption data are scaled linearly to be included in the range [0.1,0.9] to visualize their relationship by Eq. (8):
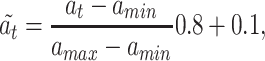 |
8 |
where 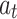 denotes the CNN values at time t, and
denotes the CNN values at time t, and 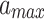 and
and  denote the minimum and maximum values of the CNN series, respectively.
denote the minimum and maximum values of the CNN series, respectively.
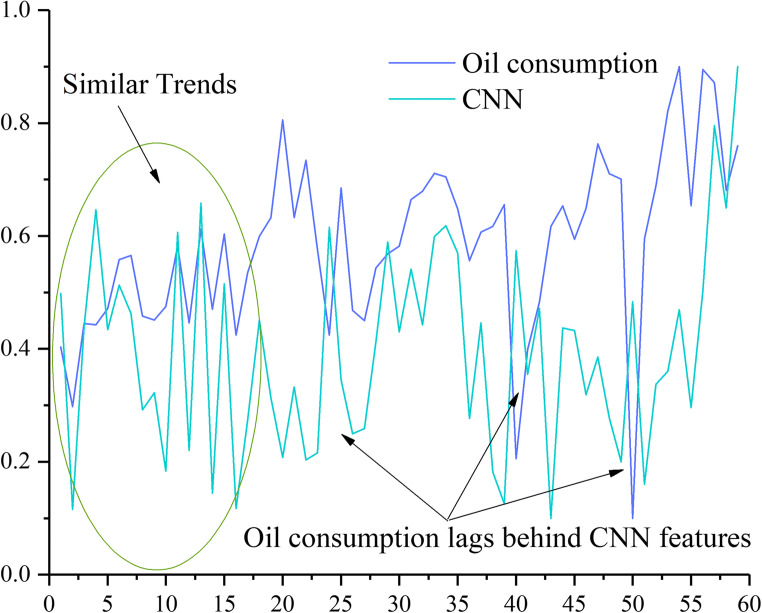
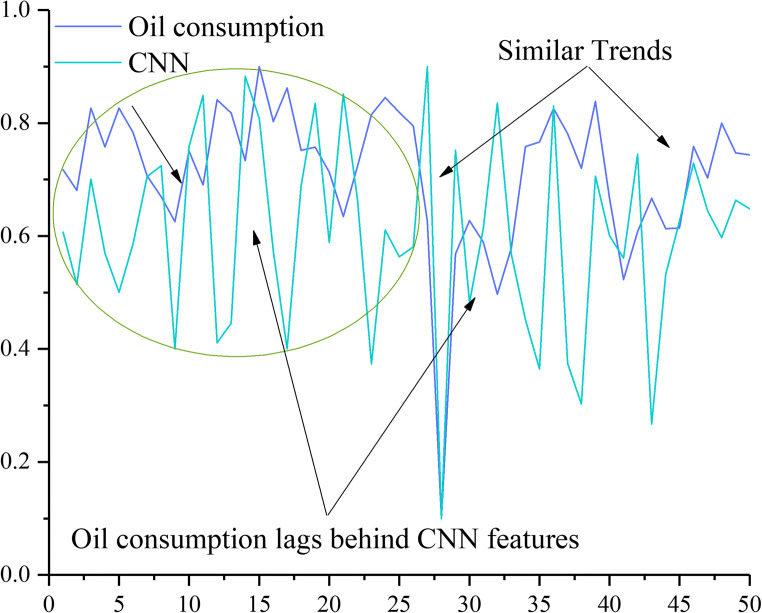
Figure 7 shows the trend chart for oil consumption compared with the CNN classifications features. The CNN values present similar trends to oil consumption, whether with a contemporary or slight lag. The data sets show good similarity between the CNN values and oil consumption. Meanwhile, in most cases, the CNN values lag behind the oil consumption, indicating that the CNN values have guiding characteristics for the oil consumption. In particular, the CNN values show better similarity or guiding characteristics to oil consumption when the oil consumption fluctuates wildly. Evidently, during the period of the COVID-19 pandemic, the U.S. oil consumption became highly volatile as shown in Fig. 7. Thus, the feature of the CNN classifications is beneficial in forecasting oil consumption.
Fig. 7.
CNN features compared with U.S. oil consumption
Oil consumption forecasting
Performance assessment
In this study, MAE, MAPE, and RMSE are employed to evaluate the forecasting accuracy over the test period. These statistical criteria are used to assess the difference between the predicted values and actual values. MAE, MAPE, and RMSE are described as follows:
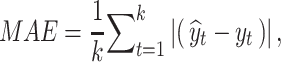 |
9 |
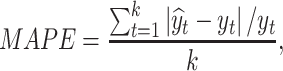 |
10 |
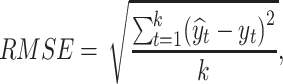 |
11 |
where 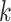 is the size of the test dataset,
is the size of the test dataset, 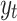 is the real value of oil consumption at month t, and
is the real value of oil consumption at month t, and 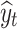 is the predicted value of oil consumption at month t. The additional explanatory power of online news features on oil consumption forecasting is quantified by improvement rate (IR):
is the predicted value of oil consumption at month t. The additional explanatory power of online news features on oil consumption forecasting is quantified by improvement rate (IR):
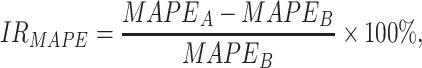 |
12 |
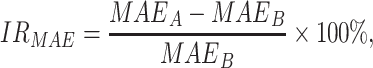 |
13 |
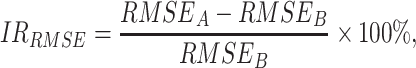 |
14 |
where 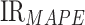 ,
, 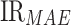 , and
, and 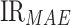 represents the improvement rate of MAPE, MAE, and MAE, respectively.
represents the improvement rate of MAPE, MAE, and MAE, respectively.
-
2)
Comparable models and parameter setting
To confirm the effectiveness and stability of the attention-based JADE-IndRNN model, its forecasting accuracy is compared with those of eight comparable models, namely, JADE-BPNN, JADE-SVM, JADE-LSTM, JADE-GRU, JADE-RNN, attention-based JADE-LSTM, JADE-IndRNN, and attention-based DE-IndRNN. Among them, backpropagation neural network (BPNN), support vector machines (SVM), long short-term memory (LSTM), gated recurrent unit (GRU), recurrent neural network (RNN), and IndRNN are compared as individual forecasting models. They are popular forecasting models for energy consumption [47–49]. For a fair comparison, the JADE algorithm is adopted to optimize the parameter of all individual models. Besides, DE and JADE are used as different intelligent optimization algorithms to search the parameters of the attention-based IndRNN model to determine a more satisfying optimization algorithm.
Meanwhile, hyperparameters of JADE are selected using the grid search process. Based on several hyperparameter experiments, we find that a combination of parameters yields excellent performance, which is sizepop = 30, maxgen = 30, initial crossover probability = 0.5, initial mutation probability = 0.5, and the rate of parameter adaptation c is set to 0.1, and the greedy degree p of the mutation strategy is set to 0.05.
The range of layers of the attention-based IndRNN is set within [1, 5], that of the number of the time step is set within [2, 5], that of the number of units of the single hidden layer is set within [1, 32], that of the number of batch size is set within [10, 23], and that of the steps of learning rate is specified within the [100,10000].
According to the search results of the JADE algorithm, we find that a combination of the attention-based IndRNN hyperparameters yields excellent forecasting performance, that is, the number of layers = 2, the number of units of the single hidden layers = 22, the number of batch size = 23, the steps of learning rate = 8542, and the number of time step = 3. Similar to the attention-based JADE-IndRNN, the lag order of online news features and historic data is both set as 3. Table 3 shows the adopted parameter values of all forecasting models based on their intelligent optimization algorithm.
Table 3.
Parameters of the used forecasting models
| Models | Parameter combination |
|---|---|
| JADE-BPNN | epochs = 98; learning rate = 0.05; hidden neurons = 3 |
| JADE-SVM | gamma = 4.9; kernel = “rbf”; C = 2.6 |
| JADE-LSTM | epochs = 387; batch size = 23; hidden neurons = 19 |
| JADE-GRU | epochs = 301; batch size = 18; hidden neurons = 22 |
| JADE-RNN | epochs = 258; batch size = 21; hidden neurons = 23 |
| Attention-based JADE-LSTM | epochs = 244; batch size = 22; hidden neurons = 15 |
| JADE-IndRNN | number of layers = 2; the steps of learning rate = 6719; batch size = 20; hidden neurons = 18 |
| Attention-based DE-IndRNN | number of layers = 2; the steps of learning rate = 9102; batch size = 21; hidden neurons = 15 |
| Attention-based JADE-IndRNN | number of layers = 2; the steps of learning rate = 8542; batch size = 23; hidden neurons = 22 |
-
3)
Results and discussion
In this study, the rolling-based forecasting procedure is used in one-step-ahead forecasting. The MAPE, RMSE, and MAE of the different models with text features and historical oil consumption are reported in Table 4. The results are analyzed as follows:
Table 4.
Performance comparison of different forecasting techniques
| Models | MAPE (%) | MAE | RMSE |
|---|---|---|---|
| JADE-SVM | 10.81 | 569.80 | 682.27 |
| JADE-BPNN | 5.89 | 291.95 | 380.61 |
| JADE-LSTM | 5.48 | 279.67 | 401.91 |
| JADE-GRU | 5.37 | 283.05 | 424.20 |
| JADE-RNN | 5.49 | 281.84 | 390.98 |
| Attention-based JADE-LSTM | 4.52 | 226.71 | 325.93 |
| JADE-IndRNN | 4.07 | 211.48 | 275.40 |
| Attention-based DE-IndRNN | 4.41 | 223.21 | 297.47 |
| Attention-based JADE-IndRNN | 2.99 | 157.63 | 191.82 |
Note: Bold values mean the best forecasting performance
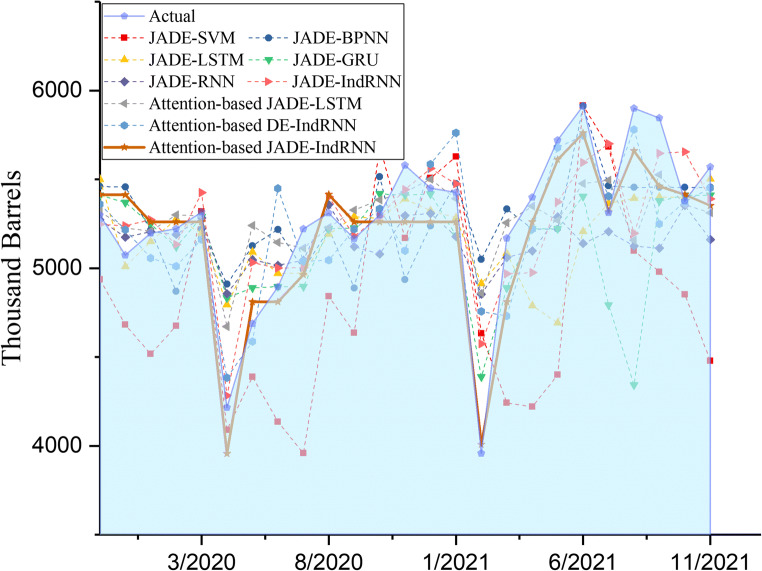
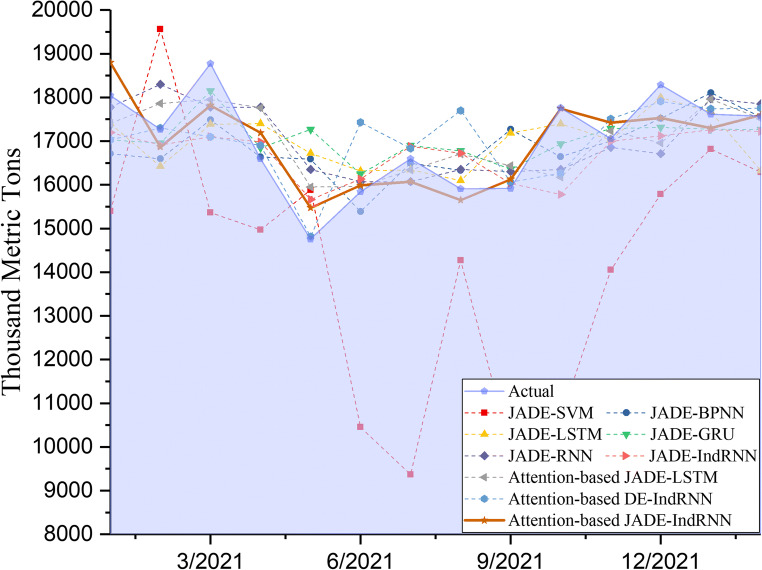
As shown in Fig. 8, attention-based JADE-IndRNN exhibits better forecasting performance as compared to the other popular models. Table 5 indicates that the MAPE value of attention-based JADE-IndRNN is 72.34%, 49.24%, 45.44%, 44.32%, 44.54%, 33.85%, 26.54%, and 32.20% lower than that of JADE-SVM, JADE-BPNN, JADE-LSTM, JADE-GRU, JADE-RNN, attention-based JADE-LSTM, JADE-IndRNN, and attention-based DE-IndRNN, respectively. Thus, the attention-based JADE-IndRNN model shows satisfactory performance in oil consumption forecasting.
Attention-based JADE-IndRNN outperforms attention-based DE-IndRNN in each evaluation index. Table 5 indicates that the MAPE value of attention-based JADE-IndRNN is 32.20% lower than that of attention-based DE-IndRNN. The results show that the attention-based IndRNN model based on JADE optimization can achieve better results than the model optimized by basic DE, which also shows that the global search ability of JADE is significantly stronger than that of the basic DE algorithm.
As shown in Table 4, attention-based JADE-LSTM and attention-based JADE-IndRNN outperform JADE-SVM, JADE-BPNN, JADE-LSTM, JADE-GRU, JADE-RNN in terms of MAPE, MAE, and RMSE. The results show that attention-based mechanisms can effectively highlight key influencing factors, thereby improving prediction performance.
Fig. 8.
Forecasting performances of different models
Table 5.
The improvement of the proposed model and comparable models
| Comparative models | 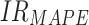 |
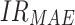 |
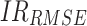 |
|---|---|---|---|
| The proposed model vs. JADE-SVM | 72.34% | 72.33% | 71.89% |
| The proposed model vs. JADE-BPNN | 49.24% | 46.01% | 49.60% |
| The proposed model vs. JADE-LSTM | 45.44% | 43.64% | 52.27% |
| The proposed model vs. JADE-GRU | 44.32% | 44.31% | 54.78% |
| The proposed model vs. JADE-RNN | 45.54% | 44.07% | 50.94% |
| The proposed model vs. attention-based JADE-LSTM | 33.85% | 30.47% | 41.15% |
| The proposed model vs. JADE-IndRNN | 26.54% | 25.46% | 30.35% |
| The proposed model vs. attention-based DE-IndRNN | 32.20% | 29.38% | 35.52% |
Note: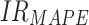 means improvement rate of MAPE;
means improvement rate of MAPE;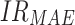 means improvement rate of MAE;
means improvement rate of MAE;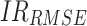 represents the improvement rate of RMSE
represents the improvement rate of RMSE
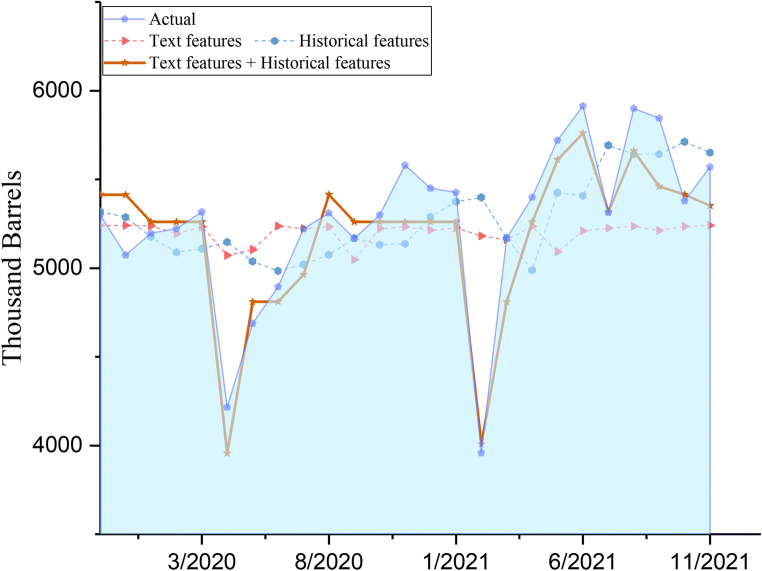
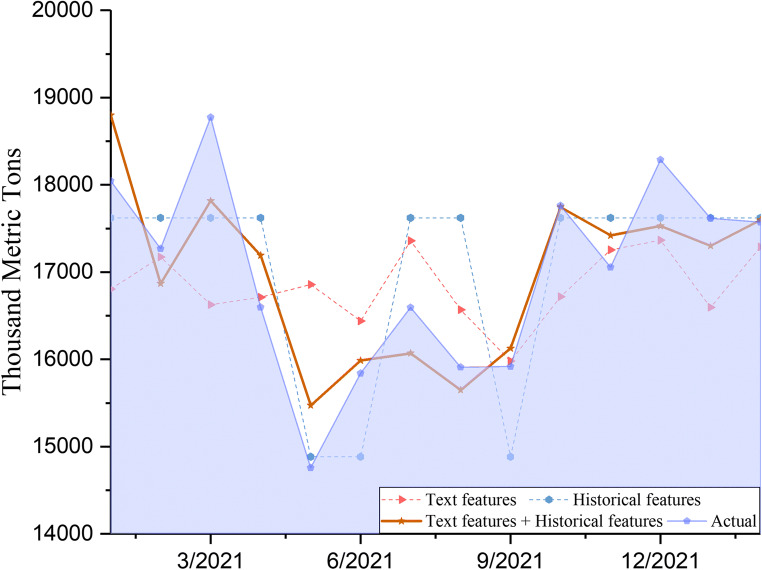
This study tested the relative predictive power of online news features through a comparison of the performances of text features (three features), historical oil consumption (three features), and by combining text features and historical oil consumption (six features). Based on the same premise when using attention-based JADE-IndRNN, the results of the IRs are described in Table 6. These results indicate that the performances of using the text feature with historical oil consumption are considerably better than that of using text features or historical oil consumption, in terms of the 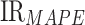 ,
, 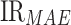 , and
, and 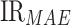 criteria. Figure 9 shows that using historical oil consumption did not accurately predict the sharply fluctuating oil consumption during the COVID-19 period. Meanwhile, using only the text features leads to poor oil consumption prediction accuracy. The results using text feature and historical oil consumption are improved by 50.90% and 48.98%, respectively compared with the results with the text features or historical oil consumption data in terms of
criteria. Figure 9 shows that using historical oil consumption did not accurately predict the sharply fluctuating oil consumption during the COVID-19 period. Meanwhile, using only the text features leads to poor oil consumption prediction accuracy. The results using text feature and historical oil consumption are improved by 50.90% and 48.98%, respectively compared with the results with the text features or historical oil consumption data in terms of 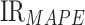 .
.
Table 6.
Forecasting performances of different predictive factors
| MAPE (%) | MAE | RMSE | |
|---|---|---|---|
| Text features (1) | 6.09 | 305.41 | 433.49 |
| Historical oil consumption features (2) | 5.86 | 285.5 | 420.02 |
| Combination: (1) + (2) | 2.99 | 157.63 | 191.82 |
| IR from (1) to (1) + (2) | 50.90% | 48.39% | 55.75% |
| IR from (2) to (1) + (2) | 48.98% | 44.79% | 54.33% |
Note: IR means improvement rate
Note: Bold values indicate the best forecasting performance
Fig. 9.
Forecasting performances of different predictors using attention-based JADE-IndRNN
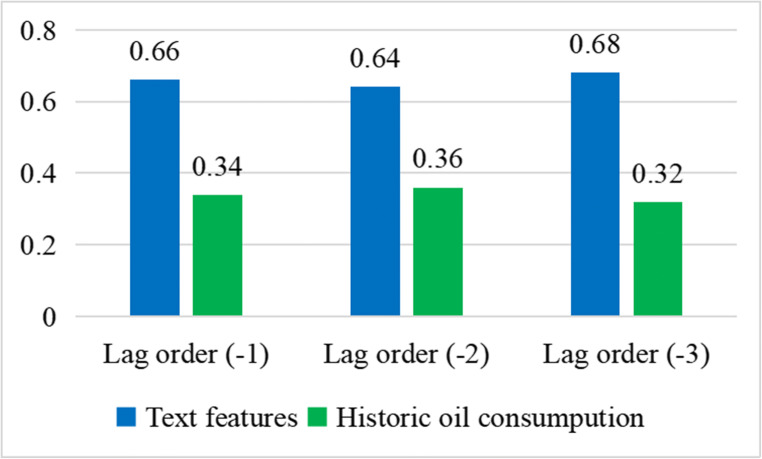
The attention weight obtained by the attention-based IndRNN is considered in the evaluation of each predictor. The relative importance of these predictors in oil consumption prediction is analyzed and discussed quantitatively. The ranking of the attention weight for oil consumption forecasting is shown in Fig. 10. The result shows that text features are more important than historical oil consumption in forecasting oil consumption. By assigning higher weights to more important factors, the predictive performance of the attention-based JADE-IndRNN model can be improved. Overall, using online text features can significantly improve the accuracy of oil consumption prediction. Therefore, the proposed methodology with oil online news as conducive predictive factors can be considered as an effective method for oil consumption predictors.
Fig. 10.
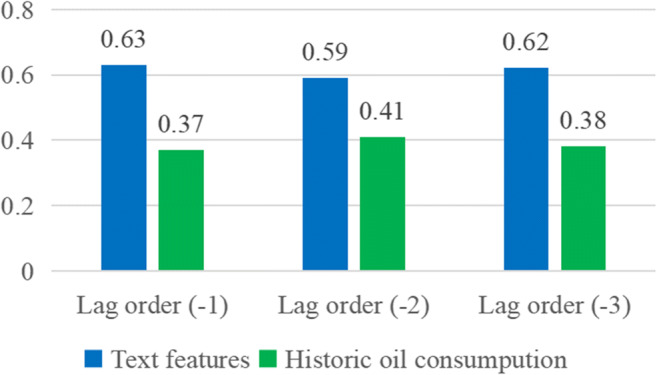
Ranking of the attention weight for U.S. oil consumption prediction
Example 2: indian oil consumption forecasting
Data retrieval
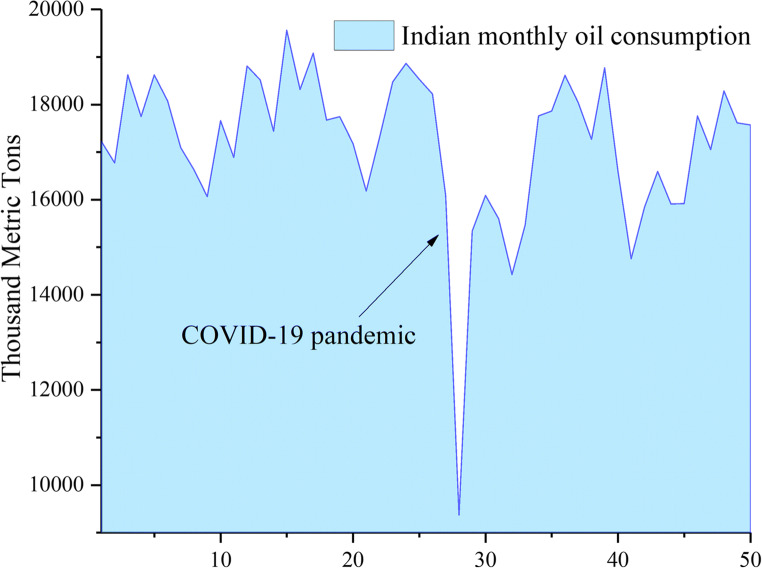
The Indian monthly oil consumption data were selected from the Indian Ministry of Petroleum and Natural Gas (MoPNG) and covered the period from January 2018 to February 2022, with a total of 50 observations. Since the beginning of the COVID-19 epidemic, Indian oil consumption has fluctuated sharply (seen in Fig. 11).
Fig. 11.
Indian monthly oil consumption
From January 2013 to February 2022, a total of 1176 oil news headlines were collected from “Crude oil news” using the keyword “India oil”. In the CNN model, the training period is January 2013–December 2017, covering 458 news headlines and 60 monthly records. The test set begins from January 2018 to February 2022, covering 718 news headlines and 50 monthly collections. The training period for the Indian oil consumption forecasting model is January 2018–April 2020 and consists of 28 monthly records. The validation set is May 2020–December 2020, including 8 monthly records. The testing set is from January 2021 to February 2022 and consists of 14 monthly records.
Text mining of oil news
Figure 12 shows the words cloud for Indian oil consumption. The top 20 words are.
Fig. 12.
Top 100 words cloud for Indian oil news
“oil,” “Iranian,” “import,” “Iran,” “U(USA),” “India,” “demand,” “coal,” “Saudi,” “India’s,” “price,” “crude,” “refiner,” “export,” “sanction,” “gas,” “cut,” “Indian,” “deal,” “OPEC,” “refinery,” “boost”. “Import,” “demand,” “price,” “export,” “sanction,” “cut,” and “boost” may suggest the oil supply, oil consumption, oil inventory, and oil price. Furthermore, “Iranian,” “Iran,” “USA,” “India,” “Saudi,” “India’s,” and “Indian,” may reflect political events related to oil. Online oil news contains various factors that affect oil consumption, so analyzing sentiment in oil news may improve the accuracy of oil consumption forecasts.
After a series of experiments, the satisfactory parameters of the CNN model are batch size = 47, number of filters = 128, filter size = 2,3,4, embedding dimension = 100, l2 regulation = 0, Drop out probability = 0.5, and the max sequence lengths = 150.
The results of CNN models are accuracy = 0.72, precision = 0.72; recall = 0.72; F-measure = 0.72. Figure 13 presents a trend graph for Indian oil consumption after scaling compared with the CNN classifications features. As seen from Fig. 13, there is a remarkable similarity between CNN value and oil consumption, which suggests that the CNN values may be helpful for Indian oil consumption prediction.
Fig. 13.
CNN features compared with Indian oil consumption
Oil consumption forecasting
Comparable models and parameter set
The comparison forecasting models are the same as the U.S. dataset. According to several hyperparameter experiments, a combination of JADE parameters yields excellent performance, which is sizepop = 25, maxgen = 30, initial crossover probability = 0.5, initial mutation probability = 0.5, and the rate of parameter adaptation c is set to 0.1, and the greedy degree p of the mutation strategy is set to 0.05.
The range of layers of the attention-based IndRNN is set within [1, 5], that of the number of the time step is set within [2, 5], that of the number of units of the single hidden layer is set within [1, 30], that of the number of batch size is set within [8, 25], and that of the steps of learning rate is specified within the [100,10000]. In the attention-based JADE-IndRNN model, the best lag order of CNN features and historical oil consumption data searched by JADE is 3. Thus, to be consistent, the input lag order of other forecasting models is also set to 3. Table 7 shows the parameter values of all forecasting models based on their intelligent optimization algorithm.
Table 7.
Parameter values of different forecasting models
| Models | Parameter combination |
|---|---|
| JADE-BPNN | epochs = 124; learning rate = 0.07; hidden neurons = 2 |
| JADE-SVM | gamma = 0.1; kernel = “rbf”; C = 2.4 |
| JADE-LSTM | epochs = 357; batch size = 21; hidden neurons = 14 |
| JADE-GRU | epochs = 281; batch size = 23; hidden neurons = 22 |
| JADE-RNN | epochs = 298; batch size = 21; hidden neurons = 24 |
| Attention-based JADE-LSTM | epochs = 268; batch size = 24; hidden neurons = 18 |
| JADE-IndRNN | number of layers = 2; the steps of learning rate = 5812; batch size = 18; hidden neurons = 19 |
| Attention-based DE-IndRNN | number of layers = 2; the steps of learning rate = 3568; batch size = 23; hidden neurons = 14 |
| Attention-based JADE-IndRNN | number of layers = 2; the steps of learning rate = 7594; batch size = 22; hidden neurons = 20 |
-
2)
Results and discussion
The forecasting performance of the different models is shown in Table 8. Table 9 provides the improvement of the proposed model and comparable models. From Tables 8 and 9, it can be found that:
Table 8.
Performance comparison of different forecasting techniques
| Models | MAPE (%) | MAE | RMSE |
|---|---|---|---|
| JADE-SVM | 19.45 | 3289.84 | 3926.28 |
| JADE-BPNN | 4.22 | 710.54 | 908.46 |
| JADE-LSTM | 4.21 | 700.89 | 897.69 |
| JADE-GRU | 4.06 | 671.69 | 885.24 |
| JADE-RNN | 4.41 | 747.69 | 904.57 |
| Attention-based JADE-LSTM | 4.04 | 685.76 | 829.60 |
| JADE-IndRNN | 3.96 | 648.80 | 886.17 |
| Attention-based DE-IndRNN | 3.95 | 676.68 | 940.48 |
| Attention-based JADE-IndRNN | 2.52 | 431.16 | 515.57 |
Note: Bold values mean the best forecasting performance
Table 9.
The improvement of the proposed model and comparable models
| Comparative model | 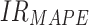 |
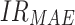 |
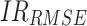 |
|---|---|---|---|
| The proposed model vs. JADE-SVM | 87.04% | 86.89% | 86.87% |
| The proposed model vs. JADE-BPNN | 40.28% | 39.32% | 43.25% |
| The proposed model vs. JADE-LSTM | 40.14% | 38.48% | 42.57% |
| The proposed model vs. JADE-GRU | 37.93% | 35.81% | 41.76% |
| The proposed model vs. JADE-RNN | 42.86% | 42.33% | 43.00% |
| The proposed model vs. attention-based JADE-LSTM | 37.62% | 37.13% | 37.85% |
| The proposed model vs. JADE-IndRNN | 36.36% | 33.55% | 41.82% |
| The proposed model vs. attention-based DE-IndRNN | 36.20% | 36.28% | 45.18% |
Compared with JADE-SVM, JADE-BPNN, JADE-LSTM, JADE-GRU, JADE-RNN, attention-based JADE-LSTM, JADE-IndRNN, and attention-based DE-IndRNN, the attention-based JADE-IndRNN model obtains all the best evaluation metrics (i.g., MAPE, MAE, and RMSE). As shown in Fig. 14, the proposed model achieves the prediction results closest to the actual oil consumption. Simply put, the attention-based JADE-IndRNN model shows better forecasting performance than any other forecasting technique.
The prediction performance of the attention-based JADE-IndRNN model is better than that of the attention-based DE-IndRNN model. The MAPE, MAE, and RMSE of the proposed model are 36.20%, 36.28%, and 45.18% lower than those of the attention-based DE-IndRNN model, highlighting the effectiveness of the JADE optimization.
Attention-based forecasting models can achieve significant improvements over general models. The MAPE of the attention-based JADE-IndRNN model decreases by 36.36% more than that of the JADE-IndRNN model, and the MAPE of the attention-based JADE-LSTM model decreases by 4.04% than that of the JADE-LSTM model, demonstrating the effectiveness and contribution of the attention mechanism.
Fig. 14.
Forecasting performances of different models
The results of using different predictive factors are shown in Table 10. The MAPE using text feature and historical oil consumption were improved by 46.72% and 36.04%, respectively compared with the results with the text features or historical oil consumption data. Figure 15 shows that using text features and historical oil consumption can more accurately predict the sharply fluctuating oil consumption amid the COVID-19 period. Overall, the results suggest that combining online text features and historical oil consumption can significantly improve the accuracy of oil consumption prediction amid the COVID-19 period.
Table 10.
Forecasting performances of different predictive factors
| MAPE (%) | MAE | RMSE | |
|---|---|---|---|
| Text features (1) | 4.73 | 803.65 | 1037.50 |
| Historical oil consumption features (2) | 3.94 | 659.59 | 821.66 |
| Combination: (1) + (2) | 2.52 | 431.16 | 515.57 |
| IR from (1) to (1) + (2) | 46.72% | 46.35% | 50.31% |
| IR from (2) to (1) + (2) | 36.04% | 34.63% | 37.25% |
Note: Bold values indicate the best forecasting performance
Fig. 15.
Forecasting performances of different predictors using attention-based JADE-IndRNN
The ranking of the attention weight for Indian oil consumption forecasting is shown in Fig. 16. By assigning higher weights to the text features, the predictive performance of the attention-based JADE-IndRNN model can be improved. The results suggest online oil news can provide more favorable forecasting value than historical oil consumption.
Fig. 16.
Ranking of the attention weight for Indian oil consumption prediction
Managerial implications
By projecting the industrial oil consumption under the COVID-19 pandemic and different policy scenarios and combined with the online social media information, some insights of interest to stakeholders are provided. To against the COVID-19, a series of confinement policies were implemented by governments of various countries. For example, affected by these confinement policies, U.S. industrial oil consumption in April 2020 was 16.40% lower than it was in March 2020. With a reopening policy in May 2020, oil consumption had a significant increase. Under the current pandemic scenario, the no-reopening policy may temporarily reduce industrial oil demand, but it could also help oil demand grow to a normal level more quickly. As the social media information contains some analyses of the relevant confinement or reopening policies, using online news can more accurately forecast the sharply fluctuating oil consumption.
The oil consumption prediction results have some implications for marketers. In particular, it could contribute to a better understanding of the internal relationship between online news information and the oil consumption movement. Media information can be employed to estimate whether the information is negative or positive to the oil market. In addition, an important positive relationship between online news and market performance was observed. That is, the oil market tends to perform better when online media shows positive sentiment towards the oil market. In contrast, the market has tended to underperform in the past when online media showed negative sentiment towards the oil market. Thus, the effect of online news on the oil market or relative fields should be considered by marketers.
Conclusion and future research
In many countries, oil consumption has exhibited uncertainty and volatility due to the effects of the COVID-19 pandemic, which poses huge difficulty to accurate predictions. This research uses qualitative information for oil consumption prediction because online news can reflect various related social events or unexpected political events that play significant roles in the volatile trend of oil consumption. Motivated by this issue, our study proposed a comprehensive text-based oil consumption prediction framework. The adaptation of CNN can generate informational time-series indicators automatically based on online oil news.
Attention-based JADE-IndRNN, a novel hybrid model that uses adaptive differential evolution (JADE) algorithm to identify hyperparameters for attention-based IndRNN was proposed. Attention mechanisms can capture key information, which can improve the accuracy of multi-factor forecasting. The effectiveness and superiority of the attention-based JADE-IndRNN were verified using the actual example of the U.S. and Indian oil consumption forecasting. The results showed that the attention-based JADE-IndRNN outperformed other popular models. A remarkable improvement in the accuracy of oil consumption forecasting can be achieved using the attention-based JADE-IndRNN model, particularly when using online oil news text features as compared with the performances of historic oil consumption data. Especially, our empirical results suggest that using online oil news text features can accurately predict the sharply fluctuating oil consumption during the COVID-19 pandemic. The additional explanatory power of online news features on oil consumption forecasting is proved.
This study has some limitations and further directions. First, using full news articles rather than just news headlines might improve the performance of CNN classifications. Second, other novel deep learning text-mining techniques can also be adapted to extract information. Third, other intelligence algorithms [50, 51], such as the fruit fly optimization algorithm and whale optimization algorithm, can also be used to identify appropriate parameters of IndRNN for oil consumption forecasting problems. We intend to further investigate these important issues.
Acknowledgements
This research is partially supported by the National Natural Science Foundation of China (No: 71771095; 71810107003).
Nomenclature
- ADE
adaptive differential evolution
- AHDE
adaptive hybrid differential evolution algorithm
- AI
artificial intelligence
- ANN
artificial neural network
- ARIMA
autoregressive integrate moving average
- BPNN
backpropagation neural networks
- CNN
convolutional neural network
- COVID-19
coronavirus disease 2019
- DE
differential evolution
- GRU
gated recurrent unit
- IndRNN
independent recurrent neural network
- JADE
adaptive differential evolution with optional external archive
- LADE
linear adaptive differential evolution
- LSTM
long short-term memory
- MAE
mean absolute error
- MAPE
mean absolute percentage error
- OBPSO
opposition-based barebones particle swarm optimization
- OPEC
Organization of the Petroleum Exporting Countries
- RMSE
root mean square error
- RNN
recurrent neural network
- SADE
S-shaped adaptive differential evolution
- SARIMA
seasonal ARIMA
- SCA
sine cosine algorithm
- SVM
support vector machines
- U.S.
the United States
- WTI
West Texas Intermediat
Biographies
Binrong Wu
is a Ph.D. candidate in the School of Management, Huazhong University of Science and Technology, Wuhan, China. His research interests are in the areas of business analytics, text mining, and time-series forecasting. He has published several papers in international journals such as Energy, Measurement, and Neural Processing Letters.

Lin Wang
is a Professor in the School of Management, Huazhong University of Science and Technology, Wuhan, China. His research interests are in the area of business analytics, and time series prediction. He has published over 50 papers in international journals such as Knowledge-Based Systems, Engineering Applications of Artificial Intelligence, Applied Soft computing, Tourism Management, Applied Energy, Energy, and European Journal of Operational Research.

Sheng-Xiang Lv
is an Assistant Professor in the School of Business Administration, Guangdong University of Finance & Economics, Guangzhou, China. His research interests are in the area of forecasting theory and method. He has published several papers in international journals such as Applied Soft computing, Applied Energy, and Energy.

Yu-Rong Zeng
is an Associate Professor in the School of Information and Communication Engineering, Hubei University of Economics, Wuhan, China. Her research interests are in the area of neural computing, text mining, and appliedintelligence. She has published more than 20 papers in international journals such as Energy, Applied Soft computing, and Knowledge-Based Systems.

Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Binrong Wu, Email: binronghust@foxmail.com.
Lin Wang, Email: wanglin982@gmail.com.
Sheng-Xiang Lv, Email: shengxianglv@foxmail.com.
Yu-Rong Zeng, Email: zyrhbue@gmail.com.
References
- 1.Yu L, Zhao Y, Tang L, Yang Z. Online big data-driven oil consumption forecasting with Google trends. Int J Forecast. 2019;35:213–223. doi: 10.1016/j.ijforecast.2017.11.005. [DOI] [Google Scholar]
- 2.Garcia Cabello J. Time-Dynamic Markov Random Fields for price outcome prediction in the presence of lobbying The case of olive oil in Andalusia. Appl Intell. 10.1007/s10489-021-02599-6
- 3.Chai L, Xu H, Luo Z, Li S. A multi-source heterogeneous data analytic method for future price fluctuation prediction. Neurocomputing. 2020;418:11–20. doi: 10.1016/j.neucom.2020.07.073. [DOI] [Google Scholar]
- 4.Xu Q, Wang L, Jiang C, Liu Y. A novel (U)MIDAS-SVR model with multi-source market sentiment for forecasting stock returns. Neural Comput Appl. 2020;32:5875–5888. doi: 10.1007/s00521-019-04063-6. [DOI] [Google Scholar]
- 5.Yu L, Yang Z, Tang L. Prediction-based multi-objective optimization for oil purchasing and distribution with the NSGA-II algorithm. Int J Inf Technol Decis Mak. 2016;15:423–451. doi: 10.1142/S0219622016500097. [DOI] [Google Scholar]
- 6.Ou S, He X, Ji W, et al. Machine learning model to project the impact of COVID-19 on US motor gasoline demand. Nat Energy. 2020;5:666–673. doi: 10.1038/s41560-020-0662-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Jo H, Kim J, Porras P, et al. GapFinder: Finding inconsistency of security information from unstructured text. IEEE Trans Inf Forensics Secur. 2021;16:86–99. doi: 10.1109/TIFS.2020.3003570. [DOI] [Google Scholar]
- 8.He J, Li L, Wang Y, Wu X. Targeted aspects oriented topic modeling for short texts. Appl Intell. 2020;50:2384–2399. doi: 10.1007/s10489-020-01672-w. [DOI] [Google Scholar]
- 9.Yoon L, Hernandez D. Energy, energy, read all about it: A thematic analysis of energy insecurity in the U.S. mainstream media from 1980 to 2019. Energy Res Soc Sci. 2021;74:101972. doi: 10.1016/j.erss.2021.101972. [DOI] [Google Scholar]
- 10.Colladon AF. Forecasting election results by studying brand importance in online news. Int J Forecast. 2020;36:414–427. doi: 10.1016/j.ijforecast.2019.05.013. [DOI] [Google Scholar]
- 11.Chu C-Y, Park K, Kremer GE. A global supply chain risk management framework: An application of text-mining to identify region-specific supply chain risks. Adv Eng Inform. 2020;45:101053. doi: 10.1016/j.aei.2020.101053. [DOI] [Google Scholar]
- 12.Song W, Fujimura S. Capturing combination patterns of long- and short-term dependencies in multivariate time series forecasting. Neurocomputing. 2021;464:72–82. doi: 10.1016/j.neucom.2021.08.100. [DOI] [Google Scholar]
- 13.Pinto T, Praca I, Vale Z, Silva J. Ensemble learning for electricity consumption forecasting in office buildings. Neurocomputing. 2021;423:747–755. doi: 10.1016/j.neucom.2020.02.124. [DOI] [Google Scholar]
- 14.AL-Musaylh MS, Al‐Daffaie K, Prasad R. Gas consumption demand forecasting with empirical wavelet transform based machine learning model: A case study. Int J Energy Res. 2021;45:15124–15138. doi: 10.1002/er.6788. [DOI] [Google Scholar]
- 15.Huang H, Jia R, Shi X, et al. Feature selection and hyper parameters optimization for short-term wind power forecast. Appl Intell. 2021;51:6752–6770. doi: 10.1007/s10489-021-02191-y. [DOI] [Google Scholar]
- 16.Wu B, Wang L, Lv S-X, Zeng Y-R. Effective crude oil price forecasting using new text-based and big-data-driven model. Measurement. 2021;168:108468. doi: 10.1016/j.measurement.2020.108468. [DOI] [Google Scholar]
- 17.Wei N, Li C, Peng X, et al. Daily natural gas consumption forecasting via the application of a novel hybrid model. Appl Energy. 2019;250:358–368. doi: 10.1016/j.apenergy.2019.05.023. [DOI] [Google Scholar]
- 18.Somu N, Raman GMR, Ramamritham K. A deep learning framework for building energy consumption forecast. Renew Sustain Energy Rev. 2021;137:110591. doi: 10.1016/j.rser.2020.110591. [DOI] [Google Scholar]
- 19.Li J, Wang R, Wang J, Li Y. Analysis and forecasting of the oil consumption in China based on combination models optimized by artificial intelligence algorithms. Energy. 2018;144:243–264. doi: 10.1016/j.energy.2017.12.042. [DOI] [Google Scholar]
- 20.Li X, Shang W, Wang S. Text-based crude oil price forecasting: A deep learning approach. Int J Forecast. 2019;35:1548–1560. doi: 10.1016/j.ijforecast.2018.07.006. [DOI] [Google Scholar]
- 21.Esteva A, Kuprel B, Novoa RA, et al. Dermatologist-level classification of skin cancer with deep neural networks. Nature. 2017;542(7639):115–118. doi: 10.1038/nature21056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Kim L, Ju J. Can media forecast technological progress?: A text-mining approach to the on-line newspaper and blog’s representation of prospective industrial technologies. Inf Process Manag. 2019;56:1506–1525. doi: 10.1016/j.ipm.2018.10.017. [DOI] [Google Scholar]
- 23.Hemmatian F, Sohrabi MK. A survey on classification techniques for opinion mining and sentiment analysis. Artif Intell Rev. 2019;52:1495–1545. doi: 10.1007/s10462-017-9599-6. [DOI] [Google Scholar]
- 24.Huang M, Xie H, Rao Y, et al. Sentiment strength detection with a context-dependent lexicon-based convolutional neural network. Inf Sci. 2020;520:389–399. doi: 10.1016/j.ins.2020.02.026. [DOI] [Google Scholar]
- 25.Yang Y, Wang J, Wang B. Prediction model of energy market by long short term memory with random system and complexity evaluation. Appl Soft Comput. 2020;95:106579. doi: 10.1016/j.asoc.2020.106579. [DOI] [Google Scholar]
- 26.Han T, Muhammad K, Hussain T, et al. An Efficient Deep Learning Framework for Intelligent Energy Management in IoT Networks. IEEE Internet Things J. 2021;8:3170–3179. doi: 10.1109/JIOT.2020.3013306. [DOI] [Google Scholar]
- 27.Peng L, Liu S, Liu R, Wang L. Effective long short-term memory with differential evolution algorithm for electricity price prediction. Energy. 2018;162:1301–1314. doi: 10.1016/j.energy.2018.05.052. [DOI] [Google Scholar]
- 28.Sheng Z, Wang H, Chen G, et al. Convolutional residual network to short-term load forecasting. Appl Intell. 2021;51:2485–2499. doi: 10.1007/s10489-020-01932-9. [DOI] [Google Scholar]
- 29.Qin Y, Xiang S, Chai Y, Chen H. Macroscopic-microscopic attention in LSTM networks based on fusion features for gear remaining life prediction. IEEE Trans Ind Electron. 2020;67:10865–10875. doi: 10.1109/TIE.2019.2959492. [DOI] [Google Scholar]
- 30.Li S, Li W, Cook C et al (2018) Independently Recurrent Neural Network (IndRNN): Building A Longer and Deeper RNN. In: 2018 Ieee/Cvf Conference on Computer Vision and Pattern Recognition (cvpr). IEEE, New York, pp 5457–5466
- 31.Chu Z, Yu J. An end-to-end model for rice yield prediction using deep learning fusion. Comput Electron Agric. 2020;174:105471. doi: 10.1016/j.compag.2020.105471. [DOI] [Google Scholar]
- 32.Ali IM, Essam D, Kasmarik K. Novel binary differential evolution algorithm for knapsack problems. Inf Sci. 2021;542:177–194. doi: 10.1016/j.ins.2020.07.013. [DOI] [Google Scholar]
- 33.Zhang J, Sanderson AC. JADE: Adaptive differential evolution with optional external archive. IEEE Trans Evol Comput. 2009;13:945–958. doi: 10.1109/TEVC.2009.2014613. [DOI] [Google Scholar]
- 34.Khodabandelou G, Kheriji W, Selem FH. Link traffic speed forecasting using convolutional attention-based gated recurrent unit. Appl Intell. 2021;51:2331–2352. doi: 10.1007/s10489-020-02020-8. [DOI] [Google Scholar]
- 35.de Medrano R, Aznarte JL. A spatio-temporal attention-based spot-forecasting framework for urban traffic prediction. Appl Soft Comput. 2020;96:106615. doi: 10.1016/j.asoc.2020.106615. [DOI] [Google Scholar]
- 36.Peng L, Wang L, Xia D, Gao Q. Effective energy consumption forecasting using empirical wavelet transform and long short-term memory. Energy. 2022;238:121756. doi: 10.1016/j.energy.2021.121756. [DOI] [Google Scholar]
- 37.Du S, Li T, Yang Y, Horng S-J. Multivariate time series forecasting via attention-based encoder-decoder framework. Neurocomputing. 2020;388:269–279. doi: 10.1016/j.neucom.2019.12.118. [DOI] [Google Scholar]
- 38.Sengupta R, Pal M, Saha S, Bandyopadhyay S. Uniform distribution driven adaptive differential evolution. Appl Intell. 2020;50:3638–3659. doi: 10.1007/s10489-020-01707-2. [DOI] [Google Scholar]
- 39.Zhan Z-H, Wang Z-J, Jin H, Zhang J. Adaptive distributed differential evolution. IEEE Trans Cybern. 2020;50:4633–4647. doi: 10.1109/TCYB.2019.2944873. [DOI] [PubMed] [Google Scholar]
- 40.Wang L, Xiong Y, Li S, Zeng Y-R. New fruit fly optimization algorithm with joint search strategies for function optimization problems. Knowl-Based Syst. 2019;176:77–96. doi: 10.1016/j.knosys.2019.03.028. [DOI] [Google Scholar]
- 41.Dhaliwal JS, Dhillon JS. A synergy of binary differential evolution and binary local search optimizer to solve multi-objective profit based unit commitment problem. Appl Soft Comput. 2021;107:107387. doi: 10.1016/j.asoc.2021.107387. [DOI] [Google Scholar]
- 42.Xu Y, Yang X, Yang Z, et al. An enhanced differential evolution algorithm with a new oppositional-mutual learning strategy. Neurocomputing. 2021;435:162–175. doi: 10.1016/j.neucom.2021.01.003. [DOI] [Google Scholar]
- 43.Lu Y, Zhou J, Qin H, et al. An adaptive hybrid differential evolution algorithm for dynamic economic dispatch with valve-point effects. Expert Syst Appl. 2010;37:4842–4849. doi: 10.1016/j.eswa.2009.12.031. [DOI] [Google Scholar]
- 44.Mirjalili S. SCA: A Sine Cosine Algorithm for solving optimization problems. Knowl-Based Syst. 2016;96:120–133. doi: 10.1016/j.knosys.2015.12.022. [DOI] [Google Scholar]
- 45.Wang H. Opposition-based barebones particle swarm for constrained nonlinear optimization problems. Math Probl Eng. 2012;2012:761708. doi: 10.1155/2012/761708. [DOI] [Google Scholar]
- 46.Wu B, Wang L, Wang S, Zeng Y-R. Forecasting the US oil markets based on social media information during the COVID-19 pandemic. Energy. 2021;226:120403. doi: 10.1016/j.energy.2021.120403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Somu N, Raman GMR, Ramamritham K. A hybrid model for building energy consumption forecasting using long short term memory networks. Appl Energy. 2020;261:114131. doi: 10.1016/j.apenergy.2019.114131. [DOI] [Google Scholar]
- 48.Bedi J, Toshniwal D. Energy load time-series forecast using decomposition and autoencoder integrated memory network. Appl Soft Comput. 2020;93:106390. doi: 10.1016/j.asoc.2020.106390. [DOI] [Google Scholar]
- 49.Li C, Li S, Liu Y. A least squares support vector machine model optimized by moth-flame optimization algorithm for annual power load forecasting. Appl Intell. 2016;45:1166–1178. doi: 10.1007/s10489-016-0810-2. [DOI] [Google Scholar]
- 50.Lv S-X, Zeng Y-R, Wang L (2018) An effective fruit fly optimization algorithm with hybrid information exchange and its applications. Int J Mach Learn Cyb 9(10):1623–1648. 10.1007/s13042-017-0669-5
- 51.Wang ZG, Zeng Y-R, Wang SR, Wang L (2019) Optimizing echo state network with backtracking search optimization algorithm for time series forecasting. Eng Appl Artif Intell 81:117–132. 10.1016/j.engappai.2019.02.009