Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2022 Jun 13;7(25):21939–21945. doi: 10.1021/acsomega.2c02291

Evaluation of Slight Changes in Aromaticity through Electronic and Density Functional Reactivity Theory-Based Descriptors

Rodrigo Báez-Grez †, Ricardo Pino-Rios ‡,*
PMCID: PMC9245093  PMID: 35785290

Abstract

graphic file with name ao2c02291_0004.jpg

Aromaticity is a useful tool to rationalize the structure, stability, and reactivity in several compounds. Although aromaticity is not directly an observable, it is well accepted that electronic delocalization around the molecular ring is a key stabilizing feature of aromatic compounds. This contribution presents a systematic evaluation of the capability of delocalization and reactivity criteria to describe aromaticity in a set of fluorinated benzenes. The aromaticity indices are compared with quantities obtained from the magnetic criteria of aromaticity, i.e., the strength of the ring current induced by an external magnetic field and the popular NICSzz(1) index. In this evaluation, the indices based on delocalization criteria used are aromatic fluctuation index (FLU), para-delocalization index (PDI), PDIπ, and the multicenter delocalization index (MCI). In addition, indices based on the bifurcation values of scalar functions are derived from electron density such as electron localization function (the π contribution, ELFπ) and the π contribution of the localized orbital locator (LOLπ). Furthermore, reactivity indices based on chemical reactivity and the information-theoretic (reactivity) approach are para-linear response (PLR), Shannon entropy, Fisher information, and Ghosh–Berkowitz–Parr (GBP) entropy. The results obtained show that the delocalization-based indicators present a high sensitivity to slight changes in aromaticity and that the reactivity criterion can be considered as a complementary tool for the study of this phenomenon, even when these changes are minimal. These results encourage the use of multiple indicators for a complete understanding of aromaticity in various chemical compounds.

Introduction

Since the aromaticity concept was introduced, it has become very useful to rationalize the structure, stability, and reactivity of various abnormally stable compounds, both organic and inorganic. Although an exact definition of aromaticity remains elusive,1 it is pertinent to this work to cite the Chen and Schleyer interpretation:2 “A manifestation of electron delocalization in closed circuits, either in two or three dimensions”. Consequently, though aromaticity is not directly observable, it is well accepted that electronic delocalization, around the molecular ring, is one key stabilizing feature of aromatic compounds.3

Different descriptors that allow us to quantify the electronic delocalization have been recently proposed and applied in several compounds. These descriptors are measurements obtained directly from electron density and derived scalar functions, such as the electron localization function (ELF).4,5 A widely used aromaticity descriptor based on this scalar function was proposed by Santos et al.6,7 who, through the bifurcation values of the σ and π contributions to the ELF, proposed an aromaticity scale. Another scalar function derived from electron density is the localized orbital locator8 (LOL) whose topology has been used to describe chemical bonding in several compounds; however, the bifurcation scheme has not been explored. In the context of electron density topology, various indices have been proposed in the context of the quantum theory of atoms in molecules (QTAIM) proposed by Bader.9 The delocalization index10 (DI), commonly used for the characterization of bond orders, has inspired the proposal of new indices that allow the quantification of aromaticity: the aromatic fluctuation index11 (FLU), which measures the uniformity of the electronic delocalization in the molecular ring and the difference with regard to a reference system (in the case of organic compounds and this case, benzene); the para-delocalization index12 (PDI) proposed for the quantification of aromaticity in six-membered rings (this index is defined as the measurement of the average electronic delocalization (DI) of the carbons in the para-related positions); and the multicenter delocalization index (MCI) proposed by Giambigi et al.13,14 as a generalization of the DI. MCI measures the number of electrons shared between n atoms, n being the number of atoms in the ring to be studied. For more information about the mentioned indices, the reader can refer to the original papers or to the excellent review by Solá and co-workers.3 Despite the limitations that electron delocalization indices may have, their predictive capability to quantify aromaticity has been confirmed and evaluated using a molecular test set proposed by Feixas et al.15,16

On the other hand, a less explored criterion for the study of aromaticity is that of reactivity. This was initially studied by Zhou, Parr, and Gharst (ZPG) in terms of global hardness,17 which was derived from the so-called density functional reactivity theory or also known as conceptual density functional theory (DFT).18 The argument used is that both properties are measures of high stability and low reactivity.19 Subsequently, Chattaraj and co-workers studied the aromaticity of atomic clusters and its relation to the maximum hardness and minimum polarizability principle.20 The global hardness has been very useful in the study of inorganic systems; however, recently, it has been shown that the energetic differences between the frontier orbitals depend on the method to be used. Báez-Grez et al.21 found opposite trends when these energies were calculated at the CCSD(T) and DFT levels, so this is not an unequivocal criterion for the study of aromaticity in heteroaromatic systems such as azines. Subsequently, Geerlings et al. proposed an analogous indicator to the PDI of Solá and co-workers, based on the linear response kernel, called para-linear response kernel100 (PLR); this indicator has shown an excellent correlation with the PDI (r2 = 0.96). The PLR indicator suffers from the same limitation as the PDI and is that it is only enabled to study six-membered rings; however, years later, the linear response kernel was used to study aromaticity in four-membered cyclic atomic clusters. It should also be noted that both indicators mentioned above are only defined to study aromaticity in the ground state, so their application to the study of aromaticity in excited states is prohibitive.

After years of attempts to study aromaticity using CDFT tools, Liu and co-workers22,23 derived a series of indicators based on the information-theoretic approach, allowing us to study aromaticity not only in the ground state but also in excited states. The most commonly used indicators are Shannon entropy, Fisher information, and Ghosh–Berkowitz–Parr entropy, whose definitions can be found in the excellent papers recently published by Liu and co-workers; however, Fisher information is a more useful indicator for the steric effect study and offers a poor description of aromaticity, so the results are shown in the Supporting Information.24,25 The interpretation of these indicators is that the higher the value, the higher the aromaticity of the system. Recently, Anjalikrishna et al.26 applied the topography of the electrostatic potential (ESP) as a tool to analyze and quantify the π-conjugation patterns and of polycyclic aromatic hydrocarbons (PAHs) based on the pictorial representation studied some years ago by Suresh et al. Furthermore, Inostroza et al.27 proposed the orbital-weighted dual descriptor (OWDD) for the study of reactivity in (quasi)degenerate systems and qualitatively applied this index for the study of Clar-sextets based on the nucleophilic character of the aromatic rings. The analysis showed that for benzene (C6H6) and hexafluorobenzene (C6F6), aromaticity is affected based on the reduction of the nucleophilic character of the ring, which is in agreement with previous results that indicate a reduction of aromaticity.28,29

The correlation among aromaticity indices remains one of the most controversial issues in modern theoretical chemistry.1,3,16,30 For instance, according to a certain index, a molecule can be highly aromatic, whereas another index may classify it as poorly or even nonaromatic. These observations have resulted in claims that aromaticity possesses multidimensional nature.31−35 However, more recently, Solà pointed out that, in many cases, contradictions between indices are due to their inherent deficiencies and that the multidimensional character of aromaticity is not fully established;18 for this reason, it has been proposed that for a complete understanding of this property, it is necessary to use more than one criterion.36

In this work, a systematic evaluation of the capability of delocalization and reactivity indices for the description of aromaticity in a set of fluorinated benzenes is presented. The indices based on delocalization criteria to be used in this evaluation are FLU,11 PDI,12 PDIπ, and MCI,13 as well as those based on the bifurcation values of ELFπ and LOLπ. In the case of the information-theoretic (reactivity) approach are those mentioned previously: para-linear response index, Shannon entropy, and Ghosh–Berkowitz–Parr entropy. The indices of aromaticity will be compared with a quantity obtained from the magnetic criteria of aromaticity: the strength of the ring current induced by an external magnetic field (perpendicular to the molecular ring). Benzene, and its fluorinated derivatives, has been selected for our analysis because it is well documented that as H is replaced in benzene by fluorine, the aromaticity decreases, and this aromaticity reduction is proportional to the number of F in the resulting fluorinated system.28,29 However, this pattern on the aromaticity behavior is not free of controversies. For instance, some magnetic or geometric-based descriptors are insensitive to these small changes in aromaticity and cannot describe it properly.37,38 Finally, the ability of OWDD to qualitatively study small changes in aromaticity will be explored due to the good performance of the indicator in discriminating the aromaticity of C6H6 and C6F6.

Computational Details

Geometrical optimizations were performed at the PBE039/6-311++G**40,41 level using Gaussian 16 program package.42 Additionally, a vibrational analysis was carried out to ensure that a minimum in the potential energy surface was obtained. Delocalization and reactivity indices were obtained using Multiwfn software43 and TAFF pipeline.44,45 Furthermore, magnetic indices such as ring current strength (RCS) and NICSzz(1) were obtained for comparison purposes. The latter values are taken from ref (28), which has been calculated at the same level of theory used in this work. In addition, RCS was recalculated at the aforementioned level in the context of QTAIM proposed by Bader and implemented by Keith in the AIMAll software.46 Calculations were done by measuring the current flow through the interatomic surfaces of the magnetically induced current density topology. The values obtained were also compared with the values computed by Kaipio et al.29 and Torres-Vega et al.28 with the aim to validate our results.

Results and Discussion

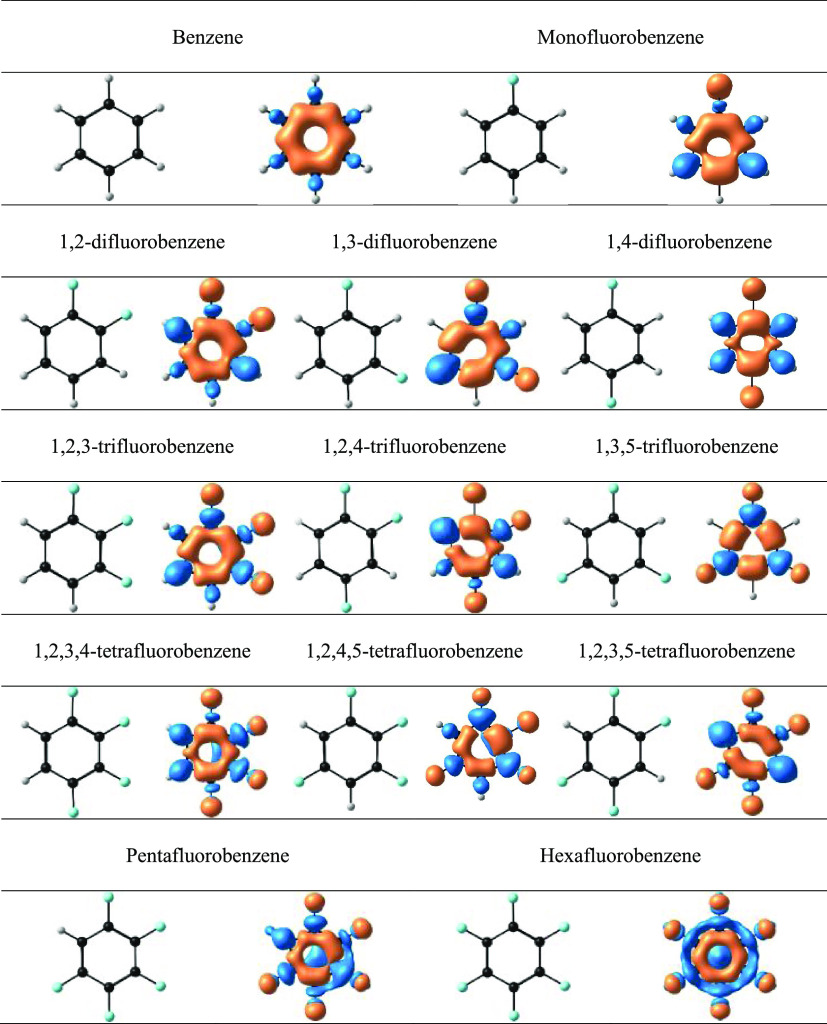
Figure 1 shows benzene and 12 fluorinated benzene derivatives, in conjunction with their RCS values obtained by calculating the current flow through the interatomic surfaces, indicating a systematic reduction of aromaticity as benzene is fluorinated. Benzene has a value of 11.96 nA·T–1, while hexafluorobenzene has a value of 9.83 nA·T–1. In between, 1,4-difluorobenzene is the most aromatic of this family of compounds, while for the case of trifluorobenzenes, it is difficult to discern between the aromaticity of 1,2,3 and 1,2,4 isomers; however, it is notorious that the 1,3,5 isomer is the least aromatic of the group. The same case is observed for tetrafluorobenzenes, where the 1,2,3,5 isomer is the least aromatic, while the other two present the same degree of aromaticity. Additionally, penta- and hexafluorobenzene are much less aromatic than benzene, the latter being the least aromatic of the whole group. These results are in agreement with those previously reported in the literature (see Figure S1).28,29Table 1 shows the percentage reduction of aromaticity with respect to benzene, clearly showing the systematic reduction of aromaticity as more fluorine atoms are added; however, it is also possible to observe that in both trifluorobenzenes and tetrafluorobenzenes, it is impossible to clearly distinguish, which is the most aromatic of each group. With regard to NICSzz(1), the results present the same trend when compared with the RCS values; it is necessary to highlight that the current density model and its quantification are one of the most reliable indicators of aromaticity in monocyclic organic systems.47 According to previous studies, it is known that fluorination has two effects on the aromatic ring: the resonant effect reduces π-delocalization, while the charge density on the ring decreases due to an inductive effect, which leads to a decrease of the paratropic current in this zone.28 Since the results between the magnetic indices have a high degree of correlation (r2 = 0.94) and present the same trends with respect to RCS, it has been decided to discuss the results only with this last indicator.

Figure 1.

Figure 1

Open in a new tab

Benzene and its fluorinated derivatives and calculated RCS values (in nA·T–1). Calculations performed at the PBE0/6-311++G** level.

Table 1. Percentage of Changes in Aromaticity Measures Based on Delocalization and Reactivity Criteria Used in this Worka.

system RCS NICSzz(1) ELFπ LOLπ MCI PDI PDIπ FLU PLR Shannon GBP
B 100.00 100.00 100.00 100.00 100.00 100.00 100.00 99.20 100.00 100.00 100.00
MFB 96.15 96.67 95.65 100.00 92.59 95.05 95.74 90.40 94.38 95.20 99.00
1,2-DFB 93.31 96.67 95.65 96.83 85.60 90.57 91.69 75.20 89.47 90.70 98.07
1,3-DFB 92.22 93.64 94.57 95.24 84.36 89.43 90.60 78.40 87.81 90.45 98.03
1,4-DFB 94.15 91.62 95.65 96.83 86.01 91.24 92.68 80.80 90.77 90.36 98.01
1,2,3-TFB 89.88 89.90 93.48 95.24 78.60 85.62 87.21 57.60 83.98 86.24 97.14
1,2,4-TFB 89.80 88.89 93.48 96.83 79.42 86.10 87.98 64.00 84.86 85.94 97.09
1,3,5-TFB 86.71 85.15 93.48 95.24 76.13 83.24 84.92 64.80 80.61 85.77 97.07
1,2,3,4-TtFB 87.04 86.97 92.39 96.83 72.84 81.62 83.93 42.40 80.24 81.75 96.21
1,2,4,5-TtFB 87.04 85.96 93.48 95.24 73.25 82.19 84.59 47.20 80.91 81.48 96.17
1,2,3,5-TtFB 85.12 84.04 92.39 95.24 72.02 80.48 82.84 44.80 78.53 81.53 96.18
PFB 83.86 83.03 92.39 95.24 67.08 76.19 80.00 24.80 75.60 77.32 95.30
HFB 82.19 80.91 91.30 95.24 65.02 73.33 77.92 0.00 76.85 76.84 94.33
Open in a new tab
a

All calculations were performed at the PBE0/6-311++G** level. Benzene (B) is taken as the most aromatic.

In relation to delocalization indices of scalar functions derived from electron density, ELFπ and LOLπ show that benzene is more aromatic than perfluorobenzene derivatives. However, only ELFπ has a notable systematic reduction. ELFπ predicts certain differences between the difluorobenzene isomers; however, ELFπ is not able to predict differences in aromaticity and the same is observed for trifluorobenzenes. In the case of LOLπ, this index is capable of establishing that 1,3-difluorobenzene is the least aromatic in that family; however, it is not capable of indicating which isomer is the most aromatic. Both ELFπ and LOLπ are unable to correctly discern small differences in the aromaticity of the fluorinated isomers; however, they do denote a systematic reduction as H atoms are replaced by F atoms.

QTAIM-based delocalization indices show a notable improvement in the description of the aromaticity of the systems under study. Although the FLU index is the one that presents the lowest sensitivity to small changes, it is able to describe the systematic reduction in aromaticity as the number of fluorine atoms increase, in the same way as ELFπ and LOLπ. PDI and its variant PDIπ, which takes into account only the contributions of the π orbitals, together with MCI, show great sensitivity in the quantification of aromaticity upon fluorination. The results allow us to say that these indicators allow to describe the reduction in aromaticity in all compounds, including in isomers where aromaticity changes are slight. Taking RCS values as reference, we can see that the indices that best correlate are, first, PDI and PDIπ, second, MCI, and finally, ELFπ, having correlation coefficients of 0.99 (both PDI and PDIπ), 0.98 (MCI), and 0.86 (ELFπ), respectively, as seen in Table 2. In contrast, FLU (r2 = 0.86) and LOLπ (r2 = 0.65) indices show a lower correlation but FLU is still useful for a qualitative description. The complete set of computed values is shown in Table S1.

Table 2. Adjusted Squared Correlation Coefficients (r2 Adj) Obtained When All of the Indices Mentioned Earlier in the Article are Used in the Analysis.

r2 (Adj) RCS NICSzz(1) ELFπ LOLπ MCI PDI PDIπ FLU PLR Shannon GBP
RCS 1.00 0.94 0.88 0.62 0.98 0.98 0.99 0.85 0.98 0.96 0.94
NICSzz(1) 0.94 1.00 0.79 0.55 0.92 0.92 0.93 0.79 0.91 0.91 0.89
ELFπ 0.88 0.79 1.00 0.56 0.88 0.86 0.87 0.71 0.88 0.86 0.83
LOLπ 0.62 0.55 0.56 1.00 0.63 0.59 0.62 0.39 0.67 0.58 0.53
MCI 0.98 0.92 0.88 0.63 1.00 0.99 0.99 0.88 0.98 0.99 0.97
PDI 0.98 0.92 0.86 0.59 0.99 1.00 1.00 0.92 0.96 0.98 0.98
PDIπ 0.99 0.93 0.97 0.62 0.99 1.00 1.00 0.89 0.98 0.97 0.97
FLU 0.85 0.79 0.71 0.39 0.88 0.92 0.89 1.00 0.79 0.89 0.95
PLR 0.98 0.91 0.88 0.67 0.98 0.96 0.98 0.79 1.00 0.95 0.91
Shannon 0.96 0.91 0.86 0.58 0.99 0.98 0.97 0.89 0.95 1.00 0.98
GBP 0.94 0.89 0.83 0.53 0.97 0.98 0.97 0.95 0.91 0.98 1.00
Open in a new tab

The para-linear response (PLR) index derived from conceptual DFT works fairly well, allowing us to differentiate between the isomers and with correlation values above 0.95 when compared to RCS, MCI, PDI, and PDIπ. Information-theoretic indices perform very well with delocalization índices and ring current strength values. In addition, Fisher entropy is unable to distinguish between the changes in aromaticity when a fluorine atom is delivered, showing that aromaticity, according to this index, remains constant, and for this reason, it does not correlate with any of the indicators used so far (see Table S1).

Finally, the orbital-weighted dual descriptor has been employed to assess the changes in the aromaticity of fluorinated compounds based on their reactivity. Recently, Inostroza et al.27 proved that the differences in aromaticity between benzene and hexafluorobenzene can be observed through the reduction in nucleophilic character (positive, orange isosurfaces). For this reason, we decided to systematically calculate the orbital-weighted dual descriptor (OWDD) using the same parameters used in the original paper.20Figure 2 shows the changes in the nucleophilic character of fluorinated benzenes. It is possible to observe that for difluorobenzene, the 1,3 isomer is the one that presents bifurcation, which coincides with its less aromatic character according to the RCS values and descriptors mentioned above. The same can be observed for 1,3,5-trifluorobenzene, which presents three nucleophilic islands that, compared to the other two isomers, indicate a less aromatic character, which also coincides with the descriptors studied. However, for the case of tetrafluorobenzenes, the OWDD shows that the 1,2,3,5 isomer is the least aromatic, but for the other isomers, it is not possible to define a reasonable difference in aromaticity. In the case of pentafluorobenzene and hexafluorobenzene, although the nucleophilicity is preserved, the electrophilic character (blue isosurfaces) becomes more and more noticeable. Although it is not yet possible to determine quantitatively the differences in the aromaticity of fluorinated benzenes using OWDD, it is very useful to understand the changes qualitatively, showing that the reactivity criteria (together with the PLR and information-theoretic indicators) are very useful for the study of slight changes in aromaticity.

Figure 2.

Figure 2

Open in a new tab

Orbital-weighted dual descriptors for benzene and fluorinated derivatives. The Δ value corresponds to that used in the original publication and isosurface = 0.001. Blue/orange (positive/negative values) represent electrophilic/nucleophilic attack susceptibility.

Conclusions

In this work, the reduction of aromaticity in benzene and its fluorinated derivatives has been evaluated by means of delocalization criteria and those based on conceptual density functional theory. Additionally, the indicators used have been compared with well-known and previously applied indices. The results show that delocalization indicators based on electron density-derived scalar functions such as ELFπ and LOLπ show a reduction in the aromaticity of benzene when fluorine atoms are systematically added but are insensitive to aromaticity differences in di-, tri-, and tetrafluorinated isomers. On the other hand, MCI, PDI, and PDIπ appropriately describe the reduction of aromaticity, even in isomers where magnetic criterion-based indicators are not able to describe. Additionally, the sensitivity of the reactivity criterion has been evaluated through indices derived from conceptual DFT and those based on information theory. The para-linear-response kernel shows results very similar to PDI because its definition is identical to that of PDI proposed by Solá and co-workers.12 The information-theoretic-based indices are also sensitive to aromaticity reduction, except for the Fisher entropy, which indicates that the aromaticity is similar in all of the systems studied; these results, however, coincide with those published by Schleyer and co-workers based on the NICS values.37 Finally, the recently proposed orbital-weighted dual descriptor has been used qualitatively to observe the aromaticity reduction of the study systems. The isosurfaces at a value of 0.001 a.u. additionally allow us to observe the differences between the isomers through bifurcations of the positive (nucleophilic) values, and furthermore, allow us to observe the reduction of aromaticity in penta- and hexafluorobenzene not only through the reduction of their nucleophilic character but also through the increase of their electrophilic character. Finally, the results obtained show that delocalization-based indicators are very sensitive to slight changes in aromaticity and that the reactivity criterion can be taken into account as a complementary tool for the study of this phenomenon, even when these changes are minimal.

Acknowledgments

R.B.-G. is grateful for financial support from FONDECYT Postdoctorado 3210037. Powered@NLHPC research was partially supported by the supercomputing infrastructure of the NLHPC (ECM-02) of the Universidad de Chile.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.2c02291.

  • Correlations between calculated RCS values in this work and values published in refs (28) and (29) and aromaticity indices computed at the PBE0/6-311++G** level; and Cartesian coordinates of the systems employed (PDF)

The authors declare no competing financial interest.

Supplementary Material

ao2c02291_si_001.pdf (171KB, pdf)

References

  1. Solà M. Why Aromaticity Is a Suspicious Concept? Why?. Front. Chem. 2017, 5, 22 10.3389/fchem.2017.00022. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Chen Z.; Wannere C. S.; Corminboeuf C.; Puchta R.; von Ragué Schleyer P. Nucleus-Independent Chemical Shifts (NICS) as an Aromaticity Criterion. Chem. Rev. 2005, 105, 3842–3888. 10.1021/cr030088+. [DOI] [PubMed] [Google Scholar]
  3. Feixas F.; Matito E.; Poater J.; Solà M. Quantifying Aromaticity with Electron Delocalisation Measures. Chem. Soc. Rev. 2015, 44, 6434–6451. 10.1039/C5CS00066A. [DOI] [PubMed] [Google Scholar]
  4. Silivi B.; Savin A. Classification of Chemical Bonds Based on Topological Analysis of Electron Locatlized Functions. Nature 1994, 371, 683–686. 10.1038/371683a0. [DOI] [Google Scholar]
  5. Becke A. D.; Edgecombe K. E. A Simple Measure of Electron Localization in Atomic and Molecular Systems. J. Chem. Phys. 1990, 92, 5397–5403. 10.1063/1.458517. [DOI] [Google Scholar]
  6. Santos J. C.; Tiznado W.; Contreras R.; Fuentealba P. Sigma–Pi Separation of the Electron Localization Function and Aromaticity. J. Chem. Phys. 2004, 120, 1670–1673. 10.1063/1.1635799. [DOI] [PubMed] [Google Scholar]
  7. Santos J. C.; Andres J.; Aizman A.; Fuentealba P. An Aromaticity Scale Based on the Topological Analysis of the Electron Localization Function Including σ and π Contributions. J. Chem. Theory Comput. 2005, 1, 83–86. 10.1021/ct0499276. [DOI] [PubMed] [Google Scholar]
  8. Jacobsen H. Localized-Orbital Locator (LOL) Profiles of Chemical Bonding. Can. J. Chem. 2008, 86, 695–702. 10.1139/v08-052. [DOI] [Google Scholar]
  9. Bader R. F. W.Atoms in Molecules: A Quantum Theory, International Series of Monographs on Chemistry; Clarendon Press, 1994. [Google Scholar]
  10. Fradera X.; Austen M. A.; Bader R. F. W. The Lewis Model and Beyond. J. Phys. Chem. A 1999, 103, 304–314. 10.1021/jp983362q. [DOI] [Google Scholar]
  11. Matito E.; Duran M.; Solà M. The Aromatic Fluctuation Index (FLU): A New Aromaticity Index Based on Electron Delocalization. J. Chem. Phys. 2005, 122, 014109 10.1063/1.1824895. [DOI] [PubMed] [Google Scholar]
  12. Poater J.; Fradera X.; Duran M.; Solà M. The Delocalization Index as an Electronic Aromaticity Criterion: Application to a Series of Planar Polycyclic Aromatic Hydrocarbons. Chem. - Eur. J. 2003, 9, 400–406. 10.1002/chem.200390041. [DOI] [PubMed] [Google Scholar]
  13. Sablon N.; De Proft F.; Solá M.; Geerlings P. The linear response kernel of conceptual DFT as a measure of aromaticity. Physical Chemistry Chemical Physics 2012, 14 (11), 3960–3967. 10.1039/c2cp23372j. [DOI] [PubMed] [Google Scholar]
  14. Bultinck P.; Ponec R.; Van Damme S. Multicenter Bond Indices as a New Measure of Aromaticity in Polycyclic Aromatic Hydrocarbons. J. Phys. Org. Chem. 2005, 18, 706–718. 10.1002/poc.922. [DOI] [Google Scholar]
  15. Giambiagi M.; de Giambiagi M. S.; Mundim K. C. Definition of a Multicenter Bond Index. Struct. Chem. 1990, 1, 423–427. 10.1007/BF00671228. [DOI] [Google Scholar]
  16. Feixas F.; Matito E.; Poater J.; Solà M. On the Performance of Some Aromaticity Indices: A Critical Assessment Using a Test Set. J. Comput. Chem. 2008, 29, 1543–1554. 10.1002/jcc.20914. [DOI] [PubMed] [Google Scholar]
  17. Solà M.; Feixas F.; Jiménez-Halla J. O. C.; Matito E.; Poater J. A Critical Assessment of the Performance of Magnetic and Electronic Indices of Aromaticity. Symmetry 2010, 2, 1156–1179. 10.3390/sym2021156. [DOI] [Google Scholar]
  18. Zhou Z.; Parr R. G.; F Garst J. Absolute Hardness as a Measure of Aromaticity. Tetrahedron Lett. 1988, 29, 4843–4846. 10.1016/S0040-4039(00)80623-1. [DOI] [Google Scholar]
  19. Geerlings P.; De Proft F.; Langenaeker W. Conceptual Density Functional Theory. Chem. Rev. 2003, 103, 1793–1874. 10.1021/cr990029p. [DOI] [PubMed] [Google Scholar]
  20. Chattaraj P. K.; Sarkar U.; Roy D. R. Electronic Structure Principles and Aromaticity. J. Chem. Educ. 2007, 84, 354. 10.1021/ed084p354. [DOI] [Google Scholar]
  21. Chattaraj P. K.; Roy D. R.; Elango M.; Subramanian V. Stability and Reactivity of All-Metal Aromatic and Antiaromatic Systems in Light of the Principles of Maximum Hardness and Minimum Polarizability. J. Phys. Chem. A 2005, 109, 9590–9597. 10.1021/jp0540196. [DOI] [PubMed] [Google Scholar]
  22. Báez-Grez R.; Arrué L.; Pino-Rios R. Quantitative Analysis of Aromaticity in Azines by Means of Dissected Descriptors Based on the Magnetic Criteria. Chem. Phys. Lett. 2021, 781, 138973 10.1016/j.cplett.2021.138973. [DOI] [Google Scholar]
  23. Wang B.; Zhao D.; Lu T.; Liu S.; Rong C. Quantifications and Applications of Relative Fisher Information in Density Functional Theory. J. Phys. Chem. A 2021, 125, 3802–3811. 10.1021/acs.jpca.1c02099. [DOI] [PubMed] [Google Scholar]
  24. Yu D.; Rong C.; Lu T.; De Proft F.; Liu S. Baird’s Rule in Substituted Fulvene Derivatives: An Information-Theoretic Study on Triplet-State Aromaticity and Antiaromaticity. ACS Omega 2018, 3, 18370–18379. 10.1021/acsomega.8b02881. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Rong C.; Wang B.; Zhao D.; Liu S. Information-Theoretic Approach in Density Functional Theory and Its Recent Applications to Chemical Problems. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2020, 10, e1461 10.1002/wcms.1461. [DOI] [Google Scholar]
  26. Liu S.-B. Information-Theoretic Approach in Density Functional Reactivity Theory. Acta Phys.-Chim. Sin. 2016, 32, 98–118. 10.3866/PKU.WHXB201510302. [DOI] [Google Scholar]
  27. Anjalikrishna P. K.; Suresh C. H.; Gadre S. R. Electrostatic Topographical Viewpoint of π-Conjugation and Aromaticity of Hydrocarbons. J. Phys. Chem. A 2019, 123, 10139–10151. 10.1021/acs.jpca.9b09056. [DOI] [PubMed] [Google Scholar]
  28. Pino-Rios R.; Inostroza D.; Cárdenas-Jirón G.; Tiznado W. Orbital-Weighted Dual Descriptor for the Study of Local Reactivity of Systems with (Quasi-) Degenerate States. J. Phys. Chem. A 2019, 123, 10556–10562. 10.1021/acs.jpca.9b07516. [DOI] [PubMed] [Google Scholar]
  29. Torres-Vega J. J.; Vásquez-Espinal A.; Ruiz L.; Fernández-Herrera M. A.; Alvarez-Thon L.; Merino G.; Tiznado W. Revisiting Aromaticity and Chemical Bonding of Fluorinated Benzene Derivatives. ChemistryOpen 2015, 4, 302–307. 10.1002/open.201402110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Kaipio M.; Patzschke M.; Fliegl H.; Pichierri F.; Sundholm D. Effect of Fluorine Substitution on the Aromaticity of Polycyclic Hydrocarbons. J. Phys. Chem. A 2012, 116, 10257–10268. 10.1021/jp308121b. [DOI] [PubMed] [Google Scholar]
  31. Omelchenko I. V.; Shishkin O. V.; Gorb L.; Leszczynski J.; Fias S.; Bultinck P. Aromaticity in Heterocyclic Analogues of Benzene: Comprehensive Analysis of Structural Aspects, Electron Delocalization and Magnetic Characteristics. Phys. Chem. Chem. Phys. 2011, 13, 20536–20548. 10.1039/c1cp20905a. [DOI] [PubMed] [Google Scholar]
  32. Cyrañski M. K.; Krygowski T. M.; Katritzky A. R.; von Ragué Schleyer P. To What Extent Can Aromaticity Be Defined Uniquely?. J. Org. Chem. 2002, 67, 1333–1338. 10.1021/jo016255s. [DOI] [PubMed] [Google Scholar]
  33. Bultinck P.; Fias S.; Ponec R. Local Aromaticity in Polycyclic Aromatic Hydrocarbons: Electron Delocalization versus Magnetic Indices. Chem. - Eur. J. 2006, 12, 8813–8818. 10.1002/chem.200600541. [DOI] [PubMed] [Google Scholar]
  34. Jusélius J.; Sundholm D. Polycyclic Antiaromatic Hydrocarbons. Phys. Chem. Chem. Phys. 2008, 10, 6630–6634. 10.1039/b808082h. [DOI] [PubMed] [Google Scholar]
  35. Krygowski T. M.; Cyrański M. Separation of the Energetic and Geometric Contributions to the Aromaticity of π-Electron Carbocyclics. Tetrahedron 1996, 52, 1713–1722. 10.1016/0040-4020(95)01007-6. [DOI] [Google Scholar]
  36. Katritzky A. R.; Karelson M.; Sild S.; Krygowski T. M.; Jug K. Aromaticity as a Quantitative Concept. 7. Aromaticity Reaffirmed as a Multidimensional Characteristic. J. Org. Chem. 1998, 63, 5228–5231. 10.1021/jo970939b. [DOI] [Google Scholar]
  37. Báez-Grez R.; Pino-Rios R. Borataalkene or Boratabenzene? Understanding the Aromaticity of 9-Borataphenanthrene Anions and Its Central Ring. New J. Chem. 2020, 44, 18069–18073. 10.1039/D0NJ03942J. [DOI] [Google Scholar]
  38. Wu J. I.; Pühlhofer F. G.; von Ragué Schleyer P.; Puchta R.; Kiran B.; Mauksch M.; van Eikema Hommes N. J. R.; Alkorta I.; Elguero J. The Effect of Perfluorination on the Aromaticity of Benzene and Heterocyclic Six-Membered Rings. J. Phys. Chem. A 2009, 113, 6789–6794. 10.1021/jp902983r. [DOI] [PubMed] [Google Scholar]
  39. Valadbeigi Y. Comparison of Effects of Charge Delocalization and π-Electron Delocalization on the Stability of Monocyclic Compounds. J. Mol. Graphics Modell. 2018, 80, 104–112. 10.1016/j.jmgm.2017.12.026. [DOI] [PubMed] [Google Scholar]
  40. Adamo C.; Barone V. Toward Reliable Density Functional Methods without Adjustable Parameters: The PBE0 Model. J. Chem. Phys. 1999, 110, 6158–6170. 10.1063/1.478522. [DOI] [Google Scholar]
  41. Ditchfield R.; Hehre W. J.; Pople J. A. Self-Consistent Molecular-Orbital Methods. IX. An Extended Gaussian-Type Basis for Molecular-Orbital Studies of Organic Molecules. J. Chem. Phys. 1971, 54, 724–728. 10.1063/1.1674902. [DOI] [Google Scholar]
  42. Hehre W. J.; Ditchfield R.; Pople J. A. Self-Consistent Molecular Orbital Methods. XII. Further Extensions of Gaussian-Type Basis Sets for Use in Molecular Orbital Studies of Organic Molecules. J. Chem. Phys. 1972, 56, 2257–2261. 10.1063/1.1677527. [DOI] [Google Scholar]
  43. Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Petersson G. A.; Nakatsuji H.. et al. Gaussian 16, revisión B.01; Gaussian, Inc.: Wallingford, CT, 2016.
  44. Lu T.; Chen F. Multiwfn: A Multifunctional Wavefunction Analyzer. J. Comput. Chem. 2012, 33, 580–592. 10.1002/jcc.22885. [DOI] [PubMed] [Google Scholar]
  45. Yañez O.; Vásquez-Espinal A.; Inostroza D.; Ruiz L.; Pino-Rios R.; Tiznado W. A Fukui Function-Guided Genetic Algorithm. Assessment on Structural Prediction of Sin (N = 12--20) Clusters. J. Comput. Chem. 2017, 38, 1668–1677. 10.1002/jcc.24810. [DOI] [PubMed] [Google Scholar]
  46. Pino-Rios R.; Yañez O.; Inostroza D.; Ruiz L.; Cardenas C.; Fuentealba P.; Tiznado W. Proposal of a Simple and Effective Local Reactivity Descriptor through a Topological Analysis of an Orbital-Weighted Fukui Function. J. Comput. Chem. 2017, 38, 481–488. 10.1002/jcc.24699. [DOI] [PubMed] [Google Scholar]
  47. Todd A.; Keith T. K.. Gristmill Software, AIMAll (Versión 19.10.12); Overland Park KS, EE. UU; 2019.
  48. Sundholm D.; Fliegl H.; Berger R. J. F. Calculations of Magnetically Induced Current Densities: Theory and Applications. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2016, 6, 639–678. 10.1002/wcms.1270. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao2c02291_si_001.pdf (171KB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES