Abstract
Likened to the economic calamity of World War Two, the COVID-19 pandemic has sparked fears of a deep economic crisis, killed more than six million people worldwide and had a ripple effect on all aspects of life. MCDM (multi-criteria decision making) methods have become increasingly popular in modeling COVID-19 problems owing to the multi-dimensionality of this crisis and the complexity of health and socio-economic systems. This paper is aimed to review 72 papers published in 37 leading peer-reviewed journals indexed in Web of Science that used MCDM methods in different areas of COVID-19 pandemic. In this paper, data retrieval follows the PRISMA protocol for systematic literature reviews. 35 countries have contributed to this multidisciplinary research and India is identified as the leading country in this field followed by Turkey and China. Also 36 articles, namely 50% of papers are presented in the form of international cooperation. “Applied Soft Computing” is the journal with the highest number of articles whereas “Journal of infection and public health” and “Operations Management Research” are ranked in the second place. The results indicate that AHP (including fuzzy AHP) is the most popular MCDM method applied in 37.5% of papers followed by TOPSIS and VIKOR. This review reveals that the use of MCDM methods is one of the most attractive research areas in the field of COVID-19. As a result, one of the main purposes of this work is to identify diverse applications of MCDM methods in the COVID-19 pandemic. Most studies i.e. 69% (49 papers) of the papers combined various fuzzy sets with MCDM methods to overcome the problem of uncertainty and ambiguity while analyzing information. Nevertheless, the main drawback of those papers has been the lack of theoretical justifications. In fact, fuzzy MCDM methods impose heavy computational load and there is no general consensus on the clear advantage of fuzzy methods over crisp methods in terms of the solution quality. We hope the researchers who applied fuzzy MCDM methods to COVID-19-related research understand the theoretical basis of MCDM methods and the serious challenges associated with basic operations of fuzzy numbers to avoid potential disadvantages. This paper contributes to the body of knowledge via suggesting a deep vision to critique the fuzzy MCDM methods from mathematical perspective.
Keywords: Multi-criteria decision making, COVID-19, Fuzzy set, Systematic review, Fuzzy arithmetic
Abbreviations
- AHP
Analytic Hierarchy Process
- ANN
Artificial Neural Network
- ANP
Analytical Network Process
- ARAS
Additive Ratio Assessment
- BWM
Best–worst Method
- CRITIC
CRiteria Importance Through Intercriteria Correlation
- COPRAS
Complex Proportional Assessment
- DEA
Data Envelopment Analysis
- DEMATEL
Decision-Making Trial and Evaluation Laboratory
- DJIA
Dow Jones Industrial Average
- ELECTRE
ELimination and Choice Expressing Reality
- FDA
Food and Drug Administration
- GLDS
Gained and lost dominance score
- GMIR
Graded mean integration representation
- GRA
Grey Relation Analysis
- ISM
Interpretive structural modeling
- IDOCRIW
Integrated Determination of Objective Criteria Weights
- JCR
Journal Citation Reports
- MACONT
Mixed Aggregation by COmprehensive Normalization Technique
- MARCOS
Measurement Alternatives and Ranking according to COmpromise Solution
- MCDM
Multi-criteria decision-making
- MCDA
Multi-criteria Decision Analysis
- MCDEA
Multicriteria Data Envelopment Analysis
- OPA
Ordinal Priority Approach
- PCA
Principal component analysis
- PRISMA
Preferred Reporting Items for Systematic Reviews and Meta-Analyses
- PROMETHEE
Preference Ranking Organization Method for Enrichment Evaluations
- OR
Operations Research
- RDM-variables
relative-distance-measure variables
- SODOSM
Subjective and objective decision by opinion score method
- SWARA
Stepwise Weight Assessment Ratio Analysis
- TISM
Total interpretive structural modeling
- TODIM
An acronym in Portuguese for Interactive Multi-criteria Decision Making
- TOPSIS
Technique for Order Preference by Similarity to an Ideal Solution
- VIKOR
VlseKriterijumska Optimizacija I Kompromisno Resenje
- WASPAS
Weighted Aggregated Sum Product Assessment
- WHO
World Health Organization
- WSM
Weighted sum model
- WPM
Weighted product model
1. Introduction
These days, many believe that COVID-19 pandemic is the unparalleled global crisis and probably the biggest challenge which is being faced by humankind in the long history. So far, COVID-19 pandemic decelerated economic activities near to stop, has caused numerous problems for businesses because of serious disruption to supply chains, has killed around six million people worldwide and no one knows when it will end. Fortunately, the use authorization by the US-FDA or WHO for several vaccines (produced by Pfizer-BioNTech, Moderna, AstraZeneca–Oxford, Johnson & Johnson, Sinopharm, Sinovac, and Bharat Biotech) has brought hope of addressing the COVID-19 pandemic.1
Nicola et al. [1] reviewed the socioeconomic effects of COVID-19 on the economy and cited “labeled as a black swan event and likened to the economic scene of World War Two, the outbreak of COVID-19 has had a detrimental effect on global healthcare systems with a ripple effect on every aspect of human life”. Sun et al. [2] reviewed the impact of COVID-19 on global air transportation system and cited “the pandemic is estimated to have caused the largest global recession since the severe worldwide economic downturn in the 1930s (the Great Depression), with millions of people falling into extreme poverty”. Jiang et al. [3] reviewed the impact of COVID-19 on energy industry during the pandemic and cited” the shock to energy demand in 2020 is set to be the largest in the last 70 y. Global energy demand in 2020 is estimated to decline by 6% compared to 2019, a fall seven times greater than the 2009 financial crisis”. Ivanov and Dolgui [4] reviewed literature on disruption propagation in supply chains and cited “the COVID-19 pandemic wreaks havoc on supply chains”. Lin et al. [5], [6] cited “on March 12, 2020, the DJIA further plunged by 9.99%, which was the largest one-day drop in DJIA’s history since Black Monday in 1987”.
By November 2021, the coronavirus disease 2019 has resulted in around 5,200,000 deaths worldwide2 and has become the main cause of death after heart disease and cancer in some countries [7], [8]. Many researchers such as Khurana et al. [9] and Özkan et al. [10] pointed out the COVID-19 pandemic has caused exceptional disruptions in all fields, especially the economic aspect and slowed economic and business activities practically to complete halt. Fortune (2020) reported over 94% of top 1000 companies were affected negatively by COVID-19 pandemic [11]. ISM (2020) mentioned in mid-April 2020, average lead times are over twice compared to common operations and also Chinese and European manufacturing is approximately one-half common capacity i.e. 53% and 50%, respectively [4]. da Silveira Pereira and de Mello [12] reported that 253 billion USD may be the loss of revenue of airlines due to Covid-19 pandemic. Beiderbeck et al. [13] pointed out the COVID-19 pandemic confronted stakeholders of the European football with extreme vagueness in terms of economic and social outcomes and Financial Times (2020) ran the headline “coronavirus threatens €10 billion hit to football transfer market”. Consequently, the COVID-19 pandemic has affected negatively every sphere of life and nearly all industries, including tourism, manufacturing, energy, education, agriculture, aviation, and sports among others.
Choi [14] provided a broad perspective on how OR (Operations Research) methods can help cope with the Covid-19 pandemic. On the other hand, according to Liao et al. [15], artificial intelligence techniques (such as machine learning, deep learning, evolutionary algorithms, etc.) and decision analysis (such as MCDM, fuzzy sets, etc.) are the most hotspots in OR in the last decades. Khan et al. [16], [17] reviewed comprehensively the applications of artificial intelligence-based methods to battle the COVID-19 pandemic. Lalmuanawma et al. [18] reviewed the role of artificial intelligence techniques in screening, predicting, contact tracing, and drug development in the context of COVID-19 pandemic. Naz et al. [19] reviewed the role of artificial intelligence in supply chain resiliency during the COVID-19 pandemic. Sarker et al. [20] reviewed the applications of artificial intelligence that are tailored to serve in the COVID-19 pandemic. Piotrowski and Piotrowska [21] provided a survey on the applications of differential evolution and particle swarm optimization (two currently the most prominent evolutionary algorithms) for problems related with COVID-19 pandemic.
As we can see, although several review papers focused on the use of artificial intelligence techniques, less attention has been paid to MCDM, fuzzy MCDM and in particular to fuzzy arithmetic in the COVID-19 situation (see for example, [22]). Fuzzy MCDM methods have been extensively employed in a huge number of applications because they can incorporate some fuzziness and ambiguity associated with qualitative judgment and provide a useful way to tackle this class of decision problems [15]. Since no comprehensive study of the applications of MCDM, fuzzy MCDM and fuzzy arithmetic to different problems in COVID-19 pandemic has been provided so far, we present this work of the most pertinent literature on this topic. Our main focus is to highlight the applications of MCDM and fuzzy MCDM methods to battle the COVID-19 pandemic and also to review the state-of-the-art solutions to deal with the challenges related to COVID-19 pandemic with the help of MCDM and fuzzy MCDM methods. Furthermore, the key challenges associated with the use of these methods are highlighted and the future recommendations based on updated studies are identified. From a mathematical point of view, the ultimate goal is to motivate the researchers to concentrate their future research on some critical aspects of MCDM and fuzzy MCDM methods which may be easily overlooked.
Salajan et al. [23] reviewed the challenges of decision making during uncertain situations and came up with three key recommendations for enhancing decision making in infectious disease outbreaks: (1) development of decision-making competencies, (2) relationship building for collaboration between main actors and (3) transparent decision-making processes. Ahmad et al. [24] pointed out decision making during a pandemic outbreak is an intricate task and has many challenges due to conflicting trade-offs between decision criteria and the variability of different stakeholders’ perceptions. Moreover, the fast-paced and non-linear characteristic of disease outbreaks may challenge the ability to totally understand decision-making procedures [23]. Fortunately, MCDM methods allow for a broader understanding of issue and help a decision maker (DM) take suitable and transparent decisions in such complex environments [23], [24]. More formally, multidimensionality is intrinsic to the COVID-19 challenges and hence, making decisions in this regard are very complex and involve many trade-offs between conflicting criteria. In such circumstances, DMs need the reliable tools that incorporate quantitative and/or qualitative data in a scientific manner rather than depending only on intuition [25], [26]. Thus, the majority of problems in the COVID-19 context can be modeled as an MCDM problem. This leads to the need of using MCDM methods for coping with decision-making problems in many real-world cases. MCDM is one of the main parts of OR and regarded as the most important research branch of decision-making theory [27], [28]. They are generally used to rank or sort the alternatives with respect to conflicting criteria and have proven to be very reliable and useful in many real-life decision making situations [29].
In general, MCDM methods are classified into two groups with respect to the decision space: MADM and MODM. Discrete decision-making problems with predetermined alternatives (the number of alternatives is finite) are tackled by MADM (multiple attribute decision making) methods and to deal with the continuous problems in which the number of alternatives is infinite, multiobjective decision-making (MODM) methods are used. In literature, the term “MCDM” is often used to represent the discrete MCDM and many papers take “MCDM” and “MADM” as interchangeable. In the rest of this article when we employ the term “MCDM” we mean “discrete MCDM”. In fact, MCDM methods refer to a set of analytical methods which cope with the assessment of a finite set of alternatives with respect to incommensurable and conflicting criteria.
As evidenced by literature, MCDM research has developed very fast leading to MCDM methods having been extensively used in many fields. Having in mind that MCDM methods have been extensively employed in different areas, many review papers have been published so far. For example, Cinelli et al. [30] reviewed the potentials of MCDM methods to conduct sustainability evaluation. Soltani et al. [31] provided a state-of-art review of the application of MCDM methods in municipal solid waste management problems. Zare et al. [32] conducted a review of the MCDM applications in E-learning. Cegan et al. [25] presented a comprehensive literature review of the applications of MCDM in environmental sciences. Gul [33] conducted a state-of-the-art review of occupational health and safety risk assessment using MCDM methods. Sitorus et al. [26] provided a comprehensive overview of the applications and trends of MCDM methods in mining and mineral processing. Nadkarni and Puthuvayi [34] presented a comprehensive literature review on the applications of MCDM methods in heritage buildings. Chen and Pan [35] reviewed comprehensively the literature of fuzzy MCDM in construction management. Widely used in nearly all sectors, Thokala et al. [36] pointed out MCDM methods are increasingly used in healthcare applications to augment the reliability, consistency and transparency of decisions. Mardani et al. [37] reviewed the traditional and fuzzy MCDM methods used in healthcare and medical problems and pointed out they have remarkable capability to tackle and evaluate the various problems within the healthcare environmental.
Also MCDM methods are mainly classified in terms of the type of data that a method employs as classical (crisp) MCDM method and fuzzy MCDM method. Although probability theories may be employed to tackle the uncertainty in MCDM problems, the uncertainty in many situations is not a probability but rather vague information [38]. Fuzzy set theory introduced by Zadeh [39] has been used to dispose vague information in different contexts, especially in decision making. Literature review shows that to tackle the subjective human thinking, a growing body of research has suggested the use of fuzzy extension of MCDM methods [40], [41]. Sitorus et al. [26] mentioned that fuzzy MCDM methods applied when some information are not clearly defined. Also Yeh and Deng [42] noted that in some applications, alternative ratings regarding criteria and relative importance of criteria may not be precisely specified and vagueness is involved. It may be owing to unquantifiable information, unobtainable information, incomplete information and partial ignorance [43]. Considering the uncertainty produced by the lack of complete information and qualitative judgments of DMs in real practice, numerous papers such as Sotoudeh-Anvari and Sadi-Nezhad [44] have been conducted to extend MCDM methods to fuzzy environments. Nevertheless, the critical point in fuzzy modeling is fuzzy arithmetic. Sotoudeh-Anvari [45] reviewed extensively the literature on fuzzy methods and revealed that fuzzy arithmetic is more problematic than is frequently assumed. Piegat [46] warned that serious drawbacks of the standard fuzzy arithmetic can hamper applications of this science domain. Also Yang et al. [47] noted although providing fuzzy or interval assessments can be more natural in real-life problems, the difficulty involved in fuzzy arithmetic may limit their practicability.
We hope this work can highlight the importance of MCDM application in COVID-19 era and give practitioners with insight into state-of-the-art in this field. Hence, the main aim of this article is to conduct a literature review of the applications of MCDM and fuzzy MCDM methods in COVID-19 pandemic. Moreover, an overview of key challenges of fuzzy arithmetic that the decision makers and researchers should know is provided. To achieve this goal, this article is arranged as follows. Section 2 reviews the background on MCDM and fuzzy sets. The details of survey methodology used are discussed in Section 3. The contents of selected papers are tabulated and analyzed in Section 4. The selected papers are reviewed in more detail with regard to application areas in Section 5. Section 6 is dedicated to key findings of this article. Theoretical challenges on fuzzy sets are briefly reviewed in Section 7. In Section 8, future directions are addressed. In Section 9, concluding remarks are presented.
2. Background
In this section, we briefly introduce and describe some concepts concerning MCDM methods and fuzzy sets.
2.1. MCDM literature
This subsection provides an overview characterizing the major features of MCDM problems and methods.
In general, an MCDM problem is to find the best solution from feasible alternatives evaluated under a number of conflicting criteria, both quantitative and qualitative. Suppose that a decision maker (DM) should rank alternatives (also known as options or choices), i.e. with respect to criteria, i.e. . Let be the score of on criteria , and also suppose is the relative weight of , where and . Now, this MCDM problem can be expressed as the following decision matrix:
In general, the main steps of MCDM methods are including problem definition, alternatives determination, criteria determination, decision matrix construction, weight elicitation (determination of criteria weight) and the ranking of alternatives. The decision criteria are often grouped into two categories, namely benefit criteria such that the higher the alternative score the better the performance (e.g. profit) and cost criteria such that the lower the alternative score the better the performance (e.g. price) [27], [30], [34], [48], [49], [50].
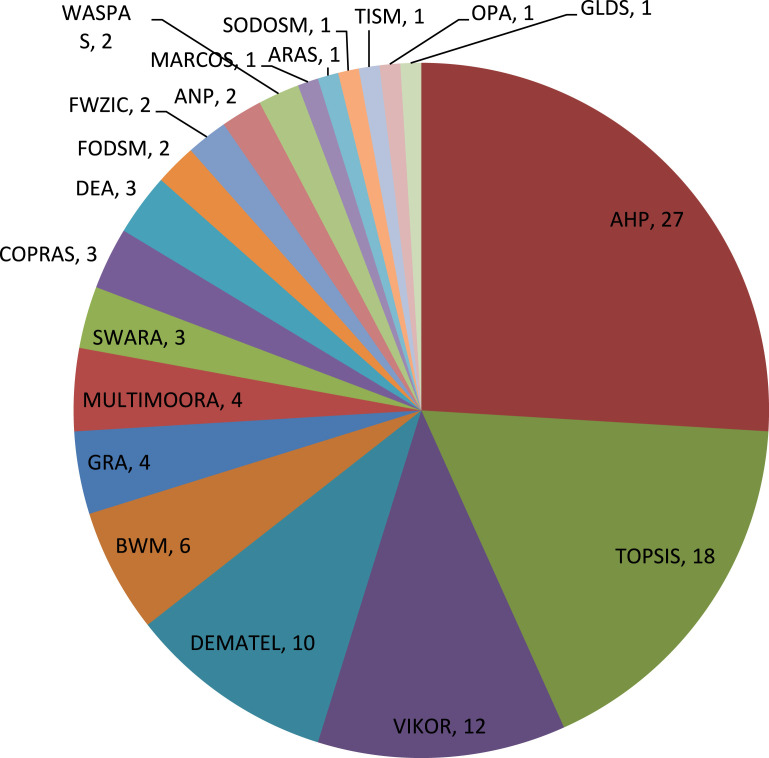
The above MCDM problem can be tackled by well-known and classical MCDM methods such as WSM, AHP, ANP, WPM, TOPSIS, VIKOR, ELECTRE, PROMETHEE, GRA and DEMATEL. Also many scholars have attempted to develop new MCDM methods to deal with real-world problems with different characteristics e.g. COPRAS, WASPAS, BWM, SWARA, MULTIMOORA, SODOSM, ARAS, OPA, MARCOS and GLDS.
Greco et al. [29] pointed out literature consists of around 100 MCDM methods (with the variations) and DMs may be uncertain about which one to apply. MCDM methods are different in the type of problems they aim to address, the theoretical background and the type of results derived [26], [51]. Accordingly, they have been created to handle problems with diverse characteristics and complexity [52]. For example, PROMETHEE has taken a very important place among the MCDM methods. However, De Keyser and Peeters [53] disclosed this method can be used only when some important remarks are taken into considerations. Dožić [54] pointed out the application of each MCDM method depends on the problem that should be tackled and the accessibility of required data. Consequently, there is no particular MCDM method that can be used to deal with all types of decision problems [48], [50], [55], [56], [57].
On the other hand, Gershon and Duckstein [58] pointed out the key criticism of MCDM methods is that different methods may yield different outcomes when applied to a given decision problem and it is relatively difficult to say which MCDM method is more reliable for a given problem. More importantly, the validity of ranking result remains an open question [48]. Needless to say, an incorrect decision in some situations may cause huge or irreparable losses. In fact, the wide variety of methods may confuse DMs and they face the critical task of selecting the most suitable MCDM method from among available methods [55]. Subsequently, many scholars have suggested guidelines for selecting an appropriate MCDM method (e.g. [27], [51], [59], [60], [61]), whereas others applied more than one MCDM methods to a given problem and compared the obtained results [50], [62]. For example, to address this problem, Chen and Pan [35] proposed a two-step method to choose suitable fuzzy MCDM methods for solving construction management problems. However, literature shows a significant research challenge which is not addressed yet is to select a suitable MCDM method for a given decision problem [61].
As documented in the literature, MCDM methods have their own strength and limitations for certain applications. For example, Sotoudeh-Anvari et al. [50] listed the benefit and weakness of some MCDM methods in optimal search problem. Chen and Pan [35] listed some advantages and disadvantages of fuzzy MCDM methods in construction management. Mousavi-Nasab and Sotoudeh-Anvari [62] studied the characteristics of MCDM methods in material selection problem. However, Cinelli et al. [30] argued many authors do not demonstrate well the reasons for choosing an MCDM method instead of another and familiarity and/or affinity seem to be the drivers for the choice of a certain MCDM method. Simply speaking, thanks to the availability of various software packages, MCDM methods are being employed extensively. However, according to Hobbs and Horn [56], if general DMs do not understand how an MCDM method works, they may not trust the obtained results.
We know that MCDM methods can be categorized in different ways. A general grouping of MCDM methods can be classified as multi-attribute utility theory (MAUT) such as TOPSIS and VIKOR and outranking methods such as ELECTRE and PROMETHEE [63]. An outranking method is on the basis of pairwise comparisons between alternatives regarding each criterion and the outranking relations are derived by aggregating the pairwise comparisons [28]. For the MAUT methods, the following steps are often included: (1) establishing a decision matrix (2) normalizing this decision matrix (3) aggregating the performance value of options with respect to all decision criteria and (4) determining the ranking of options [27], [63], [64]. Consequently, the key reason why various MCDM methods may generate different outcomes lies in the diversity of normalization methods and aggregation functions employed [27], [28], [50], [55], [64].
Everybody knows that the performance of alternatives regarding decision criteria is evaluated by different units. Normalization techniques are applied to the elements of given decision matrix to make diverse scales of measurement comparable. There are different normalization techniques and each of them has its own strength, weakness and emphasis [65]. Moreover, different normalization techniques may lead to different outcomes [64]. Milani et al. [65] evaluated the effect of different normalization techniques in MCDM methods and pointed out if not appropriately assigned, normalization within an MCDM method may fail to reach reliable decision. Nevertheless, limited attention has been paid for selecting suitable normalization technique for an MCDM method [66].
In general, MCDM methods provide a useful alternative for dealing with two major types of MCDM problems, i.e. ranking and sorting [52]. Simply speaking, the ranking methods generate a complete or partial ranking of alternatives and the sorting methods assign each alternative to predefined ordered classes [27]. The literature review shows that the ranking problems are the most common problems studied in the MCDM literature [63]. Sorting methods (such as TOPSIS-Sort) are used to classify the available alternatives into predefined ordered categories with respect to decision criteria. Alvarez et al. [52] provided a comprehensive review of MCDM sorting methods which contains 30 years of research in this field. Also as suggested by Hwang and Yoon [67], MCDM methods can be classified as compensatory methods such as TOPSIS and WSM and non-compensatory methods such as PROMETHEE. A compensatory method allows tradeoff within decision criteria and unfavorable scores of a criterion can be counterbalanced by a good score of another criterion. But in a non-compensatory method, no such trade-offs can take place [65].
On the other hand, with the increasing complexity of decision environment, it is less feasible for a DM to take into consideration all aspects of a given problem and hence, group decision making methods that involve several DMs become popular in many fields [44]. Triantaphyllou [28] proposed that MCDM methods can be classified corresponding to decision makers, such as MCDM methods involving single DM and group DMs. It should be noted that in group decision making literature, the majority of methods have utilized aggregation techniques such as arithmetic mean and geometric mean to construct a collective decision. However, Kacprzak [68] warned that such averaged information may not reflect the difference between the decisions and cause a wrong decision and introduced an extension of TOPSIS for group decision making which does not need aggregation.
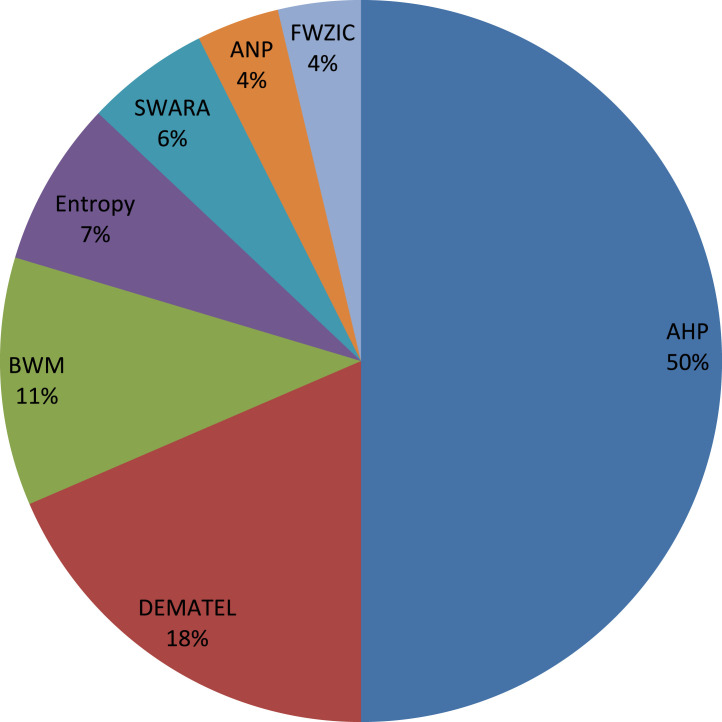
From computational point of view, MCDM methods have two main steps. In the first step, the criteria weights should be determined and in the second step, the available alternatives should be ranked.3 In fact, in nearly all MCDM problems, the significance of criteria is not necessarily identical and hence, the weights are assigned to criteria to show their relative importance [70]. For example, Altay et al. [71] pointed out the weights of majority of criteria have changed significantly between pre-COVID-19 and during COVID-19 periods. Clearly, the ranking outcomes are significantly sensitive to changes in weights and consequently, how to determine them is crucial to MCDM methods. In general, the weights can be obtained subjectively, objectively, and by combination of these methods [72]. The subjective methods such as AHP, BWM and SWARA rely completely on the subjective judgments from DM and the objective methods such as Entropy and CRITIC derive the weights by using the statistical evaluation of decision matrix or mathematical models without any preference information from DM. Hybrid methods such as SODOSM (subjective and objective decision by opinion score method) are based on the combination of subjective and objective methods and try to take advantages of both methods. Clearly, objective methods do not take into consideration human assessments which are fundamental in making a reliable decision. On the other hand, although subjective methods depend on human preference, they face inconsistency problem. In fact, the results obtained from AHP are acceptable if the pairwise comparisons pass the consistency test [73]. BWM introduced by Rezaei [74] is a subjective method that requires less pairwise comparisons than AHP and derives the weights with high consistency. In this method, pairwise comparisons are conducted between best and worst criteria and the other criteria and then a maximin problem is formulated to derive the criteria weights. Very recently, Albahri et al. [73] pointed out both subjective and objective methods pay no attention to the importance of criterion value and introduced SODOSM which integrates subjective and objective approaches to address this disadvantage.
Although there is a common assumption in MCDM problems that the decision criteria are independent of each other, it is not the case in many situations. Among the MCDM methods considered above, DEMATEL and ISM (interpretive structural modeling) have been used to uncover the complex interdependence among decision criteria [75]. In fact, DEMATEL has been widely used for the exploration of cause and effect (causal) relationships between decision criteria [76]. Also ANP which is the extension of AHP is used whenever there are interdependencies and feedback relation among the criteria whereas AHP assumes the criteria are independent among one another [77].
DEA (data envelopment analysis) introduced by Charnes et al. [78] is a nonparametric data-driven model that employs linear programming for measuring the relative efficiency of homogeneous decision making units (DMUs) with multiple inputs and multiple outputs [79]. Mathematically speaking, DEA obtains the multipliers (weights) for inputs and outputs of DMUs, so that their efficiency is maximized, following the restrictions [12]. Simply speaking, DEA estimates the efficiency of a given DMU by comparing how well that DMU converts the inputs into the outputs [80]. Some particularities of conventional DEA are that:
-
-
It does not require normalization.
-
-
The weights are not allocated by DM.
-
-
It does not employ a common set of weights.
Nevertheless, there are some inter-related disadvantages to DEA such as low discriminatory power and impractical weight distribution [12], [62], [81]. On the other words, the weights assignment by DEA may not in harmony with the fact and thus, yielding most DMUs as efficient.
Clearly, the main goals of DEA and MCDM differ and they should be utilized for different problems. However, as indicated by Stewart [82], there are interesting links and similarities between these methods. The resemblance with MCDM is notable if a user replaces “DMUs” with “alternatives”, “outputs” with “criteria to be maximized” and “inputs” with “criteria to be minimized” [81]. Although Mousavi-Nasab and Sotoudeh-Anvari [62] pointed out DEA cannot be generally considered as an MCDM method, the applications of DEA models as MCDM methods has been gaining increasing interest. Consequently, COVID-19 studies using DEA are included in this review.
2.2. Fuzzy sets
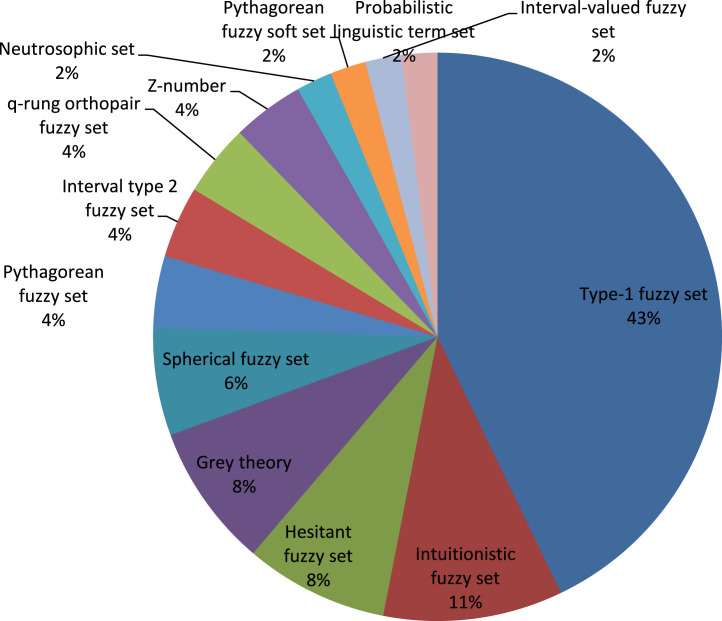
MCDM methods can be also classified in terms of the type of data that a method employs as crisp (also known as classical) or fuzzy MCDM methods. In the crisp MCDM methods, the score of alternatives on criteria and the weight of criteria can be precisely evaluated and expressed by crisp numbers, whereas in fuzzy MCDM methods, the linguistic variables linked with fuzzy numbers are used to reflect the vagueness of subjective expressions presented by DM [37], [41], [42]. In fact, crisp MCDM methods have been widely applied to the COVID-19 pandemic in the cases where all data are exactly obtained. When that is not the case, fuzzy MCDM methods (or other uncertainty theories) have been developed. Simply speaking, fuzzy MCDM methods integrate various fuzzy sets and MCDM methods to build novel approaches for resolving complex problems in COVID-19 pandemic under uncertainty.
Classical fuzzy set (also known as type-1 fuzzy set) introduced by Zadeh [39] is designed to model the vagueness and ambiguity of human cognitive processes existed in real-life world problems. The key idea of fuzzy set is that an element has a membership degree in a given set. Mathematically speaking, type-1 fuzzy set is a set of elements with the membership values ranging between 0 and 1, whereas the elements in classical set have membership values of 0 or 1. As an extension of type-1 fuzzy set, Zadeh [83] suggested type-2 fuzzy set whose membership grades are type-1 fuzzy set. Despite its advantages, the use of type-2 fuzzy set results in heavy calculations. Interval type-2 fuzzy set as a special case of a type-2 fuzzy set is characterized by an interval valued membership function which reduces the computational process [84]. Torra [85] defined the hesitant fuzzy set whose membership grade of each element includes a set of possible values between 0 and 1. Atanassov [86] extended fuzzy set and introduced intuitionistic fuzzy set by adding non-membership grade into classical fuzzy set. Intuitionistic fuzzy set is characterized by membership, non-membership and hesitancy degrees and the sum of membership and non-membership grades for each element must be . Qian et al. [87] extended hesitant fuzzy set to generalized hesitant fuzzy set by combining intuitionistic fuzzy set and hesitant fuzzy set. Cuong and Kreinovich [88] developed picture fuzzy set which is a direct extension of intuitionistic fuzzy set by incorporating the positive, neutral and negative membership grades of an element while the sum of them is . More formally, the concept of picture fuzzy set is based on four elements, namely membership (satisfaction), non-membership (dissatisfaction), abstinence, and refusal grades. Yager [89] introduced pythagorean fuzzy set as a generalization of intuitionistic fuzzy set whose interesting characteristic is that the sum of membership and non-membership grades could exceed 1 but the square sum of them is . Later, q-rung orthopair fuzzy set as a general and more flexible class of pythagorean fuzzy set and intuitionistic fuzzy set was developed. Yager [90] introduced -rung orthopair fuzzy set in which the sum of qth power of membership grade and qth power of non-membership grade is restricted to 1. In fact, intuitionistic fuzzy set and pythagorean fuzzy set are special cases of q-rung orthopair fuzzy set when and , respectively. Smarandache [91] combined the grade of indeterminacy as an independent element in intuitionistic fuzzy set and introduced the neutrosophic set to handle vagueness considering the truth-membership, indeterminacy-membership and falsity-membership while the sum of them . Spherical fuzzy set introduced by Mahmood et al. [92] is the latest extension of intuitionistic fuzzy set, pythagorean fuzzy set, neutrosophic set and picture fuzzy set. In spherical fuzzy set, the sum of membership , non-membership and hesitancy grades should satisfy . Also the concept of spherical fuzzy set is extended to T-spherical fuzzy set with a condition which can handle the situations where picture fuzzy set failed. On the other hand, in some situations, it is more reasonable to describe the membership and non-membership grades by interval-valued data owing to the complexity of real-life decision problems. Hence, various interval fuzzy sets such as interval type-2 fuzzy set, interval-valued hesitant fuzzy set, interval-valued intuitionistic fuzzy set, etc have been suggested [93]. For example, interval-valued intuitionistic fuzzy set is a generalization of intuitionistic fuzzy set in which are employed for membership and non-membership grades rather than exact values.
Zadeh [83] introduced the linguistic variables which allow DM to give his opinions in words. Literature contains different proposals about linguistic term sets. For example, Rodriguez et al. [94] pointed out a single linguistic variable sometimes cannot define the hesitation of DM among several linguistic variables and proposed hesitant fuzzy linguistic term set in which more than one word (term) are employed to represent the linguistic information. Pang et al. [95] argued that it is not reasonable to consider the importance of linguistic variables as the same and developed probabilistic linguistic term set in which the linguistic terms with probabilistic information are combined. However, none of the aforementioned fuzzy sets account for the reliability of information. Zadeh [96] developed the concept of Z-number to describe the reliability that exists in human preference and real-world information. Z-number is an ordered pair of fuzzy numbers i.e. and has two components: fuzzy restriction and fuzzy reliability. Molodtsov [97] claimed that probability theory, fuzzy sets, and interval mathematics which we use as mathematical tools for handling uncertainties have inherent insufficiencies and introduced the concept of soft set theory. By combining soft set with other fuzzy sets, various extensions of them such as intuitionistic fuzzy soft set, pythagorean fuzzy soft set, neutrosophic soft set, etc have been presented.
Since the introduction of fuzzy set into MCDM methods, numerous fuzzy MCDM methods have been used to handle a variety of problems with promising results [41]. On the other hand, many researchers have pointed out the use of fuzzy sets to MCDM methods can provide an effective way of handling subjectiveness of decision making process and DMs can efficiently express their assessments using linguistic terms with fuzzy number representation. Nevertheless, the critical point in fuzzy modeling is fuzzy arithmetic. For example, Sotoudeh-Anvari [45] revealed that fuzzy set and its extensions are not without critics. He reviewed extensively the literature on fuzzy methods and deduced that fuzzy arithmetic is more problematic than is frequently assumed. In next sections, we shall briefly explain some remarks associated with this challenge and in-depth description of this topic can be found in [45].
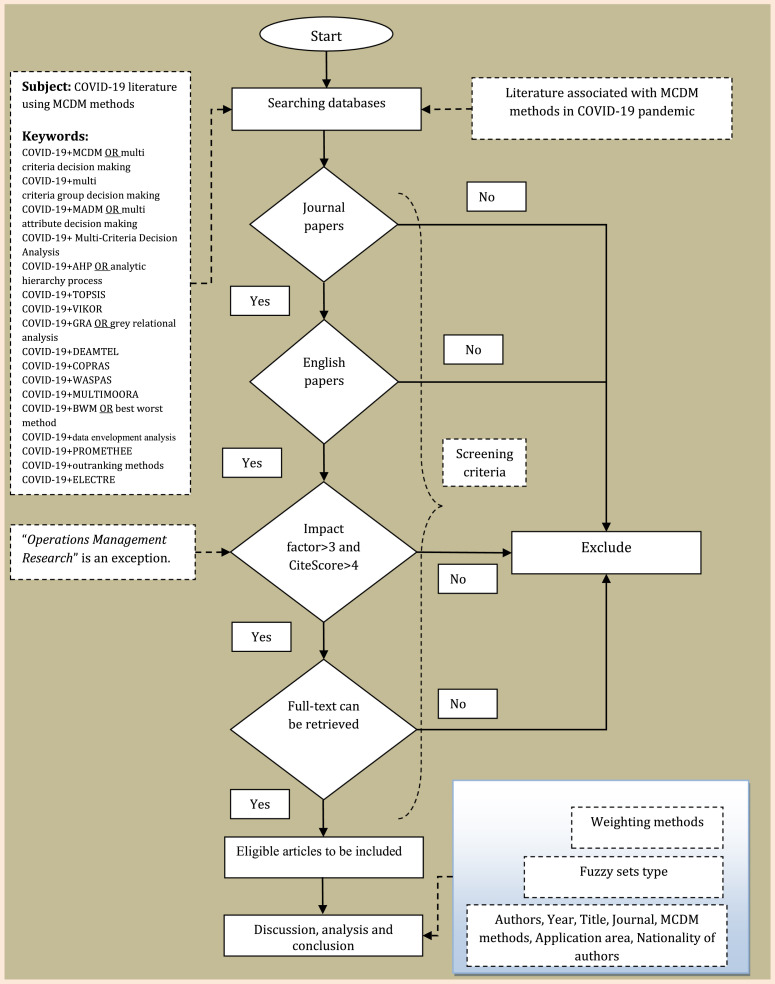
3. Research methodology
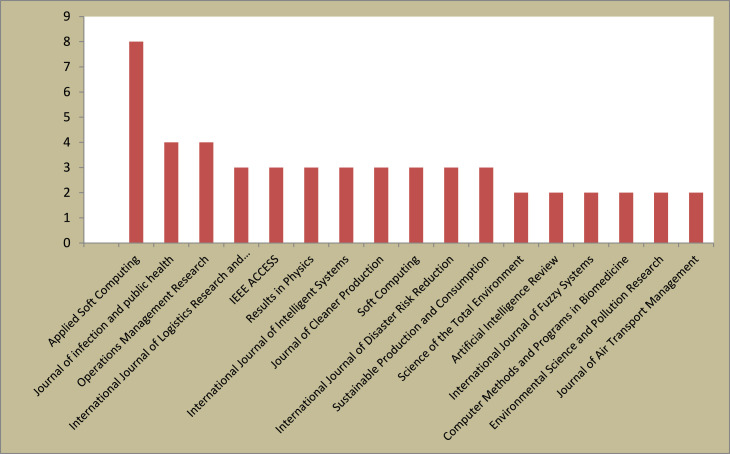
This paper has conducted a systematic review on the COVID-19 literature using MCDM methods based on PRISMA (Preferred Reporting Items for Systematic Reviews and Meta-Analyses) method, which involves three key steps: “literature search”, “selection of eligible papers”, and “data extraction and summarizing” [32]. The PRISMA statement developed by Moher et al. [98] was proposed to improve the integrity of reporting systematic reviews. In this paper, the search is done to seek only leading peer-reviewed publications. Consequently, the papers on COVID-19 under MCDM methods are collected from Web of Science with Scopus and Google Scholar also consulted in “literature search” section of PRISMA. The literature search is carried out using the main term “COVID-19” combined with “MCDM”, ”multi-criteria decision analysis”, “MCDA”, “multi-attribute decision-making”, ”MADM”, “TOPSIS”, “AHP”, ”ANP”, “BWM”, ”COPRAS”, ”VIKOR”, ”DEMATEL”, ”WASPAS”, ”SWARA”, ”MULTIMOORA”, “DEA” etc from Web of Science, Google Scholar and Scopus from January 2020 to November 2021. In fact, the term “COVID-19” and the aforementioned terms are searched using “AND” command in different ways to achieve the most narrowly-defined and appropriate outcomes. Those articles that did not use explicitly an MCDM method are excluded. To be selected (in the second stage of PRISMA), the journals should meet two inclusion criterion, namely Impact Factor>3 and CiteScore>4. Impact Factor (IF) is the most well-known metric to assess the quality of journals. Also CiteScore as the youngest metric is one of the three chief indices in Scopus to rank journals [99]. Meho [100] provided a list of key differences between CiteScore database and Journal Citation Reports (JCR) which has published IF. We know IF and CiteScore are citation-based and such metrics are criticized from various angles. Also many studies have pointed out the quality of a certain journal does not imply the quality of a specific paper necessarily. Simply speaking, every metric has its advantages and disadvantages and hence, a combination use of them can provide a more comprehensive approach to evaluate the influence of a certain journals, rather than impact factor alone [99]. Here, there is an exception. “Operations Management Research” (Impact Factor=2.706 and CiteScore=3.8) does not meet these conditions. However, this journal published the applications of two new and important MCDM methods in COVID-19 pandemic, namely GLDS (gained and lost dominance score) and OPA (ordinal priority approach) and is included in this analysis as an exception. We exclude conference proceedings and book chapters since there is no way of knowing if they go through a peer-review process. For this reason, this review contains only papers from leading journals with high impact factor. Also the papers not published in English are precluded from the analysis. Moreover, the papers from which full text can be retrieved are included. Finally, we exclude any papers that failed to suggest an explicit multi-criteria analysis using MCDM methods in COVID-19 pandemic even they have applied methods like Delphi method and aggregation operator-based methods.
Considering COVID-19 being a new phenomenon and 1 December 2019 is the start of the COVID-19 crisis, we do not limit this review to a certain period. But the retrieval end date is November 2021. The selection of papers to be included in this review is shown in Fig. 1.
Fig. 1.
Flow diagram regarding the eligibility review process.
By the strategy mentioned above, 72 articles are selected from the international scholarly journals to carry on a comprehensive analysis. These selected papers are further classified based on the kinds of MCDM methods adopted, fuzzy sets and applications. The action of summarizing and categorizing papers based on PRISMA enable us to derive impressive hints and various potential future works. In the next step, the eligible papers are summarized to classify the authors, publication years, title, journal, method, application and the country of origin. Finally, I apologize to all researchers making key findings in this field who are not cited.
Before closing this section of paper, one remark should be mentioned. At the time of writing, I became aware of the paper entitled “Rise of multiattribute decision-making in combating COVID-19: A systematic review of the state-of-the-art literature” Alsalem et al. [101]. It should be pointed out there are fundamental differences between that paper and the current review, particularly in terms of priorities and aims.
4. Analysis results
Now, we go over the articles contained in the sample. Table 1 summarizes the authors, year of publication, title, journal, method, application field and the countries of the author’s affiliation of each paper analyzed. It should be noted that some papers involved more than one method. In such cases, only MCDM methods are taken into consideration. Also if a given paper was written by researchers from diverse countries, it was counted for those countries in our analysis.
Table 1.
The papers that applied MCDM methods for COVID-19 problems.
| Author(s) | Title | Journal | Method | Application field | The nationality of authors |
|---|---|---|---|---|---|
| Mardani et al. [102 ] | A novel extended approach under hesitant fuzzy sets to design a framework for assessing the key challenges of digital health interventions adoption during the COVID-19 outbreak | Applied soft computing | SWARA–WASPAS | Digital health interventions | Viet Nam, Iran, India |
| Ashraf and Abdullah [103 ] | Emergency decision support modeling for COVID-19 based on spherical fuzzy information | International Journal of Intelligent Systems | AHP-Entropy-TOPSIS-GRA | Emergency decision support system | Pakistan |
| Ocampo and Yamagishi [104 ] | Modeling the lockdown relaxation protocols of the Philippine government in response to the COVID-19 pandemic: An intuitionistic fuzzy DEMATEL analysis | Socio-Economic Planning Sciences | DEMATEL | Lockdown relaxation protocols | Philippines |
| Sharma et al. [105 ] | Developing a framework for enhancing survivability of sustainable supply chains during and post-COVID-19 pandemic | International Journal of Logistics Research and Applications | SWARA | Sustainable supply chains | India, UK |
| Belhadi et al. [106 ] | Infectious Waste Management Strategy during COVID-19 Pandemic in Africa: an Integrated Decision-Making Framework for Selecting Sustainable Technologies | Environmental Management | AHP-VIKOR | Infectious Waste Management | Morocco, France, China, India |
| Chen and Lin [107 ] | Smart and automation technologies for ensuring the long-term operation of a factory amid the COVID-19 pandemic: an evolving fuzzy assessment approach | The International Journal of Advanced Manufacturing Technology | AHP-TOPSIS | Smart and automation technologies | Taiwan |
| Mohammed et al. [108 ] | Benchmarking Methodology for Selection of Optimal COVID-19 Diagnostic Model Based on Entropy and TOPSIS Methods | IEEE ACCESS | Entropy-TOPSIS | COVID-19 diagnostic model | Iraq, Malaysia, Saudi Arabia, Spain |
| Ashraf et al. [109 ] | A new emergency response of spherical intelligent fuzzy decision process to diagnose of COVID19 | Soft Computing | TOPSIS-COPRAS | Control of spreading of COVID19 | Pakistan, Saudi Arabia |
| Requia et al. [110 ] | Risk of the Brazilian health care system over 5572 municipalities to exceed health care capacity due to the 2019 novel coronavirus (COVID-19) | Science of The Total Environment | AHP | Community attribute | Brazil, Canada, United States |
| Albahri et al. [111 ] | Detection-based prioritization: Framework of multi-laboratory characteristics for asymptomatic COVID-19 carriers based on integrated Entropy-TOPSIS methods | Artificial Intelligence In Medicine | Entropy-TOPSIS | Prioritization of patients with COVID-19 | Iraq, Malaysia |
| Alkan and Kahraman [112 ] | Evaluation of government strategies against COVID-19 pandemic using q-rung orthopair fuzzy TOPSIS method | Applied Soft Computing | Entropy-TOPSIS | Government strategies | Turkey |
| Hezer et al. [113 ] | Comparative analysis of TOPSIS, VIKOR and COPRAS methods for the COVID-19 Regional Safety Assessment | Journal of infection and public health | TOPSIS-VIKOR-COPRAS | Regional safety | Turkey |
| Hosseini et al. [114 ] | Recovery solutions for ecotourism centers during the Covid-19 pandemic: Utilizing Fuzzy DEMATEL and Fuzzy VIKOR methods | Expert Systems with Applications | DEMATEL-VIKOR | Ecotourism centers | Iran, Mexico |
| Manupati et al. [77 ] | Selection of the best healthcare waste disposal techniques during and post COVID-19 pandemic era | Journal of Cleaner Production | VIKOR | Health-care waste disposal techniques | India |
| Das et al. [115 ] | Habitat vulnerability in slum areas of India — What we learnt from COVID-19? | International Journal of Disaster Risk Reduction | AHP | Habitat vulnerability in slum areas | India |
| Majumdar et al. [116 ] | Prioritizing risk mitigation strategies for environmentally sustainable clothing supply chains: Insights from selected organizational theories | Sustainable Production and Consumption | TOPSIS | Sustainable clothing supply chains | India, China |
| Saraji et al. [117 ] | An extended hesitant fuzzy set using SWARA-MULTIMOORA approach to adapt online education for the control of the pandemic spread of COVID-19 in higher education institutions | Artificial Intelligence Review | SWARA-MULTIMOORA | Higher education institutions | Iran, United States, Japan, India |
| Ecer and Pamucar [118 ] | MARCOS technique under intuitionistic fuzzy environment for determining the COVID-19 pandemic performance of insurance companies in terms of healthcare services | Applied Soft Computing | Intuitionistic fuzzy weighted averaging-MARCOS | Health insurance companies | Turkey, Serbia |
| Ocampo et al. [119 ] | Classifying the degree of exposure of customers to COVID-19 in the restaurant industry: A novel intuitionistic fuzzy set extension of the TOPSIS-Sort | Applied Soft Computing | TOPSIS-Sort | Restaurant industry | Philippines |
| Aydin and Seker [120 ] | Determining the location of isolation hospitals for COVID-19 via Delphi-based MCDM method | International Journal of Intelligent Systems | BWM- TOPSIS |
Location of isolation hospitals | Turkey |
| Ahmad et al. [24 ] | Identification and prioritization of strategies to tackle COVID-19 outbreak: A group-BWM based MCDM approach | Applied Soft Computing | Group BWM | Strategies to tackle outbreak | India |
| Shah et al. [121 ] | Energy trilemma based prioritization of waste-to-energy technologies: implications for post-COVID-19 green economic recovery in Pakistan | Journal of Cleaner Production | DEMATEL-ANP-VIKOR | Waste-to-energy alternatives | China, Pakistan |
| Mohammed et al. [122 ] | Convalescent-plasma-transfusion intelligent framework for rescuing COVID-19 patients across centralized/decentralized telemedicine hospitals based on AHP-group TOPSIS and matching component | Applied Intelligence | AHP-TOPSIS | Convalescent plasma transfusion | Malaysia, Iraq, Canada |
| Mishra et al. [123 ] | An extended fuzzy decision-making framework using hesitant fuzzy sets for the drug selection to treat the mild symptoms of Coronavirus Disease 2019 (COVID-19) | Applied Soft Computing | Divergence measure-ARAS | Drug selection | India |
| Altuntas and Gok [76 ] | The effect of COVID-19 pandemic on domestic tourism: A DEMATEL method analysis on quarantine decisions | International Journal of Hospitality Management | DEMATEL | Domestic tourism | Turkey |
| Lin et al. [5], [6] | Improving Service Quality of Wealth Management Bank for High-Net-Worth Customers During COVID-19: A Fuzzy-DEMATEL Approach | International Journal of Fuzzy Systems | DEMATEL | Wealth management bank | Taiwan |
| Choudhury et al. [124 ] | Evaluating the Preparedness of Indian States against COVID-19 Pandemic Risk: A Fuzzy Multi-criteria Decision-Making Approach | Risk Analysis | AHP | Preparedness of Indian States | India |
| Goker [125 ] | A novel integrated intuitionistic fuzzy decision aid for agile outsourcing provider selection: a COVID-19 pandemic-based scenario analysis | Soft Computing | Intuitionistic fuzzy cognitive map-COPRAS | Outsourcing provider selection | Turkey |
| Boyacıand Şişman [126 ] | Pandemic hospital site selection: a GIS-based MCDM approach employing Pythagorean fuzzy sets | Environmental Science and Pollution Research | AHP-TOPSIS | Pandemic hospital site selection | Turkey |
| Chai et al. [127 ] | Z-uncertain probabilistic linguistic variables and its application in emergency decision making for treatment of COVID-19 patients | International Journal of Intelligent Systems | Maximizing deviation method-TOPSIS | Emergency decision making | China |
| Shadeed and Alawna [128 ] | GIS-based COVID-19 vulnerability mapping in the West Bank, Palestine | International Journal of Disaster Risk Reduction | AHP | COVID-19 vulnerability mapping | Palestine |
| Ortiz-Barrios et al. [129 ] | A multiple criteria decision-making approach for increasing the preparedness level of sales departments against COVID-19 and future pandemics: A real-world case | International Journal of Disaster Risk Reduction | AHP-TOPSIS | The preparedness level of sales departments | Colombia, Italy, Turkey |
| Yao [130 ] | Fuzzy-based multi-criteria decision analysis of environmental regulation and green economic efficiency in a post-COVID-19 scenario: the case of China | Environmental Science and Pollution Research | AHP-VIKOR | Green economic efficiency | China |
| Özkan et al. [10 ] | Evaluation of criteria and COVID-19 patients for intensive care unit admission in the era of pandemic: A multi-criteria decision making approach | Computer Methods and Programs in Biomedicine | AHP-MULTIMOORA | COVID-19 patients for intensive care unit admission | Turkey |
| Ghorui et al. [131 ] | Identification of dominant risk factor involved in spread of COVID-19 using hesitant fuzzy MCDM methodology | Results in Physics | AHP-TOPSIS | Risk factors in spread of COVID-19 | India, Malaysia, Turkey, Italy |
| Yamagishi and Ocampo [132 ] | Utilizing TOPSIS-Sort for sorting tourist sites for perceived COVID-19 exposure | Current Issues in Tourism | TOPSIS-Sort | Tourist sites | Philippines |
| Kirişci et al. [70 ] | The novel VIKOR methods for generalized Pythagorean fuzzy soft sets and its application to children of early childhood in COVID-19 quarantine | Neural Computing and Applications | VIKOR | Children in COVID-19 quarantine | Turkey |
| Kumar et al. [133 ] | Mitigate risks in perishable food supply chains: Learning from COVID-19 | Technological Forecasting and Social Change | BWM | Perishable food supply chains | India, China |
| Petrudi et al. [134 ] | Assessing suppliers considering social sustainability innovation factors during COVID-19 disaster | Sustainable Production and Consumption | BWM-improved GRA | Social sustainability of supply chains | Iran, Taiwan, Singapore |
| Hezam et al. [135 ] | COVID-19 Vaccine: A neutrosophic MCDM approach for determining the priority groups | Results in physics | AHP-TOPSIS | Optimum allocation of COVID-19 vaccines | Saudi Arabia, Yemen, Bangladesh |
| Hartanto and Mayasari [136 ] | Environmentally friendly non-medical mask: An attempt to reduce the environmental impact from used masks during COVID 19 pandemic | Science of the Total Environment | AHP | Environmentally friendly non-medical mask | Indonesia |
| Gao et al. [137 ] | A Study of COVID-19 in the Wuhan, Beijing, Urumqi and Dalian Cities based on the Regional Disease Vulnerability Index | Journal of Infection and Public Health | AHP | Regional disease vulnerability index | China, United States |
| Khurana et al. [9 ] | Now is the time to press the reset button: Helping India’s companies to become more resilient and effective in overcoming the impacts of COVID-19, climate changes and other crises | Journal of Cleaner Production | AHP | Sustainable supply chains | India, United States |
| Khan et al. [16], [17] | q-Rung Orthopair Fuzzy Modified Dissimilarity Measure Based Robust VIKOR Method and Its Applications in Mass Vaccination Campaigns in the Context of COVID-19 | IEEE ACCESS | AHP-VIKOR | COVID-19 vaccine | Thailand, Pakistan, Taiwan, Saudi Arabia |
| Kumar and Kumar Singh [138 ] | Strategic framework for developing resilience in Agri-Food Supply Chains during COVID 19 pandemic | International Journal of Logistics Research and Applications | BWM | Agri-food supply chains | India |
| Asadi et al. [139 ] | Evaluation of Factors to Respond to the COVID-19 Pandemic Using DEMATEL and Fuzzy Rule-Based Techniques | International Journal of Fuzzy Systems | DEMATEL | Malaysia, Saudi Arabia, Australia |
|
| Paul et al. [140 ] | Supply chain recovery challenges in the wake of COVID-19 pandemic | Journal of Business Research | DEMATEL | Supply chain recovery | Australia, Bangladesh |
| Alam et al. [141 ] | Challenges to COVID-19 vaccine supply chain: Implications for sustainable development goals | International Journal of Production Economics | DEMATEL | COVID-19 vaccine supply chain | Bangladesh, Denmark, Canada |
| Shanker et al. [142 ] | Enhancing resiliency of perishable product supply chains in the context of the COVID-19 outbreak | International Journal of Logistics Research and Applications | DEMATEL-ANP | Perishable product supply chains | India, New Guinea, UK |
| Chen and Wang [143 ] | A calibrated piecewise-linear FGM approach for travel destination recommendation during the COVID-19 pandemic | Applied Soft Computing | AHP-TOPSIS | Travel destination recommendation | Taiwan |
| Palouj et al. [144 ] | Surveying the impact of the coronavirus (COVID-19) on the poultry supply chain: A mixed methods study | Food Control | AHP | Poultry supply chain | Iran |
| Altay et al. [71 ] | An intelligent approach for analyzing the impacts of the COVID-19 pandemic on marketing mix elements (7Ps) of the on-demand grocery delivery service | Complex & Intelligent Systems | AHP | On-demand grocery delivery service | Turkey |
| Samanci et al. [145 ] | Focusing on the big picture while observing the concerns of both managers and passengers in the post-COVID era | Journal of Air Transport Management | VIKOR | Service quality | Turkey |
| Razzaq et al. [8 ] | Different variants of pandemic and prevention strategies: A prioritizing framework in fuzzy environment | Results in Physics | AHP-VIKOR | Prevention strategies for COVID-19 | Pakistan |
| Alsalem et al. [146 ] | Based on T-spherical Fuzzy Environment: A Combination of FWZIC and FDOSM for Prioritizing COVID-19 Vaccine Dose Recipients | Journal of Infection and Public Health | FWZIC-FODSM | COVID-19 vaccine | Malaysia, Taiwan, Australia, Iraq |
| Albahri et al. [147 ] | Novel Dynamic Fuzzy Decision-Making Framework for COVID-19 Vaccine Dose Recipients | Journal of Advanced Research | FWZIC-FODSM | COVID-19 vaccine | Malaysia, Australia, China, Iraq |
| Albahri et al. [73 ] | Helping doctors hasten COVID-19 treatment: Towards a rescue framework for the transfusion of best convalescent plasma to the most critical patients based on biological requirements via ml and novel MCDM methods | Computer Methods and Programs in Biomedicine | SODOSM | Convalescent plasma transfusion | Malaysia, Iraq |
| Albahri et al. [148 ] | Systematic review of artificial intelligence techniques in the detection and classification of COVID-19 medical images in terms of evaluation and benchmarking: Taxonomy analysis, challenges, future solutions and methodological aspects | Journal of Infection and Public Health | AHP-VIKOR | Malaysia, Iraq | |
| Si et al. [149 ] | Picture fuzzy set-based decision-making approach using Dempster–Shafer theory of evidence and grey relation analysis and its application in COVID-19 medicine selection | Soft Computing | GRA | Medicine selection problem | India |
| Aydin and Yurdakul [79 ] | Assessing countries’ performances against COVID-19 via WSIDEA and machine learning algorithms | Applied Soft Computing | DEA | Countries’ performances against COVID-19 | Turkey |
| da Silveira Pereira and de Mello [12 ] | Efficiency evaluation of Brazilian airlines operations considering the Covid-19 outbreak | Journal of Air Transport Management | MCDEA | Efficiency evaluation of airlines | Brazil |
| Revuelta et al. [150 ] | A hybrid data envelopment analysis—artificial neural network prediction model for COVID-19 severity in transplant recipients | Artificial Intelligence Review | DEA | Prediction model for COVID-19 severity in transplant recipients | Spain, Italy |
| Mehmood et al. [151 ] | Spatiotemporal variability of COVID-19 pandemic in relation to air pollution, climate and socioeconomic factors in Pakistan | Chemosphere | GRA | China, Greece, Saudi Arabia, Pakistan |
|
| Orji and Ojadi [152 ] | Investigating the COVID-19 pandemic’s impact on sustainable supplier selection in the Nigerian manufacturing sector | Computers & Industrial Engineering | AHP-MULTIMOORA | Sustainable supplier selection | China, Nigeria |
| Wan et al. [93 ] | An integrated interval type-2 fuzzy technique for democratic–autocratic multi-criteria decision making | Knowledge-based Systems | BWM-VIKOR | Makeshift hospital selection problem | China |
| Karmaker et al. [153 ] | Improving supply chain sustainability in the context of COVID-19 pandemic in an emerging economy: Exploring drivers using an integrated model | Sustainable Production and Consumption | TISM | Sustainable supply chain | Bangladesh, Canada |
| Das et al. [154 ] | Building supply chain resilience in the era of COVID-19: An AHP-DEMATEL approach | Operations Management Research | AHP-DEMATEL | Supply chain networks | India, Turkey |
| Mahmoudi et al. [155 ] | Gresilient supplier selection through fuzzy ordinal priority approach: decision-making in post-COVID era | Operations Management Research | OPA | Supplier selection problem | China, United States |
| Wen and Liao [156 ] | Capturing attitudinal characteristics of decision-makers in group decision making: application to select policy recommendations to enhance supply chain resilience under COVID-19 outbreak | Operations Management Research | GLDS | Supply chain management | China |
| Sharma et al. [157 ] | Managing disruptions and risks amidst COVID-19 outbreaks: role of blockchain technology in developing resilient food supply chains | Operations Management Research | AHP-WASPAS | Food Supply Chains | United Kingdom, India |
| Xiaozhen et al. [158 ] | A New Computational Method Based on Probabilistic Linguistic Z-Number with Unbalanced Semantics and Its Application to Multi-Criteria Group Decision Making | IEEE Access | MULTIMOORA | Medicine selection problem | China |
| Bragatto et al. [159 ] | The impact of the COVID-19 pandemic on the safety management in Italian Seveso industries | Journal of Loss Prevention in the Process Industries | AHP | Safety management system | Italy |
5. Literature review
A final total of 72 papers have been considered to be acceptable in this review. In this section, the selected papers will be reviewed in more detail with regard to application areas.
5.1. Digital technologies
Mardani et al. [102] suggested a decision-making method under hesitant fuzzy set based on SWARA and WASPAS to assess the challenges of digital technologies (such as blockchain technology, artificial intelligence, internet of things) intervention to deal with the COVID-19 outbreak. In this method, SWARA introduced by Keršuliene et al. [160] is utilized to weigh the criteria subjectively and WASPAS introduced by Zavadskas et al. [161] is employed to rank the digital technology systems to control COVID-19 outbreak under hesitant fuzzy environment. In this paper, “health information systems” is ranked as the first factor.
5.2. Habitat vulnerability in slum areas
Das et al. [115] applied PCA (principal component analysis) and fuzzy AHP to evaluate the slum vulnerability index to COVID-19 across the states in India. They revealed that slums in the eastern and central parts of India are more susceptible to COVID-19 transmission owing to lack of availability to the basic services. In this work, for evaluation of slum vulnerability based on fuzzy AHP, twelve variables related to COVID-19 transmission are considered. Also PCA as a multivariate statistical method used to derive the most important factors.
5.3. Relaxation protocols
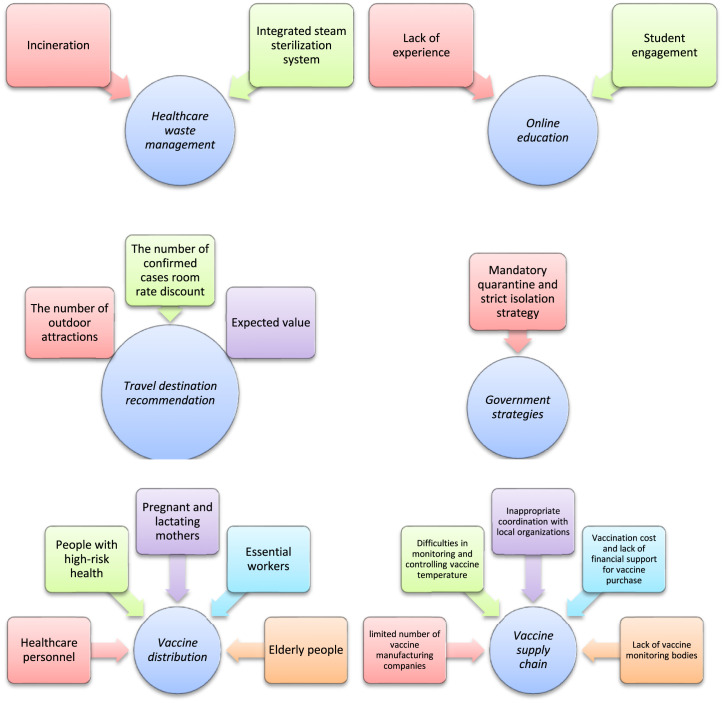
Ocampo and Yamagishi [104] applied an intuitionistic fuzzy DEMATEL in modeling the Philippine relaxation protocols. They highlighted that “compliance of minimum public health standards”, “limited movement of persons”, “suspension of physical classes”, “prohibition of mass gatherings”, “non-operation of category IV industries”, and “non-operation of hotels” are the most vital protocols. In this paper, DEMATEL deals with the causal relationships between guideline protocols for the relaxation strategy. DEMATEL introduced by Gabus and Fontela [162] is based on graph theory and divides the elements into two groups, namely cause and effect. This method is used to analyze a structural model characterized by elements as vertices and causal relationships among elements as edges.
5.4. Government strategies
Alkan and Kahraman [112] suggested a decision support system based on two different TOPSIS methods for the evaluation of government strategies that can be implemented against COVID-19 outbreak under q-rung orthopair fuzzy environment. In their methodologies, the weights of criteria are generated by an aggregation operator and entropy. According to the results of this paper, the best strategy is “mandatory quarantine and strict isolation strategy”.
5.5. Online education
Saraji et al. [117] introduced a decision-making framework based on SWARA and MULTIMOORA to obtain the criteria weights and rank the institutions, respectively for adapting online education during COVID-19 pandemic under the hesitant fuzzy environment. They pointed out the pedagogical challenges, namely “lack of experience” and “student engagement” are the key challenges in higher education institutions. MULTIMOORA was developed by Brauers and Zavadskas [163] to increase the robustness of MOORA and is one of the well-known MCDM methods, which contains three subordinate ranking models, namely ratio system, reference point and full multiplicative form.
5.6. Vaccine distribution
Hezam et al. [135] suggested an interesting MCDM method to determine the priority groups for receiving COVID-19 vaccine. In this method, AHP is employed to derive the criteria and sub-criteria weights and the COVID-19 vaccine alternatives are ranked by TOPSIS under neutrosophic environment. They concluded that “healthcare personnel”, “people with high-risk health”, “elderly people”, “essential workers”, “pregnant and lactating mothers” are the most prioritized groups to take the vaccine dose.
Albahri et al. [147] developed a new decision-making framework on the basis of fuzzy-weighted zero-inconsistency (FWZIC) and fuzzy decision by opinion score method (FDOSM) under pythagorean fuzzy information to provide a dynamic COVID-19 vaccine distribution method. In this research, pythagorean FWZIC is applied to weigh the vaccine distribution criteria and pythagorean FDOSM prioritizes the COVID-19 vaccine recipients. FDOSM is a new MCDM method under fuzzy environment that has interesting potentials to overcome some challenges of previous MCDM methods. Also FWZIC is a new weighting method and according to Albahri et al. [147], it can solve some limitations of AHP, ANP and BWM.
Alsalem et al. [146] extended FWZIC and FDOSM under T-spherical fuzzy set and used it in the distribution of COVID-19 vaccines. In this work, T-spherical FWZIC is employed to obtain the weights of criteria, whereas T-spherical FDOSM is used to rank the vaccine recipients.
5.7. Insurance companies
Ecer and Pamucar [118] proposed a multi-criteria performance assessment method based on MARCOS method to rank the insurance companies in terms of healthcare services under the intuitionistic fuzzy environment during the COVID-19 pandemic. In this work, the criteria weights are assigned by DMs using linguistic variables. Also the authors used an intuitionistic fuzzy weighted averaging operator to obtain the criteria weights. MARCOS method introduced by Stević et al. [164] is a new MCDM method and is based on the relationship between ideal and anti-ideal alternatives.
5.8. Control of spreading
Ashraf et al. [109] designed a new methodology to handle the emergency group decision-making problem of control of COVID-19 spreading by using TOPSIS and COPRAS under spherical fuzzy information. In this paper, the objective weights derived by the distance measure are combined with subjective weights in the spherical fuzzy multicriteria group decision making environment.
5.9. On-demand grocery delivery service
Altay et al. [71] suggested an intelligent comparative method based on AHP to identify the criteria weights for marketing mix elements of the on-demand grocery delivery service before and during COVID-19 outbreak under fuzzy environment. In this work, 22 criteria according to marketing mix elements (product, price, promotion, process, people, place and physical evidence) are determined. Their findings show that for example, for the price element, “relative prices” is the most important factor followed by “discount” and “delivery costs”, respectively, before the pandemic but during the pandemic, “relative prices” and “discount” factors have equal importance and the weight of “delivery costs” was decreased.
5.10. Travel destination recommendation
Chen and Wang [143] suggested a calibrated piecewise-linear fuzzy geometric mean approach to enhance the accuracy of fuzzy AHP and applied this method and fuzzy TOPSIS to rank travel destinations during the COVID-19 outbreak. They revealed that the most important factors in this field are “the number of outdoor attractions”, “confirmed cases room rate discount” and “expected value”.
5.11. Vaccine supply chain
Alam et al. [141] used DEMATEL to explore the major challenges of COVID-19 vaccine supply chain under intuitionistic fuzzy environment. They pointed out the most critical challenges in this field are “limited number of vaccine manufacturing companies”, “inappropriate coordination with local organizations”, “lack of vaccine monitoring bodies”, “difficulties in monitoring and controlling vaccine temperature”, and “vaccination cost and lack of financial support for vaccine purchase”.
5.12. Shortage of medical supplies
Chai et al. [127] extended TOPSIS to Z-uncertain probabilistic linguistic environment and used it to handle an emergency decision-making case for treating patients with COVID-19 due to shortage of medical supplies. They proposed an optimization model on the basis of the maximizing deviation method to derive the relative optimal weight of criteria.
5.13. Hospital site selection
Boyacıand Şişman [126] developed an analytical tool for hospital site selection during COVID-19 outbreak based on AHP and TOPSIS under pythagorean fuzzy information. In this work, interval-valued pythagorean fuzzy AHP and TOPSIS are utilized to determine the weights of criteria and to obtain the final ranking, respectively.
Aydin and Seker [120] suggested an MCDM framework to select the most suitable location for an isolation hospital for COVID-19 patients with mild to moderate symptoms. In this work, BWM and interval type-2 fuzzy TOPSIS are employed to weigh the decision criteria and to select the best location.
5.14. Waste-to-energy alternatives
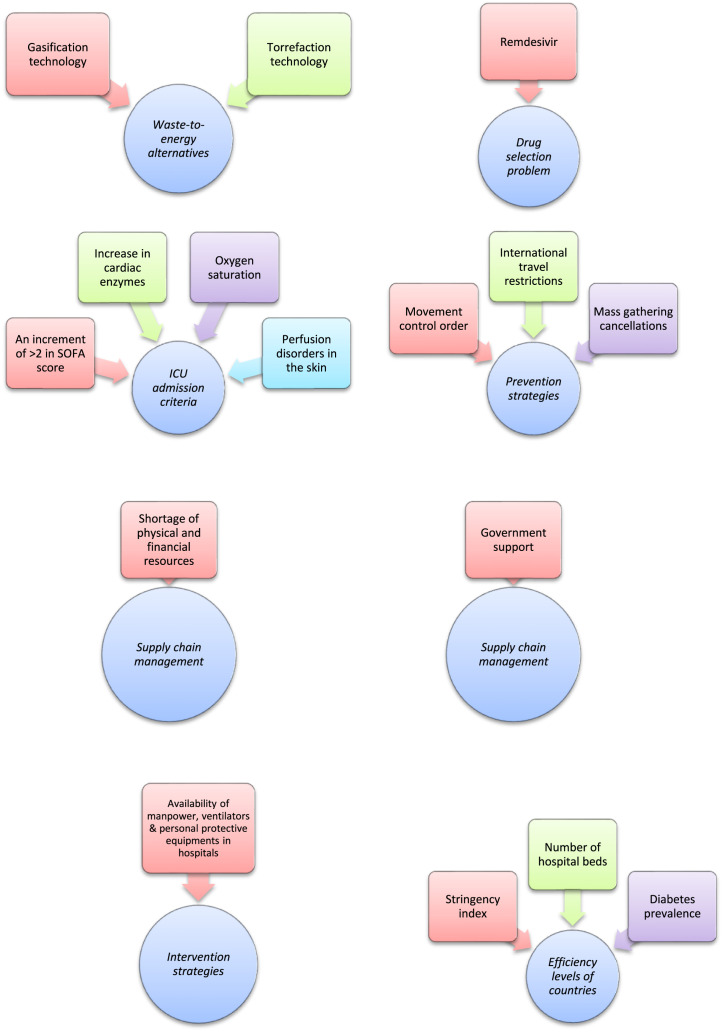
Shah et al. [121] proposed a decision support framework to rank waste-to-energy (WtE) alternatives based on the idea of energy trilemma (energy security, energy equity, and environmental sustainability) in the post-COVID-19 world. They concluded that “gasification technology” is the most feasible option and “torrefaction technology” is the least favorable for WtE generation in Pakistan. In this work, fuzzy DEMATEL is used to determine the inner dependence within the decision criteria. Fuzzy ANP is applied to analysis outer relationships among criteria and also to obtain the criteria weights. Finally, fuzzy VIKOR is utilized to rank the alternatives.
5.15. Smart and automation technology
Chen and Lin [107] developed a systematic method to assist managers in selecting the most appropriate smart and automation technology application under fuzzy environment during COVID-19 outbreak. In this work, the fuzzy AHP is applied to obtain the priorities of criteria and fuzzy TOPSIS is used to assess the performance of each smart and automation technology application.
5.16. Ecotourism centers
Hosseini et al. [114] suggested a hybrid decision-making tool based on DEMETEL and VIKOR to rank action plans as a recovery solution for ecotourism centers under fuzzy environment during the COVID-19 outbreak. They deduced that the “standardization of centers” is the optimal solution. Also “estimating demand number and increasing the capacity” and “identifying other natural tourist attractions of the region” have the lowest priority. In this work, fuzzy DEMATEL and fuzzy VIKOR are applied to obtain the weights of criteria and to prioritize the action plans, respectively.
5.17. Healthcare waste management
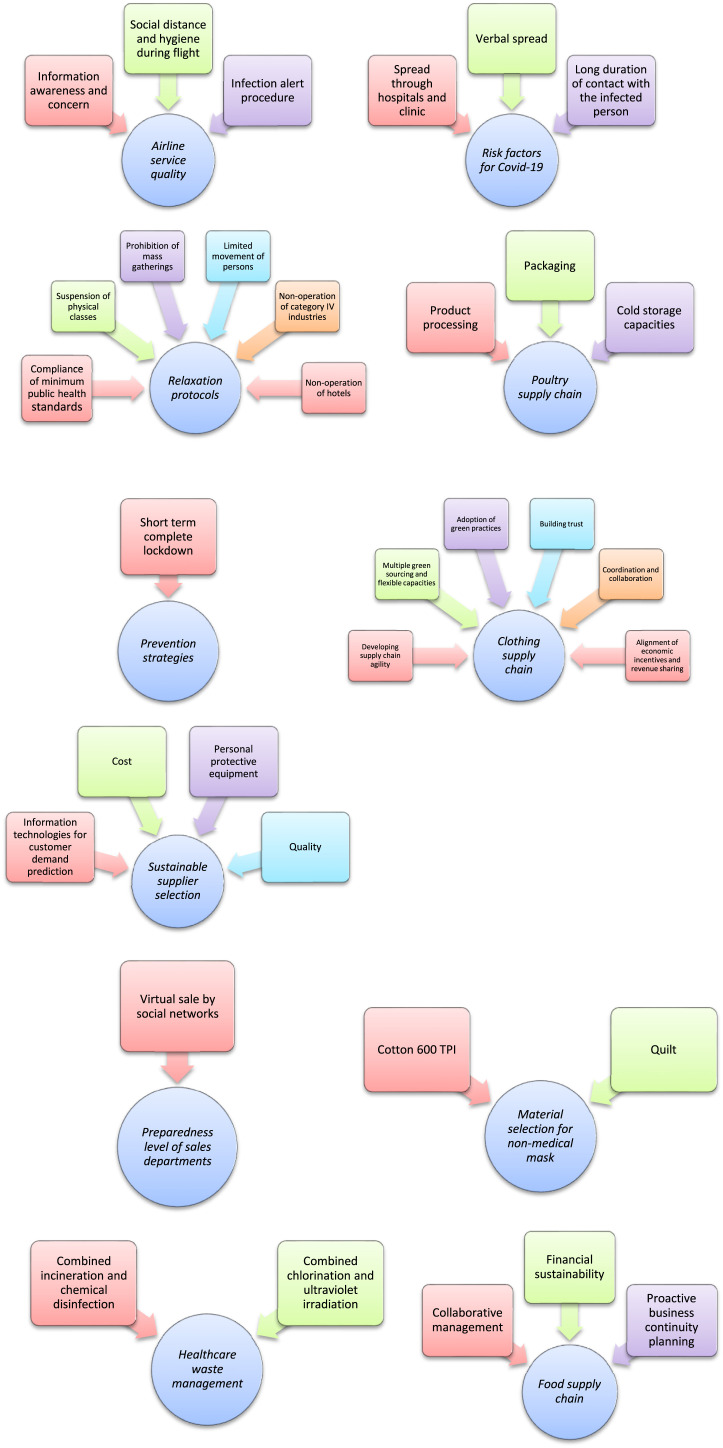
Manupati et al. [77] proposed an evaluation framework for the ranking of health care waste disposal alternatives under fuzzy environment during and post COVID-19 pandemic. In this work, fuzzy VIKOR is employed to assess nine health care waste disposal alternatives. Also linguistic variables are employed by DMs to estimate the criteria weights. They indicated that “incineration” followed by “integrated steam sterilization system” are the best alternatives in Indian.
Belhadi et al. [106] proposed a combined AHP and VIKOR to assess the infectious solid waste and wastewater alternatives from a life-cycle assessments and life-cycle costs perspective during the COVID-19 pandemic in an interval-valued fuzzy environment. They concluded that integrated “incineration” and “chemical disinfection” as well as integrated “chlorination” and “ultraviolet irradiation” are the most efficient technologies in the present context. In this method, AHP is used to determine the criteria weights and VIKOR ranks the alternatives.
5.18. Drug selection problem
Mishra et al. [123] introduced an interesting framework to deal with the drug selection problem for mild symptoms of COVID-19 under the environment of hesitant fuzzy set. They concluded that for the patients with mild symptoms, “Remdesivir” is the best medicine. In this work, a new divergence measure for hesitant fuzzy sets and modified hesitant fuzzy ARAS (Additive Ratio Assessment) are used to derive the criteria weights and to rank the alternatives, respectively. ARAS developed by Zavadskas and Turskis [165] is a new MCDM method and has relatively straightforward procedure that yields usually reliable results.
Xiaozhen et al. [158] extended MULTIMOORA in the context of probabilistic linguistic Z-number with unbalanced semantics for medicine selection problem for the patients with mild symptoms. They also concluded that “Remdesivir” is the best medicine for this group.
Si et al. [149] suggested an interesting decision-making approach on the basis of picture fuzzy set, Dempster–Shafer theory and GRA for COVID-19 medicine selection problem. They considered four factors, namely “antiviral activity”, “coolify”, “ease breathing” and “side effect” as selection criteria for the assessment of therapies and deduced that “Tocilizumab” is more applicable for a given particular patient. Dempster–Shafer theory (also called evidence theory) introduced by Dempster [166] and developed by Shafer [167] as an interesting generalization of Bayesian probability theory is a well-established mathematical framework for reasoning under uncertainty embedded in the evidence.
5.19. Preparedness of Indian states
Choudhury et al. [124] used AHP to assess the preparedness of 27 states and three union territories against the COVID-19 pandemic based on ten demographic, socioeconomic, and healthcare indicators under fuzzy environment.
5.20. Outsourcing provider selection
Goker [125] provided a decision support framework under intuitionistic fuzzy environment to assess the effects of COVID-19 pandemic on agile provider selection. In this work, intuitionistic fuzzy cognitive map technique is used to compute the weights of 13 criteria which are interrelated and the selection procedure is accomplished by intuitionistic fuzzy COPRAS.
5.21. Green economic efficiency
Yao [130] suggested an MCDM framework to evaluate and rank the alternative strategies to attain green economic efficiency in post COVID-19 pandemic in China. In this research, fuzzy AHP is employed to assess 10 criteria, 48 sub-criteria and fuzzy VIKOR is used to prioritize 5 alternative strategies. This study deduced that “resource efficiency and green purchasing” is the best strategy to achieve the goal followed by “the local production and utilization” and “green economic development”.
5.22. ICU admission criteria
Özkan et al. [10] introduced a very interesting MCDM approach under fuzzy environment to evaluate the COVID-19 suspect patient and decide which health services can be taken. In this work, fuzzy AHP is used to weigh 16 criteria and MULTIMOORA is employed to identify which patients benefit intensive care unit treatment first. They pointed out “an increment of >2 in SOFA score”, “increase in cardiac enzymes” and “oxygen saturation” are the most dominant criteria and “perfusion disorders in the skin” is the weakest.
5.23. Prevention strategies
Asadi et al. [139] used DEMATEL to study the key factors for preventing COVID-19 and also employed fuzzy rule-based techniques to show the importance of these factors. They deduced that “movement control order”, “international travel restrictions” and “mass gathering cancellations” are the most importance factors in the prevention of COVID-19.
Razzaq et al. [8] introduced a group MCDM approach in fuzzy environment to rank the prevention strategies of COVID-19 pandemic. In this research, fuzzy AHP and fuzzy VIKOR are utilized to weigh the criteria and prioritize the alternative strategies. They concluded that “complete lockdown for short term” is more effective in preventing the COVID-19 pandemic.
5.24. Mass vaccination campaigns
Khan et al. [16], [17] used a robust VIKOR for q-rung orthopair fuzzy sets in mass vaccination campaigns in the COVID-19 situation. In their method, the criteria weights were calculated by AHP.
5.25. Service quality
Samanci et al. [145] provided a hybrid method of fuzzy importance, expected performance, and priority analysis with VIKOR to improve airline service quality after the COVID-19 outbreak. In this work, 22 factors related to the airline service quality are classified in three classes as “social distance and hygiene during flight”, “information awareness and concern”, and “infection alert procedure”.
5.26. Poultry supply chain
Palouj et al. [144] employed fuzzy Delphi method and fuzzy AHP to study the impact of COVID-19 pandemic on the poultry supply chain. They noted that it is essential to take into consideration the facilities for development of “product processing”, “packaging” and “cold storage capacities” to decrease the effects of COVID-19 on poultry meat.
5.27. Clothing supply chain
Majumdar et al. [116] used fuzzy TOPSIS to rank the risk mitigation strategies for clothing supply chain. The weights of criteria (risks) are assigned by linguistic variables. They revealed that “developing supply chain agility”, “multiple green sourcing and flexible capacities”, “adoption of green practices”, “building trust”, “coordination and collaboration” and “alignment of economic incentives and revenue sharing” can be considered as main risk mitigation strategies.
5.28. Risk factors for Covid-19
Ghorui et al. [131] suggested a decision-making framework under hesitant fuzzy environment for identifying and ranking the most important risk factors for the spread of COVID-19. In this research, fuzzy AHP is applied to obtain the weights and hesitant fuzzy TOPSIS is employed to rank the key risk factor. They concluded that “long duration of contact with the infected person”, “spread through hospitals and clinic” and “verbal spread” can be considered as the most important risk factors.
5.29. Supply chain management
Paul et al. [140] applied grey DEMATEL to analyze the importance and cause-and-effect relationships of the supply chain recovery challenges owing to the COVID-19 outbreak. They mentioned in this industry, “shortage of physical and financial resources” is the most important concern of the DMs. In this paper, Delphi method determines the main supply chain recovery challenges and grey DEMATEL classifies the causal relationships among the challenges.
Wen and Liao [156] integrated probabilistic linguistic term set, ordinal k-mean clustering algorithm, GLDS and personalized quantifier with cubic spline interpolation in a large-scale group decision making problem. GLDS is a new MCDM method which takes the “group utility” and “individual regret” values into account and the optimal option obtained by this method dominates all other options.
Das et al. [154] incorporated AHP and DEMATEL to examine the factors that affected the supply chain networks with the COVID-19 pandemic. They deduced in the casual group, “government support” is the most important factor and “process automation and artificial intelligence” is the second most important factor. In this paper, AHP prioritizes the key factors that are vital to obtain a resilient supply chain network and DEMATEL evaluates the cause–effect relationship between the factors. Petrudi et al. [134] developed a decision-making model for assessing suppliers on the basis of social sustainability initiatives during the COVID-19 outbreak. In this method, the criteria weights are identified by group grey BWM and then, improved GRA is used to rank the available suppliers.
Mahmoudi et al. [155] used fuzzy OPA for tackling the supplier selection problem in post-COVID era. OPA developed by Ataei et al. [168] is a new linear programming-based method that is free from some inadequacies associated with MCDM methods. For example, OPA does not require normalization. The most distinctive feature of this interesting method is its capability to derive the weights of decision criteria, DMs, and alternatives.
5.30. Children in the quarantine
Kirişci et al. [70] suggested a new MCDM method by integrating VIKOR with generalized pythagorean fuzzy soft set to examine the problems of cognitive and behavioral development of early childhood children (children aged 5–6 years) in the COVID-19 quarantine. In this study, two types of weights are used: (1) on the basis of the expectation score function and (2) based on the evaluations of the experts.
5.31. Restaurant industry
Ocampo et al. [119] extended TOPSIS-Sort under intuitionistic fuzzy environment to assess and sort the level of exposure to COVID-19 in 40 restaurants. In this work, the weights of criteria are obtained using the intuitionistic fuzzy weighted averaging operator introduced by Xu [169] and TOPSIS-Sort assigns 17, 13 and 10 restaurants to high, moderate, and low exposure groups, respectively. In fact, in this multiple criteria sorting problem, the alternatives (restaurants) are assigned to one of a completely ordered set of homogeneous categories (degrees of exposure) on the basis of assessments of criteria.
5.32. Efficiency levels of countries
Aydin and Yurdakul [79] introduced an interesting three-staged model on the basis of DEA and machine learning techniques to evaluate the performances of 142 countries regarding the COVID19 pandemic. They revealed that the parameters such as “stringency index”, “diabetes prevalence” and “number of hospital beds” have important effects and “GDP”, “male/female cigarette smoker rate”, “extreme poverty”, and “death rate due to heart attack” have minor effects against the COVID-19 pandemic. Machine learning as one of the main branches of artificial intelligence and computer science includes a broad range of algorithms that can learn patterns from data to make predictions.
5.33. Makeshift hospital selection problem
Wan et al. [93] introduced a democratic–autocratic MCDM in trapezoidal interval type-2 fuzzy environment by integrating BWM and VIKOR and used this new method for makeshift hospital selection problem on COVID-19.
5.34. Prioritization of patients with COVID-19
Albahri et al. [111] introduced a decision-making framework that provides a ranking of patients with COVID-19. In this work, Entropy and TOPSIS are used to obtain the criteria weights and to detect and rank the COVID-19-infected patients, respectively.
5.35. Sustainable supply chains
Sharma et al. [105] utilized SWARA for identifying the significant factors for enhancing survivability of sustainable supply chains and managing buyer–supplier relationships during the pandemic COVID-19. They pointed out “supply chain network viability” is the major factor for managing buyer–supplier relationship and also enhancing survivability of sustainable supply chains during and post-COVID-19 pandemic.
Karmaker et al. [153] introduced a structural modeling by using fuzzy TISM (total interpretive structural modeling) which is an innovative version of ISM to improve the supply chain sustainability during COVID-19 pandemic. In this paper, 20 main drivers of sustainability are identified and based on Pareto chart, 13 drivers is determined for further analysis. They found that “policy development to recover the impact of COVID-19”, “development of health protocols for stakeholders” and “financial support from the government” are major drivers of sustainability.
Orji and Ojadi [152] suggested an integrated MCDM method using fuzzy AHP and MULTIMOORA to analyze the interrelationships between pandemic response strategies and triple bottom line criteria for sustainable supplier selection in the Nigerian manufacturing sector. They noted that “quality”, “cost”, “the use of personal protective equipment” and “information technologies for customer demand prediction” are very important in sustainable supplier selection during the COVID-19 pandemic.
Khurana et al. [9] used AHP to determine the crucial factors and also to improve the resilience of companies during and after the COVID-19 pandemic and future crises. In this work, the “role of governance” obtained the highest weight among the factors.
5.36. Convalescent-plasma-transfusion
Mohammed et al. [122] proposed a novel decision-making framework for efficient distribution of convalescent plasma from the eligible donors amongst patients for rescuing COVID-19 patients using AHP-TOPSIS.
Albahri et al. [73] used SODOSM as a novel MCDM method to determine the most appropriate convalescent plasma for corresponding COVID-19 patients.
5.37. Diagnostic models
Mohammed et al. [108] suggested an integrated MCDM method to assess the twelve diagnostic models (machine learning algorithms) for COVID19 such as logistic regression, K-nearest neighbors, decision tree, and support vector machine regarding the ten evaluation criteria. In this study, Entropy and TOPSIS are used to derive the weights of criteria and to rank the alternatives, respectively. Support vector machine (linear) outranks the other diagnosis models.
5.38. Safety level evaluation
Hezer et al. [113] evaluated the safety levels of 100 regions in terms of COVID-19 in the world using TOPSIS, VIKOR and COPRAS. In this paper, two ranking lists are derived. In the first phase, the weights of criteria are suggested by DKG (Deep Knowledge Group) consortium and in the second scenario, all criteria weights are assumed to be equal.
5.39. Intervention strategies
Ahmad et al. [24] used group BWM to assess and prioritize the intervention strategies to deal with the COVID-19 pandemic and considered four groups of stakeholders, i.e. health workers, social workers, academicians, and common citizens. For example, they deduced that “availability of manpower, ventilators & personal protective equipments in hospitals” is the most important criteria for health workers. Also for social workers, the topmost strategy is “complete lockdown”.
5.40. Quarantine decisions
Altuntas and Gok [76] utilized DEMATEL to help countries for quarantine decisions owing to COVID-19 outbreak. They noted that “Istanbul” has an important effect on the spread of COVID-19 pandemic on Turkey’s rest. They also demonstrated that DEMATEL can suggest suitable solutions for quarantine decisions during a pandemic
5.41. Vulnerability map
Shadeed and Alawna [128] used AHP to develop COVID-19 vulnerability map for the West Bank, Palestine. They highlighted that 82% of the West Bank population are under high to very high COVID-19 vulnerability categories.
Gao et al. [137] used AHP to investigate the importance of regional vulnerability factors related to COVID-19. In this work, four classes of vulnerability factors of infectious diseases, namely regional, pathological, medical and response attribute factors are used.
5.42. Preparedness level of sales departments
Ortiz-Barrios et al. [129] proposed an MCDM model based on AHP-TOPSIS to enhance the preparedness level of sales departments during COVID-19 pandemic and future pandemics. This problem is comprised of 7 alternatives from the electrical appliance sector, 8 criteria and 29 sub-criteria in Colombia and “virtual sale by social networks” is determined as the most important criterion.
5.43. Material selection for non-medical mask
Hartanto and Mayasari [136] employed AHP to select the suitable materials for non-medical mask for reducing the environmental impact from masks during COVID 19 outbreak. In this paper, the main criteria are “filtration efficiency”, “breathability”, and “environmental impact index” and 26 alternative materials are evaluated. They concluded “Quilt” and “Cotton 600 TPI” are suitable cloth for making non-medical mask.
5.44. Emergency decision-making problem
Ashraf and Abdullah [103] extended TOPSIS and GRA to deal with the uncertainty in emergency decision-making problems under spherical fuzzy information. In this method, TOPSIS and GRA are used to rank the alternatives and criteria weights are derived by AHP and spherical fuzzy entropy method.
5.45. Tourist sites
Yamagishi and Ocampo [132] applied TOPSIS-Sort to evaluate 20 tourist sites in a central Philippine province under 6 criteria which identify exposure to COVID-19. In this study, the criteria weights are derived from the evaluations of 208 experts on the basis of a two-part questionnaire. 12 and 8 sites are assigned to the “moderate exposure” and “high exposure” classes, respectively.
5.46. Artificial intelligence techniques
Albahri et al. [148] used AHP-VIKOR to evaluate artificial intelligence techniques in the classification of COVID-19 medical images. In this paper, a comprehensive review of artificial intelligence techniques employed in the detection of COVID-19 medical images in terms of evaluation is presented.
5.47. Community attributes
Requia et al. [110] used AHP to rank the potential effects of community attributes on COVID-19 transmission at the municipal level. Community attributes can include “demographic variation”, “economic aspects”, “transportation infrastructure”, “health condition”, and “characteristic of health care system”. They highlighted the Brazilian municipalities will have a shortage of 17 beds averagely. Moreover, they pointed out addition to “bed capacity”, “ventilator capacity”, “mask recycling capacity” and “health care worker capacity” should be considered in further studies.
5.48. Efficiency assessment of airlines
da Silveira Pereira and de Mello [12] used MCDEA to assess the operational efficiency of Brazilian airlines regarding the Covid-19 pandemic in first quarter of 2020 comparing with first quarter of 2019. They employed MCDEA to avoid disadvantages of classical DEA models.
5.49. Solid organ transplant patients with COVID-19
Revuelta et al. [150] suggested a predictive model using DEA-ANN on the basis of hospital admission data from hospitalized transplant patients to extrapolate the progression towards severe COVID-19. As a subfield of artificial intelligence, ANN which is inspired by the human brain in the organization of neurons and decision making procedure is very useful in various applications such as pattern recognition and classification [170].
5.50. Association between COVID-19 cases and PM2.5 concentrations
Mehmood et al. [151] examined the association between COVID-19 cases, air pollution and climatic and socioeconomic factors in Pakistan. The authors used GRA to study the changes in COVID-19 cases regarding respirable particle pollutants (PM2.5) concentration. This paper deduced that the relationship between COVID-19 and population density is moderate.
5.51. Food supply chain
Sharma et al. [157] developed an integrated MCDM approach based on fuzzy AHP and WASPAS for examining the factors affecting the food supply chain in the disruptive environment during COVID-19 pandemic. They pointed out that “sourcing related” is the most important factor in the disruptive environment.
Shanker et al. [142] suggested a grey-DEMATEL-ANP method to analyze the influencing factors on perishable food supply chains during the COVID-19 pandemic. They pointed out “restriction on import–export” and “fear of violation of social distancing guidelines” can be considered as the main “cause” factors, while “price variation of perishable products” and “panic buying and stockpiling” are the critical “effect” factors. In this paper, DEMATEL evaluates the mutual interrelationship among the decision criteria, where ANP is applied to determine the contribution of criteria.
Kumar et al. [133] utilized fuzzy BWM to analyze and rank the risk mitigation strategies in perishable food supply chains during the COVID-19 outbreak. According to this paper, the top risk mitigating strategies are “collaborative management”, “proactive business continuity planning” and “financial sustainability”.
Kumar and Kumar Singh [138] used BMW to identify the importance rating of COVID-19 impacts on agri-food supply chains. They concluded that “supply chain collaboration”, “coordination between the stakeholders”, “information sharing”, “digitization of the processes” and “resource sharing” are the important strategies to manage the effect of COVID-19 pandemic. Also “poor accessibility”, “high production and distribution costs”, “supply and distribution uncertainties”, “import disruption” and “the lack of trust in international trade” are the main impacts of COVID-19 on agri-food supply chains.
5.52. Wealth management banks
Lin et al. [5], [6] used DEMATEL to specify the most important criteria for wealth management banks during COVID-19 outbreak under fuzzy environment. They selected four dimensions, namely “bank performance”, “service quality”, “customer relationship”, and COVID-19 as well as 16 criteria to assess bank performance. The results revealed that “service quality” is the most important dimension and in this dimension, “customized investment information” and “innovation” are the most important factors.
Fig. 2 shows the information of selected articles with regard to their application areas.
Fig. 2.
Distribution of papers by application area.
Now, we try to depict papers in short terms by summarizing their main findings for fast access. Fig. 3 presents graphically the key results obtained from some papers and further details can be found in Table 1 and Section 5.
Fig. 3.
The key results obtained from some papers.
6. Findings
In this section, we draw the attention towards the major outcomes.
6.1. Distribution of articles by MCDM methods
Table 2 presents the frequency of MCDM methods that applied for dealing with the problems in COVID-19 pandemic. One can notice that AHP (and fuzzy AHP) applied in 37.5% of papers is the most preferred MCDM method for COVID-19 problems which is closely followed by TOPSIS applied in 25% of papers. DEMATEL and VIKOR are also MCDM methods commonly employed in this filed. Moreover, apart from the widely used classical MCDM methods in the framework of COVID-19, newly developed MCDM methods such as MARCOS, OPA, and SODOSM also exist. However, the main drawback of nearly all the reviewed papers is the lack of theoretical justifications. This challenge is owing to the fact that the validity of outcomes derived from MCDM methods remains an open problem and there is no consensus on the meaning of “valid” in the results. For example, Nadkarni and Puthuvayi [34] mentioned that the best approach to validate an MCDM method involves comparing its outcomes with the known outcomes (empirical studies). Needless to say, this is not often possible in real practice. On the other hand, many researchers have compared MCDM methods amongst each other on the basis of the final results. But Roy and Słowiński [60] highlighted such a comparison is ill-founded. This is owing to the fact that classical MCDM methods such as AHP, TOPSIS, VIKOR, PROMETHEE, TODIM, etc may suggest senseless ranking result, even if a straightforward MCDM problem is considered [53], [171], [172], [173], [174].
Table 2.
MCDM methods and the frequency of their usage in COVID-19 pandemic.
| MCDM method | Number of paper |
Total | Fuzzy papers | Crisp papers | |
|---|---|---|---|---|---|
| Fuzzy | Crisp | ||||
| AHP | 16 | 11 | 27 | Razzaq et al. [8 ], Altay et al. [71 ], Palouj et al. [144 ], Chen and Wang [143 ], Hezam et al. [135 ], Ghorui et al. [131 ], Özkan et al. [10 ], Yao [130 ], Boyacıand Şişman [126 ], Choudhury et al. [124 ], Chen and Lin [107 ], Belhadi et al. [106 ], Das et al. [115 ], Orji and Ojadi [152 ], Sharma et al. [157 ] | Khurana et al. [9 ], Gao et al. [137 ], Hartanto and Mayasari [136 ], Ortiz-Barrios et al. [129 ], Shadeed and Alawna [128 ], Mohammed et al. [122 ], Albahri et al. [148 ], Requia et al. [110 ], Das et al. [154 ], Bragatto et al. [159 ] |
| TOPSIS | 11 | 7 | 18 | Ashraf and Abdullah [103 ], Chen and Lin [107 ], Ashraf et al. [109 ], Alkan and Kahraman [112 ], Majumdar et al. [116 ], Aydin and Seker [120 ], Chai et al. [127 ], Ghorui et al. [131 ], Hezam et al. [135 ], Chen and Wang [143 ], Ocampo et al. [119 ] | Mohammed et al. [108 ], Albahri et al. [111 ], Hezer et al. [113 ], Mohammed et al. [122 ], Boyacıand Şişman [126 ], Ortiz-Barrios et al. [129 ], Yamagishi and Ocampo [132 ] |
| VIKOR | 9 | 3 | 12 | Razzaq et al. [8 ], Khan et al. [16], [17], Yao [130 ], Shah et al. [121 ], Manupati et al. [77 ], Hosseini et al. [114 ], Belhadi et al. [106 ], Kirişci et al. [70 ], Samanci et al. [145 ] | Hezer et al. [113 ], Albahri et al. [148 ], Wan et al. [93 ] |
| DEMATEL | 8 | 2 | 10 | Ocampo and Yamagishi [104 ], Hosseini et al. [114 ], Shah et al. [121 ], Lin et al. [5], [6], Asadi et al. [139 ], Paul et al. [140 ], Alam et al. [141 ], Shanker et al. [142 ] | Altuntas and Gok [76 ], Das et al. [154 ] |
| BWM | 4 | 2 | 6 | Aydin and Seker [120 ], Kumar et al. [133 ], Petrudi et al. [134 ], Wan et al. [93 ] | Ahmad et al. [24 ], Kumar and Kumar Singh [138 ] |
| GRA | 4 | – | 4 | Ashraf and Abdullah [103 ], Petrudi et al. [134 ], Si et al. [149 ], Mehmood et al. [151 ] | – |
| MULTIMOORA | 3 | 1 | 4 | Saraji et al. [117 ], Özkan et al. [10 ], Xiaozhen et al. [158 ] | Orji and Ojadi [152 ] |
| SWARA | 2 | 1 | 3 | Mardani et al. [102 ], Saraji et al. [117 ] | Sharma et al. [105 ] |
| COPRAS | 2 | 1 | 3 | Ashraf et al. [109 ], Goker [125 ] | Hezer et al. [113 ] |
| DEA | 1 | 2 | 3 | Aydin and Yurdakul [79 ] | da Silveira Pereira and de Mello [12 ], Revuelta et al. [150 ] |
| FODSM | 2 | – | 2 | Albahri et al. [147 ], Alsalem et al. [146 ] | – |
| FWZIC | 2 | – | 2 | Albahri et al. [147 ], Alsalem et al. [146 ] | – |
| ANP | 2 | – | 2 | Shanker et al. [142 ], Shah et al. [121 ] | – |
| WASPAS | 2 | – | 2 | Mardani et al. [102 ], Sharma et al. [157 ] | – |
| MARCOS | 1 | – | 1 | Ecer and Pamucar [118 ] | – |
| ARAS | 1 | – | 1 | Mishra et al. [123 ] | – |
| SODOSM | – | 1 | 1 | – | Albahri et al. [73 ] |
| TISM | 1 | – | 1 | Karmaker et al. [153 ] | – |
| OPA | 1 | – | 1 | Mahmoudi et al. [155 ] | – |
| GLDS | 1 | – | 1 | Wen and Liao [156 ] | – |
Since Saaty [175] introduced AHP, a lot of applications in real world decision situations have been reported. The clear advantage of AHP is its antiquity and simplicity and also the availability of software packages contribute to the wide usage of this method [30], [32], [35], [54], [62]. For example, e Costa and Vansnick [176] mentioned that the elicitation of pairwise comparison assessments and expressing these judgments by using verbal terms are foundations of the popularity of AHP. Nonetheless, Zare et al. [32] pointed out the application of AHP may obtain from a convenience perspective rather than a solid theoretical mathematical perspective. The literature contains serious criticisms of AHP and fuzzy AHP such as the debate with respect to the axiomatic groundwork, inconsistency problem, meaning of ratio scales, correct meaning of priorities and rank reversal [177], [178]. More importantly, Asadabadi et al. [173] exposed serious inefficiencies with AHP and warned that this method fails to give a rational ranking in many cases. Zhü [179] pointed out fuzzy AHP lacks mathematical validity and violates fundamental principles of AHP. Moreover, Asadabadi et al. [173] and Zhü [179] disclosed that ANP and fuzzy ANP are subject to similar drawbacks too. Saaty and Tran [180] warned that there is no evidence that the use of fuzzy AHP leads to greater validity of a decision. Çakır [177] discussed a fundamental problem with fuzzy AHP which was first revealed for crisp AHP by e Costa and Vansnick [176]. This problem is about the meaning of priority vector obtained from the eigenvalue method utilized in AHP. Tuljak-Suban and Bajec [181] reviewed serious incongruities in fuzzy AHP such as the inappropriate use of defuzzification techniques and consistency check of fuzzy comparison matrix that can produce contradictory results. On the other hand, the consistency issue in AHP is very vital for avoiding misleading outcomes. When a large number of options are involved, the inconsistency problem becomes a severe concern in AHP and as pointed out by Saaty and Tran [180], fuzzifying the inconsistent assessments may lead to meaningless results. For example, Kavilal et al. [75] defuzzified fuzzy pairwise comparison matrix into a crisp matrix and mentioned if this crisp matrix is consistent, the primary fuzzy matrix is also consistent. However, Bhat and Kumar [182] revealed that this crisp matrix can never be consistent and fuzzy AHP proposed by Kavilal et al. [75] produces incorrect results. As a result, ample consideration should be given to the severe disadvantages of AHP and ANP as well as their fuzzy extension.
TOPSIS (including fuzzy TOPSIS) is another widely used technique applied in 25% of papers reviewed. In general, a widely accepted consensus on popularity of TOPSIS exists and its outcome is demonstrated to be relatively convincing in practical problems [62]. Statistically speaking, TOPSIS and fuzzy TOPSIS are among the most generally used methods to handle MCDM problems of numerous kinds [40], [41], [63]. This method is applied to rank the available alternatives, where they are assessed on the basis of Euclidean distances from ideal and non-ideal solutions. However, Opricovic and Tzeng [171] revealed that TOPSIS does not take the relative importance of these two references into consideration. Pei [183] deduced that the extended fuzzy TOPSIS cannot distinguish some alternatives under linguistic environment and these indiscernible alternatives may be countless in terms of number. Dymova et al. [184] mentioned that the majority of fuzzy extensions of TOPSIS are not flawless because defuzzification or other simplifications are used in them which lead to loss of important information and may suggest wrong outcomes. Very recently, Pan and Wang [185] developed a new version of TOPSIS on the basis of interval type-2 fuzzy projection model and claimed the output of this TOPSIS is interval type-2 fuzzy set instead of crisp number, which avoids the information distortion caused by transformation. But Meniz [186] revealed that the suggested function by Pan and Wang [185] (fuzzy cosine function) cannot be employed for distance calculation and pointless result is derived from this fuzzy model. Triantaphyllou and Lin [187] introduced a fuzzy TOPSIS on the basis of fuzzy arithmetic operations. However, Wang and Elhag [188] revealed the disadvantages of this fuzzy TOPSIS and developed another fuzzy model based on cut which combines crisp TOPSIS with extension principle and implements a non-linear programming method and defuzzification at the end of decision process. Nevertheless, the shortcoming of this fuzzy TOPSIS was also demonstrated by Dymova et al. [184] and Wang [189]. Kuo et al. [190] developed a group decision-making method based on TOPSIS in which fuzzy distance values are compared by using fuzzy ranking method. Wang et al. [191] noted that fuzzy TOPSIS introduced by Kuo et al. [190] is wrong and may suggest more than one option as the best even if they are not Pareto optimal. Yatsalo et al. [192] demonstrated that the basic axiom has the place for crisp TOPSIS but it may be violated by fuzzy TOPSIS. According to the basic MCDM axiom, if option dominates option based on Pareto, is not worse on the basis of each MCDM/fuzzy MCDM method. Moreover, Yatsalo et al. [192] warned that despite the extensive use of fuzzy MCDM methods the basic axiom was not studied for those methods.
Based on Table 2, 14% of papers such as Ocampo and Yamagishi [104], Hosseini et al. [114], Shah et al. [121] and Alam et al. [141] used fuzzy DEMATEL to identify the cause–effect chain components for various decision problems. We know multiplicative inverse matrix is the main part of DEMATEL. Chou et al. [193] split the fuzzy numbers into three crisp numbers to find the multiplicative inverse of fuzzy matrix in fuzzy DEMATEL. But Pandey and Kumar [194] disclosed the elements of this inverse matrix may not be triangular fuzzy numbers and suggested method by Chou et al. [193] is incorrect. Dytczak and Ginda [195] warned that fuzzy DEMATEL requires more intricate calculations but is not better than crisp DEMATEL in terms of quality of results. It should be noted that although fuzzy DEMATEL may suggest different results than classical DEMATEL, such a difference does not give an advantage over the crisp method.
As can be seen from Table 2, fuzzy BWM is employed in 6% of papers. In fact, BWM is a linear programming based method. Literature shows modeling numerous real-life problems leads to an interval linear programming model. Two step method developed by Huang et al. [196] is the most popular technique for dealing with interval linear programming and hundreds of papers on the basis of this technique have been suggested to solve interval uncertainties in decision-making problems. Nevertheless, Wang and Huang [197] indicated that the optimum solution obtained by Huang et al. [196] may go beyond the feasible space and this phenomenon, known as solution violation, can mislead DM to unreasonable policies. All in all, Saaty and Tran [180] warned that fuzzy sets have severe difficulties in generating reliable results in decision-making problems and no theorems can be found in the literature about the workability of fuzzy set when it is used arbitrarily to numerical measurements. Simply speaking, there is no solid reason why the use of fuzzy sets should be required in MCDM methods. In fact, fuzzy MCDM methods have many critical aspects that should be more deeply scrutinized. Consequently, the researchers who want to apply fuzzy MCDM methods in their problems should be aware of disadvantages and strengths of those methods used to avoid pitfalls.
The frequency of MCDM methods used in 72 papers is visualized in Fig. 4.
Fig. 4.
Distribution of papers by MCDM methods.
6.2. Distribution of articles by weighting methods
Table 3 indicates the weighting methods adopted in the selected articles.
Table 3.
Distribution of weighting methods.
| Author (s) | Weighting method | Frequency |
|---|---|---|
| Ashraf and Abdullah [103 ], Belhadi et al. [106 ], Chen and Lin [107 ], Requia et al. [110 ], Das et al. [115 ], Mohammed et al. [122 ], Choudhury et al. [124 ], Boyacıand Şişman [126 ], Shadeed and Alawna [128 ], Ortiz-Barrios et al. [129 ], Yao [130 ], Özkan et al. [10 ], Ghorui et al. [131 ], Hezam et al. [135 ], Hartanto and Mayasari [136 ], Gao et al. [137 ], Khurana et al. [9 ], Khan et al. [16], [17], Chen and Wang [143 ], Palouj et al. [144 ], Altay et al. [71 ], Razzaq et al. [8 ], Albahri et al. [148 ], Orji and Ojadi [152 ], Das et al. [154 ], Sharma et al. [157 ] | AHP | 27 |
| Ocampo and Yamagishi [104 ], Hosseini et al. [114 ], Shah et al. [121 ], Altuntas and Gok [76 ], Lin et al. [5], [6], Asadi et al. [139 ], Paul et al. [140 ], Alam et al. [141 ], Shanker et al. [142 ], Das et al. [154 ] | DEMATEL | 10 |
| Aydin and Seker [120 ], Ahmad et al. [24 ], Kumar et al. [133 ], Petrudi et al. [134 ], Kumar and Kumar Singh [138 ], Wan et al. [93 ] | BWM | 6 |
| Ashraf and Abdullah [103 ], Mohammed et al. [108 ], Albahri et al. [111 ], Alkan and Kahraman [112 ], Ashraf and Abdullah [103 ] | Entropy | 4 |
| Mardani et al. [102 ], Sharma et al. [105 ], Saraji et al. [117 ] | SWARA | 3 |
| Shah et al. [121 ], Shanker et al. [142 ] | ANP | 2 |
| Albahri et al. [147 ], Alsalem et al. [146 ] | FWZIC | 2 |
| Karmaker et al. [153 ] | TISM | 1 |
| Albahri et al. [73 ] | SODOSM | 1 |
| Mahmoudi et al. [155 ] | OPA | 1 |
| Chai et al. [127 ] | Maximizing deviation method | 1 |
Clearly, AHP is the most common subjective method followed by BWM applied in 9% of papers. Also Entropy used in 6% of papers is the most frequent used objective method. The frequency of weighting methods used is visualized in Fig. 5.
Fig. 5.
Distribution of papers by weighting methods.
6.3. Distribution of articles by fuzzy sets
The papers that used MCDM methods under fuzzy environment in the context of COVID-19 are given in Table 4.
Table 4.
Articles that developed MCDM methods in the context of COVID-19 under fuzzy environment.
| Authors | Fuzzy sets (uncertainty theories) | Frequency |
|---|---|---|
| Chen and Lin [107 ], Hosseini et al. [114 ], Manupati et al. [77 ], Das et al. [115 ], Majumdar et al. [116 ], Shah et al. [121 ], Lin et al. [5], [6], Choudhury et al. [124 ], Yao [130 ], Özkan et al. [10 ], Kumar et al. [133 ], Chen and Wang [143 ], Palouj et al. [144 ], Altay et al. [71 ], Razzaq et al. [8 ], Orji and Ojadi [152 ], Karmaker et al. [153 ], Mahmoudi et al. [155 ], Sharma et al. [157 ], Asadi et al. [139 ], Samanci et al. [145 ] | Type-1 fuzzy set | 21 |
| Ocampo and Yamagishi [104 ], Ecer and Pamucar [118 ], Ocampo et al. [119 ], Goker [125 ], Alam et al. [141 ] | Intuitionistic fuzzy set | 5 |
| Mardani et al. [102 ], Saraji et al. [117 ], Mishra et al. [123 ], Ghorui et al. [131 ] | Hesitant fuzzy set | 4 |
| Paul et al. [140 ], Petrudi et al. [134 ], Shanker et al. [142 ], Mehmood et al. [151 ] | Grey theory | 4 |
| Ashraf and Abdullah [103 ], Ashraf et al. [109 ], Alsalem et al. [146 ] | Spherical fuzzy set | 3 |
| Boyacıand Şişman [126 ], Albahri et al. [147 ] | Pythagorean fuzzy set | 2 |
| Aydin and Seker [120 ], Wan et al. [93 ] | Interval type 2 fuzzy set | 2 |
| Alkan and Kahraman [112 ], Khan et al. [16], [17] | q-rung orthopair fuzzy set | 2 |
| Chai et al. [127 ], Xiaozhen et al. [158 ] | Z-number | 2 |
| Hezam et al. [135 ] | Neutrosophic set | 1 |
| Kirişci et al. [70 ] | Pythagorean fuzzy soft set | 1 |
| Belhadi et al. [106 ] | Interval-valued fuzzy set | 1 |
| Wen and Liao [156 ] | Probabilistic linguistic term set | 1 |
As we expected, type-1 fuzzy set is identified as the most popular set, followed by intuitionistic fuzzy set. Fig. 6 presents graphically the distribution of fuzzy sets used to introduce the extensions of MCDM methods. It is worth noting that analyzing the papers (Type-1 fuzzy set) in terms of membership function demonstrates that triangular fuzzy number is the most frequent form where 100% of all papers used this membership function. Asadi et al. [139] used different membership functions which were Gaussian membership function and triangular membership function.
Fig. 6.
Distribution of papers by fuzzy sets.
6.4. Distribution of articles by journals
Distribution of papers by journal is presented in Table 5. We can find from this table that the articles spread across 37 journals from various areas. “Applied Soft Computing” has published the largest number of articles which is a world-leading journal in the field of “soft computing” and accounts for 12% of the papers. This journal is followed by “Journal of infection and public health” and “Operations Management Research” which account for approximately 12% of papers altogether.
Table 5.
Distribution of articles on the basis of the name of journals.
| Journals | The number of papers per journal |
Impact Factora |
CiteScoreb |
|---|---|---|---|
| Applied Soft Computing | 8 | 6.725 | 11.2 |
| Journal of infection and public health | 4 | 3.718 | 4.9 |
| Operations Management Research | 4 | 2.706 | 3.8 |
| International Journal of Logistics Research and Applications | 3 | 3.821 | 5.4 |
| IEEE ACCESS | 3 | 3.367 | 4.8 |
| Results in Physics | 3 | 4.476 | 7.1 |
| International Journal of Intelligent Systems | 3 | 8.709 | 11.9 |
| Journal of Cleaner Production | 3 | 9.297 | 13.1 |
| Soft Computing | 3 | 3.643 | 5.1 |
| International Journal of Disaster Risk Reduction | 3 | 4.32 | 5.5 |
| Sustainable Production and Consumption | 3 | 5.032 | 6.7 |
| Science of the Total Environment | 2 | 7.963 | 10.5 |
| Artificial Intelligence Review | 2 | 8.139 | 8.3 |
| International Journal of Fuzzy Systems | 2 | 4.673 | 5.8 |
| Computer Methods and Programs in Biomedicine | 2 | 5.428 | 7.7 |
| Environmental Science and Pollution Research | 2 | 4.223 | 6.5 |
| Journal of Air Transport Management | 2 | 4.134 | 6.5 |
| Neural Computing and Applications | 1 | 5.606 | 7.3 |
| Socio-Economic Planning Sciences | 1 | 4.923 | 4.9 |
| Food Control | 1 | 5.548 | 9 |
| International Journal of Hospitality Management | 1 | 9.237 | 9.4 |
| Complex & Intelligent Systems | 1 | 4.927 | – |
| Applied Intelligence | 1 | 5.086 | 6.8 |
| Current Issues in Tourism | 1 | 7.43 | 8.6 |
| The International Journal of Advanced Manufacturing Technology | 1 | 3.226 | 4.9 |
| Environmental Management | 1 | 3.266 | 5.1 |
| Journal of Advanced Research | 1 | 10.479 | 13 |
| Artificial Intelligence In Medicine | 1 | 5.326 | 8 |
| Expert Systems with Applications | 1 | 6.954 | 12.7 |
| Technological Forecasting and Social Change | 1 | 8.593 | 12.1 |
| Computers & Industrial Engineering | 1 | 5.431 | 7.9 |
| Journal of Business Research | 1 | 7.55 | 9.2 |
| Risk Analysis | 1 | 4 | 5.1 |
| Chemosphere | 1 | 7.086 | 10.1 |
| International Journal of Production Economics | 1 | 7.885 | 12.2 |
| Knowledge-based Systems | 1 | 8.038 | 11.3 |
| Journal of Loss Prevention in the Process Industries | 1 | 3.66 | 5.5 |
2019 Journal Citation Reports (Clarivate Analytics, 2020).
Scopus source data, 2021.
Fig. 7 shows the journals with more than one paper on COVID-19 by using MCDM methods.
Fig. 7.
Distribution of journals with frequency 2.
6.5. Distribution of articles by countries
In order to study the distribution of articles by countries, two analyses are conducted as suggested by Dožić [54]:
(1) The distribution of papers by countries on the basis of the author’s affiliation.
(2) The distribution of papers by countries on the basis of case studies presented.
Table 6 presents the distribution of authors by affiliation countries. It can be observed from this table that MCDM methods have been applied to COVID-19 problems by authors from 35 countries. India with 18 articles is ranked as the first in terms of the number of papers followed by Turkey with 15 papers.
Table 6.
Distribution by author’s affiliation.
| Country | Number of paper |
|---|---|
| India | 18 |
| Turkey | 15 |
| China | 14 |
| Malaysia | 9 |
| Iraq | 7 |
| Pakistan | 6 |
| Taiwan | 6 |
| Saudi Arabia | 6 |
| Iran | 5 |
| United States | 5 |
| Australia | 4 |
| Bangladesh | 4 |
| Canada | 4 |
| Italy | 4 |
| Philippines | 3 |
| United Kingdom | 3 |
| Spain | 2 |
| Brazil | 2 |
| Mexico | 1 |
| New Guinea | 1 |
| Viet Nam | 1 |
| Japan | 1 |
| Palestine | 1 |
| Malaysia | 1 |
| Colombia | 1 |
| Serbia | 1 |
| Denmark | 1 |
| Thailand | 1 |
| Morocco | 1 |
| France | 1 |
| Indonesia | 1 |
| Greece | 1 |
| Singapore | 1 |
| Yemen | 1 |
| Nigeria | 1 |
Fig. 8 indicates graphically the distribution by countries with more than two publications.
Fig. 8.
Distribution by countries with more than two publications.
Also Table 7 indicates that the case studies are distributed across 14 countries.
Table 7.
Countries where the case studies are applied.
| Country | No. papers | Author(s) |
|---|---|---|
| India | 8 | Das et al. [115 ], Manupati et al. [77 ], Shanker et al. [142 ], Kumar et al. [133 ], Majumdar et al. [116 ], Choudhury et al. [124 ], Khurana et al. [9 ], Sharma et al. [157 ] |
| Turkey | 7 | Özkan et al. [10 ], Altuntas and Gok [76 ], Ecer and Pamucar [118 ], Aydin and Seker [120 ], Boyacıand Şişman [126 ], Altuntas and Gok [76 ], Goker [125 ] |
| China | 7 | Gao et al. [137 ], Yao [130 ], Ashraf et al. [109 ], Ashraf and Abdullah [103 ], Chai et al. [127 ], Mahmoudi et al. [155 ], Wan et al. [93 ] |
| Taiwan | 3 | Chen and Lin [107 ], Chen and Wang [143 ], Lin et al. [5], [6] |
| Philippine | 3 | Ocampo and Yamagishi [104 ], Ocampo et al. [119 ], Yamagishi and Ocampo [132 ] |
| Brazil | 2 | Requia et al. [110 ], da Silveira Pereira and de Mello [12 ] |
| Iran | 2 | Palouj et al. [144 ], Hosseini et al. [114 ] |
| Pakistan | 2 | Shah et al. [121 ], Mehmood et al. [151 ] |
| Bangladesh | 2 | Paul et al. [140 ], Karmaker et al. [153 ] |
| Morocco | 1 | Belhadi et al. [106 ] |
| Nigeria | 1 | Orji and Ojadi [152 ] |
| Palestine | 1 | Shadeed and Alawna [128 ] |
| Colombia | 1 | Ortiz-Barrios et al. [129 ] |
| Malaysia | 1 | Asadi et al. [139 ] |
| Italy | 1 | Bragatto et al. [159 ] |
An obvious insight from the obtained results is the increased utilization of MCDM methods for COVID-19 problems in Asian countries.
7. Note on theoretical challenges on fuzzy sets
As it was observed, many researchers claimed that fuzzy MCDM methods are efficient approach to handle real-life problems with different levels of complexity and uncertainty. In fact, these methods have incorporated the key benefits from fuzzy sets for tackling uncertainty and MCDM methods for tackling complexity. Although there are many papers to review fuzzy MCDM methods and their applications, the majority of them summarized the literature without digesting the fuzzy arithmetic and relationships between fuzzy sets and MCDM methods. Simply speaking, although the applications of fuzzy sets in MCDM methods have attracted lots of attentions, severe deficiencies are still existed. In this section and based on the selected papers in this review, we review briefly the key theoretical challenges that are associated with fuzzy sets. Through this section we highlight several claims which are at use in the fuzzy literature but having little theoretical support.
7.1. Fuzzy numbers
Two approaches have been generally used for implementing fuzzy arithmetic, namely Zadeh’s extension principle and approaches. The implementation of extension principle is computationally very demanding and to overcome this problem, the membership functions are limited to some certain forms [198]. A fuzzy number is a convex fuzzy subset of the real line and is defined by its membership function. Various types of fuzzy numbers have been employed among which triangular fuzzy numbers are the most widely used since they are simple to interpret and computationally easy to use in a fuzzy environment. A triangular fuzzy number can be indicated by a triple of real numbers as with and its membership function has the following form [45], [198], [199], [200].
Nevertheless, Piegat [46] warned that the name fuzzy number may lead to wrong interpretations of its concept. In fact, a fuzzy number is infinitely many numbers and not one and cannot be treated in the traditional way that we do for a crisp numbers. Mathematically speaking, fuzzy number is a continuous function and equivalent to infinite pairs of objects and their membership grades. For example the fuzzy number shown in Fig. 9 contains .
Fig. 9.
Triangular fuzzy number .
Nevertheless, many researchers have ignored the continuous nature of fuzzy numbers. For example, Chou et al. [193] split the triangular fuzzy number into three discrete numbers to find the inverse of fuzzy matrix for fuzzy DEMATEL. Mathematically speaking, Chou et al. [193] claimed that the multiplicative inverse of is equal to the multiplicative inverse of three matrices , and . However, Pandey and Kumar [194] revealed the multiplicative inverses of them are , and , respectively. Simply speaking, Pandey and Kumar [194] pointed out the elements of inverse matrix may not be triangular fuzzy numbers and a fuzzy number can never be split into discrete numbers.
On the other hand, interval and defuzzification are generally used approaches for approximation of fuzzy numbers yet the validity and efficiency of none of them has been proved or well addressed [45], [179]. Fuzzy number may be transformed into interval numbers corresponding to various confidence levels. The cut method or set of fuzzy number are defined as where is the membership function of and is confidence level determined by DM. In fact, interval approximation of fuzzy number is a well-known simplification approach and the -cut of triangular fuzzy number can give a set of intervals as where [200]. For example, the -cut of triangular fuzzy number with is , with is , with is and with is .
We know that values indicate the confidence level of DM over their judgments. However, there is no method to identify which is optimal for a given problem. On the other words, no reasonable method for obtaining a value for has been given, whereas value of 0.8 or 0.9 has been suggested without any justification in the majority of papers. Consequently, on the basis of different level, different results and scenarios are obtained which require heavy intervention from experts because of information distortion. For example, Rezaei [74] introduced BWM and demonstrated that the optimal weights can be derived by solving the Model (1).
| (1) |
In Model (1), and denote the preference of the best criterion over criterion and the preference of criterion over the worst criterion , respectively. Hafezalkotob and Hafezalkotob [201] extended BWM to a fuzzy environment in which the reference comparisons are expressed by linguistic terms and quantified by triangular fuzzy numbers. Mathematically speaking, and denote the fuzzy preference of the best criterion over criterion and the fuzzy preference of criterion over the worst criterion , respectively. Next, they used method to transform the fuzzy numbers to interval numbers and suggested Model (2) as follows:
| (2) |
Rahimi et al. [202] used this fuzzy BWM model to determine the weights of criteria and solved Model (2) based on . But there is no convincing argument why is appropriate. Simply speaking, if they could transform for example to , why not employ this interval number from the start instead of triangular fuzzy number for modeling the subjective evaluations? Clearly, is significantly less uncertain than . If they did, the problem could be tackled by interval numbers from beginning and there was no need to employ triangular fuzzy numbers with heavy calculation burden. Moreover, from fuzzy point of view, one can argue that if DM is certain about what level appropriate, fuzzy numbers with less uncertain such as instead of can also be used to quantify the fuzzy judgment. In fact, the information distortion arises since no membership grade is used in this transformation and according to Zhü [179], each mathematical model without considering membership grade does not belong to fuzzy sets. Zhü [179] adopted an interesting approach based on unfounded outcomes of method, ranking methods, etc to refute fuzzy AHP and ANP. Fedrizzi and Krejčí [203] tried to rebut Zhü’s [179] remarks and for example, claimed two fuzzy numbers are equal if their -cuts are equal for each . But the falsity of Fedrizzi and Krejčí’s [203] claim is obvious and it is very easy to show that two distinct fuzzy numbers are not equal under any circumstances.
On the other hand, Oussalah [204] indicated that an interval can be characterized by its mean and radius. For interval , mean and radius are determined by and , respectively. It means that with and can be approximately estimated by . Again one can argue that if DM could transform to approximately “3” why not use this crisp number instead of triangular fuzzy number from the start of problem solving? On the other words, DMs could separately solve this problem by different crisp assessments such as 2.8, 3.1, 3.15, 3.2 and obtained different scenarios. Obviously, there is no significant difference in the results of this approach based on crisp numbers and replacing fuzzy assessments and reducing them by -cut method. In fact, one may conclude that interval approach as an approximation of fuzzy number may be poor and can cause unfounded results when applied to real-world applications. More formally, it means that in the majority of fuzzy methods a single value (crisp number) is employed to represent a set of values (fuzzy number) which is barren. Let us recall that according to Saaty and Tran [180], there is no theorem or yardstick to justify the workability of the combination of fuzzy sets with MCDM methods. Saaty and Tran [180] argued “There has been some hype in the literature about “improving” some mathematics and in particular numbers, through fuzzification”. Also as pointed out by Dubois [205] “Actually, for many decision theory specialists, it is not clear that fuzzy sets have ever led to a new decision paradigm.” Finally, Saaty [206] mentioned “It is hoped that those who use fuzzy logic in the AHP would stop and examine what they are doing and explain why it is justified”.
7.2. Defuzzification
Defuzzification procedure as the biggest simplification approach of fuzzy numbers maps a fuzzy set into a crisp value [200]. In the fuzzy literature, there are many defuzzification techniques and the most generally used method to convert fuzzy number into crisp number is the center of gravity technique [181], [207]. Clearly, the defuzzification leads to the data to be degenerated and causes severe loss or distortion of information since each defuzzification method reduces infinite objects into a single point. Also various defuzzification techniques extract different levels of information and the results obtained from them may conflict with each other [207]. Some researches such as Tuljak-Suban and Bajec [181] highlighted the importance of an appropriate defuzzification technique choice and revealed how defuzzification methods can influence deeply the final assessment. For example, Bhat and Kumar [182] disclosed that the defuzzification technique, namely graded mean integration representation (GMIR) method employed by Kavilal et al. [75] leads to the senseless results and suggested another defuzzification technique, namely the weighted geometric mean for modification in Kavilal et al.’s [75] method. It means that DM faces a deep difficulty in selecting proper defuzzification method for application problems. Nevertheless, Van Leekwijck and Kerre [208] reported that in fuzzy literature, the defuzzification procedure is treated in far lesser detail than the other procedures. Although many researchers such as Grzegorzewski and Mrówka [200] claimed the fuzzy information should be processed as long as possible and early defuzzification leads to serious information loss, but the impact of defuzzification order on final outcomes has not been well addressed in literature and remains controversial [209]. The following example can illustrate this issue:
Example 1
We take four triangular fuzzy numbers , , and as an example shown in Fig. 10.
Fig. 10.
Triangular fuzzy numbers for Example 1.
Probably the center of gravity is the most commonly used defuzzification operator in general. The center of gravity of triangular fuzzy number can be obtained as follows:
According to this formula, fuzzy numbers , , and have the same defuzzification crisp number . Clearly, we can observe this method causes the serious information loss. From mathematical point of view, this defuzzification technique obtains only the average of three discrete numbers. But triangular fuzzy number is a continuous function and not discrete and hence, cannot be efficiently estimated by the average of three values. For example, we have the following equation:
Finally, we have . Now, from the beginning of operations, we use COG method to defuzzify the above fuzzy numbers and we have
Clearly, it means that .
Another well-known defuzzification technique is GMIR method and in the case of triangular fuzzy number can be obtained as4
According to GMIR, , , and have the defuzzification crisp numbers as , , , and , respectively. Clearly, different outcomes are derived from using different defuzzification methods.
Also we can see . Now, we use GMIR method to defuzzify fuzzy numbers from the beginning of operations as follows:
.
Clearly, it can be seen .
In fact, in the majority of fuzzy methods, authors only put the various average values of three crisp numbers in the equations and according to such calculation procedure, triangular fuzzy numbers can be converted to corresponding crisp numbers before the processing of data. For example, Zhü [179] revealed that the outcomes derived by triangular fuzzy AHP are the same as that derived by the geometric mean. Such examples indicate that the outcome of defuzzification at the initial step may coincide with the outcome of defuzzification at the final step. Dubois [205] pointed out in many cases, fuzzy set has only been added to existing MCDM methods such as fuzzy AHP and fuzzy ELECTRE with no apparent benefits particularly when fuzzy numbers are changed into crisp numbers via defuzzification. For example, Dytczak and Ginda [195] revealed that replacing crisp numbers with fuzzy numbers in fuzzy DEMATEL may lead to similar outcomes and pointed out that fuzzy data processing in fuzzy DEMATEL method needs a detailed rethink. Simply speaking, the simplest yet perhaps the most ineffective approach is to convert a fuzzy MCDM problem into a crisp one using defuzzification since this way generates the serious information distortion. Unfortunately, although solving fuzzy models by using fuzzy arithmetic needs to be done with special care owing to its peculiarities and very high computational complexity, they have not been addressed adequately in the fuzzy literature. More formally, in many fuzzy methods, only some linguistic variables or fuzzy assessments are represented by triangular fuzzy numbers but calculation procedures in those fuzzy models are completely separate from fuzzy arithmetic. All in all, the concept of membership grade is the foundation of fuzzy sets and the concepts of approach and defuzzification are fully opposite to this key idea of fuzzy set theory. Consequently, the author is in agreement with Zhü [179] in which and defuzzification approaches are not reliable mathematical tools for dealing with fuzzy arithmetic.
7.3. Fuzzy arithmetic
After Zadeh [83] put forward the idea of linguistic variables, the importance of associated fuzzy numbers and fuzzy arithmetic has been cited in numerous application areas. In fact, the concept of fuzzy sets lead to the definition of fuzzy number and then the arithmetic for fuzzy numbers was developed by Mizumoto and Tanaka [211] and Dubois and Prade [210]. However, many studies have warned that constructing fuzzy models through the same fashion as in the real (crisp) arithmetic may lead to dubious or senseless results [45], [46], [199], [204], [212], [213]. It arises because that reasoning in terms of standard fuzzy arithmetic which developed on the basis of interval arithmetic or extension principle may lose fundamental properties that hold for real arithmetic [204]. Accordingly, the solution of fuzzy and interval equations are not trivial even for simple linear equations such as or . Although different methods have been suggested to solve fuzzy and interval equations, the majority of those equations have no solution or particular solutions in restrictive conditions may be derived [214]. Literature shows the frequently used interval arithmetic type is Moore’s arithmetic, in spite of its serious drawbacks [215], [216]. For example, Sevastjanov and Dymova [217] developed a new operation called “interval extended zero” and used it to tackle linear fuzzy equations. Allahviranloo and Babakordi [218] suggested a new method to solve in which are fuzzy matrices and are fuzzy vectors. But different studies such as Piegat and Landowski [219] and Lodwick and Dubois [214] disclosed the ineffectiveness of such methods. For example, Piegat and Pluciński [220] pointed out the suggested method by Allahviranloo and Babakordi [218] is based on standard interval arithmetic and for this reason their approach has severe drawbacks which cause that it is incorrect. As a result, direct application of standard fuzzy arithmetic may result in questionable or senseless outcomes. Due to this fact, the basic operations of fuzzy numbers are problematic and have no fuzzy solution as follows.
Simply speaking, subtraction (division) cannot be considered as inverse operator to addition (multiplication) and it makes impossible to work out a simple equation. Moreover, Hanss [212], [216] pointed out the standard fuzzy arithmetic has a severe shortcoming which different results can be derived depending on the ordering of steps used in the solution procedure. For example, the computation of leads to one result when the form is employed and another result when the form is used.
We know a first approach to implement arithmetic operations on fuzzy numbers was made by Zadeh’s extension principle [83]. However, the extended arithmetic operators are computationally expensive and may be too complex for practical implementation due to nonlinear programming models [221]. Consequently, interval arithmetic ( approach) has been considered as the most generally used technique for implementing fuzzy arithmetic. But it leads to overestimation in the resulting fuzzy numbers [216]. Overestimation is because of the fact that the standard fuzzy arithmetic treated fuzzy numbers as independent numbers although they are not. Hanss [212] suggested a novel implementation of fuzzy arithmetic based on that avoids overestimation which often arises when fuzzy arithmetic is reduced to interval arithmetic. Klir [199] revealed that the standard fuzzy arithmetic does not take into account the known constraints when applied to linguistic variables and introduced constrained fuzzy arithmetic to reduce the overestimation effect. Although some researchers such as Boukezzoula et al. [221] suggested the use of requisite constraints, Ngan [213] warned that they may lead to incorrect outcomes. LR representation introduced by Dubois and Prade [210] can be considered as a straightforward approach to implement fuzzy arithmetic but the multiplication and division of LR numbers do not lead to a LR results which make these fuzzy numbers inappropriate for iterative purposes [204]. Also Giachetti and Young [198] warned the approximations for fuzzy multiplication and division may contain very large errors.
Very recently, Qiyas et al. [222] defined linguistic picture fuzzy set by combining picture fuzzy set and linguistic term and developed novel type of fuzzy numbers named linguistic picture fuzzy number. They also defined operational laws, two ranking methods and averaging operator for those numbers and used them to deal with an MCDM problem in which the rating scores of alternatives over criteria are represented by linguistic picture fuzzy number. For example, Qiyas et al. [222] claimed the linguistic score and linguistic accuracy functions of a linguistic picture fuzzy number can be obtained as follows: and , respectively. Also Qiyas et al. [222] argued if , , , and . But Appadoo et al. [223] disclosed that the results derived from this method are not correct as follows.
Let and be two linguistic picture fuzzy numbers that will be ranked . One can notice, and . Consequently, according to the ranking method suggested by Qiyas et al. [222], the ranking result in this case is which is counter-intuitive and illogical. Clearly, these linguistic picture fuzzy numbers are two distinct numbers and as a result, this ranking method cannot be used for solving MCDM problems in linguistic picture fuzzy environment. Moreover, Appadoo et al. [223] revealed that the aggregation operator and both ranking methods introduced by Qiyas et al. [222] are invalid too. Tao et al. [224] suggested the arithmetic operations to calculate the sum and multiplication of two intuitionistic fuzzy numbers and used them to solve an MCDM problem. But the drawbacks of those operational laws are pointed out by Kaur and Kumar [225].
Li and Chen [38] developed D-intuitionistic hesitant fuzzy set by combining D-number and generalized hesitant fuzzy set and defined some arithmetic operations for them. For example, Li and Chen [38] defined the score function of as . It should be noted that the intuitionistic fuzzy number indicates the views of th expert, denotes the belief degree of DM regarding the views of th expert and the number of DMs is represented by [226]. Li and Chen [38] claimed that if , , and . But according to Mishra et al. [226], this ranking method cannot differentiate distinct D-intuitionistic fuzzy numbers. Suppose that and are two D-intuitionistic hesitant fuzzy numbers. According to ranking method suggested by Li and Chen [38], . Thus, the ranking result is which is contrary to human intuition and incorrect. Simply speaking, Mishra et al. [226] disclosed that comparison laws of D-intuitionistic hesitant fuzzy sets suggested by Li and Chen [38] cannot differentiate distinct sets and therefore, it is not advisable to use this ranking method in MCDM methods.
Based on picture 2-tuple linguistic set, Wei et al. [227] introduced a number of operational laws and aggregation operators, namely weighted averaging and weighted geometric operators for picture 2-tuple linguistic numbers (P2TLNs). But Ju et al. [228] disclosed the serious drawbacks of those methods. For example, suppose that is a P2TLN where , , , , and . Also is a positive real number. Wei et al. [227] claimed that . But Ju et al. [228] demonstrated that this model is not correct as follows. Let be a P2TLN and . Hence, we have:
. Clearly, and hence, the aggregation result is not a P2TLN. Simply speaking, as demonstrated by Ju et al. [228], aggregation operators introduced by Wei et al. [227] are incorrect and cannot be used to solve MCDM problems.
On the other hand, Piegat and Landowski [229] pointed out the standard fuzzy arithmetic was based on vertical fuzzy numbers and this assumption can initiate serious computational paradoxes in fuzzy arithmetic and hence, introduced horizontal membership functions. Constructing horizontal membership functions became possible thanks to multi-dimensional interval arithmetic introduced by Piegat and Landowski [219] on the basis of RDM-variables. Also Kacprzak [68] used ordered fuzzy numbers to overcome the severe drawbacks of convex fuzzy numbers resulting from definition of standard fuzzy arithmetic on them such as increase of fuzziness and lack of opposite elements. Although there are some studies that suggest limited remedies to the aforementioned drawbacks, they are often intricate and useless from a practical point of view. Consequently, the authors agree with Ngan [213] in that DMs who are not well acquainted with fuzzy sets find it non-trivial to choose proper fuzzy arithmetic operators from those complicated approaches and this challenge limits its practical applicability dramatically.
8. Future direction for MCDM methods in COVID-19
This paper shows that the application of MCDM methods in COVID-19 pandemic have attracted many explorations. However, in order to address the COVID-19 problems by using MCDM methods, it requires more attentions to suggest productive models. There are research gaps and opportunities that can be addressed in the future research:
-
1.
We found from the analysis that “supply chain” is a very popular application area with MCDM methods in this context. Nevertheless, our review indicated that many problems in this field fall under MCDM and there is large room for further research to develop application domain. We expect the number of applications in vaccines assessment and equitable vaccine distribution to increase in the near future. For example, DEA can be used to assess the performance of alternative COVID-19 vaccines through a quantitative method.
-
2.
The majority of real-world problems happen in a dynamic environment. However, the classical MCDM methods concentrate on a single period and cannot model relationships among the outcomes derived at different periods. Dynamic MCDM models can take into consideration the impacts of previous outcomes on the current decision by adding time dimension to assessment. As a future suggestion, we think that it is better to treat and model some problems such as the impact of Covid-19 on women, small business, poverty, stock markets, consumer behavior, mental health, social media, and movie industry as dynamic MCDM models. Dahooie et al. [230] can be considered as the initial point.
-
3.
Our review revealed that the least number of articles can be observed in the application of outranking methods in the COVID-19 pandemic. The main feature of outranking methods such as ELECTRE and TODIM is that they avoid compensation between decision criteria which is preferred in many real-life problems. For future research, there is significant research space in this field.
-
4.
Some papers such as Asadabadi et al. [173] are critical of papers that highlight the applicability of MCDM methods such as AHP and ANP and their reason is the severe deficiencies of these methods. As a result, the key reason that a DM does not rely on MCDM methods may be owing to the fact that he/she can notice intuitively ranking errors. The authors agree with Asadabadi et al. [173] in that future studies should pay closer attention to address the possible pitfalls of existing MCDM methods. De Keyser and Peeters [53], Huang et al. [172], Asadabadi et al. [173] and Llamazares [174] can be considered as the initial points.
-
5.
The determination of criteria weights is a vital part of MCDM. We observed that the majority of papers reviewed in this study utilized AHP, BWM, and Entropy to get the criteria weights and some new weighting methods such as IDOCRIW introduced by Zavadskas and Podvezko [49] have not been used. Integrating these weighting methods into MCDM is an interesting direction for future work.
-
6.
From this literature review, it can be found that fuzziness has been incorporated in 64% of papers. The use of various fuzzy sets in MCDM problems is very interesting because fuzzy numbers can model linguistic evaluations. However, there is no doubt that the fuzzy arithmetic is more complex than it may first appear and DMs should be aware of theoretical basis of it to avoid pitfalls while using the fuzzy MCDM. For example, the researchers must pay special attention to overestimation problem which often arises when using standard fuzzy arithmetic. Also when evaluating choices in fuzzy MCDM methods, the adopted linguistic terms should be translated into fuzzy numbers and in order to reach the final decision, these fuzzy numbers should be compared and ranked. Simply speaking, in fuzzy MCDM, the ranking of alternatives are based on the ranking of fuzzy numbers. Although there are numerous techniques about how to compare and rank the fuzzy numbers, this task is one of the serious problems of fuzzy sets and there is no generally accepted ranking method. There is room for further investigations and Yatsalo et al. [192] and Sotoudeh-Anvari et al. [231] can be used as the initial points. By recalling the remarks mentioned in Section 2, Fig. 11 indicates the key theoretical challenges for future research that are associated with fuzzy sets.
-
7.
In the case when DMs face uncertainty, it is not easy to apply crisp MCDM methods to assess the performance ratings of alternatives and the relative importance of criteria or sub-criteria. Hence, many researchers extended MCDM methods in the presence of uncertainty by adding fuzzy sets to establish fuzzy MCDM methods. However, the usefulness of fuzzy MCDM methods is still controversial. Prof. Saaty argued: “For greater validity of a decision with the AHP, is there evidence that it is better to fuzzify the judgments? The answer is an unqualified no” [180]. Simply speaking, many researchers such as Dytczak and Ginda [195] warned that selecting fuzzy MCDM methods which may be lead to misleading outcomes will not essentially create different or better solution in terms of quality of results. This complexity arises since fuzzy arithmetic is more problematic than is frequently assumed. For example, Kordi and Brandt [232] concluded that by increasing the level of fuzziness in fuzzy AHP, the differences between outcomes of AHP and fuzzy AHP become more significant. Also Mosadeghi et al. [233] reaffirmed the result obtained from Kordi and Brandt [232] and pointed out AHP is sensitive to uncertainty. Future research can address whether it is essential to apply a fuzzy MCDM method to a particular problem. Dytczak and Ginda [195], Zhü [179], Kordi and Brandt [232], Mosadeghi et al. [233], Chen et al. [234], Yang et al. [47] and Chan et al. [235] can be used as the initial points
-
8.
The use of D-numbers has been obtaining in significance thanks to the interesting privileges in various fields. Another direction for future research can be to use D-numbers in combination with MCDM methods to enhance the features of COVID-19-related research. Also combination of D-numbers with DEA can be interesting for future works. For this purpose, Pamučar et al. [236] can be considered as an initial point.
-
9.
As discussed, MCDM methods have been broadly applied to this field that requires dealing with large amounts of information. However, the MCDM researchers have been facing serious challenges while using MCDM methods. Methods differ and these differences may seriously affect the final results in decision-making processes. In general, there remains the classical problem of which MCDM method to use in a particular application. Moreover, the validity of ranking result remains an open issue and can be suggested as profitable and critical line of future research. For this purpose, for a classical reference please see Hobbs and Horn [56] and Zanakis et al. [55] as well as for more updated papers please see Sotoudeh-Anvari et al. [50], Mousavi-Nasab and Sotoudeh-Anvari [62] and Kalbar and Das [57].
-
10.
Whereas fuzzy MCDM methods can be more or less useful depending on the data or situation, very few research works have been introduced to guide the selection of a fuzzy MCDM method adapted to a given problem. It can be considered to further research in MCDM problems under uncertainty. Chen and Pan [35] can be considered as the initial point.
-
11.
Appropriate MCDM methods for common problems in COVID-19 pandemic such as drug selection problem can be developed on the basis of problem or data characteristics. It is very useful and interesting for future study of the real-life problems. Mousavi-Nasab and Sotoudeh-Anvari [62] and Chen and Pan [35] can be considered as the initial points.
-
12.
Future research can also use other recently introduced techniques to make up some traditional shortcomings of MCDM methods. For example, most of the existing MCDM methods use one normalization technique which may cause information distortion. MACONT introduced by Wen et al. [64] combines three normalization techniques regarding criterion types and can enhance the reliability of decision outcome.
-
13.
In the process of setting criteria weights in MCDM problems, DMs may express the opinion dishonestly to reach their desired ranking and interest which is referred to as strategic manipulation. It can be fruitful and an interesting future study for researchers to employ this concept to study some COVID-19 issues. Dong et al. [72] can be considered as the initial point.
-
14.
We limited the search to the peer-reviewed journal articles available through Web of Science (IF> 3 and CiteScore>4). Hence, this paper cannot cover all papers related to the application of MCDM methods in COVID-19 pandemic and other literature artifacts are excluded. This limitation can be covered by future study to increase the sample papers.
Fig. 11.
Theoretical challenges associated with fuzzy sets.
9. Conclusion
The novel coronavirus first reported in Wuhan in December 2019 and declared by the WHO on March 2020 as a pandemic, has resulted in 260,000,000 laboratory-confirmed cases and 5,200,000 deaths worldwide as of November 2021.5 This paper provided a systematic literature review on peer-reviewed journal articles with high impact factor related to the application of MCDM methods in COVID-19 era. In this work, a total of 72 articles were collected from 37 leading journals and categorized into 52 types of application. First of all, this paper illustrated the potential and applicability of MCDM methods in this field. AHP (including fuzzy AHP) as the most utilized MCDM method was applied in 37.5% of articles reviewed followed by TOPSIS and VIKOR. Also the rise in COVID-19 studies using hybrid MCDM methods was documented. 35 countries contributed to this review and India was identified as the leading country in this field followed by Turkey and China. Interestingly, 50% of papers were presented in the form of international cooperation. We observed that the application of fuzzy sets in MCDM methods is one of the most attractive research areas in COVID-19-related research. The clear issue is that MCDM methods were combined with the fuzzy sets in the majority of papers, i.e. 69%. Although nearly all authors argued that MCDM methods in combination with fuzzy sets have successful application in diverse fields, solving this kind of MCDM methods, namely fuzzy MCDM methods is not computationally straightforward and it is vital to investigate other lines of evidence to prove their effectiveness. Consequently, the readers must be very cautious in interpreting the outcomes obtained from fuzzy MCDM methods. Based on literature review presented in the previous sections, some remarks can be made.
-
-
MCDM methods may suggest senseless ranking result, even if a straightforward problem is considered and hence, DM needs to understand the whole decision-making process to be able to trust the outcomes and to avoid pitfalls.
-
-
There still exist serious challenging and unsolved problems in the field of fuzzy arithmetic, in particular , defuzzification and ranking fuzzy numbers.
-
-
In general, and defuzzification approaches are not reliable mathematical tools for dealing with fuzzy arithmetic.
-
-
There is serious concern about the usefulness and validity of applying fuzzy thinking to MCDM methods and hence, this area needs much deeper investigation.
Finally, the findings of this study provide a roadmap for further research in the field of MCDM and COVID-19. We hope this work can help MCDM researchers who wish to use MCDM methods in new problems that arise in the COVID-19 pandemic.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Footnotes
Acknowledgments
I dedicate this paper to the healthcare workers around the world who are risking their lives without adequate protective equipment to save people and the COVID-19 patients.
The author is very grateful to Prof. Rocio Perez de Prado and anonymous reviewers for their valuable suggestions and constructive comments that have led to an improved version of this paper.
Unlike the most MCDM methods, PSI developed by Maniya and Bhatt [69] obtains the overall preference of criteria using the concept of statistics and there is no need to provide a relative importance between criteria.
Dubois and Prade [210] introduced the LR type for fuzzy numbers, where L and R represent the left and right shape functions, respectively and and are the inverse functions. When and are linear functions, the LR fuzzy number becomes triangular fuzzy number.
References
- 1.Nicola M., Alsafi Z., Sohrabi C., Kerwan A., Al-Jabir A., Iosifidis C., et al. The socio-economic implications of the coronavirus pandemic (COVID-19): A review. Int. J. Surg. 2020;78:185–193. doi: 10.1016/j.ijsu.2020.04.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Sun X., Wandelt S., Zheng C., Zhang A. COVID-19 pandemic and air transportation: Successfully navigating the paper hurricane. J. Air Transp. Manag. 2021 doi: 10.1016/j.jairtraman.2021.102062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Jiang P., Fan Y.Van., Klemeš J.J. Impacts of COVID-19 on energy demand and consumption: Challenges, lessons and emerging opportunities. Appl. Energy. 2021;285 doi: 10.1016/j.apenergy.2021.116441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ivanov D., Dolgui A. OR-methods for coping with the ripple effect in supply chains during COVID-19 pandemic: Managerial insights and research implications. Int. J. Prod. Econ. 2021;232 doi: 10.1016/j.ijpe.2020.107921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Lin A.J., Chang H.Y., Huang S.W., Tzeng G.H. Criteria affecting Taiwan wealth management banks in serving high-net-worth individuals during COVID-19: A DEMATEL approach. J. Financial Serv. Mark. 2021:1–21. [Google Scholar]
- 6.Lin A.J., Chang H.Y., Huang S.W., Tzeng G.H. Improving service quality of wealth management bank for high-net-worth customers during COVID-19: A fuzzy-DEMATEL approach. Int. J. Fuzzy Syst. 2021:1–18. [Google Scholar]
- 7.Woolf S.H., Chapman D.A., Lee J.H. COVID-19 as the leading cause of death in the United States. JAMA. 2021;325(2):123–124. doi: 10.1001/jama.2020.24865. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Razzaq O.A., Fahad M., Khan N.A. Different variants of pandemic and prevention strategies: A prioritizing framework in fuzzy environment. Results Phys. 2021;28 doi: 10.1016/j.rinp.2021.104564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Khurana S., Haleem A., Luthra S., Huisingh D., Mannan B. Now is the time to press the reset button: Helping India’s companies to become more resilient and effective in overcoming the impacts of COVID-19, climate changes and other crises. J. Cleaner Prod. 2021;280 doi: 10.1016/j.jclepro.2020.124466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Özkan B., Özceylan E., Kabak M., Dikmen A.U. Evaluation of criteria and COVID-19 patients for intensive care unit admission in the era of pandemic: A multi-criteria decision making approach. Comput. Methods Programs Biomed. 2021;209 doi: 10.1016/j.cmpb.2021.106348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.El Baz J., Ruel S. Can supply chain risk management practices mitigate the disruption impacts on supply chains’ resilience and robustness? Evidence from an empirical survey in a COVID-19 outbreak era. Int. J. Prod. Econ. 2021;233 doi: 10.1016/j.ijpe.2020.107972. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.da Silveira Pereira D., de Mello J.C.C.S. Efficiency evaluation of Brazilian airlines operations considering the Covid-19 outbreak. J. Air Transp. Manag. 2021;91 doi: 10.1016/j.jairtraman.2020.101976. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Beiderbeck D., Frevel N., Heiko A., Schmidt S.L., Schweitzer V.M. The impact of COVID-19 on the European football ecosystem–A Delphi-based scenario analysis. Technol. Forecast. Soc. Change. 2021;165 [Google Scholar]
- 14.Choi T.M. Fighting against COVID-19: What operations research can help and the sense-and-respond framework. Ann. Oper. Res. 2021:1–17. doi: 10.1007/s10479-021-03973-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Liao H., Tang M., Li Z., Lev B. Bibliometric analysis for highly cited papers in operations research and management science from 2008 to 2017 based on essential science indicators. Omega. 2019;88:223–236. [Google Scholar]
- 16.Khan M.J., Ali M.I., Kumam P., Kumam W., Al-Kenani A.N. q-Rung orthopair fuzzy modified dissimilarity measure based robust VIKOR method and its applications in mass vaccination campaigns in the context of COVID-19. Ieee Access. 2021;9:93497–93515. [Google Scholar]
- 17.Khan M., Mehran M.T., Haq Z.U., Ullah Z., Naqvi S.R., Ihsan M., Abbass H. Applications of artificial intelligence in COVID-19 pandemic: A comprehensive review. Expert Syst. Appl. 2021;185 doi: 10.1016/j.eswa.2021.115695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Lalmuanawma S., Hussain J., Chhakchhuak L. Applications of machine learning and artificial intelligence for Covid-19 (SARS-CoV-2) pandemic: A review. Chaos Solitons Fractals. 2020;139 doi: 10.1016/j.chaos.2020.110059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Naz F., Kumar A., Majumdar A., Agrawal R. Is artificial intelligence an enabler of supply chain resiliency post COVID-19? An exploratory state-of-the-art review for future research. Oper. Manag. Res. 2021:1–21. [Google Scholar]
- 20.Sarker S., Jamal L., Ahmed S.F., Irtisam N. Robotics and artificial intelligence in healthcare during COVID-19 pandemic: A systematic review. Robot. Auton. Syst. 2021;146 doi: 10.1016/j.robot.2021.103902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Piotrowski A.P., Piotrowska A.E. Differential evolution and particle swarm optimization against COVID-19. Artif. Intell. Rev. 2021:1–71. doi: 10.1007/s10462-021-10052-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Clemente-Suárez V.J., Navarro-Jiménez E., Ruisoto P., Dalamitros A.A., Beltran-Velasco A.I., Hormeño Holgado A., et al. Performance of fuzzy multi-criteria decision analysis of emergency system in COVID-19 pandemic. An extensive narrative review. Int. J. Environ. Res. Public Health. 2021;18(10):5208. doi: 10.3390/ijerph18105208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Salajan A., Tsolova S., Ciotti M., Suk J.E. To what extent does evidence support decision making during infectious disease outbreaks? A scoping literature review. Evid. Policy. 2020;16(3):453. [Google Scholar]
- 24.Ahmad N., Hasan M.G., Barbhuiya R.K. Identification and prioritization of strategies to tackle COVID-19 outbreak: A group-BWM based MCDM approach. Appl. Soft Comput. 2021;111 doi: 10.1016/j.asoc.2021.107642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Cegan J.C., Filion A.M., Keisler J.M., Linkov I. Trends and applications of multi-criteria decision analysis in environmental sciences: Literature review. Environ. Syst. Decis. 2017;37(2):123–133. [Google Scholar]
- 26.Sitorus F., Cilliers J.J., Brito-Parada P.R. Multi-criteria decision making for the choice problem in mining and mineral processing: Applications and trends. Expert Syst. Appl. 2019;121:393–417. [Google Scholar]
- 27.Roy B. Springer Science & Business Media; 1996. Multicriteria Methodology for Decision Aiding (Vol. 12) [Google Scholar]
- 28.Triantaphyllou E. Multi-Criteria Decision Making Methods: A Comparative Study. Springer; Boston, MA: 2000. Multi-criteria decision making methods; pp. 5–21. [Google Scholar]
- 29.Greco S., Figueira J., Ehrgott M. Springer; New York: 2016. Multiple Criteria Decision Analysis (Vol. 37) [Google Scholar]
- 30.Cinelli M., Coles S.R., Kirwan K. Analysis of the potentials of multi criteria decision analysis methods to conduct sustainability assessment. Ecol. Indic. 2014;46:138–148. [Google Scholar]
- 31.Soltani A., Hewage K., Reza B., Sadiq R. Multiple stakeholders in multi-criteria decision-making in the context of municipal solid waste management: A review. Waste Manag. 2015;35:318–328. doi: 10.1016/j.wasman.2014.09.010. [DOI] [PubMed] [Google Scholar]
- 32.Zare M., Pahl C., Rahnama H., Nilashi M., Mardani A., Ibrahim O., Ahmadi H. Multi-criteria decision making approach in E-learning: A systematic review and classification. Appl. Soft Comput. 2016;45:108–128. [Google Scholar]
- 33.Gul M. A review of occupational health and safety risk assessment approaches based on multi-criteria decision-making methods and their fuzzy versions. Hum. Ecol. Risk Assess.: Int. J. 2018;24(7):1723–1760. [Google Scholar]
- 34.Nadkarni R.R., Puthuvayi B. A comprehensive literature review of multi-criteria decision making methods in heritage buildings. J. Build. Eng. 2020 [Google Scholar]
- 35.Chen L., Pan W. Review fuzzy multi-criteria decision-making in construction management using a network approach. Appl. Soft Comput. 2021 [Google Scholar]
- 36.Thokala P., Devlin N., Marsh K., Baltussen R., Boysen M., Kalo Z., et al. Multiple criteria decision analysis for health care decision making—An introduction: Report 1 of the ISPOR MCDA emerging good practices task force. Value Health. 2016;19(1):1–13. doi: 10.1016/j.jval.2015.12.003. [DOI] [PubMed] [Google Scholar]
- 37.Mardani A., Hooker R.E., Ozkul S., Yifan S., Nilashi M., Sabzi H.Z., Fei G.C. Application of decision making and fuzzy sets theory to evaluate the healthcare and medical problems: A review of three decades of research with recent developments. Expert Syst. Appl. 2019;137:202–231. [Google Scholar]
- 38.Li X., Chen X. D-intuitionistic hesitant fuzzy sets and their application in multiple attribute decision making. Cogn. Comput. 2018;10(3):496–505. [Google Scholar]
- 39.Zadeh L.A. Information and control. Fuzzy Sets. 1965;8(3):338–353. [Google Scholar]
- 40.Kahraman C., Onar S.C., Oztaysi B. Fuzzy multicriteria decision-making: A literature review. Int. J. Comput. Intell. Syst. 2015;8(4):637–666. [Google Scholar]
- 41.Mardani A., Jusoh A., Zavadskas E.K. Fuzzy multiple criteria decision-making techniques and applications–Two decades review from 1994 to 2014. Expert Syst. Appl. 2015;42(8):4126–4148. [Google Scholar]
- 42.Yeh C.H., Deng H. 1997 IEEE International Conference on Intelligent Processing Systems (Cat. No. 97TH8335) (Vol. 2) IEEE.; 1997. An algorithm for fuzzy multi-criteria decision making; pp. 1564–1568. [Google Scholar]
- 43.Chen S.J., Hwang C.L. Fuzzy Multiple Attribute Decision Making. Springer; Berlin, Heidelberg.: 1992. Fuzzy multiple attribute decision making methods; pp. 289–486. [Google Scholar]
- 44.Sotoudeh-Anvari A., Sadi-Nezhad S. A hybrid model based on fuzzy VIKOR and the classical optimal search to detect illegal chemical warehouses. J. Environ. Sci. Health A. 2022:1–13. doi: 10.1080/10934529.2022.2053451. [DOI] [PubMed] [Google Scholar]
- 45.Sotoudeh-Anvari A. A critical review on theoretical drawbacks and mathematical incorrect assumptions in fuzzy OR methods: Review from 2010 to 2020. Appl. Soft Comput. 2020;93 [Google Scholar]
- 46.Piegat A. Cardinality approach to fuzzy number arithmetic. IEEE Trans. Fuzzy Syst. 2005;13(2):204–215. [Google Scholar]
- 47.Yang X., Yan L., Zeng L. How to handle uncertainties in AHP: The cloud delphi hierarchical analysis. Inform. Sci. 2013;222:384–404. [Google Scholar]
- 48.Yeh C.H. A problem-based selection of multi-attribute decision-making methods. Int. Trans. Oper. Res. 2002;9(2):169–181. [Google Scholar]
- 49.Zavadskas E.K., Podvezko V. Integrated determination of objective criteria weights in MCDM. Int. J. Inf. Technol. Decis. Mak. 2016;15(02):267–283. [Google Scholar]
- 50.Sotoudeh-Anvari A., Sadjadi S.J., Hadji Molana S.M., Sadi-Nezhad S. A stochastic multi-objective model based on the classical optimal search model for searching for the people who are lost in response stage of earthquake. Sci. Iran. 2019;26(3):1842–1864. [Google Scholar]
- 51.Ozernoy V.M. Choosing the best multiple criterlv decision-making method. INFOR: Inf. Syst. Oper. Res. 1992;30(2):159–171. [Google Scholar]
- 52.Alvarez P.A., Ishizaka A., Martínez L. Multiple-criteria decision-making sorting methods: A survey. Expert Syst. Appl. 2021 [Google Scholar]
- 53.De Keyser W., Peeters P. A note on the use of PROMETHEE multicriteria methods. European J. Oper. Res. 1996;89(3):457–461. [Google Scholar]
- 54.Dožić S. Multi-criteria decision making methods: Application in the aviation industry. J. Air Transp. Manag. 2019;79 [Google Scholar]
- 55.Zanakis S.H., Solomon A., Wishart N., Dublish S. Multi-attribute decision making: A simulation comparison of select methods. European J. Oper. Res. 1998;107(3):507–529. [Google Scholar]
- 56.Hobbs B.F., Horn G.T. Building public confidence in energy planning: a multimethod MCDM approach to demand-side planning at BC gas. Energy Policy. 1997;25(3):357–375. [Google Scholar]
- 57.Kalbar P.P., Das D. Life Cycle Sustainability Assessment for Decision-Making. Elsevier.; 2020. Advancing life cycle sustainability assessment using multiple criteria decision making; pp. 205–224. [Google Scholar]
- 58.Gershon M., Duckstein L. Multiobjective approaches to river basin planning. J. Water Res. Plan. Manag. 1983;109(1):13–28. [Google Scholar]
- 59.Kornyshova E., Salinesi C. 2007 Ieee Symposium on Computational Intelligence in Multi-Criteria Decision-Making. IEEE; 2007. MCDM techniques selection approaches: state of the art; pp. 22–29. [Google Scholar]
- 60.Roy B., Słowiński R. Questions guiding the choice of a multicriteria decision aiding method. EURO J. Decis. Process. 2013;1(1):69–97. [Google Scholar]
- 61.Wątróbski J., Jankowski J., Ziemba P., Karczmarczyk A., Zioło M. Generalised framework for multi-criteria method selection. Omega. 2019;86:107–124. doi: 10.1016/j.dib.2018.12.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Mousavi-Nasab S.H., Sotoudeh-Anvari A. A comprehensive MCDM-based approach using TOPSIS, COPRAS and DEA as an auxiliary tool for material selection problems. Mater. Des. 2017;121:237–253. [Google Scholar]
- 63.Zavadskas E.K., Turskis Z. Multiple criteria decision making (MCDM) methods in economics: An overview. Technol. Econ. Dev. Econ. 2011;17(2):397–427. [Google Scholar]
- 64.Wen Z., Liao H., Zavadskas E.K. MACONT: Mixed aggregation by comprehensive normalization technique for multi-criteria analysis. Informatica. 2020;31(4):857–880. [Google Scholar]
- 65.Milani A.S., Shanian A., Madoliat R., Nemes J.A. The effect of normalization norms in multiple attribute decision making models: a case study in gear material selection. Struct. Multidiscip. Optim. 2005;29(4):312–318. [Google Scholar]
- 66.Karande P., Chakraborty S. Application of multi-objective optimization on the basis of ratio analysis (MOORA) method for materials selection. Mater. Des. 2012;37:317–324. [Google Scholar]
- 67.Hwang C.L., Yoon K. Multiple Attribute Decision Making. Springer; Berlin, Heidelberg.: 1981. Methods for multiple attribute decision making; pp. 58–191. [Google Scholar]
- 68.Kacprzak D. An extended TOPSIS method based on ordered fuzzy numbers for group decision making. Artif. Intell. Rev. 2020;53(3) [Google Scholar]
- 69.Maniya K., Bhatt M.G. A selection of material using a novel type decision-making method: Preference selection index method. Mater. Des. 2010;31(4):1785–1789. [Google Scholar]
- 70.Kirişci M., Demir İ, Şimşek N., Topaç N., Bardak M. The novel VIKOR methods for generalized pythagorean fuzzy soft sets and its application to children of early childhood in COVID-19 quarantine. Neural Comput. Appl. 2021:1–27. doi: 10.1007/s00521-021-06427-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Altay B.C., Okumuş A., Mercangöz B.A. An intelligent approach for analyzing the impacts of the COVID-19 pandemic on marketing mix elements (7ps) of the on-demand grocery delivery service. Complex Intell. Syst. 2021:1–12. doi: 10.1007/s40747-021-00358-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Dong Y., Liu Y., Liang H., Chiclana F., Herrera-Viedma E. Strategic weight manipulation in multiple attribute decision making. Omega. 2018;75:154–164. [Google Scholar]
- 73.Albahri O.S., Al-Obaidi J.R., Zaidan A.A., Albahri A.S., Zaidan B.B., Salih M.M., et al. Helping doctors hasten COVID-19 treatment: Towards a rescue framework for the transfusion of best convalescent plasma to the most critical patients based on biological requirements via ml and novel MCDM methods. Comput. Methods Programs Biomed. 2020;196 doi: 10.1016/j.cmpb.2020.105617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Rezaei J. Best-worst multi-criteria decision-making method. Omega. 2015;53:49–57. [Google Scholar]
- 75.Kavilal E.G., Venkatesan S.P., Kumar K.H. An integrated fuzzy approach for prioritizing supply chain complexity drivers of an Indian mining equipment manufacturer. Resour. Policy. 2017;51:204–218. [Google Scholar]
- 76.Altuntas F., Gok M.S. The effect of COVID-19 pandemic on domestic tourism: A DEMATEL method analysis on quarantine decisions. Int. J. Hosp. Manag. 2021;92 doi: 10.1016/j.ijhm.2020.102719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Manupati V.K., Ramkumar M., Baba V., Agarwal A. Selection of the best healthcare waste disposal techniques during and post COVID-19 pandemic era. J. Cleaner Prod. 2021;281 doi: 10.1016/j.jclepro.2020.125175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Charnes A., Cooper W.W., Rhodes E. Measuring the efficiency of decision making units. European J. Oper. Res. 1978;2(6):429–444. [Google Scholar]
- 79.Aydin N., Yurdakul G. Assessing countries’ performances against COVID-19 via WSIDEA and machine learning algorithms. Appl. Soft Comput. 2020;97 doi: 10.1016/j.asoc.2020.106792. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Sotoudeh-Anvari A., Najafi E., Sadi-Nezhad S. A new data envelopment analysis in fully fuzzy environment on the base of the degree of certainty of information. J. Intell. Fuzzy Systems. 2016;30(6):3131–3142. [Google Scholar]
- 81.Giannoulis C., Ishizaka A. A web-based decision support system with ELECTRE III for a personalised ranking of British universities. Decis. Support Syst. 2010;48(3):488–497. [Google Scholar]
- 82.Stewart T.J. Relationships between data envelopment analysis and multicriteria decision analysis. J. Oper. Res. Soc. 1996;47(5):654–665. [Google Scholar]
- 83.Zadeh L.A. The concept of a linguistic variable and its application to approximate reasoning—I. Inform. Sci. 1975;8(3):199–249. [Google Scholar]
- 84.Karnik N.N., Mendel J.M., Liang Q. Type-2 fuzzy logic systems. IEEE Trans. Fuzzy Syst. 1999;7(6):643–658. [Google Scholar]
- 85.Torra V. Hesitant fuzzy sets. Int. J. Intell. Syst. 2010;25(6):529–539. [Google Scholar]
- 86.Atanassov K. Intuitionistic fuzzy sets. Fuzzy Sets and Systems. 1986;20:87–96. [Google Scholar]
- 87.Qian G., Wang H., Feng X. Generalized hesitant fuzzy sets and their application in decision support system. Knowl.-Based Syst. 2013;37:357–365. [Google Scholar]
- 88.Cuong B.C., Kreinovich V. Picture fuzzy sets-a new concept for computational intelligence problems. 2013 Third World Congress on Information and Communication Technologies; WICT 2013; IEEE; 2013. pp. 1–6. [Google Scholar]
- 89.Yager R.R. Pythagorean membership grades in multicriteria decision making. IEEE Trans. Fuzzy Syst. 2013;22(4):958–965. [Google Scholar]
- 90.Yager R.R. Generalized orthopair fuzzy sets. IEEE Trans. Fuzzy Syst. 2016;25(5):1222–1230. [Google Scholar]
- 91.Smarandache F. 1998. Neutrosophy: Neutrosophic Probability, Set, and Logic: Analytic Synthesis & Synthetic Analysis. [Google Scholar]
- 92.Mahmood T., Ullah K., Khan Q., Jan N. An approach toward decision-making and medical diagnosis problems using the concept of spherical fuzzy sets. Neural Comput. Appl. 2019;31(11):7041–7053. [Google Scholar]
- 93.Wan S.P., Chen Z.H., Dong J.Y. An integrated interval type-2 fuzzy technique for democratic–autocratic multi-criteria decision making. Knowl.-Based Syst. 2021;214 [Google Scholar]
- 94.Rodriguez R.M., Martinez L., Herrera F. Hesitant fuzzy linguistic term sets for decision making. IEEE Trans. Fuzzy Syst. 2011;20(1):109–119. [Google Scholar]
- 95.Pang Q., Wang H., Xu Z. Probabilistic linguistic term sets in multi-attribute group decision making. Inform. Sci. 2016;369:128–143. [Google Scholar]
- 96.Zadeh L.A. A note on Z-numbers. Inform. Sci. 2011;181(14):2923–2932. [Google Scholar]
- 97.Molodtsov D. Soft set theory—first results. Comput. Math. Appl. 1999;37(4–5):19–31. [Google Scholar]
- 98.Moher D., Liberati A., Tetzlaff J., Altman D.G., Prisma Group Preferred reporting items for systematic reviews and meta-analyses: The PRISMA statement. PLoS Med. 2009;6(7) doi: 10.1371/journal.pmed.1000097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Roldan-Valadez E., Salazar-Ruiz S.Y., Ibarra-Contreras R., Rios C. Current concepts on bibliometrics: a brief review about impact factor, Eigenfactor score, CiteScore, SCImago journal rank, source-normalised impact per paper, H-index, and alternative metrics. Ir. J. Med. Sci. (1971-) 2019;188(3):939–951. doi: 10.1007/s11845-018-1936-5. [DOI] [PubMed] [Google Scholar]
- 100.Meho L.I. Using Scopus’s CiteScore for assessing the quality of computer science conferences. J. Informetrics. 2019;13(1):419–433. [Google Scholar]
- 101.Alsalem M.A., Mohammed R., Albahri O.S., Zaidan A.A., Alamoodi A.H., Dawood K., et al. Rise of multiattribute decision-making in combating COVID-19: A systematic review of the state-of-the-art literature. Int. J. Intell. Syst. 2021 doi: 10.1002/int.22699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.Mardani A., Saraji M.K., Mishra A.R., Rani P. A novel extended approach under hesitant fuzzy sets to design a framework for assessing the key challenges of digital health interventions adoption during the COVID-19 outbreak. Appl. Soft Comput. 2020;96 doi: 10.1016/j.asoc.2020.106613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Ashraf S., Abdullah S. Emergency decision support modeling for COVID-19 based on spherical fuzzy information. Int. J. Intell. Syst. 2020;35(11):1601–1645. doi: 10.1002/int.22262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Ocampo L., Yamagishi K. Modeling the lockdown relaxation protocols of the philippine government in response to the COVID-19 pandemic: An intuitionistic fuzzy DEMATEL analysis. Socio-Econ. Plann. Sci. 2020;72 doi: 10.1016/j.seps.2020.100911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 105.Sharma M., Luthra S., Joshi S., Kumar A. Developing a framework for enhancing survivability of sustainable supply chains during and post-COVID-19 pandemic. Int. J. Logist. Res. Appl. 2020:1–21. [Google Scholar]
- 106.Belhadi A., Kamble S.S., Khan S.A.R., Touriki F.E., Kumar D. Infectious waste management strategy during COVID-19 pandemic in africa: An integrated decision-making framework for selecting sustainable technologies. Environ. Manag. 2020;66(6):1085–1104. doi: 10.1007/s00267-020-01375-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107.Chen T., Lin C.W. Smart and automation technologies for ensuring the long-term operation of a factory amid the COVID-19 pandemic: An evolving fuzzy assessment approach. Int. J. Adv. Manuf. Technol. 2020;111(11):3545–3558. doi: 10.1007/s00170-020-06097-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Mohammed M.A., Abdulkareem K.H., Al-Waisy A.S., Mostafa S.A., Al-Fahdawi S., Dinar A.M., et al. Benchmarking methodology for selection of optimal COVID-19 diagnostic model based on entropy and TOPSIS methods. Ieee Access. 2020;8:99115–99131. [Google Scholar]
- 109.Ashraf S., Abdullah S., Almagrabi A.O. A new emergency response of spherical intelligent fuzzy decision process to diagnose of COVID19. Soft Comput. 2020:1–17. doi: 10.1007/s00500-020-05287-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 110.Requia W.J., Kondo E.K., Adams M.D., Gold D.R., Struchiner C.J. Risk of the Brazilian health care system over 5572 municipalities to exceed health care capacity due to the 2019 novel coronavirus (COVID-19) Sci. Total Environ. 2020;730 doi: 10.1016/j.scitotenv.2020.139144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111.Albahri A.S., Hamid R.A., Albahri O.S., Zaidan A.A. Detection-based prioritisation: Framework of multi-laboratory characteristics for asymptomatic COVID-19 carriers based on integrated entropy–TOPSIS methods. Artif. Intell. Med. 2021;111 doi: 10.1016/j.artmed.2020.101983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 112.Alkan N., Kahraman C. Evaluation of government strategies against COVID-19 pandemic using q-rung orthopair fuzzy TOPSIS method. Appl. Soft Comput. 2021;110 doi: 10.1016/j.asoc.2021.107653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 113.Hezer S., Gelmez E., Özceylan E. Comparative analysis of TOPSIS, VIKOR and COPRAS methods for the COVID-19 regional safety assessment. J. Infect. Public Health. 2021;14(6):775–786. doi: 10.1016/j.jiph.2021.03.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 114.Hosseini S.M., Paydar M.M., Hajiaghaei-Keshteli M. Recovery solutions for ecotourism centers during the Covid-19 pandemic: Utilizing fuzzy DEMATEL and fuzzy VIKOR methods. Expert Syst. Appl. 2021;185 doi: 10.1016/j.eswa.2021.115594. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 115.Das M., Das A., Giri B., Sarkar R., Saha S. Habitat vulnerability in slum areas of India–What we learnt from COVID-19? Int. J. Disaster Risk Reduct. 2021;65 doi: 10.1016/j.ijdrr.2021.102553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 116.Majumdar A., Sinha S.K., Govindan K. Prioritising risk mitigation strategies for environmentally sustainable clothing supply chains: Insights from selected organisational theories. Sustain. Prod. Consum. 2021;28:543–555. doi: 10.1016/j.spc.2021.06.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 117.Saraji M.K., Mardani A., Köppen M., Mishra A.R., Rani P. An extended hesitant fuzzy set using SWARA-MULTIMOORA approach to adapt online education for the control of the pandemic spread of COVID-19 in higher education institutions. Artif. Intell. Rev. 2021:1–26. doi: 10.1007/s10462-021-10029-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 118.Ecer F., Pamucar D. MARCOS technique under intuitionistic fuzzy environment for determining the COVID-19 pandemic performance of insurance companies in terms of healthcare services. Appl. Soft Comput. 2021;104 doi: 10.1016/j.asoc.2021.107199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 119.Ocampo L., Tanaid R.A., Tiu A.M., Selerio E., Jr., Yamagishi K. Classifying the degree of exposure of customers to COVID-19 in the restaurant industry: A novel intuitionistic fuzzy set extension of the TOPSIS-sort. Appl. Soft Comput. 2021;113 doi: 10.1016/j.asoc.2021.107906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 120.Aydin N., Seker S. Determining the location of isolation hospitals for COVID-19 via delphi-based MCDM method. Int. J. Intell. Syst. 2021;36(6):3011–3034. doi: 10.1002/int.22410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 121.Shah S.A.A., Longsheng C., Solangi Y.A., Ahmad M., Ali S. Energy trilemma based prioritization of waste-to-energy technologies: implications for post-COVID-19 green economic recovery in Pakistan. J. Cleaner Prod. 2021;284 doi: 10.1016/j.jclepro.2020.124729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 122.Mohammed T.J., Albahri A.S., Zaidan A.A., Albahri O.S., Al-Obaidi J.R., Zaidan B.B., et al. Convalescent-plasma-transfusion intelligent framework for rescuing COVID-19 patients across centralised/decentralised telemedicine hospitals based on AHP-group TOPSIS and matching component. Appl. Intell. 2021;51(5):2956–2987. doi: 10.1007/s10489-020-02169-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 123.Mishra A.R., Rani P., Krishankumar R., Ravichandran K.S., Kar S. An extended fuzzy decision-making framework using hesitant fuzzy sets for the drug selection to treat the mild symptoms of coronavirus disease 2019 (COVID-19) Appl. Soft Comput. 2021;103 doi: 10.1016/j.asoc.2021.107155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 124.Choudhury S., Majumdar A., Saha A.K., Majumdar P. Evaluating the preparedness of Indian states against COVID-19 pandemic risk: A fuzzy multi-criteria decision-making approach. Risk Anal. 2021 doi: 10.1111/risa.13808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 125.Goker N. A novel integrated intuitionistic fuzzy decision aid for agile outsourcing provider selection: A COVID-19 pandemic-based scenario analysis. Soft Comput. 2021;25(21):13723–13740. doi: 10.1007/s00500-021-06037-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 126.Boyacı A.Ç., Şişman A. Pandemic hospital site selection: A GIS-based MCDM approach employing pythagorean fuzzy sets. Environ. Sci. Pollut. Res. 2021:1–13. doi: 10.1007/s11356-021-15703-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 127.Chai J., Xian S., Lu S. Z-uncertain probabilistic linguistic variables and its application in emergency decision making for treatment of COVID-19 patients. Int. J. Intell. Syst. 2021;36(1):362–402. [Google Scholar]
- 128.Shadeed S., Alawna S. GIS-based COVID-19 vulnerability mapping in the West bank, Palestine. Int. J. Disaster Risk Reduct. 2021;64 doi: 10.1016/j.ijdrr.2021.102483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 129.Ortiz-Barrios M., Borrego-Areyanes A.A., Gómez-Villar I.D., Felice F.De., Petrillo A., Gul M., Yucesan M. A multiple criteria decision-making approach for increasing the preparedness level of sales departments against COVID-19 and future pandemics: A real-world case. Int. J. Disaster Risk Reduct. 2021 [Google Scholar]
- 130.Yao S. Fuzzy-based multi-criteria decision analysis of environmental regulation and green economic efficiency in a post-COVID-19 scenario: The case of China. Environ. Sci. Pollut. Res. 2021:1–27. doi: 10.1007/s11356-021-12647-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 131.Ghorui N., Ghosh A., Mondal S.P., Bajuri M.Y., Ahmadian A., Salahshour S., Ferrara M. Identification of dominant risk factor involved in spread of COVID-19 using hesitant fuzzy MCDM methodology. Results Phys. 2021;21 doi: 10.1016/j.rinp.2020.103811. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 132.Yamagishi K., Ocampo L. Utilizing TOPSIS-sort for sorting tourist sites for perceived COVID-19 exposure. Curr. Issues Tour. 2021:1–11. [Google Scholar]
- 133.Kumar A., Mangla S.K., Kumar P., Song M. Mitigate risks in perishable food supply chains: Learning from COVID-19. Technol. Forecast. Soc. Change. 2021;166 [Google Scholar]
- 134.Petrudi S.H.H., Ahmadi H.B., Rehman A., Liou J.J. Assessing suppliers considering social sustainability innovation factors during COVID-19 disaster. Sustain. Prod. Consumpt. 2021;27:1869–1881. doi: 10.1016/j.spc.2021.04.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 135.Hezam I.M., Nayeem M.K., Foul A., Alrasheedi A.F. COVID-19 vaccine: A neutrosophic MCDM approach for determining the priority groups. Results Phys. 2021;20 doi: 10.1016/j.rinp.2020.103654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 136.Hartanto B.W., Mayasari D.S. Environmentally friendly non-medical mask: An attempt to reduce the environmental impact from used masks during COVID 19 pandemic. Sci. Total Environ. 2021;760 doi: 10.1016/j.scitotenv.2020.144143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 137.Gao Z., Jiang Y., He J., Wu J., Xu J., Christakos G. A study of COVID-19 in the Wuhan, Beijing, Urumqi and Dalian cities based on the regional disease vulnerability index. J. Infect. Public Health. 2021 [Google Scholar]
- 138.Kumar P., Kumar Singh R. Strategic framework for developing resilience in agri-food supply chains during COVID 19 pandemic. Int. J. Logist. Res. Appl. 2021:1–24. [Google Scholar]
- 139.Asadi S., Nilashi M., Abumalloh R.A., Samad S., Ahani A., Ghabban F., et al. Evaluation of factors to respond to the COVID-19 pandemic using DEMATEL and fuzzy rule-based techniques. Int. J. Fuzzy Syst. 2021:1–17. [Google Scholar]
- 140.Paul S.K., Chowdhury P., Moktadir M.A., Lau K.H. Supply chain recovery challenges in the wake of COVID-19 pandemic. J. Bus. Res. 2021;136:316–329. doi: 10.1016/j.jbusres.2021.07.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 141.Alam S.T., Ahmed S., Ali S.M., Sarker S., Kabir G. Challenges to COVID-19 vaccine supply chain: Implications for sustainable development goals. Int. J. Prod. Econ. 2021;239 doi: 10.1016/j.ijpe.2021.108193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 142.Shanker S., Barve A., Muduli K., Kumar A., Garza-Reyes J.A., Joshi S. Enhancing resiliency of perishable product supply chains in the context of the COVID-19 outbreak. Int. J. Logist. Res. Appl. 2021:1–25. [Google Scholar]
- 143.Chen T., Wang Y.C. A calibrated piecewise-linear FGM approach for travel destination recommendation during the COVID-19 pandemic. Appl. Soft Comput. 2021 doi: 10.1016/j.asoc.2021.107535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 144.Palouj M., Adaryani R.L., Alambeigi A., Movarej M., Sis Y.S. Surveying the impact of the coronavirus (COVID-19) on the poultry supply chain: A mixed methods study. Food Control. 2021;126 doi: 10.1016/j.foodcont.2021.108084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 145.Samanci S., Atalay K.D., Isin F.B. Focusing on the big picture while observing the concerns of both managers and passengers in the post-covid era. J. Air Transp. Manag. 2021;90 [Google Scholar]
- 146.Alsalem M.A., Alsattar H.A., Albahri A.S., Mohammed R.T., Albahri O.S., Zaidan A.A., et al. Based on T-spherical fuzzy environment: A combination of FWZIC and FDOSM for prioritising COVID-19 vaccine dose recipients. J. Infect. Public Health. 2021;14(10):1513–1559. doi: 10.1016/j.jiph.2021.08.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 147.Albahri O.S., Zaidan A.A., Albahri A.S., Alsattar H.A., Mohammed R., Aickelin U., et al. Novel dynamic fuzzy decision-making framework for COVID-19 vaccine dose recipients. J. Adv. Res. 2021 doi: 10.1016/j.jare.2021.08.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 148.Albahri O.S., Zaidan A.A., Albahri A.S., Zaidan B.B., Abdulkareem K.H., Al-Qaysi Z.T., et al. Systematic review of artificial intelligence techniques in the detection and classification of COVID-19 medical images in terms of evaluation and benchmarking: Taxonomy analysis, challenges, future solutions and methodological aspects. J. Infect. Public Health. 2020 doi: 10.1016/j.jiph.2020.06.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 149.Si A., Das S., Kar S. Picture fuzzy set-based decision-making approach using Dempster–Shafer theory of evidence and grey relation analysis and its application in COVID-19 medicine selection. Soft Comput. 2021:1–15. doi: 10.1007/s00500-021-05909-9. [DOI] [PMC free article] [PubMed] [Google Scholar] [Retracted]
- 150.Revuelta I., Santos-Arteaga F.J., Montagud-Marrahi E., Ventura-Aguiar P., Caprio D.Di., Cofan F., et al. A hybrid data envelopment analysis—Artificial neural network prediction model for COVID-19 severity in transplant recipients. Artif. Intell. Rev. 2021:1–32. doi: 10.1007/s10462-021-10008-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 151.Mehmood K., Bao Y., Abrar M.M., Petropoulos G.P., Soban A., Saud S., et al. Spatiotemporal variability of COVID-19 pandemic in relation to air pollution, climate and socioeconomic factors in Pakistan. Chemosphere. 2021;271 doi: 10.1016/j.chemosphere.2021.129584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 152.Orji I.J., Ojadi F. Investigating the COVID-19 pandemic’s impact on sustainable supplier selection in the Nigerian manufacturing sector. Comput. Ind. Eng. 2021;160 doi: 10.1016/j.cie.2021.107588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 153.Karmaker C.L., Ahmed T., Ahmed S., Ali S.M., Moktadir M.A., Kabir G. Improving supply chain sustainability in the context of COVID-19 pandemic in an emerging economy: Exploring drivers using an integrated model. Sustain. Prod. Consumpt. 2021;26:411–427. doi: 10.1016/j.spc.2020.09.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 154.Das D., Datta A., Kumar P., Kazancoglu Y., Ram M. Building supply chain resilience in the era of COVID-19: An AHP-DEMATEL approach. Oper. Manag. Res. 2021:1–19. [Google Scholar]
- 155.Mahmoudi A., Javed S.A., Mardani A. Gresilient supplier selection through fuzzy ordinal priority approach: decision-making in post-COVID era. Oper. Manag. Res. 2021:1–25. [Google Scholar]
- 156.Wen Z., Liao H. Capturing attitudinal characteristics of decision-makers in group decision making: application to select policy recommendations to enhance supply chain resilience under COVID-19 outbreak. Oper. Manag. Res. 2021:1–16. [Google Scholar]
- 157.Sharma M., Joshi S., Luthra S., Kumar A. Managing disruptions and risks amidst COVID-19 outbreaks: Role of blockchain technology in developing resilient food supply chains. Oper. Manag. Res. 2021:1–14. [Google Scholar]
- 158.Xiaozhen Z., Mao J., Yanan L. A new computational method based on probabilistic linguistic Z-number with unbalanced semantics and its application to multi-criteria group decision making. IEEE Access. 2020;9:2950–2965. [Google Scholar]
- 159.Bragatto P., Vairo T., Milazzo M.F., Fabiano B. The impact of the COVID-19 pandemic on the safety management in Italian seveso industries. J. Loss Prev. Process Ind. 2021;70 doi: 10.1016/j.jlp.2021.104393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 160.Keršuliene V., Zavadskas E.K., Turskis Z. Selection of rational dispute resolution method by applying new step-wise weight assessment ratio analysis (SWARA) J. Bus. Econ. Manag. 2010;11(2):243–258. [Google Scholar]
- 161.Zavadskas E.K., Turskis Z., Antucheviciene J., Zakarevicius A. Optimization of weighted aggregated sum product assessment. Elektronika Ir Elektrotechnika. 2012;122(6):3–6. [Google Scholar]
- 162.Gabus A., Fontela E. Battelle Geneva Research Center; Geneva, Switzerland: 1972. World Problems, an Invitation to Further Thought Within the Framework of DEMATEL; pp. 1–8. [Google Scholar]
- 163.Brauers W.K.M., Zavadskas E.K. Project management by MULTIMOORA as an instrument for transition economies. Technol. Econ. Dev. Econ. 2010;16(1):5–24. [Google Scholar]
- 164.Stević Ž., Pamučar D., Puška A., Chatterjee P. Sustainable supplier selection in healthcare industries using a new MCDM method: Measurement of alternatives and ranking according to compromise solution (MARCOS) Comput. Ind. Eng. 2020;140 [Google Scholar]
- 165.Zavadskas E.K., Turskis Z. A new additive ratio assessment (ARAS) method in multicriteria decision-making. Technol. Econ. Dev. Econ. 2010;16(2):159–172. [Google Scholar]
- 166.Dempster A.P. Classic Works of the Dempster-Shafer Theory of Belief Functions. Springer; Berlin, Heidelberg: 2008. Upper and lower probabilities induced by a multivalued mapping; pp. 57–72. [Google Scholar]
- 167.Shafer G. Princeton University Press; 1976. A Mathematical Theory of Evidence. [Google Scholar]
- 168.Ataei Y., Mahmoudi A., Feylizadeh M.R., Li D.F. Ordinal priority approach (OPA) in multiple attribute decision-making. Appl. Soft Comput. 2020;86 [Google Scholar]
- 169.Xu Z. Intuitionistic preference relations and their application in group decision making. Inform. Sci. 2007;177(11):2363–2379. [Google Scholar]
- 170.Acharya U.R., Bhat P.S., Iyengar S.S., Rao A., Dua S. Classification of heart rate data using artificial neural network and fuzzy equivalence relation. Pattern Recognit. 2003;36(1):61–68. [Google Scholar]
- 171.Opricovic S., Tzeng G.H. Compromise solution by MCDM methods: A comparative analysis of VIKOR and TOPSIS. European J. Oper. Res. 2004;156(2):445–455. [Google Scholar]
- 172.Huang J.J., Tzeng G.H., Liu H.H. International Conference on Multiple Criteria Decision Making. Springer; Berlin, Heidelberg: 2009. A revised VIKOR model for multiple criteria decision making-the perspective of regret theory; pp. 761–768. [Google Scholar]
- 173.Asadabadi M.R., Chang E., Saberi M. Are MCDM methods useful? A critical review of analytic hierarchy process (AHP) and analytic network process (ANP) Cogent Eng. 2019;6(1) [Google Scholar]
- 174.Llamazares B. An analysis of the generalized TODIM method. European J. Oper. Res. 2018;269(3):1041–1049. [Google Scholar]
- 175.Saaty T.L. A scaling method for priorities in hierarchical structures. J. Math. Psych. 1977;15(3):234–281. [Google Scholar]
- 176.e Costa C.A.B., Vansnick J.C. A critical analysis of the eigenvalue method used to derive priorities in AHP. European J. Oper. Res. 2008;187(3):1422–1428. [Google Scholar]
- 177.Çakır O. On the order of the preference intensities in fuzzy AHP. Comput. Ind. Eng. 2008;54(4):993–1005. [Google Scholar]
- 178.Mikhailov L. Deriving priorities from fuzzy pairwise comparison judgements. Fuzzy Sets and Systems. 2003;134(3):365–385. [Google Scholar]
- 179.Zhü K. Fuzzy analytic hierarchy process: Fallacy of the popular methods. European J. Oper. Res. 2014;236(1):209–217. [Google Scholar]
- 180.Saaty T.L., Tran L.T. On the invalidity of fuzzifying numerical judgments in the analytic hierarchy process. Math. Comput. Modelling. 2007;46(7–8):962–975. [Google Scholar]
- 181.Tuljak-Suban D., Bajec P. The influence of defuzzification methods to decision support systems based on fuzzy AHP with scattered comparison matrix: Application to 3PLP selection as a case study. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 2018;26(03):475–491. [Google Scholar]
- 182.Bhat S.A., Kumar A. An integrated fuzzy approach for prioritizing supply chain complexity drivers of an Indian mining equipment manufacturer by Kavilal, EG, Venkatesan, SP, Kumar, KDH, [Resour. Policy 51 (2017) 204–218]: Suggested modification. Resour. Policy. 2018;57:278–280. [Google Scholar]
- 183.Pei Z. A note on the TOPSIS method in MADM problems with linguistic evaluations. Appl. Soft Comput. 2015;36:24–35. [Google Scholar]
- 184.Dymova L., Sevastjanov P., Tikhonenko A. An approach to generalization of fuzzy TOPSIS method. Inform. Sci. 2013;238:149–162. [Google Scholar]
- 185.Pan X., Wang Y. An enhanced technique for order preference by similarity to ideal solutions and its application to renewable energy resources selection problem. Int. J. Fuzzy Syst. 2021;23(4):1087–1101. [Google Scholar]
- 186.Meniz B. A note on fuzzy cosine function. Int. J. Fuzzy Syst. 2021:1–2. [Google Scholar]
- 187.Triantaphyllou E., Lin C.T. Development and evaluation of five fuzzy multiattribute decision-making methods. Internat. J. Approx. Reason. 1996;14(4):281–310. [Google Scholar]
- 188.Wang Y.M., Elhag T.M. Fuzzy TOPSIS method based on alpha level sets with an application to bridge risk assessment. Expert Syst. Appl. 2006;31(2):309–319. [Google Scholar]
- 189.Wang W. On fuzzy TOPSIS method based on alpha level sets. J. Intell. Fuzzy Systems. 2017;33(6):4067–4076. [Google Scholar]
- 190.Kuo M.S., Tzeng G.H., Huang W.C. Group decision-making based on concepts of ideal and anti-ideal points in a fuzzy environment. Math. Comput. Modelling. 2007;45(3–4):324–339. [Google Scholar]
- 191.Wang Y.M., Luo Y., Hua Z.S. A note on group decision-making based on concepts of ideal and anti-ideal points in a fuzzy environment. Math. Comput. Modelling. 2007;46(9–10):1256–1264. [Google Scholar]
- 192.Yatsalo B., Korobov A., Martínez L. From MCDA to fuzzy MCDA: Violation of basic axiom and how to fix it. Neural Comput. Appl. 2021;33(5):1711–1732. [Google Scholar]
- 193.Chou Y.C., Sun C.C., Yen H.Y. Evaluating the criteria for human resource for science and technology (HRST) based on an integrated fuzzy AHP and fuzzy DEMATEL approach. Appl. Soft Comput. 2012;12(1):64–71. [Google Scholar]
- 194.Pandey A., Kumar A. Commentary on evaluating the criteria for human resource for science and technology (HRST) based on an integrated fuzzy AHP and fuzzy DEMATEL approach. Appl. Soft Comput. 2017;51:351–352. [Google Scholar]
- 195.Dytczak M., Ginda G. Is explicit processing of fuzzy direct influence evaluations in DEMATEL indispensable? Expert Syst. Appl. 2013;40(12):5027–5032. [Google Scholar]
- 196.Huang G.H., Baetz B.W., Patry G.G. Grey integer programming: An application to waste management planning under uncertainty. European J. Oper. Res. 1995;83(3):594–620. [Google Scholar]
- 197.Wang X., Huang G. Violation analysis on two-step method for interval linear programming. Inform. Sci. 2014;281:85–96. [Google Scholar]
- 198.Giachetti R.E., Young R.E. A parametric representation of fuzzy numbers and their arithmetic operators. Fuzzy Sets and Systems. 1997;91(2):185–202. [Google Scholar]
- 199.Klir G.J. Fuzzy arithmetic with requisite constraints. Fuzzy Sets and Systems. 1997;91(2):165–175. [Google Scholar]
- 200.Grzegorzewski P., Mrówka E. Trapezoidal approximations of fuzzy numbers. Fuzzy Sets and Systems. 2005;153(1):115–135. [Google Scholar]
- 201.Hafezalkotob A., Hafezalkotob A. A novel approach for combination of individual and group decisions based on fuzzy best-worst method. Appl. Soft Comput. 2017;59:316–325. [Google Scholar]
- 202.Rahimi S., Hafezalkotob A., Monavari S.M., Hafezalkotob A., Rahimi R. Sustainable landfill site selection for municipal solid waste based on a hybrid decision-making approach: Fuzzy group BWM-multimoora-GIS. J. Cleaner Prod. 2020;248 [Google Scholar]
- 203.Fedrizzi M., Krejčí J. A note on the paper fuzzy analytic hierarchy process: Fallacy of the popular methods. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 2015;23(06):965–970. [Google Scholar]
- 204.Oussalah M. On the compatibility between defuzzification and fuzzy arithmetic operations. Fuzzy Sets and Systems. 2002;128(2):247–260. [Google Scholar]
- 205.Dubois D. The role of fuzzy sets in decision sciences: Old techniques and new directions. Fuzzy Sets and Systems. 2011;184(1):3–28. [Google Scholar]
- 206.Saaty T.L. There is no mathematical validity for using fuzzy number crunching in the analytic hierarchy process. J. Syst. Sci. Syst. Eng. 2006;15(4):457–464. [Google Scholar]
- 207.Liu X. Parameterized defuzzification with maximum entropy weighting function—another view of the weighting function expectation method. Math. Comput. Modelling. 2007;45(1–2):177–188. [Google Scholar]
- 208.Van Leekwijck W., Kerre E.E. Defuzzification: Criteria and classification. Fuzzy Sets and Systems. 1999;108(2):159–178. [Google Scholar]
- 209.Li H., Wang W., Fan L., Li Q., Chen X. A novel hybrid MCDM model for machine tool selection using fuzzy DEMATEL, entropy weighting and later defuzzification VIKOR. Appl. Soft Comput. 2020;91 [Google Scholar]
- 210.Dubois D., Prade H. Operations on fuzzy numbers. Internat. J. Systems Sci. 1978;9(6):613–626. [Google Scholar]
- 211.Mizumoto M., Tanaka K. Some properties of fuzzy sets of type 2. Inf. Control. 1976;31(4):312–340. [Google Scholar]
- 212.Hanss M. The transformation method for the simulation and analysis of systems with uncertain parameters. Fuzzy Sets and Systems. 2002;130(3):277–289. [Google Scholar]
- 213.Ngan S.C. A concrete reformulation of fuzzy arithmetic. Expert Syst. Appl. 2021;167 [Google Scholar]
- 214.Lodwick W.A., Dubois D. Interval linear systems as a necessary step in fuzzy linear systems. Fuzzy Sets and Systems. 2015;281:227–251. [Google Scholar]
- 215.Moore R.E., Kearfott R.B., Cloud M.J. Society for Industrial and Applied Mathematics; 2009. Introduction to Interval Analysis. [Google Scholar]
- 216.Hanss M. Springer-Verlag; Berlin Heidelberg: 2005. Applied Fuzzy Arithmetic. [Google Scholar]
- 217.Sevastjanov P., Dymova L. A new method for solving interval and fuzzy equations: Linear case. Inform. Sci. 2009;179(7):925–937. [Google Scholar]
- 218.Allahviranloo T., Babakordi F. Algebraic solution of fuzzy linear system as: AX + BX=Y. Soft Comput. 2017;21(24):7463–7472. [Google Scholar]
- 219.Piegat A., Landowski M. Is the conventional interval-arithmetic correct. J. Theor. Appl. Comput. Sci. 2012;6(2):27–44. [Google Scholar]
- 220.Piegat A., Pluciński M. Universal algebraic solution of the interval linear system: AX+ BX=Y. Procedia Comput. Sci. 2021;192:526–532. [Google Scholar]
- 221.Boukezzoula R., Galichet S., Foulloy L., Elmasry M. Extended gradual interval (EGI) arithmetic and its application to gradual weighted averages. Fuzzy Sets and Systems. 2014;257:67–84. [Google Scholar]
- 222.Qiyas M., Abdullah S., Ashraf S., Aslam M. Utilizing linguistic picture fuzzy aggregation operators for multiple-attribute decision-making problems. Int. J. Fuzzy Syst. 2020;22(1):310–320. [Google Scholar]
- 223.Appadoo S.S., Makhan M., Kumar A. Commentary on utilizing linguistic picture fuzzy aggregation operators for multiple-attribute decision-making problems. Int. J. Fuzzy Syst. 2021:1–4. [Google Scholar]
- 224.Tao Z., Han B., Chen H. On intuitionistic fuzzy copula aggregation operators in multiple-attribute decision making. Cogn. Comput. 2018;10(4):610–624. [Google Scholar]
- 225.Kaur A., Kumar A. Commentary on on intuitionistic fuzzy copula aggregation operators in multiple-attribute decision making. Cogn. Comput. 2020;12(4):891–895. [Google Scholar]
- 226.Mishra A., Kumar A., Appadoo S.S. Commentary on D-intuitionistic hesitant fuzzy sets and their application in multiple attribute decision making. Cogn. Comput. 2021:1–2. [Google Scholar]
- 227.Wei G., Alsaadi F.E., Hayat T., Alsaedi A. Picture 2-tuple linguistic aggregation operators in multiple attribute decision making. Soft Comput. 2018;22(3):989–1002. [Google Scholar]
- 228.Ju Y., Ju D., Wang A. A note on picture 2-tuple linguistic aggregation operators in multiple attribute decision making. Soft Comput. 2020;24(6):3937–3941. [Google Scholar]
- 229.Piegat A., Landowski M. Horizontal membership function and examples of its applications. Int. J. Fuzzy Syst. 2015;17(1):22–30. [Google Scholar]
- 230.Dahooie J.H., Hajiagha S.H.R., Farazmehr S., Zavadskas E.K., Antucheviciene J. A novel dynamic credit risk evaluation method using data envelopment analysis with common weights and combination of multi-attribute decision-making methods. Comput. Oper. Res. 2021;129 [Google Scholar]
- 231.Sotoudeh-Anvari A., Sadjadi S.J., Sadi-Nezhad S. Theoretical drawbacks in fuzzy ranking methods and some suggestions for a meaningful comparison: An application to fuzzy risk analysis. Cybern. Syst. 2017;48(8):551–575. [Google Scholar]
- 232.Kordi M., Brandt S.A. Effects of increasing fuzziness on analytic hierarchy process for spatial multicriteria decision analysis. Comput. Environ. Urban Syst. 2012;36(1):43–53. [Google Scholar]
- 233.Mosadeghi R., Warnken J., Tomlinson R., Mirfenderesk H. Comparison of fuzzy-AHP and AHP in a spatial multi-criteria decision making model for urban land-use planning. Comput. Environ. Urban Syst. 2015;49:54–65. [Google Scholar]
- 234.Chen X., Fang Y., Chai J., Xu Z. Does intuitionistic fuzzy analytic hierarchy process work better than analytic hierarchy process? Int. J. Fuzzy Syst. 2021:1–16. [Google Scholar]
- 235.Chan H.K., Sun X., Chung S.H. When should fuzzy analytic hierarchy process be used instead of analytic hierarchy process? Decis. Support Syst. 2019;125 [Google Scholar]
- 236.Pamučar D., Puška A., Stević Ž., Ćirović G. A new intelligent MCDM model for HCW management: The integrated BWM–MABAC model based on d numbers. Expert Syst. Appl. 2021;175 [Google Scholar]