Multi-eGO: An in silico lens to look into protein aggregation kinetics at atomic resolution

Significance

Alzheimer’s and Parkinson’s diseases are incurable pathologies associated with the aberrant aggregation of specific proteins into amyloid fibrils. Understanding the mechanisms leading to protein aggregation, by characterizing the structures of the oligomeric species populated in the process, would have a tremendous impact on the design of therapeutic molecules. We propose that a structure-based molecular dynamics simulations approach can allow the aggregation kinetics of thousands of monomers to be followed at high resolution. Having shown that simulations can describe the aggregation of a Transthyretin amyloidogenic peptide, we demonstrate how they can provide a wealth of structural information. We foresee that integrating the latter with the many techniques developed to study protein aggregation will support the design of molecules to modulate amyloidogenesis.

Abstract

Protein aggregation into amyloid fibrils is the archetype of aberrant biomolecular self-assembly processes, with more than 50 associated diseases that are mostly uncurable. Understanding aggregation mechanisms is thus of fundamental importance and goes in parallel with the structural characterization of the transient oligomers formed during the process. Oligomers have been proven elusive to high-resolution structural techniques, while the large sizes and long time scales, typical of aggregation processes, have limited the use of computational methods to date. To surmount these limitations, we here present multi-eGO, an atomistic, hybrid structure-based model which, leveraging the knowledge of monomers conformational dynamics and of fibril structures, efficiently captures the essential structural and kinetics aspects of protein aggregation. Multi-eGO molecular dynamics simulations can describe the aggregation kinetics of thousands of monomers. The concentration dependence of the simulated kinetics, as well as the structural features of the resulting fibrils, are in qualitative agreement with in vitro experiments carried out on an amyloidogenic peptide from Transthyretin, a protein responsible for one of the most common cardiac amyloidoses. Multi-eGO simulations allow the formation of primary nuclei in a sea of transient lower-order oligomers to be observed over time and at atomic resolution, following their growth and the subsequent secondary nucleation events, until the maturation of multiple fibrils is achieved. Multi-eGO, combined with the many experimental techniques deployed to study protein aggregation, can provide the structural basis needed to advance the design of molecules targeting amyloidogenic diseases.

Amyloid fibril formation is a highly specific self-assembly process, requiring a large degree of similarity between the interacting amino acid sequences (1). Amyloids, resulting from the uncontrolled transition of normally soluble proteins, were originally found to be associated with neurodegenerative diseases (2, 3). More recently, they have also been associated with several physiologic functions (4, 5). Amyloid fibrils share a cross-β architecture in which β-strands are oriented perpendicularly to the fibril axis, allowing the formation of a dense intermolecular hydrogen bond network with sidechains contributing to both intramolecular and intermolecular interactions (6, 7). In vitro, the amyloid fold seems to be accessible to a large number of, if not all, proteins (ordered or disordered) or even short sequences of amino acids (8, 9). Thermodynamic considerations, indeed, suggest that native proteins are metastable species under physiological conditions, with the global free-energy minimum corresponding to their amyloidogenic state (10).

Protein aggregation into amyloid fibrils is an inherently dynamic process. Many interconverting species of differing sizes and structures can be populated over multiple time scales (11). The description of amyloid fibril formation thus requires an understanding of the properties of the end states, that is, monomers and fibrils, and of the different oligomeric species that are transiently populated in between. Remarkably, in diseases like Parkinson’s, Alzheimer’s, type 2 diabetes mellitus, and cardiac amyloidosis, some oligomeric species may be the primary pathogenic agents (12–16). Furthermore, toxic oligomers have been found in model proteins and associated to specific physicochemical properties like size and hydrophobicity, although it is not yet clear whether these are relevant for all amyloidogenic diseases (17–19). Structural approaches based on solid-state NMR (ssNMR) and cryogenic electron microscopy (cryo-EM) have revealed the atomic structures of amyloid fibrils formed by different proteins in diverse conditions (6, 7, 20–22). The aggregation process itself can only be studied at very low resolution, by aggregation kinetics assays, where experimental conditions are tuned to induce the in-solution interconversion of protein monomers into amyloid fibrils. Seeds obtained by previously formed fibrils can also be employed to catalyze the interconversion (23).

Chemical kinetics analyses provide a framework to dissect the microscopic mechanisms at play in fibril formation (24). Aggregation is described by a network of microscopic processes including primary nucleation and elongation, as well as secondary nucleation processes, such as fragmentation and surface-induced nucleation. By globally fitting multiple, accurate, aggregation kinetic traces obtained for multiple initial monomer concentrations, it is possible to estimate the rates for the different microscopic processes and use these to interpret the macroscopic observations. Such analyses have highlighted the preference of proteins associated with amyloidogenic diseases to aggregate through secondary nucleation mechanisms, whereas physiological amyloids are proposed to be mainly controlled by primary nucleation (25, 26). Drug design strategies have been implemented, based on the kinetic modulation of such mechanisms (27). Nonetheless, despite its power, chemical kinetics fails to provide detailed structural information on the species at play during the process.

Given the inherently transient and dynamic nature of the species populated in an assembly process, molecular dynamics (MD) simulations naturally complement current experimental approaches (27, 28). Aggregation kinetics simulations have mainly been employed to characterize the early events in the oligomerization of a few peptides at high concentrations, because of the combination of challenges resulting from system sizes and relevant time scales. Implicit solvent models have been employed to mitigate these problems and have allowed the oligomerization of 20 monomers of Aβ40 and Aβ42 over hundreds of nanoseconds to be studied (29). Simulating larger systems over longer time scales requires coarse-grain (CG) models. Notably, fibrils may, in fact, be formed by tens of thousands of monomers.

CG simulations, with simplified interactions and geometries, including HP models (30), tube models (31), and lattice models (32, 33), as well as other minimalistic approaches (34, 35), have been used to make hypotheses on the general principles of protein aggregation, also informing chemical kinetics models (36). A recent overview can be found in ref. 28. In the field of protein folding simulations, the most adopted CG models are structure based (SB), also known as Gō models (37–41), recently reviewed in ref. 38. SB models are an implementation of the principle of minimal frustration [or the folding funnel (42)]: Attractive interactions are defined only between amino acids or atoms that are close in space in the native crystal state; consequently, the minimum energy configuration is the native crystal configuration. This allows folding and unfolding transitions to be efficiently studied, by dramatically decreasing the cost of evaluating interactions and accelerating the overall diffusion in conformational space; for example, the folding time of a protein can be rescaled from milliseconds to hundreds of nanoseconds.

In keeping with the observation that the amyloid structure is the global free-energy minimum of a protein at high concentration (10), we here describe multi-eGO, a hybrid SB model that includes nonbonded interactions derived from both the dynamics of the soluble protein and the structure of the amyloid fibril, and transferable bonded interactions that are optimized to reproduce the results of state-of-the-art explicit solvent molecular force fields. While SB models, including more than one reference structure and/or hybrid terms, have been employed to study differences in protein folding pathways of homolog proteins (37–41), large conformational changes (43–45), metamorphic proteins (46, 47), and the folding upon binding of disordered proteins with different partners (48, 49), here we show that multi-eGO can be used to follow the aggregation of thousands of monomers, as a function of their initial concentration, at high resolution. Our results are qualitatively in agreement with experiments and enable the structural investigation of the aggregation of proteins into amyloid fibrils.

Results

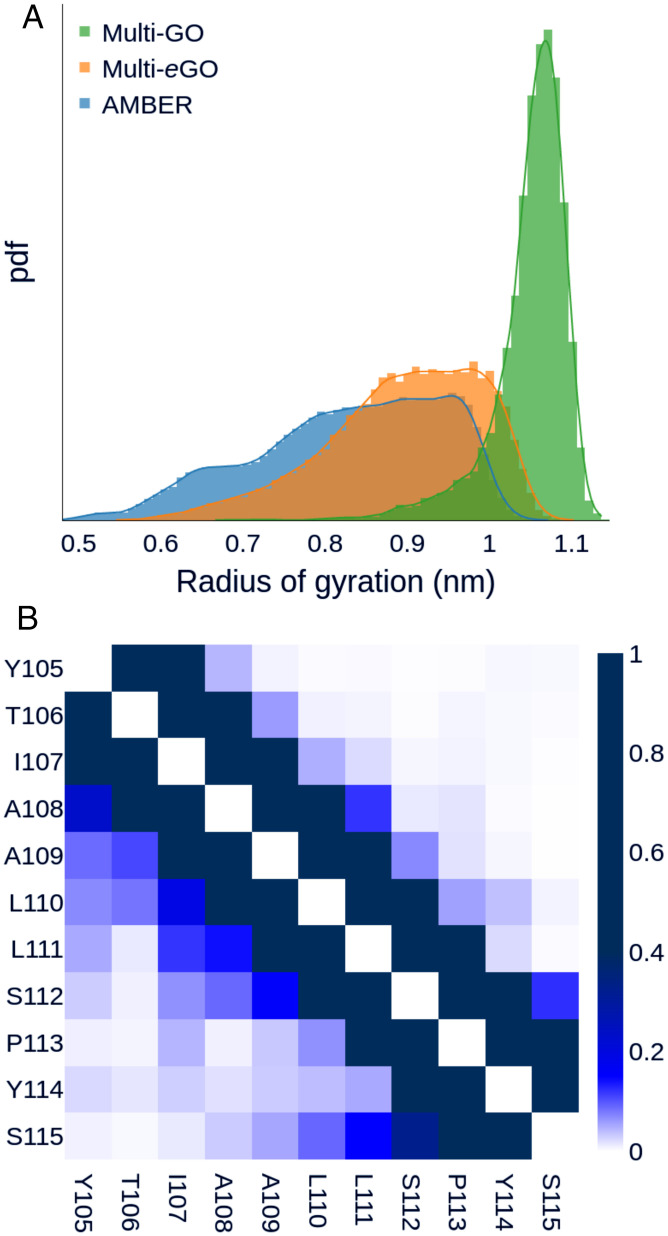
To develop multi-eGO, we used the Transthyretin 105–115 amyloidogenic peptide (TTR_105–115) (50, 51). Transthyretin is a well-studied amyloidogenic protein responsible for both sporadic and genetic cardiac and systemic amyloidosis (52). TTR_105–115 has often been used as a model system to study aggregation, and three amyloid polymorphisms have been determined at atomic resolution by a combination of multiple techniques including ssNMR and cryo-EM (20). NMR analysis of monomeric TTR_105–115 in solution indicates that it primarily populates a random-coil structure with a low percentage of turns or helical elements (53). Multi-eGO was built to include information from the structure or the dynamics of the end states and uses them to infer the properties of the intermediate oligomeric states (SI Appendix, Fig. S1). To have a realistic conformational ensemble reference of monomeric TTR_105–115, we performed an explicit solvent MD simulation using the a99SB-disp force field (54). This simulation well represented the behavior of TTR_105–115 in solution, showing a broad flexibility and sporadic turns, as reported by the radius of gyration distribution and the per-residue contact probability map in Fig. 1, as well as by a secondary structures populations analysis (SI Appendix, Fig. S2A), in agreement with previous NMR chemical shifts measurements (53).

Fig. 1.

TTR_105–115 peptide monomer dynamics. (A) Gyration radius distribution of TTR_105–115 peptide conformational ensemble according to multi-GO (green), multi-eGO (orange), and a99SB-disp (blue) simulations. The multi-GO distribution describes an open conformation with a single peak at 1.07 nm. The a99SB-disp simulation shows multiple peaks over a broad range of values. The multi-eGO distribution is shifted toward more extended conformations than a99SB-disp but still shows a broad range of values in qualitative agreement with the former. (B) Per-residue probability contact map for the a99SB-disp (Lower Left) and multi-eGO (Upper Right) simulations.

Multi-eGO Reproduces the Conformational Dynamics of TTR_105–115 in Solution.

Following previous studies on metamorphic proteins (46, 47), we initially defined the multi-GO SB force field, at all heavy atom (nonhydrogens) resolution, as a combination of terms obtained from two reference structures (Materials and Methods), namely, the protein in its native monomeric state (extracting TTR_105–115 coordinates from Protein Data Bank [PDB] 4TLT, corresponding to the crystal structure of TTR) and the amyloid fibril (PDB 2M5K) (SI Appendix, Fig. S1). A multi-GO simulation of a TTR_105–115 monomer explored only extended configurations with an average radius of gyration of 1.05 nm, in comparison with 0.83 nm of the a99SB-disp one (Fig. 1A) and the conformational ensemble did not show long range contacts (SI Appendix, Fig. S3A). The multi-GO ensemble described above did not capture the conformational freedom of the monomeric state, and consequently may not capture that of early intermediate oligomeric states.

To increase the descriptive power of the model, we introduced multi-eGO as a hybrid transferable/SB model (Materials and Methods). The most relevant differences are that all bonded interactions, and, in particular, proper dihedral angles, are transferable, while nonbonded interactions are learned from a reference simulation for the monomeric state, that is, the a99SB-disp force field simulation introduced above, and a reference amyloid fibril structure (PDB 2M5K). Remarkably, while the multi-GO simulation explored only extended configurations, the multi-eGO model could better recapitulate TTR_105–115 dynamics in solution, with an average radius of gyration of 0.90 nm. The contact probability map for a99SB-disp and multi-eGO, shown in Fig. 1B, as well as the secondary structures populations analysis in SI Appendix, Fig. S2A, indicate that multi-eGO can also qualitatively describe the intramolecular transient interactions of the peptide.

A qualitative comparison between the interaction energies of the multi-GO and multi-eGO TTR_105–115 models was obtained, summing all the native pairs strengths for all pairs of amino acids (SI Appendix, Fig. S3B). This showed limited differences in the interaction among residues between the two models. This is expected, as they are both trained on the same fibril structure. This analysis suggests that the transferable bonded interactions of multi-eGO are key to improve the agreement of the model with the a99SB-disp simulation.

Multi-eGO Can Simulate TTR_105–115 Aggregation.

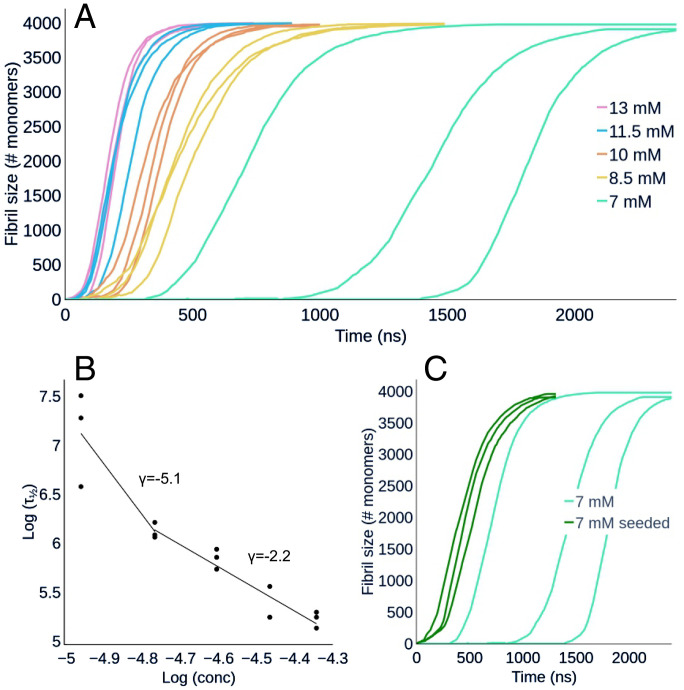
Using multi-eGO, a total of 15 simulations (each involving 4,000 TTR_105–115 monomers) as a triplicate of five different concentrations, between 7 and 13 mM, were produced (SI Appendix, legends for Datasets S1 and S2). The resulting aggregation kinetics are shown in Fig. 2A as the number of monomers forming assemblies, from decamers to larger ones, at a given time. It should be noted that the time scale of the simulations is only nominal, and comparisons with experimental data should consider a scaling factor. Simulations displayed sigmoidal concentration-dependent kinetics, where an increase in monomer concentration resulted in a reduction of the lag phase. We also observed that the variability of the curves increased inversely with the initial monomer concentration (55). From the resulting curves, we obtained the half-time, τ_1/2, shown in Fig. 2B, and the growth rate, r, as the slope of the straight line fitting the region of the curve around τ_1/2 (SI Appendix, Fig. S4). The double log plot of τ_1/2 as a function of concentration (Fig. 2B) showed a bilinear trend with a change of slope, the scaling exponent γ, at concentrations lower than 8.5 mM, suggesting that, at high monomer concentration, a dominant aggregation mechanism becomes saturated (56).

Fig. 2.

(A) Simulated aggregation kinetics. Curves represent the number of monomers involved in an aggregate of at least 10 monomers as a function of nominal simulation time. See also SI Appendix, legends for Movies S1 and S2. (B) Log–log plot of the half-times, τ_1/2, as a function of the initial monomer concentration. The points are fitted with two straight lines in the range 7 mM to 8.5 mM and 8.5 mM to 13 mM. (C) Aggregation kinetics of seeded and unseeded 7-mM simulations. Curves represent the number of monomers involved in an aggregate of at least 10 monomers as a function of nominal simulation time. The addition of the seeds reduces τ_1/2 and makes it less variable compared to the unseeded simulations, leaving the slope of the growth is unaffected. See also SI Appendix, legend for Movie S3.

To test the ability of multi-eGO to capture differences between seeded and unseeded aggregation kinetics, we also performed three seeded simulations at 7 mM by adding a 10-monomer oligomer seed, obtained from previous 13-mM simulations (compare Multi-eGO Can Provide Structural Details for TTR_105–115 Aggregation Kinetics, in the following). As shown in Fig. 2C, the addition of the seed led to a marked decrease of τ_1/2 and a reduction of its variability. The observed growth rate r, instead, remained the same as for the unseeded simulations performed at the same concentration (i.e., 7 mM).

Multi-eGO TTR_105–115 Simulations Can Form Polymorphic Fibrils.

The 18 simulations performed at five different concentrations yielded a total of 41 distinct fibrils. These fibrils grew in length from 163 Å to 515 Å, with an average length of 360 Å (Table 1 and SI Appendix, Table S1). All fibrils displayed the expected cross-β topology with a parallel and in-register stacking of chains in the same β-sheet as shown in Fig. 3. The average distance between β-strands in the cross β-sheet was 4.7 Å. Facing β-sheets were antiparallel and shifted by 2.5 Å, resulting in the even-numbered sidechains of one peptide interacting with the odd-numbered sidechains of the two opposite peptides. According to previous nomenclature (20), we define a protofilament as a structure made up of two antiparallel β-sheets; the further addition of two β-sheets in a protofilament determines a filament (Fig. 3A). The β-sheet content in a filament was shown to vary from 4 to 17, with an average of 10. Furthermore, filaments that grew in the peptide chain direction through interactions between the N- and C-terminal residues (Fig. 3B), could form a fibril. This head-to-tail interaction resulted from the Y105 sidechain interacting with both the S115 carboxyl group and the Y105 sidechain of the facing β-sheet. The number of filaments in a fibril varied from two to six, with an average of four. Mature fibrils displayed a twist per monomer between −0.1° and −0.85°, measured as the torsion angle between two vectors obtained from Y105-Cα and S115-Cα carbons of subsequent molecules in the same β-sheet. Single filaments displayed a more pronounced twist of −5° compared to mature fibrils (Fig. 3). At higher concentration, we saw the formation of more fibrils, indicating that more nuclei are produced than at lower concentration (SI Appendix, Fig. S5). Since the monomer number was fixed at 4,000, the fibrils grown at higher concentration were shorter in length than the ones obtained at lower concentration (Table 1 and SI Appendix, Table S1). At higher concentration, we also observed fibrils adhering together (Fig. 3C). Again, given the fixed and relatively small number of monomers, some protofilaments were not able to become fibrils, due to monomer depletion. We did not observe any specific differences in the fibrils formed at 7 mM in seeded and unseeded simulations.

Table 1.

Summary of the main structural features of the fibrils discussed in this work

Source	Number of fibrils	Length (Å)	Number of β-sheets in filaments	Number of filaments in fibril	Twist (deg)
13 mM	16	163 to 368	4 to 10	2 to 5	−0.18 to −0.73
11.5 mM	9	210 to 390	5 to 13	2 to 6	−0.23 to −0.85
10 mM	6	170 to 415	4 to 9	2 to 6	−0.2 to −0.79
8.5 mM	4	260 to 515	6 to 14	2 to 4	−0.15 to −0.54
7 mM	3	435 to 480	7 to 17	4 to 6	−0.11 to −0.48
7 mM seeded	3	443 to 485	13 to 14	5	−0.10 to −0.80
ssNMR model			4	2 to 4	−0.85
TEM*			4	3 to 8	−0.71 to −0.81

The first six rows indicate fibrils formed in silico in our multi-eGO simulations; ssNMR is for the fibrils corresponding to PDB codes 2M5K, 2M5M, and 3ZPK; and TEM are those observed in vitro in this work.

^*Values for TEM are estimates; SI Appendix, Table S2.

Fig. 3.

(A) A filament model observed at the end of a simulation. Colors indicate the five different β-sheets composing the filament. (B) Top and side view of a mature fibril with colors indicating the different filaments. From the top view, it is possible to see a peptide which is about to attach to the fibril and a protofilament which is perpendicular to the main fibril. (C) Multiple mature fibrils (each represented with a different color) interacting with each other from one of the 13-mM simulations.

Compared to the reference model determined by ssNMR and cryo-EM (20), the only remarkable difference is that our fibrils do not display any wet cavity within filaments. The cavity in the reference model accommodates structured water molecules that interact with exposed sidechains. In our model, all sidechains in a filament are tightly packed; therefore, we also observed a variable number of β-sheets in a filament, whereas the reference model always contained four. Indeed, there is evidence of such variations (57, 58). The reference model illustrates a structural polymorphism, based on the number of filaments, from doublet to quadruplet. In our simulations, we saw the same polymorphism but extended to six filaments in a single fibril.

Finally, we compared the multi-eGO and multi-GO aggregation kinetics by performing four multi-GO simulations of TTR_105–115 aggregation as function of the concentration (SI Appendix, Fig. S2B). Multi-GO quickly formed aggregates at concentrations, between 2 and 0.5 mM, that are lower than those used in multi-eGO simulations and experiments, that is, 10 mM to 20 mM (53). Furthermore, the multi-GO amyloid fibrils grew laterally instead of elongating (SI Appendix, Fig. S2C), indicating that multi-GO cannot correctly capture the TTR_105–115 aggregation process.

TTR_105–115 In Vitro Aggregation Experiments Recapitulate Multi-eGO Simulations.

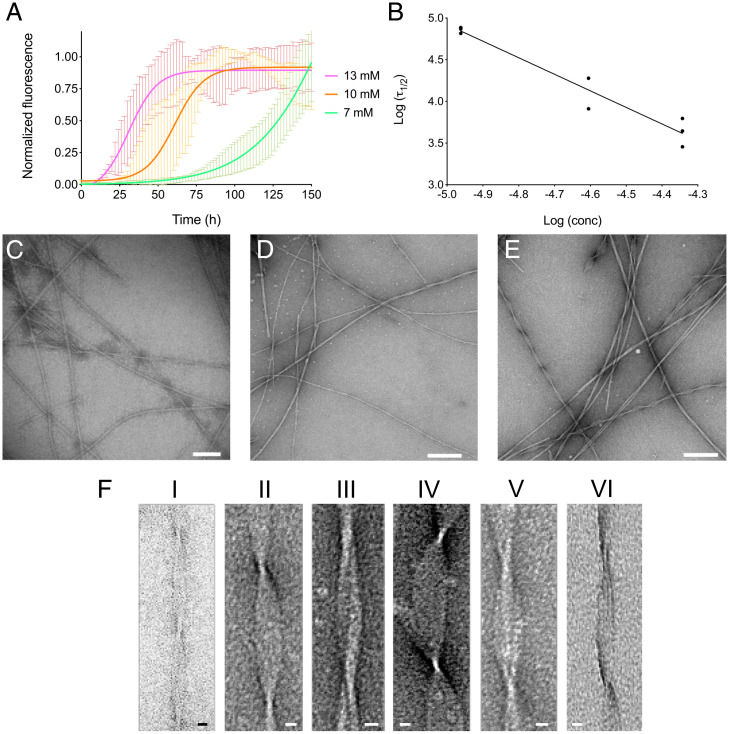
To validate the in silico aggregation kinetics, we performed aggregation assays monitored by Thioflavin T (ThT) fluorescence (Fig. 4). The TTR_105–115 peptide was incubated at 37 °C at different concentrations (i.e., 13, 10, and 7 mM), and ThT fluorescence was monitored over 150 h. ThT fluorescence increased over time, indicating (Fig. 4A) concentration-dependent aggregation kinetics. The lag phase at 13 mM was considerably shorter compared to at 10 mM or 7 mM. The fluorescence plateau was reached faster in the most concentrated samples, whereas, at the lowest concentration tested (i.e., 7mM), the plateau was not observed during the overall incubation time. The mean values of three independent experiments were subjected to nonlinear regression analysis, using a Boltzmann sigmoidal equation. From the regression, we derived the experimental τ_1/2 of 33.7 ± 4.3 h, 62.0 ± 16.6 h, and 125.7 ± 10.2 h for 13, 10, and 7 mM, respectively. Fig. 4B shows a linear correlation between peptide concentrations and half-times in a double log plot, with the slope γ comparable to that obtained from simulations in the range 8.5 mM to 13 mM (namely, −2.0 and −2.2 for the experiments and simulations, respectively; compare Fig. 2B). This is of note given the relative simplicity of our model and the fact that it does not include any specific information about the kinetics of the process.

Fig. 4.

TTR peptide aggregation kinetics in vitro. (A) Aggregation kinetics of the TTR_105–115 peptide at 13, 10, and 7 mM are shown in magenta, orange, and green, respectively. TTR peptide at 37 °C were obtained by monitoring ThT fluorescence. The mean value of three independent experiments analyzed by linear regression using Boltzmann sigmoidal equation is reported. (B) Log–log plot of the in vitro half-times, τ_1/2, as a function of the initial monomer concentration. (C–E) Electron micrographs of fibrils formed by TTR_105–115 peptide incubated at 13 mM (C), 10 mM (D), or 7 mM (E) at 37 °C for 150 h. (Scale bars, 100 nm, C; 200 nm, D and E.) (F) Representative TEM images of the six main fibrillar morphologies. The detailed structural parameters of each morphology are reported in SI Appendix, Table S2. (Scale bars: 10 nm.)

The aggregates of the TTR_105–115 peptide obtained by the aggregation kinetics experiments were negatively stained and analyzed by transmission electron microscopy (TEM). As reported in Fig. 4, we observed remarkable polymorphism in all conditions tested. Morphological analysis identified six main different types of structures (Fig. 4 C–E and SI Appendix, Table S2). The mean width at the cross-over is 37 ± 4 Å, as previously observed by Fitzpatrick et al. (20). The fibrils cross-over in the six polymorphs ranges from 1,041 ± 24 Å to 1,185 ± 43 Å; the diameter varies considerably, ranging from 115 ± 11 Å to 326 ± 21 Å. Representative pictures of each identified morphology are reported in Fig. 4F, and the main fibril parameters are summarized in SI Appendix, Table S2. Notably, the observed widths between cross-overs correspond to multiples of the peptide chain length, suggesting the presence of up to eight aligned filaments (SI Appendix, Table S2).

Multi-eGO Can Provide Structural Details for TTR_105–115 Aggregation Kinetics.

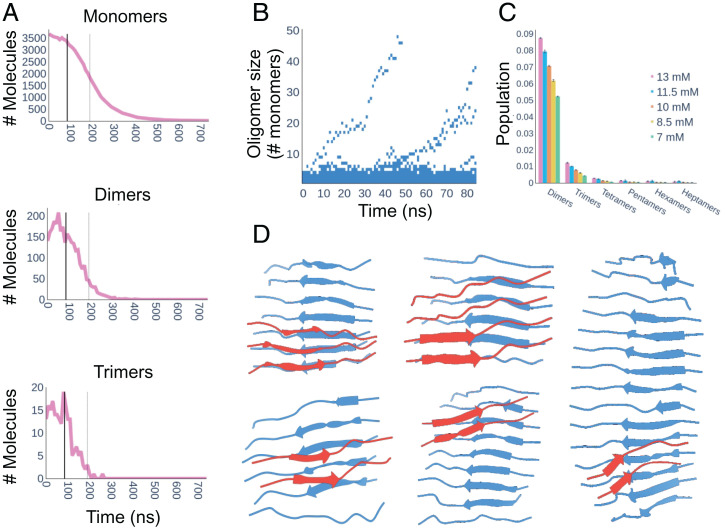
Having shown that multi-eGO could simulate the aggregation of TTR_105–115 from monomers to fibrils, with structural and kinetic features compatible with experimental data, it was possible to observe the structures populated along the self-assembly process in detail. In Fig. 5A and SI Appendix, Fig. S6, the number of monomers, dimers, and trimers in our aggregation kinetics are shown as a function of time. We observed that the number of free monomers displayed a sigmoidal behavior, symmetric with respect to that of the fibril size. The number of dimers and trimers showed, instead, a noisy but relatively constant trend until the end of the lag phase (t_lag), defined as the intersection between a straight line, tangent to the aggregation kinetic curve at τ_1/2 with slope r, and the time axis, and quickly dropped after this time. This suggests that, once fibrils start to grow, most monomers contributed to the fibril growth instead of forming new oligomers, and oligomers formed before t_lag dissolve over time.

Fig. 5.

(A) Number of monomers, dimers, and trimers over time of the first 13-mM simulation. The t_lag (solid thick line) and τ_1/2 (dashed thin line) are reported in each plot. The monomer decrease is symmetrical compared to fibril growth (compare Fig. 2A). The number of dimers and trimers is relatively constant until t_lag and quickly drops after this time. (B) Time-resolved evolution of oligomer order of the first 13-mM simulation before t_lag. (C) Oligomer order populations in the time window from zero to t_lag and averaged over the three replicates. The different colors represent the different concentrations, while the error bars represent the SD over the three simulations. In this time window, only monomers and dimers are significantly populated (C); nonetheless, one can observe the emergence of two fibrils (B). (D) Five representative structures of primary nuclei extracted from five different simulations. The β-sheets colored in blue, representing the initial oligomer, are stabilized as primary nuclei by interacting with the second β-sheet, colored in red.

The time-resolved distribution of oligomer sizes of the first 13-mM simulation before t_lag (SI Appendix, Fig. S7 for all simulations) is shown in Fig. 5B. This analysis allows the emergence and growth of primary nuclei to be followed and suggests that fibrils stem from primary nuclei composed of around 10 monomers. Assuming the simulations prior to t_lag at equilibrium, and thus averaging over this time window, we observed how, at all concentrations, dimers and trimers were the most represented oligomeric species, with populations in the 5 to 10% and 0.5 to 2% range, respectively. Higher-order oligomers were scarcely populated, stressing the need to simulate large numbers of monomers to study aggregation (compare Fig. 5C). Interestingly, apart from their populations, oligomers do not show other concentration-dependent properties (SI Appendix, legend for Dataset S3). In SI Appendix, Fig. S8 are shown the distributions of the radius of gyration, and the average β-populations per residue, of oligomers, ranging from dimers to decamers, populated in multi-eGO aggregation kinetics before t_lag. The analyses indicate that dimers, trimers, and tetramers are extended and disordered; around 20% of pentamers can form intermolecular β-sheets, and this fraction increases with higher oligomer orders. The increase in β-structure is also reflected by the distributions of the radius of gyrations that become less and less broadly distributed (SI Appendix, Fig. S8).

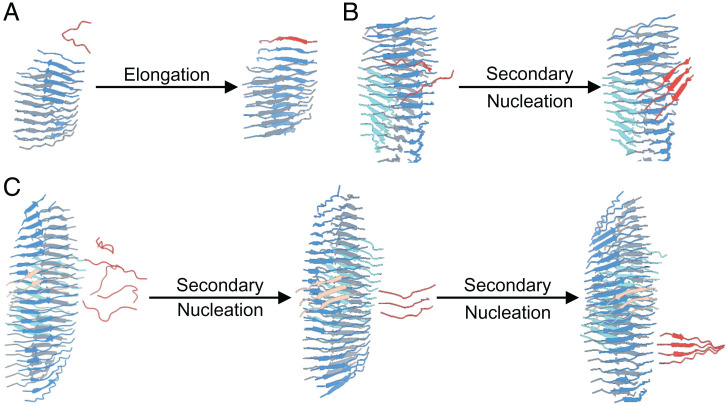
The structures of oligomers involved in primary nucleation are shown in Fig. 5D. All primary nuclei displayed two antiparallel β-sheets. Observing the trajectory, we were able to describe their formation. Free monomers spontaneously assemble into small oligomers, forming the first β-sheet. Once the β-sheet reaches a size of five to six monomers, other monomers interact with the β-sheet surface, triggering the formation of a second β-sheet docked by sidechain/sidechain interactions. Once a primary nucleus is formed, its growth can be followed. Each β-sheet provides two ends for elongation, so primary nuclei have four ends. With regards to elongation, peptides generally dock at the N terminus toward the C terminus as shown in Fig. 6A. A generally highly twisted, cross-β protofilament exposes sidechains and termini for secondary nucleation, but we observed that only the sidechain faces could trigger the formation of further β-sheets, thus forming a filament (Fig. 6B). The addition of each β-sheet decreased the twist. Filaments, made up of at least four β-sheets, can further growth, both through their sidechains faces (Fig. 6B) and through their termini, as exemplified in Fig. 6C. Growth can occur by N to N terminus (head-to-head) as well as N to C terminus (head-to-tail) interactions. Importantly, a newly N to C β-sheet can grow into a new protofilament, while a newly formed N to N β-sheet must firstly convert into an N to C sheet before further growth can occur. A fibril is thus formed when two filaments are linked head to tail. Remarkably, the formation of new β-sheets always occurs with monomers sliding on the surface before eventually docking. At high monomer concentration, we subsequently observed interactions between fibrils. Fragmentation events were not observed in any simulations.

Fig. 6.

Fibril growth secondary processes. (A) Elongation: the docking of a single monomer in red at one end of a β-sheet in blue. (B and C) Surface-induced secondary nucleation can occur both on the front surface of a β-sheet (B) and on the side surface (C). Peptides can slide on the surface before locking. At least three peptides are required to form a secondary nucleus.

To test whether the described mechanism is consistent with the macroscopic kinetics shown in Fig. 2, we performed a chemical kinetics analysis of our simulated data using Amylofit (59–61). Simulations could only be globally fitted using a “multistep secondary nucleation, unseeded model” as shown in SI Appendix, Fig. S9. This is compatible with the positive curvature with an increased slope at lower concentration displayed by τ_1/2 in a double log plot (compare Fig. 2B) that can be interpreted as the saturation of secondary nucleation (56) at high monomer concentration (e.g., all the catalytic fibril surface is occupied by monomers). Furthermore, our seeded simulations did not show variations in the rate constant r (compare Fig. 2C), supporting the hypothesis that secondary nucleation is a multistep process with a first step (monomer attachment on the surface) that is concentration dependent and a second step (monomers rearrangement on the surface) that is concentration independent (56). Amylofit analysis correlates with our observations where the addition of molecules on the cross-β surface implies the exploration of different conformations prior to latching on to and starting to form a new oligomer. Globally, the TTR_105–115 aggregation process described by our simulations is consistent with the hierarchy proposed by Fitzpatrick et al. (20).

Discussion

Amyloidogenesis is the result of an out-of-equilibrium, concentration-dependent process; thus, it cannot be easily followed by high-resolution structural biology techniques (6). Indeed, while NMR, X-ray crystallography, and cryo-EM have been instrumental to investigating, at high resolution, the early steps associated with protein misfolding, and the structures of resulting amyloid fibrils, they have only provided low-resolution information about the transient oligomers populated along the process (62, 63). In this respect, most of the fundamental mechanical understanding of protein aggregation is based on the combination of multiple low-resolution techniques, in particular, aggregation kinetics studied by ThT fluorescence, and chemical kinetics analysis (24).

MD simulations could provide the resolution, in time and space, to observe the emergence of oligomers, nuclei, and fibrils from a solution of monomeric proteins (64). This would greatly assist the understanding of the determinants of the different aggregation mechanisms at play, the observation of the effect of mutations, and, subsequently, the SB design of drugs targeting specific oligomeric species. Unfortunately, computer power is far from being able to enable such simulations, using conventional classical mechanics transferable force fields (64). Simulations have thus been employed to study the oligomerization of a few peptides (29, 65) and the interactions of peptides with preformed fibrils (66), and, in most cases, to understand the determinants of protein aggregation by only studying protein monomers (67–72). These studies, while valuable, fall short in providing indications about oligomers that are, by their nature, extremely unlikely and short lived. Alternatively, CG simulations have been used to investigate the general principles of protein aggregation, but without providing system specific information (28, 30–36).

In this study, we set out to develop a simplified force field that can allow protein aggregation, comprising thousands of monomers, to be studied with current state-of-the-art computing resources. Our force field builds on the success of SB (Gō) models to study protein folding and binding (38, 41, 48, 73, 74). The multi-eGO force field introduced here is 1) at atomic resolution (excluding hydrogens); 2) locally transferable, with bonded and excluded volume interactions derived from a transferable force field or optimized consequently; and 3) structure (or ensemble) based using multiple references and symmetrized so that, once an interacting pair is defined, this can be formed both intramolecularly as well as intermolecularly. We have shown, in Fig. 1, that this combination can describe the conformational ensemble of a disordered peptide, in qualitative agreement with more-accurate conventional explicit solvent MD simulations. Most importantly, multi-eGO can describe the aggregation kinetics of thousands of monomers, showing concentration-dependent features that are compatible with experimental data (Figs. 2–4). Indeed, the comparison of the scaling exponents γ derived from experimental and simulated τ_1/2 data (Fig. 2B and Fig. 4B) showed comparable values, confirming the robustness of the model, with a difference observed only at the lowest concentration. TEM morphological analysis of the fibrils highlighted a remarkable degree of polymorphism. Specifically, we classified six main fibril morphologies with highly variable cross-over and width (Fig. 4F and SI Appendix, Table S2). These data indicate that each fibril is formed by three to eight filaments, in agreement with in silico observed fibrils (Fig. 3, Table 1, and SI Appendix, Tables S1 and S2). On the contrary, all morphologies share a mean width at the cross-over compatible with previous measurements and associated with a hydrated cavity (20) that is not observed in silico, indicating that future improvements should try to better account for solvation effects that may only be indirectly captured by our native pair interactions (41).

Simulations can be subsequently used to formulate hypotheses on the oligomeric species populated along the process and provide a structural model for the mechanisms of primary and secondary nucleation. Interestingly, we can show how primary nuclei are on the order of 10 monomers and organized into two opposed β-sheets (Fig. 5D). These nuclei are populated for less than 0.1% in the lag phase of the kinetics, in comparison to dimers and trimers that are populated around 10 and 1%, respectively (Figs. 5 A–C and SI Appendix, Figs. S6–S8). This indicates how relevant it is to simulate aggregation using large monomer numbers. Oligomer populations drop immediately after the formation of the first nuclei. Following the growth of primary nuclei, our model also shows that elongation occurs through the preferential binding of the N-terminal region of the peptide (Fig. 6). Once a protofilament is formed, secondary nucleation can be observed. Secondary nucleation arises, initially, by the formation of nuclei on the exposed sidechains of the filament surface; then monomers can slide over the surface and eventually dock into it, triggering the formation of an additional β-sheet layer (Fig. 6). Once at least four β-sheet layers are formed, we observe additional secondary nucleation events, catalyzed by interactions with the N and C termini (Fig. 6). Secondary nucleation contributes to overall fibril growth, but it does not lead to independent oligomer formations that detach to form new protofibrils. We hypothesize that this is a size effect, resulting from the relatively small number of monomers, that are shortly depleted by fibril formation. Nonetheless, using 4,000 monomers allowed us to observe multiple primary and secondary nucleation events, with secondary nucleation remaining the main effect that contributes to the exponential growth of the fibril mass, suggesting that this number may be large enough to recapitulate the key processes occurring during the aggregation process. Notably, the mechanisms inferred by applying a chemical kinetics analysis on the simulated aggregation kinetics agrees with what was observed in the simulation (SI Appendix, Fig. S9), suggesting that multi-eGO may complement and support experimental chemical kinetics models to provide a high-resolution time-resolved description of the microscopic processes at play during aggregation (24, 36).

In conclusion, we present the development of multi-eGO, an SB model tailored to study amyloid-type protein aggregation. The model is promising in describing, at least qualitatively, the spontaneous aggregation of monomers into amyloid fibrils, as a function of the initial monomer concentration, thus providing a structural picture of the populated oligomeric species and of the associated aggregation mechanisms. We anticipate that our model can be combined with methodologies that allow the integration of simulations with the many complementary experimental techniques deployed to study protein aggregation (75–78). Eventually, the computational efficiency of multi-eGO, combined with the availability of amyloid fibrils structures (79, 80), and of already run—and publicly available—long MD simulations for disease relevant proteins (81, 82), will improve our understanding of the mechanisms and the associated oligomeric structures at play in different pathogenic and nonpathogenic self-assembly processes.

Materials and Methods

MD simulations in this work were performed with GROMACS (83). Models’ parameterization and preparation was developed in python. All scripts, including ad hoc analysis tools, are freely available on GitHub (https://github.com/emalacs/multi-eGO/tree/TTR_paper). Simulations are available on Zenodo (SI Appendix, legends for Datasets S1–S3).

Multi-GO: A Multireference Gō-Like Model for Protein Aggregation.

Multi-GO is a multireference SB force field, at all heavy atom (nonhydrogens) resolution, defined as a combination of terms obtained from two reference structures, namely, the protein in its native monomeric state and the amyloid fibril. This was originally developed to study metamorphic proteins (46, 47) using SMOG software (84). In this model, distances between covalently bonded atoms, as well as angles formed by three subsequent covalently bonded atoms, are derived only from the monomeric structure, because they describe the local geometry that is generally independent from the specific configuration. Dihedral angles are defined as in SMOG but obtained from both structures and halving the force constant to account for the double counting. Native pairs are obtained from both reference structures following SMOG rules; if two atoms are in contact in both structures, then the distance is defined as the minimum distance. All native pairs are symmetrized so that, if atom i and atom j are in contact in one reference structure, they can interact irrespectively of whether the two atoms belong to the same monomer or to two different monomers; such an approach has been successfully employed to describe domain swapped dimers (85, 86), and is needed to make intramolecular and intermolecular interactions indistinguishable.

Multi-eGO: An Enhanced Gō-Like Model for Protein Aggregation.

In contrast to multi-GO, the multi-eGO force field is partitioned so that, while nonbonded interactions are SB, bonded interactions are, instead, transferable. The multi-eGO Hamiltonian, given a reference monomer simulation X_m and a reference amyloid structure X_a, is defined as

$$\begin{array}{c}H\left(X;X_m,X_a\right)={\displaystyle \sum }_{\mathit{bonds}}{K}_r{\left(r-r_0\right)}^2+{\displaystyle \sum }_{\mathit{angles}}{K}_q{\left(\theta -{\theta }_0\right)}^2\\ +{\displaystyle \sum }_{\mathit{improper}}{K}_{\varphi }\left[1+\cos \left(n\varphi -{\varphi }_0\right)\right]+{\displaystyle \sum }_{\mathit{dihedrals}}{K}_{\psi }\left[1+\cos \left(n\psi -{\psi }_0\right)\right]\\ +{\displaystyle \sum }_{\mathit{native}}{\epsilon }_n\left[{\left(\frac{r_{ij,m,a}}{r_{ij}}\right)}^{12}-2{\left(\frac{r_{ij,m,a}}{r_{ij}}\right)}^6\right]+{\displaystyle \sum }_{\mathit{others}}\frac{C_{ij}^{(12)}}{r_{ij}^{12}},\end{array}$$

where the parameters for bonds, angles, and improper and proper dihedrals are obtained from a transferable force field, specifically, GROMOS54A7 (87), that is a united atom force field already optimized without nonpolar hydrogens. Thus, the local geometry no longer depends on the monomeric structure as in multi-GO. Proper dihedrals terms describing the ϕ and ψ backbone angles were reoptimized as describe in the next section. Interactions between native pairs are defined for pairs of atoms farther than one residue along the sequence (if they belong to the same molecule) and closer than 5.5 Å in either the native monomeric simulation or in the amyloid structure. The interactions strength for native pairs is either ε_n = ε when a pair is derived from the amyloid structure or heuristically scaled as

$${\epsilon }_n= \epsilon \left( 1-\frac{\ln P}{\ln P_{\text{threshold}}}\right)$$ [1]

when derived from a reference MD simulation. Here P is the fraction of frames in the simulation where the pair of atoms is closer than 5.5 Å, and P_threshold is a minimum fraction that should be considered, set to 0.09 in this work. This approach has the merit of giving an interaction strength equal to ε if the contact population is one, as for a single structure, and to smoothly go to zero when reaching the chosen threshold. The interaction length r_ij,m,a is defined as either the average pair distance calculated over the P frames or the pair distance in the amyloid structure. If a native pair is defined multiple times, then only the one associated with the shorter r_ij,m,a distance is retained. Care must be taken so that, if a native interaction is defined between two atoms belonging to the same or the neighbor residue, this interaction applies only intermolecularly; otherwise, once a pair interaction is defined in its length and strength, these parameters are the same irrespective of whether the interaction is formed intermolecularly or intramolecularly. Finally, excluded volume interactions for all other pairs, that is, all pairs of atoms that are not native and that are separated by more than three consecutive covalent bonds (i to i+4), are defined as in the GROMOS54A7 force field. Among the excluded volume interactions, we include all i to i+4 interactions involving a backbone nitrogen; in this case, the C⁽¹²⁾ Lennard-Jones parameter is scaled down by a factor of 0.15. This is needed to effectively account for the missing amide hydrogen, and it is critical to avoid nonphysical configurations. Of note is that, in multi-eGO, masses are correctly set to include hydrogens; also, since force constants obtained from GROMOS54A7 are tuned to work at room temperature, that is, ∼300 K, ε, the reference interaction strength between all native pairs, is the only free parameter to be set in a system-dependent manner.

Multi-eGO Backbone Dihedrals Optimization.

In the multi-eGO Hamiltonian, the intramolecular interactions between atoms belonging to consecutive amino acids are described only by transferable terms. Therefore, a dipeptide simulated with multi-eGO should closely mimic the conformational freedom of a dipeptide simulated at room temperature using a transferable force field in explicit solvent. Due to the SB nonbonded addition, parameters for the proper dihedral angles have been optimized building on the former hypothesis. Alanine, glycine, and proline dipeptides were simulated using CHARMM22* (88) and TIP3P (89) at 300 K for 1 µs each, and the resulting Ramachandran distribution was set as our target.

The same dipeptides were simulated using multi-eGO, initially setting the force constant K of the potential V_D describing proper dihedrals for the backbone ϕ and ψ angles to zero. V_D is defined as $V_D(\vartheta )=K(1+\cos (n\vartheta -{\varphi }_0))$, with force constant K, multiplicity n, and phase ϕ_0.

Target and multi-eGO Ramachandran distributions are then compared calculating the following scoring function S (i.e., the cross-entropy):

$$\mathcal{S}=P(T)\log \frac{P(T)}{P(E)},$$

where P(E) and P(T) are the multi-eGO and target Ramachandran distributions. To optimize the parameters K, n, and ϕ₀ for the proper dihedral angles, we then followed an iterative procedure combining a Monte Carlo (MC) optimization followed by MD (90, 91). In detail, the effect of a given choice of the parameters is estimated by analytically reweighting the last multi-eGO MD simulations as

$$w\left(\phi ,\psi \right)=\exp \left[-\frac{(V_D^i\left(\phi \right)+V_D^i\left(\psi \right))-(V_D^{i-1}\left(\phi \right)+V_D^{i-1}\left(\psi \right))}{k_{B}T}\right],$$

where Vⁱ_D is the potential energy from the ith iteration written as the sum of multiple proper dihedral terms, k_B is the Boltzmann constant, and T is the temperature of the MD simulation. Optimal parameters are searched by MC under the constraint that the effective information N_eff, calculated over the N configurations generated by the last MD, as

$${\text{N}}_{\mathit{eff}}=\frac{{\left[{{\displaystyle \sum }}_{i=1}^N{w}_i\right]}^2}{{{\displaystyle \sum }}_{i=1}^N{w}_i^2},$$

is greater than 0.6. This allows choosing parameters that do not dramatically alter the starting distribution. A new MD simulation is then performed with the chosen parameters, and the procedure is repeated until convergence of the scoring function (90, 91).

Data Availability

MD simulation trajectories data have been deposited in Zenodo [DOI: 10.5281/zenodo.6125995 (92), DOI: 10.5281/zenodo.6125424 (93), and DOI: 10.5281/zenodo.6414572 (94)].