Significance
Natural selection enriches a population with the best-adapted phenotypes. But collective behaviors can also shape a population’s phenotype composition, even without selection. We study this in the context of collective migration of bacteria, in which the spatial arrangement of individuals by their chemotaxis abilities determines which individuals keep up with the migrating group. Since this spatial organization is environment-dependent, we find that a slow loss of low-performing phenotypes enables an isogenic population to nongenetically adapt its phenotype composition to migrate in changing environments. An important part of this adaptation strategy is the time scale on which individuals with new phenotypes are produced. Nongenetic inheritance provides a way to tune this time scale and may be widespread among microbes.
Keywords: collective behavior, nongenetic diversity, nongenetic inheritance, bet-hedging, bacterial chemotaxis
Abstract
Collective behaviors require coordination among a group of individuals. As a result, individuals that are too phenotypically different from the rest of the group can be left out, reducing heterogeneity, but increasing coordination. If individuals also reproduce, the offspring can have different phenotypes from their parent(s). This raises the question of how these two opposing processes—loss of diversity by collective behaviors and generation of it through growth and inheritance—dynamically shape the phenotypic composition of an isogenic population. We examine this question theoretically using collective migration of chemotactic bacteria as a model system, where cells of different swimming phenotypes are better suited to navigate in different environments. We find that the differential loss of phenotypes caused by collective migration is environment-dependent. With cell growth, this differential loss enables migrating populations to dynamically adapt their phenotype compositions to the environment, enhancing migration through multiple environments. Which phenotypes are produced upon cell division depends on the level of nongenetic inheritance, and higher inheritance leads to larger composition adaptation and faster migration at steady state. However, this comes at the cost of slower responses to new environments. Due to this trade-off, there is an optimal level of inheritance that maximizes migration speed through changing environments, which enables a diverse population to outperform a nondiverse one. Growing populations might generally leverage the selection-like effects provided by collective behaviors to dynamically shape their own phenotype compositions, without mutations.
Collective behaviors enable groups to perform tasks that an individual cannot, but they require coordination (1–4). Therefore, even when collectives can accommodate individual heterogeneity, they often reduce it by removing some phenotypes from the population (1, 5). At the same time, isogenic populations with nongenetic diversity produce new phenotypes by reproducing (6–8), which can replace lost phenotypes. How do these processes of removal and production of phenotypes balance, and how do they affect collective performance of the population?
Collective migration of chemotactic bacteria is a powerful model system for studying the interaction of collective behaviors and growth. Groups of Escherichia coli can migrate collectively by consuming an attractant cue in their environment, creating a traveling gradient that they chase (5, 9–27). Experiments have recently shown that this process leads to directed range expansion of the population and can increase the overall population’s growth rate, relative to undirected expansion, by maintaining a larger fraction of the population in exponential growth (21, 28).
Even isogenic populations of E. coli exhibit a range of behavioral phenotypes (5, 29)—quantified, for example, by the fraction of time a cell spends tumbling, or tumble bias (30, 31)—which climb gradients at different speeds (32). We showed that these diverse phenotypes can migrate together by spatially sorting along the traveling gradient they create, matching individual chemotaxis ability to the local gradient steepness so that all individuals migrate at approximately the same speed (5). However, this compensatory mechanism is imperfect: The concentration of attractant at the back of the group drops below the detection limit of the cells’ receptors (21, 33–35), causing low-performing phenotypes located there to slowly fall behind (5). Thus, collective migration gradually removes these low performers.
Those experiments were performed in liquid, where cells with low tumble bias climb static attractant gradients the fastest (32, 36). However, bacteria encounter other natural environments (37), such as soil and animal hosts. In porous media, in particular, experiments indicate that cells with intermediate tumble bias navigate best (12, 16, 18, 19). Theory (38) and agent-based simulations (39) suggest that this is because cells that tumble infrequently (low tumble bias) get stuck in traps, whereas cells that tumble too frequently (high tumble bias) move very little during each run. Cells with intermediate tumble frequency balance these two competing effects to diffuse and perform chemotaxis effectively. Thus, individual and collective chemotaxis in environments of different porosity require different swimming behaviors.
If collective migration reduces diversity over time, how can populations leverage their multiple behavioral phenotypes to migrate effectively in both liquid and porous environments? One solution may be the generation of individuals with new phenotypes. Recent experiments have shown that a substantial portion of behavioral variability in E. coli populations is generated by imperfect inheritance of phenotype upon cell division (8). While daughter-cell phenotypes are correlated with those of their mothers, they are not identical. Thus, cell divisions provide a way to replenish phenotypes lost during collective behaviors.
Here, we use a generalized Keller–Segel model (10) to quantitatively study how collective migration and growth balance to determine the population’s phenotype composition and performance in multiple environments. By specifically removing low performers in each environment, we predict that collective behaviors interact with growth to dynamically adapt the population composition to the collective task. We find that a key parameter in this balance is the level of phenotypic inheritance. While higher inheritance enriches the population with high performers for the current environment, which increases migration speed, it comes at the cost of slower responsiveness to new environments. Finally, this trade-off leads to an optimal level of inheritance that maximizes average migration speed in varying environments and enables a diverse population to outperform a nondiverse one. Thus, the tension between collective behavior and individuality may generally balance with growth to enable diverse populations to dynamically and nongenetically shape their own compositions of phenotypes to match the demands of collective tasks.
Results
Collective Migration Differentially Removes Behavioral Phenotypes in an Environment-Dependent Manner.
To quantitatively study how the conflict between collective behavior and individuality shapes migrating bacterial populations, we extended the classic Keller–Segel model (10) to include multiple behavioral phenotypes, finite sensitivity for attractants, and cell growth (Methods). In this model, cells of different tumble bias, , climb gradients with drift speeds that depend on their chemotactic performance (36), and they move randomly with diffusivity .
For liquid environments, we previously showed that, despite differences in chemotactic abilities, cells of different phenotypes, are able to migrate together by spatially organizing themselves by performance, (5) (Fig. 1A; reproduced from ref. 5). However, the mapping from phenotype to performance depends on the porosity of the environment in which the cells swim. The logical, but previously unknown, consequence of this is that phenotypes should spatially organize in an environment-dependent manner during group migration. Furthermore, by placing low performers at the back, we expect that collective migration removes whichever phenotypes perform poorly in the current environment.
Fig. 1.
Collective migration differentially removes behavioral phenotypes in an environment-dependent manner. (A) Experimental data from ref. 5. Two isogenic populations with different distributions of phenotypes () travel together in liquid by spontaneously sorting themselves within the migrating group. High-performing (low-; blue) cells are in front, where the traveling gradient is shallow, and low-performing (high-; red) cells are in back, where the traveling gradient is steep, equalizing chemotactic drift speed within the group. Cells located at the back are at a higher risk of falling behind. Reprinted from ref. 5, which is licensed under CC BY 4.0. (B) The chemotactic performance of each phenotype, quantified by , depends on the physical properties of the environment in which it swims. The highest-performing phenotypes in liquid (green) and porous (orange) environments are different. (C) Schematic: Since cells in the group sort by performance , the spatial organization of phenotypes is different in different environments. (D) Since and spatial organization are environment-dependent, so is the differential loss of phenotypes. Phenotype composition of the migrating group in two simulations, in liquid (green; D, Left) and porous (orange; D, Right) environments. Black lines indicate the initial phenotype compositions. Each colored line corresponds to a snapshot in time, with lighter color corresponding to later time. Group migration removes different phenotypes in each environment.
To test these predictions, we modeled chemotaxis in porous media using a biophysical model for cell diffusion developed by Licata et al. (38). We took to be closely related to (Fig. 1B and SI Appendix) because both arise from cells’ run-and-tumble motility (21, 22, 35). To isolate the effect of collective migration on the dynamics of the migrating group’s phenotype composition, we first conducted simulations in which the cells did not grow.
Simulations confirmed our predictions (schematic in Fig. 1C and simulation results in SI Appendix, Figs. S1 and S2): Phenotypes in the migrating groups were organized differently in liquid and porous environments, but they always sorted by performance, . As a result of this different spatial organization, the phenotypes that fell behind the migrating group differed in each case, with high- cells falling behind in liquid and low- cells falling behind in porous media. To quantify this environment-dependent loss of cells based on chemotactic performance, we derive in SI Appendix a semianalytical expression for how fast cells fall behind, or “leak” out of, the migrating group:
| [1] |
Here, is the number of cells traveling in the group at time , is the time-dependent migration speed, is the cells’ sensitivity for the attractant, and is the average chemotactic performance among phenotypes located at the (moving) back edge of the group, . Individual phenotypes fall behind at rates set by their relative abundance at (SI Appendix). Due to the spatial organization of phenotypes by performance, this expression reveals that the total flux with which cells fall behind the migrating group is set by the lowest-performing phenotypes traveling.
Over time, this differential loss of phenotypes shifts the composition of the group from its initial condition toward individuals that are high-performing in each environment (Fig. 1D). These composition changes do not occur due to differences in growth or death. Instead, collective migration leaves behind phenotypes from the traveling group that perform poorly in the current environment.
Collective Migration with Growth Dynamically Adapts the Population’s Phenotype Composition to the Current Environment.
To investigate how growth and loss of cells balance during collective migration, we needed a model of cell growth. Modeling growth with diversity requires specifying which phenotypes are produced when a cell divides—that is, the extent to which daughter cells nongenetically inherit the phenotypes of their mothers (8). Imperfect inheritance may arise due to stochasticity in partitioning chemotaxis-related proteins and organelles between the two daughter cells at the time of cell division (6, 7). To make minimal assumptions, we modeled production of phenotypes as a Gaussian, auto-regressive process (Methods and SI Appendix), similar to recent work studying nongenetic inheritance of growth rate (40). Since tumble bias lies between zero and one, we defined and, instead, modeled production of the transformed phenotype .
In this model, when the population is grown in batch culture—i.e., when it is not migrating—its distribution of phenotypes approaches a Gaussian with population mean and variance . This description captures experimental measurements of the distribution in a wild-type strain of E. coli cells (SI Appendix, Fig. S3). Upon division, mother cells with phenotype produce daughter cells with phenotypes given by:
| [2] |
where is a Gaussian random variable with mean and variance , and is the correlation between mother and daughter phenotypes. When , daughter-cell phenotypes are chosen at random from the batch-culture distribution—there is no memory. As increases, daughters’ phenotypes are more similar to their mothers’ phenotypes, increasing the characteristic time, , that it takes a perturbation to the population’s phenotype composition to decay: (SI Appendix). While others have studied the role of growth rate, , and other model parameters on group migration speed in populations containing one phenotype (35), this inheritance parameter is unique to populations that exhibit nongenetic diversity. We focus on it here because we will see that it has significant effects on group migration dynamics.
Simulating the model of collective migration with growth, we found that the migrating group not only approaches a stable migration speed and population size, but also a stable phenotype composition (Fig. 2 A and B). Leakage of cells selectively removed low-performing phenotypes at the back of the group, but growth did not specifically replace the phenotypes that were lost. Therefore, the phenotype composition of the migrating group became dynamically enriched with phenotypes that perform well in the current environment, relative to the batch-culture distribution. This composition shift depended on the phenotypic inheritance parameter : With increasing , the composition shifted more because the traveling cells produced daughters that were more similar to themselves and more dissimilar to the cells that fell behind. In the limit of , the migrating population would eventually purify to the single phenotype that performs best in the current environment.
Fig. 2.
Growth and leakage balance to adapt the group’s composition to the environment, depending on nongenetic inheritance of phenotype. (A and B) Steady-state phenotype compositions in groups migrating through liquid (A; green throughout) or porous (B; orange throughout) environments, for varying values of mother–daughter phenotype correlation , which increases from dark to light lines. Black solid line: phenotype composition in batch culture, when not migrating. (C) Larger shifts in phenotype composition away from the batch-culture composition lead to faster steady-state migration, . (D) Theory captures dependence of steady-state migration speed on group composition. Line with circular markers is the predicted (Eq. 3) plotted versus in simulations. Each marker is a simulation of a population with different value of . Solid lines without markers are the predictions of Eq. 3 if , the mean performance at the back of the group, is replaced with , the average performance over the entire migrating group. Predictions in this panel used and at steady state from simulations. Dashed black line is . (E) Dynamic changes in phenotype composition circumvent the trade-offs between migrating in liquid and porous environments faced by any population with fixed composition. Black line: normalized of nondiverse populations with different phenotypes ( at the bottom right; at the top left) in a porous environment versus their in a liquid environment. Green dot: liquid specialist (highest in liquid). Orange dot: porous specialist (highest in porous). Black dot: generalist (highest minimum among the two environments). Colored dots: of diverse populations in each environment for varying values of (shown are in blue through in red, in increments of 0.2). (F) Faster steady-state migration of diverse populations trades off against the time it takes the population’s phenotype composition to adapt to a new environment. Inverse adaptation time (or adaptation rate) and from simulations were normalized to lie between zero and one. Larger values of lead to faster migration in both environments, but slower adaptation rate.
These shifts in phenotype composition were accompanied by increases in steady-state migration speed (Fig. 2C). While this seems intuitive, migration speed is set by how fast the population consumes the attractant—i.e., the size of the traveling population—not necessarily the performance of its individuals (refs. 10 and 35 and SI Appendix). Since the traveling gradient is generated by the cells’ consumption, the cells essentially make the gradient as steep as necessary to maintain the migration speed set by the pace of their consumption (SI Appendix). Therefore, for composition shifts to increase migration speed, the traveling population’s size must increase at steady state.
To quantitatively understand this, we extended an approach from a recent theoretical study of collective migration with a single phenotype (35) to include multiple phenotypes. Detailing this approach in SI Appendix, we find that the steady-state migration speed is:
| [3] |
Eq. 3 shows that is set by the diffusivity of the attractant, , and the average chemotactic performance, , among phenotypes located at the back edge of the group, . The latter quantity appears because it affects the loss of cells at the back (Eq. 1), which is exactly the net flux at (SI Appendix). Higher inheritance increases , thus reducing the rate at which all phenotypes fall behind and increasing the number of cells traveling and the migration speed at steady state. By extracting steady-state and from simulations with varying values of , Fig. 2D shows that Eq. 3 accurately captures how migration speed depends on the phenotypes traveling. These effects could not be captured by instead using the mean chemotactic abilities of the entire group—i.e., (Fig. 2D)—highlighting the importance of the lowest performers in the traveling group.
An additional consequence of these dynamic composition changes is that a diverse population with inheritance can avoid trade-offs faced by any nondiverse population. Fig. 2E shows the steady-state migration speeds of a range of nondiverse populations in each environment, scaled by the maximum migration speed in each (black line). The specialist phenotypes in agar and liquid are those that migrate the fastest in each environment, but they perform less well in the alternative environment. The generalist phenotype has the highest minimum migration speed across the two environments. The convex shape of the black line suggests that no diverse population with a fixed composition of phenotypes can outperform the nondiverse populations—i.e., by being closer to the (1, 1) point on that plot. However, dynamic adaptation enables diverse populations to outperform the nondiverse populations by enriching themselves with specialists for the current environment, relative to the batch-culture composition. This is shown by comparing the highest-performing homogeneous population (black dot in Fig. 2E) to a diverse population with the same mode phenotype (colored dots in Fig. 2E) and different values of inheritance . As increases, the diverse population approaches the (1, 1) corner of the plot, accessing a region of performance space that is inaccessible to any homogeneous population (black line in Fig. 2E). Thus, by dynamically adapting its own composition, the population is able to effectively migrate through multiple environments that require different phenotypes.
Finally, while higher inheritance leads to faster steady-state migration, we found that it also slows down the population’s response to a new environment. To quantify this trade-off, we extracted the relaxation time of migration speed near steady state for varying values of (Methods). While other quantities could be used to quantify the adaptation time scale, the relaxation time near steady state is independent of the population composition before the environment change, and it is the limiting time scale over which the composition adjusts to a new environment. Note that there is also a faster time scale in this problem: Upon encountering a new environment, the phenotypes in the population spatially reorganize according to their new values of , and some phenotypes immediately fall behind. This initial change in population composition occurs in the time it takes the migrating group to travel its own width.
Normalizing the adaptation rates and migration speeds to lie between zero and one and plotting them against each other, we visualized this trade-off (Fig. 2F). In both environments, adaptation rate decreased with steady-state migration speed with an approximate shape of . The intuition for this trade-off can be understood by making an analogy to an Ornstein–Uhlenbeck (OU) process. In an OU process, a particle diffuses in an energy-potential well, and the relaxation time of the particle’s position depends on its mass and the drag of the medium. A larger-mass particle with a shorter relaxation time is also less responsive to external forces. Likewise, lower inheritance shortens the relaxation time of the group’s phenotype composition, but makes it less responsive to the differential loss of phenotypes resulting from collective migration.
Trade-Off Leads to an Optimal Level of Nongenetic Inheritance that Maximizes Migration Speed in Changing Environments.
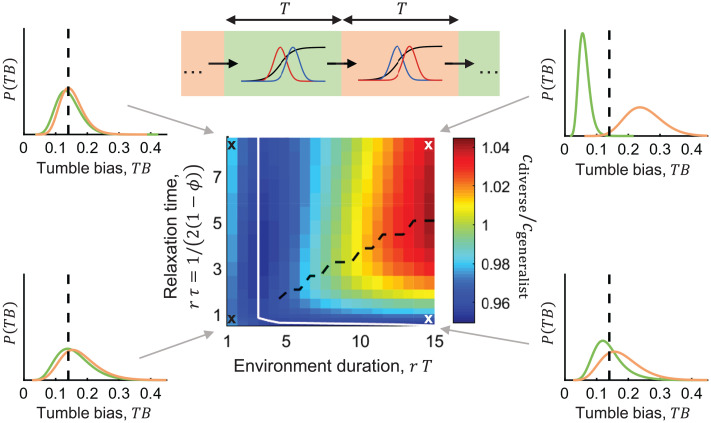
The time it takes a migrating population to adapt its composition becomes important when it encounters changing environments. How does the time scale of the environment constrain the ability of diverse populations to adapt, and when is diversity useful? To investigate this, we simulated diverse and nondiverse migrating populations that periodically encounter liquid and porous environments after fixed amounts of time (Fig. 3). We varied the level of inheritance of the diverse populations since it controls the relaxation time of their phenotype compositions. Then, we defined population performance as the time-averaged migration speed across the two environments, after many environment switches.
Fig. 3.
Diverse populations nongenetically adapt to migrate through varying environments and can outrun a single-phenotype, generalist population in slowly-varying environments. (Top) Schematic of the simulation. Populations with varying mother–daughter phenotype correlation were simulated migrating through liquid and porous environments that switch after a fixed time . (Middle) After many environment switches, the stationary, time-averaged migration speed across the two environments was computed and normalized by that of a single-phenotype, generalist population . Migration speeds (colors) are plotted against the relaxation time of the population’s composition in batch culture, , scaled by the cell-division time , and the environment duration , also scaled by . Note that increases as increases. For a plot with on the y axis, see SI Appendix, Fig. S6. White line separates two qualitatively different regimes. Insets show the phenotype composition at the end of each liquid (green) and porous (orange) environment. Black dashed lines in Insets indicate the generalist phenotype. When the environment varies rapidly (), the population narrows its composition around the generalist phenotype, and larger (larger ) increases migration speed by more effectively narrowing the phenotype composition. When the environment varies slowly (), the diverse population adapts its composition to each environment. An optimal level of inheritance (or ) maximizes migration speed in this regime (black dashed line, Middle).
Plotting the average migration speeds of the diverse population as a function of the environment duration, , and the population’s composition relaxation time in batch culture, , we found that the average migration speed exhibited two qualitatively different regimes (Fig. 3 and Methods). In environments that changed quickly compared to the cells’ doubling time (), higher inheritance (longer composition-relaxation time in batch culture) monotonically increased the average migration speed. In this regime, the population’s phenotype composition narrowed around the generalist phenotype, and higher inheritance helped the population maintain the generalist phenotype when cells divided (Fig. 3, Left). Increasing diversity by increasing reduced average migration speed in this regime because the population was less able to narrow its phenotype distribution around the generalist phenotype (SI Appendix, Fig. S6 A and B). The nondiverse, generalist population always migrated fastest in this regime.
In slowly changing environments (), the population’s phenotype composition tracked the environment. An optimal level of inheritance maximized the average migration speed by balancing the trade-off between maximally adapting the composition to each environment and the need to do so before the environment switched (Fig. 3, Right). Once the period of each environment was sufficiently long, the diverse population outperformed the nondiverse one by shifting and narrowing its composition around the specialist phenotype in each environment. Increasing diversity in this regime made the “highs higher” and the “lows lower”: Populations without inheritance () performed worse with more diversity, but populations with sufficient inheritance performed better with more diversity (SI Appendix, Fig. S6 A and B). Increasing diversity effectively increases the range of phenotypes to which the population has access, but inheritance is required to maintain the high-performing ones. These results suggest that nongenetic inheritance should be as large as the environment time scales allow. Thus, differential leakage paired with inheritance of phenotypes transiently and nongenetically adapts the population composition to migrate effectively through varying environments.
Discussion
Here, we investigated how growth in a nongenetically diverse population balances with loss of phenotypes during collective behaviors and how this balance impacts population performance. We used collective migration of chemotactic bacteria as a model system, where the demands of migration change in environments of different porosity. We realized that collective migration causes differential loss of phenotypes in an environment-dependent manner: Migration excludes whichever individuals perform poorly in the current environment. Our central finding is that, with growth and phenotypic inheritance, this differential loss dynamically enriches the population phenotype composition with high performers for the current environment, thus enhancing group migration speed in multiple environments. Growth of diverse phenotypes requires specifying how much daughters “remember” the phenotypes of their mothers, and we found that this nongenetic inheritance controls a general trade-off between larger composition shifts relative to the batch culture and slower responsiveness to new environments. In varying environments, this trade-off resulted in an optimal level of inheritance that maximized the average migration speed and enabled a diverse population to outrun a nondiverse one composed of the generalist phenotype.
Differential loss of phenotypes during group migration resembles the effects of natural selection: Individuals that are “better adapted” to the current environment become enriched in the traveling group over time. However, these composition changes were not due to differences in growth or death, by assumption. Instead, differential loss of migrating individuals emerged from their spatial arrangement by chemotaxis performance. This distinguishes our results from past work on the role of nongenetic diversity in well-mixed, growing populations (41–60) and populations undergoing undirected range expansion (61–63). Spatial structure in past work has affected population growth or evolutionary success by governing which individuals access limited nutrients in dilute conditions (64, 65), which populations occupy finite habitats (22, 23), or the ability of populations to exchange metabolites (66). Our results point to another way that spatial structure can shape the composition of a population: by dictating which individuals participate in a collective behavior. Since this spatial structure is environment-dependent, it enables migrating populations to dynamically shape their compositions to migrate effectively in multiple environments.
The dynamic nature of these nongenetic changes in phenotype composition also differentiate our results from past work by us (65) and others (47, 53, 54, 57, 67). In Frankel et al. (65), diversity enabled a population to avoid trade-offs among multiple tasks by having phenotypes in the population that performed well at each task. These tasks were performed independently by each individual cell, without collective behavior. While mutations allowed the population to evolve its standing distribution of phenotypes, this distribution was fixed for a given genotype during performance of a task. Our results here imply that, over cell divisions, diverse populations can do better: Growth and selection-like effects (either natural selection or the kind described here) dynamically shift the population’s neutral distribution of phenotypes toward those that are high performing at each task, without mutations, as the task is being performed. Likewise, approaches to studying the fitness effects of diversity that geometrically analyze Pareto fronts or optimize phenotype distributions without considering how the phenotype distribution dynamically responds to selection or selection-like effects will miss this (47, 53, 54, 57, 67, 68). The problem is that the population can have a different phenotype composition in each environment, giving it more flexibility than these procedures allow. As a result, the population is not necessarily limited to the convex hull of nondiverse populations’ performance across environments. This, in turn, affects the conditions in which a diverse population performs better than a nondiverse, generalist population.
Predicting changes in phenotype composition requires knowing how new phenotypes are produced. We modeled this as resulting from imperfect inheritance of swimming phenotypes at cell division (40, 42, 48, 69–73), consistent with recent measurements (8). Stochastic switching is another known mechanism for producing new phenotypes (41, 43, 49–52, 74, 75), such as in the case of persisters (50, 51, 55, 76). Since these mechanisms produce phenotypes independently of the cells’ environment, we expect that they are both subject to the trade-off that increasing the “susceptibility” of the population’s phenotype composition to selection-like pressures comes at the cost of slower responses to new pressures. This trade-off underlies past results showing that an optimal level of inheritance or an optimal switching frequency maximizes population growth in changing environments (41, 42, 56). Despite the very different context, we found that migrating groups of bacteria exhibit the same qualitative behavior. The existence of an optimum suggests that, on longer time scales, the population can evolve the level of nongenetic inheritance to match the time scales of environmental changes.
Emergent adaptation of phenotype composition during collective behaviors could have important effects on a range of biological processes and could interact with natural selection. For example, the adaptation studied here could play a role during competition among multiple comigrating species of bacteria (22, 23, 28). More generally, group migration with spatial ordering of phenotypes is not limited to bacterial chemotaxis: It can arise whenever individuals with diverse motility phenotypes consume or deplete a signal in the environment that they then chase. Self-generated gradients drive collective migration of eukaryotic cells during development, wound healing, and cancer metastasis (77–82), in which a leader–follower structure emerges (83–85), and, thus, adaptation mediated by spatial organization of motility phenotypes could affect these processes. A similar kind of nongenetic adaptation could potentially occur during biofilm formation, in which the collective behavior confers a selective advantage to phenotypes that produce costly biofilm-associated materials (86). Collective behaviors may generally adapt the phenotype compositions of diverse, growing populations to perform a variety of collective tasks.
Methods
Our generalized Keller–Segel model consists of the following partial differential equations (PDEs):
| [4] |
| [5] |
Here, is the density of cells with tumble bias at location and time , is the total density of cells, and is the concentration of attractant. and are the phenotype-dependent chemotactic (36) and diffusion coefficients characterizing cells’ chemotactic drift speed and random diffusive motion, respectively. Models for and in liquid and porous environments are described in SI Appendix. and are the dissociation constants of the cells’ receptors for the attractant when in the inactive and active forms (33), which roughly set the lower and upper limits of concentration that the cells can detect. We assume all phenotypes grow with rate , and is the carrying capacity. We chose sufficiently large that it had negligible effects on growth in the migrating group. encodes how divisions of a cell with phenotype contribute to production of cells with phenotype . is the diffusivity of the attractant, and and characterize consumption of the attractant by all cells. These PDEs are paired with boundary conditions stipulating that, far ahead of the wave, there are no cells, and the concentration of attractant is (i.e., there is no attractant gradient ahead of the group): , , , and . Variants of this model that simulate individual agents with a single phenotype (21, 87) and multiple phenotypes (29) have been studied in the past, finding that the large number of cells in these migrating populations [typically more than cells/mL (5, 21)] justifies modeling them with a continuous density .
In the growth term, is a kernel that maps divisions of mother cells to production of daughters. is the distribution of offspring phenotypes given the mother’s phenotype that is implied by the dynamics in Eq. 2 and by the mapping from to . The factor of two accounts for production of two daughter cells upon division (whose phenotypes may be correlated with each other; SI Appendix), and the Dirac delta function accounts for removal of the mother cell from the population upon division. We assumed that nutrients are abundant in the migrating group and distinct from the attractant (equivalent to large carrying capacity ), such that the migrating cells grow exponentially (21, 35). For simplicity, we assumed that all phenotypes divide with the same rate , and we neglected changes in a cell’s behavioral phenotype within its lifetime (8).
The code in this work built on previous code from ref. 5. Simulations were performed by converting the PDEs into a system of ordinary differential equations by discretizing space . Spatial derivatives were computed by using central differences. Integration forward in time was done by using an explicit, fourth-order Runge–Kutta scheme (88, 89). The initial condition was taken to be a steep sigmoidal function in space: , where is the initial density of cells, is the initial composition, and sets the extent of the initial inoculation. We used , where the average in is with respect to . This makes roughly the characteristic length scale (width) of the wave that would be formed by the inoculated cells. For this choice of initial condition, nearly all phenotypes in the initial inoculation join the traveling group. was always the batch-culture distribution. In simulations without growth, we used ; with growth in liquid, we used ; and with growth in porous media, we used . The spatial grid size was , using knowledge of the relevant length scale of the problem. Time steps were , where was the largest diffusion coefficient in the problem (including ).
Simulations were done over a moving segment of space with no-flux boundary conditions on both sides. Several conditions were used to decide when to move the window of space being simulated. A new segment was simulated when: the attractant concentration at the right boundary dropped below a threshold; the peak cell density (and, hence, problem length scale) changed by more than 15%; or the fraction of traveling cells that had the smallest or largest value of fell below a threshold (and could be removed from the simulation) or increased above a threshold (meaning that the new phenotypes would imminently be produced by growth). If any of these conditions were met, the simulation was stopped, space far behind the wave peak was discarded, and the spatial region of the simulation was extended ahead of the direction of motion. The spatial grid size and time step were updated during this step, with , where the average was over phenotypes currently traveling, and was the peak value of total cell density at the end of the previous simulation. The number of cells of each phenotype traveling was found by integrating over space from the location where the attractant first reached zero behind the wave to space far ahead of the group. Then, the cell density and attractant profiles were interpolated onto the new spatial grid, and the simulation was resumed.
With cell growth, phenotypes that weren’t present at the start of the simulation could be produced. In this case, if the simulation of a spatial block stopped because the fraction of edge phenotypes increased above a threshold due to growth, then the range of phenotypes in the simulation was extended. Simulations were implemented with phenotype defined as . The grid size of was chosen to be 1/10th of the SD of the offspring phenotype distribution in order to resolve the growth matrix .
For the traveling populations to reach steady state in Fig. 2, group migration was simulated for 15 h. The composition-relaxation time was determined from the time course of migration speed as it approached steady state. Once the speed was within 10% of the steady-state value, the speed profile was fit with an exponential function to extract the time scale of the slowest decaying mode, which was used to quantify the adaptation time. To compare theory to simulations, in simulations was computed by integrating cell density over the wave from to (where defines the back of the wave; SI Appendix, Steady State Migration Speed with Attractant Diffusion).
Simulations in periodically varying environments were done by first simulating migration through one environment for the fixed environment duration. Then, to make minimal assumptions about how transitions between environments occurred, we took the cell density and attractant profiles at the end of the simulation in one environment and used those profiles as the initial conditions for a simulation in the next environment. The spatial grid size was adjusted for the expected change in speed in the new environment. In order for the simulation to reach a steady state, environments were alternated 15 times this way, for a total of 30 simulations for each parameter pair . The time-averaged speed in each condition was computed by dividing the total displacement over the last two environments (one liquid, one porous) by twice the duration of each environment, . The white line in Fig. 3 that separates the regime of fast () and slow () environment switching was determined by finding, for each , the value of at which the average speed had a local minimum.
All simulations were performed on Yale’s High-Performance Computing Clusters.
Supplementary Material
Acknowledgments
We thank Jude Ong for collecting the tracking data in SI Appendix, Fig. S4, and we thank Paul Turner and Sujit Datta for helpful discussions. This work was supported by NIH Awards R01GM106189 (to H.H.M. and T.E.), R01GM138533 (to H.H.M. and T.E.), and F32GM131583 (to H.H.M.).
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2117377119/-/DCSupplemental.
Data Availability
Simulation-code data have been deposited in GitHub (https://github.com/emonetlab/ks) (90).
References
- 1.Copenhagen K., Quint D. A., Gopinathan A., Self-organized sorting limits behavioral variability in swarms. Sci. Rep. 6, 31808 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Yllanes D., Leoni M., Marchetti M. C., How many dissenters does it take to disorder a flock? New J. Phys. 19, 103026 (2017). [Google Scholar]
- 3.Bera P. K., Sood A. K., Motile dissenters disrupt the flocking of active granular matter. Phys. Rev. E 101, 052615 (2020). [DOI] [PubMed] [Google Scholar]
- 4.Peled S., et al. , Heterogeneous bacterial swarms with mixed lengths. Phys. Rev. E 103, 032413 (2021). [DOI] [PubMed] [Google Scholar]
- 5.Fu X., et al. , Spatial self-organization resolves conflicts between individuality and collective migration. Nat. Commun. 9, 2177 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Huh D., Paulsson J., Random partitioning of molecules at cell division. Proc. Natl. Acad. Sci. U.S.A. 108, 15004–15009 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Huh D., Paulsson J., Non-genetic heterogeneity from stochastic partitioning at cell division. Nat. Genet. 43, 95–100 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Pleška M., Jordan D., Frentz Z., Xue B., Leibler S., Nongenetic individuality, changeability, and inheritance in bacterial behavior. Proc. Natl. Acad. Sci. U.S.A. 118, e2023322118 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Adler J., Chemotaxis in bacteria. Science 153, 708–716 (1966). [DOI] [PubMed] [Google Scholar]
- 10.Keller E. F., Segel L. A., Traveling bands of chemotactic bacteria: A theoretical analysis. J. Theor. Biol. 30, 235–248 (1971). [DOI] [PubMed] [Google Scholar]
- 11.Novick-Cohen A., Segel L. A., A gradually slowing travelling band of chemotactic bacteria. J. Math. Biol. 19, 125–132 (1984). [DOI] [PubMed] [Google Scholar]
- 12.Wolfe A. J., Berg H. C., Migration of bacteria in semisolid agar. Proc. Natl. Acad. Sci. U.S.A. 86, 6973–6977 (1989). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Park S., et al. , Influence of topology on bacterial social interaction. Proc. Natl. Acad. Sci. U.S.A. 100, 13910–13915 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Lambert G., Liao D., Austin R. H., Collective escape of chemotactic swimmers through microscopic ratchets. Phys. Rev. Lett. 104, 168102 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Saragosti J., et al. , Directional persistence of chemotactic bacteria in a traveling concentration wave. Proc. Natl. Acad. Sci. U.S.A. 108, 16235–16240 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Koster D. A., Mayo A., Bren A., Alon U., Surface growth of a motile bacterial population resembles growth in a chemostat. J. Mol. Biol. 424, 180–191 (2012). [DOI] [PubMed] [Google Scholar]
- 17.Emako C., Gayrard C., Buguin A., Neves de Almeida L., Vauchelet N., Traveling pulses for a two-species chemotaxis model. PLOS Comput. Biol. 12, e1004843 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ni B., et al. , Evolutionary remodeling of bacterial motility checkpoint control. Cell Rep. 18, 866–877 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Fraebel D. T., et al. , Environment determines evolutionary trajectory in a constrained phenotypic space. eLife 6, e24669 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Seyrich M., Palugniok A., Stark H., Traveling concentration pulses of bacteria in a generalized Keller–Segel model. New J. Phys. 21, 103001 (2019). [Google Scholar]
- 21.Cremer J., et al. , Chemotaxis as a navigation strategy to boost range expansion. Nature 575, 658–663 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Liu W., Cremer J., Li D., Hwa T., Liu C., An evolutionarily stable strategy to colonize spatially extended habitats. Nature 575, 664–668 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Gude S., et al. , Bacterial coexistence driven by motility and spatial competition. Nature 578, 588–592 (2020). [DOI] [PubMed] [Google Scholar]
- 24.Phan T. V., et al. , Bacterial route finding and collective escape in mazes and fractals. Phys. Rev. X 10, 031017 (2020). [Google Scholar]
- 25.Bhattacharjee T., Amchin D. B., Ott J. A., Kratz F., Datta S. S., Chemotactic migration of bacteria in porous media. Biophys. J. 120, 3483–3497 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Bhattacharjee T., Amchin D. B., Alert R., Ott J. A., Datta S. S., Chemotactic smoothing of collective migration. eLife 11, e71226 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Keegstra J. M., Carrara F., Stocker R., The ecological roles of bacterial chemotaxis. Nat. Rev. Microbiol., 10.1038/s41579-022-00709-w (2022). [DOI] [PubMed] [Google Scholar]
- 28.Mattingly H., Emonet T., A rule from bacteria to balance growth and expansion. Nature 575, 602–603 (2019). [DOI] [PubMed] [Google Scholar]
- 29.Bai Y., et al. , Spatial modulation of individual behaviors enables an ordered structure of diverse phenotypes during bacterial group migration. eLife 10, e67316 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Spudich J. L., Koshland D. E. Jr., Non-genetic individuality: Chance in the single cell. Nature 262, 467–471 (1976). [DOI] [PubMed] [Google Scholar]
- 31.Dufour Y. S., Gillet S., Frankel N. W., Weibel D. B., Emonet T., Direct correlation between motile behavior and protein abundance in single cells. PLOS Comput. Biol. 12, e1005041 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Waite A. J., et al. , Non-genetic diversity modulates population performance. Mol. Syst. Biol. 12, 895 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Mello B. A., Tu Y., Quantitative modeling of sensitivity in bacterial chemotaxis: The role of coupling among different chemoreceptor species. Proc. Natl. Acad. Sci. U.S.A. 100, 8223–8228 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Wong-Ng J., Celani A., Vergassola M., Exploring the function of bacterial chemotaxis. Curr. Opin. Microbiol. 45, 16–21 (2018). [DOI] [PubMed] [Google Scholar]
- 35.Narla A. V., Cremer J., Hwa T., A traveling-wave solution for bacterial chemotaxis with growth. Proc. Natl. Acad. Sci. U.S.A. 118, e2105138118 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Dufour Y. S., Fu X., Hernandez-Nunez L., Emonet T., Limits of feedback control in bacterial chemotaxis. PLOS Comput. Biol. 10, e1003694 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Savageau M. A., Escherichia coli habitats, cell types, and molecular mechanisms of gene control. Am. Nat. 122, 732–744 (1983). [Google Scholar]
- 38.Licata N. A., Mohari B., Fuqua C., Setayeshgar S., Diffusion of bacterial cells in porous media. Biophys. J. 110, 247–257 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Kurzthaler C., et al. , A geometric criterion for the optimal spreading of active polymers in porous media. Nat. Commun. 12, 7088 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Lin J., Amir A., The effects of stochasticity at the single-cell level and cell size control on the population growth. Cell Syst. 5, 358–367.e4 (2017). [DOI] [PubMed] [Google Scholar]
- 41.Kussell E., Leibler S., Phenotypic diversity, population growth, and information in fluctuating environments. Science 309, 2075–2078 (2005). [DOI] [PubMed] [Google Scholar]
- 42.Carja O., Plotkin J. B., The evolutionary advantage of heritable phenotypic heterogeneity. Sci. Rep. 7, 5090 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Kussell E., Evolution in microbes. Annu. Rev. Biophys. 42, 493–514 (2013). [DOI] [PubMed] [Google Scholar]
- 44.Cohen D., Optimizing reproduction in a randomly varying environment. J. Theor. Biol. 12, 119–129 (1966). [DOI] [PubMed] [Google Scholar]
- 45.Slatkin M., Hedging one’s evolutionary bets. Nature 250, 704–705 (1974). [Google Scholar]
- 46.Philippi T., Seger J., Hedging one’s evolutionary bets, revisited. Trends Ecol. Evol. 4, 41–44 (1989). [DOI] [PubMed] [Google Scholar]
- 47.Haccou P., Iwasa Y., Optimal mixed strategies in stochastic environments. Theor. Popul. Biol. 47, 212–243 (1995). [Google Scholar]
- 48.Lachmann M., Jablonka E., The inheritance of phenotypes: An adaptation to fluctuating environments. J. Theor. Biol. 181, 1–9 (1996). [DOI] [PubMed] [Google Scholar]
- 49.Thattai M., van Oudenaarden A., Stochastic gene expression in fluctuating environments. Genetics 167, 523–530 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Balaban N. Q., Merrin J., Chait R., Kowalik L., Leibler S., Bacterial persistence as a phenotypic switch. Science 305, 1622–1625 (2004). [DOI] [PubMed] [Google Scholar]
- 51.Kussell E., Kishony R., Balaban N. Q., Leibler S., Bacterial persistence: A model of survival in changing environments. Genetics 169, 1807–1814 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Acar M., Mettetal J. T., van Oudenaarden A., Stochastic switching as a survival strategy in fluctuating environments. Nat. Genet. 40, 471–475 (2008). [DOI] [PubMed] [Google Scholar]
- 53.Donaldson-Matasci M. C., Lachmann M., Bergstrom C. T., Phenotypic diversity as an adaptation to environmental uncertainty. Evol. Ecol. Res. 10, 493–515 (2008). [Google Scholar]
- 54.Donaldson-Matasci M. C., Bergstrom C. T., Lachmann M., The fitness value of information. Oikos 119, 219–230 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Lewis K., Persister cells. Annu. Rev. Microbiol. 64, 357–372 (2010). [DOI] [PubMed] [Google Scholar]
- 56.Gaál B., Pitchford J. W., Wood A. J., Exact results for the evolution of stochastic switching in variable asymmetric environments. Genetics 184, 1113–1119 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Rivoire O., Leibler S., The value of information for populations in varying environments. J. Stat. Phys. 142, 1124–1166 (2011). [Google Scholar]
- 58.Grimbergen A. J., Siebring J., Solopova A., Kuipers O. P., Microbial bet-hedging: The power of being different. Curr. Opin. Microbiol. 25, 67–72 (2015). [DOI] [PubMed] [Google Scholar]
- 59.Levien E., Kondev J., Amir A., The interplay of phenotypic variability and fitness in finite microbial populations. J. R. Soc. Interface 17, 20190827 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Levien E., Min J., Kondev J., Amir A., Non-genetic variability in microbial populations: Survival strategy or nuisance? Rep. Prog. Phys. 84, 116601 (2021). [DOI] [PubMed] [Google Scholar]
- 61.Villa Martín P., Muñoz M. A., Pigolotti S., Bet-hedging strategies in expanding populations. PLOS Comput. Biol. 15, e1006529 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Patra P., Klumpp S., Phenotypically heterogeneous populations in spatially heterogeneous environments. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 89, 030702 (2014). [DOI] [PubMed] [Google Scholar]
- 63.Patra P., Klumpp S., Role of bacterial persistence in spatial population expansion. Phys. Rev. E 104, 034401 (2021). [DOI] [PubMed] [Google Scholar]
- 64.Celani A., Vergassola M., Bacterial strategies for chemotaxis response. Proc. Natl. Acad. Sci. U.S.A. 107, 1391–1396 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Frankel N. W., et al. , Adaptability of non-genetic diversity in bacterial chemotaxis. eLife 3, e03526 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Dal Co A., van Vliet S., Kiviet D. J., Schlegel S., Ackermann M., Short-range interactions govern the dynamics and functions of microbial communities. Nat. Ecol. Evol. 4, 366–375 (2020). [DOI] [PubMed] [Google Scholar]
- 67.Levins R., Theory of fitness in a heterogeneous environment. I. The fitness set and adaptive function. Am. Nat. 96, 361–373 (1962). [Google Scholar]
- 68.Xue B., Sartori P., Leibler S., Environment-to-phenotype mapping and adaptation strategies in varying environments. Proc. Natl. Acad. Sci. U.S.A. 116, 13847–13855 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Jablonka E., Lamb M. J., Avital E., ‘Lamarckian’ mechanisms in Darwinian evolution. Trends Ecol. Evol. 13, 206–210 (1998). [DOI] [PubMed] [Google Scholar]
- 70.Brock A., Chang H., Huang S., Non-genetic heterogeneity—A mutation-independent driving force for the somatic evolution of tumours. Nat. Rev. Genet. 10, 336–342 (2009). [DOI] [PubMed] [Google Scholar]
- 71.Pisco A. O., et al. , Non-Darwinian dynamics in therapy-induced cancer drug resistance. Nat. Commun. 4, 2467 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Day T., Interpreting phenotypic antibiotic tolerance and persister cells as evolution via epigenetic inheritance. Mol. Ecol. 25, 1869–1882 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Lee J. A., et al. , Microbial phenotypic heterogeneity in response to a metabolic toxin: Continuous, dynamically shifting distribution of formaldehyde tolerance in Methylobacterium extorquens populations. PLoS Genet. 15, e1008458 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Norman T. M., Lord N. D., Paulsson J., Losick R., Stochastic switching of cell fate in microbes. Annu. Rev. Microbiol. 69, 381–403 (2015). [DOI] [PubMed] [Google Scholar]
- 75.Kaufmann B. B., Yang Q., Mettetal J. T., van Oudenaarden A., Heritable stochastic switching revealed by single-cell genealogy. PLoS Biol. 5, e239 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Fisher R. A., Gollan B., Helaine S., Persistent bacterial infections and persister cells. Nat. Rev. Microbiol. 15, 453–464 (2017). [DOI] [PubMed] [Google Scholar]
- 77.Streichan S. J., Valentin G., Gilmour D., Hufnagel L., Collective cell migration guided by dynamically maintained gradients. Phys. Biol. 8, 045004 (2011). [DOI] [PubMed] [Google Scholar]
- 78.Scherber C., et al. , Epithelial cell guidance by self-generated EGF gradients. Integr. Biol. 4, 259–269 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Donà E., et al. , Directional tissue migration through a self-generated chemokine gradient. Nature 503, 285–289 (2013). [DOI] [PubMed] [Google Scholar]
- 80.Tweedy L., Knecht D. A., Mackay G. M., Insall R. H., Self-generated chemoattractant gradients: Attractant depletion extends the range and robustness of chemotaxis. PLoS Biol. 14, e1002404 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Tweedy L., et al. , Seeing around corners: Cells solve mazes and respond at a distance using attractant breakdown. Science 369, eaay9792 (2020). [DOI] [PubMed] [Google Scholar]
- 82.Cochet-Escartin O., et al. , Hypoxia triggers collective aerotactic migration in Dictyostelium discoideum. eLife 10, e64731 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.McLennan R., et al. , Neural crest migration is driven by a few trailblazer cells with a unique molecular signature narrowly confined to the invasive front. Development 142, 2014–2025 (2015). [DOI] [PubMed] [Google Scholar]
- 84.Mayor R., Etienne-Manneville S., The front and rear of collective cell migration. Nat. Rev. Mol. Cell Biol. 17, 97–109 (2016). [DOI] [PubMed] [Google Scholar]
- 85.Hopkins A., Camley B. A., Leader cells in collective chemotaxis: Optimality and trade-offs. Phys. Rev. E 100, 032417 (2019). [DOI] [PubMed] [Google Scholar]
- 86.Nadell C. D., Bassler B. L., A fitness trade-off between local competition and dispersal in Vibrio cholerae biofilms. Proc. Natl. Acad. Sci. U.S.A. 108, 14181–14185 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Erban R., Othmer H. G., From individual to collective behavior in bacterial chemotaxis. SIAM J. Appl. Math. 65, 361–391 (2004). [Google Scholar]
- 88.Runge C., Ueber die numerische Auflösung von Differentialgleichungen. Math. Ann. 46, 167–178 (1895). [Google Scholar]
- 89.Kutta W., Beitrag zur Näherungsweisen Integration Totaler Differentialgleichungen (B. G. Teubner, Leipzig, Germany, 1901). [Google Scholar]
- 90.H. H. Mattingly, T. Emonet, Matlab code for “Collective behavior and non-genetic inheritance allow bacterial populations to adapt to changing environments.” GitHub. https://github.com/emonetlab/ks. Deposited 5 May 2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Simulation-code data have been deposited in GitHub (https://github.com/emonetlab/ks) (90).