Selective excitation localized by the Bloch-Siegert shift and a $B_1^{+}$ gradient

Abstract

Purpose:

To perform $B_1^{+}$-selective excitation using the Bloch-Siegert shift for spatial localization.

Theory and Methods:

A $B_1^{+}$-selective excitation is produced by an RF pulse consisting of two summed component pulses: an off-resonant pulse that induces a $B_1^{+}$-dependent Bloch-Siegert frequency shift and a frequency-selective excitation pulse. The passband of the pulse can be tailored by adjusting the frequency content of the frequency-selective pulse, as in conventional B₀ gradient-localized excitation. Fine magnetization profile control is achieved by using the Shinnar-Le Roux algorithm to design the frequency-selective excitation pulse. Simulations analyzed the pulses’ robustness to off-resonance, their suitability for multi-echo spin echo pulse sequences, and how their performance compares to that of rotating-frame selective excitation pulses. The pulses were evaluated experimentally on a 47.5 mT MRI scanner using an RF gradient transmit coil. Multiphoton resonances produced by the pulses were characterized and their distribution across $B_1^{+}$ predicted.

Results

With correction for varying $B_1^{+}$ across the desired profile, the proposed pulses produced selective excitation with the specified profile characteristics. The pulses were robust against off-resonance and RF amplifier distortion, and suitable for multi-echo pulse sequences. Experimental profiles closely matched simulated patterns.

Conclusion

The Bloch-Siegert shift can be used to perform B₀-gradient-free selective excitation, enabling the excitation of slices or slabs in RF gradient-encoded MRI.

Introduction

Gradients in the static B₀ magnetic field are used in nearly all modern magnetic resonance imaging systems. Although B₀ gradients are versatile tools capable of performing a variety of functions in the imaging process, their use also creates substantial challenges. Gradient hardware is expensive and occupies a large portion of the scanner’s bore, constraining scanner design; gradient switching is loud and induces peripheral nerve stimulation, compromising patient comfort; and eddy currents and concomitant non-linear magnetic fields induced by gradients require correction to prevent image artifacts (1, 2).

Imaging with magnitude or phase gradients of the RF transmit field $\left(B_1^{+}\right)$ rather than the static B₀ magnetic field has long been investigated as an alternative to B₀ gradient encoding (3–6). $B_1^{+}$ gradients can be switched in near-negligible time without acoustic noise, eddy currents, or peripheral nerve stimulation resulting from large dB/dt (7). However, replacing B₀ gradients with RF magnitude gradients in an imaging system introduces a new challenge: how to spatially localize excitation utilizing only the RF transmit field. A number of methods exist which exploit an inhomogeneous transmit field for spatial discrimination, such as early techniques for localized spectroscopy in $B_1^{+}$ gradients utilizing composite 180° hard pulses (8–10). These pulse trains achieve a rudimentary degree of spatial localization but require multiple FID acquisitions to define the ROI and do not provide strict profile definition. Another approach, the related depth pulse sequence technique, requires a smaller number of FID acquisitions and is somewhat more robust to off-resonance than composite pulses, but similarly provides only minimal control over the excitation profile (11). A third method proposed by Hoult is rotating-frame $B_1^{+}$-selective excitation (RFSE) by means of an RF pulse with constant B_1,x and modulated B_1,y (12). These pulses selectively excite magnetization based on the strength of the B_1,x component. The selectivity of the rotating frame method was improved over time (13–15), and a later recasting of the problem as a rotated Shinnar-Le Roux (SLR) design enabled pulse designers to meet target slice profile characteristics in $B_1^{+}$ (16). Although this most recent method provides fine control of the excitation profile, these pulses face some practical challenges, including unintended excitation at low $B_1^{+}$ with off-resonance and sensitivity to RF amplifier distortions due to the pulses’ strict envelope area requirements (16).

This work describes a class of $B_1^{+}$-selective RF pulses that use the Bloch-Siegert shift (17) to localize excitation. The Bloch-Siegert shift is a temporary shift in the resonance frequency of a nucleus, produced by the application of an off-resonant RF field. The size of the frequency shift induced by the off-resonant RF field depends on the frequency offset of the applied pulse and the strength of the RF field. This property has allowed the Bloch-Siegert shift to be used for mapping $B_1^{+}$ fields in MRI (18) and calibrating decoupling field strength in NMR (19, 20). More recently, the phenomenon has been exploited as an encoding mechanism for B₀ gradient-free imaging (5, 21, 22). In this work, the Bloch-Siegert shift is used to localize excitation. Preliminary aspects of the pulse design algorithm were presented in Ref. (23).

The proposed $B_1^{+}$-selective pulses comprise the summation of 1) a far-off-resonant Bloch-Siegert frequency-shift-inducing pulse, and 2) a frequency-selective excitation pulse (Fig. 1a). The two pulses work in analog to the paired B₀ z-gradient and frequency-selective excitation pulse used in conventional imaging slice selection. The Bloch-Siegert pulse creates a nonlinear frequency gradient that varies with $B_1^{+}$ field strength, and the frequency-selective pulse is designed with a frequency passband that excites a range of $B_1^{+}$‘s of interest (Fig. 1b). If the transmit coil generates a spatially inhomogeneous $B_1^{+}$ field, the $B_1^{+}$ selectivity of the summed pulse translates to spatial selectivity.

Figure 1.

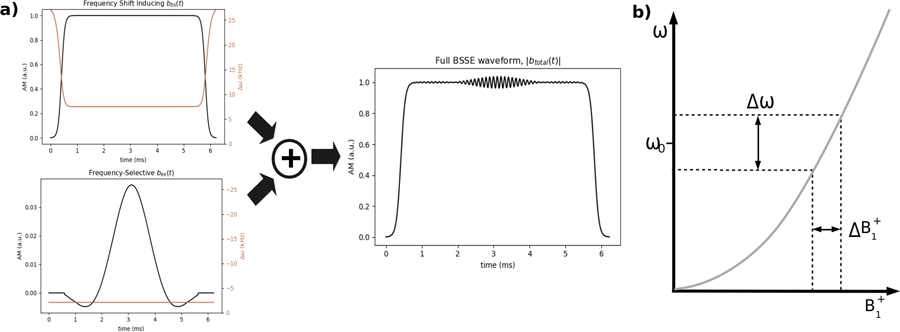
a) Construction of a BSSE RF pulse. The Bloch-Siegert shift producing pulse b_bs(t) (top left) and slice-selective pulse b_ex(t) (bottom left) are designed independently and summed into the full BSSE waveform b_total(t). b_bs(t) has Fermi AM (black) and adiabatic frequency sweeps towards and away from a constant frequency offset ω_off (orange). b_ex(t) has SLR-designed AM (black) and a constant frequency offset (orange). The amplitude of the b_bs(t) waveform is generally much larger than that of the b_ex(t) waveform; in |b_total(t)|, b_ex(t) is visible as a small ripple in the plateau of the Fermi waveform. b) Bloch-Siegert shift-localized slice selection, in which an off-resonant RF pulse produces an approximately quadratic variation in resonant frequencies across field strengths $B_1^{+}$. When paired with a frequency-selective excitation pulse, this results in the excitation of spins across a range $\Delta B_1^{+}$, which can be mapped to space using an amplitude gradient transmit coil.

The primary resonance used for excitation by the proposed pulses is the Bloch Siegert-shifted single-photon resonance. However, the new pulse class is reliant on the simultaneous application of two off-resonant pulses in the xy plane, which also produces additional multiphoton resonances (24, 25). Although imaging techniques that use multiphoton resonances for excitation have recently been demonstrated (26), these additional resonances are here regarded as nuisances and their mitigation is discussed.

In the following, the design of the two component pulses that make up a Bloch-Siegert-localized $B_1^{+}$-selective excitation pulse is described. Although there are many feasible choices for both the off-resonant Bloch-Siegert-shift inducing pulse and the frequency-selective pulse, this work focuses on the promising combination of an amplitude- and frequency-swept off-resonant pulse and an SLR frequency-selective pulse which allows the designer to directly specify and analytically trade off pulse and $B_1^{+}$ profile parameters (27). Design of these two pulses is analytic, simple, and fast. Simulations show the pulses’ suitability for selective excitation, inversion, and refocusing. Off-resonance behavior is simulated and shown to be predictable and similar to that of conventional spatially slice-selective excitation pulses, without the out-of-band excitation produced by the RFSE pulses of Ref (16). The pulses are also shown to have improved robustness against RF amplifier distortions over RFSE pulses. Selective excitation is experimentally demonstrated on a 47.5 mT MRI scanner with a gradient solenoid transmit-receive coil.

Theory

The design of a Bloch-Siegert $B_1^{+}$-selective excitation (BSSE) pulse comprises the design of two distinct component pulses: 1) an off-resonant pulse, b_bs(t), which produces a $B_1^{+}$-dependent shift in resonant frequencies via the Bloch-Siegert effect, and 2) a frequency-selective SLR pulse, b_ex(t), which excites a desired $B_1^{+}$ passband. Although these two pulses could be transmitted by separate coils, we here assume that they are generated together by the same transmit coil, so they are complex-summed once individually designed, i.e.,

$$b_{total}\left(t\right)=b_{bs}\left(t\right)+b_{ex}\left(t\right).$$

Component Pulse 1: The Bloch-Siegert Shift-Inducing Pulse

In the absence of externally applied RF, the magnetic resonance frequency is the Larmor frequency, ω₀ = γB₀. If an RF field is applied with amplitude $B_1^{+}$ and frequency offset ω_off relative to ω₀, then a Bloch-Siegert frequency shift of the resonance is produced, given by (28):

$${\omega }_{bs}\left(B_1^{+},{\omega }_{off}\right)\approx -{\omega }_{off}\left(\sqrt{1+{\left(\frac{\gamma B_1^{+}}{{\omega }_{off}}\right)}^2}-1\right).$$ (1)

This shift is away from the frequency of the applied off-resonance RF, i.e., a positive ω_off results in a negative ω_bs.

The Bloch-Siegert shift-inducing pulse is defined as an amplitude- and phase-modulated function

$$b_{bs}\left(t\right)=A_{bs}\left(t\right)e^{i{\varphi }_{bs}\left(t\right)},$$

where ${\varphi }_{bs}\left(t\right)={\int }_{-T/2}^t\Delta {\omega }_{rf}\left(t^{\prime }\right)d{t}^{\prime }$ is the time integral of the pulse’s time-varying frequency modulation ∆ω_rf (t), and T is the pulse duration. For A_bs(t) we use a Fermi pulse which was previously used in Ref. (18) to produce a large BS frequency shift with little out-of-band excitation. The Fermi envelope provides an additional benefit for this application: its plateau results in a constant ω_bs for the majority of the pulse duration, which simplifies the design of the b_ex(t) pulse so long as b_ex(t) is restricted to be nonzero only on the plateau. Thus for A_bs(t) a normalized Fermi pulse is used which is centered at t = 0:

$$A_{bs}\left(t\right)=\frac{1}{1+e^{\frac{\left|t\right|-t_0}{a}}},$$ (2)

where t₀ and a are parameters with units of seconds that control the duration of the pulse and the width of the transition, respectively. The duration of this Fermi pulse is T = 2t₀ + 13.81a. To ensure that b_ex(t) is only nonzero during the plateau when A_bs(t) ≈ 1, we derive from Eq. 2 that t₀ should be set to:

$$t_0=\frac{T_{ex}}{2}-a\ln \left(\frac{1}{A_{th}}-1\right),$$

where T_ex is the duration of b_ex(t) required to excite the desired bandwidth and A_th is a user-specified constant. This t₀ setting creates a central plateau in the Fermi envelope of duration T_ex with A_bs(t) ≥ A_th. Herein, all pulse designs used a = 6 × 10⁻⁵ s and A_th = 0.95.

A modification is made to the conventional constant frequency-offset Fermi by starting and ending the pulse’s FM waveform far-off resonance and sweeping adiabatically towards and away from the central constant frequency offset ω_off. This modification spin-locks the magnetization during the Fermi’s amplitude sweeps, reducing undesired excitation by A_bs(t) (29, 30). The analytic adiabatic sweep of Ref. (30) is used, with modification to allow for time-varying A_bs(t). A frequency sweep adapted from the analytic adiabatic sweep of Ref. (30) is used, with modification to allow for time-varying A_bs(t). The first half of the symmetric frequency sweep is given by:

$$\Delta {\omega }_{sweep}\left(t\right)=\frac{\gamma A_{bs}\left(t\right)}{\sqrt{{\left(1-\frac{\gamma A_{bs}\left(t\right)}{K}{t}_d\right)}^{-2}-1}},t\in \left(0,T/2\right),$$

where T is the duration of the full A_bs(t) waveform, t_d is the hardware dwell time, and K is a design parameter which trades off the maximum offset of the frequency sweeps and undesired excitation by A_bs(t). K = 0.2 was used for all pulses in this work, which produces a maximum frequency offset of ∼10–30 kHz for a practical ω_off range of 5 − 20 kHz. The full FM waveform with constant frequency plateau ω_off is then given by:

$$\Delta {\omega }_{rf}\left(t\right)=\left\{\begin{array}{cc}-\Delta {\omega }_{sweep}\left(t+T/2\right)+\max \left(\Delta {\omega }_{sweep}\left(t\right)\right)+{\omega }_{off},& -T/2<t<0,\\ -\Delta {\omega }_{sweep}\left(T/2-t\right)+\max \left(\Delta {\omega }_{sweep}\left(t\right)\right)+{\omega }_{off},& 0\le t<T/2.\end{array}\right.$$

An example of an amplitude- and frequency-modulated b_bs(t) is shown in Fig. 1a. Note that the frequency modulation of this pulse is positive for all t, producing a negative Bloch-Siegert shift for all $B_1^{+}$. As a result, the frequency-selective excitation pulse described in the next section is modulated to a negative frequency relative to Larmor, to excite the desired $B_1^{+}$ passband.

Component Pulse 2: The Frequency-Selective SLR Excitation Pulse

For a given desired passband between field strengths $B_{1,L}^{+}$ and $B_{1,H}^{+}$, the bandwidth of resonant frequencies that must be excited by the frequency selective SLR pulse b_ex(t) is:

$$B={\omega }_{bs}\left(B_{1,L}^{+},{\omega }_{off}\right)-{\omega }_{bs}\left(B_{1,H}^{+},{\omega }_{off}\right).$$

b_ex(t) must further be frequency modulated to the center of the passband, which has frequency:

$${\omega }_{cent}=\frac{1}{2}\left({\omega }_{bs}\left(B_{1,L}^{+},{\omega }_{off}\right)+{\omega }_{bs}\left(B_{1,H}^{+},{\omega }_{off}\right)\right).$$

The Shinnar Le-Roux (SLR) pulse design algorithm is used to design b_ex(t) since it allows for direct design of pulses to meet design constraints including bandwidth (B), duration (T_ex), flip angle (θ), transition width, and magnetization profile ripple (${\delta }_1^e$ and ${\delta }_2^e$) (27). Based on these parameters, SLR designs a pair of polynomials that are transformed to the discretized excitation pulse by the inverse SLR transform. Given the designer’s choice of time-bandwidth product T_exB, the duration of the excitation pulse T_ex is determined by B. The RF pulse output by SLR is interpolated to the target dwell time and scaled to produce the desired flip angle θ for the $B_1^{+}$ at its passband center, based on the relationship:

$$\theta =\gamma {\Delta }_t{B}_1^{+}\left({\omega }_{cent}\right)\sum _{i=0}^{N-1}{A}_{ex}\left(t_i\right),$$ (3)

where ∆_t is the dwell time, N is the number of time points in the pulse, and A_ex(t) is the baseband RF pulse waveform generated by SLR after interpolating it to the target dwell time. $B_1^{+}\left({\omega }_{cent}\right)$ is derived from Eq. 1 after rearranging it to give the $B_1^{+}$ producing a Bloch-Siegert shift of ω during an RF pulse with frequency offset ω_off > 0:

$$B_1^{+}\left(\omega \right)\approx \frac{w_{off}}{\gamma }\sqrt{{\left(1-\frac{\omega }{{\omega }_{off}}\right)}^2-1}.$$ (4)

After scaling A_ex(t) to the desired flip angle, b_ex(t) is obtained by frequency modulating it to ω_cent. The final pulse is then:

$$b_{ex}\left(t\right)=A_{ex}\left(t\right)e^{i{\omega }_{cent}t}.$$

Before summing b_ex(t) with b_bs(t), b_ex(t) is zero-padded to match the full duration T of b_bs(t). An example b_ex(t) with T_exB = 4 and θ = 90° is shown in Figure 1a.

However, under the assumption that both b_ex(t) and b_total(t) are played from the same transmit coil, b_ex(t) will produce a sloped magnetization profile (or a distorted profile, in the case of 180° excitation) due to the fact that b_ex(t) is played out slightly weaker than designed at passband locations where $B_1^{+}<B_1^{+}\left({\omega }_{cent}\right)$ and slightly stronger than designed where $B_1^{+}>B_1^{+}\left({\omega }_{cent}\right)$. The degree of distortion will depend on the width of the passband relative to its center, $\left(B_{1,H}^{+}-B_{1,L}^{+}\right)/B_1^{+}\left({\omega }_{cent}\right)$, and is therefore more pronounced for wide passbands and center positions closer to zero. Modifications can be made to the SLR algorithm to correct for these distortions, and the procedure adopted is outlined in Fig. 2a. For small-tip and 90° excitation, the distortion is approximately compensated by scaling the SLR algorithm’s B_N (ω) polynomial by the inverse of the transmit field strength corresponding to each frequency ω in the profile, with normalization to $B_1^{+}\left({\omega }_{cent}\right)$, prior to applying the inverse SLR transform:

$$B_N\left(\omega \right)\leftarrow \frac{B_1^{+}\left({\omega }_{cent}\right)}{B_1^{+}\left(\omega +{\omega }_{cent}\right)}{B}_N\left(\omega \right).$$

Figure 2.

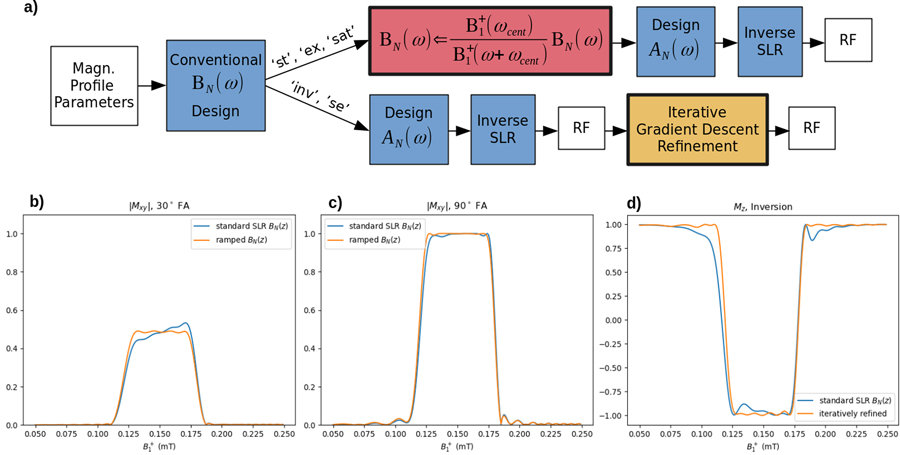
a) SLR design algorithm to compensate for a sloped excitation profile across $B_1^{+}$. In the case of small-tip (‘st’) or 90° (‘ex’, ‘sat’) excitation, a pointwise scaling of the B_N(ω) profile is sufficient. For an inversion (‘inv’) or refocusing (‘se’) pulse, iterative refinement is required. b) Uncorrected and corrected 30°, PBC = 0.15 mT, PBW = 0.06 mT, T_exB = 8 excitation. c) Uncorrected and corrected 90° excitation. d) Uncorrected and corrected inversion profile after autodifferentiated gradient descent optimization of the pulse with respect to its magnetization profile, Iterative refinement corrected the highly distorted transition bands of the profile.

For 180° inversion or refocusing, profile distortion cannot be corrected with this analytic method. Instead, an iterative optimization of the RF pulse is used to alleviate profile distortion caused by varying $B_1^{+}$ (described further in Methods).

Overall Pulse Design Procedure

The overall pulse design procedure is to first select the $B_1^{+}$ passband edges $B_{1,H}^{+}$ and $B_{1,L}^{+}$, the excitation pulse’s SLR algorithm parameters and flip angle, and the BS pulse’s frequency offset ω_off. With these parameters, the SLR pulse is designed, interpolated to the target dwell time, scaled to the desired flip angle, and frequency modulated to the center frequency ω_cent of the slice, yielding the pulse b_ex(t). Knowing the duration T_ex of b_ex(t) the BS pulse b_bs(t) is calculated, b_ex(t) is zero-padded to the same length as b_bs(t), and the two pulses are complex-summed to obtain the total pulse b_total(t) = b_bs(t) + b_ex(t). It should be noted that the choice of ω_off is critical to the performance of the pulse. Figure 3a shows the relationship between ω_off and total pulse duration. For all BSSE pulses duration is minimized by minimizing ω_off (which maximizes the Bloch-Siegert frequency gradient). However, as shown in Figure 3b, bringing ω_off too close to the Larmor resonance produces undesirable out-of-band excitation.

Figure 3.

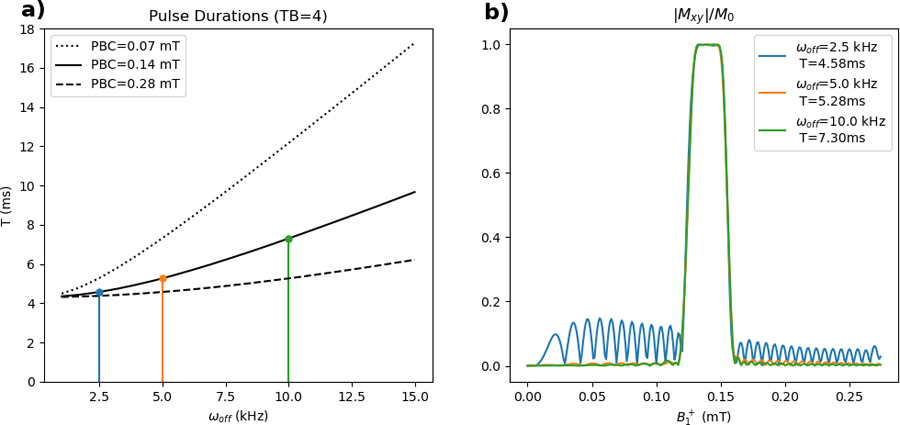
a) Variation in BSSE pulse duration with ω_off and PBC in $B_1^{+}$. Pulse duration increases with increasing ω_off and decreases with increasing $B_1^{+}$ PBC. The magnetization profiles of pulses designed at the three points of interest are plotted in (b). b) Magnetization profiles of BSSE pulses with PBC=0.14mT. Out-of band excitation can be large if ω_off is set too small: a pulse with ω_off = 2.5 kHz produces a substantial amount of out-of-band excitation, which is reduced to within design specifications when ω_off → 5.0 kHz. Further increasing ω_off to 10.0 kHz produced only marginal improvement.

As in conventional B₀ gradient-selective excitations, at the end of a BSSE excitation pulse there will be a phase ramp across the slice that must be refocused if the slice dimension will not be resolved by subsequent spatial encoding. For BSSE pulses, the phase ramp depends on the b_ex(t) pulse’s isodelay and the K_BS of the b_bs(t) pulse (18). A BSSE rewinding pulse can be constructed in the same manner as b_bs(t), but with opposite frequency sign and a central constant frequency offset section with duration equal to the isodelay of b_ex(t). That is, the rewinding pulse should have a K_BS equal to the negative of b_bs(t)’s K_BS, and scaled by b_ex(t)’s isodelay divided by the total duration of b_bs(t).

Motion of the Magnetization Vector

With the full BSSE waveform defined, the trajectory of a magnetization vector $\overrightarrow{\mathbf{M}}$ during application of a BSSE RF pulse b_total(t) can be described. Figures 4b and 4c show the motion of the normalized magnetization vector $\overrightarrow{\mathbf{M}}$ in a frame rotating at ω_off for spin isochromats in $B_1^{+}$ fields at 0.17 mT (in the stopband) and at 0.14 mT (in the passband), respectively, during application of the BSSE pulse of. During the first adiabatic sweep of the RF pulse, both magnetization vectors rotate down from equilibrium to an axis that is slightly tilted away from the x-y axis. At the end of the initial sweep, when $\left|b_{total}\left(t\right)\right|\approx \left||b_{bs}\left(t\right)\right|$ and $\Delta {\omega }_{rf}\left(t\right)\approx {\omega }_{off}$, $\overrightarrow{\mathbf{M}}$ is approximately colinear with the tilted effective field

$${\overrightarrow{\mathbf{B}}}_{1,eff}=\left[\begin{array}{ccc}\gamma B_1^{+}& 0& {\omega }_{off}\end{array}\right]/\gamma$$

at which point the frequency-selective b_ex(t) pulse begins. For the stopband isochromat of Fig. 4b this pulse is not resonant, but it is resonant with the isochromat of Fig. 4c and the magnetization is nutated by the component of b_ex(t) perpendicular to ${\overrightarrow{\mathbf{B}}}_{1,eff}$ to the opposite side of the unit sphere. After b_ex(t) is completed, the second adiabatic frequency sweep returns $\overrightarrow{\mathbf{M}}$ to being approximately colinear with the main magnetic field. The stopband isochromat in Fig. 4b is coaligned and approximately unperturbed from equilibrium, while the passband isochromat of Fig. 4c is successfully inverted. An video illustrating the magnetization motion is included as Supporting Information Video V1.

Figure 4.

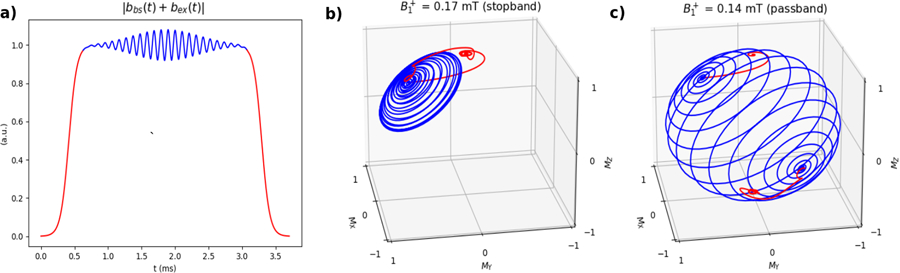
a) Magnitude of a T = 3.7 ms BSSE inversion pulse. The pulse is colored red during the adiabatic frequency sweeps when b_ex(t) = 0, and blue during the constant portion of b_bs(t) when b_ex(t) ≠ 0. b) Motion of the net magnetization vector in the ω_off rotating frame for a stopband isochromat. Simulation timestep was 4 µs. At the end of the pulse, magnetization is essentially unperturbed. c) Motion of the net magnetization vector in the ω_off rotating frame for a passband isochromat. At the end of the pulse, magnetization is successfully inverted.

Compensating flip angle errors

The pulse design algorithm described above is based on the implicit approximation that the effect of applying b_bs(t) is to produce a pure $B_1^{+}$-dependent resonance frequency shift. In reality, as illustrated in Fig. 4, b_bs(t) rotates magnetization to precess in a plane that is slightly tilted from the x-y plane, at an angle ${\tan }^{-1}\left(\frac{\gamma B_1^{+}}{{\omega }_{off}}\right)$ from the z-axis. Ideally, b_ex(t) would also be applied in this tilted plane, but it remains in the x-y plane, and the actual flip angle produced by b_ex(t) will be slightly smaller than expected because its projection onto the tilted plane will be elliptical and smaller than its full amplitude. This results in a flip angle attenuation that increases as ω_cent/ω_off becomes large. Similar effects have been previously observed in other dual-frequency RF applications (32, 33). Given the difficulty of describing and correcting this effect analytically, a normalized empirical correction is given herein for the amplitude of A_ex(t) based on Bloch simulations of slice profiles across a wide range of ω_cent and ω_off. The model is shown in Fig. 5a, and the equations for the correction predicted by the model is provided in the Appendix. Deviations are generally small and require minimal correction for pulses where ω_cent/ω_off < 1 as suggested by the example profile correction shown in Fig. 5b. This comprises the majority of practical BSSE pulses. Pulses with ω_cent substantially larger than ω_off are in general encountered when designing a pulse to select a PBC at very large $B_1^{+}$ (which produces a large Bloch-Siegert shift and thus large ω_cent relative to ω_off ), or when a very small ω_off is used, which is typically impractical due to the large out-of-band excitation produced.

Figure 5.

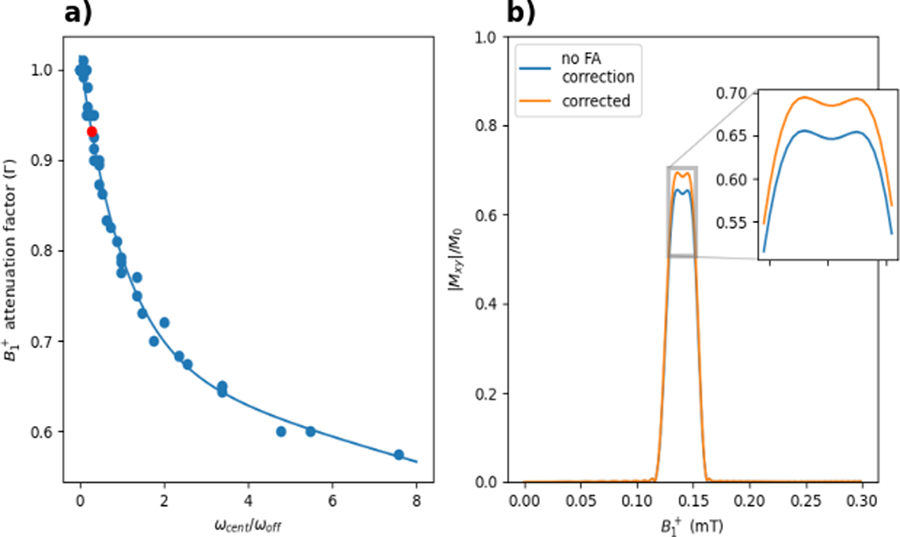
a) Flip angle attenuation factor versus ω_cent/ω_off. Data points are empirical correction factors found through simulation, with an exponential fit to the data shown as a continuous line. The red dot indicates the parameters of the pulse simulated in (b). b) Excited slice profile of a PBC =0.14 mT, PBW = 0.03 mT, 45°, ω_off =7.5 kHz pulse with and without the empirical FA correction. For this pulse, ω_cent/ω_off = 0.279, which the model predicts will result in a flip angle attenuation of 6.9% if uncorrected. Applying the correction improves the effective flip angle of the pulse, bringing it closer to the anticipated |M_xy|/M₀ = 0.7

Multiphoton Resonances

As discussed in the previous section, the simultaneous application of two off-resonance RF pulses in BSSE excitation leads to non-linear effects including small flip angle errors. A second effect is the appearance of subsidiary multiphoton resonances, in addition to the single-photon resonance. These are a consequence of the BSSE pulse’s simultaneous irradiation of nuclei at two frequencies near (generally within 10’s of kHz) but not at the Larmor frequency (24). While unwanted higher-order multiphoton resonances cannot be corrected simply by adjusting the b_ex(t) pulse’s amplitude or frequency, their positions can be predicted analytically as follows and used to guide the pulse design.

The off-resonance frequencies of the two component pulses b_ex(t) and b_bs(t) are ω_cent and ω_off, with an average frequency of the two off-resonant pulses ${\omega }_{av}=\frac{1}{2}\left({\omega }_{cent}+{\omega }_{off}\right)$. Multiphoton resonances occur at frequencies ω_0,N for which the following is satisfied:

$$\left|\frac{{\omega }_1-{\omega }_{av}}{{\omega }_{0,N}-{\omega }_{av}}\right|\approx \frac{1}{N},N=1,3,5,\dots ,$$

where ω₁ is equivalently either ω_off or ω_cent (25). N = 1 corresponds to the single-photon resonance while N = 3, 5, 7 . . . correspond to multiphoton resonances. Arbitrarily taking ω₁ = ω_off, two solutions exist for ω_0,N :

$${\omega }_{0,N}\approx {\omega }_{av}\pm N\left({\omega }_{off}-{\omega }_{av}\right)$$ (5)

In this application, because ω_off > 0 will produce a negative frequency shift for all $B_1^{+}$, only ω_0,N < 0 are of interest. These resonances are given by the solution ${\omega }_{0,N}\approx {\omega }_{av}+N\left({\omega }_{off}-{\omega }_{av}\right)$. To determine the locations of the multiphoton resonances on the $B_1^{+}$ axis, we can substitute Eq. 5 into Eq. 4, giving:

$$B_{1,mp}^{+}\left(N,{\omega }_{av},{\omega }_{off}\right)\approx \frac{{\omega }_{off}}{\gamma }\sqrt{{\left(1-\frac{{\omega }_{av}+N\left({\omega }_{off}-{\omega }_{av}\right)}{{\omega }_{off}}\right)}^2-1},N=1,3,5,\dots$$ (6)

Pulses with two combinations of ω_off and ω_cent but with the same PBC for the N = 1 excitation are shown in Figure 6a: the red pulses have ω_off =10 kHz and ω_cent=−1.655 kHz, and the black pulses have ω_off =7.5 kHz and ω_cent=−2.094 kHz. Figure 6b shows the distribution of multiphoton resonances across $B_1^{+}$ for the two ω_off. For both ω_off, the combination of RF frequencies place the N = 1 resonance at 0.14 mT. For the 90° and 180° pulses there is a small amount of excitation produced at the N = 3 resonance (maximum |M_xy|/M₀ = 0.075 for the excitation and maximum M_z/M₀ = 0.918 for the inversion), but excitation at N > 3 is below the stopband ripple level of the pulses. In the case of the pulse scaled up to produce a 720° flip, a greater number of multiphoton resonances can be appreciated. These simulated resonances shown in Figure 7b are at the approximate locations predicted by Equation 6; in the case of the black pulse (ω_off = 7.5 kHz), the resonances (aside from N = 1) are at $B_{1,mp}^{+}=\left[0.14,0.41,0.65,0.88,1.11,1.34\right]$ mT. In the case of the red pulse (ω_off = 10 kHz), the predicted locations of the N = 1 to 11 resonances shift up to $B_{1,mp}^{+}=\left[0.14,0.49,0.79,1.07,1.35,1.62\right]$ mT. Using a larger ω_off can shift multiphoton resonances upward in $B_1^{+}$ and out of the imaging bandwidth, although this decreases the Bloch-Siegert frequency gradient and thus requires longer pulse durations.

Figure 6.

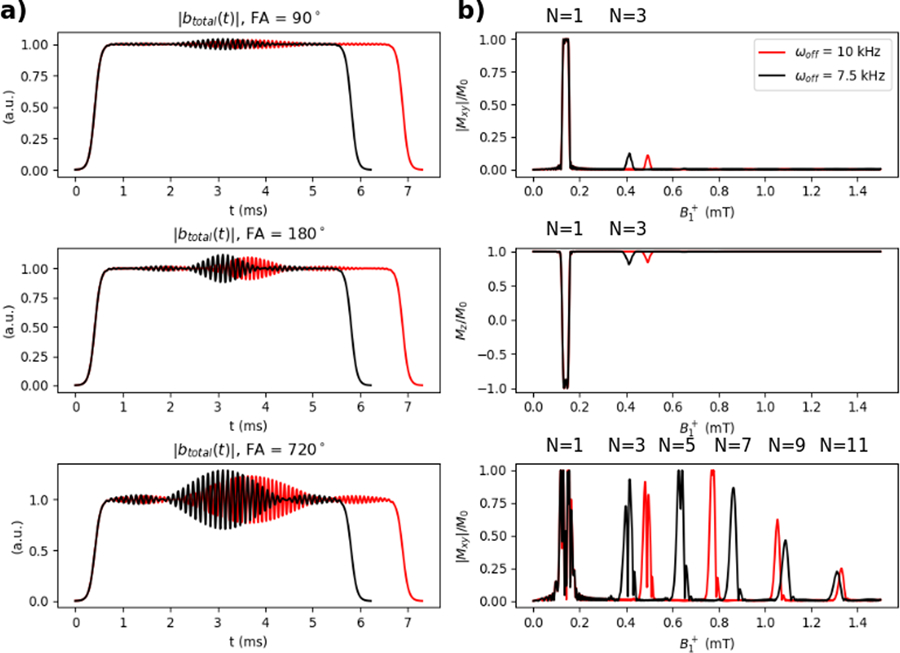
a) Magnitudes of 90°, 180°, and 720° BSSE pulses with ω_off = 7.5 kHz (black) and ω_off = 15.0 kHz (red). b) The corresponding simulated magnetization profiles. Multiphoton resonances are visible at the locations in $B_1^{+}$ predicted by Equation 6. Increasing ω_off shifts resonances N ≥ 3 upward in $B_1^{+}$.

Figure 7.

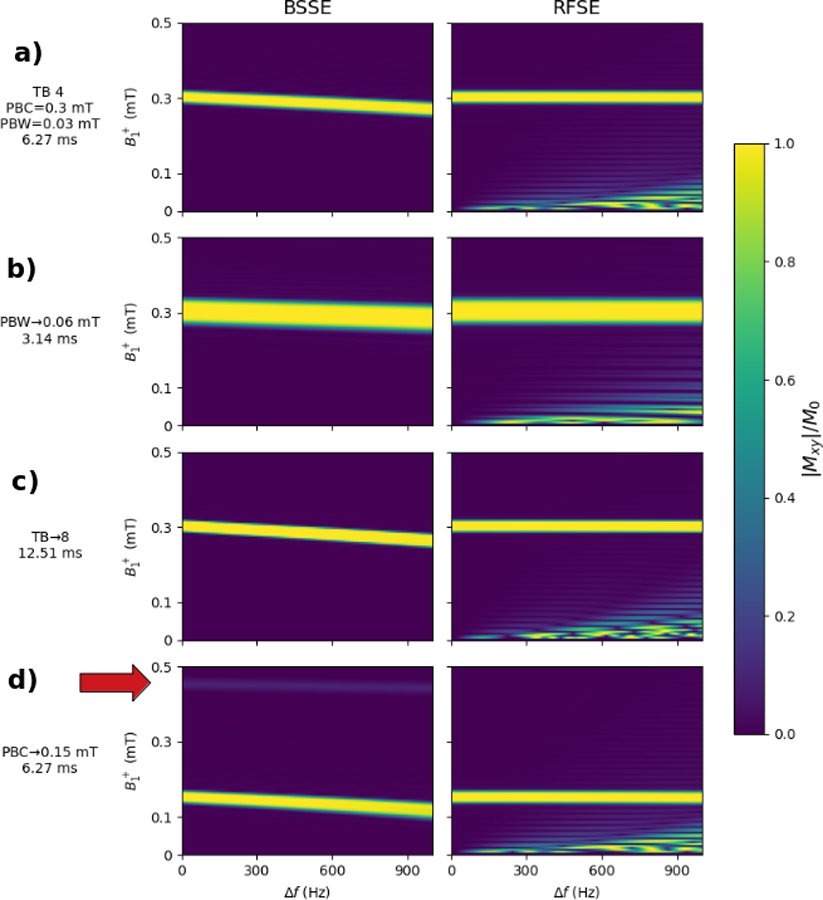
Simulations of BSSE and RFSE pulse off-resonance sensitivity. a) Simulation of the “base” 6.27ms BSSE and RFSE pulses with TB=4, PBC=0.4 mT, PBW=0.03 mT, FA=90°. ω_off was set to 16.37 kHz to match the RFSE pulse duration. b) Same as base pulse but with PBW set to 0.06 mT. ω_off was set to 9.48 kHz to match durations. c) Same as base but with TB set to 8. ω_off was set to 19.25 kHz to match durations. d) Same as base but with PBC set to 0.15. ω_off was set to 8.17 kHz to match durations. In all cases, the BSSE magnetization profiles show a bulk shift in the magnetization profile with increasing off-resonance. The red arrow in d) shows the location of an N = 3 multiphoton resonance. This multiphoton resonance also experiences a bulk shift downward in $B_1^{+}$ with increasing off-resonance. The RFSE profiles show no bulk shift, but have substantial unintended excitation at low $B_1^{+}$.

Methods

Simulations

Simulations were performed to demonstrate the effectiveness of SLR B_N (ω) ramp correction, to evaluate the pulses’ suitability for refocusing in an RF gradient slice-selective CPMG pulse sequence, and to compare their performance to RFSE $B_1^{+}$-selective excitation pulses (16) in the presence of B₀ inhomogeneity and nonideal RF hardware. All simulations were performed using a hard pulse approximation-based Bloch simulator (27) in SigPy.RF (35) with 1 µs dwell time. All BSSE and RFSE pulses were designed using SigPy.RF pulse design functions. Code for BSSE pulse design is available at: https://github.com/jonbmartin/sigpy-rf.

Profile Ramp Correction

Simulations were performed to verify the ability of the BSSE ramp correction algorithm to correct passband distortions caused by varying $B_1^{+}$. A 30° small-tip pulse, a 90° excitation pulse, and a 180° inversion pulse were constructed and their magnetization profiles were simulated across $B_1^{+}$. For all three pulses, PBC = 0.14 mT, PBW = 0.06 mT, T_exB = 8, $d_1^e=d_2^e=0.01$, ω_off = 7.5 kHz; these parameters were chosen to create a profile in which uncorrected distortions were clearly visible. In profiles with smaller T_exB or PBW, the distortion is not easily observable. The small-tip and 90° excitation pulses were designed using the analytic B_N (ω) ramp correction. In the inversion case, an uncorrected BSSE inversion pulse was designed to meet the profile parameters specified above as well as possible. This pulse was used as the initializer for an iterative gradient descent refinement to eliminate distortions. The following general unconstrained problem was solved:

$$\underset{{\mathit{b}}_{total}}{\min }\sum _{i=0}^{N_b-1}{w}_i{\left|M_z\left({\mathit{b}}_{total},B_{1,i}^{+}\right)-M_{z,d}\left(B_{1,i}^{+}\right)\right|}^2,$$ (7)

where ${\left\{M_z\left({\mathit{b}}_{total},B_{1,i}^{+}\right)\right\}}_{i=0}^{N_b-1}$ is the Bloch-simulated M_z Profile of the BSSE pulse vector b_total across transmit field strengths ${\left\{B_{1,i}^{+}\right\}}_{i=0}^{N_b-1}$, and ${\left\{M_{z,d}\left(B_1^{+}\right)\right\}}_{i=0}^{N_b-1}$ is the desired inversion profile across the same $B_1^{+}$ range. The $\left\{w_i\right\}$ are error weights used to specify the transition regions of the profile as ‘don’t care’ regions for the optimization. The gradient of the loss was calculated across a grid of 250 points in $B_1^{+}$ from 0 to 0.25 mT using an automatic differentiation function from the JAX software toolbox (36). Gradient descent steps were taken to minimize this loss, with a fixed step size of 1e−4. Iterations were performed until convergence, defined as a difference in loss between iterations of less than 1%.

Off-Resonance Simulation

Four BSSE pulses and four RFSE pulses were designed, with ω_off of the BSSE pulses set to give the pulses the same duration as the RFSE pulses. The ‘base’ pulse for both pulse classes was a 6.27 ms T_exB = 4 pulse at 90° flip angle, centered at PBC = 0.4 mT with PBW = 0.03 mT and M_xy passband and stopband maximum errors of ${\delta }_1^e={\delta }_2^e=0.01$. The other three pulses each had one parameter changed from the base pulse (Pulse 1): Pulse 2 had its’ PBW doubled to 0.06 mT (decreasing the duration to 3.14 ms), Pulse 3 had its’ time bandwidth product doubled to 8 (increasing the duration to 12.53 ms), and Pulse 4 had its’ PBC shifted to 0.15 mT (keeping the duration of the pulses fixed at 6.27 ms). ω_off for the four BSSE pulses were set to 16.370 kHz, 9.485 kHz, 19.250 kHz, and 8.170 kHz, respectively, to match RFSE pulse durations. Magnetization was simulated over a $B_1^{+}$ range of 0–0.5 mT and an off-resonance range of 0–1 kHz.

RF Amplifier Droop Simulation

A weakness of RFSE $B_1^{+}$-selective pulses is their requirement that the pulse AM envelope be carefully balanced (16), since the pulses operate by spinning magnetization in the y-z plane while tipping magnetization in the passband towards x, and any errors in the envelope will result in large undesired excitation in y. This is a challenging demand for many RF amplifiers. RF amplifier droop was simulated for both a BSSE and an RFSE pulse to compare their robustness. Both pulses were designed with PBC=0.14 mT, PBW=0.03 mT, T_exB = 4, 45° flip angle, and ${\delta }_1^e={\delta }_2^e=0.01$. ω_off of the BSSE pulse was set to 7.608 kHz to match the durations of the two pulses (6.22 ms). Droops of −0.5 dB and −1.5 dB in the relative pulse amplitudes across the total duration were simulated (Figures 8a, 8c).

Figure 8.

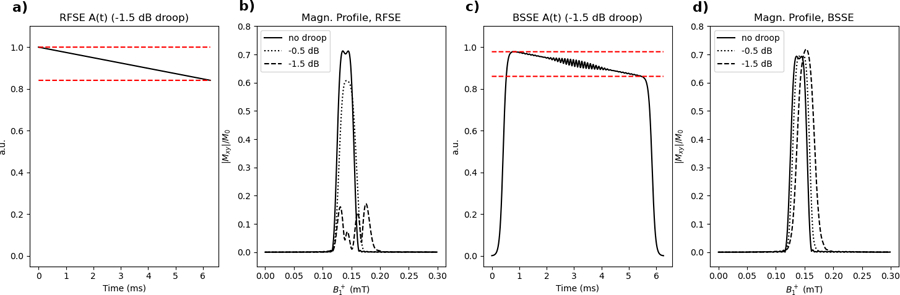
Simulation of RF amplifier droop. AM waveforms for RFSE (a) and BSSE (c) RF pulses are shown with −1.5dB of droop. In the case of the RFSE pulse, the magnetization profile (b) is severely degraded by RF amplifier distortion. However, the magnetization profile of the BSSE pulse (d) experiences only a slight shift upward in $B_1^{+}$, with minimal profile distortion.

CPMG Sequence Simulation

A multi-echo spin echo pulse sequence was constructed using BSSE excitation and refocusing pulses. The same BSSE pulse parameters were used as in the previous experiment (PBC = 0.14 mT, PBW = 0.03 mT, T_exB = 4, ω_off =7.5 kHz, T = 6.22 ms) to design a 90° excitation pulse and a 180° refocusing pulse. The BSSE refocusing pulse was iteratively refined to eliminate any ramped $B_1^{+}$ distortion.

The b_bs(t) design algorithm was used to generate a pair of RF pulses serving as $B_1^{+}$ phase pre- and rewinder gradients. These pulses were given an equal-magnitude/opposite-signed ω_off as the BSSE pulse to produce a shift in resonant frequency opposite that of the refocusing pulse, with |K_BS| half that of the refocusing pulse (32.2 vs 16.1 rad²/G). The 90° BSSE excitation pulse was applied along the x-axis and was followed by eight refocusing pulses applied along the y-axis for an echo train length of 8, with TE = 2τ = 33 ms. The RF pulse sequence diagram is shown in Figure 9a. The pulses were simulated across a $B_1^{+}$ range of 0 to 0.3 mT and a range of frequency offsets between −200 and 200 Hz, with T₁ = T₂ = ∞.

Figure 9.

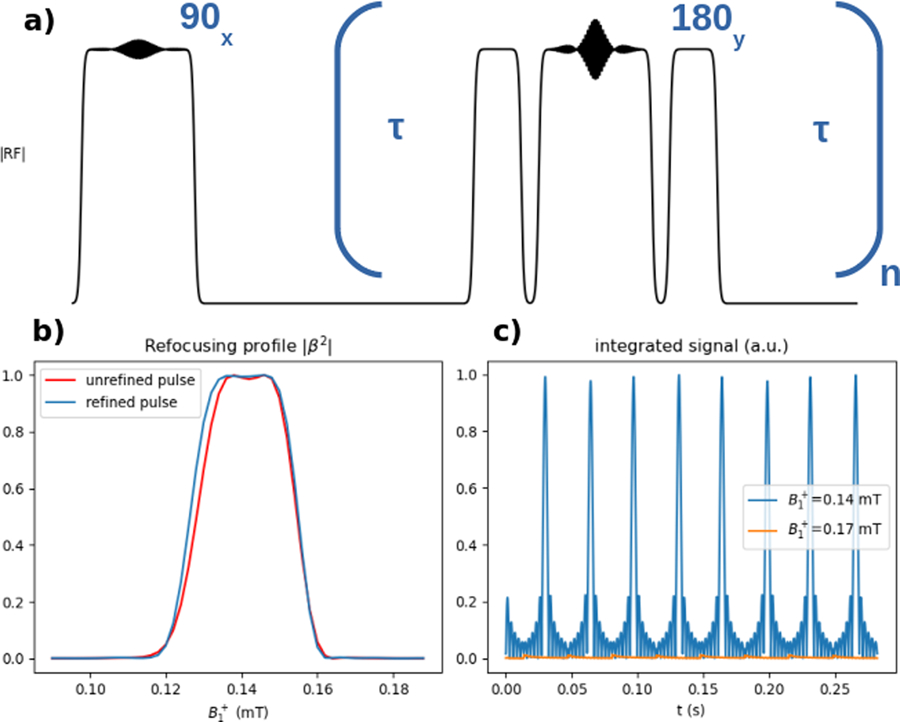
BSSE Multi-echo CPMG pulse sequence. a) Pulse sequence diagram. A 90° excitation pulse was followed by a train of 180° pulses. To satisfy the CPMG phase conditions, RF pre- and re-winders were inserted before and after the 180° refocusing pulses. b) |β²| refocusing efficiency profile for the refocusing pulse. Refocusing was selective and nearly complete across the passband. The gradient descent-refined 180° pulse had a slightly improved profile, although the unrefined pulse also performs well given the narrow PBW. c) Signal timecourse in the passband and stopband. Regularly spaced echos of uniform amplitude were produced in the passband.

Experiments

Phantom experiments were performed to verify the magnetization profiles produced by BSSE pulses. A base BSSE pulse with flip angle 90°, PBC = 0.14 mT, PBW = 0.03 mT, ω_off = 7.5 kHz, T_exB = 4, and total duration T = 6.22 ms was designed. Three copies of the pulse were created in which a single parameter was varied: passband center (0.14 mT → 0.11 mT), flip angle (90° → 45°), and time-bandwidth product (4 → 1.5). The pulses were deployed on a 47.5 mT permanent magnet (Fig 10a) (Sigwa MRI, Boston, MA, USA) and image data were acquired using a Tecmag Redstone MRI Console (Tecmag, Houston, Texas, USA). The system used a 1 µs transmit dwell time and amplitude/phase tables for RF waveform definition. A 2 kW BT02000-AlphaS Tomco RF power amplifer (Tomco Rechnologies, Stepney, Australia) was used to drive a 20-turn variable-pitch solenoid RF T/R coil producing a linearly decreasing $B_1^{+}$ gradient (Fig 10b). A 50 mL 1 mM CuSO4 vial phantom with 30 mm diameter and 115mm length was imaged using a 3D gradient-recalled echo pulse sequence (TR/TE = 27/425 ms, dx/dy/dz = 2.0/3.5/3.5 mm, matrix size = 128×49×3, 5 signal averages), where the BSSE pulses were used for excitation. Phase variation produced across the excitaton profile by the BSSE excitation pulse was not rewound in this pulse sequence. Conventional B₀ gradients were used for image spatial encoding. $B_1^{+}$ mapping was also performed using the BS shift method (18) with the same 3D gradient-recalled echo sequence but with the addition of a hard pulse excitation. The 6.22 ms, ω_off =7.5kHz component of the BSSE pulse was kept as the $B_1^{+}$-dependent phase shift-generating pulse (K_BS = 32.2 rad²/G) for $B_1^{+}$ mapping, producing no excitation without the addition of the b_ex(t) component pulse. To process the images, a mask was created by thresholding a 90° hard pulse GRE acquisition with the same matrix size and resolution to 20% of the maximum signal intensity. This mask was applied to the phase images of the $B_1^{+}$-mapping sequence and magnitudes of the BSSE-excitation images. The $B_1^{+}$ mapping phase image was unwrapped along the coil’s gradient dimension, and background phase was subtracted out using a reference scan without a BS shift pulse. $B_1^{+}$ strength was then calculated using the K_BS of the off-resonant pulse. The BSSE excitation images were divided by the $B_1^{+}$ map to remove the receive sensitivity of the T/R coil, since $\left|B_1^{+}\right|~\left|B_1^{-}\right|$ at this low frequency.

Figure 10.

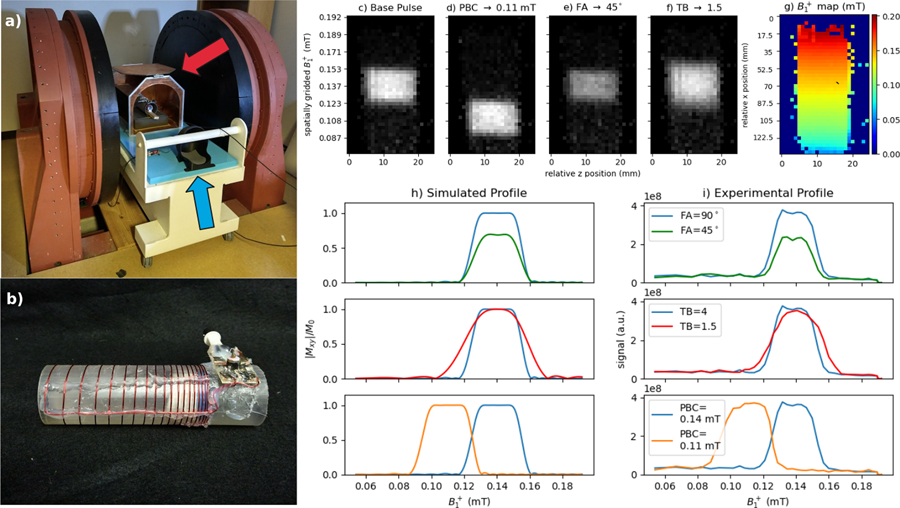
a) 47.5 mT permanent magnet system used for experimental results. A Faraday cage (red arrow) and pickup coil (blue arrow) are used to reduce EMI. b) variable-pitch T/R solenoid coil used in experiments. The tube phantom is placed inside in this image. c-f) middle slice of 3D GRE acquisition with varying BSSE excitation pulse. g) $B_1^{+}$ map corresponding to the same slice h) 1D simulated profiles for the pulses, and i) corresponding experimental 1D profiles. The 45° excitation (green) produces reduced signal intensity in relation to the 90° excitation (blue). The TB=1.5 excitation (red) produces a profile with a broader transition region. Designing the pulse with PBC shifted to 1.1 G (orange) produces the corresponding change in the magnetization profile.

Results

Ramp Correction Simulation

Figures 2b–d shows the improved small-tip excitation, 90° excitation, and inversions with ramp correction. The small-tip excitation had a substantial ramp across $B_1^{+}$ when uncorrected which was flattened by the analytic correction, with differences between normalized $\left|M_{xy}\right|/M_0$ at passband edges reduced from 0.0893 in the uncorrected case to less than 0.001 in the corrected case. The 90° excitation also had substantially reduced distortion in the passband, particularly on the rising edge of the profile. Iterative optimization of the inversion pulse reached convergence after 37 gradient descent iterations. The final optimized pulse produced a substantially improved magnetization profile which met the desired ripple levels $\left(d_1^e=d_2^e=0.01\right)$ and transition width. The substantial ripple produced by over-flipping on the falling edge of the profile was eliminated, and the broad transition on the rising edge of the profile was sharpened.

Off-Resonance Simulations

The results of the off-resonance simulation are shown in Fig. 7. All RFSE pulses produced a triangular pattern of erroneous excitation where the effective size of the off-resonance field was large compared to the $B_1^{+}$ field. This effect is absent from the BSSE pulse profiles. At the same time, all four BSSE pulses show a small bulk downward shift in the excitation profile with increasing off-resonance, similar to a conventional B₀ gradient-selective excitation pulse. For the four BSSE pulses shown in Figures 8a–d, the shift was −0.033 mT/kHz, −0.019 mT/kHz, −0.038 mT/kHz, and −0.036 mT/kHz. As expected, the slope of the shift correlated with pulse duration: the pulse with the shortest duration (3.14 ms) also had the smallest bulk shift (−0.019 mT/kHz). A faint N = 3 multiphoton resonance is visible in Figure 8d at approximately 0.45 mT. The N = 3 resonance also exhibited a shift downward in $B_1^{+}$ with off-resonance.

RF Amplifier Droop Simulation

The effect of RF amplifier droop on the magnetization profile is shown in Figures 8b and 8d. For the RFSE pulse, pulse droop significantly distorted the excitation profile. −0.5 dB of droop reduced the transverse magnetization by approximately 13%; −1.5 dB of droop completely degraded the magnetization profile. In the case of the BSSE pulse, however, the same droop produced minimal distortion, manifesting primarily as a small shift in the magnetization profile. This shift was approximately 0.004 mT (13% of slice width) in the case of −0.5 dB of droop and 0.013 mT (43% of slice width) in the case of the −1.5 dB droop.

CPMG Simulation

Figures 9b and 9c show the results of the multi-echo spin echo sequence simulation. The refocusing profile in Fig. 9b shows close to full refocusing efficiency within the pulses’ 0.03 mT-wide passband. This is supported by Fig. 9c, which shows the signal integrated across off-resonance at a location in the passband (0.14 mT) and the stopband (0.17 mT). In the passband evenly spaced echoes are formed, with near-identical signal amplitude produced at each echo. In the stopband, no appreciable signal was produced at the echo times.

Experimental Results

Figures 10c–f show the measured experimental profiles for the pulses played out in the experiment in the central slice of the 3D acquisition. Figure 10g shows the corresponding $B_1^{+}$ map from the same slice. 1D profiles of the simulated (Fig 10h) and experimental (Fig 10i) are shown as well. In the experimental case these were generated by averaging across the z dimension of the profile. For the two-flip angle (90° to 45°) experiment, a decrease in signal intensity was observed consistent with the expected 30% decrease based on the nominal flip angles. The ratio of the signals from the 45° and 90° excitations between the passband edges was 0.705 in simulation and 0.627 in the experiment. In the case of decreasing T_exB from 4 to 1.5, the T_exB = 1.5 profile had a wider transition width resulting from the decrease in selectivity. The ratio of the full width at half-maximum of the profiles from the T_exB = 1.5 excitation and the T_exB = 4 excitation was 1.29 in simulation and 1.21 in the experiment, showing close agreement. The pulse with PBC shifted to 0.11 mT produced a magnetization profile centered at the intended locations, and the transition bands of the pulses intersected at approximately 0.125 mT, where each profile was expected to reach its half-maximum.

The phase produced by the BSSE excitation pulses across the magnetization profile is shown in Supporting Information Figure S1. For all four of the BSSE pulses that were examined, the phase of the spins increased in an approximately linear manner across the magnetization profile, with uniform spacing between successive phase wraps over the linearly increasing $B_1^{+}$ transmit field.

Discussion

A class of excitation pulses that apply the Bloch-Siegert shift for the purpose of selective excitation was introduced. Although the Bloch-Siegert shift has been widely used in MRI for $B_1^{+}$ mapping (18, 30) and in NMR for the calibration of decoupling field power (20, 37), to our knowledge the present work represents its first use to localize selective excitation. Simulation results showed that the pulses are robust against system imperfections and can be used in pulse sequences requiring phase control, making them a viable choice for a wide range of pulse sequences. Overall, BSSE pulses enable the replacement of one axis of B₀ gradient encoding with $B_1^{+}$ gradient encoding in an imaging system. Most RF encoding systems experimentally implemented thus far including the imaging experiments performed in this work have relied on at least one axis of B₀ encoding for 3D imaging (5, 6), and further development is needed to achieve fully RF-encoded 3D imaging. More immediately, BSSE selective excitation could be combined with other pulsed B₀ gradient-free imaging systems, such as systems with built-in B₀ field inhomogeneities (39–41).

As in the RFSE design algorithm of (16), the proposed BSSE pulse design method is based on the Shinnar-Le Roux algorithm, giving BSSE pulses the same advantage in speed of design and ability to predict and trade off design parameters. However the proposed method also has a number of advantages over RFSE pulses, including the ability to refocus magnetization for spin-echo based pulse sequences, and reduced out-of-band excitation in response to B₀ inhomogeneity. RFSE pulses can also be challenging to implement experimentally because they place strict requirements on the integrated area of the RF envelope, which must be accurately balanced between pulse segments to prevent large distortions of the magnetization profile. In this work BSSE pulses were shown to be more tolerant of moderate amplifier errors in the amplitude of the RF pulse, such as amplifier droop, which led primarily to relatively benign slice shifts which could be mostly corrected by transmit gain adjustment.

BSSE pulse designers should keep several practical considerations in mind. First, the BSSE pulses demonstrated here had relatively longer durations than conventional B₀ gradient-selective excitations (several ms versus a few ms). For a fixed b_ex(t) time-bandwidth product T_exB, BSSE pulse length is principally determined by two factors: the $B_1^{+}$ gradient strength for a given b_bs(t) amplitude and ω_off, the central constant frequency offset of b_bs(t). These variables determine the magnitude of the Bloch-Siegert frequency gradient produced by b_bs(t), which in turn sets the duration of the full BSSE pulse. If the Bloch-Siegert spatial frequency gradient were of the same magnitude as a B₀ spatial frequency gradient, a BSSE pulse would have approximately the same duration as an equivalent conventional B₀ gradient selective excitation pulse. For example, to create a frequency gradient of 1 MHz/m (produced by a B₀ gradient of approximately 23.5 mT/m) using the Bloch-Siegert shift, using the ω_off =7.5kHz value used throughout this work, a $B_1^{+}$ gradient of approximately the same strength, 23.5 mT/m, would be required. Though a much weaker $B_1^{+}$ gradient of ∼2 mT/m was used here experimentally, this stronger gradient is not difficult to achieve in practice (5, 7). In general, ω_off should be minimized to maximize the Bloch-Siegert frequency gradient. However, excessive reduction of the frequency offset can produce out-of band excitation (Figure 3b, at ω_off =2.5kHz) or move multiphoton resonances closer in $B_1^{+}$ to the single-photon resonance (Figure 6) and potentially into the FOV. Although their rapid dropoff in amplitude with N makes their use for imaging challenging, it may be possible to use BSSE pulses for multiband multiphoton excitation in implementations similar to those previously described (26). However in general ω_off should be increased to move multiphoton resonances outside the FOV.

The RF power and consequently the specific absorption rate (SAR) contribution of BSSE pulses is increased compared to an equivalent B₀ gradient-selective excitation by the addition of the large, near-constant AM waveform of the off-resonant b_bs(t) pulse to the on-resonant b_ex(t) pulse. Since the pulses are well-separated in frequency, the power increase compared to a conventional pulse is approximately equal to the power of the b_bs(t) component. For example, for the 6.22 ms BSSE pulse shown in Figure 1, operating at 47.5 mT, the integrated power of b_ex(t) normalized by that of the full b_total(t) was 4 × 10⁻⁴ (a.u.), and the integrated power of b_bs(t) normalized by that of b_total(t) was 0.9996 (a.u.). Nearly all power is contributed by the b_bs(t) pulse. At the same time, SAR is much less a concern in low-field MRI such as the 47.5 mT imager used in this work (42).

Like conventional B₀ gradient-selective excitations, as demonstrated experimentally, BSSE pulses leave a phase gradient across the excited slice that should be refocused if subsequent imaging will not resolve the slice dimension. Refocusing can be achieved with a rewinding off-resonant b_bs(t) pulse, to cancel phase accrued during the pulse’s isodelay. At the same time, like conventional B₀ gradient-selective excitations, there are many situations where this is not necessary, including when using the pulses for saturation, inversion, or for slab selection in 3D imaging sequences. When used for slice-selective excitation, using a minimum-phase b_ex(t) pulse shape with a small isodelay would also reduce or eliminate the need for a rewinder. When using BSSE pulses for balanced or spin echo pulse sequences, RF pre- and rewinders may be inserted into the pulse sequence.

The experimental setup in this work used a single gradient coil for transmit and receive which is nonideal in practice, since although profiles with uniform flip were excited across the slice, the coil’s nonuniform receive sensitivity would result in spatially varying SNR. To alleviate this, the gradient transmit coil could be paired with a saddle receive coil with uniform receive sensitivity, which has been demonstrated on the 47.5 mT system described here (43).

The pulse design algorithm described here could be extended in numerous ways. Applying the VERSE algorithm (44) may allow the frequency-selective excitation pulse to extend onto the time-varying portion of the Bloch-Siegert shift inducing pulse, to shorten overall pulse duration. Additionally, BSSE pulse designs may benefit from joint gradient-based optimization of the two component pulses, in analogy to previously demonstrated joint optimization of RF and gradient waveforms (45). Further optimizing the waveforms this way could be used to, e.g., reduce multiphoton effects, decrease pulse duration, produce uniform excitation across a broad range of $B_1^{+}$, or constrain the pulses to have a flat amplitude so they can be more easily generated by current-mode amplifiers(46). Finally, the pulses could be extended to produce Hadamard or other multiband excitations, by designing the excitation pulse b_ex(t) using multiband pulse designers developed for B₀ gradient-based selective excitation (47–49).

Conclusion

In this work, we presented a novel class of pulses for $B_1^{+}$-selective excitation which localize excitation using frequency gradients produced by the Bloch-Siegert shift. Simulations demonstrate that these pulses produce magnetization profiles of excellent quality with phase control, and that the pulses are robust against off-resonance. Experimental results on an ultra-low-field 47.5 mT verified the design algorithm’s ability to control magnetization profile parameters. BSSE pulses may help enable new methods of B₀-gradient-free acquisition and novel imaging approaches.

Supplementary Material

vS1

Supporting Information Video V1 a) Magnitude of a T = 3.7 ms BSSE inversion pulse. The red trace is 10 µs long. b) Stopband magnetization trajectory in the ω_off rotating frame. The Simulation timestep was 4 µs. c) Passband magnetization trajectory in the ω_off rotating frame.

supinfo

Supporting Information Figure S1 a-d) Top: middle slice of experimental 3D GRE acquisition with varying BSSE excitation pulse. Bottom: corresponding phase across profile. Several wraps in phase are visible across all profiles, since a phase rewinder was not applied following the BSSE pulse. However the phase behavior is regular and can be rewound. Note that in d), in which the TB was decreased to 1.5, the phase increases more slowly due to the reduced isodelay of the excitation pulse. e) $B_1^{+}$ map corresponding to the same slice.

Appendix

The models used to correct for flip angle inaccuracy is as follows. The observed flip angle attenuation was fit by a biexponential model, using MATLAB’s fit() function. This attenuation model is:

$$\Gamma \left(x\right)=0.335e^{-1.116x}+0.678e^{-0.028x},$$

where x = ω_cent/ω_off. The correction is applied by accounting for Γ(x) in the flip angle relation of Eq. 3:

$$\theta =\gamma {\Delta }_t\Gamma \left(x\right)B_1^{+}\left({\omega }_{cent}\right)\sum _{i=0}^{N-1}{A}_{ex}\left(t_i\right),$$

The goodness-of-fit of this model was R² = 0.9899.