Modeling Bias Error in 4D flow MRI Velocity Measurements

Abstract

We present a model to estimate the bias error of 4D flow magnetic resonance imaging (MRI) velocity measurements. The local instantaneous bias error is defined as the difference between the expectation of the voxel’s measured velocity and actual velocity at the voxel center. The model accounts for bias error introduced by the intra-voxel velocity distribution and partial volume (PV) effects. We assess the intra-voxel velocity distribution using a 3D Taylor Series expansion. PV effects and numerical errors are considered using a Richardson extrapolation. The model is applied to synthetic Womersley flow and in vitro and in vivo 4D flow MRI measurements in a cerebral aneurysm. The bias error model is valid for measurements with at least 3.75 voxels across the vessel diameter and signal-to-noise ratio greater than 5. All test cases exceeded this diameter to voxel size ratio with diameters, isotropic voxel sizes, and velocity ranging from 3–15mm, 0.5–1mm, and 0–60cm/s, respectively. The model accurately estimates the bias error in voxels not affected by PV effects. In PV voxels, the bias error is an order of magnitude higher, and the accuracy of the bias error estimation in PV voxels ranges from 67.3% to 108% relative to the actual bias error. The bias error estimated for in vivo measurements increased two-fold at systole compared to diastole in partial volume and non-partial volume voxels, suggesting the bias error varies over the cardiac cycle. This bias error model quantifies 4D flow MRI measurement accuracy and can help plan 4D flow MRI scans.

I. INTRODUCTION

4D flow magnetic resonance imaging (MRI) is a phase contrast-MRI (PC-MRI) technique that provides time-resolved velocity measurements in three directions and has medical utility for quantifying cardiovascular flows in vivo. 4D flow MRI accuracy is of paramount importance for calculating flow-derived biomarkers such as wall shear stress (WSS) which can affect the progression of vascular disease [1]–[6].

4D flow MRI spatiotemporal resolution and velocity encoding parameter (venc) are prescribed according to the vascular territory being imaged. Spatial and temporal resolutions are reported to range from 0.5–3.0mm³ and 40–60ms, respectively [7], [8]. Jarvis et al. report setting the velocity encoding parameter (venc) as high as 150cm/s to capture the maximum expected velocity in the heart and aorta. [8]. Suboptimal spatiotemporal resolution of 4D flow MRI may result in reduced accuracy of the measured velocity field. The measured velocity error propagates into derived hemodynamic metrics. Szajer et al. compared the WSS obtained from 4D flow MRI and computational fluid dynamics (CFD) simulations. They found that 4D flow MRI-derived WSS was lower compared to CFD. This underestimation was attributed to the insufficient spatial resolution of 4D flow MRI and partial volume (PV) effects [9]. Van Ooij et al. reported that 4D flow MRI-derived WSS was underestimated by 50% compared to CFD-derived WSS. Increasing the imaging resolution resulted in higher WSS values [3]. Brindise et al. compared hemodynamic metrics derived from in vivo 4D flow MRI measurements in cerebral aneurysms to CFD and volumetric particle tracking velocimetry (PTV). Although the velocity fields were similar between modalities, considerable differences were found in the WSS-based metrics. The accuracy of WSS obtained from 4D flow MRI in smaller vessels was compromised due to insufficient spatial resolution [10].

Despite the imprecision imposed by 4D flow MRI’s resolution and PV effects, no method exists to estimate the resulting bias error. This bias error arises due to intra-voxel phase dispersion (IVPD), which sums the signal of all isochromats (i.e., spins precessing at the same frequency) [11] to yield a single value, thereby spatially under-resolving the flow measurement [12]. Several groups have introduced models to estimate or correct for IVPD. However, these approaches assume an ideal cylindrical geometry and only assess flow rate error across the vessel cross-section [11], [13], [14]. Methods to model the intra-voxel velocity distribution have been introduced by Dyverfeldt et al. but only quantify turbulent flow variables [15].

In this work, we develop a model to estimate the instantaneous and local bias error of 4D flow MRI velocity measurements by considering the intra-voxel velocity distribution and PV effects. This bias error is defined as the difference between the expectation of the velocity measurement and the actual velocity at the center of the voxel. The intra-voxel velocity distribution is assessed using a 3D Taylor Series expansion. PV effects and numerical error are modeled using a Richardson extrapolation according to the model’s order of accuracy. Using 4D flow MRI noise estimates, we calculate a 68% confidence interval to assess the accuracy of the bias error estimation. The bias error model is validated using synthetic Womersley flow and applied to in vitro and in vivo 4D flow measurements in a cerebral aneurysm.

II. THEORY

We introduce a method to evaluate the bias error (β_i) for each component of the velocity vector (i = x, y, z) due to insufficient measurement resolution. This bias error estimation is resolved in space and time. We express β_i as its bias error estimate $({\widehat{\beta }}_i)$ with 68% confidence interval bounds (σ_i,β):

$${\beta }_i={\widehat{\beta }}_i\pm {\sigma }_{i,\beta }$$ (1)

Fig. 1 presents the workflow for evaluating the bias error estimate and 68% confidence interval for the MRI-measured velocity field. In Section II-A, we derive a bias error model for a single voxel by modeling the intra-voxel velocity distribution using a Taylor Series expansion. The bias error model is then generalized in Section II-B for all voxels in the field-of-view (FOV) and expressed as a system of linear equations. We account for numerical error and PV effects using a Richardson extrapolation in Section II-C according to estimates of the order of accuracy in PV voxels. The bias error is estimated for the measured velocity field. We model the propagation of measurement noise through the model to arrive at a 68% confidence interval for the bias error estimates. A 68% confidence interval corresponds to one standard deviation for normally distributed noise. Additional details of the derivations are provided in the Appendices.

Fig. 1:

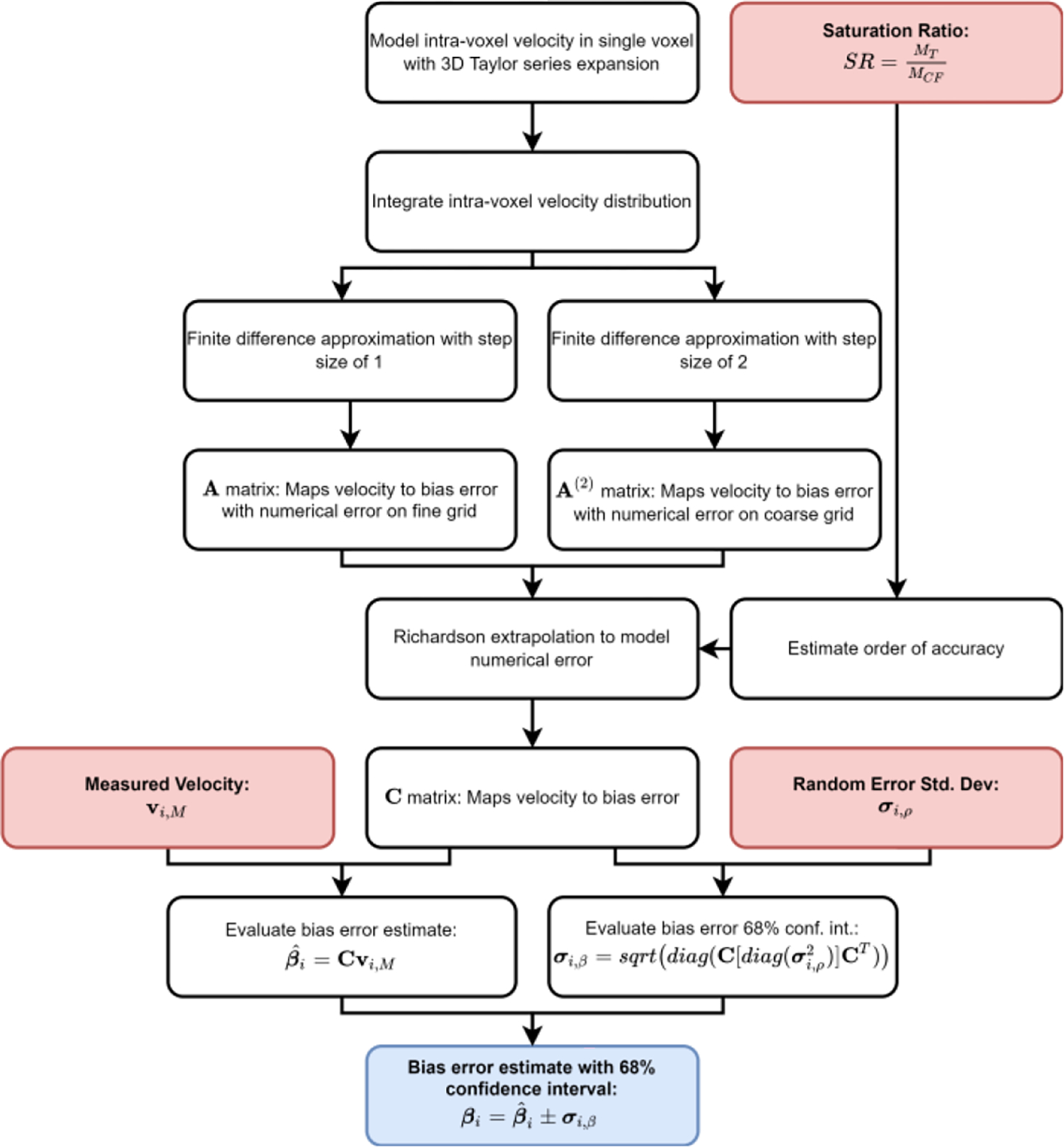
Bias error model workflow. Red boxes indicate inputs, black boxes indicate intermediate steps, and the blue box is the model output. The saturation ratio (SR) is defined for a PV voxel as the signal magnitude of the tissue (M_T) adjacent to the vessel relative to the magnitude of the neighboring core flow (M_CF).

A. Bias Error Model for a Single Voxel

We define the intra-voxel position vector $(\overrightarrow{a}\in {ℝ}^3)$ relative to the center of the voxel as shown in Fig. 2a, with voxel dimensions in each Cartesian direction denoted by δ_x, δ_y, and δ_z. It is assumed that each component of the measured velocity (ν_i,M) can be represented as the superposition of the actual velocity component (ν_i), bias error (β_i), and the zero-mean random error component (ρ_i) at the voxel’s center $(\overrightarrow{a}=\overrightarrow{0})$ [16]. The measured velocity component is expressed as:

$$v_{i,M}=v_i(\overrightarrow{a}=\overrightarrow{0})+{\beta }_i+{\rho }_i$$ (2)

Herein, the correct velocity component at the voxel’s center will be simply referred to as ν_i,0 or the “voxel-centered” velocity component. Assuming the measured velocity is represented by a stationary and ergodic process with zero-mean noise, the expectation of the measured velocity component (ν_i,0 + β_i) can be expressed as the integral of the intra-voxel velocity component distribution $(v_i(\overrightarrow{a}))$ within the limits of the voxel, divided by the total voxel volume (V):

$$v_{i,0}+{\beta }_i=\frac{1}{V}{\int }_0^V{v}_i(\overrightarrow{a})dV$$ (3)

In (3), we assume that the bias error is dominated by IVPD effects as other error sources, such as concomitant gradients and eddy currents, are corrected prior to analysis [2]. The expected velocity was evaluated using (3) by Boussel et al. when downsampling high-resolution velocity fields to the resolution of 4D flow MRI [17]. Furthermore, in the 4D flow MRI consensus statement by Dyverfeld et al., it is indicated that the expected velocity agrees well with the mean of the velocity field in voxels that are entirely composed of fluid flow [2]. This motivates the formulation of $\frac{1}{V}{\int }_0^V{v}_i(\overrightarrow{a})dV$ in (3), which is equivalent to the mean velocity in the voxel.

Fig. 2.

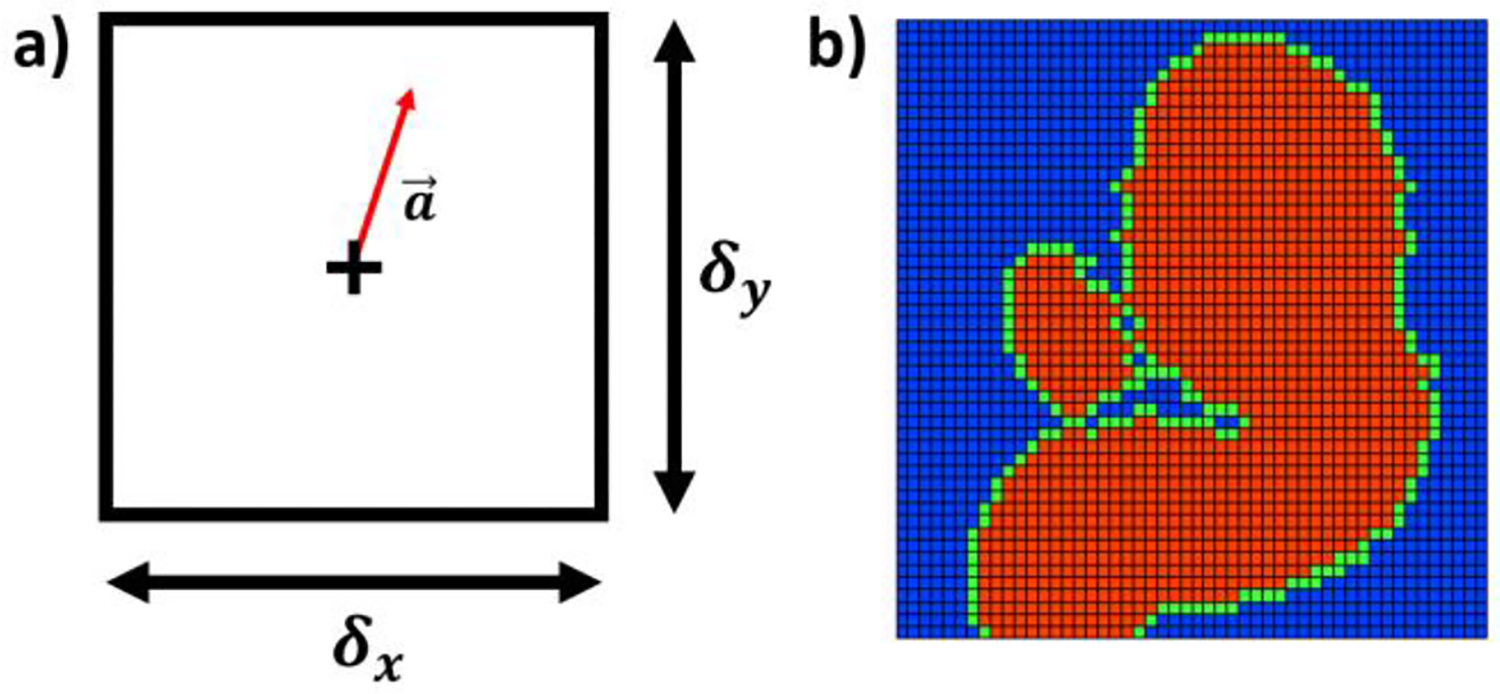
a) Intra-voxel coordinate system defined inside the voxel. The “+” denotes the voxel-center and the arrow indicates the intra-voxel position relative to the center; b) Cross-section of in vitro MR data for an internal carotid artery aneurysm indicating the tissue domain (blue), partial volume (PV) domain (green), and core flow (CF) domain (red).

The intra-voxel velocity component is approximated using a 3D Taylor Series expansion centered about $\overrightarrow{a}=\overrightarrow{0}$ (i.e., Maclaurin series):

$$v_i(\overrightarrow{a})=v_{i,0}+{\nabla v_i|}_{\overrightarrow{a}=\overrightarrow{0}}\overrightarrow{a}+{\frac{1}{2}{\overrightarrow{a}}^T\nabla \nabla v_i|}_{\overrightarrow{a}=\overrightarrow{0}}\overrightarrow{a}+\cdots$$ (4)

The Taylor Series expansion represents the intra-voxel velocity distribution as a combination of ν_i,0, odd gradient (e.g. ∇) and even gradient terms (e.g. ∇∇). The bias error is calculated by substituting (4) into (3) and simplifying:

$${\beta }_i=\frac{1}{V}{\int }_0^V\left({\nabla v_i|}_{\overrightarrow{a}=\overrightarrow{0}}\overrightarrow{a}+{\frac{1}{2}{\overrightarrow{a}}^T\nabla \nabla v_i|}_{\overrightarrow{a}=\overrightarrow{0}}\overrightarrow{a}+\cdots \right)dV$$ (5)

It is worth noting that simplification eliminates ν_i,0. Upon integrating, the odd gradient terms reduce to zero. Moreover, we found that the fourth-order and higher terms have negligible effects on the numerical approximation. As a result, even gradient terms greater than second-order are neglected. Thus, the bias error of a given voxel is:

$${\beta }_i={\frac{1}{24}\left({\delta }_x^2\frac{{\partial }^2}{\partial x^2}+{\delta }_y^2\frac{{\partial }^2}{\partial y^2}+{\delta }_z^2\frac{{\partial }^2}{\partial z^2}\right)v_i|}_{\overrightarrow{a}=\overrightarrow{0}}+\mathcal{O}\left({\delta }^4\right)$$ (6)

Equation (6) shows that each voxel dimension can be different when assessing the bias error. The fourth-order accuracy of (6) is indicated using $\mathcal{O}\left({\delta }^4\right)$ [18]. We expect (6) to remain valid so long as the velocity gradient profile is monotonic.

Equation (6) is fourth-order accurate as the gradient terms fourth-order and higher are truncated in (5). Equation (6) matches Jasak et al.’s derivation of truncation error estimates for assessing the accuracy of Finite Volume solutions [19].

B. Bias Error Model for the Field-of-View

We expand the local bias error defined by (6) to describe the bias errors for all voxels in the FOV as a linear system. This expansion is possible considering the basis vectors expressing the intra-voxel, and FOV coordinates have the same orientation. We assign all the voxels in the FOV into one of three domains: the core flow (CF) domain, the partial volume (PV) domain, and the tissue domain (Fig. 2b). We assume the velocity distribution at all points in the tissue domain is zero. The domains are generated using a mask of the vessel geometry. Voxels outside of the mask are in the tissue domain, while voxels in the mask are either in the CF or PV domain. Any masked voxels that neighbor a tissue voxel are part of the PV domain. Masked voxels that neighbor only masked voxels are CF voxels.

From (6), the $v_i{\mid }_{\overrightarrow{a}=\overrightarrow{0}}$ term is expressed as a vector (ν_i,0) of length N for every voxel in the FOV. We use ν_i,0 to compute partial derivatives based on the voxel-centered velocities. The operator applied to $v_i{\mid }_{\overrightarrow{a}=\overrightarrow{0}}$ in (6) is written as an N-by-N matrix, A, where each row numerically approximates partial derivatives using second-order accurate finite difference schemes. This allows us to express (6) as a linear system of equations and calculate the vectorized bias error component (β_i) for all N voxels in the FOV:

$${\mathit{\beta }}_i+{\mathit{\epsilon }}_i=\mathit{A}{\mathit{v}}_{i,0}$$ (7)

where ε_i represents the numerical error of the finite difference schemes and added bias error due to PV effects, which (6) does not model. A similar approach was implemented by Zhang et al. for estimating pressure gradients from 4D flow MRI velocity measurements [20]. Finite difference schemes for CF voxels use velocities only from other CF voxels, while schemes for PV voxels use velocities from all domains. Rows of A which correspond to voxels in the tissue domain are set to zeros. This enforces the assumed uniform intra-voxel velocity of zero for tissue voxels.

We express the velocities measured with 4D flow MRI (ν_i,M) in the entire FOV using the same superposition principle that was used for a single voxel in (2):

$${\mathit{v}}_{i,M}={\mathit{v}}_{i,0}+{\mathit{\beta }}_i+{\mathit{\rho }}_i$$ (8)

where ν_i,M and ρ_i are vectors of the same size as β_i, ν_i,0, and ε_i. Upon substituting (7) into (8) to eliminate ν_i,0, β_i is expressed as:

$${\mathit{\beta }}_i={(\mathit{I}+\mathit{A})}^{-1}\mathit{A}{\mathit{v}}_{i,M}-{(\mathit{I}+\mathit{A})}^{-1}\mathit{A}{\mathit{\rho }}_i-{(\mathit{I}+\mathit{A})}^{-1}{\mathit{\epsilon }}_i$$ (9)

where I is an N-by-N identity matrix. Defining (I + A)⁻¹ as B, we rewrite (9) as:

$${\mathit{\beta }}_i=\mathit{B}A{\mathit{v}}_{i,M}-\mathit{B}A{\mathit{\rho }}_i-\mathit{B}{\mathit{\epsilon }}_i$$ (10)

Equation (10) provides a linear equation for the bias error as a function of the one known parameter, ν_i,M, and two unknown parameters, ρ_i and ε_i.

C. Bias Error Estimate and Confidence Interval

Numerical error is introduced into the bias error estimates as the partial derivatives in (6) are approximated using a finite difference scheme. There is also an added bias error due to PV effects contributing to the term ε_i in (10). Herein, we refer to Bε_i as the “numerical error term” in (10) and estimate it using a Richardson extrapolation. The Richardson extrapolation evaluates numerical error by comparing numerical solutions on grids with different spatial resolutions. To generate a coarse grid solution, we double the step size of the finite difference schemes in A. We write A with twice the step size as A⁽²⁾, and the corresponding matrix B calculated using A⁽²⁾ as B⁽²⁾. Details of the derivation for the Bε_i estimate are provided in Appendix A.

As shown in the Appendix, Bε_i is expressed as:

$$\mathit{B}{\mathit{\epsilon }}_i=\mathit{P}\left({\mathit{B}}^{(2)}{\mathit{A}}^{(2)}-\mathit{B}A\right){\mathit{v}}_{i,M}-\mathit{P}\left({\mathit{B}}^{(2)}{\mathit{A}}^{(2)}-\mathit{B}A\right){\mathit{\rho }}_i$$ (11)

in which P is a scaling factor dependent on the step size difference between A⁽²⁾ and A, along with the order of accuracy of A. Substituting (11) into (10), simplifying, and denoting BA − P(B⁽²⁾A⁽²⁾ − BA) as a matrix C, the bias error is rewritten as:

$${\mathit{\beta }}_i=\mathit{C}{\mathit{v}}_{i,M}-\mathit{C}{\mathit{\rho }}_i$$ (12)

Henceforth, Cν_i,M will be referred to as the bias error estimate $({\widehat{\mathit{\beta }}}_i):$

$${\widehat{\mathit{\beta }}}_i=\mathit{C}{\mathit{v}}_{i,M}$$ (13)

Equation (13) corresponds to the bias error estimate defined in (1) for all voxels in the FOV.

The estimate provided by (13) is affected by the unknown random error (ρ_i). We use the estimated statistical properties of ρ_i to define the 68% bias error confidence interval (CI) in (1). Each element in ρ_i is assumed to be normally distributed with a mean of zero and a variance of ${\sigma }_{i,\rho }^2$. The random error is assumed to be normally distributed for voxels with signal-to-noise ratio (SNR) greater than 5, according to Friman et al. [16]. The random error variance in the FOV is represented as a vector of length N (${\mathit{\sigma }}_{i,\rho }^2$). The value of ${\mathit{\sigma }}_{i,\rho }^2$ can be estimated using the SNR, according to Pelc et al. [21].

In Appendix B, the random error variance is propagated through the linear operator, C, defined in (12). The 68% bias error CI vector (σ_i,β) is then evaluated as:

$${\mathit{\sigma }}_{i,\beta }=sqrt\left(diag\left(\mathit{C}\left[diag\left({\mathit{\sigma }}_{i,\rho }^2\right)\right]{\mathit{C}}^T\right)\right)$$ (14)

in which diag(·) indicates the diagonal operator.

This 68% CI corresponds to one standard deviation assuming normally distributed noise. According to (13) and (14), the bias error in (1) is expressed as a bias error estimate with a 68% CI for all voxels.

III. METHODOLOGY

A. Synthetic Womersley Flow

The bias error model’s performance was first assessed using synthetic Womersley flow, representing arterial flow in the cardiovascular system [22]. The velocity profile is dictated by the non-dimensional Womersley number $(\alpha =R\sqrt{\omega /v})$ indicating the ratio of pulsatile inertial forces to viscous forces, where R is the pipe radius, ω is the frequency owing to the flow pulsatility, and ν is the kinematic viscosity of the fluid. The flow in a cylindrical pipe has only the axial component along the z-axis, with no radial and circumferential components.

4D flow MRI provides phase images for each velocity component, along with a magnitude image, which quantifies the intensity of the MR signal. We synthetically generate this complex signal (Z) for each voxel as the summation of intra-voxel isochromatic complex signal (ζ_j) with additive complex noise (η) [23]. A total of N_ISO isochromats (N_ISO = 20³) for each voxel were generated uniformly inside each voxel on a 20 × 20 × 20 grid with j indicating the isochromat index:

$$Z=\left({\sum }_j^{N_{ISO}}{\zeta }_j\right)+\eta$$ (15)

The details on the generation of ζ_j and η are provided in Appendix C. PV effects are introduced when the voxel contains both tissue and flow isochromats. The extent of PV effects is quantified according to the saturation ratio (SR) defined for a PV voxel as the signal magnitude of the tissue adjacent to the vessel relative to the magnitude of the neighboring flow [24]. Different levels of PV effects are investigated by generating data with SR values ranging from 0 to 1. We generate ζ_j with a venc of 100 cm/s. The variance of random error for each voxel was assessed using the SNR [21]:

$${\sigma }_{\rho }^2=\frac{2}{{\pi }^2}\frac{ven{c}^2}{SN{R}^2}$$ (16)

The random error variance is used with (14) to generate bias error CIs in (1).

The isochromat velocity (u_j) is a function of the mean axial velocity in the pipe $(\overline{u})$, the radial distance of the j isochromat from the pipe centerline (r_j) and the pipe radius, R [25]:

$$u_j=Real\left\{\frac{\mathrm{\Lambda }{J}_0(\mathrm{\Lambda })-\mathrm{\Lambda }{J}_0\left(\raisebox{1ex}{$r_j$}\!\left/ \!\raisebox{-1ex}{$R$}\right.\right)}{\mathrm{\Lambda }{J}_0(\mathrm{\Lambda })-2J_1(\mathrm{\Lambda })}\right\}\overline{u}$$ (17)

where J₀(·) and J₁(·), respectively, are the zeroth- and first-order Bessel functions of the first kind, Real{·} indicates the real component, and Λ is a complex number determined by the Womersley number:

$$\mathrm{\Lambda }=\left(\frac{i-1}{\sqrt{2}}\right)\alpha$$ (18)

The mean velocity was set to 30 cm/s, which is in the range of blood flow velocity in carotid arteries. Equation (17) generates u_j for a single timeframe. Womersley numbers from 0 to 6 were considered, providing a range of physiologically relevant velocity profiles for cerebral circulation. Pipe diameters (D) ranged from 3 to 15mm, with isotropic voxel sizes ranging from 0.5 to 1mm.

4D flow MRI velocimetry includes a reference acquisition (Z_ref) to remove inhomogeneous magnetic field effects. The axial velocity measurements for the synthetic Womersley flow (ν_M) is evaluated as the difference in phase between the flow-sensitive acquisition and reference acquisition, both multiplied by $\frac{venc}{\pi }$:

$$v_M=\frac{venc}{\pi }\left(\angle Z-\angle Z_{ref}\right)$$ (19)

We assume the reference acquisition is not sensitive to flow and model isochromats with zero phase in (15). The synthetic velocity measurements obtained from (19) are used to assess bias error estimates defined in (1).

We can compare our bias error estimates to a synthetic bias error (β_synth) as we know the intra-voxel velocity distribution and the size of the voxel. As a result, β_synth is independent of numerical error, noise, and PV effects, unlike the bias error estimates. The synthetic bias error is calculated for each voxel in the FOV as the difference between the expected velocity measurement and the velocity at the center of the voxel:

$${\beta }_{synth}=E\left(v_M\right)-v_0$$ (20)

The E(ν_M) is evaluated from ${\sum }_j^{N_{ISO}}{\zeta }_j$ in (15), and ν₀ using (17).

The comparison to synthetic bias error is used to assess the accuracy of the bias error estimates. In CF voxels, we found that the numerical error is negligible. In PV voxels, the numerical error and PV effects are accounted for using a Richardson extrapolation, as explained in Section II-C. Appendix D outlines how the order of accuracy in the PV domain $\left({\widehat{p}}_{PV}\right)$ is evaluated.

A total of 3,549 unique synthetic MR acquisitions were generated to investigate the effects of Womersley flow conditions and imaging parameters on ${\widehat{p}}_{PV}$. These acquisitions were generated by varying the Womersley number between 0 and 6, relative pipe diameters $\left(D^{*}=\raisebox{1ex}{$D$}\!\left/ \!\raisebox{-1ex}{${\delta }_i$}\right.\right)$ in the range of 3.75 to 18.75, and the SR from 0 to 1.

The impact of voxel size and SR on the bias error in PV voxels was assessed by reporting the maximum synthetic bias error as a function of these parameters. We also demonstrate that the numerical error in CF voxels can be neglected relative to the synthetic bias error. The synthetic and estimated bias error were compared by plotting these as functions of the voxel’s radial location in the pipe. The model’s accuracy in PV voxels is quantified by assessing the maximum estimated bias error relative to the maximum synthetic bias error.

B. In Vitro 4D flow in ICA Aneurysm

The bias error model was applied to in vitro 4D flow measurements in 3D-printed flow phantoms replicating an internal carotid artery (ICA) aneurysm with complex flow patterns. According to IRB-approved protocol, in vivo 4D flow and time-of-flight (TOF) MRI data of the cerebral vasculature were acquired at Northwestern University. The flow phantom geometries were generated from TOF data segmented with open-source software ITK-SNAP [26]. Thresholding and region growth algorithms were used to segment the images. The images were imported into Geomagic Design software (3D Systems, Rock Hill, SC) to model the aneurysm’s luminal surface with the proximal and distal ICA segments and add extensions connecting the model to a flow loop. A 1-to-1 and a scaled-up 2-to-1 in vitro phantoms were created. The phantoms were printed using a high-resolution ProJet MJP 2500 Plus printer (3D Systems, Rock Hill, SC) with VisiJet M2R-CL material.

A flow loop was created to conduct in vitro 4D flow measurements of the intra-aneurysmal flow at a steady flow rate. The flow rate for the 1-to-1 model was determined from the in vivo 4D flow data by calculating the flow rate in the proximal ICA at peak systole. The flow rate prescribed to the 2-to-1 model was determined by matching the Reynolds number to that of the 1-to-1 model to maintain flow similarity in both models. Both geometries had Reynolds numbers of 313, while the 1-to-1 and 2-to-1 geometries had flow rates of $4.45\frac{mL}{s}$ and $8.90\frac{mL}{s}$, respectively. The working fluid was a water-glycerol mixture (60:40 by volume) with a respective density and viscosity of $1110\frac{kg}{m^3}$ and 0.00372 Pa · s. In vitro velocity measurements in both phantoms were acquired on Siemens 3T PRISMA scanner using dual-venc 4D flow MRI [27], with a flip angle of 15 degrees for these measurements. Table I contains a list of sequence parameters used to acquire the flow. Doubling the phantom size halves the velocities since the Reynolds number is held constant. The 1-to-1 and 2-to-1 phantoms were imaged with voxel sizes of 0.8 × 0.8 × 0.8 mm³ and 0.85 × 0.85 × 0.8 mm³, respectively. Similar voxel sizes achieve comparable SNR between the two phantoms while providing different spatial resolution levels of the flow. To maintain similar velocity-to-noise (VNR) values, we set the venc of the 2-to-1 phantom to be half that of the 1-to-1 phantom. The 4D flow MRI sequence used requires ECG-gating. We prescribed an artificial pulse to collect 18 timeframes (phases) of the steady flow in the in vitro phantoms according to the gating provided. However, only 15 timeframes exhibiting stationary noise were used since a stationary noise assumption was made in (3). These non-stationary effects are introduced during the k-t GRAPPA reconstruction.

TABLE I.

Imaging parameters for In vitro and in Vivo Studies

	Low Venc (cm/s)	High Venc (cm/s)	Time Frames	TE (ms)	TR (ms)
1-to-1 An.	30	60	18 (15)	4.08	6.8
2-to-1 An.	15	30	18 (15)	4.80	7.5
In vivo An.	50	100	16 (16)	3.39	6.1

Imaging parameters for the in vitro and in vivo aneurysm (An.) studies. The timeframe values in parenthesis indicate the number of cardiac phases used for analysis out of the total number of cardiac phases acquired per cardiac cycle.

The bias error model was applied to each velocity component in the 4D flow datasets acquired for the aneurysm flow. Values of ${\widehat{p}}_{PV}$ from the synthetic study were used to define P in (11). The numerical error in CF voxels is neglected according to our findings presented in Section IV-A-2. The estimated bias error in the 1-to-1 and 2-to-1 phantoms were qualitatively compared for cross-sectional planes in the flow. Quantitative comparisons were made for the root mean square (RMS) values of the estimated bias error in the two phantoms.

C. In Vivo 4D flow in ICA Aneurysm

The bias error model was applied to in vivo 4D flow MRI measurements of the flow in the ICA aneurysm described above in Section III-B, as the in vitro experiments were conducted for the same patient. The 4D flow imaging parameters are shown in Table I. A pseudo-complex angiography algorithm generated a mask after thresholding combined velocity and magnitude data [28]. The bias error model was applied to all three velocity components at 16 timeframes within the cardiac cycle. This produced a spatiotemporally resolved bias error vector field for the in vivo 4D flow measurements. PV order of accuracy estimates from the synthetic study were used to define the scaling factor P in (11), and numerical error in CF voxels was expected to be negligible.

Quantitative comparisons between the bias error at systole and diastole were made to investigate its variability throughout the cardiac cycle. We also compared the magnitude of bias error in CF voxels to PV voxels and the magnitude of the bias error to the bias error CI.

IV. RESULTS

A. Synthetic Womersley Flow

1). Velocity and Signal Effects on Synthetic Bias Error

The synthetic Womersley velocity profiles and corresponding synthetic bias error profiles are shown in Fig. 3. The relative axial velocity (ν*) and relative synthetic bias error $\left({\beta }_{synth}^{*}\right)$ were normalized by the mean velocity. The voxel center’s relative radial location (r*) was normalized by the pipe radius. Fig. 3a displays the velocity profiles for α of 0, 4, and 6. Fig. 3b shows the relative synthetic bias error corresponding to the velocity profiles in Fig. 3a for an isotropic voxel size of 0.75mm, pipe diameter of 1cm, and SR of 0.5. The synthetic bias error was evaluated using (20).

Fig. 3:

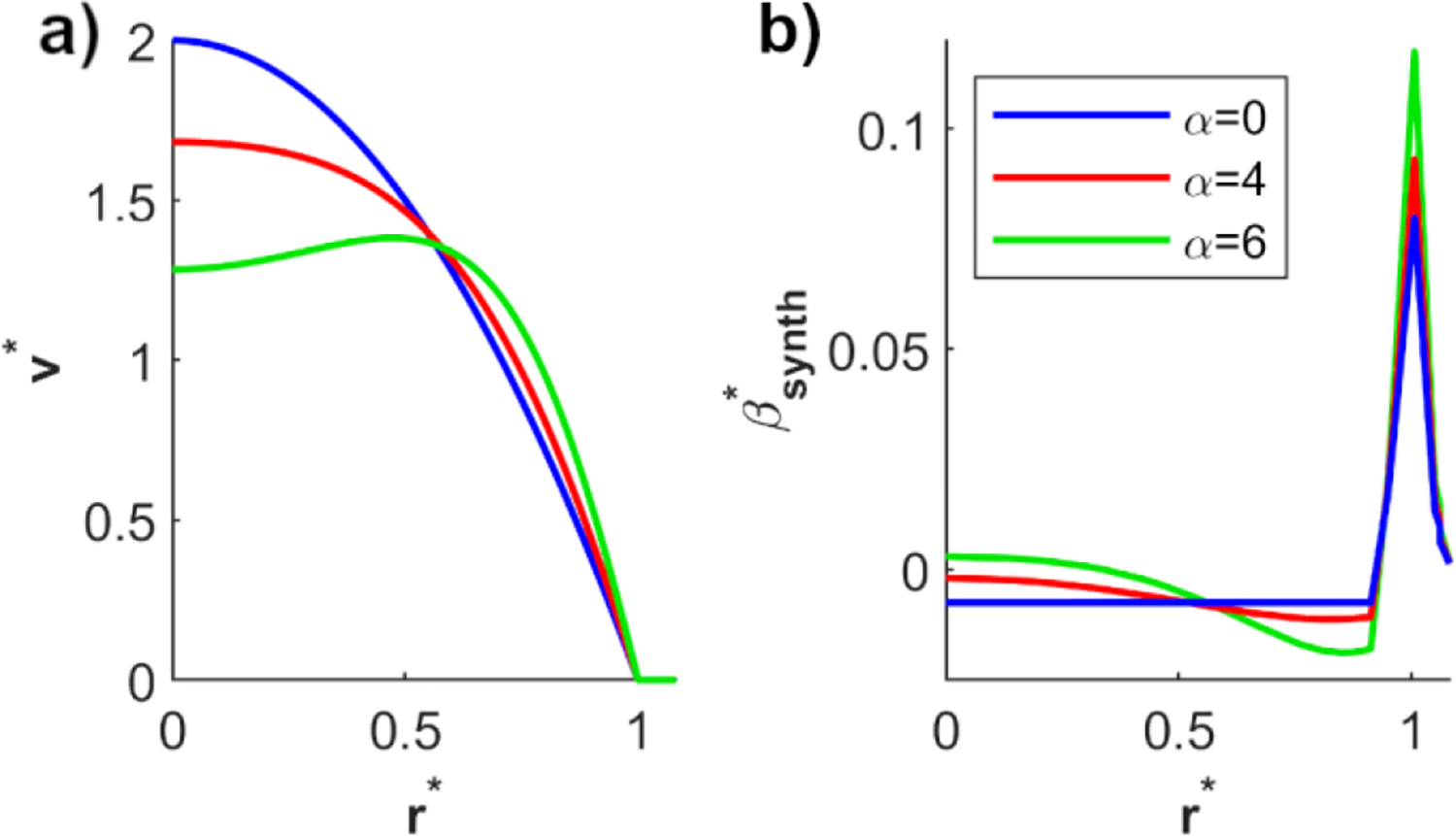
a) Relative velocity and b) corresponding relative synthetic bias error as a function of the relative radial location and Womersley number. The bias error was evaluated for an isotropic voxel size of 0.75mm, pipe diameter of 1cm, and SR of 0.5.

For α = 0, the velocity profile is parabolic, which has a constant second-order derivative. This produces a constant bias error in CF voxels. At α = 4 and 6, the velocity profile has variable second order derivatives in CF voxels and therefore fluctuating bias error. The bias error peaks in PV voxels located at the wall (r* = 1). Fig. 3b includes values of r* greater than 1 as the center of some PV voxels may reside outside the pipe but have edges of the voxel still in the flow.

Table II reports the maximum relative bias error at different levels of isotropic voxel sizes and SR for Womersley number α = 6. At SR=0.5, there is a 91.3% increase in maximum bias error at δ_i = 1mm relative to δ_i = 0.5mm. We observe that the maximum bias error increases with a decrease in SR. For a constant voxel size (δ_i = 0.75mm), the maximum bias error increases by 125% at SR=0 relative to SR=1. These findings indicate that 4D flow MRI measurements’ bias error is dictated by the intra-voxel velocity distribution and signal properties of flow relative to the tissue.

TABLE II.

Maximum Relative Bias Error as a Function of Voxel Size and SR (α = 6)

	SR=1	SR=0.5	SR=0
δi = 0.5mm	0.069	0.092	0.140
δi = 0.75mm	0.085	0.117	0.191
δi = 1mm	0.131	0.176	0.268

2). Order of Accuracy Estimates in PV Voxels

Fig. 4 presents the order of accuracy in PV voxels for the 3,549 synthetic MR datasets with different values of D*, α, and SR. The lowest value for D* was set to 3.75 because smaller values did not provide enough CF voxels across the vessel diameter to inform bias error estimates in PV voxels adequately.

Fig. 4:

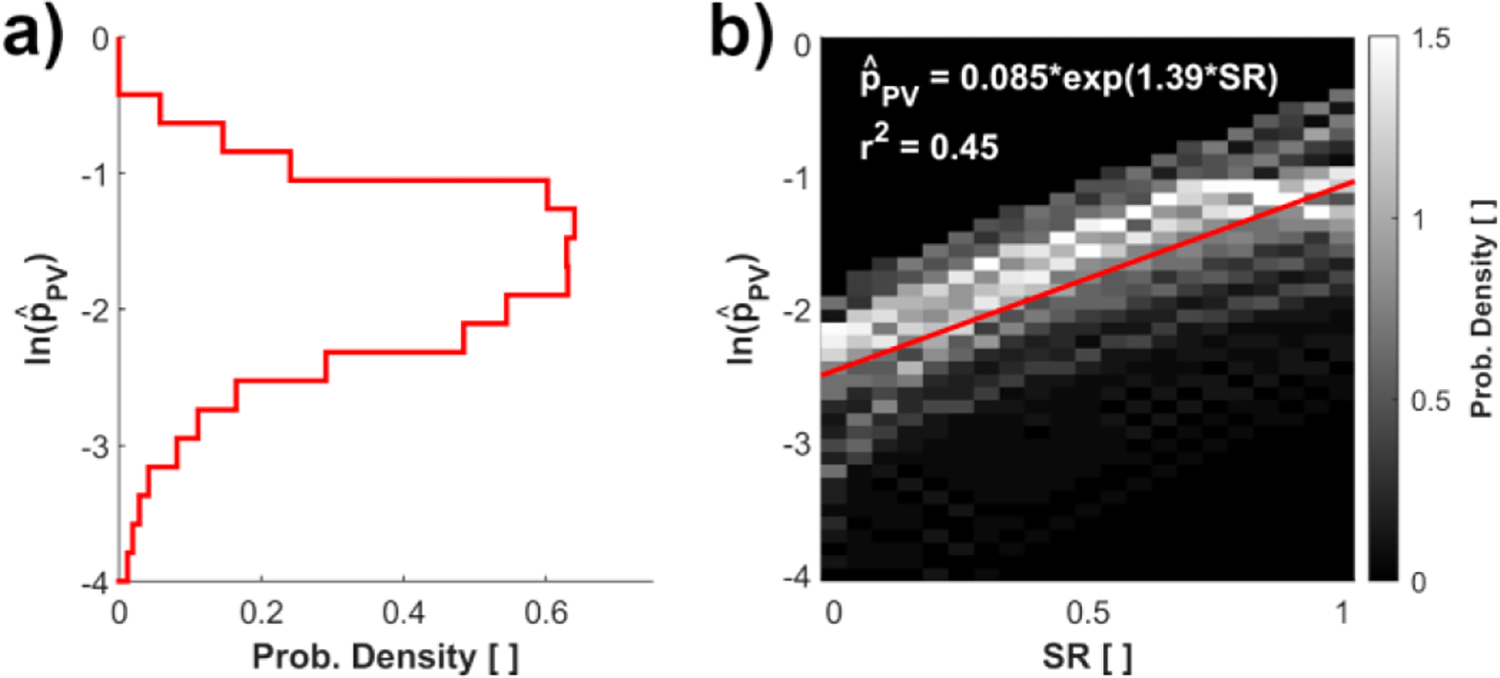
a) Probability density with respect to the natural log order of accuracy at PV voxels; b) Heat map of the PV natural log order of accuracy vs. SR. The intensity of the heat map indicates the probability density of the datapoint in the cell. Note that panel a is the projected probability density of panel b onto the y-axis.

We found the values of ${\widehat{p}}_{PV}$ to resemble a log-normal distribution, hence the natural log scale used in Fig. 4a and Fig. 4b. The median value of the ${\widehat{p}}_{PV}$ distribution was 0.181. Hereafter, the bias error model estimates will evaluate ${\widehat{p}}_{PV}$ for each PV voxel based on the best exponential fit of PV voxel’s value of SR as presented in Fig. 4b:

$${\widehat{p}}_{PV}=0.085\exp (1.39*SR)$$ (21)

The SR dictates the degree of PV effects in the measurements (Table II). It can be observed that as SR increases from 0 to 1, the order of accuracy increases according to (21) as the PV effects are reduced. As the SR is increased from 0 to 1, the PV order of accuracy also increases from 0.085 to 0.34. While for an SR of 1 the PV effects are minimized, a high numerical error is still introduced due to steep changes of velocity gradients, which results in a low order of accuracy relative to that expressed in (6).

We evaluated the numerical error in CF voxels relative to the synthetic bias error. When considering all CF voxels across all 3,549 synthetic cases, we observed that the median absolute numerical error of the bias error estimate was only 2.45% of the median absolute synthetic bias error. This confirms our expectation that the numerical error in CF voxels is negligible.

3). Bias Error Model Validation

Fig. 5 compares the estimated and synthetic bias errors for the axial velocity at SNR_CF of 100, SR of 0.5, and pipe diameter of 1cm. The estimated and synthetic bias errors are represented according to their distance from the pipe center relative to the pipe radius. The synthetic and estimated bias errors are non-dimensionalized relative to the mean velocity. Bias error CIs are reported as bounds around the expected bias error estimate using (14).

Fig. 5:

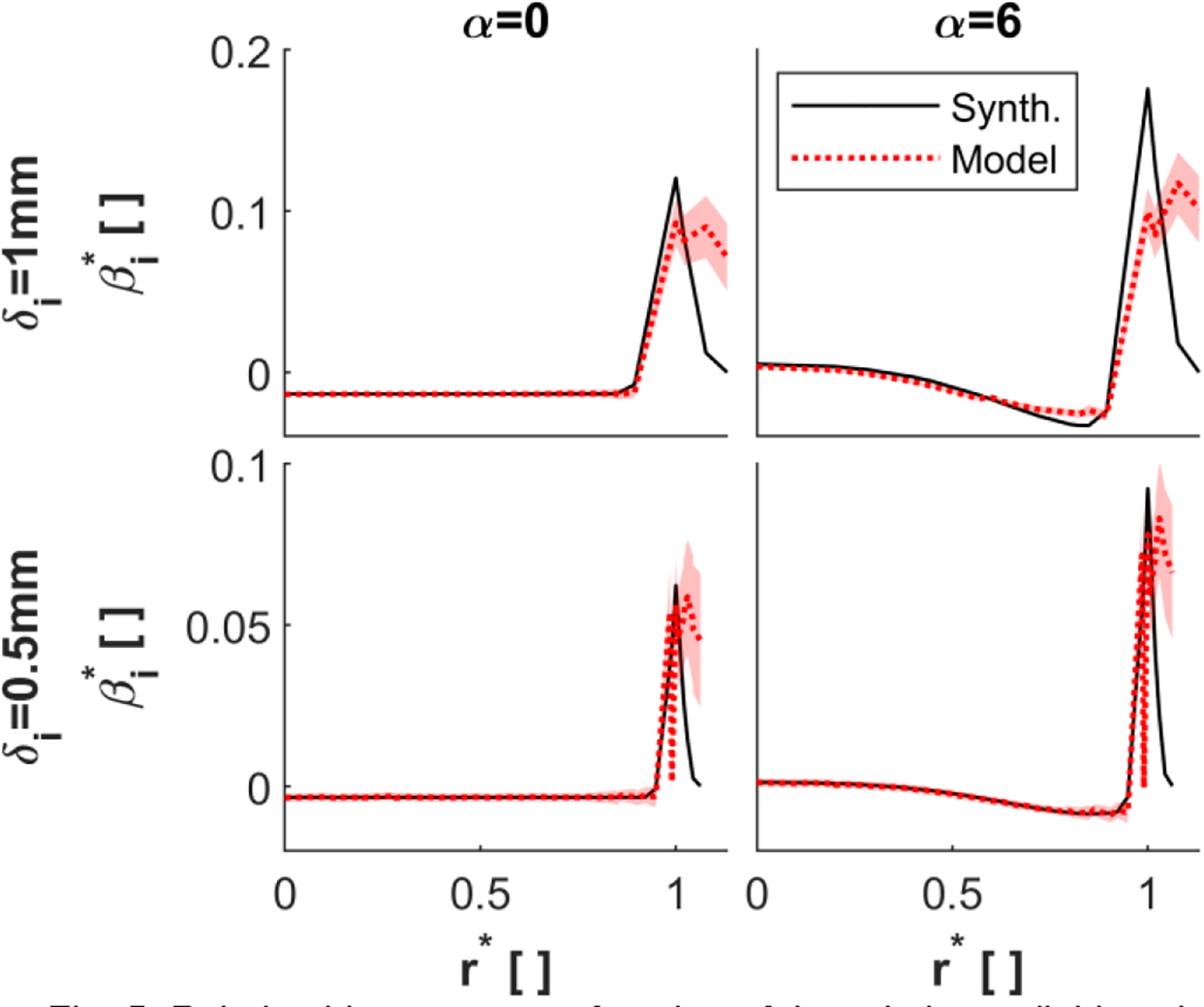
Relative bias error as a function of the relative radial location of the voxel-center for an SNR_CF of 100, pipe diameter of 1cm, and SR of 0.5. The bias error was evaluated using isotropic voxel sizes of 1mm (top row) and 0.5mm (bottom row) and Womersley numbers of 0 (left column) and 6 (right column). The solid lines indicate the synthetic bias error and the dotted lines indicate the expectation of the bias error estimate. The bounds indicate the 68% confidence interval. Note the change in y-axis limits for the two different voxel sizes.

Decreasing the voxel size reduces the estimated bias error. This bias error reduction is due to a smaller dynamic range of velocities in the voxel. The estimated bias error appears to agree with the synthetic bias error in CF voxels. For α = 0, the estimated bias error in CF voxels for the 0.5mm voxel is reduced by 75.2% relative to the 1mm voxel. This reduction is similar to the 75% reduction observed in the synthetic bias error.

The bias error estimates capture the sharp increase in bias error in PV voxels relative to CF voxels for a range of Womersley numbers, voxel sizes, and SR. We quantify the accuracy of the bias error model in PV voxels according to the relative maximum bias error $\left({\beta }_{max}^{*}\right)$. The relative maximum bias error is quantified in PV voxels as the ratio of the maximum estimated bias error and the maximum synthetic bias error. In Fig. 6, a good agreement is observed for a voxel size of 0.75mm and 0.5mm. The bias error model underestimates the maximum PV bias error for 1mm voxels. There is no strong dependence of the model’s accuracy on either SR or Womersley number. The variable accuracy of the model is due to residuals in approximating the best fit in Fig. 4b.

Fig. 6:

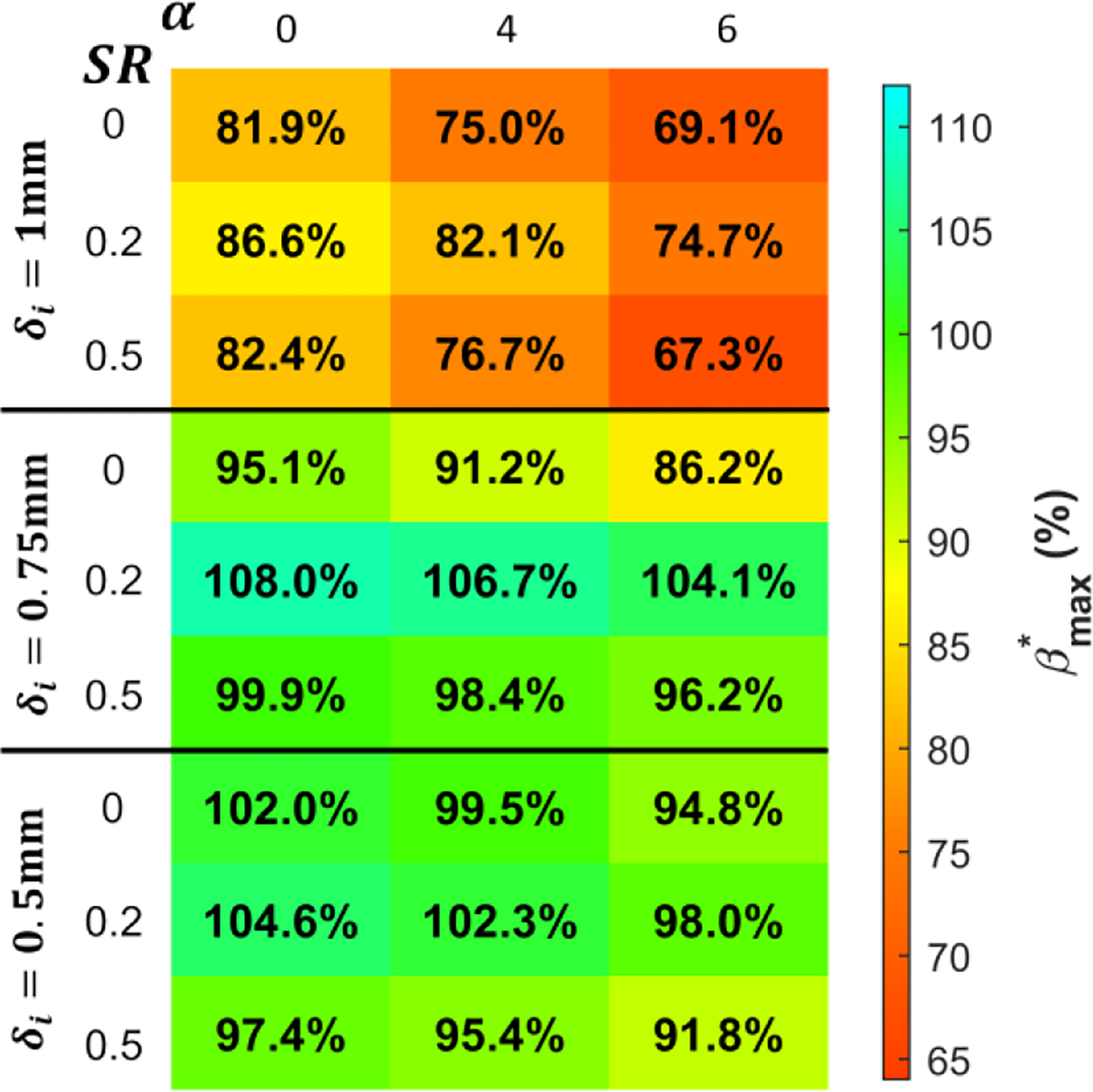
The relative maximum bias error is evaluated as a function of the Womersley number, SR, and voxel size.

B. In Vitro 4D flow in Scaled ICA Aneurysm

For the steady flow measurements in the 1-to-1 and 2-to-1 phantoms of the ICA aneurysm, the measured velocities were arithmetically averaged over the timeframes to form spatially resolved velocity and bias error fields. To assess the model’s order of accuracy using (21), SR is estimated for each PV voxel in the phantom measurements using the magnitude image. Noise in the magnitude image was minimized by first averaging magnitude images with respect to time, followed by applying a median filter to remove outliers. For each PV voxel, we considered a 3 × 3 × 3 neighborhood centered on the PV voxel of interest. The PV voxel’s SR is calculated as the neighborhood’s minimum tissue magnitude and the maximum CF magnitude ratio. This value of SR is then used to evaluate ${\widehat{p}}_{PV}$. Table III reports the 25%, 50%, and 75% quantiles of SR and ${\widehat{p}}_{PV}$ for the 1-to-1 and 2-to-1 aneurysm flow phantoms. We see similar quantile values for the measurements in the two phantoms. The low SR values were expected as the phantoms were surrounded by air, which provides little signal.

TABLE III.

Saturation Ratio and Order of Accuracy Quantiles in 1-to-1 and 2-to-1 Aneurysm (An.) Phantoms

	SR25%	SR50%	SR75%	${\widehat{p}}_{PV,25\mathrm{\%}}$	${\widehat{p}}_{PV,50\mathrm{\%}}$	${\widehat{p}}_{PV,75\mathrm{\%}}$
1-to-1 An.	0.085	0.099	0.119	0.096	0.098	0.100
2-to-1 An.	0.079	0.093	0.110	0.095	0.097	0.099

Fig. 7 presents cross-sections of the relative velocity magnitude and relative bias error magnitude for the 4D flow acquisition within the 1-to-1 and 2-to-1 phantoms. The velocity magnitude and bias error magnitude fields were normalized by each flow phantom’s mean inlet flow velocity. Since the Reynolds number was the same for both phantoms, the distributions of the velocity magnitude are similar.

Fig. 7:

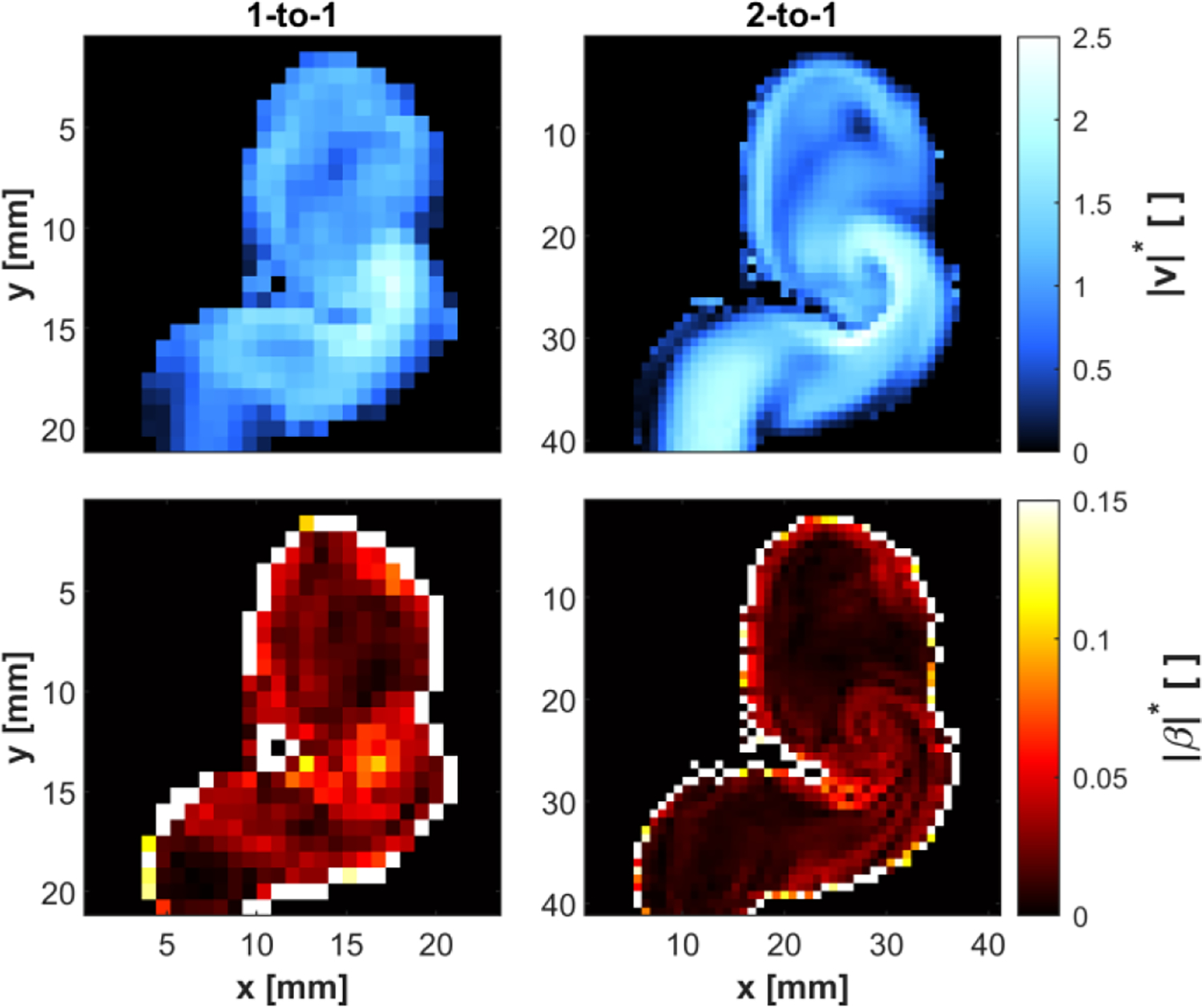
Cross-section of in vitro ICA aneurysm phantoms. The relative velocity magnitude was calculated from the 4D flow velocity in the 1-to-1 phantom (upper-left) and the 2-to-1 phantom (upper-right). The bias error magnitude was assessed from the 4D flow velocity in the 1-to-1 phantom (lower-left) and the 2-to-1 phantom (lower-right).

Phantom scaling had a pronounced effect on the bias error. In CF voxels, the bias error for the 2-to-1 phantom was reduced due to the decreased range of intra-voxel velocities. The map of velocity magnitude for the 2-to-1 phantom shows a high-speed jet entering the aneurysm (x=30mm, y=25mm). The model captures elevated bias error in the flow layers surrounding the jet, which was characterized by steep changes of velocity gradients. Furthermore, there was a band of low bias error in the center of the jet corresponding to a more uniform velocity region. This behavior is best observed in the 2-to-1 geometry due to the higher resolution of the bias error field than that of the 1-to-1 geometry. Despite this, the velocity measurements in the 1-to-1 geometry still captured the elevated region of bias error at the bend of the ICA.

The RMS values for the CF and PV voxels in the 1-to-1 and 2-to-1 phantoms are listed in Table IV. The PV relative bias error is an order of magnitude higher than that in CF voxels. This is consistent with our synthetic results, which demonstrated a similar increase in PV voxels’ bias error. The RMS bias error in the 2-to-1 phantom relative to the 1-to-1 phantom decreased by 46.4% in CF voxels but only 20.5% in PV voxels. Increased MR resolution restricts the dynamic range of velocities in voxels, thus reducing the bias error; however, this does not address the bias error due to PV effects, leading to lower error reduction in PV voxels.

TABLE IV.

RMS Relative bias Error Magnitude and RMS Relative bias Error Confidence intervals In 1-to-1 and 2-to-1 Aneurysm Phantoms

	$\mathrm{RMS}\left(|\beta {|}_{CF}^{*}\right)$	$\mathrm{RMS}\left(|\beta {|}_{PV}^{*}\right)$	$\mathrm{RMS}\left({\sigma }_{\beta ,CF}^{*}\right)$	$\mathrm{RMS}\left({\sigma }_{\beta ,PV}^{*}\right)$
1-to-1 An.	0.0424	0.438	0.00119	0.0202
2-to-1 An.	0.0227	0.348	0.00108	0.0274

We evaluated bias error CIs for each voxel and velocity component according to (14). The SNR in (16) was calculated using the “SNR Mult” method described by Dietrich et al., using the 15 timeframes acquired for each geometry [29]. To account for averaging the velocity field for the 15 timeframes, we multiplied the SNR for each voxel by $\sqrt{15}$. Additionally, since the magnitude image is the average across the four acquisitions obtained from the dual-venc sequence, we divided the SNR for each voxel by 2. The RMS SNR values in CF voxels were 115 and 94 for the 1-to-1 and 2-to-1 measurements. The RMS SNR values in PV voxels were 51 and 38 for the 1-to-1 and 2-to-1 measurements.

Bias error CIs were non-dimensionalized similar to the bias error using the mean inlet velocity. The RMS relative bias error CI for the CF and PV voxels ($\mathrm{RMS}\left({\sigma }_{\beta ,CF}^{*}\right)$ and $\mathrm{RMS}\left({\sigma }_{\beta ,PV}^{*}\right)$) in the 1-to-1 and 2-to-1 phantoms are presented in Table IV. Similar to the bias error, we observe an order of magnitude increase in the RMS CI in PV voxels compared to CF voxels. For the same domain type and phantom scale, the ratio between the RMS bias error and the RMS CI ratio ranged from 12.7 to 35.6. This indicates that the bias estimates are robust to measurement noise.

C. In Vivo 4D flow in ICA Aneurysm

The velocity magnitude and bias error magnitude fields were calculated for each voxel for the in vivo 4D flow MRI in the ICA aneurysm. These calculations were performed for each timeframe in the measured cardiac cycle. The median SR value at all time points was 0.279. The SNR was calculated as described in Section IV-B. However, the SNR at each voxel was not multiplied by $\sqrt{15}$ because the velocity fields were not averaged over the cardiac cycle. The RMS SNR was 6.36 and 6.13 in CF and PV voxels, respectively. We evaluated the bias error CI for each velocity component and voxel. The velocity magnitude, bias error magnitude, and bias error CI fields were normalized with respect to the mean inlet velocity across all timeframes. The velocity magnitude and bias error magnitude at peak systole and diastole are shown in Fig. 8.

Fig. 8:

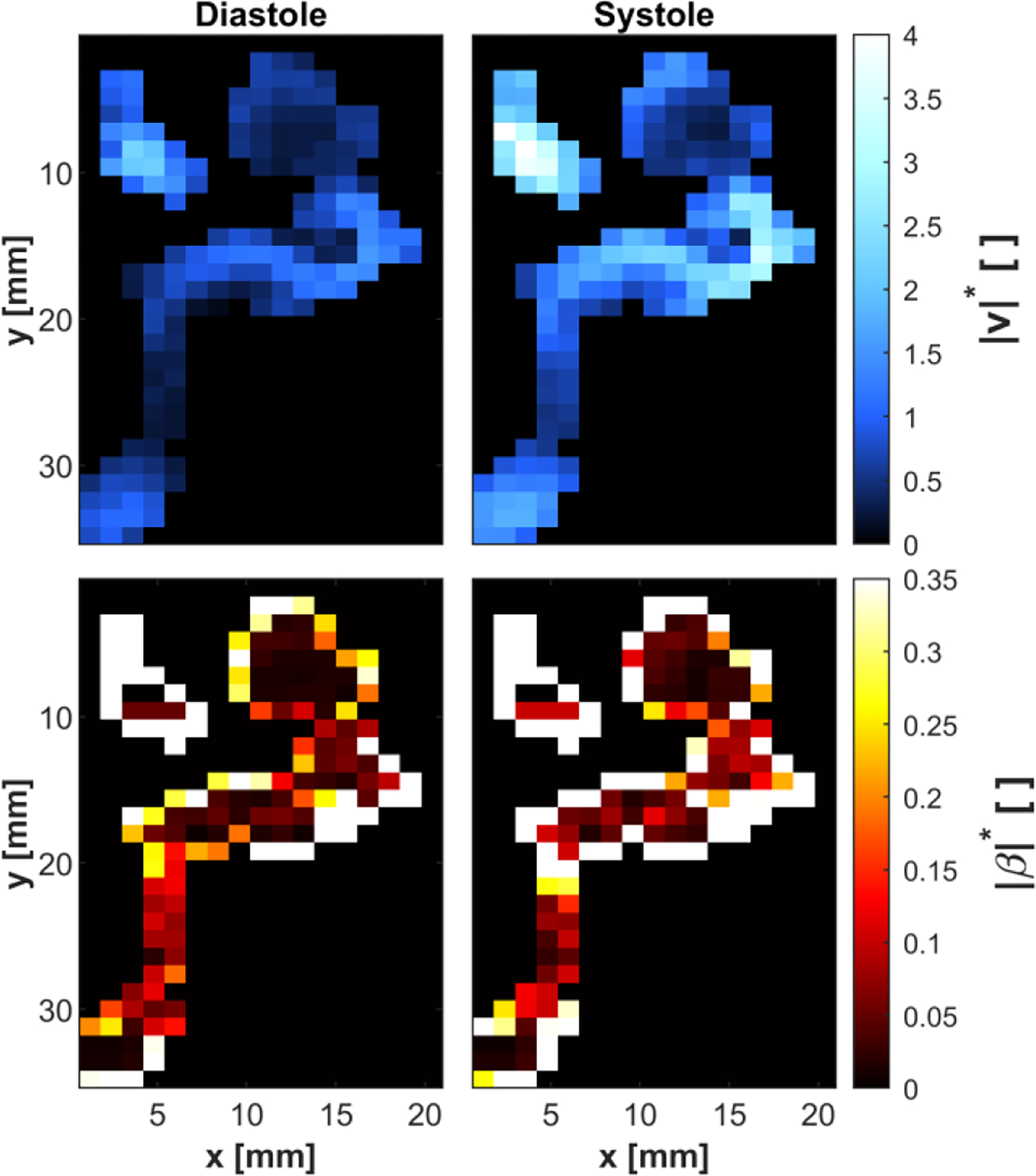
Cross-section of an in vivo ICA aneurysm. Note that although this is the same patient data as in Fig. 7, the chosen cross-sections differ slightly. The relative velocity magnitude was calculated from 4D flow MRI data at diastole (upper-left) and peak systole (upper-right). The bias error magnitude was assessed from the dual venc 4D flow velocity at diastole (lower-left) and peak systole (lower-right). The bias error is shown to be higher at systole relative to diastole, particularly at the jet entering the aneurysm.

Fig. 8 qualitatively shows that the bias error magnitude is higher at systole compared to diastole. Additionally, PV voxels appear to have a much higher bias error than CF voxels.

Table V reports the RMS bias error magnitude and RMS bias error CI for CF and PV voxels at systole and diastole. The RMS bias error magnitude in PV relative to CF voxels is 16.4 times larger at systole and 21.6 times larger at diastole. This increase in bias error in PV voxels is similar to that seen in our synthetic and in vitro studies. The bias error relative to the bias error CI is comparable in CF voxels, but the bias error in PV voxels is a factor of 2.90 to 5.08 times larger than the bias error CI at systole and diastole, respectively.

TABLE V.

RMS relative bias error magnitude and RMS relative bias error confidence intervals at diastole and systole for in vivo ICA 4D flow MRI measurements

	$\mathrm{RMS}\left(|\beta {|}_{CF}^{*}\right)$	$\mathrm{RMS}\left(|\beta {|}_{PV}^{*}\right)$	$\mathrm{RMS}\left({\sigma }_{\beta ,CF}^{*}\right)$	$\mathrm{RMS}\left({\sigma }_{\beta ,PV}^{*}\right)$
Systole	0.0732	1.20	0.0347	0.236
Diastole	0.0317	0.685	0.0347	0.236

V. DISCUSSION AND CONCLUSION

In this study, we assess the local and instantaneous bias error of 4D flow MRI velocimetry due to IVPD. Our model demonstrates the bias error to be an interplay between the intra-voxel velocity distribution and PV effects. Specifically, the intra-voxel velocity distribution determines the bias error trend, and PV effects amplify this trend. The propagation of noise into the model is expressed using a 68% CI. The viability of the bias error model is demonstrated on synthetic velocity fields and those obtained from in vitro and in vivo 4D flow MRI measurements.

The intra-voxel velocity distribution effects on the bias error are expressed in (6) for a single voxel. Equation (6) shows that the bias error is a function of the velocity profile’s concavity (i.e., second-order derivative) and mediated by voxel size choice. This model serves as a priori guide to predict the bias error trend according to the velocity profile. We expect a positive bias error for velocity profiles that are concave upward and a negative bias error for velocity profiles that are concave downward; inflection points in the velocity profile correspond to zero bias error. This trend is observed in Fig. 3 for the Womersley number of 6, in which the velocity profile changing from an upward to downward concavity with increasing relative radial position corresponds to a transition from positive to negative bias error. Fig. 5 reports our bias error estimates alongside the synthetic bias error. Qualitatively, the estimates capture the trend of bias error in both CF and PV voxels. In CF voxels, the estimates closely follow the synthetic bias error at different Womersley numbers and capture the expected decrease in bias error with a reduction in voxel size, as predicted by (6).

In Section IV-B, scaling the in vitro phantom allowed us to reduce the range of the intra-voxel velocity distribution while maintaining similar voxel sizes and SR values between the two phantoms. This change in the intra-voxel velocity distribution reduces bias error magnitude for the larger size phantom, as observed qualitatively (Fig. 7) and quantitatively (Table IV). We expect the bias error to be highest in flow regions characterized by sharp changes in velocity gradients. This is most notably demonstrated in the 2-to-1 in vitro ICA aneurysm when comparing the velocity magnitude to the bias error magnitude map (Fig. 7). Steep changes of velocity at the edge of the jet entering the aneurysm correspond to elevated bias error magnitude. Contrastingly, in the core of this jet, we observe a relatively low bias error as the intra-voxel velocity profile is almost uniform.

Further evidence for the intra-voxel velocity distribution impact on the bias error is observed in the in vivo study (Section IV-C). Fig. 8 shows that the bias error is higher at systole than at diastole. Table V reports that the RMS bias error approximately doubles at systole compared to diastole in both CF and PV voxels. A higher flow rate increases the range of velocities in voxels, resulting in elevated bias error at systole compared to diastole, as suggested by our model. This dependence of the bias error on the phase of the cardiac cycle should be considered when evaluating hemodynamic metrics and planning 4D flow MRI scans.

Sharp changes in the intra-voxel velocity profile typically occur in PV voxels, where high-velocity gradients at the wall meet the stationary tissue. According to (6), this is expected to result in high levels of bias error. These near-wall voxels are also affected by PV effects, which exacerbate the bias error introduced by the intra-voxel velocity. This work quantified the PV effects using SR similar to Tang et al. [24]. The SR of each PV voxel is used to quantify the order of accuracy of the numerical scheme in (21) and assess the bias error using a Richardson extrapolation. The Richardson extrapolation acts to amplify the estimated bias error according to the PV voxel’s SR. For synthetic Womersley flow, this amplification of the synthetic bias error is observed in Table II. With a decrease in SR (higher PV effects), the maximum bias error is increased for all voxel sizes. Figs. 5 and 6 demonstrate that our model is sensitive to the bias error in PV voxels for a range of SR values along with varying Womersley number and voxel size. The model predicts that the bias error should generally be much higher in PV voxels than in CF voxels due to the sharp changes in velocity profile and PV effects. In the synthetic Womersley flow and in vitro and in vivo aneurysm studies, the bias error in PV voxels was an order of magnitude larger than that in CF voxels. This high bias error in PV voxels can contribute to errors in WSS derived from 4D flow MRI, as reported by other researchers [3], [9], [10].

Our model accounts for noise propagating into the bias error estimates by reporting a 68% bias error CI, as shown in (1). According to the model, higher levels of σ_i,β are expected in PV voxels compared to CF voxels. This increase in CI bounds results from lower SNR values in PV voxels which, in turn, owes to higher noise variance according to (16). Additionally, the noise is amplified when propagated through the Richardson extrapolation used for PV voxels. Tables IV and V demonstrate that the CI bounds are wider in PV voxels than in CF voxels.

The bias error model presented in this work serves as an a priori guide for planning 4D flow MRI scans. The venc will affect the dynamic range and level of noise propagated into the measured velocity, and the choice of voxel size directly affects the bias error level, as shown in (6). Hoogeveen et al. show that SR is a function of proton density, relaxation parameters (T1 and T2), echo time (TE), repetition time (TR), and flip angle [30]. From these parameters, MR users can adjust TE, TR, and the flip angle to modulate SR and, as a result, the level of bias error in PV voxels.

The presented method is applicable for vessels with a diameter greater than or equal to 3.75 of the voxel size. Our synthetic Womersley flow study demonstrated that finite difference scheme stencils could not be generated for velocity fields with less than 3.75 voxels across the diameter. This constraint is likely to have broader applications to the estimation of metrics based on velocity gradients from 4D flow MRI data. Additionally, the bias error model assumes that the velocity gradient profile is monotonic, and the SNR is greater than 5. A further limitation of our model is its reliance on the order of accuracy estimates obtained from synthetic flow for in vitro and in vivo measurements. The best fit used to determine the model’s order of accuracy in PV voxels has large residuals (Fig. 4b). These residuals cause underestimation of the maximum bias error for an isotropic voxel size of 1mm, as shown in Fig. 6.

Furthermore, despite investigating a range of SR values in the synthetic Womersley flow datasets, we assumed that the SR is constant throughout the FOV. Our model is limited by the definition of the tissue, CF, and PV domains (Fig. 2b) since this relies on an accurate mask of the vessel geometry. As described in Section II-B, the PV domain is evaluated directly from the mask of the entire vessel. If the vessel mask is inaccurate, then the assessment of the PV domain is likely also to be inaccurate. Fig. 5 shows that mischaracterization of these domains can lead to over- or under-estimation of the bias error in voxels near the vessel wall.

While Womersley flow represents pulsatile flow in straight vessels, it is not representative of all velocity profiles in the cardiovascular system. Our work is limited by only considering a subset of possible velocity profiles in the synthetic test cases. Furthermore, although our in vitro test investigates more complex velocity fields, there is no ground truth solution. Although CFD simulations could provide high-resolution velocity fields, these simulations would not serve as a ground truth due to their own sources of error [10]. Rather, this work compares the change in bias error with model scale to the expected trend for similar signal properties and Reynolds number.

In conclusion, this study presents an approach to estimate the bias error of velocity measured with 4D flow MRI. The model indicates that bias error is introduced by the rate of change of velocity gradients. This bias error is mediated by the choice of the voxels size and amplified by PV effects in the near-wall voxels. The accuracy of the bias error estimates is reported according to its 68% confidence interval. The method is validated with synthetic Womersley flow and applied to in vitro and in vivo 4D flow in a cerebral aneurysm. The bias error model can assess the accuracy of 4D flow MRI measurements and serve as an a priori guide for planning 4D flow MRI scans. 4D flow MRI users could optimize their MR settings (e.g., voxel size and signal-related settings) according to expected flow dynamics to mitigate the bias error level.

APPENDIX A. RICHARDSON EXTRAPOLATION

Richardson extrapolations are used to estimate the exact solution in numerical methods [31]. For two numerical solutions, with an exact solution (f), solved on a fine grid (f₁) and coarse grid (f₂) the numerical error of the fine grid (f₁ − f) can be expressed as:

$$f_1-f=\frac{1}{m^p-1}\left(f_2-f_1\right)$$ (A1)

where m is the refinement factor quantifying the coarse grid’s size relative to the fine grid, and p is the order of accuracy of the numerical scheme used to solve for f₁ and f₂ [32].

When (10) is solved for Bε_i, with β_i being the exact solution, the numerical solution of the bias error on the native (fine) 4D flow MRI structured grid (f₁) is:

$${\mathit{f}}_1=\mathit{B}A{\mathit{v}}_{i,M}-\mathit{B}A{\mathit{\rho }}_i$$ (A2)

The coarse grid numerical solution of (10) is assessed by doubling the finite difference schemes’ step size to generate the operator A. We write A with twice the step size as A⁽²⁾ and the operator B calculated using A⁽²⁾ as B⁽²⁾. Therefore, the coarse numerical solution (f₂) is expressed as:

$${\mathit{f}}_2={\mathit{B}}^{(2)}{\mathit{A}}^{(2)}{\mathit{v}}_{i,M}-{\mathit{B}}^{(2)}{\mathit{A}}^{(2)}{\mathit{\rho }}_i$$ (A3)

The numerical error term can be expressed as a scaling factor (P) multiplied by the difference between f₂ and f₁, P(f₂ − f₁). P is defined as an N-by-N diagonal matrix with each diagonal entry evaluating $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$m^p-1$}\right.$ for each voxel. Since the step size of A⁽²⁾ relative to A is doubled everywhere in the FOV, m = 2 for all voxels. The order of accuracy, p, is estimated by comparing f₁ to the known bias error as described in Section III-A. Furthermore, in Section IV-A-2, we demonstrate that the additional bias error due to PV effects is modeled by the selection of p. Using the definitions of f₁ and f₂ in (A2) and (A3), we evaluate the numerical error term as:

$$\mathit{B}{\mathit{\epsilon }}_i=\mathit{P}\left({\mathit{B}}^{(2)}{\mathit{A}}^{(2)}-\mathit{B}A\right){\mathit{v}}_{i,M}-\mathit{P}\left({\mathit{B}}^{(2)}{\mathit{A}}^{(2)}-\mathit{B}A\right){\mathit{\rho }}_i$$ (A4)

APPENDIX B. BIAS ERROR CONFIDENCE INTERVAL

Given that β_i in (12) is independent of noise, the variance of ${\widehat{\mathit{\beta }}}_i$ is only due to Cρ_i We define the variance of ${\widehat{\mathit{\beta }}}_i$ as ${\mathit{\sigma }}_{i,\beta }^2$ and evaluate ${\mathit{\sigma }}_{i,\beta }^2$ according to (12) and (13):

$${\mathit{\sigma }}_{i,\beta }^2=var\left(\mathit{C}{\mathit{\rho }}_i\right)$$ (A5)

For a linear system of equations (e.g., Y = MX), the variance-covariance of the output (Σ_Y) is generally written as a function of the input variance-covariance matrix (Σ_X) and the linear operator, Σ_Y = 𝑴Σ_X𝑴^T [33]. Given C is a linear operator and assuming no spatial correlation of noise, the variance of Cρ_i is expressed as:

$$var\left(\mathit{C}{\mathit{\rho }}_i\right)=\mathit{C}\left[diag\left({\mathit{\sigma }}_{i,\rho }^2\right)\right]{\mathit{C}}^T$$ (A6)

where diag(·) in (A6) is the diagonal operator expressing ${\mathit{\sigma }}_{i,\rho }^2$ as an N-by-N matrix. Equations (A5) and (A6) are combined by eliminating var(Cρ_i) from both equations. The 68% bias error confidence interval vector (σ_i,β) is evaluated as the square root of ${\mathit{\sigma }}_{i,\beta }^2$:

$${\mathit{\sigma }}_{i,\beta }=sqrt\left(diag\left(\mathit{C}\left[diag\left({\mathit{\sigma }}_{i,\rho }^2\right)\right]{\mathit{C}}^T\right)\right)$$ (A7)

In (A7), diag(·) expresses the diagonal elements of $\mathit{C}\left[diag\left({\mathit{\sigma }}_{i,\rho }^2\right)\right]{\mathit{C}}^T$ as a vector of length N. The sqrt(·) operator evaluates each element’s square root in $diag\left(\mathit{C}\left[diag\left({\mathit{\sigma }}_{i,\rho }^2\right)\right]{\mathit{C}}^T\right)$.

APPENDIX C. SYNTHETIC WOMERSLEY FLOW

Equation (15) assesses Z as the summation of isochromats in the voxel with additive noise. The isochromat complex signal (ζ_j) is assessed according to the isochromatic modulus (|ζ|_j), velocity encoding parameter (venc), and intra-voxel axial velocity (u_j) at each j location:

$${\zeta }_j=|\zeta {|}_j\exp \left(i\frac{\pi }{venc}{u}_j\right)$$ (A8)

The isochromat modulus is uniform in the flow and tissue regions. We evaluate |ζ|_j according to the prescribed values of saturation ratio (SR), CF voxel signal magnitude (|Z|_CF = 100), and the number of isochromats modeled in each voxel (N_ISO = 20³). In the flow domain, |ζ|_j is evaluated as the ratio of |Z|_CF and N_ISO, and in the tissue domain, this ratio is multiplied by the SR:

$$|\zeta {|}_j=\left\{\begin{array}{c}|Z{|}_{CF}/N_{ISO},whenj\in flow\\ (SR)\left(|Z{|}_{CF}/N_{ISO}\right),whenj\in tissue\end{array}\right\}$$ (A9)

We compute u_j according to the analytical Womersley solution in (17).

After summing ζ_j for all isochromats in the voxel, complex noise (η) is added to the signal. Both the real and imaginary components of η are normally distributed, zero-mean, uncorrelated, with a variance, ${\sigma }_{\eta }^2$ [34]. We quantify ${\sigma }_{\eta }^2$ using |Z|_CF and the prescribed value of the SNR in CF voxels (SNR_CF = 100). For synthetic Womersley flow, both |Z|_CF and SNR_CF were set to 100 to represent values found from in vitro MRI measurements [29]. The noise variance is then calculated using the ratio of CF magnitude and SNR_CF [35]:

$${\sigma }_{\eta }^2={\left(\raisebox{1ex}{$|Z{|}_{CF}$}\!\left/ \!\raisebox{-1ex}{$SN{R}_{CF}$}\right.\right)}^2$$ (A10)

This value of ${\sigma }_{\eta }^2$ is constant for all voxels in the FOV. The SNR for each voxel is quantified as the ratio of the voxel’s signal magnitude (|Z|) relative to σ_η.

APPENDIX D. ORDER OF ACCURACY ESTIMATES

The order of accuracy is evaluated by solving for p in (A1). We evaluate ${\widehat{p}}_{PV}$ using an L2-norm [36]:

$${\widehat{p}}_{PV}=\frac{1}{\ln (m)}\ln \left(\frac{{\Vert {\mathit{f}}_2-{\mathit{\beta }}_{synth}\Vert }_2}{{\Vert {\mathit{f}}_1-{\mathit{\beta }}_{synth}\Vert }_2}\right)$$ (A11)

where β_synth is a vector of length N for the synthetic bias error at all voxels in the FOV and ‖·‖₂ evaluates the norm for vector elements only in the PV domain.

The order of accuracy estimates in (A11) are used to define rows corresponding to PV voxels of P in (A4). Rows of P corresponding to tissue and CF voxels are defined as zeros.