The impact of transfer learning on 3D deep learning convolutional neural network segmentation of the hippocampus in mild cognitive impairment and Alzheimer disease subjects

Abstract

Research on segmentation of the hippocampus in magnetic resonance images through deep learning convolutional neural networks (CNNs) shows promising results, suggesting that these methods can identify small structural abnormalities of the hippocampus, which are among the earliest and most frequent brain changes associated with Alzheimer disease (AD). However, CNNs typically achieve the highest accuracy on datasets acquired from the same domain as the training dataset. Transfer learning allows domain adaptation through further training on a limited dataset. In this study, we applied transfer learning on a network called spatial warping network segmentation (SWANS), developed and trained in a previous study. We used MR images of patients with clinical diagnoses of mild cognitive impairment (MCI) and AD, segmented by two different raters. By using transfer learning techniques, we developed four new models, using different training methods. Testing was performed using 26% of the original dataset, which was excluded from training as a hold‐out test set. In addition, 10% of the overall training dataset was used as a hold‐out validation set. Results showed that all the new models achieved better hippocampal segmentation quality than the baseline SWANS model (p _s < .001), with high similarity to the manual segmentations (mean dice [best model] = 0.878 ± 0.003). The best model was chosen based on visual assessment and volume percentage error (VPE). The increased precision in estimating hippocampal volumes allows the detection of small hippocampal abnormalities already present in the MCI phase (SD = [3.9 ± 0.6]%), which may be crucial for early diagnosis.

In this study, we used transfer learning technique for the segmentation of the hippocampus, considering three datasets of patients with a clinical diagnosis of mild cognitive impairment and Alzheimer disease, scanned with different protocols. We started from a previously developed deep learning algorithm, trained with a different dataset, and we quantified the benefits given by the transfer learning, both in a numerical and visual way, using manual segmentations from two raters as a gold standard.

1. INTRODUCTION

Many neurodegenerative diseases cause volume loss in the brain region of the hippocampus (Albert et al., 2011; Minkova et al., 2017; Persson et al., 2017; Ten Kate et al., 2017), usually due to cellular death and synaptic loss (Adriano, Caltagirone, & Spalletta, 2012; Courchesne et al., 2000; Moodley et al., 2015).

Among them, Alzheimer disease (AD) is a neurodegenerative disease clinically characterized by progressive decline of cognitive function, which in most cases starts with the isolated impairment of memory (a phase indicated as mild cognitive impairment [MCI]) and eventually evolves to overt dementia, defined by the loss of social and occupational function due to cognitive impairment (McKhann et al., 2011). One of the major questions in dementia research is which MCI subjects are more likely to progress to dementia (Fischer et al., 2007; Petersen et al., 2005; Ravaglia et al., 2006). With this purpose, several studies found that lower hippocampal volume in the MCI phase is related to progression to AD dementia (Jack Jr. et al., 2010). Indeed, hippocampal atrophy has been included among the imaging biomarkers suggestive of neurodegeneration in the criteria for “MCI due to AD” (Albert et al., 2011). Thus, assessing hippocampal atrophy is crucial for a timely diagnosis of syndromes characterized by cognitive impairment, especially in their early phases (Winblad et al., 2004).

Segmentation of magnetic resonance (MR) images allows in vivo volumetric assessments to be made of structures of interest and has been widely used for measurement of the hippocampus (Minkova et al., 2017; Tondelli et al., 2012; Yushkevich et al., 2015). Segmentation maps can be produced manually or automatically. Manual segmentations of the hippocampus are time consuming and rater‐dependent, and therefore there is increasing need for reliable automatic segmentation tools to be used in clinical practice, which can be used flexibly, independently of protocol and scanner.

Convolutional neural networks (CNNs) are a deep learning (DL) strategy for image processing, that has proved to be an effective technique for medical image segmentation (Novosad, Fonov, Collins, & Alzheimer's Disease Neuroimaging, 2020; Sarvamangala & Kulkarni, 2021; Zavaliangos‐Petropulu et al., 2020). In CNNs, there are many processing blocks that implement convolution operations followed by nonlinear (activation) functions and downsampling (pooling) operations, along with other potential elements such as ways of rescaling output values (i.e., batch normalization). Each convolution kernel consists of a set of numbers, and these are the main parameters in the network, which are adjusted during training (along with other parameters associated with some of the other operations, for example, batch normalization). In each block there is a set of convolution kernels, and each produces a separate image, which are stacked together (often referred to as different channels) and typically the number of channels (or depth) in the block outputs increases as we go further into the network. It is also common for the pooling operations to continually decrease the spatial size of the images in the outputs, while at the same time the number of these channels is increasing. An exception to this is in the U‐Net where initially (in the encoder) the spatial size is decreased until a certain point and then (in the decoder) the spatial size is increased (upsampling, often via specialized steps such as a transpose convolutional layer) to bring the information back to the size of the original image (e.g., to do segmentation). In addition, the U‐Net also directly transfers information across from earlier stages, in the encoder, to the decoder (these are called skip connections) which provides precise spatial localization to the network, while the images being upsampled provide contextual information. As opposed to fully connected neural networks, CNNs maintain local spatial information and translational invariance, making them the most suitable networks for computer vision problems (Kayhan & Gemert, 2020).

However, one of the main limitations of CNN‐based models is that they often perform poorly when applied to images belonging to a domain (defined by the type of scanner, MRI sequences, and patient variety) that is different from the training dataset (Cheplygina, de Bruijne, & Pluim, 2019; Dinsdale, Jenkinson, & Namburete, 2021). In order to be able to transfer the ability of the CNN to work accurately in another domain with only a small labeling effort, it is possible to use the transfer learning technique. This partially maintains the knowledge from the original training dataset, but also adds new information from a limited number of examples from the new domain (Cheplygina et al., 2019; Pan & Yang, 2010).

Here, we test the efficacy of using transfer learning with SWANS (spatial warping network for segmentation), a fully supervised CNN method recently developed (Dinsdale, Jenkinson, & Namburete, 2019), for hippocampal segmentation of T1‐weighted images. The original training dataset used for the development of the SWANS network consisted of images from patients with AD, MCI, and cognitively healthy elderly controls from the Alzheimer Disease Neuroimaging Initiative (ADNI) project that were labeled according to the EADC‐ADNI Harmonized Hippocampal Protocol (HarP) (Boccardi et al., 2015; Dinsdale et al., 2019; Frisoni & Jack, 2015).

In the present study, we tested the performance of transfer learning on three image datasets of patients with MCI and AD, that were different to the ADNI dataset in terms of scanners and acquisition protocols. The aim of this study was to fine‐tune the SWANS network to automatically perform accurate hippocampal volume assessments in domains different from the training one, so that it will be possible to observe small changes in a wide range of patient scans.

2. MATERIALS AND METHODS

First, we tested the performance of SWANS directly, only trained with the original HarP/ADNI data, on three new imaging datasets. The code is publicly available (https://github.com/ericabalboni/SWANS), as well as the used image datasets (https://identifiers.org/neurovault.collection:12227).

Second, we performed transfer learning and assessed if it introduced significant and meaningful changes. Evaluations were done by comparing SWANS' segmentations to raters' segmentations: hippocampi in all the datasets were manually segmented using FSLeyes (from FSL) (Jenkinson, Beckmann, Behrens, Woolrich, & Smith, 2012) twice, by two different raters, who had been trained to perform hippocampal segmentation according to the harmonized hippocampal protocol (HarP) (Frisoni & Jack, 2015).

The subset of the ADNI dataset, on which SWANS had been originally trained, consisted of 100 T1‐weighted images, segmented according to the HarP protocol in MNI 1 mm resolution space (Boccardi et al., 2015; Frisoni & Jack, 2015). This dataset had been used to train the DL CNN, consisting of an initial 3D encoder‐decoder U‐Net architecture (Ronneberger, Fischer, & Brox, 2015), from which the network learns a warping transformation map to be applied to an initial ellipsoidal mask, which ultimately becomes the segmentation map of the hippocampus (Figure 1) (Dinsdale et al., 2019). The last CNN section is a spatial transformer network (Jaderberg, Simonyan, Zisserman, & Kavukcuoglu, 2015) adapted to perform local transformations.

FIGURE 1.

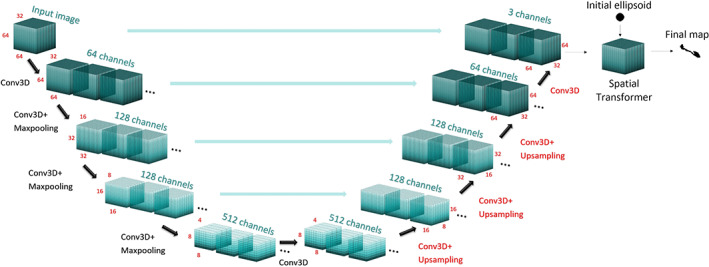
Structure of the u‐net: black layers were kept fixed for the transfer learning, while red layers were trained. Each layer uses a ReLu activation function (Nicola K. Dinsdale et al., 2019). The final section of the network, the spatial transformer, is not shown but only has fixed parameters

3. DATASETS

The three new datasets used in the present study differ in population demographics, scanner, and image protocol. Each dataset had been acquired as part of a study approved by the local ethical committee, for which participants had given written consent.

3.1. Dataset 1

The first dataset included 31 T1‐weighted brain images from 31 patients with MCI. They had been acquired with the sequence detailed in Table 1, on the 3 T General Electric (GE) Signa Architect scanner of the University Hospital of Modena, Italy. Participants had undergone extended clinical and biomarker assessment as detailed in a previous study (Chiari et al., 2021).

TABLE 1.

Characteristics of the acquisition sequences

DS	Scanner	Field	Voxel size	Field of view	Sequence	TE (ms)	TR (ms)	TI (ms)	FA	Ch.	Acquisition time (min)	Acceleration factor	SMS factor
1	General Electric Signa Architect	3T	0.5 mmisotropic	328 X 512 X 340	MP‐rage	3.1	2,150	900	8°	48	5.5	2	2
2	Philips Achieva	3T	1 mm isotropic	160 X 205 X 140	MP‐rage	4.6	9,360	900	15°	8	4.7	2	1
3	Siemens Magnetom	3T	1 mm isotropic	192 X 174 X 192	MP‐rage	4.7	2040	900	8°	32	5.56	1	1

Abbreviations: Ch., number of channels in the head coil; DS, dataset; FA, flip angle; SMS, simultaneous multislice imaging; TE, echo time; TR, repetition time.

3.2. Dataset 2

This dataset consisted of 30 T1‐weighted brain images from patients with MCI. Images were acquired on the 3 T Philips Achieva scanner of the OCSAE Hospital of Modena (see Table 1 for acquisition parameters). Participants had undergone extended clinical and biomarker assessment as detailed in a previous study (Tondelli et al., 2018).

3.3. Dataset 3

The dataset included 12 T1‐weighted brain images from patients with AD. They were acquired on the 3 T Siemens Magnetom scanner of the Oxford Centre for Magnetic Resonance (OCMR) at the John Radcliffe Hospital in Oxford, UK (Table 1). Participants had undergone extended clinical and neurological assessment as detailed in a previous study (Zamboni et al., 2013).

3.4. Preprocessing

Brain extraction was performed with BET (Smith, 2002), part of FMRIB Software Library (FSL) (Jenkinson et al., 2012). SWANS takes as input images in standard MNI152 1 mm space (Grabner et al., 2006), therefore all the brain volumes and the manually segmented hippocampal maps were registered to it, using the FLIRT and FNIRT tools from FSL (Greve & Fischl, 2009; Jenkinson, Bannister, Brady, & Smith, 2002; Jenkinson & Smith, 2001). Manual segmentation maps were thresholded at 0.5 and binarized after applying the same spatial transformation obtained from the registration of the T1‐weighted image.

SWANS also needs inputs to be cropped images of a single hippocampus with size 32 × 64 × 64. Image cropping was included in the algorithm. Moreover, intensity values were scaled to be largely between 0 and 1: the automated algorithm divided the registered image by the 99th percentile and cropped the volume around each hippocampus.

3.5. Training

Transfer learning was performed by keeping the weights of the encoder fixed, consisting of the first five layers, and fine‐tuning the subsequent weights, associated with the decoder, consisting of the remaining four layers (Figure 1).

We split the original datasets into training, validation, and testing using the proportions 64%, 10%, and 26%, respectively. Testing and validation images were never used during training. The validation images were used to prevent the model overfitting to the training data during the tuning process and the testing images were used to independently evaluate the network's performance on new images after training and tuning. Training, testing, and validation datasets contained images from all the three different original datasets in almost equal proportions.

In particular, 19 subjects (with a total of 38 hippocampi) including 8 subjects with MCI from Dataset 1, 8 subjects with MCI from Dataset 2, and 3 subjects with AD from Dataset 3 were separated from the training dataset and kept as a hold‐out test dataset.

We used four methods of training, combining different training datasets, and learning approaches. For each method we performed data augmentation by flipping the images left–right, exploiting brain symmetry. The dataset was then further doubled, because we used, as a gold standard, both of the two manual segmentations.

The loss function to be used was the same as in a previous study (Dinsdale et al., 2019). It was a combination of binary cross‐entropy and Dice coefficient loss, with a relative weighting factor α of 0.6:

$$1-\frac{2·\sum _i{\widehat{y}}_i·y_i+\epsilon }{\sum _i{\widehat{y}}_i+\sum _i{y}_i+\epsilon }-\alpha \frac{1}{N}\sum _i{y}_i\log \left({\widehat{y}}_i\right)+\left(1-y_i\right)·\log \left(1-{\widehat{y}}_i\right)$$

where ${\widehat{y}}_i$ and $y_i$ are respectively predicted and gold standard voxel values, N is the total number of voxels and $\epsilon$ is a regularization parameter set to 1.

We used Python version 3.6.9, with Keras (version 2.3.1) and Tensorflow (version 1.15.0). Training was optimized with the Adam optimizer. Adam is a generalization of the stochastic gradient descent optimization method, using a different learning rate for each parameter and updating the rates based on the statistics (moments) of recent gradients. This is useful in CNNs as different layers show highly diverse loss function gradients (Kingma & Ba, 2015). The learning rate was chosen to be 10 times smaller than the default ($1\bullet {10}^{-4}$), as the default behavior was fast but unstable, while other hyperparameters were left at their default values. The mini‐batch method was chosen for training, using a batch size of 2 during the training.

It took 50 epochs with an Intel Xeon CPU E5 2620 version 2. The training time varied with the size of the dataset: with a training dataset of 54 images the time per epoch was of 1 hr, while with 22 and 23 images the time was of half an hour. In contrast, prediction time was only a few seconds. Outputs of SWANS were thresholded at 0.5, and changes to this threshold had little influence as all the output values were either higher than 0.9 or lower than 0.1, meaning that voxels had a probability of belonging to the hippocampus that was either higher than 90% or smaller than 10%.

3.6. Training methods

Below, we describe the characteristics of the four training methods for transfer learning, which gave rise to the four new models. In addition, the baseline model is included in the evaluations, alongside these four new versions:

• “Transfer All” model. This was constructed by varying the parameters (weights and biases) of the four last layers and with the training dataset consisting of 54 images (23 MCI from dataset 1, 22 MCI from dataset 2, and 9 AD from dataset 3). Five hippocampi were excluded from training and used as validation data (2 MCI from dataset 1, 2 MCI from dataset 2, and 1 AD from dataset 3).

• “Training All” model. In this case, the weights of the “Baseline” model were used for initialization and all the weights (and biases) in the network were allowed to vary during training. The training and validation datasets were the same as for the “Transfer All” model.

• “Transfer DS1” model. This was again obtained through transfer learning, only varying the parameters in the four last layers (as in the “Transfer All” model). The training dataset, for this case, only included images belonging to the first dataset. It consisted of 23 images, among which 1 was excluded from training and used as validation. It was the same image included in the validation dataset of the “Transfer All” and “Training All” models.

• “Transfer DS2” model. This was obtained through transfer learning, only varying the parameters in the four last layers. The training dataset included 22 images, all belonging to dataset 2. Of these, one of them was used for validation and excluded from training. It was the same image included in the validation dataset of the “Transfer All” and “Training All” models.

• “Baseline” model (Dinsdale et al., 2019).

The “Transfer DS1” and “Transfer DS2” models were constructed to investigate if it was better to customize SWANS for a specific acquisition method or to have more variability in the training for transfer learning. The “Transfer All” model was, instead, introduced to compare the performance of transfer learning on a complete training set.

3.7. Validation metrics

We evaluated SWANS' voxel‐wise segmentation accuracy and its volume accuracy. Segmentation accuracy was estimated both visually and numerically, using the Dice coefficient, estimating the overlap between segmentation maps from SWANS with the manual ones from the two raters (Zou et al., 2004). Dice coefficients associated with SWANS were calculated using separately rater 1 and rater 2 as gold standard, without calculating a mean value for hippocampus. Visual assessment was performed by the two raters.

Hippocampal volume accuracy was evaluated by the volume percentage error (VPE), calculated in the following way:

$$\mathrm{VPE}=100\bullet \frac{V^{\exp }-V^{\mathrm{th}}}{V^{\mathrm{th}}}$$

where V ^exp is the hippocampal volume from SWANS and V ^th is the mean of the manually segmented hippocampal volumes (i.e., the gold standard volume) from the two raters. The mean of the VPE values represents systematic difference from the gold standard and the SD of the VPE values represents SWANS' precision in measuring hippocampal volume.

3.8. Statistical analysis

All the statistical analyses were performed with Matlab 2020b (The MathWorks, 2020). First, we evaluated the reliability between the two raters in measuring hippocampal volume by calculating the intraclass correlation coefficient (ICC), without considering the systematic difference, that is, as norm‐referenced reliability (Salarian, 2021). We interpreted the outcome ICC > 95% as excellent reliability, meaning that one rater would have been enough for gold standard, 75% < ICC < 95% as good reliability, meaning that both raters were necessary, ICC < 75% as not acceptable expertise of at least one of the two raters (Koo & Li, 2016). The calculation was performed in subject space to avoid normalization bias.

Second, we tested SWANS “Baseline” segmentation maps and hippocampal volumes for all the datasets. We compared Dice coefficients between the two raters to Dice coefficients between SWANS and the two raters, using a graphical boxplot representation. Hippocampal volumes from SWANS were compared to the mean volume from the two raters, through a Bland Altman Plot (Rik, 2021).

Third, we tested new models, evaluating them using manual segmentations from the hold‐out test sets that were not used in the training phase. We verified that all distributions of Dice coefficients and VPE values were Gaussian through Kolmogorov Smirnov tests (p < .05). Then, we used a nonparametric Kruskal–Wallis test, evaluating Dice coefficients associated with segmentations from the new models and from the “Baseline” model. The null hypothesis was that segmentations from the new models and the “Baseline” model were all equivalent.

Hippocampal volumes obtained from the baseline SWANS model and from the new models were compared to the gold standard volumes with Bland Altman plots. To test if the new models were more precise than the “Baseline” model in measuring hippocampal volume, we performed Bartlett's test for homoscedasticity using VPE values from the different models (Bartlett, 1937). The null hypothesis was that VPE values from the new models had a variance that was equal to that of the “Baseline” model.

4. RESULTS

The ICC evaluating the agreement between the two raters in measuring the hippocampal volume was 85%. Boxplots comparing Dice coefficients associated with the raters and SWANS (Figure 2) showed that the compatibility between the two raters was significantly higher (p < .001) than that between SWANS and the two raters, as can also be seen from the summary statistical parameters (Table 2). A Bland Altman plot comparing SWANS and the gold standard (Figure 3) showed that SWANS systematically estimated smaller hippocampal volumes and had more difficulty for larger hippocampi. From these results, we could see that models constructed with transfer learning had the capacity to perform better.

FIGURE 2.

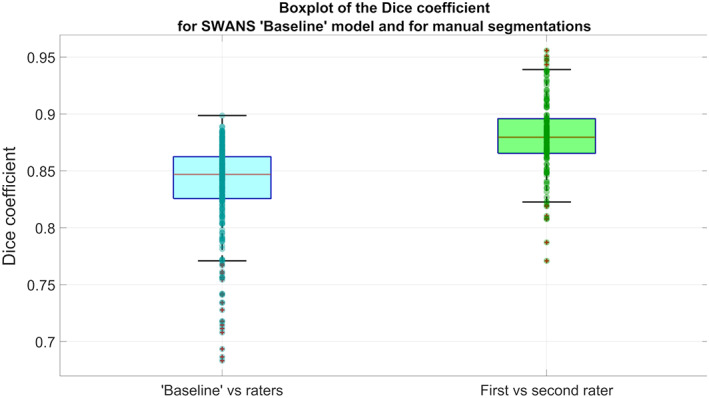
Boxplots of Dice coefficients for the SWANS network with the “Baseline” model (using separately labels from rater 1 and 2 as ground truth) on the left and for the manual raters (comparing the raters with each other) on the right, using the whole dataset of 146 hippocampi

TABLE 2.

Statistical values of the Dice coefficients for SWANS with the “Baseline” model (comparing SWANS separately to rater 1 and rater 2) and for the two raters

	SWANS “Baseline”	Raters
Dice coefficient:
Median	0.847	0.880
Interquartile range	0.826–0.862	0.866–0.896
Mean	0.838	0.880
SD	0.04	0.03

FIGURE 3.

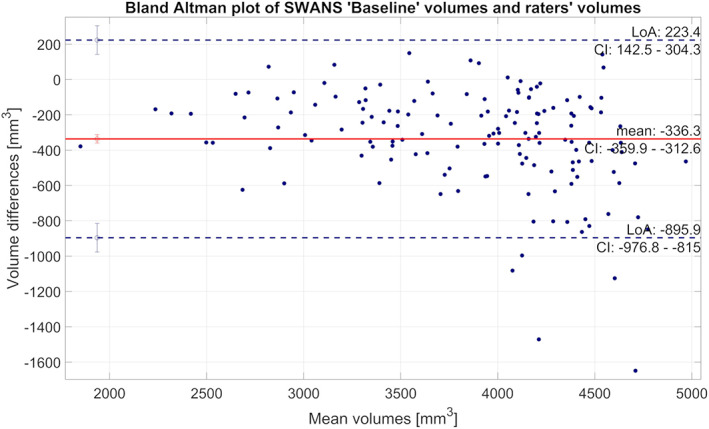
Bland Altman plot comparing hippocampal volumes from the SWANS network with the “Baseline” model to the gold standard (the average of the two manual labels). Positive values indicate that hippocampal volumes from SWANS were larger than gold standard and vice versa

From the Kruskal–Wallis test results it can be seen that the mean Dice coefficients from the different models were significantly different (p < .001, Figure 4). Following this, paired Wilcoxon rank sum tests were performed, showing that all the new models had significantly higher Dice coefficients than the “Baseline” model (p < .001) and that the new models did not differ from each other.

FIGURE 4.

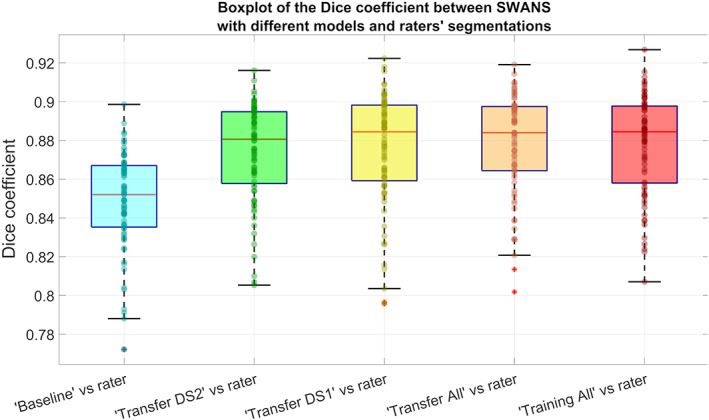
Boxplot of Dice coefficients for the SWANS network with different transfer learning models (considering separately labels from rater 1 and 2 as ground truth), using a hold‐out test dataset of 38 hippocampi

The results of Bartlett's test on VPE values from both the “Baseline” model and the new models showed no significant differences among models (p = .06), even though all new models had better precision than the “Baseline” model (i.e., lower SDs, Table 3, Figure 5).

TABLE 3.

Statistical values of VPEs and Dice coefficients for each SWANS model

	Baseline	Transfer DS2	Transfer DS1	Transfer all	Training all
Dice coefficient
Median	0.852	0.881	0.884	0.884	0.885
25th to 75th percentiles	0.835 to 0.867	0.858 to 0.895	0.859 to 0.898	0.864 to 0.898	0.858 to 0.898
Mean	0.848	0.874	0.876	0.878	0.878
SD	0.03	0.03	0.03	0.03	0.03
VPE
Median	−6.4%	3.1%	1.2%	5.0%	2.4%
25th to 75th percentiles	−9.7% to −1.4%	0.46% to 5.4%	−1.9% to 4.5%	2.1% to 7.1%	0.48% to 4.8%
Mean	−5.7%	2.9%	1.1%	4.1%	2.1%
SD	5.8%	4.9%	4.2%	4.5%	3.9%

Note: The mean and median values of VPE highlight systematic difference with the gold standard, while SDs and quartile ranges (between the 25th and 75th percentiles) show the precision of the algorithm in estimating hippocampal volume.

FIGURE 5.

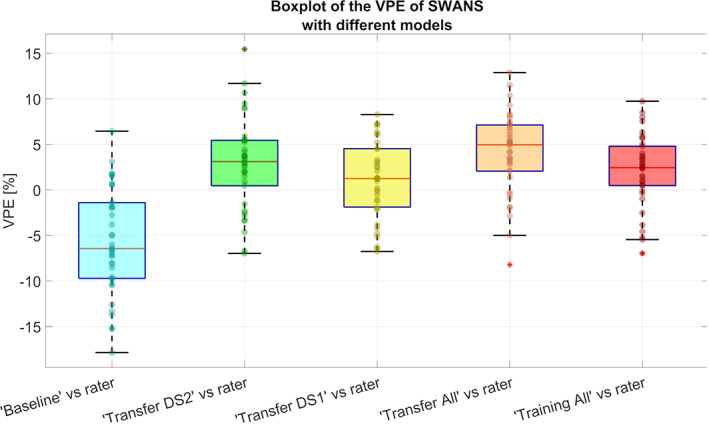
Boxplots of VPE values for the SWANS network with different transfer learning models, using a hold‐out test dataset of 38 hippocampi. The median values highlight a systematic difference with the gold standard, while the interquartile ranges show the precision of the algorithm in estimating hippocampal volumes

Bland Altman plots (Figure 6) showed that hippocampal volume estimates from the new models were slightly larger than the gold standard. Also, “Transfer DS2” model clearly had the worst performance for larger hippocampal volumes.

FIGURE 6.

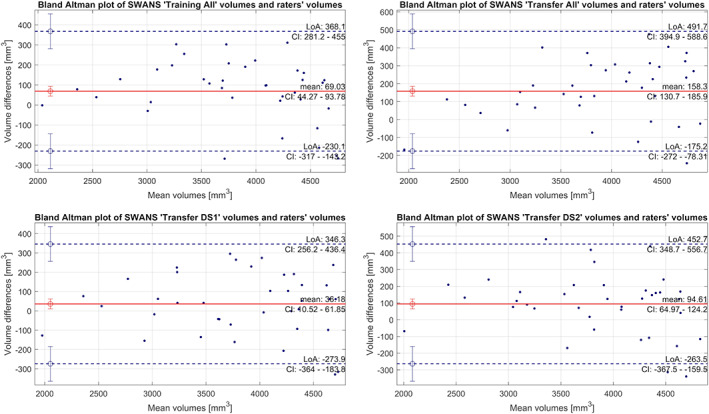
Bland Altman plot comparing hippocampal volumes from the SWANS network, for the different transfer learning models, to the gold standard. Positive values indicate that hippocampal volumes from SWANS were larger than gold standard and vice versa

4.1. Visual assessment

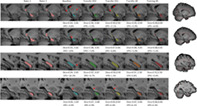
Figure 7, whose elements are presented separately in Figures S1‐S32, Supporting Information, shows four characteristic examples from the three datasets, with their corresponding segmentations performed by different models and by the two raters. It shows that, qualitatively, segmentations were performed in a satisfactory way by all models, but we categorized four types of issues associated with the segmentations of the network from the “Baseline” model that were completely or partially absent in the new models' segmentations. No additional problems were introduced by the new models. Each example shown in Figure 7 corresponds to a different type of issue that the “Baseline” model had in segmenting the hold‐out test dataset of 38 hippocampi. We comment them on below.

FIGURE 7.

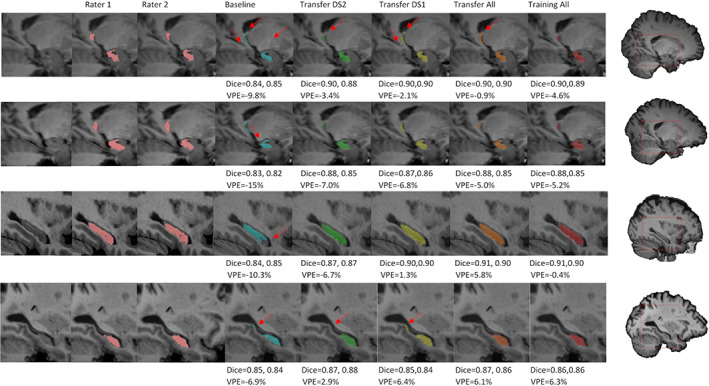
Hippocampal segmentation maps produced by different models, compared to ones from the two raters. In the first row the red arrows highlight the presence of isolated voxel labels, in the second row they show incomplete portions of the hippocampal head, in third row they indicate incomplete portions in the lateral side, and in the fourth row they highlight an additional tract in the caudal region. Dice coefficient and VPE scores of each segmentation are showed below the corresponding image. Subjects in rows 1 and 2 come from dataset 2, subject in row 3 from dataset 1 and subject in row 4 from dataset 3; all views are sagittal and all views except row 4 are from the right hippocampus; rows 1 and 2 show medial slices and rows 3 and 4 show lateral slices

4.1.1. Isolated voxel allocation

For 22 hippocampi, the “Baseline” model included a few isolated voxels that were completely outside of the hippocampal region within its segmentation. In the first row of Figure 7 this can be seen for the right hippocampus of a subject of the second dataset. All the other models showed an improvement in hippocampus localization, especially with regards to the white matter region. However, the “Transfer DS1” model still included some voxels under the parahippocampal white matter, and only the “Training All” model eliminated the caudal part that is close to the temporal horn.

4.1.2. Incomplete hippocampal head

For 13 hippocampi, the “Baseline” model had difficulties in completely segmenting the most anterior part of the hippocampus. For the subject shown in the second row of Figure 7, a considerable portion was ignored. Other models still neglected a tiny area close to cerebrospinal fluid, but their segmentation was more complete.

4.1.3. Incomplete lateral side

For 11 hippocampi, the “Baseline” model excluded a large part of the lateral side. In the third row of Figure 7, the “Baseline” model segmentation missed a large portion of anterior‐right part, while all the other models covered almost the whole area.

4.1.4. Additional tract in the caudal region

For three hippocampi, from two subjects, the “Baseline” model segmented a white matter and enthorinal cortex tract in the most caudal region. In the fourth row of Figure 7, an AD subject from the third dataset is shown. The other subject in which this phenomenon occurred belongs to the first dataset. For the case shown in the figure, it is possible to notice that additional voxels were partially removed by the “Transfer DS2” and “Transfer All” models, and completely removed by the “Training All” model.

5. DISCUSSION OF RESULTS

In this study, we performed transfer learning on a CNN called SWANS (Dinsdale et al., 2019), that produces hippocampal segmentations, to improve the accuracy of hippocampal volume estimates, with the ultimate aim of being able to detect, in clinical settings, very small volume abnormalities in the hippocampi of patients with MCI.

Through intraclass correlation coefficient values, we determined that the agreement between the two raters was good, but not perfect, meaning that one rater alone would not have been sufficient to build a reliable gold standard. We used three types of validation: quantitative evaluation of segmentation maps using Dice coefficients, quantitative hippocampal volume evaluation using VPE, and visual assessments of segmentation maps.

Dice coefficient values reflected how much the segmentation maps from the algorithms overlapped with the average of the raters' gold standard maps. We demonstrated that all of the new models obtained through transfer learning had higher Dice coefficient values than the ones from the “Baseline” model. This was expected, as the loss function of the network included a Dice coefficient score. The new models did not show a significant difference in their mean Dice coefficient, and therefore, they were deemed statistically equivalent.

VPE values showed differences in hippocampal volumes calculated from a segmentation map of a model and the average of the ones from the two raters. Its SD represents the precision associated with the volume estimates, while its mean represents any systematic difference. Although the systematic difference was reduced by the new models, precision was not significantly improved after the training. However, all new models did present smaller SDs in VPE compared to the “Baseline” model, though this difference, and the differences in mean Dice coefficient, might not have been detected in this instance because of the limited size of the hold‐out test dataset.

From visual assessment, the problems associated with the “Baseline” model were completely or partially corrected by the new models. The model that had best visual performance was “Training All,” which also had the highest mean Dice coefficient and the smallest variance in VPE. Therefore, the “Training All” model was chosen as the best of all the models tested.

The VPE associated with the chosen model has a SD of (3.9 ± 0.6)%, meaning that for approximately 68% of the time the error committed by the algorithm is less than 3.9%. This precision can be useful for assessments in hippocampal volume changes in the MCI stage, as AD hippocampi show reductions of the order of 25% and MCI of roughly 11% compared to matched healthy controls (Thompson et al., 2003, 2007).

The chosen model (“Training All”) required the longest time to train, due to the large number of images to be labeled. Its better performance is probably related to the size of its training dataset, which is comparable in size to that of the Baseline model, so it was sufficient to also optimize the parameters belonging to the first layers. More specifically, the effort to create manual segmentation labels for the “Training All” model involved two raters, with 2 weeks of initial training, and nearly another 1.5 months to segment the images in datasets 1, 2, and 3, while the computational training time was only 2 days. The computational time needed to perform all the preprocessing and processing steps to obtain the two segmentation maps of the hippocampi, from the all the datasets, was about 20 min per subject for all the models, which is a lot less than the time needed to generate manual segmentations per subject.

Although the “Training All” model showed the best segmentation quality, it also required a major effort. If possible, performing transfer learning by using previous parameters (weights and biases) only as an initialization and using as many images as possible (almost 50 subjects in our case) for training is the best strategy. However, there is a substantial cost in time for manually segmenting the images, so that it might not be feasible to reach such numbers. In the case where fewer manual segmentations are available, it would still be recommended to use the transfer learning technique, as clear benefits were seen even with the smaller subsets of data. Finally, it is important to evaluate the benefits in a visual way, since the simpler quantitative measures were not as useful in showing the important changes.

In fact, the quantitative assessment of the segmentation maps was not particularly helpful in establishing whether there had been an improvement in the segmentation that could be potentially clinically useful. In particular, Dice coefficients were too sensitive to systematic changes, while VPE values wrongly improved when the segmentation was overall smaller and included areas outside the hippocampus. Instead, visual assessment clearly showed the superiority of the new models and, in particular, of “Training All.” The most important improvement in terms of clinical implication given by transfer learning techniques consisted of eliminating the cases where the “Baseline” model had produced segmentations with several critical inaccuracies. These cases were not found in the majority of subjects but could have been sufficient to bias a clinical study that used, as an example, the value of hippocampal volume in predicting conversion to dementia. Indeed, in clinical settings the outliers frequently make a big difference. In this sense, we can conclude that the “Training All” strategy delivered a clinically useful level of performance, with segmentations that otherwise would have not been considered of sufficient quality for clinical purposes. To test if this improvement could have been already detected at a clinical level, we used Spearman rank‐order test to evaluate a possible correlation between hippocampal volume and mini mental state examination (MMSE). Hippocampal volumes from both models had a significant positive correlation with MMSE score (p < .05) with no evident difference between models, suggesting that further analyses are needed to fully demonstrate the clinical benefits of transfer learning.

The main limitation of this study was the relatively small number of subjects used to test the new models, which constrains the statistical power of the results. The main strengths were having two expert raters perform the segmentations of each hippocampus, as we could more reliably construct the gold standard and perform key visual assessments over the varying datasets.

6. CONCLUSION

Transfer learning has been successfully deployed on a DL CNN in this work, demonstrating that we could improve the performance of the network, in a clinically meaningful way, on new datasets with different domains than the one used for the original training. This has important implications for the utility of DL methods across a wide range of clinical settings, since pre‐trained models often underperform in data collected in different hospitals and on different machines. An estimate for the possible improvement that can be obtained from an extra set of manually labeled images is indicated by this work, but highlights that expert visual assessments are more valuable than simple statistical measures. Future work should examine the limits regarding size of the additional datasets, and how this impacts the possible improvements, as well as ways of quantifying performance that are more clinically relevant.

CONFLICT OF INTEREST

The authors declare that the research reported here was conducted in the absence of any commercial or financial relationships that can be construed as potential conflicts of interest.

AUTHOR CONTRIBUTIONS

Giovanna Zamboni designed the study and formed the research group. Nicola Dinsdale, Ana I. L. Namburete, and Mark Jenkinson realized the baseline model and supported. Erica Balboni and Luca Nocetti in implementing the code. Erica Balboni and Chiara Carbone manually segmented the images and collected the data. Maurilio Genovese and Marcella Malagoli controlled the segmentations and resolved major disagreements between Erica Balboni and Chiara Carbone. Erica Balboni and Luca Nocetti trained the network and performed the statistical analysis. Mark Jenkinson and Gabriele Guidi supervised the statistical analysis. Giovanna Zamboni and Annalisa Chiari performed the clinical and neurological assessment of the patients. Erica Balboni wrote the initial draft of the manuscript and all the authors contributed to the review of the manuscript.

ETHICS STATEMENT

This study used data from protocols approved by local ethics committees in accordance with the principles of the Helsinki Declaration (1983). Written consent was obtained from all the subjects involved: Ethical approval from Comitato Etico dell'Area Vasta Emilia Nord, code 832/2018, on January 23, 2019 (dataset 1). Ethical approval from Comitato Etico Provinciale di Modena, code 252.09, on April 21, 10 (dataset 2). Ethical approval the Bristol Frenchay Research Ethics Committee, code 09/H0107/8, on April 16, 2010 (dataset 3).

Supporting information

Appendix S1 Supplementary figures

Balboni, E. , Nocetti, L. , Carbone, C. , Dinsdale, N. , Genovese, M. , Guidi, G. , Malagoli, M. , Chiari, A. , Namburete, A. I. L. , Jenkinson, M. , & Zamboni, G. (2022). The impact of transfer learning on 3D deep learning convolutional neural network segmentation of the hippocampus in mild cognitive impairment and Alzheimer disease subjects. Human Brain Mapping, 43(11), 3427–3438. 10.1002/hbm.25858

DATA AVAILABILITY STATEMENT

The authors confirm that the data supporting the findings of this study are available within the article and from the corresponding authors upon reasonable request.