PERSPECTIVE: TEMPERATURE-DEPENDENT DENSITY AND THERMAL EXPANSION OF CRYOPROTECTIVE AGENTS

Abstract

The density is a key thermophysical property, affecting the response of the material to temperature changes in different ways, consistent with the phase of state. In fluids, temperature variation across the domain leads to colder areas being heavier than warmer areas, where buoyancy effects drive fluid flow and thereby increase heat transfer. This phenomenon is known as natural heat convection, which in general is a more efficient heat transfer mechanism than heat conduction in the absence of flow. In solids, where the material is locked in place, colder areas tend to contract while warmer areas tend to expand, leading the material to deform. When this deformation is constraint by the geometry of the domain and/or its container, mechanical stresses develop. This phenomenon is known as thermomechanical stress (or thermal stress), which can lead to structural damage such as fractures. The picture becomes even more complex during vitrification (or glass formation), where the material gradually changes from liquid to an amorphous solid over a significant temperature range. There, due to temperature variation across the domain, fluid mechanics and solid mechanics effects may coexist. It follows that characterization of the density as a function of temperature is crucial for the analyses of thermal, fluid, and mechanical effects during cryopreservation, with the goals of protocol planning, optimization, and preserving structural integrity. For this purpose, the current study focuses on the density of the material and its companion property of thermal expansion. Specifically, this paper reviews literature data on thermal expansion of cryoprotective agents (CPAs), discusses the mathematical relationship between thermal expansion and density, and presents new calculated density data. This study focuses on the CPA cocktails DP6, VS55, M22, and their key ingredients at various concentrations, including DMSO, Propylene Glycol, and Formamide. Data for DP6 combined with a selection of synthetic ice modulators (SIMs) are further presented.

INTRODUCTION

The long-term preservation of organs and tissues will not only help tens of thousands of patients on the official transplant waiting list, but also millions of others suffering from end-stage organ disease (1). A promising means for long-term preservation of large-size specimens is cryopreservation via vitrification (vitreous means glassy in Latin) (2). Vitrification involves relatively high cooling and rewarming rates of cryoprotective agents (CPAs), which are loaded into the tissue in order to suppress crystallization and, thereby, avoid its associated devastating effects on mammalian cells and tissues (2,3).

Cooling and rewarming rate limits imposed by the sheer size of organs, the underlying principles of heat transfer, and the kinetics of crystallization often require additional means to promote vitrification, with the addition of synthetic ice modulators (SIMs) as a promising alternative (4). In general, while CPAs promote vitrification by exponential increase in viscosity with decreasing temperature, and thereby suppress molecular motion, SIMs are compounds which inhibit ice nucleation and growth by various mechanisms not directly related to viscosity (4). For example, compounds such as 1,3-cyclohexanediol limits the growth of ice crystals owing to its special chemical structure (5), while synthetic compounds like the very-low-molecular-weight polyvinyl alcohol (PVA) copolymer inhibit heterogeneous nucleation of ice (6).

An additional and potentially devastating effect on the recovery of preserved tissues and organs from cryogenic storage is the thermomechanical stress, which is driven by differential expansion of the cryopreserved material due to thermal effects. Such differential thermal expansion may result from temperature gradients in the specimen and the tendency of the material to change its volume with temperature, thereby leading to thermal expansion gradients (7,8). Another source of variable thermal expansion is partial ice formation, where pure water expands by about 9% upon freezing in standard conditions (9). Yet another source of thermomechanical stress is the thermal expansion mismatch between the specimen and the container (10,11), between the specimen and its surrounding solution (12), and even between the different constituents of the tissue (12). Either way, excessive thermomechanical stress can lead to structural damage, with fracture formation and plastic deformation as possible outcomes (10,11,13–15).

Successful vitrification is the result of a multiphysics process optimization associated with the coupled effects of CPA toxicity, thermal effects, kinetics of crystallization, and thermomechanical stresses (16). Given the virtually endless combination of key parameters involved, physical modeling (17–19) and computer simulations (20–24) appear to be critical and cost-effective tools in seeking for improved cryopreservation protocols. The current study summarizes experimental data relating to a key thermophysical property of the material – the density. In heat transfer analysis, the heat capacity of the material is proportional to its density (that is the product of the intrinsic properties of density and the specific heat), in fluid mechanics analysis it is associated with the buoyancy effects and convection, while in the solid mechanics analysis, the intrinsic property of thermal expansion—the driving mechanism of thermomechanical stress—is in fact inversely proportional to the density. For this purpose, the current study presents the mathematical relationship between the thermal expansion coefficient and the density of the material. In addition, this study presents compiled experimental data from literature for the benefit of physical modeling and computational cryobiology.

THE RLEATIONSHIP BETWEEN THERMAL EXPANSION AND DENSITY

The linear thermal expansion coefficient is a relative property describing how much a unit length of the material changes with temperature compared with its known original length at a reference temperature. For this purpose, a small isotropic cube of mass m is assumed:

$$m= \rho l^3$$ [1]

where its density is ρ and its typical dimension is l. Assuming mass conservation, changes in density and dimensions is given by:

$${\rho }_0{l}_0^3 =\rho l^3$$ [2]

where the subscript 0 refers to a reference value at temperature T₀.

Using the linear thermal expansion coefficient, β, the length of the cube as a function of temperature can be calculated as:

$$l=l_0\left(1+\epsilon \right) ; \epsilon \equiv \underset{T_0}{\overset{T}{\int }}\beta \left(T\right)dT$$ [3]

The integral of the thermal expansion coefficient over temperature is defined as the thermal strain, ε, in solid mechanics analyses. Since the integral in Eq. [3] is at least one order of magnitude smaller than 1, the corresponding expansion of the unit volume can be approximated as:

$$l^3=l_0^3{\left(1+\epsilon \right)}^3\cong l_0^3\left(1+3\epsilon \right)$$ [4]

while ignoring higher order terms of the cubic expansion. In practice, the approximation presented in Eq. [4] leads up to 2% error in the calculation of the change in volume, which is less than the uncertainty in the experimental measurement of the thermal expansion coefficient β (25).

Finally, by substituting the volume in Eq. [4] into Eq. [2], the density can be calculated as:

$$\rho ={\rho }_0{\left(1+3\epsilon \right)}^{-1}$$ [5]

For the purpose of this study, a reference temperature of 25°C is selected, where the thermal expansion coefficient is extrapolated to the reference temperature using polynomial approximation listed in Table 1. When not readily available, the reference density was calculated by assuming the CPA to be an ideal solution (26). Since the total volume of an ideal solution is equal to the sum of the volumes of the components (26), the reference density can be derived as:

$${\rho }_0={\left(\sum _{i=1}^{n_c}\frac{w_i}{{\rho }_i}\right)}^{-1}$$ [6]

where n_c is the number of components, and w_i and ρ_i are the mass fraction and density of the i^th component, respectively. The uncertainty of this assumption is addressed in the discussions section below.

Table 1:

Coefficients of best-fit polynomial approximation for thermal strain, ε = a₂T²+a₁T+a₀, and the coefficient of thermal expansion, β=2a₂T+a₁, °C⁻¹.

Solution	Material	Temperature Range, °C	a0 × 103	a1 × 104	a2 × 107	Ref.
DP6	Pure Solution	−41.9…25	−3.621	2.142	9.504	(34)
DP6+UCV		−87.8…25	−7.442	2.279	6.839
DP6+UCV+1% X1000		−84.4…25	−7.326	2.321	6.571
DP6+UCV+1% Z1000		−84.3…25	−7.374	2.487	6.548
DP6+UCV+1% X1000+1%Z1000		−84.4…25	−5.748	2.432	6.723
DP6+UCV+0.5M Sucrose		−81.7…25	−5.069	2.274	5.157
M22		−91.1…25	−4.709	2.520	6.235
2.2 M Propylene Glycol		−4.1…25	−1.923	0.583	16.77	(33)
3 M Propylene Glycol		−6.6…25	−2.346	0.847	14.53
3.1 M Formamide		−3.4…25	−2.0	0.849	13.33
3.1 M DMSO		−7.7…25	−1.983	0.956	9.324
6 M DMSO		−36.2…25	−4.609	1.981	2.296
8.4 M DMSO		−95.6…25	−5.205	2.383	−1.014
DP6 + EC	Pure Solution	−55…25	0.247	1.992	2.705	(4)
	Bovine Muscles	−45…25	−0.428	1.957	11.50
	Goat Artery	−40.5…25	−4.447	1.653	10.41
		−167.2…25	−4.321	1.564	3.825	(31)
DP6 + 12% PEG400	Pure Solution	−95…25	−0.496	2.313	−0.219	(4)
	Bovine Muscles	−85…25	0.982	2.118	1.697
	Goat Artery	−80…25	−0.487	2.392	1.777
DP6 + 6% 1,3 - CHD	Pure Solution	−80…25	2.699×10−2	1.957	−0.627
	Bovine Muscles	−80…25	−1.366	2.175	4.411
	Goat Artery	−80…25	−0.548	2.232	1.054
DP6 + 6% 2,3 - BD	Pure Solution	−90…25	0.452	2.080	0.631
	Bovine Muscles	−85…25	−1.117	2.094	1.431
	Goat Artery	−90…25	−1.104	1.912	0.738
VS55	Pure Solution	−77.1…25	−3.838	1.841	2.012	(32)
	Bovine Muscles	−47.8…25	−2.655	1.852	4.118
	Goat Artery	−63.6…25	−3.711	2.081	9.425
		−165.3…25	−3.652	1.911	5.312	(31)
7.05M DMSO	Pure Solution	−95.8…25	−4.462	2.084	0.563	(32)
	Bovine Muscles	−58.3…25	−3.373	2.215	7.578
	Goat Artery	−93.1…25	−4.895	1.995	6.127
		−167.7…25	−4.939	1.890	4.796	(31)

A previous study on density in freshly isolated tissues (27) demonstrated that the fat-free and water-free density of fresh tissues is in a close range for different tissues at about 1390 ± 102 kg/m³. The water content is found to be 76.5% for bovine muscles (27) and 72.1% for carotid arteries (28). For the case of tissue permeated with CPA, the permeation time is assumed to be sufficiently long such that all the water in the specimen is replaced by CPA. The reference density for the CPA permeated tissue systems is given by Eq. [6].

Finally, uncertainty in density calculations is calculated by applying the technique presented previously (29) on Eq. [5]:

$$\Delta \rho =\sqrt{{\left(\frac{\partial \rho }{\partial {\rho }_0}\Delta {\rho }_0\right)}^2+{\left(\frac{\partial \rho }{\partial \epsilon }\Delta \epsilon \right)}^2}=\sqrt{{\left(\frac{\Delta {\rho }_0}{1+3\epsilon }\right)}^2+{\left(\frac{-3{\rho }_0}{{\left(1+3\epsilon \right)}^2}\Delta \epsilon \right)}^2}$$ [7]

where Δ represent the uncertainty range.

CALCULATED DENSITY DATA

Literature data on the thermal expansion coefficient (4,30–34) is used to calculate the temperature dependent density. The materials analyzed include DMSO, VS55, M22 and DP6 in combination with various SIMs, in presence and absence of tissues, Table 1. There, EC refers to EuroCollins carrier solution (35), UCV is Unisol cryoprotectant vehicle solution (35), PEG is polyethylene glycol, 1,3-CHD is 1,3 cyclohexanediol and 2,3-BD is 2,3 butanediol. Distilled water is used instead of a vehicle solution wherever EC or UCV are not listed.

Tables 1 and 2 list the coefficients of polynomial approximations for the literature data on thermal strain and the currently compiled data on density, respectively. Note that, due to the dramatic change of twelve orders of magnitude in CPA viscosity during vitrification, two different techniques have been employed to measure the thermal expansion coefficient: on a volumetric basis at higher temperatures when the material is free to flow (4,32–34), and on a linear basis at lower temperatures when the material is highly viscous (30,31,36), where the cutoff is roughly around −90°C. Further note that due to the experimentation techniques used, thermal expansion of CPAs in the presence and absence of tissues were measured in the upper part of the cryogenic temperature range, while only CPA-loaded tissues were measured in lower temperatures.

Table 2:

Coefficients of best-fit polynomial approximation for density, ρ = b₂T²+b₁T+b₀, kg/m³.

Solution	Material	Temperature Range, °C	b0 × 10−3	b1 × 10	b2 × 103	Ref. for β
DP6	Pure Solution	−41.9…25	1.048	−6.839	−2.683	(34)
DP6+UCV		−87.8…25	1.062	−7.425	−1.946
DP6+UCV+1% X1000		−84.4…25	1.064	−7.570	−1.825
DP6+UCV+1% Z1000		−84.3…25	1.066	−8.137	−1.757
DP6+UCV+1% X1000+1%Z1000		−84.4…25	1.067	−7.963	−1.844
DP6+UCV+0.5M Sucrose		−81.7…25	1.124	−7.822	−1.402
M22		−91.1…25	1.092	−8.452	−1.692
2.2 M Propylene Glycol		−4.1…25	1.013	−1.791	−5.027	(33)
3 M Propylene Glycol		−6.6…25	1.017	−2.611	−4.334
3.1 M Formamide		−3.4…25	1.025	−2.641	−3.989
3.1 M DMSO		−7.7…25	1.039	−3.005	−2.798
6 M DMSO		−36.2…25	1.078	−6.502	−0.373
8.4 M DMSO		−95.6…25	1.104	−8.019	1.037
DP6 + EC	Pure Solution	−55…25	1.056	−6.405	−0.518	(4)
	Bovine Muscles	−45…25	1.124	−6.691	−3.659
	Goat Artery	−40.5…25	1.134	−5.691	−3.378
		−167.2…25	1.132	−5.463	−1.264	(31)
DP6 + 12% PEG400	Pure Solution	−95…25	1.069	−7.543	0.659	(4)
	Bovine Muscles	−85…25	1.133	−7.322	−0.156
	Goat Artery	−80…25	1.149	−8.399	−5.054×10−2
DP6 + 6% 1,3 - CHD	Pure Solution	−80…25	1.042	−6.204	0.609
	Bovine Muscles	−80…25	1.113	−7.398	−1.142
	Goat Artery	−80…25	1.127	−7.674	0.148
DP6 + 6% 2,3 - BD	Pure Solution	−90…25	1.054	−6.682	0.222
	Bovine Muscles	−85…25	1.121	−7.160	−6.372×10−2
	Goat Artery	−90…25	1.133	−6.595	0.121
VS55	Pure Solution	−77.1…25	1.068	−5.985	−0.362	(32)
	Bovine Muscles	−47.8…25	1.133	−6.383	−1.108
	Goat Artery	−63.6…25	1.149	−7.297	−3.046
		−165.3…25	1.147	−6.811	−1.805	(31)
7.05M DMSO	Pure Solution	−95.8…25	1.090	−6.922	0.257	(32)
	Bovine Muscles	−58.3…25	1.154	−7.804	−2.298
	Goat Artery	−93.1…25	1.164	−7.134	−1.991
		−167.7…25	1.162	−7.147	−1.780	(31)

Figure 1 displays the temperature-dependent density of selected combinations of CPAs and SIMs in higher cryogenic temperatures. Figure 2 displays the temperature-dependent density for tissues loaded with representative CPAs in higher cryogenic temperatures. Figure 3 displays the combined density curves over the entire cryogenic temperature range of interest, where the combination includes different measurement techniques in higher (32) and lower temperatures (31).

Figure 1:

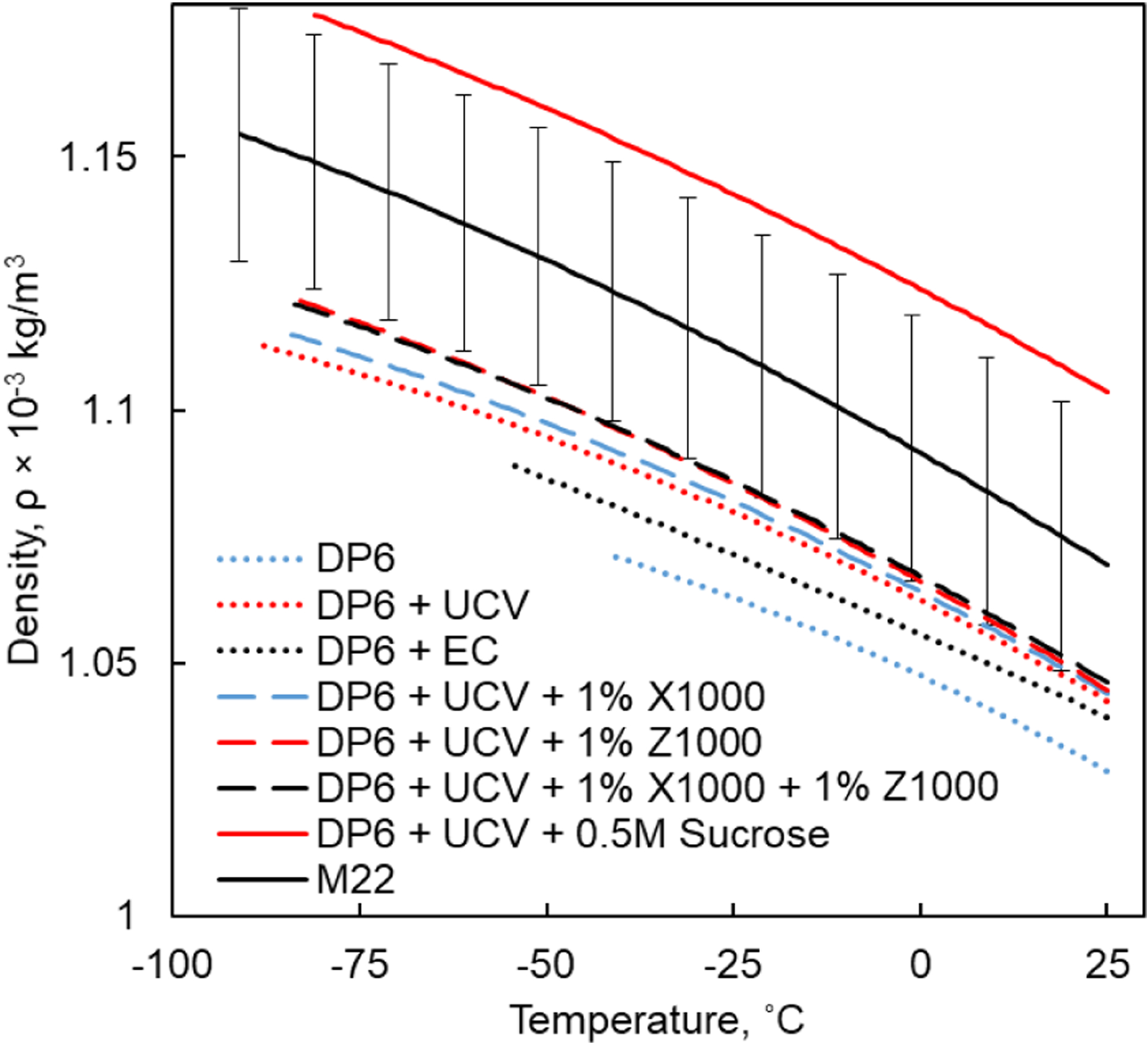
Density of CPA+SIM cocktails in higher cryogenic temperatures, where the coefficients for polynomial approximations are listed in Table 1.

Figure 2:

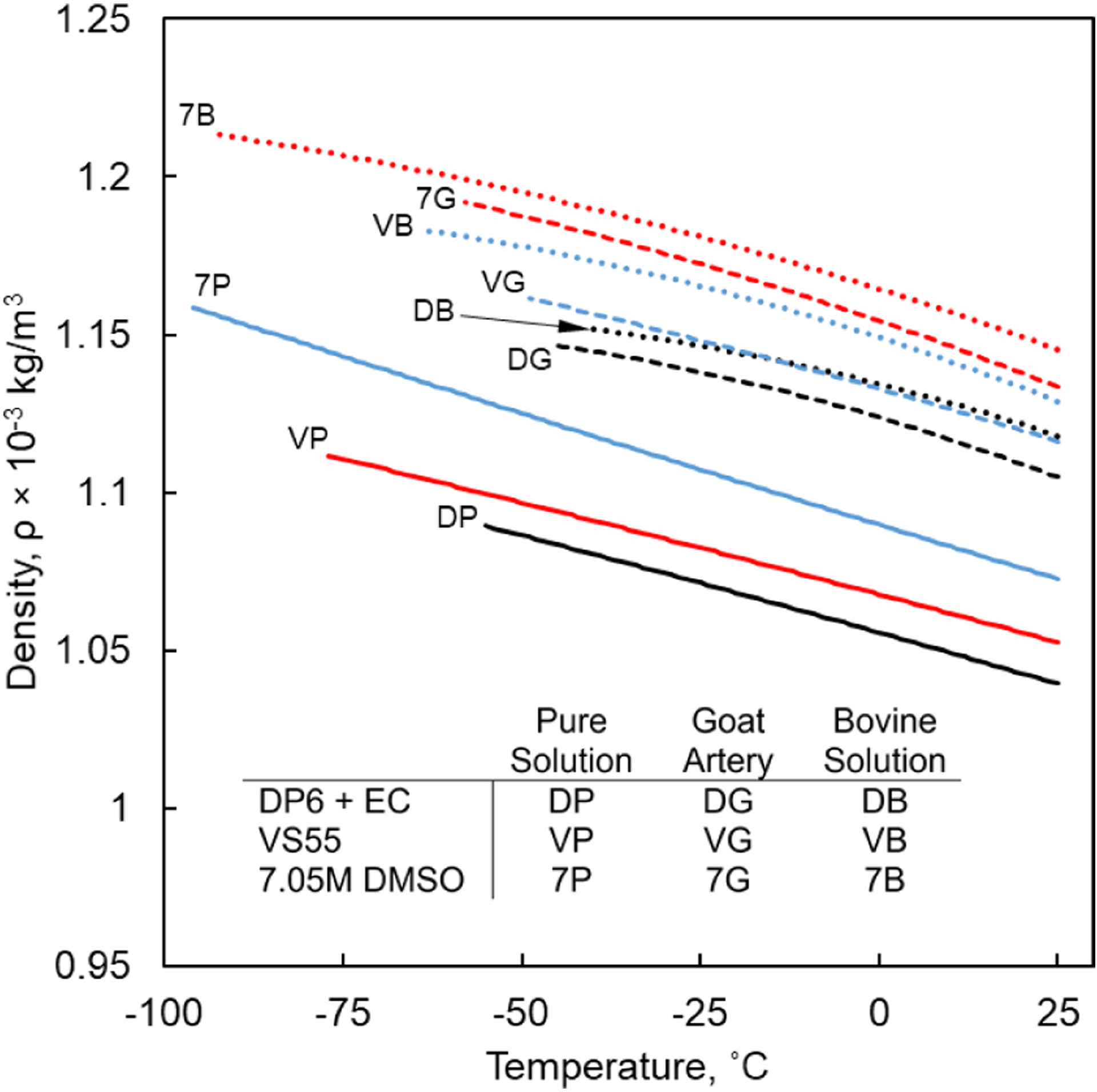
Density of CPA cocktails in presence and absence of tissues in higher cryogenic temperatures, where the coefficients for polynomial approximations are listed in Table 1.

Figure 3:

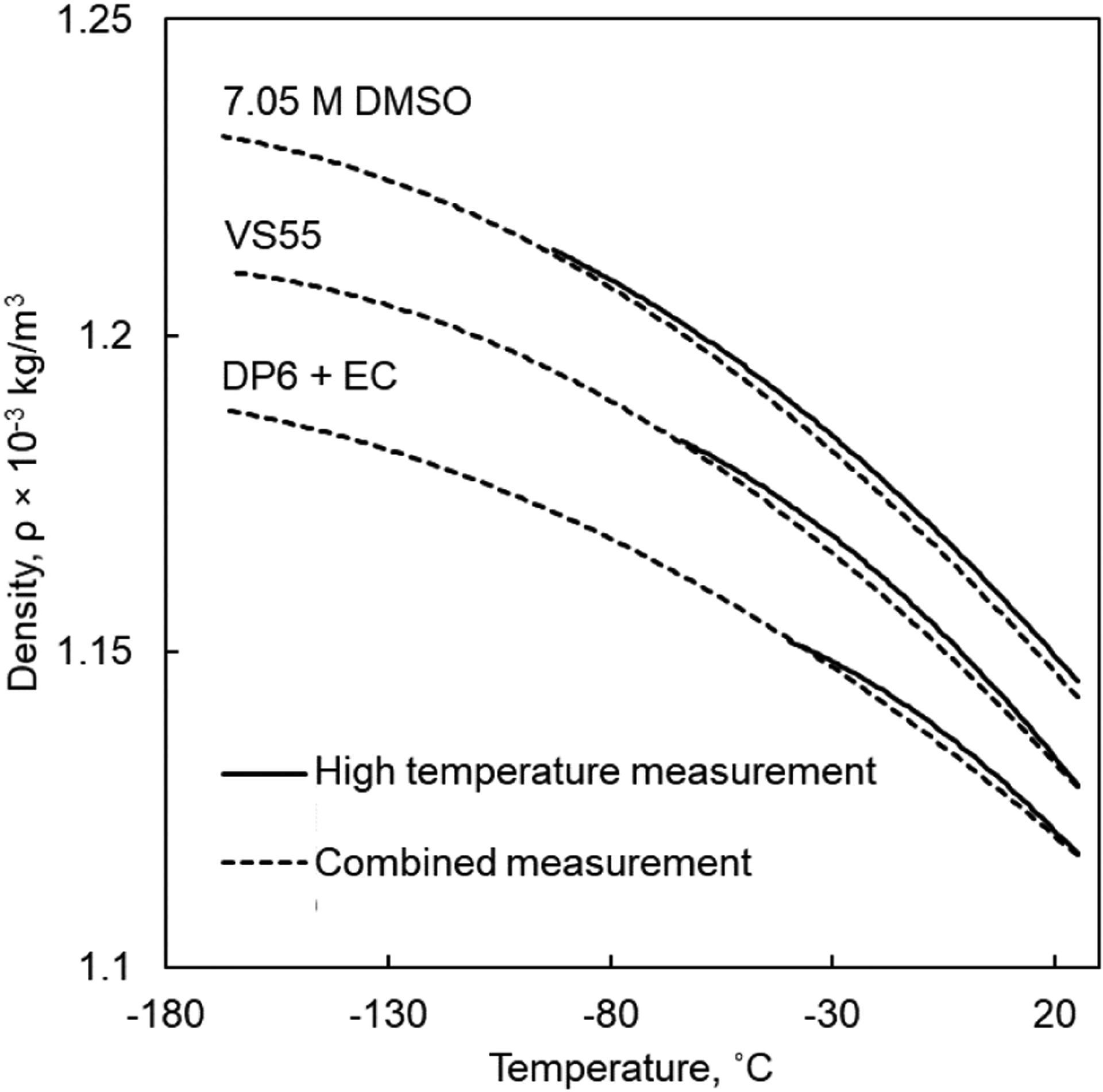
Comparison of selected temperature-dependent density curves of CPAs in presence of tissues calculated from two sources of measurements in different temperature ranges (4,31,32).

Figure 4 displays a summary of thermal properties compiled for 7.05M DMSO, which is a reference solution shown useful for thermomechanical stress analysis of cryopreservation by vitrification of highly concentrated CPA solutions (24,37).

Figure 4:

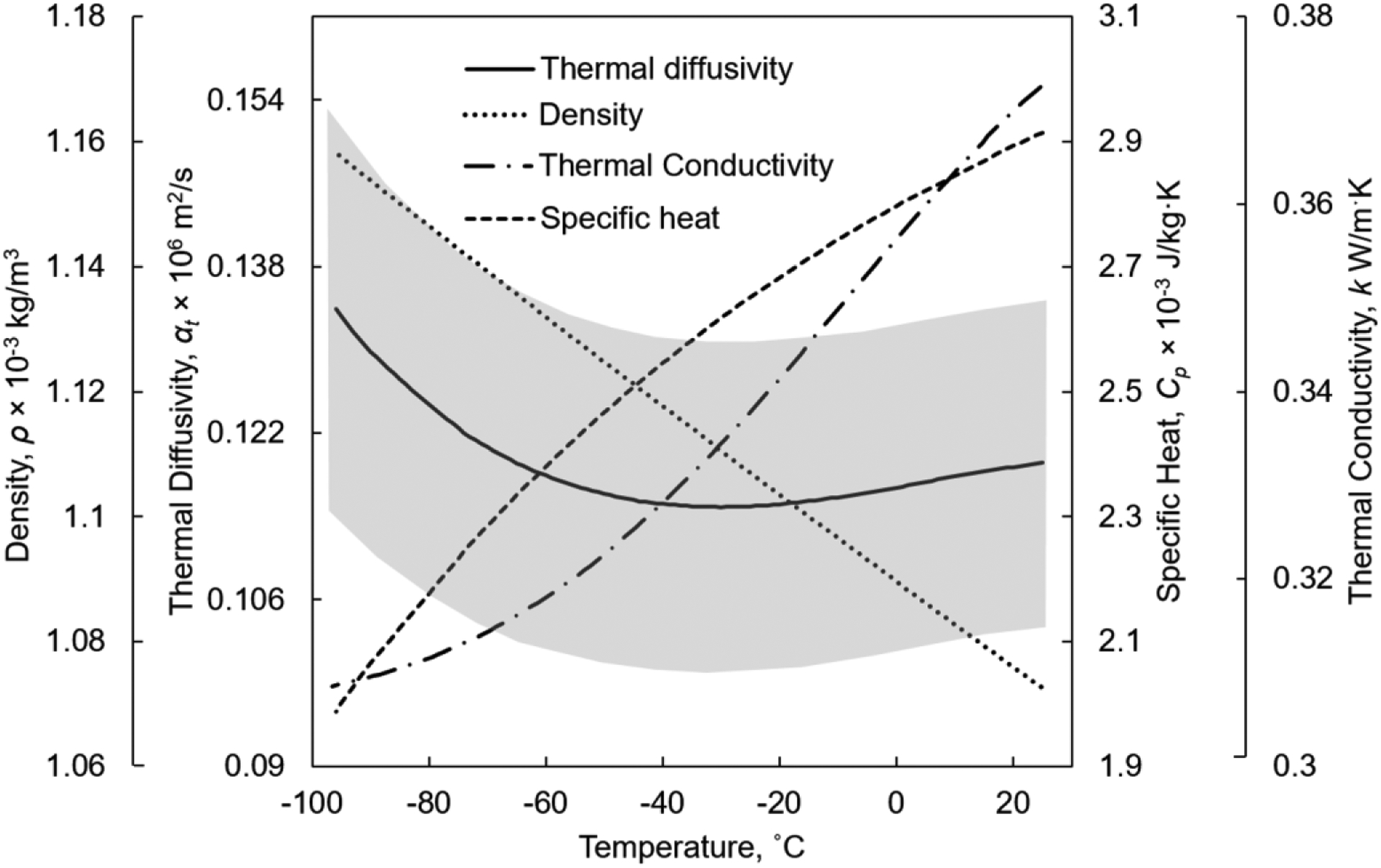
Thermophysical properties for 7.05 M DMSO, where the density and thermal diffusivity are compiled in the current study, while the thermal conductivity (7) and specific heat (42) are taken from literature data. The uncertainty in thermal diffusivity estimation is displayed by the gray region.

DISCUSSION

In broad terms, in the absence of phase change during vitrification, the material contracts continuously (negative thermal strain) while its density increases monotonically, although at a variable rate. The tendency to contract is somewhat higher at higher temperatures. For example, the density of DP6 increases by 4.11% when the temperature is reduced from 25°C to −41°C, Fig. 1.

The addition of the reported SIMs results in increased density as can be observed from Fig. 1. For example, the addition of 0.5M Sucrose results in the largest density increase compared to the density of DP6+UCV, amounting to 6.35% at 25°C. The density of DP6+UCV+0.5M Sucrose increases by 6.76% as the temperature decreases from 25°C to −82°C.

While the above density changes are significant for fluid mechanics analysis when calculating free convection effects during vitrification (13,38), and for solid mechanics analysis when calculating thermomechanical stress (20,22,24), it is important to compare it with the uncertainty in measurement. For example, the compiled density of M22 increases by 7.43% as the temperature decreases from 25°C to −91°C. The uncertainty in the measured thermal strain within this range has been estimated as 4% (34), while the uncertainty in the compiled density value is 2.5% based on Eq. [7] (Fig. 1). Note that the experimental techniques and corresponding literature data used as the basis for the current study were designed to filter out random errors in measurements (25), and the uncertainty analysis presented here refers essentially to systematic (bias) errors.

A different source of uncertainty in the data compilation in the current study is associated with the calculation of the reference density by means of Eq. [6]. For DMSO, this uncertainty is estimated as 2.5%, based on comparing the outcome of Eq. [6] and literature data for aqueous DMSO solutions (39). Recall that Eq. [6] assumes DMSO solution to follow an ideal mixture law, where the ingredients do not chemically interact with one another, while the DMSO solution is in fact known to be a complex solution (39). Nonetheless, the ideal solution simplification serves well for the compilation of the density, when compared with other sources of uncertainty. Furthermore, the uncertainty associated with this assumption is expected to lead a bias in the density profile, while maintaining its trend, and not to a random uncertainty as would be expected from a discrete measurement. For this reason, the effect of this assumption further diminishes when the data is used to calculate fluid mechanics or solid mechanics effects.

The presence of tissues is demonstrated to increase the density of the specimen At any specific temperature, Figs. 2 and 3. For example, the density of VS55 is 6.05% and 7.25% higher in the presence of bovine muscle and goat artery, respectively, compared to the pure solution at the reference temperature of 25°C. However, the rate of change of density with temperature is not significantly affected by the presence of tissues. For example, as the temperature decreases from 25°C to −45°C, the density of pure solution VS55 increases by 3.93%, while the density of VS55 in presence of bovine muscle and goat artery increases by 3.86% and 4%, respectively. For DP6+EC, as the temperature decreases from 25°C to −45°C, the density for pure solution, solution with bovine muscle and solution with goat artery increases by 4.24%, 3.77% and 3.26%, respectively. Similarly for 7.05 M DMSO, as the temperature decreases from 25°C to −45°C, the density for pure solution, solution with bovine muscle and solution with goat artery increases by 4.55%, 4.53% and 4.16%, respectively.

Recall that the reference densities for tissues permeated with CPA is calculated using Eq. [6] which assumes that total volume of the specimen is the linear sum of the tissue and constituents of the CPA solution. The validity of this assumption remains untested. Possible deviations from this assumption might occur if the tissue swells or shrinks when permeated with CPA (40,41).

Of particular interest for thermal analyses of cryopreservation is the physical property of thermal diffusivity, which represents the ratio of thermal conductivity to the product of density and specific heat $(\alpha =\frac{k}{\rho Cp})$. While the thermal conductivity relates to the ability of the material to conduct heat, the thermal diffusivity relates to the rate at which this tends to happen. Figure 4 displays the dependency of all those thermophysical properties for 7.05M DMSO, which has been used repeatedly as a reference solution for thermo-fluids and thermo-mechanics analyses. Interestingly, while the density of 7.05M DMSO increases almost linearly with the decreasing temperature, the specific heat and thermal conductivity display an opposing trend, and the thermal diffusivity is only moderately and non-monotonically changing with temperature. For this solution, the thermal diffusivity varies from a minimum value of 1.15×10⁻⁷ m²/s at −30°C to a maximum value of 1.34×10⁻⁷ m²/s at −96°C, which represents a range of 16.5 %. At the same time, the uncertainty in thermal diffusivity compilation is estimated within the range of 14.1%. The uncertainty in the compiled thermal diffusivity value is calculated using the propagation of uncertainty in the basic thermophysical properties following Eq. [7] (29). The uncertainties in the thermophysical properties was taken as 2.5% for calculation of the reference density based on Eq.[6], 10% for the calculation of the specific heat (42), ±0.3 W/m°C for the measurement of the thermal conductivity (7) and 3% for the measurement of the thermal strain (32). While the uncertainty in thermal diffusivity is significant, as with other thermophysical properties, the trend of property change is noteworthy, even if it may be shifted.

SUMMARY

All materials change volume with temperature, where the thermal expansion coefficient is a physical property that describes the corresponding rate of change. Those volume changes are inversely proportional to the density of the material. In general, direct density measurements are more convenient in fluids, while linear thermal expansion measurements are more convenient in solids. However, from a practical perspective in the extreme conditions of cryogenic temperatures, thermal expansion of CPAs is more commonly available in the literature.

In fluids, thermal expansion may intensify heat transfer by the mechanism of natural convection. In solid, thermal expansion may drive the development of thermomechanical stresses, potentially causing structural damage. During vitrification, fluid mechanics and solid mechanics effects may coexist, leading to complex effects such as macro-scale deformations. In this context, vitrification is widely considered as the only alternative for long-term preservation of organ and large-size tissues. Furthermore, the anomalous expansion of water upon freezing may lead to unexpected thermal stresses, an effect which should be considered when only partial vitrification is achieved during vitrification attempts.

In order to account for the above effects during modeling and computer-assisted analyses of experiments, the current study reviews literature data on thermal expansion, discusses the mathematical relationship between thermal expansion and density, and presents calculated density data relevant to cryopreservation by vitrification.

Specifically, the current study derives density data for selected CPAs and CPAs+SIMs in the presence and absence of tissues. The reported materials include M22 which has shown promising results for kidney cryopreservation (43), VS55 which demonstrated high vitrification tendencies, and DP6 mixed with SIMs, such as sucrose which has drawn significant attention in recent years (44).

The broader impact of the current study on the overall interpretation of thermomechanical effects is presented using the example of thermal diffusivity of 7.05 M DMSO.

In conclusion, this study addresses only one but a very significant aspect of the unmet need for temperature-dependent material properties for improved theoretical investigations and computer modeling of cryopreservation.