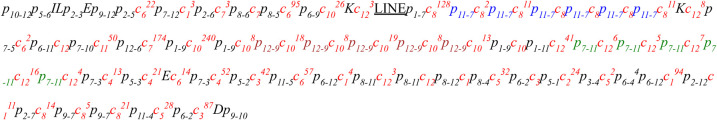Automated annotation of human centromeres with HORmon

Abstract

Recent advances in long-read sequencing opened a possibility to address the long-standing questions about the architecture and evolution of human centromeres. They also emphasized the need for centromere annotation (partitioning human centromeres into monomers and higher-order repeats [HORs]). Although there was a half-century-long series of semi-manual studies of centromere architecture, a rigorous centromere annotation algorithm is still lacking. Moreover, an automated centromere annotation is a prerequisite for studies of genetic diseases associated with centromeres and evolutionary studies of centromeres across multiple species. Although the monomer decomposition (transforming a centromere into a monocentromere written in the monomer alphabet) and the HOR decomposition (representing a monocentromere in the alphabet of HORs) are currently viewed as two separate problems, we show that they should be integrated into a single framework in such a way that HOR (monomer) inference affects monomer (HOR) inference. We thus developed the HORmon algorithm that integrates the monomer/HOR inference and automatically generates the human monomers/HORs that are largely consistent with the previous semi-manual inference.

Recent advances in long-read sequencing technologies led to rapid progress in centromere assembly in the past year (Bzikadze and Pevzner 2020; Miga et al. 2020; Nurk et al. 2020, 2022; Logsdon et al. 2021; Altemose et al. 2022) and, for the first time, opened a possibility to address the long-standing questions about the architecture and evolution of human centromeres (Rice 2019; Thakur et al. 2021). “Alpha satellite arrays” of live human centromeres that organize the kinetochore (which we refer to simply as “centromeres”) are tandem DNA repeats that are formed by units repeating thousands of times with limited nucleotide-level variations but extensive variations in copy numbers in the human population (Black and Giunta 2018). We refer to “live” centromeres as those that host the kinetochore as revealed by CENPA = CENH3 binding (“live” corresponds to “active” in Altemose et al. 2022). Each such unit represents a tandem repeat formed by smaller repetitive building blocks (referred to as “monomer blocks”), thus forming a “stacked tandem repeat” (Fig. 1). Partitioning all monomer blocks into clusters of similar monomer blocks defines “monomers,” where each monomer represents the consensus of all monomer blocks in a given cluster. The emergence of centromere-specific stacked tandem repeats is a fascinating and still poorly understood evolutionary puzzle (Smith 1976; Malik and Henikoff 2009; Rice 2019; Uralsky et al. 2019).

Figure 1.

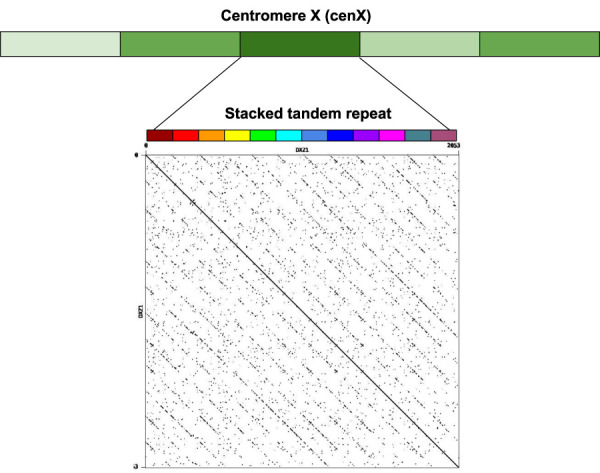
The architecture of centromere on Chromosome X. The centromere of Chromosome X (cenX) consists of ∼18,100 monomers of length ≅171 bp each based on the cenX assembly in Bzikadze and Pevzner (2020); the T2T assembly (Nurk et al. 2022) represents a minor change to this assembly. These monomers are organized into ∼1500 units. Five units are colored by five shades of green illustrating unit variations. Each unit is a stacked tandem repeat formed by various monomers. The vast majority of units in cenX correspond to the canonical HOR, which is formed by 12 monomers (shown by 12 different colors). The figure on top represents the dot plot of the nucleotide sequence of the canonical HOR that reveals 12 monomers. Although the canonical units are 95%–100% similar, monomers are only 65%–88% similar. In addition to the canonical 12-monomer units, cenX has a small number of partial and auxiliary HORs with varying numbers of monomers.

Each human monomer is of length ≅171 bp, and each higher-order unit is formed by multiple monomers that differ from each other. A monomer is “frequent” if the number of monomer blocks in its cluster exceeds a frequency threshold, and “infrequent,” otherwise. Recently, Uralsky et al. (2019), Bzikadze and Pevzner (2020), and Dvorkina et al. (2020, 2021) revealed still underexplored “hybrid” monomers (each hybrid monomer is a concatenate of two or even more frequent monomers) and hypothesized that they may drive the “birth” of new frequent monomers. Different human centromeres typically have different monomers and units, and the number of the frequent monomers in a unit varies from two for Chromosome 19 to 19 for Chromosome 4.

A “canonical (cyclic) order of monomers” (referred to as a “higher-order repeat” [HOR]) is specific to each centromere and is defined evolutionarily as the ancestral and chromosome-specific order of frequent nonhybrid monomers that has evolved into the complex organization of extant centromeres. This definition, however, is computationally nonconstructive because the ancestral order is unknown and no algorithm for its inference has yet been described. The current view of centromere evolution can be summarized by the following framework that we refer to as the “Centromere Evolution (CE) Postulate”:

• Each extant human centromere has evolved from a “single” ancestral HOR formed by “k different” monomers. Hence, each monomer occurs in a HOR only once. The parameter k (number of monomers in a HOR) varies between various centromeres.

• Each frequent nonhybrid monomer in a centromere has evolved from a single ancestral monomer. The number of ancestral monomers equals the number of frequent nonhybrid monomers in the extant centromere.

• Each hybrid monomer has evolved from a concatenate of two (or even more) ancestral monomers and does not participate in the ancestral HOR.

• In addition to units formed by canonical HORs, there exist units formed by “partial HORs” (substrings of canonical HORs). All other units consist of a single hybrid monomer and are referred to as “auxiliary HORs.” Although the canonical HOR corresponds to the most frequent unit for most human centromeres, it is not always the case.

Although the CE postulate is widely accepted (Waye and Willard 1987; Alexandrov et al. 2001; McNulty and Sullivan 2018; Altemose et al. 2022), we are not aware of a rigorous proof of this postulate or an algorithm that, given an extant centromere, derives its canonical HOR (Supplemental Note 1). Moreover, because the concept of a HOR is parameter-dependent, the CE postulate may hold for some parameters and fail for others. However, it is not clear how to select various parameters such as the frequency threshold parameter (for defining the concept of a frequent monomer), the percent identity parameter (for deciding which monomer blocks correspond to the same monomer), and parameters for classifying a monomer as a hybrid (Dvorkina et al. 2021).

Moreover, the CE postulate implicitly assigns the inferred HOR to a particular (and unspecified) moment in the past. For example, although the HOR for centromere X (referred to as cenX) consists of 12 monomers, this 12-monomer HOR evolved from an even more ancient 5-monomer ancestral HOR (Waye and Willard 1987; Alexandrov et al. 2001). It is thus not clear how an algorithm for HOR inference should choose between a 12-monomer HOR and a 5-monomer HOR for cenX. Further, even if the CE postulate holds, it may be impossible to infer canonical HORs if nearly all information about the ancestral HOR was erased by millions of years of evolution; for example, it is unclear how to derive HORs in mouse centromeres (Thakur et al. 2021).

Recent evolutionary studies of centromeres (Uralsky et al. 2019; Bzikadze and Pevzner 2020; Suzuki et al. 2020) revealed the importance of partitioning them into monomers, the problem that was addressed by the StringDecomposer algorithm (Dvorkina et al. 2020). Given a nucleotide string Centromere and a monomer set Monomers, StringDecomposer decomposes Centromere into monomer blocks (each block is similar to one of the monomers) and transforms it into a “monocentromere” string Centromere* over the alphabet of monomers. For each monomer M, it generates the set of “M blocks” in the centromere that are more similar to M than to other monomers (ties broken arbitrarily).

StringDecomposer opened a possibility to automatically generate all HORs and annotate human centromeres (i.e., partition them into canonical, partial, and auxiliary HORs), the problem that remains unsolved despite multiple studies in the last four decades (Waye and Willard 1985; Alexandrov et al. 2001; Paar et al. 2005; Alkan et al. 2007; Shepelev et al. 2015; Sevim et al. 2016; McNulty and Sullivan 2018; Uralsky et al. 2019). However, the challenge of properly defining the set of all human monomers remained outside the scope of the StringDecomposer tool. Although Sevim et al. (2016) presented a large set of human monomers, it is unclear if this set is compatible with the CE postulate. As a result, it remains unclear how to computationally define the complete set of monomers (a prerequisite for launching StringDecomposer) and HORs in human centromeres.

Previous semi-manual studies inferred many HORs and greatly contributed to our understanding of the architecture of human centromeres (Alexandrov et al. 2001; McNulty and Sullivan 2018). However, they did not specify an “algorithmically constructive definition” of a HOR. Instead, an order of monomers in a consensus HOR was implicitly defined as the “ancestral order” without specifying how to derive this order and how to prove that it is correct and unique. Although Paar et al. (2005), Alkan et al. (2007), and Sevim et al. (2016) described various HOR inference heuristics (ColorHOR, HORdetect, and Alpha-CENTAURI, respectively), these studies have not specified the exact objective function for HOR inference (Table 1). As such, the concept of a HOR is highly dependent on the parameters used for generating the monomer set. Moreover, the nucleotide sequences for human HORs of live human centromeres have been manually extracted at the dawn of the sequencing era and used reads (often sampled from a single clone from a specific centromere) rather than completely assembled centromeres, raising questions about their accuracy (Bzikadze and Pevzner 2020; Miga and Alexandrov 2021). For example, HOR DXZ1 (S3CXH1L) on cenX, the first inferred human HOR, was derived based on limited sequencing data from a single clone (Waye and Willard 1985). The sequence of this HOR differs from the HOR extracted from the complete cenX assembly, suggesting that either (1) reads used for deriving DXZ1 were limited to a small region of cenX that does not adequately represent the entire centromere, or (2) HORs extracted from different individuals may be different.

Table 1.

Comparison of methods for monomer/HOR inference and annotation

These limitations prevent future evolutionary studies of centromeres across multiple species. Addressing them is important because long and accurate Pacific Biosciences (PacBio) HiFi reads have already been used for centromere assembly in fish (Xue et al. 2021) and because various HiFi assembly projects are currently underway, opening a possibility to assemble vertebrate centromeres in the near future. On the other hand, the Telomere-to-Telomere (T2T) Consortium and the Human Pangenome Reference Consortium (HPRC) are now assembling centromeres from multiple humans. Because their manual annotation (including monomer and HOR inference) is prohibitively time-consuming, automated annotation is a prerequisite for any centromere analysis in the future.

Dvorkina et al. (2021) developed the CentromereArchitect tool that addressed the monomer and HOR inference as two separate problems. In particular, the HOR inference was addressed as a data compression problem rather than an evolutionary problem that takes into account the CE postulate. Thus, although CentromereArchitect enabled an automated inference of monomers, it remains unclear whether its HORs inference adequately reflects the centromere evolution. Our analysis revealed that to generate a biologically adequate centromere annotation, the monomer and HOR inference should be viewed as two interconnected problems in such a way that HOR (monomer) generation affects monomer (HOR) generation.

In the past, the monomer generation problem was addressed as clustering of monomer blocks without considering the follow-up inference of HORs derived from the resulting monomers (Dvorkina et al. 2021). Because this is a complex clustering problem, any clustering algorithm may merge some biologically distinct monomer blocks into a single cluster and split a single cluster into multiple ones. Another complication is the inference of hybrid monomers that by definition do not participate in canonical HORs.

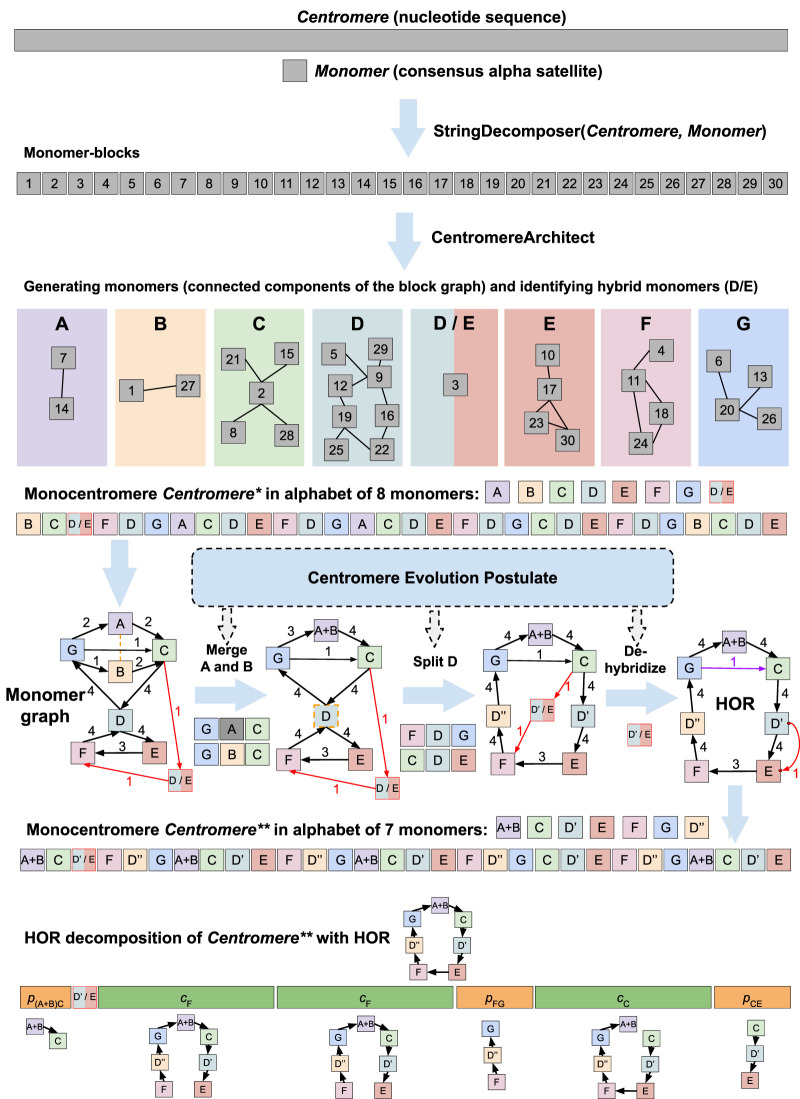
Below, we describe the HORmon algorithm that addresses these complications by incorporating the monomer and HOR generation into a single pipeline (Fig. 2). HORmon generated the first automated centromere annotation that is largely consistent with the CE postulate and previous manual centromere annotations. Recognizing that HORs represent an important evolutionary concept, we show how HORmon can be used to automatically derive the currently known HORs.

Figure 2.

HORmon pipeline. Given the nucleotide sequence Centromere and a consensus alpha satellite sequence Monomer, HORmon iteratively launches StringDecomposer (Dvorkina et al. 2020) to partition Centromere into monomer blocks. After each launch of StringDecomposer, HORmon launches CentromereArchitect (Dvorkina et al. 2021) to cluster similar monomer blocks into monomers, identify hybrid monomers (represented by a single hybrid D/E of monomers D and E), and transform Centromere into the monocentromere Centromere*. Afterward, HORmon uses the generated monocentromere to construct a monomer graph (red edges connect the hybrid monomer D/E with the rest of the monomer graph). To comply with the centromere evolution postulate, HORmon performs split/merge transformations and dehybridizations on the initial monomer set. The orange dotted undirected edge connects similar monomers A and B to indicate that they represent candidates for merging. The breakable monomer D is shown as a dotted vertex to indicate that it is a candidate for splitting into monomers D′ and D′′. The dehybridization substitutes the hybrid vertex D′/E by a single red edge that connects the prefix of D′ with the suffix of E. Split, merge, and dehybridization operations result in a new monomer set and transform Centromere into the monocentromere Centromere**. The black cycle in the monomer graph of Centromere* represents the HOR; the purple edge connecting monomers G and C is a low-frequency chord in this cycle. HORmon uses this HOR to generate the HOR decomposition of Centromere** into the canonical (c_F, c_C), partial (p_{(A + B)C}, p_FG, p_CE), and auxiliary (the single block D′/E) HORs. c_F and c_C refer to traversing the (canonical) HOR starting from monomers F and C, respectively. p_{(A + B)C}, p_FG, and p_CE refer to partial traversals of the HOR from monomer A + B to C, from F to G, and from C to E, respectively.

Results

A brief description of the HORmon algorithm

Figure 2 illustrates the various steps of the HORmon algorithm for monomer and HOR inference. Supplemental Note 2 summarizes the notation that we use throughout the paper.

Data sets

We extracted the alpha satellite arrays from the assembly (public release v1.0) of the effectively haploid CHM13 human cell line constructed by the T2T Consortium (Miga et al. 2020; Logsdon et al. 2021; Altemose et al. 2022; Nurk et al. 2022). We also extracted the alpha satellite array of the newly assembled centromeres of Chromosome X and Chromosome Y from the HG002 cell line sequenced by the HPRC. For simplicity, we refer to these two genomes as the CHM13 and HG002 genomes. Supplemental Note 3 provides information about the extracted regions for all live human centromere arrays.

Monomer inference

HORmon launches CentromereArchitect (Dvorkina et al. 2021) to generate the initial monomer set and further modifies it by using the monomer-HOR feedback loop described in Methods (Fig. 2). Because all chromosomes considered in this study except Chromosome Y originated from the CHM13 cell line, we launch HORmon three times: on centromeres that originated from the CHM13 cell lines, on Chromosome X from the HG002 cell line, and on Chromosome Y from the HG002 cell line. Supplemental Note 4 describes how HORmon assigns names to monomers and provides correspondence between these names and the traditional names described in Uralsky et al. (2019).

Because CentromereArchitect identifies many infrequent monomers, comparing its monomer set with the previously identified monomer sets, for example, the monomer set MonomersT2T (Altemose et al. 2022) used by the T2T Consortium (based on the monomer set derived in Shepelev et al. 2015; Uralsky et al. 2019), is not straightforward. HORmon thus filters the monomer set generated by CentromereArchitect as described below.

We refer to the set of frequent monomers obtained from CentromereArchitect as MonomersNew. Supplemental Note 5 describes the procedure for construction of MonomersNew and shows that it provides a minor improvement over the (manually constructed) MonomersT2T monomer set with respect to standard clustering metrics. However, as with any clustering approach, the parameter-dependent CentromereArchitect may both split and aggregate monomers as compared to the biologically adequate clustering. Moreover, the monomer set MonomersT2T does not attempt to solve the monomer inference problem that CentromereArchitect addresses (Dvorkina et al. 2021). Instead, it generates clustering that is consistent with CE postulate, which can be suboptimal with respect to standard clustering metrics that do not take into account any evolutionary assumptions.

The challenge of monomer generation

Although it is unclear what is a biologically adequate clustering of monomer blocks, positional information about these blocks (i.e., pairs, triples, etc., of consecutive monomers in the monocentromere) often reveals monomers that were erroneously split/aggregated. This positional information helps one to generate a more adequate monomer set with respect to the CE postulate, not unlike the positional information about orthologs in comparative genomics studies (Jun et al. 2009). Two monomers are called “similar” if the percent identity between them exceeds a threshold minPI (default value 94%). In the subsection “Positionally similar monomers” (Fig. 2), we define the concept of positional similarity and classify two similar monomers as “positionally similar” if their positional similarity exceeds a threshold minPosSim (default value 0.4).

To illustrate the challenge of generating a biologically adequate clustering, we consider similar frequent monomers M′ and M′′ from the monomer set Monomers that would be merged into a single monomer if the clustering parameters were slightly relaxed. Because it is unclear how to select clustering parameters, it is also unclear whether such merging would represent a biologically adequate clustering as opposed to the clustering that separates these monomers. However, one may argue that if M′ and M′′ are always flanked by the same frequent monomers X and Y in a monocentromere (resulting in triples XM′Y and XM′′Y), these two monomers are likely erroneously split and should be merged into a single monomer M, defined as the consensus of all M′ blocks and M′′ blocks. Such merging is justified from the perspective of the CE postulate because each nonhybrid monomer occurs exactly once in a HOR. Specifically, unless monomers M′ and M′′ are merged, the HOR cannot traverse monomers X and Y exactly once as required by the CE postulate.

On the other hand, a frequent monomer M that is flanked either by frequent monomers X′ and Y′ (resulting in a triple X′MY′) or by different frequent monomers X′′ and Y′′ (resulting in a triple X′′MY′′) conflicts with the CE postulate. Because this monomer is likely erroneously aggregated from two different monomers, it can be split into monomers M′ and M′′, resulting in triples X′M′Y′ and X′′M′′Y′′, respectively. The monomers M′ (M′′) can be defined as the consensus of all M′ blocks (M′′ blocks) in triples X′M′Y′ (X′′M′′Y′′).

Although such transformations are not necessarily justified with respect to optimizing the standard clustering metrics, Supplemental Note 5 illustrates that the monomer set transformed by merging/splitting operations in HORmon is largely comparable to the monomer set generated by CentromereArchitect with respect to various clustering metrics.

In addition to generating the monomer set, CentromereArchitect includes a HOR inference algorithm based on iteratively defining the units as the “heaviest” substrings of a monocentromere (Dvorkina et al. 2021). Although this definition is adequate from the perspective of data compression, it does not necessarily reflect the evolutionary history of a centromere (although many resulting units correspond to canonical, partial, and auxiliary HORs). Moreover, Dvorkina et al. (2021) derived monomers independently from HORs without accounting for hybrid monomers, positional information, and the CE postulate. Below, we show that positional information, as well as information about hybrid monomers, is important for both monomer and HOR inference. The Methods section describes how to identify erroneously aggregated/split monomers and split/merge them.

We further introduce the concept of a “breakable” monomer, that is, a monomer that is amenable to splitting into two or more monomers in such a way that the enlarged monomer set still adequately represents the centromere architecture. In contrast, splitting an unbreakable monomer results in an inadequate representation of the centromere architecture. We show that a series of split and merge operations results in unbreakable monomers for cen1, cen13, and cen18 that prevent HORmon from reporting HORs in these centromeres. We further describe a special procedure for splitting unbreakable monomers in these problematic centromeres (subsection “Splitting unbreakable monomers reveals HORs in cen1, cen13, and cen18”).

Split and merge operations on the monomer set MonomersNew result in a monomer set MonomersNew⁺, whereas further hybridization of hybrid monomers (Fig. 2) and splitting of unbreakable monomers result in the monomer set MonomersFinal described in Supplemental Table S1.

Monomer graph

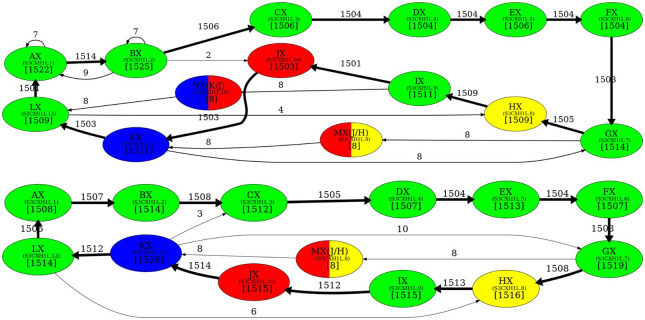
Given a monocentromere, its directed “monomer graph” is constructed on the vertex set of all its monomers and the edge set formed by all pairs of its consecutive monomers. The “multiplicity” of an edge (M,M′) in the monomer graph is defined as the number of times the monomer M′ follows the monomer M in the monocentromere (Fig. 2). We note that the monomer graph of a monocentromere Centromere* is the “de Bruijn graph” DB(Centromere*, 2) (Compeau et al. 2011). Figure 3 presents the monomer graph for cenX in the CHM13 genome (top) and the HG002 genome (bottom) built using the monomer set extracted by CentromereArchitect from CHM13 genome (Dvorkina et al. 2021). Both graphs reveal the cycle formed by 12 high-multiplicity edges that form the canonical 12-monomer HOR in cenX. In addition, the monomer graph for CHM13 reveals two infrequent hybrid monomers and 10 low-multiplicity edges. In contrast, the monomer graph for HG002 reveals only one infrequent hybrid monomer and only five low-multiplicity edges. These differences suggest that hybrid monomers represent a rather recent evolutionary innovation and illustrate large variations in centromeres across the human population.

Figure 3.

The monomer graph of cenX in the CHM13 (top) and HG002 (bottom) genomes. The monomer graphs of cenX were constructed on the monocentromere that was generated from the monomer sets consisting of two infrequent hybrid monomers (labeled as MX and NX) and 12 frequent canonical monomers (labeled as AX, BX, CX, …, KX, and LX) that contribute to the canonical DXZ1 HOR in cenX (Dvorkina et al. 2021). Small font corresponds to the naming conventions introduced in Shepelev et al. (2015). The hybrid monomers M and N are inferred in Dvorkina et al. (2020). A hybrid monomer formed by frequent monomers X and Y is represented as a bicolored vertex (two colors correspond to the colors of X and Y) and is denoted as (X/Y). Only edges of the monomer graph with multiplicity exceeding 1 are shown (edges with multiplicity exceeding 100 are shown in bold). The cycle formed by bold edges (with multiplicities above 1500) traverses the 12 most frequent monomers that form the canonical cenX HOR.

Figure 3 creates a false impression that simply ignoring the low-multiplicity edges and hybrid monomers in the monomer graph of a centromere would result in a graph with a single cycle that forms a HOR. Although this is indeed true for centromeres 3, 11, 14, 16, 17, 19, 20, 21, 22, X, and Y (after performing a series of split/merge transformations on the monomer set generated by CentromereArchitect) (Dvorkina et al. 2021), the remaining human centromeres have a more complex evolutionary history, resulting in complex architectures that we analyze below.

Monomer graphs of human centromeres

Given a monomer set Monomers and a monocentromere Centromere*, we define minCount(Monomers) min_{all monomers M in Monomers} count(M,Centromere*). HORmon uses the set MonomersNew⁺ to generate the monocentromere Centromere** (split and merge operations on the monomer set MonomersNew result in the monomer set MonomersNew⁺), generates the monomer graph as the de Bruijn graph DB(Centromere**, 2), and removes edges that have multiplicity below min(MinEdgeMultiplicity, minCountFraction × minCount(MonomersNew⁺)) with the default values MinEdgeMultiplicity = 100, minCountFraction = 0.9 (Fig. 2). Supplemental Figure S1 provides information about the generated monomer graphs for all human centromeres.

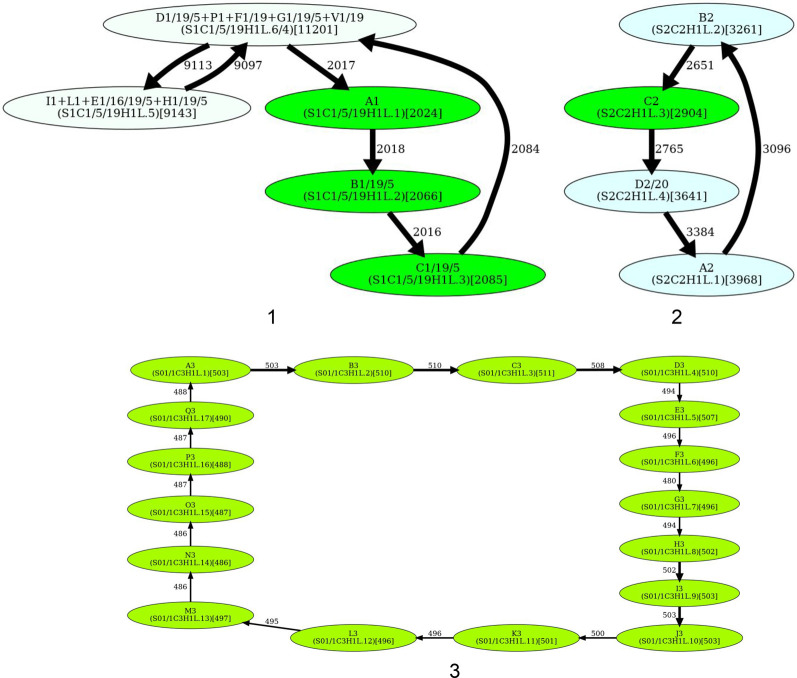
The monomer graphs of 10 centromeres (3, 11, 14, 16, 17, 19, 20, 21, 22, X, and Y) are formed by cycles that immediately reveal HORs. The monomer graph for cen17 contains two cycles: the higher-multiplicity cycle corresponds to the D17Z1 HOR, whereas the lower-multiplicity cycle corresponds to its sister HOR D17Z1-B (for discussion of sister HORs, see Miga and Alexandrov 2021). The remaining monomer graphs contain (albeit implicitly) information about HORs but represent a more detailed view of the evolutionary history of centromeres. To reveal HORs in these monomer graphs, HORmon constructs simplified monomer graphs described in Methods.

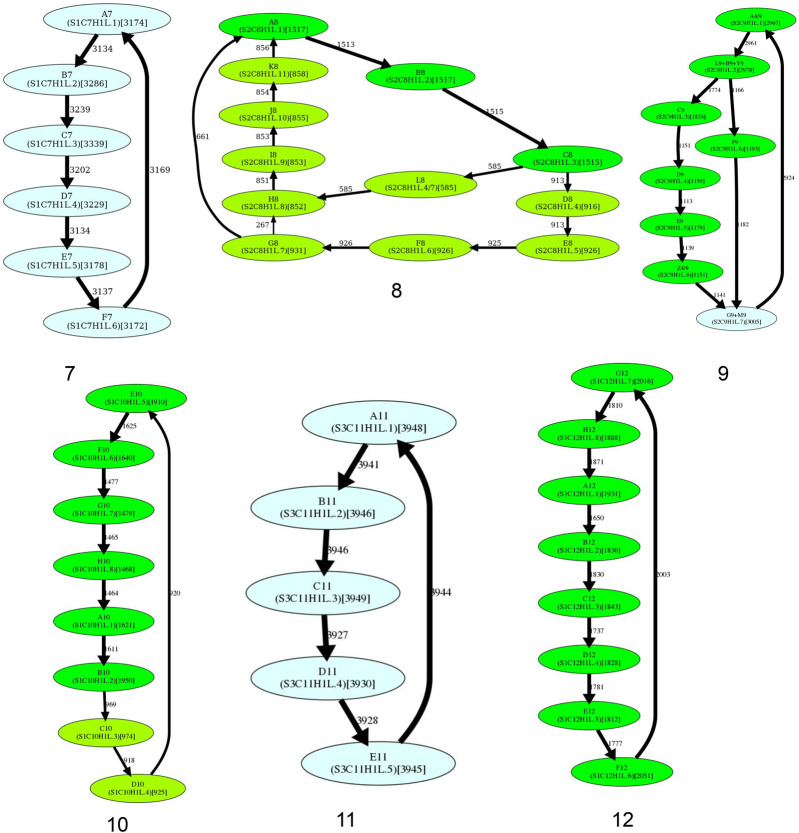
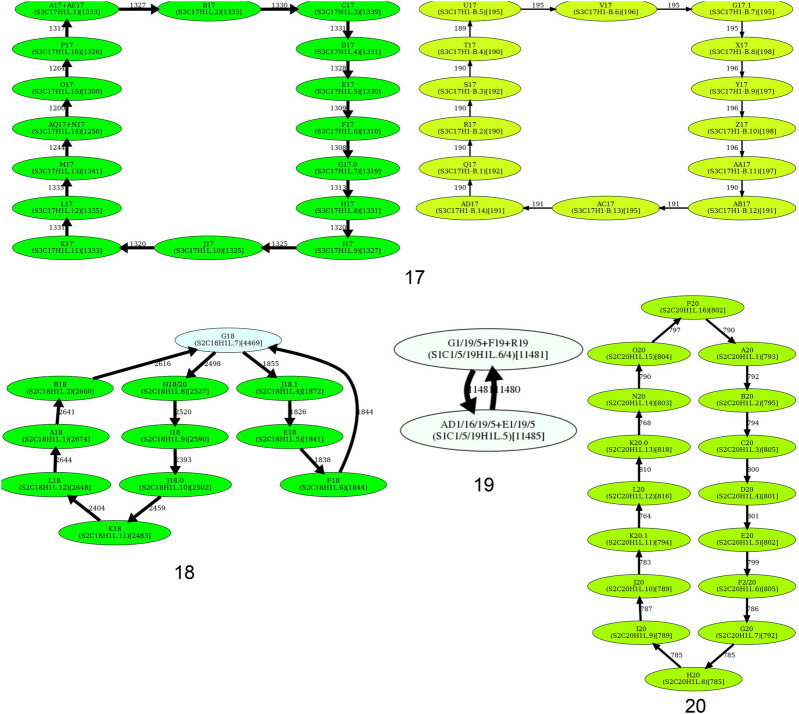
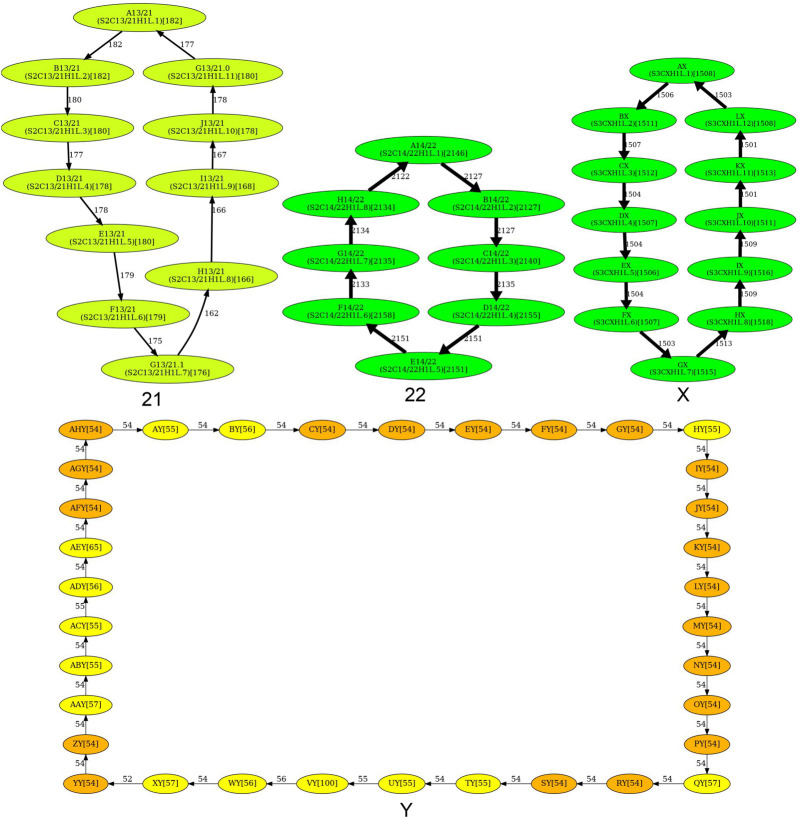
Figure 4 shows that the simplified monomer graphs represent cycles (corresponding to HORs) for all centromeres but centromeres on Chromosomes 1, 5, 8, 9, 13, and 18 that do not have Hamiltonian cycles and represent special cases that we consider below.

Figure 4.

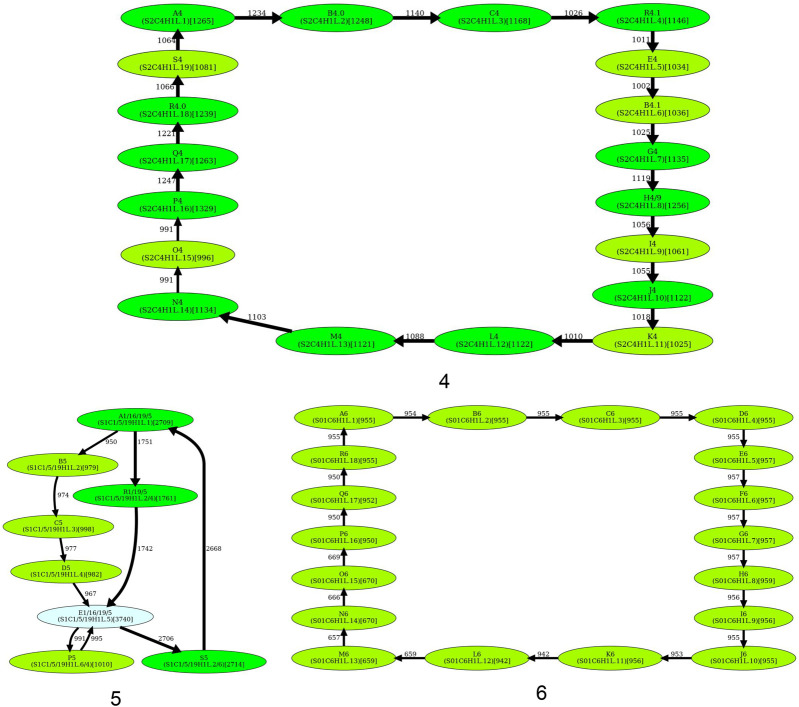
The simplified monomer graphs of human centromeres. The first 23 subfigures contain simplified monomer graphs for all live human centromeres in the CHM13 cell line (centromere ID shown in the subcaption). The 24th subfigure corresponds to the centromere on Chromosome Y in the HG002 genome. In each graph, vertices represent the monomer set Monomers of the corresponding Centromere. The label of each vertex represents the monomer ID and its count in the monocentromere Centromere* (in parentheses). The ID of the monomers follow the naming convention introduced in Shepelev et al. (2015). Two monomers are connected by an edge if they are consecutive in monocentromere Centromere*. The weight of an edge connecting monomers M and M′ is defined as the number of times M is followed by M′ in Centromere*. The width of an edge (color of a vertex) reflects its multiplicity (count of a monomer). In each graph, HORmon detects heavy nonoverlapping cycles and paths and removes chords in such cycles (for details, see Methods). The isolated cycles in 18 centromeres (2, 3, 4, 6, 7, 10, 11, 12, 14, 15, 16, 17, 19, 20, 21, 22, X, and Y) represent HORs in these centromeres. (Figure continues on following pages.)

Splitting unbreakable monomers reveals HORs in cen1, cen13, and cen18

A monomer is breakable if it is amenable to splitting into two or more monomers in such a way that the enlarged monomer set still adequately represents the centromere architecture (Methods). In contrast, splitting an unbreakable monomer leads to conflicts and results in an inadequate representation of the centromere architecture. Even if a monomer is breakable, splitting it into two very similar monomers (e.g., monomers M′ and M′′ that differ in a single position) may lead to a misclassification of monomer blocks because all centromere decomposition tools, including StringDecomposer, often misclassify an M′ block as a very similar M′′ block and vice versa. Such misclassified monomer blocks may lead to downstream challenges in analyzing centromere architecture and evolution.

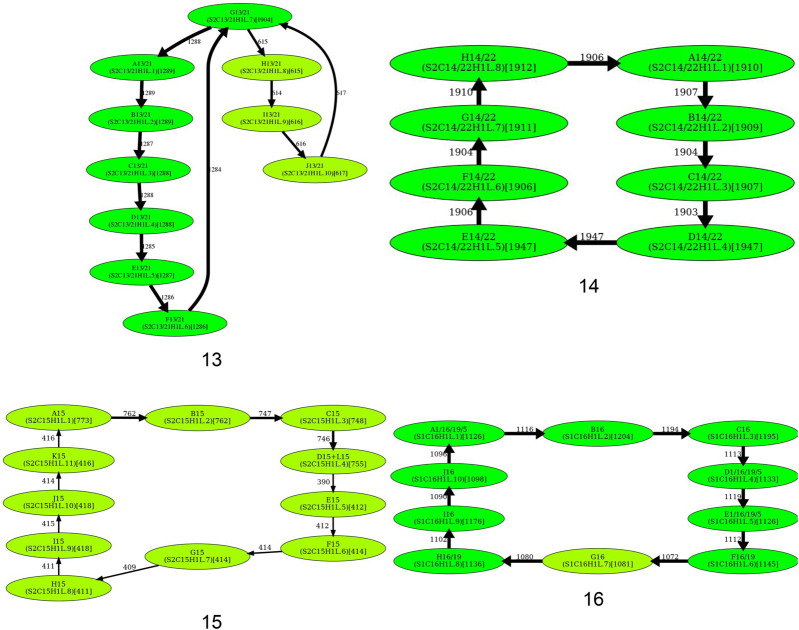
Although the simplified monomer graphs of cen1, cen13, and cen18 are formed by two cycles that share a junction vertex (that deviate from the definition of a HOR as a single cycle), these two cycles can be transformed into a single cycle by splitting the junction vertices (Fig. 5). However, because these junction vertices correspond to unbreakable monomers, splitting them raises concerns. Indeed, it either conflicts with some frequent traversals through the junction vertex or results in a pair of highly similar monomers that would be merged into a single monomer even under extremely stringent values of HORmon parameters.

Figure 5.

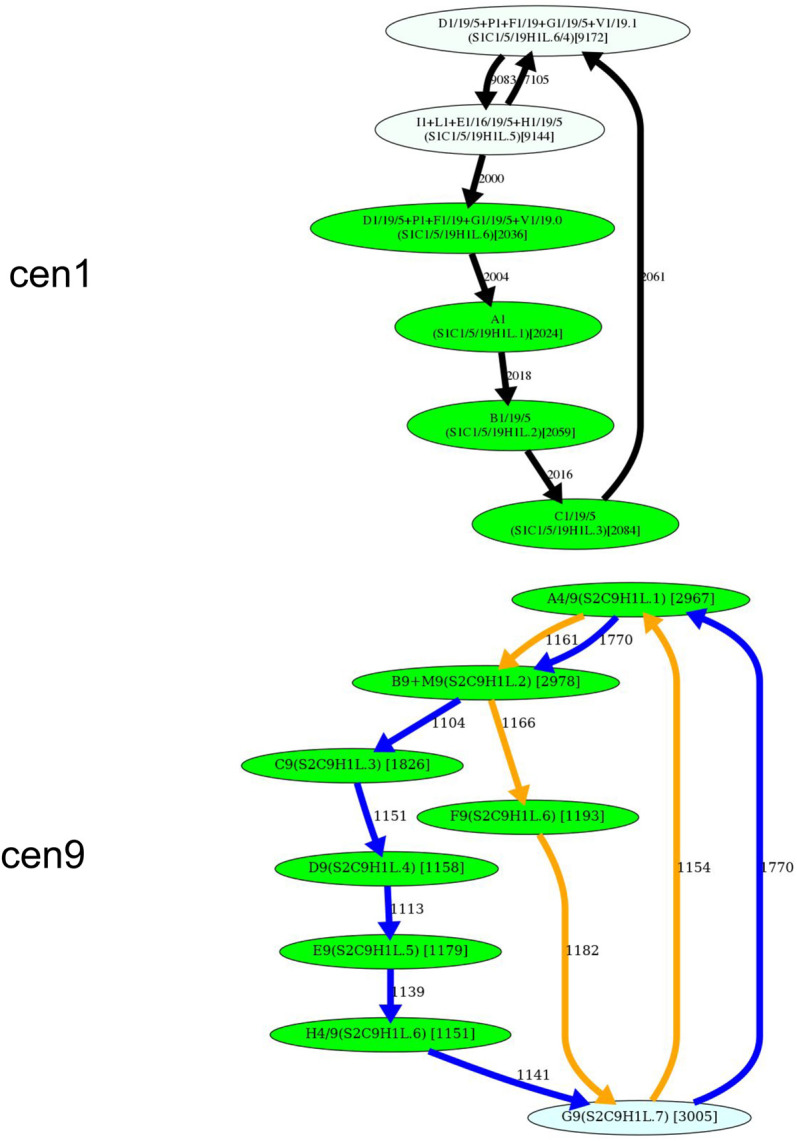
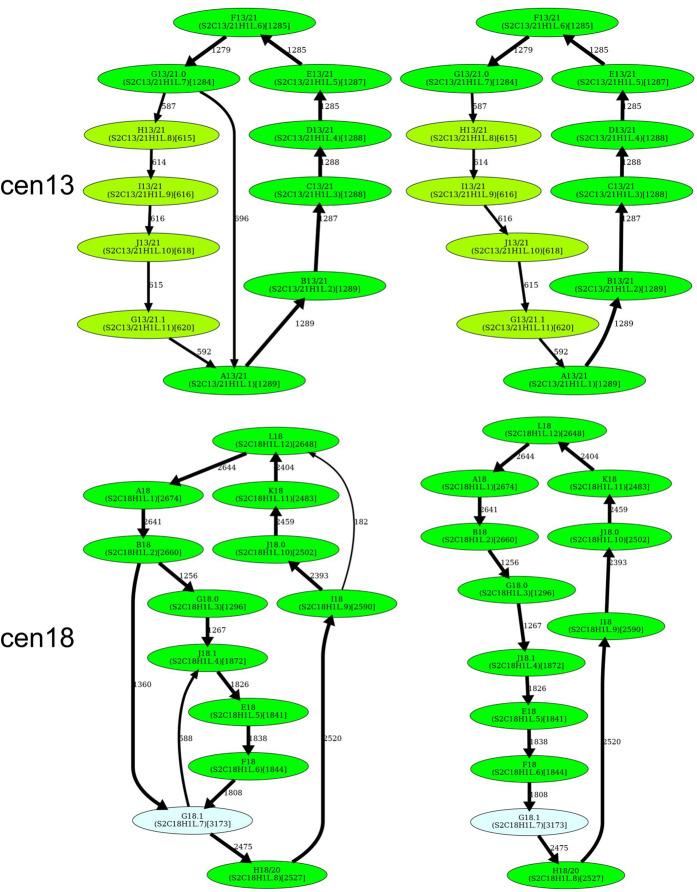
Inferring HORs for cen1, cen9, cen13, and cen18. (First row) Splitting an unbreakable junction monomer in cen1 results in two monomers with an 11-nt difference and transforms the monomer graph of cen1 into a cycle with a single chord. (Second row) The manually inferred HOR of cen9 (McNulty and Sullivan 2018), shown as the blue cycle, is in conflict with the CE postulate because the frequently traversed yellow cycle contains a monomer that does not belong to the blue cycle. (Third row) Splitting an unbreakable junction monomer in cen13 results in two similar monomers with an only 3-nt difference and transforms the monomer graph of cen13 (Fig. 4) into a cycle with a single chord shown on the left. The resulting simplified monomer graph (shown on the right) reveals the canonical 11-monomer HOR in cen13. (Fourth row) Splitting an unbreakable junction monomer in cen18 results in two monomers with only a single-nucleotide difference and transforms the simplified monomer graph of cen18 (Fig. 4) into a cycle with three chords (shown on the left). The resulting simplified monomer graph (shown on the right) reveals the canonical 12-monomer HOR in cen18. (Figure continues on following page.)

Splitting a junction monomer in cen1 results in two monomers that differ in 11 nt. This transformation results in a simplified monomer graph that contains a cycle that corresponds to a HOR and a dimer formed by two high-multiplicity anti-parallel edges (Fig. 5). In fact, this dimer was originally reported as a HOR in cen1 (Carine et al. 1989; Alexandrov et al. 2001; McNulty and Sullivan 2018).

Splitting a junction monomer in cen13 (cen18) results in two monomers that differ in only 3 (1) nt. The split of the unbreakable vertex G into vertices G.0 and G.1 results in two traversals F-G.0-H and J-G.1-A (Fig. 5). Further launch of StringDecomposer (using monomers G.0 and G.1 instead of G) confirms that there are no traversals F-G.0-A and J-G.1-H.

Splitting a junction monomer in cen18 results in two nearly identical monomers that differ in a single nucleotide and raises a concern about the applicability of the CE postulate to cen18. Splitting the unbreakable monomer G in cen18 should result in two traversals B-G.0-J and F-G.1-H. However, the further launch of StringDecomposer shows 547 B-G.1-J traversals and 10 F-G.0-H traversals. Importantly, in all B-G.1-J (F-G.0-H) traversals, the monomer block G.1(G.0) is more similar (or even identical) to the monomer G.1(G.0). Although this raises a concern about the validity of splitting the unbreakable monomer G in cen18, we proceed with the split to be consistent with the CE postulate.

Dehybridization reveals HORs in cen5 and cen8

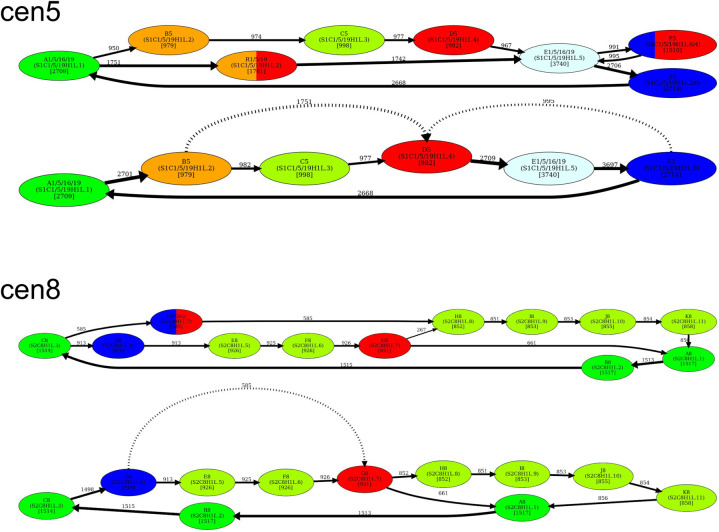
We identified all hybrid monomers (among monomers in MonomersNew⁺ across all centromeres) using the approach described in Methods (“Inference of hybrid monomers”). This analysis revealed only three frequent hybrid monomers: P5, R1/5/19, and L8. Below, we describe the “dehybridization” operation on monomer graphs that reveals HORs in cen5 and cen8.

Dehybridization in cen5

P5 is a hybrid monomer of S5 and D5 that differs from S5(50)/D5(120) in 5 nt, whereas R1/5/19 is a hybrid monomer of B5 and D5 that differs from B5(92)/D5(78) in 6 nt. Figure 6 (top) illustrates that dehybridization of P5 and R1/5/19 results in a graph with a single Hamiltonian cycle that is classified as a HOR.

Figure 6.

Dehybridization substitutes hybrid vertices (monomers) by hybrid edges in the monomer graph. (Top) Dehybridization of P5 and R1/5/19 in cen5. (Bottom) Dehybridization of L8 in cen8.

Dehybridization in cen8

L8 is a hybrid monomer of D8 and G8 which differs from the consensus D8(60)/G8(111) by only 2 nt (Supplemental Note 4). Figure 6 (bottom) illustrates the dehybridization of L8 that models it as a hybrid edge of the monomer graph, resulting in a graph with a single Hamiltonian cycle (and two chords) that is classified as a HOR.

What is a HOR in cen9?

Splitting unbreakable junction vertices (cen1, cen13, and cen18) and dehybridization (cen5 and cen8) reveal HORs for all centromeres except for cen9. This centromere represents a difficult case from the perspective of the CE postulate because it is unclear how to infer a HOR from the monomer graph of this centromere. The blue traversal of this graph (Fig. 5) corresponds to the currently known (manually inferred) HOR. The monomer F9 (that does not belong to the HOR in cen9) cannot be represented as a hybrid monomer and is quite different from its most similar monomer in cen9 (it differs from Z4/9 by 12 nt). Thus, it is not clear how to automatically derive a HOR for cen9.

One can argue that merging monomers F9 and Z4/9 would reveal a Hamiltonian cycle (HOR) in the resulting monomer graph, thus extending the CE postulate to cen9. This argument reflects the difficulty of developing an automated approach to centromere annotation and defining parameters of these approaches that work across all centromeres. Indeed, the CE postulate is highly dependent on parameters; for example, relaxing the parameter for monomer merging will affect the monomer graphs for all centromeres and may “break” the CE postulate for some of them. Although by manually fitting parameters for each centromere, one can make it look consistent with the CE postulate, such an approach does not represent solid supporting evidence for this postulate. As described in Supplemental Note 6, because of the limited data (only a single human genome has been completely assembled so far), it is challenging to avoid overfitting even for the default parameters of HORmon, let alone for a more complex procedure. Our approach represents the first automated analysis (with the same parameters for all centromeres) demonstrating that the CE postulate holds for nearly all centromeres. Subsection “Limitations of the CE postulate” (Methods) highlights further limitations of the CE postulate.

Generating the centromere decomposition into HORs

HORmon decomposes each monocentromere into canonical, partial, and auxiliary HORs as described in subsection “Decomposing a centromere into HORs” in Methods (Fig. 2). Given a canonical HOR H = M₁, …, M_n, each canonical HOR M_i, …, M_n,M_{n + 1}, …, M_i−1, in the decomposition is labeled as c_i. We use the notation c^m_i to denote m consecutive occurrences of a canonical HOR and refer to each such element in the HOR decomposition as a “HOR run.” According to the CE postulate, hybrid and infrequent monomers do not belong to the HOR. Supplemental Note 7 discusses the advantages of the HORmon approach over more traditional methods.

The “length” of the HOR decomposition is defined as the total number of elements in this decomposition (each entry x^y is counted as a single element). Figure 7 shows the HOR decompositions of cenX under the assumption that the monomer set includes 12 monomers AB…KL forming the HOR on cenX, as well as hybrid monomers M and N identified in Dvorkina et al. (2020). Supplemental Table S2 and Supplemental File 1 provide information about the HOR decompositions for all human centromeres. Supplemental Note 8 describes how these HOR decompositions are used to generate the nucleotide consensus of each HOR. Supplemental Note 4 summarizes information about these consensuses for live human centromeres. Because these consensus sequences are computed for the first time using a complete human genome assembly, they characterize the CHM13 cell line more accurately than previously inferred sequences. The question of whether they are representative for other individuals remains open.

Figure 7.

Decomposition of cenX into HORs. The 12-monomer HOR for cenX is represented as M₁… M₁₂ = AB…KL. The monomer set includes these 12 frequent monomers as well as hybrid monomers M (a hybrid of monomers J and H) and N (a hybrid of monomers K and J) identified in Dvorkina et al. (2020). Each occurrence of this HOR that starts from the monomer M_i is labeled as c_i (shown in red). Each occurrence of a partial HOR that includes monomers from i to j is labeled as p_i,j. We use the notation c^m (p^m) to denote m consecutive occurrences of a canonical (partial) HOR. The most frequent partial monomers p_3-7, p_7-3, and p_5-2 in cenX are colored in blue, green, and brown, respectively. The HOR decomposition of cenX has a length 72 and includes 1486 complete HORs that form 34 HOR runs. Only 257 of 18,089 (1.4%) monomer blocks in cenX are not covered by complete HORs. The “LINE” entry shows the position of the LINE element. To ensure that all monomers are shown in the forward strand, we decompose the reverse complement of cenX and take reverse-complements of all monomers in cenX (Supplemental Note 4).

Pairs of centromeres (13, 21) and (14, 22), as well as triple of centromeres (1, 5, 19), have been reported to share the same HOR (McNulty and Sullivan 2018). Contrary to previous studies, we conclude that HORs in these centromeres are rather different, at least in the CHM13 cell line. The edit distance between the consensus of HORs in cen13 and cen21 is rather high (20 differences, 1% divergence), whereas the edit distance between the consensus of HORs in cen14 and cen22 is much lower (three differences, 0.2% divergence). Previous studies reported two frequent nonhybrid monomers for centromeres 1, 5, and 19 (McNulty and Sullivan 2018). We report six frequent nonhybrid monomers for cen1 and cen5, and two for cen19. We hypothesize that these differences are a result of the absence of a complete genome assembly in prior studies. Sequence comparison shows that the edit distance between the consensus of HOR in cen1 and cen5 is large (34 differences, 3.3% divergence).

Discussion

Recent advances in long-read sequencing technologies and genome assembly algorithms opened new horizons for centromere genomics. For the first time, studies of human alpha satellite arrays can be based on a complete centromere assembly rather than individual reads or “satellite reference models” (Miga et al. 2014). The development of an automated centromere annotation tool is a prerequisite for future centromere research that quickly moves to the stage when the complete genomes of hundreds of individuals will be assembled. These studies include population-wide analysis of human monomers and HORs, evolutionary studies of centromeres across primates and other species, and biomedical studies of diversity of human centromeres and their associations with genetic diseases.

We developed HORmon, the first annotation tool for live alpha satellite arrays that considers monomer and HOR inference as two interconnected problems and automatically generates the monomer and HOR set that mirror the four decades of centromere research. HORmon not only provides the first automatic procedure for extracting monomers and HORs in live alpha satellite arrays but also establishes their nucleotide consensus sequences. This is important because the currently used nucleotide sequences for many of these monomers and HORs have been extracted more than two decades ago (Alexandrov et al. 2001) in the absence of centromere assemblies. In centromeres 1, 2, 5, and 15, HORmon reported a different number of monomers than McNulty and Sullivan (2018). We hypothesize that these differences result from the absence of a complete genome assembly in prior studies. Contrary to previous studies, we found that HORs in pairs of centromeres (13, 21) and (14, 22) are rather different (“Generating the centromere decomposition into HORs”). We note that because human centromeres are very divergent between individuals, it remains unclear how well the inferred nucleotide consensus of HORs in the CHM13 cell line represents other individuals.

HORmon uses a heuristic approach for monomer and HOR inference rather than popular clustering algorithms (such as k-means or hierarchical clustering) because the monomer inference problem differs from the classical clustering problem. For example, the set of data points (monomer blocks) is not explicitly given but is implicitly encoded in the centromere and depends on the selection of centers (monomers). Although the choice of the consensus alpha satellite results in the initial set of monomer blocks, each selection of a monomer set affects this initial set and results in a slightly different clustering problem. Moreover, it is not clear how to select the biologically adequate function to measure the distances between data points and centers. For example, the sequence divergence function that HORmon uses is clearly limited (it does not take into account the positional information), necessitating the merging/splitting modules in HORmon. It is also unclear how to incorporate hybrid monomers in the framework of the classical clustering problems. To address all these complications, we have designed the HORmon heuristic instead of using the standard clustering approaches. Supplemental Note 9 presents information about time and memory footprint of HORmon.

HORmon introduced a procedure for decomposing a centromere into HORs and generated the UCSC Genome Browser tracks representing this decomposition for the CHM13 genome. Although the recently assembled CHM13 genome does not include Chromosome Y, we project that HORmon will be able to generate monomers and HORs for cenY once its complete assembly becomes available. Uralsky et al. (2019) classified a HOR as “homogeneous (divergent)” if its copies have an average divergence <5% (>10%). In addition to live centromeres that we analyzed in this paper, human chromosomes have nearly 60 pseudocentromeric and divergent HOR arrays. Our next goal is to use HORmon for generating monomers and HORs for these HOR arrays that are still only manually annotated (inferred) in the T2T assembly.

Although HORmon relies on the CE postulate to rationalize the series of splits, merges, and dehybridizations, computational validation of this postulate remains outside the scope of this paper (Supplemental Note 1). Indeed, rigorous statistical analysis of the CE postulate (together with formulating and analyzing alternative evolutionary hypotheses) is currently lacking. Because the CE postulate was formed implicitly at the dawn of the sequencing era, we do not rule out a possibility that it might be revised once the statistical significance of HOR extraction for all centromeres is rigorously assessed. In fact, development of HORmon already revealed difficulties of extending CE postulate to cen9 (subsection “What is a HOR in cen9?”) and cen18 (subsection “Splitting unbreakable monomers reveals HORs in cen1, cen13, and cen18”).

Because only a single human genome remains completely assembled, the selection of HORmon parameters was based on this genome only and thus may suffer from overfitting. Supplemental Note 6 provides intuition and justification for parameter selection. Moreover, without a rigorous statistical assessment of the CE postulate versus alternative models of centromere evolution (Mestrovic et al. 1998; Henikoff et al. 2001; Rice 2019), it is unclear how to verify that the HORs extracted by HORmon represent the most likely solution of the HOR inference problem. To complicate the issue even further, the existing nucleotide sequences of canonical HORs have been extracted decades ago, limiting the available “ground truth” to benchmark HORmon against. We anticipate that the HORmon pipeline will become an important stepping stone for the development of a fully automatic tool for the extraction of HORs and centromere annotation across the human population once more complete assemblies become available. In fact, Altemose et al. (2022) already show that extracting monomers and HORs and centromere annotation assists with analysis of CENPA ChIP-seq enrichment and DNA methylation in satellite arrays.

Because the rapidly evolving centromeres are very diverse across the human population (Miga et al. 2014; Suzuki et al. 2020), we anticipate that the concepts of the monomer graph will assist in comparing centromeres across multiple individuals. Supplemental Notes 10 and 11 show early application of HORmon to centromeres beyond the human genome. Although HORmon proved to be useful for analyzing live centromeres, automatic procedures for annotating other alpha satellite domains (both HOR and monomeric) are currently not established. We project that HORmon will work just as well on all homogeneous HORs (not only the live ones). Other HOR arrays however are known to be more divergent than the live arrays, and monomeric arrays are yet more divergent, so it is currently unclear how to universally select HORmon parameters to annotate all alpha satellite arrays in the human genome.

Methods

Positionally similar monomers

Given a monomer M in a monomer set Monomers for a given monocentromere, we identify all triples of consecutive blocks XMY that appear in this monocentromere, and construct the |Monomers|*|Monomers| matrix Triples_M, where Triples_M(X,Y) is the count of the number of triples XMY in the monocentromere. We further construct a normalized matrix NormalizedTriples_M(X,Y) by multiplying Triples_M(X,Y) by a constant so that the squared sum of all its entries is equal to one.

Given two equally sized n × m matrices A and B, we define their similarity as the dot-product of the n × m-dimensional vectors representing these matrices:

$$sim(A,B)=\sum _{\mathrm{each}\mathrm{row}i,\mathrm{eachcolumn}j}A(i,j)\times B(i,j).$$

Given two monomers M and M′, we define their positional similarity PosSim(M,M′) as

$$sim(NormalizedTriple{s}_M,NormalizedTriple{s}_{M^{\mathrm{\prime }}}).$$

Two monomers are called “similar” if the percent identity between them exceeds a threshold minPI (default value 94%). Two similar monomers are called “positionally similar” if their positional similarity exceeds a threshold minPosSim (default value 0.4).

Merging positionally similar monomers

Because two different positionally similar monomers point to a potentially erroneous splitting of a single monomer, HORmon checks if there are positionally similar monomer pairs in the monomer set Monomers. If such monomer pairs exist, it iteratively identifies a pair of the most positionally similar monomers (similar monomers with the highest positional similarity of all similar monomers), merges them into a new monomer, recomputes the consensus of the new monomer, launches StringDecomposer on the new (smaller) monomer set, and iterates until there are no positionally similar monomers left. Similarly to constructing the triple matrices for all triples XMY of a monomer M, HORmon constructs similar matrices for all triples XYM and MXY and merges monomers based on these two matrices in the same way it merges monomers for all triples XMY.

Splitting aggregated monomers

To decide whether to split a monomer M, HORmon analyzes all frequent triples XMY in a monocentromere. Given a monomer M, we refer to the largest element in the matrix NormalizedTriples_M (X,Y) as the “M champion.” We classify elements (X,Y) and (X′,Y′) in the matrix NormalizedTriples_M(X,Y) as “M comparable” if

$$NormalizedTriple{s}_M(X^{\mathrm{\prime }},Y^{\mathrm{\prime }})/NormalizedTriple{s}_M(X,Y)$$

exceeds a “splitting threshold” splitValue (default value 1/8). HORmon uses the single linkage clustering to iteratively identify all monomer pairs (X,Y) that are M comparable with the M champion and refer to them as “M-candidate pairs.”

Monomer pairs (X,Y) and (X′,Y′) are called “independent” if all four monomers X, Y, X′, and Y′ are different. A monomer M that has M-candidate-pairs is called breakable if all M-candidate pairs are (pairwise) independent, and “unbreakable,” otherwise. Given a breakable monomer M, HORmon considers all M-candidate pairs (X₁,Y₁),…, (X_t,Y_t) and splits the monomer M into t monomers M₁, …, M_t by separately deriving the monomers M_i as the consensus of all M blocks that arise from triples X_iMY_i in the monocentromere for 1 ≤ i ≤ t.

Supplemental Note 12 describes the pseudocode of the SplitAndMerge module that HORmon uses for modifying the initial monomer set.

Simplified monomer graphs

Given a monomer graph, HORmon constructs the “complete bipartite graph” where each part represents all vertices (monomers) of the monomer graph. A monomer M′ in the “upper” part is connected with a monomer M′′ in the “bottom” part by an edge of the weight equal to the multiplicity of the edge (M′,M′′) in the monomer graph. Afterward, HORmon solves the “assignment problem” to find the “maximum weight bipartite matching” in the bipartite graph (Ahuja et al. 1993). Edges of this bipartite matching, which also represent edges of the monomer graph, form a set of nonoverlapping cycles and paths in the monomer graph. An edge of a monomer graph is classified as “removable” if it forms a chord in one of these cycles/paths (a chord of a path is defined as an edge connecting two internal vertices of this path). Removal of all removable edges from the monomer graph results in the “simplified monomer graph.”

Inference of hybrid monomers

HORmon's algorithm for inferring hybrid monomers differs from the approach in Dvorkina et al. (2021). For monomers A, B, and C, we define HybridDivergence_A(B, C) as the divergence between A and a concatenate of a prefix of B and a suffix of C that is most similar to A. A monomer A from a monomer set Monomers is a “hybrid candidate” of monomers B and C if HybridDivergence_A(B,C) is below the maxResolvedDivergence threshold and HybridDivergence_A(B,C) does not exceed divergence between A and any another monomer from Monomers. HORmon first generates a set HybridCandidates by iterating over concatenates of all possible prefixes and suffixes for every pair of distinct monomers B and C. Afterward, if there is a single pair of monomers B and C that give rise to a hybrid candidate A, we classify A as a hybrid of B and C. If several pairs of such monomers exist, we select a pair of monomers B and C that are not hybrid candidates themselves, form a concatenate with the minimal divergence from the monomer A, and classify A as a hybrid of B and C.

Decomposing a centromere into HORs

We defined the monomer graph as the de Bruijn graph with low-multiplicity vertices and edges removed. We now consider the complete de Bruijn graph DB(Centromere*, 2) and classify an edge in this graph as a “HOR edge” if it connects two consecutive monomers in a HOR, and a “non-HOR edge,” otherwise. A monocentromere defines a traversal of edges in the de Bruijn graph (that contains both HOR edges and non-HOR edges) and each non-HOR edge in this traversal corresponds to two consecutive monomers in the monocentromere that we refer to as “breakpoint.” We break the monocentromere at all breakpoints defined by non-HOR edges, resulting in multiple short substrings. These substrings, that define the HOR decomposition of a centromere, represent one of the following scenarios:

• a canonical HOR or multiple consequently traversed canonical HORs that may be followed by a partial HOR;

• a partial HOR that includes monomers from i to j denoted p_i,j. Because a HOR is a cycle, i might exceed j, for example, p_4,2 corresponds to the partial 4-monomer HOR M₄,M₅,M₁,M₂ for a 5-monomer HOR M₁,M₂,M₃,M₄,M₅; and

• an auxiliary HOR represented by a hybrid or an infrequent monomer (denoted by the identifier of this monomer).

Limitations of the CE postulate

Figure 8 shows a toy example of two “monocentromeres” that result in identical monomer graphs (formed by cycles AB and BC connected via the junction vertex B) yet represent very different evolutionary scenarios. Although one can come up with a plausible “evolutionary” scenario for these centromeres, it is not clear how to find out their HORs that would be compliant with the CE postulate. The first monocentromere can be described as two cycles (one formed by vertices A and B and another formed by vertices C and B), whereas the second one can be described by a single cycle (formed by vertices A, B, C, and B) in the monomer graph (Fig. 8).

Figure 8.

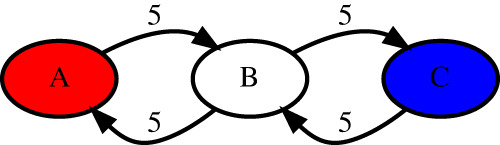
Two different “monocentromeres” BABABABABABCBCBCBCBCB and BABCBABCBABCBABCBABCB have the identical monomer graphs.

The concept of a HOR does not allow one to adequately describe the differences between the monocentromeres shown in Figure 8 because it requires that each monomer participates in a HOR once, necessitating the sequence ABC (that does not adequately reflect the centromere architecture) as the only possible HOR candidate. Although this example might be considered artificial, any algorithm for centromere annotation should adequately handle such cases, even if they rarely appear in the human centromeres. As we show below, cen13 and cen18 represent an evolutionary scenario that is similar to the toy centromere described in Figure 8.

The previous approaches to centromere annotation were based on the CE postulate and described centromeres in terms of complete and partial HORs. Given toy monocentromeres ABCABCABCABCABABABAB and ABCABABCABABCABABCAB, they described these very different architectures in the same way: as the complete HOR ABC and the partial HOR AB, each repeating five times. Because this representation does not distinguish these two very different centromere architectures, there is a need for a more general representation of the centromere architecture that will adequately reflect all complete and partial HORs.

Data access

The codebase of HORmon is available at GitHub (https://github.com/ablab/HORmon/tree/HORmon) and as Supplemental Code. Monomer and HOR decompositions of alpha satellite arrays in the CHM13 cell line are available at Figshare (https://figshare.com/articles/dataset/HORmon/16755097/2) and as Supplemental Material. Jupyter notebook that reproduces figures in this paper is available at GitHub (https://github.com/TanyaDvorkina/hormon_paper/blob/dev/HORmon_paper.ipynb).

Competing interest statement

The authors declare no competing interests.