Skip to main content
NCBI home page
Molecular Biology of the Cell logoLink to Molecular Biology of the Cell
. 2022 Feb 18;33(3):ar27. doi: 10.1091/mbc.E20-01-0087

A mechanistic motor-clutch model that explains cell shape dynamics to cyclic stretch

Benjamin W Scandling a,b,†, Jia Gou c,†,‡, Jessica Thomas a, Jacqueline Xuan a, Chuan Xue c,*, Keith J Gooch a,b,*
Editor: Alex Mogilnerd
PMCID: PMC9250388  PMID: 35020463

Abstract

Many cells in the body experience cyclic mechanical loading, which can impact cellular processes and morphology. In vitro studies often report that cells reorient in response to cyclic stretch of their substrate. To explore cellular mechanisms involved in this reorientation, a computational model was developed by adapting previous computational models of the actin–myosin–integrin motor-clutch system developed by others. The computational model predicts that under most conditions, actin bundles align perpendicular to the direction of applied cyclic stretch, but under specific conditions, such as low substrate stiffness, actin bundles align parallel to the direction of stretch. The model also predicts that stretch frequency impacts the rate of reorientation and that proper myosin function is critical in the reorientation response. These computational predictions are consistent with reports from the literature and new experimental results presented here. The model suggests that the impact of different stretching conditions (stretch type, amplitude, frequency, substrate stiffness, etc.) on the direction of cell alignment can largely be understood by considering their impact on cell–substrate detachment events, specifically whether detachments preferentially occur during stretching or relaxing of the substrate.

INTRODUCTION

Cell alignment in response to cyclic stretch

Many tissues and organs in the body experience cyclic mechanical loading, including the cardiovascular systems with the beating of the heart and subsequent pulse wave through the vasculature, the lungs with breathing, the digestive system with peristalsis, and the muscular skeletal system with locomotion. The cyclic mechanical loading and resulting cyclic stretch are thought to impact the structure and functions of these tissues as well as the associated cells in vivo, as summarized in various review articles (Gupta and Grande-Allen, 2006; Birukov, 2009; Morita et al., 2013; Qiu et al., 2014; Yu et al., 2016). In vitro studies have shown that stretch plays a role in cellular proliferation (Gorfien et al., 1989; Sumpio et al., 1990; Butt and Bishop, 1997), apoptosis (Sotoudeh et al., 2002), migration (Hasaneen et al., 2005; Zhang et al., 2015), extracellular matrix maintenance and production (Gorfien et al., 1989; Sumpio et al., 1990; Butt and Bishop, 1997), and phenotype alteration (Cui et al., 2015). Similarly, various morphological responses of cells to cyclic stretch have been reported, including spreading, elongation, and alignment (Moretti et al., 2004; Barron et al., 2007; Greiner et al., 2013; Cui et al., 2015). While some cellular and molecular responses to cyclic loading are highly dependent on cell type and alterations in stretch type, many cell types tend to alter their orientation similarly in response to cyclic stretch. Specifically, cells cultured on deformable substrates with initially random orientations align nearly perpendicular to the direction of principal strain, or along an axis of minimal strain, after exposure to cyclic substrate deformation (Dartsch and Betz, 1989; Sumpio et al., 1990; Iba and Sumpio, 1991; Kada et al., 1999; Standley et al., 2002; Moretti et al., 2004; Barron et al., 2007; Jungbauer et al., 2008; Matsugaki et al., 2013).

Biophysical processes that could potentially lead to cytoskeletal alignment

Several cellular components have been hypothesized to play a role in cellular realignment, with most of them focusing on the actin cytoskeleton. Cells under tension from internal (e.g., cellular contraction) (Chrzanowska-Wodnicka and Burridge, 1996) or external loads form highly organized actin fiber bundles terminating at substrate-linking focal adhesions known as actin stress fibers (Burridge et al., 1988; Pellegrin and Mellor, 2007). Applied cyclic load reorganizes stress fibers along an axis of minimal strain (roughly perpendicular to the direction of applied stretch) with the whole cell typically also aligning in this direction (Dartsch and Betz, 1989; Ghibaudo et al., 2008; Faust et al., 2011). When stress fiber formation is inhibited, cells lose the ability to reorient when exposed to cyclic stretching (Kaunas et al., 2005). Similarly, disruption of actin cytoskeletal organization with various pharmacological agents also inhibits cellular reorientation (Goldyn et al., 2010). These observations suggest that the actin cytoskeleton plays a vital role in the cellular morphological response to cyclic stretch. While there exists a wealth of knowledge on the cellular response to cyclic stretch, and data have begun to emerge on potential molecular players, the specific mechanisms behind cellular sensing of cyclic stretch and reorientation of cells remain unknown. On a broad level, one can consider three mechanisms by which changes in the actin cytoskeleton can result in reorganization of cells in response to cyclic stretch (Figures 1 and 2): 1) Actin bundles can preferentially lengthen and/or shorten, depending on their orientation; 2) Actin bundles can preferentially depolymerize or form, again depending on their orientation; 3) Intact bundles can change their orientation or rotate within the cells.

FIGURE 1:

FIGURE 1:

Open in a new tab

Cellular morphological response to applied mechanical cyclic stretch. (A) In vitro HUVEC exposed to no stretch control (top) and 10% stretch conditions (bottom). Representative images show overall culture perpendicular realignment (left) and individual cell actin fiber realignment (right, yellow circle). (B) Three general processes by which changes in the actin cytoskeleton (actin fibers) can result in reogranization of cells in response to cyclic stretch. Fibers may lengthen or shorten due to polymerization or depolymerization, based on their orientation with respect to the direction of applied stretch. Fibers may rotate as a function of applied strain. Fibers may disassemble in directions where applied strain is greatest and reassemble in directions where strain is reduced.

FIGURE 2:

FIGURE 2:

Open in a new tab

Experimental application of mechanical cyclic stretch to cultured cells. (A) Schematic of custom mechanical stretch device capable of applying cyclic strain to cell cultures. Device consists of two clamps attached to a motorized stage, where one clamp moves cyclically to stretch a PDMS slab. The PDMS slab contains wells in which cells are seeded. (B) Graphical representation of cyclic stretch waveform. Cultures are stretched from initial length L0 to final length Lε according to a sine function with period t.

Existing mathematical models of fiber and cell alignment

Several computational models have been previously developed to predict cellular reorientation in response to cyclic stretch. Generally, models of stress fiber alignment make predictions by focusing on ways that actin bundles are altered by applied cyclic stretch. Many of these models utilize the pivoting of bundles in response to applied cyclic stretch. Models such as the one developed by Wang and Grood (1992) include preexisting fibers with initially random orientations. Fibers then change their orientation if their perceived level of stress exceeds a certain threshold value. Fibers continue to sense applied stresses and change orientation until they reorient in a direction where perceived stress is below a specified strain threshold. In a similar model, Civelekoglu et al. (1998) consider the rate of actin fiber unbinding with the extracellular substrate as a determinant of final fiber orientation. They reasoned that fibers aligned in the direction of stretch would exert greater forces on the proteins connecting them to the substrate and thus hypothesized that fibers initially oriented perpendicular to the direction of stretch are less likely to unbind with the substrate as it is stretched, while fibers oriented parallel to the direction of stretch are more likely to break their bonds with the substrate and are free to pivot. Notably, their model did not directly account for force-dependent effects on unbinding, but instead assumed that the unbinding constant was a specified function of the angle of the fiber relative to the stretch. A separate model developed by De et al. (2007) also utilizes fiber pivoting and rotation phenomena, but further describes how cells adjust a force dipole within the cell to maintain constant levels of cellular and matrix stress.

Another commonly modeled phenomenon as a means of describing cellular reorientation in response to cyclic stretch is the assembly, disassembly, and subsequent reassembly of actin fibers under stress. Hsu et al. (2009) and Kaunas and Hsu (2009) developed a model in which stress fibers have a defined rate of turnover dependent on applied stretch, where fibers tend to disassemble in directions with greater amounts of stretch and reassemble in directions where strain is decreased. Similar models, developed by Obbink-Huizer et al. (2014), Qian et al. (2013), and Wang (2000), also utilize assembly and disassembly of fibers to predict an alignment response.

While previously developed mathematical models can predict certain experimental results, some models are phenomenological in nature, for example, assuming fibers exposed to higher stresses rotate without giving insight into why this rotation might occur. Other models do not consider processes likely important for cellular reorientation, including the impact of force on the binding and unbinding of the actin fibers via integrins to the substrate and the impact of myosin motors on the motion of actin fibers. Therefore, we developed a mechanistic, mathematical model that utilizes specific cell–substrate interactions to examine how cells are linked with their substrate, sense externally applied forces, alter their morphology, and reorient along their substrate as a function of applied cyclic stretch. This model builds upon the work of Chan and Odde (2008) and Bangasser et al. (2013, 2017), who developed a computational model of the actin–myosin–integrin motor-clutch system hypothesized by Mitchison and Kirschner (1988).

RESULTS

Motor-clutch model of cell–substrate interactions

The motor-clutch model describes the interactions between myosin motors, actin bundles, and molecular clutches that link the actin bundle and the extracellular substrate (Figure 3A). Myosin motors pull the actin bundle toward the center of the cell (i.e., retrograde motion). Molecular clutches (e.g., integrin complexes) link the intracellular actin bundle to the extracellular substrate. The binding and unbinding of the multiple clutches are assumed to be independent of one another. The bound clutches apply a resisting force to the actin bundle, thereby decreasing the speed of the retrograde motion. Actin subunits are continuously added to the leading edge of the actin bundle. This addition of new subunits tends to extend the end of the actin fiber away from the center of the cell while individual subunits within the fiber move toward the center of the cell. If the rate of fiber elongation is greater than the rate of retrograde motion, the actin fiber can push against the plasma membrane, thereby elongating the cell in that direction.

FIGURE 3:

FIGURE 3:

Open in a new tab

(A) The motor-clutch model of Chan and Odde (2008) was adapted to incorporate the effects of cyclic stretch on actin bundle dynamics. The original model of Chan and Odde is shown in black and consists of an F-actin bundle, molecular clutches, and myosin motors. Myosin motors pull on the actin bundle, which moves at a velocity Vactin. In the diagram, only one of the 50 clutches is shown for simplicity. Clutches can bind from the substrate to the actin bundle with a probability of kon. One end of each clutch originates from the current location of the substrate (Xsub), and other end of each clutch binds to the actin bundle at X(i). At the moment of binding, there is no load on the clutch, so Xsub = X(i). Owing to the relative motion of the substrate and actin, after bonding the clutch can be stretched (i.e., Xsub ≠ X(i)) and the clutch applies forces to the actin bundle and substrate. In the adapted model used here, the substrate anchor is moved sinusoidally to introduce stretch (shown in red). (B) Illustration of three forms of cyclic stretch: purely uniaxial, simple elongation, and equibiaxial.

Chan and Odde (2008) and Bangasser et al. (2013, 2017) developed a set of equations that embody the concepts of the motor-clutch model and applied it to a cell on a deformable substrate. The model consists of an F-actin bundle, molecular clutches, and a compliant substrate. The actin bundle is treated as a rigid rod. The velocity of the actin (Vactin) is assumed to be a linear function of the sum of the forces applied by all clutches (∑Fclutch(i)). Specifically,

graphic file with name mbc-33-ar27-e001.jpg 1

where Vu is the unloaded velocity of the bundle. The stall force (Fstall) is the force that would prevent bundle motion and is calculated as the force of a single motor (Fm) times the number of motors (nm). Thus, when ∑ Fclutch(i) is equal and opposite to Fstall, Vactin = 0. The velocity of actin polymerization at the leading edge is a function of available free actin. While addition of new actin monomers to the leading edge impacts bundle length, it does not impact bundle velocity directly. Each individual clutch bond is treated as a single, Hookean spring with the magnitude of the force it exerts (Fclutch(i)) proportional to its deformation. Specifically,

graphic file with name mbc-33-ar27-e002.jpg 2

where Xi is the position of the ith clutch, Xsub is the position of the substrate, and Kc is the clutch spring constant. The sum of the forces for all clutches is applied to and deforms the substrate, which is treated as a single, Hookean spring with a spring constant Ksub. Specifically,

graphic file with name mbc-33-ar27-e003.jpg 3

Ksub is related to the modulus of the substrate, with 1 pN/nm corresponding to 1 kPa (Chan and Odde, 2008). Clutch binding and unbinding occurs stochastically with a binding rate constant (kon) and a detachment rate constant (koff*). To account for the fact that mechanically loading the clutch bond can increase the probability that it breaks, the Bell relationship is used to calculate koff(i)* for each clutch given the force it is currently experiencing. Specifically,

graphic file with name mbc-33-ar27-e004.jpg 4

where koff is the unloaded off-rate, Fb is a characteristic bond rupture force, and abs represents the absolute value function.

The length of the actin bundle is influenced by both depolymerization on the nuclear edge, or minus end, and polymerization on the leading edge, or plus end. The depolymerization rate at the minus end is assumed to be equal to Vactin. The polymerization rate (Vp) is allowed to increase as L decreases, which is consistent with the notion that as the bundle shortens there would be more globular (G-actin), or free, actin, which could increase polymerization rate. This behavior is captured by the equation

graphic file with name mbc-33-ar27-e005.jpg 5

where Vpmax is the maximum actin polymerization rate and Lmax is the maximum allowable bundle length.

Values for the free parameters were obtained by Chan and Odde from the literature or their own experimental work (Supplemental Table 1; Chan and Odde, 2008).

Modifications to model cyclic stretch

To consider the impact of cyclic stretch, we adapted the original Chan and Odde (2008) motor-clutch model described above. To mimic different experimental systems, the motor-clutch model was adapted to include three distinct types of cyclic stretch, following the convention of Wang et al. (2001): purely uniaxial stretch, simple elongation, and equibiaxial (Figure 3B). Purely uniaxial stretch involves movement of the substrate anchor in the x-direction only. Simple elongation involves movement of the substrate anchor in both the x- and y-directions, where the substrate is stretched in the x-direction and compressed in the y-direction as a result of the incompressible nature of deformable substrates commonly used in in vitro stretch experiments. Equibiaxial stretch involves stretching of the substrate anchor equally in both the x- and y-directions.

Cyclic stretch of the substrate in the x-direction is modeled through movement of the substrate anchor (Xanchor) according to a sinusoidal function,

graphic file with name mbc-33-ar27-e006.jpg 6

where X is the Lagrangian x-coordinate of the actin bundle tip at time of the first clutch binding in relation to the stretch cycle, P is the period of stretch, and εrtx is the percent cyclic stretch in the direction parallel (x-) to applied stretch. For the case of purely uniaxial stretch, Eq. 6 was the only application of strain to the system. The functional form 1 – cos(constant*t) was chosen so that at the beginning of the simulation (i.e., time = 0) there would be no applied stretch on the bundle, which matches the conditions of our experiments and those of most others. The position of the substrate following movement of the anchor is then updated such that the sum of the forces acting on the substrate is zero by using the equation

graphic file with name mbc-33-ar27-e007.jpg 7

where neng is the number of engaged (bound) clutches. Recognizing that the force exerted by the substrate (Ksub * [Xsub – Xanchor]) is equal and opposite to ∑ Fclutch(i), Eq. 1 yields

graphic file with name mbc-33-ar27-e008.jpg 8

In the simple elongation case, strain in the y-direction, which is perpendicular to the direction of applied stretch, the y-coordinate of the substrate anchor (Yanchor) changes following the equation

graphic file with name mbc-33-ar27-e009.jpg 9

where Y is the Lagrangian y-coordinate of the actin bundle tip at the time of the first clutch binding in relation to the stretch cycle, P is the period of stretch, and εrty is the applied cyclic compression ratio in the direction perpendicular (y-) to applied stretch as a result of elongation in the parallel direction (x-). The compression ratio was calculated as a function of stretch applied in the parallel (x-) direction and the estimated Poisson’s ratio of the modeled substrate. Our in vitro experimental system applied stretch in the x-direction, and the substrate was not confined in the y-direction. By recording the motion of fiduciary markers placed on our in vitro polydimethylsiloxane (PDMS) deformable substrate, we determined the Poisson’s ratio to be 0.52, similar to that reported for elastomers (specifically silicone rubbers) (O’Hara, 1983), which we approximated as 0.5 in simulations of simple elongation.

In simulations with cyclic equibiaxial stretch, stretch was applied equally in both the parallel (x-) and the perpendicular (y-) directions by moving the x- and y-coordinates of the substrate simultaneously with equal magnitude,

graphic file with name mbc-33-ar27-e010.jpg 10

where Lxy is the Lagrangian tip of the actin bundle at the time of the first clutch binding in relation to the stretch cycle and εrtxy is the applied cyclic stretch ratio.

In vitro cell and actin fiber orientation as a function of the amplitude of simple cyclic elongation

Changes in the morphology of cells exposed to cyclic stretch are well-documented (Dartsch and Betz, 1989; Sumpio et al., 1990; Iba and Sumpio, 1991; Kada et al., 1999; Standley et al., 2002; Moretti et al., 2004; Barron et al., 2007; Jungbauer et al., 2008; Matsugaki et al., 2013). The large majority of these studies, however, analyze either cell or actin fiber orientation without quantifying other metrics of cellular morphology such as shape (e.g., aspect ratio) and elongation. Because our computational model can make predictions related to changes in both actin bundle orientation and length, which in turn influence cell shape, it is useful to have experimental data for each of these metrics. Owing to differences in the cyclic loading experiments across reports including stretch type, magnitude, and frequency of stretch as well as cell types used, it is difficult to compare the effects of cyclic stretch on different metrics taken from different experiments. Thus, we collected a self-consistent set of experimental data that explored how these metrics changed as the amplitude of stretch was varied (Figure 4).

FIGURE 4:

FIGURE 4:

Open in a new tab

In vitro cellular morphology changes as a function of applied cyclic stretch. (A) Representative images of HUVEC exposed to no stretch control and 10% stretch conditions. (B–D) Cellular morphological measurements collected as a function of applied cyclic stretch. From left to right, visual descriptions of each measurement collected, average measurements (* denotes statistical significance with p value < 0.0125 according to Bonferroni multiple comparisons correction; bars on data points represent SEM), and representative frequency distribution histograms from no stretch control and 10% stretch conditions, n = 50–100 cells for each condition.

In our experiments, exposing cultured cells to simple uniaxial cyclic elongation, cells reoriented their major axis away from the direction of applied stretch (Figure 4, B–D, row 1). Similar to that reported by others (Faust et al., 2011), increasing the magnitude of stretch increased the angle (from 49.94° with 1% stretch to 73.88° with 10% stretch) (Figure 4, B–D, row 1). Similarly, actin fibers within the cell tend to realign to a similar angle when exposed to cyclic stretch (Figure 4, B–D, row 2). With increasing stretch amplitude, cells also tend to be longer along the axis perpendicular to the direction of stretch compared with their length along the axis parallel to stretch (Figure 4, B–D, row 3). However, data suggest that cell shape is not altered by cyclic stretch as the cellular aspect ratio (ratio of major axis length to minor axis length) is unchanged, with the exception of the 4% amplitude case (Figure 4, B–D, row 4). Histograms showing major axis, fiber orientation, perpendicular elongation, and aspect ratio for all strain levels studied are shown in Supplemental Figure 1.

Experimental data inform biophysical processes that could potentially lead to actin reorientation

As noted in Figure 1B, there are at least three nonexclusive mechanisms that could lead to changes in cellular alignment in response to cyclic stretch. By measuring only changes in cell shape or orientation, it is not possible to exclude any of these three mechanisms. Experimental measurements, however, reveal a change in actin orientation, which can be accounted for only by cyclic stretch preferentially altering fiber rotation or actin assembly/disassembly (Figure 1B). Thus, we explored the case where actin bundles can rotate as a potential mechanism of cellular reorientation in response to applied cyclic stretch.

Type of cyclic stretch and actin reorientation

To directly compare our model results with our experimental observations of cellular and actin fiber reorientation, we analyzed the effect of cyclic stretch on simulated actin bundle orientation. Under simulation conditions most comparable to our experimental conditions (simple elongation, high substrate stiffness [10 kPa], cyclic stretch frequency of 1 Hz, and 24 h of stretching), bundles align to an angle of 55.44 ± 0.12° relative to the direction of applied stretch (Figures 5A and 6A). Notably, this angle is similar to the angle calculated for the axis of minimal strain for simple elongation of an incompressible material (54.74°) (Livne et al., 2014) (Figure 5A, red dotted line). As noted by others, the calculated angle of minimal strain is similar to the orientation of cells cultured on a substrate subjected to simple cyclic elongation (Figure 5A and Table 1, row 1, type of stretch) (Barron et al., 2007; Faust et al., 2011; Matsugaki et al., 2013).

FIGURE 5:

FIGURE 5:

Open in a new tab

Experimentally measured actin fiber and/or cell orientation compared with our simulation results. Angle is relative to the direction of applied stretch. Because different stretch amplitudes or durations can yield different fiber orientations, the maximum value of the average fiber orientation reported in a study was used. (A) Actin fiber and/or cell orientation following exposure to simple elongation cyclic stretch. (B) Actin fiber and/or cell orientation following exposure to purely uniaxial cyclic stretch.

FIGURE 6:

FIGURE 6:

Open in a new tab

Simulated actin bundle reorientation as a function of cyclic stretch type, amplitude, and substrate stiffness. Bundles with initial orientations ranging from 0 to 90° are grouped into cells to create a single figure representing a whole cell. Single bundles in each cell represent the average final orientation and length of 10 simulated bundles (n = 10). Individual bundles were modeled using the adapted motor-clutch model with an initial length of 5000 nm, orientation ranging from 0 to 90°, and on substrate stiffnesses ranging from 0.1 to 10 kPa. Modeled actin bundles were then exposed to simulated simple substrate elongation (A), purely uniaxial cyclic stretch (B–D), or equibiaxial cyclic stretch (E) with frequency of 1 Hz and variable amplitude, following which bundle length and final orientation were collected. Red circles around bundles represent average size of bundles under no stretch control condition for each substrate stiffness.

TABLE 1:

Comparison of simulation predictions and in vitro experimental observations.

Simulation predictions In vitro experimental observations
Type of stretch
Simple elongation: Actin bundles typically (with many parameters sets) align ∼55–60° relative to direction of applied unconfined cyclic stretch (Figure 6A). In vitro experiments utilizing unconfined cyclic stretch, both we and others report actin alignment along an axis of minimal strain, ∼55–65° relative to direction of applied stretch (Figures 4 and 5A) (Wang et al., 2001; Barron et al., 2007; Faust et al., 2011; Matsugaki et al., 2013).
Purely uniaxial stretch: Actin bundles typically (with many parameters sets) align perpendicular relative to direction of applied purely uniaxial confined cyclic stretch (Figure 6, B and C). Others report actin realignment ∼90° relative to direction of applied cyclic strain Figure 5B) (Wang et al., 2001; Standley et al., 2002).
Equibiaxial stretch: Actin bundle orientation is not changed following exposure to equibiaxial cyclic stretch (Figure 6E). Randomly oriented cell populations remain randomly oriented following exposure to equibiaxial cyclic stretch (Wang et al., 2001; Kaunas et al., 2006).
Magnitude of stretchDose response: For moderate and high substrate stiffness, final angle of reorientation increases (toward perpendicular) with increasing amplitude of cyclic stretch (Figure 6), until reaching perpendicular.For high substrate stiffness, amplitude of cyclic stretch affects rate of actin bundle realignment, where increasing amplitude increases rate of realignment (Supplemental Figure 2).Minimal effective dose: Significant realignment is noticeable with stretch amplitudes as low as 1% (Figure 6). We and others show increasing cellular and actin fiber reorientation with increasing stretch amplitude (Faust et al., 2011).Rate of reorientation is affected by amplitude of cyclic stretch., where characteristic time of reorientation decreases linearly with increasing stretch amplitude (Jungbauer et al., 2008).We and others show significant realignment with stretch amplitudes as low as 1% (Faust et al., 2011), while others report minimum stretch amplitudes greater than 1% required for reorientation response (Nava et al., 2020).
Frequency of stretchRate of reorientation: For high substrate stiffness, frequency of cyclic stretch affects rate of actin bundle realignment with increasing frequency increasing rate of realignment (Figure 7A).Final angle of orientation: Frequency has no effect on final angle of orientation (Figure 7). Rate of cellular reorientation is affected by frequency of cyclic stretch, where the characteristic time required for reorientation decreases with increasing frequency. For confluent cell cultures, characteristic time decreases exponentially (Jungbauer et al., 2008).Frequency affects final angle of orientation, where final angle of reorientation increases with increasing frequency (Jungbauer et al., 2008).
Substrate stiffnessFor low substrate stiffness, actin bundles align parallel to the direction of applied cyclic stretch (Figure 6D). Others have reported realignment parallel to the direction of applied cyclic stretch on soft collagen substrates (Tondon and Kaunas, 2014).
Myosin motorsReducing myosin motor stall force by one order of magnitude completely eradicates actin bundle reorientation in response to cyclic stretch (Figure 8). Blocking myosin II function through the use of blebbistatin eliminates perpendicular reorientation of cells in response to cyclic stretch (Goldyn et al., 2010; Greiner et al., 2013).
Open in a new tab

In simulations of actin bundles exposed to purely uniaxial stretch (i.e., no deformation of the substrate in the direction perpendicular to the applied stretch), actin bundles align to an angle of 89.74 ± 0.38° relative to the direction of applied stretch (Figures 5B and 6B). Again, the direction that the actin bundles orient in the simulation is similar to the direction of minimal strain (90° for purely uniaxial strain). This simulation finding is consistent with the experimental results of others who used systems that generated purely uniaxial stretch (Figure 5B and Table 1, row 2, magnitude of stretch) (Sumpio et al., 1990; Iba and Sumpio, 1991; Standley et al., 2002). Thus, for both simple elongation and purely uniaxial cyclic stretch, the simulations predict that actin bundles reorient to the direction on minimal strain, which is generally consistent with experimental observations (Figure 5).

Others have reported that both cells and actin fibers do not align with a preferred orientation following exposure to cyclic equibiaxial stretch (Wang et al., 2001; Kaunas et al., 2006). For example, initially randomly oriented cell populations remain randomly oriented following equibiaxial stretch. Following 24 h of equibiaxial cyclic stretch, simulated actin bundles do not alter their orientation (e.g., a bundle with an initial orientation of 15° remains at 15° following stretching) (Figure 6E and Table 1, row 3 frequency of stretch). Therefore, our adapted model accurately predicts the experimental observation of no preferential realignment of actin fibers following equibiaxial cyclic stretch.

Amplitude of stretch and actin reorientation

In general, actin bundle orientation moves toward perpendicular to the direction of applied stretch with increasing stretch amplitude for moderate and high substrate stiffness and toward parallel for low substrate stiffness (Figure 6). To compare simulation results to experimental observations, we first focused on the high-substrate-stiffness case because we and most others used this condition in experiments. For simulations of high substrate stiffness (Figure 6, A and B), bundle reorientation begins for stretch amplitudes as small as 0.1%. Most of the reorientation occurs by 1% stretch, and there is very little difference in final orientation as the amplitude increases from 1 to 20% (Figure 6, A and B). Our in vitro studies (Figure 4) and the work of others (Faust et al., 2011) report significant realignment of fibers with stretch amplitudes as small as 1%, with further realignment with increasing amplitude. Some have reported no significant realignment with amplitudes lower than 5% but significant realignment following exposure to 40% stretch (Nava et al., 2020). Thus, across various in vitro studies, there is a range of stretch amplitudes required for significant cell and actin alignment, but the amplitude required by our simulations is less than this range (Table 1, row 2, magnitude of stretch). It is not surprising that we did not see quantitative agreement between the stretch amplitude required to achieve significant alignment in simulation and experimental results because we did not attempt to optimize our model parameters to better fit the experimental data. Odde and coworkers have shown that varying the parameters in a version of the motor-clutch model that does not account for cyclic stretch can vary the mechanical stimuli required for a specific response by several orders of magnitude (Bangasser et al., 2013, 2017). Though beyond the scope of the current study, model parameters likely could be optimized to provide better quantitative agreement.

Jungbauer et al. (2008) reported that increasing the stretch amplitude decreased the characteristic time of reorientation. We ran simulations with a range of amplitudes from 1% to 20% with other parameters held constant. As amplitude was increased, the time it took for actin bundles to reach their final orientation decreased (Supplemental Figure 2 and Table 1, row 2, magnitude of stretch), consistent with the experimental results. Therefore, the motor-clutch model can predict the qualitative effects of stretch amplitude on both the rate and steady-state value of actin alignment in response to cyclic stretch.

Frequency of stretch and actin reorientation

Relative to studies of the effect of stretch amplitude, there have been far fewer experiments studying the impacts of stretch frequency on cell and actin reorientation. Jungbauer et al. (2008) reported that increasing the frequency of cyclic stretch of a PDMS substrate decreased the characteristic time required for two different types of fibroblasts to reorient. Under simulation conditions most comparable to their experimental conditions (simple elongation, 10% stretch, and high substrate stiffness [10 kPa], 24 h of stretching), we observed that increasing the stretch frequency decreased the characteristic time required for reorientation (Figure 7A). However, stretch frequency has no impact on the final bundle orientation seen after ∼500 s (Figure 7, A and B), which is in contrast to Jungbauer et al.’s observation of increasing final orientation with increasing stretch frequency (Table 1, row 3, frequency of stretch).

FIGURE 7:

FIGURE 7:

Open in a new tab

Actin bundle reorientation as a function of cyclic stretch frequency. Actin bundles are modeled with 10% simple elongation cyclic stretch for 24 h on a substrate stiffness of 10 kPa. (A) Reorien­tation over time with variable cyclic stretch frequency (top) and resultant characteristic time required for reorientation, or time required for a bundle to reach an orientation that is equal to 98% of its steady state orientation (bottom). (B) Reorientation as a function of number of cyclic stretch cycles with variable stretch frequency (top) and resultant characteristic number of cycles required for reorientation, or number of cycles required for a bundle to reach 98% of its steady state orientation (bottom).

We reasoned that one potential explanation for actin bundles aligning more quickly when stretched at higher frequencies is that they simply experience a greater number of stretch cycles over a given time. Plotting the average actin bundle angle as a function of the number of cycles (Figure 7B) reveals that curves that represent lower frequencies (0.1–0.33 Hz) largely overlap. Similarly, curves representing higher frequencies (>2 Hz) tended to overlap, but they were clearly distinct from those for lower frequencies. The curve for an intermediate frequency of 1 Hz fell between the two groups of curves. Taken together, these results suggest that the number of cycles is an important determinant of the extent of fiber reorientation but not that other factors impacted by strain rate also play a role.

Substrate stiffness and actin reorientation

While holding all other parameters constant, decreasing substrate stiffness by one order of magnitude (from 10 to 1 kPa) diminishes the perpendicular reorientation response to purely uniaxial cyclic stretch (Figure 6, B and C) and simple elongation cyclic stretch (Supplemental Figure 3). That is, at a given stretch amplitude, actin bundles aligned closer to the perpendicular direction with the higher substrate stiffness (Figure 6, B vs. C) and a smaller stretch amplitude was required to approach maximal alignment with higher stiffness. However, decreasing substrate stiffness further (from 1 to 0.1 kPa) results in a more complex behavior (Figure 6D). At the lowest stretch investigated (0.1% stretch), there was negligible reorientation of actin bundles. With increasing levels of stretch, a greater fraction of the actin bundles aligned parallel to the applied stretch until the highest stretch where all bundles are aligned nearly parallel to the stretch. While we used only a single, relatively stiff, substrate in our in vitro cyclic stretch experiments, others have previously reported the in vitro parallel alignment of cells on soft extracellular substrates exposed to simple elongation (Tondon and Kaunas, 2014). Thus, our model can reproduce both the perpendicular alignment of fibers when cells are stretched on relatively stiff substrates and the parallel alignment seen on relatively soft substrates (Table 1, row 4, substrate stiffness).

Myosin motor function is required for actin bundle reorientation response

Blocking myosin motor function with the myosin II muscle and nonmuscle myosin ATPase inhibitor blebbistatin significantly reduces or eliminates the reorientation response to cyclic stretch in vitro (Goldyn et al., 2010; Greiner et al., 2013). Blebbistatin alters myosin motor function by binding to the myosin complex at the actin-binding interface, effectively blocking any actin–myosin interaction (Kovács et al., 2004).

We interpret the effects of blebbistatin to be incorporated in the motor-clutch model through alterations to the myosin motor stall force parameter, Fm. As blebbistatin decouples actin–myosin bonds, the actin bundle is free to move without influence from the myosin motors. In the model, decreasing Fm decreases the amount of force required to stall myosin motors and, therefore, allow the actin bundle to move independently. Reducing Fm approximately one order of magnitude nearly eradicates reorientation response, especially when analyzing stretch amplitudes comparable to those utilized in in vitro experiments (Figure 8). Specifically, a stall force of 0.1 pN results in no changes in actin bundle reorientation on any substrate stiffness, even with increased levels of stretch amplitude, up to 10% stretch (Figure 8B). Final average orientation also decreases with decreasing Fm (Figure 8B), suggesting a potential dose response to myosin motor function. Thus, our model accurately predicts the effects of blebbistatin and proper myosin motor function on the reorientation response to cyclic stretch through alterations to myosin motor stall force (Fm; Table 1, row 5, myosin motors).

FIGURE 8:

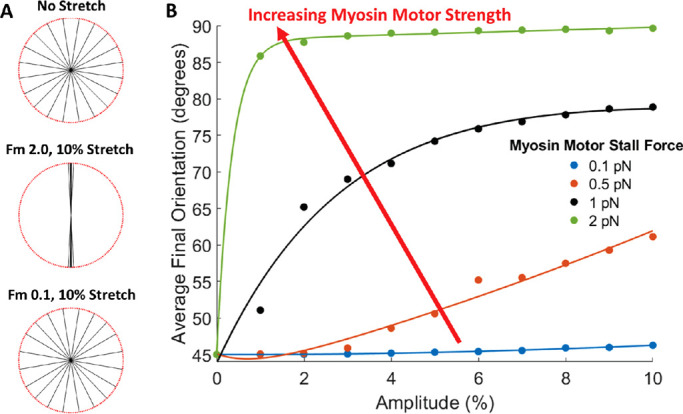
FIGURE 8:

Open in a new tab

Simulated actin bundle reorientation as a function of motor-clutch model myosin motor function. (A) Actin bundle final orientation as a function of cyclic stretch and myosin motor stall force, Fm. (B) Average final bundle orientation as a function of stretch amplitude and myosin motor stall force, Fm.

Mechanism by which cyclic stretch causes changes in actin bundle orientation

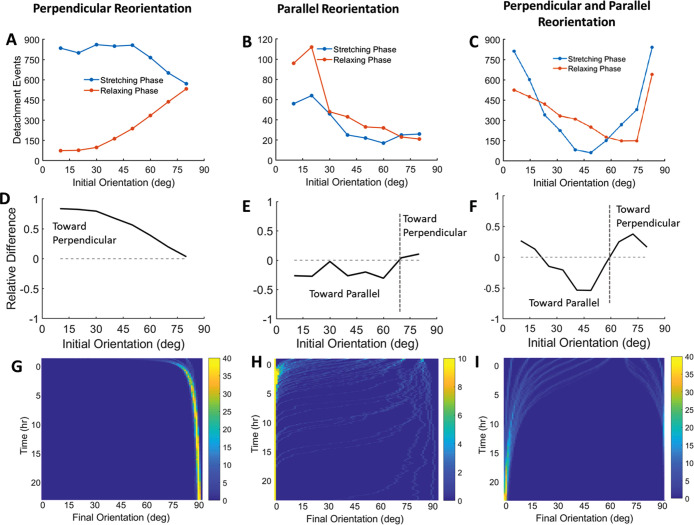
Experimental (Figures 4 and 5) and computational (Figure 6) results show that cells and/or actin bundles within cells alter their orientation in response to applied cyclic stretch. While most conditions result in perpendicular reorientation, under certain conditions (Figure 6D) bundles may align parallel to the direction of applied stretch. Factors such as initial bundle orientation, type of cyclic stretch, cyclic stretch frequency, stretch magnitude, and extracellular substrate stiffness all impact the direction of bundle realignment (Figure 6 and Supplemental Figure 3). We considered whether these factors work through a common mechanism. We reasoned that during the relatively rare times when there were no clutches bound to the substrate, a condition that we call a cell–substrate detachment event, both the actin bundle and the extracellular substrate are free to move independent of one another. Independent movement then allows for large changes in the relative position between the bundle and the substrate resulting in changes in overall fiber orientation. Moreover, as illustrated in Figure 9, we anticipated that the timing of the detachment event in relation to the cyclic stretch cycle will influence how the angle of the bundle will change, where failure during stretching of the substrate will increase the angle between the bundle and substrate (i.e., toward perpendicular) and failure during relaxing will decrease the angle between the bundle and substrate (toward parallel). Thus, we hypothesized that conditions that lead to a greater chance for bond failure to occur during the stretching phase will favor perpendicular alignment, while conditions that lead to a greater chance for bond failure to occur during the relaxing phase will favor parallel alignment.

FIGURE 9:

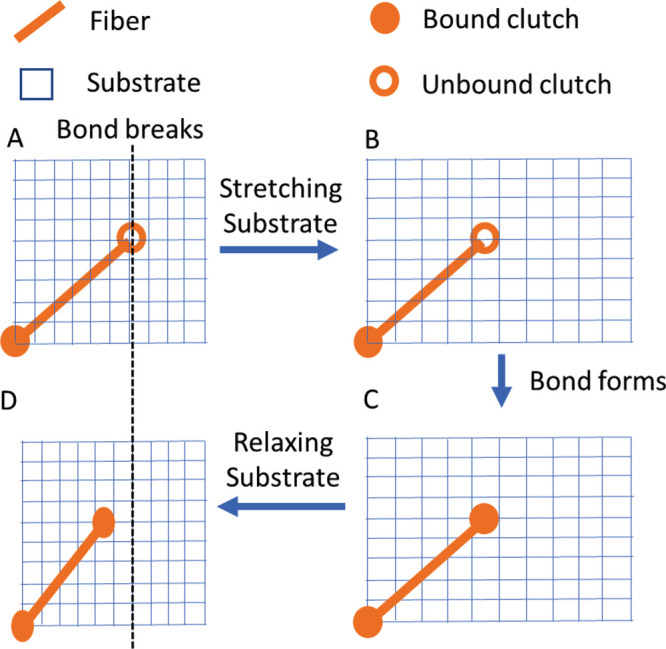
FIGURE 9:

Open in a new tab

Timing of clutch bond failure influences direction of fiber alignment. A clutch unbinds as the substrate is stretching (A), allowing the substrate to move relative to the fiber (B). The clutch bond reforms (C), allowing the fiber and substrate to move together, where (D) the final position of the fiber has rotated relative to its initial position (dotted line).

To test this hypothesis, we first calculated how often detachment events (i.e., no bound clutches) occurred during the stretching and relaxing phases of cyclic stretch of the substrate (Figure 10, top row). In some stretch conditions, the number of detachment events is consistently greater during the stretching phase (Figure 10A), while other stretching conditions tend to have more detachment events during the relaxing phase (Figure 10B). For some stretching conditions, however, whether more detachment events occur during stretching or relaxing is dependent on the initial orientation of the actin bundle (Figure 10C). Because our hypothesis focuses on whether detachment events were more likely during the stretching or relaxing phase, we calculated the difference between the two (Figure 10, middle row). A difference greater than 0 corresponds to a greater number of detachment events occurring during the stretching phase, and a difference less than 0 corresponds to a greater number of detachment events occurring during the relaxing phase. Therefore, a positive difference would predict perpendicular reorientation while a negative difference would predict parallel reorientation. Consistent with our hypothesis, conditions that caused more detachment events during stretching of the substrate than during relaxing (Figure 10D) corresponded to rotation of the actin toward the perpendicular direction (Figure 10G). Conversely, conditions that caused more detachment events during relaxation (Figure 10E) led to parallel realignment (Figure 10H).

FIGURE 10:

FIGURE 10:

Open in a new tab

Proposed mechanism for changes in actin bundle orientation following exposure to cyclic stretch. (A–C. top row) Detachment events, moments where the actin bundle is completely detached from the substrate (i.e., no bound clutches), are counted during both the stretching and relaxing phase of the cyclic stretch regime for bundles with initial orientations over the initial 1000 s. (D–F, middle row) Relative differences in stretching-phase detachment events and relaxing-phase detachment events are plotted; differences > 0 predict perpendicular reorientation and differences <0 predict parallel reorientation. (G–I, bottom row) Simultaneously, actin bundle reorientation is tracked over a course of 24 h of cyclic stretch. (A, D, G, left column) Perpendicular realignment of all actin bundles on stiff substrates (10 kPa). Detachment events are significantly increased during the stretching phase compared with the relaxing phase, which corresponds to rapid perpendicular realignment. (B, E, H, middle column) Parallel realignment of actin bundles on soft substrates (0.1 kPa). For many bundles, detachment events are increased during the relaxing phase of stretching, which corresponds to parallel realignment. (C, F, I. right column) Increased detachment events fluctuate between the stretching and relaxing phase corresponding to both parallel and perpendicular realignment of actin bundles for cases with decreased frequency and stiffness (0.5 kPa, 0.5 Hz). Bundles with initial orientations <65° align parallel to stretch, while bundles initially oriented >65° orient perpendicular to stretch. Color bars represent number of bundles at each data location.

Interestingly, bundles exposed to the same extracellular conditions (stiffness, frequency and amplitude of stretch) can experience changes in reorientation based solely on their initial orientations. For example, this behavior is seen in the simulation results for 10% stretch on a soft substrate (Figure 6). Other conditions lead to more pronounced changes where bundles align either parallel or perpendicular to that applied stretch, depending on the initial angle of the bundle (Figure 10C). Again, consistent with our hypothesis, the relative number of detachment events in the stretching and relaxing phase correctly predicts the direction of fiber rotation (Figure 10, F and I).

While these observations support the hypothesis relating timing of detachment events to direction of bundle rotation, not all observations can be explained solely by this hypothesis. For example, in Figure 10C, for initial angles from 10° to 25°, the relative number of detachment events predicts bundle rotation perpendicular to the direction of stretch, when the bundles actually reorient parallel to the direction of stretch (i.e., difference between detachment events is greater than 0, which would typically correspond to perpendicular realignment). The ability of the relative number of detachment events to explain the direction of bundle rotation in most but not all cases suggests that other factors also play a role. Other potential factors could be related to the stretch rate during detachment events (which varies through the sinusoidal cyclic stretch) or where within either the stretching- or relaxing-phase detachment occurs (e.g., detaching at the beginning of a stretch phase could have an effect different from that of detaching at the end of the same stretching phase even though stretch rates are the same).

DISCUSSION

Model capabilities, limitations, and opportunities for improvements

The motor-clutch model is based on established molecular processes and has been shown to describe previously known cell-–substrate interactions and make specific predictions that were subsequently observed experimentally (Chan and Odde, 2008; Bangasser et al., 2013, 2017). Our modifications to the model to account for exogenously applied substrate stretch predict and give mechanistic insights into changes in actin bundle orientation as well as cellular morphology in response to cyclic stretch. Despite these accomplishments, the model has several limitations. As with other computational models of the motor-clutch, the equations used to describe specific behaviors are reasonable but simplified descriptions and not all potentially relevant processes are modeled. For example, in our model, each bundle is considered independent of others. In cells, however, one would expect steric interactions between fibers preventing one to move independent of its neighbors. The ability of the modeled bundles, but not ones in real cells, to rotate independently of one another is likely why the model can predict two different preferred orientations of bundles within a given cell (Figure 6D) while experimental observations reveal that most actin bundles within a given stretched cell have similar alignment (Figure 4). One can envision a model of multiple actin bundles that considers steric interactions between fibrils, but this is beyond the scope of the work here. As a simpler alternative, we suggest that the probability that an experimental cell will have most of its bundles in a given direction after exposure to cyclic stretch is the percentage of bundles in that direction at the end of a model simulation where the bundles were originally uniformly distributed.

In addition to predicting bundle orientation, this model can predict the effects of cyclic stretch on bundle length, another potential mechanism by which cyclic stretch alters cellular morphology (Figure 1B). Examples of this can be seen in Figure 6, where simulating 5 and 10% stretch for 24 h changed the initially uniform bundle lengths to different lengths. Notably, bundles oriented more parallel to applied stretch were shorter than those oriented more perpendicular, which is consistent with cells aligning away from the direction of applied stretch. The ability of this model to explore how cyclic stretch alters bundle lengths merits further investigation but is beyond the scope of this study.

The parameters used in our adapted model are the same as those selected by Chan and Odde (2008) and Bangasser et al. (2013, 2017) in their investigation of how substrate stiffness alters clutch binding and actin bundle motion. The parameters selected were often chosen from a range of experimental values and could be considered as useful for a generic cell. As they showed in their later work, altering model parameters can be used to better match model predictions for experimental data from specific cell types (Bangasser et al., 2013, 2017). Similarly, there is an opportunity in future work to improve the agreement between our model predictions and experimental results by altering model parameters.

Conclusions

Subconfluent endothelial cells subjected to cyclic stretch alter their cell and actin alignment but not their aspect ratio, which is consistent with a fiber rotation–mediated model of alignment. A computational simulation of the motor-clutch system that allows for fiber rotation and accounts for cyclic stretch of the substrate was developed. The major findings from the computational model are 1) actin bundles align roughly perpendicular to the direction of the applied stretch, ∼90° for pure uniaxial stretch and ∼56° for simple elongation stretch. In both cases these directions coincide with the direction of minimal strain. 2) Under specific conditions, such as low substrate stiffness, actin bundles are predicted to align parallel to the direction of stretch. 3) Increasing stretch amplitude tends to promote a greater degree of predicted actin bundle alignments while increasing the stretch frequency tends to increase the rate at which fibers reorient. 4) Myosin motor function is critical in the perpendicular reorientation response. All these model predictions are generally in good agreement with the experimental data (Table 1). The model suggests that though a number of factors including stretch amplitude, stretch frequency, substrate stiffness, and initial bundle orientation can influence the reorientation of bundles, the impact of all of these factors can largely be understood in light of their impact on cell–substrate detachments events. Conditions that lead to more detachment events occurring when the substrate is stretching than when the substrate is relaxing cause the bundles to orient away from the direction of applied stretch. Conversely, conditions that lead to more detachment events when the substrate is relaxing cause alignment toward the direction of applied stretch.

MATERIALS AND METHODS

Request a protocol through Bio-protocol.

Cyclic stretch of in vitro cell cultures

Lonza (Morristown, NJ) human umbilical vein endothelial cells (HUVEC) were cultured with EGM-2 Bullet Kit media (Lonza, Morristown, NJ) and maintained below passage 8 to ensure constant cellular proliferation. A PDMS substrate was created with a 10:1 mixture of Sylgard 184 base and curing agent (Dow Corning, Auburn, MI), which was then degassed, poured into molds, and cured at 56°C for 1.5 h until fully hardened. The stiffness of this substrate is estimated to be about 1 MPa (Palchesko et al., 2012). The casting was then removed from the mold and autoclaved. A solution of 10 μg/ml human fibronectin in phosphate-buffered saline was added to each well of the sterilized cast and allowed to coat overnight at 4°C and then aspirated. Cells were trypsinized, counted, and seeded on the cast at a concentration of 4300 cells per well and incubated for 24 h at 37°C with 5% CO2 to allow for cell adhesion. The casting was then placed in a customized NSC-A1 Single Axis Stepper Motor Controller + Micro-step Driver (Newmark Systems, Rancho Santa Margarita, CA). The setup was placed in an incubator at 37°C with 5% CO2 with the stepper motor subjecting the casting and cells to cyclic stretch (Figure 2). The control casting was similarly incubated with no cyclic stretch. After ∼24 h, the castings were removed from the incubator and the cells were fixed with 4% paraformaldehyde.

Cells were permeabilized and stained for actin with 488 AlexaFluor phalloidin and counterstained for nuclei with 4′,6-diamidine-2′-phenylindole dihydrochloride (DAPI), after which they were imaged for fluorescence and differential interference contrast. Microscopy images were exported as TIFF images and processed using ImageJ software for cell size, shape, and orientation. Stained actin fibers were analyzed using the ImageJ plug-in FibrilTool (Boudaoud et al., 2014) for average actin fiber orientation and anisotropy for each cell. For each condition, 50–100 cells were analyzed, and results are presented as means. Independent simultaneous t tests were performed to determine the statistical significance of each stretch condition compared with the no stretch control condition. To control for multiple comparison–associated Type I error, the Bonferroni correction (Miller, 1981) was utilized to determine a new statistical significance level. Specifically, the initial significance criterion of 0.05 was reduced to 0.0125.

Code availability

MATLAB code is available by contacting the corresponding authors.

Supplementary Material

Click here for additional data file. (1.9MB, pdf)
Click here for additional data file. (263.5KB, pdf)

Acknowledgments

This work was supported by an award from the American Heart Association (17GRNT33700288, to K.J.G.) and an award from the National Science Foundation (CMMI-1334757 to K.J.G.).

Abbreviations used:

DAPI

4′,6-Diamidine-2′-phenylindole dihydrochloride

HUVEC

human umbilical vein endothelial cells

PDMS

polydimethylsiloxane.

Footnotes

This article was published online ahead of print in MBoC in Press (http://www.molbiolcell.org/cgi/doi/10.1091/mbc.E20-01-0087) on January 12, 2022.

REFERENCES

  1. Bangasser BL, Shamsan GA, Chan CE, Opoku KN, Tüzel E, Schlichtmann BW, Kasim JA, Fuller BJ, McCullough BR, Rosenfeld SS, Odde DJ (2017). Shifting the optimal stiffness for cell migration. Nat Commun 8, 15313. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Bangasser BL, Rosenfeld SS, Odde DJ (2013). Determinants of maximal force transmission in a motor-clutch model of cell traction in a compliant microenvironment. Biophys J 105, 581–592. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Barron V, Brougham C, Coghlan K, McLucas E, O’Mahoney D, Stenson-Cox C, McHugh PE (2007). The effect of physiological cyclic stretch on the cell morphology, cell orientation and protein expression of endothelial cells. J Mater Sci Mater Med 18, 1973–1981. [DOI] [PubMed] [Google Scholar]
  4. Birukov KG (2009). Cyclic stretch, reactive oxygen species, and vascular remodeling. Antioxid Amp Redox Signal 11, 1651–1668. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Boudaoud A, Burian A, Borowska-Wykręt D, Uyttewaal M, Wrzalik R, Kwiatkowska D, Hamant O (2014). FibrilTool, an ImageJ plug-in to quantify fibrillar structures in raw microscopy images. Nat Protoc 9, 457–463. [DOI] [PubMed] [Google Scholar]
  6. Burridge K, Fath K, Kelly T, Nuckolls G, Turner C (1988). Focal adhesions: transmembrane junctions between the extracellular matrix and the cytoskeleton. Annu Rev Cell Biol 4, 487–525. [DOI] [PubMed] [Google Scholar]
  7. Butt RP, Bishop JE (1997). Mechanical load enhances the stimulatory effect of serum growth factors on cardiac fibroblast procollagen synthesis. J Mol Cell Cardiol 29, 1141–1151. [DOI] [PubMed] [Google Scholar]
  8. Chan CE, Odde DJ (2008). Traction dynamics of filopodia on compliant substrates. Science 322, 1687–1691. [DOI] [PubMed] [Google Scholar]
  9. Chrzanowska-Wodnicka M, Burridge K (1996). Rho-stimulated contractility drives the formation of stress fibers and focal adhesions. J Cell Biol 133, 1403–1415. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Civelekoglu G, Tardy Y, Meister J-J (1998). Modeling actin filament reorganization in endothelial cells subjected to cyclic stretch. Bull Math Biol 60, 1017–1037. [DOI] [PubMed] [Google Scholar]
  11. Cui Y, Hameed FM, Yang B, Lee K, Pan CQ, Park S, Sheetz M (2015). Cyclic stretching of soft substrates induces spreading and growth. Nat Commun 6, 6333. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Dartsch PC, Betz E (1989). Response of cultured endothelial cells to mechanical stimulation. Basic Res Cardiol 84, 268–281. [DOI] [PubMed] [Google Scholar]
  13. De R, Zemel A, Safran SA (2007). Dynamics of cell orientation. Nat Phys 3, 655–659. [Google Scholar]
  14. Faust U, Hampe N, Rubner W, Kirchgeßner N, Safran S, Hoffmann B, Merkel R (2011). Cyclic stress at mHz frequencies aligns fibroblasts in direction of zero strain. PLoS One 6, e28963. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Ghibaudo M, Saez A, Trichet L, Xayaphoummine A, Browaeys J, Silberzan P, Buguin A, Ladoux B (2008). Traction forces and rigidity sensing regulate cell functions. Soft Matter 4, 1836. [Google Scholar]
  16. Goldyn AM, Kaiser P, Spatz JP, Ballestrem C, Kemkemer R (2010). The kinetics of force-induced cell reorganization depend on microtubules and actin. Cytoskeleton 67, 241–250. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Gorfien SF, Winston FK, Thibault LE, Macarak EJ (1989). Effects of biaxial deformation on pulmonary artery endothelial cells. J Cell Physiol 139, 492–500. [DOI] [PubMed] [Google Scholar]
  18. Greiner AM, Chen H, Spatz JP, Kemkemer R (2013). Cyclic tensile strain controls cell shape and directs actin stress fiber formation and focal adhesion alignment in spreading cells. PLoS One 8, e77328. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Gupta V, Grande-Allen KJ (2006). Effects of static and cyclic loading in regulating extracellular matrix synthesis by cardiovascular cells. Cardiovasc Res 72, 375–383. [DOI] [PubMed] [Google Scholar]
  20. Hasaneen NA, Zucker S, Cao J, Chiarelli C, Panettieri RA, Foda HD (2005). Cyclic mechanical strain-induced proliferation and migration of human airway smooth muscle cells: role of EMMPRIN and MMPs. FASEB J 19, 1507–1509. [DOI] [PubMed] [Google Scholar]
  21. Hsu H-J, Lee C-F, Kaunas R (2009). A dynamic stochastic model of frequency-dependent stress fiber alignment induced by cyclic stretch. PLoS One 4, e4853. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Iba T, Sumpio BE (1991). Morphological response of human endothelial cells subjected to cyclic strain in vitro. Microvasc Res 42, 245–254. [DOI] [PubMed] [Google Scholar]
  23. Jungbauer S, Gao H, Spatz JP, Kemkemer R (2008). Two characteristic regimes in frequency-dependent dynamic reorientation of fibroblasts on cyclically stretched substrates. Biophys J 95, 3470–3478. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Kada K, Yasui K, Naruse K, Kamiya K, Kodama I, Toyama J (1999). Orientation change of cardiocytes induced by cyclic stretch stimulation: time dependency and involvement of protein kinases. J Mol Cell Cardiol 31, 247–259. [DOI] [PubMed] [Google Scholar]
  25. Kaunas R, Hsu H-J (2009). A kinematic model of stretch-induced stress fiber turnover and reorientation. J Theor Biol 257, 320–330. [DOI] [PubMed] [Google Scholar]
  26. Kaunas R, Nguyen P, Usami S, Chien S (2005). Cooperative effects of Rho and mechanical stretch on stress fiber organization. Proc Natl Acad Sci USA 102, 15895–15900. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Kaunas R, Usami S, Chien S (2006). Regulation of stretch-induced JNK activation by stress fiber orientation. Cell Signal 18, 1924–1931. [DOI] [PubMed] [Google Scholar]
  28. Kovács M, Tóth J, Hetényi C, Málnási-Csizmadia A, Sellers JR (2004). Mechanism of blebbistatin inhibition of myosin II. J Biol Chem 279, 35557–35563. [DOI] [PubMed] [Google Scholar]
  29. Livne A, Bouchbinder E, Geiger B (2014). Cell reorientation under cyclic stretching. Nat Commun 5, 3938. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Matsugaki A, Fujiwara N, Nakano T (2013). Continuous cyclic stretch induces osteoblast alignment and formation of anisotropic collagen fiber matrix. Acta Biomater 9, 7227–7235. [DOI] [PubMed] [Google Scholar]
  31. Miller RGJ (1981). Simultaneous Statistical Inference, New York: Springer-Verlag. [Google Scholar]
  32. Mitchison T, Kirschner M (1988). Cytoskeletal dynamics and nerve growth. Neuron 1, 761–772. [DOI] [PubMed] [Google Scholar]
  33. Moretti M, Prina-Mello A, Reid AJ, Barron V, Prendergast PJ (2004). Endothelial cell alignment on cyclically-stretched silicone surfaces. J Mater Sci Mater Med 15, 1159–1164. [DOI] [PubMed] [Google Scholar]
  34. Morita N, Takada S, Okita K (2013). Influence of stretch and pressure as mechanical stresses on skeletal muscle. J Phys Fit Sports Med 2, 347–350. [Google Scholar]
  35. Nava MM, Miroshnikova YA, Biggs LC, Whitefield DB, Metge F, Boucas J, Vihinen H, Jokitalo E, Li X, García Arcos JM, et al. (2020). Heterochromatin-driven nuclear softening protects the genome against mechanical stress-induced damage. Cell 181, 800–817.e22. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Obbink-Huizer C, Oomens CWJ, Loerakker S, Foolen J, Bouten CVC, Baaijens FPT (2014). Computational model predicts cell orientation in response to a range of mechanical stimuli. Biomech Model Mechanobiol 13, 227–236. [DOI] [PubMed] [Google Scholar]
  37. O’Hara GP (1983). Mechanical Properties of Silicone Rubber in a Closed Volume, Technical Report ARLCB-TR-83045, Army Armament Research and Development Center, Watervliet NY, Large Caliber Weapon Systems Lab.
  38. Palchesko RN, Zhang L, Sun Y, Feinberg AW (2012). Development of polydimethylsiloxane substrates with tunable elastic modulus to study cell mechanobiology in muscle and nerve. PLoS O 7, e51499. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Pellegrin S, Mellor H (2007). Actin stress fibres. J Cell Sci 120, 3491–3499. [DOI] [PubMed] [Google Scholar]
  40. Qian J, Liu H, Lin Y, Chen W, Gao H (2013). A mechanochemical model of cell reorientation on substrates under cyclic stretch. PLoS One 8, e65864. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Qiu J, Zheng Y, Hu J, Liao D, Gregersen H, Deng X, Fan Y, Wang G (2014). Biomechanical regulation of vascular smooth muscle cell functions: from in vitro to in vivo understanding. J R Soc Interface 11, 20130852. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Sotoudeh M, Li Y-S, Yajima N, Chang C-C, Tsou T-C, Wang Y, Usami S, Ratcliffe A, Chien S, Shyy JY-J (2002). Induction of apoptosis in vascular smooth muscle cells by mechanical stretch. Am J Physiol-Heart Circ Physiol 282, H1709–H1716. [DOI] [PubMed] [Google Scholar]
  43. Standley PR, Camaratta A, Nolan BP, Purgason CT, Stanley MA (2002). Cyclic stretch induces vascular smooth muscle cell alignment via NO signaling. Am J Physiol-Heart Circ Physiol 283, H1907–H1914. [DOI] [PubMed] [Google Scholar]
  44. Sumpio BE, Banes AJ, Link GW, Iba T (1990). Modulation of endothelial cell phenotype by cyclic stretch: inhibition of collagen production. J Surg Res 48, 415–420. [DOI] [PubMed] [Google Scholar]
  45. Tondon A, Kaunas R (2014). The direction of stretch-induced cell and stress fiber orientation depends on collagen matrix stress. PLoS One 9, e89592. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Wang H, Grood ES (1992). Cell orientation response to cyclically deformed substrates: experimental validation of a cell model. J Biomech 28, 1543–1552. [DOI] [PubMed] [Google Scholar]
  47. Wang JH, Goldschmidt-Clermont P, Wille J, Yin FC (2001). Specificity of endothelial cell reorientation in response to cyclic mechanical stretching. J Biomech 34, 1563–1572. [DOI] [PubMed] [Google Scholar]
  48. Wang JH-C (2000). Substrate deformation determines actin cytoskeleton reorganization: a mathematical modeling and experimental study. J Theor Biol 202, 33–41. [DOI] [PubMed] [Google Scholar]
  49. Yu H-S, Kim J-Ju, Kim H-W, Lewis MP, Wall I (2016). Impact of mechanical stretch on the cell behaviors of bone and surrounding tissues. J Tissue Eng 7, 1–24. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Zhang B, Luo Q, Chen Z, Sun J, Xu B, Ju Y, Song G (2015). Cyclic mechanical stretching promotes migration but inhibits invasion of rat bone marrow stromal cells. Stem Cell Res 14, 155–164. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Click here for additional data file. (1.9MB, pdf)
Click here for additional data file. (263.5KB, pdf)

Articles from Molecular Biology of the Cell are provided here courtesy of American Society for Cell Biology

RESOURCES