Brain MR Atlas Construction Using Symmetric Deep Neural Inpainting

Abstract

Modeling statistical properties of anatomical structures using magnetic resonance imaging is essential for revealing common information of a target population and unique properties of specific subjects. In brain imaging, a statistical brain atlas is often constructed using a number of healthy subjects. When tumors are present, however, it is difficult to either provide a common space for various subjects or align their imaging data due to the unpredictable distribution of lesions. Here we propose a deep learning-based image inpainting method to replace the tumor regions with normal tissue intensities using only a patient population. Our framework has three major innovations: 1) incompletely distributed datasets with random tumor locations can be used for training; 2) irregularly-shaped tumor regions are properly learned, identified, and corrected; and 3) a symmetry constraint between the two brain hemispheres is applied to regularize inpainted regions. Henceforth, regular atlas construction and image registration methods can be applied using inpainted data to obtain tissue deformation, thereby achieving group-specific statistical atlases and patient-to-atlas registration. Our framework was tested using the public database from the Multimodal Brain Tumor Segmentation challenge. Results showed increased similarity scores as well as reduced reconstruction errors compared with three existing image inpainting methods. Patient-to-atlas registration also yielded better results with improved normalized cross-correlation and mutual information and a reduced amount of deformation over the tumor regions.

I. INTRODUCTION

MAGNETIC resonance imaging (MRI) has been extensively used to capture an internal organ’s anatomical structures and functional properties [1], [2]. Data composed of large collections of subjects from a population of interest are often involved in modern imaging studies. Since the size and shape of the internal tissue vary from subject to subject [3], [4], to evaluate tissue structure’s similarity and unique features in a comprehensive common space, statistical atlases are constructed from a collection of data from the target population [5], [6], [7], [8], which acts as a summarization of the group statistics. An atlas 1) provides a normalized space in which all subjects from this group are mapped into and compared against and 2) acts as a computational tool to map any future data acquired in a similar condition to enable quantitative evaluation. In brain imaging studies, MRI atlases of the brain have been used to provide label maps for segmentation [9], normalize individual image data [10], and classify different tissue distributions [11].

A common application for MRI in brain imaging is tumor diagnosis [12]. MRI data with tumors can cause a few challenges in atlas construction: 1) tumor growth deforms its neighboring tissue, distorts ventricles, and makes it difficult to seek alignment with registration; 2) mapping a new patient’s tumor image to a previously established atlas space becomes unreliable since the tumor region has no matching structure in a healthy brain regardless of the similarity measure used [13], [14]. However, in practice, datasets composed of only pathological brains are often collected due to resource limitations and scanning costs. When statistical analysis of such data collections is desired, atlas construction using only pathological data becomes necessary.

There have been prior works that tackle patient-to-normal tissue registration [14]. The seeding method [15] was good at handling small tumor cases and was updated to include a tumor growth model [16]. The tumor-induced deformation method was proposed to use image simulation to deal with large tumor cases [17]. Tumor growth simulations have proven to be useful in inducing symmetry in the computations [18], [19]. Recently, Tang et al. [20] proposed a normal tissue-appearance estimation method to inpaint brain tumor regions using a low-rank plus sparse matrix decomposition technique. They summarized all methods that tackle the pathological brain registration problem into three main categories (mask-based methods, pathology simulations, and inpainting) and proposed that inpainting is a better choice to deal with groupwise pathological images.

In this work, we aim to develop an image inpainting method to reconstruct pathological brain MRI into pseudo-normal images. Inpainting reconstructs abnormal structures in defective “holes” of an image, caused by missing information or deterioration, to closely resemble peripheral intensities [21], [22]. When tumor regions in brain MRI are treated as holes, inpainting can be applied to reconstruct the region with synthetic normal tissue, yielding a synthesized normal brain. The new brain can be used in regular atlas construction processes, and the tumor region can be eventually re-applied after image registration and space mapping. We propose a novel learning-based, context-aware inpainting method that contributes to targeting three major difficulties in restoring brain tumor MRI:

• Since images from patient MRI data are either impacted (with tumor or distorted by an adjacent tumor) or minimally affected, the slices that can be used as training data are incomplete within each subject and inconsistent across all subjects.

• Patient MRI data are associated with randomly distributed lesions. Their irregular mask shape causes further inconsistencies, when matching multiple tumor spots [23].

• On a slice, without but adjacent to a tumor, its global structure could be asymmetrically distorted.

The proposed framework is capable of making effective predictions within irregularly-shaped holes with a pixel-wise conditional refinement module trained on both complete and incomplete slices. A symmetry constraint is used to explicitly recreate quasi-symmetry of the human brain for additional structural representation. Classic image registration can then be performed using the inpainted volumes, achieving atlas construction with an all-patient population.

II. RELATED WORK

A. Learning-based Inpainting

Although conventional non-learning inpainting methods are available, they work on the image space and are therefore insensitive to the high-level semantic information in the latent feature space [24], [25]. Recent learning-based methods with generative adversarial networks (GANs) [26] have gained remarkable progress since GAN’s inception in 2014. Pathak et al. [27] proposed an unsupervised visual feature learning algorithm by context encoders to apply the adversarial training on a novel encoder-decoder pipeline for missing region predictions. However, it has limitations in generating fine-detailed textures and filling in large holes. Armanious et al. [28] applied the context encoders [27] to fill in rectangular-shaped holes in the brain. Izuka et al. [29] proposed local and global discriminators to improve inpainting quality. However, they require sophisticated post-processing steps to maintain coherence between inpainted regions and their boundaries. Armanious et al. [30] applied a global-local discriminator [29] to medical image inpainting problems. Yang et al. [31] developed a refinement to [27] by increasing the texture details to make high-resolution predictions, which however greatly increased computational costs. Yu et al. [32] proposed stacked generative networks to improve coherence between inpainted regions and their boundaries. Those methods were trained on rectangular masks and were not generalized for irregularly-shaped holes [33].

B. Inpainting for Irregular Holes

In order to deal with irregular holes, Liu et al. [34] updated the mask in each network layer and re-normalized the convolution weights with the mask value to ensure that partial convolution filters concentrate on valid information from known regions. Wei et al. [35] adopted the work by Liu et al. [34] for liver tumor inpainting and registration. Following this line of research, a number of partial convolution operations have been used for conditional image generation, while demanding more training and test time [36]. Yu et al. [33] proposed to learn the mask automatically with gated convolutions and used the SN-Patch-GAN discriminator to achieve better predictions. However, these methods did not explicitly consider the correlation between valid features, resulting in inconsistencies on the inpainted images [36].

Recent deep attention-based image inpainting methods [37], [32], [25] adopted the patch-based non-learning texture refinement idea to iteratively optimize the texture on the feature-level by matching the closest patches in the latent feature space. Specifically, Song et al. [25] introduced a two-step scheme to produce a rough inference first, followed by a patch-swap step to replace each patch inside the missing regions of a feature map with the most similar patch within the contextual region. The patch-swap operation allows to mine the semantic and contextual information. While the patch-swap operation can potentially be used for filling in irregular holes, the 3×3 patch may not be well suited to deal with irregular shapes. Moreover, these attention-based methods failed to model the correlation between the refined patches inside the hole regions and their neighboring patches. To address this, we propose to use a multi-step approach, by performing a 1×1 patch swap operation in the latent feature space to recover the high-frequency information, following a coarse image-to-image translation inference step.

Based on these ideas, we proposed a preliminary inpainting network structure in [38]. The network was designed for typical image registration tasks and had a few shortcomings in more general inpainting tasks. The network only considers the correlation between the patches in and out of the hole region as in [37], [32], [25]. Since the correlation between the neighboring and the previously refined patches is largely ignored, its inpainted result lacks ductility and continuity in the holes and their boundaries. The network only trains with normal control images, by which bias in patient images data can be induced. In this work, we aim to expand this existing network [38] as a major workhorse for brain atlas construction. Upgrades are made to adapt the method to this task. 1) We include a masking scheme for image and feature level reconstruction loss. 2) The set difference operator is adopted to address real tumors spanning across the middle brain. 3) To further utilize the correlation between the neighboring and previously refined patches, a soft attention scheme is proposed. 4) Both normal and pathological MRI slices are used as training input to efficiently exploit patient features at the training stage and avoid any potential bias between normal and tumor slices. Rather than T1-weighed MRI slices only, the network was also tested on T2-weighted and T1-weighted contrast-enhanced MRI slices. Its effect on atlas construction was thoroughly evaluated as well.

C. Symmetry Assumption of the Human Brain

The normal human brain exhibits a large degree of symmetry with respect to the mid-sagittal plane, though not perfect [39]. Tumors break the symmetric appearance of a healthy brain within and around the legions [40]. We note that although no real-life brain is expected to possess completely symmetric lobes, compared to blind guesses, assuming symmetry using available information from the other hemisphere is a feasible strategy to simulate lost information in the tumor region. Besides, symmetry has been one of the key features sought for in tumor segmentation [40], [41]. In traditional segmentation methods, several works [39], [42], [39], [43] proposed to use symmetry with handcrafted textures or intensity features. Recent works adopted the symmetry map for deep convolutional neural network-based brain tumor segmentation [40], [41]. Although brain symmetry information has been used in segmentation or tumor detection tasks, this constraint has not been explored in inpainting. In this work, in order to better recover tumor regions with normal appearances, a specialized quasi-symmetric prior [44], [45] reflecting brain anatomy is incorporated to achieve better structural understanding.

III. METHODOLOGY

Given an MRI slice $X_0\in {ℝ}^{1\times 240\times 240}$ with tumors, the goal of our framework is to refill the segmented tumor region with synthetic normal brain tissue. We use $R$ to denote the tumor regions (holes) and $\overline{R}$ to denote the remaining regions of normal tissue. The training input is $X_0=\{R\cup \overline{R}\}$. Mathematically, we aim to learn a parametric mapping function $f:X_0\to X$ to generate a complete image $X\in {ℝ}^{1\times 240\times 240}$ with plausible content in R region by exploring the cues in $\overline{R}$. We note that the images are processed in 2D slices, because the structure of the deep network requires the third dimension to be a stack of the image features. Maintaining 3D spatial information with our proposed network structure remains a goal in our future development.

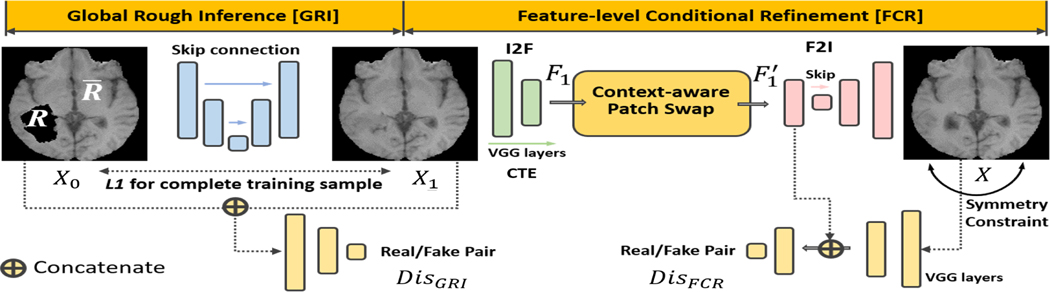
Given that the tumor regions could involve larger holes with irregular shapes, an inpainting method with a simple one-step model, $f\left(X_0\right)\to X$, cannot accurately recover this region. Therefore, in this work, we opt to use a multi-step approach for fine-grained texture rendering. Based on the multi-stage context-based inpainting method of [25], we propose to use a coarse-to-fine network structure to achieve high-quality images. Specifically, we split $f:X_0\to X$ into a global rough inference (GRI) module, $f_{GRI}:X_0\to X_1$, and a feature-level conditional refinement (FCR) module, $f_{FCR}:X_1\to X$, where $X_1\in {ℝ}^{1\times 240\times 240}$ is the preliminary inpainted result of GRI, which will then be post-processed by FCR. We note that both GRI and FCR can be trained on slices with and without tumors with any irregular shapes.

In this work, we only use patient datasets for our image inpainting task for the following reasons. First, in contrast to the image inpainting task used in computer vision and machine learning, training on images with manually segmented holes from healthy controls and testing on images from patients could introduce the problem of domain shift due to the pathology and potential differences in imaging acquisitions [46], [47], [48], [49]. Second, since tumor regions do not usually spread over all brain areas, we have sufficient and redundant normal parts across patient samples from which we can train our network. Therefore, in order to efficiently use patient datasets only and avoid any potential bias in our training, our strategy is to use both tumor and non-tumor regions in our training. The proposed architecture is illustrated in Fig. 1. We detail each module of our framework below.

Fig. 1.

The proposed deep network. Context-aware patch swap propagates boundary high frequencies to fill the hole. The symmetry loss is used to constrain the complete F2I translated image. Of note, the training images include both normal and pathological images with irregular holes.

A. Global Rough Inference

Our global rough inference (GRI) module, $f_{GRI}:X_0\to X_1$, takes an irregularly-holed image as input and predicts a coarse X₁. To concatenate features between every encoder and its corresponding decoder, we adopt the conditional adversarial network for image translation in [50] following the context-based inpainting network in [25]. The network uses skip connections and 4×4 convolutions. The channels of each layer are modified to adapt to only grayscale MRI slices.

The training objectives of image translation-based inpainting [25], [50], [51] consist of an adversarial loss and an L₁ loss between the generated image X₁ and its ground truth X_gt. The unstable training of the adversarial objective is a long-lasting problem [52] and therefore the pairwise ${\mathcal{L}}_1$ constraint has been demonstrated necessary for image translation-based inpainting [50], [25], [51] and general image transfer tasks [53]. However, images with tumors cannot be directly used as the target reference X_gt. To get the complete X_gt, we pick images without any tumors from the datasets and manually make holes as in [25], [50] to construct the paired training data X_gt and X₀. Specifically, we use tumor masks to cover normal MRI slices. In our case, the tumor masks are randomly chosen from the other training subjects.

We configure a general adversarial optimization objective using images with or without irregular tumor regions. GAN-based approaches have shown promising performance for content generation by adaptively aligning the distribution of generated images and real images [26]. It enforces the semantic similarity rather than pixel-wise matching, thereby producing a much richer and sharper texture and more visually accurate content [26] than conventional methods. Following the adversarial training in [25], the adversarial loss of discriminator $D_{{is}_{GRI}}$ can be defined as:

$$\begin{array}{c}{\mathcal{L}}_{adv}={\mathbb{E}}_{X_0,X_N}\left[\log \left(Di{s}_{GRI}\left(X_0,X_N\right)\right)\right]\\ +{\mathbb{E}}_{X_0,X_1}\left[\log \left(1-Di{s}_{GRI}\left(X_0,X_1\right)\right)\right],\end{array}$$ (1)

where X_N is a randomly sampled normal MR image from the training set, which does not need to be the paired ground truth image of X₀. The discriminator $Di{s}_{GRI}:{ℝ}^{2\times 240\times 240}\to [0,1]$ takes the concatenation of two images, and predicts a value with the sigmoid output unit. In contrast, the image-to-image network $f_{GRI}$ is trained in a round based adversarial game with $Di{s}_{GRI}$, and expected to minimize ${\mathcal{L}}_{adv}$. $Di{s}_{GRI}$ takes a pair of images as input as in the adversarial training of [50]. The real pair is the incomplete X₀ and the sampled normal MRI X_N. The fake pair is the incomplete X₀ and the predicted X₁.

With Eq. (1), the discriminator tries to predict $Di{s}_{GRI}\left(X_0,X_N\right)=1$, while $Di{s}_{GRI}\left(X_0,X_1\right)=0$. Therefore, the real image and the generated image should be well separated by $Di{s}_{GRI}$. With the adversarial objective, $f_{GRI}$ tries to confuse $Di{s}_{GRI}$, and progressively learns to generate X₁ similar to the real images.

To exploit both normal and pathological MRI slices in the ${\mathcal{L}}_1$ constraint, we propose to enforce the ${\mathcal{L}}_1$ similarity on these normal training images and the normal parts of patient MRI slices, which can be formulated as

$${\mathcal{L}}_1\left(X_1,\widetilde{X_0}\right)={\Vert N\circ \left(X_1-\widetilde{X_0}\right)\Vert }_1,$$ (2)

where $\widetilde{X_0}$ is the unsegmented X₀, which can be either the normal or original pathological MRI slices without holes. N is a binary mask in our setting. Its element has value 0 for the tumor parts, and value 1 for the normal parts. It yields the loss only on the normal parts of $\widetilde{X_0}$, and for the normal image, N represents the whole image.

Enforcing the identical ${\mathcal{L}}_1$ loss conditioned on the availability of the ground truth normal region also shares similarity with the fixed-point translation learning [54], which applies the additional ${\mathcal{L}}_1$ loss to adversarial training for the cross domain style translation [55], [56], [57], if the ground truth of some translation is available. The fixed-point learning also has been proven to help the network learn a minimal cost transformation [54]. During training, the overall optimization objective of $f_{GRI}$ is to minimize

$${\mathcal{L}}_{GRI}={\lambda }_1{\mathcal{L}}_1+{\lambda }_2{\mathcal{L}}_{adv},$$ (3)

where λ₁ and λ₂ are the balancing hyperparameters. We note that $Di{s}_{GRI}$ is only updated to maximize ${\mathcal{L}}_{adv}$.

B. Feature-level Conditional Refinement

Feature-level conditional refinement (FCR) module $f_{FCR}:X_1\to X$ consists of three components: image-to-feature encoder (I2F), feature-to-image translator (F2I), and context-aware patch swapping (CPS). We detail each step below.

• Image-to-feature encoder (I2F)

First, $X_1\in {ℝ}^{1\times 240\times 240}$ is encoded as $F_1\in {ℝ}^{256\times 60\times 60}$ by a content extractor (CTE). We simply choose the widely used pre-trained VGG19-based fully convolutional network (FCN) as in [25] and modify its first layer convolution channel to one to adapt the grayscale MRI slice X₁. For the CTE, we only use the VGG-network before the third maxpooling layer. Specifically, the utilized layers are 24×conv (64 kernels), maxpooling, 24×conv (128 kernels), maxpooling, and 4×conv (256 kernels). We use zero padding to keep the size of convolutional layers. Maxpooling layer halves the spatial size. Therefore, we have the feature with a size of 256 × 60 × 60.

• Contextual-aware patch swapping (CPS)

The feature-level patch-swap maintains high frequency details in R, while propagating textures from $\overline{R}$ to R. Similar to R and $\overline{R}$ in X₁, we use r and $\overline{r}$ to represent corresponding regions in F₁.

Considering the potential random distribution of tumor locations, the 3×3 rectangular hole generation module used in [25] may not handle the irregular holes. Instead, we follow [37] to explore the 1×1 neural patch.¹ The matching feature patch q_j of each 1×1 feature patch p_i in $\overline{r}$ can be found by

$$d\left(p_i,q_j\right)=\frac{\langle p_i,q_j\rangle }{\Vert p_i\Vert \cdot \Vert q_j\Vert }.$$ (4)

This process is illustrated in Fig. 2(a). After the searching of all 1×1 patches, we follow [25], [37] to replace these p_i by their corresponding q_j directly as shown in Fig. 2(b). Practically, searching for the most similar patch can be sped up by a parallel convolution operation [25], [58]. Every patch is swapped with its similar patch, producing a new feature map $F_1^{\prime }$ in the output.

Fig. 2.

The patch-swap operation. (a) Find the 1×1 boundary patch (most similar) by minimizing d(p_i,q_j). (b) Replace p_i with q_j directly as in [25]. (c) Refine p₁ with its neighboring patches and the most similar patch with an soft attention scheme. (d) Refine p₂ based on the previously refined p₁. We note that this patch-swap operation is carried out in the FCN-based CTE’s feature space.

However, this operation only considers the correlation between r and $\overline{r}$ in the feature map to make the refinement as in [37], [32], [25]. Since the correlation between the neighboring and the previously refined patches are largely ignored, the results may lack ductility and continuity in the holes and their boundaries.

To further explore the correlation between the neighboring and previously refined patches, for each patch p_i, we consider its most similar q_j, and the eight neighboring patches of p_i to achieve the smooth content generation. Toward this goal, we propose a soft attention scheme [59] to aggregate the information based on their cross-correlation metric. We start the refinement process from the top left corner with the zigzag order traversal on r. We then update p_i with:

$$p_i=\frac{d\left(p_i,w_n\right)}{{\sum }_{n=1}^9{l}_n\times d\left(p_i,w_n\right)}\times w_n,$$ (5)

where w_n with $n\in \{1,2,\cdots ,9\}$ indexes the eight neighboring patches, searching for the most similar patch. $l_n\in \{0,1\}$ is a binary mask with value 0 if the neighboring patch, w_n, has not been refined. Otherwise, it has value 1.

The first 1×1 patch on r is denoted by p₁ without the previously refined reference. Fig. 2(c) has three bottom patches, and the right patches of p₁ have not been refined yet. Therefore, the corresponding l_n should be zero. After p₁ has been refined, we start to refine p₂. Here we will also take the refined p₁ into consideration. We note that the most similar patch can also be one of the neighboring patches, and will be calculated twice using Eq. (5) to further emphasize this patch.

• Feature-to-image network (F2I)

A complete image $X\in {ℝ}^{1\times 240\times 240}$ is finally learned by the F2I network. It uses a generator with a U-Net structure, where six of its deconvolution layers are skip-connected with its convolution layers. $Di{s}_{FCR}$ is a patch-GAN discriminator. In practice, our underlying framework is based on [25], and we adapt it to use patient MRI slices for training. Unlike the GRI network which inputs a pair of images, the input to $Di{s}_{FCR}$ is an image and its corresponding feature map.

Specifically, a randomly sampled normal and complete MR image X_N or the generated X, and $F_1^{\prime }=\text{patch\_swap}\left(F_1\right)$ are the input to $Di{s}_{FCR}$. To concatenate $F_1^{\prime }\in {ℝ}^{256\times 60\times 60}$ with an image, we also use the same modified VGG-based CTE network in I2F to encode X_N or X as CTE(X_N) or CTE(X), respectively. The to be maximized adversarial loss of the discriminator $Di{s}_{FCR}$ can be expressed as

$$\begin{array}{c}{\mathcal{L}}_{adv}={\mathbb{E}}_{X_N}[\text{log}\left(Di{s}_{FCR}\left(F_1^{\prime },\text{CTE}\left(X_N\right)\right)\right]\\ +{\mathbb{E}}_X[\text{log}\left(1-Di{s}_{FCR}\left(F_1^{\prime },\text{CTE}(X)\right)\right].\end{array}$$ (6)

The real pair are $\left(F_1^{\prime },CTE\left(X_N\right)\right)$ and the fake pair are $\left(F_1^{\prime },CTE(X)\right)$, respectively. Of note, the output unit of $Di{s}_{FCR}$ is also the sigmoid unit, which predicts the value from zero to one.

The second loss is perceptual of the entire image:

$${\mathcal{L}}_{perceptual}\left(X,\widetilde{X_0}\right)={\Vert M\circ \left[CTE(X)-CTE\left(\widetilde{X_0}\right)\right]\Vert }_2,$$ (7)

where $\circ$ is the Hadamard product, and M is the weighted mask, yielding the loss only on the feature map of the normal region of ${\tilde{X}}_0$. For the normal MR image, M is the whole feature map. ${\tilde{X}}_0$ is the unsegmented X₀, which can be either normal or pathological complete MRI.

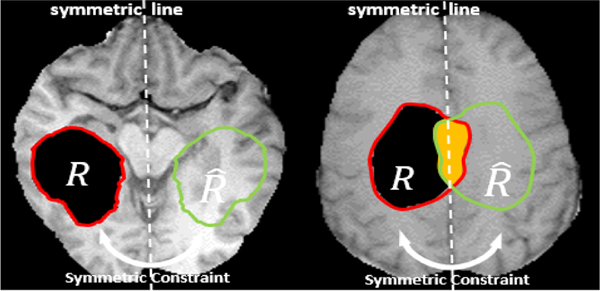
C. Symmetry Constraint

As discussed before, the quasi-symmetry property is an inherent feature of the human brain [44], [45]. Realizing this anatomical feature during image synthesis could greatly improve image quality if incorporated correctly, since image inpainting is inherently ill-posed. We denote the hole as R, while using $\widehat{R}$ to denote its corresponding region mirrored with respect to the mid-sagittal plane. If the ground truth of $\widehat{R}$ is available in training, we can simply enforce the ${\mathcal{L}}_1$ similarity measure between R and $\widehat{R}$ in the feature space. However, if the tumor region is located around the mid-line, an intersected zone appears as in Fig. 3 right. To address this, we use the Boolean operation to not calculate the loss for this region. The symmetry loss of an MR image in its feature map is given by

$$\begin{array}{c}{\mathcal{L}}_{sym}(X)=\mathbb{E}{\Vert \text{CTE}\left(X_{\{R-R\cap \widehat{R}\}}\right)-\text{CTE}\left(X_{\{\widehat{R}-R\cap \widehat{R}\}}\right)\Vert }_2\\ =\mathbb{E}{\Vert \text{CTE}\left(X_{\{R-\widehat{R}\}}\right)-\text{CTE}\left(X_{\{\widehat{R}-R\}}\right)\Vert }_2,\end{array}$$ (8)

where the minus sign between sets denotes the set difference operation². Since $X_{\{R-\widehat{R}\}}$ does not have the ground truth in either R or $\widehat{R}$, the symmetry loss is not applied to this area.

Fig. 3.

The symmetry constraint: when using patient MRI slices in training, we have the ground truth of the orange region $X_{\{R-\widehat{R}\}}$.

There are a few advantages by using a deep network following the new symmetry constraint. 1) With maxpooling’s inherent downsampling step, the networks are in general robust facing a small amount of brain rotation [60]. The feature space has a 60×60 resolution, and the original image has a 240×240 resolution. 2) The deep network automatically simulates the missing parts in the tumor hole by finding their corresponding normal tissue structures from the mirrored hemisphere.

Finally, the total network loss after incorporating the symmetry constraint is defined as

$${\mathcal{L}}_{F2I}={\lambda }_3{\mathcal{L}}_{perceptual}+{\lambda }_4{\mathcal{L}}_{adv}+{\lambda }_5{\mathcal{L}}_{sym},$$ (9)

where λ₃, λ₄, and λ₅ are weighting hyperparameters.

IV. EXPERIMENTAL RESULTS

A. MRI Data Acquisition

The proposed framework was evaluated using the 2018 Multimodal Brain Tumor Segmentation (BraTS) database³ [61]. The database consists of ∼210 routine clinical 3T multimodal MRI scans of glioblastoma and lower grade glioma with pathologically confirmed diagnosis. The tumor locations were manually identified by expert neuroradiologists as ground truth. Fifteen patients were randomly selected at the testing stage. The other fifteen subjects were used for hyperparameter validation. The training group comprised all remaining 180 subjects. Each dataset has around 150 MRI slices. We used T1-weighted, T2-weighted, and T1-weighted contrast-enhanced (T1ce) MRI with gadolinium contrast agent in this work. The inpainting framework of these three modalities was trained and tested independently. The training masks were randomly selected with irregular tumor shapes from the provided labels.

B. Implementation Details

Our framework was implemented using the PyTorch deep learning toolbox [62]. Training was performed on four NVIDIA TITAN Xp GPUs, which took about 15 hours. We trained all of the networks for 100 epochs consistently. The batch size was set to 16 for each GPU in our implementation. With each loss, we set its unique weight using grid searching on the validation set. We used grid searching to select proper combinations of hyperparameters. For GRI training, we set λ₁ = 1 and λ₂ = 1. We used Adam optimizer here. The learning rate were $l{r}_{GRI}=1\text{e}-3$ and $l{r}_{Di{s}_{GRI}}=1\text{e}-4$ with a momentum of 0.5. For F2I training, we set λ₃ = 3, λ₄ = 3, and λ₅ = 1. Here we used $l{r}_{F2I}=2\text{e}-4$ and $l{r}_{Di{s}_{FCR}}=2\text{e}-4$ with a momentum of 0.5. The time it took to process each feature map was about 0.1 second. 180 subjects were used in training. Around 20–30 almost blank slices of each subject in the top or bottom were removed. The training set has 21,268 slices, which is sufficient for our training for which no data augmentation was used. We note that increasing training epochs linearly increases training time, thus we do not gain significant improvements with more epochs.

C. MRI Inpainting and Comparisons

The inpainting results using our framework from three subjects are shown in Fig. 4. The proposed network successfully recovered the holes in that the filled regions were semantically consistent with the non-tumor region with smooth translation as visually assessed. In addition, our framework performed equally well on T1-weighted, T2-weighted, and T1ce MRI.

Fig. 4.

Illustration of inpainting results of a few sampled MRI slices with different modalities from three patients.

For quantitative evaluation, since there is no ground truth, we manually dug circular holes on normal-labeled regions with random radius (size) and center (position) throughout the brains of all test subjects. The proposed framework generated visually reasonable results as shown in Fig. 5. Tables I, II, and III list performances of different networks: the proposed framework, GLC [51], Patch-match [63], and Partial Convolution [34] for T1-weighted, T2-weighted, and T1ce MRI. For a fair comparison, we chose the same backbone network with the same sets of training data for these compared methods. The comparison results using tumor masks are shown in Fig. 6. Our framework outperformed the other three comparison methods as both qualitatively and quantitatively assessed.

Fig. 5.

Illustration of inpainting results in comparison to the ground truth.

TABLE I.

Comparison of four methods on T1 test data.

Methods	mean L1 error ↓	SSIM ↑	PSNR ↑	Inception Score ↑
Patch-match [63]	445.8	0.9460	29.55	9.13
GLC [51]	432.6	0.9506	30.34	9.68
Partial Conv [34]	373.2	0.9512	33.57	9.77
Proposed [38]	254.8	0.9682	34.52	10.58
Proposed	211.7	0.9823	35.85	11.74
Proposed-IC	244.7	0.9707	34.72	10.95
Proposed-NB	227.4	0.9772	35.16	11.28
Proposed-sym	232.5	0.9765	35.24	11.26

↑: larger value = higher similarity. ↓: smaller value = higher similarity.

TABLE II.

Comparison of four methods on T1ce test data.

Methods	mean L1 error ↓	SSIM ↑	PSNR ↑	Inception Score ↑
Patch-match [63]	375.4	0.9275	27.54	9.06
GLC [51]	352.8	0.9343	28.31	9.74
Partial Conv [34]	326.6	0.9345	28.86	9.81
Proposed	263.7	0.9595	31.06	10.67
Proposed-IC	304.7	0.9502	30.35	10.05
Proposed-NB	287.4	0.9537	30.64	10.16
Proposed-sym	292.5	0.9542	30.57	10.18

↑: larger value = higher similarity. ↓: smaller value = higher similarity.

TABLE III.

Comparison of four methods on T2 test data.

Methods	mean L1 error ↓	SSIM ↑	PSNR ↑	Inception Score ↑
Patch-match [63]	395.6	0.9360	28.55	9.56
GLC [51]	354.8	0.9304	29.34	10.13
Partial Conv [34]	339.4	0.9425	30.57	10.31
Proposed	254.3	0.9573	31.82	11.58
Proposed-IC	297.5	0.9512	30.94	10.94
Proposed-NB	273.8	0.9547	31.15	11.25
Proposed-sym	284.1	0.9549	31.21	11.06

↑: larger value = higher similarity. ↓: smaller value = higher similarity.

Fig. 6.

Illustration of comparison of different inpainting methods including partial Conv, GLS, and PatchMatch.

D. Ablation Study

To demonstrate the necessity of multi-step inpainting for our inpainting task, we displayed the intermediate result of GRI and the final result of FCR in Fig. 7. Our GRI module was used as an initialization for FCR with a single global discriminator, which can be regarded as a simplified GLC. Our GRI model was efficient at generating the result with coarse details. FCR further corrected the artifacts by aggregating the cues around the target tumor regions. Especially, the compared baseline works [51], [34] based on a 1-step structure were inferior to our framework as shown in Fig. 6.

Fig. 7.

Illustration of comparison of GRI and GRI+FCR. Note that the FCR step yielded vivid and visually reasonable results compared with GRI only as visually assessed.

Another ablation study was also performed to test symmetry loss, neighboring refinement, and incomplete data training. We used the suffix “w/o sym”, “w/o NB”, and “w/o IC” to denote the proposed framework without the symmetry loss (sym), the neighboring (NB) refinement, and incomplete (IC) data training, respectively. Four measurements were tested to reflect the performance: mean L1 error, peak signal-to-noise ratio (PSNR), structural similarity index (SSIM), and inception score [64]. Specifically, PSNR shows the ratio between the maximum signal power and noise power that affects the fidelity of its representation. SSIM measures the similarity between two images, predicting the perceived quality of the image with respect to an initial distortion-free reference image. Inception score measures both the variety and the distinguishability of a group of output images, and is widely used for judging how realistic the image outputs from GANs are. All these metrics reflect the performance of our tested networks from various aspects. Tables I, II, and III show our framework outperformed the three comparison methods by a large margin.

First, we show the effect of the symmetry loss in Fig. 8. Without the symmetry loss, the filled hole regions presented distorted structure, which was caused by training instability and the lack of image semantic understanding. However, the proposed symmetry constraint improved the quality with marginal training cost but without additional test cost.

Fig. 8.

Illustration of the ablation study on the use of the symmetry constraint (sym), neighboring (NB) refinement, and incomplete (IC) data training.

Second, in FCR, we proposed to make the patch refinement based on the available neighboring patches instead of only searching for the most similar one as in [25]. Although the patch swap in [25] improved the performance compared with conventional 1-step inpainting schemes, without the neighborhood refinement, the inpainting results still lacked fine texture details and were not consistent with the surrounding region (see Fig. 8 w/o NB). With our framework using the neighborhood refinement, the continuity was better preserved.

Third, we used only the normal MRI slices without tumors for our training and simply discarded slices with tumors. Therefore, we obtained the ground truth for the symmetry loss. Therefore, Eq. (8) can be simplified as ${\mathcal{L}}_{sym}(X)=\mathbb{E}{\Vert \text{CTE}\left(X_{\left\{R\right\}}\right)-\text{CTE}\left(X_{\left\{\widehat{R}\right\}}\right)\Vert }_2$. However, since the database used in this work included slices with tumors mostly distributed in the center region rather than top or bottom regions, the relatively small number of normal slices made it difficult to train the network reliably, leading to unsatisfactory inpainting results (see Fig. 8 w/o IC). In comparison to these baselines, our model was able to handle these challenges effectively, generating satisfactory results.

In our implementation, the same proportion (1:1) of normal and pathological MRI slices are used as training input to efficiently exploit patient features in training. In Table IV, we provide the comparison of using different proportion of normal and pathological MR slices. Using too many normal slices (i.e., 2:1) leads to a small performance drop presumably related to bias to the normal tissue. Setting the normal and pathological proportion to 1:2 leads to larger performance drop. Since training highly relies on the L1 loss, which needs the normal tissue as ground truth. The normal parts in the pathological MRI slices can be relatively limited.

TABLE IV.

Comparison of different proportion of normal and pathological MRI slices on T1, T1ce, and T2 test data.

Proportion	mean L1 error ↓	SSIM ↑	PSNR ↑	Inception Score ↑
1:1	243.2	0.9664	32.91	11.33
2:1	241.5	0.9584	31.32	10.97
1:2	237.3	0.9630	32.17	11.08

↑: larger value = higher similarity. ↓: smaller value = higher similarity.

E. Atlas Construction and Registration Evaluation

After inpainting of all the fifteen test datasets, to construct structural atlases from each modality including T1- weighted, T2-weighted, and T1ce MRI, we applied the Advanced Normalization Tools (ANTs) for registration between datasets [65]. In preprocessing we performed an N4 bias correction to fix low frequency intensities and non-uniformity in the patient images [66]. For atlas construction, an initial template was first created by averaging all input data. Then, a coarse atlas from only rigid transformations was created, which was used to initialize the symmetric and diffeomorphic atlas formation. We used cross-correlation as similarity measure throughout the whole atlas formation process.

The first column of Fig. 9 shows a few sample slices from resulting atlases of the three modalities (T1-weighted, T1ce, and T2-weighted MRI) created from the fifteen test patient subjects after inpainting. Visual assessment through all slices showed crisp and clear brain structures without any tumor presence. We used the symmetric and diffeomorphic transformation with cross-correlation as similarity metric [65]. For quantitative atlas evaluation, we compared patient-to-atlas registration quality between direct patient image registration and inpainted registration. Fig. 9 column 2 shows sample slices from six randomly selected patients of corresponding modalities, and their corresponding inpainting results are shown in column 3. Both the original volumes (column 2) and the inpainted volumes (column 3) were registered in 3D volumes to the atlas (column 1), and the results are shown in the fourth and fifth columns of Fig. 9, respectively. To clarify registration details, since we would rather avoid spatially aligning tumor images to non-tumor images, the tumor region was inpainted first and then registered to the healthy atlas tissue. After registration, since we already had the deformation fields, we used them to warp the original tumor images to the atlas space as if they appeared directly registered, thus improving the alignment process over direct patient-to-atlas registration. The ANTs registration we used was based on diffeomorphic demons and the average Jacobian of all deformation fields from all registrations was 1.00 ± 0.02.

Fig. 9.

Registration results from six sample subjects in the atlas space using three modalities. Registered images with and without inpainting are shown in columns four and five. Tumor regions are marked in red boxes.

To compare the quality of these two groups of results,we computed both normalized cross correlation (NCC) and mutual information (MI) for the similarity measures between the registration results and their corresponding atlas. Since one group used volumes with tumors for similarity computation, it was expected to yield lower similarity scores compared to the inpainted group without tumors, nullifying the purpose of this experiment. To achieve a fair comparison, for direct patientto-atlas registration, we used the tumor masks provided by the BraTS datasets to cut off the tumor regions after registration and computed similarities only in the remaining normal tissue regions. These similarities scores were then used to compare against the scores from the inpainted group with full normal tissues. Fig. 10 shows the boxplots over all fifteen warped subjects of their NCC and MI to the atlas on three modalities, where the left box shows the similarity using direct patient registration, and the right box shows the similarity using inpainted volume registration. The mean of these metrics are shown as cross marks and the median as middle bars.

Fig. 10.

Similarity evaluation between the atlas and volumes from fifteen subject registered to the atlas. Both NCC and MI are shown on all three modalities using either direct registration or registration after inpainting. The middle bar marks the median and the cross marks the mean in the boxplots.

The mean of NCC and MI in all six scenarios (three modalities with two registration groups) are shown in Table V. Besides NCC and MI, we also computed the average magnitude of the final deformation fields estimated in the registration process. The magnitude of deformation (MoD) is a quantity in mm that measures the general extent of deformation that is required to match the patient to the atlas. A smaller value means that less deformation is needed to align the corresponding tissues. All three measures yielded lower deformation scores and higher similarities of inpainting registration, indicating an improved matching quality over direct patient registration. To show statistical significance, we performed a one-tailed paired t-test for each of the NCC, MI, and MoD metrics comparing improvements over direct registration with inpainted registration, yielding p-values of 2.09 × 10⁻⁶, 1.85 × 10⁻⁸, and 0.014, respectively.

TABLE V.

Normalized cross-correlation (NCC), mutual information (MI), and magnitude of deformation (MoD, in mm) between the atlas and fifteen registered subjects.

Measures	T1	T1ce	T2
NCC Direct Patient Reg	0.961	0.932	0.905
NCC Inpainted Reg ↑	0.968	0.946	0.914
MI Direct Patient Reg	0.511	0.476	0.493
MI Inpainted Reg ↑	0.520	0.484	0.503
MoD Direct Patient Reg	5.296	5.379	5.803
MoD Inpainted Reg ↓	5.135	5.182	5.116

↑: larger value = higher similarity. ↓: smaller value = higher similarity.

V. DISCUSSION

We presented a context-aware, two-step inpainting framework to fill in tumor regions in the human brain and compared it against the other widely used inpainting methods, e.g., Patch-match [63], GLC [51], and Partial Conv [34]. To the best of our knowledge, this is the first attempt at achieving the irregular hole inpainting with both complete—MRI slices without any tumors—and incomplete—MRI slices with tumors—datasets. The correlation between patches in the hole regions and their neighboring patches was further examined using the conventional attention-based inpainting methods [25], [37] to achieve sharp and vivid content generation. To accurately reflect brain anatomy, we introduced a quasi-symmetry constraint due to a degree of anatomical symmetry.

Because of diffuse infiltration of glioma cells into normal brain tissue, the shape of tumors is highly irregular in all brain areas when imaged with structural MRI including T1-weighted, T2-weighted, or T1ce. While many conventional deep learning-based inpainting methods [27], [31] attempted to fill in large rectangular masks, they cannot be easily generalized on irregularly-shaped holes. Thus we revisited the non-learning patch match method [63] as well as the recent translation-based method [51], partial convolution-based method [34], and attention-based method [25]. Based on previous approaches and our prior work [25], we adapted its patch-swap to 1×1 patch in the feature space to address irregular holes and further explored the correlation between the patches in the hole regions and their neighboring patches.

Our proposed framework demonstrated superior performance over the other compared methods as qualitatively and quantitatively assessed as shown in Fig. 6 and Tables I, II, and III. For the evaluations on T1-weighted, T1ce, and T2-weighted testing samples, we adopt the one-tailed paired ttest, the p-value between our method and partial conv is 0.0497. There are a few key differences that provide important insights into their relative performances. First, patch-match [63] is the classical non-learning inpainting method, which makes the patch swap based on the low-level features. Its predictions, therefore, were to some extent blurry and detail-missing when applied to brain MRI data. In contrast, our patch swap was implemented in the latent feature space which inherits the high-level semantic information. Second, GLC [51] applies both the global and local discriminator to enhance the generation quality, which is also the backbone of [30]. However, the combination of multiple discriminators was challenging, and the results showed distorted structure and confusing texture when applied to brain MRI data. Third, partial Conv [34] uses the partial convolution operation. Partial Conv produced smooth and plausible results, but the continuity did not hold well and some artifacts were still observed on generated MRI slices. Because these methods do not consider the correlations between the deep features in the hole regions.

In addition to the two-stage inpainting framework, we tailored several approaches for our brain tumor inpainting task (i.e., symmetry constraint, neighboring conditioned refinement, and incomplete data training) with detailed ablation study in Fig. 8. First, the symmetry constraint was adopted to improve the inpainting quality with minimal cost. While prior knowledge has been investigated for tumor segmentation [40], [41], we introduced this prior knowledge for the inpainting task and demonstrated its effectiveness for the first time. Second, due to the difficulty in generating satisfactory results with the limited number of normal images and biased tumor distributions, we proposed to efficiently explore the incomplete training data. Without the need for additional training data from an external database, we were able to achieve visually reasonable inpainting results. We only enforced the identical ${\mathcal{L}}_1$ loss conditioned on the availability of the ground truth normal region, sharing similarity with the fixed-point translation learning [54]. This has been proven helpful for the network to learn a minimal cost transformation [54]. The qualitative results were further evidenced by the quantitative evaluations (see Tables I, II, and III). Third, the patch refinement based on the available neighboring patches was proposed in FCR. Patch swap has shown improved inpainting performance over the conventional 1-step inpainting approaches [25]. However, the results of the conventional approaches lacked fine texture details and were not consistent with the normal tissues around tumor. As shown in Fig. 8, the better continuity illustrates the fact that the global semantic structure and local coherency were well balanced by the proposed FRI module.

Although our decision to incorporate a symmetry constraint has been quantitatively demonstrated effective, we clarify that our fundamental purpose is not to simulate a real-life anatomically perfect human brain. In fact, in medical image analysis, assuming symmetry has been a frequently discussed topic. Especially in tumor inpainting, trying to recover lost information from a “hole” in an image is essentially an illposed problem since the healthy tissue information is in fact nonexistent. Naturally, obtaining extra information from prior knowledge such as an image atlas is deemed a better solution. However, our data setup requires us to look for such an atlas to provide prior knowledge in the first place. As a result, rather than using no information, a more improved solution is to obtain this extra information from the mirrored hemisphere. We point out that human organs such as the brain are not strictly anatomically symmetric [67], so the symmetry constraint is aimed for the construction of a statistical image atlas, which is often used as a tool for the followed image registration and spatial alignment operations on a population of interest. Any synthetic inpainted brain image should not be used for the purpose of disease diagnosis or clinical treatment. The ablation studies in Tables I, II, and III have demonstrated mathematical quality improvements with the symmetry constraint. Statistically, the combination of fifteen subjects after groupwise registration inherently helps in eliminating any inconsistency in the atlas from the varying tumor locations.

From a registration point of view, we constructed a fine quality atlas using only pathological MRI data and achieved better patient-to-atlas registration results. Fig. 9 showed that although the atlases were created using inpainted brain tumor volumes, the influence of the tumor regions was minimal and the brain structures were complete, symmetrical, and intact. Visually, despite having tumor regions, the result of direct patient registration also seemed to have good quality. However, quantitative analysis showed that results were further improved by a better registration with higher similarity using inpainted volumes. The boxplots in Fig. 10 showed that every subject group on all three modalities had both increased NCC and MI values using inpainted registration over direct patient registration, and both the mean and median were increased in all six comparing scenarios. Note that MI measures the joint entropy between two images using the statistical distribution of their intensity histograms and their joint histogram, while NCC measures similarity by computing the covariance between two image intensities. MI and NCC are two independent metrics in different ranges not comparable to each other. Therefore, the registered results were more similar to the atlas on all normal tissues after the restoration resulting from our inpainting. This confirms that 1) the existence of tumors impedes the computation in the registration process and reduces similarity even in the normal tissue regions and 2) the proposed method is able to simulate normal tissues to a satisfying extent that the pseudo-normal region helps in matching the inpainted image with the atlas. The increased mean values on all the six similarity measures in Table V further confirmed this observation. Besides NCC and MI, the average magnitude of the deformation field, MoD, was decreased in all three modalities. A greater extent of deformation was needed to directly align a patient image to the atlas and fix the distortions caused by the tumors even in its nearby normal tissue, while less deformation was needed to align the corresponding tissue after inpainting now that the tumors were replaced.

There are several aspects not fully explored. First, we proposed to exploit the information from the surrounding contextual area, but did not take the correlation between neighboring MRI slices into consideration. Second, the proposed symmetry constraint works well when the mid-sagittal brain is roughly centered. Enforcing symmetry for largely misaligned datasets may mislead the learning process. Third, the choice of weights λ to balance the different loss functions could influence the inpainting performance. While our experiments showed that results were not sensitive to these weights, they needed to be carefully tuned to optimize our objectives. Fourth, modeling the approach to deal with 2D slices limits the demonstration of this network setup’s full potential, and we presume that utilizing a neighboring slice’s depth information in the third dimension could help recover more lost structure information. Exploring additional network structures such as a 3D U-Net to reconstruct the 3D aspects of the human brain is an important direction for our future work.

VI. CONCLUSION

We presented a deep network-based image inpainting framework that replaces tumor regions with synthetic normal tissues. Our framework excels at tackling incomplete training datasets, irregularly-shaped tumor regions, and asymmetric hemisphere restoration. Experimental results demonstrated reduced error as well as increased image quality and structural similarity when compared with the three widely used image inpainting methods. Brain atlases on three modalities were successfully constructed with good quality. Patient-to-atlas registration also yielded better results with improved NCC and MI, and reduced tissue distortion near the tumor region.