Stage Shift as an Endpoint in Cancer Screening Trials: Implications for Evaluating Multi-Cancer Early Detection Tests

Abstract

Background:

Disease-specific mortality is a consensus endpoint in cancer screening trials. New liquid biopsy-based screening tests, including multi-cancer early detection (MCED) tests, are creating a need to reduce the typically lengthy screening trial process. Endpoints based on the reduction in late-stage disease (stage shift) have been proposed but it is unclear how well they predict the impact of screening on disease-specific mortality across a variety of cancers potentially detectable by MCED tests.

Methods:

We develop a mathematical formulation relating the reduction in late-stage cancer to the expected reduction in disease-specific mortality if cases diagnosed early via screening receive a corresponding shift in mortality. We investigate the similarity between the expected mortality reduction and the observed mortality reduction in published trials of screening for breast, lung, ovarian, and prostate cancer.

Results:

The expected mortality reduction for a given stage shift varies significantly depending on cancer- and stage-specific survival distributions, with some cancer types showing little possibility for mortality improvement even under substantial stage shift. The expected mortality reduction fails to consistently match the mortality outcomes of published trials.

Conclusions:

In MCED, any mortality benefit is likely to vary substantially across target cancers. Stage shift does not appear to be a reliable basis for inference about mortality reduction across cancers potentially detectable by MCED tests.

Impact:

Stage shift may be an appealing endpoint for evaluation of cancer screening tests but it appears to be an unreliable predictor of mortality benefit; further, the same stage shift can mean different things for different cancers.

Introduction

A fundamental intuition drives cancer early detection research: that advancing the diagnosis of tumors that would otherwise be detected at late stage will extend disease-specific life expectancy. A stage-shift model of screening benefit predicts the change in disease-specific mortality based on the shift in stage at diagnosis and the survival of early-stage cases in the absence of screening. This model is established in the literature on cancer early detection. Connor et al [1] postulated a stage-shift model in their analysis of incidence and mortality patterns from one of the earliest screening trials, the Health Insurance Plan breast screening trial. Wever et al [2] hypothesized a stage-shift model as an explanation for the results of another large trial, the European Randomized Study of Screening for Prostate Cancer (ERSPC).

A primary application of the stage-shift model is to project the mortality benefit of screening programs with a specific downstaging profile in the absence of screening trial results. Feuer et al [3] used a stage-shift model to translate the observed decline in distant-stage prostate cancer under PSA screening into a projection of mortality reduction. Koopman et al [4] used a stage-shift model in their analysis of the factors likely to influence effectiveness of pancreatic cancer screening. And Clarke et al [5] used a stage-shift model to suggest that if new multi-cancer early detection (MCED) tests shifted stage IV diagnoses evenly across stages I to III, this could lead to a 24% reduction in cancer-related deaths.

Advances in liquid biopsy technology are generating a growing number of early detection tools for cancer, including MCED tests which offer to detect multiple cancers with a single blood draw ([6], [7], [8], [9]). It is likely that some of these tests will become available before they can be rigorously evaluated via the usually lengthy trial process. This creates a need for more expeditious ways to generate evidence regarding screening benefit. Endpoints based on disease incidence and disease features at diagnosis are more proximal than mortality and offer the potential for much timelier evaluation.

Endpoints based on stage shift have been proposed as surrogate endpoints in a number of cancer screening trials. The National Bowel Cancer Screening Program in South Australia reported stage shift as a surrogate for colorectal cancer mortality [10]. Putcha and colleagues [11] suggested stage shift as a surrogate endpoint in MCED trials. Cuzik et al [12] proposed using the projected mortality based on stage shift in the UK Flexible Sigmoidoscopy Screening Trial.

While the criteria for an endpoint to be a valid surrogate in treatment trials are well established [13], what constitutes a surrogate endpoint in screening trials is not as well defined. However, a key requirement for a surrogate endpoint in general is that it should be predictive of the effect of the intervention on the outcome of interest.

In this article, we investigate the validity and implications of the stage-shift model in principle and in practice. We first develop a theoretical formulation for the relationship between the stage shift and the expected reduction in disease-specific mortality. We use this formulation to predict the mortality reduction in hypothetical screening trials for multiple cancers, examining how the predicted mortality reduction for a given stage shift varies across cancers. We then investigate whether the stage-shift model holds in practice by examining results from published screening trials for breast, lung, ovarian, and prostate cancer. We use our findings to derive some general conclusions about the likely impact of multi-cancer screening tests on disease-specific mortality and the validity of stage shift as a predictor of screening benefit.

Methods

General model

We begin with a general model for cancer-specific mortality in the absence of screening. For a given population without a diagnosis of the cancer of interest, suppose the time from the start of a study until clinical diagnosis is a random variable with density function f, and suppose the time to disease-specific death following diagnosis is a random variable with cumulative distribution function G. Then at time t = T, the cumulative probability of cancer mortality in the absence of other causes is given by

$$M\left(T\right)={\int }_0^{T}f\left(t\right)G\left(T-t\right)\text{d}t$$ (1)

reflecting that for a person to die by time T, they must have become diagnosed at time t before T and had a survival less than T−t.

We partition cancers by stage at diagnosis into K stages. Here we focus on the case where K = 2, representing early- and late-stage disease, but this general formulation can be applied to any number of stages. Let p_k be the probability that the cancer is at stage k at the time of diagnosis (in the case where K = 2, k = 0 represents early stage and K = 1 represents late stage) and let G_k(t) be the post-diagnosis cumulative mortality for stage k at time t from diagnosis. Then equation (1) can be expanded into:

$$M\left(T\right)={\int }_0^{T}f\left(t\right)\left({\sum }_k{p}_k{G}_k\left(T-t\right)\right)\text{d}t=\sum _k{p}_k{\int }_0^{T}f\left(t\right)G_k\left(T-t\right)\text{d}t=p\cdot r$$ (2)

where p is the vector of the probabilities p_k and the components of the vector r are defined as

$$r_k\left(T\right)={\int }_0^{T}f\left(t\right)G_k\left(T-t\right)\text{d}t$$ (3)

The quantities r_k(t) represent the cumulative mortality at time T if all cases of the disease were stage k. In the case where K = 2, equation (2) reduces to M(T) = r₀(T)p₀ + r₁(T)p₁. In the rest of this section for notational simplicity we write r₀ and r₁ for r₀(T) and r₁(T).

Now, suppose that for the same population, a screening program results in a reduction in late-stage disease at diagnosis. We model only cases that would have been diagnosed without screening, i.e., excluding overdiagnosed cases. Given the relative reduction in late- stage incidence, we move that fraction of late-stage cases to be diagnosed in early stage. The stage-shift model specifies that cases shifted earlier have their disease-specific life-expectancy altered to that of an early-stage diagnosis, thus, we take the survival origin for stage-shifted cases to be their original time of clinical diagnosis. Given these specifications, we can write the new distribution of early- and late-stage diagnoses as Sp, where S is a transition matrix representing the shift in the proportions of (non-overdiagnosed) cases diagnosed in late- versus early-stage. In the two-stage setting, if p₁ is the probability that the disease is late stage in the absence of screening and α the fraction of late-stage cases shifted to early-stage by screening, we have:

$$S=\left[\begin{array}{cc}1& \alpha \\ 0& 1-\alpha \end{array}\right],\hspace{1em}p=\left[\begin{array}{c}1-p_1\\ p_1\end{array}\right]$$ (4)

The implied absolute reduction in the cumulative disease-specific mortality at time T is then:

$$M^{\text{abs}}=p\cdot r-Sp\cdot r=\left(I-S\right)p\cdot r$$ (5)

and the relative reduction is:

$$M^{\text{rel}}=\frac{M^{\text{abs}}}{M}=1-\frac{\left(Sp\right)\cdot r}{p\cdot r}$$ (6)

In the two-stage setting, this reduces to:

$$M^{\text{rel}}=\frac{p_1\left(r_1-r_0\right)}{\left(1-p_1\right)r_0+p_1{r}_1}\alpha$$ (7)

Thus, a specified change in the incidence of late-stage diagnosis induces a relative change in cumulative mortality that can be written in terms of the mortality curves that would be expected if all cases were early- or late-stage at diagnosis. In the two-stage setting the mortality reduction is linear in the reduction in late-stage cases α. We define ρ, or the “stage-shift multiplier”, to be the multiplier that converts the reduction in late-stage disease to the reduction in disease-specific cumulative mortality, i.e.,

$$\rho =\frac{p_1\left(r_1-r_0\right)}{\left(1-p_1\right)r_0+p_1{r}_1}.$$

It is apparent that the quantity ρ is less than or equal to 1, with equality only in the case where r₀ = 0. In other words, the relative reduction in disease-specific mortality, M^rel, is always more modest than the reduction in late-stage incidence α and is only equal to the reduction in late-state incidence if all cases detected in early stage are cured of disease.

Modeling under exponentially distributed event times

An expression for the improvement in disease-specific mortality given a screening-induced stage shift can be derived in closed form under exponentially distributed failure times. Let λ_d be the hazard of disease incidence and let λ_k be the hazard of disease-specific death following clinical diagnosis in stage k. Then for each k, equation (3) evaluates to

$$r_k=1-\frac{{\lambda }_k{e}^{-{\lambda }_{d}T}-{\lambda }_d{e}^{-{\lambda }_{k}T}}{{\lambda }_k-{\lambda }_d}$$ (8)

This expression for r_k can be substituted into expression (7) to yield a formula for M^rel that depends on p₁ and the hazards of disease incidence and survival by stage in the absence of screening. Thus, for example, two cancers may have similar stage distributions in the absence of screening, and similar reductions in late-stage incidence under screening, but if their early-stage survival differs, then the expected mortality reductions induced by a given stage shift will not be the same.

Modeling hypothetical trials using registry data

We implement expression (7) for a selection of cancers based on parameters estimated from registry data over a 10-year hypothetical screening period. We sourced inputs for disease incidence and stage from the Surveillance, Epidemiology, and End Results (SEER) registry (November 2020 submission, [14]) for diagnosis years 2000 – 2009. Our calculations focused on the 50–54 age group; we also examined ages 60–64 and 70–74 and found that key results did not vary significantly. We considered bladder, lung, pancreatic, liver, ovarian, and stomach cancer, and lymphoma. Breast, colorectal, and prostate cancer were not considered due to the widespread use of screening during this time period.

For each cancer, we estimated the overall incidence parameter λ_d by averaging the annual incidence for the 50–54 and 55–59 age groups in order to account for the average risk over the 10-year hypothetical trial period. Late-stage cancers were defined as SEER historic stage distant, while early-stage cancers were SEER historic stage local or regional. Unknown or blank stages were excluded; thus we assumed that those with missing stage were partitioned into stages similarly to those with recorded stage at diagnosis. The fraction with late- stage disease at diagnosis was used as the parameter p₁ in equation (7) above. The post-diagnosis mortality hazards λ₀ and λ₁ were calculated from the SEER 10-year net cause- specific survival for each cancer.

Modeling published screening trials

To determine how this formulation for mortality reduction as a function of stage shift matches observed results in practice, we considered four published screening trials, estimating the required inputs from study results and comparing the expected with the observed mortality reduction.

The National Lung Screening Trial (NLST [15]) was a trial of low-dose computed tomography (CT) screening for lung cancer in high-risk individuals conducted between 2002 and 2009 in the United States. Individuals randomized to the screening arm received annual low-dose CT scans during their first 3 years of enrollment in the trial, with up to 7 years of follow-up. Individuals randomized to the control arm were screened with chest X-ray. The trial showed a reduction of 20% in disease-specific mortality associated with screening.

The European Randomized Study of Screening for Prostate Cancer (ERSPC [16]) examined the effect of screening using prostate-specific antigen (PSA) in seven European countries beginning in the early 1990s. The primary trial publication in 2009 reported that PSA screening as conducted in the trial reduced prostate cancer mortality by 21%, and this estimate remained robust across reports with longer follow-up.

The UK Collaborative Trial of Ovarian Cancer Screening (UKCTOCS [17]) examined the effect of screening for ovarian cancer, with recruitment beginning in 2001 and annual screening though 2011. Women were screened annually with either multimodal screening (MMS arm) including the biomarker CA-125 and ultrasound or with transvaginal ultrasound. The primary report from the trial based on follow-up through 2015 estimated a mortality reduction of 15% on the MMS arm relative to the control arm, however this was not statistically significant. A later report with follow-up through 2020 reported a non-significant mortality reduction of 4% in the MMS arm.

The UK Age Trial ([18]) investigated the effect of screening for breast cancer among women ages 39–41 years. The trial enrolled between 1991 and 1997 and randomized women to either annual mammography or usual care. The primary report for this trial reported a reduction in breast cancer mortality of 17% associated with screening after 10 years of follow-up.

We defined late-stage disease differently for each trial depending on the trial’s stage definitions and on the availability of the required inputs, as follows:

• In the NLST, cancers were classified according to the sixth edition of the American Joint Committee on Cancer (AJCC) staging system. We classified late-stage disease as stages III and IV.

• For the ERSPC, we defined late-stage cancer as metastatic disease or a measured PSA of greater than 100 ng/ml. Because PSA levels are not available in the SEER data, we considered only metastatic disease as late stage when sourcing inputs from that data (described below).

• In the UKCTOCS, cancers were classified according to the Federation of Gynecology and Obstetrics 2014 staging system. We classified stages II-IV of this system as late stage.

• For the UK Age Trial, we relied on a meta-analysis by Autier et al [19] which extracted the incidence of cancers by tumor size as a proxy for disease progression. Cancers greater than 20 mm were classified as late stage.

The proportion late stage p₁ was based on cases in the control arm for each trial. The parameter α was set equal to the relative reduction in cumulative incidence of late-stage disease in the screen versus the control arm over the follow-up period.

Ideally, we would use data from the control arm of each trial to estimate the relevant parameters. In the UKCTOCS trial, sufficient information was available in the published data. In the NLST, ERSPC, and UK Age Trial, however, we were not able to identify stage- specific mortality hazards from the published data. Therefore, we supplemented the trial data with survival estimates from the SEER database by stage. This data was filtered to age ranges consistent with the populations included in the trials. The lung cancer survival was based on cases diagnosed in 2000–2009, while the prostate cancer survival was based on cases diagnosed in 1980–1989, before widespread PSA testing. The breast cancer survival was based on SEER cases diagnosed from 1992 – 2004, consistent with the duration of the trial. The hazard rates were then scaled up uniformly by stage to target the overall cancer-specific mortality observed in the corresponding trials.

Data Availability

The data and code underlying this analysis has been made publicly available at the following page: https://codeocean.com/capsule/1574902/tree/v1

Results

Hypothetical trials

For each of the seven cancers examined, we calculated the stage-shift multiplier (ρ) shown in formula (7) to convert the reduction in late-stage disease to a mortality reduction. Table 1 shows the relevant parameters extracted from the SEER data and the calculated stage- shift multiplier for each cancer. Figure 1 demonstrates the relationship between mortality reduction (M^rel) and reduction in late-stage disease (α). In this plot, the slope of each line is the stage-shift multiplier displayed in Table 1. Ovarian cancer has the steepest slope (corresponding to ρ = 0.636), due to the large differential in mortality between early- and late-stage disease. Conversely, liver cancer has the lowest stage-shift multiplier due to the low survival rate of early-stage cancer. Pancreatic cancer also has a very low multiplier due to the low survival rates at any stage of the disease, while the low multiplier of bladder cancer is due mainly to the fact that late-stage disease is rare. All curves have a slope that is less than one indicating that, if only between-stage shifts confer benefit, the expected mortality reduction will be below the reduction in late-stage incidence.

Table 1:

Mortality reduction for hypothetical cancer screening trials with ten years of follow-up and incidence and stage-specific survival estimated from SEER

Cancer Site	Incidence Hazard Rate (λd)	Early-Stage Mortality Hazard Rate (λ0)	Late-Stage Mortality Hazard Rate (λ1)	Late-Stage Disease Percent (p1)	Stage-Shift Multiplier (ρ)
Ovary	7.38 × 10−6	0.030	0.198	56%	0.636
Lymphoma	0.16 × 10−6	0.027	0.064	51%	0.367
Lung	0.33 × 10−6	0.157	0.570	62%	0.292
Stomach	4.56 × 10−6	0.133	0.586	41%	0.261
Bladder	7.35 × 10−6	0.022	0.489	4%	0.211
Pancreas	6.83 × 10−6	0.319	0.658	61%	0.115
Liver	6.99 × 10−6	0.238	0.692	19%	0.070

Figure 1:

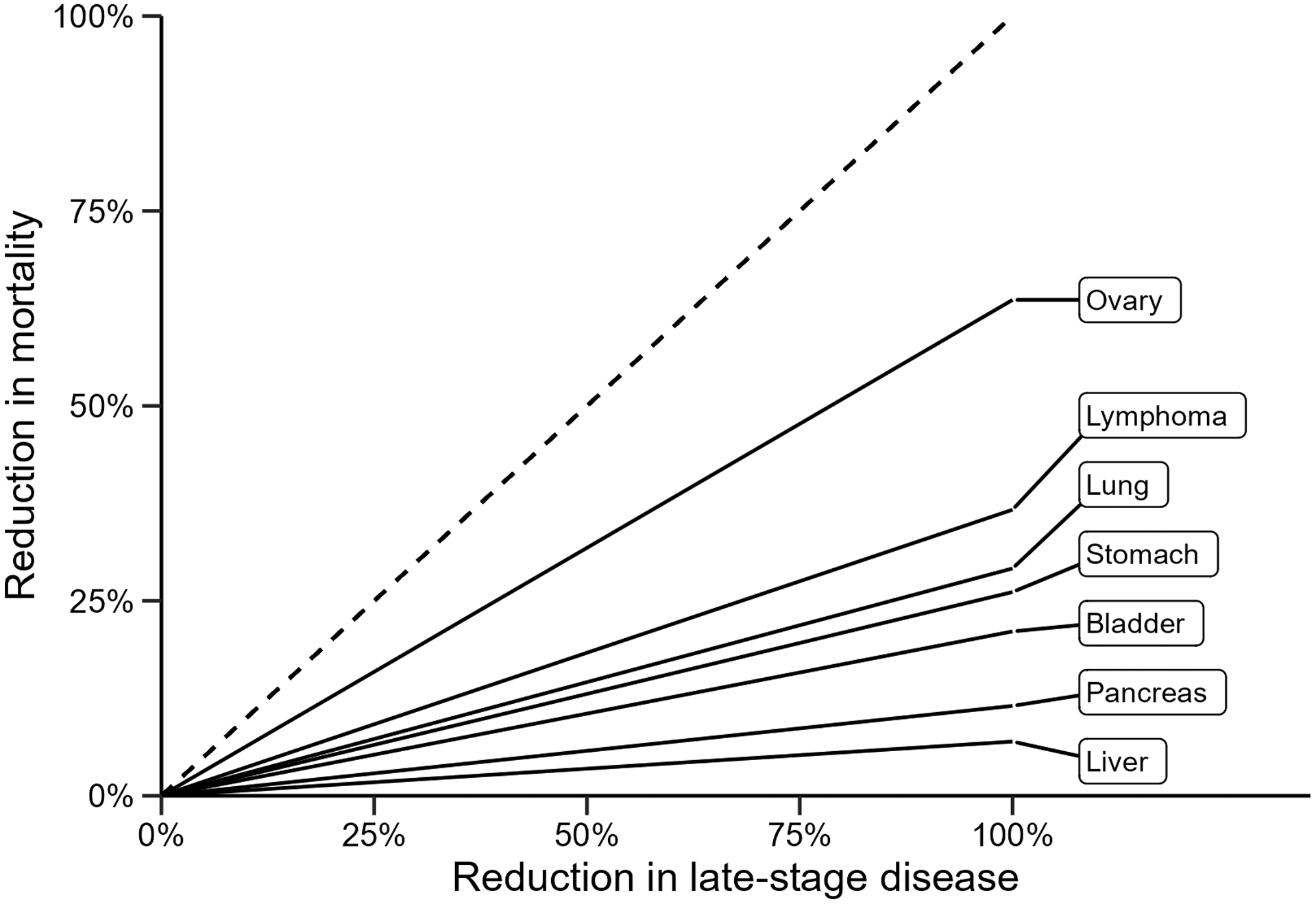
Mortality reduction for selected hypothetical cancer screening trials

The figure shows that the same reduction in late-stage disease has a different implication for mortality depending on the characteristics of the cancer. For example, in ovarian cancer, ρ = 0.636, so a 20% reduction in late-stage disease is expected to result in a 13% mortality reduction, but for liver cancer, the value of the stage-shift multiplier is only 0.070, so a similar 20% reduction in late-stage disease would be expected to produce a 1% mortality reduction.

Published trials

Table 2 displays the expected and observed mortality reduction for each trial based on the stage-shift model. It also displays the relevant inputs extracted from the trials (and from SEER data where indicated), and the multiplier used for converting the reduction in late- stage disease into reduction in mortality. Figure 2 displays the line with slope ρ as well as the expected mortality reduction (circle) and observed mortality reduction (cross). For each trial, the predicted mortality reduction falls within the bounds of the 95% confidence interval for the observed result, as shown in Figure 2. However, the expected mortality reduction can be either above or below that observed.

Table 2:

Calculation of expected mortality reductions given stage-shift and follow-up duration in screening trials

Trial	Incidence Hazard Rate (λd)a	Early-Stage Mortality Hazard Rate (λ0)	Late-Stage Mortality Hazard Rate (λ1)	Late-Stage Disease Percent (p1)a	Stage-Shift Multiplier (ρ)a	Reduction in Late-Stage Disease (α)a	Expected Mortality Reduction (Mrel)a	Observed Mortality Reduction (95% CI)a
NLST	0.006	0.088b	0.380b	61%	0.479	21%	10%	20% (7% to 27%)
ERSPC	0.005	0.016b	0.537b	9%	0.443	48%	21%	21% (9% to 32%)
UKCTOCS	0.001	0.010a	0.198a	79%	0.845	9%	7%	4% (−10% to 17%)
UK Age Trial	0.001	0.022b	0.091b	26%	0.371	12%	5%	17% (−4% to 34%)

^aindicates value obtained from published trial data

^bindicates value taken from SEER and calibrated to overall trial results

Figure 2:

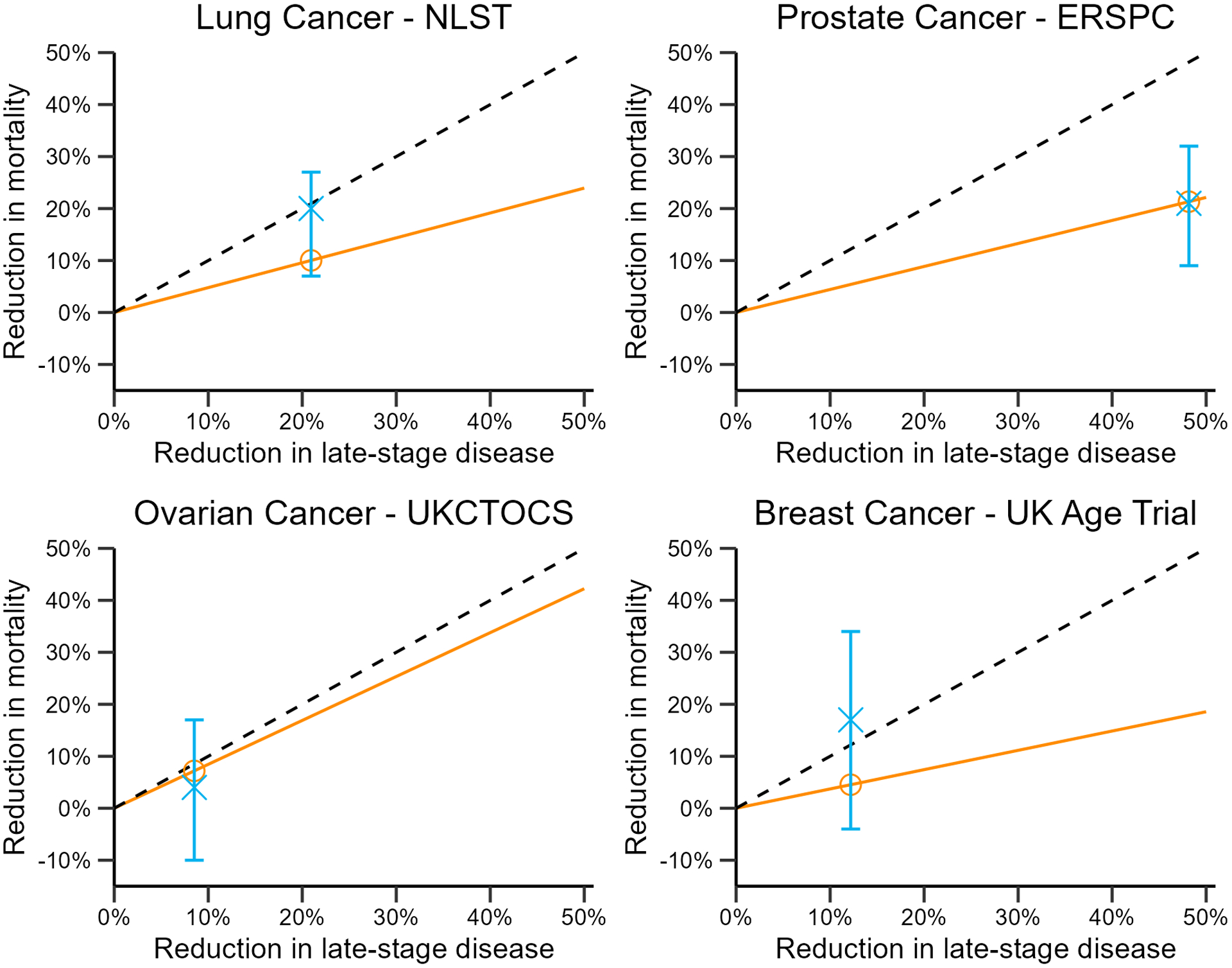
Actual (blue cross) versus expected (orange circle) mortality reduction in published trials. Dashed line is the y = x line; slope of the orange line is the stage-shift multiplier (ρ) in each trial; blue error bars are 95% confidence intervals for actual trial results.

In the NLST, the cumulative incidence of late-stage (stage III and IV) cases was reduced by 21%. The calculated stage-shift multiplier based on the control arm of the trial was 0.479, implying a mortality reduction of 10%. The actual mortality reduction observed in the trial was 20%, twice what was expected. We also examined alternate definitions of late-stage disease, including classifying stage II-IV as late-stage and classifying only stage IV as late-stage. The expected mortality reductions under these alternate scenarios were 10% and 7%, respectively.

In the ERSPC, the cumulative incidence of late-stage cases was reduced by 48% and the implied mortality reduction was 21%, based on a multiplier of 0.444. The trial also observed a mortality reduction of 21%, matching the prediction made by the model.

In the UKCTOCS, the cumulative incidence of late-stage cases was reduced by 9% in the MMS screening arm. The multiplier for this trial was the highest of the three trials (0.845) but the low reduction in late-stage disease resulted in low predicted mortality reduction (7% for the MMS arm). The trial showed a 4% mortality reduction in the MMS arm, even less than predicted.

In the UK Age Trial, the cumulative incidence of late-stage cases was reduced by 12% in the screening arm and the multiplier was 0.365, implying a mortality reduction of 4%. The trial reported a reduction in mortality of 17%.

Interactive calculator

We provide an online calculator developed using the R Shiny package [20] to project the expected mortality reduction given disease-specific inputs and stage shift. The calculator can be accessed at: https://lukasowens.shinyapps.io/stage-shift/.

Discussion

The advent of MCED technologies is creating a need for efficient and timely evaluation of novel screening tests. While screening trials have focused on disease-specific mortality as a primary endpoint, the reduction in late-stage incidence under screening (stage shift) is more proximal and has been proposed as an alternative basis for evaluation of screening benefit. Our analysis shows that the expected mortality reduction given a specified stage shift is likely to vary considerably across cancers. Moreover, it may deviate widely from the mortality reduction observed in trials.

This investigation is timely because the idea behind MCED testing is that advancing diagnosis will generate benefits across the targeted cancers, but our analysis suggests that the cancer-specific impacts may be quite heterogeneous. Indeed, given the variability in prevalence and stage-shift multipliers for each cancer, it is possible that any mortality reductions observed under a MCED test might be attributable to a modest subset of cancers included in the test. Although some stage-shift multipliers might suggest a modest impact on cancer-specific mortality for each cancer individually, aggregation across cancers may lead to a reduction in the absolute number of cancer deaths over all cancers included in the test. Our model makes several simplifying assumptions. We focus on the setting where cases are partitioned into two stage groups, early stage and late stage. This simplification induces an implicit distribution of late-stage cases shifted under screening. For example, in a model that groups AJCC stages I-III as early stage and defines stage IV as late stage, a specified reduction in late-stage incidence will imply the redistribution of the shifted cases across stages I-III in proportion to their original relative frequencies. If the redistribution is different in practice (e.g., stage IV cases are mostly shifted to stage I), then the predictions may not match the observed mortality reductions. The framework as formulated can model more than two stages by specifying the full set of stage-transition probabilities; however, these are not uniquely determined by cross-sectional data on stage distributions with and without screening.

Further simplifications include the application of the cumulative stage reduction uniformly over time so that the same relative reduction in late-stage incidence occurs across all years of follow-up. In practice, we may observe time dependence of the stage shift particularly in trials with a stop-screen implementation such as the NLST and UKCTOCS. Technical simplifications include our use of exponential distributions to obtain closed-form expressions for the stage-shift multiplier and our exclusion of other causes of death to project disease-specific mortality. In practice we expect our results would not differ significantly under alternative distributions (e.g. Weibull) especially over our modest 10-year time horizon. Including other causes of death would likely reduce the absolute cumulative risk of disease-specific death on each arm of a hypothetical or published trial and could therefore lead to an attenuation of the predicted mortality reductions over our current projections.

The fundamental assumption underlying the stage-shift model is that cases shifted via screening to early stage have the same survival as cases detected in early stage without screening. This may not be correct if certain cancer subtypes are more likely to be detected early by the screening test. In the UKCTOCS [17], for example, the case fatality rate for localized cases on the MMS arm was higher than among localized cases on the control arm, suggesting a possibly different biology between stage-shifted cases and clinically localized cases. Similarly, the low dose CT scans considered by the NLST are particularly sensitive for adenocarcinoma, which generally have high early-stage survival relative to other subtypes. One possible approach to address this issue would be to model mortality outcomes within prognostic subgroups. Further investigation may be warranted to see if incorporation of features in addition to stage improves mortality prediction. For example, we note that Cuzick et al [12] examined the predicted mortality reduction based on age as well stage-shift in the UK Flexible Sigmoidoscopy Screening Trial.

We note that the stage-shift model focuses on screening benefit and does not account for harms that may occur due to screening, such as overdiagnosis, unnecessary biopsy or other adverse events. These events depend on the screening and diagnostic process and can, in principle, be evaluated on a more proximal timeline than mortality. In conclusion, there is an urgent need for trial designs and analysis plans that can evaluate novel screening technologies efficiently and rapidly. Our analysis of four screening trials suggests that stage-shift alone may not constitute a reliable endpoint in terms of its ability to predict mortality reduction in cancer screening trials. It is possible that extensions of the basic stage-shift model may be more accurate as a basis for inference about screening benefit. In the setting of MCED, any evaluation that relies on stage-shift should account for the varying stage-shift multipliers of each cancer in projecting eventual benefit. Published trials show that we are not in a one-size-fits-all situation, and this must be taken into account as we develop best practices for expeditious and efficient evaluation of multi-cancer screening tests.