Interaction Potential for NaCs for Ultracold Scattering and Spectroscopy

Abstract

We obtain the interaction potential for NaCs by fitting to experiments on ultracold scattering and spectroscopy in optical tweezers. The central region of the potential has been accurately determined from Fourier transform spectroscopy at higher temperatures, so we focus on adjusting the long-range and short-range parts. We use coupled-channel calculations of binding energies and wave functions to understand the nature of the molecular states observed in ultracold spectroscopy and of the state that causes the Feshbach resonance used to create ultracold NaCs molecules. We elucidate the relationships between the experimental quantities and features of the interaction potential. We establish the combinations of experimental quantities that determine particular features of the potential. We find that the long-range dispersion coefficient C₆ must be increased by about 0.9% to 3256(1)E_ha₀⁶ to fit the experimental results. We use coupled-channel calculations on the final potential to predict bound-state energies and resonance positions.

1. Introduction

Ultracold polar molecules have many potential applications, ranging from precision measurement,¹⁻¹¹ quantum simulation,¹²⁻¹⁷ and quantum information processing¹⁸⁻²⁴ to state-resolved chemistry.²⁵⁻³⁰ A very important class of ultracold molecules are the alkali-metal diatomic molecules; these are usually produced by the association of pairs of ultracold atoms, by magnetoassociation, or by photoassociation, followed by coherent optical transfer to the ground rovibronic state. The ground-state molecules produced in this way include KRb,^31,32 Cs₂,^33,34 Rb₂,³⁵ RbCs,^36,37 NaK,³⁸⁻⁴⁰ NaRb,⁴¹ NaLi,⁴² and NaCs.⁴³

A particular success in the past few years has been the production of ultracold NaCs molecules in optical tweezers. Configurable arrays of polar molecules in tweezers offer many possibilities for studying few-body physics involving dipolar species and constructing designer Hamiltonians for quantum logic and quantum simulation. In 2018, Liu et al.⁴⁴ succeeded in loading one atom each of Na and Cs into a single optical tweezer and photoassociated them to form a single electronically excited NaCs molecule in the tweezer. Liu et al.⁴⁵ measured the binding energy of the least-bound triplet state of NaCs by two-photon Raman spectroscopy. Hood et al.⁴⁶ measured interaction shifts for flipping the spin of one or both atoms in the tweezer and located magnetically tunable Feshbach resonances in an excited spin channel. They used these measurements to model the interaction using multichannel quantum defect theory (MQDT). Zhang et al.⁴⁷ located an s-wave Feshbach resonance in the lowest spin channel, allowing them to form a single NaCs molecule in the tweezer by magnetoassociation. Yu et al.⁴⁸ used a different route to form a single NaCs molecule in the tweezer by coherent Raman transfer. Most recently, Cairncross et al.⁴³ transferred a molecule formed by magnetoassociation to the absolute ground state by a coherent Raman process.

Studies of ultracold molecule formation typically need close collaboration between experiment and theory. Initial experiments identify properties of the system that can be used to determine an initial interaction potential. The interaction potential is then used to predict new experimental properties. Once these are measured, they are used to refine the interaction potential, and the process repeats. The studies of NaCs in tweezers have followed this cycle several times. In the process, we have learned a considerable amount, both about the specific system and more generally about the ways in which experimental properties are influenced by features of the interaction potential. The purpose of the present article is to present the fitted potential for Na + Cs, describe its relationships to experimental observables, and explain the insights that have been gained. Accurate interaction potentials have applications not only for ultracold molecules but also for precise control of atomic collisions, for example, in studies of Efimov physics⁴⁹ and quantum droplet formation.⁵⁰

The structure of this article is as follows. Section 2 describes the underlying theory and the methods used in the present work. Section 3.1 describes the measured quantities from ultracold scattering and spectroscopy, the wave functions of the underlying weakly bound states, and their relationship to the singlet and triplet potential curves. Section 3.2 describes our procedure for fitting potential parameters, with a focus on how each parameter is related to and constrained by the measured quantities. Section 3.3 describes the near-threshold bound states calculated for our final interaction potential and the resulting scattering properties, including predictions for additional resonances. It compares additional measurements for p-wave and d-wave resonances and gives assignments for the states involved. Finally, Section 4 summarizes our conclusions and the insights gained from the present work.

2. Theoretical Methods

2.1. Atomic States

The Hamiltonian for an alkali-metal atom X in its ground ²S state may be written as

1

where ζ_X is the hyperfine coupling constant, ŝ_X and î_X are the operators for the electron and nuclear spins, respectively, and ŝ_z,X and î_z,X represent their z components along an axis defined by the external magnetic field B. We follow the convention of using lowercase letters for operators and quantum numbers of individual atoms and uppercase letters for those of the diatomic molecule or colliding pair of atoms. The constants g_S,X and g_n,X are the electron and nuclear g-factors, and μ_B is the Bohr magneton. The numerical values are taken from Steck’s compilations.^51,52

The nuclear spin is i = 3/2 for ²³Na and i = 7/2 for ¹³³Cs. These are the only stable isotopes for each element, so in the following we omit the mass numbers. The hyperfine splitting at zero field is 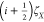and is approximately 1.77 GHz for Na and 9.19 GHz for Cs. Because of these differences, the free atoms have quite different Zeeman structures, as shown in Figure 1.

Figure 1.

Breit–Rabi plots showing the hyperfine structure and Zeeman splitting for ²³Na and ¹³³Cs atoms. The zero of energy is the hyperfine centroid in each case. Each state is identified by a Roman letter in alphabetic order from the lowest, which is designated as a.

At low fields, the atomic states may be labeled with 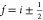and its projection m_f onto the axis of the magnetic field. However, at higher fields the magnetic field mixes states of different f values, particularly for Na. Here we label the states alphabetically in increasing order of energy, with Roman letters from a to h for Na and from a to p for Cs, as shown in Figure 1. In each case, the highest-energy state is spin-stretched, with .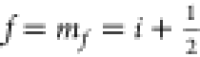

We label a state of an atom pair with two letters, with Na first. For example, ha indicates that Na is in its uppermost state and Cs is in its lowest. The threshold for a particular pair state is the energy of the separated atom pair at the appropriate magnetic field. There are 128 = (3 + 5) × (7 + 9) of these thresholds but no more than 16 for a particular value of M_F = m_f,Na + m_f,Cs, which is a nearly conserved quantity in a magnetic field.

2.2. Two-Atom Hamiltonian

When two alkali-metal atoms in their ground ²S states approach one another, their electron spins couple to form either a singlet state X¹Σ⁺ with total electron spin S = 0 or a triplet state a³Σ⁺ with S = 1. Their interaction is governed mostly by the electrostatic potential curves V₀(R) and V₁(R) for the singlet and triplet states, respectively, but there are also small spin-dependent terms as described below.

The Hamiltonian for an interacting pair of atoms may be written as

2

where R is the internuclear distance, μ is the reduced mass, and L̂ is the operator for the end-over-end angular momentum of the two atoms about one another.

The interaction between the atoms is described by the interaction operator, which for a pair of alkali-metal atoms takes the form

3

Here 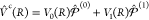is an isotropic potential operator that accounts for the potential energy curves V₀(R) and V₁(R) for the singlet and triplet states. The singlet and triplet projectors and project onto subspaces with S = 0 and 1, respectively. Figure 2 shows the two potential energy curves for NaCs. The functional forms used for these are described in Section 2.5.

Figure 2.

Potential curves of Docenko et al.⁵³ for the X¹Σ⁺ and a³Σ⁺ states of NaCs. The inset shows an expanded view of the zero-field hyperfine structure at long range, with thresholds labeled (f_Na, f_Cs) and energies shown relative to the hyperfine centroid.

The term V̂^d(R) describes the dipole–dipole interaction between the magnetic moments of the electrons at long range, together with terms due to second-order spin–orbit coupling at short range. This makes only small contributions for the experimental observables that we fit to in the present article, but it is important for some of the predicted observables described in Section 3.3. It is described in Appendix A.

2.3. Calculations of Bound States and Scattering

We carry out calculations of both bound states and scattering using coupled-channel methods,⁵⁴⁻⁵⁶ as described in Appendix B. The total wave function is expanded in a complete basis set of functions for electron and nuclear spins and end-over-end rotation, producing a set of coupled differential equations that are solved by propagation with respect to the internuclear distance R. The coupled equations are identical for bound states and scattering, but the boundary conditions are different.

Scattering calculations are performed with the MOLSCAT package.^57,58 Such calculations produce the scattering matrix S for a single value of the collision energy and magnetic field each time. The complex s-wave scattering length a(k₀) is obtained from the diagonal element of S in the incoming channel, S₀₀, using the identity⁵⁹

4

where k₀ is the incoming wavenumber related to the collision energy E_coll by E_coll = ℏ²k₀²/(2μ). The scattering length a(k₀) becomes constant at sufficiently low E_coll, with limiting value a. In the present work, s-wave scattering lengths are calculated at E_coll/k_B = 1 nK, which is low enough to neglect the dependence on k₀.

A zero-energy Feshbach resonance occurs where a bound state of the atomic pair (diatomic molecule) crosses a scattering threshold as a function of the applied field. At the lowest threshold, or in the absence of inelastic processes, the scattering length is real. Near a resonance, a(B) passes through a pole and is approximately

5

where B_res is the position of the resonance, Δ is its width, and a_bg is a slowly varying background scattering length. In the presence of inelastic processes, a(B) is complex and the pole is replaced by an oscillation.⁵⁹ MOLSCAT can converge on Feshbach resonances automatically and characterize them to obtain B_res, Δ, and a_bg (and the additional parameters needed in the presence of inelasticity) as described in ref (60).

Coupled-channel bound-state calculations are performed using the packages BOUND and FIELD,^58,61 which converge upon bound-state energies at fixed field and upon bound-state fields at fixed energy, respectively. The methods used are described in ref (62). Once bound states have been located, their wave functions may be obtained by back-substitution using matrices saved from the original propagation.⁶³ Alternatively, the expectation value of any operator may be calculated by finite differences, without requiring explicit wave functions.⁶⁴ This capability is used here to calculate overall triplet fractions for bound states.

Zero-energy Feshbach resonances can be fully characterized using MOLSCAT as described above. However, if only the position of the resonance is needed, it is more convenient simply to run FIELD at the threshold energy to locate the magnetic field where the bound state crosses the threshold.

A key capability of both MOLSCAT and FIELD, used in the present work, is automated convergence of any one parameter in the interaction potential to reproduce a single observable quantity, such as a bound-state energy, scattering length, or resonance position. This uses the same algorithms as are used to converge on such quantities as a function of the external field.^60,62

In the present work, the coupled equations for both scattering and bound-state calculations are solved using the fixed-step symplectic log-derivative propagator of Manolopoulos and Gray⁶⁵ from R_min = 4a₀ to R_mid = 30a₀, with an interval size of 0.002a₀, and the variable-step Airy propagator of Alexander and Manolopoulos⁶⁶ between R_mid and R_max = 10 000a₀. The exception to this is calculations used to plot wave functions, which use the fixed-step log-derivative propagator of Manolopoulos.^63,67

2.4. Basis Sets for Angular Momentum

To carry out coupled-channel calculations, we need a basis set that spans the space of electron and nuclear spins and of relative rotation. We do not require a basis set where the atomic Hamiltonians ĥ₁ and ĥ₂ are diagonal because MOLSCAT transforms the solutions of the coupled equations into an asymptotically diagonal basis set before applying scattering boundary conditions.

There are five sources of angular momentum for an interacting pair of alkali-metal atoms: the electron spins s₁ and s₂, the nuclear spins i₁ and i₂, and the rotational angular momentum L. These may be coupled together in several different ways, and different coupling schemes are useful when discussing different aspects of the problem. The separated atoms are conveniently represented by quantum numbers (s, i)f, m_f, where the notation (a, b)c indicates that c is the resultant of a and b and m_c is the projection of c onto the z axis. Conversely, the molecule at short range (and low field) is better represented by S and the total nuclear spin I, together with their resultant F and its projection M_F. In the present work, we carry out coupled-channel calculations in two different basis sets. The first is

6

which we term the coupled-atom basis set. The second is

7

which we term the SIF basis set. The only conserved quantities in a magnetic field are M_tot = m_f,Na + m_f,Cs + M_L = M_F + M_L and parity (−1)^L. We take advantage of this to perform calculations for each M_tot and parity separately. In each calculation, we include all basis functions of the required M_tot and parity for 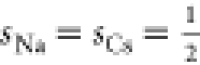, , 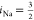and 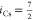, subject to the limitation L ≤ L_max. In most of the calculations in the present work, L_max = 0, except that we use L_max = 1 for calculations of p-wave states and resonances in Section 3.3.4 and L_max = 2 for the calculations in Section 3.3.3.

2.5. Singlet and Triplet Potential Curves

Our starting points for fitting the interaction potentials are the singlet and triplet potential curves of Docenko et al.,⁵³ shown in Figure 2. These were fitted to extensive Fourier transform (FT) spectra involving vibrational levels of up to v = 83 in the singlet state, which has a total of 88 levels, and of up to v = 21 in the triplet, which has 25. These curves give an excellent representation of the levels they were fitted to, but their behavior at higher energies depends sensitively on how they are extrapolated, and they do not reproduce the near-threshold states important for ultracold scattering.

In a central region from R_SR,S to R_LR,S, with S = 0 for the singlet and S = 1 for the triplet, each curve is represented as a finite power series in a nonlinear function ξ_S that depends on the internuclear separation R,

8

where

9

The quantities a_i,S and b_S are fitting parameters, and R_m,S is chosen to be near the equilibrium distance for the state concerned. The values of the parameters fitted to FT spectroscopy for NaCs are given in Tables 1 and 2 of ref (53); the values R_SR,0 = 2.8435 Å and R_SR,1 = 4.780 Å, which specify the minimum distance at which the power-series expansion is used for each state, are particularly important for the present work.

At long range (R > R_LR,S), the potentials are

10

where the dispersion coefficients C_n are common to both potentials. The long-range matching points are chosen as R_LR,0 = R_LR,1 = 10.2 Å. The exchange contribution is⁶⁸

11

where a₀ is the Bohr radius. It makes an attractive contribution for the singlet and a repulsive contribution for the triplet. The value of C₆ used by Docenko et al.⁵³ was fixed at the theoretical value of Derevianko et al.,⁶⁹ whereas C₈, C₁₀, and A_ex were fitting parameters. The mid-range potentials are adjusted to match the long-range potentials at R_LR,S by setting the constant terms a_0,S in eq 8 as required.

Finally, the potentials are extended to short range (R < R_SR,S) with simple repulsive terms,

12

where A_SR,S is chosen so that V_SR,S and V_mid,S match at R_SR,S. In the present work, B_SR,S is chosen to match the derivative of these two functions. However, this latter constraint was not applied in ref (53), producing discontinuities in the derivatives of the potential curves at R_SR,S.

3. Results and Discussion

3.1. Observables from Ultracold Scattering and Spectroscopy

The recent experimental studies on Na + Cs in tweezers^43,45−48 have measured a number of quantities that could be used in fitting potential curves. Each observable is associated with one or more molecular bound states of a particular spin character. In this section, we consider each observable quantity and the nature of the corresponding state in order to understand how the observable depends on features of the singlet and triplet potential curves. The calculations in this section are based on “lightly fitted” potential curves, with approximately correct scattering lengths. Calculations based on the final potential would be visually almost identical.

3.1.1. General Features of Near-Threshold States

The near-threshold states that are important in studies of ultracold molecules and ultracold collisions are typically bound by less than a few GHz. Their wave functions extend several nm to distances where hyperfine coupling is stronger that the spacing between the singlet and triplet curves. This long-range region is shown as an inset in Figure 2. Each curve represents a different zero-field hyperfine threshold, labeled (f_Na, f_Cs). For an interaction potential of the form −C₆/R⁶ at long range, the bound states below each threshold are located within “bins” given by multiples of an energy scale E̅ = ℏ²/(2μa̅²),⁷⁰ where a̅ is the mean scattering length⁷¹ and depends only on C₆ and μ. For NaCs, a̅ = 59.17a₀ and E̅ = 26.30 MHz. The first (top) bin is 36.1E̅ = 950 MHz deep, implying that the top (least-bound) bound state for each spin combination lies 0 to 950 MHz below its threshold; the position of the state within the bin is governed by the actual scattering length a, which differs for different thresholds. The least-bound state is designated n = −1. The second and third bins extend to depths of 249E̅ and 796E̅, so the second and third bound states (with n = −2 and −3) lie between 950 MHz and 6.6 GHz and between 6.6 and 21 GHz below the threshold, respectively. We focus here on states with binding energies within the three uppermost bins; accurately modeling this region of the potential is crucial for obtaining reliable scattering lengths and resonance positions, among other properties.

3.1.2. Binding Energy of the Absolute Ground State

Cairncoss et al.⁴³ have measured the energy of the absolute ground state of NaCs, initially with respect to the near-threshold state formed by magnetoassociation. After correcting for hyperfine and Zeeman effects and the binding energy of the near-threshold state, they infer that the binding energy E₀₀ of the lowest rovibrational level of the singlet state, relative to the hyperfine centroid of free atoms, is 147 044.63(11) GHz.

This state is located thousands of cm^–1 below the minimum of the triplet state, so singlet–triplet mixing is negligible. Its binding energy is sensitive only to the singlet curve. Its wave function is tightly confined around the minimum of the singlet curve near 3.85 Å, and the zero-point energy is very well determined by the FT spectra, so it is mostly sensitive to the well depth of the singlet curve.

3.1.3. Binding Energy of the Least-Bound Pure Triplet State

The binding energy of the least-bound state in the hp channel, E_–1^hp, has been measured by Liu et al.⁴⁵ and refined by Hood et al.⁴⁶ This channel corresponds to (f, m_f) = (2, 2) for Na and (4, 4) for Cs. Both of these states are spin-stretched, with f = m_f = s + i, so states that lie in the hp channel are pure triplet in character. The binding energy of the state, relative to the hp threshold, is 297.6(1) MHz at 8.8 G.

The binding energy E_–1^hp is sensitive only to the triplet curve. It is also very closely related to the triplet scattering length a_t, with only slight sensitivity to the dispersion coefficient C₆ and even less to C₈ and C₁₀.

3.1.4. Binding Energy of the Least-Bound State in the ha Channel

Yu et al.⁴⁸ have measured the binding energy of the least-bound state in the ha channel, E_–1^ha, with respect to the ha threshold. The binding energy is 770.1969(2) MHz at B = 8.83 G.

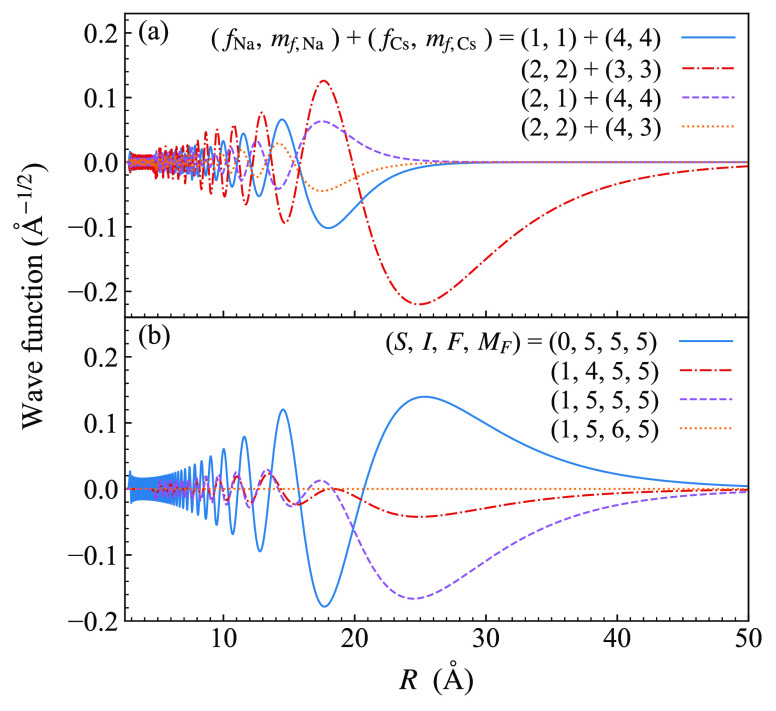
The ha channel corresponds to (f, m_f) = (2, 2) for Na and (3, 3) for Cs, so M_F = 5. Because there are four atomic pair states with M_F = 5, which are mixed by the interaction potential, this state has a mixture of singlet and triplet character. To quantify this, Figure 3 shows the components of the wave function for this state. In the coupled-atom representation, the main contribution is provided by the ha channel, with smaller contributions arising from the other three channels with M_F = 5. In the SIF representation, there are similar contributions from singlet and triplet channels. The overall triplet fraction obtained from the expectation value of the triplet projector is 49.7%.

Figure 3.

Components of the wave function for the least-bound state in the ha channel, shown in both the (a) coupled-atom and (b) SIF representations. Components in all four contributing channels are plotted in each case.

The binding energy E_–1^ha is approximately equally sensitive to the singlet and triplet curves. It is closely related to the scattering length in the ha channel. However, because the triplet scattering length is determined independently by E_–1, the role of E_–1^ha is to provide information on the singlet scattering length a_s.

3.1.5. Position of Feshbach Resonance in the aa Channel

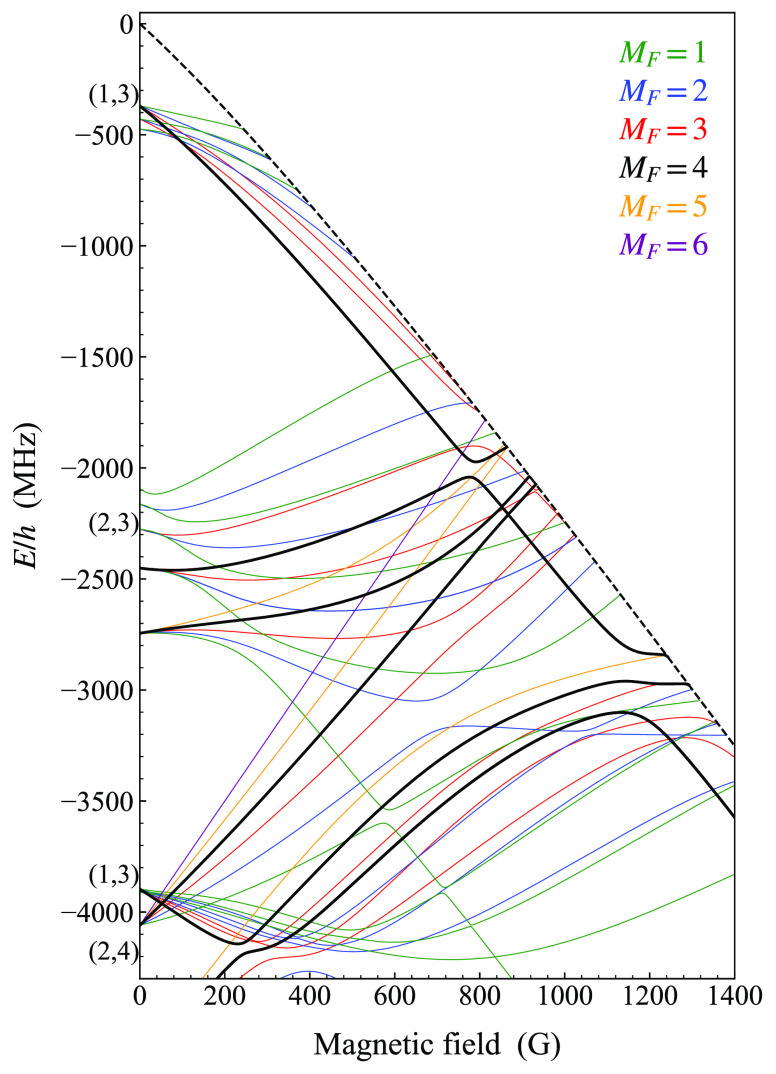
Zhang et al.⁴⁷ have observed a strong s-wave resonance in the lowest hyperfine channel at 864.11(5) G and used it to form NaCs molecules by magnetoassociation. The atoms collide at the aa threshold, corresponding to (f, m_f) = (1, 1) + (3, 3) at low field. The resonance position is designated B_res^aa.

Figure 4 shows the pattern of s-wave bound states below the aa threshold as a function of magnetic field, obtained from coupled-channel bound-state calculations, together with the calculated scattering length. The bound state originating at −400 MHz and running parallel to the aa threshold has the same spin character (i.e., the same spin quantum numbers) as the aa threshold. The resonance near 864 G occurs when this state is pushed up and across the threshold by a more deeply bound state through an avoided crossing.

Figure 4.

(a) Calculated s-wave scattering length in the aa channel as a function of magnetic field. (b) Energies of weakly bound s-wave molecular states with M_F = 4 (solid lines) and of the aa threshold (dashed line). The zero of energy is the zero-field threshold energy. Feshbach resonances occur where bound states cross the threshold and are indicated by vertical lines extending up to the corresponding position on the plot of the scattering length.

The more deeply bound state originates from −2450 MHz below the aa threshold at zero field. Its depth and behavior with magnetic field ultimately determine the location and nature of the resulting resonance. The components of its wave function at zero field are plotted in Figure 5. In the coupled-atom representation, the dominant components are from channels corresponding to (f_Na, f_Cs) = (2, 3) (solid brown and dotted–dashed green curves). The calculated zero-field binding energy is 4220 MHz below the (2, 3) threshold, indicating that the state corresponds to n = −2. Because of this, the wave function is concentrated at significantly shorter range than those for the least-bound states in Figure 3. The components of the wave function in the SIF representation are shown in Figure 5(b). There are significant contributions from both singlet and triplet channels. The overall triplet fraction is 69.5%.

Figure 5.

Components of the wave function at zero field for the state responsible for the resonance near 864 G in the aa channel, shown in both the (a) coupled-atom and (b) SIF representations. Components in the four most prominent channels are plotted in each case.

3.1.6. Position of Feshbach Resonance in the cg Channel

Hood et al.⁴⁶ have measured the position of an inelastic loss feature in the cg channel at 652.1(4) G. This channel corresponds to (f, m_f) = (1, −1) + (3, −3) at low field. They attributed this feature to an s-wave Feshbach resonance, and its position is designated B_res^cg.

The state that causes this resonance crosses downward across the threshold with increasing magnetic field. It is bound at fields above the crossing but is quasibound at fields below it, so it cannot as simply be traced back to its origin at zero field with BOUND. Figure 6 shows the bound states and atomic thresholds with M_F = −4 relevant to this resonance. A least-squares fit to the crossing state (solid yellow line) at fields above the crossing gives a gradient of −0.76 MHz/G and a zero-field intercept of −5140 MHz. The state is reasonably parallel to the df threshold with (f, m_f) = (2, −2) + (3, −2), which has a gradient of about −0.7 MHz/G; we conclude that the state is mostly of df character. Calculation of the wave function at a field 80 G above the crossing confirms this, though there is developing coupling to the state in the cg channel (solid blue line) with increasing field. The state is bound by about 640 MHz with respect to the df threshold, indicating that it lies in the top bin. Its overall triplet fraction is 60.6%.

Figure 6.

(a) Calculated s-wave scattering length in the cg channel as a function of magnetic field. (b) Energies of weakly bound s-wave molecular states with M_F = −4 (solid lines) and of nearby thresholds (dashed lines). The zero of energy is the zero-field energy of the cg and aa thresholds. The resonant state (yellow) is approximately parallel to the df threshold, and there is another state (blue) roughly parallel to the cg threshold. The resonance position is marked by a vertical line extending up toward the scattering-length plot. The dotted–dashed yellow line shows a linear extrapolation of the resonant state to zero field.

This state has a roughly similar triplet fraction and binding energy (with respect to the threshold that supports it) as the least-bound state in the ha channel. However, the interpretation of the position of the loss peak is somewhat uncertain. First, the resonance is quite broad, as seen in Figure 6(a), with width Δ of around 40 G. Secondly, Brooks et al.⁷² have shown that inelastic loss features for atom pairs in tweezers may be significantly shifted from the actual resonance position. We therefore conclude that the information on the interaction potential available from this feature is similar to but less reliable than that available from E_–1^ha; we therefore do not use B_res in fitting.

3.1.7. Interaction Shifts and Derived Scattering Lengths

Hood et al.⁴⁶ have measured interaction shifts for spin-flip transitions of Na atoms (transition a ↔h) and Cs atoms (transition a↔p) in tweezers. The shifts are defined as the difference in transition frequency between a tweezer containing one atom of each species and a tweezer containing a single atom. They are made up of shifts for individual pair states that depend on the scattering length for the particular pair of atomic states. However, modeling the shift for two different atoms in a nonspherical tweezer involves a complicated forward calculation to take account of the anisotropy of the trap and the coupling between the relative and center-of-mass motions of the atoms.⁴⁶

Hood et al. used their measurement of E_–1^hp to extract a triplet scattering length a_t = 30.4(6)a₀. They used this to calculate the interaction shift for the hp state of Na + Cs and hence to extract interaction shifts for the ha and ap states from the transition frequencies. They found an interaction shift of −30.7 kHz for the ha state, from which they inferred a large negative scattering length of −693.8a₀. From this, they used MQDT to extract a singlet scattering length a_s = 428(9)a₀.

The measurements of interaction shifts are principally sensitive to the scattering length for the ha state. They contain information that is very similar to E_–1^ha but is less precise and far less direct. We therefore do not use them in fitting.

3.2. Fitting Potential Parameters

The interaction potentials of Docenko et al.⁵³ were fitted primarily to FT spectra, which accurately determine the deeper part of the potential but not the near-threshold part. Our goal is to adjust the potential curves to fit the ultracold observables described above while retaining as much as possible their ability to reproduce the FT spectra. We therefore keep the two power series that represent the singlet and triplet potential wells fixed, with the coefficients obtained in ref (53), and vary only the short-range and long-range extrapolations. As will be seen below, we found it necessary to make small changes in the long-range dispersion coefficients C₆ and C₈ of eq 10 as well as to vary the parameters of the short-range extrapolations, R_SR,S and N_S of eq 12.

There is no advantage in varying R_LR,S, the point at which the mid-range power series (eq 8) is matched to the long-range exchange-dispersion potential (eq 10). As described above, continuity of the curves at R_LR,S is achieved by shifting the midrange curves bodily using the constant terms a_0,S in the power series. Any change in the dispersion coefficients C₆ and C₈ thus shifts the minima of both curves and is directly reflected in the binding energy E₀₀ of the absolute ground state. The measured value of E₀₀ effectively provides a constraint that relates C₈ to C₆.

For a single potential curve V(R) that varies as −C₆/R⁶ at long range, the scattering length a is approximately related to a phase integral Φ by⁷¹

13

where

14

and R_in is the inner classical turning point at the threshold energy E_thresh. With the mid-range and long-range parts of the curve fixed by other observables, the only way to adjust a is to vary the short-range potential in the region between R_in and R_SR, where it is given by eq 12. Because the relationship between a and the binding energy E_–1 is only very weakly affected by the dispersion coefficients, the same applies to E_–1. These considerations apply independently to the singlet and triplet curves, so we have dropped the S subscript here.

If A_SR and B_SR are chosen to give continuity of the potential and its derivative at R_SR, then the short-range extrapolation (eq 12) for each curve has free parameters R_SR and N. The short-range power N controls the hardness of the repulsive wall and can substantially affect the extrapolation of the potential to energies above dissociation, which are important for higher-energy collisions. Nevertheless, in potentials fitted to FT spectra, N has commonly been assigned an arbitrary fixed value, which has ranged from 3 for NaCs⁵³ to 12 for K₂.⁷³ A requirement to reproduce a particular value of a or E_–1 is satisfied along a line in the space of R_SR and N. However, because of the longer-range contribution to the phase integral Φ, this line depends significantly on the values of C₆ and C₈.

We apply this approach first to the potential curve for the triplet state. As described above, the FIELD package can automatically converge on the value of a potential parameter (here R_SR,1) required to reproduce a particular observable (here E_–1^hp). The resulting curves that relate N₁ and R_SR,1 are shown in Figure 7. The curves do depend on C₆ and the associated C₈ and so are shown for values of C₆ that vary by up to ±1% from the theoretical value in ref (69). As described below, N₁ will ultimately be chosen on physical grounds, and the inset of Figure 7 shows how the required value of R_SR,1 depends on C₆ for the choice N₁ = 10.

Figure 7.

Relationship between the inverse power N₁ and the short-range matching point R_SR,1 required to reproduce the experimental binding energy E_–1^hp of the least-bound triplet state of NaCs. The relationship is given for various values of the dispersion coefficient C₆, expressed as percentage differences from the theoretical value.⁶⁹ The solid brown line shows the value used in ref (53), and the solid red line shows the final value of the present work. The inset shows the dependence of R_SR,1 on C₆ for the choice N₁ = 10.

Once values are chosen for C₆, C₈, N₁, and R_SR,1, the triplet curve is fully defined. The same procedure may then be applied to vary the short-range part of the singlet curve to reproduce E_–1^ha. Because this state has multiple components as shown in Figure 3, this requires coupled-channel bound-state calculations, but it is nevertheless conceptually similar. The resulting relationship between R_SR,0 and N₀ is shown by the green lines in Figure 8, again for a range of values of C₆.

Figure 8.

Relationship (green dashed lines) between the inverse power N₀ and the short-range matching point R_SR,0 required to reproduce the experimental binding energy E_–1^ha of the least-bound state of NaCs in the ha channel. The relationship is given for various values of the dispersion coefficient C₆, expressed as percentage differences from the theoretical value.⁶⁹ The solid green curve shows the value used in ref (53). The blue lines show the analogous relationships required to reproduce the experimental position B_res of the s-wave resonance in the aa channel of Na + Cs. The solid red line is for the values of C₆ required to reproduce E_–1^ha and B_res simultaneously. The inset shows the dependence of R_SR,1 on C₆ required to fit each observable for the choice N₁ = N₀ = 10.

We initially carried out this procedure with the dispersion coefficient C₆ of ref (69), as used in ref (53). This produced the relationship between R_SR,1 and N₁ shown by the solid brown line in Figure 7 and between R_SR,0 and N₀ shown by the solid green line in Figure 8. It may be seen that, for the original value of C₆, there is no value of R_SR,0 that fits E_–1^ha for N₀ ≳ 5. Furthermore, the resulting potential curves fail to reproduce B_res, the position of the resonance near 864 G in the aa channel; they place it near 873 G. This is because they place the zero-field binding energy of the state that causes this resonance significantly too deep, about 2470 MHz below the (f_Na = 2, f_Cs = 3) thresholds that support it. As seen in Figure 5, this is still a long-range state whose binding energy is controlled by the singlet and triplet scattering lengths and the dispersion coefficients. However, its wave function does not extend as far to long range as the least-bound states in Figure 3, so its binding energy is more sensitive to the dispersion coefficients than theirs. Because the relationship between C₆ and C₈ is determined by the binding energy of the absolute ground state and the singlet and triplet scattering lengths are determined by E_–1^ha and E_–1, the only way to adjust B_res^aa is by varying C₆ and C₈.

We therefore repeat the calculation of the relationship between R_SR,0 and N₀, but by fitting to B_res^aa instead of E_–1. This produces the blue lines in Figure 8, again for a range of values of C₆. It may be seen that the lines fitted to B_res^aa and to E_–1 are incompatible unless C₆ is increased from its original value by approximately 0.9%. The inset of Figure 8 shows the values of R_SR,0 obtained from each of the two fits for the choice N₀ = N₁ = 10. The requirement to fit both quantities produces a single value of C₆ (and the corresponding C₈ as required to reproduce E₀₀ as above).

These results led us to an iterative procedure for fitting the experimental observable. We (i) choose values for N₀, N₁, and C₆; (ii) vary C₈ to fit E₀₀; (iii) vary R_SR,1 to fit E_–1^hp; (iv) vary R_SR,0 to fit E_–1; and (v) evaluate B_res^aa, adjust C₆, and return to (ii). We repeat this cycle until convergence is achieved. This can be done for any reasonable values of N₀ and N₁, with results shown by the red line in Figure 7 and by the red line in Figure 8 for the choice N₁ = 10. Any potential along these lines reproduces the four observables E₀₀, E_–1, E_–1^ha, and B_res, and they differ very little in their predictions for other observable quantities. For our final interaction potential, we choose N₀ = N₁ = 10 to avoid the very soft repulsive wall of the triplet curve in ref (53).

It would have been possible to obtain the same final potential by a “blind” minimization procedure, but it conveys important insights to understand the interplay between parameters and the lines in parameter space that are capable of fitting each observable.

The parameters that differ from those in ref (53) are given in Table 1, together with the resulting singlet and triplet scattering lengths. Compared to ref (53), R_SR,0 and R_SR,1 have changed by 0.03 and −0.0072 Å, respectively; N_S has been fixed at a more physically reasonable value of 10 for both states, compared to its original value of 3; C₆ has increased by 0.9%; in atomic units it is 3257(1)E_ha₀⁶, compared with 3227(18)E_ha₀⁶ from ref (69); and C₈ has decreased by 3% from the fitted value of ref (53), but our fitted value corresponds to C₈ = 3.568(4) × 10⁵E_ha₀⁸, which is closer to the theoretical value of C₈ = 3.62(12) × 10⁵E_ha₀⁸ from ref (74) and well within its uncertainty.

Table 1. Parameters of the Fitted Interaction Potential, Including the Resulting Singlet and Triplet Scattering Lengths^a.

	singlet	triplet
RSR,S (Å)	2.873240(6000)	4.772797(1600)
NS (Å)	10	10
ASR,S/hc (cm–1)	–3798.0168	–420.536
BSR,S/hc (cm–1 Å10)	1.30971 × 108	2.56041 × 109
a0,S/hc (cm–1)	–4954.229 485	–217.146766
C6/hc (107 cm–1 Å6)	1.568975(400)
C8/hc (108 cm–1 Å8)	4.815171(5000)
as or at (a0)	433.05(65)	30.55(22)

^aOnly quantities that are different from those in ref (53) are listed. The derived parameters A_SR, B_SR, and a_0,S, which arise from the continuity constraints applied to V(R) and V′(R), are included for convenience in evaluating the potential curves. The rounded values of A_SR correspond to the rounded values of B_SR and differ slightly from the values obtained with the exact B_SR.

Key differences between our potential curves and those in ref (53) are shown in Figure 9. The derivative discontinuity in the triplet potential of ref (53) is clearly visible at 4.78 Å. The present triplet potential continues smoothly through R_SR,1 and so has a zero-energy turning point at slightly shorter range, 4.7693 Å, compared to 4.7702 Å for the potential of ref (53). The effect of the larger values of N₀ and N₁ is seen in the steeper short-range repulsive walls shown in the inset.

Figure 9.

Comparison of the short-range region of the triplet curve of the present work (blue) with that of ref (53) (dashed black). The derivative discontinuity in the potential curve of ref is clearly visible.⁵³ The inset shows the complete potential wells and the extrapolations onto the repulsive wall, including the singlet curve (red for the present work).

3.2.1. Uncertainties in Fitted Parameters

The interaction potential determined here is obtained by fitting four potential parameters to four experimental quantities. The 4-parameter space is actually a subspace of a much larger space, of approximately 50 parameters, that were fitted to FT spectra in ref (53). Reference (53) itself gave no uncertainties for the fitted parameters or estimates of the correlations between them. It is therefore not appropriate or practical to use error estimates based on deviations between observed and calculated properties. We can nevertheless make estimates of errors based on the derivatives of the calculated observables with respect to potential parameters, as described in Appendix C, and these are included in Table 1.

3.3. Predictions of the Fitted Potential

3.3.1. Scattering Lengths

The singlet and triplet scattering lengths given in Table 1 are within the uncertainties of those obtained by Hood et al.,⁴⁶a_s = 428(9)a₀ and a_t = 30.4(6)a₀. Their value of a_t was obtained from E_–1^hp, so it is of similar accuracy to ours, though ours is shifted slightly because we have determined improved values of the dispersion coefficients. Their value of a_s was obtained by combining a_t with measurements of interaction shifts, as described above. Our value of a_s is considerably more precise, both because of the greater precision of E_–1 compared to the interaction shifts and because of the use of full coupled-channel calculations.

Hood et al. also gave the scattering length for the ha channel as −693a₀, without an error estimate. This quantity is important because the large negative value enhances the intensity of photoassociation transitions originating from atoms in the ha state.⁴⁷ Our interaction potential gives an even larger negative value of −860(2)a₀. The value of ref (46) arose fairly directly from their measurements of interaction shifts, which are dominated by the ha channel. Our value is principally based on the more reliable and precise measurement of E_–1^ha, so it is expected to be more accurate.

In recent work, Warner et al.⁷⁵ have created overlapping Bose–Einstein condensates of Na and Cs and measured the scattering length for the aa channel to be 18(4)a₀ at B = 23 G and 29(4)a₀ at B = 894 G. Our fitted interaction potential gives 14a₀ at 23 G and 30a₀ at 894 G, in good agreement with the measurements.

3.3.2. Bound States with L = 0

Figure 10 shows the energies of bound states of NaCs below the lowest (aa) threshold as a function of magnetic field. All states with M_F between 1 and 6 are included (but not states with M_F from −6 to 0). The calculation uses a basis set with L_max = 0, so only states with L = 0 are shown. At zero field, the states can be grouped according to their hyperfine characters. The uppermost group, with zero-field binding energies from 350 to 500 MHz, are n = −1 states with character (f_Na, f_Cs) = (1, 3). The next group, from 2000 to 2800 MHz, are n = −2 states with character (2, 3). The group near 3900 MHz has character (1, 3) but with n = −2. Finally, the deepest group shown, which starts slightly deeper than 4000 MHz and extends off the bottom of the plot, is made up of n = −3 states with character (2, 4).

Figure 10.

Weakly bound states of NaCs with L = 0 below the aa threshold as a function of magnetic field. The aa threshold is shown as a dashed black line. States with M_F = 4 that can cause s-wave Feshbach resonances are shown as solid black lines; other values of M_F are color-coded as shown in the legend. Only states with M_F from 1 to 6 are shown. The zero of energy is the threshold energy at zero field, which lies 6278.1 MHz below the hyperfine centroid.

For each group, f_Na couples to f_Cs to give a resultant F, which is a good quantum number at zero field. The allowed values of F run from f_Cs – f_Na to f_Cs + f_Na in steps of 1. In a magnetic field, each state splits into components with different M_F values (though not all possible values of M_F are shown). The value of F for a zero-field state can therefore be inferred from the largest M_F present. M_F is a good quantum number when L_max = 0, but at moderate fields (between 30 and 500 G), states of the same M_F but different F approach one another and mix; above these fields, m_f,Na and m_f,Ca are better quantum numbers than F.

3.3.3. Resonances in s-Wave Scattering

It is important to distinguish between L_in for the incoming wave and L for a bound state. The widest resonances in s-wave scattering (L_in = 0) are due to s-wave bound states (with L = 0) and are referred to as s-wave resonances. Because M_tot = M_F + M_L is conserved and is 4 for an incoming s wave at the aa threshold, bound states with L = 0 can cause resonances at this threshold only if they have M_F = 4. These states are shown as solid black lines in Figure 10.

Bound states with even L > 0 can also cause Feshbach resonances in s-wave scattering, which are usually narrower. The widest of these are d-wave resonances due to d-wave states (with L = 2). In this case, M_L can take values from −2 to 2, so d-wave states with M_F = 2 to 6 can have M_tot = 4 and cause resonances in s-wave scattering at the aa threshold.

Figure 11(a) shows all states with M_tot = 4 that lie close to the aa threshold, as a function of magnetic field. This calculation uses a basis set with L_max = 2, so it includes states with both L = 0 and 2. States with L = 0 and M_F = 4 are again shown in black, whereas states with L = 2 are color-coded according to M_F. To allow this labeling, the small couplings off-diagonal in M_F are neglected in the bound-state calculations (but not in the corresponding scattering calculations). The pattern of zero-field states for each hyperfine group is similar in structure to Figure 10, but the states with L = 2 are shifted upward by a rotational energy. Figure 11(b) shows an expanded view of the bound states, plotted as energies below the aa threshold, and Figure 11(c) shows the resulting s-wave scattering length. A resonance occurs at every field where a state with M_tot = 4 crosses the threshold, but some of them are too narrow to be visible on the grid of magnetic fields used for Figure 11(c). Nevertheless, all of them can be characterized in scattering calculations, using the methods of ref (60), to give values for B_res, Δ, and a_bg from eq 5.

Figure 11.

(a) Weakly bound states of NaCs with M_tot = 4 and L = 0 or 2 below the aa threshold as a function of magnetic field. The aa threshold is shown as a dashed black line. States with L = 0 and M_F = 4 that can cause s-wave Feshbach resonances are shown as solid black lines; states with L = 2 that can cause d-wave resonances are color-coded according to M_F as shown in the legend. The zero of energy is the threshold energy at zero field. (b) Expanded view of (a), with energies shown as binding energies with respect to the aa threshold. (c) s-wave scattering length at the aa threshold, showing resonances where bound states cross the threshold. Some of the resonances that exist are too narrow to see on the 0.2 G grid used for the calculation of the scattering length.

Table 2 gives the parameters of all s-wave and d-wave resonances with Δ > 10^–4 G, together with quantum numbers for the states that cause them. It may be noted that the s-wave resonance near 864 G, which appeared at 864.11 G in a calculation with L_max = 0, is shifted to 864.13 G in the calculation with L_max = 2. This demonstrates the small effect of basis functions with L = 2 on s-wave properties and justifies the use of L_max = 0 in fitting.

Table 2. Feshbach Resonances with Widths Greater Than 10^–4 G in s-Wave and p-Wave Scattering at the aa Threshold^a.

resonances in s-wave scattering (34 total)
Bres (G)	Δ (G)	abg (a0)	L	MF
161.23	0.0007	19.8	2	2
218.30	0.0002	21.6	2	2
230.24	0.0007	21.9	2	3
366.36	0.0010	24.8	2	3
668.14	0.066	28.9	2	6
699.69	0.0012	29.2	2	5
712.89	0.011	29.4	2	5
756.80	0.0016	29.9	2	4
773.90	0.0002	30.2	2	4
853.50	0.0008	34.2	2	2
864.13	1.27	30.7	0	4
864.42	–0.0001	–105	2	3
917.07	0.0003	30.6	0	4
932.20	0.0003	30.9	0	4
1032.90	0.0035	33.2	2	4
1036.15	0.022	33.0	2	5
1080.00	0.001	34.3	2	3
1133.52	0.0005	36.9	2	3
1243.02	14.4	40.2	0	4
1252.53	–0.026	–22.6	2	2
1292.57	17.7	20.5	0	4

resonances in p-wave scattering (17 total)
Bres (G)	Δ (G)	vbg (107 a03)	L	MF
805.41	0.021	–1.50	1	4
806.80	0.0083	–1.53	1	5
1173.87	0.42	–1.50	1	4
1216.83	0.0067	–1.47	1	3
1222.78	0.21	–1.53	1	4

^aThe p-wave calculations are for M_tot = 4 only.

Zhang et al.⁴⁷ observed a weak d-wave Feshbach resonance at 864.5 G on the shoulder of the s-wave resonance at 864.11 G. The bound state responsible for this is visible in Figure 11(a) and crosses the threshold at 864.42 G, causing a resonance of width Δ = −10^–4 G. It is an impressive demonstration of the quality of our interaction potential that it can reproduce the position of this resonance to within 0.1 G and identify the bound state responsible: it is a state with L = 2, M_F = 3 (brown in Figure 11) involving a pair of states originating from (f_Na, f_Cs, F) = (2, 3, 5) and (2, 4, 6) that experience an avoided crossing at around 700 G.

3.3.4. Resonances in p-Wave Scattering

Resonances can also occur in p-wave scattering (L_in = 1) due to either p-wave states (with L = 1) or states with higher odd L. In the gas phase, such resonances are usually observed only at relatively high temperatures (several μK), but in optical tweezers it is possible to enhance them selectively by promoting one atom to a motionally excited state. Zhang et al.⁴⁷ observed a group of p-wave resonances at around 807 G for Na + Cs, with complicated structure, and used them to produce a single p-wave molecule in the tweezer.

For p-wave scattering, M_L,in can be −1, 0, or −1 and M_tot = M_F,in + M_L,in. Thus, even at the aa threshold, M_tot can be 3, 4, or 5. If the resonant state has L = 1, M_L can be −1, 0, or −1 too. For each of the three values of M_tot, p-wave resonances arise from bound states with M_F = M_tot and M_tot ± 1. Figure 12(c) shows the p-wave bound states below the aa threshold and the corresponding scattering volume v, but only for the case M_tot = 4. The bound states show considerable similarities to the s-wave and p-wave ones in Figures 10 and 11. Figure 12(c) shows that s-wave and p-wave states share several similarities, but with shifts due to the different rotational energy in each case. The positions, widths, and assignments of the widest resulting resonances are given in Table 2, but it must be remembered that this is for only one of the three possible values of M_tot for p-wave scattering at the aa threshold. Figure 12 and Table 2 show that the group of resonances observed⁴⁷ near 807 G are mainly the p-wave analogs of the s-wave resonance near 864 G.

Figure 12.

(a) Weakly bound p-wave states of NaCs, with M_tot = 4 and L = 1, below the aa threshold as a function of magnetic field. The aa threshold is shown as a dashed black line. Only states with M_tot = 4 are shown. The states are color-coded according to M_F as shown in the legend. The zero of energy is the threshold energy at zero field. (b) Expanded view of (a), with energies shown as binding energies with respect to the aa threshold. (c) p-wave scattering volume at the aa threshold, calculated at a collision energy of 2 μK × k_B. Some of the resonances that exist are too narrow to see on the 0.2 G grid used for the calculation of the scattering volume.

3.3.5. Resonance in the cg Channel

As described above, Hood et al.⁴⁶ measured the position of an inelastic loss feature in the cg channel at 652.1(4) G. Our fitted potential produces a resonance at 654.3 G. However, its width is Δ = 43 G, so the difference between the resonance position and the observed loss peak is only 5% of the width. The calculated background scattering length is −41a₀.

4. Conclusions

We have used measurements on ultracold scattering and spectroscopy in optical tweezers,^43,45−48 combined with previous work using Fourier transform spectroscopy,⁵³ to determine improved potential curves for the singlet and triplet states of NaCs. We have used coupled-channel calculations based on these curves to characterize the weakly bound states involved and to make predictions for additional bound states and Feshbach resonances.

Each measurement of a spectroscopic transition or resonance position is sensitive to the properties of one or two specific bound states of the molecule. These properties are in turn sensitive to particular features of the interaction potentials. Our work has produced important insights into these relationships and the ways that combinations of measurements can be used to determine features of the potential curves.

For NaCs, as for many other diatomic molecules, the mid-range parts of the potential curves had previously been accurately determined from spectroscopy at relatively high temperatures. For NaCs, this mid-range part extends from just outside the inner turning point at the dissociation energy to 10.2 Å and is expressed as a power-series expansion for each of the singlet and triplet curves.⁵³ Our approach is to change the mid-range part by as little as possible to retain its ability to fit the higher-temperature spectra. We thus retain the mid-range expansion unchanged and adjust only the extrapolations to long and short range. This gives sufficient flexibility to reproduce the ultracold observables.

The binding energy of the least-bound (uppermost) state in a particular scattering channel, E_–1, is closely related to the scattering length a for that channel. The relationship between E_–1 and a depends on the dispersion coefficients for the long-range interaction, particularly C₆, but only weakly. Because the dispersion coefficients are often known fairly accurately from independent theory,⁶⁹E_–1 is a good surrogate for a. If it can be measured for two channels that represent significantly different mixtures of singlet and triplet states, the singlet and triplet scattering lengths a_s and a_t can be disentangled. This is the case for NaCs, where E_–1 has been measured both for a spin-stretched channel that is pure triplet in character^45,46 and for the ha channel,⁴⁸ which has about 50% singlet character. Because the mid-range part of the potential is held fixed to reproduce the higher-temperature spectra and the dispersion coefficients have only limited influence, the two values of E_–1 determine the short-range parts of the singlet and triplet curves.

Magnetic Feshbach resonances exist where a weakly bound molecular state crosses a scattering threshold as a function of magnetic field. These states are often supported by thresholds in which one or both atoms are in excited hyperfine states. States that cause resonances at the lowest threshold are thus often bound by considerably more than the least-bound state. In NaCs, the state that causes the resonance observed in the lowest channel⁴⁷ is bound by more than 4 GHz with respect to the threshold that mostly supports it. Because of this, it is much more sensitive to the dispersion coefficients than the least-bound states. The requirement to reproduce this resonance position as well as the least-bound states places a strong constraint on the dispersion coefficients, particularly C₆.

In potential curves from higher-temperature spectroscopy, the dissociation energy (and thus the absolute binding energies of all of the deeply bound states) is usually obtained from extrapolation rather than measured directly. However, Raman transfer of ultracold molecules to a deeply bound state provides a direct measurement of its absolute binding energy. If the mid-range part of the potential is held fixed to reproduce the higher-temperature spectra, this provides a second (and different) constraint on the dispersion coefficients. Satisfying this along with the constraint from the resonance position allows C₆ and C₈ to be disentangled.

There is an important general insight here. The spectroscopy of ultracold molecules often provides measurements of the energies of the least-bound molecular states supported by one or more thresholds. Measurements of tunable Feshbach resonances are often sensitive to somewhat deeper states, with binding energies in the GHz range. When such measurements are combined, they can provide very precise values for dispersion coefficients. The same principle applies when different Feshbach resonances provide implicit information on two or more states with substantially different binding energies with respect to the thresholds that support them.

For NaCs, we find that the different ultracold observables can be fitted simultaneously only if C₆ is increased by about 0.9% from the theoretical value. Our fitted value corresponds to 3256(1)E_ha₀⁶, compared to 3227(18)E_ha₀⁶ from ref (69). Our fitted value C₈ = (3.568(4) × 10⁵)E_ha₀⁸ is well within the error bounds of the value of ref (74).

Accurately fitted interaction potentials are key to progress in ultracold scattering and spectroscopy. They provide predictions of new experimental observables, which are often crucial in designing experiments and locating new spectroscopic lines. They also provide calculated scattering lengths, as a function of magnetic field, which are unavailable from other sources. These are often crucial in experiments that need precise control of the scattering length, such as those exploring Efimov physics or quantum phase behavior.

Appendix A: Magnetic Dipole Interaction and Second-Order Spin–Orbit Coupling

At long range, the coupling V̂^d(R) of eq 3 has a simple magnetic dipole–dipole form that varies as 1/R³.^55,76 However, for heavy atoms such as Cs, second-order spin–orbit coupling provides an additional contribution that has the same tensor form as the dipole–dipole term and dominates at short range.^77,78 In the present work, V̂^d(R) is written as

15

where e⃗_R is a unit vector along the internuclear axis and λ is an R-dependent coupling constant. This term couples the electron spins of Na and Cs atoms to the molecular axis.

The second-order spin–orbit splitting is not known for NaCs. However, it contributes only when L_max > 0 and makes only very small contributions for s-wave states and resonances due to them. We model it here using the functional form used for RbCs,⁷⁹

16

where E_h is the Hartree energy and α ≈ 1/137 is the atomic fine-structure constant. To account for the smaller size of Na compared to Rb, we adjust the values of A_2SO^short and A_2SO for RbCs to shift the second-order spin–orbit contribution to short range by 0.757a₀. This gives parameters A_2SO^short = −27.8, A_2SO = −0.027, β_2SO^short = 0.80, and β_2SO = 0.28 for NaCs. Future experiments may allow the determination of these parameters, but changing them would have little effect on the singlet and triplet curves obtained here (though it might have a significant effect on the widths of predicted d-wave resonances).

Appendix B: Coupled-Channel Methods

We expand the total wave function of the molecule or colliding pair of atoms in a coupled-channel representation,

17

Here, ξ represents all coordinates of the pair except the internuclear distance R. The functions Φ_j(ξ) form a complete orthonormal basis set for motion in the coordinates ξ, and the factor R^–1 serves to simplify the action of the radial kinetic energy operator. The component of the wave function in each channel j is described by ψ_j(R), and these are the functions shown in Figures 3 and 5. The expansion (eq 17) is substituted into the total Schrödinger equation, and the result is projected onto a basis function Φ_i(ξ). The resulting coupled differential equations for the functions ψ_i(R) are

18

where δ_ij is the Kronecker delta, , E is the total energy, and

19

The different equations are coupled by the off-diagonal terms W_ij(R) with i ≠ j.

The coupled equations may be expressed in matrix notation,

20

If there are N basis functions included in the expansion (eq 17), ψ(R) is a column vector of order N with elements ψ_j(R), I is the N × N unit matrix, and W(R) is an N × N interaction matrix with elements W_ij(R).

In general, there are N linearly independent solution vectors ψ(R) that satisfy the Schrödinger equation subject to the boundary condition that ψ(R) → 0 in the classically forbidden region at short range. These N column vectors form a wave function matrix Ψ(R).

Appendix C: Uncertainties in Fitted Parameters

Our objective is to fit a set of M parameters p_j, collectively represented by the vector p, to a set of N observables y_i^obs. We minimize the weighted sum of squares of residuals,

21

where u_i is an uncertainty for observable i. In standard least-squares methods, with N ≫ M, the common uncertainty of the measurements is usually estimated statistically from the minimum value of χ² achieved in the fit, generally with a denominator N – M. In the present work, N = M = 4, so this is not possible. Instead, we choose the values u_i as the experimental uncertainties.

To estimate uncertainties in the fitted parameters, we follow the usual procedures for nonlinear least-squares fitting. At the final values of the parameters, we calculate a 4 × 4 Jacobian matrix J with ele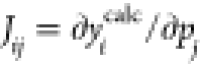ments . We scale this by the chosen uncertainties to define the matrix A with elements A_ij = J_ij/u_i and the Hessian matrix H = A^TA; the elements of the latter are half the second partial derivatives of χ² with respect to potential parameters. We choose uncertainties in the parameters defined by a contour at χ² = 1. The variance–covariance matrix is then Θ = H^–1. The resulting correlated uncertainties Θ_jj^1/2 are ±0.006 Å in R_SR,0, ±0.0016 Å in R_SR,1, ±4 × 10³ cm^–1 Å⁶ in C₆, and ±5 × 10⁵ cm^–1 Å⁸ in C₈. The correlation matrix has elements 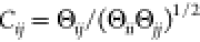; all elements have a magnitude below 0.6 except that between R_SR,0 and R_SR,1, which is −0.995.

It should be noted that these uncertainties do not take account of model dependence due to fixing the parameters of the mid-range potential. These are hard to estimate in a systematic way because ref (53) did not discuss uncertainties in the parameters or the correlations between them.

In correlated fits, it often is not sufficient to specify parameters to within their uncertainties. The sensitivity of calculated properties to the parameters depends on the Hessian matrix H rather than its inverse Θ.⁸⁰ To reproduce the observables to within their uncertainties, each parameter must be specified to a precision of at least H_jj^–1/2, which may be much smaller than Θ_jj. The parameters in Table 1 are given to a precision based on these values.

The authors declare no competing financial interest.

Special Issue

Published as part of The Journal of Physical Chemistry virtual special issue “Cold Chemistry”.