Alternating Learning Approach for Variational Networks and Undersampling Pattern in Parallel MRI Applications

Abstract

This work proposes an alternating learning approach to learn the sampling pattern (SP) and the parameters of variational networks (VN) in accelerated parallel magnetic resonance imaging (MRI). We investigate four variations of the learning approach, that alternates between improving the SP, using bias-accelerated subset selection, and improving parameters of the VN, using ADAM. The variations include the use of monotone or non-monotone alternating steps and systematic reduction of learning rates. The algorithms learn an effective pair to be used in future scans, including an SP that captures fewer k-space samples in which the generated undersampling artifacts are removed by the VN reconstruction. The quality of the VNs and SPs obtained by the proposed approaches is compared against different methods, including other kinds of joint learning methods and state-of-art reconstructions, on two different datasets at various acceleration factors (AF). We observed improvements visually and in three different figures of merit commonly used in deep learning (RMSE, SSIM, and HFEN) on AFs from 2 to 20 with brain and knee joint datasets when compared to the other approaches. The improvements ranged from 1% to 62% over the next best approach tested with VNs. The proposed approach has shown stable performance, obtaining similar learned SPs under different initial training conditions. We observe that the improvement is not only due to the learned sampling density, it is also due to the learned position of samples in k-space. The proposed approach was able to learn effective pairs of SPs and reconstruction VNs, improving 3D Cartesian accelerated parallel MRI applications.

I. INTRODUCTION

The acquisition of high-resolution three-dimensional (3D) volumetric data of the human body in magnetic resonance imaging (MRI) is time-consuming. Furthermore, shortening the scan time is necessary for capturing high-resolution images, dynamic processes, quantitative imaging, and reducing health-care costs with increased patient comfort.

The reduction of MRI acquisition time, also known as accelerated MRI, has been obtained by different approaches. Fast magnetic resonance (MR) pulse sequences (FPS) [1]–[3], parallel imaging (PI) [4]–[6], compressed sensing (CS) [7]–[10], and deep learning (DL) image reconstructions [11]–[14] are some examples of the advancements in the accelerated MRI field. These approaches have different mechanisms, FPS can collect more k-space data per unit of time [3], PI uses a receiver array with different coil sensitivities to capture more data in parallel [15] to overcome k-space undersampling, CS relies on incoherent sampling and sparse reconstruction, while DL uses neural networks able to learn non-linear filters to remove artifacts from undersampling.

The quality of image reconstruction in accelerated MRI depends on the sampling process. CS theory shows that specific properties of the sampling process (such as incoherence) [7], [16] are necessary to effectively recover images with specific reconstruction approaches (such as sparse reconstruction) [17]. In this sense, properties such as restricted isometry properties (RIP) and incoherence have guided the design of sampling patterns [7], [9], [18] for sparse reconstructions in MRI. However, new theoretical results [19], [20] showed that incoherence is not a strict requirement in MRI, which are also supported by several studies [21], [22]. In other words, justifying that empirical designs for sampling patterns (SP) such as variable density [23]–[25] or Poisson-disc [26], [27] (also written as “Poisson disk”) can also be effective in MRI. Recently, combined variable density and Poisson-disc [28], [29] has been introduced to MRI and it is currently one of the best SPs for CS-MRI.

Many accelerated MRI studies have shown that the design of the SP can be customized using reference k-space data of other similar images of particular anatomies [30]–[34]. One class of such approaches, called adaptive sampling, adjusts the probability of the k-space points of variable density SP according to the magnitude of the k-space. Another approach, known as statistical experimental design techniques [35], [36], uses optimization of Cramér-Rao lower bounds for finding good sampling patterns. In both approaches, the particularities of the reconstruction algorithm are not considered in the design of the SP, even though some general formulation is usually assumed.

In data-driven approaches, the customization of the SP is done by optimization algorithms, considering images or datasets containing several images of particular anatomy and a specific method for image reconstruction [37]–[42]. The main idea is that the designed SP should perform well with other images of the same anatomy when the same reconstruction method is used. If one considers that the parameters of the image reconstruction methods can also be learned, then these approaches can be extended to jointly learning the reconstruction and the SP, as seen in [43]–[49]

Most prior data-driven approaches to learning the SP, as in [37]–[40], formulate the SP learning as a subset selection problem and implement it using greedy search algorithms, which lead to extremely high computational costs for SPs of large sizes, particularly the ones used in Cartesian 3D acquisitions. To circumvent this problem, some methods extended deep learning approaches to jointly learn SP and the reconstruction network [43], [44], by implementing the SP as a neural network parameter to be learned. One approach for jointly learning the sampling and reconstruction, called Learning based Optimization of the Under-sampling PattErn (LOUPE), has been originally proposed in [43] for one-coil MRI problems and extended in [50] for multi-coil, or parallel, MRI. Unfortunately, LOUPE does not learn a unique SP, but a sampling density. This way LOUPE does not learn the advantages of the relative position and the distance between k-space samples. For example, studies [26]–[29] on the Poisson-disc SPs have shown that the distance between the sampled points is fundamental to the success of SPs used in CS and parallel MRI. In [44], [46], [47], parametric formulation of non-Cartesian k-space trajectories are learned. Although they are very interesting approaches, they require non-uniform Fourier transforms, which is not the best fit for our Cartesian 3D problem, as described next in Section I.A.

In [42], a fast learning approach for SPs of large sizes was proposed. This approach, called bias-accelerated subset selection (BASS), is still based on the subset selection formulation, as the greedy approaches, but it is as fast as any neural network training algorithm. BASS has shown great results for parallel and CS problems in MRI. However, BASS was never combined with deep learning reconstructions before.

The difficulty in using BASS in a combined learning approach arises because it is originally a monotone algorithm, while deep learning training algorithms are usually done with non-monotone stochastic methods. Because of this, we investigate four variations of the alternating learning approach for the jointly learning SP and reconstruction problem. These variations exploit the use or not of monotonicity and/or reduced initial learning rate.

The SP learning approach is formulated as a subset selection problem, solved either with the original BASS or with its new non-monotone version presented in this paper. The parameters of the reconstruction network are learned using backpropagation algorithms, such as ADAM [51]. The four variations consider the use or not of monotonicity check after each execution of ADAM, and the use or not of reduced initial learning rates.

The version with monotonicity and the reduced initial learning rate is referred to as the proposed one when compared to other kinds of methods. We illustrate through several experiments that this approach is stable and obtains a better pair of SPs and learned reconstruction, superior to other joint learning approaches for the same problem, such as LOUPE, and superior to reconstructions trained with the currently best human-designed SPs for MRI, the combined variable density with Poisson-disc [28], [29].

A. The specific content of this paper

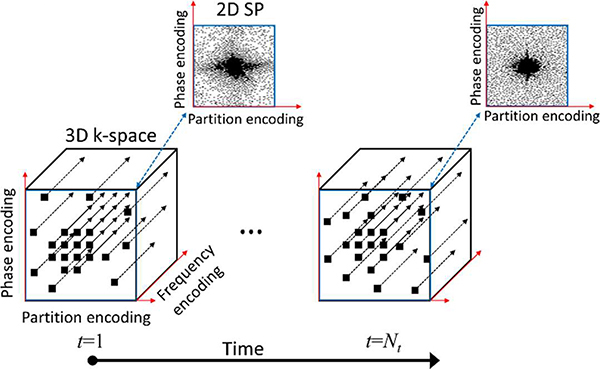
We propose and validate the new alternating learning approach to jointly learning the SP and the parameters of a variational network (VN) [11] used for image reconstruction in accelerated parallel MRI applications. We focus on Cartesian 3D problems used in high-resolution and quantitative MRI, in which the data are collected along multiple k-space lines in a frequency-encoding direction with the SP specifying the 2D phase/partition-encoding positions to be acquired, as illustrated in Fig. 1. The acquisition is a 3D process, but we assume that a Fourier transform is applied in the frequency-encoding direction and the volume is separated into multiple slices for 2D reconstructions. We assume that both, the learned SP and VN, would be saved in the MRI scanner for future acquisitions of images of the same anatomy.

Fig. 1.

Illustration of the 3D+time data collection scheme considered in this work. The SP is in 2D+time, it comprises the time-varying phase and partition encoding positions, for each of which data are to be collected by the MRI scanner for all frequency encoding positions.

II. Methods

A. Models used

Parallel MRI methods such as SENSE [52], [53] and many CS approaches [54], including VN, are based on the image-to-k-space forward model, such as

$$\mathbf{m}=\mathbf{F}\mathbf{C}\mathbf{x}=\mathbf{E}\mathbf{x}.$$ (1)

Here x represents 2D+time images, of size N_y × N_z × N_t, where N_y and N_z are horizontal and vertical dimensions and N_t is the number of time frames, C denotes the coil sensitivities transform, which maps x into multi-coil-weighted images of size N_y × N_z × N_t × N_c, with N_c coils. F represents the spatial Fourier transforms (FTs), which are N_t × N_c repetitions of the 2D-FT, and m is the fully sampled data, of size NN_s, where N = N_yN_zN_t and N_s = N_c. Both systems combine in the encoding system E. When accelerated MRI by undersampling is used, then the SP is included in the model as

$$\overline{\mathbf{m}}={\mathbf{S}}_{\text{Ω}}\mathbf{F}\mathbf{C}\mathbf{x}={\mathbf{E}}_{\text{Ω}}\mathbf{x},$$ (2)

where S_Ω is the sampling function using the SP specified by Ω ⊂ Γ (same for all coils) which is a subset of the fully sampled Cartesian set Γ, and $\overline{\mathbf{m}}={\mathbf{S}}_{\text{Ω}}\mathbf{m}$ is the undersampled multi-coil k-space data (or k-t-space when N_t > 1), with MN_s elements, where M is the number of sampled points in the undersampled k-space. Essentially, the operation S_Ωm maintains the k-space points that are sampled and it eliminates the ones that are not sampled. The acceleration factor (AF) in MRI is given by N/M. Depending on the approach used to obtain coil sensitivity, additional sampling might be necessary. Here, we assume a central area of the k-space will be always fully sampled and used to compute coil sensitivities with auto-calibration methods, such as [55].

B. Variational networks for image reconstruction:

The VNs are inspired by the minimization problem [56], given by

$$\widehat{\mathbf{x}}\in \underset{\mathbf{x}}{\arg \min }\frac{1}{2}{\Vert {\mathbf{E}}_{\text{Ω}}\mathbf{x}-\overline{\mathbf{m}}\Vert }_2^2+{\sum }_{f=1}^{N_f}\langle \text{Φ}\left({\mathbf{K}}_f\mathbf{x}\right),\mathbf{1}\rangle ,$$ (3)

where the complex-valued images x, undersampled k-space data $\overline{\mathbf{m}}$, and the encoding system E_Ω are described in (1) and (2). The first term in (3) is the data-discrepancy term, modeled by a squared Euclidean norm, and the second term is a regularizing penalty, composed of N_f linear operators K_f, with potential function Φ, and 1 is a vector of ones.

However, instead of minimizing the cost function in (3), the VN approximates a solution by a fixed number of iterations, denoted by J, of a gradient descent-like algorithm [11], given by

$${\mathbf{x}}_{j+1}={\mathbf{x}}_j-\left({\text{α}}_j{\mathbf{E}}_{\text{Ω}}^{\ast }\left({\mathbf{E}}_{\text{Ω}}{\mathbf{x}}_j-\overline{\mathbf{m}}\right)+{\sum }_{f=1}^{N_f}{\mathbf{K}}_{j,f}^b{\mathrm{\Phi }}^{\prime }\left({\mathbf{K}}_{j,f}{\mathbf{x}}_j\right)\right).$$ (4)

In (4), 1 ≤ j ≤ J + 1 represents the iteration index, where J = 10 was chosen in this work. In the context of deep learning [57], [58], it corresponds to the number of layers. All the VN parameters, i.e. convolutional filters ${\mathbf{K}}_{j,f}^b$, K_j,f (N_f = 24) and step-sizes α_j, are learned from data [11]. In this study, activation functions Φ′ are fixed rectified linear units (ReLu) [57]. The set of convolutional filters ${\mathbf{K}}_{j,f}^b$, K_j,f are typical convolutional filters implemented in deep learning packages. Each convolutional filter K_j,f, maps the complex-valued images (represented as a multichannel image of size N_y × N_z with 2N_t channels, where real and imaginary components of the complex-valued images are treated as separate channels) into one filter output of size N_y × N_z. A 2D convolution is performed on each channel with a learned kernel of size 11 × 11 (different for each channel), and their output are added to a one-channel output. The linear filter ${\mathbf{K}}_{j,f}^b$_, maps the one-channel output, after applying the activation function Φ′, back to the original image representation using other learned kernels of the same size.

Note that the VN in equation (4) resembles a general iterative regularized reconstruction algorithm. The central term in (4), ${\text{α}}_j{\mathbf{E}}_{\text{Ω}}^{\ast }\left({\mathbf{E}}_{\text{Ω}}{\mathbf{x}}_j-\overline{\mathbf{m}}\right)$, is responsible for reducing k-space error, while the right term in (4), ${\sum }_{f=1}^{N_f}{\mathbf{K}}_{j,f}^b{\mathrm{\Phi }}^{\prime }\left({\mathbf{K}}_{j,f}{\mathbf{x}}_j\right)$, reduces undesired artifacts in the image. These components are different for each layer j. The output of a VN can be written as

$$\widehat{\mathbf{x}}=R_{\mathrm{\theta }}(\overline{\mathbf{m}},\text{Ω}),$$ (5)

where R_θ represents the VN reconstruction with network parameters $\mathrm{\theta }={\left\{{\left\{{\mathbf{K}}_{j,f}^b,{\mathbf{K}}_{j,f}\right\}}_{f=1}^{N_f},{\text{α}}_j\right\}}_{j=1}^J$, input sampling pattern Ω and undersampled data $\overline{\mathbf{m}}={\mathbf{S}}_{\text{Ω}}\mathbf{m}$, and output reconstructed image $\widehat{\mathbf{x}}$. Note that coil sensitivity maps used in C (that is part of E_Ω) are also input parameters for image reconstruction, but since they are obtained from $\overline{\mathbf{m}}$, and they are not considered a learned parameter, we will not make them explicit in (5).

C. Adjoint followed by U-net for direct reconstruction:

VN architectures resemble CS iterative reconstructions, however, different approaches for reconstruction with neural networks (NNs) are often used [13], [14], [58]. In [43], image reconstruction is composed of a NN as aliasing removal post-filtering after the adjoint operator ${\mathbf{E}}_{\text{Ω}}^{\ast }$. For parallel MRI, it can be written as:

$$\overline{\mathbf{x}}={\mathbf{E}}_{\text{Ω}}^{\ast }\overline{\mathbf{m}},$$ (6)

followed by:

$$\widehat{\mathbf{x}}=U_{\mathrm{\theta }}(\overline{\mathbf{x}}).$$ (7)

Compared to the VN, this approach does not use the image-to-k-space model in the network itself, in (7). It only uses the adjoint operator, ${\mathbf{E}}_{\text{Ω}}^{\ast }$, in (6), to compute the initial aliased image $\overline{\mathbf{x}}$. Nevertheless, we can still represent both steps as in (5), with $\widehat{\mathbf{x}}=R_{\mathrm{\theta }}(\overline{\mathbf{m}},\text{Ω})=U_{\mathrm{\theta }}\left({\mathbf{E}}_{\text{Ω}}^{\ast }\overline{\mathbf{m}}\right)$. In [43], the NN is a U-net. In this study, we will call this approach UNET.

D. Joint learning the sampling pattern and image reconstruction:

The joint learning process can be formulated through the following criterion:

$$\widehat{\mathrm{\Omega }},\widehat{\mathrm{\theta }}=\underset{\begin{array}{c}\text{Ω}\subset \text{Γ},\mathrm{\theta }\in \text{Θ}\\ s.t.\left|\text{Ω}\right|=M\end{array}}{\text{argmin}}\frac{1}{N_i}{\sum }_{i=1}^{N_i}f\left({\mathbf{x}}_i,R_{\mathrm{\theta }}\left({\overline{\mathbf{m}}}_i,\text{Ω}\right)\right),$$ (8)

where $R_{\mathrm{\theta }}\left({\overline{\mathbf{m}}}_i,\text{Ω}\right)={\widehat{\mathbf{x}}}_i$ is the reconstructed image using undersampled data ${\overline{\mathbf{m}}}_i$, with sampling pattern Ω and network parameters θ. Note that i represent the index of the image and k-space data in the dataset with N_i elements. Ideally, undersampled data from true k-space data should be used, as ${\overline{\mathbf{m}}}_i,={\mathbf{S}}_{\text{Ω}}{\mathbf{m}}_i$, and reference images can be produced by x_i= R(m_i, Γ), as a reference for fully sampled image reconstruction (which do not necessarily need to be a deep learning reconstruction). Under some limited circumstances [59], the undersampled data could be synthetically generated using ${\overline{\mathbf{m}}}_i={\mathbf{E}}_{\text{Ω}}{\mathbf{x}}_i$, if images and coil sensitivities are available.

The criterion (8) is defined in the image domain. This approach is useful when fully-sampled k-space data are not directly available, but images reconstructed from fully-sampled data and coil sensitivities are available, or when one wants to weigh differently particular regions of interest of the image to obtain better quality in more relevant structures. In this study, we will consider $f\left({\mathbf{x}}_i,R_{\mathrm{\theta }}\left({\overline{\mathbf{m}}}_i,\text{Ω}\right)\right)={\Vert {\mathbf{x}}_i-R_{\mathrm{\theta }}\left({\overline{\mathbf{m}}}_i,\text{Ω}\right)\Vert }_2^2$, since it is a criterion easily available in most deep learning tools and it is the same criterion used in the other compared approaches.

III. Proposed alternating learning approach:

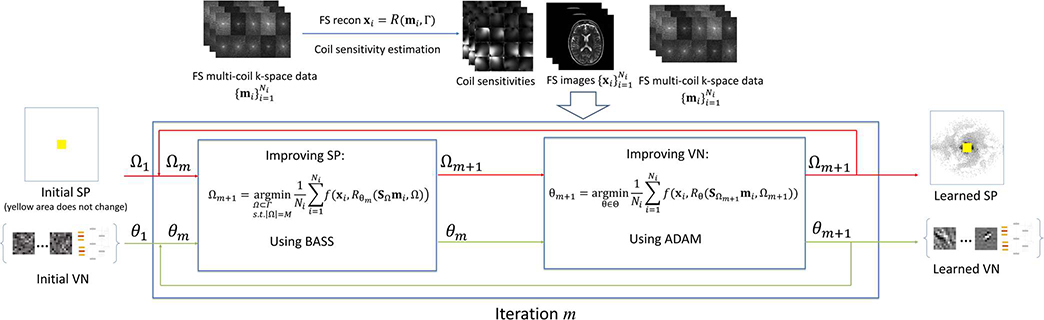
In this work, we propose an alternating approach for this joint learning process in (8), represented as:

$${\text{Ω}}_{m+1}=\underset{\begin{array}{c}\text{Ω}\subset \text{Γ}\\ s.t.\left|\text{Ω}\right|=M\end{array}}{\text{argmin}}\frac{1}{N_i}{\sum }_{i=1}^{N_i}f\left({\mathbf{x}}_i,R_{{\mathrm{\theta }}_m}\left({\mathbf{S}}_{\text{Ω}}{\mathbf{m}}_i,\text{Ω}\right)\right),$$ (9)

$${\mathrm{\theta }}_{m+1}=\underset{\mathrm{\theta }\in \text{Θ}}{\text{argmin}}\frac{1}{N_i}{\sum }_{i=1}^{N_i}f\left({\mathbf{x}}_i,R_{\mathrm{\theta }}\left({\mathbf{S}}_{{\text{Ω}}_{m+1}}{\mathbf{m}}_i,{\text{Ω}}_{m+1}\right)\right),$$ (10)

where the problem in (9) is a subset selection problem and the problem in (10) is a neural network training. For fast solving the subset selection problem, the BASS algorithm [42] was chosen, and for neural network parameters learning the ADAM algorithm was chosen [51]. An overview of the proposed approach is shown in Fig. 2. BASS has been proven effective in learning the SP for CS and parallel MRI methods before, however it was never tested with deep learning algorithms. ADAM is currently one of the most used approaches to train deep neural networks.

Fig. 2.

General overview of the proposed approach for jointly learning the SP and the parameters of a VN on Parallel MRI problems.

We investigate four variations for the joint alternating approach, testing the effect of two different techniques for the alternating decrease of the cost function: a) forced monotonicity, by checking the reduction of the cost functions at each alternating step; and b) reducing initial learning rate. The forced monotonicity is used to make sure the parameters θ_m+1 learned in a particular iteration are better than the previous θ_m (the improvement strongly depends on the choice of the parameters used in ADAM, including initial learning rate and the number of iterations). Reducing the learning rate is typically used in deep learning algorithms, including ADAM. In our proposed approach the learning rate is always reduced during ADAM executions, however, the initial learning rate of each ADAM run can be reduced or can be fixed.

A. Bias-Accelerated Subset Selection:

BASS is a heuristic optimization approach for subset selection based on bit change, such as Pareto optimization for subset selection (POSS) [60]–[62]. In general, bit change algorithms are much faster than greedy algorithms. While greedy algorithms compute many candidates before choosing the one with maximum improvement, bit-wise mutation algorithms change the current best SP, adding and removing some elements of it, according to some heuristic rule, accepting the new solution if it is better. BASS is faster because it uses heuristics rules to choose the new k-space points based on large observed errors in the k-space [42].

The learning process can start with any known SP, such as Poisson-disc, variable density, or even an empty SP. It is also possible to constrain some regions of the SP, such as the central area that is used for coil sensitivity auto-calibration. BASS, originally proposed in [42], is detailed in Algorithm 1, for completeness, where the cost function $F(\text{Ω})=\frac{1}{N_i}{\sum }_{i=1}^{N_i}{\Vert {\mathbf{d}}_i\Vert }_2^2$, for ${\mathbf{d}}_i={\mathbf{x}}_i-R_{\mathrm{\theta }}\left({\overline{\mathbf{m}}}_i,\text{Ω}\right)$, is different from [42] in this study.

Algorithm 1:

BASS | Non-monotone BASS

1.	Ω ← Ωinit
2.	K ← Kinit
3.	l ← 1
4.	While l ≤ L do
5.	Ωr ← select-remove (Ω, K, ρr(K, M, l))
6.	Ωa ← select-add(Ω, K, ρa(K, M, N, l))
7.	Ω′ ← (Ω\Ωr) ⋃ Ωa
8.	if |Ω| ≠ M, Ω ← Ω′
9.	if |Ω| = M
10.	if F(Ω′) ≤ F(Ω), Ω ← Ω′ |or 10. Ω ← Ω′
11.	else K ← ⌊(K − 1)α⌋ + 1 |or 11. K ← ⌊(K − 1)α + 1
12.	l ← l + 1
13.	return Ω

In this paper, we also present a new non-monotone version of BASS. In the non-monotone version, line 10 of Algorithm 1 is replaced by Ω ← Ω′, and line 11 is simply replaced by K ← ⌊(K − 1)α⌋ + 1.

In Algorithm 1, K_init is the initial number of elements of the SP that change at each iteration, α < 1 is the decreasing rate of K, and ρ_a and ρ_r are the probabilities of selecting an element to be added to or removed from the SP. The probabilities can be constant or a function of K, M, N, l, as discussed next.

B. Modification in the heuristics used in BASS:

In BASS, the elements of Ω_a and Ω_r are selected by the functions select-add and select-remove in similar ways. The functions select-add(Ω, K, ρ_a(K, M, N, l)) and select-remove(Ω, K, ρ_r(K, M, l)) in Algorithm 1 are used to modify Ω in the composition of a new candidate Ω′. The number K of elements to be added/removed varies with iteration. For 1 ≤ i ≤ N_i, let ${\mathbf{e}}_i=\mathbf{F}\mathbf{C}{\mathbf{d}}_i=\mathbf{F}\mathbf{C}\left({\mathbf{x}}_i-R_{{\mathrm{\theta }}_m}\left({\overline{\mathbf{m}}}_i,\text{Ω}\right)\right)$, which is essentially the transformation of the residual error of the image reconstruction d_i to the multi-coil k-space. Note that each of the N components of e_i is an N_s-dimensional vector. For 1 ≤ k ≤ N, and 1 ≤ s ≤ N_s, where [e_i]_k,s, denotes the s-th component (corresponding to the coil) of the k-th component (corresponding to the k-space position) of e_i. For select-add, we define the measure of importance (MI) used in this work, for 1 ≤ k ≤ N, as

$${\mathbf{\epsilon }}_k=\frac{1}{N_i{N}_s}{{\sum }_{i=1}^{N_i}{\sum }_{s=1}^{N_s}|{[{\mathbf{e}}_i]}_{k,s}|}^2,$$ (11)

which is referred to as the ε-map. The purpose of select-add is to select K elements from Γ\Ω in a randomly biased manner [42], and its MI prioritizes to add unselected k-space elements with large error, which may significantly reduce the cost function. Note that in the non-monotone version F(Ω) is never computed. Then, the convergence relies on the correlation between F(Ω) and the chosen MI. For select-remove, a sequence with K elements that are in Ω, is generated in the same way, but using r_k as the MI, instead of ε_k. The MI for select-remove is

$${\mathbf{r}}_k=\frac{1}{N_i{N}_s}{\sum }_{i=1}^{N_i}\frac{{\sum }_{s=1}^{N_s}{|{[{\mathbf{e}}_i]}_{k,s}|}^2+\delta }{{\sum }_{s=1}^{N_s}{|{[{\mathbf{m}}_i]}_{k,s}|}^2+\delta },$$ (12)

for 1 ≤ k ≤ N, which is referred to as the r-map, with δ a small constant to avoid zero/infinity in the definition of r_k. This MI prioritizes the removal of k-space sampled elements that still have large errors compared to their size. Essentially, the large elements of r_k are elements that do not fit well in the recovery, and their removal may not significantly increase the cost function.

The probability of pre-selecting elements should respect predefined ranges, K/M < ρ_r(K, M, l) ≤ 1 and K/(N − M) < ρ_a(K, M, N, l) ≤ 1. We used constant probabilities for ρ_a = 1/4 and ρ_r = 1/8, and we used the same positional constraints (PC) rules proposed in [42]. The most expensive part of select-add and select-remove is the computation of the recoveries given by $R_{{\mathrm{\theta }}_m}\left({\overline{\mathbf{m}}}_i,\text{Ω}\right)$. However, these computations are cheap because they are just forward propagations of a VN, which are much faster than iterative CS reconstructions [63].

IV. Experimental Setup:

A. Datasets:

In these experiments, we utilized two MRI datasets to test the proposed approach. One dataset, denominated brain, contains 335 brain T₂-weighted images from the fast MRI dataset [64]. Of these, 260 were used for training, 60 for validation, and 15 for testing. Validation and testing images are never used for learning, however, the validation images are used to monitor the generalizability of the learning process by computing the cost function of each iteration with similar data that are not used for training. The k-space data has a size N_y × N_z × N_t × N_c = 320 × 320 × 1 × 16, and the reconstructed images are N_y × N_z × N_t = 320 × 320 × 1. The brain T₂-weighted images from the fast MRI dataset are originally acquired with multislice 2D pulse sequences, which would allow only 1D undersampling. However, we can use them as an illustrative example of learning a hypothetical 2D SP for 3D Cartesian brain acquisitions [65].

The second dataset comprises the knee joint, denominated knee, contains 335 T_1ρ-weighted knee images for quantitative T_1ρ mapping [66], of size N_y × N_z × N_t × N_c = 256 × 64 × 2 × 16, and the reconstructed images are N_y × N_z × N_t = 256 × 64 × 2. Of these, 260 were used for training, and 60 for validation, and 15 for testing. The k-space data for all images are normalized by the largest component. These images were acquired with the 3D Cartesian acquisitions as described in [66].

B. Compared approaches:

The proposed alternating approach was compared with the following training approaches for VN:

• General training VN, VD+PD SP

• Specific training VN, VD+PD SP

• VN trained with LOUPE, LOUPE SP

The two best learned VN approaches, the VN with the proposed alternating approach and the one with specific training were compared against other learned and CS reconstructions:

• Specific training UNET, VD+PD SP

• Proposed alternating approach with UNET

• Compressed Sensing, VD+PD SP

The details of each method are described below. We trained and tested the SPs and the reconstructions for AF from 2 to 20, spaced by 2.

C. General training of a VN:

The VN was trained with several randomly generated SPs of several kinds, including Poisson-disc [27], [67], variable density [25], uniform density [67], and combined variable density with Poisson-disc (VD+PD) [28] and different AF. One VN training is performed for all AF, the VD+PD SP used for testing may have not been used for training. Each of the N_i elements of the datasets contains an image sequence, with respective coil sensitivities and SP. The SP is different in each element, randomly assigned between the kinds of SP mentioned above. We used 80 epochs of the ADAM algorithm [51] with an initial learning rate of 1×10⁻⁴, with a learning rate drop factor of 1/10 applied every 5 epochs, and a batch size of 8 images.

D. Specific training of a VN or UNET:

A VN or UNET [43] were trained with only one specific SP, the same SP for all N_i elements, a combined variable density with Poisson-disc (VD+PD), for each AF. One VN or UNET training is performed for each AF. We used 80 epochs of the ADAM algorithm [51] with an initial learning rate of 1×10⁻⁴, with a learning rate drop factor of 1/10 applied every 5 epochs, and a batch size of 8 images.

E. Joint SP and VN training with LOUPE:

We trained a VN (also UNET, in some specific experiments) within LOUPE framework [43], [50], where the VN and the sampling density (SD) are learned. The VN is tested with a specific SP that is one realization obtained from the learned sampling density (SD), named LOUPE SP. One joint SD and VN training is performed for each AF. We used 80 epochs of ADAM with an initial learning rate of 1×10⁻⁴, for the VN weights, and 1 for the SD, with a learning rate drop factor of 1/10 applied every 5 epochs, and a batch size of 8 images. The slope parameter of LOUPE is 0.25.

F. Configuration of the training process of the proposed approach:

The proposed alternating learning algorithm consists of alternating executions of BASS and ADAM. Each run of BASS starts with K_init=1024 and α=0.5 and stops when K=1 (or when L=31 in the non-monotone version). Each run of ADAM uses 8 epochs with an initial learning rate of 1×10⁻⁴, with a learning rate drop factor of 0.25 applied every 2 epochs, and batch size of 8 images. The alternating procedure is repeated until the cost function stops decreasing for 5 cycles or a maximum of 100 alternating cycles passed. When a reduced initial learning rate is used, each ADAM run starts with the previous initial learning rate multiplied by a reduction factor of 0.9.

G. Compressed sensing reconstructions:

We included CS reconstructions using sparsity on spatial finite differences for the brain dataset, as in [42], and using spatio-temporal finite differences for the knee dataset, as in [68], [69]. The CS is used as a reference for non-deep learning methods. The training dataset was used to optimize the regularization parameter, as in [69].

H. Assessment:

The quality of the results obtained with the SP and reconstructions was evaluated using the root mean squared error (RMSE), structural similarity index (SSIM), and high-frequency energy norm (HFEN). All measurements of individual images are averaged among the tested images. The RMSE is defined as:

$$RMSE\left({\mathbf{x}}_i,{\widehat{\mathbf{x}}}_i\right)=\sqrt{{\Vert {\mathbf{x}}_i-{\widehat{\mathbf{x}}}_i\Vert }_2^2}.$$ (13)

The SSIM is defined in [70] and HFEN in [71]. Only RMSE is computed for training and validation images along the training process. The testing images have RMSE, SSIM, and HFEN values computed only with the final SPs and reconstructions.

V. Results:

A. Illustration of convergence of the proposed approaches:

We illustrate several aspects of the convergence of the proposed approaches, showing the curves of the cost function for validation or training images. We compare the four alternating approaches, showing the convergence with or without monotonicity and reduced initial learning rate. We compare the proposed alternating approach with one long run of BASS, as in [42] without alternating learning, using an already learned VN. Finally, we illustrate the performance of the proposed approach with other deep learning solvers, such as stochastic gradient descent with momentum (SGDM) and root mean square propagation (RMSprop) [72].

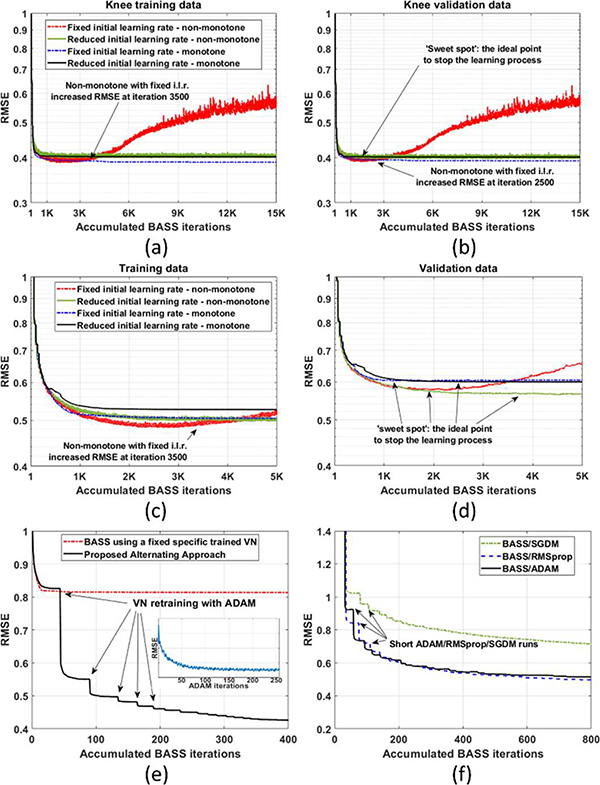
In Fig. 3(a)–(d), we show the RMSE over the accumulated BASS iterations of the proposed approach when forced monotonicity is enabled (monotone) and disabled (non-monotone for both: BASS and ADAM), and we also show the convergence of both methods with a fixed or reducing initial learning rate for ADAM, as a way to stabilize and improve convergence. This experiment uses the knee dataset in 3(a)–(b) and brain dataset in 3(c)–(d), both at AF=16. The forced monotonicity only assure a monotone decrease of the cost with training images, while the validation images are used to monitor generalizability. When monotonicity is disabled, the convergence has some small oscillations, but the local average behavior is similar to the monotone version. Except that, the cost starts to increase again on the non-monotone version with a fixed initial learning rate. The increase of the RMSE with training data (divergence of the algorithm) happened due to the use of a large initial learning rate combined with a short number of epochs. Proper reduction of the initial learning rate solves this problem (a factor of 0.9 was used).

Fig. 3:

Curves of cost function over accumulated BASS iterations for the (a) training images and the (b) validation images for knee dataset, and (c)-(d) for brain dataset, showing the performance of the four alternating approaches. In (e), the original BASS with a fixed specific trained VN (no re-training) is compared with the proposed alternating approach, with the same initial conditions. In these figures, the discontinuities are due to the short runs of the ADAM algorithm. Only some runs are marked with arrows and an illustrative convergence curve for ADAM is shown in the small box. In (f) the convergence using other deep learning solvers, instead of ADAM, is shown.

In Fig. 3(e), the original BASS [42] with a fixed specific trained VN is compared with the proposed alternating approach. The convergence curves in Fig. 3(e) illustrate the importance of retraining the VN to learn how to improve the reconstruction with the current SP. In Fig. 3(f) we illustrate the RMSE over the accumulated BASS iterations for ADAM, RMSprop, and SGDM. All methods use the same parameters except SGDM, in which the initial learning rate was 1×10⁻⁵ because it diverged with the same initial rate of the other methods. Due to the lower initial learning rate, the SGDM was slower than the others were.

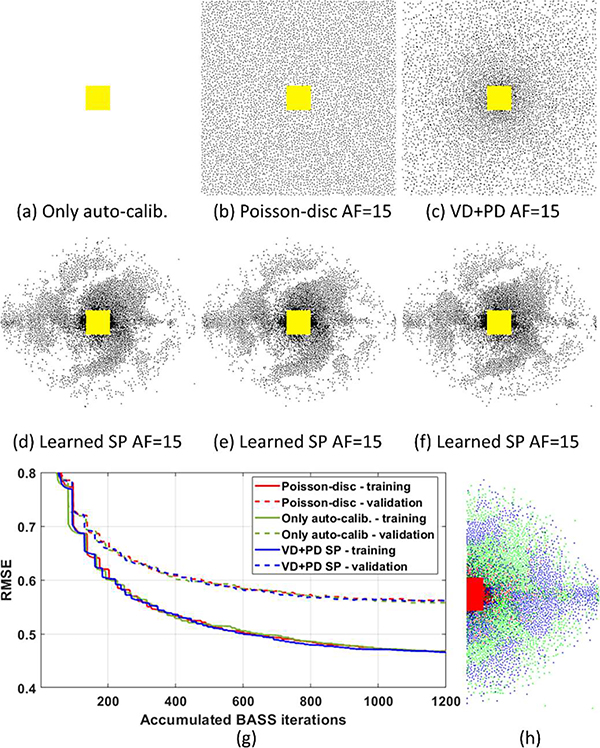
In Fig. 4 we illustrate the learned SPs considering different initial SPs: an empty SP, only with the fixed central auto-calibration area, shown in Fig. 4(a), a Poisson-disc SP, shown in Fig. 4(b), and the VD+PD SP, in Fig. 4(c). The RMSE curves for the training and validation datasets are shown in Fig. 4(g), while the resulting learned SPs with AF=15 are shown in figures 4(d)–(f), respectively. All resulting learned sets, SP and VN, obtained a final RMSE between 0.555 and 0.560 for the validation images with very similarly-looking learned SPs. In Fig. 4(h), we briefly observe what was learned in the SPs related to the position of the samples in the k-space. One can see comparing in Fig. 4(f) and Fig. 4(h) that many empty areas in one side of the k-space (with original samples in green) were sampled in the negative side of the k-space (with projected sampled positions shown in blue). There are very few coincident samples (in red) outside the auto-calibration area, where both sides of the k-space were sampled.

Fig. 4:

Convergence of the proposed approach with different initial SPs and randomly initialized VNs. The initial SPs are shown in (a) an empty SP, only with the fixed auto-calibration area in yellow, in (b) a Poisson-disc SP, and in (c) a VD+PD SP. The corresponding learned SPs are shown in (d)-(f). In (g), the RMSE over accumulated BASS iterations is shown, where the discontinuities are due to short runs of the ADAM algorithm. In (h) we illustrate some aspects of the position of the samples in the learned SP: in green the original positions of the left-hand side of the learned SP, in blue the projected samples from the negative side of the k-space (equivalent to horizontal and vertical flipping), and in red the coincident samples.

The results in Fig. 4 essentially mean that the proposed approach learned to exploit complex-conjugated symmetry of the k-space, as in half-Fourier, or partial-Fourier, acquisitions in MRI [73]. Moreover, the sampling density of the SP decreases from the center to the outer areas, indicating it learned variable density, and that there is a very regular spacing between samples that increases from the center to the outer areas, indicating it learned the importance of spacing between samples, like in Poisson-disc and VD+PD SPs.

B. Comparison between the tested approaches:

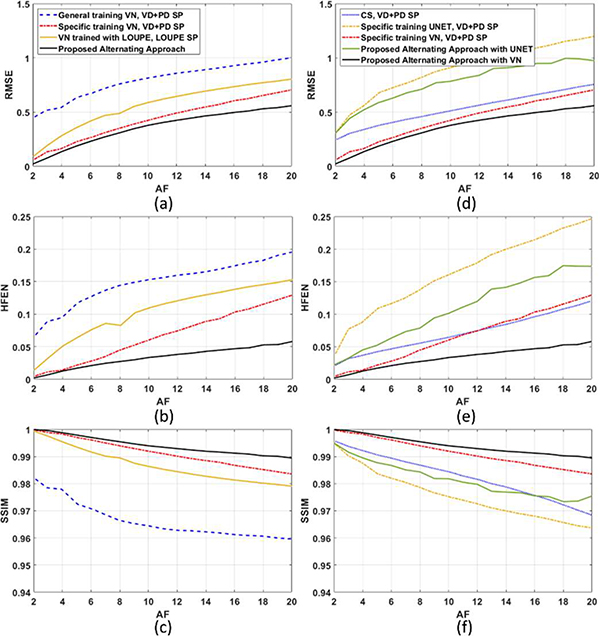
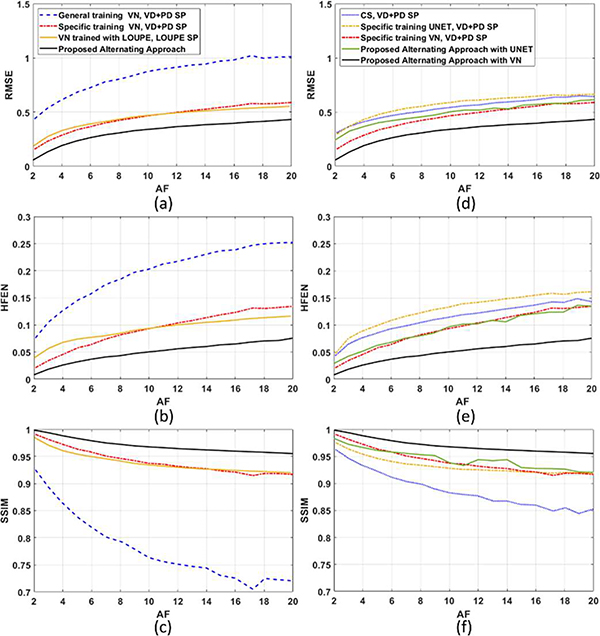
We compare the performance of the proposed approach against the approaches cited in Section IV.B. The resulting RMSE, HFEN, and SSIM for the testing dataset at different acceleration factors (AF) are shown in Fig. 5 for the brain dataset and in Fig. 6 for the knee joint dataset.

Fig. 5:

RMSE, HFEN, and SSIM of the tested approaches on the brain dataset. In (a)-(c) the results for the VN with different learning approaches are shown, and in (d)-(f) the results comparing VN, UNET, and CS are shown.

Fig. 6:

RMSE, HFEN, and SSIM of the tested approaches on the knee dataset. In (a)-(c) the results for the VN with different learning approaches are shown, and in (d)-(f) the results comparing VN, UNET, and CS are shown.

The performance of the VN depends significantly on the type of SP, and also on the way it was trained. Particularly, the quality of the reconstructions was better when the VN was trained for one specific SP (note that the same learned SP was used for testing and should be used in new scans that will be reconstructed with the trained VN). In LOUPE, the training process randomly generates different SPs from a learned sampling density. The weakness of this approach is that the specific k-space positions of the samples are disregarded, and LOUPE is not able to learn the advantages of the relative position between k-space samples. The relative position of the k-space samples is key in Poisson-disc SPs, as well as VD+PD SPs, and it is also learned by the proposed approach.

The UNET reconstructions performed worse than VN, as shown before in [58]. UNET with specific training performed poorly with the brain dataset, as seen in Fig. 5, but was better with the knee dataset, as seen in Fig. 6. In both cases, the proposed alternating approach improved the quality of the UNET reconstructions and VN over their versions with specific training with VD+PD SP.

The proposed approach with VN was able to surpass the performance of the other alternatives, including CS, UNET, and even the VN trained with LOUPE or specifically for a VD+PD SP. On average, the improvements obtained by the proposed alternating approach ranged from 1.0% (SSIM, Brain, AF=4) to 62.0% (HFEN, Knee, AF=2) over the second-best approach (Specific training VN, VD+PD SP). Note that the VD+PD SP is among the best know SPs for parallel MRI. It has an excellent asymptotic performance (which means it performs well with different kinds of reconstructions and different data). Nevertheless, it is interesting that the proposed approach learned in hours a different SP that performed better than the VD+PD SP for the given data.

In Table 1 we included the difference in training time. Note that the proposed approach consumes more training time than the other ones because it requires multiple (average of 40) short retraining (8 epochs each) of the VN.

Table 1:

Approximate training times for the datasets on an NVIDIA GTX 1660 GPU 4GB memory with Intel i5-4570S CPU and 32GB memory.

	General or Specific VN training	VN training with LOUPE	Proposed Approach
VN training or retraining epochs	80	80	Average of 40×8
Accumulated BASS iterations	0	0	Average of 1000
Training time brain dataset	5.4 hours	5.6 hours	23.0 hours
Training time knee dataset	3.2 hours	3.8 hours	12.5 hours

C. Visual comparison of the resulting images and SPs:

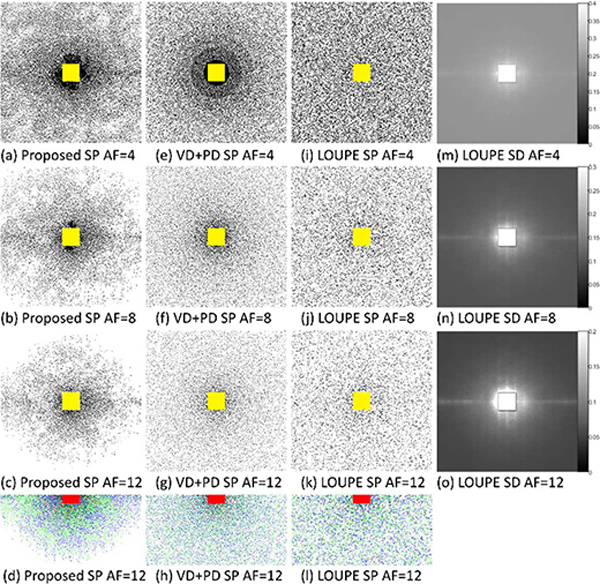
In Fig. 7 we compared the SPs learned by the proposed approach and LOUPE for VN, and also compared them with the VD+PD SP. Note that all of them show variable density behavior, with more samples near the center of the k-space (just outside the fixed central auto-calibration area). VD+PD SP has an isometric behavior (by design), while LOUPE and the proposed approach have not. Curiously, the proposed approach learned that more samples in the lower and mid frequencies are necessary for proper reconstruction, and, as discussed in Fig. 4(h), the proposed approach learned to exploit complex-conjugated symmetry of the k-space, variable density, and the importance of spacing between samples. The sampling density learned by LOUPE was very similar (apart from the scaling due to AF) across different AF. One can compare these aspects of the SP learned with the proposed approach with VD+PD SP and LOUPE SP in figures 7(d), 7(h), and 7(l).

Fig. 7:

Comparing SPs for VN at different AFs for the brain dataset. In (a)-(c) the SPs learned by the proposed approach, for AF=4, 8, and 12, are shown. In (e)-(g) the VD+PD SPs are shown, for the same AFs. In (i)-(k) the SPs generated from the sampling densities (SD) learned in LOUPE are shown. The corresponding SDs learned by LOUPE are shown in (m)-(o). Yellow areas correspond to fixed auto-calibration areas of the SP. In (d), (h), and (l) we compare the position of the samples in the SPs: in green the original positions of the lower side of the SP, in blue the projected position of the samples of the negative side of the k-space (equivalent to horizontal and vertical flipping), and in red coincident samples.

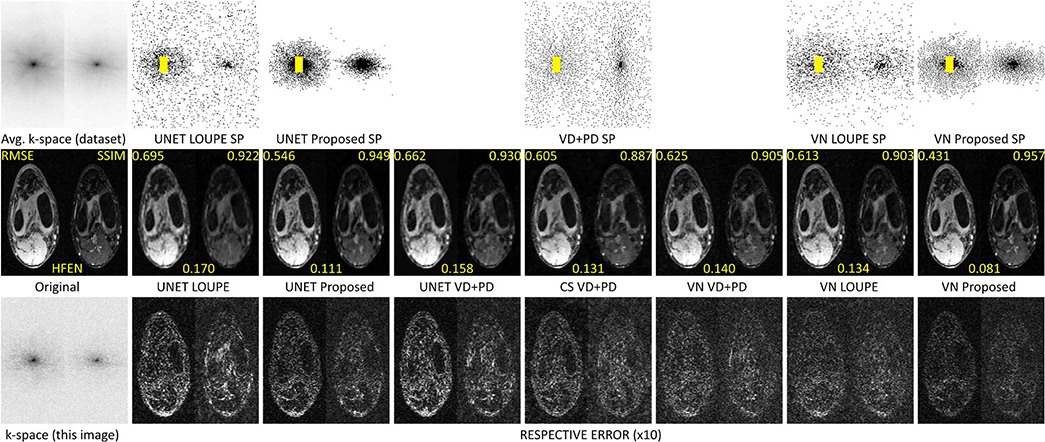
In Fig. 8, some visual results for the brain dataset are shown. We compared the images obtained by LOUPE and by specific trained VN with VD+PD SP against the proposed approach. We also show the results with UNET and CS, with their corresponding RMSE, SSIM, and HFEN. One can observe improvements obtained by the proposed approach in the reconstructed images, in the error maps, and the details on the bottom row, with arrows pointing to relevant structures that were better recovered by the proposed approach.

Fig. 8:

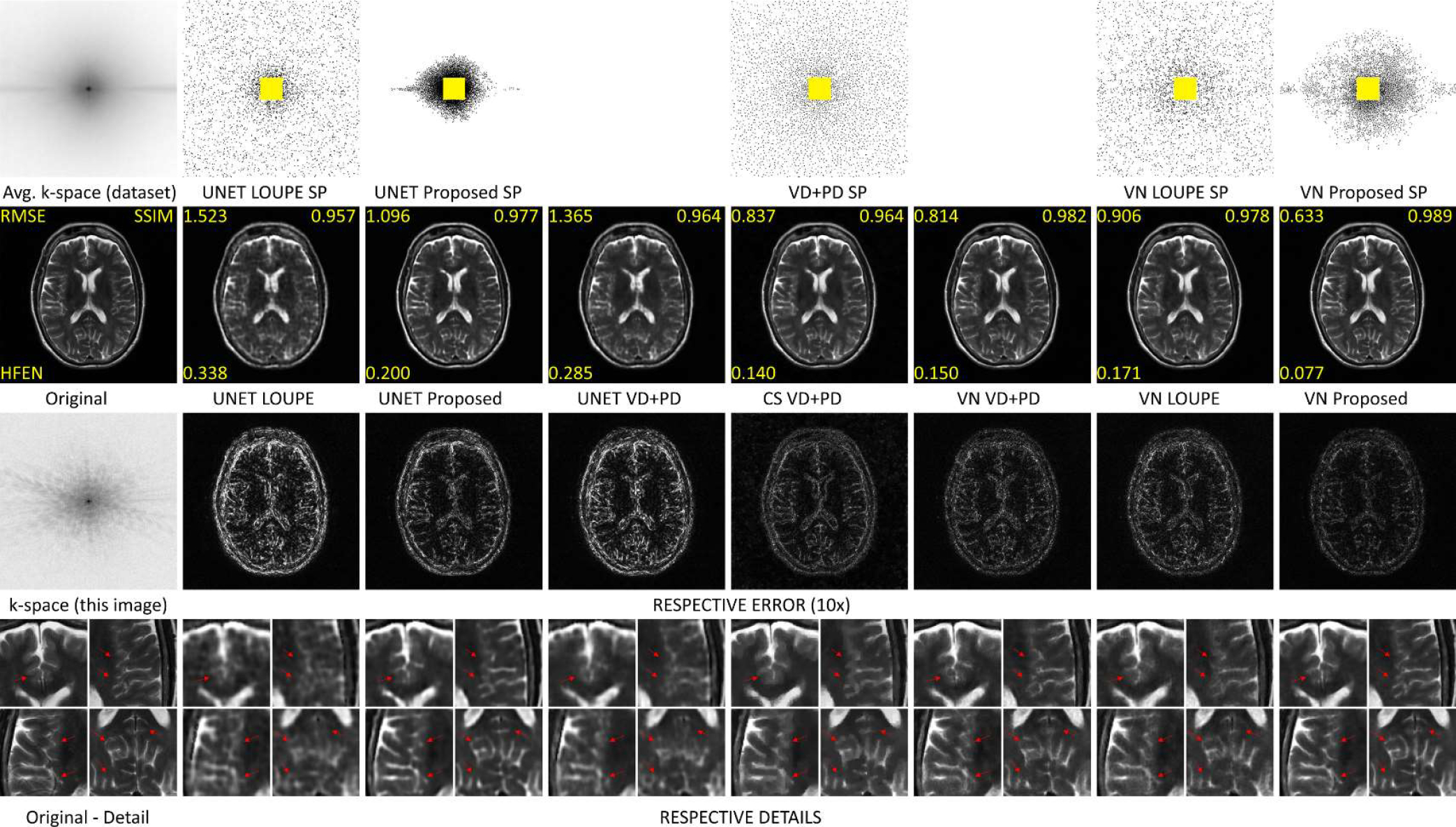
Comparing SP and images with brain dataset at AF=20. In the top row the average of the magnitude of the k-space of the training dataset and the SPs are shown. In the second row, the original reference image and the reconstructed images are shown, with their respective RMSE, SSIM, and HFEN. In the third row, the k-space of the reference image is shown, as well as the corresponding error maps of the reconstructions right above them. In the bottom row, the details of the reconstructed images of the same column are shown. Arrows point to the relevant structures in the detailed reconstructed images.

In Fig. 9, some visual results for the knee joint dataset are shown. Note that LOUPE and the proposed approach learned that the sampling density should follow the average magnitude of the k-space. However, LOUPE performed worse than the proposed approach because it does not learn the importance of the relative position of the samples. The sampling density of the VD+PD SP does not follow well the average of the k-space data, resulting in an RMSE worse than the other methods. Also, the proposed approach learned that a variable number of samples over time is beneficial, allocating more samples in the first frame, as previously observed in [42].

Fig. 9:

Comparing SP and images with knee dataset at AF=12. In the top row the average of the magnitude of the k-space of the training dataset and the SPs are shown. In the second row, the original reference image and the reconstructed images are shown, with their respective RMSE, SSIM, and HFEN. In the bottom row, the k-space of the reference image is shown, as well as the corresponding error maps of the reconstructions right above them.

D. Using larger datasets:

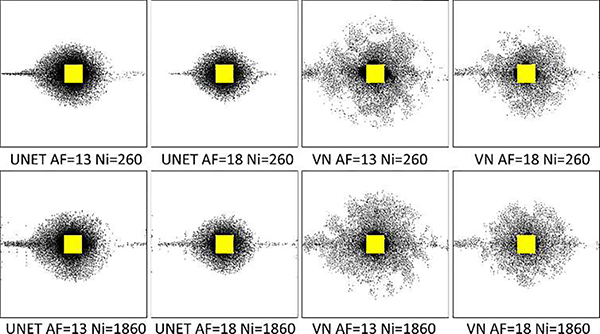
Depending on the network architecture and application, using 260 images for training may not be enough. In Fig. 10, we observe the effect of the training size, comparing the results of VN and UNET with a training size of 1860 images, 7 times larger. Note that the RMSE with UNET reduced 17% and with VN it reduced only 2% on the testing data. Only minor changes in the learned SP are seen.

Fig. 10:

Comparing SP and reconstruction error of UNET and VN when training was performed with 260 or 1860 images. For AF=18, VN reduced the RMSE from 0.50 to 0.49, and UNET from 0.80 to 0.67, and for AF=13, VN reduced the RMSE from 0.43 to 0.42, and UNET from 0.69 to 0.57 on the testing dataset.

E. T1ρ mapping:

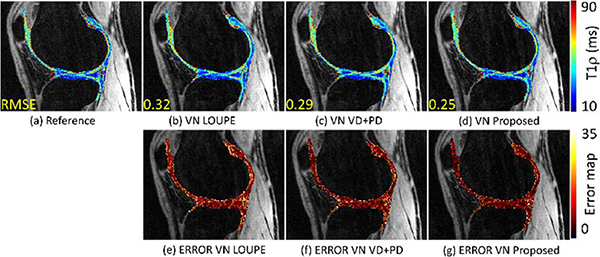
We illustrate the performance of the proposed approach for T_1ρ mapping of the knee cartilage following [66]. We compare the proposed approach against LOUPE and the VN with specific training with VD+PD SP. The T_1ρ mapping is performed in the cartilage region on the longitudinal plane (in-plane) of the recovered 3D volume. The 3D+time volume has N_x × N_y × N_z × N_t = 256 × 256 × 64 × 2, where N_x = 256 corresponds to the samples in the frequency-encoding direction, field-of-view of 130 × 130 × 130 mm³, with in-plane resolution of 0.5× 0.5 mm², and slice thickness of 2 mm. In Fig. 11(a)–(d) we illustrate the resulting T_1ρ maps and in Fig. 11(e)–(g) the pixel-wise error maps.

Fig. 11:

Comparing T_1ρ mapping results with knee joint dataset at AF=4. In (a) the reference T_1ρ map produced from fully-sampled images is shown. In (b)-(d) T_1ρ map produced by the VN reconstruction using LOUPE, using VD+PD SP, and using the proposed approach. In (e)-(g) the error maps are shown.

VI. Discussion:

The proposed approach is an interesting alternative for combined learning of the SP and the reconstruction parameters in 3D Cartesian parallel MRI applications. It performed better than LOUPE, mainly because LOUPE does not learn the relative position between samples in k-space, which are relevant in parallel MRI. Some other joint approaches that can potentially be used for this problem are [44], [46], [47], however, they require non-Cartesian Fourier transforms in their network. These approaches have more freedom in learning arbitrary k-space trajectories, while the proposed approach is limited to subset selection formulation to the SP learning, but they require more processing due to the need for non-uniform Fourier transform [74].

The SP learning algorithm used in the proposed approach, known as BASS, has been proven effective with different CS algorithms [42] in large-scale problems. However, it is the first time it has been merged with deep learning algorithms for MR image reconstruction. Four different versions of the alternating approach are shown. The non-monotone alternating approach should stop when the RMSE of the validation images increases. However, the convergence of the non-monotone approach can be stabilized by using a reduced initial learning rate on the VN retraining. This is also the most indicated variation for further development on batch training on very large datasets.

In [42], it was also shown that BASS can work with different cost functions. There is no need for differentiability in BASS, which is a requirement in neural networks trained with backpropagation algorithms. In this study, we illustrate the performance of the proposed approach with the squared l₂-norm of the error as the cost function. However, other criteria can improve the sampling and reconstruction in different aspects for specific MRI applications or problems.

An important aspect of the joint learning approaches is the stability of the results. Due to the non-convex nature of the problem, the learning approach is likely to converge to a local minimum. In other words, several parameters of the learning algorithm are relevant (like the initial solution, step-sizes, decaying rates). In this sense, we observe that the proposed approach was very stable, as seen in figures 3 and 4. The stability of the joint learning approaches is important, as mentioned in [44], [47].

As seen in the results of figures 7, 8, and 9, the proposed approach learned SPs that are more densely sampled in low and mid frequencies than VD+PD and LOUPE. The learned SPs look different from the others and the disposition of the k-space samples is, to say, non-intuitive. However, as seen in Fig. 4(h) and figures 7(d), 7(h), and 7(l), many properties of the SPs learned through the years by human research seems to be learned by the proposed approach, such as partial-Fourier (or conjugated symmetry), variable density, and the relative distance between the samples. There are likely even more properties learned about the SP that we cannot identify right now. The improvements in the reconstructed images obtained by a learned SP and VN are visible and measured by different figures of metrics. Particularly in figures 8 and 9, where brain and knee joint structures were better recovered by the proposed approach than by the other pairs of reconstruction and SP. The VN was also superior to the UNET, as previously reported [58]. Those interesting results support the fact that joint learning of SP and neural network parameters, using algorithms like the proposed one, is important in accelerated parallel MRI.

In this work, we tested the joint learning approach with the original VN for MRI [11] and the UNET, however, the proposed approach is not restricted to these networks. Other recent deep learning networks, such as the ones discussed in [13], [14], [58], can be used.

V. Conclusion

This paper proposes a new alternating learning approach to learn the sampling pattern and the parameters of a variational network in accelerated parallel 3D Cartesian MRI problems. The proposed approach learned a set (SP and VN) that jointly produces better images than other approaches such as LOUPE with VN or a VN with a variable density with Poisson-disc fixed SP. The proposed approach can also be used with other NN-based reconstructions. The results were observed with two different datasets, and performed stably across different acceleration factors, improving the quality from small AF, such as AF=2, up to very high AF, such as AF=20.

Biographies

Marcelo Victor Wust Zibetti (member IEEE) received his doctoral degree in Electrical Engineering from Universidade Federal de Santa Catarina in 2007. He received the IBM Best Student Paper Award at the IEEE ICIP’06. From 2007 to 2008 he was a researcher at the Department of Statistics and Applied Mathematics, University of Campinas, SP, Brazil. From 2008–2015 he was an assistant professor at the Universidade Tecnológica Federal do Paraná at Curitiba, Brazil, teaching in the Mechanical (DAMEC) and Electronic (CPGEI) engineering departments, where he headed the research group on image reconstruction and inverse problems. From 2015 to 2016 he was a visiting scholar in the Department of Computer Science at the Graduate Center of the City University of New York.

Currently he is assistant professor at the New York University Grossman School of Medicine and a researcher at the Center for Advanced Imaging Innovation and Research (CAI2R). His research interests include image reconstruction algorithms, machine learning algorithms for imaging, magnetic resonance imaging, ultrasound imaging and computed tomography.

Ravinder R. Regatte received his doctoral degree in Physics from Osmania University in 1996, India. From 1997–2004, he worked as a post-doctoral fellow and research associate in the Department of Radiology at the University of Pennsylvania. In 2004 he joined the NYU School of Medicine as a faculty member, where he now heads the Quantitative Multinuclear Musculoskeletal Imaging Group (QMMIG) at the Center for Biomedical Imaging, in the Department of Radiology. Currently he is a Professor of Radiology, working on development of novel multinuclear (1H, 23Na, 31P and gagCEST) imaging techniques for early metabolic and biochemical changes in host of chronic diseases. He has successfully mentored number of undergraduate students, medical students, graduate students, radiology residents, fellows, post-doctoral fellows, research scientists and junior faculty. He has published more than 150 peer-reviewed papers in scientific journals including PNAS, MRM, NeuroImage, JMRI and Radiology and is currently serving as a deputy editor for JMRI. He was recognized for his excellence in medical imaging research and was awarded to be the 2014 Distinguished Investigator of Academy of Radiology Research & Biomedical Imaging Research. He was also awarded to be a Fellow from AIMBE and ISMRM.

Florian Knoll (member IEEE) received his PhD in electrical engineering in 2011 from Graz University of Technology. From 2015 to 2021, he was Assistant Professor for Radiology at the Center for Biomedical Imaging at NYU Grossman School of Medicine. Since 2021, he is Professor and head of the Computational Imaging Lab at the Department Artificial Intelligence in Biomedical Engineering at Friedrich-Alexander University Erlangen Nuremberg. His research interests include iterative MR image reconstruction, parallel MR imaging, Compressed Sensing and Machine Learning.