A LAG FUNCTIONAL LINEAR MODEL FOR PREDICTION OF MAGNETIZATION TRANSFER RATIO IN MULTIPLE SCLEROSIS LESIONS

Abstract

We propose a lag functional linear model to predict a response using multiple functional predictors observed at discrete grids with noise. Two procedures are proposed to estimate the regression parameter functions: (1) an approach that ensures smoothness for each value of time using generalized cross-validation; and (2) a global smoothing approach using a restricted maximum likelihood framework. Numerical studies are presented to analyze predictive accuracy in many realistic scenarios. The methods are employed to estimate a magnetic resonance imaging (MRI)-based measure of tissue damage (the magnetization transfer ratio, or MTR) in multiple sclerosis (MS) lesions, a disease that causes damage to the myelin sheaths around axons in the central nervous system. Our method of estimation of MTR within lesions is useful retrospectively in research applications where MTR was not acquired, as well as in clinical practice settings where acquiring MTR is not currently part of the standard of care. The model facilitates the use of commonly acquired imaging modalities to estimate MTR within lesions, and outperforms cross-sectional models that do not account for temporal patterns of lesion development and repair.

1. Introduction.

Multiple sclerosis (MS) is an inflammatory disease of the central nervous system in which the myelin sheaths around the axons of the neurons in the brain and spinal cord are damaged. Focal areas of tissue damage in the brain and spinal cord are known as “lesions.” These lesions appear in various locations in the brain at different time points. Magnetic resonance imaging (MRI) is sensitive to these lesions and is the most important tool used by clinicians to diagnose and monitor the disease. One benchmark diagnostic criterion that is observed via MRI is the number of white matter lesions [McDonald et al. (2001), Polman et al. (2005)]. Conventional MRI modalities that are used in routine clinical practice to observe lesions are T1-weighted (T1w), T2-weighted (T2w) and T2-weighted fluid attenuated inversion recovery (FLAIR) images. However, it has been argued that rudimentary measures of lesion burden, including the number and volume of lesions, only moderately correlate with disability [Barkhof (2002), Brex et al. (2002), Hawkins et al. (1990), Schmierer et al. (2004)]. Therefore, much research in the field has centered on investigating the use of images that quantify tissue damage (e.g., white matter) and are believed to correlate with disability, such as magnetization transfer ratio (MTR) maps, which are sensitive to the degree of demyelination as well as lesion remyelination. Axons of the neurons in the white matter of the brain are insulated with a myelin sheath, which increases the speed at which impulses propagate along the axon. Demyelinating diseases, such as MS, destroy this layer of myelin, in a process called demyelination. Remyelination is the process of creating new myelin sheaths along these axons.

Here, we estimate MTR within lesions after lesion incidence using only the T1w and FLAIR images. MTR is not typically acquired in clinical settings, yet it would be a valuable addition to the typically acquired images and is believed to contain information about the disease process in MS [Chen et al. (2007, 2008)]. While MTR is not typically collected in clinical practice, the FLAIR and T1w volumes are routinely collected. Prediction of MTR in lesions will be useful in research applications where MTR was not acquired, as well as in clinical practice settings where acquiring MTR is not currently part of the standard of care. In practice, MTR is also an imaging sequence known to contain much noise [Reich et al. (2015)]. Predicting MTR within lesions with the longitudinal information in the FLAIR and T1w volume could therefore potentially provide a less noisy measurement of the MTR.

We propose a voxel-level model that uses sparsely sampled functional measurements of the T1w and FLAIR images over a fixed window of time to predict MTR within lesions. The model yields improvement over cross-sectional models that do not account for temporal patterns of early lesion evolution. This will ultimately allow researchers to study the effect of treatments on tissue damage in patients with MS.

We analyze data that were obtained from a group of 53 MS patients at the National Institute of Neurological Disorders and Stroke (NINDS). Each patient was scanned between 9 and 38 times over a period of 5.5 years. In this longitudinal study, the number of visits varies for each patient; MTR maps, T1w, and FLAIR images were acquired at each of the visits. For our analysis, the voxels in all of the images are temporally registered to obtain voxel-level intensity trajectories over time. The images are also segmented to obtain the set of voxel trajectories that correspond to areas of white matter containing MS lesions. Our objective is to relate current MTR intensity in a given voxel (within a lesion) to the T1w and FLAIR intensities in the same voxel observed over time. The observed voxel-level trajectories are discrete observations arising from a continuous process over time. Therefore, to predict MTR, we employ a function-on-function regression framework.

We propose a model for prediction of the functional response (MTR) beginning 6 months after lesion incidence, using the prior six months of the observed intralesional functional predictors (T1w and FLAIR) at the voxel level. As documented by Van Den Elskamp et al. (2008), MTR values may decrease subtly in areas of future lesion formation within a six-month period. Current methods in the functional data analysis literature do not model the relationship between a functional response and more than one functional predictor when it is assumed that only the recent past of the predictors affect the current value of the response. We develop a model that is able to use only the intensity of the T1w and FLAIR images observed in the previous six months of historical data to predict MTR at the current time point.

Functional data analysis has been a very active research area due to a surge of applications; see Besse and Ramsay (1986), Ferraty, Vieu and Viguier-Pla (2007), Horváth and Kokoszka (2012), Ramsay and Silverman (2005), Rice and Silverman (1991), to name a few. In particular, function-on-function regression has attracted increasing interest, starting with the functional linear model introduced in Ramsay and Silverman (2005) for which Scheipl and Greven (2015) address identifiability issues. Meyer et al. (2015) proposes a multilevel, wavelet-based, Bayesian function-on-function regression framework. Additionally, Scheipl, Staicu and Greven (2015) proposed a framework that incorporates additive regression models in penalized function-on-function regression. Recently, Ivanescu et al. (2015) developed a penalized regression method for association models between functional responses and multiple functional predictors, where the current response is allowed to depend on the entire trajectory of the predictor. Until recently, the work related to function-on-function regression has been able to account for only one functional predictor; see He et al. (2010), Ramsay and Dalzell (1991), Ramsay and Silverman (2005), Wu, Fan and Müller (2010), Yao, Müller and Wang (2005b). For a complete review of the current literature in this area, see Morris (2015).

Motivated by the medical application, we focus on the scientific problem of estimating the functional response at a specific time point using only a fixed window of history of the functional predictors. To address this problem when there is only one covariate, Malfait and Ramsay (2003) introduced the Historical Functional Linear Model (HFLM). In their model, they represent the coefficient function using a triangular basis function that is estimated using information from the predictor, and estimate a coefficient function at each observation point. Harezlak et al. (2007) present a penalized approach that allows for varying lags for the HFLM. Kim, Şentürk and Li (2011) propose a least-squares approach to fitting this model by estimating the coefficient function at each timepoint known as the Recent HFLM. However, their methods do not account for more than one predictor.

In this paper we study function-on-function regression where the response and predictors are functions defined on the same domain, multiple functional predictors are considered, and the response depends solely on a fixed window of the functional predictors. To estimate the regression parameter functions, we propose two methods: (1) a semi-local smoothing approach; and (2) a global smoothing approach.

We introduce the modeling framework in Section 2. Two estimation procedures are presented in Sections 2.1 and 2.2. Medically relevant extensions to sparse and noisy predictors are discussed in Section 2.3. We evaluate the proposed methods in a simulation experiment in Section 3. In Section 4, the proposed estimation approaches are then applied for predicting MTR trajectories using the recent past of T1w and FLAIR voxel-level intensities.

2. Methodology.

Suppose we observe data, [Y_ij, t_ij : i ∈ {1, …, n} and j ∈ {1, …, m_0i}], [X_1ij, r_1ij : i ∈ {1, …, n} and j ∈ {1, …, m_1i}] and [X_2ij, r_2ij : i ∈ {1, …, n} and j ∈ {1, …, m_2i}], where t_ij, r_1ij, $r_{2ij}\in \mathcal{T}$, a bounded and closed interval. For example, Y_ij corresponds to the MTR measurement at voxel i at time t_ij. In our data, there are n voxels under consideration and m_0i observations for voxel i. The variables X_1ij and X_2ij correspond to the smooth T1w and FLAIR intensities for voxel i at times r_1ij and r_2ij, respectively. Our data analysis relies on the working assumption that the measurements are independent across voxels. Additionally, we assume the voxels in the scans of patients are properly registered over time. Throughout the rest of this section we consider r_1ij = t_ij and r_2ij = t_ij, and make use of r_1ij and r_2ij again in Section 3 where we present simulations.

Let X_1ij = X_1i(t_ij) and X_2ij = X_2i(t_ij), and assume that X_1i(·) and X_2i(·) are independent and square-integrable random smooth functions over $\mathcal{T}$. Without loss of generality, let us assume E[X_1i(t)] = E[X_2i(t)] = 0. Assume that the predictor functions are observed on a dense grid of points and without noise, and the response is observed on a dense and equidistant grid of points t_ij = t_j; more realistic sampling designs and scenarios will be considered in Section 2.3. We assume the fixed-lag HFLM with multiple covariates for the response Y_ij,

$$\begin{array}{l}{Y}_{ij}=f_i\left(t_j\right)+{\epsilon }_i\left(t_j\right),\\ f_i\left(t_j\right)={\beta }_0\left(t_j\right)+{\int }_0^{{\Delta }_1}{\beta }_1\left(s,t_j\right)X_{1i}\left(t_j-s\right)ds\\ +{\int }_0^{{\Delta }_2}{\beta }_2\left(s,t_j\right)X_{2i}\left(t_j-s\right)ds,\end{array}$$ (2.1)

where i ∈ {1, …, n}, j ∈ {1, …, m_i}, ${\beta }_0:\mathcal{T}\to ℝ$ and β₁, ${\beta }_2:[0,\Delta ]\times \mathcal{T}\to ℝ$ are continuous functions, and ε_i(·) is an independent (across i) measurement error with zero-mean and covariance ${\sigma }_{\epsilon }^2$. ε_i(·)is also assumed to be independent of X_1i(·) and X_2i(·).

This model (2.1) is used throughout the paper. For intuition, notice that $f_i\left(t_j\right)={\beta }_0\left(t_j\right)+{\int }_{t_j-{\Delta }_1}^{t_j}{\beta }_1\left(t_j-s,t_j\right)X_{1i}(s)ds+{\int }_{t_j-{\Delta }_2}^{t_j}{\beta }_2\left(t_j-s,t_j\right)X_{2i}(s)ds$. The model assumes that, given the entire predictor trajectories, the response is affected by the predictor values over only recent time windows of length Δ₁ and Δ₂, respectively; these lag parameters are chosen based on scientific knowledge. For simplicity of illustration, we let Δ = Δ₁ = Δ₂. The time-varying coefficient functions, β₁(·, ·) and β₂(·, ·), weigh the predictor values over the Δ lag-window, and quantify the effect of the predictors on the current response. While historical functional linear models have been presented in the current literature [Kim, Şentürk and Li (2011), Malfait and Ramsay (2003)] they have not accounted for multiple covariates as model (2.1) does.

We discuss two approaches for estimating the model parameters β₀(·), β₁(·, ·) and β₂(·, ·). The first approach considers a pointwise (PW) estimation procedure for each observed time point t_ij. The second approach considers a basis function expansion using prespecified bases for each model parameter and conceptually controls the smoothness over $\mathcal{T}$ globally (GB). The two approaches are detailed in the next two sections.

2.1. PW model representation.

Model assumption.

As is common in the nonparametric regression literature, we assume that smooth coefficient functions can be represented using a basis function expansion. Specifically, let {B_s1,k(s)}_k and {B_s2,k(s)}k be two prespecified functional bases on [0, Δ]. Then β₁(s, t) is assumed to be represented as a tensor product of the form ${\beta }_1(s,t)={\sum }_{k=1}^{K_1}{B}_{s1,k}(s){\alpha }_{1k}(t)$, where K₁ is large enough to capture the flexibility of the model and the α_1k(t)’s are unknown time-varying coefficient functions defined on $\mathcal{T}$. We use a similar basis expansion for ${\beta }_2(s,t)={\sum }_{k=1}^{K_2}{B}_{s2,k}(s){\alpha }_{2k}(t)$, where α_2k(t)’s are unknown functions defined on $\mathcal{T}$.

Without loss of generality, we assume that K₁ = K₂ = K. Although many choices for basis functions are possible, we use B-spline functions of degree 4 with 6 equally spaced interior knots over [0, Δ], which correspond to K = 10, as the sets {B_s1,k(s)}_k and {B_s2,k(s) k}. B-splines are determined by the degree of the polynomial, and the number and location of the knots. The degree usually does not have a strong effect on the model performance [Wood (2006)]. Typically the knots are placed at equally spaced locations or equally spaced quantile locations. Furthermore, it is common practice to use a large number of basis functions and use a smoothness parameter to determine the smoothness of the fit [Ruppert, Wand and Carroll (2003)]. The value of K in our application was selected empirically. Substituting the expressions for the coefficient functions into equation (2.1) yields

$$\begin{array}{l}{f}_i\left(t_j\right)={\beta }_0\left(t_j\right)+\sum _{k=1}^K{\alpha }_{1k}\left(t_j\right){\int }_0^{\Delta }{X}_{1i}\left(t_j-s\right)B_{s1,k}(s)ds\\ +\sum _{k=1}^K{\alpha }_{2k}\left(t_j\right){\int }_0^{\Delta }{X}_{2i}\left(t_j-s\right)B_{s2,k}(s)ds.\end{array}$$ (2.2)

Furthermore, by denoting ${\tilde{X}}_{1k,i}\left(t_j\right)={\int }_0^{\Delta }{X}_{1i}\left(t_j-s\right)B_{s1,k}(s)ds$ and ${\tilde{X}}_{2k,i}$ similarly, equation (2.2) reduces to

$$f_i\left(t_j\right)={\beta }_0\left(t_j\right)+\sum _{k=1}^K{\tilde{X}}_{1k,i}\left(t_j\right){\alpha }_{1k}\left(t_j\right)+\sum _{k=1}^K{\tilde{X}}_{2k,i}\left(t_j\right){\alpha }_{2k}\left(t_j\right).$$ (2.3)

Fitting.

This representation captures the dependence between the precomputed covariates (${\tilde{X}}_{1k,i}$ and ${\tilde{X}}_{2k,i}$) and the response using a varying-coefficient model. Nevertheless, when the functional predictors are observed at sparse sampling points for each i and possibly contaminated with error, these derived quantities may not be directly computable. In this section, we develop an estimation procedure of the HFLM model that depends on the continuous second moments of the additive predictors. It does not require direct computation of ${\tilde{X}}_{pk,i}(t)$ and accounts for the correlation between the functional predictors. A working independence assumption over time for the error process ε_i(·) is assumed for fitting. This representation of the function-on-function regression model will allow us to obtain smooth pointwise estimates for the coefficient functions. A similar approach was considered by Kim, Şentürk and Li (2011) for the recent history functional linear model with one functional predictor. Here we present estimation of the coefficient functions and prediction of the response for the dense case; and extensions to more realistic settings are considered in Section 2.3.

Fix t_j, and define α_1kj = α_1k(t_j) and α_2kj = α_2k(t_j). Notice that β₀(t_j) = E[Y_ij], and thus β₀(·) can be estimated by smoothing Y_ij ’s and using a working independence assumption. By an abuse of notation, in the rest of the subsection, let Y_ij denote $Y_{ij}-{\widehat{\beta }}_0\left(t_j\right)$, where ${\widehat{\beta }}_0(\cdot )$ is a smooth estimator of β₀(·). We estimate α_1kj ’s and α_2kj ’s by minimizing the following penalized criterion:

$$\sum _i{\left\{Y_{ij}-f_i\left(t_j\right)\right\}}^2+{\lambda }_1\sum _k{\alpha }_{1kj}^2+{\lambda }_2\sum _k{\alpha }_{2kj}^2,$$ (2.4)

where λ₁ > 0 and λ₂ > 0 are the regularization parameters. Let α_pj = [α_p1j ⋯ α_pKj]^⊤ for p = 1, 2. Then the minimizer is

$$\left[\begin{array}{c}{\widehat{\alpha }}_{1j}\\ {\widehat{\alpha }}_{2j}\end{array}\right]={\left(Z_j^{\top }{Z}_j+\left[\begin{array}{cc}{\lambda }_1{I}_K& 0\\ 0& {\lambda }_2{I}_K\end{array}\right]\right)}^{-1}\left(Z_j^{\top }\left(Y_j-{\mu }_Y\left(t_j\right)\right)\right),$$ (2.5)

where I_K is the K × K identity matrix, Y_j is the vector of all observations at time t_j, μ_Y (t) = E[Y (t)], and

$$Z_j=\left[\begin{array}{cccccc}{\tilde{X}}_{11,1}\left(t_j\right)& \cdots & {\tilde{X}}_{1K,1}\left(t_j\right)& {\tilde{X}}_{21,1}\left(t_j\right)& \cdots & {\tilde{X}}_{2K,1}\left(t_j\right)\\ ⋮& & ⋮& ⋮& & ⋮\\ {\tilde{X}}_{11,n}\left(t_j\right)& \cdots & {\tilde{X}}_{1K,n}\left(t_j\right)& {\tilde{X}}_{21,n}\left(t_j\right)& \cdots & {\tilde{X}}_{2K,n}\left(t_j\right)\end{array}\right].$$ (2.6)

For fixed t_j, the analytic solution (2.5) is the solution in a ridge regression framework for fixed values of the tuning parameters λ₁ and λ₂. In our case, α_1kj ’s and α_2kj ’s represent the evaluations of smooth functions α_1k(t) and α_2k(t) at times t = t_j. However, selecting optimal values of λ₁ and λ₂ for each t could lead to high variability of the tuning parameters over t. One approach to accommodate this situation is to assume that the tuning parameters are constant across t.

The parameter functions α_1k(t) and α_2k(t) can be estimated using the probability limits of the standardized block submatrices, $Z_j^{\top }{Z}_j$ and $Z_j^{\top }{Y}_j$, that are included in expression (2.5). Specifically, for arbitrary t,

$$\left[\begin{array}{l}{\widehat{\alpha }}_1(t)\hfill \\ {\widehat{\alpha }}_2(t)\hfill \end{array}\right]={\left(\left[\begin{array}{ll}{\widehat{G}}_{11}(t)\hfill & {\widehat{G}}_{12}(t)\hfill \\ {\widehat{G}}_{21}(t)\hfill & {\widehat{G}}_{22}(t)\hfill \end{array}\right]+\left[\begin{array}{cc}\frac{{\lambda }_1}{n}{I}_K& 0\\ 0& \frac{{\lambda }_2}{n}{I}_K\end{array}\right]\right)}^{-1}\left[\begin{array}{l}{\widehat{G}}_{1Y}(t)\hfill \\ {\widehat{G}}_{2Y}(t)\hfill \end{array}\right],$$ (2.7)

where ${\widehat{G}}_{pY}(t)={\left[{\widehat{G}}_{pY1}(t)\cdots {\widehat{G}}_{pYK}(t)\right]}^{\top }$ is a vector, ${\widehat{G}}_{pYl}(t)$ is an estimator of $G_{pYl}(t)=\text{cov}\left({\tilde{X}}_{pl,i}(t),Y_i(t)\right)$, ${\widehat{G}}_{pq}(t)={\left[{\widehat{G}}_{{\tilde{X}}_{pl},{\tilde{X}}_{qk}}(t)\right]}_{kl}$ is a K × K matrix, and ${\widehat{G}}_{{\tilde{X}}_{pl},{\tilde{X}}_{qk}}(t)$ is an estimator of $G_{{\tilde{X}}_{pl},{\tilde{X}}_{qk}}(t)=\text{cov}\left({\tilde{X}}_{pl,i}(t),{\tilde{X}}_{qk,i}(t)\right)$ for p, q ∈ {1, 2}. Although the model framework and estimation are discussed for two functional predictors, it is straightforward to extend it to accommodate three or more functional predictors.

To obtain the necessary quantities, observe that

$$\begin{array}{l}\text{cov}\left({\tilde{X}}_{pl,i}(t),{\tilde{X}}_{qk,i}(t)\right)\\ ={\int }_0^{\Delta }{\int }_0^{\Delta }E\left[X_{pi}\left(t-s_1\right)X_{qi}\left(t-s_2\right)\right]B_{sp,l}\left(s_1\right)B_{sq,k}\left(s_2\right)d{s}_{1}d{s}_2\\ ={\int }_0^{\Delta }{\int }_0^{\Delta }{G}_{X_p{X}_q}\left(t-s_1,t-s_2\right)B_{sp,l}\left(s_1\right)B_{sq,k}\left(s_2\right)d{s}_{1}d{s}_2,\end{array}$$ (2.8)

where $G_{X_p{X}_q}\left(s_1,s_2\right)$ is the covariance between X_pi(s₁) and X_qi(s₂). Similarly, we also have that $\text{cov}\left({\tilde{X}}_{pl,i}(t),Y(t)\right)={\int }_0^{\Delta }{G}_{X_{p}Y}(t-s,t)B_{sp,l}(s)ds$, where $G_{X_{p}Y}\left(s_1,s_2\right)$ is the covariance between X_pi(s₁) and Y_i(s₂).

To use expression (2.7), we first need to obtain estimates of G₁₁(t), G₁₂(t), G₂₁(t), G₂₂(t), G_1Y (t) and G_2Y (t). Once estimates of α₁(t) and α₂(t) are available, estimates for the coefficient functions are given by ${\widehat{\beta }}_1(s,t)={\sum }_{k=1}^{K_1}{B}_{s1,k}(s){\widehat{\alpha }}_{1kj}(t)$ and similarly for ${\widehat{\beta }}_2(s,t)$. We note that this estimation is restricted to the class of regression parameter functions that can be expanded using B_s1,k(s) and B_s2,k(s) for k ∈ {1, …, K}. It follows that the response for the ith voxel can be predicted at any time point t by

$${\widehat{Y}}_i(t)={\int }_0^{{\Delta }_1}{\widehat{\beta }}_1(s,t)X_{1i}(t-s)ds+{\int }_0^{{\Delta }_2}{\widehat{\beta }}_2(s,t)X_{2i}(t-s)ds.$$ (2.9)

Selection of the smoothing parameters λ₁ and λ₂ is very important. To ensure that the regularization parameters are the same for all t_j, these parameters can be selected using cross-validation (CV) to minimize an error-based criterion that we call the Normalized Prediction Error,

$$NP{E}_{\left({\lambda }_1,{\lambda }_2\right)}=\frac{1}{n}\sum _{i=1}^n\left\{\frac{1}{m}\left[\sum _{j=1}^m\left|{\widehat{Y}}_{ij}-Y_{ij}\right|\right]/\left[\frac{1}{m}\sum _{j=1}^m\left|Y_{ij}\right|\right]\right\};$$ (2.10)

a similar criterion is used in Kim, Şentürk and Li (2011). The algorithm for fitting of the model using the PW approach is included in the Supplementary Material [Pomann et al. (2016)].

2.2. GB model representation.

Model assumption.

In this section, we propose the BG method, which takes a global smoothing approach to estimate the regression coefficient functions of the HFLM. This method estimates all the parameter functions β₀(·), β₁(·,·) and β₂(·,·) simultaneously. To do this, we assume an expansion of the coefficient functions of the form ${\beta }_0(t)={\sum }_{l=1}^{M_0}{B}_{t0,l}(t)b_{0l}$, ${\beta }_1(s,t)={\sum }_{l=1}^{M_1}{B}_{1,l}(s,t)b_{1l}$, and ${\beta }_2(s,t)={\sum }_{l=1}^{M_2}{B}_{2,l}(s,t)b_{2l}$, where M₀, M₁ and M₂ are large enough constants to capture the variability of the coefficient functions. The discussion on the choice of K in the PW approach is applicable for M₀, M₁ and M₂. {B_t0,l(·)}, {B_1,l(·, ·)} and {B_2,l(·, ·)} are preselected basis functions; and b_0l, b_1l and b_2l are unknown basis coefficients. For this study, the bivariate thin plate regression splines (TPRS) are selected as the sets {B_p,l(·, ·)} with M₁ = M₂ = 30, and one-dimensional TPRS are chosen as the set {B_t0,l(·)} with M₀ = 10. These basis functions are commonly used in the literature, and they are the default choices for the package mgcv [Wood (2006, 2011)] in R that is used in our study. As in the PW approach, other choices of basis functions could also be used with this framework.

Similar to Section 2.1, the conditional mean, f_i(t_j), can be represented as

$$f_i\left(t_j\right)=\sum _{l=1}^{M_0}{B}_{0t,l}\left(t_j\right)b_{0l}+\sum _{l=1}^{M_1}{\check{X}}_{1l,i}\left(t_j\right)b_{1l}+\sum _{l=1}^{M_2}{\check{X}}_{2l,i}\left(t_j\right)b_{2l},$$ (2.11)

where ${\check{X}}_{1l,i}\left(t_j\right)={\int }_0^{\Delta }{X}_{1i}\left(t_j-s\right)B_{1,l}\left(s,t_j\right)ds$ and ${\check{X}}_{2l,i}\left(t_j\right)$ is defined analogously. This representation is inspired by Ivanescu et al. (2015), which presents a penalized function-on-function regression framework that uses the entire range for the predictor functions. Equation (2.11) looks similar to equation (2.3); the main difference is that the unknown coefficients, b_0k, b_1k and b_2k are not time varying. This modeling approach ensures smoothness of the regression parameter functions β₁(s, t) and β₂(s, t) over both s and t.

Fitting.

The coefficient vectors, $b_0={\left[b_{01}\cdots b_{0M_0}\right]}^{\top }$, $b_1={\left[b_{11}\cdots b_{1M_1}\right]}^{\top }$ and $b_2={\left[b_{21}\cdots b_{2M_2}\right]}^{\top }$, are estimated by minimizing the following penalized criterion:

$$\sum _{i,j}{\left\{Y_i\left(t_j\right)-f_i\left(t_j\right)\right\}}^2+{\lambda }_0{P}_0\left(b_0\right)+{\lambda }_1{P}_1\left(b_1\right)+{\lambda }_2{P}_2\left(b_2\right),$$ (2.12)

where λ₀, λ₁ and λ₂ are smoothing parameters and P₀, P₁ and P₂ are the penalty terms [Ivanescu et al. (2015), Wood (2011)]. In particular, the integral of the square of the second derivative is a common measure for smoothness, in which case $P_0\left(b_0\right)={\int }_{\mathcal{T}}{\left\{{\beta }_0^{\prime \prime }(t)\right\}}^{2}dt=b_0^{\top }{S}_0{b}_0$ and $P_p\left(b_p\right)={\int }_{\mathcal{T}}{\int }_0^{\Delta }[{\left\{{\partial }^2{\beta }_p(s,t)/\partial s^2\right\}}^2+{\left\{{\partial }^2{\beta }_p(s,t)/\partial s\partial t\right\}}^2+{\left\{{\partial }^2{\beta }_p(s,t)/\partial t^2\right\}}^2]dsdt=b_p^{\top }{S}_p{b}_p$, where S₀ and S_p are penalty matrices specified by the choice of basis functions for p = 0, 1, 2 [Wood (2006)]. A working independence assumption over time for the error process ε_i(·) is assumed for fitting.

Selection of the optimal regularization parameters can be done via generalized cross-validation (GCV). However, empirical evidence suggests that GCV leads to undersmoothing [Reiss and Ogden (2009), Wood (2011)]. Instead, the problem can be posed as a mixed model of the form X_f b_f + Zb_r, where b_f contains the fixed effect parameters and b_r is a random effect vector [Wood (2006, 2011)]. In this context, λ₀, λ₁ and λ₂ represent variance components of the random effect covariance structure. This framework allows us to use a restricted maximum likelihood (REML) to estimate λ₀, λ₁ and λ₂ [Reiss and Ogden (2009), Wood (2006, 2011)]. This approach is also more robust to nonindependent error assumptions [Ivanescu et al. (2015), Krivobokova and Kauermann (2007)]. The algorithm for fitting of the model using the GB approach is included in the Supplementary Material [Pomann et al. (2016)].

Predictions of the functional response can be obtained using the same methodology presented for the PW method. In particular, given that ${\widehat{\beta }}_0(t)={\sum }_{l=1}^{M_0}{B}_{t0,l}(t){\widehat{b}}_{0l}$ and ${\widehat{\beta }}_1(s,t)={\sum }_{l=1}^{M_1}{B}_{1,l}(s,t){\widehat{b}}_{1l}$ with a similar expression for ${\widehat{\beta }}_2(s,t)$, then ${\widehat{Y}}_i(t)={\widehat{\beta }}_0(t)+{\int }_0^{{\Delta }_1}{\widehat{\beta }}_1(s,t)X_{1i}(t-s)ds+{\int }_0^{{\Delta }_2}{\widehat{\beta }}_2(s,t)X_{2i}(t-s)ds$.

2.3. Noisy and sparsely observed data.

The estimation approach presented above is applicable to smooth predictors observed on a fine grid of time points. However, the response MTR and both covariates T1w and FLAIR are observed at few time points for each voxel. Additionally, the measurements are contaminated with noise. To accommodate this situation, let W_pi(t) X_pi(t) ε_pi(t) for p = 1, 2, where ε_pi(·) is a zero mean white noise process with variance ${\sigma }_p^2$. Assuming the same sampling design for the functional covariates, we distinguish 4 different scenarios according to whether the response is sparse or dense, and whether the functional predictors are sparse or dense. Namely, the scenarios are as follows: sparse/sparse, dense/sparse, sparse/dense and dense/dense. In the following we discuss in detail the case sparse/sparse which is the most relevant for our application; the remaining cases are detailed in the Supplementary Material [Pomann et al. (2016)].

PW method.

This approach requires smooth estimators of $G_{X_1{X}_1}\left(s_1,s_2\right)$, $G_{X_2{X}_2}\left(s_1,s_2\right)$, $G{X}_1{X}_2\left(s_1,s_2\right)$, $G_{X_{1}Y}\left(s_1,s_2\right)$ and $G_{X_{2}Y}\left(s_1,s_2\right)$, which can be obtained using functional principal component analysis (FPCA). Mercer’s theorem yields the spectral decomposition of the covariance $G_{X_p{X}_p}\left(s_1,s_2\right)={\sum }_{l=1}^{\infty }{\omega }_{pl}{\psi }_{pl}\left(s_1\right){\psi }_{pl}\left(s_2\right)$ in terms of non-negative eigenvalues ω_p1 ≥ ω_p2 ≥ ⋯ ≥ 0 and orthogonal eigenfunctions ψ_pl(t) with ${\int }_{\mathcal{T}}{\psi }_{pl}(t){\psi }_{p{l}^{\prime }}(t)dt=1\left(l=l^{\prime }\right)$, where 1(l = l′) is the indicator function which equals 1 when l = l′ and 0=otherwise [Bosq (2000)]. Given that E [X_pi(t)] = 0, the above decomposition of the covariance implies that X_pi (t) can be represented via the Karhunen–Loève (KL) expansion as $X_{pi}(t)={\sum }_{l=1}^{\infty }{\zeta }_{pl,i}{\psi }_{pl}(t)$, where ${\zeta }_{pl,i}={\int }_{\mathcal{T}}{X}_{pi}(t){\psi }_{pl}(t)dt$ are commonly called the functional principal component (FPC) scores and are uncorrelated random variables with zero mean and variance equal to ω_pl. For practical and theoretical reasons, the KL expansion is often truncated [Di et al. (2009), Hall, Müller and Wang (2006), Yao, Müller and Wang (2005a)]; let $X_{1i}^{L_1}={\sum }_{l=1}^{L_1}{\zeta }_{1l,i}{\psi }_{1l}(t)$ and $X_{2i}^{L_2}={\sum }_{2i}^{L_2}{\zeta }_{2l,i}{\psi }_{2l}(t)$ be the truncated KL expansions of X₁(t) and X₂(t), respectively, for finite L₁ and L₂. The spectral decomposition of the smooth estimates of $G_{X_1{X}_1}\left(s_1,s_2\right)$ and $G_{X_2{X}_2}\left(s_1,s_2\right)$ yields the pairs of estimated eigenfunctions and eigenvalues ${\left\{{\widehat{\psi }}_{1l},{\widehat{\omega }}_{1l}\right\}}_l$ and $\left\{{\widehat{\psi }}_{2l},{\widehat{\omega }}_{2l}\right\}l$, respectively. Then one can obtain consistent estimators of the scores ${\widehat{\zeta }}_{1l,i}={\int }_{\mathcal{T}}{X}_{1i}(t){\widehat{\psi }}_{1l}dt$ and ${\widehat{\zeta }}_{2l,i}={\int }_{\mathcal{T}}{X}_{2i}(t){\widehat{\psi }}_{2l}dt$ [Hall, Müller and Wang (2006), Zhang and Chen (2007)].

Since the response is observed on a sparse grid of points, bivariate kernel smoothing [Yao, Müller and Wang (2005a)] or spline-based smoothing [Wood (2006)] can be used to estimate the covariance functions. In our implementation, we make use of B-spline-based smoothing techniques [Crainiceanu, Staicu and Di (2009), Di et al. (2009)]. To account for the measurement error, the diagonal elements are left out when smoothing is carried out. The resulting covariance estimator is adjusted to be symmetric and positive semidefinite. Then the variance of the noise, ${\sigma }_1^2$ and ${\sigma }_2^2$, can be estimated based on the difference between the empirical pointwise variance of the corresponding observed predictors and the estimated pointwise variance ${\widehat{G}}_{X_1{X}_1}\left(s_1,s_2\right)$, ${\widehat{G}}_{X_2{X}_2}\left(s_1,s_2\right)$, [Staniswalis and Lee (1998)]. In this setting, the conditional expectation formula should be employed to estimating the scores, ${\widehat{\zeta }}_{1l,i}=\widehat{E}\left[{\zeta }_{1l,i}\mid W_{1i}\right]={\widehat{\eta }}_{1l}{\widehat{\psi }}_{1l}^{\top }{\left({\widehat{G}}_{X_1,X_1}+{\widehat{\sigma }}_1^2{I}_{m_{1i}\times m_{1i}}\right)}^{-1}{W}_{1i}$ [Yao, Müller and Wang (2005a)]. Here W_1i is a vector of length m_1i containing the observed values of the first predictor function, ${\widehat{\psi }}_{1l}^{\top }$ is a vector of length m_1i with the jth entry equal to ${\widehat{\psi }}_{1l}\left(t_{ij}\right)$, ${\widehat{G}}_{X_1,X_1}$ is a m_1i × m_1i-dimensional matrix with the (j, j′)th entry equal to ${\widehat{G}}_{X_1,X_1}\left(t_{ij},t_{i{j}^{\prime }}\right)$ and $I_{m_{1i}\times m_{1i}}$ is the m_1i × m_1i identity matrix. ${\widehat{\zeta }}_{2l,i}$ can be estimated similarly. Yao, Müller and Wang (2005a) showed that, under the assumption that the predictors and their errors are jointly Gaussian, this equation yields the empirical best linear unbiased predictor of the scores.

In this case, there is an alternative approach to predict the response trajectory. Specifically, let $X_{pi}(t)={\sum }_{l=1}^{L_p}{\zeta }_{pl,i}{\psi }_{pl}(t)$ be the KL expansion for the covariate functions. Then by substituting this into equation (2.2) we obtain

$$\begin{array}{l}{\widehat{Y}}_i(t)={\widehat{\beta }}_0(t)+\sum _{k=1}^K{\widehat{\alpha }}_{1k}(t){\int }_0^{\Delta }\sum _{l=1}^{L_1}{\widehat{\zeta }}_{1l,i}{\widehat{\psi }}_{1l}(t-s)B_{s1,k}(s)ds\\ +\sum _{k=1}^K{\widehat{\alpha }}_{2k}(t){\int }_0^{\Delta }\sum _{l=1}^{L_2}{\widehat{\zeta }}_{2l,i}{\widehat{\psi }}_{2l}(t-s)B_{s2,k}(s)ds\\ ={\widehat{\beta }}_0(t)+\sum _{l=1}^{L_1}{\widehat{\zeta }}_{1l,i}{\widehat{P}}_{1l}(t)+\sum _{l=1}^{L_2}{\widehat{\zeta }}_{2l,i}{\widehat{P}}_{2l}(t),\end{array}$$ (2.13)

where ${\widehat{\alpha }}_{1k}(t)$ and ${\widehat{\alpha }}_{2k}(t)$ are the estimators of α_1k(t) and α_2k(t), respectively, ${\widehat{P}}_{1l}(t)={\sum }_{k=1}^K{\widehat{\alpha }}_{1k}(t){\int }_0^{\Delta }{\widehat{\psi }}_{1l}(t-s)B_{s1,k}(s)ds$ and ${\widehat{P}}_{2l}(t)$ is defined similarly.

GB method.

Densely sampled covariate functions are needed for the GB method; hence, smooth estimators for the covariates can be obtained using the predicted scores, eigenfunctions and KL expansion; that is, ${\widehat{X}}_{pi}(t)={\sum }_{l=1}^{L_p}{\widehat{\zeta }}_{pl,i}{\widehat{\psi }}_{pl}(t)$. The methodology can be applied by using the predicted functional covariates in place of the true smooth functions.

3. Simulation studies.

This section presents results from an extensive simulation study used to evaluate the predictive performance of the two proposed methods, PW and GB. We consider two settings for data generated as in model (2.1): (I) the response and functional predictors are observed densely so that m_0i, m_1i and m_2i are large and the predictors are observed without measurement error; and (II) the functional predictors and response are observed on a sparse grid of points so that m_0i, m_1i and m_2i are small and the predictors are observed with measurement error.

We first generate the response and predictor functions on a dense and equally spaced grid of points, $t_{ij}\in \mathcal{T}=\{j/99:j=0,1,2,\dots ,99\}$. In setting (I), we generate observed data, {t_ij, Y_ij, W_1ij, W_2ij}j, where Y_ij is the response function and W_1ij = X_1i(t_ij) and W_2ij = X_2i (t_ij) are the predictor functions measured without error. We define the predictors, $X_{1i}(t)={\sum }_{k=1}^2{u}_{ik1}\text{sin}(k\pi t)+u_{ik2}\text{cos}(k\pi t)$ and $X_{2i}(t)={\sum }_{k=1}^3{v}_{ik}\text{cos}(2k\pi t)$ for u_ik1, u_ik2 and $v_{ik1}\stackrel{\text{ i}.\text{i}.\text{d}.}{~}N\left(0,1/k^4\right)$. We use regression parameter functions ${\beta }_0(t)=e^{-{(t-.5)}^2}$, β₁(s, t) = cos(2πt) cos(πs) and β₂(s, t) = cos(πt) cos(πs). We take Δ = 0.4 so that β₁, β₂ : [0, 0.4] × [0, 1] → [0, 1] and β₀ [0, 1] → [0, 1]. Illustrations of the simulated data and predictions are included in the Supplementary Material [Pomann et al. (2016)].

The response for voxel i ∈ 1, …, n is generated from model (2.1) via numerical integration for each $t_{ij}\in \mathcal{T}$. The measurement error in model (2.1) is taken to be ε_i(t) = ε_a,i(t) + ε_g,i(t), where ε_g,i(t) is a zero-mean i.i.d. normal random variable with variance ${\sigma }_{\epsilon }^2/2$, and ε_a,i(t) is a zero-mean AR(1) process with covariance structure given by $\Sigma \left(t_j,t_{j^{\prime }}\right)=\left({\sigma }_{\epsilon }^2/2\right){\rho }^{\left|t_j-t_{j^{\prime }}\right|}$ with ρ = 0.5. It follows that $\text{var}\left({\epsilon }_i(t)\right)={\sigma }_{\epsilon }^2$. Note that an AR(1) process is considered in the simulation study to analyze the effect of nonindependent (over time) noise structure in the fitting process. We simulate data under a framework similar to Ivanescu et al. (2015) and McLean et al. (2014) by using a version of the empirical signal to noise ratio (eSNR_ε), which we define as $eSN{R}_{\epsilon }=\left[{\sum }_{i,j}{\left\{E\left(Y_{ij}\right)-{\sum }_{i}E\left(Y_{ij}\right)/n\right\}}^2/\left\{{\sigma }_{\epsilon }^2(n-\text{ 1) }m\right\}\right]$. The value of ${\sigma }_{\epsilon }^2$ is chosen by specifying the eSNR_ε for each Monte Carlo (MC) replication. In this section, we present results for eSNR_ε = 5. It was observed that the predictive error decreases (increases) as eSNR_ε is increased (decreased). Results for eSNR_ε = 1 as well as for responses generated with a white noise error process are included in the Supplementary Material [Pomann et al. (2016)].

In setting (II) the response and predictors are first generated as in setting (I). Then, to generate the sparse data, we evaluate the functions at points $r_{ik}\in {\mathcal{R}}_i$ for a randomly sampled subset ${\mathcal{R}}_i\subset \mathcal{T}$ of size m_i. To determine the number of observations for each voxel, we take $m_i\stackrel{\text{ i}.\text{i}.\text{d}.}{~}\text{ Uniform }$ on {10, 11, …, 15}. This level of sparsity is consistent with the 13.6 average number of samples observed per curves in the real data (see the Data Analysis Details section in the Supplementary Material [Pomann et al. (2016)]). To generate the predictors that are observed with error, we take W_1ik = X_1i(r_ij) + ε_1ik and W_2ik = X_2i(r_ij) + ε_2ik, where ε_1ik ~ N(0, 0.1) and ε_2ik ~ N(0, 0.05). The latter error variances were selected to correspond to a signal-to-noise ratio of 5.

The main simulation factors of interest are the number of observations and the lag parameter used for fitting the model. We present results for n ∈ {20, 50, 100}. To understand how the model performs when the lag parameter is misspecified, we let Δ_F be the lag parameter used for fitting the model and present results for Δ_F ∈ {0.4, 0.6}. As expected, when Δ_F < Δ, both estimation methods have poor predictive accuracy and results in increased bias. Intuitively, this case corresponds to fitting a misspecified model, as it enforces the two regression parameters to be null on domains where they are not. Namely, β₁(s, t) = 0 and β₂(s, t) = 0 are enforced for s ∈ [Δ_F, Δ].

To fit the model, the predictors are first standardized to have a zero mean function and pointwise variance equal to 1. For the model using the PW method, we consider the bases sets {B_s1,k} and {B_s2,k} to be the set of K = 10 B-spline basis functions o degree 4 with 6 interior knots over [0, Δ_F]. This value of K was selected empirically. We use one tuning parameter λ that is selected using a grid search over I_λ = [0.0001, 0.01] and cross-validation. The range was determined empirically. Using a larger range and two tuning parameters produced similar results. To obtain the smooth covariance and cross-covariance functions, ${\widehat{G}}_{X_1{X}_1}\left(s_1,s_2\right)$, ${\widehat{G}}_{X_2{X}_2}\left(s_1,s_2\right)$, ${\widehat{G}}_{X_1{X}_2}\left(s_1,s_2\right)$, ${\widehat{G}}_{X_{1}Y}\left(s_1,s_2\right)$ and ${\widehat{G}}_{X_{2}Y}\left(s_1,s_2\right)$, we use bivariate smoothing, via tensor products of 20 univariate cubic regression splines with 15 equally spaced interior knots. The positive semidefiniteness of the covariance functions is ensured by truncating the eigenvalues to be positive.

For the GB method, the functions B_p,k(s, t) are chosen to be 30 thin plate spline basis functions with 30 knots equally spaced. The penalty for equation (2.12) is taken to be $P_l\left(b_l\right)=b_l^{\top }{S}_l{b}_l$, where S_l is chosen to be the thin plate spline penalty [Wood (2006)]. In setting (II), the reconstructed trajectories are estimated using FPCA with 20 basis functions to smooth the covariance and cross-covariance functions; the percent variance explained is set to 99%. The smooth predictor trajectories are sampled over a grid of 100 equally spaced observation points on [0, 1]. To obtain the necessary smooth estimates, we use fpca.sc function of the package refund [Di et al. (2009), Goldsmith, Greven and Crainiceanu (2012), Staniswalis and Lee (1998), Yao, Müller and Wang (2005b)]. To obtain predictions, we use the gam function of the mgcv package [Wood (2006, 2011)].

The computational cost and empirical performance of the PW method depends directly on the range of values I_λ used to search for the optimal regularization parameter. Since the estimation of regression parameters for the PW method uses only the smooth covariance and cross-covariance estimates at each time t_ij, it is more computationally efficient than the GB method which uses large matrices that grow linearly with ${\sum }_{i=1}^n{m}_i$; see the Supplementary Material [Pomann et al. (2016)] for algorithms that outline the implementation details.

3.1. Simulation results.

To evaluate model performance, we present the relative mean square error (reMSE) for Y (t) as $\text{reMSE}(Y)=\left({\sum }_i{\int }_{\Delta }^T\{{\widehat{Y}}_i(t)-{f_i(t)\}}^{2}dt\right)/\left({\sum }_i{\int }_{\Delta }^T{\left\{f_i(t)\right\}}^{2}dt\right)$. Since our main objective is prediction, we report the mean and standard error of the reMSE(Y) values over 500 Monte Carlo (MC) replications. We compare the resulting prediction errors by evaluating improvement of quantity “A” over “B,” defined to be [(B − A)/B] 100%. The discussion in this section focuses on the comparison of the reMSE(Y) values found in the last column of the tables provided.

First we describe and compare the results for the two estimation methods under the dense setting. Table 1 reports the simulation results for the PW and the GB methods under setting (I). On average, the GB method yields an improvement of 92% over the PW method in reMSE of prediction for this setting. For both the PW and GB methods, the case Δ_F = Δ has smaller prediction errors than the case when Δ_F ≥ Δ. As expected, the prediction error decreases in both cases as the sample size increases. For the PW method, n = 50 yields an average improvement of 47% over the case of n = 20, and for n = 100 we observe an improvement over the case when n = 50. Using the GB method with n = 50 yields an average improvement of 56% over the case when n = 20, and a clear improvement as the sample size increases.

Table 1.

Prediction Error—Setting (I), Average Error Variance = 0.012

n	Δ	ΔF	reMSE(Y) (SE)—PW Method	reMSE(Y) (SE)—GB Method
20	0.4	0.4	5.1e–3 (5.9e–3)	5.2e–4 (1.6e–4)
20	0.4	0.6	6.5e–3 (1.1e–2)	6.5e–4 (2.3e–4)
50	0.4	0.4	2.9e–3 (4.6e–3)	2.3e–4 (6.4e–5)
50	0.4	0.6	3.2e–3 (2.8e–3)	2.9e–4 (8.4e–5)
100	0.4	0.4	1.8e–3 (1.4e–3)	1.2e–4 (3.2e–5)
100	0.4	0.6	2.1e–3 (2.0e–3)	1.5e–4 (4.3e–5)

Next, we compare performance under the dense and sparse settings for each of the estimation methods. As expected, the performance of both approaches is affected by the sparse sampling design of the functional covariates and response. For the PW method, prediction errors in setting (I) are on average 70% smaller than in setting (II). Similarly, for the GB method the prediction errors in setting (I) are on average 95% smaller than in setting (II).

Last, we describe and compare the results for the two estimation methods under the sparse setting (II) (see Table 2). On average, in these datasets, the GB method yields an improvement of 55% over the PW method. For PW, we observe that the case when Δ_F = Δ has smaller prediction errors than the case when Δ_F ≥ Δ. For GB, on average, having Δ_F = Δ yields a slight improvement over having Δ_F ≥ Δ. As expected, the prediction error decreases in both cases as the sample size increases.

Table 2.

Prediction Error–Setting (II), Average Error Variance = 0.012

n	Δ	ΔF	reMSE(Y) (SE)—PW Method	reMSE(Y) (SE)—GB Method
20	0.4	0.4	1.6e–2 (2.4e–2)	7.1e–3 (1.9e–2)
20	0.4	0.6	2.2e–2 (7.7e–2)	9.0e–3 (6.1e–2)
50	0.4	0.4	9.6e–3 (4.3e–3)	4.2e–3 (3.2e–3)
50	0.4	0.6	1.0e–2 (4.6e–3)	4.0e–3 (2.4e–3)
100	0.4	0.4	6.7e–3 (4.3e–3)	3.6e–3 (5.7e–3)
100	0.4	0.6	7.1e–3 (3.1e–3)	3.2e–3 (3.9e–3)

4. Prediction of Magnetization Transfer Ratio within lesions of MS patients.

Recall that the data consist of MTR maps and T1w and FLAIR images obtained for 53 MS patients who were imaged as part of a natural history study at the National Institute of Neurological Disorders and Stroke. Time to each observed scan is measured from the first scan after lesion incidence. With this definition of observation times, each patient had between 9 and 38 observed scans with the maximum time ranging from 20 weeks to 5.5 years. Our objective is to predict MTR at voxels within lesions using the T1w and FLAIR measurements acquired within the previous six months. This is important as MTR is not typically acquired in clinical settings, yet it would be a valuable addition to the typically acquired images and is believed to contain information about the disease process in MS [Chen et al. (2007, 2008)]. Predicting the MTR in MS lesions from the T1w and FLAIR information will provide information within lesions, without needing to acquire the MTR volume. This information will be of use in research for retrospective analysis where the MTR is not available as well as in clinical practice in settings where the MTR is not acquired. For this model, the window is chosen to be six months because it has been reported that MTR values may decrease subtly in areas of future lesion formation within a six-month period [Van Den Elskamp et al. (2008)]. Previously, Mejia et al. (2016) proposed a cross-sectional model to predict quantitative T₁ maps, which estimate T₁ relaxation times as a function of T₁-weighted, T₂-weighted, PD-weighted and FLAIR images; and Suttner et al. (2015) applied this method to predict DTI measures. To the best of our knowledge, this is the only other work in the literature that has been presented to estimate images of quantitative MR values. Jog et al. (2013a) do attempt to estimate average quantitative tissue properties, but not the quantitative images themselves. In addition, work has been done to predict standard nonquantitative clinical images using cross-sectional models [Jog et al. (2013b); Roy, Carass and Prince (2011, 2013)].

It is common practice to use cross-sectional linear models to make other voxel-level predictions [Pomann et al. (2015), Sweeney et al. (2013a, 2013b)]. Therefore, we evaluate the performance of the proposed approaches against two cross-sectional models that do not take temporal dependence of the data into account. Section 4.1 discusses the preprocessing of the data, and Section 4.2 presents implementation details and results for this analysis.

4.1. Data processing.

Details about the data acquisition, preprocessing, image registration and normalization are provided in Sweeney et al. (2015). After image preprocessing, we temporally align the voxel trajectories by aligning the voxels to the time point when it first is identified as belonging to a new or enlarging lesion. We identify this time of incidence for each voxel using the Subtraction-Based Logistic Inference for Modeling and Estimation (SuBLIME) procedure [Sweeney et al. (2013a)]. For each voxel, we obtain the time marker that corresponds to the time when the voxel is first identified as being part of a lesion (“time zero”). We then measure all following time points as the time difference in weeks from this marker. The alignment is appropriate because our goal is to predict MTR in the time window after the lesion develops; see the Supplementary Material [Pomann et al. (2016)] for more details.

4.2. Model implementation and results.

After normalization and spatiotemporal registration, we measure time in weeks, and let Y_ij be the MTR at voxel i in the brain of a subject at week t_ij ∈ [0, 190]. Similarly, we let the predictors W_1ij and W_2ij be the normalized T1w and FLAIR intensities, respectively, of voxel i at time t_ij, which are assumed to be observed with noise. We consider these two predictors as they are commonly acquired images as part of clinical MRI studies. We omit times after 190 weeks, as there are too few observations beyond this point. After Δ_F = 26 weeks (approximately six months), lesion evolution is approximately stable [Meier, Weiner and Guttmann (2007)], which justifies our choice for lag window.

Figure 1 presents images for a lesion for one of the patients with MS in our study. From top to bottom, the FLAIR, T1w and MTR images are displayed for this patient obtained over time in weeks from left to right (indicated below in white text). Time zero corresponds to lesion incidence for each voxel. The lesion is the hypointense region in the center of the image on the T1w and MTR images and the hyperintense on the FLAIR. Figure 2(a), (b) and (a) present the corresponding T1w, FLAIR and MTR voxel-level trajectories for this image.

Fig. 1.

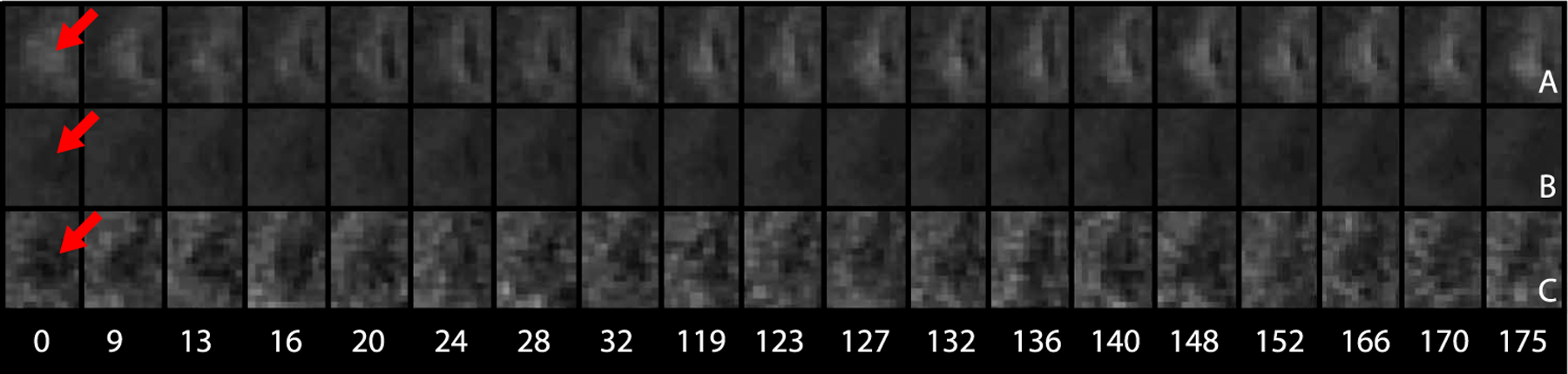
From top to bottom, axial slices of an MS lesion in the FLAIR (A), T1w (B) and MTR (C) sequences. This MS patient is imaged over time in weeks from left to right. Time zero corresponds to lesion incidence, and the lesion on each sequence is denoted at time zero with a red arrow. On the MTR and T1w images the lesion is the hypointense region; on the FLAIR the lesion is hyperintense.

Fig. 2.

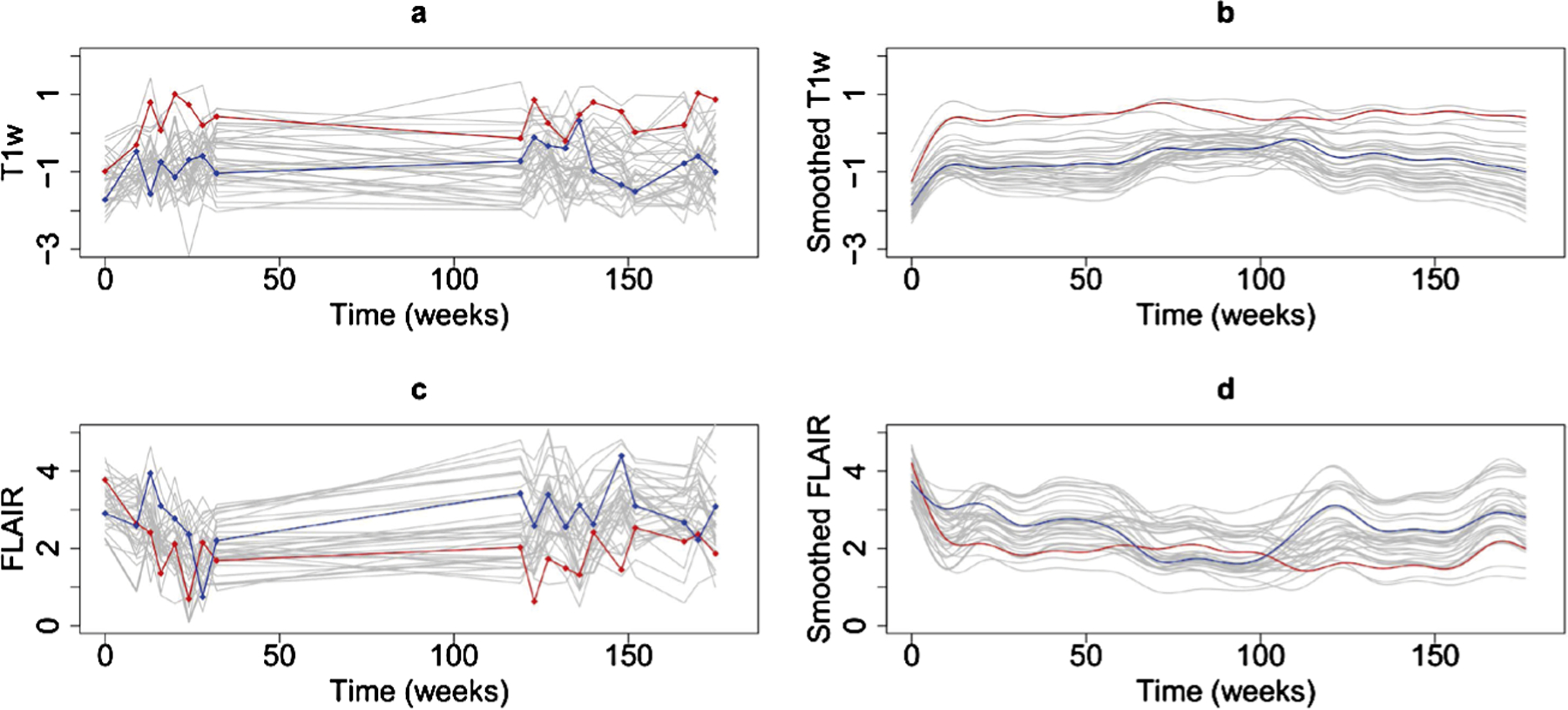
(a) Normalized T1w voxel intensities for a subset of the lesion voxels in the same patient as in Figure 1; (b) corresponding smoothed T1w voxel intensities using 20 basis functions to smooth all of the data; (c) corresponding FLAIR voxel intensities; (d) corresponding smoothed FLAIR voxel intensities using 20 basis functions to smooth all of the data. The red and blue curves are two particular curves.

In order to determine the benefit of the HFLM model for predicting MTR, we compare its performance against a cross-sectional model (CS),

$$Y_{ij}={\beta }_0+{\beta }_1{W}_{1ij}+{\beta }_2{W}_{2ij}+{\epsilon }_{ij}.$$ (4.1)

Additionally, we compare the performance against a cross-sectional nonlinear model (CSNL),

$$Y_{ij}={\beta }_0+g_1\left[W_{1ij}\right]+g_2\left[W_{2ij}\right]+{\epsilon }_{ij},$$ (4.2)

where g₁(·) and g₂(·) are unknown nonlinear functions. These models do not account for any temporal dependencies that may be present in the data. To fit the cross-sectional models, the predictors are standardized to have a mean zero and standard deviation of one. Predictions for the CSNL model are obtained using the gam function of the mgcv package in R with 10 thin plate basis functions with 10 equally spaced knots.

To fit the HFLM models, the predictors are first standardized to have a zero mean function and pointwise variance equal to 1. Prediction is performed only for voxels in lesions at times after the corresponding lesion incidence. The analysis is performed on the logit transform of the MTR trajectories since the response values lie in the range [0, 1]. The same analysis is also conducted on the raw data which yields comparable results (see the Supplementary Material [Pomann et al. (2016)]). There are some zero values in the response but no values of 1, and most of the MTR values are concentrated between 0.2 and 0.5. Hence, in order to avoid division by zero, we shift the data by 0.01 when performing the logit transformation; that is, for our analysis we define $\text{logit}(y)=\text{log}\left(\frac{(y+0.01)}{1-(y+0.01)}\right)$ and ${\text{logit}}^{-1}(\alpha )=\frac{e^{\alpha }}{e^{\alpha }+1}-0.01$. When using the logit option in the implementation, the response data is transformed before fitting the model. Then predictions are transformed back to the probabilities using the logit⁻¹ function. All analysis is conducted using R version 2.15.1.

For the PW method, the basis set ${\left\{B_{s1,k}(s)\right\}}_{k=1}^K$ and ${\left\{B_{s2,k}(s)\right\}}_{k=1}^K$ are taken to be the set of K = 10 B-spline basis functions of degree 4 with 6 interior knots over [0, 26]. The value of K was selected empirically. Similar results were observed for K = 20. We use one tuning parameter, λ, that is selected using GCV over [0.1,100]. To obtain the smooth covariance and cross-covariance functions, ${\widehat{G}}_{X_1{X}_1}\left(s_1,s_2\right)$, ${\widehat{G}}_{X_2{X}_2}\left(s_1,s_2\right)$, ${\widehat{G}}_{X_1{X}_2}\left(s_1,s_2\right)$, ${\widehat{G}}_{X_{1}Y}\left(s_1,s_2\right)$, and ${\widehat{G}}_{X_{2}Y}\left(s_1,s_2\right)$, we use bivariate smoothing, via tensor products of univariate bases. The positive semidefiniteness of the covariance and cross-covariance functions is ensured by truncating the eigenvalues to be positive. The results are based on using the tensor product of 20 univariate cubic regression splines with 15 equally spaced interior knots.

For the GB method, the functions B_p,k(s, t) are chosen to be 30 thin plate spline basis functions with 30 knots equally spaced. The penalty for equation (2.12) is taken to be $P_l\left(b_l\right)=b_l^{\top }{S}_l{b}_l$, where S_l is obtained by using the thin plate spline penalty [Wood (2006)]. The reconstructed trajectories are estimated for t_ij ∈ [0, 190] using FPCA with 20 basis functions to smooth the covariance and cross-covariance functions and the percent variance explained set to 99%. To obtain the necessary smooth estimates, we use the fpca.sc function of the package refund. To obtain predictions, we use the bam function of the mgcv package [Wood (2006, 2011)].

Using this smoothing procedure, we are able to capture the natural variation in the predictor functions. To see this, we display a subset of voxels in the brain of a patient in this study; Figure 2(a) and (c) display the observed voxel-level predictor trajectories of the T1w and FLAIR images, respectively, and Figure 2(b) and (d) show the respective smoothed trajectories. The voxel-level trajectories in these figures correspond to the voxels in the lesion displayed on the observed images in Figure 1.

Since the true underlying MTR functions are unknown, we perform a 10-fold cross-validation of the data based on subject ID. The subject IDs are first randomly sorted, and then the corresponding voxel observations are split into groups. The first three groups consist of six subjects, and the other seven groups consist of five subjects. The validation was designed in this manner in order to produce a more realistic scenario in which imaging information is observed from entire subjects and prediction is also done for all voxels in the scan of a subject. Histograms of the number of voxels and observations per subject are included in the Supplementary Material [Pomann et al. (2016)].

We evaluate prediction by comparing the integrated mean squared error (MSE) of the models. We also compare this prediction error with the empirical measurement error of the MTR voxel-level trajectories. To do this, for each cross-validation step, we compute $MSE/s_0^2$ such that $s_0^2=\left[{\sum }_{i=1}^n{\sum }_{j=1}^{m_i}\{Y_i\left(t_{ij}\right)-{{\tilde{Y}}_i\left(t_{ij}\right)\}}^2\right]/\left[{\sum }_{i=1}^n{m}_i\right]$, where m_i is the number of time samples per curve, and n is the total number of observed voxels, and ${\tilde{Y}}_i\left(t_{ij}\right)$ are the smoothed response trajectories without noise. A ratio of 1 indicates that the prediction is as good as smoothing the observed data. The smooth trajectories are obtained by using the fpca.sc function in the refund package in R with 20 basis functions to smooth the covariance and 99% variance explained to obtain the number of eigenfunctions used to reconstruct the data.

Figure 3(a) and (b) display the observed and smoothed MTR voxel-level trajectories, respectively, for the voxels in the lesion of Figure 1. For these same voxel-level trajectories, Figure 3(c) and (d) present the predicted response trajectories from using the PW and GB methods. Due to the lag window being fixed at six months, the estimation is restricted to t > 26 weeks. We see that the predictions obtained using our model are similar to the smoothed MTR trajectories.

Fig. 3.

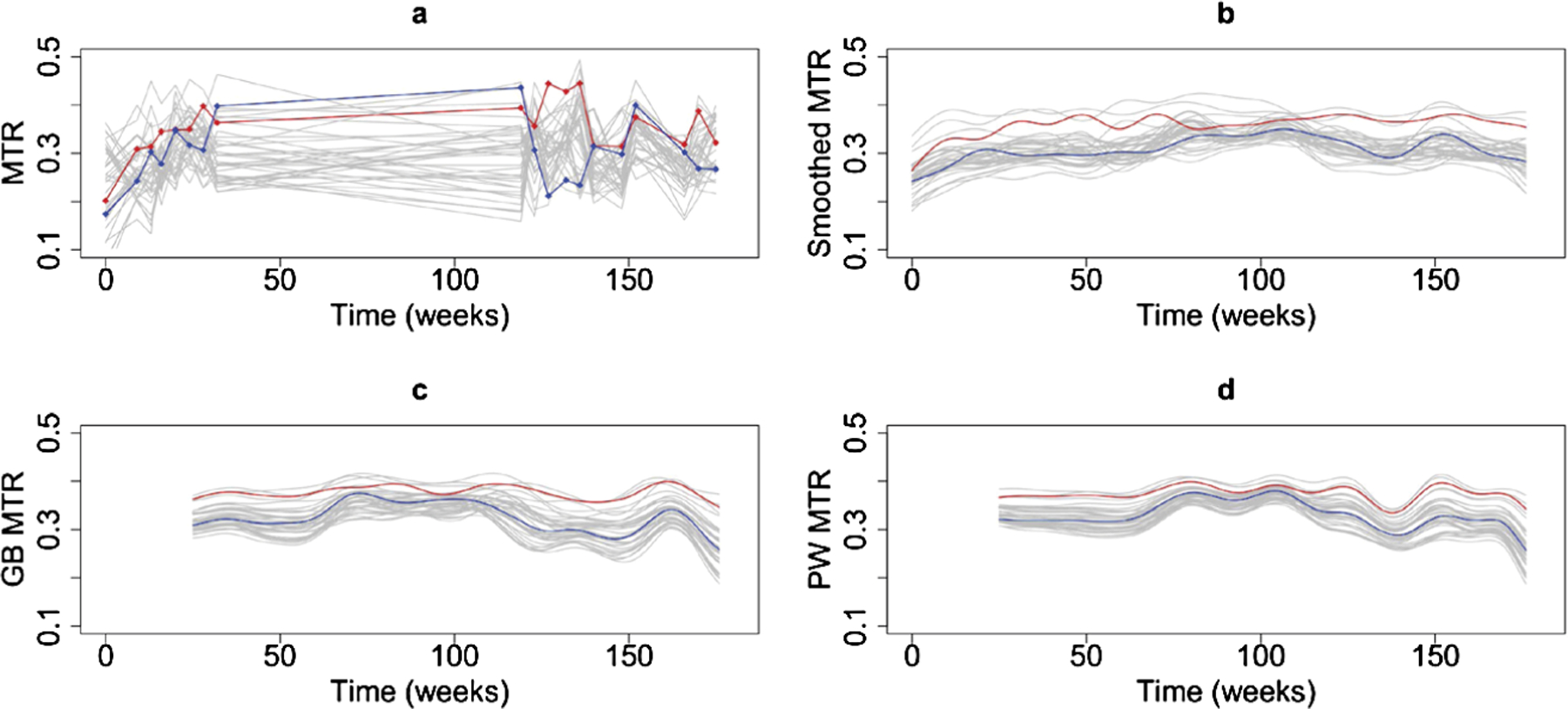
(a) MTR voxel intensities for a subset of the lesion voxels in the same patient as in Figure 1; (b) smoothed MTR voxel intensities using 20 basis functions to smooth all of the data; (c) predicted MTR voxel intensities using the GB method; (d) predicted MTR voxel intensities using the PW method. The values for the predicted MTR are not available for the first 26 weeks since this is the window used for prediction. The red and blue curves are two particular curves.

Table 3 displays the prediction error results for the different approaches. The HFLM model consistently has higher predictive accuracy than the corresponding cross-sectional models. Both estimation approaches for the HFLM model perform comparably. This model yields a 61% improvement over the CS model and a 48% improvement over the CSNL model. These improvements indicate the importance of accounting for temporal dependence over the previous six months when predicting MTR. Similar results were observed for the average in-sample error.

Table 3.

Prediction error from 10-fold cross-validation on MTR data with T1w and FLAIR predictors. Integrated mean squared error (MSE) along with the average $MSE/s_0^2$, where $s_0^2$ is the estimated measurement error in the observed MTR voxel trajectories for all models and estimation approaches. The last two columns show the improvement for each approach over the CS and CSNL models

Model	MSE[SE] · (103)	$MSE/s_0^2$	Imp. over CS	Imp. over CSNL
CS	12.7 [3.4]	4.1	0%	−32%
CSNL	9.6 [2.7]	3.1	31%	0%
HFLM (GB)	5.0 [2.1]	1.6	61%	48%
HFLM (PW)	4.9 [2.1]	1.6	61%	49%

This analysis was repeated for a lag window of 3 and 9 months, and it was observed that the error between the different window sizes was the same up to the third significant digit for both methods. It may be of future interest to explore the model with interactions as well as other commonly acquired predictors such as proton density volumes or T2w images. This analysis can provide further insight regarding which commonly acquired images can be used to predict MTR and analyze tissue damage. Observe that using both predictors in the HFLM model yields a 9% improvement over the model with only one predictor (see the Supplementary Material [Pomann et al. (2016)]). However, when using the cross-sectional models, this relationship is not maintained; each of the two-predictor models does not perform as well as the corresponding model with only the T1w intensities used as a predictor. The models with only FLAIR intensities used as a predictor consistently do worse than all of the corresponding cross-sectional two-predictor models. These results confirm the qualitative assessment that the T1w image on its own contains detailed information about tissue damage. Furthermore, adding the FLAIR intensities to any of the cross-sectional models does not improve predictive power.

5. Conclusion.

We propose using the HFLM to estimate the current value of MTR in lesions using only the previous six months of both the T1w and FLAIR voxel intensities. We provide two methods to estimate the regression parameter functions: the PW method, a pointwise least squares approach; and the GB method, a global penalized functional regression approach. The PW method directly accounts for the covariance of the predictor functions by using a pointwise least squares approach to estimate the regression parameters. Additionally, in the case of sparse data, this method does not require the estimation of smooth trajectories as the GB method does. However, the GB method has a few advantages over the PW method. First, the performance of the PW method depends on the choice of the range of λ values for cross-validation. It was observed experimentally that if this range were not properly selected, then high out-of-sample prediction errors would be observed. Second, the PW method does not guarantee smoothness across time since estimated coefficients and predictions are performed at each time value. Finally, the PW method assumes that the β functions can be modeled as a sum of tensor products of basis functions, whereas the GB method makes use of general bivariate basis functions.

Our findings from the study suggest that the MRI signal within lesions depends on the local recent history of the signal at that location. Thus, the proposed model can facilitate the study of tissue damage in lesions of patients with MS. Furthermore, estimation of MTR using the HFLM model with the recent six months of both the T1w and FLAIR voxel trajectories outperforms cross-sectional models that do not take temporal dependence of the voxel-level trajectories into account. Future work will explore the use of this HFLM model to predict other quantitative imaging modalities and its application to other tissue classes. Estimability should be investigated further when making inference about the β coefficients is of interest.

The estimation of MTR in lesions using the traditional clinical FLAIR and T1w sequences has implications for both research and clinical practice. Estimating MTR within lesions with these sequences will provide additional information about lesions without needing to acquire MTR. As MTR has not been a traditional imaging modality, most retrospective data will not have MTR measured. Estimating the MTR in lesions may allow us to answer important research questions in large historical databases of MRI images. The proposed methods facilitate the estimation of MTR within lesions, providing additional information to clinicians to make treatment decisions in patients with MS.