Machine Learning-Based Continuous Intracranial Pressure Prediction for Traumatic Injury Patients

Abstract

Structured Abstract—Objective: Abnormal elevation of intracranial pressure (ICP) can cause dangerous or even fatal outcomes. The early detection of high intracranial pressure events can be crucial in saving lives in an intensive care unit (ICU). Despite many applications of machine learning (ML) techniques related to clinical diagnosis, ML applications for continuous ICP detection or short-term predictions have been rarely reported. This study proposes an efficient method of applying an artificial recurrent neural network on the early prediction of ICP evaluation continuously for TBI patients. Methods: After ICP data preprocessing, the learning model is generated for thirteen patients to continuously predict the ICP signal occurrence and classify events for the upcoming 10 minutes by inputting the previous 20-minutes of the ICP signal. Results: As the overall model performance, the average accuracy is 94.62%, the average sensitivity is 74.91%, the average specificity is 94.83%, and the average root mean square error is approximately 2.18 mmHg. Conclusion: This research addresses a significant clinical problem with the management of traumatic brain injury patients. The machine learning model data enables early prediction of ICP continuously in a real-time fashion, which is crucial for appropriate clinical interventions. The results show that our machine learning-based model has high adaptive performance, accuracy, and efficiency.

I. Introduction

Patients diagnosed with traumatic brain injury (TBI), a major cause of death and disability worldwide, require immediate treatments in an ICU with restless support from different medical specialists [1]. In prevalent cases of TBI, the occurrence of hemorrhage causes an increased ICP. The elevated ICP, along with impaired cerebrovascular autoregulation, can lead to brain ischemia and subsequent hypoxia [2]. Besides that, the brain tissue is sensitive to compression. During the high ICP, vital brainstem structures have an increased incidence of pressure exposures, shortly resulting in dangerous or even fatal outcomes [2], [3]. Referring to the guidelines for TBI management [4], continuous ICP monitoring is assigned to the patients to detect prolonged elevated ICP events, which is believed to improve the survival rate. Targeted treatments to maintain the ICP below a critical threshold for a sufficiently long term are considered to decrease the likelihood of unfavorable outcomes.

There have been previous efforts on developing noninvasive ICP monitoring methods, including the transcranial Doppler techniques [5], optic nerve sheath diameter measurements [6]–[9], and imaging-based methods (e.g., computed tomography (CT) [9], [10], magnetic resonance imaging (MRI)) [11]. Machine learning (ML) techniques have become a powerful tool to make predictions or perform classifications for medical diagnoses [12]. Three previous studies proposed a noninvasive methodology on early intracranial hypertension detections based on ML techniques using ICP waveform analysis or image features (including midline shift, intracranial cavities, and ventricle size) extracted from medical imaging modalities (e.g., CT or MRI) [13]–[15] with varying degrees of prediction accuracy. The classification accuracy in the first study [13] was about 74% in ICP levels predicted with multiple features sources. The second study [14] reported an accuracy of 91% for predicting increased ICP classification for children. Another study based on noninvasive ICP data with thirteen patients reported a root-mean-square error (RMSE) of 3.7 mmHg with their ICP estimation [15]. All these three studies [13]–[15] used noninvasive methods to achieve ICP estimates. The first two methods [13], [14] predicted the ICP based on CT scans. The CT scan can only be executed on the patients a limited number of times due to the risks of ionizing radiation exposure. Also, the CT scan requires a particular time to be performed, which causes the real-time ICP estimation to be unachievable. The ICP signal is a time series of physiological data. Thus, models to provide binarized classification may still be too simple to achieve ICP tracking and predictions in a real-time and continuous manner. The third study [15] highly relies on the excellent quality signal, which may not apply to real-world medical scenarios. The waveform-targeted method may be sensitive to the noise components of ICP signals that occur during TBI patients’ routine care (e.g., patient movements, bed adjustment, or simple connection problems), which may hinder the accuracy and unavoidably yield unreliable diagnosis predictions [10]. Compared to their methods, our machine learning pipeline provides continuous ICP estimation in real-time. Furthermore, our method is designed to compensate for the noise/artifact frequently evident in clinical data. Overall, our proposed method provided a better performance on ICP predictions, confirmed by the higher accuracy and the lower RMSE.

The accurate way to monitor ICP is using invasive techniques (including fluid-based systems and implantable micro-transducers) along with certain risks of intracranial infection and hemorrhage [10], [16]. ML applications on ICP data collected invasively are not commonly found. ML techniques were applied to the ICP data collected invasively by Scalzo et al. [17]. They suggested using extremely randomized decision trees to predict intracranial hypertension with ICP wave morphology-related features and obtain improved results compared to multiple linear regression models and the adaptive boosting algorithm. Time components intrinsically increase the complexity of a sequenced dependence among the ordered data. Thus, conventional regression models may not perform well with the time series forecasting problems. Our study is a step forward as it proposes an ML application for early detection of the upcoming intracranial hypertension in a real-time manner. In this work, a Long Short-Term Memory (LSTM) model [18], as an artificial recurrent neural network (RNN), is used for predicting ICP events. First, a statistical-based method is applied for smoothing the ICP data and minimizing the negative effect caused by the noisy data. Second, with the processed ICP data, an LSTM model was generated for each patient and predicted the following ICP signal in every next 10-min period after the model initialization. The normal adult ICP is typically within a range of 5 to 15 mmHg; mild intracranial hypertension is described with an ICP readout from 20 to 30 mmHg [19], [20]. Thus, 20 mmHg on ICP readouts is selected conservatively as the criterion for the ICP event classification in this study. Lastly, accuracy, sensitivity, specificity, and RMSE were calculated to evaluate the models’ performance.

II. Methods and Procedures

A. Database

The CHARIS database [21] used in this study was obtained from the PhysioNet [22]. The studies were approved by the Rutgers Research Ethics Committee (IRB) and have been performed in accordance with the ethical standards as laid down in the 1964 Declaration of Helsinki and its later amendments or comparable ethical standards. The study was exempt from informed consent since no patient contact nor identity was involved, and no procedures were performed [21]. The ICP data (unit: mmHg) were monitored with either a subarachnoid bolt or ventriculostomy of thirteen patients diagnosed with traumatic brain injury (TBI). All the data acquisitions were initialized from patients arriving in surgical ICU rooms of Robert Wood Johnson Medical center of Rutgers University (NJ, USA). During the data acquisition, the sampling rate was 0.02 seconds per sample. The resolution of 1.41 mV at ±5 V analog input range was equivalent to a pressure resolution of 0.14 mmHg and a dynamic range of ±500 mmHg. The sampling duration was varied for different subjects. The data involved high-frequency noise and signal distortion. Additionally, patient demographic information was not originally included.

B. Data Preprocessing

Due to the appearance of the noise and signal distortion, data preprocessing steps, including denoising and smoothing, were critical for achieving better prediction outcomes from the neural network model. As the first step, based on the visual inspection of the histogram of all the ICP data, global thresholding values were selected, and all reasonable ICP data ranges (from −5 to 50 mmHg) were kept. All other data points that fall out of the ranges were set to null and forward filled with the first available previous values to maintain the data continuity. In the second step, the processed data was input into the smoothing algorithm. In this algorithm, a sliding smoothing window with a length of 60000 data points (a 20-min period) was activated at the beginning of the data. The mean and the standard deviation (SD) of all the data points inside the window were calculated. Any value out of +/−3 times the standard deviation was classified as an outlier and replaced with the mean of the current smoothing window. Next, the window was moved toward the end with a step of 3000 data points (5% of the window length) until reaching the end of the data. As the last step of the data preprocessing, the ICP data was compressed from 0.02 seconds per sample (50 Hz) to 60 seconds per sample (0.017 Hz). The average of every 3000 data points was assigned as one data point in the compressed data. Although effective data processing techniques were applied to the raw data, visual inspection was still needed for removing the meaningless data segments (continuous abnormal high/low ICP measurements) from the input data. One patient’s ICP data is randomly selected to illustrate the data preprocessing steps; raw data and processed data are shown in the results section for comparison.

Data Preprocessing Procedure*

• Input:x: raw ICP signal
• Output:

  y: processed ICP signal

• 1:initialize: w 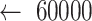: Size of the sliding window; st 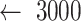: Steps of window moving
• 2:i ;
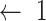• 3:while i + w <= Length(x) do
• 4:Segment: seg x[i: i + w]
• 6:for j in Range(1, w) do
• 7:if seg[j] >50 or seg[j] < −5 do
• 8:seg[j] NULL
• 9:end if
• 10:end for
• 11:seg FillNull(seg): Forward filling NULL with the first available previous data
• 12:Mean: m Average(seg); Standard deviation: s 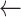SD(seg)
• 13:for k in Range(1, w) do
• 14:if seg[k] > m +3*s or seg[k] < m - 3*s do
• 15:seg[k] 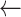m
• 16:end if
• 17:end for
• 18:i 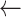i + st
• 19:end while
• 20:y 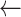Compress(seg): down sampling to 60 seconds per sample
• 21:return y

• *Annotation: 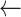: value assigning; Length(): the function return the length of input; Average(): the function return the average of input; SD(): the function return the standard deviation of input; Compress(): the down sampling function.

C. Model Training

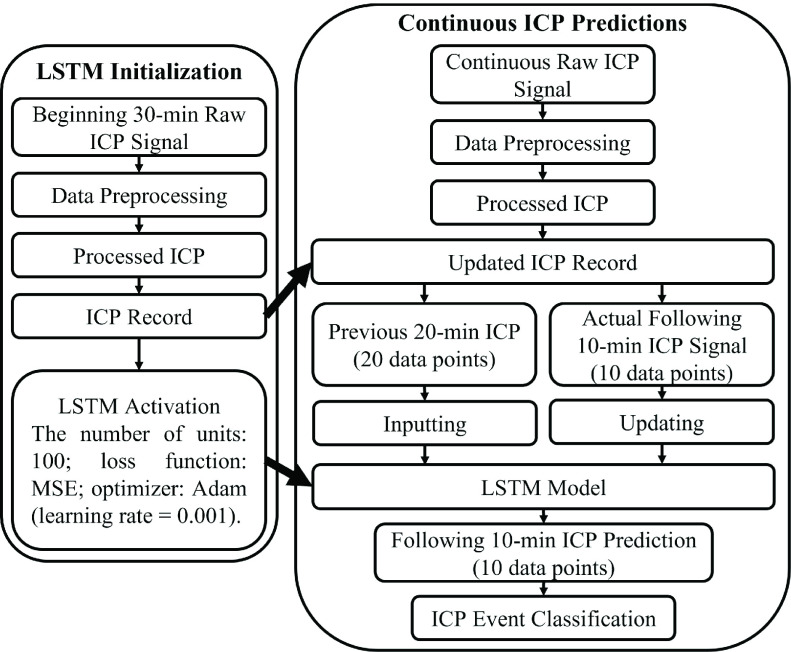
The machine learning code was written using Python 3.6 [23]. The LSTM model was from Keras [24], a popular open-source library for artificial neural networks on Python. After preprocessing the raw ICP data of each subject, a scalar (50 mmHg) was used for normalizing the processed ICP data. For compiling the LSTM model, the number of units was set to 100. The training epoch was set to 15, the mean square error (MSE) was chosen as the loss function during the model training, and Adam (learning rate = 0.001) [25] was selected as the optimizer algorithm. The first 30-min ICP data was used for starting the LSTM model. To ensure the model training efficiency, the model takes 20 data points to predict one data point representing the ICP data for the following 1-min, and this predicted value was appended to the previous input to predict the next data point until a total of 10-min ICP data (10 data points) were generated. After the model’s activation, every 1-min of the upcoming raw ICP data (3000 data points) was preserved for data preprocessing in a real-time fashion. All the processed ICP data was stored historically (by expanding the ICP record). With every last 20-min ICP data on the ICP record, LSTM predicted a result representing the following 10-min (10 data points) after 10-min from the previous prediction. Simultaneously, this 10-min prediction was classified as an incident of high or low ICP (intracranial hypertension or intracranial normotension) compared with the ground-true label (generated from the smoothed ICP data within the same time frame). To determine a high or low ICP event, if there were more than 60% of data (6 data points) above 20 mmHg, this whole 10-min ICP segment was labeled as a high event; otherwise, it was labeled as low. The accuracy, sensitivity, and specificity as additional metrics for the model validation were calculated after classification. The model was trained recursively along with the passing time. After each prediction, the ground-true data served as the next input for training the model to yield an updated model. These prediction steps were continued until the end of the ICP signal for each patient. A flowchart is shown in Fig. 1 for clarification.

FIGURE 1.

Flowchart of the data processing pipeline.

D. Statistics

For analyzing the statistical significance of the difference between the actual and predicted ICP data, regression analysis was performed. The Pearson correlation was calculated for evaluating the linear relationship, and the Spearman rank-order correlation was used to quantify the strength of a monotonic relationship. The RMSE, accuracy, sensitivity, and specificity were calculated to further validate the accuracy of the model. By defining a high ICP incident as a positive case, the sensitivity value was calculated by dividing true-positive counts with the sum of true-positive counts and false-negative counts. The specificity value was calculated by dividing true-negative counts by the sum of true-negative counts and false-positive counts.

III. Results

Statistical analysis of the raw ICP data and the processed ICP data are shown in Table 1 to demonstrate the effectiveness of the proposed data preprocessing method. Among the original ICP data from the 6th patient, the range of the raw ICP data was from −395.51 to 400.66 mmHg, and artifacts were evident (Fig. 2A). After global thresholding, nearly all the significant artifacts with abnormal high/low readouts were removed, as shown in Fig. 2B. By applying the described data smoothing methods, the ICP data were further smoothened, and abnormal peaks were removed, as shown in Fig. 2C. During this step, outliers were recognized and discarded locally. Lastly, the processed ICP data were downsampled (the outcome is shown in Fig. 2D). The overall trend of ICP data for the 6th patient can be clearly observed. Considering the fact that the ICP waveform information was prone to distortion and would yield false diagnosis predictions, it would not be much beneficial to maintain the physiological ICP waveforms during the data preprocessing. Instead, the features related to the ICP trend were focused on in this study. After the data preprocessing, statistical analysis results (Table 1) showed that the range of the processed ICP data was close to a physically reasonable range (from 1.60 to 31.34 mmHg) with lower SD values. For the other patients, similar statistical analysis results are obtained, as shown in Table 1; the effectiveness of the proposed data preprocessing method was observed among all the patients’ data.

TABLE 1. Statistical Analysis of the Raw ICP Data and the Processed ICP Data.

Patient #	Min (mmHg)	Max (mmHg)	Average (mmHg)	SD	Duration (hours)	Min* (mmHg)	Max* (mmHg)	Average* (mmHg)	SD*
1	−320.95	369.77	21.11	15.17	68	6.65	32.24	17.99	5.86
2	−394.68	396.13	24.92	24.43	320.56	−1.19	49.25	22.75	5.72
3	−409.18	407.59	15.96	9.46	49.44	12.64	27.66	16.34	1.96
4	−389.77	389.89	22.96	34.14	40	0.08	24.51	18.48	2.22
5	−386.54	401.18	22.74	9.76	167.61	13.56	40.57	22.23	4.97
6	−395.51	400.66	21.91	27.5	46	1.6	31.34	18.35	6.8
7	−309.24	358.93	15.93	28.83	114.69	0.39	32.29	12.39	3.79
8	−396.4	390.56	18.87	34.03	46.67	−1.56	41.97	11.23	6.28
9	−65.26	64.33	4.21	4.21	68.89	−3.63	16.86	4.08	3.68
10	−98.48	47.86	12.31	6.31	23.55	3.91	31.84	12.2	5.67
11	−374.8	388.21	27.26	49.25	69.44	−4.91	49.95	14.71	11.87
12	−362.11	371.24	11.85	26.87	107	−4.69	30.26	8.86	5.55
13	−408.13	408.21	23.26	48.79	73.89	0.16	27.43	14.13	2.89

^*after data preprocessing.

FIGURE 2.

Resulting plots illustrating the data preprocessing steps (all sampling points are plotted). A. the raw ICP data plot (from the 6th patient); B. the resulting data plot after data thresholding; C. the resulting data plot after applying the smoothing technique. In A, B, and C, the sampling frequency is 50 samples per second (0.02 second per sample), and the scale of the x-axis is 10⁶ samples D. an outcome plot of the data preprocessing steps where the sampling frequency is reduced to 1 sample per minute (60 seconds per sample), and the unit of the x-axis is one sample per minute.

Table 2 shows the regression analysis performed for each patient to reveal the high degree of similarity between the model predictions and the actual ICP data. The Pearson correlation coefficients of determination (R²) ranged from 0.58 to 0.97, and the p-values indicated significant correlations between the predictions and the actual ICP data. The linear relations between the predictions and the actual data varied among the patients. According to [26], a strong linear correlation (R > 0.7) was found in all patients. The strength of the relation between the actual data and the predicted ICP was shown during Spearman’s rank correlation. The minimal Spearman’s rank correlation coefficients were 0.82, which was considered a strong correlation (in a monotonic relationship), and the p-values indicated the significant correlations between the predictions and the actual ICP data. With a positive Spearman correlation coefficient, when the actual ICP data increase, the predicted ICP data increase with a nonconstant rate, whereas the rate of increase (or decrease) in a linear relationship is constant. When the input data to the LSTM model is abnormally lower (or higher), the prediction will decrease (or increase) but in a nonlinear manner. Thus, the LSTM predictions should show more stability following the overall trend and less likely to be affected by extreme input values. In this study, the LSTM models were able to follow the data trends during the entire period.

TABLE 2. Regression Analysis of the ICP Predictions With the Actual ICP Data for all 13 Patients.

Patient #	Pearson Correlation (R2)	p-value* (Pearson)	Spearman Rank Correlation ( )	p-value** (Spearman)
1	0.90	p < 0.001	0.95	p < 0.001
2	0.74	p < 0.001	0.87	p < 0.001
3	0.75	p < 0.001	0.89	p < 0.001
4	0.58	p < 0.001	0.89	p < 0.001
5	0.90	p < 0.001	0.95	p < 0.001
6	0.97	p < 0.001	0.98	p < 0.001
7	0.69	p < 0.001	0.87	p < 0.001
8	0.60	p < 0.001	0.82	p < 0.001
9	0.95	p < 0.001	0.98	p < 0.001
10	0.79	p < 0.001	0.90	p < 0.001
11	0.89	p < 0.001	0.93	p < 0.001
12	0.80	p < 0.001	0.92	p < 0.001
13	0.79	p < 0.001	0.89	p < 0.001

^*the null hypothesis was rejected at p < 0.05.

^**the null hypothesis was rejected at p < 0.05.

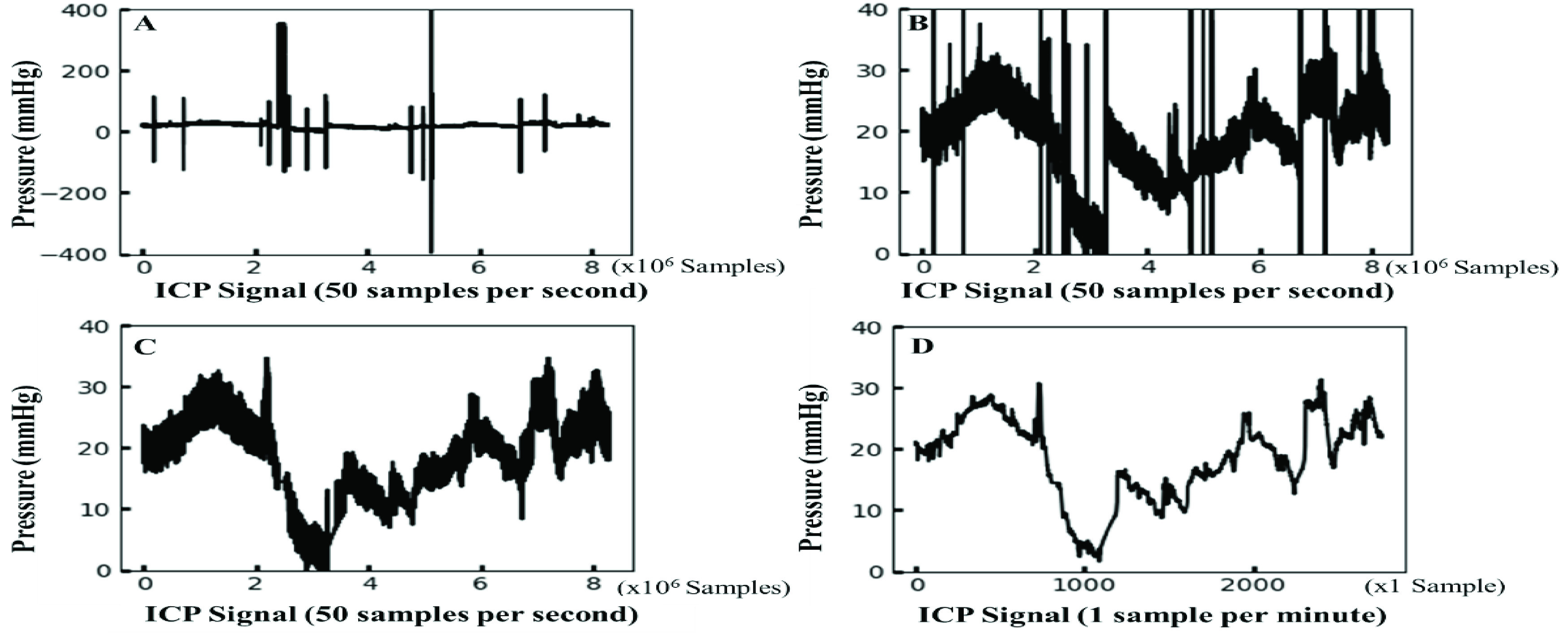
In Figure 3, the predicted ICP data (labeled in red) resulting from the proposed method were plotted against the actual ICP data (labeled in black) for all patients. Our models’ ICP predictions accurately followed the trend of the actual ICP data with small errors. It is difficult to visually distinguish subtle differences between the actual ICP data and the predicted ICP data, even if different colors are used. In Table 3, a total of 7127 ICP incidents (2452 high ICP incidents) were detected among all the patients, and the number of ICP incidents ranged between 138 and 1920. Since the ICP signals included inconsistent amounts of noise close to the end of the data collection, these portions of noise were truncated manually. Thus, the incident number and the duration of hospital stays were not in a linear relationship after the proposed data processing steps. The percentage of high ICP incidents ranged from 0% to 69.69%, and the average was 22.06%. The 9th patient had an absence of a high ICP event. Thus, the sensitivity was shown with NaN (Not a Number). After excluding the 9th patient, the overall LSTM model performance was as follows: the average accuracy was 94.62%, the average sensitivity was 74.91%, and the average specificity was 94.83%. A minimum of 93.70% accuracy was found among nine patients, and a minimum of 96.14% accuracy was found among seven patients. The lowest accuracy (88.91%) was found for the 2nd patient. A minimal 87.50% sensitivity was found among six patients, and a sensitivity of less than 70% was found among 5 patients. The sensitivity values were lower for the 3rd, 7th, 8th, 12th, and 13th patients who had a low percentage of high ICP incidents (ranging from 1.72% to 6.88%). The relatively small number of high ICP events caused underfitting problems for predicting high ICP incidents. A minimal 92.75% specificity was found among 11 patients. Among all the patients, the minimal specificity was 80.41% and was found in the 2nd patient who had the highest ICP incidence rate. Since high ICP events were found more frequently and the low ICP events were rare with the 2nd patient, this unbalanced event ratio could cause a relatively higher sensitivity value with a lower specificity value. Among all the patients, the average RMSE was 2.18 mmHg and ranged from 0.89 to 4.31 mmHg, indicating that the model predictions followed the target data trend quite well without large errors. Besides the imbalanced data effect, the proposed ML method can achieve high accuracy, high specificity, and good sensitivity for all the patients for the continuous real-time ICP event predictions in the short-term period.

FIGURE 3.

The ICP prediction plots for all 13 patients. The predicted ICP data from the proposed method are labeled in red; the actual ICP data are labeled in black. The patient ID numbers (from 1 to 13) are labeled alphabetically from A to M.

TABLE 3. Summary of the Scoring Metric for Each Individual LSTM Model (all the 13 Patients).

Patient #	Total Events	High ICP Incidence Rate (%)	RMSE (mmHg)	Accuracy (%)	Sensitivity (%)	Specificity (%)
1	404	37.13	1.89	95.54	94.00	96.46
2	1920	69.69	3.04	88.91	92.60	80.41
3	293	3.75	1.00	96.93	63.64	98.23
4	236	18.22	1.60	91.10	83.72	92.75
5	1002	60.38	1.56	92.22	94.05	89.42
6	272	47.43	1.19	96.69	96.12	97.2
7	685	1.75	2.19	97.08	33.33	98.22
8	276	6.88	4.31	92.03	47.37	95.33
9	410	0.00	0.89	99.76	NaN	99.76
10	138	11.59	2.70	96.38	87.50	97.54
11	413	23.97	4.04	93.70	88.89	95.22
12	638	1.72	2.55	98.75	54.55	99.52
13	440	4.32	1.37	96.14	63.16	97.62
Average	548	22.06	2.18	* 94.62	* 74.91	* 94.83

^*The 9th patient data were excluded.

IV. Discussion

In this study, an effective smoothing method was developed which selectively suppressed the native noise from raw ICP signals. After the ICP data were preprocessed, an LSTM model was applied to monitor the next ICP event in the upcoming 10-min period for each patient. Despite the varying degrees of noise and data imbalance, the LSTM model can correctly identify ‘low’ events (with 95.62% precision) and ‘high’ events (with 90.21% precision). The low RMSE and the strong correlation coefficients between the actual and the predicted ICP data show that the model follows the trend quite well. The significant difference test results also verify that. In a real-world scenario, varying degrees of noise/artifact will always exist. These noise/artifact components are efficiently compensated in the data preprocessing steps in our method. Therefore, our method is highly feasible and practical in performing transfer learning to new patients.

Although an experienced doctor may be able to predict the trend when looking at the preprocessed data, this relies on some well-trained doctors who may not always be available. Also, continuous ICP assessment for days and nights during the long duration of patient stays might be challenging. Additionally, the ICP estimation obtained via visual inspection is prone to subjective errors, especially with the existence of noise/artifact. Thus, the ICP assessment performed by continuously monitoring a screen may not be feasible or efficient. The proposed model in this study predicts the ICP trend in the following 10 minutes, which can provide extra assistance for decision-making on arranging medical treatments. Furthermore, continuous ICP evaluation shows that mannitol can lower the ICP after intravenous administration [27]. The ICP trends and predictions can be integrated into infusion pumps for automatically controlled intravenous injections. The availability of infusion treatments in real-time could be useful in generating a personalized ICP monitoring/therapy plan for future intracranial hypertension prediction tasks. The ICP data applied in our study were collected from actual clinical settings. During signal collections, any artifact or sensor disturbance caused in surgical procedures are not labeled in the original data. Despite the noise involved with the ICP data, our method provides accurate ICP estimations continuously with high applicability. There are only limited ICP predictions using ML models, and this work would be a beneficial step forward for future time-series machine modeling of ICP predictions.

There are some similar studies focusing on machine learning methods for ICP event prediction. In the first study [13], the dataset contains CT scans from 17 patients with mild to severe TBI. The CT scan features were combined with demographic information to predict a raised ICP event. Their model achieved 73.7% accuracy, 76.6% specificity, and 68.6% sensitivity. In the second study [14], the dataset also consists of CT scans collected from 475 children. Their model predicted ICP increases based on CT scans and achieved an accuracy of 91% for the testing data. Compared to these two studies, our model performed better and achieved 94.62% accuracy, 74.91% sensitivity, and 94.83% specificity. The dataset in the third study [15] was collected from 13 patients. The mean ICP value was estimated from measured blood pressure and cerebral blood flow volume. Nearly 7-hours of data were analyzed (in comparison, we analyzed 1195 hours of data). Their method yielded ICP estimations with an RMSE of 3.7 mmHg. Still, our model performed better, and the RMSE in our work was 2.18 mmHg.

In the past, Scalzo et al. [17] used ML to improve the temporal accuracy of finding changes in ICP values for finding intracranial hypertension events. Their method relies on monitoring both the arterial blood pressure (ABP) and ICP and changes in the slope of a linear relationship between the two signals [21]. However, they cannot predict the spurious ICP events in advance. Differently, our models uniquely provided a prediction of a future (10-minutes) ICP event with good accuracy. Another recent outcome prediction model was developed using statistical and frequency features of ICP, ABP, and carotid perfusion pressure to predict neurological outcomes in patients with TBI using Gaussian processes [28]. They tried to predict an intracranial hypertension event 30 minutes in advance based on 4-hour continuous data from TBI patients. Instead of focusing singularly on predicting classification, our model predicts ICP estimation and classifies the ICP events with real-time ICP pressure signals accurately alone without knowing other physiological parameters; this capability distinguishes our work from previous studies. Extra medical monitoring activity unavoidably increases the cost of critical care medicine for the patients and introduces task complexity for the medical staff. Even though ABP data is available in the CHARIS database, the tremendous amount of noise made the blood pressure data unbeneficial to be included in this study. Additionally, our model could be initialized quickly with a half-hour ICP signal from the beginning of ICP monitoring, which provides fast installation and flexibility. Furthermore, the short-term ICP data prediction will be more practical than knowing the ICP event classification in the long term. For the one-hour case, it may turn out high-risk ICP events could have happened earlier or later within an hour, but knowing the ICP events in the next 10 mins could largely reduce this uncertainty. Therefore, the proposed method can help monitor patients’ ICP and efficiently forecast the occurrence of short-term ICP escalations.

Due to the individual differences between the patients, one conventional model/method may not always perform well for all the subjects. Personalized healthcare is currently receiving more and more attention [29]. In this work, the ICP prediction model is generated uniquely for each patient. The major benefit of creating a unique model for each new patient is to better fulfill personalized medicine needs. Our machine learning pipeline can provide continuous ICP estimation for the following 10 min at a real-time pace. Additionally, the LSTM model featured with fast installation/deployment only required the first 30 min of ICP data to be initiated. After the activation, the predictions are generated accurately until the release of the patients. Since the LSTM model is applicable to high-dimensional data, for future research, combining additional patient information (e.g., simultaneous and continuous blood pressure) with the current ICP readout might help provide long-term ICP prediction (more than 10 min ahead in time). Additionally, a pre-trained LSTM model capable of being activated instantly without initialization could be tested. This approach might ease the transfer learning of the proposed method. As suggested by [30], cerebral hemodynamics models can generate simulated ICP data to develop a pre-trained LSTM model. This approach might improve the efficiency of the LSTM model development. Additionally, the patients’ demographic information (e.g., age, gender) and anatomical features (e.g., brain width) extracted from CT scans would be valuable for designing a patient-specific cerebral hemodynamics model geared toward precision medicine. There is room for future improvement on the proposed method; however, this research showed the feasibility of using the LSTM model to predict ongoing ICP for patients in a crucial short-term period.

V. Conclusion

This study introduces an efficient artificial recurrent neural network model for the following 10-min prediction of ICP changes and events in a real-time fashion for 1195 hours. The proposed ML method achieved good accuracy in terms of continuous predictions of the ICP event. The high adaptive performance of the LSTM model has been demonstrated among varying patients’ data. Continuous ICP prediction and detection of future incidents of high ICP might help save the lives of TBI patients. This technology can help perform timely and appropriate treatment plans.