Influence of impact velocity and impact attack angle of bullets on damage of human tissue surrogate —— ballistic gelatin

Abstract

Purpose

Terminal performance of a bullet in human body is critical for the treatment of gunshot injury and optimization of bullet design. The effects of the impact velocity (v₀) and the impact attack angle (δ₀) of the bullet on its terminal performance was investigated, using a new evaluation method (called expansion method) based on the expansion of cracks and the permanent cavity wall in ballistic gelatin.

Methods

Ballistic gelatin was used to simulate human body. The 7.62 mm × 39 mm rifle bullets with different v₀ (600–760 m/s) and δ₀ (0°–6°) were fired into the gelatin blocks. The gelatin block was cut into slices of about 20 mm thickness. The cracks and the permanent cavity on each slice were obtained manually. The damaged gelatin was determined using two methods: expanding the permanent cavity but ignoring the cracks, and expanding both the permanent cavity and the cracks. The relations between the damaged gelatin and v₀ and δ₀ were obtained using linear fitting method.

Results

According to the distribution of the damaged gelatin along the penetration depth, the damaged gelatin block could be divided into two parts: the less damaged part and the severely damaged part. The length of the less damaged part depends mostly on δ₀; while the average damaged area of this part depends on both δ₀ as well as v₀. The cracks contributed significantly to the total volume of damaged gelatin, particularly when the expansion was larger than 1.9 mm. The total damaged gelatin increases with v₀, δ₀ and the expansion extent. The average length of equivalent cracks grew with v₀ and δ₀ when considering the cracks, and decreased with v₀ when ignoring the cracks.

Conclusion

The expansion method is suitable to investigate the influence of different factors of bullets on their terminal performance. The characteristics of the damaged gelatin have a linear relationship with the initial attack angle (δ₀) and the initial velocity (v₀) of the bullet.

Introduction

The knowledge of the terminal performance of a projectile in human body is critical for surgeons to treat the wounded and for weapon experts to optimize the projectile.1, 2, 3 To visualize how the projectile generates wounds in human body, various animal models (pig models, goat models, etc.) have been established since these animal tissue has similar structures and functions to human tissue.4, 5, 6, 7, 8 However, due to the difference in terms of anatomy, physiology and behavior of animals, none of the experimentally created wound channels are identical or can be repeated. This variability complicates the evaluation of the terminal performance of projectiles, necessitating the use of a large number of animals in the experiments.

Homogeneous simulants such as water, soap, and ballistic gelatin are then proposed to model the properties of human tissues.⁹ Although they are inanimate objects and their structure differs from that of human beings, their densities are all approximately 1 g/cm³, a value close to that of human soft tissues. Ballistic gelatin is the most frequently used homogenous simulant, not only because of its elastic mechanical characteristics similar to the muscle tissue but also due to its transparency.10, 11, 12, 13, 14 The second property ensures that the motion of the projectile and the formation of the temporary cavity can be recorded by a high-speed camera.^1,2

Three terminal effects will present after a projectile penetrating the ballistic gelatin, respectively temporary cavity, permanent cavity, and the cracks. Of note, when permanent cavity is not formed in ballistic gelatin, the term “permanent track” should be used instead. For high speed rifle bullets, previous study¹⁵ and our experiments both documented the formation of permanent cavity.

The temporary cavity can reach a remarkably large size, with the diameter up to 200 mm. Attempts have been made to correlate the motion of the temporary cavity with the motion of the bullet.16, 17, 18, 19 However, the temporary cavity is just a boundary. It cannot indicate which part of the gelatin is damaged directly. Moreover, accurate measurement of the temporary cavity is difficult since the temporary cavity changes rapidly and its shape is quite irregular. These characteristics render that the temporary cavity is inappropriate for quantification of penetration damage produced by bullets, in our view. In contrast to the temporary cavity, the permanent cavity and the cracks are two types of real damage of the gelatin. They can be both measured using slices of the gelatin or the CT images.^17,20, 21, 22, 23, 24 These merits make them more suitable as the damage evaluation basis of the gelatin than the temporary cavity. At present, the crack damage in gelatin has been correlated with the dissipated energy of the bullet.20, 21, 22, 23, 24 However, the damage produced by the permanent cavity is ignored. The dissipated energy cannot independently reflect the influences of other factors to the gelatin damage, such as the shape of the bullet, the deformation of the bullet, the impact velocity (v₀) and the impact attack angle (δ₀) of the bullet.

In our work, a new evaluation method of the gelatin damage based on both the cracks and the permanent cavity is proposed. Then the gelatin damage resulted from the rifle bullet of different impact v₀ and impact attack δ₀ are evaluated. Finally, the influences of v₀ and δ₀ to gelatin damage are analyzed.

Methods

Ballistic test

Ballistic gelatin blocks were used as the human body surrogate in our tests. The ballistic gelatin was prepared with water (90%) and photographic gelatin (10%) (Qinghai Gelatin Company Limited, Qinghai Province, China) to obtain gel strength corresponding to the Bloom value between 250 g and 300 g. The mixture was kept at 60 °C in a water bath for 3 h, and then poured into molds and transferred to a refrigerator (4 °C, 160 kW) for 24 h before use.¹⁶ The dimensions (mm) of the ballistic gelatin blocks were approximately 300 × 300 × 300.

Placement of the gelatin block is shown in Fig. 1. The gelatin block was placed on a transparent polymethyl methacrylate plate. A reflective mirror was set on the top of the gelatin block. A horizontal lamp and a vertical lamp were used to increase the brightness of the gelatin block. The bullet penetration process was recorded with a high-speed camera (Phantom v211, York Technologies Ltd. HongKong, China) located at the lateral side of the gelatin block. The camera is capable of simultaneous recording of both the direct image and the reflective image of the gelatin block. The camera speed was set at 30,000 frames per second. The exposure time was 2 μs, and the resolution was 640 × 480 pixels.

Fig. 1.

Placement of the gelatin block. PMMA: polymethyl methacrylate plate.

A ballistic gun was used to fire the tested full metal jacketed rifle bullets, 7.62 × 39 mm. The barrel length is 508 mm and the twist is 31.5. One gelatin block was shot by only one bullet. The impact longitudinal velocity of the bullet was measured using the photoelectric targets at the muzzle of the gun. The distance between the muzzle of the gun and the gelatin block was about 4 m, as shown in Fig. 2.

Fig. 2.

Locations of the gun and the camera.

Four tests were performed in this study. The v₀ and δ₀ of the bullet (the angle between the velocity and the axis of the bullet) were derived by analysis of the movement of the bullet using the previously developed ballistic model---The impact moving parameters of the bullet including the velocity components, the angular velocity components and the spatial positions are firstly determined, and then the v₀ and δ₀ are derived, shown in Table 1.^25,26

Table 1.

Impact velocity and impact attack angle of the bullets.

Test	v0 (m/s)	δ0 (°)
1	760	0.065
2	732	5.09
3	650	4.83
4	620	1.76

Penetration images by the bullets in the tests are shown in Fig. 3. No obvious deformation of the bullets was identified during the penetration. Thus, the bullets were taken as rigid. The influence of v₀ and δ₀ on gelatin damage could be analyzed.

Fig. 3.

Penetration of the ballistic gel by a rigid bullet. (A–D): Test 1–4.

Evaluation of gelatin damage

The proposed new method --- expansion method

The wound profile (WP) and polygon procedure (PP) methods are typical methods of wound evaluation on the basis of cracks. The WP method takes the sum of two longest cracks as the diameter of the circle reflecting the range of damage. The PP method takes the polygon formed by the cracks as the shape of the damaged area.²⁴ While the proposed new method, expansion method, considers that the gelatin damage around every point of the cracks is the same. Comparison of the three methods is shown in Fig. 4.

Fig. 4.

Comparison of wound profile (WP) method; polygon procedure (PP) method and expansion method for evaluation of gelatin damage: (crack: heavy line; damaged gelatin: yellow area).

The WP method yields a much larger area than the other two methods, and the number and distribution of cracks do not affect the calculated area, as illustrated in Fig. 4A-D. The number and distribution of cracks have some influence in the PP method and the expansion method. However, in some instances, the PP method generates unreasonable results. Fig. 4E has the same total length of the cracks as Fig. 4F, but it has a much smaller area of damage. In comparison with Fig. 4F and G has one additional small crack. However, its damaged area is significantly reduced. For the expansion method, small alterations in the cracks would cause small changes in the damaged area, as shown in Fig. 4I–L. The results from the expansion method comply with the common sense. Thus, it is employed in our study.

The expansion method can also be used to evaluate the gelatin damage around the permanent cavity if the cavity wall is treated as a special kind of crack.

Application of the expansion method

The gelatin blocks were cut into consecutive slices with a blade. The thickness of the slice was about 20 mm. Accurate thickness of each slice is shown in Appendix A1-A4. The wall of the permanent cavity and the cracks in each slice were painted manually with an ink pen and then the marks were scanned to images at 600 dpi resolution. The permanent cavity and the cracks were then highlighted in the Adobe Photoshop software, as shown in Fig. 5.

Fig. 5.

Recognition of the permanent cavity and the cracks.

When contribution of the cracks to the gelatin damage is ignored, the damaged gelatin on the surface of the slice is considered to be the sum of the permanent cavity and the expanded area of the permanent cavity wall, using the expansion method. The latter is acquired using the expansion tool in the Photoshop software.²⁷ Fig. 6 illustrates the changes of the damaged gelatin with the extent of expansion (the distance the boundary moves outwards the original region) from 0 mm to 0.21 mm, 1.9 mm, and 3.6 mm.

Fig. 6.

Expansion of the permanent cavity (white area represents the damaged gelatin).

When contribution of the cracks to the gelatin damage is included, the damaged area on each slice surface is considered to be the sum of the permanent cavity, the expanded area of the permanent cavity, and the expanded area of the cracks. Fig. 7 depicts the increase of the gelatin damage with the different extents of the expansion: 0.21 mm, 1.9 mm, and 3.6 mm.

Fig. 7.

Expansion of the permanent cavity and the cracks (white area represents the damaged gelatin).

The total damaged gelatin in the gelatin block is indicated using the volume of the damaged gelatin, which is estimated using the following equation:

$$V=\sum A_i\cdot h_i$$ (1)

Where A_i is the area of the damaged gelatin in the i_th slice, and h_i is the thickness of the slice.

Results

The cracks and the permanent cavities in the tested gelatin blocks are shown in Appendix A1, at an expansion of 0.21 mm. These data were analyzed using the proposed expansion method, and the results are listed below.

Distribution of the gelatin damage

Ignoring the cracks

Fig. 8 illustrates the size of the damaged gelatin along the penetration when contribution of cracks to gelatin damage is ignored. It is found that the gelatin block from each test can be divided into two parts along the penetration depth according to the range of the permanent cavity (0 mm of expansion): the less damaged part at the entry of the gelatin block and the severely damaged part at the exit. The size of the damaged gelatin in the less damaged part changes slowly along the penetration depth but fluctuates significantly in the severely damaged part. The size of the damaged gelatin in the severely damaged part was much larger than at in the less damaged part, and moreover, more sensitive to the expansion extent than the less damaged part. According to these criteria, the length of the less damaged part in the 4 tests was measured as 214 mm, 135 mm, 106 mm, and 159 mm, respectively.

Fig. 8.

Distribution of gelatin damage ignoring the cracks with different extents of expansion.

Other features about the gelatin damage distribution could also be acquired. The largest damaged area in the less damaged part was located at the entry of the bullet into the gelatin block. The most damaged area in the severely damaged part changed with the expansion extent. Without expansion, the largest area was at the exit of the bullet from the gelatin block. With the increasing expansion, the largest area showed up inside the gelatin block (Fig. 8C and D). The smallest damaged area was zero lying in the less damaged part, meaning no permanent cavity has been created at that location.

Considering the cracks

Fig. 9 illustrates the area of damaged gelatin when contribution of the cracks to gelatin damage was considered. It was apparent that inclusion of the cracks had a significant effect on the gelatin damage, particularly when the expansion was large enough (>1.9 mm), compared with Fig. 8. The damaged gelatin increased with the expansion extent, both in the less damaged part and the severely damaged part. The expansion extent dramatically influenced the tendency of the damaged gelatin along the penetration. When the expansion became larger, the damaged gelatin in the less damaged part may keep changing slowly (Figs. 9A and D) or started to change dramatically (Figs. 9B and C).

Fig. 9.

Distribution of gelatin damage considering the cracks with different extents of expansion.

Quantification of the gelatin damage

The motion of the rigid bullet was determined mostly by its v₀ and δ_0.²⁸ Thus, the gelatin damage was also expected to be determined by these two factors. Given the limited tests performed, quantification of the gelatin damage was correlated with v₀ and δ₀ using the fitting method.

Length of the less damaged part

Let the length of the less damaged part of the gelatin block, L_I be a function of v₀ and δ₀:

$$L_I=a_1+a_2\cdot v_{\text{0}}+a_3\cdot {\delta }_{\text{0}}$$ (2)

Fitting the coefficients a₁ - a₃ with the least square method, we can yield: a₁ = 25.96 mm, a₂ = 2.523 × 10⁻⁴/s, and a₃ = −15.89 mm/° while the r-squared value is 0.98. Since a₂ is positive and a₃ is negative, a higher velocity makes the less damaged part longer, and a higher attack angle makes the less damaged part shorter. However, a₂ is very small compared with a₃. A change in v₀ of only 100 m/s has the same effect as the change of δ₀ of 1.6e⁻³°. Thus, the length of the less damaged part is determined mostly by δ₀.

Average damaged gelatin area in the less damaged part

When ignoring the contribution of the cracks to the gelatin damage, the damaged gelatin in the less damaged part differed little at different locations. The average damaged area in this part can be expressed as:

$$A_{I\text{ave}}=\frac{V_I}{L_I}$$ (3)

Where V_I is the total damaged gelatin in the less damaged part. The calculated values of A_Iave are listed in Table 2. It can be seen that the average damaged area may increase several-fold with a small increase in the expansion extent.

Table 2.

Average damage A_Iave in the less damaged part with different expansions.

Test	0 mm (mm2)	0.21 mm (mm2)	1.9 mm (mm2)	3.6 mm (mm2)
1	1.9	3.6	24.5	64.3
2	6.1	8.2	35.4	81.2
3	5	7.1	33.2	77.6
4	1.8	2.9	21.1	56.5

Let the average damaged area has a linear relationship with v₀ and δ₀, then:

$$A_{I\text{ave}}=b_1+b_2\cdot v_{\text{0}}+b_3\cdot {\delta }_{\text{0}}$$ (4)

The fitting parameters b₁ - b₃ are listed in Table 3.

Table 3.

Fitting of the relations between A_Iave and v₀, δ₀ with different expansions.

Fitted parameters	0 mm	0.21 mm	1.9 mm	3.6 mm
b1 (mm2)	−6.849	−8.650	−12.240	−5.105
b2 (10−4 mm s)	0.1141	0.1589	0.4543	0.8955
b3 (mm2/°)	0.9086	1.065	2.738	4.485
r2	1.00	0.99	0.98	0.96

The r²-values are all greater than 0.95, documenting a linear relationship. Both b₂ and b₃ are positive, indicating that a higher velocity and greater attack angle would increase average gelatin damage in the less damaged segment. A change of 100 m/s in v₀ is equivalent to a change of 1°–2° in δ₀. Given that δ₀ is usually smaller than 5°, both v₀ and δ₀ are important determinants of the amount of gelatin damage in the less damaged part.

Total damaged gelatin

The total damaged gelatin in the tested gelatin block is shown in Table 4. For the same expansion extent, the total volume of damaged gelatin is assumed to be:

$$V=c_1+c_2\cdot v_{\text{0}}+c_3\cdot {\delta }_{\text{0}}$$ (5)

Table 4.

Total volume of damaged gelatin at different degrees of expansion.

Test	Ignoring the cracks (cm3)				Considering the cracks (cm3)
	0 mm	0.21 mm	1.9 mm	3.6 mm	0.21 mm	1.9 mm	3.6 mm
1	10.5	12.3	29.0	51.1	14.4	82.4	151.8
2	14.7	17.7	46.7	78.7	21.0	114.8	207.2
3	13.8	17.0	45.8	80.9	20.1	110.9	199.3
4	8.8	11.1	32.2	58.9	12.9	73.4	136.4

The fitting parameters c₁ - c₃ are listed in Table 5. Since the r²-values of all fitting parameters are greater than 0.95, Equation (5) could adequately describe the relations.

Table 5.

Fitting of the relation between the total gelatin damage and v₀, δ₀.

Fitted parameters	Ignoring the cracks				Considering the cracks
	0 mm	0.21 mm	1.9 mm	3.6 mm	0.21 mm	1.9 mm	3.6 mm
c1 (cm3)	−57.90	−26.60	155.00	493.00	−4.20	−17.20	−20.70
c2 (mm2·s)	0.211	0.192	0.170	0.008	0.024	0.128	0.222
c3 (cm3/°)	10.80	13.40	38.00	59.80	1.64	8.28	14.00
r2	0.97	0.97	0.99	0.98	0.97	0.96	0.96

Both c₂ and c₃ are positive at all degrees of expansion no matter ignoring the cracks or considering the cracks, indicating that both the larger v₀ and the larger δ₀ contribute to the total gelatin damage.

Increasing rate of the total damaged gelatin

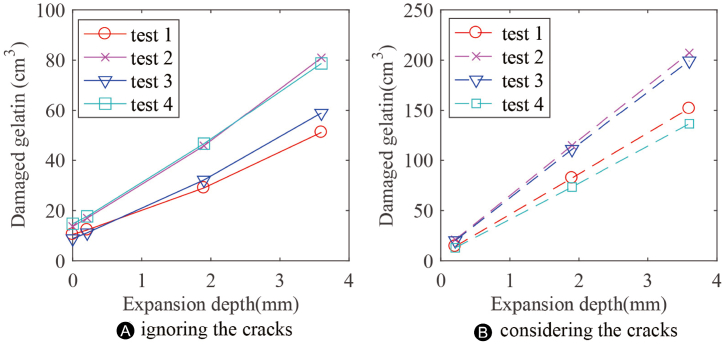
Changes of the total damaged gelatin with the expansion extent are shown in Fig. 10. The total volume of damaged gelatin increased linearly with the expansion extent, regardless of whether the cracks were ignored or considered. The damaged gelatin considering the cracks can be 2–3 folds the damaged gelatin ignoring the cracks, showing that the permanent cavity and the cracks were both important for the damage. The increasing rates k are listed in Table 6. It can be seen that the cracks could enlarge the increasing rates by one to three times.

Fig. 10.

Relation between the total damaged gelatin and the expansion extent.

Table 6.

Increasing rate of the total gelatin damage.

Test	Ignoring the cracks (cm3/mm)	Considering the cracks (cm3/mm)
1	11.2	40.5
2	17.8	54.9
3	18.6	52.9
4	13.8	36.4

When ignoring the cracks, the damaged gelatin is the sum of the permanent cavity and the contribution of the cavity wall. As mentioned in section The proposed new method - expansion method, the cavity wall can be seen as an equivalent crack. As the permanent cavity does not change with the expansion extent, the contribution of the equivalent crack is the increased damaged gelatin with the expansion extent. When the expansion is little, the increased damaged gelatin is equal to the average length of the equivalent crack times the expansion extent and the length of the gelatin block. This means the increasing rate k can be seen as the average length of the equivalent crack times the length of the gelatin block. When considering the cracks, the equivalent cracks consist of the cavity wall and the real cracks. As the length of the gelatin block is a constant, k reflects the average length of the equivalent cracks. As k can be seen as constant as shown in Fig. 10, the length of the equivalent cracks can be seen as constant.

Let k be:

$$k=d_1+d_2\cdot v_{\text{0}}+d_3\cdot {\delta }_{\text{0}}$$ (6)

The fitting parameters d₁ - d₃ are listed in Table 7. The results show that d₂ is negative when the cracks are ignored, indicating that the higher velocity of the bullet would diminish the average length of the equivalent cracks. Conversely, when the cracks are considered, d₂ is positive, indicating that the higher velocity would enhance the increasing rate. d₃ is positive in both cases, showing that the larger δ₀ would raise the average length of the equivalent cracks.

Table 7.

Fitting parameters of the relation between k and v₀, δ₀.

Case	d1 (cm3/mm)	d2 (mm·s)	d3 (cm3/mm·°)	r2
Ignoring the cracks	14.73	−4.98e−3	1.38	0.98
Considering the cracks	−4.705	5.81e−2	3.66	0.96

Discussion

Distribution characteristics of gelatin damage along the penetration have been revealed in the present work. The results indicate that the same kind of bullet does not necessarily result in the same ballistic wound in human. The impact velocity and impact attack angle of the bullet matter a lot for the ballistic wound. For the underweight, there is a possibility that only the less damaged part happens in the body; while the severely damaged part is more likely to happen in the overweight. With the help of other information such as the trajectory of the bullet, the surgeons may predict the seriousness of the wounded more objectively.

The changing tendencies of the gelatin damage with the expansion extent are studied in our work. The results may help to recognize the development of the ballistic wound in human, as the ballistic wound in the human body is affected by multiple factors such as the progressive neurologic deficit, the bacterial contamination, and the time from injury to treatment.²⁹

The permanent cavity in the gelatin is created by the crushing and cutting effects of the bullet. The cracks are torn by the temporary cavity.^2,29 The different mechanisms of formation of these features indicate that the gelatin around the permanent cavity must be under different stress state than the gelatin around the cracks. Therefore, the expansion extent of the permanent cavity and the expansion extent of the cracks may not be identical. As the stress states at different locations of the permanent cavity or the cracks are not the same, the expansion extent of the permanent cavity or the cracks may not be identical. However, in this work, only two extreme cases were analyzed for simplicity: If the cracks are not considered, the expansion extent of the cracks is zero, and only the expansion of the permanent cavity wall is considered; and if the cracks are considered, the expansion extent of the cracks and that of the permanent cavity are assumed to be identical.

In the present study, the relations between the characteristics of gelatin damage and v₀ or δ₀ are established. Based on these relations and other information such as the distribution characteristics of v₀ and δ₀ of the bullet, the expansion extent, etc., experts may evaluate how good the bullet is. Then the experts may optimize v₀ and δ₀ of the bullet. As the relations are built for the tested rigid bullet, the influence of other factors such as the shape and the structure of the bullet to the gelatin damage needs to be further studied.

In conclusion, the expansion method proposed in this study has several advantages to infer the damaged gelatin over other methods. It may be used to investigate the influences of other factors of the bullet on the terminal performances in human. With this method, the distribution characteristics of the damaged gelatin are revealed. The quantities of the gelatin damage are found to have a linear relationship with the δ₀ and v₀ of the bullet. The influences of the cracks and the expansion extent to the gelatin damage are also revealed. The results may help experts to evaluate the wound potential of the bullets, and help surgeons to predict the possible ballistic wound in human.

Funding

The experimental work is supported by the Senior Talent Foundation of Jiangsu University (15JDG038), the Foundation of National Laboratory (601010417) and the Natural Science Research of Jiangsu Higher Education Institutions of China (19KJB130003).

Ethical statement

This experiment is not related to animals or humans and is not harmful to others.

Declaration of competing interest

All the authors declare no competing interest.

Author contributions

Gen-Lin Mo: Draft of the manuscript; Jing Liu: Revising of the manuscript; Qian-Wen Ma: Picture editing; Yong-Xi Jin: Experiment; Wen-Min Yan: Experiment.

Appendix ASupplementary data

The following is the Supplementary data to this article: