Modeling of Combined Processing Steps for Reducing Escherichia coli O157:H7 Populations in Apple Cider

Abstract

Probabilistic models were used as a systematic approach to describe the response of Escherichia coli O157:H7 populations to combinations of commonly used preservation methods in unpasteurized apple cider. Using a complete factorial experimental design, the effect of pH (3.1 to 4.3), storage temperature and time (5 to 35°C for 0 to 6 h or 12 h), preservatives (0, 0.05, or 0.1% potassium sorbate or sodium benzoate), and freeze-thaw (F-T; −20°C, 48 h and 4°C, 4 h) treatment combinations (a total of 1,600 treatments) on the probability of achieving a 5-log₁₀-unit reduction in a three-strain E. coli O157:H7 mixture in cider was determined. Using logistic regression techniques, pH, temperature, time, and concentration were modeled in separate segments of the data set, resulting in prediction equations for: (i) no preservatives, before F-T; (ii) no preservatives, after F-T; (iii) sorbate, before F-T; (iv) sorbate, after F-T; (v) benzoate, before F-T; and (vi) benzoate, after F-T. Statistical analysis revealed a highly significant (P < 0.0001) effect of all four variables, with cider pH being the most important, followed by temperature and time, and finally by preservative concentration. All models predicted 92 to 99% of the responses correctly. To ensure safety, use of the models is most appropriate at a 0.9 probability level, where the percentage of false positives, i.e., falsely predicting a 5-log₁₀-unit reduction, is the lowest (0 to 4.4%). The present study demonstrates the applicability of logistic regression approaches to describing the effectiveness of multiple treatment combinations in pathogen control in cider making. The resulting models can serve as valuable tools in designing safe apple cider processes.

Fresh apple cider is a ready-to-eat product which often receives no microbial inactivation steps in its manufacturing. Although rare, Escherichia coli O157:H7 has become the pathogen most frequently transmitted by cider (3, 8, 9). To improve the safety of cider, the U.S. Food and Drug Administration (FDA) is currently evaluating comments on a proposed Hazard Analysis Critical Control Point (HACCP) regulation which, if approved, must be implemented in fresh fruit juice plants. In addition, the proposal states that processors must adopt at least one treatment that reduces the numbers of target pathogens by 5 log₁₀ units (17). Today, the only FDA-approved method for pathogen control is pasteurization, which is, however, viewed by many consumers and cider producers as detrimental to the taste and texture of cider and, for small cider producers, may not be financially feasible (23). The need for other effective intervention treatments has led to numerous research projects (6, 10, 16, 24, 36, 46).

E. coli O157:H7 cannot grow in apple juice, with a pH of typically 3.3 to 4.1 (25), but it can survive for long periods (28, 47). Low pH and the presence of naturally present organic acids, such as malic and citric acids, or added organic acid preservatives may cause sublethal cellular injury (37, 41, 42). The numbers of E. coli O157:H7 in cider may be reduced by exposing injured cells to further stresses such as exposure of the cider to a warm temperature or else freezing and thawing the cider (43). There are several steps in cider processing at which E. coli O157:H7 may be stressed. In a noncontinuous process, commonly used by small cider processors, a sufficient amount of cider must be first collected before proceeding to the next step. Cider may, therefore, sit in the holding tank for a time ranging from a few hours to overnight (44), a period during which cells may become injured. Injury and cell death are enhanced as this storage temperature increases (42, 43, 47). Many cider makers also freeze their cider for later sale (44), which further stresses cells and may result in cell death (34). Although individual studies have demonstrated the potential lethality of these steps, a systematic approach to describe microbial responses to such treatments and their combinations is needed for use in developing effective pathogen control strategies for cider.

Multifactor kinetic models have been developed to describe the growth, survival, and inactivation of E. coli O157:H7 in foods or synthetic media (1, 4, 7, 40). Single endpoint modeling is used to predict a single phenomenon, e.g., lag-phase duration, the time required to reach a predetermined population density, toxin production, or the probability of these events occurring (27). Such models have been referred to as the first attempts to predict the risk associated with foods (38).

Many investigators have found turbidimetric methods to be convenient and cost-efficient for generating large data sets in model development (11, 18, 26, 31, 33). These methods can simplify the detection of growth, resulting in binary results (1 = growth, 0 = no growth) for which logistic regression techniques are appropriate. This technique was successfully used in describing the growth limits (the growth-no growth interface) of E. coli as a function of temperature, pH, lactic acid concentration, and water activity (31, 33). Models based on similar techniques have also been used to predict the most probable number of Listeria monocytogenes (5), the probability of growth and toxigenesis of Clostridium botulinum (14, 19), and the occurrence of Campylobacter spp. in water (39).

Our earlier work demonstrated the potential for combinations of commonly used preservation methods to reduce E. coli O157:H7 populations by at least 5-log₁₀ units in apple cider (43). The present study extends this work to develop a model using logistic regression techniques to relate the probability of a 5-log₁₀-unit reduction of E. coli O157:H7 to cider pH, post-pressing storage temperature and time, type and concentration of organic acid preservatives, and use of a freeze-thaw (F-T) treatment. This model may be used to design novel processes wherein common steps are used to achieve the 5-log₁₀-unit reduction in E. coli O157:H7 numbers in unpasteurized fresh cider.

MATERIALS AND METHODS

Apple cider.

Unpasteurized, preservative-free apple cider was obtained from three different local cider plants (ciders A, B, and C) and kept frozen (−20°C) until use. Participating cider mills were about 200, 20, and 35 km, respectively, from Madison, Wis. For each cider pH, the titratable acidity (expressed as percent malic acid) and the degree Brix (percent soluble solids; Temperature-Compensated Hand-Held Refractometer; Leica, Inc., Buffalo, N.Y.) were determined. For cider A, the pH was 3.5, the titratable acidity was 0.32, and the Brix value was 12.4°. For cider B, the respective values were 3.7, 0.35, and 11.0°, and for cider C the respective values were 3.5, 0.33, and 10.0°.

For each cider, 56 different combinations of treatment variables were applied (see experimental design section, below). First, pH adjustments from 3.1 to 6.5 were done in 200-ml portions by adding 1, 3, or 6 N HCl or NaOH. Next, cider was further divided into seven 25-ml volumes to which 2.5 and 5% (wt/vol) filter-sterilized stock solutions of potassium sorbate (K-Sorbate; Sigma) or sodium benzoate (Na-Benzoate; Aldrich Chemical Company, Inc., Milwaukee, Wis.) were added to attain final concentrations of 0.05 or 0.1% (wt/vol). In addition, cider samples with equal volumes of added sterilized distilled water were used as controls. Finally, cider was dispensed (5 ml) in 10-ml polystyrene tubes with flanged plugs (Fisher Scientific, Itasca, Ill.). For sterilization, tubes were shipped overnight in dry ice to the Linear Accelerator Facility at Iowa State University, Ames. Tubes were exposed to electron beam radiation (first load, 29.5 kGy [range, 28.5 to 31.4 kGy]; second load, 29.4 kGy [range, 27.9 to 30.6 kGy]) the same day and returned in dry ice to our laboratory by the following day. Upon arrival tubes were placed in a freezer (−20°C) until use. There were no cells detected (0 CFU/ml) in five control tubes of irradiated cider as tested by spread plating on Trypticase soy agar (TSA; BBL Becton Dickinson and Company, Cockeysville, Md.) and incubation for 48 h at 35°C.

Cultures and inoculum preparation.

A mixture of three E. coli O157:H7 strains (ATCC 43895, C7927, and USDA-FSIS-380-94) was used as an inoculum. The characteristics of these strains and their maintenance have been previously described (43). All of these E. coli O157:H7 strains are commonly used for challenge studies. For inoculating the cider, a three-strain mixture was prepared from stationary-phase cultures (18 h, 35°C) as previously described (43). The inoculum was prepared separately for each cider and trial because, due to time constraints, only one cider sample could be treated daily. The final concentration of cells in saline (0.85% [wt/vol]) was ca. 9.0 log₁₀ CFU/ml.

Experimental design.

In a complete factorial design, all combinations of the following variables were tested: pH (3.1, 3.3, 3.5, 3.7, 3.9, 4.1, and 4.3), temperature (5, 15, and 25°C for 0, 2, 4, 6, and 12 h and 35°C for 0, 2, 4, and 6 h), preservatives (0, 0.05, or 0.1% sodium benzoate or potassium sorbate), and F-T treatment (−20°C, 48 h and 4°C, 4 h) or no F-T treatment. A total of ca. 1,600 treatments were tested in three different ciders. For one of the three ciders duplicate testing was done; triplicate testing was done for the other two ciders. All tests were independent.

Treatments of cider.

Apple cider samples (5 ml) with or without preservatives were tempered to 5, 15, 25, and 35°C; inoculated at 7.0 log₁₀ CFU/ml (50 μl of the inoculum); and kept at 5, 15, and 25°C for 12 h and at 35°C for 6 h. During this storage, 1.0-ml samples were taken from the 5, 15, and 25°C ciders at 0, 2, 4, 6, and 12 h and from the 35°C ciders at 0, 2, 4, and 6 h and placed in sterile 1.5-ml microcentrifuge tubes (Fisher). Of each sample, 30 μl (three 10-μl samples) was immediately used to determine the presence of viable cells, and the rest was placed in a −20°C freezer for 48 h. After 48 h of freezing, apple cider samples were thawed at 4°C for 4 h and then analyzed for the presence of viable cells as described below.

Determination of 5-log₁₀-unit reduction.

Our approach was to determine the combinations of treatments that resulted in a 5-log₁₀-unit reduction in the cell population. This reduction was determined by a turbidimetric method in microtiter plates (96-Well Cell Culture Cluster; Corning Costar, Corning, N.Y.) containing 240 μl of Trypticase soy broth (TSB) each. Inoculated cider (10⁷ CFU/ml) was first exposed to appropriate treatment(s), after which a 10-μl sample was removed from the cider and transferred to a well containing TSB. If a 5-log₁₀-unit reduction in cell numbers occurred during the treatment, this 10-μl sample would contain <1 CFU and result in no growth in TSB upon the subsequent incubation. If, however, the treatment did not lead to at least 5-log₁₀-unit reduction, >1 CFU would be transferred to TSB, resulting in turbid TSB after incubation. Three replicate wells were used for each sample point. In each 96-well plate, 12 wells were left uninoculated and used as negative controls. Wells were examined after 48 h of incubation at 35°C for visible turbidity (<5-log₁₀-unit reduction) or the absence of turbidity (≥5-log₁₀-unit reduction). The number of turbid wells (0 to 3) for each sample point was recorded. Confirmation tests to eliminate the possibility of any bacteriostatic effects in the well, i.e., cell survival but no growth in the well, were carried out by plating the contents of the first clear wells on TSA as described earlier. An approximate probability for the 5-log₁₀-unit reduction was calculated by using the relative frequency concept of probability (30): P(5-log₁₀-unit reduction) ≈ n_e/n, where n_e is the number of observed 5-log₁₀-unit reductions and n is the total number of observations.

Yeast, mold, and aerobic plate counts.

The effects of selected treatment combinations on cider's natural (potential spoilage) flora were determined. Nonirradiated fresh cider, with the pH adjusted to 3.3, 3.7, and 4.1 and with no additives, 0.1% sorbate, or 0.1% benzoate added was incubated at 5 or 25°C for 12 h or at 35°C for 6 h. Samples were taken at the beginning and the end of storage for cell enumerations. Yeasts and molds were enumerated on Dichloran Rose Bengal Chloramphenicol (Oxoid/Unipath, Ltd., Basingstoke, Hampshire, England) as described before (43). The aerobic plate count (APC) was determined using Plate Count Agar (Difco, Detroit, Mich.) supplemented with 0.01% (wt/vol) cycloheximide (Sigma) for the inhibition of yeast and mold growth. All results were expressed as the log₁₀ CFU per milliliter of cider. A Student t test (22) was used to test for significant (P < 0.05) differences in mean (n = 3) cell concentrations between 0 and 6 h or between 0 and 12 h samples for each type of cider.

Data analysis and construction of models.

Seven predictor variables were included in the data set: cider type, F-T treatment, storage temperature, storage time, preservative concentration, preservative type, and cider pH. Among them were three class variables: cider type, F-T treatment, and preservative type. The other four variables were continuous: cider pH, storage temperature, storage time, and preservative concentration. To determine the grouping of data, the three class variables were analyzed by using SAS PROC analysis of variance. Before the analysis, each class variable was given numerical codings (cider type, three levels, values 1, 2, and 3; F-T treatment, two levels, values 0 and 1; and preservative type, three levels, values 0, 1, and 2).

The response variable in this research has two possible values: (i) achieving a 5-log₁₀-unit reduction or (ii) not achieving a 5-log₁₀-unit reduction. Logistic regression is the most commonly used technique to model such a binary response. Logistic regression uses a logit transformation of the binary response variable so that the transformed response variable extends from −∞ to ∞ just as the predictor variables do (29). A response surface model describing the probability of achieving a 5-log₁₀-unit reduction by different combinations of treatments was developed using PROC LOGISTIC (35). All of the fitted models were of the following form: logit(P) = ln(P/[1 − P]) = a + b₁(T) + b₂(t) + b₃(C) + b₄(pH), where P is the overall predicted probability of achieving a 5-log₁₀-unit reduction, T is storage temperature, t is the storage time, C is the preservative concentration, pH is the cider pH, a is the intercept, and b₁ to b₄ are the corresponding parameter estimates. Models with quadratic [i.e., b₅(T²)] and interaction [i.e., b_q(Tt)] terms were evaluated and were not found to offer any significant benefit compared to the simple models presented here.

An equivalent equation,

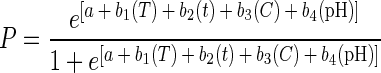where e is the Naperian base, was solved to generate all response surface plots at a given probability level for each parameter as a function of two independent variables, while the other variables were held constant.

RESULTS

Effects of experiment variables on achieving a 5-log₁₀-unit reduction in cider.

Figure 1 illustrates the effects of pH, storage temperature, and storage time on achieving a 5-log₁₀-unit reduction in the numbers of E. coli O157:H7 populations in cider. At each storage temperature tested, the lower the cider pH, the shorter the storage time at which a 5-log₁₀-unit reduction was achieved. Also, the higher the storage temperature at any given pH, the shorter the storage time at which the desired reduction in cell numbers was achieved. Figure 1A further shows that, with increased cider pH, higher temperatures were required to obtain a 5-log₁₀-unit reduction. For example, at pH 3.1 a 5-log₁₀-unit reduction was achieved at a 5°C storage temperature, but at pH 3.5 and 3.9 this reduction was only achieved at temperatures of at least 25 and 35°C, respectively. The same trend was observed when sorbate (Fig. 1B) or benzoate (Fig. 1A) was added, although benzoate had a greater antibacterial activity.

FIG. 1.

Effects of storage time, storage temperature, and cider pH on achieving a 5-log₁₀-unit reduction in E. coli O157:H7 populations in apple cider containing 0.1% benzoate (A) and 0.1% sorbate (B) after F-T treatment. The height of a given bar indicates the time, for a given temperature and pH, at which the observed probability of achieving a 5-log₁₀-unit reduction was at least 0.5. A bar with no height indicates 0 h, and no bar present indicates >12 h (5, 15, and 25°C) or >6 h (35°C) for a given temperature and pH at which the observed probability of achieving a ≥5-log₁₀-unit reduction was at least 0.5.

The effects of preservative type and concentration, pH, and F-T treatment on achieving a 5-log₁₀-unit reduction are shown in Fig. 2. The storage time required to achieve a 5-log₁₀-unit reduction decreased when the preservative concentration was increased. Furthermore, at increased preservative concentrations the pH of cider at which a 5-log₁₀-unit reduction was achieved increased. For example, in the presence of 0, 0.05, or 0.1% benzoate after F-T treatment the maximum pHs where desired cell reduction was observed were <3.1, 3.5, and 3.9, respectively (Fig. 2). The F-T treatment always further increased the pH and decreased the storage time where a 5-log₁₀-unit reduction was achieved. Of the organic acid preservatives used, benzoate always had a greater effect compared to sorbate. The presence of either preservative was necessary in nearly all treatment combinations to achieve the desired 5-log₁₀-unit reduction. Achieving a 5-log₁₀-unit reduction was most probable when cider contained 0.05 or 0.1% sorbate or benzoate, had pH of 3.1 to 3.9, was stored at 25°C for up to 12 h or at 35°C for up to 6 h, and went through F-T treatment (Fig. 1 and 2). These results demonstrate the potential of the described treatment combinations to decrease the numbers of E. coli O157:H7 populations by 5-log₁₀ units in apple cider.

FIG. 2.

Effects of storage time, preservative concentration, and pH on achieving a 5-log₁₀-unit reduction in E. coli O157:H7 populations in apple cider at 35°C before and after an F-T treatment. The height of a given bar indicates the time, for a given preservative concentration and pH, at which the observed probability of achieving a 5-log₁₀-unit reduction was at least 0.5. A bar with no height indicates 0 h, and no bar present indicates >6 h for a given preservative concentration and pH at which the observed probability of achieving a ≥5-log₁₀-unit reduction was at least 0.5.

Yeasts, molds, and APC as affected by selected treatment combinations.

The effect of selected treatment combinations on yeast and mold populations and APC in cider is presented in Table 1. Most of the treatments tested significantly (P < 0.05) decreased or had no significant effect on the yeast and mold populations and APC in cider. A significant (P < 0.05) increase in yeast and mold counts, although less than 1-log₁₀ unit, was observed only when no preservatives were present and storage lasted 12 h at 25°C. The APC increased significantly in most ciders tested when no preservatives were present during 12 h of storage at 25°C or when no preservatives were present during 6 h of storage at 35°C. While decreases in yeasts and molds and in APC were less than those for E. coli O157:H7 in corresponding experiments, the same general trends were observed. Significant decreases were only observed when an organic acid preservative, particularly sodium benzoate, was added. Population decreases were greater with decreasing cider pH and with increasing storage temperature.

TABLE 1.

Effect of storing apple cider with or without 0.1% sorbate or benzoate for 6 or 12 h at 5, 25, or 35°C on yeast and mold counts and on APC

Temp (°C), time (h)	Preservative (%)	Change from initial cell concna (Log10 CFU/ml)
		Yeast and mold count at pH:			Aerobic plate count at pH:
		3.3	3.7	4.1	3.3	3.7	4.1
5, 12	None (0)	0.1	0.1	0.4	−0.2	0.1	0.1
	Sorbate (0.1)	−0.1	0.0	0.2	−0.5	−0.2	−0.1
	Benzoate (0.1)	−0.9	−0.2	−0.3	−1.6*	−0.6	−0.2
25, 12	None (0)	0.8*	0.6	0.8*	1.2*	1.7*	1.8*
	Sorbate (0.1)	−0.4	−0.1	−0.3	−1.4*	−0.8	−0.7
	Benzoate (0.1)	−0.9*	−1.0	0.0	−2.4*	−1.3*	−1.0*
35, 6	None (0)	0.1	0.2	0.3	0.4	0.7*	0.8*
	Sorbate (0.1)	−0.5	−0.2	0.1	−2.2*	−1.1*	−0.9*
	Benzoate (0.1)	−1.5*	−1.0	−0.2	−2.7*	−1.6*	−1.4*

^aThe initial yeast and mold count was 2.4 ± 0.1 log₁₀ CFU/ml, and the initial aerobic plate count was 3.4 ± 0.0 log₁₀ CFU/ml. Asterisks indicate statistically (P < 0.05) significant changes in cell concentrations compared to the 0-h values. 

Modeling.

The data set contained 36,480 cases of observations, 2,294 of which had response of “a 5-log₁₀-unit reduction achieved” and 34,186 of which had a response of “a 5-log₁₀-unit reduction not achieved.”

Statistical analysis of the three class variables (preservative type, F-T treatment, and cider type) revealed their high significance (Table 2). Although it had a significant effect, cider type was not used in further data classification because the model was meant to represent the average of three different ciders. Thus, the final grouping of the data was based on preservative type and F-T treatment.

TABLE 2.

Analysis of class variables

Source	df	Sum of squares	Mean square	F	P
Cider type	2	7.84	3.92	70.06	0.000
F-T treatment	1	46.61	46.61	833.45	0.000
Preservative type	2	54.77	27.38	489.63	0.000

The four continuous variables were modeled in separate segments of the data set, segments based on preservative type and before or after F-T treatment. The models were for the following data groups: (i) 0% preservatives, before F-T treatment; (ii) 0% preservatives, after F-T treatment; (iii) benzoate, before F-T treatment; (iv) benzoate, after F-T treatment; (v) sorbate, before F-T treatment; and (vi) sorbate, after F-T treatment. Summaries of parameter estimates for fitted response surface equations (models 1 to 6) are presented in Table 3. Three-dimensional surface response plots were developed to graphically illustrate the effects of treatment combinations on the probability of achieving a 5-log₁₀-unit reduction (Fig. 3). The data set for model 1 (no preservatives, before F-T) cannot be modeled because all observations had the same response (no 5-log₁₀-unit reduction was observed). The lowest number of observations of 5-log₁₀-unit reductions compared to data sets of the other models was expected for this model, because two important factors contributing to cell death, preservatives and F-T treatment, were not included in these treatment combinations.

TABLE 3.

Summary of logistic models^a for six different data subsets describing the probability of achieving a 5-log₁₀-unit reduction in numbers of E. coli O157:H7 in cider by applying various combinations of inactivation treatments^b

Model	Parameter	Coefficient	SE	Wald chi-square (P)	Probably of a greater valued	Standardized coefficient
1 (no preservatives, before F-T)		–c
2 (no preservatives, after F-T)	a	21.44	4.81	19.91	0.0001	–
	T	0.22	0.03	45.48	0.0001	1.3
	t	0.37	0.06	45.61	0.0001	0.8
	C	0.00	–	–	–	–
	pH	−10.13	1.52	44.17	0.0001	−5.58
3 (benzoate, before F-T)	a	−20.64	4.44	21.62	0.0001	–
	T	1.77	0.17	107.33	0.0001	10.64
	t	2.39	0.22	114.99	0.0001	5.09
	C	64.88	8.41	59.50	0.0001	0.89
	pH	−17.51	1.62	116.80	0.0001	−9.64
4 (benzoate, after F-T)	a	12.62	1.29	95.88	0.0001	–
	T	0.45	0.02	357.21	0.0001	2.71
	t	0.75	0.04	337.81	0.0001	1.6
	C	10.84	3.29	10.87	0.001	0.15
	pH	−9.59	0.51	352.32	0.0001	−5.28
5 (sorbate, before F-T)	a	−26.21	3.30	62.97	0.0001	–
	T	1.52	0.12	156.72	0.0001	9.12
	t	1.79	0.14	155.91	0.0001	3.83
	C	75.33	7.08	113.34	0.0001	1.04
	pH	−12.13	0.92	175.41	0.0001	−6.68
6 (sorbate, after F-T)	a	18.15	0.72	626.85	0.0001	–
	T	0.15	0.01	615.66	0.0001	0.93
	t	0.31	0.02	426.07	0.0001	0.66
	C	53.42	2.44	478.71	0.0001	0.74
	pH	−8.22	0.27	962.71	0.0001	−4.52

^aLogistic regression models followed the form logit(P) = ln(P/1 − P) = a + b₁(T) + b₂(t) + b₃(C) + b₄(pH), where P is the probability to achieve a 5-log₁₀-unit reduction, T is the storage temperature, t is the storage time, C is the preservative concentration, pH is the cider pH, a is the intercept, and b₁ to b₄ are the corresponding coefficients. 

^bTreatments included storage of cider samples of pH 3.1, 3.3, 3.5, 3.7, 3.9, 4.1, and 4.3 at 5, 15, and 25°C for 0, 2, 4, 6, and 12 h or at 35°C for 0, 2, 4, and 6 h in the presence of 0, 0.05, and 0.1% of a given preservative. 

^c–, all observations had the same response; no model was developed. 

^dNo preservative was used and, therefore, preservative concentration was not part of the model. 

FIG. 3.

Observed (points) and predicted (surfaces) probabilities of achieving a 5-log₁₀-unit reduction in E. coli O157:H7 populations in apple cider as a function of cider pH and storage temperature after 12 h storage at 5 to 25°C or 6 h storage at 35°C. Model 1, 0% preservatives, before F-T treatment; model 2, 0% preservatives, after F-T treatment; model 3, benzoate, before F-T treatment; model 4, benzoate, after F-T treatment; model 5, sorbate, before F-T treatment; and model 6, sorbate, after F-T treatment.

Values of standardized coefficients (Table 3) were used to rank the significance of the variables affecting E. coli O157:H7 survival in cider. Of all continuous variables, pH stood out as the most important factor (largest absolute value for standardized coefficient) determining the probability of the 5-log₁₀-unit reduction. It ranked as the most important factor in three of the models and as the second (but relatively close to the most important factor) in two of the other models. In the presence of sorbate, the pH played a relatively more significant role after F-T treatment than before the treatment in achieving a 5-log₁₀-unit reduction. The second most important variable in three of the models was temperature, followed closely by time. The preservative concentration was also always significant (P < 0.001). However, increasing the concentration of benzoate from 0.05 to 0.1% had a less significant role relative to the other factors in achieving a 5-log₁₀-unit reduction than if the sorbate concentration was increased the same amount. The significance of the benzoate concentration was further decreased when F-T treatment was applied. It should be noted, however, that benzoate is clearly more effective in attempts to achieve a 5-log₁₀-unit reduction than is sorbate (Fig. 1 and 2).

As expected, parameter estimates of the four continuous variables all had the same sign (pH always negative and the others always positive) throughout the six models, indicating that their effects were generally the same no matter which preservative type was considered and no matter whether the effect was noted before or after F-T treatment (Table 3).

Next, predicted values were compared with observed values to determine the goodness of fit of the models. The observed binary data responses are either a 5-log₁₀-unit reduction (event) or not a 5-log₁₀-unit reduction (nonevent). The predicted response is a real number between 0 and 1. To compare observed and predicted values, any predicted probability greater than 0.5 (i.e., there is a 50% or greater chance that the event will occur) was categorized as an event; any predicted probability less than 0.5 was deemed a nonevent. As shown in Table 4, at a 0.5 probability all five models predicted more than 92% (range, 92 to 99%) of responses correctly. While a value of 0.5 gives the highest percent correct in prediction, a probability value of 0.9 is stricter in predicting events, which can offer safety where human pathogens are involved. Table 5 shows that an increase in probability from 0.5 to 0.9 decreased the range of false positives from 0 to 19.9% to 0 to 4.4%, respectively. Decreasing the probability level to 0.1 had the opposite effect, resulting in less conservative, or more dangerous, models (Table 5). Three-dimensional plots of predicted and approximate observed probabilities for models 2 to 6 are shown in Fig. 3. Any prediction is considered safe when a 5-log₁₀-unit reduction is predicted to occur at lower pH values and higher temperatures than what was actually observed. For example, in pH 3.5 at 25°C for 12 h (Fig. 3), model 4 predicted a lower (safer) probability than the observed probability, i.e., 0.60 and 0.75, respectively. For the same conditions (Fig. 3), model 6 predicted a higher (less safe) probability than the observed probability, i.e., 0.91 and 0.46, respectively.

TABLE 4.

Goodness of fit of models predicting the probability of achieving a 5-log₁₀-unit reduction in the numbers of E. coli O157:H7 in cider as a result of applying various combinations of inactivation treatments

Model	P	No. correcta		No. incorrecta		%
		Event	Nonevent	Event	Nonevent	Correct	Sensitivity	Specificity	False positiveb	False negativec
1 (no preservatives, before F-T)	0.5
2 (no preservatives, after F-T)	0.5	0	3,596	0	52	98.6	0	100	0	1.4
3 (benzoate, before F-T)	0.5	187	7,048	29	32	99.2	85.4	99.6	13.4	0.5
4 (benzoate, after F-T)	0.5	325	6,774	59	138	97.3	70.2	99.1	15.4	2
5 (sorbate, before F-T)	0.5	233	6,965	55	43	98.7	84.4	99.2	19.1	0.6
6 (sorbate, after F-T)	0.5	942	5,778	234	342	92.1	73.4	96.1	19.9	5.6

^aEvent, 5-log₁₀-unit reduction achieved; nonevent, 5-log₁₀-unit reduction not achieved. 

^bThat is, among all positive results. 

^cThat is, among all negative results. 

TABLE 5.

Comparison of models at different probability levels

Model	% Correct at P of:			% False positive at P of:			% False negative at P of:
	0.1	0.5	0.9	0.1	0.5	0.9	0.1	0.5	0.9
1 (no preservatives, before F-T)
2 (no preservatives, after F-T)	96.5	98.6	98.6	77.9	0	0	0.6	1.4	1.4
3 (benzoate, before F-T)	98.8	99.2	98.6	27.4	13.4	0.8	0.1	0.5	1.4
4 (benzoate, after F-T)	93.9	97.3	95.9	49.1	15.4	0.6	0.4	2.0	4.2
5 (sorbate, before F-T)	97.6	98.7	98.1	38.5	19.1	3.5	0.2	0.6	1.9
6 (sorbate, after F-T)	85.8	92.1	87.8	44.4	19.9	4.4	1.1	5.6	12.7

DISCUSSION

Survival curves of bacteria that are subjected to combined stress conditions are often complicated and multiphasic (32). In some cases, it may be less important to predict the rates of inactivation in each step than to focus on the resulting end point. For example, Whiting (45) determined the time for a 4-log₁₀-unit reduction in numbers of L. monocytogenes in fermented sausage, a reduction that would eliminate the numbers of a pathogen likely to be present in products made under good manufacturing practices. Similarly, Ratkowsky and Ross (33) and Presser et al. (31) focused on the bacterial growth-no growth interface and adopted a probabilistic approach using logistic regression to develop models defining this interface. Considering the complexity of treatments applied in the present work, determining the probability of desired reduction was thus considered the most appropriate approach.

In the present study, data to be modeled were collected from three different ciders. We considered this the minimum number of ciders upon which to base our model, since the composition of apple ciders from different sources can vary considerably (25). Expectedly, such differences resulted in the cider type having a significant (P < 0.0001) effect on achieving the 5-log₁₀-unit reduction. Reasons for compositional differences between ciders may include the type and the maturity of the apples used to make cider (13). Furthermore, the number of different apple varieties used in one batch of cider varies, usually from 3 to 10 (44). These results highlight the importance of testing several types of cider to validate intervention treatments.

Cider pH was found to be a significant factor affecting a 5-log₁₀-unit reduction of E. coli O157:H7. Cider pH affects the concentration of the undissociated (more bactericidal) form of naturally present organic acids and added organic acid preservatives. The concentration of the undissociated form increases with decreasing pH. The important role of low pH in injuring the cell becomes evident when sorbate was present (models 5 and 6). Such injury can well be taken advantage of by subjecting the cell to further stress, e.g., F-T treatment. Interestingly, while benzoate was clearly more effective than sorbate in reducing cell populations, the significance of the benzoate concentration was less than in the case of sorbate, and the significance was further decreased when F-T treatment was applied. This suggests that benzoate was already relatively effective in injuring and killing cells before F-T treatment at the 0.05% concentration. It could be concluded that if a lower preservative concentration is preferred for optimal organoleptic properties, benzoate allows the user to reduce concentration with less decrease in the overall effectiveness of the preservative, especially if F-T treatment is applied.

At refrigeration temperatures, it may take several days (47) or weeks (28) before the presence of commonly used preservatives, such as benzoate or sorbate, result in a 5-log₁₀-unit reduction in E. coli O157:H7 populations in cider. Similarly, in our study at low temperatures a 5-log₁₀-unit reduction was seldom seen and there was only a minimal decline in yeast and mold counts and in APC in the presence of either preservative. However, holding the cider for a short time at a warm temperature was essential in increasing the lethality of tested preservatives against E. coli O157:H7 and other microflora. When E. coli O157:H7 was eliminated, the numbers of yeasts and molds and aerobic plate counts also declined, i.e., improving the safety and shelflife of the cider. At the higher end of the typical pH range of cider, however, the preservatives became less effective, regardless of the holding temperature.

It is generally desirable to find models that predict the data as closely as possible. When making predictions about food safety, however, the possibility of predicting that a food is safe when the food actually contains pathogens must be considered. If the model predicted a 5-log₁₀-unit reduction, but this level of reduction did not occur in actuality, the model would be considered “fail-dangerous” for this condition. A model can be made more “fail-safe” by raising the probability level from 0.5 to 0.9 (Table 5). This means that a 5-log₁₀-unit reduction would only be predicted when the predicted probability value of the model is ≥0.9. To lower the probability level to 0.1 would have the opposite effect, making a model more fail-dangerous.

The model's accuracy in predicting new datum points can be improved by increasing the number of cider samples tested or by decreasing the sampling intervals. Smaller sampling intervals would allow for a more precise determination of the transition value for the factor studied. For example, under one set of conditions, a 5-log₁₀-unit reduction might be achieved by holding at 35°C but not at 25°C. Another experimental design (that includes additional observations at 30°C) would improve the accuracy of predictions, especially in the temperature range of ca. 30°C.

To best resemble the practices used in small cider mills, several adjustments were made to the previously reported procedure (43). All conditions were tested with three different ciders, compared to only one in our previous study. The ciders used were sterilized by ionizing irradiation instead of by heat to prevent precipitation of the pulp. The presence of pulp was desired because it may provide extra protection for cells to survive applied treatments, as was previously observed (20). Heat sterilization may also have chemically altered the sugars present. Sugars may protect the survival of E. coli O157:H7 since a faster decline in cell numbers has been shown in diluted forms of apple cider and juice (21). In our previous work, we aimed to demonstrate the inverse relation between the cider pH and the survival of E. coli O157:H7; therefore, all pH adjustments were done after addition of organic acids. In the present study, preservatives were added after pH adjustment, resembling the order used in real cider making. The addition of benzoate and sorbate salts increased the pH of the cider by ca. 0.2 pH unit. Compared to our previous study, an increased pH due to the added organic acids or preservatives may therefore have weakened the effectiveness of further treatments. One or several of these differences in the experimental procedure may have contributed to the differences seen in the effectiveness of the treatments.

Our study has documented effectiveness of treatment combinations in reducing the E. coli O157:H7 populations in apple cider and how probabilistic modeling can be used to define these combinations for production of safe cider. To understand the effects of these treatment combinations in other types of juices and/or against other pathogens, further experiments are warranted. However, the laboratory and modeling techniques used could be applied to a variety of treatment combinations in such experiments. Furthermore, if one prefers modeling the microbial death rate instead of modeling the point of 5-log₁₀-unit reduction during treatment combinations in juice, then several considerations should be taken into account. Different bacterial strains in an inoculum mixture may respond differently to each stress, with the numbers of the most sensitive strain declining the fastest. Prediction becomes more complicated in the presence of two or more stresses where the proportion of sensitive cells increases due to increasing injury during each stress applied. The effect of preservatives should be known, i.e., whether the preservative can inhibit, injure, or inactivate the cells or whether the cells can grow in its presence. The rate of freezing controls water loss, relocation, and the size and shape of ice crystals formed (2), all of which affect the chemical and physical structure of cells and the degree of disruption of cellular constituents. Variation in the natural microflora in unpasteurized juice would further complicate the model development. Competing microbes have been shown to have a protective effect during inactivation treatments when present in high numbers (15), but during a long-term survival the opposite occurred (47).

We report here a probabilistic modeling approach describing the effects of treatment combinations in pathogen control in cider. In further research, the described modeling strategy can be used to evaluate additional treatments and their combinations. The present study was conducted as full factorial design; however, information gathered in the present study may be used in further studies to determine the combinations that could be left out of the design, and effort could be concentrated on combinations near the point of 5-log₁₀-unit reduction, as in a partial factorial design (12). Suggestions to improve the applicability and the prediction capability of the model would include testing more types of ciders, testing additional pathogens, and testing the addition of naturally occurring organic acids (malic and citric), ascorbic acid, and/or their combinations. Once fully evaluated, such a model would provide a good first step for making decisions in HACCP plan development in cider mills and/or for further development of the described processes. The use of multiple antimicrobial treatments has provided an effective way to increase the safety of many food products, and the present study also demonstrates its potential for unpasteurized apple cider.