3D-printed auxetic-structured intervertebral disc implant for potential treatment of lumbar herniated disc

Abstract

In this study, a novel artificial intervertebral disc implant with modified “Bucklicrystal” structure was designed and 3D printed using thermoplastic polyurethane. The new implant has a unique auxetic structure with building blocks joined “face-to-face”. The accompanied negative Poisson’s ratio enables its excellent energy absorption and stability under compression. The deformation and load distribution behavior of the implant under various loading conditions (bending, torsion, extension and flexion) has been thoroughly evaluated through finite element method. Results show that, compared to natural intervertebral disc and conventional 3D implant, our new implant exhibits more effective stress transfer and attenuation under practical loading conditions. The implant's ability to contract laterally under compression can be potentially used to alleviate the symptoms of lumbar disc herniation. Finally, the biocompatibility of the implant was assessed in vitro and its ability to restore the physiological function of the disc segment was validated in vivo using an animal model.

Graphical abstract

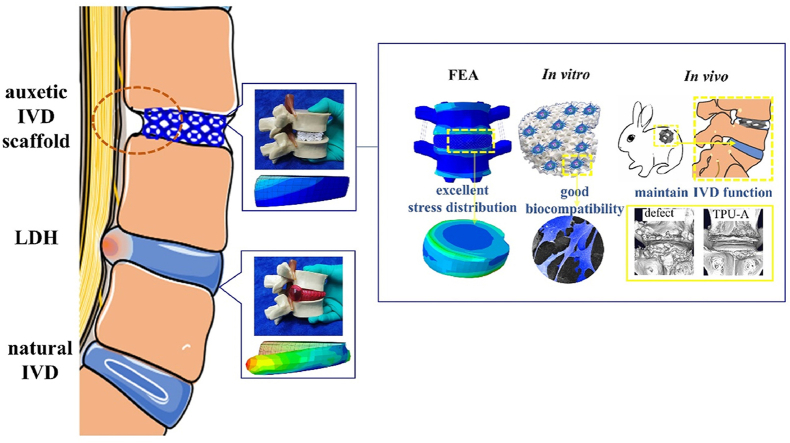
An auxetic scaffold with uniquely modified “Bucklicrystal” structure prepared by 3D printing, which can effectively alleviate lumbar disc herniation (LDH) due to auxetic effect. The superior mechanical properties (stress distribution, stiffness, strength, energy absorption and dissipation), biocompatibility and potential to restore the disc physiological functions been proved by FEA, in vitro and in vivo studies.

Highlights

• •Auxetic-structured IVD implant features negative Poisson's ratio (NPR) behavior.
• •Modified “Bucklicrystal”structure exhibits better energy absorption and stability.
• •The stress effectively and evenly transfers/attenuates in the auxetic implant.
• •Auxetic implant potentially alleviates the symptoms of lumbar disc herniation.

1. Introduction

The rapid developments in biomedical implant design necessitate the use of smart and high-performance materials to meet the ever-increasing demands in patient specific applications. Since the first auxetic foam structures created by Lake in 1987 [1], auxetic materials have attracted huge research interest and are increasingly integrated into smart advanced materials/structures for wide ranging applications in science, engineering and the biomedical field. Auxetic materials feature negative Poisson's ratio (NPR), i.e., they expand in the transverse direction when stretched and contract when compressed. Such counter-intuitive property has presented unprecedented advantages, particularly for load bearing implant applications [[2], [3], [4]]. For instance, three-dimensional (3D) auxetic materials with re-entrant honeycomb structures have been used as bone screws [5], total hip replacements [6], vascular stents [7], tissue scaffolds [8], etc. Despite the highly effective kinematic mechanism (e.g., the buckling and folding of ligaments) of the conventional re-entrant honeycomb auxetic architectures, they suffer from low stiffness and strength. To address this limitation, novel 3D auxetic structures such as “Bucklicrystals” have been developed [9]. “Bucklicrystals” possess body center cubic (bcc) or simple cubic (sc) structures, which consist of elastomeric spherical shells with 6 or 12 periodically arranged holes. Through buckling of the spherical shells and rotation of the connecting nodes, “Bucklicrystals” can achieve excellent auxetic effects while retaining their mechanical properties [[10], [11], [12]]. However, the building blocks of conventional “Bucklicrystals” are joined by nodes (point connections) [13], hence suffers from low structural stability. As such, this unique structure is yet to be optimized to fulfill its full potential in vital/novel applications in the biomedical field.

Intervertebral disc (IVD), the cartilaginous tissue maintaining the deformable space between adjacent vertebrae, plays a crucial role in providing shock absorption and flexibility of human spine [14]. Due to the nature of the human anatomy, IVDs are often subjected to long-term axial compression. As a result, small tears in the annulus fibrosus (AF) would develop and deteriorate over time, which could eventually lead to lumbar disc herniation (LDH) [15]. The associated bulging of gelatinous nucleus pulposus (NP) often compresses the neighboring spine cord and nerves, leading to severe back pain, impaired patient mobility [16] and in the worst case scenario, disability [[17], [18], [19]]. Surgery to removal of herniated IVD is a standard treatment protocol [20,21], however, this suffers from high recurrence rate (5%–26%) [22]. Other common treatments such as spinal fusion can severely restrict the spinal motion/flexibility and may accelerate the adjacent segments degeneration [23]. Lumbar disc replacement is another alternative surgical option. Despite the wide range of commercially available IVD replacement products available (such as ProDisc-L®, FlexiCore™ and Mobi-C with “ball-and-socket” structure), most of these implants cannot fully restore the spine's physiological motion/functions due to their rigidity. Several studies also reported accelerated facet joints degeneration due to the abnormal patterns of motion and the lack of shock stress attenuation in some IVD replacements [24,25].

According to the literature, the structure/composition of auxetic materials can be tailored to provide desirable mechanical properties (e. g., high energy absorption capacity, indentation/shear resistance, maximum elastic strain, and shock absorption) [26,27]. These promising features could inspire new IVD replacement design with reduced interference of implant with the surrounding nerves. To date, research in this exciting area is still in its infancy [28,29] and no work has been reported on the design and development of 3D printed auxetic material with bespoke architecture optimized for LHD treatment.

In this study, we designed and developed a 3D printed an auxetic structured IVD implant using thermoplastic polyurethane (TPU) (see Scheme 1). The implant has a modified Bucklicrystal structure (i.e., building blocks joined face-to-face, see Scheme 1A yellow surfaces), which enhances the structure's mechanical stability under loading. The behavior of the auxetic implant under various practical loading conditions (bending, torsion, extension and flexion) has been analyzed using finite element (FE) simulation. The results were compared with natural IVD as well as a conventional 3D TPU implant with positive Poison's ratio (PPR). Finally, the biocompatibility of the implant was assessed in vitro and its ability to alleviate LHD was demonstrated in vivo using an animal model.

Scheme 1.

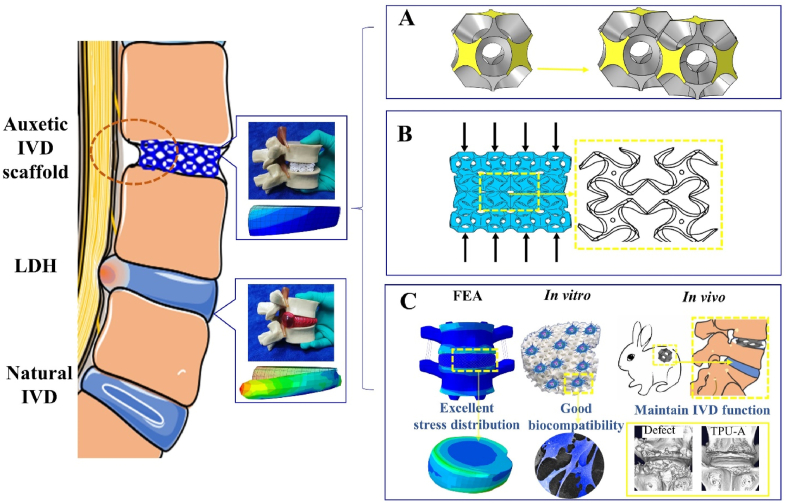
Schematic showing the auxetic IVD implant subjected to compression. A. Construction of the modified Bucklicrystal structure. B. The deformation mechanism of Bucklicrystal structure under compression. C. Advantages of the auxetic IVD prosthesis.

2. Experimental section

2.1. Construction of numerical models and 3D printing of TPU implants

Numerical models for our NPR auxetic implant (TPU-A) and the conventional PPR implant (TPU-X) were constructed using Rhino software. As shown in Fig. S2, the unit cell of TPU-A consist of a hollow shell cuboctahedron block. This is generated by removing regular cone arrays from a hollow cuboctahedron, leaving twelve holes on the surfaces. It is noteworthy that all the models were constructed with the same volume fraction. The models were exported into STL format for rapid prototyping using a selective laser sintering (SLS) equipment (EP- 3650, China). The laser power was 40W and the laser scanning speed was 4000 m/s. The part bed temperature was set at 95 °C. The TPU powder used for 3D printing was supplied by Beijing Mohou Co., China.).

2.2. Microscopic characterization

The surface morphology of the implants was observed using scanning electron microscope (SEM, thermo scientific, Apreo S, America) under a voltage of 10 kV. All samples were freeze dried (LGJ-12, China) for 48h followed by gold sputtering (SBC-12, China) prior to SEM analysis.

2.3. Uniaxial compression test

Uniaxial compression test was carried out using a universal testing machine (AG-IC-50KN, China) following ISO 815-1:2019. Strain-rate sensitivity tests were carried out at different compression loading speed (1 mm/min, 10 mm/min and 100 mm/min, respectively). The cyclic loading behaviors of the TPU implants were investigated following established method by subjecting the samples to cyclic compressive loading (0%–50% compressive strain at a strain rate of 100 mm/min) for five cycles. The Young's modulus of all samples was calculated for the linear region of the stress-strain curve (i.e., 5% strain). The Poisson's ratio (ν_zr) of the implant was calculated following Eq. (1) [30].

$${\nu }_{\text{zr}}={\epsilon }_{\text{r}}\text{/}{\epsilon }_{\text{z}}$$ (1)

Where ε_r is the transverse strain and ε_z is the longitudinal strain.

For all mechanical testing, five samples from each group were tested for repeatability.

2.4. Finite element simulation

In order to model the mechanical response of the implants under practical bending, torsion, flexion and extension conditions, ABAQUS (a commercial FE software) was used for the buckling and post-buckling analysis. To select the appropriate TPU material constitution model for the simulation, standard tensile tests were carried out on 3D-printed TPU dumbbell shaped tensile specimens, and the experimental and simulation data can be found in Figure S1. 3rd order Ogden hyperelastical material constitution model was chosen for the next compression simulation in this study as it gives the best fit in accuracy and stability to our experimental data. The strain energy density function is based on the left Cauchy-Green strain tensor and principal stretches (Eqs (2), (3), (4))):

$$W=\sum _{\text{i}=1}^N\frac{{\mu }_{\text{i}}}{{\alpha }_{\text{i}}}({\bar{\lambda }}_1^{{\alpha }_{\text{i}}}+{\bar{\lambda }}_2^{{\alpha }_{\text{i}}}+{\bar{\lambda }}_3^{{\alpha }_{\text{i}}})+\sum _{k=1}^N\frac{1}{D_k}{(J-1)}^{2k}$$ (2)

$${\bar{\lambda }}_{\text{i}}=J^{-\frac{1}{3}}{\lambda }_{\text{i}}$$ (3)

$${\bar{\lambda }}_1{\bar{\lambda }}_2{\bar{\lambda }}_3=1$$ (4)

Where N is the order of the constitution model, μ is the initial shear modulus, $\alpha$ is the strain hardening index, λ is the principal stretches in X-Y-Z directions, D is the material stiffness and J is the volume ratio.

Since TPU-A is a buckling-induced structure, two steps were carried out to simulate its auxetic behavior. Firstly, linear perturbation with subspace eigensolver was applied to trigger the desired buckling pattern with auxetic behavior. 10-node quadratic tetrahedral hybrid elements were used for meshing and the mesh sensitivity was analyzed upon convergence of the Young's modulus. The top and bottom plates of natural IVD, TPU-X and TPU-A were modeled as a rigid body and meshed by 4-node 3D bilinear rigid quadrilateral. The bottom plate was constrained with a concentrated force applied to the top plate. In addition, symmetric boundary conditions for x = 0 and y = 0 planes were deployed taking into consideration of the computational efficiency and geometric symmetry [31]. In the second step, post-buckling analysis was conducted. The first overall mode obtained from the linear buckling computation results was deployed as a geometric imperfection and the imperfection scale factor was set to be 0.05 due to its negligible difference from the original model [13].

For TUP-X with a stretch-domain structure, a single step analysis (dynamic, explicit) was carried out for its compression simulation. Finally, a compressive displacement was applied to the top plate of both TPU-X and TPU-A to achieve a 33% strain and a general contact condition was used for all possible interactions. For comparison, the mechanical response of the natural IVD was also modeled under similar compressive boundary conditions.

To further investigate the feasibility of TPU-A as an implant, FE simulations of the IVD with TPU-A or TPU-X implants were analyzed in Section 3.3 under practical bending, torsion, extension, and flexion conditions. In our analysis, a load of 500 N was selected as a typical human loading in line with the literature [[32], [33]]. The detailed lumber reconstruction process and mechanical response can be found in Section 3.3.

2.5. In vitro studies

Chondrocytes were extracted following established procedure [34] and were cultivated for two passages before use. Rabbit nucleus pulposus cells (NPCs) were isolated and cultured following [35]. Natural IVD tissues were obtained from 2-week-old male New Zealand rabbits (Animal Center, Sichuan University). The nucleus pulposus tissue was separated from the surrounding annulus fibrous tissue and washed twice with PBS (Invitrogen). The NP tissue was then treated with collagenase II (Sigma-Aldrich, USA) at 37 °C for 4 h, and the obtained cell solution was filtered through a 180 μm nylon mesh filter, followed by centrifugation at 1000 rpm for 5 min. Isolated cells were then suspended and cultured in low-glucose DMEM medium containing 10% FBS and 1% P/S. All cells were incubated at 37 °C with 5% CO₂ and the culture medium was refreshed every 48h.

According to ISO 10993-5 and ISO 10993-12, TPU-A was incubated with serum-supplied medium (extraction ratio = 3 cm²/ml) at 37 °C for 24 h to obtain the extracts. We employed two different cell lines (chondrocytes and NPCs) to evaluate the cell viability and proliferation. The cells were cultured in 24-well plates with a seeding density of 10⁴ cells/well, and exposed to the extraction medium for 1, 3, 5, and 7 days, respectively. The cells were then stained using a Live/Dead Assay Kit (DOJINDO) according to the manufacturer's instructions. Finally, the cells were visualized using an inverted fluorescence microscope (OBSERVER D1/AX10 cam HRC; Zeiss, Germany) after incubation at 37 °C for 15 min. For each cell type, five randomly regions were analyzed to calculate the cell viability. The morphology of NPCs on TPU-A was observed by scanning electron microscopy (SEM, JEOL, JSM-6510LV, Japan). A Cell Counting Kit-8 (CCK-8; Dojindo, Japan) assay was performed to determine the cell proliferation rates of the two cell lines. After cultured for 1, 3, 5, and 7 days in a 96-well plate (4000 cells/well), the fresh medium and CCK-8 solution with a 9:1 ratio was used to incubate chondrocytes and MC-3T3 E1 cells for 2 h at 37 °C. The optical density (OD) of the supernatants was measured using a microplate reader at 450 nm (Gen5, BioTek, USA).

2.6. In vivo studies

20 New Zealand white rabbits (4 months old, 2.5–3.0 kg, male) were obtained from the Laboratory Animal Research Center of Sichuan University. All procedures in this study were conducted under the approval of the Institutional Animal Care and Use Committee of West China Hospital, Sichuan University (approval number: 2020406A).

2.7. Disc degeneration model and implantation of TPU-A

All animals were given X-ray and magnetic resonance imaging (MRI) scans of the spine prior to implantation to ensure no IVD degeneration-related diseases were present. Each rabbit was anesthetized with pentobarbital at 30 mg/kg. Specifically, the rabbits were anesthetized with pentobarbital (30 mg/kg). After shaving and sterilization, the anterior surfaces of four consecutive lumbar IVDs (disc segments L3–L4 to L6–L7) were exposed by a posterolateral retroperitoneal approach. L3–L4 and L6–L7 receiving no treatment were used as the control group. L4/5 was used as the defect group. To induce disc degeneration, a 21-gauge needle was inserted into the center of the L4/5 disc through the annulus fibrosus (AF) into the nucleus pulposus (NP) for 30 s. L5/6 was chosen for TPU-A implantation (TPU-A group). Annular defects (3 mm diameter, 1.5 mm height) and discectomy were performed to prepare the disc space for implant insertion. TPU-A was press-fit into the disc space (2 mm depth) at the center of the L5/6 to ensure the initial implantation stability, followed by sealing with fibrin glue (Tisseel, Baxter) into the defect area. The muscles on the surface of the exposed spine were then sutured. After the surgery, cefazolin (22 mg/kg) was given to the animals in the initial 48 h for infection prevention and meloxicam was used daily for 3 consecutive days for pain relief.

2.8. Radiographic analysis

Lateral radiographs were taken for each rabbit in week 2, 4, and 8. To avoid axial rotation of the spine and minimize the error from the beam divergence, radiographs were repeated twice for each animal. The IVD height and body height were measured using Image J. Disc height (DHI) was calculated based on established method (see Figure S8) [36]. The normalized DHI defined by Eq. (5) reveals the changes in DHI.

%DHI = (I₂ / I₁) × 100% (5)

Where I₁ is the preoperative bone volume, I₂ is the postoperative bone volume.

Micro-computed tomography (μCT) analysis was performed using Quantum GX Micro-CT (Quantum GX, PerkinElmer, American) with a resolution of 4.5 μm. All 3D reconstructions images were generated by Analyze 12.0 software (PerkinElmer, American) to visualize bony surfaces and the osteophyte volume. The pre-and post-surgery bone volumes were evaluated and the osteophyte bone volume was calculated by Eq. (6).

Osteophyte bone volume = V₂–V₁ (6)

Where V₁ is the pre-surgery bone volume, V₂ is the post-surgery bone volume.

Magnetic resonance imaging was performed using a 1.5-T imager (SIGNA Creator, USA). The T2-weighted spin-echo images in the sagittal plane were obtained under the following settings: repetition time (TR) = 2500 ms; echo time (TE) = 120 ms; excitations = 12; matrix = 320 × 288 mm; field of view = 164 cm; slice thickness = 2 mm with a 0-mm gap. Three researchers used the modified pfirrmann grading system [37] to evaluate the changes in signals before and after the surgery.

2.9. IVD histology

The disc specimens were harvested and fixed in 4% paraformaldehyde for 48 h, decalcified in 10% EDTA for 6 weeks, paraffin-embedded, and sectioned into 5 μm thick slices. The sectioned specimens were then stained with hematoxylin and eosin (H&E), Safranin O/Fast Green (SO), and Masson staining for further histological analysis.

2.10. Statistical analysis

All experiments were repeated at least 3 times. The data from all experiments were presented as the mean ± SEM. Statistical analyses were performed using SPSS Statistical software (SPSS Statistics 20, Chicago, IL, USA). The statistical significance between groups was analyzed using one-way ANOVA, and a P < 0.05 was considered statistically significant.

3. Results and discussion

3.1. 3D printing and FE simulation

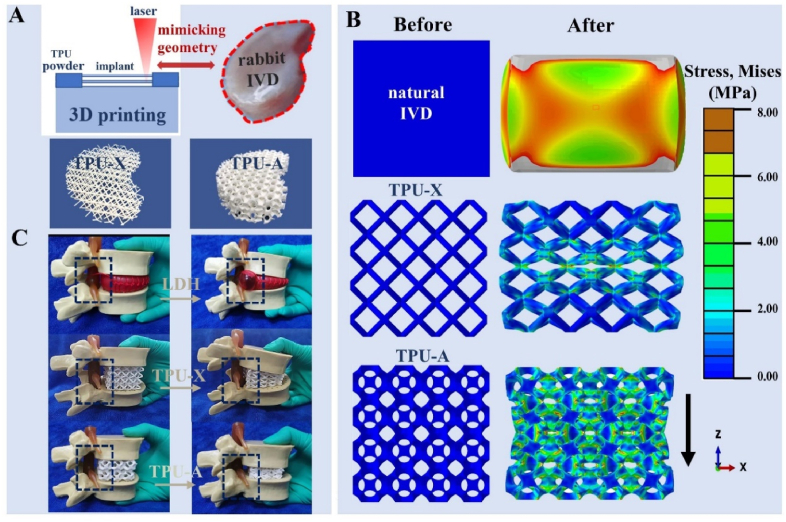
TPU is a durably, biocompatible elastomer widely used as the raw material for tissue implants [38]. Its low cost and thermoplastic nature enabled its wide application in 3D printed prototypes with complex structures. Fig. 1A illustrates the 3D printing process deploying selective laser sintering (SLS) and the printed implant with geometry replicating that of a natural rabbit IVD. The implant with modified Bucklicrystal structure was named as TPU-A, whereas the implant with a conventional lattice structure (with PPR) was named as TPU-X. The construction of TPU-A consists of hollow cells (“cuboctahedron blocks”) with 12 holes (see Figure S2). The thin ligaments and the adequate internal void spaces allow ligaments bending and shell rotation in the out-of-plane direction under compression, resulting in an inwards contraction of the adjacent curved cell edges (see Scheme 1B). Fig. 1B shows the FEM simulation results for natural IVD, TPU-X and TPU-A under uniaxial compressive loading condition. It can be seen that the Von Mises stress contours are denser at the center of the natural IVD and TPU-X, whereas for TPU-A, the stress is evenly more distributed across the entire implant. For TPU-A, the stress transfer between the Bucklicrystal structure layers is more conducive to energy dissipation, hence the stress concentration is less severe. It is worth noting that natural IVD and TPU-X both expand in the transverse direction under compression. In contrast, TPU-A under compression contracts in the transverse direction, exhibiting the typical auxetic characteristics. The corresponding strain distribution and deformation distribution of natural IVD, TPU-X and TPU-A were illustrated in Figure S3. The real-time simulation results can be found in Supplementary Movie S1. Fig. 1C and Movie S2 provide visual illustrations on the concept of LDH using a commercial IVD model and how TPU-A can be used to alleviate this problem.

Fig. 1.

A. Schematic illustrating the SLS fabrication process and printed implants with geometry mimicking the rabbit IVD. B. The stress and deformation distribution within natural IVD, TPU-X and TPU-A under compression (the mid-sagittal plane of 3D analyses). C. The behavior of TPU-X and TPU-A under compression using a commercial LDH model.

3.2. Mechanical testing

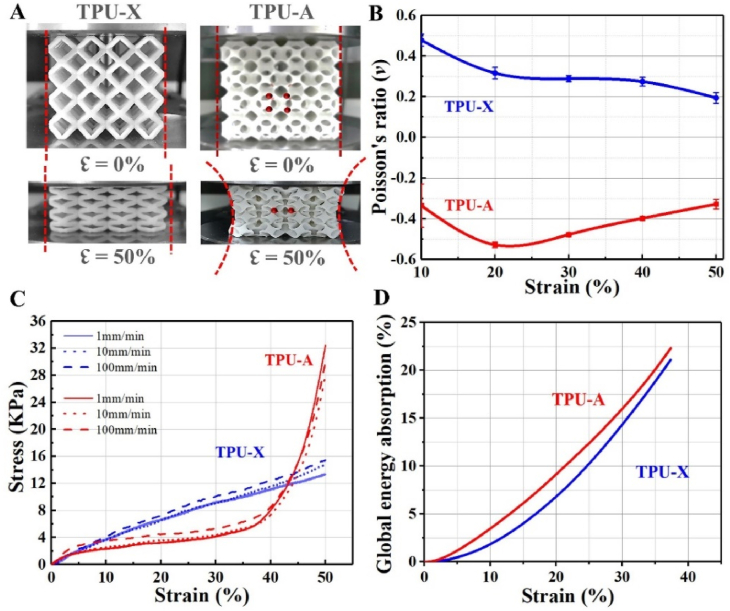
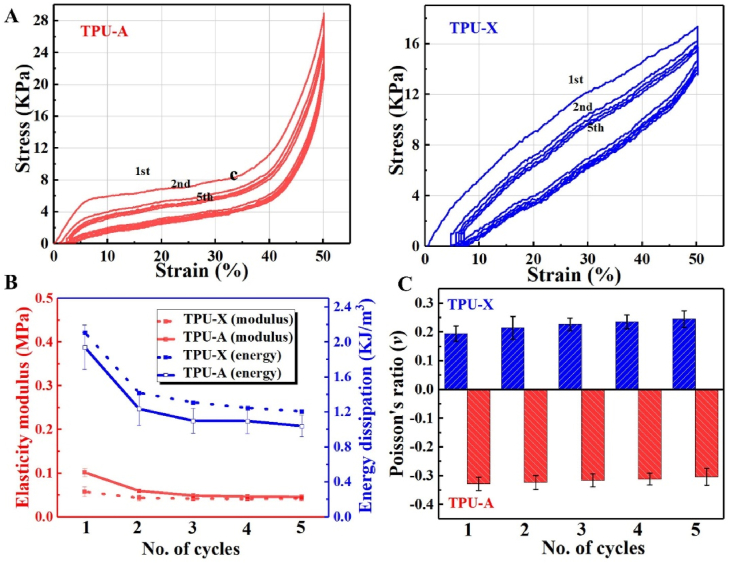
Uniaxial compression testing results are illustrated in Fig. 2. Under 50% strain, TPU-X showed expansion in the transverse direction, whereas TPU-A demonstrated distinct contraction confirming its auxetic behavior (see Fig. 2A and Supplementary Movie S3). The Poisson's ratios for both implants at different compressive strains are plotted in Fig. 2B. The Poisson's ratio of TPU-X dropped from 0.47 to 0.19. In contrast, TPU-A showed initial decline (from −0.33 to −0.52) in strain ranging from 10% to 20%. The Poisson's ratio then gradually recovered to −0.32 at 50% strain. The behavior observed for TPU-A differs from that of the traditional Bucklicrystal auxetic structures [10]. This is because in TPU-A, the linkage between the building blocks is through surface rather than point contact. There will be no adequate space to allow further structural elements to collapse once the ligaments contact each other under the applied stress. Fig. 2C shows the stress-strain curves of TPU-X and TPU-A under different strain rates. From the results, it can be seen that both implants are largely strain rate independent. The slope of TPU-A in the linear elastic stage (5% strain) is larger than that of the TPU-X, suggesting the greater stiffness of TPU-A. Under all conditions, both implants demonstrated remarkably different deformation behaviors. For TPU-X, the stress shows a quasi-linear increase with increasing strain and it achieves a compressive strength of ∼15 KPa at 50% strain. TPU-A on the other hand, only showed a brief linear response up to 5% strain, which is followed by a stress plateau (up to 40% strain). This is due to the inward buckling and bending of the ligaments (i.e., the densification regime) causing the impingement of the structural elements. Subsequently, TPU-A showed rapidly increased stress in strain ranging from 40 to 50%, where the structure behaved like a dense material. The compressive strength corresponds to the strength value at which the weakest layer of cells collapse. The total global energy absorption, W, was defined by the area under the stress-strain curves up to the densification point by Eq (7) [39].

$$W\left(\epsilon d\right)=\frac{1}{\sigma m}{\int }_0^{\epsilon d}\mathrm{\sigma }\left(\epsilon \right)\text{ d}\epsilon$$ (7)

where, ε is the strain, $\mathrm{\sigma }\left(\epsilon \right)$ is the corresponding stress and ↋d is the densification strain which was calculated by the energy absorption efficiency method. The energy absorption efficiency is defined by Eq (8).

$$\eta \left(\epsilon \right)=\frac{1}{\mathrm{\sigma }\left(\mathrm{\epsilon }\right)}{\int }_{\text{0}}^{\epsilon }\mathrm{\sigma }\left(\epsilon \right)\text{ d}\epsilon$$ (8)

Fig. 2.

A. Optical images showing TPU-X and TPU-A in compression; B. The Poisson's ratio of TPU-X and TPU-A during compression testing; C. The compressive stress-strain curves and D. The global energy absorption curves of TPU-X and TPU-A, respectively.

The onset of densification determined by the energy absorption efficiency is given by Eq (9).

$${\frac{d\eta \left(\epsilon \right)}{d\epsilon }|}_{\epsilon =\epsilon d}=0$$ (9)

Fig. S4 further illustrates how the densification strain can be extracted from the energy absorption efficiency curves and the stress-strain curve of the testing coupons.

The energy absorbing capacity of auxetic materials strongly depends on the extended plateau in the stress-strain curve [40]. In comparison to TPU-X, TPU-A undergoes a large volume reduction upon compression. The larger degree of mechanical energy dissipation associated with the volume reduction indicates the better global energy absorption efficiency of TPU-A [12], also see Fig. 2D.

Fig. 3A shows the hysteresis loops of TPU-A and TPU-X obtained from cyclic loading/unloading tests. The hystereses show partial recovery of energy at unloading due to the phase lag between the strain and the stress arise from the delay of the structure rearrangement. In comparison, TPU-A shows a better recovery (less residual strain) as compared to TPU-X. The corresponding energy dissipation is illustrated in Fig. 3B (blue lines), implying the more superior energy dissipation of TPU-A during the loading–unloading cycles. Fig. 3B (red lines) also shows that with increasing number of cycles, the elastic moduli of both implants decline gradually and stabilize after 4 cycles. Fig. 3C shows that the Poisson's ratio of TPU-A was maintained at a constant level throughout the cyclic test, while that of the TPU-X showed gradual increase due to its plastic deformation. The results suggest the better stability of TPU-A under cyclic loading condition.

Fig. 3.

A. Loading/unloading stress-strain curves; B. Elasticity moduli and energy dissipation curves in five loading–unloading cycles; C. The Poisson's ratio values in five loading–unloading cycles.

It should be noted that the results regarding cyclic loading does not fully represent the material's behavior under realistic fatigue testing condition (millions of cycles, the required resource of which is unavailable to the authors). However, we followed the established protocol in the published literature and believe that such preliminary results would provide a fair indication on the potential cyclic behavior of our implants. More comprehensive fatigue test has been planned for future work to fully justify the material's long term performance.

3.3. FE simulation

FE model was conducted to further evaluate the feasibility of our TPU-A in LHD management. The stress distribution and the deformation behavior of natural IVD, TPU-X and TPU-A were analyzed and compared. The equivalent entity method is well established in the literature [41], to address the challenges (in consideration of the computation time and accuracy) arise from the complex porous FE modeling. Published literature [42] has confirmed the validity of such method in analyzing the dynamic properties of complex porous structures. Stress-mapping method [43] was used (see Figure S5) to achieve balanced simulation accuracy and computational speed.

A detailed 3D human lumbosacral spine (L4-L5) non-linear FE model was obtained from high-resolution computed tomography (CT) images of a human in the axial, sagittal, and coronal planes with 1-mm scan interval. Digital CT data were imported to a software (Mimics, Materialise Inc., Leuven, Belgium), and 3D geometrical surface of the lumbosacral spine was generated. The exported IGES files from the Mimics software were inputted to hypermesh to create hexahedral finite element mesh. The initial gap between the articulating surfaces was based on CT images.

Fig. 4 shows the typical views of the reconstructed 3D model which consists of 27586 elements and 29262 nodes. The edge of the spinal disc was obtained from the enhanced CT images. As the disc nucleus cannot be clearly distinguished from the CT image, we followed [44] for its geometry. The ligaments were defined as truss elements which are connected to the adjacent vertebrae, including anterior longitudinal ligament (ALL), posterior longitudinal ligament (PLL), ligamentum flavum (LF), interspinous ligament (ISL), and capsular ligaments (CL). The properties of the biological tissues involved in the model were referred from the literature [45].

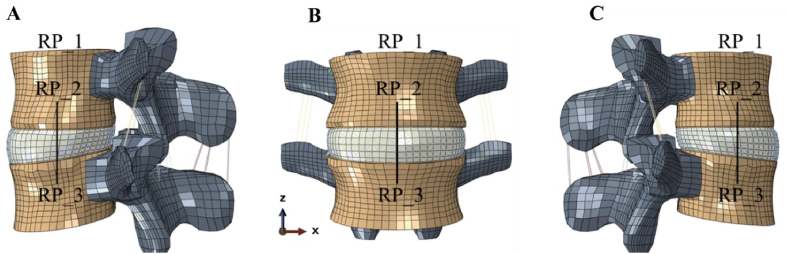
Fig. 4.

The spine FE model showing A. side view (right); B. front view and C. side view (left). Reference points RP_1, 2, 3 were selected for the simulation of the implants under bending, torsion, flexion and extension.

In order to reproduce the loading conditions of natural human IVD, the dynamics response of L4-L5 lumbar under bending, torsion, extension, and flexion conditions were analyzed following established method [46]. The boundary conditions were based on practical loading within human body [47], see Tabel S1. To facilitate the modeling, reference points RP_1, 2, 3 were defined, where RP_1 is the center point on the top surface of L4, RP_2, 3 are in the center of L4 and L5, respectively. A connector was established between RP_2 and RP_3 in order to exert the force moment.

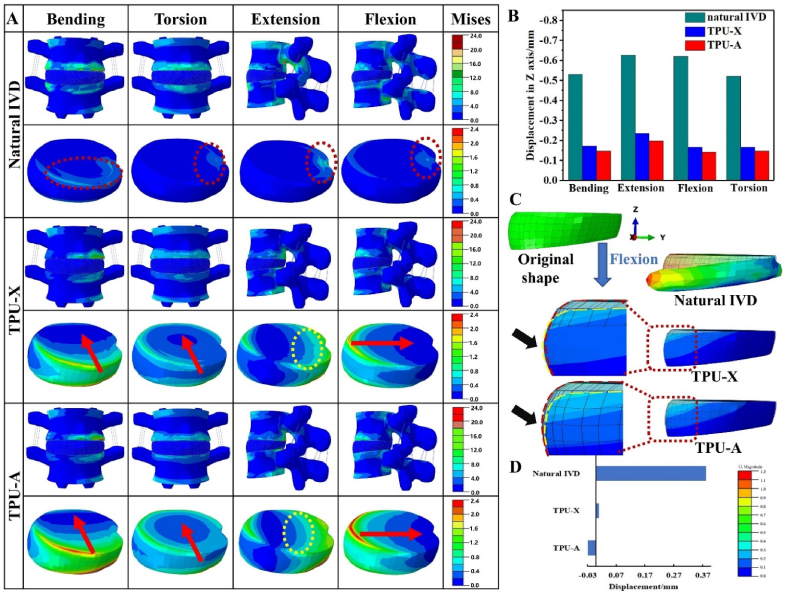
Fig. 5A compares the Von Mises stress distribution of L4-L5 lumbar for natural IVD, TPU-X, and TPU-A under the four typical loading conditions. The arrows in Fig. 5A show the stress diffusion direction [48] (i.e., the pathway of stress propagation) in the TPU-A and TPU-X implants. It is worth noting that under all conditions, the equivalent stress for natural IVD is very much concentrated (red dashed circles in Fig. 5A). In contrast, for TPU-A and TPU-X, the stress is diffused from the periphery towards the center (see red arrow) and the stress decreased along the propagation direction. Additionally, more domains within the TPU-A and TPU-X were engaged in the stress dissipation process. Although the TPU-A and TPU-X can effectively attenuate stress, TPU-A presents smoother stress diffusion front. This can be particularly evident under extension loading (yellow dashed circles in Fig. 5A), indicating the more even stress transfer/attenuation within such structure. To quantify the mechanical response of different implants under various loading conditions, the displacement at reference point RP_1 (Fig. 4) in the z-axis direction was analyzed and the results can be found in Fig. 5B. The results demonstrated that TPU-A is stiffer than TPU-X under the same loading condition due to its smaller lateral displacement (consistent with Fig. 2Ac). Results show that TPU-A demonstrates lower compressibility as compared to the natural IVD, indicating its better resistance to the external mechanical loading and its excellent stress dissipation performance.

Fig. 5.

A. The equivalent stress distribution and deformation distribution of L4-L5 lumbar under bending, torsion, extension and flexion conditions. B. Displacement of reference point in Z direction. C. Comparing local deformation of natural IVD, TPU-X and TPU-A under flexion. D. Final displacement of node 54620 in U2 (Z axis) direction.

It is accepted that disc failure is prone to occur under an accelerated compression rate and a flexed posture. Flexion loading was therefore chosen as a typical loading condition for more in-depth investigation. Fig. 5C shows the deformation characteristics of natural IVD, TPU-A, and TPU-X implants under flexion. The stress contour is referenced against the undeformed IVD in order to highlight any change with different structures. Note the black arrows denote magnified image (5X) for easy observation, red dashed lines show the contour of unformed IVD and yellow dashed lines highlight the contour of the implant after deformation. Fig. 5C shows that natural IVD displays the greatest degree of bulging. Slight bulging was observed in TPU-X, whereas TPU-A exhibits the NPR behavior (contraction). The final displacement of node 54620 in U2 (Z axis) direction is plotted in Fig. 5D. The results further confirm that TPU-A displays the desirable auxetic behavior under practical loading conditions, and further details can be found in Figure S6 and Movie S4.

In the present FE analysis, we utilized a simplified model based on equivalent entity method to demonstrate the NPR effect of our TPU-A scaffold. Since the NPR behavior is dominant by the buckling of the ligaments, bending of the ligament would lead to local stress concentration sites which are prone to failure. More future work is required to include micromechanics based material model into the FE method. In addition, the development/exploration of other advanced 3D printable biomaterials with more superior mechanical properties for the auxetic structure would also help enhance the feasibility of the scaffold for the proposed application.

3.4. In vitro analysis

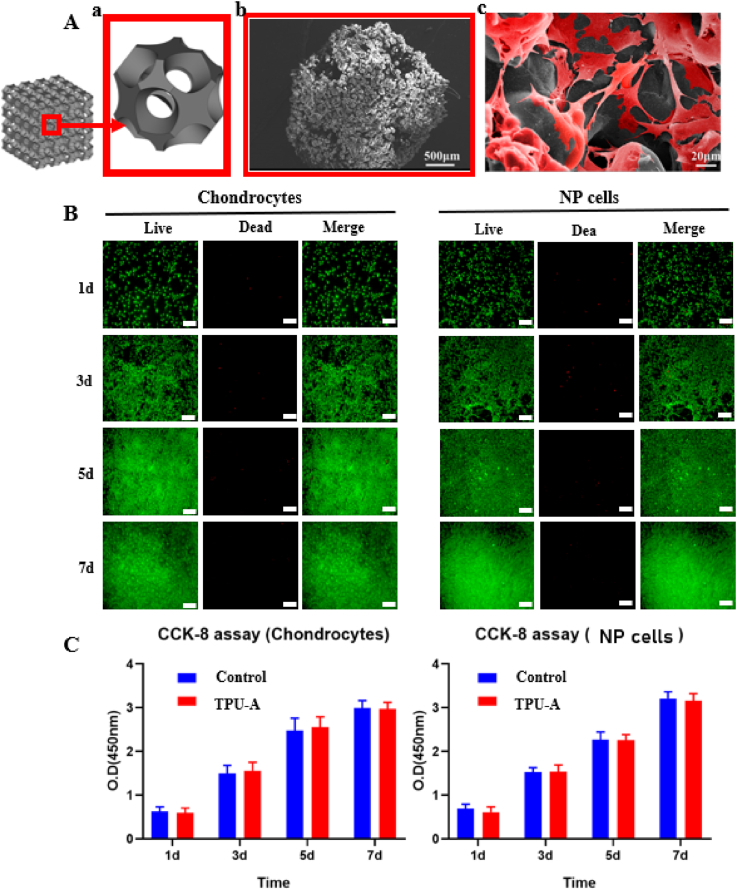
The cytocompatibility of TPU-A was investigated. Fig. 6Aa shows a single unit cell (2 mm × 2 mm) extracted from TPU-A implant with interconnected microporous structures. Fig. 6Ab shows the 3D printed implant features rough surface resulted from the SLS process, which is ideal for cell adhesion. This is further confirmed by Fig. 6Ac where NPCs adhered and spread extensively on the implant surface after 24h of culturing. After the chondrocytes and NPCs were seeded on TPU-A for 1, 3, 5, and 7 days, cell viability staining was performed. Fig. 6B suggests live chondrocytes and NPCs cultured with TPU-A were greater than 90% (green stain) for day 1,3,5 and 7, suggesting TPU-A is highly biocompatible. CCK-8 assay was used to determine the proliferation of chondrocytes and NPCs, with cells cultured in petri dish being the control. The CCK-8 values of the chondrocytes andNPCs in the TPU-A group were similar to that of the control for day 1,3,5 and 7 (see Fig. 6C).

Fig. 6.

A. (a) Schematic showing a single unit cell extracted from TPU-A, (b) SEM image showing the surface morphology of TPU-A and (c) NP cells adhesion on TPU-A. B. Live/dead assay of chondrocytes and NP cells at different point of time (green: live; red: dead; scale bar: 200 μm). C. CCK8 assay for proliferation of chondrocytes and NP cells. Error bars represent S.D., and significant differences were assessed with Student's t-test; *P < 0.05.

3.5. In vivo analysis

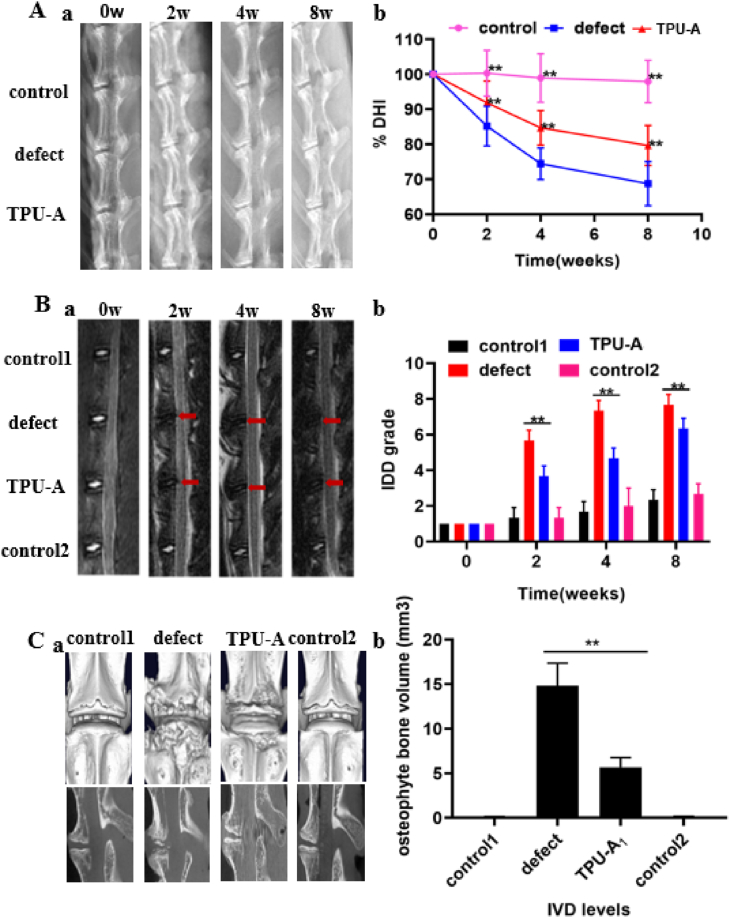
To investigate the feasibility of using TPU-A as an IVD replacement and verify its potential in restoring the physiological function of natural IVD, TPU-A (in the size of a rabbit IVD) was implanted in vivo using a rabbit disc replacement model for up to 8 weeks (see Figure S7). X-ray and MRI were performed prior to surgery and 2, 4 and 8 weeks post-surgery. As shown in Fig. 7A and B, the disc height index (%DHI) and Pfirrmann grading system were used to quantify the X-ray and MRI results. From the X-ray results in Fig. 7Aa, disc height loss and the blurring of the endplate boundary can be seen from the week 2 defect group. The disc height loss and endplate blurring were exacerbated in the week 4 defect group. The TPU-A group displayed narrowed disc height, however, no blurring or structural failure of the endplate was found. Moreover, the disc height indices of the TPU-A group were significantly higher than that of the defect group for week 2, 4 and 8 post-surgery (see Fig. 7Ab). MRI images in Fig. 7Ba show decreasedT2-weighted imaging signal intensity in the defect group as compared with the control in week 2. Further aggravation occurred in week 4 and 8 in the defect group. In contrast, TPU-A group demonstrated higher T2-weighted signal intensity in week 2, 4 and 8 post-surgery. The pfirrmann grades in TPU-A were also significantly higher than that in the defect group (see Fig. 7Bb). 8 weeks after surgery, the rabbit spine samples were harvested for μCT scan and further histology assessment. From Fig. 7Ca, b, 3D reconstruction of cross-sectional μCT scans of the rabbit lumbar spine confirmed the complete absence of heterotopic ossification in the normal control group. There was significantly smaller heterotopic ossification area in the TPU-A group than those in the defect group. Optical images in Figure S9 show that the defect group had an obvious tear in the spine under compression after 8W and TPU-A as an artificial IVD could help alleviate this problem.

Fig. 7.

A. Radiographic changes of spine after the TPU-A implantation: (a) X-ray images and (b) measurements of DHI% changes. B. (a) MRI images and (b) IDD grading score (modified pfirrmann grading) at different time points after surgery. C. (a) 3D reconstructions of μCT scans of the rabbit lumbar spines and the representative cross-sections 8 weeks after implantation, (b) Quantification of osteophyte bone volumes after different treatment. Error bars represent S.D., and significant differences were assessed with Student's t-test; *P < 0.05, **P < 0.01.

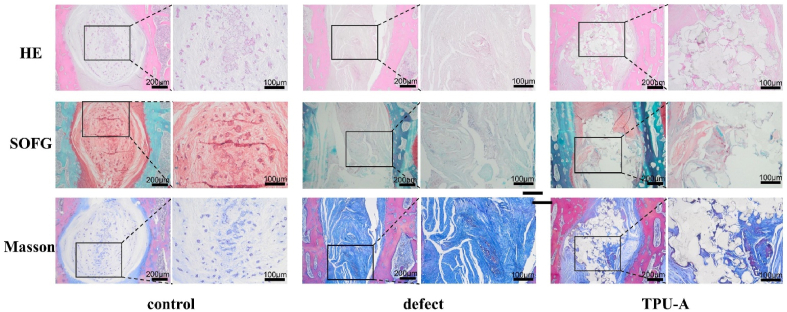
From Fig. 8, the implantation efficacy was further evaluated using histological analysis 8 weeks post-surgery. In the control group, large volume of the oval-shaped nucleus pulposus can be seen in the specimen stained by H&E and safranin-O method. In the defect group, the disc space collapsed with evident extracellular matrix (ECM) loss and fibrous tissue invasion. This was further confirmed by the positive staining of Masson's Trichrome. The nucleus pulposus area in the TPU-A group was similar to that of the control by H&E and safranin-O staining. Negative staining by Masson's Trichrome method in the TPU-A group also demonstrated decreased fibrosis when compared with the defect group. In accordance with radiographic findings, histological data further demonstrated that TPU-A is stable over an 8-week period in vivo, maintaining its structure and function. It should be noted in this preliminary study, an IVD implantation model [49] was adopted due to the restriction present in the rabbit spine autonomy. Thorough validation of the implant as a total IVD replacement would call for future research which involves large animal models (such as goats and pigs), however it is beyond the scope of this study.

Fig. 8.

Histology analysis of intervertebral disc after implantation. TPU-A alleviated IVD degeneration and fibrosis formation when compared to the defect group. H&E staining showing cellular distribution and degree of inflammation in NP area; Safranin-O staining showing the proteoglycan distributions; Masson staining showing the fibrosis formation.

4. Conclusion

In this study, we design and construct a novel 3D printed auxetic-structured implant (TPU-A) for potential IVD application. The uniquely modified “Bucklicrysal” auxetic design endows the implant with the desirable negative Poisson's ratio and the geometry of the implant can be customized to match the anatomy of natural IVD. The implant has been characterized for its stiffness, strength, energy absorbing and dissipation and cyclic loading behavior. FEA modeling has been conducted to simulate the deformation of the implant under bending, torsion, tension and flexion conditions and the results were compared with natural IVD as well as a conventional 3D printed TPU implant with positive poison's ratio. Simulation results show that TPU-A could re-establish the mechanical function of native spine motion segments and alleviate LDH. In vitro studies shows that TPU-A has excellent biocompatibility and in vivo implantation using the rabbit disc model confirmed TPU-A can maintain the natural motion segment mechanical function after implantation and can withstand the demanding practical loading conditions. The promising results obtained from this proof-of-concept study points to the new direction in future design and development of IVD implants with novel auxetic structures. In future work, more follow-up studies will be required to further validate the practicality of the scaffolds. Future work would include developing micromechanics based constitutive model in the finite element method, development/exploration of new and advanced 3D printable biomaterials with more superior mechanical properties, and in vivo studies in larger animal models (e.g., pig, goat) to fully validate the implant's long-term performance in vivo.

Credit Author Statement

Li Zhang, Yong Yi and Ganjun Feng designed the project and modified the paper. Yulin Jiang, Kun Shi and Luonan Zhou performed the experiments and wrote the manuscript. Miaomiao He and Ce Zhu helped performed cytotoxicity evaluation experiments. Jingcheng Wang and Jianhua Li helped performed animal experiments. Yubao Li and Limin Liu provided Fund support. Dan Sun revised the language of the manuscript. All authors discussed the results and contributed to the data interpretation.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following is/are the supplementary data to this article: