A multivariate Bayesian classification algorithm for cerebral stage prediction by diffusion tensor imaging in amyotrophic lateral sclerosis

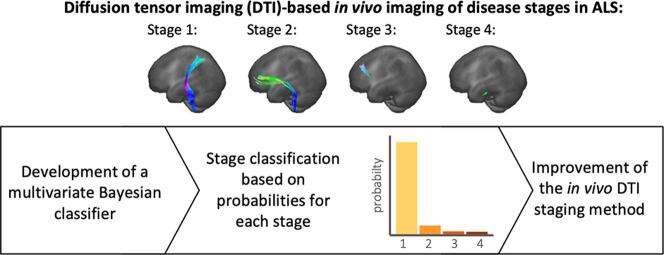
Graphical abstract

Highlights

• •Novel DTI-based classification of ALS disease stages by a Bayesian approach is applied.
• •Bayesian classification algorithm improves threshold-based staging method.
• •Step forward in MRI-based patient stratification in ALS in vivo.

Abstract

Background and Objective

Diffusion tensor imaging (DTI) can be used to tract-wise map correlates of the sequential disease progression and, therefore, to assess disease stages of amyotrophic lateral sclerosis (ALS) in vivo. According to a threshold-based sequential scheme, a classification of ALS patients into disease stages is possible, however, several patients cannot be staged for methodological reasons. This study aims to implement a multivariate Bayesian classification algorithm for disease stage prediction at an individual ALS patient level based on DTI metrics of involved tract systems to improve disease stage mapping.

Methods

The analysis of fiber tracts involved in each stage of ALS was performed in 325 ALS patients and 130 age- and gender-matched healthy controls. Based on Bayes’ theorem and in accordance with the sequential disease progression, a multistage classifier was implemented. Patients were categorized into in vivo DTI stages using the threshold-based method and the Bayesian algorithm. By the margin of confidence, the reliability of the Bayesian categorizations was accessible.

Results

Based on the Bayesian multistage classifier, 88% of all ALS patients could be assigned into an ALS stage compared to 77% using the threshold-based staging scheme. Additionally, the confidence of all classifications could be estimated.

Conclusions

By the application of the multi-stage Bayesian classifier, an individualized in vivo cerebral staging of ALS patients was possible based on the sequentially involved tract systems and, furthermore, the reliability of the respective classifications could be determined. The Bayesian classification algorithm is an improvement of the threshold-based staging method and could provide a framework for extending the DTI-based in vivo cerebral staging in ALS.

1. Introduction

During the disease progression of amyotrophic lateral sclerosis (ALS), four neuropathological stages are progressed based on the distribution of phosphorylated 43 kDa TAR DNA-binding protein (pTDP-43) in the brain as defined in postmortem studies (Braak et al., 2013, Brettschneider et al., 2013, Tan et al., 2015). Using diffusion tensor imaging (DTI), the analysis of white matter neuronal tracts and, in a hypothesis-guided approach, the in vivo identification of tracts involved in the progression of ALS is possible (Kassubek et al., 2014). During the course of ALS, the following tracts were demonstrated to become sequentially involved: the corticospinal tract (CST) at stage 1, the corticorubral and corticopontine tracts at stage 2, the corticostriatal pathway at stage 3, and the proximal portion of the perforant pathway at stage 4 (Kassubek et al., 2014, Kassubek et al., 2018). The analysis of the fractional anisotropy (FA) using a tract of interest (TOI)-based method allowed for a stage classification at an individual level and, moreover, quantitative mapping of disease progression in the brain (Kassubek et al., 2018). This in vivo staging method, based on the stereotypical sequential involvement of tract systems, uses a fixed FA threshold for each tract system based on a healthy control group to provide an individual disease stage classification for ALS patients. However, for a substantial percentage of the patients investigated so far, a classification according to this scheme is not possible due to methodological reasons (Kassubek et al., 2014, Kassubek et al., 2018): the general inter-subject variability of FA values (Vollmar et al., 2010) contributes to an incomplete separation of ALS patients’ and healthy controls’ FA values in the CST (Kassubek et al., 2014) so that in patients with rather high FA values at the cross-sectional level, the question remains open whether their FA values are not altered or their FA is altered but per se is within the range of FA values of controls. While combining the FA of involved tract systems with structural parameters can improve the separation of patients and healthy controls for general disease diagnosis (Kocar et al., 2021), this uncertainty in the assessment of a patient’s FA value in the range of overlapping distributions of patients and controls should be incorporated into disease stage imaging.

Bayesian predictions have already shown their usefulness in the medical field in general (Bours, 2021, Webb and Sidebotham, 2020) and in combination with brain imaging in particular (Morales et al., 2013): Bayesian statistics can be used to calculate the probabilities that a measured value belongs to either the patient or the healthy control class based on the distributions of the observed values in those two classes. This is especially helpful in cases where measured values of a patient group cannot be sharply separated from those of a healthy control group as it is the case for the in vivo staging approach. Based on a two-class scenario, the classification algorithm can also be extended for the prediction of different multiple stages along an observed variable (Ichikawa et al., 2017). In contrast, established threshold- or cut-off-based classification schemes provide binary decisions, e.g., ‘altered’ or ‘not altered’, for observed values.

In this study, we developed a Bayesian classifier with multiple staging alternatives based on multi-dimensional data sets of diffusion metrics of tract systems involved during the progression of ALS. The a priori knowledge about sequential involvement of tracts was considered as a boundary condition and thus, individual probability statements for each in vivo DTI stage of ALS. Providing a probability for the classification into a certain stage and therefore confidence of classification might have the potential to improve the stratification of quantitative DTI results at the individual level.

2. Methods

2.1. Subjects and clinical characterization

In total, 325 patients (61.5 ± 12.0 years, 198 male/126 female) with clinically definite or probable sporadic ALS according to the revised version of the El Escorial World Federation of Neurology criteria (Brooks et al., 2000) were included in the study. All patients underwent standardized clinical-neurological and routine laboratory examinations. None of the patients had any history of other neurological or psychiatric disorders. Severity of physical symptoms of patients as measured with the revised ALS functional rating scale (ALS-FRS-R) (Cedarbaum et al., 1999) was 40 ± 6 (range 17 – 47). MiToS functional staging was obtained from ALS-FRS-R domains (Chiò et al., 2015). King’s clinical staging was estimated based on the ALS-FRS-R domains (Balendra et al., 2014) which provides high agreement with the original staging scheme (Roche et al., 2012). Due to the retrospective nature of this study, the points reached in the single ALS-FRS-R questions were not available for all patients in addition to the total ALS-FRS-R score. Therefore, functional and clinical staging could only be obtained for 206 of the 325 patients. Magnetic Resonance Imaging (MRI) data were acquired either on a 1.5 T scanner (248 patients) or a 3.0 T scanner (77 patients). About half (52%) of these patients with ALS were already included in an earlier DTI-based staging analysis (Kassubek et al., 2018), i.e., the results of this prior report could be confirmed by the application of the staging approach to additional 156 patients who had not received this analysis before. Longitudinal data sets were available for a limited number of patients. In these cases, the baseline data were used for further analysis. In addition, 130 age- and sex-matched healthy controls (57.6 ± 12.1 years, 72 male/58 female, 80 acquired on a 1.5 T scanner and 50 acquired on a 3 T scanner) were used to define statistical comparison. All subjects gave written consent for the MRI protocol according to institutional guidelines. The study was approved by the Ethical Committee of the University of Ulm, Germany (reference # 19/12).

2.2. MRI acquisition

For scanning, a 1.5 T MRI scanner (Magnetom Symphony, Siemens Medical, Erlangen, Germany) and a 3.0 T MRI scanner (Allegra, Siemens Medical, Erlangen, Germany) were used. The 1.5 T protocol consisted of 52 gradient directions including four b0 directions (b = 1000 s/mm², voxel size 2.0 mm × 2.0 mm × 2.8 mm, 128 × 128 × 64 matrix, TE = 95 ms, TR = 8000 s). The 3.0 T protocol consisted of 49 gradient directions including one b0 directions (b = 1000 s/mm², voxel size 2.2 mm × 2.2 mm × 2.2 mm, 96 × 128 × 52 matrix, TE = 85 ms, TR = 7600 s).

2.3. DTI analysis

The DTI analysis software ‘Tensor Imaging and Fiber Tracking’ (TIFT) (Müller et al., 2007a) was used for data postprocessing. First, DTI data sets were corrected for eddy current distortions and underwent quality control (Müller et al., 2011). In the next step, on all data sets a non-linear spatial normalization to the Montreal Neurological Institute (MNI) stereotaxic standard space (Brett et al., 2002) was performed by using study-specific DTI templates from all patients and controls (Müller et al., 2007b) as described previously (Müller et al., 2012). For each data set, FA maps were calculated and smoothed with a Gaussian filter with 8 mm full width-at-half-maximum.

Based on FA maps of healthy controls (27 data sets each recorded at 1.5 T and 3 T), three-dimensional correction matrices were calculated and used to correct all 3 T data sets as described previously (Rosskopf et al., 2015). An averaged data set from MNI transformed controls' data was used for the identification of the relevant tract systems by a seed-to-target TOI-based approach. The brain structures to be identified were defined according to the ALS-associated staging system (Brettschneider et al., 2013, Kassubek et al., 2014, Kassubek et al., 2018), i.e., the CST (according to ALS stage 1), the corticorubral and corticopontine tracts (according to ALS stage 2), the corticostriatal pathway (according to ALS stage 3), and the proximal portion of the perforant pathway (according to ALS stage 4). Fiber tracking was a deterministic streamline tracking approach (Müller et al., 2009) at which the FA threshold was set at 0.2 (Kunimatsu et al., 2004), the Eigenvector scalar product threshold was set at 0.9, the seed regions had a radius of 5 mm, and the target regions had a radius of 10 mm. In a final step, the technique of tract-wise FA statistics was applied to select FA values underlying the fiber tracks for arithmetic averaging. Bihemispheric FA values were averaged and tract-wise corrected for age (Behler et al., 2021). The results of corticopontine and corticorubral tracts were averaged since both were involved in ALS stage 2.

2.4. Threshold-based disease staging categorization

The well-established fiber tract-based staging scheme (Kassubek et al., 2014) is based on FA thresholds $({\mu }_{\mathit{HC}}-0.47{\sigma }_{\mathit{HC}})$ utilizing the mean ${\mu }_{\mathit{HC}}$ and standard deviation ${\sigma }_{\mathit{HC}}$ of the healthy control group in the respective tract systems. After applying the sequential staging cascade, a staging categorization was obtained at the individual level.

2.5. Bayesian statistics

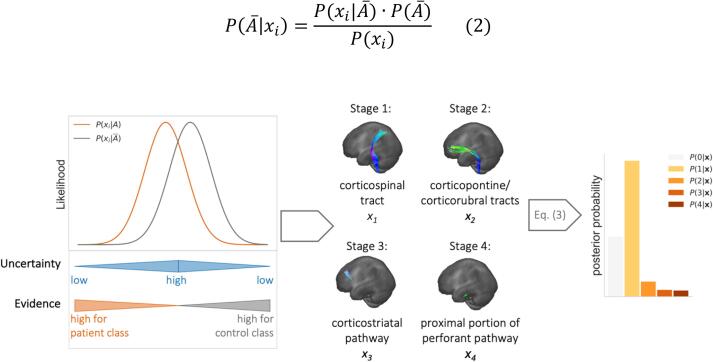
In a particular tract system subject to disease-related alterations, based on Bayes’ theorem, the posterior probability that the observed FA value $x_i$ of a tract system would be assigned to the patient class, i.e., would be considered as ‘altered’ (noted as $A$), is given by:

$$P\left(A\text{|}{x}_i\right)=\frac{P(x_i|A)·P\left(A\right)}{P\left(x_i\right)}$$ (1)

where $P\left(A\right)$ is the prior probability for class $A$, $P\left(x_i|A\right)$ is the likelihood of observing $x_i$ given $A$, i.e., in the patient group, and $P\left(x_i\right)$ is the overall probability of $x_i$ being observed. For the condition that a value is considered as belonging to the controls class, i.e., ‘not altered’ (notated as $\overline{A}$), the formula applies analogously:

$$P\left(\overline{A}\text{|}{x}_i\right)=\frac{P(x_i|\overline{A})·P\left(\overline{A}\right)}{P\left(x_i\right)}$$ (2)

A schematic example of a Bayesian prediction between these two classes $A$ (the patient class) and $\overline{A}$ (the controls class) is schematically shown in Fig. 1. The likelihood for $x_i$ being observed in the ALS patient class, $P\left(x_i|A\right),$ and the likelihood for $x_i$ being observed in the healthy control class, $P\left(x_i|\overline{A}\right)$, overlap for a broad range of $x_i$. For $P\left(x_i|A\right)=P\left(x_i|\overline{A}\right),$ the confidence of a classification of $x_i$ into one of both classes is reasonably the lowest, and, therefore, the risk for misclassification the highest. Starting from this point, with decreasing or increasing $x_i$ the difference between $P\left(x_i|A\right)$ and $P\left(x_i|\overline{A}\right)$ increases resulting in increasing confidence in classification. The confidence of a classification is highest when there is just evidence for one of both classes.

Fig. 1.

Schematic illustration of likelihoods and posterior probabilities for the Bayesian prediction of measured FA values $x_{\mathit{i}}$ belonging either to the patient (orange) or the healthy control class (grey) in a tract system associated with disease progression. The superposition of the two likelihoods leads to a range of greater uncertainty in the classification. Therefore, the evidence for the respective class membership increases with decreasing or increasing $x_{\mathit{i}}$. Based on this simple case in one tract system, the likelihoods of FA values of four tract systems are evaluated for the classification of ALS patients and posterior probabilities are calculated for each ALS stage.

2.6. Modeling a multistage Bayesian classifier

The binary case just described for classifying an FA value as ‘altered’ or ‘not altered’ can be extended to consider all four tract systems simultaneously without a priori knowledge of the patients’ stages. The multivariate Bayesian algorithm then calculates the posterior probabilities for each stage based on the likelihood of FA values in each of the four tract systems to be ‘altered’ or ‘not altered’. The vector $\mathit{x}=\left(x_1,x_2,x_3,x_4\right)$ contains all four FA values observed in the stage-defining tract systems (see Fig. 1). The likelihood $P\left(\mathit{x}|S\right)$ of $\mathit{x}$ in each class $S\in \left\{0,1,2,3,4\right\}$ is obtained by multiplication of the likelihoods $P\left(x_i|A\right)$ of tract systems involved in the corresponding stage and likelihoods $P\left(x_i|\overline{A}\right)$ of tract systems not yet involved. It should be noted that the condition of all four $x_i$ to be considered as 'not altered' is referred to as class $S=0$ here. The posterior probabilities of ALS stages are therefore calculated as.

$$P\left(S|\mathit{x}\right)=\frac{1}{P\left(\mathit{x}\right)}\prod _{k}P\left(x_k\right|A)·\prod _{l}P\left(x_l\right|\overline{A})·P\left(S\right)$$ (3)

with $k\in \left\{0,1,2,3,4\right\}$ in class $S$ affected tract systems and the number of non-involved tract systems $l=4-k$, in order to take the sequential order into account in which the tracts are affected during the disease. An exemplary illustration of the resulting posterior probabilities for each class is given in Fig. 1. The classifier assigns $\mathit{x}$ to ALS stage $C$ according to the following classification rule:

$$C=\left\{\begin{array}{cc}\text{'not}\text{stageable'}& \mathrm{if}P\left(0|\mathit{x}\right)>\sum _{S=1}^{4}P\left(S|\mathit{x}\right)\\ \underset{S}{\mathrm{argmax}}P\left(S|\mathit{x}\right)& \text{otherwise}\end{array}\right)$$ (4)

To use Bayes’ theorem in this multi-stage setting, two assumptions were made:

• 1)likelihoods are normal distributed with mean $\mu$ and standard deviation $\sigma$
• 2)standard deviations from the patients and controls group are equal in each tract system: $P\left(x_k\right|A)~\mathcal{N}\left({\mu }_A,{\sigma }_{\mathit{HC}}\right)$ and $P\left(x_k\right|\overline{A})~\mathcal{N}\left({\mu }_{\mathit{HC}},{\sigma }_{\mathit{HC}}\right)$,

3) prior probabilities $P(S)$ are equal.

The assumption of a normal distributed FA values in the tract systems was tested using D'Agostino's K-squared test (D’Agostino, 1971), rejecting the null hypothesis at p < 0.05; in the control group, FA values outside $\mu \pm 3\sigma$ were removed. Since the CST is involved in every ALS stage, the variation between the distributions of the respective mean FA of patients and healthy controls were the starting points for defining the mean ${\mu }_A$ of ‘altered’ FA values in tract systems involved in a later (i.e., higher) stage.

The computational implementation of the Bayesian classifier and the statistical analysis was performed using Python 3.9 with the following machine learning modules: Scikit-learn 1.7 (Pedregosa et al., 2018) and PyTorch 1.9 (Paszke et al., 2019).

2.7. Margin of confidence

Since the decision of the multilevel Bayesian classifier is based on probabilities, the risk of misclassification is accessible (Li and Ma, 2020). The margin of confidence can be used as a confidence variable and is calculated as the difference between the posterior probabilities of the two most probable classes. If those two classes have equal probability, the classification then is ‘least confident’.

3. Results

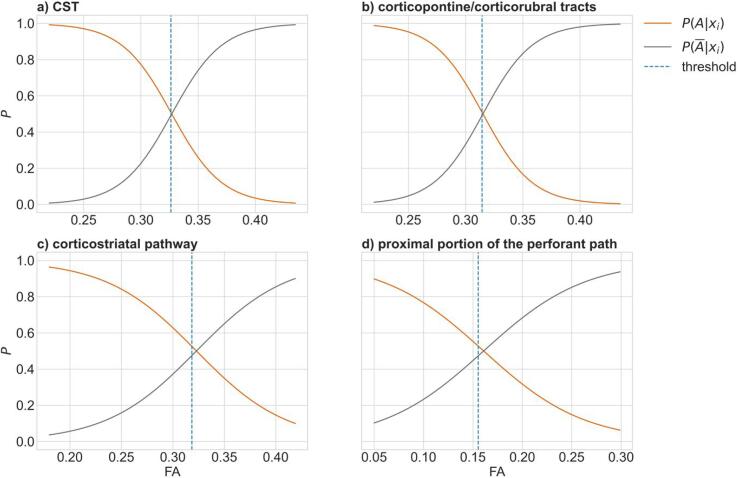
In the healthy control group, the means and standard deviations of FA values in the tract systems considered were obtained as follows: CST, 0.335 ± 0.019: corticopontine and corticorubral tracts, 0.323 ± 0.018; corticostriatal tract, 0.331 ± 0.026; proximal portion of perforant pathway, 0.165 ± 0.020. Among the patient measurements, the mean FA in the CST was 0.319. Based on the differences between patients and healthy controls in the CST, the means of the distribution for the tract systems involved in stages 2 to 4 were calculated to 0.307 for the corticopontine and corticorubral tracts, 0.315 for the corticostriatal tract, and 0.157 for the perforant pathway. Standard deviations of FA in the altered tract systems, according to the stages, were equated with those of healthy controls according to the assumptions made. Based on these values, the likelihoods were estimated. For a comparison with the decision rules of the threshold method, the posterior probabilities were calculated for each tract system according to the Eqs. (1), (2) (Fig. 2). In the CST (Fig. 2a) and the corticopontine and corticorubral tracts (Fig. 2b), the threshold of a FA considered as altered was equal to the FA with the same posterior probability for class $A$ and $\overline{A}.$ In the corticostriatal pathway (Fig. 2c) and the proximal portion of the perforant pathway (Fig. 2d), the threshold was 0.020 and 0.012, respectively, below the FA with equal posterior probabilities.

Fig. 2.

Posterior probabilities for fractional anisotropy (FA) values in a) the corticospinal tract (CST), b) the corticopontine and corticorubral tracts, c) the corticostriatal pathway, and d) the proximal portion of the perforant pathway to be classified as ‘altered’ ($P\left(A|x_i\right)$, orange) or ‘not altered’ ($P\left(\overline{A}|x_i\right),$ grey). The individual tract systems were analyzed independently and the respective threshold of the threshold-based staging method is shown as dashed blue line.

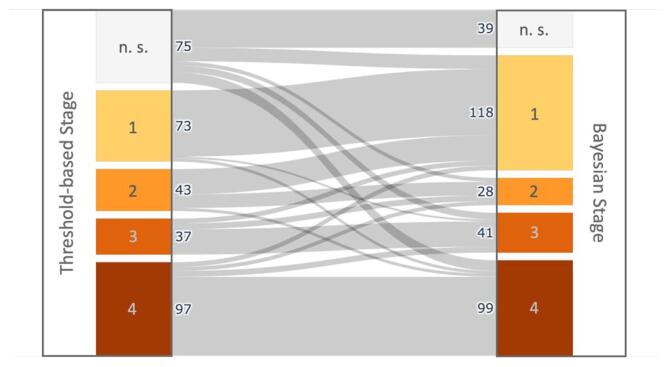
After implementing the Bayesian multi-stage classifier (Eqs. (3), (4)), 88% of the ALS patients could be assigned to a DTI stage. In comparison, only 77% of the ALS patients could be assigned using the threshold-based method. The detailed distribution of patients across the stages is shown in Fig. 3 for both staging approaches. 229 patients showed no difference in their stage association between the two classification methods. Out of the 75 patients who could not be classified using the threshold method, Bayesian staging could be used to assign 14 of them to Stage 1, 4 to Stage 2, 7 to Stage 3, and 11 to Stage 4. The margin of confidence for the Bayesian classifications ranged from < 0.001% to 75.7%.

Fig. 3.

Number of patients with amyotrophic lateral sclerosis (ALS) in each DTI stage. Staging categorization was performed for 325 patients using the established threshold-based method and the Bayesian classifier. Patients who could not be classified into one of the four DTI stages are categorized as ‘not stageable’ (‘n. s.’).

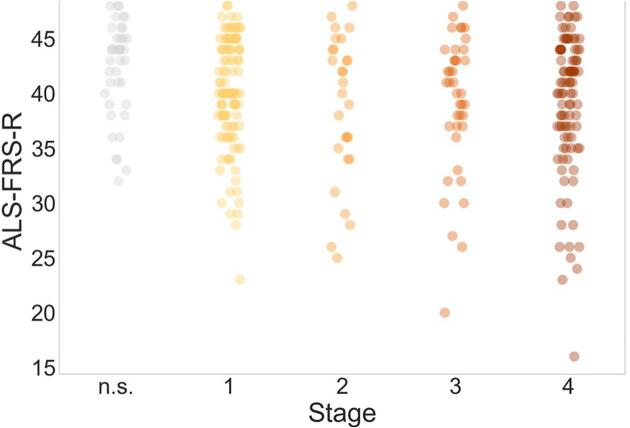
Disease duration and ALS-FRS-R did not differ between patients in different DTI stages. For the ALS-FRS-R, however, a trend for a lower score at higher stages could be identified (Fig. 4). An analysis of MiToS and King’s staging of the patients in the different DTI stages also did not show a significant association between the clinical staging and the DTI-based staging (see Supplementary Material Table S1).

Fig. 4.

Revised ALS functional rating score (ALS-FRS-R) of patients with ALS in different stages as classified according to tract-based Bayesian classification. Patients who could not be classified into one of the four DTI stages are categorized as ‘not stageable’ (‘n.s.’). ALS = Amyotrophic Lateral Sclerosis, DTI = Diffusion Tensor Imaging.

4. Discussion

It could be shown how a Bayesian classifier for a multivariate setting with several staging alternatives can be developed and used to classify ALS patients into in vivo DTI stages based on their diffusion metrics in the sequentially involved tract systems. The algorithm evaluated the posterior probabilities for each stage based on likelihoods of altered or non-altered FA values in the tract systems involved or not involved according to the respective disease stage. The development of a multi-variable Bayesian prediction algorithm has shown that it is possible to obtain probability statements about the impairment of stage-defining tract systems and the staging categorization itself at an individual level for ALS patients in accordance with the sequential involvement of the tract systems during the course of the disease. The transition from fixed ‘either-or‘ decisions to probability statements represents a substantial improvement in the DTI staging approach. Compared to the threshold-based staging method, the new Bayesian multistage classifier reduced the number of not-stageable patients by half. Comparison of the classification of patients using both classification methods (Fig. 3) showed that for most patients, the classification remained the same. Also, the tract-wise comparison of the threshold with the FA values for equal posterior probabilities (Fig. 2) suggests that Bayesian classification should be seen as an extension and improvement of the previous threshold-based approach but does not invalidate it. These advantages of the multivariate Bayesian classification support the use of machine learning approaches to interpret and categorize imaging data at the single-patient level in ALS (Meier et al., 2020, Bede et al., 2022).

Another advantage of the Bayesian approach over a threshold-based classification is the availability of probability statements for each stage, and, therefore, a measure of confidence for each classification. The threshold-based approach cannot provide any information about how certain a specific classification is, although due to the uncertainty of an observed value, misclassification could occur, especially for values in whose measurement uncertainty the threshold lies. Due to the higher information content compared to the threshold method, the Bayesian classification of a given patient into a stage can be evaluated differently. For example, if the certainty is low, the DTI measurement could be repeated to obtain more confidence in the staging classification or unnecessary tests could be avoided if the classification is certain. As a quantitative measure, FA values are subject to a certain degree of uncertainty (Tanno et al., 2021) and while the inclusion of such measurement uncertainty at the individual level is not possible with the threshold-based method, the Bayesian classifier could be extended accordingly (Qin et al., 2011).

The prior probabilities within the Bayesian staging algorithm correspond to the probability for the stages prior to DTI and provide the opportunity to incorporate existing knowledge about a patient, e.g., prevalence or previous test results. Additional specifications of the prior probabilities might further reduce the number of not stageable patients; other measures that are associated with disease progression, such as performance in cognitive tests (Lulé et al., 2018), could be used to estimate prior probabilities and to assess disease progression in a multimodal approach. Such a combination of factors would be consistent with the natural decision-making process of physicians (Gill et al., 2005) and might help to enhance the potential role of DTI-based MRI as a biomarker in ALS (Baek et al., 2020, Kalra et al., 2020).

Given the disease’s clinical heterogeneity, it is not surprising that a higher DTI stage was not associated with higher disease duration. The DTI staging approach in general assesses only the ALS-associated neuropathological changes in the brain according to the proposed propagation pattern (Brettschneider et al., 2013), which can only be reflected to a limited extent by assessing functionality with the ALS-FRS-S and clinical MiToS and King’s staging, given that many clinical deficits and dysfunctions are determined by the degeneration of the second motor neuron.

This study is not without limitations. The likelihoods were assumed to be normally distributed with equal standard deviations for altered and normal FA values in each tract system. In tract systems affected during the disease, the standard deviation of FA values could be higher since the FA values decrease continuously during the course. The patients’ ALS stages were not confirmed by post-mortem examination; calculation of the likelihoods based on autopsy-confirmed data could improve the confidence of the classifications.

In summary, we demonstrated how Bayesian statistics can be used to design an algorithm that improves the in vivo classification of ALS patients into a neuropathological stage according to the sequential scheme of disease progression. In addition to classification, confidence statements can be made about the stage categorization itself at the individual level. This approach could be a further step ahead to form a basis for combining DTI with other modalities to stratify MRI data according to the neuropathological stages in vivo and thus could improve the accuracy of DTI-based imaging biomarkers in ALS.

CRediT authorship contribution statement

Anna Behler: Formal analysis, Investigation, Visualization, Writing – original draft. Hans-Peter Müller: Formal analysis, Investigation, Software, Supervision, Writing – original draft. Albert C. Ludolph: Investigation, Writing – review & editing. Dorothée Lulé: Data curation, Formal analysis, Writing – review & editing. Jan Kassubek: Project administration, Conceptualization, Supervision, Investigation, Writing – original draft.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following are the Supplementary data to this article: