Pathologic mechanobiological interactions between red blood cells and endothelial cells directly induce vasculopathy in iron deficiency anemia

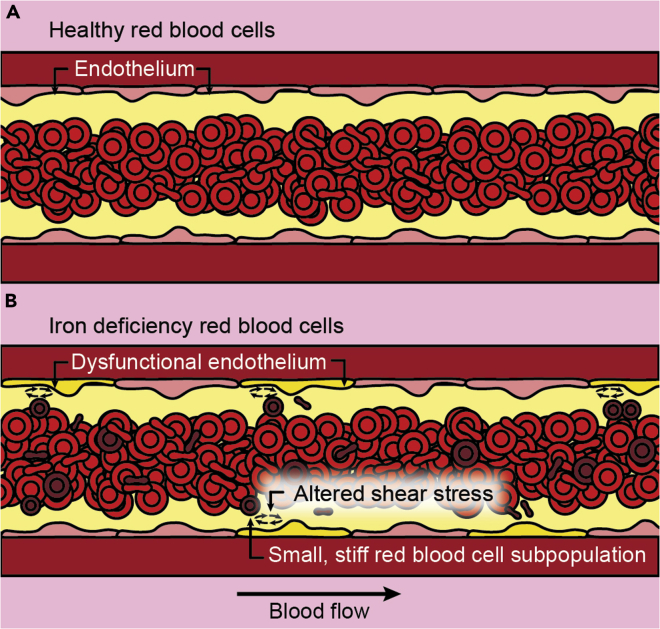
Summary

The correlation between cardiovascular disease and iron deficiency anemia (IDA) is well documented but poorly understood. Using a multi-disciplinary approach, we explore the hypothesis that the biophysical alterations of red blood cells (RBCs) in IDA, such as variable degrees of microcytosis and decreased deformability may directly induce endothelial dysfunction via mechanobiological mechanisms. Using a combination of atomic force microscopy and microfluidics, we observed that subpopulations of IDA RBCs (idRBCs) are significantly stiffer and smaller than both healthy RBCs and the remaining idRBC population. Furthermore, computational simulations demonstrated that the smaller and stiffer idRBC subpopulations marginate toward the vessel wall causing aberrant shear stresses. This leads to increased vascular inflammation as confirmed with perfusion of idRBCs into our “endothelialized” microfluidic systems. Overall, our multifaceted approach demonstrates that the altered biophysical properties of idRBCs directly lead to vasculopathy, suggesting that the IDA and cardiovascular disease association extends beyond correlation and into causation.

Graphical abstract

Highlights

• •Subpopulations of stiff and small red blood cells (RBCs) exist in iron deficiency anemia (IDA)
• •Small and stiff cells marginate toward vessel walls, causing aberrant shear stress
• •Increased cell margination leads to increased vascular inflammation in vitro
• •Altered biophysical properties of iron-deficient RBCs induce vasculopathy

Mechanobiology; Disease; Biological sciences; Human Physiology; Cell biology; Biophysics

Introduction

Anemia, a condition in which the number of RBCs or the hemoglobin concentration within them is lower than normal, affects over two billion people of all ages worldwide. IDA, or anemia caused by low iron stores, is defined as blood iron levels of <10 μmol/L or blood ferritin levels of <10 μg/L and accounts for over 50% of all cases of anemia (Kassebaum et al., 2014; Lopez et al., 2016). Morphologically, IDA RBCs (idRBCs) appear smaller, paler, and have more variability in size and shape in comparison to healthy RBCs. Iron not only plays a critical role in erythropoiesis but is crucial to many organ systems including the CNS, immune system, and cardiovascular system (von Haehling et al., 2015). IDA has been linked to poor cognitive and motor development in infants and young children (McCann and Ames, 2007) and adverse outcomes in individuals with cardiovascular disease, with recent work looking at the role of iron supplementation in those with heart failure, coronary artery disease, and pulmonary hypertension. In patients diagnosed with acute heart failure, iron deficiency was linked to both increased in-hospital and 12-month mortality rates (Jankowska et al., 2014). A link between IDA and increased mortality was also seen in individuals with moderate to severe aortic stenosis (Ng et al., 2015). Iron deficiency was found to be associated with pulmonary hypertension exacerbations; however, intravenous (IV) iron infusion helped prevent the increased acute hypoxic pulmonary vasoconstrictive response normally induced by pre-exposure to hypoxia (Rhodes et al., 2011). Studies have also shown that the treatment of patients with iron-deficient heart failure with IV iron resulted in improvement in symptoms, functional capacity, and quality of life (Ponikowski et al., 2015). More recent studies continue to show improved outcomes when IDA is corrected with iron supplementation in cardiovascular disease (Zhou et al., 2019); however, the underlying pathophysiologic basis for the association remains unknown. Although cardiovascular disease and other chronic diseases are definitively associated with underlying inflammation and iron deficiency, is it possible that idRBCs actually play a causal role in inflammation and vasculopathy?

Here we explored the hypothesis that the biophysical alterations of idRBCs may, in and of themselves, directly induce endothelial inflammation. This hypothesis comprises several specific questions: (1) while idRBCs are known in general to be microcytic (smaller in size than healthy RBCs) and increased in stiffness, how heterogeneous are these cellular biophysical properties? (2) How do idRBC microcytosis and increased stiffness correlate, if at all? (3) How do idRBC microcytosis and increased stiffness affect RBC margination towards the vessel wall and the local shear stresses thereof? (4) If aberrant RBC margination does occur in IDA, what are the mechanobiological consequences on the endothelial cells, if any? To those ends, we leveraged a multi-disciplinary approach involving atomic force microscopy (AFM), microfluidics including “endothelialized” systems, and high-throughput single-cell modeling of patient blood samples to address these questions.

Results

How can the heterogeneity of red blood cell stiffness and shape in iron deficiency anemia be quantified?

Past studies have assessed RBC deformability and stiffness in IDA, but the data have been inconsistent, with some studies finding idRBC deformability to be decreased (Yip et al., 1983; Anderson et al., 2000; Vayá et al., 2005), increased (Reinhart, 1992; Izzo et al., 1999), or unchanged (Reinhart, 1992). A multitude of methods can be used to quantify the deformability of RBCs, likely contributing to some of the variability across these studies. Ektacytometry can offer bulk analysis but cannot accurately capture deformability at the single-cell level (Sosa et al., 2014). Atomic force microscopy (AFM) can assess mechanical variations at the single-cell level; however, it is a low-throughput technique yielding measurements that would not necessarily be representative of an entire RBC population (Costa, 2003). Microfluidic devices that mimic the microvascular environment allow for single RBC deformability measurements by utilizing transit time, or the time it takes a cell to pass through a channel with a diameter even smaller than the cell (Hoelzle et al., 2014). Although high-throughput measurements initially proved problematic owing to issues with image processing inaccuracy, recent work has shown that coupling microfluidic technology with accurate image-processing software is both feasible and can generate robust RBC deformability analysis across a range of hematologic conditions (Guruprasad et al., 2019). Here we ask: can coupling single-cell biophysical techniques such as AFM and microfluidics definitively determine whether idRBCs are less deformable than healthy RBCs and how heterogeneous that phenomena may be?

Atomic force microscopy identifies idRBC subpopulations of increased cell stiffness and decreased cell size

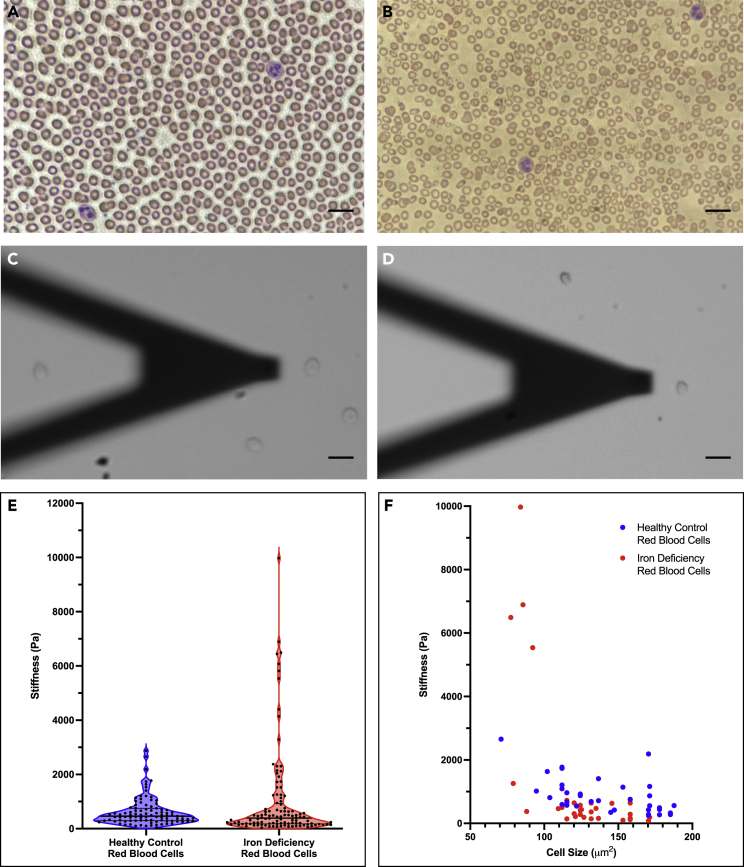
In order to assess mechanical variations between healthy RBCs and idRBCs at the single-cell level, AFM was performed on isolated RBCs from three healthy control and three patients with IDA (Figures 1A and 1B) (www.github.com/nstone8/pyrtz). In total, 95 control RBCs and 112 idRBCs were probed and analyzed (Figures 1C and 1D). idRBCs were found to have a higher mean stiffness than control RBCs, 1024 ± 1715 Pa compared to 616.6 ± 517.8 Pa, respectively. idRBCs also had a higher 75^th percentile stiffness value than control RBCs (931.3 Pa compared to 750.8 Pa, respectively). Despite this, the 25^th percentile and median stiffness values were lower in idRBCs than in their healthy RBC counterparts (176.9, 388.3 Pa) and (292.3, 460.7 Pa), respectively (Figure 1E). What accounts for this apparent discrepancy is a small subpopulation (9% of analyzed cells) of very stiff idRBCs, all with a stiffness of greater than 3000 Pa, greater than the stiffest of all control RBCs. The difference in stiffness between groups was found to be statistically significant (p < 0.05).

Figure 1.

Quantification of iron deficiency red blood cell (idRBC) stiffness and size via atomic force microscopy (AFM) identifies significant biophysical heterogeneity

(A and B) Peripheral blood smears were viewed at 40x magnification from a healthy control subject (A) and a patient with iron deficiency anemia (IDA) (B). The RBCs from the healthy control are uniform in appearance and normal in size, color, and morphology. Comparatively, the IDA patient’s RBCs exhibit the classic findings of IDA, including small size (microcytic), pale color (hypochromic), and an increased variation in cell size and shape (elevated red cell distribution width (RDW)). Abnormally shaped RBCs, such as elongated cells referred to as “pencil cells” are also present.

(C and D) Brightfield microscopy images were taken during AFM prior to cell stiffness measurements of a typical healthy control RBC (C) and an idRBC (D). The cantilever probe can be seen with the cell about to be analyzed with the end of the probe. A total of 95 healthy control RBCs and 112 idRBCs were probed and analyzed. The healthy control RBC seen in (C) exhibited a stiffness of 758.99 Pa and a pixel area of 158 μm². The idRBC in (D) had a measured stiffness of 1259.67 Pa with a pixel area of 79 μm².

(E) Violin plot from our AFM experiments showing stiffness results (measured in pascal (Pa)) of healthy control RBCs (blue) and idRBCs (red). Although idRBCs had a higher mean and 75^th percentile stiffness value than control RBCs, the 25^th percentile and median values were lower in the idRBCs than control RBCs. The higher mean observed in the idRBCs occurs because of a small subpopulation (9% of total cells) of very stiff idRBCs measuring >3000 Pa.

(F) Scatterplot of cell size (x axis) versus stiffness (y axis) of healthy control RBCs (blue) and idRBCs (red) from one AFM experiment. idRBCs were smaller than control RBCs, and 13% of the stiffest idRBCs were also some of the smallest. Scale bars are equal to 20 μm.

Using the microscopy images of each individual RBC obtained during one AFM experiment (1 healthy control and one patient with IDA), we were able to generate an approximate cell size (μm²) to determine if there was any correlation between cell size and membrane stiffness (Figure 1F). Overall, idRBCs were smaller than their healthy counterparts, with a mean cell size of 125.27 ± 26.38 μm² compared to 141.67 ± 31.33 μm², which is expected given a hallmark of IDA is microcytosis. This difference was statistically significant (p < 0.05). Interestingly, for this AFM experiment, the 13% of idRBCs that were the least deformable (i.e., the stiffest) were also some of the smallest cells, having a cell size between 77.4 and 92.2 μm², with only two other cells smaller than any of the 13%. These findings, in which a subpopulation of idRBCs is significantly smaller and less deformable than the overall population of idRBCs as well as healthy RBCs, are in support of our computational and endothelialized microfluidic experiments discussed later.

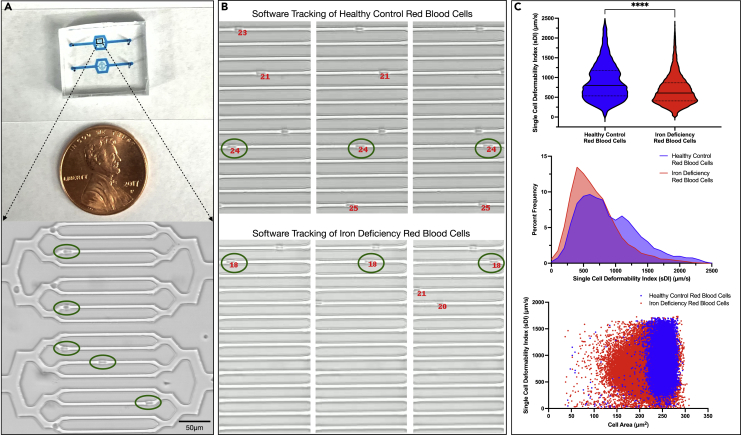
High-throughput microfluidic experiments complement atomic force microscopy in the detection and quantification of idRBC subpopulations of decreased cell deformability and size

RBCs from 10 IDA patient samples and corresponding healthy controls were isolated and perfused through our single-cell microfluidic device designed to mimic a capillary bed (Figure 2A) and paired with our custom hematology microscopy assay analysis software (www.github.com/iCLOTS) (Figure 2B), to obtain a single-cell deformability index (sDI), defined as the cellular tracking velocity (in μm/s) of a cell through a microchannel, for each RBC. The sDI is used as a surrogate for RBC deformability, meaning more deformable cells exhibit a relatively higher velocity and less deformable cells a relatively lower velocity. In total, a unique sDI and a corresponding cell size were obtained for over 10,000 healthy control RBCs and 30,000 idRBCs. idRBCs were found to have a slower mean sDI (678.6 ± 371.2 μm/s) and median sDI (607.3 μm/s) than healthy control RBCs (890.9 ± 461.5 μm/s and 800.4 μm/s, respectively), indicating the overall population of idRBCs are less deformable than healthy RBCs. The difference in the overall mean was statistically significant between healthy control RBCs and idRBCs (p < 0.0001). Furthermore, histogram plots of healthy control RBCs versus idRBCs revealed a “left shift” in the idRBC population, which had both a subpopulation of slow, poorly deformable RBCs and lacked a subpopulation of the most deformable RBCs observed in healthy control RBCs (Figure 2C).

Figure 2.

High-throughput microfluidic single-cell deformability experiments complement AFM in the quantification of RBC deformability and size

(A) Macroscopic view (top) of our single-cell microfluidic device designed to mimic the capillary bed, with a brightfield microscopy image (bottom) of the region of interest of the microfluidic device at 20x magnification. RBCs can be seen transversing the microchannels and are circled in green. The smallest channels are approximately 5.9 μm in diameter, allowing only one cell to transverse the channel at a time. The cellular transit velocity is used as a surrogate for RBC deformability (i.e., more deformable cells exhibit a relatively higher velocity, less deformable cells exhibit a relatively lower velocity).

(B) Select images from our custom hematology microscopy assay analysis software showing a representative healthy control RBC labeled “24” (top) and an idRBC labeled “18” (bottom) being tracked across various frames. A single-cell deformability index (sDI), defined as the cellular transit velocity (in μm/s) of a cell through a microchannel, was then calculated for each tracked cell. Control RBC 24 was present for three total frames and “traveled” a total of 122.24 μm in 0.08 s for an sDI of 1528 μm/s. idRBC 18 was present for six total frames and traveled 145.09 μm in 0.2 s for an sDI of 725.4 μm/s. Cell size of each RBC was also recorded by the software prior to the cell’s entry into the smallest microfluidic channel.

(C) Cumulative graphical analyses from 10 patients with IDA and corresponding healthy controls. sDI measurements for >10,000 healthy control RBCs (blue) and 30,000 idRBCs (red) were obtained, and idRBCs were found to have slower mean and median sDIs than control RBCs (p < 0.0001). Histogram plots (middle) showed that idRBCs demonstrate a “left shift” compared to control RBCs, meaning there is an idRBC subpopulation of slow, poorly deformable RBCs. Additionally, idRBCs lacked a subpopulation of highly deformable RBCs observed in the control RBCs. Finally, a “flow cytometry-like” scatterplot of RBC size versus sDI (bottom) reveals an increased variability in cell size for idRBCs, consistent with the elevated RDW observed in patients with IDA as well as a significantly stiff (low sDI) subpopulation of relatively microcytic (smaller) idRBCs, which is consistent with the lower throughput, but more direct idRBC AFM stiffness measurements in Figure 1. Scale bar is equal to 50 μm.

Similar to our AFM data, idRBCs were found to be smaller than healthy control RBCs, with a mean area of 213.85 μm² ± 32.55 and 252.0 μm² ± 18.21, respectively. This difference was statistically significant (p < 0.0001). Additionally, when plotting RBC cell size versus sDI for the healthy control RBCs and idRBCs (Figure 2C, bottom graph), the increased variability of cell size within the idRBC group became apparent; while the first through 99^th percentiles for cell size in healthy RBCs only varied by an area of 76.9 μm², the idRBCs had a 2-fold higher area range (153.4 μm²) across the same percentiles. This is consistent with the elevated red cell distribution width (RDW) which is classically observed in patients with IDA. A significantly stiff (low sDI) subpopulation of relatively microcytic (smaller) idRBCs was also seen, which is consistent with the lower throughput, but more direct idRBC AFM stiffness measurements in Figure 1.

How do idRBC microcytosis and increased stiffness affect red blood cell margination toward the vessel wall and the local shear stresses thereof?

How idRBCs interact with the endothelium and whether such interactions can cause vasculopathy remain unknown. Can computational models and in vitro modalities be leveraged to address such questions? RBCs are known to migrate toward the center of blood vessels leaving an RBC-depleted cell-free layer (CFL) near vessel walls. White blood cells and platelets tend to reside in these layers, a flow-induced segregation phenomenon known as margination (Firrell and Lipowsky, 1989; Tangelder et al., 1985; Bishop et al., 2002). A growing understanding of this process is emerging with the help of computational modeling (Kumar and Graham, 2011; Rivera et al., 2015), but much remains unknown about its dependence on various parameters of blood flow or the role it plays in various diseases.

Cellular properties such as shape, size, and deformability all contribute to the segregation of the various cell types during blood flow. In the past decade, numerous computational models have been made using direct simulations to understand the individual roles of a host of physical properties on segregation behavior and margination in suspensions designed to mimic physiologic blood flow. In one such simulation focused on the effect of rigidity in a suspension containing both deformable and stiff capsules, the stiff capsules displayed substantial margination when they were the minority component, while the flexible majority remained in the center of the channel (Tangelder et al., 1985). Additionally, in a mixture of large and small capsules, the smaller capsules were found to marginate while the larger ones did not (Kumar et al., 2014). Margination may be of particular importance in hematologic disorders such as sickle cell disease (SCD). Chronic sickle vasculopathy, in which the endothelial cells lining blood vessels are dysfunctional and in a pro-inflammatory state, is a common and important complication of SCD. Sickled RBCs are both smaller and stiffer than healthy RBCs, and recent simulations showed that these sickled RBCs, indeed, strongly marginate toward channel walls, generating large fluctuations in local wall shear stress (Zhang et al., 2020). Given the success in modeling blood flow in other hematologic disorders, here we leverage high-throughput, single-cell computational models to aid in our understanding of how the biophysical RBC alterations in IDA affect their margination and flow patterns within the circulation.

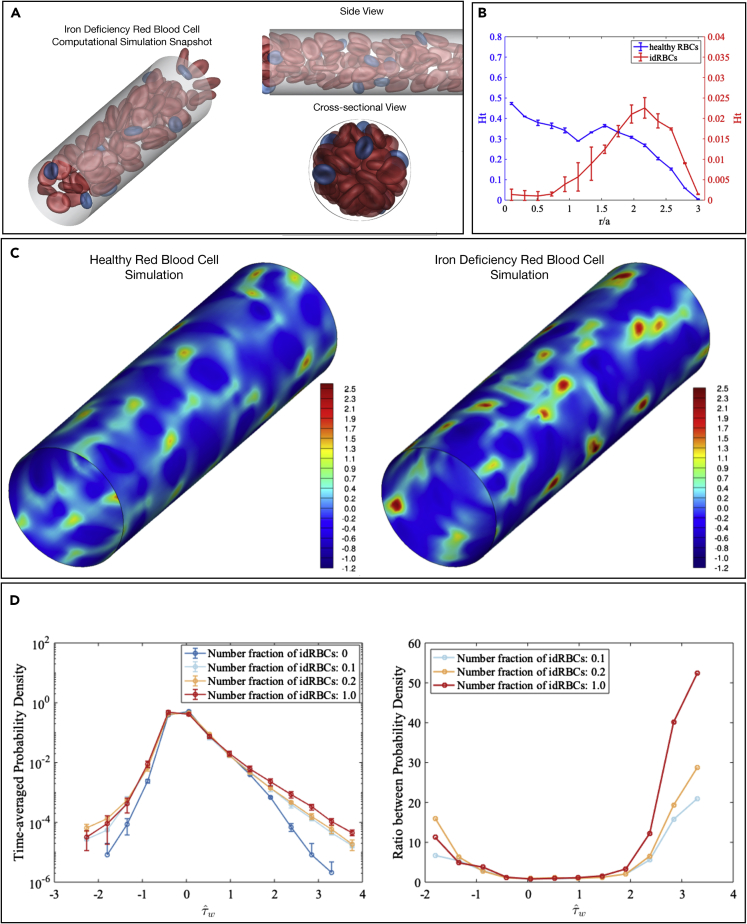
idRBCs demonstrate increased margination and local wall shear stress fluctuations in computational simulations

Computational simulations were created for four types of RBC suspensions, including one uniform suspension containing only healthy RBCs, one uniform suspension of only stiff idRBCs, and two binary suspensions of healthy RBCs (the “primary” component, denoted as “p”) with stiff idRBCs (the “trace” component, denoted as “t”), in which the number fraction of stiff idRBCs was 0.1 and 0.2, respectively. As shown in our experimental data described in Figures 1 and 2, stiff idRBCs have the same shape but a smaller radius and decreased deformability in comparison to healthy RBCs, which we integrated into our simulations (Figure 3A). Compared with the uniform suspension of healthy RBCs, these two binary suspensions have the same overall hematocrit φ ≈ 0.20, while the pure idRBCs suspension has the same cell-number density as the healthy cell suspension, but smaller overall hematocrit φ ≈ 0.09,because the idRBC cells are smaller than healthy cells. In reality, an idRBC population exhibits a range in cell stiffness (normal to increased) and size (normal to microcytic), but for the purposes of these simulations, “idRBCs” comprise only the microcytic and stiff subpopulation to allow for tracking the margination of that RBC subpopulation and the subsequent shear stresses those cells induce at the vessel wall. Suspensions were subjected to unidirectional flow in a rigid tube and run for an adequate amount of time to reach a statistical steady-state distribution of cells in the radial directions in the tube. To measure this distribution, the root-mean-square (RMS) distance of each cell from the center of the channel was calculated using the equation $s={\left(r_{cm}^2\right)}^{1/2}/a$, where r_cm is the center-of-mass position of a cell in the radial direction and angle brackets denote averaging over the cells in the system. It was found that at the beginning of the simulations, s decreased for healthy RBCs while increasing for idRBCs until reaching a plateau at S_p ≈ 1.7 and S_t ≈ 2.1, respectively, suggesting a segregation behavior within the binary suspension; on average the small and stiff idRBCs are much closer to the walls than larger and more deformable healthy RBCs.

Figure 3.

idRBC Subpopulations of increased stiffness and smaller size demonstrate increased margination and local wall shear stress fluctuations in computational simulations

(A) Angled (left) with side and cross-sectional (right) views of snapshots taken from a computational simulation of a binary suspension of RBCs with a majority population of large and deformable healthy RBCs (red) with a minority population of smaller and less deformable idRBCs (blue). This suspension is designed to mimic the heterogeneity observed in IDA and was then compared to a uniform suspension containing only healthy RBCs. In reality, an idRBC population exhibits a range in cell stiffness (normal to increased) and size (normal to microcytic), but for the purposes of these simulations, “idRBCs” comprise only the microcytic and stiff subpopulation to allow for tracking the margination of that RBC subpopulation and the subsequent shear stresses those cells induce at the vessel wall.

(B) Steady-state radial hematocrit profiles (Ht) for healthy RBCs (blue) and idRBCs (red). The x axis depicts distance from the center of the channel scaled with the radius of a healthy RBC, with 0 being the center of the channel and 3.1 representing the channel walls. idRBCs significantly marginate and travel in higher percentages close to channel walls, whereas RBCs of normal size and stiffness concentrate around the center of the channel.

(C) Snapshot of the spatial distribution of additional wall shear stress $\left({\widehat{\text{τ}}}_{\text{w}}\right)$ induced by healthy RBC (left) and idRBC (right) suspensions, respectively. Red regions indicate large fluctuations and are more numerous in the presence of idRBCs.

(D) Probability density (left) of excess wall shear stress induced by healthy RBCs only (blue), the binary suspensions with the number fraction of idRBCs being 0.1 (light blue) and 0.2 (yellow), and idRBCs only (red). The idRBC suspension created excess large fluctuations in wall shear stress in comparison to the healthy RBCs. The ratio between probability densities (right) show that large positive fluctuations in wall shear stress are an order of magnitude more likely in the presence of idRBCs than without them, meaning that even a small number of idRBCs can create a high relative probability of large stress fluctuations.

The segregation behavior is further illustrated in Figure 3B, where the steady-state radial hematocrit profiles (Ht) for healthy RBCs and idRBCs in the binary suspension with idRBC number fraction 0.1 are shown. The horizontal axis depicts the distance from the center of the channel scaled with the radius of a healthy RBC, with 0 being the center of the channel and 3.1 representing the channel walls. idRBCs were found to strongly marginate and travel in higher percentages close to channel walls, whereas healthy RBCs tend to concentrate around the center of the channel. This margination behavior is also illustrated in the simulation snapshots (Figure 3A), demonstrating that differences in size and deformability are sufficient to drive segregation behavior within this computational system.

To characterize the hydrodynamic effects of the cell distribution on the blood vessel wall, we computed the wall shear stress for the four types of RBC suspensions mentioned above, in which the number fraction of idRBCs varies from 0, 0.1, 0.2, to 1, correspondingly. Figure 3C depicts a snapshot of the spatial distribution of additional wall shear stress $\left({\hat{\tau }}_w\right)$ induced by the healthy RBC suspension (left) and the binary suspension with idRBC number fraction 0.1 (right), respectively. The red regions indicate large fluctuations of wall shear stress, which are more numerous in the presence of idRBCs and arise at positions corresponding to a near-wall idRBC interaction. These differences are further quantified in Figure 3D, which shows the probability density function (PDF) of excess wall shear stress in these four cases. The two cases with idRBC number fractions of 0.1 and 0.2 demonstrate a disproportionate excess of large wall shear stress fluctuations, which is attributable to the margination of these small and stiff cells toward the vessel wall. Figure 3D also shows the ratio between these probability densities (right graph), highlighting that large positive fluctuations in wall shear stress are an order of magnitude more likely in the presence of idRBCs than in their absence. Thus, even for these cases where the relative number of idRBCs is small, the relative probability of large stress fluctuations is quite large.

Finally, Figure 3D also shows the PDF of excess wall shear stress for the pure idRBC suspension. Here the probability of high wall shear stress is higher than in the other cases, indicating that increased overall cell stiffness leads, as expected, to increased additional wall shear stress fluctuations. Nevertheless, the increase in the high shear stress “tail” of the PDF is only about a factor of two over that of the cases where the idRBCS are dilute, while the increase of those cases over the pure healthy RBC suspension approaches an order of magnitude. For the binary suspensions in which the relative number of idRBCs is small (0.1 and 0.2), the margination of idRBCs is, therefore, the principal mechanism to promote idRBC-induced wall shear stress fluctuations.

How does the aberrant margination of idRBCs and the pathologic local wall shear stresses thereof affect the mechanobiology of endothelial cells?

While computational models have demonstrated alteration in blood flow can cause local increases in wall shear stress, cardiovascular bioengineering research has definitively demonstrated that endothelial cells mechanotransduce biophysical cues, such as the shear forces of the hemodynamic microenvironment, into cellular biological signals (Abe and Berk, 2014; Chien, 2007). Additionally, pathological alteration of those forces leads to the activation of pro-inflammatory signals within endothelial cells including the upregulation of VCAM-1, ICAM-1, and E-selectin and the subsequent development of atherosclerotic plaques in situ that are prone to myocardial infarction and stroke (Abe and Berk, 2014). By leveraging endothelialized microfluidics and computational models, endothelial mechanobiology can be studied in vitro. Microfluidic models of the microvasculature comprised of endothelial cells that are cultured throughout the entire 3-dimensional surface of a standard microfluidic system have demonstrated that the hemodynamic conditions recapitulate those of the microvasculature in vivo, endothelial cells are functional, and they appropriately express VE-cadherin at cellular junctions and nitric oxide (Myers et al., 2012). Here we leverage in vitro endothelialized microfluidic devices to develop a more comprehensive understanding of the physiologic implications of IDA on the body.

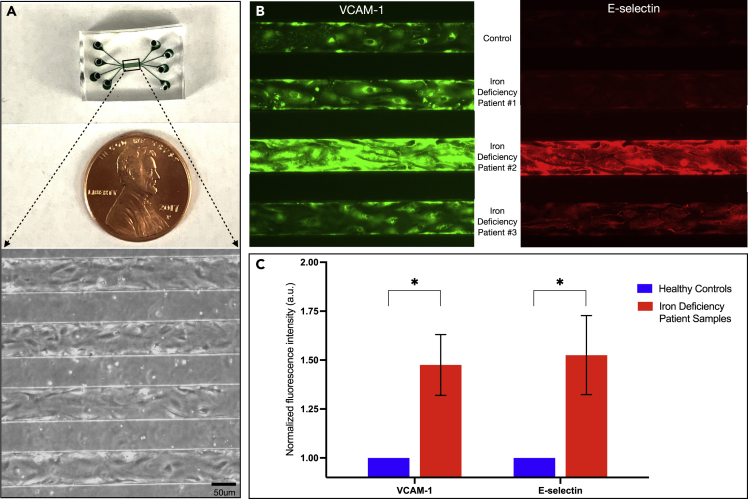
idRBCs induce vascular inflammation in “endothelialized” microfluidic devices

RBCs from five IDA patient samples and five corresponding healthy controls were isolated and resuspended in media to a hematocrit of 25%, simulating a hematocrit observed in patients with IDA, and perfused into individual channels in a straight-channel microfluidic device endothelialized to confluence with human umbilical vein endothelial cells (HUVECs) for 4 h (Figure 4A). Devices were then fixed, permeabilized, and immunostained with antibodies against VCAM-1 and E-selectin, known markers of endothelial inflammation (Figure 4B). Florescence intensity was quantified and normalized mean fluorescence intensity was then calculated (endothelium exposed to healthy control RBCs normalized to 1). Endothelium exposed to idRBCs exhibited increased expression of both VCAM-1 (1.45 ± 0.155 SEM normalized fluorescence intensity) and E-selectin (1.52 ± 0.20 SEM normalized fluorescence intensity) over endothelium exposed to healthy RBCs (Figure 4C). The difference in both VCAM-1 and E-selectin expression was statistically significant (p < 0.05). These findings experimentally confirm what was observed in the computational simulations, that increased, pathologic idRBC-endothelial cell interactions at the vessel walls occur in the setting of IDA directly leading to increased inflammation via mechanobiological mechanisms. Given that altered shear stress is known to incite pro-inflammatory signaling within endothelial cells leading to atherosclerotic lesions in cardiovascular disease (Abe and Berk, 2014; Simmons et al., 2016), the importance of such findings cannot be understated.

Figure 4.

idRBCs induce vascular inflammation in “Endothelialized” microfluidic devices

(A) Macroscopic view (top) and brightfield microscopy image (bottom) at 10x magnification of a straight, 4-channel microfluidic device endothelialized to confluence with human umbilical vein endothelial cells. The microchannels are 50 μm in height by 100 μm wide, mimicking large venules.

(B) Endothelial VCAM-1 (green) and E-selectin (red) expression in the 4-channel device after 4 h perfusion of healthy control RBCs versus idRBCs from 3 separate patients with IDA. All RBC suspensions were diluted in media to a hematocrit of 25% and perfused at a constant venular shear rate.

(C) Mean normalized fluorescence intensity for VCAM-1 (left) and E-selectin (right), both markers of inflammation, in endothelial cells exposed to healthy RBCs (blue) and idRBCs (red). A total of five IDA patient samples and corresponding healthy control RBC samples were analyzed. Increased VCAM-1 and E-selectin expression were observed in all idRBC samples (p < 0.05), experimentally confirming what was observed in the computational simulations, that increased, pathologic idRBC-endothelial cell interactions at the vessel walls occur in the setting of IDA directly leading to increased inflammation via mechanobiological mechanisms. Scale bar is equal to 50 μm. Data are represented as mean ± SEM.

Discussion

Here, we have demonstrated that a multifaceted approach utilizing single-cell modalities such as AFM, computational simulations, and an array of microfluidic models creates a more comprehensive understanding of the role idRBCs play systemically on the microvasculature. To definitively determine the biophysical alterations present in idRBCs, single-cell mechanical variations were analyzed using AFM and coupled with a system utilizing a high-throughput microfluidic device paired with a custom hematologic microassay analysis software to create sDI measurements of thousands of individual RBCs. AFM identified a subpopulation of very small and poorly deformable idRBCs, and our high-throughput microfluidic assay confirmed that idRBCs overall are less deformable, smaller, and are more heterogeneous than healthy RBCs.

Such biophysical alterations serve as the basis of our hypothesis; that changes in the size and deformability of idRBCs are enough to induce endothelial inflammation and dysfunction through margination and localized changes in vascular wall shear stress (Figure 5). Computer simulations were created to explore our hypothesis, comparing a uniform suspension of healthy RBCs with a less homogeneous suspension containing a minority population of small and stiff idRBCs within a majority suspension of normal RBCs that are both larger and more deformable, mimicking the heterogeneity observed in IDA. These simulations showed that the small and stiff RBC subpopulation exhibits increased margination toward channel walls, leading to subsequently increased fluctuations in localized shear stress not apparent in homogeneous suspensions of healthy RBCs. In vitro experiments were performed to confirm the results of these simulations utilizing endothelialized microfluidic models of the microvasculature. Increased VCAM-1 and E-selectin expression was seen in endothelium exposed to idRBCs in comparison to endothelium exposed to healthy RBCs, demonstrating that physical interactions between endothelial cells and idRBCs are sufficient to cause endothelial inflammation.

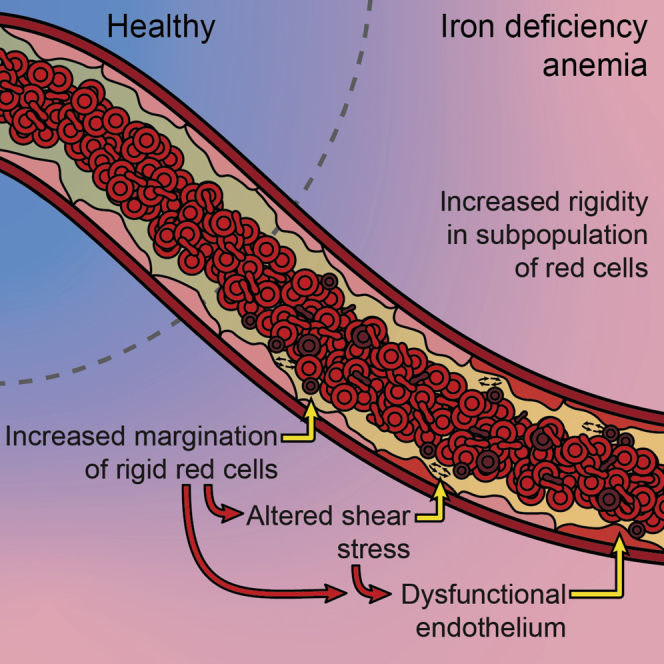
Figure 5.

Biophysical alterations of idRBCs directly induce endothelial inflammation via aberrant margination

Cartoon representation of our hypothesis, showing that when uniform suspensions comprised of healthy RBCs (A) travel through vessels large enough for cells to travel side-by-side cells generally travel in the center of the vessel and have limited direct interactions with the endothelium and vessel walls. When RBC suspensions are not uniform, such as in IDA (B), a subpopulation of the smallest and stiffest idRBCs will tend to marginate closer to vessel walls. These marginating RBCs not only come into direct contact with the endothelium but also create altered local wall shear stress simply from coming into close proximity to the vessel wall, inducing endothelial inflammation via mechanobiological mechanisms.

Previously, idRBCs had not been viewed as pro-inflammatory; iron deficiency in individuals with chronic diseases and underlying vasculopathy was merely viewed as correlative associations. This work demonstrates, for the first time, to the best of our knowledge, that the association between iron deficiency and chronic inflammation may extend past correlation and actually be causative. This could, in turn, lead to a new paradigm in the investigation and treatment of iron deficiency, particularly amongst those with underlying cardiovascular disease or other chronic inflammatory disorders. We still do not understand the exact mechanotransducive pathways affected in the endothelium, and next steps will focus on teasing these out. Additionally, the development of a mouse model to study these processes in vivo could also yield additional valuable insight into the underlying mechanisms at play.

Even in hematologic disorders in which RBCs are known to have altered biophysical properties, such as thalassemia major, RBC margination and RBC-endothelium interactions have not been studied. These results could lead to further investigations across a multitude of hematologic disorders. Finally, the finding that biophysical alterations in RBCs alone are enough to cause endothelial dysfunction raises the question if RBCs are in fact altered in other chronic diseases in which RBCs are not generally viewed as “problematic,” and if so, should similarly work as performed here be proposed in other chronic diseases or inflammatory conditions, such as diabetes mellitus. Given the multifaceted approach leveraged here to address both the RBC and direct RBC-endothelial interactions, potential studies across both hematologic disorders and other chronic diseases are numerous.

Limitations of the study

Although an array of modalities was leveraged to investigate the differences between healthy RBCs and idRBCs, a small total IDA sample size was used (10 IDA samples for high-throughput microfluidic experiments and five IDA samples for endothelialized microfluidic experiments). Although results in these experiments did find statistically significant differences between the groups, additional experiments aimed at increasing the overall sample size could be performed. Additionally, endothelialized microfluidic experiments were performed in just one microfluidic system (i.e., vascular geometry and size were not varied) and using only one endothelial cell type (HUVECs). Future endothelialized microfluidic experiments could be performed in microfluidics of different sizes and geometries as well as with other endothelial cell types from different vascular regions to better quantify changes in endothelial inflammation in vivo. Although straight-channel microfluidics are ideal for understanding margination effects given the simple geometry, microfluidics with different geometrical configurations, such as those with varied channel diameters, curved channels, or bifurcations could allow us to assess localized changes in endothelial inflammation specific to a geometric configuration, such as around a curved vessel or at a branchpoint. Finally, our computer simulations created a binary suspension to mimic IDA containing a majority population of larger and more deformable healthy RBCs mixed with a minority population of smaller and stiffer idRBCs. This is perhaps a simplified model of IDA given what we know about the heterogeneity of idRBCs. Future simulations could address this by creating more complex ternary or quaternary suspensions.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Antibodies
Rabbit monoclonal to VCAM-1	ABCAM	Cat. #Ab134047; RRID: AB_2721053
Mouse monoclonal to E-selectin	Thermo Fisher Scientific	Cat. #MA1-34486; RRID: AB_1955403
Goat anti-mouse IgG secondary Ab, Alexa Fluor 568	Thermo Fisher Scientific	Cat. #A-11031; RRID: AB_144696
Goat anti-rabbit IgG secondary Ab, Alexa Fluor 488	Thermo Fisher Scientific	Cat. #A-11034; RRID: AB_2576217
Biological samples
Healthy adult whole blood	Adult Volunteers	No stored samples or data
Iron deficiency anemia patient whole blood	Emory University School of Medicine Department of Hematopathology	De-identified patient samples in Redcap
Chemicals, peptides, and recombinant proteins
Cell-Tak Cell and Tissue Adhesive	Corning	Cat. # 354240
Sylgard 184 (PDMS)	Ellsworth Adhesives	Cat. # 4019862
Paraformaldehyde 16%	Thermo Fisher Scientific	Cat. # 50-980-487
EGM-2 growth media	Lonza	Cat. #CC-3162
Bovine Serum Albumin	Sigma-Aldrich	Cat. # A7906-50G
Deposited data
Raw and analyzed data	This paper; Mendeley data	[Mendeley]: [https://doi.org/10.17632/gtv74r5zt5.1].
Experimental models: Cell lines
Human umbilical vein endothelial cells (HUVECs)	Lonza	Cat. #CC-2519
Software and algorithms
ImageJ version 1.53a	National Institute of Health	http://imagej.nih.gov/ij
GraphPad Prism version 9.2.0	GraphPad Software	www.graphpad.com
Custom Hematology Analysis Software	The Lam Lab; This paper	www.github.com/iCLOTS
AFM Hertzian contact model	PYTHON	www.github.com/nstone8/pyrtz
Other
EDTA blood collection tubes	Beckton Dickinson	Cat. #367856
Atomic Force Microscopy	Asylum Research	Model: MFP-3D Bio-AFM
AFM Fluorodish	World Precision Instruments	Cat. #FD35-100
Syringes	Beckton Dickinson	Cat. #309628
Syringe Pump	Harvard Apparatus	Cat. #70-3007
Inverted Optical Microscope	Nikon	Model: Eclipse TE2000-U

Resource availability

Lead contact

Further information and requests for resources and reagents should be directed to the lead contact, Wilbur A. Lam (wilbur.lam@emory.edu).

Materials availability

New unique reagents were not generated during this study.

Experimental model and subject details

Acquisition and preparation of blood samples

Consent for all patient blood samples was obtained in accordance with Emory University IRB 105125. Consent for all healthy human blood samples was obtained in accordance with Emory University and Georgia Institute of Technology IRB H15258. Individuals undergoing laboratory evaluation for and who met criteria for IDA (defined as hemoglobin below the normal reference range for age and ferritin <10 ng/mL) had 1 mL of whole blood collected via venous blood draw in ethylenediaminetetraacetic acid (EDTA) phlebotomy tubes (Beckton Dickinson) set aside for this study. IDA patient samples were de-identified of all patient information, and only hemoglobin and ferritin values were disclosed. Samples of blood from healthy male and female adult volunteers were also obtained via venous blood draw in EDTA tubes on the same day as IDA patient samples. Following collection, blood was stored at 4°C until the time of experiments. All AFM experiments were performed less than 24 h from sample collection. Endothelialized microfluidic experiments were performed less than 72 h from sample collection, with an average storage time of 48 h. Single cell deformability experiments were performed less than 120 h from sample collection, with an average storage time of 72 h. To isolate RBCs from other blood components, blood samples were first centrifuged under a low acceleration of 150xg for 15 min, washed with Phosphate Buffered Saline (PBS), and centrifuged at 201xg for 10 min. An additional wash and centrifugation were done to ensure complete isolation of RBCs.

Method details

Atomic force microscopy (AFM)

AFM measurements were performed with a MFP-3D Bio-AFM (Asylum Research). RBCs from both a healthy control and a patient with IDA were attached to the bottom of a Fluorodish (World Precision Instruments) coated with 3.5 μg/cm² CellTak Cell and Tissue Adhesive (Corning). Cells were gently centrifuged to attach to the glass at 300xg for 10 min. A 5.24 μm spherical silica bead was attached to a tipless silicon nitride cantilever (MLCT-D, nominal spring constant k = 0.03 N/m, Bruker Probes) using a two-part epoxy and cured for 48 h. The thermal method (Hutter and Bechhoefer, 1993) was used to calibrate the cantilever spring constant immediately prior to use by indenting the glass bottom of a Fluorodish and performing a Lorentzian fit to the thermal spectrum. The cantilever probe was visually aligned with the RBC center using an integrated inverted optical microscope (Nikon) and translated with a vertical velocity of 2 μm/s to indent the cell with increasing compressive force until a force trigger of 5 nN was reached. One measurement per cell was obtained, and approximately 35 healthy control RBCs and iron deficiency RBCs were probed, respectively. A Hertzian contact model was used to calculate Young’s modulus for stiffness characterization through customized PYTHON code (www.github.com/nstone8/pyrtz). We only used the early contact portion of 10% of the force trigger to calculate the cell stiffness to avoid non-linear stiffening which occurs when a large strain is applied to cells (Xu et al., 2011).

Microfabrication of microfluidic devices

The microfluidic devices used in this paper were made from polydimethylsiloxane (PDMS) (Ellsworth Adhesives) using standard soft lithography techniques (Hoelzle et al., 2015). Master molds of the microvasculature devices were fabricated using SU-8 photoresist patterned onto silicon wafers. PDMS was poured over the master molds and cured at 60°C for at least 2 h. The PDMS devices were removed from the mold and device-appropriate inlet and outlet ports were created by punching holes ranging from 0.75 to 1.5 mm through the inlet and outlet channels of the device. Devices were then plasma-bonded onto clean glass slides and placed at 60°C for at least 1 h prior to use.

The microchannels in the single cell microfluidic device (Figure 2) have dimensions of 5.9 ± 0.08 μm (width) by 13.3 μm (height) and are meant to simulate a capillary bed in vivo, as only 1 cell can transverse each channel at a time. The device contains 64 microcapillary channels, with large bypass channels aimed to prevent flow rate oscillations that can occur from obstruction of any of the microchannels. The microchannels of the straight 4-channel device (Figure 4) are 50 μm (height) by 100 μm (width) and are designed to mimic large venules.

Cell deformability microfluidic experiments

Microfluidic devices were injected and perfused with a 20 mg/mL solution of bovine serum albumin (BSA) (Sigma-Aldrich) in PBS for >30 min at 22°C to prevent non-specific adhesion to the microfluidic channel walls (Schrott et al., 2009). Isolated control RBCs or idRBCs, respectively, were diluted in PBS to a ratio of 1:100, mixtures drawn into 1 mL syringes (Beckton Dickinson) attached to microfluidic tubing, loaded onto syringe pumps (Harvard Apparatus), and infused into the microfluidic devices at a rate of 1 μL/min. Videos were then taken at 20x magnification with an inverted optical microscope (Nikon) at a frame rate of approximately 25 frames per second. The videos were then run through particle tracking software in order to create a single cell deformability index (sDI), defined as the transit velocity (in μm/s) of a cell through a microfluidic channel, for each RBC in the video.

Computational analysis using hematology software

Videos were analyzed using the freely available python module Trackpy (Rose et al., 2020), adapted for use with blood cells within a hematology microscopy assay analysis software developed within our lab (www.github.com/iCLOTS). Trackpy detects particles represented by small image regions with a 2-D Gaussian-like distribution of pixel brightness. A linking algorithm connects individual particles detected across different frames into pathways representing their movement. Our custom software adapts the Trackpy algorithms for use with blood cells in a microfluidic device. Users interactively choose parameters specific to their microscopy data, such as maximum cell diameter and pixel intensity. The software chooses the highest-quality data points by imposing requirements for the number of frames detected and minimum observed distance traveled. Individual cells are labeled with an identification number that corresponds to its characteristics, including sDI and size, in an excel file so that the user can verify data veracity.

Computational model of IDA formulation

We considered a flowing suspension of RBCs, which we modeled as deformable fluid-filled elastic capsules, in a rigid tube with radius R = 12.5 μm (Figure 3). No-slip boundary conditions were imposed on the walls of the tube, while periodic boundary conditions were applied in the axial direction. The suspension was subjected to a unidirectional pressure-driven flow, and the velocity field in the absence of RBCs field is given by the Poiseuille flow result

$$u^{\infty }\left(r,\theta ,z\right)=U_0\left(1-{\left(\frac{r}{R}\right)}^2\right)e_z$$

where U₀ is the undisturbed centerline velocity e_z the unit vector in the axial direction. In this study, the flow was driven by a constant pressure gradient, which is equivalent to fixing the mean wall shear rate at γ_w = 2U₀/R.

For this study, we considered a binary suspension of healthy RBCs (“primary” component, denoted as “p”) and idRBCs (“trace” component, denoted as “t”). A healthy RBC was modeled as a flexible capsule with a biconcave discoidal rest shape with radius α = 4 μm. The idRBCs have the same rest shape as healthy RBCs, except the radius of idRBCs is 0.76a. The cell membranes were modeled as isotropic and hyperelastic surfaces with interfacial shear modulus G, and incorporate shear elasticity, area dilatation, volume conservation, and bending resistance. Sinha and Graham detail the membrane mechanics model and validation against experimental observations (Sinha and Graham, 2015).

The deformability of a capsule in pressure-driven flow was measured by the dimensionless capillary number Ca = ηγ_wa/G. In this study, G of the idRBCs was assumed to be five times that of healthy RBCs, which leads to a Ca_t for idRBCs always around 0.15 times that of Ca_p for healthy RBCs. In this study, Ca_p is set to 1.0 for healthy RBCs and Ca_t is 0.15 for idRBCs, which corresponds to γ_w ∼100 - 1000s^-1 . In the binary suspension, the number fractions for healthy RBCs X_p was set to 0.9 or 0.8 and for idRBCs X_t is 0.1 or 0.2. The total volume fraction of the cells (hematocrit) is φ ≈ 0.20. To simplify the computations in this initial study, the suspending fluid and the fluid inside the cells were assumed to have the same viscosity.

In our simulation, the particle Reynolds number, defined as Re = ργ_wa²/η, was set to 0.05 and the fluid assumed to be incompressible and Newtonian, therefore the flow was governed by the unsteady Stokes and continuity equations. A projection method was used to advance the velocity field in time. The tube was embedded in a cuboidal computational domain with size of 20a×7a×7a and an Eulerian grid of 182 × 64×64 was used. Sample simulations with doubled tube length (40a×7a×7a) and the same mesh spacing were also conducted, to test whether the system considered here is large enough to characterize the hydrodynamics of RBC suspensions. Negligible changes in the results were found. The immersed boundary method (IBM) was used to handle fluid-structure interaction. Specifically, two types of immersed boundaries were considered in the current model: deformable moving cellular membrane as well as rigid non-moving cylindrical walls. The capsule membrane was discretized into N_Δ piecewise flat triangular elements; N_Δp = 1280 for healthy RBCs, while N_{Δt =} 816 for idRBCs. Different N_Δ were chosen to ensure that the triangular elements on both healthy RBCs and idRBCs were close in size. We used “continuous forcing” IBM and “direct forcing” IBM methods for the RBC membranes and tube wall, respectively. Approaches by Balogh and Bagchi (2017) and Mittal et al. (2008) were closely followed for the numerical methodology.

Endothelialized microfluidic experiments

After creating the straight 4-channel microfluidic device designed to mimic large venules (Figure 4), it is “endothelialized” with approximately 1,000,000 cells/mL of human umbilical vein endothelial cells (HUVECs) (Lonza) in endothelial growth media (EGM-2) (Lonza) with 8% dextran. The device is then connected to a syringe and tubing filled with EGM-2 and infused at a volumetric flow rate of 1.25 μL/min at 37°C and 5% CO₂ until a confluent monolayer of endothelial cells is present, which usually occurs after approximately 48 h. When the microfluidic device was endothelialized to confluence, RBCs from healthy controls and idRBCs were isolated, resuspended in media to a hematocrit of 25% to mimic conditions seen in IDA patients, and perfused into separate channels of the microfluidic device for 4 h. After 4 h, the microfluidic device was fixed with 4% paraformaldehyde in PBS, permeabilized, and immunostained with antibodies against VCAM-1 (ABCAM) and E-selectin (Themo Fisher). The microfluidic device was then imaged at 10x magnification using an inverted optical microscope (Nikon), and mean fluorescence intensity was then measured using ImageJ to quantify endothelial inflammation.

Quantification and statistical analysis

All data was analyzed in GraphPad Prism (GraphPad Software). Mean ± standard deviation was presented unless otherwise stated, however depending on the experiment, various additional measurements are reported, including mean with standard error of mean and median. Throughout all experiments, when comparing healthy control RBCs and idRBCs, unpaired t-tests were used, unless results did not fit a Gaussian distribution, in which case a Mann Whitney test was utilized. Unless otherwise stated, p < 0.05 was considered statistically significant.

Published: July 15, 2022

Data and code availability

Original AFM and microfluidic images have been deposited at Mendeley and are publicly available as of the date of publication. The DOI is listed in the key resources table. De-identified patient sample data is stored in RedCAP and can be made available upon request. Microfluidic videos, additional microscopy data, and computational model data reported in this paper will be shared by the lead contact upon request.

All original code has been deposited at Github and is publicly available as of the date of publication. DOIs are listed in the key resources table.

Any additional information necessary for reanalysis of the data reported in this paper is available upon request from the lead contact.