Abstract
Purpose:
Patient motion artifacts present a prevalent challenge to image quality in interventional cone-beam CT (CBCT). We propose a novel reference-free similarity metric (DL-VIF) that leverages the capability of deep convolutional neural networks (CNN) to learn features associated with motion artifacts within realistic anatomical features. DL-VIF aims to address shortcomings of conventional metrics of motion-induced image quality degradation that favor characteristics associated with motion-free images, such as sharpness or piecewise constancy, but lack any awareness of the underlying anatomy, potentially promoting images depicting unrealistic image content. DL-VIF was integrated in an autofocus motion compensation framework to test its performance for motion estimation in interventional CBCT.
Methods:
DL-VIF is a reference-free surrogate for the previously reported Visual Image Fidelity (VIF) metric, computed against a motion-free reference, generated using a CNN trained using simulated motion-corrupted and motion-free CBCT data. Relatively shallow (2-ResBlock) and deep (3-Resblock) CNN architectures were trained and tested to assess sensitivity to motion artifacts and generalizability to unseen anatomy and motion patterns. DL-VIF was integrated into an autofocus framework for rigid motion compensation in head/brain CBCT and assessed in simulation and cadaver studies in comparison to a conventional gradient entropy metric.
Results:
The 2-ResBlock architecture better reflected motion severity and extrapolated to unseen data, whereas 3-ResBlock was found more susceptible to overfitting, limiting its generalizability to unseen scenarios. DL-VIF outperformed gradient entropy in simulation studies (yielding average multi-resolution structural similarity index (SSIM) improvement over uncompensated image of 0.068 and 0.034, respectively, referenced to motion-free images. DL-VIF was also more robust in motion compensation, evidenced by reduced variance in SSIM for various motion patterns (σDL-VIF = 0.008 vs σgradient entropy= 0.019). Similarly, in cadaver studies, DL-VIF demonstrated superior motion compensation compared to gradient entropy (an average SSIM improvement of 0.043 (5%) vs. little improvement and even degradation in SSIM, respectively) and visually improved image quality even in severely motion-corrupted images.
Conclusion:
The studies demonstrated the feasibility of building reference-free similarity metrics for quantification of motion-induced image quality degradation and distortion of anatomical structures in CBCT. DL-VIF provides a reliable surrogate for motion severity, penalizes unrealistic distortions, and presents a valuable new objective function for autofocus motion compensation in CBCT.
1. Introduction
Cone-beam CT (CBCT) has seen increased presence in the interventional suite, providing pre-, intra-, and post-procedural 3D imaging for procedure planning, guidance, and assessment. Robotic C-arm CBCT systems are used in applications spanning from abdominal vascular and soft-tissue interventions,1–3 vascular procedures on extremities,4 emergency hemorrhage control,5,6 to brain/head diagnostic and interventional procedures.7,8 CBCT of the head/brain is integral to a wide variety of imaging scenarios, including brain perfusion, image-guided radiotherapy, stroke diagnosis and treatment guidance, and mechanical thrombectomy.9–12 CBCT provides isotropic spatial resolution but with a number of challenges to image quality, including a moderately long acquisition time (often 4 to 30 seconds) which creates potential for involuntary patient movement. The first and most widespread strategy to address patient motion is to restrict the possible range of motion through immobilization and fixation devices attached to the surface of the head. However, patient immobilization often proves insufficient, with previous studies showing residual motion resulting in noticeable artifacts, shape distortion, and blurring in up to 82.7% of interventional brain CBCT instances,13 with 6.2% of motion-corrupted images exhibiting severe artifacts and structure deformation that rendered images uninterpretable.
Residual motion artifacts can be mitigated with motion compensated reconstruction methods, which integrate an estimation of the patient motion trajectory into the backprojection process to form a motion-compensated CBCT volume.14 Methods to obtain such estimate of the motion trajectory often invoke temporal periodicity assumptions (e.g. respiratory or cardiac periodic cycles), which allow splitting of the projection dataset into discrete motion phases that contribute to individual CBCT volumes with sparse angular sampling. Motion trajectory can then be estimated via 3D-3D registration of the individual volumes.15–17 Further approaches make use of prior periodic motion models extracted from a planning 4D CT.18,19 However, motion trajectories observed in head CBCT present relatively sudden, variable, and non-periodic amplitude transitions, rendering such methods unsuitable.
Previous approaches demonstrated successful compensation of non-periodic motion in head CBCT 20,21 and in extremities CBCT,22 with a combination of skin fiducials and 2D-3D registration. Fiducial-based motion estimation, however, fits poorly with the demanding interventional imaging workflow, and is subject to inaccuracies in the position of the fiducial markers and in the correspondence between the motion of the skin surface and internal structures, particularly so when motion restraining devices (e.g., holding straps) are placed on the patient skin. Fiducial-free, non-periodic, motion estimation was achieved 23,24 by registering a motion-free 3D prior image (CT or CBCT) of the same patient to the acquired 2D projection data. However, those methods rely on the availability of such prior scan, and their performance might be degraded in presence of mismatched image content between the prior CT and the interventional CBCT (e.g., anatomical changes induced by the interventional procedure). Therefore, motion estimation approaches that use solely the motion-contaminated CBCT scan are necessary to remove such requirements. For example, motion estimation can be achieved by simple measures of distance between consecutive projection views 25 or by enforcement of more advanced consistency conditions of the CBCT sinogram data, based on its Fourier properties 26 or its epipolar symmetry.27,28 Consistency based methods present a fairly limited sensitivity to certain motion components (e.g. translations/rotation out of the detector plane) and their applicability is limited to certain acquisition orbits (often variations of simple circular CBCT orbits) and to a field-of-view constrained to the vicinity of the central slice, beyond which most consistency conditions are no longer valid. Further approaches translate the concept of 3D-2D registration with a prior motion-free image to prior-free scenarios involving registration between the motion-corrupted CBCT volume and the projection data.29,30 While those methods removed the necessity for a prior patient model, they pose limitations on the severity of motion, since registration accuracy degrades significantly in presence of strong blurring and distorted anatomy.
Another category of methods draws from the “autofocus” concept, usually applied to optical imaging, to estimate patient motion. Autofocus methods model motion estimation as a numerical optimization problem that finds trajectories maximizing some desired characteristic of motion-free images, such as image sharpness or piecewise constancy. Autofocus-based motion estimation has been successfully applied to CBCT for rigid motion estimation in extremities,31,32 head,7,33,34 and cardiac imaging,35 and in conventional MDCT, for cardiac 35–37 and head 38 applications. Recent work proved the feasibility of autofocus motion estimation beyond rigid motion and high-contrast CBCT, demonstrating successful deformable motion estimation in interventional soft-tissue CBCT of the abdomen via multi-region autofocus.32,39 One critical aspect of autofocus approaches is proper selection of the autofocus metric which must be tuned to the particularities of the system and imaging task. Numerous autofocus functions have been proposed for CBCT autofocus, including metrics promoting image sharpness (e.g., image gradient magnitude or variance), metrics favoring piecewise constancy (e.g., histogram entropy or total variation), and metrics quantifying higher order properties of the image texture (e.g., Haralick co-occurrence features or Tamura texture features).31,39,40 Previous studies show varying performance of autofocus metrics as a function of image content and scanner geometry. For example, Wicklein et al 40 showed that metrics based on histogram entropy provided optimal assessment of motion severity in CBCT applications involving piecewise constant images, motivating its use for cardiac CBCT autofocus.41 Sisniega et al 31 showed lower performance of entropy for quantification of motion effects in scenarios involving high-frequency, high-contrast, image content, as is the case of extremities CBCT, favoring metrics quantifying pure image sharpness, such as variance of the image gradient. In the case of autofocus for soft-tissue deformable motion, Ref 39 showed that better motion quantification was obtained with metrics combining measures of image sharpness and contrast uniformity, such as the entropy of the image gradient. Common to all conventional autofocus metrics is the enforcement of image properties that are agnostic to the underlying anatomy and can, potentially, favor motion trajectories resulting in images that satisfy the metric (e.g., sharp image content), but depict unrealistic image appearance. With metrics agnostic to the correct presentation of anatomy, the optimizer is more prone to fall into local minima, particularly within the complex, non-convex, space defined by autofocus cost functions.
Image quality metrics incorporating terms to assess the structural similarity between a test image and a reference image provide quantitative evaluation of the distance between two images including not only generic image properties, but also alignment between the structures depicted in the images. Reference similarity metrics include structural similarity index 42 (SSIM), often used to quantify image quality in CT and CBCT,43–45 and visual information fidelity 46 (VIF) that was shown to appropriately quantify distortion and artifacts in CT images.47 If a motion-free image were available for reference, image blurring, and artifacts induced by patient motion could then be appropriately quantified, together with distortion of the structural content of the reference, making VIF a suitable metric for estimation of motion while preserving image structure. Nonetheless, similarity metrics require that motion-free reference image, ideally offering a perfect match for structural content, position, and acquisition settings of the motion-corrupted image. While methods using an approximate prior reference in combination with a structural similarity metric could be envisioned, imperfect image matching would deteriorate performance, and the necessity of a prior volume poses an obvious limitation that defies the purpose of purely image-based autofocus.
Recent advances in machine learning for image processing and analysis have demonstrated the capability of deep convolutional neural networks (CNNs) to extract image features characterizing varied image properties, including artifacts associated with different image degradation effects in CBCT. In the context of motion compensation for CT and CBCT, that capability to identify features associated with motion degradation was explored for the development of image synthesis approaches in which deep CNNs are used to synthesize an image free of motion artifacts directly from the motion-corrupted volume.48–50 The synthesized images depicted substantially reduced motion artifacts, but the lack of mechanisms to enforce fidelity to the original projection data raises questions on the validity of the synthesized anatomy in regions affected by motion.51 The ability to identify motion effects with deep CNNs have enabled the development of “deep autofocus” methods in which CNNs are used as part of an autofocus motion estimation framework. Recent approaches to deep autofocus include methods for cardiac CBCT motion estimations in which deep CNNs acting on partial angle reconstructed volumes are coupled to spatial transformer modules to find a set of rigid transformations acting on the partial angle reconstructions, effectively building a piecewise constant rigid motion trajectory.52 Other approaches trained deep-CNNs with motion-corrupted image patches and motion amplitude pairs, to obtain direct estimations of the motion amplitude affecting that patch. Those estimations were applied for detection of regions affected by motion artifacts,53 preconditioning of the autofocus problem,54,55 or as distance metrics that act directly as autofocus cost functions.56–58 Further applications used deep-CNNs to extract anatomical landmarks in the projection and volume ensemble to replace physical fiducials in fiducial-based autofocus,59 or to directly derive realistic autofocus metrics, such as per-projection reprojection errors for head motion estimation.60
This work leverages the capabilities of deep-CNNs to identify features associated with motion in CBCT, the ability of structural similarity metrics to provide quantification of motion-induced image degradation and preservation of anatomical structures, and recent work on derivation of reference-free image similarity metrics with deep CNNs for general image quality assessment,61,62 to create a novel reference-free, anatomy aware, autofocus metric. The proposed metric, named DL-VIF and first reported in Ref 63, aims at replicating VIF values without the need of a motion-free reference image, via a specifically designed deep CNN. The network was trained on simulated motion-corrupted and motion-free paired CBCTs for head/brain imaging. The resulting metric was evaluated in simulated datasets featuring distinct anatomical features and motion properties from those in the training set and was integrated in an autofocus motion estimation framework. Motion-compensation with DL-VIF was assessed in simulated and cadaver brain CBCT datasets obtained on a clinical interventional robotic C-arm system. The motion compensation results were evaluated in comparison with conventional, anatomy agnostic metrics, illustrating the potential of DL-VIF for anatomy aware autofocus motion compensation.
2. Material and Methods
2.1. DL-VIF: A reference-free similarity metric for motion quantification
Visual Information Fidelity (VIF) is a reference-based image similarity metric first proposed in Ref 46 for quantification of visual and structural similarity between a reference image and an equivalent image that has undergone a distortion process. VIF quantifies similarity as the degree of information preserved in the image after the distortion process, weighted by the effect of the perception process of the human vision system (HVS) that affects both the distorted and the reference images. Thus, VIF provides estimation of image similarity emphasizing image features and frequency content most commonly considered by human observers. Previous studies47 showed that VIF of CT images can provide a measure of image quality that largely agrees with subjective image quality scores from human observers for a wide variety of distortion processes. In the case considered here, the distortion process is the patient motion corrupting the 3D reconstructed images.
To define VIF for motion-corrupted CBCT, expressions for the information carried by the motion free, static, image (μMF) and by the motion-corrupted image (μMC) need to be defined. The information contained in motion-corrupted image, after being filtered by the HVS channel, is denoted IMC, and it is obtained as follows, neglecting constant scaling terms:
| (1) |
| (2) |
| (3) |
| (4) |
where H is a convolution kernel modelling the HVS and built as a cascade of four three-dimensional isotropic Gaussian kernels of size Ni x Ni x Ni, with Ni = 17, 9, 5, and 3 (i = 1, … , 4), and standard deviation of Ni/5. The term , represents the noise in the HVS channel and was set as described in 46. The term g in Eq. 1 and Eq.2 estimates the degradation of information induced by patient motion, dependent on the covariance between the motion-corrupted and motion-free images, , computed according to Eq. 3. The term models the variance caused by motion artifacts, and it is computed as , where is obtained analogously to (Eq. 4) but using the motion-corrupted volume.
The information carried by the motion-free image, IMF, is obtained in an analogous fashion but drops out g and terms related to motion degradation. The VIF is computed as the ratio of the information carried by the motion corrupted image and the motion-free image, measuring the amount of information preserved in the presence of motion. The following expressions are used to compute IMF and VIF:
| (5) |
| (6) |
The VIF obtained with Eq. 6 provides an estimation of motion-induced image quality degradation that captures both the presence of motion artifacts through the modified noise term and distortion of anatomical structures via the structural degradation term g. Both terms are the result of applying linear convolution operators to the motion-free reference image, to the motion-corrupted image, or to a combination of both. Considering the characteristic appearance of motion artifacts (e.g., distortion and streaks), it is expected that a manifold of features representing artifacts and distortions degrading VIF could be learned via observation of a large case cohort capturing the variability of motion-corrupted images in interventional head CBCT. The DL-VIF metric presented below builds on that hypothesis and uses a deep-CNN for performing the learning of such feature manifold.
2.1.1. DL-VIF Network Architecture
The structure of the proposed network is inspired by previous approaches for estimation of approximate local motion amplitude in interventional CBCT.54,58 The DL-VIF network acts on three-dimensional inputs of 128 x 128 x 128 voxels. The base architecture of the convolutional network, depicted in Fig. 1A, featured an initial instance normalization stage combined with an input convolutional layer. This initial layer is followed by a cascade of residual blocks (denoted ResBlock, similar to ResNet designs.64 The ResBlock unit consists of three convolution stages, each followed by an instance normalization layer, and a final leaky rectified linear unit (leaky-ReLU), acting on the addition of the main and the residual paths (see Fig. 1A). Each ResBlock was followed by a max pooling layer to reduce the dimensionality in the volume and the last ResBlock also has a 1x1x1 convolution layer followed by leaky-ReLU inserted before pooling, to condense the number of channels. The output of the ResBlock cascade was input to a fully connected layer that integrates all extracted features across channels and volume dimensions to obtain a single scalar estimation of the reference VIF value.
Figure 1:
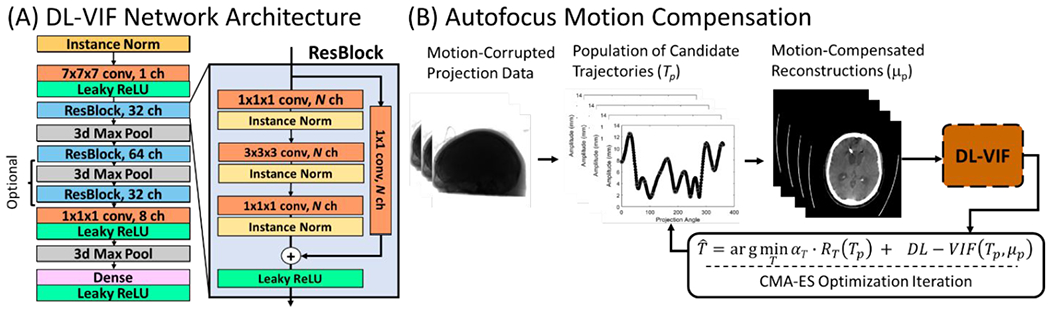
(A) Deep CNN architecture for estimation of DL-VIF. The resulting reference-free DL-VIF metric provides estimation of motion-induced artifacts and distortion, as well as realism of the structural content by learning trends shown by the reference VIF trained against matched motion-free references. (B) DL-VIF was used as the cornerstone of a Deep Autofocus framework in which the trajectory of motion is estimated by iteratively finding the motion trajectory that optimizes the DL-VIF autofocus cost function. The complete autofocus cost function combines DL-VIF with a regularization term that encourages smooth, non-abrupt, motion.
Two different alternative network architectures were considered for DL-VIF: i) a first design, referred to as “2-ResBlock” including a cascade of two ResBlocks (with 32 and 64 channels, respectively), yielding a receptive field of 80 x 80 x 80 pixels for each output value before the fully connected layer; and, ii) a deeper configuration, called “3-ResBlock”, that uses a concatenation of three ResBlocks (with 32, 64, and 32 channels, respectively), resulting in a receptive field of 164 x 164 xl64 voxels, spanning the complete image. The shallower alternative contains a lower number of parameters, potentially resulting in easier training and reduced risk of overfitting. The alternate deep network on the other hand is expected to better integrate the contribution from the entire volume and, potentially, extract more complex artifact patterns. However, the increased depth implies a more complex model that challenges training, and with higher potential for overfitting.
2.1.2. Autofocus Motion Compensation with DL-VIF
The DL-VIF metric was integrated into an autofocus framework for rigid motion compensation, similar to previous approaches for rigid motion compensation in extremities 31 and head CBCT,33 and for soft-tissue deformable motion compensation in abdominal interventional CBCT.39 The algorithm, illustrated in Fig. 1B, minimizes the following cost function:
| (7) |
where Tp is the candidate rigid motion trajectory at the current iteration and population member p, and μp is the reconstructed volume for motion trajectory Tp. The term S(Tp,μp) is an autofocus metric that encourages images free of motion artifacts. The term RT is a regularization term that acts on the quadratic first order difference of the temporal motion trajectory to penalize unrealistic abrupt motion patterns.31 The relative contributions of the penalty and autofocus terms are weighted by the scalar αT. The motion trajectory T is modelled as a set of 6 degree of freedom (DoF) transformations, one per angular projection in the scan (cf., time point). To reduce the problem dimensionality, the temporal trajectory for each DoF was obtained as a superposition of NK cubic b-spline kernels, each centered at one of the NK knots, equally distributed along the scan length.
To evaluate the suitability of DL-VIF for autofocus in comparison with conventional autofocus metrics, the autofocus metric S was set in this work to: i) the proposed DL-VIF metric; and, ii) gradient entropy, shown in Ref 55 to perform relatively well compared to other entropy and gradient-based metrics.
The autofocus cost-function in Eq. 7 defines an optimization space that might be non-convex. Therefore, a derivative-free stochastic numerical optimization method was used, namely the covariance matrix adaptation evolutionary strategy (CMA-ES), proposed in Ref 65. CMA-ES was successfully applied in previous autofocus motion compensation approaches in CBCT.31,39,54
2.2. Data Generation and Training
The training strategy is illustrated in Fig. 2, using paired motion-corrupted and ideally compensated datasets of brain CBCT featuring rigid motion of the head. The datasets were generated via simulated forward projection of motion-free MDCT data. Motion-free volumes were extracted from 39 MDCT head scans acquired as part of a previous IRB-approved study, and the use of the data is retrospective. Each volume has a size of 600 x 500 x 500 voxels with 0.5 x 0.4 x 0.4 mm3 voxel size. For each data instance, a volume was randomly selected from the MDCT data cohort and two CBCT projection datasets were synthesized, one contaminated with motion, and one ideally compensated. CBCT projections were generated using a high-fidelity CBCT forward model, with a separable footprint forward projector,66 and an acquisition geometry pertinent to interventional robotic C-arms, with source-to-axis distance (SAD) of 785 mm, source-to-detector distance (SDD) of 1200 mm, and 360 projections over 360 degrees. The detector was modelled as a flat panel detector with 864 x 660 pixels, and 0.64 x 0.64 mm2 pixel size. The x-ray source was modelled as a monochromatic point source.
Figure 2.
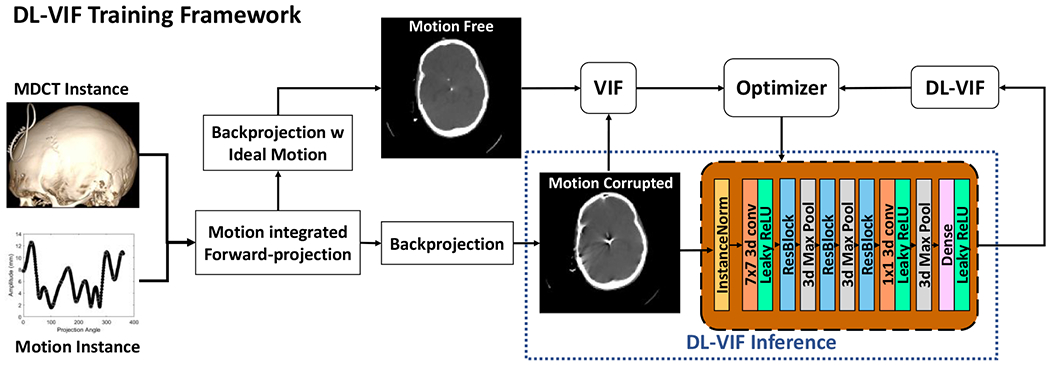
Training strategy for the DL-VIF deep CNN. Motion-free MDCT datasets were used as base instances for the generation of motion corrupted CBCT data. The motion-corrupted data were reconstructed without any motion compensation and with motion compensation using the same motion pattern used to generate the motion corrupted dataset, providing a ground truth for ideal motion compensation. Conventional VIF values were computed for each motion-corrupted volume, using the ideal compensation as reference, to serve as training labels for DL-VIF training. Note that at inference time (see dashed box), only the motion corrupted image is needed, making DL-VIF a true reference-free metric.
Motion contaminated projection datasets were simulated by inducing a projection-wise varying rigid transformation with 6 DoF, applied to the volume during the forward projection process, as shown in Fig 3A. The motion trajectories contained both translational and rotational components. Translational motion amplitude is chosen randomly from 0 mm to 8 mm, with random direction. Random rotations between 0 degrees and 5 degrees were imparted around each of the three axes (superior-inferior – SUP, antero-posterior – AP, and lateral – LAT), with a 50% chance of rotation for each individual axis. The motion trajectories followed cosine temporal patterns with frequency ranging from 0.75 to 1.25 cycles per scan, and random phase. For training purposes, both the motion-corrupted and ideally compensated (motion-free) images were reconstructed on a 128 x 128 x 128 voxel grid with 2.0 x 2.0 x 2.0 mm3 voxel size. For each instance a ground truth VIF label was obtained using the motion-corrupted volume as the distorted image and the ideally compensated volume as the reference.
Figure 3.
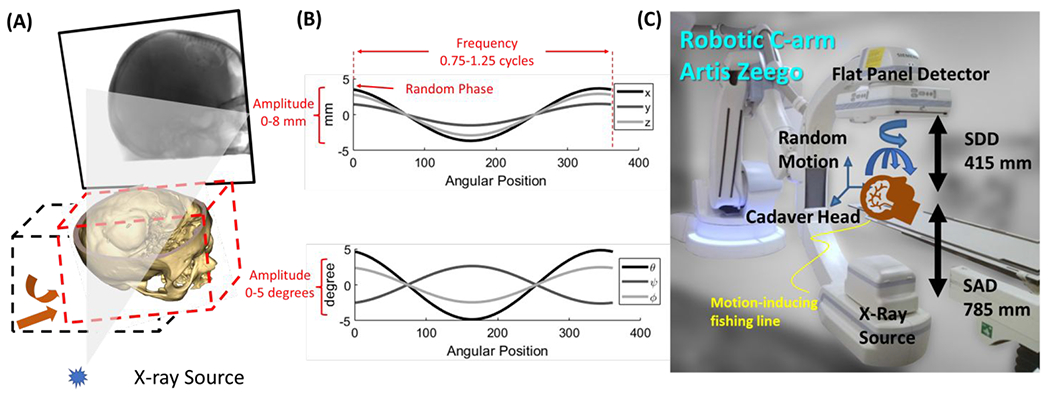
(A) Simulation of motion during the CBCT scan acquisition. Rigid motion trajectories were modelled as set of rigid transformations (one per projection angle) that were applied to the volume before forward projection. (B) Example of rigid motion trajectory in the simulated dataset, with randomly selected amplitude between 0 mm and 8 mm (0 deg to 5 deg for rotational motion components), frequency ranging from 0.75 to 1.25 cycles per scan, and phase ranging from 0 to 18 deg. (C) Experimental setup for the clinically realistic study using a cadaver specimen scanned on an interventional robotic C-arm.
A total of 7,500 instances were generated and the dataset was split as follows: i) 6000 instances generated from a subset of 33 out of the total 39 anatomical subjects were used for training; ii) 750 instances were reserved for validation, generated from 3 anatomical samples distinct from the ones included in the training set; and, iii) 750 instances were allocated to the testing set, generated from the remaining 3 anatomical samples. Although the dataset included distinct anatomical instances, all base datasets were consistent in terms of anatomical site. The network was trained using mean square error (MSE) as the loss function acting on the DL-VIF and the ground truth VIF. The loss function was minimized using the Adam optimizer for a total of 250 epochs, with a batch size of 24, and initial learning rate of 5×10−3. The training was considered converged when clear signs of overfitting were observed in the validation dataset. Overfitting was detected when a continuous increase in the validation loss was observed for a period of 20 epochs. The final trained network was obtained by recovering the network state at the first epoch marking convergence (i.e., the first of the 20 epochs with continuous increase in validation loss), point at which the training is conventionally considered converged before entering overfitting.
2.3. DL-VIF Validation Studies
2.3.1. Correlation Between VIF and DL-VIF
Both network designs (2-ResBlocks and 3-ResBlocks) were evaluated for generalizability to unseen anatomy and motion patterns using the test dataset described in section 2.2. Further validation of generalizability was obtained in scenarios with controlled motion parameters, in terms of motion amplitude and motion temporal frequency. Such controlled validation was obtained with an expanded test dataset, denoted “controlled-motion dataset,” based on the test anatomies. The controlled-motion dataset systematically covered motion patterns with controlled amplitude and frequency, spanning a wider range of temporal motion frequencies than the one used in the original test dataset. Motion amplitudes were set to 2, 4, 6, and 8 mm, while temporal frequencies were set to 0.5, 1, 2, and 3 cycles per scan. Each motion pattern was applied with 4 different starting phases (72, 144, 216, and 288 degrees), resulting in a total of 192 motion-corrupted volumes in the controlled-motion dataset. The generalizability of each network was assessed as the linear correlation between the inferred DL-VIFs and the corresponding true VIF values. Linear correlation was quantified in terms of slope and R-squared estimations.
2.3.2. DL-VIF as a metric of Residual Motion
As stated above, conventional autofocus metrics are challenged by degenerate motion solutions that show desired image properties (e.g., sharpness) but unrealistic anatomical structure. To test the robustness of DL-VIF against such degenerate solutions, a motion perturbation study was performed. Systematic evaluation of DL-VIF robustness was achieved in 15 motion corrupted CBCTs generated using the test dataset anatomies. The 15 cases featured motion trajectories with random amplitude between 0 mm and 10 mm, random 0-5 degrees rotation around each axis, and random frequency between 0.75 and 1.25 cycles per scan. Motion compensated reconstructions were then performed using the known motion trajectories modified but inducing a set of random perturbations, thus simulating intermediate solutions that might be encountered by the numeric optimizer during the motion estimation process. The induced perturbations span a set of increasing amplitude values ranging between 0.5 mm (degrees when applied to rotational motion trajectory) and 20 mm (degrees), in 0.5 mm increments. For each amplitude setting, 5 perturbation patterns were induced, each featuring a random perturbation direction selected independently for each scan angle (viz. projection number). DL-VIF values were computed after reconstruction with the perturbed trajectories.
The DL-VIF values in presence of motion were compared to those obtained with an established conventional autofocus metric, gradient entropy, as reported in Ref. 39. Since the baseline motion-free value of gradient entropy might vary across anatomical instances, and only its variation from that baseline value is relevant for motion estimation, comparison studies were based on percentage rates of metric change (instead of absolute metric values) using the metric value obtained for the corresponding motion-free images as the baseline reference.
2.3.3. Rigid Motion Compensation on Simulated CBCT
Autofocus motion compensation was performed in the 15 simulated brain/head CBCT scans, obtained as described in section 2.3.2. Motion compensation with DL-VIF and gradient entropy was performed for each motion instance using 12 b-spline knots for each of the 6 DoFs, yielding a total of 72 parameters. The weight for the abruptness penalty term, αT, was set empirically based on preliminary tests for each metric (DL-VIF and gradient entropy) on a typical CBCT head image. The value of αT was thus set to yield a contribution of the penalty term approximately equivalent to 1 % of the absolute value of the autofocus metric, resulting in αT = 0.5 for gradient entropy, and αT = 10 −7 for DL-VIF. Further validation of conventional, reference-based, VIF as a metric for rigid motion estimation (and therefore of DL-VIF as its reference-free surrogate), was obtained by performing motion compensation with VIF as autofocus metric, leveraging the availability of motion-free references in the simulated data. Motion compensation with reference VIF was achieved for the same 15 simulated datasets using exact the same optimization settings described above for DL-VIF.
To further test the robustness of DL-VIF to degenerate solutions leading to local minima, for each motion-corrupted instance, autofocus motion compensation was performed 5 times, each with a different random initialization for the motion parameters to estimate. In particular, each b-spline coefficient for translational motion was initialized to a random value between −4.0 mm and 4.0 mm, while rotational components were randomly initialized between −2.5° and 2.5°. The seed of the random number generator was explicitly set to guarantee repeatability of initialization across instances of motion compensation with DL-VIF and gradient entropy.
CMA-ES parameters for the autofocus optimization were maintained fixed across autofocus metrics. Optimization was performed with a CMA-ES population size of 15 members, an initial search space of σCMA – ES = 0.1, and a total of 1000 iterations.
The performance of autofocus motion compensation was quantified with the structural similarity index (SSIM) 42 using a multiscale approach. SSIM values were calculated using the motion-free image as reference on a 5-level resolution scale featuring a cascade of downsampling factors of 16x, 8x, 4x, 2x, and 1x. The SSIM obtained at different resolutions were then combined into a single score following a Gaussian weighting strategy with maximum centered at 4x-downsampling, to approximate human vision sensitivity which is usually assumed to be tuned to mid-frequency imaging tasks.67 To accommodate the large dynamic range of CBCT volumes to the SSIM measurement range, a clipping window between 0.0185 mm−1 and 0.0205 mm−1 was applied to both the motion free reference and the test image (i.e., motion-corrupted, gradient entropy-based autofocus, or DL-VIF autofocus) before SSIM computation.
2.3.4. Rigid Motion Compensation on Cadaver Scans
Assessment of motion compensation with DL-VIF in comparison with conventional autofocus in clinically realistic imaging scenarios was achieved with experimental studies using a cadaver specimen obtained through the Anatomy Board Donation Program of the Maryland State Anatomy Board. We state that every effort was made to follow all local and international ethical guidelines and laws that pertain to the use of human cadaveric donors in anatomical research.
The experimental setup is shown in Fig. 3C. CBCT scans were obtained on an interventional robotic C-ann (Siemens Artis Zeego, Siemens Healthineers, Forchheim, Germany) with a geometrical configuration with SDD = 415 mm, and SAD = 785 mm. A total of 496 projections spanning 198 degrees were acquired with 100 kV and 0.195 mAs during the 20-second Dyna-CT scan. A fishing line was attached to the head and was manually pulled randomly during the scan to induce motion. The experiment involved the acquisition of five scans: one stationary, free of motion artifacts, and four with artifacts, blurring, and distortion resulted from random motion induced by the fishing line.
Motion compensation was obtained with DL-VIF and gradient entropy as autofocus metrics. The motion compensation parameters were empirically set for each dataset, based on preliminary tests. In each case, all the compensation parameters were kept consistent between DL-VIF and gradient entropy, except for the regularization strength, αT, which was scaled according to the value range of each metric, as described above. Motion compensation was obtained with 5 random initialization patterns, as described in section 2.3.3.
3. Results
3.1. DL-VIF for VIF Inference
The performance of DL-VIF to reproduce reference VIF values is illustrated in Fig. 4 for the two 2-ResBlocks and 3-ResBlocks architectures. DL-VIF fidelity in Fig. 4 was computed using the test datasets that featured subjects not included in the training and validation sets. Motion trajectories in the test set were distinct to those in training and validation, but they both were uniformly sampled for the same range of motion parameters (i.e., amplitude and frequency range). Results for fully trained 3-ResBlocks and 2-ResBlocks configurations showed good linearity between DL-VIF and true VIF for both configurations, with slope of 0.884 and 0.890 and correlation coefficient values of R2 = 0.96 and R2 = 0.97 for 3-ResBlocks and 2-ResBlocks, respectively. The value of the loss function, aggregated over the complete test dataset, also reflected the same trend, with the 2-ResBlocks configuration achieving a total test loss of 1.9 x 10−3, yielding a reduction of 42%, compared to the 3-ResBlocks design that achieved a test loss of 3.3 x 10−3. While both configurations showed good agreement with the true, reference-based, VIF, the test results suggested slightly increased performance for the 2-ResBlocks architecture, despite its shallower structure and lower number of parameters. This suggests that the 2-ResBlocks configuration provides adequate representation of features associated with motion-induced image-quality degradation and benefits from somewhat improved robustness to overfitting, potentially, yielding better generalizability to unseen scenarios.
Figure 4.
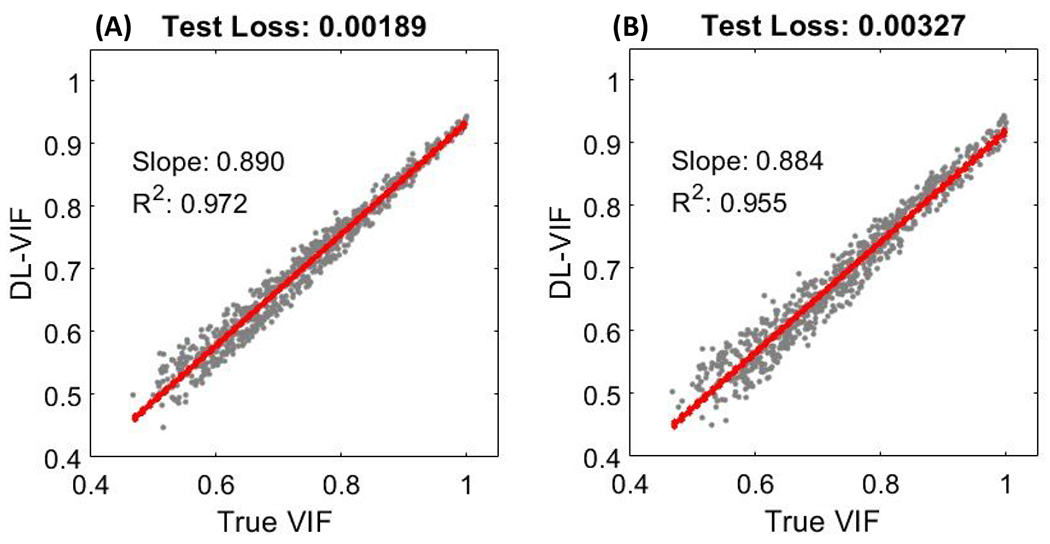
Fidelity ot DL-VIF inferences (obtained without a motion-free image reference) to ground truth VIF values obtained using paired, motion-free, reference images. DL-VIF was obtained for the test dataset that featured subjects not included in the training dataset and motion trajectories analogous to those included in the training set. Results for both tested configurations, 2-ResBlocks (A) and 3-ResBlocks (B) showed appropriate linearity with the reference VIF values.
Fig. 5 shows DL-VIF inferences for the controlled-motion dataset that featured motion trajectories spanning a larger temporal frequency range, compared to the test dataset in Fig. 4. Both network designs reproduced the trend observed in reference-based VIF. Slow motion patterns (0.5 cycles per scan, depicted by circular markers in Fig. 5) resulted in less severe distortion of the shape of anatomical structure, and mild to moderate global blurring and double contours, compared to higher frequency trajectories. This is reflected in overall higher motion-corrupted VIF values for slow motion patterns and a decrease in motion-corrupted VIF with increasing motion frequency. Both DL-VIF architectures were able to capture this trend and achieved good linearity between inferred DL-VIF and reference VIF, albeit with lower R2 values (R2 = 0.86 for both the 3-ResBlocks and the 2-ResBlocks configurations), compared to the test dataset in Fig. 4 that yielded R2 = 0.97. However, the configuration with 2-ResBlocks showed substantially better absolute agreement with VIF, as indicated by a slope of 0.83, closer to unity, compared with that obtained with the 3-ResBlocks configuration (slope = 0.69). This better correspondence with the true reference-based VIF agrees with the better generalization capabilities observed in the test dataset for the 2-ResBlocks architecture (see Fig. 4). In light of those observations, the remaining results in this work were obtained with the 2-ResBlocks architecture.
Figure 5.
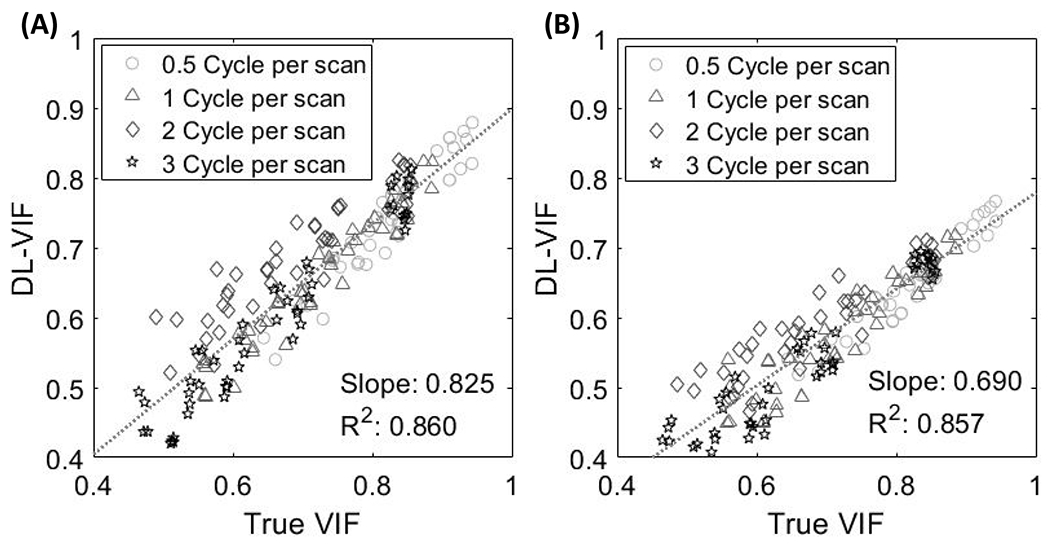
Fidelity of DL-VIF to ground truth reference-based VIF measures in the controlled-motion dataset, featuring a larger range of temporal frequency and motion amplitude. (A) Results for the 2-ResBlocks configuration and (B) for the 3-ResBlocks configuration.
3.2. Performance of DL-VIF with Residual Motion
In Fig.6, DL-VIF and gradient entropy are compared in terms of their capability to quantify motion-induced quality degradation for perturbations in the vicinity of the true motion trajectory. Error bars in Fig.6 represent the range of variation for a set of 5 random perturbations of the same amplitude. For low amplitude perturbations (below 3 mm) both metrics show comparable performance, albeit with a steeper slope and lower variation range for DL-VIF. The larger variability of gradient entropy compared to DL-VIF became more evident with increasing perturbation magnitude. In the case of DL-VIF the metric change rate remains moderately stable across the range of perturbations explored. Thus, the rate of metric net change due to departures from the true motion remained comparable or larger to the variability induced by random perturbations at any given perturbation magnitude, resulting in a rate change of 2.24 %/mm(degree) vs an average of ±4.63% variability across instances for perturbation amplitude larger than 5 mm (which represents the motion patterns with larger variability across perturbation instances). Gradient entropy, on the other hand, showed a plateau for perturbations larger than ~4 mm. Thus, for moderate to large perturbations around the solution, the rate of metric change became almost an order of magnitude smaller than the variability across instances (0.73 %/mm(degree) vs an average of ±6.99% across instances for perturbation amplitude larger than 5 mm). Consequently, gradient entropy showed increased sensitivity to perturbation and larger difficulty to correctly identify the direction of decreasing motion-induced image quality degradation. The observed trends illustrate the sensitivity of DL-VIF to motion-induced image quality degradation and shape distortion, throughout the explored perturbation range, pointing to better robustness against local minima compared to gradient entropy that showed comparatively larger susceptibility to local minima that might promote degenerate solutions with residual motion artifacts and unrealistic shape of anatomical structures.
Figure 6.
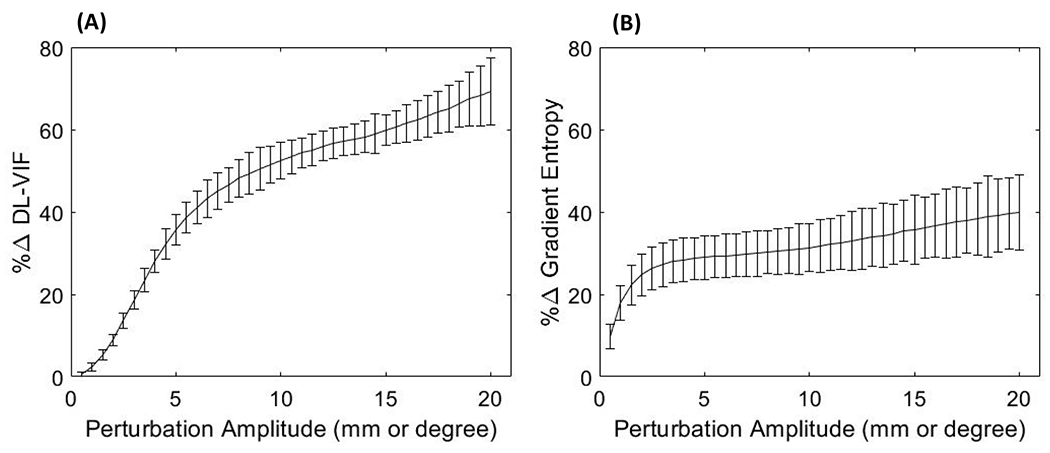
The percentage change rate tor DL-VIF (A) and gradient entropy (B) for motion trajectories featuring random perturbations around the true motion trajectory with increasing perturbation amplitude. Large change rate is associated with higher sensitivity to small motion variations around the vicinity of the true solution. Low measurement variability (as quantified by the error bars) results in increased robustness to distinct motion patterns with similar severity but resulting in different artifacts and distortion patterns. Large change rate, combined with low variability, points to a better conditioning of the autofocus optimization problem, with lower number and strength of local minima.
3.3. Motion Compensation with DL-VIF
3.3.1. Simulation Studies
The results of autofocus motion compensation in simulation studies are shown in Fig. 7. Image quality after motion compensation is quantified with SSIM, computed using the volume reconstructed with the ideal simulated motion trajectory as the motion-free reference. As a baseline for comparison, autofocus motion compensation with full reference VIF achieved nearly perfect compensation, demonstrated by an average SSIM value of ~1.00, with standard deviation of 4.06×10−4, regardless of the severity of the initial motion-induced quality degradation. Motion compensation results in Fig. 7 are presented as a function of the initial image quality in the motion-corrupted reconstruction (Fig. 7A), also measured using SSIM; as a function of the total distance traveled by a corner point in the reconstruction volume for the complete motion trajectory (Fig. 7B); and as a function of the abruptness of motion, estimated as the motion speed, computed as the average derivative of the traveled distance along the scan time (Fig. 7C). Baseline SSIM in presence of motion showed a relatively high value indicating a reasonably high overall alignment of structures even in the presence of motion, associated to the high dynamic range of the structural image content and reasonable preservation of the structural content of the image, compared to the intensity of motion artifacts and the magnitude of motion distortion. However, as indicated in Fig 7, motion induced a net decrease in SSIM, that was reduced from 1.0 (motion-free) to a minimum SSIM of 0.85 in presence of severe motion. The error bars in Fig. 7 indicate different initializations of the trajectory in the autofocus optimization. Results in Fig. 7 show average improvement in SSIM of 0.068 for DL-VIF, yielding superior compensation of motion effects compared to gradient entropy, that yielded a lower average SSIM increase of 0.034. Furthermore, DL-VIF showed more stable performance across initializations (σDL-VIF = 0.008, σgradient entropy= 0.019, obtained as the ensemble across instances), confirming the better robustness against local minima illustrated in section 3.1. The trend in Fig. 7A indicates degraded performance of gradient entropy for cases with lower initial motion-corrupted SSIM, associated with severe motion artifacts and significant distortion of anatomical structures. In such cases, gradient entropy was trapped in degenerate solutions with reasonably sharp image content but unrealistic appearance. Motion compensation results as a function of total distance traveled (Fig. 7B) suggest that increasing total motion distance, often resulting in lower initial SSIM, challenged the performance of gradient entropy autofocus motion compensation. Fig. 7C showed reasonably stable performance for both DL-VIF and gradient entropy across the range of motion speed included in the study, however with slight larger variability across initializations for rapid motions when using gradient entropy-based autofocus, compared to the consistent performance showed by DL-VIF. Nevertheless, SSIM values after motion compensation are consistently higher for DL-VIF compared to gradient entropy, confirming its superior performance across the motion patterns and anatomies included in the study.
Figure 7.
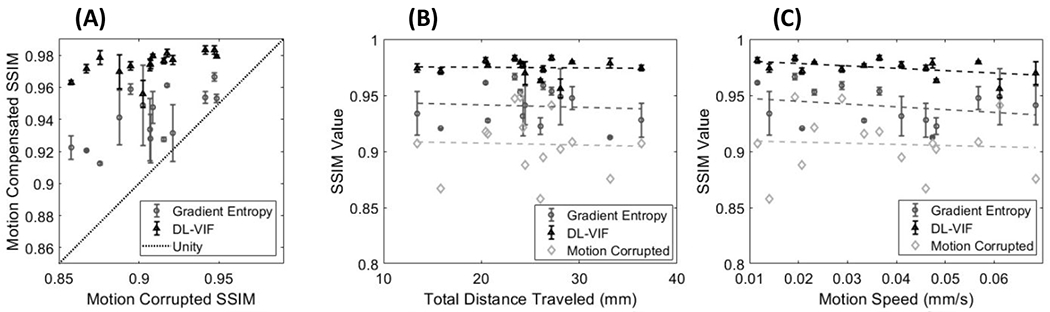
(A) As the motion-corrupted SSIM decreases, the performance of gradient entropy becomes more unstable, while the DL-VIF remains robust. (B) SSIM after motion compensation as a function of the total motion distance, showing degraded compensation stability with gradient entropy-based autofocus, compared to more stable and in general superior SSIM with DL-VIF. (C) SSIM as a function of motion speed points to slight larger susceptibility to local minima for faster motion when using gradient entropy, compared to stable performance with DL-VIF autofocus.
The trends shown by aggregated motion compensation results in Fig. 7 are explored in Fig. 8 via individual examples of motion compensation. The instances included in Fig. 8 were selected to illustrate scenarios with motion trajectories that challenged motion compensation or that resulted in large discrepancies between SSIM values obtained with DL-VIF and gradient entropy. Fig. 8A–8D depicts motion compensation in the data instance with the worse initial image quality (i.e., the lowest SSIM value before motion compensation). Motion resulted in severe image quality degradation, as can be appreciated in Fig. 8B that depicts severe streak artifacts, blurring and shape distortions that hamper identification of any anatomical feature. Motion compensation substantially improved image quality and restored the overall shape of the head for both gradient entropy (Fig. 8C) and DL-VIF (Fig. 8D). However, gradient entropy was not able to achieve full convergence in this challenging scenario, favoring a local minimum with sharp high-contrast structures. This degenerate solution was anatomically inaccurate, featuring a ring structure (see zoom-in window in Fig. 8C), instead of the single shunt in Fig. 8A, and overall blurring and mild distortion of soft-tissue structures, yielding SSIM = 0.92. DL-VIF, on the other hand, converged to a solution that effectively combined sharp high-contrast features with anatomically realistic soft-tissue structures. The result provided by DL-VIF yielded an improved SSIM = 0.96. Analogous behavior was observed for the instance with the largest total distance traveled, shown in Fig. 8E–8H. In that case, there was a large discrepancy between the true motion trajectory and the initialization, posing a complex, non-convex, search space for the CMA-ES optimizer. In particular, the random initialization of the motion parameters resulted in an average difference of 42.84 mm to the true motion trajectory, compared to an average difference of 33.43 mm for all other cases. Similar to the case in Fig. 8C, the gradient entropy motion compensation result (Fig. 8G) enforced a solution with sharp high-contrast features (a ring-shaped distorted ventricular shunt – see zoom-in) but resulting in residual blurring, distortion of soft-tissue anatomy, and only modest improvement in image quality: SSIM = 0.92, vs SSIM = 0.91 before motion compensation (Fig. 8F). Motion compensation with DL-VIF posed a simpler optimization space and resulted in better restoration of anatomy accompanied by conspicuous reduction of motion artifacts and image blurring, yielding an enhanced similarity with the motion-free reference, with SSIM = 0.98.
Figure 8.
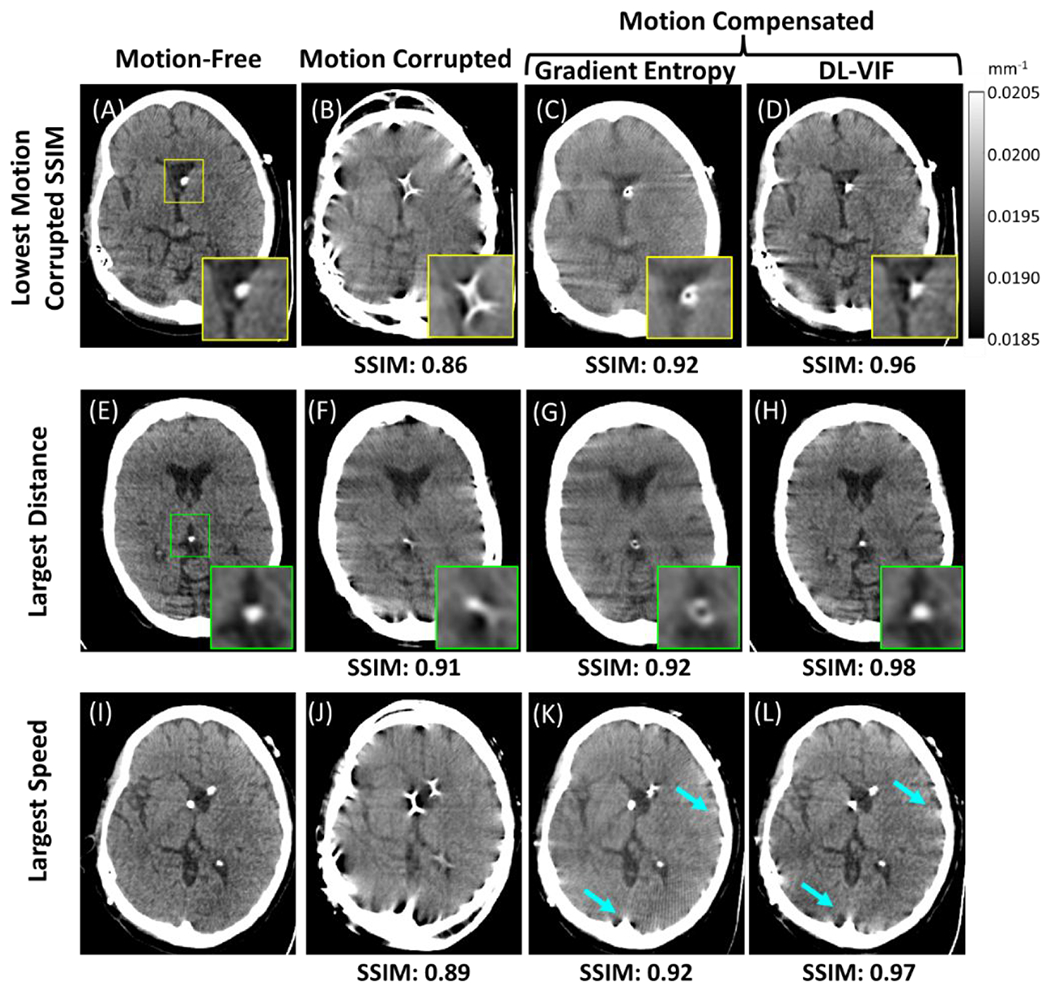
Example cases of motion compensation with gradient entropy and DL-VIF as autofocus metrics. Results are shown for three representative cases: (A-D) The case showing the most severe image quality degradation within the cohort, resulting in the worst SSIM for the motion-corrupted image; (E-H) the case with the motion trajectory resulting in the largest total distance traveled, used as a surrogate for the total magnitude of accumulated motion; and, (I-L) the case with the fastest motion speed, resulting in a distinct motion degradation pattern with a higher number of streaks and high-frequency artifacts. The first column depicts reference motion-free images obtained applying the ideal motion trajectory during image reconstruction. The second column shows motion corrupted images reconstructed directly from simulated projections without applying any motion trajectory. The third and fourth columns illustrate the motion compensation results with gradient entropy and DL-VIF respectively. Zoom-in windows indicate regions containing sharp high-contrast features that are enforced by sharpness-based metrics, such as gradient entropy, despite their anatomical unfeasibility. Blue arrows indicate streak artifacts that are more efficiently mitigated by gradient entropy, however resulting in overall degradation of image quality and distorted intra-cranial structures.
The final example in Fig. 8I–8L, shows motion compensation results for the motion trajectory with fastest transitions, as measured by motion speed. In this case, both metrics resulted in significant mitigation of motion artifacts and restoration of the underlying anatomy. This case posed a somewhat different scenario than those observed in the two previous instances, with gradient entropy providing larger reduction of residual motion artifacts around bone structures than DL-VIF (see arrows). However, reduction of such streak artifacts resulted in slightly degraded conspicuity of the intra-cranial anatomy and residual distortion of high-contrast intra-ventricular structures, that reduced the similarity with the motion-free reference, obtaining an SSIM value of 0.92 (compared to SSIM = 0.89 before motion compensation). In the case of DL-VIF, the motion compensation produced an image with mild residual streak artifacts around bone regions, but with otherwise sharp delineation of anatomical structures and intraventricular high-contrast features, providing a larger similarity with the reference (SSIM = 0.97).
3.3.2. Experimental validation in cadaveric studies
Results of motion compensation on experimental data of the cadaver head acquired on the Siemens Artis Zeego robotic C-arm are illustrated in Fig. 9. A total of 4 motion-corrupted scans were obtained, with motion induced manually as described in section 2.3.2. The resulting motion trajectories were more abrupt compared to the simulation study in Section 3.3.1 SSIM values against motion-free (static) reference scan of the same cadaver were used to assess compensation performance. Aggregated motion compensation results are presented in Fig. 9A as a function of the initial image quality before compensation (SSIM value of the motion-corrupted image, computed against the static reference). Error bars in Fig. 9A indicate the range of resulting SSIM values for the set of 5 initializations used for the autofocus optimization. In all experiments, motion compensation with DL-VIF achieved noticeable mitigation of motion artifacts and recovered the shape of anatomical structures across cases. The SSIM was improved over motion-corrupted image by 0.043 (5.0%) on average. Successful motion compensation was thus achieved despite the different nature of the experimental motion trajectories compared to the training cohort. In addition to a net average increase in SSIM, DL-VIF maintained consistent performance across random initializations, as indicated by the small variability in SSIM for each motion instance, represented by the small size of the error bars in Fig. 9A (light gray markers). Gradient entropy, on the other hand, was generally unable to noticeably mitigate motion artifacts. The gradient entropy SSIM was typically no better, and often worse, than the initial uncorrected image, with average SSIM below the identity line in Fig. 9A. Lower overall SSIM was accompanied by a higher sensitivity to trajectory initialization, reflected by larger error bars indicating inconsistent performance across initializations.
Figure 9.
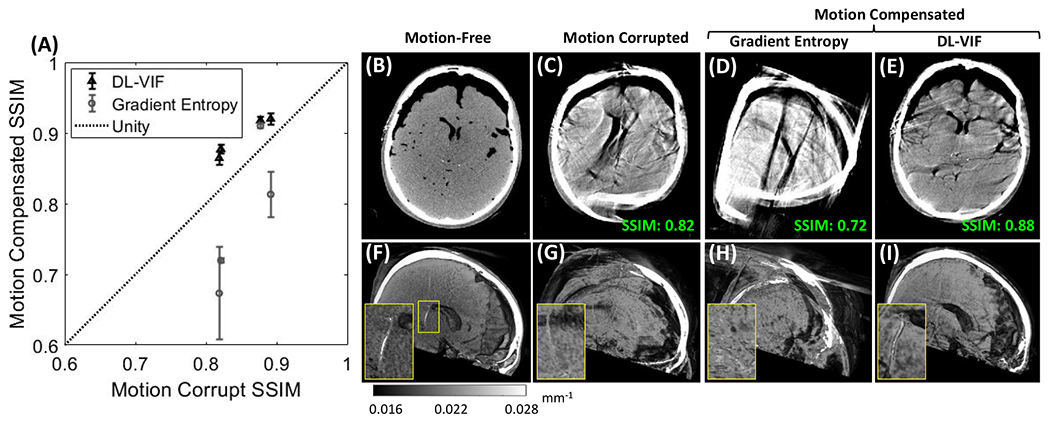
Motion compensation results with DL-VIF and gradient entropy in data of a cadaver specimen acquired on a clinical robotic C-arm. (A) Quantification of SSIM before and after motion compensation showed a net increase in SSIM values when using DL-VIF autofocus. The motion-free reference (B, F) showed conspicuous bony and soft-tissue anatomy and appropriate visualization of the intraventricular shunt (F, zoom-in). (C, G) Example motion-corrupted case showed severe distortion of bony and soft-tissue anatomy that challenged visibility of the shunt. (D, H) Motion compensation with gradient entropy for the example case resulted in net degradation of image quality compared to the uncompensated case. (E, I) Motion compensation using DL-VIF managed to recover most of the highly degraded soft tissue and bone features on the example case, allowing visualization of the shunt, as illustrated in the zoom-in window, and increased SSIM, pointing to a better agreement with the motion-free reference.
A representative example result is depicted in Fig 9B–9I. Reference reconstruction of a motion-free scan is in Fig.9B, motion-corrupted scan is in Fig. 9C. Axial views after motion compensation with gradient entropy (Fig. 9D) show degraded image quality compared to the initial motion-corrupted image (Fig. 9C); the SSIM is 0.72 after compensation compared to SSIM 0.82 for the uncorrected volume. Motion compensation with DL-VIF, on the other hand, resulted in noticeable (although not complete) mitigation of the severe distortions caused by motion, yielding an increase in SSIM to 0.88, in a scenario involving severe image quality degradation and shape distortion. Reduced motion artifacts were accompanied by partial restoration of anatomical structures, as evidenced by the restored shape of the skull surface, ventricles, and overall brain boundaries (Fig. 9E). Sagittal cuts of three-dimensional volumetric renders show that the majority of soft tissue and high-contrast features were undiscernible in the motion-corrupted volume (Fig. 9G), evidenced by the complete degradation of the shunt depicted in the zoom-in window. Consistent with axial views, motion compensation with gradient entropy, did not improve the visibility of the shunt or anatomical structures (Fig. 9H). Motion compensation with DL-VIF was able to restore the majority of cranial bone and soft tissue boundaries and improved the visibility of the shunt, as depicted in the zoom-in view in Fig. 9I.
4. Discussion and conclusions
A novel metric, denoted DL-VIF, was developed for quantification of motion artifacts and motion-induced distortion of anatomical structures. The proposed metric aims at quantifying motion effects in CBCT with a comprehensive measurement that combines aspects purely related to image quality and agnostic to the structural content of the image (e.g., image sharpness), with measures quantifying the realistic appearance of the image contents. In this case, image contents are assumed to be anatomical structures pertinent to a particular imaging task with properties (e.g., contrast and spatial resolution) compatible with acquisition protocols commonly used in interventional CBCT. This work draws from previous efforts on reference-free image quality metrics developed in the context of general image quality evaluation. Analogously to DL-VIF, those approaches leveraged the capability of deep CNNs to extract image patterns underlying in large image data cohorts to learn a set of features associated to image quality degradation.61,62 The learning is usually performed in a supervised fashion, via exploration or pairs of distorted images and corresponding distortion-free image references, to reproduce the behavior of reference-based image quality metrics. DL-VIF used a similar approach to infer estimations of VIF values in motion distorted CBCT images, without a corresponding motion-free reference.
In this work, DL-VIF was implemented with a deep CNN based on a concatenation of ResBlocks modules, consisting of convolutional layers and instance normalization layers joined with a residual connection before a leaky ReLU activation. Two alternative designs were tested. A deeper design integrating 3-ResBlocks, and a shallower one featuring 2-ResBlocks. The 3-ResBlocks architecture was expected to be capable of extracting more complex feature patterns, but at the price of a larger number of network parameters, which might challenge the training and make the network more prone to overfitting. The 2-ResBlocks configuration, on the other hand, was expected to achieve representations of a more limited variety of feature combinations, but with correspondingly lower number of parameters and less potential for overfitting. The results for the test dataset showed similar level of agreement between DL-VIF and reference VIF for both architectures. However, for the expanded test dataset, that featured controlled motion trajectories deviating from the range of amplitude and frequency in the training dataset, the 3-ResBlocks configuration showed degraded performance compared to the 2-ResBlocks network. This implied that the simpler 2-ResBlocks configuration resulted in lower overfitting and was thus able to provide better generalization to unseen motion artifacts patterns. This result is likely dependent on the design of the training dataset, and the particular imaging task, rigid motion in interventional CBCT for neuroradiological applications in this work. Deeper configurations might be better suited for inference of DL-VIF in scenarios encompassing a variety of motion sources interacting in complex ways, such as soft-tissue deformable motion. In such cases training would require realistic datasets spanning a larger variety of motion patterns and anatomical features.
The training strategy for DL-VIF included motion as the only source of artifacts and distortion and, therefore, any deviation from unity VIF in the training set was attributable only to motion-induced artifacts and shape distortion. However, while only motion contamination was induced in the training data, the variety of source CT volumes used as reference anatomy induced variations naturally appearing in VIF (and other structural similarity metrics) from interaction of motion with different structural content. For instance, anatomies containing a larger fraction of skull base depict richer high-frequency content that would result in a more conspicuous distribution of motion artifacts and lower VIF compared to a relatively homogeneous brain region affected by similar motion severity. The agreement between the target VIF and the inferred DL-VIF suggests that the learning process successfully conveyed the interplay between the structural content of the image and the appearance of motion artifacts and distortion. Analogously to the dependency of the network architecture with the type of motion considered in the development of DL-VIF, application of DL-VIF to other types of image distortion and artifacts, with appearance significantly different to motion effects would require the design of a different training strategy and, possibly, the use of a different network architecture.
The performance of DL-VIF as a metric of motion severity and its integration into an autofocus framework for rigid motion compensation was assessed in comparison with a conventional autofocus metric that estimates motion-induced image quality degradation from purely image-based measurements. DL-VIF showed better quantification of motion effects, reflected as a better agreement with trends shown by image-based similarity metrics (multi-resolution SSIM) computed using the motion-free counterpart image as reference. The better agreement was also accompanied by a lower variability of DL-VIF values for data cases with similar motion degradation, again quantified as SSIM. These combined better agreement and lower variability indicates that a cost function based on DL-VIF would define a smoother space, with a lower number of local minima that are in turn also of lower magnitude difference compared to their vicinity. Those characteristics are desirable to provide better conditioning to the autofocus optimization, and it is translated to better robustness to initialization, motion trajectory, and underlying anatomical instance. As a result, better motion compensation performance and more consistent results across patients, motion trajectories, and parameter initialization were achieved with DL-VIF, as illustrated in section 3.3. Motion compensation results with gradient entropy could be improved with better preconditioning of the autofocus optimization problem, achieved, e.g., via estimations of the magnitude and direction of motion, as illustrated in previous work for autofocus preconditioning.54,55 The experiments in section 3.3 were designed to assess the baseline conditioning of the autofocus problem for DL-VIF vs a state-of-the-art conventional autofocus metric (gradient entropy), showing a better conditioning of the search space that largely removed the need for advanced preconditioning. Such advanced preconditioning would, in any case, not degrade the baseline performance of DL-VIF-based autofocus illustrated in section 3.3. The results in our current work are only strictly applicable to the specific metric (gradient entropy) used in this work. However, while other conventional metrics might perform differently, previous studies showed that the performance of such metrics is highly dependent on the imaging task, magnitude of motion, and underlying anatomical features, hampering the selection of a global gold-standard metric for CBCT motion compensation. For example, previous works on autofocus motion compensation found histogram entropy as a suitable metric for motion compensation in head CBCT 41 and in cardiac CBCT.35 Despite its successful application in those scenarios, further work on motion compensation for high-resolution bone imaging in extremities CBCT found that histogram entropy can enforce degenerate solutions for such application and moderate to large motion amplitude (>10 mm), and that variance of the gradient provided a more favorable autofocus optimization space.31 Furthermore, recent work on deformable motion compensation for abdominal CBCT, in a scenario that effectively combined high-contrast features (bone and contrast-enhanced vascularity) with low-contrast soft-tissue structures, found that both previous metrics offered sub-par performance compared to entropy of the gradient, which promoted more consistent motion quantification.39 Our selection of gradient entropy as the reference metric for conventional autofocus was motivated by its superior performance compared to other candidate metrics, reflected in previous literature. Gradient entropy was, therefore, selected as our best estimation of a state-of-the-art conventional autofocus metric, recognizing that, within the vast pool of possible metrics of image quality, others, not evaluated in this context, might be better suited to the particular imaging task and motion characteristics considered in this work. However, common to those metrics is their lack of evaluation of the feasibility of underlying anatomical structures, and their possible enforcement of artifacts compatible to the particular metric (e.g., sharp streaks or uniform regions). While DL-VIF was evaluated only in comparison to one candidate metric, the general trends of better robustness and more consistent motion assessment are expected to hold when compared to any autofocus metric enforcing image characteristics not aware of underlying image structures.
The autofocus framework with DL-VIF showed certain desirable characteristics compared to other approaches to deep autofocus. Full deep autofocus methods directly estimate the motion trajectory from motion-corrupted data, without iterative optimization of an autofocus cost-function. For example, in 52 partial angle reconstructions and spatial transformer modules were combined to extract rigid transforms applied individually to each partial angle reconstructions. Each of those partial angle reconstructions were then transformed in the image domain and added to form the final motion-compensated reconstruction. This approach had several advantages compared to iterative autofocus, the most important being the reduced computational burden. However, downsides to this approach include a simplification of the temporal characteristics of the motion trajectory. For instance, application of a single transformation to a partial angle reconstruction effectively results in a nearest-neighbor interpolation of the motion pattern for the scan time covered by each partial angle reconstruction. A second difference is that by applying the transformation directly in the image domain via a spatial transformer, a second interpolation stage is applied, besides intrinsic interpolation during backprojection, resulting in potential degradation of image resolution. Finally, and, perhaps more important in comparison to DL-VIF, direct estimation of the motion trajectory from the data requires extensive training with a variety of motion trajectories fully incorporating most possible artifacts patterns resulting in similar image artifacts but caused by different motion patterns, posing difficulties for generalization of the trained network to motion deviating from training instances. Similar observations could be made for methods that aim at building an autofocus metric that estimates motion amplitude and direction directly from motion-corrupted data.56,58,68 While not solving the deep autofocus problem in one stage and requiring an iterative optimization, accurate estimation of motion characteristics from the motion-corrupted data poses a similar problem when the training data do not capture enough variety of trajectories resulting in similar artifact patterns but distinct amplitude or direction.
Similar to DL-VIF, other deep autofocus approaches aimed at estimating surrogate metrics of motion severity. Along those lines, Preuhs et al 60 proposed a deep autofocus metric for head CBCT that estimates several reprojection error measures (average reprojection error, per-projection reprojection error, in-plane reprojection error, and out-of-plane reprojection error) by extracting features from 9 orthogonal planes of a motion-corrupted reconstruction. Such approach relies on the ability of the network to identify anatomical landmarks contributing to reprojection error in the projection. While that is reasonably feasible for scenarios involving high-contrast bone imaging with distinct anatomy (e.g. cranial structures in head imaging), this approach might be challenged in scenarios which much less defined and homogeneous across patients anatomical landmarks, such as abdominal soft-tissue imaging. In addition, the current approach in Preuhs et al 60 estimates reprojection error as a projection-wise global perturbation to the system geometry, which limits its application to rigid motion patterns. The general architecture of DL-VIF, on the other hand, is not limited to rigid motion in high contrast CBCT, and can be extended to deformable, soft-tissue motion scenarios, as shown in preliminary results in our previous work.63 Derivation of DL-VIF for quantification of image quality degradation from soft-tissue deformable motion poses a more challenging problem, arising from limited contrast in soft-tissue structures and from the complex distribution of artifacts and motion distortion induced by deformable motion fields. Ongoing work on DL-VIF addresses such extension to soft-tissue deformable motion with application to scenarios ranging from abdominal to breast imaging.
DL-VIF was applied in this work for compensation of patient motion in interventional neuroradiology applications involving the same rigid motion of the head and all other objects present in the field of view. Such assumption, while commonly applied in literature for head/brain motion compensation 60,69 might result in residual, non-mitigable, artifacts arising from objects inside the field of-view or in its vicinity that follow a different motion trajectory than the head, such as head holders and patient positioning hardware, or articulated parts of the anatomy (e.g., lower jaw).33 Previous work showed that rigid autofocus approach, such as the one introduced here will not mitigate artifacts from regions moving independently of the cranium in such scenarios. That might be one of the reasons for the comparatively reduced image quality observed in the cadaver experiments in Section 3.3.2. However, while a multi-region autofocus framework will be needed in that situation, the definition of DL-VIF is fully applicable to that scenario and the similar appearance of artifacts arising from outside elements compared to those from structures within the head makes it plausible for DL-VIF to provide appropriate estimation of motion-induced image quality degradation without need of further training.
Similar to the effect of objects outside of the field of view, the performance of DL-VIF might be affected by the presence of high-attenuating objects (e.g., metallic implants or metal instrumentation) that might induce artifacts with an appearance similar to motion-induced streak artifacts. Application of DL-VIF in such scenarios might require of alternative training approaches including configurations with metal elements to enable the metric to distinguish between high-frequency artifacts not related to motion and similar, motion-induced, artifact patterns.
One limitation of the current DL-VIF network design is the reasonably coarse voxel size (2 mm) associated with the 128 x 128 x 128 voxels volumes input to the network. While this limitation is to a large extent associated with memory and computational burden limits of the GPU devices used for training, they pose a limit on the smallest features associated with motion degradation that can be observed with the network. Extension to higher-resolution volumes, while possible with the current architecture, might result in different learning trends and more computationally and memory intensive training. Ongoing and future work targets such extension to high-resolution and complex deformable motion patterns with possible approaches including multi-resolution, patch-based, architectures building on previous work on context awareness for deep-learning applications in multi-modality image synthesis,70 or in image analysis applications.71
In summary, a novel metric for quantification of motion-induced image quality degradation, DL-VIF, was presented and evaluated in the context of autofocus patient motion compensation for rigid motion trajectories in head CBCT. Validation experiments in simulation studies and experimental data of a cadaver specimen acquired in a clinical robotic C-arm showed improved performance for motion estimation compared with conventional autofocus metrics that only consider generic image properties. Better robustness to scenarios involving similar image-quality degradation but with variations in the source motion pattern was demonstrated, and resulted in superior, more consistent performance of motion compensation. The concept of learning reference-free structural similarity metrics, introduced with DL-VIF, provides a new set of metrics towards reliable autofocus rigid and deformable motion compensation in interventional CBCT.
Acknowledgments
This research was supported by NIH-R01EB030547, and academic-industry research collaboration with Siemens Healthineers.
References
- 1.Orth, Robert C, MD, PhD, Wallace MJ, MD, Kuo MD, MD. C-arm cone-beam CT: General principles and technical considerations for use in interventional radiology. Journal of vascular and interventional radiology. 2008;19(6):814–820. https://www.clinicalkey.es/playcontent/1-s2.0-S1051044308002133. doi: 10.1016/j.jvir.2008.02.002. [DOI] [PubMed] [Google Scholar]
- 2.Kapoor Baljendra S., MD, FSIR, Esparaz A, BA, Levitin A, MD, McLennan Gordon, MD, FSIR, Moon E, MD, Sands Mark, MD, FACR. Nonvascular and portal vein applications of cone-beam computed tomography: Current status. Techniques in vascular and interventional radiology. 2013;16(3):150–160. https://www.clinicalkey.es/playcontent/1-s2.0-S1089251613000310. doi: 10.1053/j.tvir.2013.02.010. [DOI] [PubMed] [Google Scholar]
- 3.Kakeda S MD, Korogi Y, MD, Ohnari N, MD, et al. Usefulness of cone-beam volume CT with flat panel detectors in conjunction with catheter angiography for transcatheter arterial embolization. Journal of vascular and interventional radiology. 2007;18(12):1508–1516. https://www.clinicalkey.es/playcontent/1-s2.0-S1051044307011074. doi: 10.1016/j.jvir.2007.08.003. [DOI] [PubMed] [Google Scholar]
- 4.Lightfoot Christopher B., MD, FRCPC, Ju Y, MD, Dubois Josée, MD, FRCPC, et al. Cone-beam CT: An additional imaging tool in the interventional treatment and management of low-flow vascular malformations. Journal of vascular and interventional radiology. 2013;24(7):981–988.e2. https://www.clinicalkey.es/playcontent/1-s2.0-S1051044313008592. doi: 10.1016/j.jvir.2013.03.035. [DOI] [PubMed] [Google Scholar]
- 5.Grosse U, Syha R, Ketelsen D, et al. Cone beam computed tomography improves the detection of injured vessels and involved vascular territories in patients with bleeding of uncertain origin. British journal of radiology. 2018;91(1088):20170562. https://www.ncbi.n1m.nih.gov/pubmed/29848014. doi: 10.1259/bjr.20170562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Carrafiello G, Ierardi AM, Duka E, et al. Usefulness of cone-beam computed tomography and automatic vessel detection software in emergency transarterial embolization. Cardiovasc Intervent Radiol. 2015;39(4):530–537. 10.1007/s00270-015-1213-1. doi: 10.1007/s00270-015-1213-1. [DOI] [PubMed] [Google Scholar]
- 7.Wu P, Sisniega A, Stayman JW, et al. Cone-beam CT for imaging of the head/brain: Development and assessment of scanner prototype and reconstruction algorithms. 2020;47(6):2392–2407. 10.1002/mp.14124. doi: 10.1002/mp.14124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Orth, Robert C, MD, PhD, Wallace MJ, MD, Kuo MD, MD. C-arm cone-beam CT: General principles and technical considerations for use in interventional radiology. Journal of vascular and interventional radiology. 2008;19(6):814–820. https://www.clinicalkey.es/playcontent/1-s2.0-S1051044308002133. doi: 10.1016/j.jvir.2008.02.002. [DOI] [PubMed] [Google Scholar]
- 9.Niu K, Yang P, Wu Y, et al. C-arm conebeam CT perfusion imaging in the angiographic suite: A comparison with multidetector CT perfusion imaging. 2016;37(7):1303–1309. http://www.ajnr.org/content/37/7/1303. doi: 10.3174/ajnr.A4691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Wagner A, Schicho K, Kainberger F, Birkfellner W, Grampp S, Ewers R. Quantification and clinical relevance of head motion during computed tomography. Investigative radiology. 2003;38(11):733–741. http://ovidsp.ovid.com/ovidweb.cgi?T=JS&NEWS=n&CSC=Y&PAGE=fulltext&D=ovft&AN=00004424-200311000-00008. doi: 10.1097/01.rli.0000084889.92250.b0. [DOI] [PubMed] [Google Scholar]
- 11.Nicholson P, Cancelliere NM, Bracken J, et al. Novel flat-panel cone-beam CT compared to multi-detector CT for assessment of acute ischemic stroke: A prospective study. 2021;138(109645). 10.1016/i.ejrad.2021.109645. doi: . [DOI] [PubMed] [Google Scholar]
- 12.Eckert M, Gölitz P, Lücking H, Struffert T, Knossalla F, Doerfler A. Optimized flat-detector CT in stroke imaging: Ready for first-line use? Cerebrovasc Dis. 2017;43(1-2):9–16. 10.1159/000450727. doi: 10.1159/000450727. [DOI] [PubMed] [Google Scholar]
- 13.Spin-Neto R, Wenzel A. Patient movement and motion artefacts in cone beam computed tomography of the dentomaxillofacial region: A systematic literature review. Oral Surgery, Oral Medicine. 2016;121(4):425–433. https://www.sciencedirect.com/science/article/pii/S2212440315013449. doi: 10.1016/j.oooo.2015.11.019. [DOI] [PubMed] [Google Scholar]
- 14.Rit S, Nijkamp J, van Herk M, Sonke J. Comparative study of respiratory motion correction techniques in cone-beam computed tomography. Radiotherapy and oncology. 2011;100(3):356–359. https://www.clinicalkey.es/playcontent/1-s2.0-S0167814011004956. doi: 10.1016/j.radonc.2011.08.018. [DOI] [PubMed] [Google Scholar]
- 15.Sonke J, Zijp L, Remeijer P, van Herk M. Respiratory correlated cone beam CT. Medical physics (Lancaster). 2005;32(4):1176–1186. https://www.narcis.nl/publication/RecordID/oai:pure.amc.nl:publications%2F110b96a1-474f-4f72-b681-f1bb9b5a6313. doi: 10.1118/1.1869074. [DOI] [PubMed] [Google Scholar]
- 16.Bergner F, Berkus T, Oelhafen M, et al. An investigation of 4D cone-beam CT algorithms for slowly rotating scanners. Medical physics (Lancaster). 2010;37(9):5044–5053. 10.1118/1.3480986. doi: 10.1118/1.3480986. [DOI] [PubMed] [Google Scholar]
- 17.Yan H, Wang X, Yin W, et al. Extracting respiratory signals from thoracic cone beam CT projections. PMB. 2013;58(5):1447–1464. 10.1088/0031-9155/58/5/1447. doi: 10.1088/0031-9155/58/5/1447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Rit S, Wolthaus JWH, van Herk M, Sonke J. On-the-fly motion-compensated cone-beam CT using an a priori model of the respiratory motion. Medical physics (Lancaster). 2009;36(6):2283–2296. https://www.narcis.nl/publication/RecordID/oai:pure.amc.nl:publications%2F4e9f1b45-9747-4208-b0f1-58cee4510708. doi: 10.1118/1.3115691. [DOI] [PubMed] [Google Scholar]
- 19.Zhang Q, Hu Y, Liu F, Goodman K, Rosenzweig KE, Mageras GS. Correction of motion artifacts in cone-beam CT using a patient-specific respiratory motion model. Medical physics (Lancaster). 2010;37(6):2901–2909. 10.1118/1.3397460. doi: 10.1118/1.3397460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Jacobson MW, Stayman JW. Compensating for head motion in slowly-rotating cone beam CT systems with optimization transfer based motion estimation. NSSMIC. Oct 2008:5240–5245. 10.1109/NSSMIC.2008.4774416. DOI: 10.1109/NSSMIC.2008.4774416 [DOI] [Google Scholar]
- 21.Kim J, Nuyts J, Kyme A, Kuncic Z, Fulton R. A rigid motion correction method for helical computed tomography (CT). PMB. 2015;60(5):2047–2073. 10.1088/0031-9155/60/5/2047. doi: 10.1088/0031-9155/60/5/2047. [DOI] [PubMed] [Google Scholar]
- 22.Choi J, Maier A, Keil A, et al. Fiducial marker-based correction for involuntary motion in weight-bearing C-arm CT scanning of knees. II. experiment. Medical physics (Lancaster). 2014;41(6Part1):61902. doi: 10.1118/1.4873675. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Berger M, Müller K, Aichert A, et al. Marker-free motion correction in weight-bearing cone-beam CT of the knee joint. Medical physics (Lancaster). 2016;43(3):1235–1248. 10.1118/1.4941012. doi: 10.1118/1.4941012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Ouadah S, Jacobson M, Stayman JW, Ehtiati T, Weiss C, Siewerdsen JH. Correction of patient motion in cone-beam CT using 3D-2D registration. PMB. 2017;62(23):8813–8831. 10.1088/1361-6560/aa9254. doi: 10.1088/1361-6560/aa9254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ens S, Ulrici J, Hell E, Buzug TM. Automatic detection of patient motion in cone-beam computed tomography. 2010 IEEE International Symposium on Biomedical Imaging: From Nano to Macro. Apr 2010:1257–1260. 10.1109/ISBI.2010.5490224. DOI: 10.1109/ISBI.2010.5490224 [DOI] [Google Scholar]
- 26.Berger M, Xia Y, Aichinger W, et al. Motion compensation for cone-beam CT using fourier consistency conditions. PMB. 2017;62(17):7181–7215. 10.1088/1361-6560/aa8129. doi: 10.1088/1361-6560/aa8129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Preuhs A, Maier A, Manhart M, Fotouhi J, Navab N, Unberath M. Double your views – exploiting symmetry in transmission imaging. In: Medical image computing and computer assisted intervention – MICCAI 2018. Cham: Springer International Publishing; 2018:356–364. 10.1007/978-3-030-00928-1_41. 10.1007/978-3-030-00928-1_41. [DOI] [Google Scholar]
- 28.Preuhs A, Maier A, Manhart M, et al. Symmetry prior for epipolar consistency. Int J CARS. 2019;14(9):1541–1551. 10.1007/s11548-019-02027-8. doi: 10.1007/s11548-019-02027-8. [DOI] [PubMed] [Google Scholar]
- 29.Rohkohl C, Lauritsch G, Biller L, Prümmer M, Boese J, Hornegger J. Interventional 4D motion estimation and reconstruction of cardiac vasculature without motion periodicity assumption. Medical image analysis. 2010;14(5):687–694. 10.1016/j.media.2010.05.003. doi: 10.1016/j.media.2010.05.003. [DOI] [PubMed] [Google Scholar]
- 30.Klugmann A, Bier B, Müller K, Maier A, Unberath M. Deformable respiratory motion correction for hepatic rotational angiography. Computerized medical imaging and graphics. 2018;66:82–89. 10.1016/j.compmedimag.2018.03.003. doi: 10.1016/j.compmedimag.2018.03.003. [DOI] [PubMed] [Google Scholar]
- 31.Sisniega A, Stayman JW, Yorkston J, Siewerdsen JH, Zbijewski W. Motion compensation in extremity cone-beam CT using a penalized image sharpness criterion. PMB. 2017;62(9):3712–3734. 10.1088/1361-6560/aa6869. doi: 10.1088/1361-6560/aa6869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Sisniega A, Thawait GK, Shakoor D, Siewerdsen JH, Demehri S, Zbijewski W. Motion compensation in extremity cone-beam computed tomography. Skeletal Radiol. 2019;48(12):1999–2007. 10.1007/s00256-019-03241-w. doi: 10.1007/s00256-019-03241-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Sisniega A, Zbijewski W, Wu P, et al. Multi-motion compensation for high-quality cone-beam CT of the head. The Fifth International Conference on Image Formation in X-Ray Computed Tomography. 2018. https://ct-meeting.org/wp-content/uploads/2021/11/ProceedingsCTMeeting2018.pdf [Google Scholar]
- 34.Kingston A, Sakellariou A, Varslot T, Myers G, Sheppard A. Reliable automatic aligmnent of tomographic projection data by passive auto-focus. Medical physics (Lancaster). 2011;38(9):4934–4945. 10.1118/1.3609096. doi: 10.1118/1.3609096. [DOI] [PubMed] [Google Scholar]
- 35.Hahn J, Bruder H, Rohkohl C, et al. Motion compensation in the region of the coronary arteries based on partial angle reconstructions from short-scan CT data. Medical physics (Lancaster). 2017;44(11):5795–5813. 10.1002/mp.12514. doi: 10.1002/mp.12514. [DOI] [PubMed] [Google Scholar]
- 36.Rohkohl C, Bruder H, Stierstorfer K, Flohr T. Improving best-phase image quality in cardiac CT by motion correction with MAM optimization. Medical physics (Lancaster). 2013;40(3):031901–n/a. 10.1118/1.4789486. doi: 10.1118/1.4789486. [DOI] [PubMed] [Google Scholar]
- 37.Kim S, Chang Y, Ra JB. Cardiac motion correction for helical CT scan with an ordinary pitch. TMI. 2018:37(7):1587–1596. https://ieeexplore.ieee.org/docmnent/8320379. doi: 10.1109/TMI.2018.2817594. [DOI] [PubMed] [Google Scholar]
- 38.Jang S, Kim S, Kim M, Son K, Lee K, Ra JB. Head motion correction based on filtered backprojection in helical CT scanning. TMI. 2020;39(5):1636–1645. https://ieeexplore.ieee.org/docmnent/8903230. doi: 10.1109/TMI.2019.2953974. [DOI] [PubMed] [Google Scholar]
- 39.Capostagno S, Sisniega A, Stayman JW, Ehtiati T, Weiss CR, Siewerdsen JH. Deformable motion compensation for interventional cone-beam CT. 2021;66(5):055010. 10.1088/1361-6560/abb16e. doi: 10.1088/1361-6560/abb16e. [DOI] [PubMed] [Google Scholar]
- 40.Wicklein J, Kunze H, Kalender WA, Kyriakou Y. Image features for misalignment correction in medical flat-detector CT. Medical physics (Lancaster). 2012;39(8):4918–4931. 10.1118/1.4736532. doi: 10.1118/1.4736532. [DOI] [PubMed] [Google Scholar]
- 41.Wicklein J, Lauritsch G, Müller K, Kunze H, Kalender WA, Kyriakou Y. Aortic root motion correction in c-arm flat-detector ct. 12th International Meeting on Fully Three-Dimensional Image Reconstruction in Radiology and Nuclear Medicine. 2013:481–484. https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.434.8826&rep=rep1&type=pdf [Google Scholar]
- 42.Wang Zhou, Bovik AC, Sheikh HR, Simoncelli EP. Image quality assessment: From error visibility to structural similarity. TIP. 2004;13(4):600–612. https://ieeexplore.ieee.org/document/1284395. doi: 10.1109/TIP.2003.819861. [DOI] [PubMed] [Google Scholar]
- 43.Tien H, Yang H, Shueng P, Chen J. Cone-beam CT image quality improvement using cycle-deblur consistent adversarial networks (cycle-deblur GAN) for chest CT imaging in breast cancer patients. Scientific reports. 2021;11(1):1133. https://www.ncbi.nlm.nih.gov/pubmed/33441936. doi: 10.1038/s41598-020-80803-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Gao Q, Li S, Zhu M, et al. Blind CT image quality assessment via deep learning framework. 2019 IEEE Nuclear Science Symposium and Medical Imaging Conference (NSS/MIC). 2019:1–4. doi: 10.1109/NSS/MIC42101.2019.9059777. [DOI] [Google Scholar]
- 45.Oyama A, Kumagai S, Arai N, et al. Image quality improvement in cone-beam CT using the super-resolution technique. Journal of radiation research. 2018;59(4):501–510. https://www.ncbi.nlm.nih.gov/pubmed/29659997. doi: 10.1093/jrr/rry019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Sheikh HR, Bovik AC. Image information and visual quality. TIP. 2006;15(2):430–444. https://ieeexplore.ieee.org/document/1576816. doi: 10.1109/TIP.2005.859378. [DOI] [PubMed] [Google Scholar]
- 47.Xie H, Lei Y, Wang T, et al. High through-plane resolution CT imaging with self-supervised deep learning. PMB. 2021:66(14):145013. 10.1088/1361-6560/ac0684. doi: 10.1088/1361-6560/ac0684. [DOI] [PubMed] [Google Scholar]
- 48.Küstner T, Armanious K, Yang J, Yang B, Schick F, Gatidis S. Retrospective correction of motion-affected MR images using deep learning frameworks. Magnetic resonance in medicine. 2019;82(4):1527–1540. 10.1002/mrm.27783. doi: 10.1002/mrm.27783. [DOI] [PubMed] [Google Scholar]
- 49.Latif S, Asim M, Usman M, Qadir J, Rana R. Automating motion correction in multishot MRI using generative adversarial networks. 2018. https://arxiv.org/abs/1811.09750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Ko Y, Moon S. Baek J, Shim H Rigid and non-rigid motion artifact reduction in X-ray CT using attention module. 2021;67:101883. https://www.sciencedirect.com/science/article/pii/S1361841520302474. doi: 10.1016/j.media.2020.101883. [DOI] [PubMed] [Google Scholar]
- 51.Huang Y, Preuhs A, Lauritsch G, Manhart M, Huang X, Maier A. Data consistent artifact reduction for limited angle tomography with deep learning prior.. 2019. https://arxiv.org/abs/1908.06792. [Google Scholar]
- 52.Maier J, Nitschke M, Choi J, et al. Rigid and non-rigid motion compensation in weight-bearing cone-beam CT of the knee using (noisy) inertial measurements. 2021. https://arxiv.org/abs/2102.12418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Oksuz I, Ruijsink B, Puyol-Antón E, et al. Automatic CNN-based detection of cardiac MR motion artefacts using k-space data augmentation and curriculum learning. 2019;55:136–147. https://www.sciencedirect.com/science/article/pii/S1361841518306765. doi: 10.1016/j.media.2019.04.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Sisniega A, Capostagno S. Zbijewski W. et al. Estimation of local deformable motion in image-based motion compensation for interventional cone-beam CT. 6th International Conference on Image Formation in X-Ray Computed Tomography. 2020;11312:113121M. 10.1117/12.2549753 [DOI] [Google Scholar]
- 55.Sisniega A, Capostagno S, Zbijewski W, et al. Local motion estimation for improved cone-beam CT deformable motion compensation. Proceedings of the 6th International Conference on Image Formation in X-Ray Computed Tomography. 2020:236–239. https://ct-meeting.org/wp-content/uploads/2021/11/ProceedingsCTMeeting2020.pdf. [Google Scholar]
- 56.Elss T, Nickisch H, Wissel T, Bippus R, Morlock M, Grass M. Motion estimation in coronary CT angiography images using convolutional neural networks. 2018. https://hannes.nickisch.org/papers/conferences/elss18motion_artifact2.pdf [DOI] [PubMed] [Google Scholar]
- 57.Lossau T, Nickisch H, Wissel T, et al. Motion artifact recognition and quantification in coronary CT angiography using convolutional neural networks. 2019;52:68–79. https://www.sciencedirect.com/science/article/pii/S1361841518308624. doi: 10.1016/j.media.2018.11.003. [DOI] [PubMed] [Google Scholar]
- 58.Sisniega A, Huang H, Zbijewski W, et al. Deformable image-based motion compensation for interventional cone-beam CT with a learned autofocus metric. 2021;11595:241. 10.1117/12.2582140. doi: 10.1117/12.2582140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Bier B, Aschoff K, Syben C, et al. Detecting anatomical landmarks for motion estimation in weight-bearing imaging of knees: First international workshop, MLMIR 2018, held in conjunction with MICCAI 2018, granada, spain, september 16, 2018, proceedings. In: Machine learning for medical image reconstruction. ; 2018:83–90. 10.1007/978-3-030-00129-2_10. 10.1007/978-3-030-00129-2_10. [DOI] [Google Scholar]
- 60.Preuhs A, Manhart M, Roser P, et al. Appearance learning for image-based motion estimation in tomography. TMI. 2020;39(11):3667–3678. https://ieeexplore.ieee.org/document/9117090. doi: 10.1109/TMI.2020.3002695. [DOI] [PubMed] [Google Scholar]
- 61.Kang Le, Ye Peng, Li Yi, Doermann D. Convolutional neural networks for no-reference image quality assessment. CVPR. Jun 2014:1733–1740. 10.1109/CVPR.2014.224. DOI: 10.1109/CVPR.2014.224 [DOI] [Google Scholar]
- 62.Bosse S, Maniry D, Muller K, Wiegand T, Samek W. Deep neural networks for no-reference and full-reference image quality assessment. TIP. 2018;27(1):206–219. https://ieeexplore.ieee.org/document/8063957. doi: 10.1109/TIP.2017.2760518. [DOI] [PubMed] [Google Scholar]
- 63.Huang H, Siewerdsen JH, Zbijewski W, Weiss CR, Ehtiati T, Sisniega A. Reference-free, learning-based image similarity: Application to motion compensation in cone-beam CT. 16th Virtual International Meeting on Fully 3D Image Reconstruction in Radiology and Nuclear Medicine. Oct 7, 2021:67–71. https://arxiv.org/abs/2110.04143 [Google Scholar]
- 64.He K, Zhang X, Ren S, Sun J. Deep residual learning for image recognition. 2015. https://arxiv.org/abs/1512.03385. [Google Scholar]
- 65.Hansen N. CMA-ES: A function value free second order optimization method. 2014. https://hal.inria.fr/hal-01110313. [Google Scholar]
- 66.Long Yong, Fessler JA Balter JM. 3D forward and back-projection for X-ray CT using separable footprints. TMI. 2010;29(11):1839–1850. https://ieeexplore.ieee.org/document/5482021. doi: 10.1109/TMI.2010.2050898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Wang Z., Simoncelli EP, Bovik AC. Multiscale structural similarity for image quality assessment. The Thrity-Seventh Asilomar Conference on Signals, Systems & Computers, 2003. 2003;2:1398–1402 Vol.2. doi: 10.1109/ACSSC.2003.1292216. [DOI] [Google Scholar]
- 68.Lossau (née Elss) T, Nickisch H, Wissel T, et al. Motion estimation and correction in cardiac CT angiography images using convolutional neural networks. Computerized medical imaging and graphics. 2019;76:101640. 10.1016/j.compmedimag.2019.06.001. doi: 10.1016/j.compmedimag.2019.06.001. [DOI] [PubMed] [Google Scholar]
- 69.Zhang Y, Zhang L, Sun Y. Rigid motion artifact reduction in CT using the phase correlation method. Recent Advances in Electrical & Electronic Engineering. 2020;13(8):1119–1128. http://www.eurekaselect.com/openurl/content.php?genre=article&issn=2352-0965&volume=13&issue=8&spage=1119. doi: 10.2174/2352096513999200606224154. [DOI] [Google Scholar]
- 70.Kläser K, Borges P, Shaw R, et al. A multi-channel uncertainty-aware multi-resolution network for MR to CT synthesis. Applied sciences. 2021;11(4):1667. https://www.ncbi.nlm.nih.gov/pubmed/33763236. doi: 10.3390/app11041667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Ehteshami Bejnordi B, Zuidhof GCA, Balkenhol MC, et al. Context-aware stacked convolutional neural networks for classification of breast carcinomas in whole-slide histopathology images. Journal of medical imaging (Bellingham, Wash.). 2017;4(4):044504. https://www.narcis.nl/publication/RecordID/oai:repository.ubn.ru.nl:2066%2F181885. doi: 10.1117/1.JMI.4.4.044504. [DOI] [PMC free article] [PubMed] [Google Scholar]


