A bit-vector differential model for the modular addition by a constant and its applications to differential and impossible-differential cryptanalysis

Abstract

ARX algorithms are a class of symmetric-key algorithms constructed by Addition, Rotation, and XOR. To evaluate the resistance of an ARX cipher against differential and impossible-differential cryptanalysis, the recent automated methods employ constraint satisfaction solvers to search for optimal characteristics or impossible differentials. The main difficulty in formulating this search is finding the differential models of the non-linear operations. While an efficient bit-vector differential model was obtained for the modular addition with two variable inputs, no differential model for the modular addition by a constant has been proposed so far, preventing ARX ciphers including this operation from being evaluated with automated methods. In this paper, we present the first bit-vector differential model for the n-bit modular addition by a constant input. Our model contains $O({log}_2(n))$ basic bit-vector constraints and describes the binary logarithm of the differential probability. We describe an SMT-based automated method that includes our model to search for differential characteristics of ARX ciphers including constant additions. We also introduce a new automated method for obtaining impossible differentials where we do not search over a small pre-defined set of differences, such as low-weight differences, but let the SMT solver search through the space of differences. Moreover, we implement both methods in our open-source tool ArxPy to find characteristics and impossible differentials of ARX ciphers with constant additions in a fully automated way. As some examples, we provide related-key impossible differentials and differential characteristics of TEA, XTEA, HIGHT, LEA, SHACAL-1, and SHACAL-2, which achieve better results compared to previous works.

Introduction

Low-end devices such as RFID tags, sensor networks, and the Internet of Things (IoT) are becoming ubiquitous. In 2018, Gartner, Inc. forecasted that there would be more than 25 billion connected devices forming the IoT by 2021 [24], and following the COVID-19 lockdowns Gartner also revealed that the unprecedented event led IoT implementers to increase IoT investments to reduce costs [25]. Traditional cryptographic algorithms are not suitable for these resource-constrained devices, and several lightweight cryptographic algorithms have been recently proposed to meet this growing demand. In this regard, the National Institute of Standards and Technology (NIST) has started a process to evaluate and standardize lightweight cryptographic algorithms [59].

ARX primitives, composed exclusively of modular Additions, cyclic Rotations, and XORs, are a promising class of lightweight cryptographic algorithms with the most efficient software implementations on low-end microcontrollers [17]. There are many noteworthy ARX algorithms, such as the hash function BLAKE [1], the stream cipher Salsa20 [7], the MAC algorithm Chaskey [58] and notable block ciphers like HIGHT [31], LEA [32], SPECK [6], SPARX [16] or CHAM [41]. Usually, ciphers that are exclusively composed of ARX operations and other common bit-vector operations (e.g., modular multiplication or logical shifts) are also considered in the class of ARX ciphers, such as IDEA [43], TEA [73], or XTEA [60].

The security of ARX ciphers is evaluated by analysing their robustness against various attacks. Some of the most successful attacks applied to ARX algorithms are differential cryptanalysis and their variants, such as boomerang or related-key differential attacks [32, 41]. These attacks exploit differences in the inputs that propagate through the cipher with high probability. Another powerful attack based on non-random propagation of differences is impossible-differential cryptanalysis [8, 37], which exploits input differences propagating to differences in the outputs with zero probability.

The standard approach to show an ARX cipher is secure against differential and impossible-differential attacks is by finding the optimal characteristics (i.e., trails of differences with the highest probabilities) and the longest impossible differentials and checking that no high-probability characteristic and no impossible differential cover most rounds of the cipher [31, 32]. When the best attack in the design stage is a differential or an impossible-differential attack, the number of rounds of the cipher is determined by the longest observed high-probability characteristic or impossible differential. Thus, searching for optimal characteristics and impossible differentials is a crucial step in the design and security analysis of a cipher.

Two main techniques have been applied to search for optimal characteristics of ARX algorithms: branch-and-bound algorithms [11, 13] based on Matsui’s algorithm [54], and the recent automated methods based on Constraint Satisfaction Problems (CSP), such as SMT (Satisfiability Modulo Theories) or MILP (Mixed Integer Linear Programming) problems [21, 57]. CSP-based methods have also been recently applied to find impossible differentials [14, 65, 66]. These automated methods formulate the characteristic or impossible-differential search problem as a CSP and delegate the solving task to one of the powerful off-the-shelf CSP solvers available nowadays [5, 49]. While some CSP-based open-source tools automate the search of ARX characteristics (e.g., CryptoSMT [38]), no CSP-based open-source tool has been published to search for impossible differentials of ARX ciphers.

The main difficulty in formulating a CSP-based search problem lies in the differential models of the non-linear operations, that is, the constraints describing the differential probability of the non-linear operations of the cipher. ARX ciphers can be efficiently described using the bit-vector theory of SMT, and several bit-vector differential models have been proposed so far [39, 47, 48]. For the modular addition with two n-bit operands, the foremost non-linear operation in ARX primitives, Lipmaa and Moriai found a bit-vector algorithm for computing the differential probability with complexity $O({log}_{2}n)$ [47]. This algorithm can be straightforwardly translated to a bit-vector differential model, and it has been used in several SMT-based methods to search for characteristics [48, 57, 68] and impossible differentials [65] of ARX ciphers.

However, no CSP-based differential model has been proposed for the modular addition with a constant input, preventing from searching for characteristics or impossible differentials of ARX ciphers that contain constant additions. Lipmaa’s algorithm is restricted to the modular addition with two operands, and it cannot be applied when one of the inputs is fixed to a constant, as we will discuss later. Machado proposed an algorithm to compute the differential probability of the constant addition [53], but it cannot be translated to an efficient bit-vector differential model due to its recursive nature and the use of floating-point arithmetic.

Contributions

We propose an efficient bit-vector differential model for the modular addition by an n-bit constant. Our model contains $O({log}_{2}n)$ basic bit-vector constraints and it is composed of a bit-vector formula that determines whether a differential over the constant addition has non-zero probability, and a bit-vector function that computes the binary logarithm of the differential probability. Our bit-vector model exploits the properties of the carry chain of the modular addition and relies on efficient well-known bit-vector functions, such as the Hamming weight or the bit-reversal, and new bit-vector functions that we have developed for the binary logarithm.

Furthermore, we describe an SMT-based automated method to search for characteristics of ARX ciphers, including constant additions. Our method is composed of an iterated search of optimal characteristics of round-reduced versions of the cipher and an automated encoding technique that formulates the SMT problems from the cipher’s Single Static Assignment (SSA) form. Moreover, we describe a new automated method to search for impossible differentials of ARX ciphers which does not depend on any pre-defined sets of input and output differences.

We have implemented our methods in an SMT-based open-source tool ArxPy,1 which fully automated the search of ARX characteristics and impossible differentials. ArxPy is the first open-source tool that can search for the characteristics of ARX ciphers with constant additions, and it is also the first CSP-based open-source tool that automates the search of ARX impossible differentials. ArxPy offers a simple interface to represent any ARX cipher, different types of characteristics and impossible differentials to search, and a complete documentation.

We have applied our characteristic and impossible-differential search methods to several ARX ciphers containing constant additions to provide some examples. In particular, we have searched for different types of related-key characteristics alongside related-key impossible differentials of TEA, XTEA, HIGHT, LEA, SHACAL-1, and SHACAL-2. With our automated approach, we have revisited results previously found with manual and ad-hoc techniques. We have obtained better characteristics in terms of probability and number of rounds, and longer impossible differentials.

With our bit-vector model for the constant addition, the SMT-based automated methods, and our open-source tool ArxPy, we provide cipher designers with the resources to design ARX ciphers, including constant additions that are secure against differential and impossible-differential attacks. Thus, cipher designers can choose the best constants for the modular additions and optimize the number of rounds to balance security and efficiency.

Differences to the conference version

This paper is an extended full version of the conference paper [3]. Thus, the content of the conference paper is included in this paper, namely the bit-vector differential model for the constant addition, the SMT-based method and tool to search for ARX differential characteristics and the related-key differential characteristics found for TEA, XTEA, HIGHT, and LEA. Apart from this content, the rest of this paper is new material. This new content includes the SMT-based method to search for impossible differentials of ARX ciphers, the tool to search for ARX impossible differentials, the related-key differential characteristics found for SHACAL-1 and SHACAL-2 and the related-key impossible differentials found for TEA, XTEA, HIGHT, LEA, SHACAL-1 and SHACAL-2. Furthermore, this paper enhances the description of the bit-vector differential model of the constant addition with improved proofs and new examples.

Outline

The notations and preliminaries are introduced in Sect. 2, and the bit-vector model for the modular addition by a constant is described in Sect. 3. Section 4 illustrates the formulation of the search of characteristics and impossible differentials as sequences of SMT problems. Section 5 presents the characteristics and impossible differentials found for TEA, XTEA, HIGHT, LEA, SHACAL-1, and SHACAL-2 using our automated approaches. Finally, Sect. 6 concludes the paper and addresses future works.

Preliminaries

Notations

Let x be an integer such that its n-bit vector representation when $0\le x<2^n$ is $x=(x[n-1],\cdots ,x[0])$, where x[0] and $x[n-1]$ denote respectively the least and the most significant bit. For ease of notation, we define $x[i]=0$ when $i<0$ and the symbol $\ast$ stands for an undetermined bit. The usual integer operations are denoted by $(+,-,\times ,/)$ and the basic bit-vector operations are gathered in Table 1.

Table 1.

Basic bit-vector operations for n-bit vectors

x[i, j]	The bit-vector $(x[i],\cdots ,x[j])$, $n>i\ge j\ge 0$
$\neg x$	Bit-wise NOT of x
$x\Vert y$	Concatenation of x and y
$x\wedge y$	Bit-wise AND of x and y
$x\vee y$	Bit-wise OR of x and y
$x\oplus y$	Bit-wise XOR of x and y
$x\ll i$	(Logical) left shift of x by i bits
$x\gg i$	Right shift of x by i bits
$x⋘i$	Left cyclic rotation of x by i bits
$x⋙i$	Right cyclic rotation of x by i bits
$x⊞y$	Modular addition of x and y
$x\boxminus y$	Modular subtraction of x and y
$\mathsf{Equals}(x,y)$	Bit-vector equality of x and y, returning True
	If x and y are the same, otherwise False

A mathematical expression only involving bit-vector variables and basic bit-vector operations is called a bit-vector expression. A bit-vector formula is a bit-vector expression returning $\mathtt{True}$ or $\mathtt{False}$, such as $\mathsf{Equals}$, whereas an n-bit vector function is a bit-vector expression returning an n-bit vector. In order to measure the complexity of the bit-vector differential model that we propose in this paper, we define the bit-vector complexity of a bit-vector expression as the number of basic bit-vector operations that the expression is composed of.

In the literature of the bit-vector theory, the set of basic bit-vector operations usually includes the operations gathered in Table 1 and few additional operations, such as modular multiplication or modular division [42]. However, modular multiplication and modular division are much more costly than the other operations in practice, and we have excluded them from our set of basic bit-vector operations, which resembles the unit-cost RAM model used in [47].

Apart from the basic bit-vector operations listed in Table 1, we will also employ the following well-known bit-vector functions: $\mathsf{Carry},\mathsf{Rev},\mathsf{RevCarry},\mathsf{HW}$ and $\mathsf{LZ}$. The carry function $c=\mathsf{Carry}(x,y)$ returns the n-bit carry chain of the n-bit modular addition $x⊞y$. It is defined iteratively as $c[0]=0$ and $c[i+1]=(x[i]\wedge y[i])\oplus (x[i]\wedge c[i])\oplus (y[i]\wedge c[i])$ for $0<i<n-1$. Note that the carry has bit-vector complexity O(1), since $\mathsf{Carry}(x,y)=x\oplus y\oplus (x⊞y)$. The carry function is an efficient function that allows propagating information from the least significant bits to the most significant bits, a property that we will exploit for our bit-vector differential model.

The bit-reversal function $\mathsf{Rev}(x)$ reverses the order of bits of x, i.e., $\mathsf{Rev}(x)=(x[0],x[1],\cdots ,x[n-1])$. This function can be computed using a divide and conquer method with bit-vector complexity $O({log}_{2}n)$ [29, Fig. 7-1]. We will use this function to define the reverse carry, $\mathsf{RevCarry}(x,y)=\mathsf{Rev}(\mathsf{Carry}(\mathsf{Rev}(x),\mathsf{Rev}(y)))$, which allows to propagate information from right to left and also has bit-vector complexity $O({log}_{2}n)$.

The Hamming weight $\mathsf{HW}(x)$ returns an n-bit vector denoting the number of non-zero bits of the n-bit input x. Similar to the bit-reversal, the Hamming weight can be computed using a divide and conquer approach with bit-vector complexity $O({log}_{2}n)$ [29, Fig. 5-2]. The Hamming weight will be one of the main building blocks to obtain an efficient bit-vector representation of the binary logarithm.

The last bit-vector function we will consider is the leading zeros function $\mathsf{LZ}(x)$. This function marks the leading zeros of an n-bit input x, that is, for $0\le i<n$, $\mathsf{LZ}(x)[i]=1⟺x[n-1,i]=0$. This function is used as a subroutine for the well-known function to compute the number of leading zeros. Similar to the previous bit-vector functions, $\mathsf{LZ}$ can be computed with bit-vector complexity $O({log}_{2}n)$ [29, Fig. 5-16].

Differential and impossible-differential cryptanalysis

A block cipher is a family of permutations parametrized by a $\kappa$-bit key k, mapping n-bit plaintexts p to n-bit ciphertexts c. Most block ciphers consist of a key scheduling algorithm $\mathsf{KS}$, which derives round keys $k_1,\cdots ,k_r$ from the master key k, and an encryption algorithm $E_k$, which processes the plaintext by iterating a round function f and injecting a round key at each round, i.e., $E_k=f_{k_r}\circ \cdots \circ f_{k_1}$.

Block ciphers are shown to be secure by analysing their resistance against all known attacks. One of the most potent attacks, especially to ARX primitives, is differential cryptanalysis [10]. It exploits the non-random propagation of differences in the input to recover the secret key.

Let F be an n-bit to n-bit function and $({\mathrm{\Delta }}_p,{\mathrm{\Delta }}_c)$ be the XOR of a pair of inputs $(p,p^{\prime })$ and their corresponding outputs $(c,c^{\prime })$, i.e., ${\mathrm{\Delta }}_p=p\oplus p^{\prime }$ and ${\mathrm{\Delta }}_c=c\oplus c^{\prime }$. The pair $({\mathrm{\Delta }}_p,{\mathrm{\Delta }}_c)$ is called a differential and its probability is defined as

$$\begin{array}{c}\hfill Pr\left[{\mathrm{\Delta }}_p,\stackrel{F}{\to },{\mathrm{\Delta }}_c\right]=\frac{\#\{p:F(p)\oplus F(p\oplus {\mathrm{\Delta }}_p)={\mathrm{\Delta }}_c\}}{2^n}.\end{array}$$

A differential is valid if it has non-zero probability. In this case, its weight is defined as

$$\begin{array}{c}\hfill {\mathsf{weight}}_F({\mathrm{\Delta }}_p,{\mathrm{\Delta }}_c)=-{log}_2\left(Pr,\left[{\mathrm{\Delta }}_p,\stackrel{F}{\to },{\mathrm{\Delta }}_c\right]\right).\end{array}$$

The differential $0\stackrel{F}{\to }0$ has probability 1 for any function F, and a differential with non-zero input difference over a random n-bit permutation has probability $2^{-n}$. Differential cryptanalysis [10] exploits a differential over the n-bit block cipher with probability $p>2^{-n}$ to recover the secret key with roughly $O(p^{-1})$ encryption calls.

Related-key differential cryptanalysis [34] extends differential cryptanalysis by considering key differences. A related-key differential is given by a pair of differentials over the key schedule and the encryption function respectively,

$$\begin{array}{c}\hfill \left({\mathrm{\Delta }}_k,\stackrel{\mathsf{KS}}{\to },\left({\mathrm{\Delta }}_{k_1},,,\cdots ,,,{\mathrm{\Delta }}_{k_r}\right)\right),\left({\mathrm{\Delta }}_p,\stackrel{E}{\to },{\mathrm{\Delta }}_c\right),\end{array}$$

where the ciphertext difference is computed using the related round-key pairs,

$$\begin{array}{c}\hfill {\mathrm{\Delta }}_c=\left(f_{k_r},\circ ,\cdots ,\circ ,f_{k_1}\right)(p)\oplus \left(f_{k_r\oplus {\mathrm{\Delta }}_{k_r}},\circ ,\cdots ,\circ ,f_{k_1\oplus {\mathrm{\Delta }}_{k_1}}\right)\left(p,\oplus ,{\mathrm{\Delta }}_p\right).\end{array}$$

The probability of a related-key differential is the product of the probability of key schedule differential $p_{\mathsf{KS}}$ and the probability of encryption differential $p_E$.

A related-key attack exploits a related-key differential with $p_{\mathsf{KS}}>2^{-\kappa }$ and $p_E>2^{-n}$ to recover the secret key with complexity $O({(p_{\mathsf{KS}}\times p_E)}^{-1})$. The attacker takes about $p_{\mathsf{KS}}^{-1}$ key pairs to find one key, on average, that satisfies the key schedule differential. Next and for each key pair, the attacker runs a differential attack over the encryption using $O(p_E^{-1})$ encryption calls.

Related-key differential cryptanalysis requires a very powerful attacker that can query the encryption function $E_{k\oplus {\mathrm{\Delta }}_k}$ for many keys $k\oplus {\mathrm{\Delta }}_k$. In fact, if an adversary can query $E_{k\oplus {\mathrm{\Delta }}_k}$ for $2^m$ key differences ${\mathrm{\Delta }}_k$, any block cipher is vulnerable to a related-key attack with complexity $O(2^m+2^{n-m})$ [74]. Thus, we distinguish between weak related-key differentials (i.e., $p_{\mathsf{KS}}<1$) and strong related-key differentials (i.e., $p_{\mathsf{KS}}=1$), which can be exploited in practice with a single related-key pair. Furthermore, we define equivalent keys as pairs of related keys $(k,k\oplus {\mathrm{\Delta }}_k)$ such that $\forall p,E_k(p)=E_{k\oplus {\mathrm{\Delta }}_k}(p\oplus {\mathrm{\Delta }}_p)\oplus {\mathrm{\Delta }}_c$, for some $({\mathrm{\Delta }}_p,{\mathrm{\Delta }}_c)$. Note that a related-key differential with $p_E=1$ leads to $2^{\kappa }{p}_{\mathsf{KS}}$ pairs of equivalent keys.

Lastly, we consider (related-key) impossible differentials. A differential $({\mathrm{\Delta }}_p,{\mathrm{\Delta }}_c)$ over a function F is called impossible if its probability is zero, and a related-key differential $({\mathrm{\Delta }}_k,{\mathrm{\Delta }}_p\to {\mathrm{\Delta }}_c)$ over a block cipher is called impossible if its probability is zero for all keys. Impossible-differential cryptanalysis [8] is an attack on block ciphers that exploits an impossible differential over the block cipher holding for every key. Related-key impossible-differential cryptanalysis is a combination of impossible-differential cryptanalysis and related-key cryptanalysis. Using the known difference of the key pairs and the input and the output of the impossible differential, the attacker discards the wrong keys to obtain the correct key.

Searching for characteristics and impossible differentials.

The most challenging step to launch a differential attack is finding a differential with high probability. The main approach is to analyse how differences traverse through the round function and search for a characteristic, that is, a trail of differences

$$\begin{array}{c}\hfill \mathrm{\Omega }=\left({\mathrm{\Delta }}_p,=,{\mathrm{\Delta }}_{x_0},\stackrel{f_{k_1}}{\to },{\mathrm{\Delta }}_{x_1},\to ,\cdots ,\to ,{\mathrm{\Delta }}_{x_{r-1}},\stackrel{f_{k_r}}{\to },{\mathrm{\Delta }}_{x_r},=,{\mathrm{\Delta }}_c\right).\end{array}$$

Similar to differentials, a characteristic $\mathrm{\Omega }$ is valid if it has non-zero probability and its weight is defined as $-{log}_2(Pr[\mathrm{\Omega }])$. Furthermore, we denote a related-key characteristic by a pair of characteristics $({\mathrm{\Omega }}_{\mathsf{KS}},{\mathrm{\Omega }}_E)$, where ${\mathrm{\Omega }}_{\mathit{KS}}$ is the key schedule characteristic containing the trail of differences from the master key to the round keys and ${\mathrm{\Omega }}_E$ is the encryption characteristic containing the trail of differences through the encryption.

Obtaining the exact probability of a characteristic is computationally infeasible. Thus, two assumptions are commonly made. First, it is assumed that the differential probabilities over each round are independent, which allows computing the weight of a characteristic by summing the round weights, i.e.,

$$\begin{array}{c}\hfill \mathsf{weight}(\mathrm{\Omega })=\sum _{i=0}^r\mathsf{weight}({\mathrm{\Delta }}_{x_i}\to {\mathrm{\Delta }}_{x_{i+1}}).\end{array}$$

Second, it is assumed that the probability of a characteristic does not strongly depend on the choice of the secret key, also known as the hypothesis of stochastic equivalence [44], which allows computing the weight of a characteristic by averaging over all keys.

On top of that, designers also assume that the probability of a differential $({\mathrm{\Delta }}_p,{\mathrm{\Delta }}_c)$ is close to the probability of the best characteristic $({\mathrm{\Delta }}_p\to \cdots \to {\mathrm{\Delta }}_c)$, and they prove a cipher is secure against differential cryptanalysis by showing that characteristics with high probability cannot cover most rounds of the cipher. While these assumptions do not always hold, currently this is the best systematic approach to argue security against differential cryptanalysis, and this heuristic approach is widely used for ARX ciphers in practice [21, 39, 57, 68–70].

Searching for characteristics is usually dependent on some assumptions, as mentioned earlier. In contrast, the process of obtaining an impossible differential typically results in a sound proof, guaranteeing that the probability of the achieved differential is equal to zero. Therefore, most of the impossible-differential search methods are sound but not complete. In other words, any differential found by these methods is assuredly impossible, yet there may be many impossible differentials that the search methods cannot detect.

SMT solvers

A recent approach to search for characteristics and impossible differentials of ARX ciphers is by formulating the search problem as an SMT problem in the bit-vector theory [2, 39, 48, 57, 65, 68]. Satisfiability Modulo Theories (SMT) refers to the problem of determining whether a first order formula is satisfiable with respect to some logical theory. SMT problems are a generalization of SAT problems; while the latter problems are expressed in propositional logic, SMT formulas can be expressed in richer logics, such as the theory of bit-vectors or the theory of integers.

SMT has grown in recent years into a very active research field, and several off-the-shelf SMT solvers are available nowadays [5]. Most SMT solvers can determine the satisfiability of a problem and obtain an assignment of the variables that satisfies the problem. This feature allows SMT solvers to be applied in search problems.

An SMT problem in the bit-vector theory is given by a set of bit-vector variables and a set of bit-vector formulas or constraints. The constraints can be defined with the usual logical operations (e.g., $\mathsf{Equals},\mathsf{NotEquals},\mathsf{Implies}$, etc.) and the usual bit-vector operations (e.g., $\oplus ,⊞,⋘$, etc.).

For example, a bit-vector SMT problem to find an 8-bit preimage of $y=f(x)=x\oplus ((x⊞x)\vee 1)$, given the 8-bit image $y=3=\mathtt{00000011}$, is the following:

$$\begin{array}{c}\hfill \exists x\in {\{0,1\}}^8:\mathsf{Equals}(\mathtt{00000011},x\oplus ((x⊞x)\vee 1).\end{array}$$

This problem is satisfiable and the only assignment that satisfies the problem is $x=\mathtt{11111110}$.

Differential models

To represent a characteristic in a constraint satisfaction problem, it is necessary to find a differential model of the round function f. For an SMT problem in the bit-vector theory, a differential model of a function $y=f(x)$ is given by a bit-vector formula ${\mathsf{valid}}_f({\mathrm{\Delta }}_x,{\mathrm{\Delta }}_y)$ and a bit-vector function ${\mathsf{weight}}_f({\mathrm{\Delta }}_x,{\mathrm{\Delta }}_y)$. The formula ${\mathsf{valid}}_f({\mathrm{\Delta }}_x,{\mathrm{\Delta }}_y)$ is True if and only if the differential $({\mathrm{\Delta }}_x\to {\mathrm{\Delta }}_y)$ over f is valid, and the function ${\mathsf{weight}}_f({\mathrm{\Delta }}_x,{\mathrm{\Delta }}_y)$ returns the weight of a valid differential $({\mathrm{\Delta }}_x\to {\mathrm{\Delta }}_y)$.

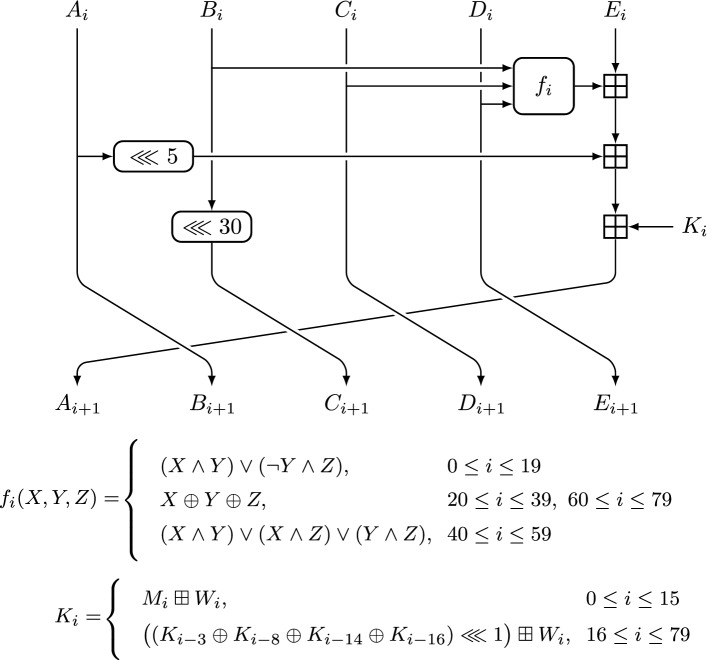
Characteristics over ARX ciphers are usually defined by considering the difference after each ARX operation. The differential models of the XOR and the cyclic rotations are very simple since these operations propagate differences deterministically, that is,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathrm{\Delta }}_{x_1},{\mathrm{\Delta }}_{x_2}& \stackrel{f(x_1,x_2)=x_1\oplus x_2}{\to }{\mathrm{\Delta }}_{x_1}\oplus {\mathrm{\Delta }}_{x_2},\hfill \\ \hfill {\mathrm{\Delta }}_x& \stackrel{f_a(x)=x⋘a}{\to }{\mathrm{\Delta }}_x⋘a,\hfill \end{array}\begin{array}{cc}\hfill {\mathrm{\Delta }}_x& \stackrel{f_a(x)=x\oplus a}{\to }{\mathrm{\Delta }}_x,\hfill \\ \hfill {\mathrm{\Delta }}_x& \stackrel{f_a(x)=x⋙a}{\to }{\mathrm{\Delta }}_x⋙a.\hfill \end{array}\end{array}$$

For the modular addition with two n-bit inputs, $y=f(x_1,x_2)=x_1⊞x_2$, the algorithm by Lipmaa and Moriai [47] can be translated into the following differential model with bit-vector complexity $O({log}_{2}n)$.

Theorem 1

Let $(({\mathrm{\Delta }}_{x_1},{\mathrm{\Delta }}_{x_2}),{\mathrm{\Delta }}_y)$ be a differential over the modular addition $y=x_1⊞x_2$ and denote $\overleftarrow{x}=x\ll 1$ and $\mathrm{eq}(a,b,c)=(\neg a\oplus b)\wedge (\neg a\oplus c)$. Then, the differential is valid if and only if the bit-vector formula

$$\begin{array}{c}\hfill {\mathsf{valid}}_{⊞}(({\mathrm{\Delta }}_{x_1},{\mathrm{\Delta }}_{x_2}),{\mathrm{\Delta }}_y)=\mathsf{Equals}(0,\mathrm{eq}(\overleftarrow{{\mathrm{\Delta }}_{x_1}},\overleftarrow{{\mathrm{\Delta }}_{x_2}},\overleftarrow{{\mathrm{\Delta }}_y})\wedge ({\mathrm{\Delta }}_{x_1}\oplus {\mathrm{\Delta }}_{x_2}\oplus {\mathrm{\Delta }}_y\oplus \overleftarrow{{\mathrm{\Delta }}_{x_2}}))\end{array}$$

is True. In this case, the differential weight is given by the bit-vector function

$$\begin{array}{c}\hfill {\mathsf{weight}}_{⊞}(({\mathrm{\Delta }}_{x_1},{\mathrm{\Delta }}_{x_2}),{\mathrm{\Delta }}_y)=\mathsf{HW}(\neg \mathrm{eq}({\mathrm{\Delta }}_{x_1},{\mathrm{\Delta }}_{x_2},{\mathrm{\Delta }}_y)\ll 1).\end{array}$$

For the modular addition with a constant input ${⊞}_a(x)=x⊞a$, Machado [53] obtained the following algorithm to compute the differential probability [53].

Theorem 2

Let (u, v) be a differential over the n-bit constant addition ${⊞}_a$. Then, the differential probability is given by

$$\begin{array}{c}\hfill Pr[u\stackrel{{⊞}_a}{\to }v]={\phi }_0\times \cdots \times {\phi }_{n-1},\end{array}$$

where ${\phi }_i$ depends on the ${\delta }_{i-1}$ and $S_i$, each one defined for $0\le i<n$ by

$$\begin{array}{cc}\hfill S_i& =(u[i-1],v[i-1],u[i]\oplus v[i]),\hfill \\ \hfill {\delta }_i& =\left\{\begin{array}{cc}(a[i-1]+{\delta }_{i-1})/2,\hfill & S_i=\mathtt{000}\hfill \\ 0,\hfill & S_i=\mathtt{001}\hfill \\ a[i-1],\hfill & S_i\in \{\mathtt{010},\mathtt{100},\mathtt{110}\}\hfill \\ {\delta }_{i-1},\hfill & S_i\in \{\mathtt{011},\mathtt{101}\}\hfill \\ 1/2,\hfill & S_i=\mathtt{111}\hfill \end{array}\right)\hfill \\ \hfill {\phi }_i& =\left\{\begin{array}{cc}1,\hfill & S_i=\mathtt{000}\hfill \\ 0,\hfill & S_i=\mathtt{001}\hfill \\ 1/2,\hfill & S_i\in \{\mathtt{010},\mathtt{011},\mathtt{100},\mathtt{101}\}\hfill \\ 1-(a[i-1]+{\delta }_{i-1}-2a[i-1]{\delta }_{i-1}),\hfill & S_i=\mathtt{110}\hfill \\ (a[i-1]+{\delta }_{i-1}-2a[i-1]{\delta }_{i-1}),\hfill & S_i=\mathtt{111},\hfill \end{array}\right)\hfill \end{array}$$

For $i=-1$, $S_i$ and ${\delta }_i$ are defined by $S_{-1}=\perp$ and ${\delta }_{-1}=0$.

Unfortunately, the algorithm illustrated in Theorem 2 is not suitable for constraint satisfaction problems due to its recursive nature and the use of floating-point arithmetic.

Some authors [46, Corollary 2] [4] have adapted the differential model of the 2-input addition (i.e., the modular addition with two independent inputs) for the constant addition by setting the difference of the second operand to zero, that is,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathsf{valid}}_{{⊞}_a}({\mathrm{\Delta }}_x,{\mathrm{\Delta }}_y)& \leftarrow {\mathsf{valid}}_{⊞}(({\mathrm{\Delta }}_x,0),{\mathrm{\Delta }}_y),\hfill \\ \hfill {\mathsf{weight}}_{{⊞}_a}({\mathrm{\Delta }}_x,{\mathrm{\Delta }}_y)& \leftarrow {\mathsf{weight}}_{⊞}(({\mathrm{\Delta }}_x,0),{\mathrm{\Delta }}_y).\hfill \end{array}\end{array}$$ 1

The approximation given by Eq. (1) models the differential $({\mathrm{\Delta }}_x\stackrel{{⊞}_a}{\to }{\mathrm{\Delta }}_y)$ by averaging over all a. While this approach can be used to model the constant addition by a round key, since the characteristic probability is also computed by averaging over all keys, for a fixed constant this approach is rather inaccurate.

Surprisingly, the differential properties of the 2-input addition and the constant addition are very different. The 2-input addition was shown to be CCZ-equivalent to a quadratic function [67], that is, the differential properties of the 2-input addition are the same as some quadratic functions. In particular, the set of inputs $(x_1,x_2)$ satisfying a differential $(({\mathrm{\Delta }}_{x_1},{\mathrm{\Delta }}_{x_2})\to {\mathrm{\Delta }}_y)$ over the 2-input addition forms a subspace of ${\mathbb{F}}_2^n$, which allows to describe its differential model using few basic operations.

On the other hand, the constant addition is not CCZ-equivalent to a quadratic function, since the set of inputs $(x_1,x_2)$ satisfying a differential $({\mathrm{\Delta }}_x,{\mathrm{\Delta }}_y)$ over ${⊞}_a$ does not form a subspace for many a. In other words, the probability of a differential over the constant addition is not necessarily of the form $2^{-\alpha }$ for a positive integer $\alpha$, and finding a differential model for the constant input addition is a much harder problem.

We experimentally checked the accuracy of the approximation given by Eq. (1) for 8-bit constants a. For most values of a, validity formulas differ roughly in $2^{13}$ out of all $2^{16}$ differentials. For those differentials where they did not differ, the difference between their weights was significantly high on average.

Consequently, no differential model of the constant addition suitable for constraint satisfaction problems has been proposed so far. In the next section, we present the first differential model of the constant addition for SMT problems in the bit-vector theory.

Bit-vector differential model of the constant addition

We present a bit-vector differential model of the constant addition, composed of a bit-vector formula to determine whether a given differential is valid and a bit-vector function that computes the weight of the valid differential. Our model takes benefit from Theorem 2 [53]; however, we avoid bit iterations, floating-point arithmetic, multiplications and look-up tables, in order to obtain efficient bit-vector constraints to be used in bit-vector SMT problems.

Before we illustrate our model, we remark an essential property of Theorem 2. When the state $S_i$ is not $\mathtt{110}$ or $\mathtt{111}$, the probability of the step i, ${\phi }_i$, depends exclusively on $S_i$; otherwise, ${\phi }_i$ depends on $S_i$ and ${\delta }_{i-1}$. When $S_i=\mathtt{11}\ast$, $S_{i-1}\in \{\mathtt{010},\mathtt{100},\mathtt{110},\mathtt{000}\}$ and for the first three cases, ${\delta }_{i-1}$ is equal to $a[i-2]$. However, considering the forth case, i.e., $S_{i-1}=\mathtt{000}$, ${\delta }_{i-1}$ depends on ${\delta }_{i-2}$ and this dependency will proceed until we obtain a state $S_{i-{\ell }_i}\ne \mathtt{000}$ for some positive integer ${\ell }_i$. Thus, ${\delta }_{i-1}$ has the following expression when $S_i=\mathtt{11}\ast$,

$$\begin{array}{c}\hfill {\delta }_{i-1}=\frac{a[i-{\ell }_i-1]}{2^{{\ell }_i-1}}+\sum _{j=2}^{{\ell }_i}\frac{a[i-j]}{2^{j-1}}.\end{array}$$ 2

Therefore, when $S_i=\mathtt{11}\ast$, ${\phi }_i$ also depends on the previous states $S_{i-1},\dots ,S_{i-{\ell }_i}$, which motivates the following definition.

Definition 1

Let $S_i=\mathtt{11}\ast$. The chain ${\mathrm{\Gamma }}_i$ is defined as the smallest set of previous states $\{S_{i-1},S_{i-2},\dots ,S_{i-{\ell }_i}\}$ that completely determine ${\phi }_i$, and the positive integer ${\ell }_i$ is called the length of ${\mathrm{\Gamma }}_i$.

Given a chain ${\mathrm{\Gamma }}_i=\{S_{i-1},S_{i-2},\dots ,S_{i-{\ell }_i}\}$, note that $S_{i-{\ell }_i}\ne \mathtt{000}$ and the remaining states in the chain (if any) are all equal to $\mathtt{000}$.

In the next example, we illustrate how to calculate the differential probability using the iterative method of Theorem 2 and we learn more about the intermediate variables used for obtaining the probability.

Example 1

Consider the differential $(u,v)=(\mathtt{1010001110},\mathtt{1010001010})$ over the modular addition by the 10-bit constant $a=\mathtt{1000101110}$. According to Theorem 2, the differential probability of (u, v) is given by

$$\begin{array}{c}\hfill Pr[u\stackrel{{⊞}_a}{\to }v]=\frac{\#\{x:(x{⊞}_a)\oplus ((x\oplus u){⊞}_a)=v\}}{2^{10}}=\prod _{i=0}^9{\phi }_i.\end{array}$$

Table 2 displays the variables we need to compute to obtain the differential probability. As we mentioned earlier, if $S_i=(u_{i-1},v_{i-1},u_i\oplus v_i)\ne \mathtt{11}\ast$, each ${\phi }_i$ can be computed in a straightforward way without any further dependencies of previous states.

Table 2.

The intermediate variables for finding the differential probability of Example 1

i	9	8	7	6	5	4	3	2	1	0	$-1$
a[i]	1	0	0	0	1	0	1	1	1	0	0
u[i]	1	0	1	0	0	0	1	1	1	0	0
v[i]	1	0	1	0	0	0	1	0	1	0	0
$S_i$	$\mathtt{000}$	$\mathtt{110}$	$\mathtt{000}$	$\mathtt{000}$	$\mathtt{000}$	$\mathtt{110}$	$\mathtt{100}$	$\mathtt{111}$	$\mathtt{000}$	$\mathtt{000}$	$\perp$
${\delta }_i$	0	0	$\frac{3}{8}$	$\frac{3}{4}$	$\frac{1}{2}$	1	1	$\frac{1}{2}$	0	0	0
${\phi }_i$	1	$\frac{5}{8}$	1	1	1	1	$\frac{1}{2}$	1	1	1

For the remaining states equal to $\mathtt{110}$ or $\mathtt{111}$, we first obtain their associated chains as

$$\begin{array}{cc}\hfill S_2& =\mathtt{111},{\mathrm{\Gamma }}_2=\{S_1=\mathtt{000},S_0=\mathtt{000},S_{-1}=\perp \},{\ell }_2=3,\hfill \\ \hfill S_4& =\mathtt{110},{\mathrm{\Gamma }}_4=\{S_3=\mathtt{100}\},{\ell }_4=1,\hfill \\ \hfill S_8& =\mathtt{110},{\mathrm{\Gamma }}_8=\{S_7=\mathtt{000},S_6=\mathtt{000},S_5=\mathtt{000},S_4=\mathtt{110}\},{\ell }_8=4.\hfill \end{array}$$

Then, we compute the associated ${\delta }_{i-1}$ using Eq. (2), and finally we obtain ${\phi }_i$ from the values of $a[i-1]$ and the computed ${\delta }_{i-1}$.

Multiplying each ${\phi }_i$ listed in Table 2 leads to the differential probability,

$$\begin{array}{c}\hfill Pr\left[u,\stackrel{{⊞}_a}{\to },v\right]=\prod _{i=0}^9{\phi }_i=\frac{5}{16}.\end{array}$$

Validity

Let (u, v) be a differential over ${⊞}_a$, the modular addition by n-bit constant a. According to Theorem 2, the differential probability of (u, v) can be expressed as ${\phi }_0\times \cdots \times {\phi }_{n-1}$. Thus, (u, v) is a valid differential, i.e., with non-zero probability, if and only if all ${\phi }_i$ are non-zero. If ${\phi }_i=0$, note that $S_i$ must be $\mathtt{001},\mathtt{110}$ or $\mathtt{111}$. While $S_i=\mathtt{001}$ always implies ${\phi }_i=0$, the other two cases require an extra condition to result in ${\phi }_i=0$, as shown in the next lemma.

Lemma 1

Let the state $S_i$ be $\mathtt{11}\mathtt{b}$, for $\mathtt{b}\in \{\mathtt{0},\mathtt{1}\}$. Then, ${\phi }_i$ is equal to 0 if and only if $\neg \mathtt{b}\oplus a[i-1]=a[i-2]=\cdots =a[i-{\ell }_i-1].$

Proof

Having $S_i=\mathtt{11}\mathtt{b}$, ${\phi }_i=0$ if and only if $\neg \mathtt{b}={\delta }_{i-1}\oplus a[i-1]$. Let ${\ell }_i$ be the chain length of $S_i$. The case for ${\ell }_i=1$ is trivial, since ${\delta }_{i-1}=a[i-2]$. To achieve ${\delta }_{i-1}=a[i-1]\oplus \neg b$ when ${\ell }_i>1$, the non-negative rational number ${\delta }_{i-1}$ must be equal to 0 or 1. Since ${\delta }_{i-1}$ is a monotonically increasing function of $(a[i-2],\cdots ,a[i-{\ell }_i-1])$ regarding Eq. (2), ${\delta }_{i-1}$ reaches its extrema in $(0,\cdots ,0)$ and $(1,\cdots ,1)$, that is,

$$\begin{array}{c}\hfill {\delta }_{i-1}=c⟺a[i-2]=a[i-3]=\cdots =a[i-{\ell }_i-1]=c,\forall c\in \{\mathtt{0},\mathtt{1}\},\end{array}$$

Thus, ${\delta }_{i-1}=a[i-1]\oplus \neg \mathtt{b}⟺{\delta }_{i-1}=a[i-2]=\cdots =a[i-{\ell }_i]$. $\square$

The next lemma provides a bit-vector expression to check Lemma 1 by exploiting the fact that the carry chain allows a bit to affect the bits to its left.

Lemma 2

Consider the following n-bit values,

$$\begin{array}{cc}\hfill s_{\mathtt{00}\ast }& =\neg (u\ll 1)\wedge \neg (v\ll 1),s_{\ast \ast \mathtt{1}}=u\oplus v,a^{\prime }=(a\oplus (a\ll 1))\ll 1,\hfill \\ \hfill c& =\mathsf{Carry}(s_{\mathtt{00}\ast }\wedge \neg a^{\prime },\neg (s_{\mathtt{00}\ast }\ll 1)),g=(s_{\ast \ast \mathtt{1}}\oplus a^{\prime })\wedge (c\vee \neg (s_{\mathtt{00}\ast }\ll 1)).\hfill \end{array}$$

Then, for all states $S_i=\mathtt{11}\ast$, we have ${\phi }_i=0$ if and only if $g[i]=1$.

Proof

Let $S_i=\mathtt{11}\mathtt{b}$ with chain length ${\ell }_i$. Note that $a^{\prime }[i]=a[i-1]\oplus a[i-2]$ and that $s_{\mathtt{00}\ast }[i]=1$ (resp. $s_{\ast \ast \mathtt{1}}[i]=1$) if and only if $S_i=\mathtt{00}\ast$ (resp. $S_i=\ast \ast \mathtt{1}$).

The first operand of g[i], i.e., $(s_{\ast \ast \mathtt{1}}\oplus a^{\prime })[i]$, is equal to one if and only if $\mathtt{b}=\neg (a[i-1]\oplus a[i-2])$. For ${\ell }_i=1$ it is easy to see that $S_{i-1}\ne \mathtt{00}\ast$; therefore, the second operand of g[i] is 1, and by Lemma 1$g[i]=1$ if and only if ${\phi }_i=0$.

When ${\ell }_i>1$, $S_{i-1}=\mathtt{000}$ and the second major operand of g[i] reduces to c. In particular, the two major operands of the $\mathsf{Carry}$ function of c are given by

$$\begin{array}{cc}\hfill (s_{\mathtt{00}\ast }\wedge \neg a^{\prime })[i,i-{\ell }_i]& =(\neg (a[i-1]\oplus a[i-2]),\cdots ,\neg (a[i-{\ell }_i]\oplus a[i-{\ell }_i-1]),0),\hfill \\ \hfill \neg (s_{\mathtt{00}\ast }\ll 1)[i,i-{\ell }_i]& =(0,\cdots ,0,1,\ast ).\hfill \end{array}$$

Thus, $c[i]=c[i-1]\wedge \neg a^{\prime }[i-1]$ and $c[i-{\ell }_i+1]=c[i-{\ell }_i]\wedge \neg s_{\mathtt{00}\ast }[i-{\ell }_i-1]=0$; otherwise, for $0\le j\le i-{\ell }_i-1$ we will obtain $s_{\mathtt{00}\ast }[j]=0$ which does not conform to $S_0=\mathtt{00}\ast$. By unrolling the recursive definition of c[i], we see that $c[i]=\neg a^{\prime }[i-1]\wedge \cdots \wedge \neg a^{\prime }[i-{\ell }_i+1]$. In other words, $c[i]=1$ if and only if $a[i-2]=\cdots =a[i-{\ell }_i-1]$. Together with the condition for $(s_{\ast \ast \mathtt{1}}\oplus a^{\prime })[i]=1$, we have that $g[i]=1$ exactly when ${\phi }_i=0$, regarding Lemma 1. $\square$

Lemma 2 provides a bit-vector variable g that detects the states $S_i=\mathtt{11}\ast$ leading to invalidity. The next theorem presents the final bit-vector formula for the validity by taking into account the states $S_i=\mathtt{001}$ as well.

Theorem 3

Let (u, v) be a differential over the n-bit constant addition ${⊞}_a$. Consider the n-bit value g defined in Lemma 2 and the following n-bit values

$$\begin{array}{c}\hfill s_{\mathtt{001}}=\neg (u\ll 1)\wedge \neg (v\ll 1)\wedge (u\oplus v),s_{\mathtt{11}\ast }=(u\ll 1)\wedge (v\ll 1).\end{array}$$

Then, the bit-vector formula ${\mathsf{valid}}_{{⊞}_a}(u,v)=\mathsf{Equals}(s_{\mathtt{001}}\vee (s_{\mathtt{11}\ast }\wedge g),0)$ is True if and only if the differential (u, v) is valid.

Proof

By the definition of $s_{\mathtt{001}}$ and $s_{\mathtt{11}\ast }$, $s_{\mathtt{001}}[i]=1$ (respectively $s_{\mathtt{11}\ast }[i]=1$) if and only if $S_i=\mathtt{001}$ (respectively $S_i=\mathtt{11}\ast$). Moreover, ${\phi }_i=0$ exactly when $S_i=001$, or when $S_i=11\ast$ and $g[i]=1$ (Lemma 2). Thus, ${\phi }_i=0$ if and only if $s_{\mathtt{001}}\vee (s_{\mathtt{11}\ast }\wedge g)[i]=1$. $\square$

Since the number of basic bit-vector operations of our bit-vector validity formula is independent of the bit-size of the inputs, the bit-vector complexity of ${\mathsf{valid}}_{{⊞}_a}$ is O(1).

Example 2

Consider the valid differential of Example 1, i.e. $a=\mathtt{1000101110}$, $u=\mathtt{1010001110}$, and $v=\mathtt{1010001010}$. Previously, we showed that its differential probability is non-zero and equal to 5/16. In this example, we will illustrate our bit-vector validity formula step by step.

Table 3 provides some of the essential bit-vector values used in Theorem 3. Since there is no state equal to $\mathtt{001}$, $s_{\mathtt{001}}$ is the all-zero bit-vector. As we have shown in Example 1, there are three states equal to $\mathtt{11}\ast$, and the associated bit of $s_{\mathtt{11}\ast }$ is equal to one in the corresponding bits. In this example, no state $\mathtt{11}\ast$ leads to invalidity, and g is equal to the all-zero bit-vector. Thus, $s_{001}[i]\vee (s_{11\ast }[i]\wedge g[i])=0$ for all i, and our validity formula

$$\begin{array}{c}\hfill {\mathsf{valid}}_{{⊞}_a}(u,v)=\mathsf{Equals}(s_{001}\vee (s_{11\ast }\wedge g),0)\end{array}$$

evaluates to True.

Table 3.

The intermediate variables for evaluating the bit-vector validity formula of Example 2

i	9	8	7	6	5	4	3	2	1	0
a[i]	1	0	0	0	1	0	1	1	1	0
u[i]	1	0	1	0	0	0	1	1	1	0
v[i]	1	0	1	0	0	0	1	0	1	0
g[i]	0	0	0	0	0	0	0	0	0	0
$s_{\mathtt{11}\ast }[i]$	0	1	0	0	0	1	0	1	0	0
$s_{\mathtt{001}}[i]$	0	0	0	0	0	0	0	0	0	0

Weight of a valid differential

In this section, we propose a bit-vector function that computes the weight of a valid differential over the constant addition. Working with differential weights has the advantage that multiple differential weights can be combined by adding them up, while probabilities need to be multiplied, a very costly operation in a bit-vector SMT problem.

The weight of a valid differential over the constant addition is an irrational value in general, and it cannot be represented as a fixed-sized bit-vector. Thus, our bit-vector function computes a close approximation of the weight, and we provide almost tight bounds for the approximation error.

Through the rest of the section, let (u, v) be a valid differential over the n-bit constant addition ${⊞}_a$. According to Theorem 2, the weight can be obtained by

$$\begin{array}{c}\hfill {\mathsf{weight}}_{{⊞}_a}(u,v)=-{log}_2\left(\prod _{i=0}^{n-1},{\phi }_i\right)=-\sum _{i=0}^{n-1}{log}_2({\phi }_i).\end{array}$$ 3

Let $\mathcal{I}$ denote the set of indices corresponding to the states $\mathtt{11}\ast$ with chain length bigger than one, i.e., $\mathcal{I}=\{1\le i\le n-1|S_i=\mathtt{11}\ast ,{\ell }_i>1\}$. For $i\notin \mathcal{I}$, the probability ${\phi }_i$ only depends on the current state $S_i$ and ${\phi }_i$ is either 1 or 1/2. Based on the aforementioned fact, we show how to acquire the summation of all ${log}_2({\phi }_i)$ when $i\notin \mathcal{I}$ using bit-vector expressions.

Lemma 3

Let $\mathcal{I}=\{1\le i\le n-1|S_i=\mathtt{11}\ast ,{\ell }_i>1\}$. Then,

$$\begin{array}{c}\hfill -\sum _{i\notin \mathcal{I}}{log}_2({\phi }_i)=\mathsf{HW}((u\oplus v)\ll 1).\end{array}$$

Proof

To prove the lemma, we divide the set $\{i|i\notin \mathcal{I}\}$ into two parts as $\{i|S_i\ne \mathtt{11}\ast \}$ and $\{i|S_i=\mathtt{11}\ast ,{\ell }_i=1\}$. For each state $S_i\ne 11\ast$, there are two possible cases. If $S_i$ is equal to $\mathtt{000}$, the corresponding step probability is ${\phi }_i=1$. Otherwise, $S_i\in \{010,011,100,101\}$ and we obtain ${\phi }_i=1/2$. Considering these two cases leads to

$$\begin{array}{cc}\hfill \sum _{\begin{array}{c}i\\ S_i\ne 11\ast \end{array}}{log}_2({\phi }_i)& =\sum _{\begin{array}{c}i\\ S_i=000\end{array}}{log}_2(1)+\sum _{\begin{array}{c}i\\ S_i\in \{010,011,100,101\}\end{array}}{log}_2(1/2),\hfill \\ \hfill & =-\#\{S_i\in \{010,011,100,101\}:0\le i<n\}.\hfill \end{array}$$

Since the second case $S_i\in \{010,011,100,101\}$ occurs when $u[i-1]\oplus v[i-1]=1$, we can use $\mathsf{HW}((u\oplus v)\ll 1)$ to compute the number of times this case happens.

Now for $S_i=\mathtt{11}\ast$ when ${\ell }_i=1$, we know that ${\delta }_{i-1}=a[i-2]\in \{0,1\}$. Since the probability is not equal to zero, we obtain ${\phi }_i=1$. Thus we get

$$\begin{array}{c}\hfill \sum _{\begin{array}{c}i\\ S_i=11\ast \\ {\ell }_i=1\end{array}}{log}_2({\phi }_i)=0.\end{array}$$

By and large, the sum of ${log}_2({\phi }_i)$ when $i\notin \mathcal{I}$ is

$$\begin{array}{c}\hfill \sum _{i\notin \mathcal{I}}{log}_2({\phi }_i)=\sum _{\begin{array}{c}i\\ S_i\ne 11\ast \end{array}}{log}_2({\phi }_i)+\sum _{\begin{array}{c}i\\ S_i=11\ast \\ {\ell }_i=1\end{array}}{log}_2({\phi }_i)=-\mathsf{HW}((u\oplus v)\ll 1).\end{array}$$

$\square$

Lemma 3 describes the sum of ${log}_2({\phi }_i)$ when $i\notin \mathcal{I}$ as a bit-vector expression with complexity $O({log}_{2}n)$. To describe the logarithmic summation when $i\in \mathcal{I}$ as a bit-vector, we will first show how to split ${\phi }_i$ as the quotient of two integers.

Lemma 4

Let $i\in \mathcal{I}$ and let $p_i$ be the positive integer defined by

$$\begin{array}{c}\hfill p_i=\left\{\begin{array}{c}a[i-2,i-{\ell }_i]+a[i-{\ell }_i-1],u[i]\oplus v[i]\oplus a[i-1]=1\hfill \\ 2^{{\ell }_i-1}-(a[i-2,i-{\ell }_i]+a[i-{\ell }_i-1]),u[i]\oplus v[i]\oplus a[i-1]=0\hfill \end{array}\right)\end{array}$$

where ${\ell }_i>1$ is the chain length of the state $S_i=\mathtt{11}\ast$. Then, ${\phi }_i={\displaystyle \frac{p_i}{2^{{\ell }_i-1}}}$.

Proof

Considering the definition of ${\phi }_i$ when $S_i=\mathtt{11}\ast$,

$$\begin{array}{c}\hfill {\phi }_i=\left\{\begin{array}{cc}{\delta }_{i-1},\hfill & u[i]\oplus v[i]\oplus a[i-1]=1\hfill \\ 1-{\delta }_{i-1},\hfill & u[i]\oplus v[i]\oplus a[i-1]=0\hfill \end{array}\right)\end{array}$$

and following the definition of ${\delta }_{i-1}$ given by Eq. (2),

$$\begin{array}{c}\hfill 2^{{\ell }_i-1}{\delta }_i=\sum _{j=0}^{{\ell }_i-2}{2}^{j}a[i-{\ell }_i+j]+a[i-{\ell }_i-1]=a[i-2,i-{\ell }_i]+a[i-{\ell }_i-1],\end{array}$$

we obtain that ${\phi }_i=p_i/2^{{\ell }_i-1}$. Moreover, having $0<{\phi }_i\le 1$ and ${\ell }_i>1$ results in $0<p_i\le 2^{{\ell }_i-1}$. Thus, $p_i$ is always a positive integer. $\square$

Due to Lemma 4, we can decompose the logarithmic summation over $\mathcal{I}$ as

$$\begin{array}{c}\hfill \sum _{i\in \mathcal{I}}{log}_2({\phi }_i)=\sum _{i\in \mathcal{I}}{log}_2(p_i)-\sum _{i\in \mathcal{I}}({\ell }_i-1).\end{array}$$

The next lemma shows how to describe the summation involving the chain lengths with basic bit-vector operations.

Lemma 5

Consider the n-bit vector $s_{000}=\neg (u\ll 1)\wedge \neg (v\ll 1)$. Then,

$$\begin{array}{c}\hfill \sum _{i\in \mathcal{I}}({\ell }_i-1)=\mathsf{HW}(s_{000}\wedge \neg \mathsf{LZ}(\neg s_{000})).\end{array}$$

Proof

Recall that there are exactly $({\ell }_i-1)$ states in each chain ${\mathrm{\Gamma }}_i$ such that

$$\begin{array}{c}\hfill S_{i-1}=S_{i-2}=\cdots =S_{i-({\ell }_i-1)}=\mathtt{000}.\end{array}$$

Therefore, we have ${\sum }_{i\in \mathcal{I}}({\ell }_i-1)=\#\{S_j|S_j=\mathtt{000}\text{and}\exists i\in \mathcal{I}s.t.S_j\in {\mathrm{\Gamma }}_i\}.$ When $S_j=\mathtt{000}$, the next state $S_{j+1}$ will be a member of the set $\{\mathtt{000},\mathtt{11}\ast \}$. As a result, it is easy to see that for an arbitrary j, if $S_j$ is equal to $\mathtt{000}$, then either $S_j$ is included in some chain ${\mathrm{\Gamma }}_i,i\in \mathcal{I}$, or $S_j$ belongs to the set ${\mathrm{\Gamma }}^{\prime }$ defined by

$$\begin{array}{c}\hfill {\mathrm{\Gamma }}^{\prime }=\{S_{n-1}=\mathtt{000},\dots ,S_{n-k}=\mathtt{000}\},\end{array}$$

for some $k>0$, where $S_{n-k-1}\ne 000$. Concerning Definition 1, one can observe that ${\mathrm{\Gamma }}^{\prime }$ is not a chain. Therefore, ${\sum }_{i\in \mathcal{I}}({\ell }_i-1)=\#\{S_j|S_j=\mathtt{000}\text{and}{S}_j\notin {\mathrm{\Gamma }}^{\prime }\}$.

Since we are assuming that the differential is valid, there are no states $S_j=\mathtt{001}$, and $s_{000}[j]=1$ if and only if $S_j=\mathtt{000}$. On the other hand, the function $\mathsf{LZ}$ can be used to detect the states from the set ${\mathrm{\Gamma }}^{\prime }$. In particular, $\mathsf{LZ}(\neg s_{000})[i]$ is equal to $\mathtt{1}$ if and only if $S_i\in {\mathrm{\Gamma }}^{\prime }$. Therefore, we obtain

$$\begin{array}{c}\hfill \sum _{i\in \mathcal{I}}({\ell }_i-1)=\mathsf{HW}(s_{000}\wedge (\neg \mathsf{LZ}(\neg s_{000}))).\end{array}$$

$\square$

Representing the sum of ${log}_2(p_i)$ by a bit-vector expression is the most complex and challenging part of our differential model. Thus, we will proceed in several steps. First, we will show how to obtain a bit-vector w that contains all the $p_i$ as some sub-vectors.

Lemma 6

Consider the following n-bit values,

$$\begin{array}{ccc}& s_{\mathtt{000}}=\neg (u\ll 1)\wedge \neg (v\ll 1),\hfill & \hfill s_{\mathtt{000}}^{\prime }=s_{\mathtt{000}}\wedge \neg \mathsf{LZ}(\neg s_{\mathtt{000}}),\\ \hfill & t=\neg s_{\mathtt{000}}^{\prime }\wedge (s_{\mathtt{000}}^{\prime }\gg 1),\hfill & \hfill t^{\prime }=s_{\mathtt{000}}^{\prime }\wedge (\neg (s_{\mathtt{000}}^{\prime }\gg 1)),\\ \hfill & s=((a\ll 1)\wedge t)⊞(a\wedge (s_{\mathtt{000}}^{\prime }\gg 1)),\hfill & \hfill q=((\neg ((a\ll 1)\oplus u\oplus v))\gg 1)\wedge t^{\prime },\\ \hfill & d=\mathsf{RevCarry}(s_{\mathtt{000}}^{\prime },q)\vee q,\hfill & \hfill w=(q\boxminus (s\wedge d))\vee (s\wedge \neg d).\end{array}$$

Then, for all states $S_i=\mathtt{11}\ast$ with $i\in \mathcal{I}$, $w[i-1,i-{\ell }_i]=p_i$.

Proof

For each $i\in \mathcal{I}$ and $0\le j<n$, note that $s_{\mathtt{000}}^{\prime }[j]=1$ exactly when $S_j=\mathtt{000}$ and $S_j\in {\mathrm{\Gamma }}_i$, and $t[j]=1$ (resp. $t^{\prime }[j]=1$) if and only if $S_j=S_{i-{\ell }_i}$ (resp. $S_j=S_{i-1}$). Denoting $s=s_1⊞s_2$, where $s_1=(a\ll 1)\wedge t$ and $s_2=a\wedge (s_{000}^{\prime }\gg 1)$, when $i\in \mathcal{I}$ the sub-vectors

$$\begin{array}{c}\hfill \begin{array}{cccccccc}\hfill s_1[i-1,i-{\ell }_i-1]& =\hfill & (0,\hfill & 0,\hfill & \cdots ,\hfill & 0,\hfill & a[i-{\ell }_i-1],\hfill & 0),\hfill \\ \hfill s_2[i-1,i-{\ell }_i-1]& =\hfill & (0,\hfill & a[i-2],\hfill & \cdots ,\hfill & a[i-{\ell }_i+1],\hfill & a[i-{\ell }_i],\hfill & 0),\hfill \end{array}\end{array}$$

result in $s[i-1,i-{\ell }_i]=a[i-2,i-{\ell }_i]+a[i-{\ell }_i-1]$. In particular, $s[i-1,i-{\ell }_i]\le 2^{{\ell }_i-1}$ and the equality holds when $s[i-1,i-{\ell }_i]=\mathtt{10}\cdots \mathtt{0}$.

It is easy to see that $q[i-1]=\neg (a[i-2]\oplus u[i-1]\oplus v[i-1])$ when $i\in \mathcal{I}$ and q is zero elsewhere. Then, the sub-vectors $d[i-1,i-{\ell }_i]$ are composed of repeated copies of $q[i-1]$ when $i\in \mathcal{I}$, as shown by the following sub-vectors

$$\begin{array}{c}\hfill \begin{array}{ccccccccc}\hfill s_{000}^{\prime }[i,i-{\ell }_i-1]& =\hfill & (0,\hfill & 1,\hfill & 1,\hfill & \cdots ,\hfill & 1,\hfill & 0,\hfill & \ast ),\hfill \\ \hfill q[i,i-{\ell }_i-1]& =\hfill & (0,\hfill & q[i-1],\hfill & 0,\hfill & \cdots ,\hfill & 0,\hfill & 0,\hfill & \ast ),\hfill \\ \hfill \mathsf{RevCarry}(s_{000}^{\prime },q)[i,i-{\ell }_i-1]& =\hfill & (\ast ,\hfill & 0,\hfill & q[i-1],\hfill & \cdots ,\hfill & q[i-1],\hfill & q[i-1],\hfill & 0),\hfill \\ \hfill d[i,i-{\ell }_i-1]& =\hfill & (\ast ,\hfill & q[i-1],\hfill & q[i-1],\hfill & \cdots ,\hfill & q[i-1],\hfill & q[i-1],\hfill & \ast ).\hfill \end{array}\end{array}$$

The only exception for the above equations is when $i-{\ell }_i=-1$, where the two least significant bits of the above sub-vectors will be equal to zero.

Let $w=w_1\wedge w_2$, where $w_1=q\boxminus (s\wedge d)$ and $w_2=s\wedge \neg d$. Regarding the acquired patterns for q and d, we prove the following inequalities for $i\in \mathcal{I}$

$$\begin{array}{cc}\hfill (s\wedge d)[i-1,i-{\ell }_i]& \le q[i-1,i-{\ell }_i],\hfill \\ \hfill (s\wedge d)[i-{\ell }_i-1,0]& \le q[i-{\ell }_i-1,0],\hfill \end{array}$$

which imply the identity $w_1[i-1,i-{\ell }_i]=q[i-1,i-{\ell }_i]\boxminus (s\wedge d)[i-1,i-{\ell }_i]$.

The first inequality can be derived from the fact that $s[i-1,i-{\ell }_i]\le \mathtt{10}\cdots \mathtt{0}$. For the second inequality, consider the index set $\mathcal{J}=\{j|\forall i\in I,S_j\notin {\mathrm{\Gamma }}_i\}$. Then, the second inequality holds since for $j\in \mathcal{J}$ and $c\in \{0,1\}$ we can see that

$$\begin{array}{c}\hfill s_{\mathtt{000}}^{\prime }[j+1-c]=0\Rightarrow s_1[j-c]=s_2[j-c]=0.\end{array}$$

We are now ready to evaluate $w[i-1,i-{\ell }_i]$ when $i\in \mathcal{I}$. If $q[i-1]=0$, then $d[i-1,i-{\ell }_i]=(0,\cdots ,0)$, $w_1[i-1,i-{\ell }_i]$ reduces to 0, and

$$\begin{array}{c}\hfill w[i-1,i-{\ell }_i]=w_2[i-1,i-{\ell }_i]=a[i-2,i-{\ell }_i]+a[i-{\ell }_i-1].\end{array}$$

If $q[i-1]=1$, then $d[i-1,i-{\ell }_i]=(1,\cdots ,1)$, $w_2[i-1,i-{\ell }_i]$ reduces to 0, and

$$\begin{array}{cc}\hfill w[i-1,i-{\ell }_i]& =w_1[i-1,i-{\ell }_i]=(1,0,\cdots ,0)\boxminus s[i-1,i-{\ell }_i]\hfill \\ \hfill & =2^{{\ell }_i-1}-(a[i-2,i-{\ell }_i]+a[i-{\ell }_i-1]).\hfill \end{array}$$

Hence, for $q[i-1]=\neg (a[i-1]\oplus u[i]\oplus v[i])$ and regarding Lemma 4, we obtain that $w[i-1,i-{\ell }_i]=p_i$. $\square$

Recall that both $\mathsf{LZ}$ and $\mathsf{RevCarry}$ have bit-vector complexity $O({log}_{2}n)$. Therefore, w can be described with $O({log}_{2}n)$ basic bit-vector operations.

Since $p_i$ is not always a power of two, ${log}_2(p_i)$ cannot be represented by a fixed-sized bit-vector. Thus, we will use the following approximation for the binary logarithm of a positive integer x,

$$\begin{array}{c}\hfill {\mathsf{apxlog}}_2(x)\triangleq m+\frac{\mathsf{Truncate}(x[m-1,0])}{2^4},\end{array}$$ 4

where $m=\lfloor {log}_2(x)\rfloor$ and $\mathsf{Truncate}(z)$ for an m-bit vector z is defined by

$$\begin{array}{c}\hfill \mathsf{Truncate}(z)=\left\{\begin{array}{cc}z[m-1,m-4],\hfill & m\ge 4\hfill \\ z[m-1,0]\Vert (\stackrel{4-m}{\overbrace{0,\cdots ,0}}),\hfill & m<4\hfill \end{array}\right)\end{array}$$

In other words, ${\mathsf{apxlog}}_2$ includes the integer part of the logarithm and takes the four bits right after the most significant one as the “fraction” bits. While $\mathsf{Truncate}$ can be generalized to consider more fraction bits, we will show later that four fraction bits are enough to minimize the bounds of our approximation error.

To describe ${\sum }_{i\in \mathcal{I}}{\mathsf{apxlog}}_2(p_i)$ with basic bit-vector operations, we will introduce in the next proposition two new bit-vector functions $\mathsf{ParallelLog}$ and $\mathsf{ParallelTrunc}$. Given a bit-vector x with sub-vectors delimited by a bit-vector y, $\mathsf{ParallelLog}(x,y)$ computes the sum of the integer part of the logarithm of the delimited sub-vectors, whereas $\mathsf{ParallelTrunc}(x,y)$ calculates the sum of the four most significant bits of the delimited sub-vectors.

Proposition 1

Let x and y be n-bit vectors such that y has r sub-vectors

$$\begin{array}{c}\hfill y[i_t,j_t]=(1,1,\cdots ,1,0),t=1,\cdots ,r\end{array}$$

where $i_1>j_1>i_2>j_2>\cdots >i_r>j_r\ge 0$, and y is equal to zero elsewhere.

We define the bit-vector functions $\mathsf{ParallelLog}$ and $\mathsf{ParallelTrunc}$ by

where $z_{\lambda }=x\wedge (y\gg 0)\wedge \cdots \wedge (y\gg \lambda )\wedge \neg (y\gg (\lambda +1))$.

1. If $x[i_t,j_t]>0$ for $t=1,\cdots ,r$, then

   $$\begin{array}{c}\hfill \sum _{t=1}^r\lfloor {log}_2(x[i_t,j_t])\rfloor =\mathsf{ParallelLog}(x,y).\end{array}$$
2. If at least $\lfloor {log}_2(n)\rfloor +4$ bits are dedicated to $\mathsf{ParallelTrunc}(x,y)$, then

   $$\begin{array}{c}\hfill \sum _{t=1}^r\mathsf{Truncate}(x[i_t,j_t+1])=\mathsf{ParallelTrunc}(x,y).\end{array}$$

Proof

Case (a) Let $m=\lfloor {log}_2(x[i_1,j_1])\rfloor$ and $c=\mathsf{RevCarry}(x\wedge y,y)$. Note that $c[n-1,i_1]=0$, since $y[n-1,i_1+1]=0$. For $m\ge 1$, we obtain the sub-vectors

$$\begin{array}{c}\hfill \begin{array}{ccccccccccc}\hfill & \hfill & i_1,& \cdots ,& j_1+m+1,& j_1+m,& j_1+m-1,& \cdots ,& j_1+1,& j_1,& j_1-1\\ \hfill y[i_1,j_1-1]& \hfill =& (1,& \cdots ,& 1,& 1,& 1,& \cdots ,& 1,& 0,& \ast ),\\ \hfill (x\wedge y)[i_1,j_1-1]& \hfill =& (0,& \cdots ,& 0,& 1,& \ast ,& \cdots ,& \ast ,& 0,& \ast ),\\ \hfill c[i_1,j_1-1]& \hfill =& (0,& \cdots ,& 0,& 0,& 1,& \cdots ,& 1,& 1,& 0).\end{array}\end{array}$$

In particular, $c[i_1,j_1]$ has m bits set to one. If $m=0$, $x[i_1,j_1+1]=0$ and $y[j_1]=0$, which implies that there is no carry chain, i.e., $c[i_1,j_1]=0$. Therefore, in both cases $\mathsf{HW}(c)[i_1,j_1])=m=\lfloor {log}_2(x[i_1,j_1])\rfloor$.

Note that the reversed carry chain stops at $j_1$, and $c[j_1-1,i_2]=\mathtt{0}\cdots \mathtt{0}$. Therefore, the same argument can be applied for $t=2,\cdots ,r$, obtaining

$$\begin{array}{c}\hfill \mathsf{HW}(c[i_t,j_t])=\lfloor {log}_2(x[i_t,j_t])\rfloor ,c[j_t-1,i_{t+1}]=0.\end{array}$$

Finally, it is easy to see that $c[j_r-1,0]=0$, concluding the proof for this case.

Case (b) First note that for $\lambda =0,\cdots ,3$ and $t=1,\cdots ,r$, the variable $z_{\lambda }$ is

$$\begin{array}{c}\hfill z_{\lambda }[i]=\left\{\begin{array}{cc}x[i],\hfill & \text{if}i=i_t-\lambda >j_t\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}\right)\end{array}$$

Therefore, the Hamming weight of $z_{\lambda }$ computes the following summation:

$$\begin{array}{c}\hfill \mathsf{HW}(z_{\lambda })=\sum _{\begin{array}{c}t\\ i_t-\lambda >j_t\end{array}}x[i_t-\lambda ].\end{array}$$

While we define $\mathsf{HW}$ as a bit-vector function returning an n-bit output given an n-bit input, $\lfloor {log}_2(n)\rfloor +1$ bits are sufficient to represent the output of $\mathsf{HW}$. Therefore, by representing each $\mathsf{HW}(z_{\lambda })\ll (3-\lambda )$ in a $(\lfloor {log}_2(n)\rfloor +4)$-bit variable $h_{\lambda }$, the bit-vector expression $h_0⊞h_1⊞h_2⊞h_3$ does not overflow, and we obtain

$$\begin{array}{c}\hfill \sum _{t=1}^r\mathsf{Truncate}(x[i_t,j_t+1])=\sum _{t=1}^r\sum _{\begin{array}{c}\lambda =0\\ i_t-\lambda >j_t\end{array}}^{3}x[i_t-\lambda ]\times 2^{3-\lambda }=h_0⊞h_1⊞h_2⊞h_3,\end{array}$$

which concludes the proof. $\square$

Since both $\mathsf{HW}$ and $\mathsf{Rev}$ have $O({log}_{2}n)$ bit-vector complexities, so do the functions $\mathsf{ParallelLog}$ and $\mathsf{ParallelTrunc}$. The next lemma applies $\mathsf{ParallelLog}$ and $\mathsf{ParallelTrunc}$ to provide a bit-vector expression of the sum of ${\mathsf{apxlog}}_2(p_i)$.

Lemma 7

Let r and f be the bit-vectors given by

If at least $\lfloor {log}_2(n)\rfloor +5$ bits are dedicated to r and f, then

$$\begin{array}{c}\hfill 2^4\sum _{i\in \mathcal{I}}{\mathsf{apxlog}}_2(p_i)=(r\ll 4)⊞f.\end{array}$$

Proof

Regarding Lemma 6, $w[i-1,i-{\ell }_i]$ represents the ${\ell }_i$-bit vector of $p_i$ and $s_{\mathtt{000}}^{\prime }[i-1,i-{\ell }_i]$ conforms to the pattern $(1,\dots ,1,0)$ for any $i\in \mathcal{I}$. Therefore,

$$\begin{array}{c}\hfill \sum _{i\in \mathcal{I}}\lfloor {log}_2(p_i)\rfloor =\mathsf{HW}(\mathsf{RevCarry}((w\wedge s_{\mathtt{000}}^{\prime })\ll 1,s_{\mathtt{000}}^{\prime }\ll 1)),\end{array}$$

following Proposition 1. For the second case, let c be the n-bit vector given by $c=\mathsf{RevCarry}((w\wedge s_{\mathtt{000}}^{\prime })\ll 1,s_{\mathtt{000}}^{\prime }\ll 1)$. Denoting by $j=i-l_i$ and $m=\lfloor {log}_2(p_i)\rfloor$ for a given $i\in \mathcal{I}$, note that $p_i[m]$ is the most significant active bit of $p_i$ and

$$\begin{array}{c}\hfill \begin{array}{ccccccccccc}\hfill & \hfill & i+1,& \cdots ,& j+m+2,& j+m+1,& j+m,& \cdots ,& j+2,& j+1,& j\\ \hfill (w\ll 1)[i+1,j]& \hfill =& (0,& \cdots ,& 0& p_i[m],& p_i[m-1],& \cdots ,& p_i[1],& p_i[0]& 0),\\ \hfill c[i+1,j]& \hfill =& (0,& \cdots ,& 0& 0,& 1,& \cdots ,& 1,& 1& 0).\end{array}\end{array}$$

Thus $c[j+m,j]$ conforms to the pattern $(1,\dots ,1,0)$ and Proposition 1 leads to

$$\begin{array}{c}\hfill \sum _{\begin{array}{c}i\in \mathcal{I}\\ m=\lfloor {log}_2(p_i)\rfloor \end{array}}\mathsf{Truncate}(p_i[m-1,0])=\mathsf{ParallelTrunc}(w\ll 1,c).\end{array}$$

For any n-bit variables x and y, it is easy to see that $\mathsf{ParallelLog}(x,y)<n$. Thus, $\lfloor {log}_2(n)\rfloor +4$ bits are sufficient to represent $(r\ll 4)$, and f can also be represented with the same number of bits following Proposition 1. Therefore, by representing $(r\ll 4)$ and f in $(\lfloor {log}_2(n)\rfloor +5)$-bit variables, the bit-vector expression $(r\ll 4)⊞f$ does not overflow. $\square$

Recall that the differential weight of constant addition can be decomposed as

$$\begin{array}{c}\hfill {\mathsf{weight}}_{{⊞}_a}(u,v)=-\sum _{i\notin \mathcal{I}}{log}_2({\phi }_i)-\sum _{i\in \mathcal{I}}{log}_2\left({\displaystyle \frac{1}{2^{{\ell }_i-1}}}\right)-\sum _{i\in \mathcal{I}}{log}_2(p_i).\end{array}$$

If the binary logarithm of $p_i$ is replaced by our approximation of the binary logarithm ${\mathsf{apxlog}}_2(p_i)$, we obtain the following approximation of the weight,

$$\begin{array}{c}\hfill {\mathsf{apxweight}}_{{⊞}_a}(u,v)\triangleq -\sum _{i\notin \mathcal{I}}{log}_2({\phi }_i)-\sum _{i\in \mathcal{I}}{log}_2\left({\displaystyle \frac{1}{2^{{\ell }_i-1}}}\right)-\sum _{i\in \mathcal{I}}{\mathsf{apxlog}}_2(p_i).\end{array}$$ 5

Our weight approximation can be computed with the bit-vector function $\mathsf{BvWeight}$ described in Algorithm 1, as shown in the lemma.

Lemma 8

If at least $\lfloor {log}_2(n)\rfloor +5$ bits are dedicated to $\mathsf{BvWeight}(u,v,a)$, then

$$\begin{array}{c}\hfill 2^4{\mathsf{apxweight}}_{{⊞}_a}(u,v)=\mathsf{BvWeight}(u,v,a).\end{array}$$

Proof

Regarding Lemmas 3 and 5 and 7 we respectively obtain

All in all, we get the following identities,

$$\begin{array}{c}\hfill 2^4{\mathsf{apxweight}}_{{⊞}_a}(u,v)=2^4((int\ll 4)\boxminus frac)=\mathsf{BvWeight}(u,v,a).\end{array}$$

$\square$

Note that the four least significant bits of $\mathsf{BvWeight}(u,v,a)$ correspond to the fraction bits of the approximate weight. In other words, the output of $\mathsf{BvWeight}(u,v,a)$ represents the rational value

$$\begin{array}{c}\hfill \sum _{i=0}^{\lfloor {log}_2(n)\rfloor +4}{2}^{i-4}\mathsf{BvWeight}(u,v,a)[i].\end{array}$$

The bit-vector complexity of $\mathsf{BvWeight}$ is dominated by the complexity of $\mathsf{LZ}$, $\mathsf{Rev}$, $\mathsf{HW}$, $\mathsf{ParallelLog}$, and $\mathsf{ParallelTrunc}$. Since these operations can be computed with $O({log}_{2}n)$ basic bit-vector operations, so does $\mathsf{BvWeight}$.

Theorem 4 shows that $\mathsf{BvWeight}$ leads to a close approximation of the differential weight and provides explicit bounds for the approximation error.

Theorem 4

Let (u, v) be a valid differential over the n-bit constant addition ${⊞}_a$, let ${\mathsf{weight}}_{{⊞}_a}(u,v)$ be the differential weight of (u, v), and let $\mathsf{BvWeight}$ be the bit-vector function defined by Algorithm 1. Then, the approximation error,

$$\begin{array}{c}\hfill E={\mathsf{weight}}_{{⊞}_a}(u,v)-{\mathsf{apxweight}}_{{⊞}_a}(u,v)={\mathsf{weight}}_{{⊞}_a}(u,v)-2^{-4}\mathsf{BvWeight}(u,v,a)\end{array}$$

is bounded by $-0.029(n-1)\le E\le 0.$

Section 3.3 is devoted to the proof of Theorem 4, where we will also analyse the error caused by our approximated binary logarithm. Before proving Theorem 4, we will describe an example to understand this theorem and Algorithm 1.

Example 3

Consider the same conditions as defined in Example 1, i.e., $(u,v)=(\mathtt{1010001110},\mathtt{1010001010})$ and the constant input $a=\mathtt{1000101110}$. The weight for our differential is

$$\begin{array}{cc}\hfill {\mathsf{weight}}_{{⊞}_a}(u,v)& =-{log}_2(Pr[u\stackrel{{⊞}_a}{\to }v])=-{log}_2\left(\frac{5}{16}\right)\approx 1.678.\hfill \end{array}$$

Let’s find the approximate weight ${\mathsf{apxweight}}_{{⊞}_a}$ based on Algorithm 1. Table 4 presents some of the variables we obtain to compute the aforementioned approximate weight.

Table 4.

Intermediate variables for computing ${\mathsf{apxweight}}_{{⊞}_a}(u,v)$ of Example 3

i	9	8	7	6	5	4	3	2	1	0
a[i]	1	0	0	0	1	0	1	1	1	0
u[i]	1	0	1	0	0	0	1	1	1	0
v[i]	1	0	1	0	0	0	1	0	1	0
$s_{\mathtt{000}}[i]$	1	0	1	1	1	0	0	0	1	1
$s_{\mathtt{000}}^{\prime }[i]$	0	0	1	1	1	0	0	0	1	1
w[i]	0	0	0	1	0	1	0	0	1	0
$\mathsf{BvWeight}(u,v,a)[i]$	0	0	0	0	0	1	1	1	0	0

The set $\mathcal{I}=\{1\le i\le n-1|S_i=\mathtt{11}\ast ,{\ell }_i>1\}$ in this example is equal to $\mathcal{I}=\{2,8\}$. The variable int in Algorithm 1 consists of three parts. The first part of the variable int calculated in Algorithm 1 is

$$\begin{array}{c}\hfill \mathsf{HW}((u\oplus v)\ll 1)=\mathtt{0000000001}=1,\end{array}$$

which is equal to $-{\sum }_{i\notin \mathcal{I}}{log}_2({\phi }_i)=-{\sum }_{i\in \{0,1,3,4,5,6,7,9\}}{log}_2({\phi }_i)=-{log}_2({\phi }_3)$.

The second part uses the variable $s_{\mathtt{000}}^{\prime }$ which is the same as $s_{\mathtt{000}}$ except that the leading one bits of $s_{\mathtt{000}}$ are replaced in $s_{\mathtt{000}}^{\prime }$ by zeros. In other words, $s_{\mathtt{000}}^{\prime }[9]=0$ but the remaining bits of these two bit-vectors are exactly equal. Computing the second part results in

$$\begin{array}{c}\hfill \mathsf{HW}(s_{\mathtt{000}}^{\prime })=\mathtt{0000000101}=5,\end{array}$$

and it is equal to ${\sum }_{i\in \mathcal{I}}({\ell }_i-1)=({\ell }_2-1)+({\ell }_8-1)$.

For the third and last part of int, we compute w, obtaining $w=\mathtt{0001010010}$. We remark that the bit-vector w for $i\in \mathcal{I}$ in fact includes $p_i$ as some subvectors, i.e.

$$\begin{array}{cc}\hfill i=& 2:w[2-1,2-{\ell }_2]=w[1,-1]=\mathtt{100}=4=p_2,\hfill \\ \hfill i=& 8:w[8-1,8-{\ell }_8]=w[7,4]=\mathtt{0101}=5=p_8.\hfill \end{array}$$

Hence, the third part of int is computed as

$$\begin{array}{c}\hfill \mathsf{ParallelLog}((w\wedge s_{\mathtt{000}}^{\prime })\ll 1,s_{\mathtt{000}}^{\prime }\ll 1)=\mathtt{0000000100}=4,\end{array}$$

which is equal to ${\sum }_{i\in \mathcal{I}}\lfloor {log}_2(p_i)\rfloor =\lfloor {log}_2(p_2)\rfloor +\lfloor {log}_2(p_8)\rfloor$. Considering all three parts, the bit-vector int is obtained by

$$\begin{array}{c}\hfill int=\mathtt{0000000001}⊞\mathtt{0000000101}\boxminus \mathtt{0000000100}=\mathtt{0000000010}=2.\end{array}$$

Moreover, the frac bit-vector in Algorithm 1 is calculated by

Considering the third major operand of int and the bit-vector frac, we can obtain the summation of all approximate logarithms

$$\begin{array}{c}\hfill \sum _{i\in \mathcal{I}}{\mathsf{apxlog}}_2(p_i)={\mathsf{apxlog}}_2(p_2)+{\mathsf{apxlog}}_2(p_8)=4+\frac{4}{2^4}=4.25.\end{array}$$

To summarize, the output of Algorithm 1 is

$$\begin{array}{cc}\hfill \mathsf{BvWeight}(u,v,a)& =(int\ll 4)\boxminus frac,\hfill \\ \hfill & =\mathtt{0000100000}\boxminus \mathtt{0000000100}=\mathtt{0000011100}=28.\hfill \end{array}$$

Therefore, the approximate weight will be equal to

$$\begin{array}{c}\hfill {\mathsf{apxweight}}_{{⊞}_a}(u,v)=2^{-4}\mathsf{BvWeight}(u,v,a)={\displaystyle \frac{28}{2^4}}=1.75.\end{array}$$

The total error of our approximation is

$$\begin{array}{c}\hfill E={\mathsf{weight}}_{{⊞}_a}(u,v)-{\mathsf{apxweight}}_{{⊞}_a}(u,v)\approx 1.678-1.75=-0.072,\end{array}$$

which is a negative value and lower bounded by $-0.029(n-1)=-0.261$ as suggested by Theorem 4.

Error analysis: proof of Theorem 4

In this subsection, we will prove Theorem 4 by gradually analysing the error produced by our approximation of the binary logarithm. As we can see from Eqs. (3) and (5), the gap between ${\mathsf{weight}}_{{⊞}_a}(u,v)$ and ${\mathsf{apxweight}}_{{⊞}_a}(u,v)$ is

$$\begin{array}{cc}\hfill \mathsf{weight}& {}_{{⊞}_a}(u,v)-{\mathsf{apxweight}}_{{⊞}_a}(u,v)=-\sum _{i\in \mathcal{I}}({log}_2(p_i)-{\mathsf{apxlog}}_2(p_i)).\hfill \end{array}$$

Note that the integer part of ${\mathsf{apxlog}}_2$ is equal to the integer part of ${log}_2$ and the error is caused by the fraction part of the logarithm.

Given a positive integer x and the corresponding $m=\lfloor {log}_2(x)\rfloor$, we define ${\mathsf{apxlog}}_2^{\kappa }$ as

$$\begin{array}{c}\hfill {\mathsf{apxlog}}_2^{\kappa }(x)=\left\{\begin{array}{cc}m+x[m-1,0]/2^m,\hfill & m\le \kappa \hfill \\ m+x[m-1,x-\kappa ]/2^{\kappa },\hfill & m>\kappa \hfill \end{array}\right)\end{array}$$

The non-negative integer $\kappa$ is called the precision of the fraction part. Note that ${\mathsf{apxlog}}_2^{\kappa }$ is the generalization of ${\mathsf{apxlog}}_2$, which considers $\kappa =4$ bits for the fraction part. While Theorem 4 only focuses on $\kappa =4$, we will use ${\mathsf{apxlog}}_2^{\kappa }$ in this section to additionally prove that our error bound also applies to $\kappa \ge 4$.

The following lemma bounds the approximation error of ${\mathsf{apxlog}}_2$ when $\kappa \ge \lfloor {log}_2(x)\rfloor$, with a similar proof as [56] for the sake of completeness. The main idea is that after extracting integer part of the logarithm in base 2, one can estimate ${log}_2(1+\gamma )$ by $\gamma$ when $0\le \gamma <1$.

Lemma 9

Consider a positive integer x and the binary logarithm approximation ${log}_2(x)\approx m+x[m-1,0]/2^m,$ where $m=\lfloor {log}_2(x)\rfloor$. Then, the approximation error $e={log}_2(x)-(m+x[m-1,0]/2^m)$ is bounded by $0\le e\le B$, where B is given by

$$\begin{array}{c}\hfill B=1-(1+ln(ln(2)))/ln(2)\approx 0.086.\end{array}$$

Proof

Let $x=2^m+b$, where b is a non-negative integer such that $0\le b<2^m$. Therefore, $x[m-1,0]=x-2^m=b$ and the error is given by

$$\begin{array}{cc}\hfill e=& {log}_2(x)-\left(m,+,\frac{x[m-1,0]}{2^m}\right)={log}_2(2^m+b)-\left(m,+,\frac{b}{2^m}\right)\hfill \\ \hfill =& {log}_2\left(1,+,\frac{b}{2^m}\right)-{\displaystyle \frac{b}{2^m}}.\hfill \end{array}$$

For $\gamma =b/2^m$, we obtain $0\le \gamma <1$ and $e={log}_2(1+\gamma )-\gamma$. Note that e is a concave function of $\gamma$ where $e\ge 0$ if and only if $0\le \gamma \le 1$. By deriving $e=e(\gamma )$, one can see that $max(e)=B=1-(1+ln(ln(2)))/ln(2)\approx 0.086$ is reached when $\gamma =1/ln(2)-1\approx 0.44$. $\square$

The bound B is an almost tight bound, e.g., when $x=3$, the obtained error is ${log}_2(3)-(1+\frac{1}{2})\approxeq 0.085$. The following example sheds more light on our binary logarithm approximation.

Example 4

Consider the positive integer $x=\mathtt{11101}$. Note that ${log}_2(x)\approxeq 4.85798$ and $m=\lfloor ({log}_2(x))\rfloor =4$. In order to obtain the approximation defined in Proposition 9, we first find and omit the greatest "one" in binary representation of x, and we get $x[m-1,0]=\mathtt{1101}$. By interpreting the remaining bits as a binary fraction, we have $x[m-1,0]/2^m=\mathtt{0.1101}$. Therefore, the approximated binary logarithm of $x=\mathtt{11101}$ in binary representation is

$$\begin{array}{c}\hfill m+{\displaystyle \frac{x[m-1,0]}{2^m}}=\mathtt{100.1101},\end{array}$$

which is equal to 4.8125. In addition, the corresponding error of such approximation is $e\approx 0.04548$, which is a positive value and upper bounded by $B\approx 0.086$.

Finally, we can now prove Theorem 4, which basically states that if we dedicate 4 bits to the fraction precision $\kappa$, the approximation error E is bounded by $-0.029·(n-1)\le E\le 0$. While Theorem 4 focuses on $\kappa =4$, we will show in the proof that we can also bound the error for $\kappa \ge 4$. To this end, we generalize the approximated weight ${\mathsf{apxweight}}_{{⊞}_a}$ and the approximated weight error $E_{\kappa }$ as follows

$$\begin{array}{cc}\hfill {\mathsf{apxweight}}_{{⊞}_a}^{\kappa }(u,v)& =-\left(\sum _{i\in \mathcal{I}},{\mathsf{apxlog}}_2^{\kappa },(p_i),+,\sum _{i\in \mathcal{I}},{log}_2,\left({\displaystyle \frac{1}{2^{{\ell }_i-1}}}\right),+,\sum _{i\notin \mathcal{I}},{log}_2,({\phi }_i)\right)\hfill \\ \hfill E_{\kappa }& ={\mathsf{weight}}_{{⊞}_a}(u,v)-{\mathsf{apxweight}}_{{⊞}_a}^{\kappa }(u,v),\hfill \end{array}$$

where ${\mathsf{apxweight}}_{{⊞}_a}^4(u,v)={\mathsf{apxweight}}_{{⊞}_a}(u,v)$ is defined by Eq. (5) and $E_4=E$ is defined in Theorem 4.

Fig. 1.

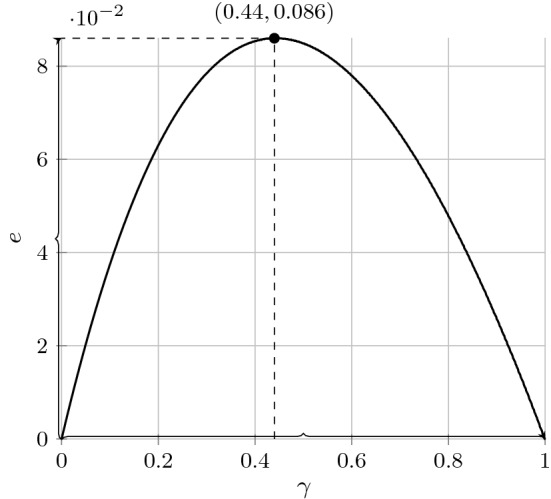
The error $e={log}_2(1+\gamma )-\gamma$, over $0\le \gamma <1$

Proof (Theorem 4)

First, we mention that ${log}_2({\phi }_i)$ is an integer number when $S_i\ne \mathtt{11}\ast$ or for $S_i=\mathtt{11}\ast$ we see ${\ell }_i<3$. For these cases, ${log}_2({\phi }_i)=\lfloor {log}_2({\phi }_i)\rfloor$ and the approximation error is equal to zero.

Next, for each $i\in \mathcal{I}$ when ${\ell }_i\ge 3$, let $p_i=2^{m_i}+b_i$ such that $m_i$ and $b_i$ are two non-negative integers, $m_i\le {\ell }_i-2$ and $0\le b_i<2^{m_i}$. If ${\ell }_i\le \kappa +2$, we obtain $m_i\le \kappa$ and ${\mathsf{apxlog}}_2^{\kappa }(p_i)=m_i+b_i·2^{-m_i}$. Thus, the resulting error

$$\begin{array}{c}\hfill e_i={log}_2(p_i)-{\mathsf{apxlog}}_2^{\kappa }(p_i)={log}_2(p_i)-(m_i+b_i·2^{-m_i})\end{array}$$

is exactly the same as the error defined in Proposition 9, and $0\le e_i\le B\approx 0.086$.

On the other hand, for $m_i>\kappa$, i.e., ${\ell }_i\ge \kappa +3$, let $p_i=2^{m_i}+t_i·2^{m_i-\kappa }+{\zeta }_i$, where $t_i$ and ${\zeta }_i$ are two non-negative integers such that $0\le t_i<2^{\kappa }$ as well as $0\le {\zeta }_i<2^{m_i-\kappa }$. In this case, the approximated binary logarithm is ${\mathsf{apxlog}}_2^{\kappa }(p_i)=m_i+t_i·2^{-\kappa }$. We now define a new error $e_i^{\prime }$ as

$$\begin{array}{cc}\hfill e_i^{\prime }& ={log}_2(p_i)-{\mathsf{apxlog}}_2^{\kappa }(p_i)={log}_2(1+t_i·2^{-\kappa }+{\zeta }_i·2^{-m_i})-t_i·2^{-\kappa }.\hfill \end{array}$$

Due to the fact that ${\zeta }_i\ge 0$, we can see that

$$\begin{array}{c}\hfill e_i^{\prime }={log}_2(p_i)-(m_i+t_i·2^{-\kappa })\ge {log}_2(p_i)-(m_i+t_i·2^{-\kappa }+{\zeta }_i·2^{-m_i})=e_i\ge 0.\end{array}$$

Since ${\zeta }_i<2^{m_i-\kappa }$ and by reforming the error, we obtain the upper bound of $e_i^{\prime }$

$$\begin{array}{c}\hfill e_i^{\prime }\le {log}_2(1+t_i·2^{-\kappa }+2^{-\kappa })-t_i·2^{-\kappa }=({log}_2(1+{\gamma }_i^{\prime })-{\gamma }_i^{\prime })+2^{-\kappa },\end{array}$$

where ${\gamma }_i^{\prime }=(t_i+1)·2^{-\kappa }$ and $2^{-\kappa }\le {\gamma }_i^{\prime }<1$. Regarding Proposition 9, the new error $e_i^{\prime }$ is bounded by $0\le e_i^{\prime }\le B+2^{-\kappa }$.

Note that for a valid differential (u, v) over the constant addition ${⊞}_a$ we can see that $S_0=\mathtt{000}$ which for some $i^{\ast }$ belongs to the chain

$$\begin{array}{c}\hfill {\mathrm{\Gamma }}_{i^{\ast }}=\{S_{i^{\ast }-1},\dots ,S_0,S_{-1}=\perp \},{\ell }_{i^{\ast }}=i^{\ast }+1.\end{array}$$

Hence, we obtain

$$\begin{array}{cc}\hfill {\delta }_{i^{\ast }-1}& =\frac{a[i^{\ast }-{\ell }_{i^{\ast }}-1]}{2^{{\ell }_{i^{\ast }}-1}}+\sum _{j=2}^{{\ell }_{i^{\ast }}}\frac{a[i^{\ast }-j]}{2^{j-1}}=\sum _{j=2}^{{\ell }_{i^{\ast }}-1}\frac{a[i^{\ast }-j]}{2^{j-1}}.\hfill \end{array}$$

Similar to the proof of Lemma 4 we have

$$\begin{array}{c}\hfill {\phi }_{i^{\ast }}=\frac{p_{i^{\ast }}}{2^{{\ell }_{i^{\ast }}-1}}=\frac{p_{i^{\ast }}^{\ast }}{2^{{\ell }_{i^{\ast }}-2}},\end{array}$$

where $p_{i^{\ast }}^{\ast }=p_{i^{\ast }}/2$ is an integer. Therefore, by replacing ${\ell }_{i^{\ast }}$ with ${\ell }_{i^{\ast }}^{\ast }={\ell }_{i^{\ast }}-1$, the previous statements considering the error bounds of our approximation for the state $S_{i^{\ast }}=\mathtt{11}\ast$ and its new ${\ell }_{i^{\ast }}^{\ast }$ are still correct. We now define two bits $\mathtt{b}$ and ${\mathtt{b}}^{\prime }$ as

$$\begin{array}{c}\hfill \mathtt{b}=\left\{\begin{array}{cc}1,\hfill & 3\le {\ell }_{i^{\ast }}^{\ast }\le \kappa +2\hfill \\ 0,\hfill & o.w.\hfill \end{array}\right),{\mathtt{b}}^{\prime }=\left\{\begin{array}{cc}1,\hfill & {\ell }_{i^{\ast }}^{\ast }>\kappa +2\hfill \\ 0,\hfill & o.w.\hfill \end{array}\right)\end{array}$$

Finally, by defining the conditional index set ${\mathcal{I}}_{\alpha }^{\beta }=\{i\in \mathcal{I}-\{i^{\ast }\}|\alpha \le {\ell }_i\le \beta \}$ we obtain

$$\begin{array}{cc}\hfill E_{\kappa }& ={\mathsf{weight}}_{{⊞}_a}(u,v)-{\mathsf{apxweight}}_{{⊞}_a}^{\kappa }(u,v)\hfill \\ \hfill & =-\sum _{i\in \mathcal{I}}({log}_2(p_i)-{\mathsf{apxlog}}_2^{\kappa }(p_i))\hfill \\ \hfill & =-\left(\sum _{i\in {\mathcal{I}}_3^{\kappa +2}},,,,e_i,+,,,,\sum _{i\in {\mathcal{I}}_{\kappa +3}^n},,,,e_i^{\prime },+,\mathtt{b},e_{i^{\ast }},+,{\mathtt{b}}^{\prime },e_{i^{\ast }}^{\prime },\right)\hfill \\ \hfill & \ge -\left(B,,,,\sum _{i\in {\mathcal{I}}_3^{\kappa +2}},,,,1,,+,,(B+2^{-\kappa }),,,,\sum _{i\in {\mathcal{I}}_{\kappa +3}^n},,,,1,+,\mathtt{b},B,+,{\mathtt{b}}^{\prime },(B+2^{-\kappa }),\right)\hfill \\ \hfill & \ge -\left({\displaystyle \frac{B}{3}},,,,\sum _{i\in {\mathcal{I}}_3^{\kappa +2}},,,,{\ell }_i,,+,,\left({\displaystyle \frac{B+2^{-\kappa }}{\kappa +3}}\right),,,,\sum _{i\in {\mathcal{I}}_{\kappa +3}^n},,,,{\ell }_i,+,\mathtt{b},\frac{B}{3},{\ell }_{i^{\ast }}^{\ast },+,{\mathtt{b}}^{\prime },\left(\frac{B+2^{-\kappa }}{\kappa +3}\right),{\ell }_{i^{\ast }}^{\ast },\right).\hfill \end{array}$$

For $\kappa \ge 4$, we can see that ${\displaystyle \frac{B+2^{-\kappa }}{\kappa +3}}\le {\displaystyle \frac{B}{3}}$, resulting in

$$\begin{array}{cc}\hfill 0\ge E_{\kappa }& \ge -\left({\displaystyle \frac{B}{3}},\sum _{i\in {\mathcal{I}}_3^n},{\ell }_i,+,{\displaystyle \frac{B}{3}},{\ell }_{i^{\ast }}^{\ast }\right)=-\left({\displaystyle \frac{B}{3}},\sum _{i\in {\mathcal{I}}_3^n},{\ell }_i,+,{\displaystyle \frac{B}{3}},({\ell }_{i^{\ast }}-1)\right)\hfill \\ \hfill & \ge -{\displaystyle \frac{B}{3}}(n-1)\approx -0.029(n-1).\hfill \end{array}$$

Since for $\kappa =4$, we have $E_4=E={\mathsf{weight}}_{{⊞}_a}(u,v)-{\mathsf{apxweight}}_{{⊞}_a}(u,v)$, the above inequalities hold for the approximation error E as well. $\square$

While dedicating $\kappa =4$ bits as the fraction precision is enough to obtain the same error bounds as $\kappa >4$, considering $\kappa <4$ creates a trade-off between the lower bound of the error and the complexity of Algorithm 1. As an example, choosing $\kappa =3$ removes one $\mathsf{HW}$ call in Algorithm 1. However, by following the proof of Theorem 4 for $\kappa =3$, the error will be lower bounded by $-0.035(n-1)$, which potentially is an acceptable trade-off.

The differential model of the constant addition as well as the approximation error will be used in the automated method that we will present in the next section to search for characteristics and impossible differentials of ARX ciphers.

SMT-based search of characteristics and impossible differentials

In this section, we describe how to formulate the search of optimal characteristics and impossible differentials as a sequence of SMT problems, which can be solved by an off-the-shelf SMT solver such as Boolector [62] or STP [22]. Our methods are inspired by the approach of Mouha and Preneel [57] to search for single-key characteristics of Salsa20 [57] and the approach by Sasaki and Todo to search for impossible differentials using Mixed Integer Linear Programming (MILP) [66].

Searching for characteristics

To search for characteristics up to probability $2^{-n}$, the probability space is decomposed into n intervals $I_w=\left(2^{-w-1},,,2^{-w}\right]$, where $w=0,1,\cdots ,n-1$, and for each interval, the decision problem of whether there exists a characteristic with probability $p\in I_w$ is encoded as an SMT problem. Note that a characteristic $\mathrm{\Omega }$ has probability $p\in I_w$ if and only if its integer weight $\lfloor \mathsf{weight}(\mathrm{\Omega })\rfloor$ is equal to w. Section 4.2 describes the encoding process for an ARX cipher.

The SMT problems are provided to the SMT solver, which checks their satisfiability in increasing weight order. When the SMT solver finds the first satisfiable problem, an assignment of the variables that makes the problem satisfiable is obtained, and the search finishes. The assignment contains a characteristic with integer weight $\widehat{w}$, and it is optimal in the sense that there are no characteristics with integer weight strictly smaller than $\widehat{w}$. If the n SMT problems are found to be unsatisfiable, then it is proved there are no characteristics with probability higher than $2^{-n}$.

To speed up the search, we perform the search iteratively on round-reduced versions of the cipher. First, we search for an optimal characteristic for a small number of rounds r; let $\widehat{w}$ denote its integer weight. Then, we search for an optimal $(r+1)$-round characteristic, but skipping the SMT problems with weight strictly less than $\widehat{w}$. Since these SMT problems were found to be unsatisfiable for r rounds, they will also be unsatisfiable for $r+1$ rounds. This procedure is repeated until the total number of rounds is reached. Algorithm 2 describes in pseudo-code this search strategy. Our strategy prioritises SMT problems with low weight and small number of rounds, which are faster to solve. In addition, our search also finds optimal characteristics of round-reduced versions, which can be used in other differential-based attacks, such as rectangle or boomerang attacks [9, 71].

This automated method can be used to search for either single-key or related-key characteristics. Furthermore, additional SMT constraints can be added to the SMT problems in order to search for different types of characteristics. For related-key characteristics and by default, this method searches characteristics minimizing the total weight $\mathsf{weight}(\mathrm{\Omega })=\mathsf{weight}({\mathrm{\Omega }}_{\mathit{KS}})+\mathsf{weight}({\mathrm{\Omega }}_E)$. Strong related-key characteristics can be searched by adding the constraint $\mathsf{weight}({\mathrm{\Omega }}_{\mathit{KS}})=0$ in the SMT problems. Similarly, equivalent keys can be found by adding the constraint $\mathsf{weight}({\mathrm{\Omega }}_E)=0$.

Algorithm 2 returns the characteristic with the minimum SMT integer weight, obtained from the bit-vector differential models used within the SMT problems. When some of these models compute approximations of the intermediate weights, the SMT integer weight and the actual integer weight of the characteristic might differ, and the returned characteristic might not be optimal. However, if we have alternative models that compute the exact intermediate weights (that cannot be represented in the SMT problems) and a bound for the error of the SMT integer weight, Algorithm 2 can be adapted to obtain the optimal characteristic as follows. First, Algorithm 2 is used to obtain the characteristic $\mathrm{\Omega }$ with the minimum SMT integer weight $\widehat{w}$. Then, one finds all2 characteristics with SMT integer weights $\{\widehat{w},\widehat{w}+1,\cdots ,\widehat{w}+\lfloor ϵ\rfloor \}$, where $ϵ$ is the absolute bound for the error of the SMT integer weight. Finally, the weights of the found characteristics are recomputed with the alternative models, and the characteristic with the minimum integer weight is returned. This adaptation can be used for ARX ciphers with constant additions, as the error bound can be computed from Theorem 4 and Machado’s algorithm [53] can be used to compute the exact weights of the constant additions.

This method only ensures optimality if the differential probabilities over each round are independent and the characteristic probability does not strongly depend on the choice of the secret key. When these assumptions do not hold for a cipher, we empirically compute the weight of each characteristic found by sampling many input pairs satisfying the input difference and counting those satisfying the difference trail. In this case, this method provides a practical heuristic to find characteristics with high probability, and it is one of the best systematic approaches for some families of ciphers, such as ARX.

Encoding the SMT problems

In this section, we explain how to formulate the decision problem of determining whether a characteristic $\mathrm{\Omega }$ exists with integer weight W of an ARX cipher as an SMT problem in the bit-vector theory.

First, the ARX cipher is represented in Static Single Assignment (SSA) form, that is, as an ordered list of instructions $y\leftarrow f(x)$ such that each variable is assigned exactly once and each instruction is a modular addition, a rotation, or an XOR.

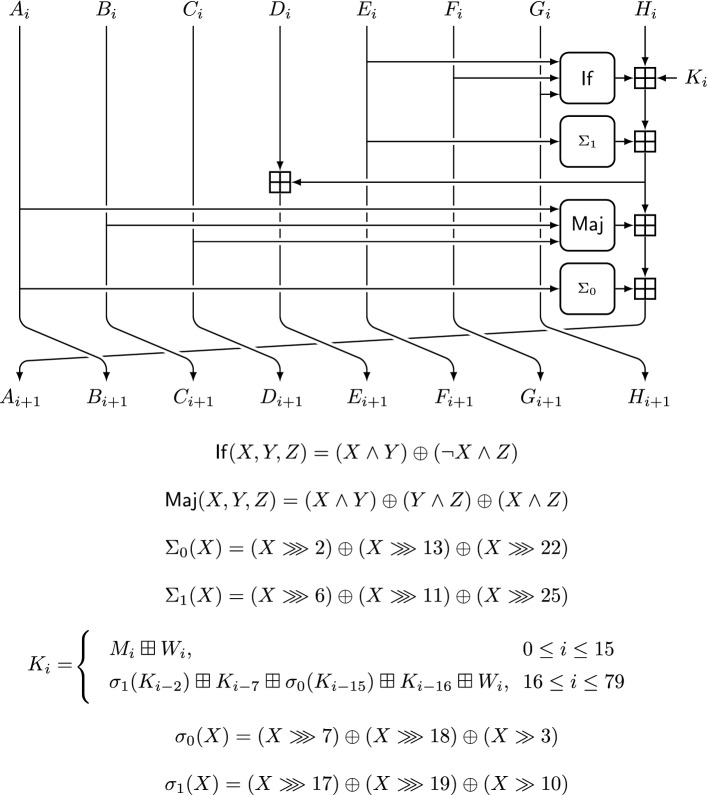
For each variable x in the SSA representation, a bit-vector variable ${\mathrm{\Delta }}_x$ denoting the difference of x is defined in the SMT problem. Then, for every instruction $y\leftarrow f(x)$, the weight and the differential model of f are added to the SMT problem as a bit-vector variable w and bit-vector constraints ${\mathsf{valid}}_{f_i}({\mathrm{\Delta }}_x,{\mathrm{\Delta }}_y)$ and $\mathsf{Equals}(w,{\mathsf{weight}}_{f_i}({\mathrm{\Delta }}_x,{\mathrm{\Delta }}_y))$, following Table 5.

Table 5.

Bit-vector differential models of ARX operations

$y=f_a(x)$	Validity	Weight
$y=x_1\oplus x_2$	$\mathsf{Equals}({\mathrm{\Delta }}_y,{\mathrm{\Delta }}_{x_1}\oplus {\mathrm{\Delta }}_{x_2})$	0
$y=x\oplus a$	$\mathsf{Equals}({\mathrm{\Delta }}_y,{\mathrm{\Delta }}_x)$	0
$y=x⋘a$	$\mathsf{Equals}({\mathrm{\Delta }}_y,{\mathrm{\Delta }}_x⋘a)$	0
$y=x⋙a$	$\mathsf{Equals}({\mathrm{\Delta }}_y,{\mathrm{\Delta }}_x⋙a)$	0
$y=x_1⊞x_2$	Theorem 1	Theorem 1
$y=x⊞a$	Theorem 3	Theorem 4

Finally, the following bit-vector constraints are added to the SMT problem,

$$\begin{array}{c}\hfill \mathsf{NotEquals}({\mathrm{\Delta }}_p,0),\mathsf{Equals}(W,w_1⊞\cdots ⊞w_r),\end{array}$$

where ${\mathrm{\Delta }}_p$ denotes the input difference and $(w_1,\cdots ,w_r)$ denote the weight of each operation. The first constraint excludes the trivial characteristic with zero input difference, while the second constraint fixes the weight of the characteristic to the target weight. Note that the bit-size of the weights might need to be increased to prevent an overflow in the modular addition of the last constraint.

Example 5

Consider the keyed function $f_k$ with key k and input $p=(p_1,p_2)$,

$$\begin{array}{c}\hfill f_k(p_1,p_2)=(((p_2⊞1)\oplus k)⊞p_1,p_1⋘1).\end{array}$$

This function can be written as a list of simple instructions (SSA form) as

$$\begin{array}{cc}& x_1\leftarrow p_2⊞1,\hfill \\ \hfill & x_2\leftarrow x_1\oplus k,\hfill \\ \hfill & x_3\leftarrow x_2⊞p_1,\hfill \\ \hfill & x_4\leftarrow p_1⋘1,\hfill \end{array}$$

where the output is the pair $(x_3,x_4)$. Figure 2 depicts the function $f_k$ together with its intermediate variables.

Fig. 2.

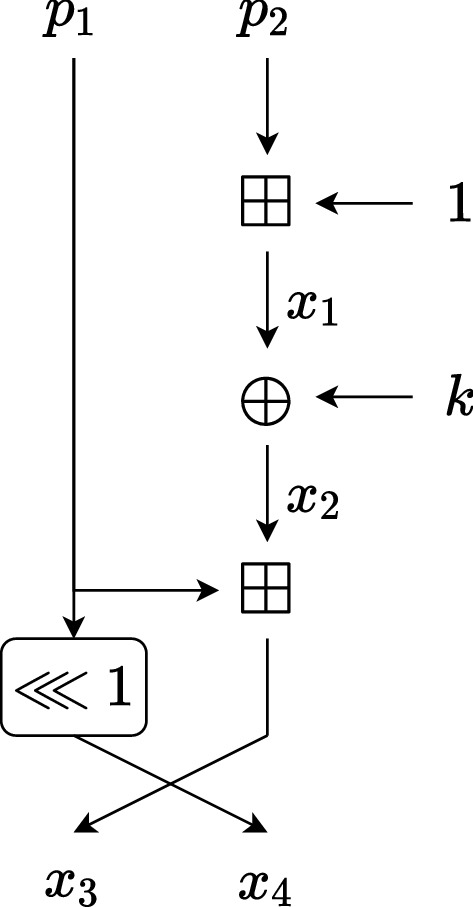
The function $f_k$

An SMT problem in the bit-vector theory denoting whether $f_k$ has a characteristic with integer weight W is as follows:

$$\begin{array}{cc}\hfill \exists {\mathrm{\Delta }}_{p_1},& {\mathrm{\Delta }}_{p_2},{\mathrm{\Delta }}_{x_1},{\mathrm{\Delta }}_{x_2},{\mathrm{\Delta }}_{x_3},{\mathrm{\Delta }}_{x_4},w_1,w_2,w_3,w_4:\hfill \\ \hfill & {\mathsf{valid}}_{{⊞}_1}({\mathrm{\Delta }}_{p_2},{\mathrm{\Delta }}_{x_1}),\hfill \\ \hfill & \mathsf{Equals}(w_1,\mathsf{BvWeight}({\mathrm{\Delta }}_{p_2},{\mathrm{\Delta }}_{x_1},1)),\hfill \\ \hfill & \mathsf{Equals}({\mathrm{\Delta }}_{x_2},{\mathrm{\Delta }}_{x_1}),\hfill \\ \hfill & \mathsf{Equals}(w_2,0),\hfill \\ \hfill & {\mathsf{valid}}_{⊞}(({\mathrm{\Delta }}_{x_2},{\mathrm{\Delta }}_{p_1}),{\mathrm{\Delta }}_{x_3}),\hfill \\ \hfill & \mathsf{Equals}(w_3,{\mathsf{weight}}_{⊞}(({\mathrm{\Delta }}_{x_2},{\mathrm{\Delta }}_{p_1}),{\mathrm{\Delta }}_{x_3})),\hfill \\ \hfill & \mathsf{Equals}({\mathrm{\Delta }}_{x_4},{\mathrm{\Delta }}_{d_{p_1}}⋘1),\hfill \\ \hfill & \mathsf{Equals}(w_4,0),\hfill \\ \hfill & \mathsf{NotEquals}(({\mathrm{\Delta }}_{p_1},{\mathrm{\Delta }}_{p_2}),0),\hfill \\ \hfill & \mathsf{Equals}(W,(w_1⊞((w_2⊞w_3⊞w_4)\ll 4)\gg 4)).\hfill \end{array}$$

The shifts in the last constraint are due to the fact that the last four bits of $w_1$ denote fraction bits. Furthermore, depending on the bit-size of $f_k$, it might be necessary to extend the bit-size of the weights in order to prevent an overflow in the last modular additions.

Searching of impossible differentials

In [66], Sasaki and Todo [66] propose a MILP-based method to search for impossible differentials that employs the MILP problems used to search for characteristics. Since this method can also be adapted to SMT problems, we will explain the method within the SMT context.

The method’s main idea is that one can check whether a particular differential $({\mathrm{\Delta }}_p,{\mathrm{\Delta }}_c)$ is impossible by querying a simple SMT problem. While it is infeasible to check all differentials, one can check those with a low number of active bits since most of the known impossible differentials have this property.

The subroutine to check whether a particular differential $({\mathrm{\Delta }}_{p_0},{\mathrm{\Delta }}_{c_0})$ is impossible can be done as follows. First, the SMT problem of whether there exists a characteristic over the cipher is encoded as in Sect. 4.2. However, only the validity constraints are added; the weight constraints and the target weight W are ignored. Second, the constraints that fix the input and output differences $({\mathrm{\Delta }}_p,{\mathrm{\Delta }}_c)$ to $({\mathrm{\Delta }}_{p_0},{\mathrm{\Delta }}_{c_0})$ are added to the SMT problem, that is,

$$\begin{array}{c}\hfill \mathsf{Equals}({\mathrm{\Delta }}_p,{\mathrm{\Delta }}_{p_0}),\mathsf{Equals}({\mathrm{\Delta }}_c,{\mathrm{\Delta }}_{c_0}).\end{array}$$

Then, the SMT solver checks the satisfiability of the SMT problem. If the problem is found to be unsatisfiable, the differential is impossible.

This method can be used to search for single-key and related-key impossible differentials. For the former case, the validity constraints of the key schedule are ignored, while for the latter case they are included in the SMT problems.

As opposed to the previous SMT-based characteristic search method, the impossible check subroutine is a sound method. In other words, a characteristic found by Algorithm 2 could be invalid due to the independence assumptions, but a differential found impossible by the check subroutine is always impossible. While the check subroutine is a sound method, it is not complete; there are some impossible differentials that cannot be detected by the check subroutine.

While the check subroutine is fast, checking all differentials is infeasible and only a small subset can be checked with the method by [66]. Thus, we propose a new automated method to search for impossible differentials that does not restrict the search over any pre-defined small subset and let the SMT solver efficiently search through the space of differentials. Our automated method proceeds as follows.

First, we split the cipher $E=E_2\circ E_1\circ E_0$ into three parts $E_2,E_1$ and $E_0$. Let $\mathrm{\Omega }=({\mathrm{\Delta }}_{x_0},{\mathrm{\Delta }}_{x_1},{\mathrm{\Delta }}_{x_2},{\mathrm{\Delta }}_{x_3})$ denote a partial characteristic over E, that is, any characteristic verifying

$$\begin{array}{c}\hfill Pr({\mathrm{\Delta }}_{x_0}\stackrel{E_0}{\to }{\mathrm{\Delta }}_{x_1})=1,Pr({\mathrm{\Delta }}_{x_2}\stackrel{E_2}{\to }{\mathrm{\Delta }}_{x_3})=1.\end{array}$$

Note that no relation is imposed between ${\mathrm{\Delta }}_{x_1}$ and ${\mathrm{\Delta }}_{x_2}$.

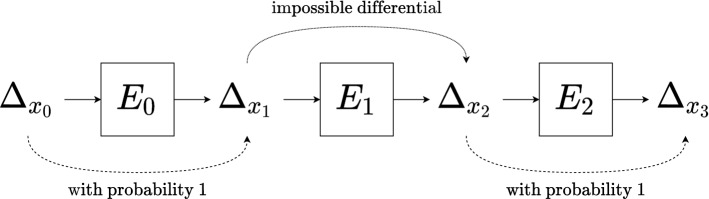
Then, we search for all partial characteristics using our SMT-based method from Sect. 4.1. For each partial characteristic $\mathrm{\Omega }=({\mathrm{\Delta }}_{x_0},{\mathrm{\Delta }}_{x_1},{\mathrm{\Delta }}_{x_2},{\mathrm{\Delta }}_{x_3})$, we apply the check subroutine to the differential $({\mathrm{\Delta }}_{x_1},{\mathrm{\Delta }}_{x_2})$ over $E_1$. If $({\mathrm{\Delta }}_{x_1},{\mathrm{\Delta }}_{x_2})$ is found to be impossible over $E_1$, then $({\mathrm{\Delta }}_{x_0},{\mathrm{\Delta }}_{x_3})$ is an impossible differential over E, since $({\mathrm{\Delta }}_{x_0},{\mathrm{\Delta }}_{x_1})$ and $({\mathrm{\Delta }}_{x_2},{\mathrm{\Delta }}_{x_3})$ are differentials with probability one (see Fig. 3).

Fig. 3.

The partial characteristic $\mathrm{\Omega }=({\mathrm{\Delta }}_{x_0},{\mathrm{\Delta }}_{x_1},{\mathrm{\Delta }}_{x_2},{\mathrm{\Delta }}_{x_3})$ over $E=E_2\circ E_1\circ E_0$, alongside the condition that the inner part $({\mathrm{\Delta }}_{x_1},{\mathrm{\Delta }}_{x_2})$ over $E_1$ is an impossible differential

Like the characteristic search method, we start searching for impossible differentials over a round-reduced version of the cipher and keep increasing the number of rounds iteratively. This procedure is described in Algorithm 3. While FindPartialCh in Algorithm 3 is responsible for finding partial characteristics, IsImpossible subroutine checks the corresponding inner differential to be impossible. Impossible differentials starting after a few rounds are useful in practice, and our method can easily be adapted by splitting the cipher into four parts, $E=E_2\circ E_1\circ E_0\circ E_{-1}$, where $E_{-1}$ denotes the skipped rounds.

The main advantage of our method is that the subset of differentials to check does not need to be specified. Thus, it can find impossible differentials that other methods cannot. Moreover, the search of partial characteristics is quite fast, as for many operations f (including the modular addition and the constant addition) the constraint $\mathsf{Equals}(0,{\mathsf{weight}}_f({\mathrm{\Delta }}_x,{\mathrm{\Delta }}_y))$ is much simpler than the constraint for the general case $\mathsf{Equals}(w,{\mathsf{weight}}_f({\mathrm{\Delta }}_x,{\mathrm{\Delta }}_y))$.

As opposed to the search of characteristics, the search of $r+1$-round impossible differentials cannot reuse information obtained from the search of r-round impossible differentials. In other words, Algorithm 2 exploits the fact that if no r-round characteristics were found with weight w, then no $r+1$-round characteristics can be found with the same weight. However, for some key schedules, Algorithm 2 might find $r+1$-round impossible differentials even if no r-round impossible differentials were found.

Implementation

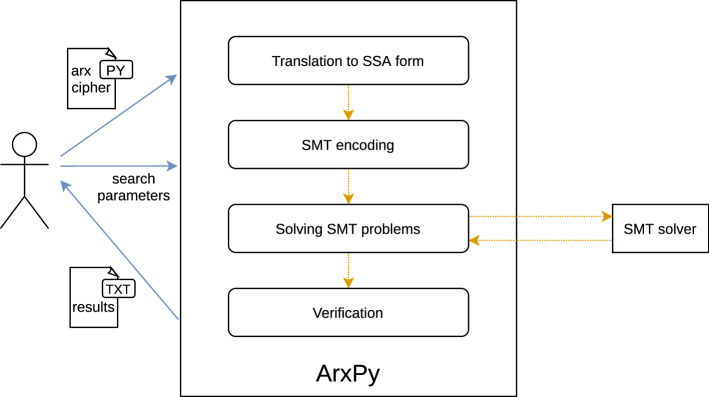
We have developed an open-source tool ArxPy3 to find characteristics and impossible differentials of ARX ciphers implementing the methods described earlier. Originally, ArxPy was a tool to search for rotational-XOR characteristics using SMT solvers [64]. However, we have extended it to support (related-key) differential characteristics and impossible differentials containing the constant addition. ArxPy provides high-level functions that automate the search, a simple interface to represent ARX ciphers, and complete documentation in HTML format, among other features.

ArxPy workflow is represented in Fig. 4. The user first defines the ARX cipher using the interface provided by ArxPy and chooses the parameters of the search (e.g., the type of the characteristic to search, the SMT solver to use, etc.). Then, ArxPy automatically translates the python implementation of the ARX cipher into SSA form, encodes the SMT problems associated to the type of search selected by the user, and solves the SMT problems by querying the SMT solver. When searching for characteristics, for each satisfiable SMT problem found, ArxPy reconstructs the characteristic from the assignment of the variables that satisfies the problem and empirically verifies the weight of the characteristic. Finally, ArxPy returns the results of the search to the user.

Fig. 4.

Workflow of ArxPy

Internally, ArxPy is implemented in Python 3 and uses the libraries SymPy [55] to obtain the SSA representation through symbolic execution and PySMT [23] for the communication with the SMT solvers. Thus, all the SMT solvers supported by PySMT can be directly used for ArxPy.

Experiments

We have applied our methods for finding characteristics and impossible differentials to some ARX ciphers that include constant additions. In particular, we have searched for related-key characteristics and related-key impossible differentials of TEA, XTEA, HIGHT, LEA, SHACAL-1, and SHACAL-2.

Due to the difficulty of searching for characteristics of ciphers with constant additions this far, cipher designers have avoided constant additions in the encryption functions so that they could search for single-key characteristics, the most threatening ones. Only a few ciphers include constant additions in the encryption function, and their ad-hoc structures make them more suitable to be analysed with other types of differences, such as additive differences in the case of TEA [11]. As a result, we have focused on searching related-key characteristics and impossible differentials of some well-known ciphers.

Regarding the search for characteristics, we used Algorithm 2 to find related-key characteristics starting from the first round of each cipher. For the case of impossible differentials, we applied Algorithm 3 to search for related-key impossible differentials but skipping the first rounds of the cipher. To this end, we repeatedly call Algorithm 3 while increasing the number of skipped rounds in each call.

For related-key characteristics, the usual assumptions (i.e., round independence and the hypothesis of stochastic equivalence) do not always hold. Thus, we empirically verify each characteristic and stopped each round-reduced search after the first valid characteristic is found.

To verify a related-key characteristic $\mathrm{\Omega }$, we split $\mathrm{\Omega }$ in smaller characteristics ${\mathrm{\Omega }}_i=({\mathrm{\Delta }}_{x_i}\to \cdots \to {\mathrm{\Delta }}_{y_i})$ with weight $w_i$ lower than 20, and empirically compute the probability of each differential $({\mathrm{\Delta }}_{x_i},{\mathrm{\Delta }}_{y_i})$ by sampling a small multiple of $2^{w_i}$ input pairs for $2^{10}$ related-key pairs. After combining the probability of each differential, we obtain $2^{10}$ characteristic probabilities, one for each related-key pair. If the characteristic probability is non-zero for several key pairs, we consider the characteristic valid and we define its empirical probability (resp. weight) as the arithmetic mean of the $2^{10}$ characteristic probabilities (resp. weights), but excluding those key pairs with zero probability.

Thus, for each characteristic that we have found, i.e. strong related-key characteristic ($w_{\mathsf{KS}}=0$) and weak related-key characteristic ($w_{\mathsf{KS}}>0$), Table 6 provides: (1) the theoretical key schedule and encryption weights $(w_{\mathsf{KS}},w_E)$, computed by summing the weight of each ARX operation; (2) the empirical key schedule and encryption weights $(\overline{w_{\mathsf{KS}}},\overline{w_E})$, computed by sampling input pairs as explained before; and (3) the percentage of the valid key pairs that empirically lead to non-zero probability in the weight verification. In the appendix, we provide the round weights and the round differences for the characteristics covering the most rounds.

Table 6.

Best related-key differential characteristics of XTEA, HIGHT, LEA, SHACAL-1, and SHACAL-2

Cipher	Ch. Type	Rounds	$(w_{\mathsf{KS}},\overline{w_{\mathsf{KS}}})$	$(w_E,\overline{w_E})$	% valid keys	References
XTEA	Strong	16	0	32	–	[52]
		16	(0,0)	(37, 32.02)	46%	This paper
		18	(0,0)	(57, 49.79)	48%	This paper
	Weak	18	17	19	–	[45, 52]
		18	(4.83, 3.15)	(16, 14.46)	100%	This paper
		27	(6.89, 5.74)	(40, 39.39)	7%	This paper
HIGHT	Strong	10	0	12	–	[50]
		10	(0, 0)	(12, 9.97)	34%	This paper
		15	(0, 0)	(45, 42.59)	8%	This paper
	Weak	12	2	19	–	[40]
		12	(2.48, 3.19)	(19, 17.65)	40%	This paper
		14	(13.09, 9.85)	(14, 11.46)	17%	This paper
LEA	Weak	11	–	–	–	[32]
		6	(1.56, 1.22)	(24, 22.50)	100%	This paper
		7	(2.56, 4.68)	(36, 34.35)	100%	This paper
SHACAL-1	Strong	27	0	29	–	[36]
		30	(0, 0)	(63, 47.36)	97%	This paper
	Weak	35	10	29	–	[18, 72]
		25	(1, 0.87)	(22, 13.31)	47%	This paper
SHACAL-2	Strong	24	0	38${}^{\mathrm{a}}$	–	[51]
		23	(0, 0)	(58, 48.06)	100%	This paper
	Weak	24	–	52	–	[12]
		22	(6.67, 2.38)	(29, 24.03)	100%	This paper

${}^{\mathrm{a}}$Imposes extra conditions on plaintext values or intermediate values

When searching for impossible differentials with skipped rounds, Algorithm 3 splits the cipher into four parts. More specifically, the cipher E is represented as $E=E_2\circ E_1\circ E_0\circ E_{-1}$, where $E_{-1}$ denotes the skipped rounds, $E_1$ stands for the rounds of the inner impossible differential, and $E_0$ and $E_2$ respectively denote the backward and the forward rounds of the partial characteristics. In Table 7 we provide the number of rounds of each part for the best related-key impossible differentials that we found, and in Table 8 we provide the input and output differences of our longest impossible differentials.

Table 7.

Best related-key impossible differentials of XTEA, HIGHT, LEA, SHACAL-1, and SHACAL-2

Cipher	Rounds	Start	Backward	Inner ID	Forward	References
XTEA	$25(19\sim 43)$	19	–	–	–	[15]
	$25(0\sim 24)$	0	7	13	5	This paper
HIGHT	$22(6\sim 27)$	6	–	–	–	[63]
	$22(0\sim 21)$	0	4	14	4	This paper
LEA	$4(0\sim 3)$	0	0	4	0	This paper
SHACAL-1	$30(20\sim 49)$	20	2	16	12	This paper
SHACAL-2	$18(0\sim 17)$	0	–	–	–	[75]
	$24(0\sim 23)$	0	1	12	11	This paper

Table 8.

Input, output, and key differences of our longest related-key impossible differentials

Cipher	Differences
XTEA	${\mathrm{\Delta }}_{\mathit{mk}}$	$(\mathtt{0}\mathtt{x}\mathtt{80000000},\mathtt{0}\mathtt{x}\mathtt{00000000},\mathtt{0}\mathtt{x}\mathtt{00000000},\mathtt{0}\mathtt{x}\mathtt{00000000})$
	${\mathrm{\Delta }}_p$	$(\mathtt{0}\mathtt{x}\mathtt{80000000},\mathtt{0}\mathtt{x}\mathtt{00000000})$
	${\mathrm{\Delta }}_c$	$(\mathtt{0}\mathtt{x}\mathtt{00000000},\mathtt{0}\mathtt{x}\mathtt{80000000})$
HIGHT	${\mathrm{\Delta }}_{\mathit{mk}}$	$(\mathtt{0}\mathtt{x}\mathtt{00},\mathtt{0}\mathtt{x}\mathtt{00},\mathtt{0}\mathtt{x}\mathtt{00},\mathtt{0}\mathtt{x}\mathtt{00},\mathtt{0}\mathtt{x}\mathtt{00},\mathtt{0}\mathtt{x}\mathtt{00},\mathtt{0}\mathtt{x}\mathtt{00},\mathtt{0}\mathtt{x}\mathtt{00},$
		$\mathtt{0}\mathtt{x}\mathtt{00},\mathtt{0}\mathtt{x}\mathtt{00},\mathtt{0}\mathtt{x}\mathtt{00},\mathtt{0}\mathtt{x}\mathtt{00},\mathtt{0}\mathtt{x}\mathtt{00},\mathtt{0}\mathtt{x}\mathtt{00},\mathtt{0}\mathtt{x}\mathtt{80},\mathtt{0}\mathtt{x}\mathtt{00})$
	${\mathrm{\Delta }}_p$	$(\mathtt{0}\mathtt{x}\mathtt{00},\mathtt{0}\mathtt{x}\mathtt{00},\mathtt{0}\mathtt{x}\mathtt{00},\mathtt{0}\mathtt{x}\mathtt{00},\mathtt{0}\mathtt{x}\mathtt{80},\mathtt{0}\mathtt{x}\mathtt{00},\mathtt{0}\mathtt{x}\mathtt{00},\mathtt{0}\mathtt{x}\mathtt{00})$
	${\mathrm{\Delta }}_c$	$(\mathtt{0}\mathtt{x}\mathtt{00},\mathtt{0}\mathtt{x}\mathtt{80},\mathtt{0}\mathtt{x}\mathtt{00},\mathtt{0}\mathtt{x}\mathtt{00},\mathtt{0}\mathtt{x}\mathtt{00},\mathtt{0}\mathtt{x}\mathtt{00},\mathtt{0}\mathtt{x}\mathtt{00},\mathtt{0}\mathtt{x}\mathtt{00})$
LEA	${\mathrm{\Delta }}_{\mathit{mk}}$	$(\mathtt{0}\mathtt{x}\mathtt{00000001},\mathtt{0}\mathtt{x}\mathtt{00000000},\mathtt{0}\mathtt{x}\mathtt{00000000},\mathtt{0}\mathtt{x}\mathtt{00000000})$
	${\mathrm{\Delta }}_p$	$(\mathtt{0}\mathtt{x}\mathtt{00000000},\mathtt{0}\mathtt{x}\mathtt{00000000},\mathtt{0}\mathtt{x}\mathtt{00000000},\mathtt{0}\mathtt{x}\mathtt{00000000})$
	${\mathrm{\Delta }}_c$	$(\mathtt{0}\mathtt{x}\mathtt{00000000},\mathtt{0}\mathtt{x}\mathtt{00000000},\mathtt{0}\mathtt{x}\mathtt{00000000},\mathtt{0}\mathtt{x}\mathtt{00000000})$
SHACAL-1	${\mathrm{\Delta }}_{\mathit{mk}}$	$(\mathtt{0}\mathtt{xa}\mathtt{0000000},\mathtt{0}\mathtt{x}\mathtt{80000000},\mathtt{0}\mathtt{xa}\mathtt{0000000},\mathtt{0}\mathtt{x}\mathtt{00000000},$
		$\mathtt{0}\mathtt{x}\mathtt{80000000},\mathtt{0}\mathtt{x}\mathtt{00000000},\mathtt{0}\mathtt{xc}\mathtt{0000000},\mathtt{0}\mathtt{x}\mathtt{00000000},$
		$\mathtt{0}\mathtt{x}\mathtt{80000000},\mathtt{0}\mathtt{x}\mathtt{80000000},\mathtt{0}\mathtt{x}\mathtt{40000000},\mathtt{0}\mathtt{x}\mathtt{00000000},$
		$\mathtt{0}\mathtt{x}\mathtt{80000000},\mathtt{0}\mathtt{x}\mathtt{80000000},\mathtt{0}\mathtt{x}\mathtt{40000000},\mathtt{0}\mathtt{x}\mathtt{00000000})$
	${\mathrm{\Delta }}_p$	$(\mathtt{0}\mathtt{x}\mathtt{00000000},\mathtt{0}\mathtt{x}\mathtt{00000000},\mathtt{0}\mathtt{x}\mathtt{00000000},\mathtt{0}\mathtt{x}\mathtt{80000000},\mathtt{0}\mathtt{x}\mathtt{00000000})$
	${\mathrm{\Delta }}_c$	$(\mathtt{0}\mathtt{x}\mathtt{00000000},\mathtt{0}\mathtt{x}\mathtt{00000000},\mathtt{0}\mathtt{x}\mathtt{00000000},\mathtt{0}\mathtt{x}\mathtt{00000000},\mathtt{0}\mathtt{x}\mathtt{00000000})$
SHACAL-2	${\mathrm{\Delta }}_{\mathit{mk}}$	$(\mathtt{0}\mathtt{x}\mathtt{00000000},\mathtt{0}\mathtt{x}\mathtt{00000000},\mathtt{0}\mathtt{x}\mathtt{00000000},\mathtt{0}\mathtt{x}\mathtt{00000000},$
		$\mathtt{0}\mathtt{x}\mathtt{00000000},\mathtt{0}\mathtt{x}\mathtt{00000000},\mathtt{0}\mathtt{x}\mathtt{00000000},\mathtt{0}\mathtt{x}\mathtt{00000000},$
		$\mathtt{0}\mathtt{x}\mathtt{94857}\mathtt{ee}\mathtt{6},\mathtt{0}\mathtt{x}\mathtt{00000000},\mathtt{0}\mathtt{x}\mathtt{00000000},\mathtt{0}\mathtt{x}\mathtt{00000000},$
		$\mathtt{0}\mathtt{x}\mathtt{00000000},\mathtt{0}\mathtt{x}\mathtt{00000000},\mathtt{0}\mathtt{x}\mathtt{00000000},\mathtt{0}\mathtt{x}\mathtt{00000000})$
	${\mathrm{\Delta }}_p$	$(\mathtt{0}\mathtt{x}\mathtt{00000000},\mathtt{0}\mathtt{x}\mathtt{00000000},\mathtt{0}\mathtt{x}\mathtt{00000000},\mathtt{0}\mathtt{x}\mathtt{00000000},$
		$\mathtt{0}\mathtt{x}\mathtt{00000000},\mathtt{0}\mathtt{x}\mathtt{00000000},\mathtt{0}\mathtt{x}\mathtt{00000000},\mathtt{0}\mathtt{x}\mathtt{00000000})$
	${\mathrm{\Delta }}_c$	$(\mathtt{0}\mathtt{x}\mathtt{80000000},\mathtt{0}\mathtt{x}\mathtt{00000000},\mathtt{0}\mathtt{x}\mathtt{00000000},\mathtt{0}\mathtt{x}\mathtt{00000000},$
		$\mathtt{0}\mathtt{x}\mathtt{80000000},\mathtt{0}\mathtt{x}\mathtt{00000000},\mathtt{0}\mathtt{x}\mathtt{00000000},\mathtt{0}\mathtt{x}\mathtt{00000000})$

Apart from all of the best-known impossible differentials that are indicated in Table 7, we also implemented and searched impossible differentials using the automated method of Sasaki and Todo  [66] to compare the results with the ones observed by Algorithm 3. While for XTEA, LEA, and HIGHT, both methods find impossible differentials with the same number of rounds, for SHACAL-1 and SHACAL-2 Algorithm 3 achieves impossible differentials covering more rounds. For XTEA and HIGHT, the longest impossible differentials found by Algorithm 3 include a few active bits, and thus they could also be found by the other method. However, for SHACAL-1 and SHACAL-2, our algorithm found impossible differentials containing multiple active bits, which cannot be obtained by other methods that restrict to predefined differential subsets with a low number of active bits.

For the experiments, we have used ArxPy equipped with the SMT solver Boolector [62], winner of the SMT competition SMT-COMP 2019 in the bit-vector track [26]. We run the characteristic search for one week on a single core of an Intel Xeon 6244 at 3.60GHz. The search of impossible differentials was done on similar hardware during one week as well. Note that better characteristics and impossible differentials could be found if the round-reduced searches are not stopped after the first valid characteristic or if more time is employed.

TEA

Designed by Wheeler and Needham, TEA [73] is a block cipher with 64-bit block size and 128-bit key size. It iterates 64 times an ARX round function, including constant additions and logical shifts, depicted in Fig. 5. Since the logical shifts propagate XOR differences deterministically, the encoding method presented in Sect. 4.2 can be easily extended to include these operations.

Fig. 5.

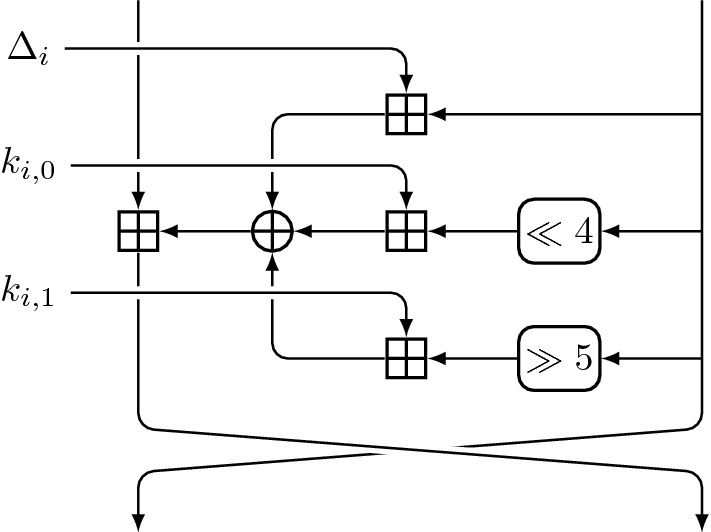
The i-th round of TEA, $i=0,1\cdots ,63$. The master key mk is split into four 32-bit words $(m{k}_0,m{k}_1,m{k}_2,m{k}_3)$ and the i-th round key is defined as $(k_{i,0},k_{i,1})=(m{k}_0,m{k}_1)$ if i is even and $(k_{i,0},k_{i,1})=(m{k}_2,m{k}_3)$ if i is odd. The i-th round constant is defined as ${\mathrm{\Delta }}_i={\mathrm{\Delta }}_{i-2}⊞{\mathrm{\Delta }}_0$, where ${\mathrm{\Delta }}_{-1}={\mathrm{\Delta }}_0=2654435769$

Kelsey et al. [35] presented the best related-key characteristics in [35]. They found a 2-round iterative strong related-key characteristic $\mathrm{\Omega }$ with weight $(w_k,w_e)=(0,1)$, which they extended to a 60-round characteristic with weight (0, 30). They also discovered in [34] that each TEA key has three other equivalent keys.

Using ArxPy, we revisited the results by Kelsey et al. [34], but in a fully automated way. We found three related-key characteristics with weight zero over the full cipher, confirming that each key is equivalent to exactly three other keys. Excluding these three characteristics, we also obtained a 60-round strong related-key characteristic with weight (0, 30), and all the 60-round SMT problems with smaller weights were found to be unsatisfiable. Since a 60-round related-key characteristic is sufficient to mount the related-key differential cryptanalysis on full-round TEA [35], there is no need to search for characteristics containing more rounds of TEA, and we stop at 60 rounds.

There is also no need to search for related-key impossible differentials of TEA, as each of the three full-round zero-weight related-key characteristics induces roughly $2\times 2^{64}$ full-round related-key impossible differentials, simply by alternating either the plaintext or the ciphertext difference.

XTEA

The block cipher XTEA [60] is designed by the same authors of TEA to fix the weakness of the former cipher (in the related-key setting). XTEA has a 64-bit block size and 128-bit key size, and it iterates 64 times the round function depicted in Fig. 6. Like TEA, the round function also includes logical shifts, but the constant additions are included in the key schedule.

Fig. 6.

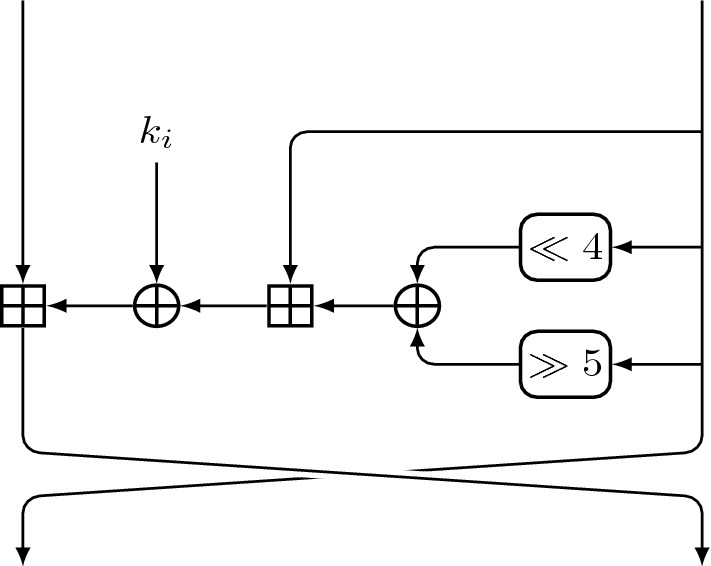
The i-th round of XTEA, $i=0,1\cdots ,63$. The master key mk is split into four 32-bit words $(m{k}_0,m{k}_1,m{k}_2,m{k}_3)$ and the i-th round key is defined as $k_i=s_i⊞m{k}_{s_i\wedge 3}$ if i is even and $k_i=s_i⊞m{k}_{(s_i\ll 11)\wedge 3}$ if i is odd. The i-th constant $s_i$ is defined as $s_i=s_{i-2}⊞s_0$, where $s_{-1}=s_0=2654435769$

The longest related-key characteristics found so far are the 16-round strong related-key differential with weight 32, manually found by Lu in [52], and the 18-round weak related-key characteristic with weights $(w_{\mathsf{KS}},w_E)=(19,19)$, manually found by Lee et al. [45] but later improved to (17, 19) by Lu [52].

The results of our automated search for related-key characteristics are listed in Table 6. In the strong related-key search, we found an 18-round characteristic with weight 57; all the SMT problems for 19 rounds were found to be unsatisfiable. In the weak related-key search, we found characteristics up to 27 rounds, where the 27-round characteristic has total weight $6+40=46$. No equivalent keys were found for XTEA.

In our automated search for related-key impossible differentials of XTEA, we observed impossible differentials spanning 25 rounds, similar to the best impossible differential found this far by Darbuka [15]. Denoting the cipher XTEA with 25 rounds by $E=E_2\circ E_1\circ E_0$, our related-key impossible differential contains a 13-round inner impossible differential over $E_1$, extended by a deterministic 7-round backward trail over $E_0$ and a deterministic 5-round forward trail over $E_2$ as depicted in Table 7. Our automated tool was also able to complete the search of related-key impossible differentials up to 31 rounds, but no impossible differentials spanning more than 25 rounds were found.

HIGHT

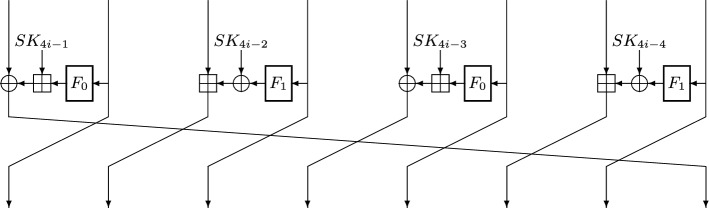
Adopted as an international standard by ISO/IEC [33], HIGHT [31] is a lightweight cipher with a block size of 64 bits and a key size of 128 bits. The encryption function performs initial and final key whitening transformations, and iterates 32 times a round function including XORs, 2-input additions and rotations; the constant additions are performed in the key schedule.

Fig. 7.

The i-th round function of HIGHT, $i=0,1\cdots ,31$ [31]. The i-th round key is denoted by $k_i=(S{K}_{4i-1},S{K}_{4i-2},S{K}_{4i-3},S{K}_{4i-4})$ and the functions $F_0$ and $F_1$ are defined as $F_0(x)=(x⋘1)\oplus (x⋘2)\oplus (x⋘7)$ and $F_1(x)=(x⋘3)\oplus (x⋘4)\oplus (x⋘6)$

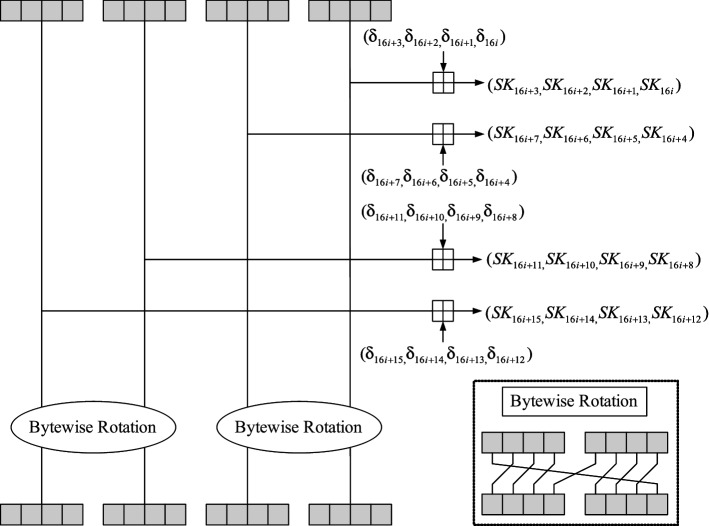
Fig. 8.

The key schedule of HIGHT [31]. The round key words are denoted by $S{K}_i$ and the key schedule constants are denoted by ${\delta }_j$

The longest related-key characteristics found for HIGHT are a 10-round strong characteristic with weight 12 found by Lu [50], and a 12-round weak characteristic with weights $(w_{\mathsf{KS}},w_E)=(2,19)$ found by Koo et al. [40]. In our automated search, we found related-key characteristics up to 15 rounds, listed in Table 6. The longest strong related-key characteristic we found covered 15 rounds with weights (0, 45), whereas the longest weak related-key characteristic covered 14 rounds with total weight $13+14=27$.

Özen et al. introduced the best-known 22-round related-key impossible differential for HIGHT [63]. Using ArxPy, we found a new impossible differential covering the same number of rounds, as shown in Table 7. Our impossible differential consists of a 14-round inner impossible differential, extended by two zero-weight 4-round backward and forward related-key trails. The mentioned 22-round impossible differential is the longest related-key impossible differential that ArxPy could obtain in one week by checking up to 32 rounds of HIGHT.

LEA

Among the family of ARX ciphers LEA [32], we analysed LEA-128, the version with 128-bit block size, 24 rounds, and 128-bit key size. The encryption round function of LEA performs 2-input additions, rotations, and XORs, whereas the key schedule contains constant additions and rotations.

Fig. 9.

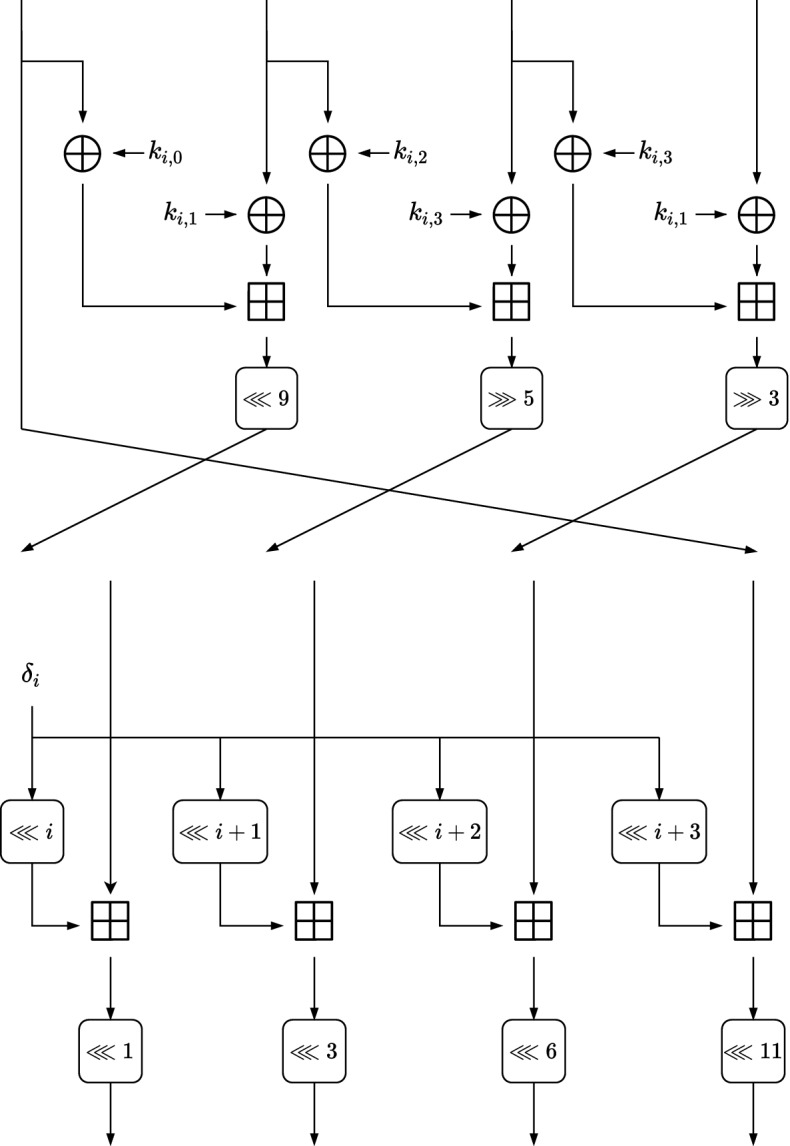
The i-th round function of the encryption (top) and the key schedule (bottom) of LEA-128, $i=0,1\cdots ,23$. The tuple $(k_{i,0},\cdots ,k_{i,3})$ denotes the i-th round key and ${\delta }_i$ denotes the i-th key schedule constant

The designers of LEA found related-key characteristics up to 11 rounds, but only specifying that the 11-round characteristics are valid for a small part of the key space and without providing the weights of such characteristics [32]. Excluding these characteristics, there are no others examples of related-key characteristics of LEA. Our automated search found weak related-key characteristics up to 7 rounds valid for the full key space, listed in Table 6. Strong characteristics with weight smaller than 128 were found up to 4 rounds, and all the strong related-key SMT problems for 5 rounds were found unsatisfiable. No equivalent keys were found for LEA.

We applied ArxPy on LEA to automatically search for related-key impossible differentials. While our method completed the search for a large number of rounds, only impossible differentials with non-zero key difference spanning up to four rounds were found. The lack of related-key impossible differentials, with low Hamming weight or with key schedule transitions with probability 1, seems to be due to the heavy and robust key schedule of LEA. By and large, ciphers with lightweight key schedule algorithms tend to have longer related-key impossible differentials in comparison to their single-key counterparts. However, the key schedule and the round function of LEA are of the same complexity. Thus, finding an impossible differential that covers more rounds in related-key setting instead of single-key setting seems infeasible. We confirmed this by applying our tool to LEA in the single-key setting, obtaining multiple 10-round single-key impossible differentials within a few hours.

SHACAL-1

Based on the compression function of the NIST standard hash function SHA-1 [19], the block cipher SHACAL-1 was initially suggested in [27] and submitted by Handschuh and Naccache to the NESSIE project [61]. SHACAL-1 uses 160-bit block size and 80 rounds, where its round function is similar to the SHA-1 compression function. The key size can be variable from 0 to 512 bits, although a minimum of 128-bit key size is required in [28] and we analysed SHACAL-1 for 512-bit keys.

There are some ad-hoc differential characteristics presented in [18, 30, 36]. However, Wang et al. [72] indicated that many of the previous characteristics are invalid. The longest valid XOR differential characteristic is a 35-round weak related-key characteristic that appeared in [18] and was later corrected in [72] to obtain the corrected weights $(w_{\mathsf{KS}},w_E)=(10,29)$. Moreover, the longest strong related-key XOR differential characteristic that is not found to be invalid by [72] spans 27 rounds of SHACAL-1 with the corresponding weights $(w_{\mathsf{KS}},w_E)=(0,29)$ [36].

These characteristics do not necessarily start from the first round of SHACAL-1 since they are not used for a differential attack but rather for a rectangle attack [9]. Note that the round function of SHACAL-1 changes in different rounds (see Fig. 10), and these characteristics could take advantage of the variable definition of the round function. However, we are only looking for the characteristics starting from the first round and for the particular case of SHACAL-1 with variable round functions, we do not necessarily obtain the best possible characteristics.

Fig. 10.

The i-th round of SHACAL-1, $i=0,1\cdots ,79$. The 160-bit input is divided into five 32-bit words $A_i$, $B_i$, $C_i$, $D_i$, and $E_i$. The function $f_i$ significantly changes regarding the round number. For a given 512-bit master key $mk=(M_0,M_1,\cdots ,M_{15})$, the round keys $K_i$ are computed as described above, where $W_i$ is the round constant

Our automated tool ArxPy obtained a weak-key 25-round characteristic with $(w_{\mathsf{KS}},w_E)=(1,22)$. Moreover, the tool could also find a 30-round characteristic in the strong-key setting with the corresponding weights $(w_{\mathsf{KS}},w_E)=(0,63)$. In our search, a large amount of SHACAL-1 characteristics found by the SMT solver did not pass our empirical validation test, which significantly increased the running time for finding each valid characteristic. More specifically and in the weak-key setting, we found more than 100 empirically invalid characteristics until we detected a valid 25-round one; we also obtained multiple 26-round weak characteristics within a week, but they were found invalid by our empirical test. We discarded more than 900 empirically invalid characteristics for the strong-key setting before finding a valid 30-round characteristic, and none of the 31-round trails obtained in a week could pass the test.

One of the main reasons for the large number of empirically invalid characteristics is the 5-input modular addition within the round function of SHACAL-1. Since the differential model of the modular addition with three or more inputs is unknown, we had to approximate the differential model of the 5-input addition with a chain of 2-input addition models. In other words, to model the 5-input addition $y=x_1⊞x_2⊞x_3⊞x_4⊞x_5$, we split it into four 2-input additions

$$\begin{array}{c}\hfill z_1=x_1⊞x_2,z_2=z_1⊞x_3,z_3=z_2⊞x_4,y=z_3⊞x_5,\end{array}$$

and we model the four 2-input additions independently. Thus, we are approximating the differential probability of the 5-input addition

$$\begin{array}{c}\hfill Pr[({\mathrm{\Delta }}_{x_1},\cdots ,{\mathrm{\Delta }}_{x_5})\stackrel{⊞}{\to }{\mathrm{\Delta }}_y]\end{array}$$

with the multiplication of the differential probabilities of the four 2-input additions

$$\begin{array}{cc}\hfill Pr[({\mathrm{\Delta }}_{x_1},{\mathrm{\Delta }}_{x_2})\stackrel{⊞}{\to }{\mathrm{\Delta }}_{z_1}]\times & Pr[({\mathrm{\Delta }}_{z_1},{\mathrm{\Delta }}_{x_3})\stackrel{⊞}{\to }{\mathrm{\Delta }}_{z_2}]\times \hfill \\ \hfill & Pr[({\mathrm{\Delta }}_{z_2},{\mathrm{\Delta }}_{x_4})\stackrel{⊞}{\to }{\mathrm{\Delta }}_{z_3}]\times Pr[({\mathrm{\Delta }}_{z_3},{\mathrm{\Delta }}_{x_5})\stackrel{⊞}{\to }{\mathrm{\Delta }}_y].\hfill \end{array}$$

For many differentials, this approximation is not accurate, and this caused the appearance of many empirically invalid characteristics in our search.

As depicted in Table 7, our automated tool found the first known related-key impossible differential of SHACAL-1, extending to 30 rounds of the cipher from rounds 20 to 49. The backward and forward trails respectively traverse 2 and 12 rounds of SHACAL-1, delimiting the inner 16-round impossible differential. The search for 31-round impossible differentials did not finish after one week, and we stopped the search. Thus, we expect that dedicating more time to the search may result in obtaining longer impossible differentials.

Fig. 11.

The i-th round of SHACAL-2, $i=0,1\cdots ,63$. The 256-bit input is divided into eight 32-bit words $A_i$, $B_i$, $C_i$, $D_i$, $E_i$, $F_i$, $G_i$, and $H_i$. The special operators used in the round function of SHACAL-2 are $\mathsf{If}$, $\mathsf{Maj}$, ${\mathrm{\Sigma }}_0$, and ${\mathrm{\Sigma }}_1$ that are defined as above. For a given 512-bit master key $mk=(M_0,M_1,\cdots ,M_{15})$, the key schedule generates round keys $K_i$ as described in above, where $W_i$ is the round constant

SHACAL-2

Similar to SHACAL-1, the block cipher SHACAL-2 [28] was designed based on the compression function of the NIST standard hash function SHA-256 [20]. The cipher was submitted to the NESSIE project [61] and was approved as one of the NESSIE final selections. SHACAL-2 is a 256-bit block cipher, has 64 rounds, and supports a variable key size up to 512 bits. We analysed SHACAL-2 for 512-bit keys.

The longest ad-hoc related-key XOR differential characteristic in the strong-key setting is a 24-round characteristic presented in [51] with $(w_{\mathsf{KS}},w_E)=(0,38)$, which relies on some additional conditions on specific values alongside the differences to improve the weights. Moreover, in the weak-key setting, Biryukov et al. [12] provided two 24-round related-key XOR differential characteristics of SHACAL-2, each has encryption weight $w_E=52$. However, they did not explicitly mention the key schedule weight $w_{\mathsf{KS}}$ for each characteristic.

Our automated search resulted in a 23-round characteristic in the strong-key setting with encryption weight $w_E=58$ and a 22-round characteristic in the weak-key setting with total weight $w_{\mathsf{KS}}+w_E=6+29=35$. Like SHACAL-1, our automated search could not find longer characteristics of SHACAL-2 within a week due to the large number of empirically invalid characteristics found. The round function of SHACAL-2 also contains a modular addition with multiple inputs (i.e., seven operands), and modelling it with 2-input additions is one of the main reasons for the inaccurate differential behaviour for some special differences.

Table 7 lists the results of the best related-key impossible differentials of SHACAL-2. The 18-round impossible differential presented by Yang et al. in [75] has been the longest known related-key impossible differential for SHACAL-2 so far. Our automated tool ArxPy obtained a 24-round impossible differential, improving the previous best result by 6 rounds. This impossible differential includes a 12-round inner impossible differential, extended by two deterministic 1-round backward and 11-round forward trails. We checked up to 28-rounds of SHACAL-2 in one week, and the longest impossible differential we observed was the 24-round related-key impossible differential.

Conclusion

In this paper, we proposed the first bit-vector differential model of the n-bit modular addition with a constant. We described a bit-vector formula, with bit-vector complexity O(1), that determines whether a differential is valid and a bit-vector function, with complexity $O({log}_{2}n)$, that provides a close approximation of the differential weight. In this regard, we carefully studied our approximation error and obtained almost tight bounds. Moreover, we described two new SMT-based automated methods to search for characteristics and impossible differentials of ARX ciphers including constant additions, respectively.

Each of our methods formulates the search problem as a sequence of bit-vector SMT problems, encoded from the cipher’s SSA representation and the bit-vector differential models of each operation. We have implemented our methods in ArxPy, an open-source tool to find characteristics and impossible differentials of ARX ciphers in a fully automated way. To show some examples, we have applied our automated methods to search for equivalent keys, related-key characteristics, and related-key impossible differentials of TEA, XTEA, HIGHT, LEA, SHACAL-1, and SHACAL-2.

Regarding the characteristic results, for TEA we revisited previous results obtained in a manual approach. In contrast, for XTEA, HIGHT, and LEA, we improved the previous best-known related-key characteristics in both the strong-key and the weak-key settings. Our characteristic results of SHACAL-1 and SHACAL-2 did not outperform previous works in all settings due to the presence of modular additions with more than two inputs, for which no efficient differential model has been proposed yet.

Concerning the impossible differentials, our results for TEA, XTEA, and HIGHT are of the same length, compared to the best-known related-key impossible differentials. On the other hand, we obtained the longest related-key impossible differentials for LEA, SHACAL-1, and SHACAL-2.

Our differential model relies on a bit-vector-friendly approximation on the binary logarithm. Thus, future works could explore other approximations improving the bit-vector complexity or the approximation error, which could also be applied to other SMT problems involving the binary logarithm. While we have focused on the modular addition by a constant, there are other simple operations for which no differential model has been proposed so far, such as the modular multiplication, and the modular addition with more than two inputs. Obtaining differential models for more operations will allow designing ciphers with more flexibility, leading to new designs that potentially are more efficient.

Appendix A: Characteristics

We describe the characteristics covering most rounds that we obtained in Sect. 5. For each characteristic, we provide the difference of the master key words ${\mathrm{\Delta }}_{\mathit{mk}}$, the difference of the plaintext words ${\mathrm{\Delta }}_p$ and the difference of the ciphertext words ${\mathrm{\Delta }}_c$. Furthermore, for each round $i=0,1,\cdots$ of the cipher, we provide the difference of the i-th round key words, the output difference of the i-th round function ${\mathrm{\Delta }}_{x_i}$, the (cumulative) weight of the operations that compute the i-th round key words $w_{k_i}$ and the weight of the i-th round function $w_{x_i}$. The differences are given in hexadecimal values.

Table 9.

The 60-round strong related-key characteristic of TEA

i-th round	${\mathrm{\Delta }}_{x_i}$	$w_{x_i}$
0	(0x00000000, 0x80000000)	0
1	(0x80000000, 0x00000000)	1
2	(0x00000000, 0x80000000)	0
3	(0x80000000, 0x00000000)	1
4	(0x00000000, 0x80000000)	0
5	(0x80000000, 0x00000000)	1
6	(0x00000000, 0x80000000)	0
7	(0x80000000, 0x00000000)	1
8	(0x00000000, 0x80000000)	0
9	(0x80000000, 0x00000000)	1
10	(0x00000000, 0x80000000)	0
11	(0x80000000, 0x00000000)	1
12	(0x00000000, 0x80000000)	0
13	(0x80000000, 0x00000000)	1
14	(0x00000000, 0x80000000)	0
15	(0x80000000, 0x00000000)	1
16	(0x00000000, 0x80000000)	0
17	(0x80000000, 0x00000000)	1
18	(0x00000000, 0x80000000)	0
19	(0x80000000, 0x00000000)	1
20	(0x00000000, 0x80000000)	0
21	(0x80000000, 0x00000000)	1
22	(0x00000000, 0x80000000)	0
23	(0x80000000, 0x00000000)	1
24	(0x00000000, 0x80000000)	0
25	(0x80000000, 0x00000000)	1
26	(0x00000000, 0x80000000)	0
27	(0x80000000, 0x00000000)	1
28	(0x00000000, 0x80000000)	0
29	(0x80000000, 0x00000000)	1
30	(0x00000000, 0x80000000)	0
31	(0x80000000, 0x00000000)	1
32	(0x00000000, 0x80000000)	0
33	(0x80000000, 0x00000000)	1
34	(0x00000000, 0x80000000)	0
35	(0x80000000, 0x00000000)	1
36	(0x00000000, 0x80000000)	0
37	(0x80000000, 0x00000000)	1
38	(0x00000000, 0x80000000)	0
39	(0x80000000, 0x00000000)	1
40	(0x00000000, 0x80000000)	0
41	(0x80000000, 0x00000000)	1
42	(0x00000000, 0x80000000)	0
43	(0x80000000, 0x00000000)	1
44	(0x00000000, 0x80000000)	0
45	(0x80000000, 0x00000000)	1
46	(0x00000000, 0x80000000)	0
47	(0x80000000, 0x00000000)	1
48	(0x00000000, 0x80000000)	0
49	(0x80000000, 0x00000000)	1
50	(0x00000000, 0x80000000)	0
51	(0x80000000, 0x00000000)	1
52	(0x00000000, 0x80000000)	0
53	(0x80000000, 0x00000000)	1
54	(0x00000000, 0x80000000)	0
55	(0x80000000, 0x00000000)	1
56	(0x00000000, 0x80000000)	0
57	(0x80000000, 0x00000000)	1
58	(0x00000000, 0x80000000)	0
59	(0x80000000, 0x00000000)	1
Total		30
${\mathrm{\Delta }}_p$	(0x80000000, 0x00000000)
${\mathrm{\Delta }}_c$	(0x80000000, 0x00000000)
${\mathrm{\Delta }}_{\mathit{mk}}$	(0x00000000, 0x00000000, 0x00000000, 0x84000000)

Table 10.

The three full-round related-key characteristics with total weight 0 of TEA

${\mathrm{\Delta }}_{\mathit{mk}}$	${\mathrm{\Delta }}_p$	${\mathrm{\Delta }}_c$
(0x80000000, 0x80000000, 0x80000000, 0x80000000)	(0x00000000, 0x00000000)	(0x00000000, 0x00000000)
(0x00000000, 0x00000000, 0x80000000, 0x80000000)	(0x00000000, 0x00000000)	(0x00000000, 0x00000000)
(0x80000000, 0x80000000, 0x00000000, 0x00000000)	(0x00000000, 0x00000000)	(0x00000000, 0x00000000)

Table 11.

The 18-round strong related-key characteristic of XTEA

i-th round	${\mathrm{\Delta }}_{k_i}$	$w_{k_i}$	${\mathrm{\Delta }}_{x_i}$	$w_{x_i}$
0	0x00000000	0	(0x00010000, 0x44200000)	9
1	0x00000000	0	(0x44200000, 0x04000000)	6
2	0x00000000	0	(0x04000000, 0x80000000)	6
3	0x80000000	0	(0x80000000, 0x00000000)	2
4	0x80000000	0	(0x00000000, 0x00000000)	0
5	0x00000000	0	(0x00000000, 0x00000000)	0
6	0x00000000	0	(0x00000000, 0x00000000)	0
7	0x00000000	0	(0x00000000, 0x00000000)	0
8	0x00000000	0	(0x00000000, 0x00000000)	0
9	0x00000000	0	(0x00000000, 0x00000000)	0
10	0x00000000	0	(0x00000000, 0x00000000)	0
11	0x00000000	0	(0x00000000, 0x00000000)	0
12	0x80000000	0	(0x00000000, 0x80000000)	0
13	0x80000000	0	(0x80000000, 0x04000000)	2
14	0x00000000	0	(0x04000000, 0x44200000)	6
15	0x00000000	0	(0x44200000, 0x00010000)	6
16	0x00000000	0	(0x00010000, 0xc4310800)	9
17	0x00000000	0	(0xc4310800, 0x01010040)	11
Total		0		57
${\mathrm{\Delta }}_p$	(0xc4310800, 0x00010000)
${\mathrm{\Delta }}_c$	(0xc4310800, 0x01010040)
${\mathrm{\Delta }}_{\mathit{mk}}$	(0x00000000, 0x00000000, 0x80000000, 0x00000000)

Table 12.

The 27-round weak related-key characteristic of XTEA

i-th round	${\mathrm{\Delta }}_{k_i}$	$w_{k_i}$	${\mathrm{\Delta }}_{x_i}$	$w_{x_i}$
0	0x00000000	0	(0x00000000, 0x00000000)	0
1	0x80000000	0	(0x00000000, 0x80000000)	0
2	0x80000000	0	(0x80000000, 0x04000000)	2
3	0x40200000	1.179	(0x04000000, 0x04000000)	4
4	0x40200000	0	(0x04000000, 0x80000000)	4
5	0x80000000	0	(0x80000000, 0x00000000)	2
6	0x80000000	0	(0x00000000, 0x00000000)	0
7	0x00000000	0	(0x00000000, 0x00000000)	0
8	0x00000000	0	(0x00000000, 0x00000000)	0
9	0x00000000	0	(0x00000000, 0x00000000)	0
10	0x80000000	0	(0x00000000, 0x80000000)	0
11	0x80000000	0	(0x80000000, 0x04000000)	2
12	0x40200000	1.006	(0x04000000, 0x04000000)	4
13	0x40200000	0.734	(0x04000000, 0x80000000)	4
14	0x80000000	0	(0x80000000, 0x00000000)	2
15	0x80000000	0	(0x00000000, 0x00000000)	0
16	0x00000000	0	(0x00000000, 0x00000000)	0
17	0x00000000	0	(0x00000000, 0x00000000)	0
18	0x80000000	0	(0x00000000, 0x80000000)	0
19	0x00000000	0	(0x80000000, 0x84000000)	2
20	0x40600000	2.067	(0x84000000, 0x80000000)	4
21	0x80000000	0	(0x80000000, 0x80000000)	2
22	0x80000000	0	(0x80000000, 0x84000000)	2
23	0xc0600000	1.907	(0x84000000, 0x80000000)	4
24	0x00000000	0	(0x80000000, 0x00000000)	2
25	0x80000000	0	(0x00000000, 0x00000000)	0
26	0x80000000	0	(0x00000000, 0x80000000)	0
Total		6.893		40
${\mathrm{\Delta }}_p$	(0x00000000, 0x00000000)
${\mathrm{\Delta }}_c$	(0x80000000, 0x00000000)
${\mathrm{\Delta }}_{\mathit{mk}}$	(0x00000000, 0x80000000, 0xc0200000, 0x80000000)

Table 13.

The 15-round strong related-key characteristic of HIGHT. The round -1 corresponds to the initial key whitening

i-th round	${\mathrm{\Delta }}_{k_i}$	$w_{k_i}$	${\mathrm{\Delta }}_{x_i}$	$w_{x_i}$
− 1	(0x00, 0x00, 0x00, 0x00)	0	(0x00, 0x00, 0x09, 0x20, 0xb8, 0xe9, 0x80, 0x00)	1
0	(0x00, 0x00, 0x80, 0x00)	0	(0x00, 0x00, 0x20, 0xb8, 0xe9, 0x80, 0x00, 0x00)	3
1	(0x00, 0x00, 0x00, 0x00)	0	(0x00, 0x00, 0xb8, 0x2c, 0x80, 0x00, 0x00, 0x00)	6
2	(0x00, 0x00, 0x00, 0x00)	0	(0x00, 0x00, 0x2c, 0x80, 0x00, 0x00, 0x00, 0x00)	3
3	(0x00, 0x00, 0x00, 0x00)	0	(0x00, 0x00, 0x80, 0x00, 0x00, 0x00, 0x00, 0x00)	3
4	(0x00, 0x80, 0x00, 0x00)	0	(0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00)	0
5	(0x00, 0x00, 0x00, 0x00)	0	(0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00)	0
6	(0x00, 0x00, 0x00, 0x00)	0	(0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00)	0
7	(0x00, 0x00, 0x00, 0x00)	0	(0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00)	0
8	(0x80, 0x00, 0x00, 0x00)	0	(0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x80)	0
9	(0x00, 0x00, 0x00, 0x00)	0	(0x00, 0x00, 0x00, 0x00, 0x00, 0xd4, 0x80, 0x00)	5
10	(0x00, 0x00, 0x00, 0x00)	0	(0x00, 0x00, 0x00, 0x90, 0xd4, 0x80, 0x00, 0x00)	1
11	(0x00, 0x00, 0x00, 0x00)	0	(0x00, 0xe9, 0x90, 0x95, 0x80, 0x00, 0x00, 0x00)	7
12	(0x00, 0x00, 0x00, 0x00)	0	(0xe9, 0x00, 0x95, 0x80, 0x00, 0x00, 0x00, 0x80)	1
13	(0x00, 0x00, 0x00, 0x80)	0	(0x00, 0xe9, 0x80, 0x00, 0x00, 0xa4, 0x80, 0xe9)	9
14	(0x00, 0x00, 0x00, 0x00)	0	(0x80, 0xe9, 0x80, 0x00, 0x89, 0xa4, 0x2b, 0xe9)	6
Total		0		45
${\mathrm{\Delta }}_p$	(0x00, 0x00, 0x09, 0x20, 0xb8, 0xe9, 0x80, 0x00)
${\mathrm{\Delta }}_c$	(0x80, 0xe9, 0x80, 0x00, 0x89, 0xa4, 0x2b, 0xe9)
${\mathrm{\Delta }}_{\mathit{mk}}$	(0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x80, 0x00)

Table 14.

The 14-round weak related-key characteristic of HIGHT. The round -1 corresponds to the initial key whitening

i-th round	${\mathrm{\Delta }}_{k_i}$	$w_{k_i}$	${\mathrm{\Delta }}_{x_i}$	$w_{x_i}$
-1	(0x00, 0x00, 0x00, 0x40)	0	(0x62, 0xc0, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00)	1
0	(0x40, 0x00, 0x00, 0x00)	0.791	(0xc0, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00)	2
1	(0x00, 0x00, 0x00, 0x00)	0	(0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0xc0)	0
2	(0x00, 0x00, 0x00, 0x3a)	1.0	(0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0xc0, 0x00)	0
3	(0x00, 0x00, 0x00, 0x40)	0.752	(0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00)	1
4	(0x00, 0x00, 0x00, 0x00)	0	(0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00)	0
5	(0x00, 0x00, 0x00, 0x40)	0.791	(0x00, 0x00, 0x00, 0x00, 0x00, 0xc0, 0x00, 0x00)	1
6	(0x00, 0x00, 0x2e, 0x00)	4.0	(0x00, 0x00, 0x00, 0x00, 0xc0, 0x00, 0x00, 0x00)	5
7	(0x00, 0x00, 0x40, 0x00)	1.093	(0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00)	1
8	(0x00, 0x00, 0x00, 0x00)	0	(0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00)	0
9	(0x00, 0x00, 0xc0, 0x00)	0.046	(0x00, 0x00, 0x00, 0x40, 0x00, 0x00, 0x00, 0x00)	1
10	(0x00, 0x16, 0x00, 0x00)	4.0	(0x00, 0x00, 0x40, 0x00, 0x00, 0x00, 0x00, 0x00)	0
11	(0x00, 0x40, 0x00, 0x00)	0.142	(0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00)	1
12	(0x00, 0x00, 0x00, 0x00)	0	(0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00)	0
13	(0x00, 0x00, 0xc0, 0x00)	0.476	(0x00, 0x00, 0x40, 0x00, 0x00, 0x00, 0x00, 0x00)	1
Total		13.091		14
${\mathrm{\Delta }}_p$	(0x62, 0xc0, 0x00, 0x00, 0x00, 0x00, 0x00, 0x40)
${\mathrm{\Delta }}_c$	(0x00, 0x00, 0x40, 0x00, 0x00, 0x00, 0x00, 0x00)
${\mathrm{\Delta }}_{\mathit{mk}}$	(0x00, 0x00, 0x00, 0x40, 0x00, 0x00, 0x00, 0x7a, 0x00, 0x00, 0x00, 0x00, 0x40, 0x00, 0x00, 0x00)

Table 15.

The 7-round weak related-key characteristic of LEA

i-th round	${\mathrm{\Delta }}_{k_i}$	$w_{k_i}$	${\mathrm{\Delta }}_{x_i}$	$w_{x_i}$
0	(0x20000000, 0x00000000, 0x00000000, 0x00000000)	0.408	(0x80000000, 0x40000000, 0xc0000010, 0x4000000c)	14
1	(0x40000000, 0x00000000, 0x00000000, 0x00000000)	0.462	(0x00000000, 0x80000000, 0x80000000, 0x80000000)	7
2	(0x80000000, 0x00000000, 0x00000000, 0x00000000)	0.695	(0x00000000, 0x00000000, 0x00000000, 0x00000000)	0
3	(0x00000001, 0x00000000, 0x00000000, 0x00000000)	0	(0x00000200, 0x00000000, 0x00000000, 0x00000000)	1
4	(0x00000002, 0x00000000, 0x00000000, 0x00000000)	0	(0x00040400, 0x00000000, 0x00000000, 0x00000200)	2
5	(0x00000004, 0x00000000, 0x00000000, 0x00000000)	0	(0x08080800, 0x00000000, 0x00000040, 0x00040400)	4
6	(0x00000008, 0x00000000, 0x00000000, 0x00000000)	1.0	(0x10101010, 0x00000002, 0x00008088, 0x08080800)	8
Total		2.565		36
${\mathrm{\Delta }}_p$	(0x4000000c, 0x2040000c, 0x20400004, 0x20400082)
${\mathrm{\Delta }}_c$	(0x10101010, 0x00000002, 0x00008088, 0x08080800)
${\mathrm{\Delta }}_{\mathit{mk}}$	(0x10000000, 0x00000000, 0x00000000, 0x00000000)

Table 16.

The 30-round strong related-key characteristic of SHACAL-1

i-th round	${\mathrm{\Delta }}_{k_i}$	$w_{k_i}$	${\mathrm{\Delta }}_{x_i}$	$w_{x_i}$
0	0x80000000	0	(0x00000000, 0x00000002, 0x00000000, 0x80100008, 0x00008000)	7
1	0x80000000	0	(0x00008000, 0x00000000, 0x80000000, 0x00000000, 0x80100008)	5
2	0x00000000	0	(0x00000008, 0x00008000, 0x00000000, 0x80000000, 0x00000000)	5
3	0x00000000	0	(0x00000100, 0x00000008, 0x00002000, 0x00000000, 0x80000000)	5
4	0x80000000	0	(0x00000008, 0x00000100, 0x00000002, 0x00002000, 0x00000000)	6
5	0x00000000	0	(0x00000102, 0x00000008, 0x00000040, 0x00000002, 0x00002000)	8
6	0x00000000	0	(0x00000000, 0x00000102, 0x00000002, 0x00000040, 0x00000002)	8
7	0x00000000	0	(0x00000000, 0x00000000, 0x80000040, 0x00000002, 0x00000040)	5
8	0x80000000	0	(0x00000000, 0x00000000, 0x00000000, 0x80000040, 0x00000002)	5
9	0x00000000	0	(0x00000002, 0x00000000, 0x00000000, 0x00000000, 0x80000040)	3
10	0x80000000	0	(0x00000000, 0x00000002, 0x00000000, 0x00000000, 0x00000000)	3
11	0x00000000	0	(0x00000000, 0x00000000, 0x80000000, 0x00000000, 0x00000000)	1
12	0x80000000	0	(0x00000000, 0x00000000, 0x00000000, 0x80000000, 0x00000000)	1
13	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000, 0x80000000)	1
14	0x80000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000, 0x00000000)	0
15	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000, 0x00000000)	0
16	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000, 0x00000000)	0
17	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000, 0x00000000)	0
18	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000, 0x00000000)	0
19	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000, 0x00000000)	0
20	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000, 0x00000000)	0
21	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000, 0x00000000)	0
22	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000, 0x00000000)	0
23	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000, 0x00000000)	0
24	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000, 0x00000000)	0
25	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000, 0x00000000)	0
26	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000, 0x00000000)	0
27	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000, 0x00000000)	0
28	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000, 0x00000000)	0
29	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000, 0x00000000)	0
Total		0		63
${\mathrm{\Delta }}_p$	(0x00000002, 0x00000000, 0x80100008, 0x00008000, 0x80000040)
${\mathrm{\Delta }}_c$	(0x00000000, 0x00000000, 0x00000000, 0x00000000, 0x00000000)
${\mathrm{\Delta }}_{\mathit{mk}}$	(0x80000000, 0x80000000, 0x00000000, 0x00000000,
	0x80000000, 0x00000000, 0x00000000, 0x00000000,
	0x80000000, 0x00000000, 0x80000000, 0x00000000,
	0x80000000, 0x00000000, 0x80000000, 0x00000000)

Table 17.

The 25-round weak related-key characteristic of SHACAL-1

i-th round	${\mathrm{\Delta }}_{k_i}$	$w_{k_i}$	${\mathrm{\Delta }}_{x_i}$	$w_{x_i}$
0	0x00000000	0	(0x00000000, 0x00000000, 0x80000040, 0x00000002, 0x80000000)	3
1	0x80000000	0	(0x00000000, 0x00000000, 0x00000000, 0x80000040, 0x00000002)	3
2	0x00000000	0	(0x00000002, 0x00000000, 0x00000000, 0x00000000, 0x80000040)	3
3	0x80000000	0	(0x00000000, 0x00000002, 0x00000000, 0x00000000, 0x00000000)	3
4	0x00000000	0	(0x00000000, 0x00000000, 0x80000000, 0x00000000, 0x00000000)	1
5	0x80000000	0	(0x00000000, 0x00000000, 0x00000000, 0x80000000, 0x00000000)	1
6	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000, 0x80000000)	1
7	0x80000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000, 0x00000000)	0
8	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000, 0x00000000)	0
9	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000, 0x00000000)	0
10	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000, 0x00000000)	0
11	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000, 0x00000000)	0
12	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000, 0x00000000)	0
13	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000, 0x00000000)	0
14	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000, 0x00000000)	0
15	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000, 0x00000000)	0
16	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000, 0x00000000)	0
17	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000, 0x00000000)	0
18	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000, 0x00000000)	0
19	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000, 0x00000000)	0
20	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000, 0x00000000)	0
21	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000, 0x00000000)	0
22	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000, 0x00000000)	0
23	0x00000003	1	(0x00000001, 0x00000000, 0x00000000, 0x00000000, 0x00000000)	4
24	0x00000000	0	(0x00000020, 0x00000001, 0x00000000, 0x00000000, 0x00000000)	3
Total		1		22
${\mathrm{\Delta }}_p$	(0x00000000, 0x00000102, 0x00000002, 0x80000000, 0x80000000)
${\mathrm{\Delta }}_c$	(0x00000020, 0x00000001, 0x00000000, 0x00000000, 0x00000000)
${\mathrm{\Delta }}_{\mathit{mk}}$	(0x00000000, 0x80000000, 0x00000000, 0x80000000,
	0x00000000, 0x80000000, 0x00000000, 0x80000000,
	0x00000000, 0x00000000, 0x00000000, 0x00000000,
	0x00000000, 0x00000000, 0x00000000, 0x00000000)

Table 18.

The 23-round strong related-key characteristic of SHACAL-2

i-th round	${\mathrm{\Delta }}_{k_i}$	$w_{k_i}$	${\mathrm{\Delta }}_{x_i}$	$w_{x_i}$
0	0x00000000	0	(0x00000000, 0x00000000, 0x221c0240, 0x80000000,	12
			0x00000000, 0x00082200, 0x20040000, 0x80000000)
1	0x00000000	0	(0x80000000, 0x00000000, 0x00000000, 0x221c0240,	26
			0x00000000, 0x00000000, 0x00082200, 0x20040000)
2	0x00000000	0	(0x00000000, 0x80000000, 0x00000000, 0x00000000,	7
			0x02100040, 0x00000000, 0x00000000, 0x00082200)
3	0x00000000	0	(0x00000000, 0x00000000, 0x80000000, 0x00000000,	4
			0x00000000, 0x02100040, 0x00000000, 0x00000000)
4	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x80000000,	3
			0x00000000, 0x00000000, 0x02100040, 0x00000000)
5	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000,	4
			0x80000000, 0x00000000, 0x00000000, 0x02100040)
6	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000,	1
			0x00000000, 0x80000000, 0x00000000, 0x00000000)
7	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000,	1
			0x00000000, 0x00000000, 0x80000000, 0x00000000)
8	0x80000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000,	0
			0x00000000, 0x00000000, 0x00000000, 0x80000000)
9	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000,	0
			0x00000000, 0x00000000, 0x00000000, 0x00000000)
10	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000,	3
			0x00000000, 0x00000000, 0x00000000, 0x00000000)
11	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000,	0
			0x00000000, 0x00000000, 0x00000000, 0x00000000)
12	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000,	0
			0x00000000, 0x00000000, 0x00000000, 0x00000000)
13	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000,	0
			0x00000000, 0x00000000, 0x00000000, 0x00000000)
14	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000,	0
			0x00000000, 0x00000000, 0x00000000, 0x00000000)
15	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000,	0
			0x00000000, 0x00000000, 0x00000000, 0x00000000)
16	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000,	0
			0x00000000, 0x00000000, 0x00000000, 0x00000000)
17	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000,	0
			0x00000000, 0x00000000, 0x00000000, 0x00000000)
18	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000,	0
			0x00000000, 0x00000000, 0x00000000, 0x00000000)
19	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000,	0
			0x00000000, 0x00000000, 0x00000000, 0x00000000)
20	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000,	0
			0x00000000, 0x00000000, 0x00000000, 0x00000000)
21	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000,	0
			0x00000000, 0x00000000, 0x00000000, 0x00000000)
22	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000,	0
			0x00000000, 0x00000000, 0x00000000, 0x00000000)
Total		0		58
${\mathrm{\Delta }}_p$	(0x00000000, 0x00000000, 0x221c0240, 0x80000000,
	0x00000000, 0x00082200, 0x20040000, 0x80000000)
${\mathrm{\Delta }}_c$	(0x00000000, 0x00000000, 0x00000000, 0x00000000,
	0x00000000, 0x00000000, 0x00000000, 0x00000000)
${\mathrm{\Delta }}_{\mathit{mk}}$	(0x00000000, 0x00000000, 0x00000000, 0x00000000,
	0x00000000, 0x00000000, 0x00000000, 0x00000000,
	0x80000000, 0x00000000, 0x00000000, 0x00000000,
	0x00000000, 0x00000000, 0x00000000, 0x00000000)

Table 19.

The 22-round weak related-key characteristic of SHACAL-2

i-th round	${\mathrm{\Delta }}_{k_i}$	$w_{k_i}$	${\mathrm{\Delta }}_{x_i}$	$w_{x_i}$
0	0x00000000	0	(0x00000000, 0x00020000, 0x00000000, 0x00000000,	6
			0x01000840, 0x00000000, 0x00000000, 0x88000020)
1	0x00000000	0	(0x00000000, 0x00000000, 0x00020000, 0x00000000,	4
			0x00000000, 0x01000840, 0x00000000, 0x00000000)
2	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00020000,	4
			0x00000000, 0x00000000, 0x01000840, 0x00000000)
3	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000,	4
			0x00020000, 0x00000000, 0x00000000, 0x01000840)
4	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000,	1
			0x00000000, 0x00020000, 0x00000000, 0x00000000)
5	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000,	1
			0x00000000, 0x00000000, 0x00020000, 0x00000000)
6	0x00020000	0.405	(0x00000000, 0x00000000, 0x00000000, 0x00000000,	3
			0x00000000, 0x00000000, 0x00000000, 0x00020000)
7	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000,	0
			0x00000000, 0x00000000, 0x00000000, 0x00000000)
8	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000,	0
			0x00000000, 0x00000000, 0x00000000, 0x00000000)
9	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000,	0
			0x00000000, 0x00000000, 0x00000000, 0x00000000)
10	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000,	0
			0x00000000, 0x00000000, 0x00000000, 0x00000000)
11	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000,	0
			0x00000000, 0x00000000, 0x00000000, 0x00000000)
12	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000,	3
			0x00000000, 0x00000000, 0x00000000, 0x00000000)
13	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000,	0
			0x00000000, 0x00000000, 0x00000000, 0x00000000)
14	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000,	0
			0x00000000, 0x00000000, 0x00000000, 0x00000000)
15	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000,	0
			0x00000000, 0x00000000, 0x00000000, 0x00000000)
16	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000,	0
			0x00000000, 0x00000000, 0x00000000, 0x00000000)
17	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000,	0
			0x00000000, 0x00000000, 0x00000000, 0x00000000)
18	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000,	0
			0x00000000, 0x00000000, 0x00000000, 0x00000000)
19	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000,	0
			0x00000000, 0x00000000, 0x00000000, 0x00000000)
20	0x00000000	0	(0x00000000, 0x00000000, 0x00000000, 0x00000000,	0
			0x00000000, 0x00000000, 0x00000000, 0x00000000)
21	0x80004400	6.262	(0x00000000, 0x00000000, 0x00000000, 0x00000000,	6
			0x00000000, 0x00000000, 0x00000000, 0x00000000)
Total		6.67		29
${\mathrm{\Delta }}_p$	(0x00000000, 0x00020000, 0x00000000, 0x00000000,
	0x01000840, 0x00000000, 0x00000000, 0x88000020)
${\mathrm{\Delta }}_c$	(0x80004400, 0x00000000, 0x00000000, 0x00000000,
	0x80004400, 0x00000000, 0x00000000, 0x00000000)
${\mathrm{\Delta }}_{\mathit{mk}}$	(0x00000000, 0x00000000, 0x00000000, 0x00000000,
	0x00000000, 0x00000000, 0x00020000, 0x00000000,
	0x00000000, 0x00000000, 0x00000000, 0x00000000,
	0x00000000, 0x00000000, 0x00000000, 0x00000000)